Решение примеров дроби 5 класс: Действия с дробями

Действия с дробями, подробно с примерами

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь список материалов и изучать последовательно.

1. Сумма дробей, разность дробей.

Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.

Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь  – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.

Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…

Вариант 1 – можно перевести их в обыкновенные и далее вычислять.

Вариант 2 – можно отдельно «работать» с целой и дробной частью.

Примеры (2):

Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.

Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.

Ещё пример:

 

Вывод: имеется универсальный подход  – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.

Выше мы рассмотрели примеры с дробями, у которых равные знаменатели.  А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.

Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.

Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ.

То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

Теперь посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.

Способ ВТОРОЙ.

Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.

Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.

Рассмотрим пример:

Видно что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.

Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?

Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но  пары чисел могут быть и другими, например 51 и 119.

Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:

— разложить каждое из чисел на ПРОСТЫЕ множители

— выписать разложение БОЛЬШЕГО из них

— умножить его на НЕДОСТАЮЩИЕ множители других чисел

Рассмотрим примеры: 

50 и 60   =>  50 = 2∙5∙5    60 = 2∙2∙3∙5

в разложении большего числа не хватает одной пятёрки

 =>   НОК(50,60) = 2∙2∙3∙5∙5 = 300

48 и 72   =>   48 = 2∙2∙2∙2∙3    72 = 2∙2∙2∙3∙3            

в разложении большего числа не хватает двойки и тройки

=>   НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Наименьшее общее кратное двух простых чисел равно их произведению

Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.

Рассмотрим примеры:

*51 = 3∙17    119 = 7∙17

в разложении большего числа не хватает тройки

 =>   НОК(51,119) = 3∙7∙17

А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.

Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!

— приводим дроби к обыкновенным, если есть целая часть.

— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).

— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).

— если необходимо, то результат сокращаем.

— если необходимо, то выделяем целую часть.

2. Произведение дробей.

Правило простое. При умножении дробей умножаются их числители и знаменатели:

Примеры:

Если есть возможность сократить дробь на стадии вычисления, то лучше это сделать:

Ещё правило относящееся к умножению!

Примеры, которые мы уже рассмотрели:

Определить, сколько составляет 3/7 от числа 63?

Задача. Весь путь составляет 180 километров. Турист в первый день прошёл 3/10 пути. Сколько километров турист прошёл в первый день?

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм  картофеля завезли на базу?

С произведением закончим.

*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.

Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Делитесь информацией в социальных сетях.

Обыкновенные дроби 🐲 СПАДИЛО.РУ

Определение

Обыкновенная дробь – это запись числа в виде:

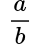
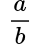
где число a называют числителем, а число b – знаменателем дроби.

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Пример №1. У первой дроби  можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби  можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.

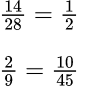
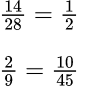Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.

• Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
• Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.

Сокращение дробей

Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.

Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:

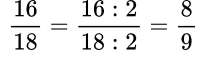
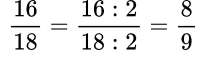
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.

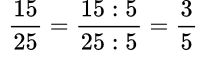
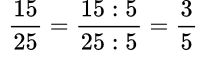Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями

При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.

Пример №4.

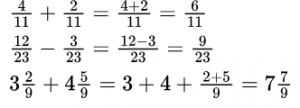
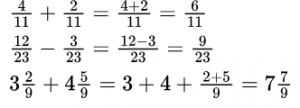
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.

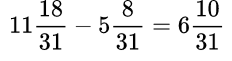
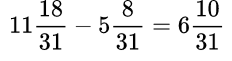
Вычитание обыкновенной дроби из целого числа

Вычитание обыкновенной дроби из единицы

Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.

Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).

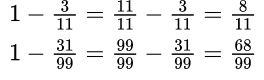
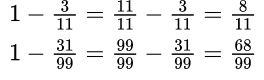Вычитание обыкновенной дроби из бóльшего числа

Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.

Пример №6.

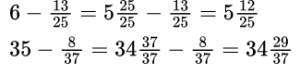
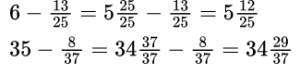
Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.

Нахождение общего знаменателя

Наименьшее общее кратное. Приём №1.

Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.

Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:

12=2×2×3

15=3×5

2. Затем найти одинаковые множители (подчеркиваем):

12=2×2×3

15=3×5

В данном случае это только множитель 3.

3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:

12 домножаем на 5: 12×5=60, или

15 домножаем на 2 и 2: 15×2×2=60

Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.

Перемножение знаменателей. Приём №2.

Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.

Пример №8.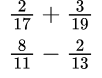

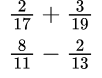
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.

Последовательный подбор. Приём №3.

Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.

Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.

После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.

Алгоритм сложения (вычитания)

1. Находим общий знаменатель данных дробей.
2. Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
3. Умножаем каждый числитель на дополнительный множитель.
4. Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.

Пример №10.

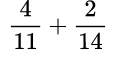
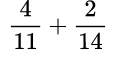
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:

Выполняем умножение в числителе: 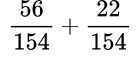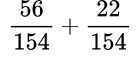Выполняем сложение дробей с одинаковыми знаменателями:

Умножение обыкновенных дробей

Как перемножить дроби?

При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).

Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.

Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.

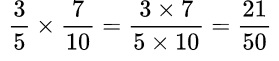
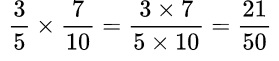
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.

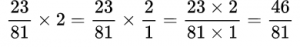
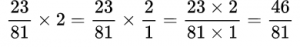
Пример №13. Нам даны смешанные дроби, переводим их  в неправильные для выполнения умножения.

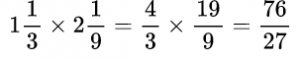
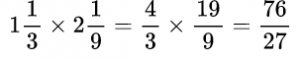
Деление обыкновенных дробей

Как разделить одну дробь на другую?

При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.

Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.

Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.

Пример №14. Делимое умножаем на число, обратное делителю.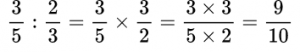 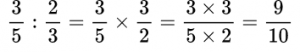Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.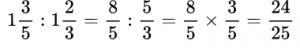

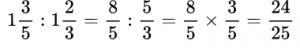
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.

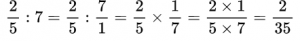
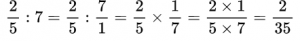
Формулы для решения задач на дроби для 5 класса

В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.

Обыкновенная дробь — это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.

То есть дробь $\frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.

Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.

Как найти дробь от числа

В задачах на дробь от  числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу

Пример 1.1.
В самолёте 120 пассажиров. $\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?

Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $\frac{2}{5}$
Нужно найти, чему равны две пятых от 120.

Решаются задачи на нахождение дроби от числа так.

Решение
Задаём себе два вопроса:
1. Чему равна $\frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $\frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.

Значит, $\frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.

Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?

Решение
1. Чему равна $\frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $\frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000

Ответ: 180 000 школьников.

Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель

Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?

Решение
Умножим 14 на $\frac{2}{7}$:
$14\cdot \frac{2}{7} = \frac{14\cdot 2}{7} = 2\cdot 2 = 4$

Ответ: 4 автомобиля.

Теперь рассмотрим задачи второго типа:

Как найти число по дроби

В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.

Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?

Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($\frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.

Ответ: 120 пассажиров всегов самолёте

Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($\frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?

Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $\frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $\frac{1}{25}$ от населения города. Разделим 180 000 на 3:

180 000:3 = 60 000

Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000

Ответ: в городе 1 500 000 жителей

Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:

Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель

Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?

Решение
Разделим 4 на $\frac{2}{7}$:
$4: \frac{2}{7} = \frac{4\cdot 7}{2} = 2\cdot 7 = 14$

Ответ: 14 автомобилей завезли в салон.

И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:

Как найти отношение двух чисел и выразить его в виде дроби

В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего

Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?

Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $\frac{48}{120}$.

И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$\frac{48}{120}=\frac{24}{60}$

Сократим ещё раз на 2:
$\frac{24}{60} = \frac{12}{30}$

И ещё раз:
$\frac{12}{30} = \frac{6}{15}$

Теперь можно сократить на 3:

$\frac{6}{15} = \frac{2}{5}$

Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $\frac{2}{5}$ пассажиров летят впервые.

Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.

Обратите внимание, что дробь $\frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.

Разберём ещё два примера.

Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?

Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$\frac{180000}{1500000}=\frac{18}{150}=\frac{9}{75}=\frac{3}{25}$

Ответ: школьники составляют $\frac{3}{25}$ от общего населения города

Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?

Решение
Точно так же, берём дробь $\frac{4}{14}$ и сокращаем:
$\frac{4}{14}=\frac{2}{7}$

Ответ: продали $\frac{2}{7}$ от общего количества автомобилей.

Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».

Неправильные дроби — примеры для 5 класса с решением и объяснением

Математика — это не просто цифры. С её помощью познаётся окружающий мир. Умение работать с числами позволяет прогрессировать всему человечеству. Особое положение занимает раздел, изучающий действия с дробными отношениями. Именно с ними приходится чаще всего встречаться в жизни. Поэтому нужно пристальное внимание обратить в 5 классе на неправильные дроби. Примеры с объяснением помогут лучше разобраться в теме и построят важный мост для дальнейшего изучения науки.

Общие сведения

Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.

В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.

Это легко проверить: 11/ 8 пиццы — это тоже что 8 / 8 плюс 3 / 8. То есть одна была полностью съедена, а с другой взяли только три кусочка. Так как отношение 8 / 8 – это целое (единица), то можно утверждать, что 8 / 8 = 1. Значит, произошедшее можно представить в виде равенства: 11 / 8 = 1 + 3 / 8.

Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:

Правильные. Рациональные выражения, в которых числитель меньше или неравен делителю. Например, 1 / 16; 4 / 45; -78 / 123.

Неправильные. Обыкновенные дроби, у которых знаменатель количественно меньше значения делимого или равен ему по численности. Например, 7 / 6; 19 / 19; 453 / 21.

Смешанные. Отношения, включающие в свою запись как натуральное число, так и правильную дробь. Фактически они представляют собой их сумму: 4 (4 / 5) = 4 + 4 / 5

Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.

Так как, по сути, дроби – это числа, только чаще всего не целые, над ними можно выполнять любые операции. Для того чтобы школьника научить правильно решать дроби, в 5 классе, кроме теоретического материала несколько уроков уделяют практике. На ней, кроме непосредственного выполнения арифметических операций, учат преобразовывать дробные отношения из одного вида в другой.

Суть отношения

Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.

Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.

Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.

Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.

Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:

• натуральным числом — в случае когда числитель количественно совпадает со знаменателем;
• суммой правильной дроби и простого числа — если делимое не делится нацело на делитель.

Как и любое число, дробь может быть положительной и отрицательной. В первом случае она обозначает изменение чего-то в сторону увеличения, а во втором — уменьшения. Например, -6 / 5 может обозначать недостачу равную шесть пятых.

Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.

Превращение дробей

По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.

Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).

Поняв смысл такого перехода, можно выполнить превращение и в обратную сторону. Чтобы разобраться, как это сделать лучше, проще рассмотреть пример. Пусть имеется смешанное число 4 (5/8), его нужно превратить в неправильную дробь. Иными словами, определить, сколько восьмых долей содержится в четырёх и пяти восьмых. Так как одной единице соответствует 8 / 8, то четырём – 8 * 4 / 8 = 32 / 8. Соответственно в четырёх и 5 / 8 будет 37 / 8 долей.

Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:

• перемножить единицы целой части со знаменателем дробного числа;
• сложить полученное произведение и числитель дроби;
• результат сложения записать в числитель, а знаменатель оставить без изменений.

Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.

Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.

Выполнение действий

Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.

Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.

Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:

• исследовать числитель и знаменатель на возможность сокращения;
• определить наименьший общий знаменатель (НОЗ) среди делителей;
• найти дополнительные множители;
• выполнить умножение числителей на найденные аргументы;
• в знаменатель записать НОЗ, а в числитель сумму или разность произведений делимых.

Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).

Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).

Возведение в степень и извлечение корня выполняют способом разделения. То есть, делимое от делителя возводится или извлекается отдельно: (s / m) ^j = s^j / m^j и √(s / m) = √s / √m. Например, 3 / 2 * 9 / 6 : 7 / 5 * (3 / 2)³. С какого действия начинать решение не принципиально, но следует обратить внимание, что 9 / 6 можно сократить на три. В итоге получится 9 / 6 = 3 / 2. Далее, решение будет выглядеть следующим образом: 3 / 2 * 3 / 2 : 7 / 5 * 3 ³ / 2³ = (3 * 3) / (2 * 2): 7 / 5 * 27 / 8 = 9 / 4 * 5 / 7 * 27 / 8 = (9 * 5 * 27) / (4* 7 * 8) = 1215 / 224 = 5 (95 / 224).

Предыдущая

МатематикаВозрастание и убывание функции — свойства, характеристики и примеры

Следующая

МатематикаУмножение и деление натуральных чисел — правила и примеры для 5 класса

Как объяснить ребенку дроби: 5 класс

Выходим на битву с домашним заданием по математике! Враг — непокорные дроби. Программа 5 класса. Стратегически важная задача — объяснить ребенку дроби. Поменяемся ролями с учителем и попробуем сделать это «малой кровью», без нервов и в доступной форме. Обучить одного солдата куда легче, чем роту…

ria.ru

Как объяснить ребенку дроби

Не ждите, пока ребенок пойдет в 5 класс и встретится с дробями на страницах учебника по математике. Ответ на вопрос «Как объяснить ребенку дроби» рекомендуем поискать на кухне! И сделать это прямо сейчас! Даже если вашему малышу только 4-5 лет, смысл понятия «дроби» он в состоянии уяснить и даже может научиться простейшим действиям с дробями.

Мы делили апельсин.
Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.

Помните стихотворение? Вот самый наглядный пример и самое эффективное руководство к действию! Объяснить ребенку дроби проще всего на примере еды: режем яблоко на половинки и четвертинки, делим пиццу между членами семьи, разрезаем буханку хлеба перед обедом и т.п. Главное, перед тем, как съесть «наглядное пособие» не забудьте озвучить, какую часть от целого вы «уничтожаете».

• Введите понятие «доли».

Сделайте акцент на том, что ЦЕЛЫЙ апельсин (яблоко, шоколадка, арбуз и пр.) — это 1 (обозначаем цифрой 1).

• Введите понятие «дробь».

Апельсин или шоколадку мы делим, можно еще сказать «дробим» на несколько частей.

Покажите ребенку хорошо знакомый предмет — линейку. Объясните, что между числами есть промежуточные значения — части. 

i.ytimg.com

• Объясните, как записывать дроби: что значит числитель, и на что указывает знаменатель.

Смысл понятия «дроби» и правильную запись легко показать на примере конструктора. В числителе НАД чертой пишем какая часть, а в знаменателе ПОД чертой — на сколько таких частей было разделено целое.

gladtolearn.ru

spacemath.xyz

Обязательно на наглядном примере покажите разницу между дробями с одинаковым числителем, но разными знаменателями.

gladtolearn.ru

На примере 4-х квадратов одинакового размера покажите, как можно разделить их на одинаковое/разное количество частей. Пусть ребенок сам разрежет ножницами бумажные заготовки, а затем запишет при помощи дробей результаты.

gladtolearn.ru

• Объясните, как записать целое через дробь.

Вспомните квадрат и то, как мы делили его на 4 части. Квадрат — это целое, мы можем записать его как 1. Но как записать в виде дроби: что в числителе, что в знаменателе? Если мы делили квадрат на 4 части, то целый квадрат, это 4/4. Если мы делили квадрат на 8 частей, то целый квадрат это 8/8. Но это все равно квадрат, т.е. 1. И 4/4, и 8/8 — это единица, целое!

Как объяснить ребенку дроби: задаем ПРАВИЛЬНЫЕ вопросы

Чтобы ученик 5 класса понял тему «Дроби» и научился выполнять вычисления с дробями, заглянем в методику. Нам, родителям, важно понимать, как объясняет детям дроби учитель в школе, иначе мы можем окончательно запутать своего «солдата».

Дробь — это число, которое является частью целого предмета. Оно всегда меньше единицы.

Пример 1. Яблоко — это целое, а половинка — одна вторая. Она же меньше, чем целое яблоко? Половинки делим еще раз пополам. Каждая долька — одна четвертая от целого яблока, и она меньше, чем одна вторая.

Дробь — это количество частей от целого.

Пример 2. Например, в магазин одежды завезли новый товар: 30 рубашек.  Продавцы успели разложить и развесить лишь одну треть всех рубашек из новой коллекции. Сколько рубашек они развесили?
Ребенок легко устно посчитает, что треть (одна третья) — это 10 рубашек, т.е. 10 развесили и вынесли в торговый зал, а еще 20 осталось на складе.

ВЫВОД: Дробями можно измерять все, что угодно, не только куски пиццы, но и литры в бочках, поголовье диких животных в лесу, площадь и т.п.

Приводите самые разные примеры из жизни, чтобы ребенок 5 класса понял СУТЬ дробей: это поможет в дальнейшем в решении задач и выполнении вычислений с правильными и неправильными дробями, и обучение в 5 классе будет не в тягость, а в радость.

Как убедиться, что ребенок усвоил, что в записи дробей обозначают числа в числителе и в знаменателе?

Пример 3. Спросите, что значит 5 в дроби 4/5?

— Это на сколько частей поделили.
— А что значит 4?
— Это сколько взяли.

Сравнение дробей — самая, пожалуй, сложная тема.

Пример 4. Предложите ребенку сказать, какая дробь больше: 3/10 или 3/20? Кажется, что раз 10 меньше 20, то и ответ очевиден, но это не так! Вспомните про квадраты, которые мы разрезали на части.  Если два одинаковых по размеру квадрата разрезать — один на 10, второй на 20 частей — ответ очевиден? Так какая дробь больше?

Действия с дробями

Если вы видите, что ребенок хорошо усвоил смысл записи в виде дроби, можно переходить к простым арифметическим действиям с дробями. На примере конструктора можно сделать это очень наглядно.

Пример 5. 

edinstvennaya.ua

Пример 6. Математическое лото на тему «Дроби».

www.kakprosto.ru

Уважаемые читатели, если вы знаете другие эффективные методики, как объяснить ребенку дроби, делитесь в комментариях. С радостью пополним нашу копилочку дельных школьных советов.

Тренажер «ДРОБИ» | тренажер дробей онлайн | дроби для 5 и 6 класса | Клуб любителей математики

Данный тренажер является третьим в линейке тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.

Работа тренажера также основана на генерации примеров по математике с различными видами дробей, изучаемых в средних классах школы. Решение примеров способствует развитию скорости и качества устного счёта.

Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.

Режимы счёта

На странице настроек режима можно задавать необходимые параметры генерации примеров с дробями для любого класса.

Онлайн тренажер «Дроби» позволяет генерировать примеры с любыми видами дробей, с любым из четырёх арифметических действий.

Кнопки на панели настроек работают по принципу «Вкл/Выкл». Если цвет кнопки зелёный — значит в примерах будут использоваться дроби того типа, который описывает кнопка. Если же цвет серый — этот тип дробей использоваться не будет.

В приложении отсутствуют режимы «Уравнение» и «Сравнение» из-за их избыточной сложности. Работа проходит только в режиме «Пример» с возможным использованием следующих типов дробей:

Разные знаменатели — в примере будут появляться обыкновенные дроби с разными знаменателями.

Неправильные дроби — в примере будут появляться обыкновенные неправильные дроби (числитель больше знаменателя).

Смешанные числа — в примере будут появляться смешанные числа (числа, состоящие из целой и дробной частей).

Десятичные дроби — в примере будут появляться дроби в десятичной записи.

Также имеется возможность включить обязательную проверку ответа на сокращение дробной части числа и выделение целой части числа (если имеется). Понять, нужно ли сокращать ответ можно по красному индикатору * на странице настроек и странице ввода ответа.

Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». Когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.

Процесс счёта

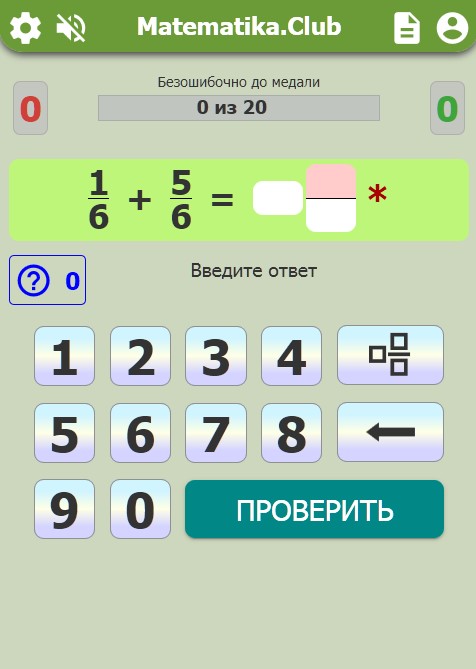
Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.

Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.

Прогресс и достижения

Приложение также предусматривает небольшой соревновательный момент через получение медалей за безошибочность — правильное решение N примеров подряд.

Для получения медали, в зависимости от степени её «классности» (бронзовая, серебряная или золотая), необходимо безошибочно решить 20, 50 и 100 примеров соответственно. Медаль высшей категории заменяет собой предыдущую, и выдается единоразово. На полоске прогресса наглядно видно сколько примеров осталось решить для достижения цели. При получении медали прогресс не сбрасывается, таким образом чтобы получить, например, серебряную медаль достаточно решить еще 30 примеров безошибочно.

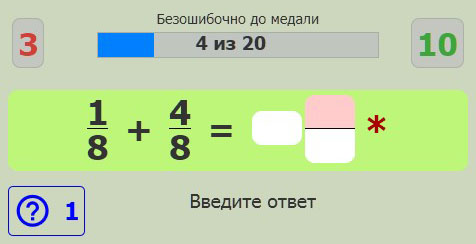
Если во время решения была использована подсказка, то верный ответ не идет в зачет прогресса. Ошибка же сразу обнуляется весь прогресс. Поэтому будьте максимально осторожны, если хотите получить медаль — один неверный шаг и придется начинать все с начала.

Узнать, получили ли Вы уже медаль за конкретный режим можно на странице «Статистика» в профиле или в самом приложении.

Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.

Подробное решение примеров

В любой момент работы с тренажером вы можете перейти в разделу «Подробного решения примера», если обычной подсказки в виде верного ответа вам не достаточно. Для этого кликните на соответствующую иконку сверху, либо перелестнув страницу вниз.

Здесь вы сможете посмотреть подробное решение примера с дробями со всеми преобразованиями, сокращениями и упрощениями.

Дополнительная информация

Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:

домен сайта + раздел приложения + кодировка данного режима

например: matematika.club/drobi/#60101

Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.

5 класс Смешанные дроби (памятка ученику)

Смешанные дроби

Смешанная Неправильная

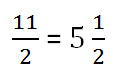
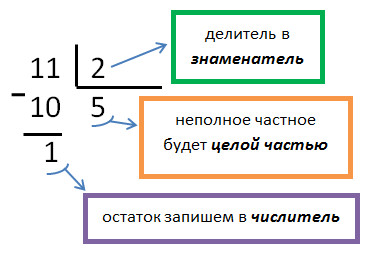
5 =

Сложение и вычитание смешанных дробей

Чтобы сложить смешанные числа, нужно:

1) привести к наименьшему общему знаменателю дробные части;

2) сложить отдельно целые и дробные части;

3) если необходимо, сократить дробную часть;

4) если дробная часть суммы окажется неправильной дробью, выделить из нее целую часть и полученное число прибавить к целой части суммы.

Например:

Чтобы вычесть смешанные числа, нужно:

1) привести к наименьшему общему знаменателю дробные части;

2) если дробные части «не вычитаются» (дробная часть уменьшаемого меньше дробной части вычитаемого),то нужно «занять» единицу из целой части;

3) вычесть отдельно целые и дробные части;

4) если необходимо, сократить дробную часть.

Например:

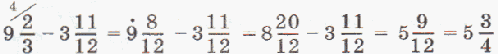
Например:

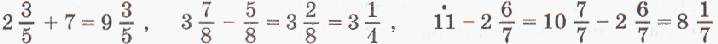
Смешанные дроби

Сложение:

1 шаг: к общ. знам. (НОЗ)

2 шаг: + цел1+цел2,

др1+др2 (числ1+числ2)

3 шаг: неправ. смеш.

4 шаг: сократить

Вычитание:

1 шаг: к общ. знам. (НОЗ)

2 шаг: занять ед. (если нужно)

3 шаг: — цел1 — цел2

др1 — др2 (числ1 — числ2)

4 шаг: сократить

Умножение:

1 шаг: смеш. неправ.

2 шаг: числ1 числ2

зн1 зн2 сократить!

3 шаг: вычислить

4 шаг: неправ. смеш.

Деление:

1 шаг: смеш. неправ.

2 шаг: числ1 зн2

зн1 числ2 сократить!

3 шаг: вычислить

4 шаг: неправ. смеш.

Рабочие листы с дробями и десятичными знаками для 3-го класса — бесплатно и для печати

Определение дробей	Пример
Определить дроби — цвет дроби
Определить дроби — написать дробь
Дробная часть набора
Эквивалентные дроби
Эквивалентные фракции — цвет в дроби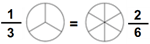
Определить эквивалентные дроби
Эквивалентные дроби (числители отсутствуют)	__ / 3 = 20/30
Эквивалентные фракции (более сложная версия)	6/8 = __ / 56
Эквивалентные дроби (числители или знаменатели отсутствуют)	2/3 = 10 / __
3 эквивалентных дроби	1/3 = 3 / __ = 6 / __
Сравнение дробей
Сравнить 2 дроби, тот же знаменатель (с круговой диаграммой)
Сравните 2 дроби, разные знаменатели (с круговыми диаграммами)
Сравните 2 правильные или неправильные дроби (с круговыми диаграммами)
Сравните смешанные числа и дроби (с круговыми диаграммами)
Сравнение дробей (как и знаменатели)	4/5> 3/5
Сравнение дробей (в отличие от знаменателей)	9/10> 1/2
Сравнение дробей (неправильных дробей)	3/2> 3/4
Сравнение дробей (смешанные числа)	1 1/2 <3 1/6
Упрощающие дроби
Упрощающие дроби (собственные дроби)	20/24 =
Упрощающие дроби (правильные и неправильные)	26/10 =
Сложение и вычитание дробей
Сложение одинаковых дробей — знаменатели от 2-12	1/6 + 2/6 =
Сложение смешанных чисел (например, знаменателей)	3 1/6 + 4 2/6 =
Заполнение целых чисел (неправильных дробей)	1/2 + ___ = 2
Заполнение целых чисел (смешанные числа)	3 1/3 + ____ = 4
Вычитание одинаковых дробей (знаменатели 2-12)	3/10 — 1/10 =
Вычитание неправильных дробей (например, знаменателей)	8/6 — 5/6 =
Вычитание дроби из целого числа	6 — 2/3 =
Вычитание дроби из смешанного числа	2 4/5 — 1/5 =
Вычтем смешанное число из целого	10 — ___ = 5 3/4
Вычесть смешанные числа (например, знаменатели)	8 3/7 — 3 6/7 =
Преобразование дробей в смешанные числа и обратно
Преобразование чисел в дроби	9 1/5 =
Дроби в смешанные числа	46/5 =
Преобразование дробей в / из десятичных
От десятичных до смешанных чисел	7.3 =
Дроби до десятичных	1/10 =
Смешанные числа с десятичными знаками	1 1/10 =
Сравнение и порядок десятичных знаков
Сравнение десятичных знаков	0,9 <1,2
Порядок десятичных знаков	9,3, 42,7, 89, 706
Сложение десятичной дроби
1 десятичная цифра — легко	0.8 + 1,8 =
Добавить в столбцы (1 десятичная цифра)	0,8 + 1,8
Десятичное вычитание
Вычесть однозначные десятичные дроби из целых чисел	8 — 0,8 =
Вычесть однозначные десятичные дроби из целых чисел (пропущенное уменьшение / вычитание)	10 — ___ = 9,1
Вычесть однозначные десятичные знаки в столбцах	50.0 –3,8
Проблемы со словами
Задачи на дробное слово для 3 класса

.

Сложение дробей

Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.

Чтобы сложить дроби, выполните три простых шага:

• Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают.
• Шаг 2: сложите верхние числа (числители), поместите полученный ответ над знаменателем
• Шаг 3: Упростите дробь (при необходимости)

Пример:

Шаг 1 .Нижние цифры (знаменатели) уже одинаковые. Переходите сразу к шагу 2.

Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:

1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4

Шаг 3 . Упростим дробь:

2 4 знак равно 1 2

На картинке это выглядит так:

1 4	+	1 4	=	2 4	=	1 2

… и ты видишь как 2 4 проще как 1 2 ? (см. Эквивалентные дроби.)

Пример:

Шаг 1 : Нижние числа разные. Видите, как ломтики бывают разных размеров?

1 3	+	1 6	=	?

Нам нужно сделать их такими же, прежде чем мы сможем продолжить, потому что не может, добавить их вот так.

Число «6» вдвое больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:

× 2

× 2

Важно: вы умножаете как верхний, так и нижний на одинаковую величину,
, чтобы сохранить значение дроби одинаковым

Теперь у дробей одинаковое нижнее число («6»), и наш вопрос выглядит так:

2 6	+	1 6

Нижние числа теперь те же, поэтому мы можем перейти к шагу 2.

Шаг 2 : сложите верхние числа и поместите их над тем же знаменателем:

2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6

На картинке это выглядит так:

2 6	+	1 6	=	3 6

Шаг 3 : Упростите дробь:

3 6 знак равно 1 2

На картинке весь ответ выглядит так:

2 6	+	1 6	=	3 6	=	1 2

С ручкой и бумагой

А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

Рифма, которая поможет вам вспомнить

♫ «Если ваша цель — сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫» Измените нижнее значение с помощью умножения или деления,
Но то же самое и к верхнему,
♫ » И не забудьте упростить,
Пока не пришло время прощаться «

Пример:

1 3 + 1 5

Опять же, нижние цифры разные (срезы разного размера)!

1 3	+	1 5	=	?

Но давайте попробуем разделить их на меньшие размеры, чтобы каждый был одинаковым :

5 15	+	3 15

Первая дробь: умножив верхнюю и нижнюю части на 5, мы получили 5 15 :

× 5

× 5

Вторая дробь: умножив верхнюю и нижнюю части на 3, мы получили 3 15 :

× 3

× 3

Нижние числа теперь такие же, поэтому мы можем продолжить и сложить верхние числа:

5 15	+	3 15	=	8 15

Результат настолько прост, насколько это возможно, вот и ответ: 8 15

1 3 + 1 5 знак равно 8 15

Делаем знаменатели одинаковыми

В предыдущем примере, как мы узнали, что нужно разрезать их на ¹ / ₁₅ тысяч, чтобы знаменатели совпадали? Мы просто умножили два знаменателя вместе (3 × 5 = 15).

Прочтите о двух основных способах сделать знаменатели одинаковыми здесь:

Они оба работают, используйте тот, который вам больше нравится!

Пример: Cu

.

Рабочие листы по дробям для 4-го класса — бесплатно и для печати

Дроби — сложение (как знаменатели)		Пример
Сложить подобные дроби		1/3 + 2/3 =
Сложить дроби и смешанные числа		1/3 + 2 2/3 =
Сложить смешанные числа		1 1/3 + 2 2/3 =
Заполнение целых чисел (неправильных дробей)		7/2 + ___ = 8
Заполнение целых чисел (смешанные числа)		3 1/2 + ___ = 8
Дроби — вычитание (как знаменатели)
Вычесть подобные дроби		2/3 — 1/3 =
Вычесть дроби из целых чисел		20 — 4/5 =
Вычесть дроби из смешанных чисел		2 3/4 — 1/4 =
Вычесть смешанные числа из целых чисел		4 — ___ = 1 7/11
Вычесть смешанные числа		4 2/3 — 1 1/3 =
Вычесть смешанные числа (отсутствующее число)		4 2/3 — ___ = 3 1/3
Преобразование дробей в / из смешанных чисел
Преобразование чисел в дроби		3 2/3 =
Преобразование чисел в дроби — сложнее		17 6/17 =
Дроби к смешанным числам		11/3 =
Дроби в смешанные числа — сложнее		37/12 =
Сравнение дробей
Сравните две дроби с круговой диаграммой
Сравните две неправильные или правильные дроби
Сравните смешанные числа и дроби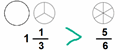
Сравните две дроби		1/2> 1/4
Сравните две правильные или неправильные дроби		8/7> 1/2
Заказ 3 фракции		6/7 <6/5 <6/2
Эквивалентные дроби
Фракции эквивалента цвета
Запишите эквивалентные дроби
Эквивалентные дроби, пропущенные числа		3/4 = ___ / 12
Эквивалентные дроби (правильные и неправильные)		5/4 = ___ / 20
Дробная часть набора
Дробная часть набора		1/3 из 9 = ___
Задачи с дробными словами
Задачи о написании и сравнении дробей		Проблемы со словами
Сложение и вычитание дробей		Проблемы со словами
Умножение дробей на целые числа		Проблемы со словами

.

Обзор урока в шестом классе: упрощение дробей

На этом уроке я покажу ученикам два метода упрощения дробей. Первый метод предназначен для студентов, которым было трудно найти GCF на предыдущих уроках, но которые комфортно понимают правила делимости. Второй метод предназначен для студентов, которым не только удобно находить GCF, но и они могут делать это с помощью мысленной математики.

Мы обсудим оба метода и рассмотрим примеры для каждого метода.

Метод 1 — Найдите общий множитель

Пр. 1 — Упростить 40/48

Шаг 1. Найдите общий множитель для числителя и знаменателя.

Напомню студентам, что для нахождения общего множителя можно использовать правила делимости. Что такое общий множитель 40 и 48? Большинство студентов скажут 2, потому что они оба четные числа. На доске я буду использовать 2, чтобы показать студентам повторяющиеся шаги использования наименьшего общего множителя.

Шаг 2 — Разделите числитель и знаменатель на общий множитель.

Студенты должны иметь ответ 20/24. Можно ли снова уменьшить дробь? Откуда вы знаете?

Шаг 3 — Повторяйте процесс, пока не исчезнут общие факторы.

Окончательный ответ будет 5/6. Как узнать, что вы полностью упростили дробь? Какие наблюдения вы можете сделать?

У студентов может быть несколько ответов:

• 5 — простое число
• 5 нечетное и 6 четное
• Единственное число, которое можно разделить на 5 и 6, — 1.
• 5 и 6 являются взаимно простыми.

Хотя все приведенные выше наблюдения верны, я хочу, чтобы студенты подумали, какое из них верно для всех упрощенных дробей. При необходимости приведу еще несколько примеров упрощенных дробей. Студенты должны прийти к выводу, что если числитель и знаменатель имеют gcf равное 1, относительно простое, то дробь полностью упрощается.

Метод 2 — Найдите GCF

Пр. 2 — Упростить 36/84

Шаг 1 — Найдите GCF числителя и знаменателя.

У учащихся есть 2 метода поиска GCF (см. Урок «Поиск GCF»). Некоторые студенты могут попытаться найти GCF с помощью ментальной математики и подумать, что ответ равен 4. Хотя я хочу развить у студентов умственные математические навыки, я брошу им вызов, чтобы доказать, что их ответ правильный, найдя GCF с помощью одного из методов, которые мы работали. в классе. Студенты должны найти, что GCF составляет 12.

Шаг 2 — Разделите числитель и знаменатель на GCF.

Студенты получат 3/7 ответа. Можно ли еще упростить эту дробь? Почему нет? Опять же, студенты должны прийти к выводу, что числитель и знаменатель взаимно просты.

.