Решение задач с показателями — SAT Mathematics
Все ресурсы SAT Mathematics
137 Практические тесты Вопрос дня Карточки Learn by Concept
SAT Mathematics Help » Экспоненты и корни » Решение задач с экспонентами
Если , то что?
Возможные ответы:
Правильный ответ:
4
Объяснение:
Это задание проверяет ваше владение правилами экспоненты и дает полезные подсказки, которые помогут вам в их использовании. Здесь вы можете увидеть, что и 27, и 9 являются степенями числа 3. и . Это позволяет вам выражать как и как . Затем вы можете упростить эти показатели, чтобы получить . Поскольку, когда вы делите степени одного и того же основания, вы вычитаете степени, теперь у вас есть , и поскольку у вас действительно есть:
Это говорит вам об этом.
Обратите внимание: если бы вы сразу не увидели, что все числа в этой задаче выражены как степени 3, тот факт, что вопрос требует такой комбинации переменных, должен быть вашей подсказкой; вам дали задачу об экспоненте и попросили дать ответ на вычитание, так что это должно заставить вас задуматься о делении экспонент одного и того же основания, чтобы вычесть экспоненты, и, по крайней мере, дать вам немного корма для игры с правилами экспоненты, пока вы не найдете способ прогрессировать.
Сообщить об ошибке
Какое из следующих значений является решением приведенного выше уравнения?
Возможные ответы:
10
3
30
9
Правильный ответ: 5
01 Объяснение:
Эта задача связана с творческим разложением на множители, а разложение на множители всегда следует делать всякий раз, когда вы видите несколько показателей степени среди какого-либо сложения или вычитания.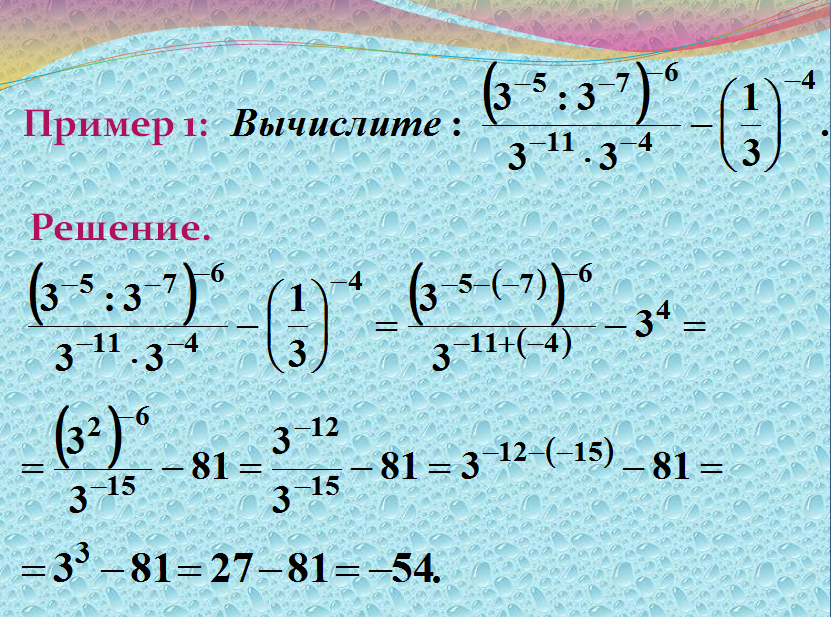
Может стать:
И если вы разложите общий термин, вы получите:
Единственное доступное решение для действительных чисел , поэтому правильный ответ .
Сообщить об ошибке
Если , каково значение ?
Возможные ответы:
14
13
15
16
Правильный ответ: 50
150004 Объяснение:Важным принципом проверки степени здесь является то, что когда вы умножаете/делите степени одного и того же основания, вы складываете/вычитаете эти степени. Здесь вы можете сделать следствие; если бы вы , вы бы сложили вместе эти показатели, чтобы получить . Но в этом случае вам дан комбинированный показатель степени , и вы можете преобразовать его в , чтобы можно было разложить:
позволяет разложить термины на множители, чтобы получить:
Вы можете выполнить арифметические действия для упрощения , что позволит вам разделить обе части на 3 и получить:
Итак .
Сообщить об ошибке
Если , каково значение ?
Возможные ответы:
Правильный ответ:
3
Пояснение:
Эта задача зависит от вашей способности распознавать числа 16, 4 и 64 как степени числа 4 (или числа 2). Если вы сделаете это признание, вы можете использовать правила экспоненты, чтобы выразить термины как степени 4:
Поскольку преобразование одного показателя в другой означает, что вы умножаете показатели степени, вы можете упростить числитель и получить:
И затем, поскольку при делении показателей степени одного и того же основания вы можете вычесть показатели степени, вы можете выразить это как:
Это означает, что .
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Ключом к получению заданного выражения в действенной форме при решении этой проблемы экспоненты является поиск общих оснований.
Поскольку и 9, и 27 являются степенями числа 3, вы можете переписать данное выражение как:
Когда вы это сделаете, вы будете готовы применить основные правила экспоненты. Когда вы переводите один показатель в другой, вы умножаете показатели. Таким образом, числитель становится , а знаменатель становится . Ваша новая дробь:
Теперь займитесь отрицательными показателями степени, что означает, что вы перевернете каждый член на полосе дроби и сделаете показатель степени положительным. Это делает вашу дробь:
Поскольку при делении показателей степени одного основания вы вычитаете их показатели степени, это упрощается до .
Сообщить об ошибке
эквивалентен какому из следующих?
Возможные ответы:
Правильный ответ:
Объяснение:
Эта задача вознаграждает вас за то, что вы умеете множить с показателями степени.
Теперь вы можете произвести некоторые арифметические действия в скобках, поскольку каждый из этих показателей степени вы должны распознать или уметь быстро вычислять вручную. У вас есть:
Что равно:
Здесь, даже если вы не узнаете как , вы должны посмотреть на варианты ответа, чтобы увидеть множество двоек с показателями степени, и это может быть вашей подсказкой. Вы можете упростить это до:
Теперь у вас есть несколько вариантов. Вы могли заметить, что если два разных основания привести к одному и тому же показателю степени, вы можете объединить умножение, чтобы получить или . Или вы можете перейти к вариантам ответов и исключить те, которые близки, но явно неверны.
Сообщить об ошибке
Если , какое из следующих уравнений должно быть верным?
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче вы должны увидеть, что используемые числа 2, 4 и 8 являются степенями двойки. Таким образом, чтобы получить степени таким образом, чтобы их можно было использовать вместе, вы можете разложить каждое основание в основание 2. Это дает вам:
Затем вы можете применить правило, согласно которому, когда вы переводите один показатель степени в другой, вы умножаете степени. Это затем упрощает ваше уравнение до:
А теперь к левой части уравнения можно применить другое правило экспоненты: когда вы умножаете две степени одного и того же основания, вы складываете степени вместе:
Поскольку основания здесь все одинаковые , вы можете установить показатели равными.
Это дает вам:
Сообщить об ошибке
Что из следующего представляет собой среднее значение и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Хотя на первый взгляд это может показаться быстрой задачей, если вы просто возьмете показатель степени между 61 и 63 и скажете , быстрый тест с небольшими числами должен показать вам, что вы не можете просто сделать это. Среднее значение и , например, равно 5, а не . Итак, здесь вам нужно будет найти способ использовать правило, согласно которому Среднее = (Сумма терминов)/(Количество терминов).
Таким образом, алгебраически среднее значение равно , но, конечно, эти числа слишком велики, чтобы их можно было вычислить, а затем сложить. Вы можете, однако, использовать две подсказки в свою пользу: 1) всякий раз, когда вы складываете или вычитаете показатели степени, хорошей идеей является факторизация (помните, показатели степени представляют собой повторяющееся умножение, а факторизация создает большее умножение).
И 2) все варианты ответов имеют степени 11 без добавления, поэтому вам следует попытаться исключить общий 11-член, чтобы ваша математика больше походила на ответы. Если вы сделаете это, вы обнаружите, что у вас есть:
Отсюда вы можете вычислить числа в скобках. Это дает вам:
Если вы закончите математику, вы увидите, что вы можете сложить 121 + 1, чтобы получить 122, что при делении на 2 дает вам 61. Таким образом, ваш окончательный ответ выглядит так:
Сообщить об ошибке
равно чему из следующих?
Возможные ответы:
Правильный ответ:
Объяснение:
Эта задача вознаграждает вашу способность вычислять показатели степени. Здесь, если вы вычеркнете общие термины в данном уравнении, вы сможете увидеть, как математика выглядит как правильный ответ. Факторинг отрицательных показателей может немного отличаться от более традиционного факторинга, который вы делаете чаще, но механика такая же.
Если вы разложите на множители общие , выражение станет следующим:
Здесь вы можете выполнить арифметические действия с меньшими показателями. Они преобразуются в:
Если сложить дроби (и 1) в круглых скобках, вы получите:
И поскольку теперь вы можете выразить это как:
, что преобразуется в правильный ответ:
Примечание. которую вы также могли бы начать с вынесения из заданного выражения. Если бы вы пошли по этому пути, факторизация привела бы к:
Это также дает вам правильный ответ, так как, когда вы суммируете термины в скобках, вы получаете:
Сообщить об ошибке
Если , то каково значение ?
Возможные ответы:
Правильный ответ:
7
Объяснение:
Всякий раз, когда вам дают сложение или вычитание двух экспоненциальных членов с общим основанием, первым побуждением будет решить задачу на сложение или вычитание, чтобы создать умножение.
Большинство правил экспоненты имеют дело с умножением/делением и очень немногие — сложением/вычитанием, поэтому, если вы застряли на задаче экспоненты, факторинг может быть вашим лучшим другом.
Уравнение может быть переписано как , используя правило, согласно которому при умножении показателей степени одного и того же основания вы складываете показатели степени. Это позволяет вам разделить общий член в левой части уравнения, чтобы получить:
И, конечно же, вы можете упростить небольшую задачу на вычитание в круглых скобках, чтобы получить:
И вы можете сделать еще один шаг : так как все в уравнении является показателем степени, кроме 4, вы можете выразить 4 как , чтобы все члены выглядели одинаково:
Теперь вам нужно увидеть, что может быть выражено как или как . Таким образом, уравнение может выглядеть так:
Затем вы можете разделить обе части на и получить:
Это доказывает, что .
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по математике SAT
137 Практические тесты Вопрос дня Карточки Learn by Concept
РЕШЕННЫЕ УПРАЖНЕНИЯ: ПОКАЗАТЕЛИ УПРОЩЕНИЯ: ВТОРИЧНЫЙ
Содержание этой страницы:
Введение
Степень является выражением этого типа
a b = a · a · · · a · a 12 база , , сама по себе столько раз, сколько показывает показатель степени , b .
Мы читаем это как « a в степени b ».Например, 2 3 = 2·2·2 = 8 (основание равно 2, показатель степени равен 3).
Как правило, основание и показатель степени могут быть любым числом (действительные или комплексные) или они могут быть даже переменными, неизвестными факторами или параметрами. Уравнения с неизвестным множителем в показателе степени известны как показательных уравнений .
Особым случаем являются степени, показатели степени которых являются дробями. В этом случае мощность представляет собой квадратный корень. Они появляются из-за к необходимости решить уравнение типа х n = а.
Другим особым случаем являются степени с основанием 10 , с этим
внешний вид 10 n . Если n является натуральным числом (0, 1, 2, 3,…)
результат 10…0 , то есть n количество нулей. Если n является отрицательным число (-1, -2, -3, -4,.
..), результат 0.00…1 где значение n положительное указывает количество нулей, считая 0 перед запятой. Эти
тип полномочий, используемых в научное обозначение .
Наконец, мы скажем, что степень, возведенная в 0, всегда равна 1 , поэтому x 0 = 1 .
В этом разделе задания расположены в порядке возрастания сложности: мы используем свойства экспонент (мощность произведений, степень частного, степень степени,..) и, после того, как мы упростим выражения, образованные степенями (круглые скобки, дроби, отрицательные показатели, параметры…).
| СВОЙСТВА ПОЛНОМОЧИЙ | ||
| Продукт | Мощность | |
| Частное | Отрицательный показатель степени | |
| Обратный | Инверсия инверсии | |
Упражнение 1
Шоу раствор
УПРАЖНЕНИЕ 2
Покат.