правила, примеры, решения, арифметические действия с рациональными числами
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5+1 4возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Определение 1Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство:
Используя переместительное свойство сложения, получим также верное равенство:
Пара простых примеров: сумма рационального числа 2,1 и числа 0 равно 2,1 и: 645+0 = 645.
Сложение противоположных рациональных чисел
Определение 2Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a+(-a)=0 (для любого рационального числа a).
К примеру, числа 45,13 и -45,13 являются противоположными, т.е. их сумма равно нулю: 45,13+(-45,13) = 0.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Пример 1Необходимо произвести сложение рациональных чисел: 0,6 и 59.
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0,6 + 59 = 610 + 59.
Осуществим сложение дробей с разными знаменателями:
610+59= 5490+ 5090= 10490=1745
Ответ: 0,6 + 59= 1745.
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Определение 3Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Пример 2Необходимо осуществить сложение рациональных чисел с разными знаками 8,2 и -234 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: |8,2| = 8,2 и|-234|=234. Проведя сравнение модулей — рациональных чисел, получим: 8,2 > 234 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым.
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8,2 +(-234)= 5920.
Сложение отрицательных рациональных чисел
Определение 4Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Пример 3Необходимо произвести сложение чисел: -4,0203 и -12,193.
Решение
Модули заданных чисел соответственно равны: 4,0203 и 12,193. Сложим их:
Полученному результату присваиваем знак минус: -16,2133.
Ответ: (-4,0203)+(-12,193) =-16,2133.
Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b=a следует, что a-b=c и a-c=b. И наоборот: из равенств a-b =c и a-c=b следует, что c+b=a.
И наоборот: из равенств a-b =c и a-c=b следует, что c+b=a.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Определение 5При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Пример 4Необходимо вычислить разность рациональных чисел: 4,(36)– 15.
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4,(36) = 4+(0,36 + 0,0036 +…)= 4+0,361-0,01=4 + 3699=4+ 411= 4411
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4, (36)-15= 4411- 15=4 + 411-15=4+2055- 1155=4+955=4955
Ответ: 4,(36)-15= 4955
Определение 6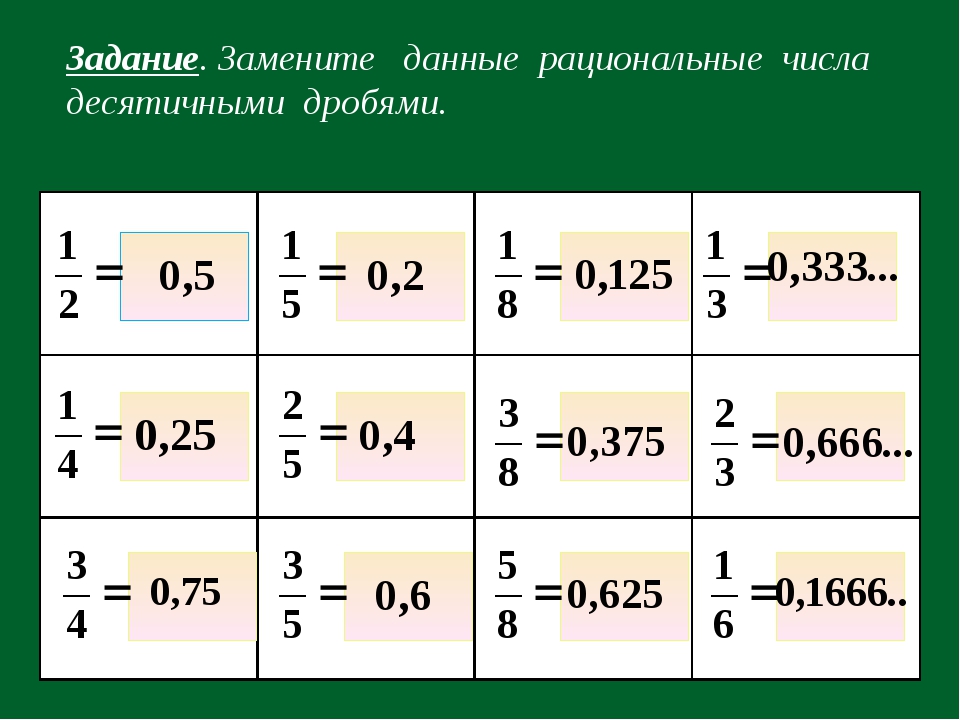
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: (a+(-b))+b=a+((-b)+b)=a+0=a. Отсюда в силу смысла действия вычитания следует, что сумма a+(-b) есть разность чисел a и b.
Пример 5Необходимо из рационального числа 27 вычесть рациональное число 537
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. -537. Тогда: 27-537=27+-537
Далее произведем сложение рациональных чисел с разными знаками: 27+-537=-537-27=-537-27= -517
Ответ:27+-537=-517
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Определение 7Произведение любого рационального числа a на нуль есть нуль.
Т.е. a·0=0.
Используя переместительное свойство умножения, получим: 0·а=0.
К примеру, умножение рационального числа 713 на 0 даст 0. Перемножив отрицательное рациональное число -718и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0·0=0
Умножение на единицу
Определение 8Умножение любого рационального числа a на 1 дает число a.
Т.е. a·1=a или 1 · a = a (для любого рационального a). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5,46 на 1 даст в итоге число 5,46.
Умножение взаимообратных чисел
Определение 9Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а·а-1=1.
Т.е. : а·а-1=1.
К примеру, результатом произведения чисел 56 и 65 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Пример 6Необходимо вычислить произведение положительных рациональных чисел 0,5 и 625.
Решение
Представим заданную десятичную дробь в виде обыкновенной 0,5 = 510= 12.
Далее произведем умножение обыкновенных дробей: 12 · 625= 650= 325.
Ответ: 0,5 ·625= 325
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Пример 7Необходимо вычислить произведение рациональных чисел 2,121 и 3,4.
Решение
Перемножим десятичные дроби столбиком:
Ответ: 2,121 · 3,4 = 7,2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Определение 10Необходимо найти произведение чисел: -338и 212
Решение
Согласно вышеуказанному правилу получим: -338·212=-338·212=-338·212
Заменим смешанные дроби неправильными и найдем искомое произведение: -338·212=-278·52=-13516=-8716
Ответ: -338·212=-8716
Умножение отрицательных рациональных чисел
Определение 11Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Пример 9Необходимо найти произведение отрицательных рациональных чисел -3,146 и -56.
Решение: модули заданных чисел соответственно равны 3,146 и 56.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b·c =a следует, что a:b =c и a:c=b. И наоборот: из равенств a:b=c и a:c=b следует, что b·c=a.
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Определение 12Разделить число а на число b, отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a·b-1.
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств (a·b-1)· b=a·(b-1·b)=a·1=a, которая и доказывает равенство

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Пример 10Необходимо выполнить действие деления 313:-116
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: -116= -76.
Число, обратное этой дроби, будет: -67. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 313-116=313·-67=103·(-67) =-(103·67)=-207= -267
Ответ: 313:-116=-267
правила, примеры, решения, арифметические действия с рациональными числами
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5+1 4возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Определение 1Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a.
Пара простых примеров: сумма рационального числа 2,1 и числа 0 равно 2,1 и: 645+0 = 645.
Сложение противоположных рациональных чисел
Определение 2Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a+(-a)=0 (для любого рационального числа a).
К примеру, числа 45,13 и -45,13 являются противоположными, т.е. их сумма равно нулю: 45,13+(-45,13) = 0.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Пример 1Необходимо произвести сложение рациональных чисел: 0,6 и 59.
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0,6 + 59 = 610 + 59.
Осуществим сложение дробей с разными знаменателями:
610+59= 5490+ 5090= 10490=1745
Ответ: 0,6 + 59= 1745.
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Определение 3Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Необходимо осуществить сложение рациональных чисел с разными знаками 8,2 и -234 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: |8,2| = 8,2 и|-234|=234. Проведя сравнение модулей — рациональных чисел, получим: 8,2 > 234 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8,2-234= 8210- 234= 59 20.
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8,2 +(-234)= 5920.
Сложение отрицательных рациональных чисел
Определение 4Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Пример 3Необходимо произвести сложение чисел: -4,0203 и -12,193.
Решение
Модули заданных чисел соответственно равны: 4,0203 и 12,193. Сложим их:
Полученному результату присваиваем знак минус: -16,2133.
Ответ: (-4,0203)+(-12,193) =-16,2133.
Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b=a следует, что a-b=c и a-c=b. И наоборот: из равенств a-b =c и a-c=b следует, что c+b=a.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Определение 5При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Пример 4Необходимо вычислить разность рациональных чисел: 4,(36)– 15.
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4,(36) = 4+(0,36 + 0,0036 +…)= 4+0,361-0,01=4 + 3699=4+ 411= 4411
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4, (36)-15= 4411- 15=4 + 411-15=4+2055- 1155=4+955=4955
Ответ: 4,(36)-15= 4955
Определение 6В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a–b=a+(-b).
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: (a+(-b))+b=a+((-b)+b)=a+0=a. Отсюда в силу смысла действия вычитания следует, что сумма a+(-b) есть разность чисел a и b.
Пример 5Необходимо из рационального числа 27 вычесть рациональное число 537
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. -537. Тогда: 27-537=27+-537
Далее произведем сложение рациональных чисел с разными знаками: 27+-537=-537-27=-537-27= -517
Ответ:27+-537=-517
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Определение 7Произведение любого рационального числа a на нуль есть нуль.
Т.е. a·0=0.
Используя переместительное свойство умножения, получим: 0·а=0.
К примеру, умножение рационального числа 713 на 0 даст 0. Перемножив отрицательное рациональное число -718и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0·0=0.
Умножение на единицу
Определение 8Умножение любого рационального числа a на 1 дает число a.
Т.е. a·1=a или 1 · a = a (для любого рационального a). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5,46 на 1 даст в итоге число 5,46.
Умножение взаимообратных чисел
Определение 9Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а·а-1=1.
Т.е. : а·а-1=1.
К примеру, результатом произведения чисел 56 и 65 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Пример 6Необходимо вычислить произведение положительных рациональных чисел 0,5 и 625.
Решение
Представим заданную десятичную дробь в виде обыкновенной 0,5 = 510= 12.
Далее произведем умножение обыкновенных дробей: 12 · 625= 650= 325.
Ответ: 0,5 ·625= 325
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Пример 7Необходимо вычислить произведение рациональных чисел 2,121 и 3,4.
Решение
Перемножим десятичные дроби столбиком:
Ответ: 2,121 · 3,4 = 7,2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Определение 10Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Пример 8Необходимо найти произведение чисел: -338и 212
Решение
Согласно вышеуказанному правилу получим: -338·212=-338·212=-338·212
Заменим смешанные дроби неправильными и найдем искомое произведение: -338·212=-278·52=-13516=-8716
Ответ: -338·212=-8716
Умножение отрицательных рациональных чисел
Определение 11Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Пример 9Необходимо найти произведение отрицательных рациональных чисел -3,146 и -56.
Решение: модули заданных чисел соответственно равны 3,146 и 56.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Ответ: (-3,146) · (-56) = 176,176
Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b·c =a следует, что a:b =c и a:c=b. И наоборот: из равенств a:b=c и a:c=b следует, что b·c=a.
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Определение 12Разделить число а на число b, отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a·b-1.
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств (a·b-1)· b=a·(b-1·b)=a·1=a, которая и доказывает равенство a : b = a · b-1.
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Пример 10Необходимо выполнить действие деления 313:-116
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: -116= -76.
Число, обратное этой дроби, будет: -67. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 313-116=313·-67=103·(-67) =-(103·67)=-207= -267
Ответ: 313:-116=-267
правила, примеры, решения, арифметические действия с рациональными числами
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5+1 4возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Определение 1Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a.
Пара простых примеров: сумма рационального числа 2,1 и числа 0 равно 2,1 и: 645+0 = 645.
Сложение противоположных рациональных чисел
Определение 2Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a+(-a)=0 (для любого рационального числа a).
К примеру, числа 45,13 и -45,13 являются противоположными, т.е. их сумма равно нулю: 45,13+(-45,13) = 0.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Пример 1Необходимо произвести сложение рациональных чисел: 0,6 и 59.
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0,6 + 59 = 610 + 59.
Осуществим сложение дробей с разными знаменателями:
610+59= 5490+ 5090= 10490=1745
Ответ: 0,6 + 59= 1745.
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Определение 3Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Необходимо осуществить сложение рациональных чисел с разными знаками 8,2 и -234 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: |8,2| = 8,2 и|-234|=234. Проведя сравнение модулей — рациональных чисел, получим: 8,2 > 234 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8,2-234= 8210- 234= 59 20.
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8,2 +(-234)= 5920.
Сложение отрицательных рациональных чисел
Определение 4Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Пример 3Необходимо произвести сложение чисел: -4,0203 и -12,193.
Решение
Модули заданных чисел соответственно равны: 4,0203 и 12,193. Сложим их:
Полученному результату присваиваем знак минус: -16,2133.
Ответ: (-4,0203)+(-12,193) =-16,2133.
Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b=a следует, что a-b=c и a-c=b. И наоборот: из равенств a-b =c и a-c=b следует, что c+b=a.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Определение 5При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Пример 4Необходимо вычислить разность рациональных чисел: 4,(36)– 15.
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4,(36) = 4+(0,36 + 0,0036 +…)= 4+0,361-0,01=4 + 3699=4+ 411= 4411
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4, (36)-15= 4411- 15=4 + 411-15=4+2055- 1155=4+955=4955
Ответ: 4,(36)-15= 4955
Определение 6В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a–b=a+(-b).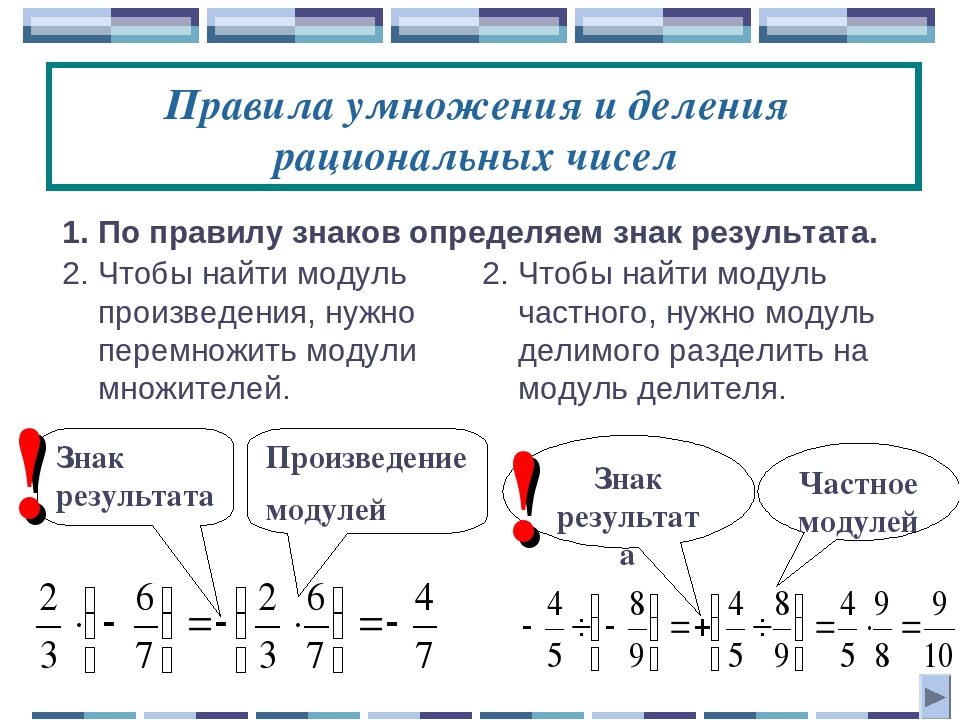
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: (a+(-b))+b=a+((-b)+b)=a+0=a. Отсюда в силу смысла действия вычитания следует, что сумма a+(-b) есть разность чисел a и b.
Пример 5Необходимо из рационального числа 27 вычесть рациональное число 537
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. -537. Тогда: 27-537=27+-537
Далее произведем сложение рациональных чисел с разными знаками: 27+-537=-537-27=-537-27= -517
Ответ:27+-537=-517
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Определение 7Произведение любого рационального числа a на нуль есть нуль.
Т.е. a·0=0.
Используя переместительное свойство умножения, получим: 0·а=0.
К примеру, умножение рационального числа 713 на 0 даст 0. Перемножив отрицательное рациональное число -718и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0·0=0.
Умножение на единицу
Определение 8Умножение любого рационального числа a на 1 дает число a.
Т.е. a·1=a или 1 · a = a (для любого рационального a). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5,46 на 1 даст в итоге число 5,46.
Умножение взаимообратных чисел
Определение 9Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а·а-1=1.
Т.е. : а·а-1=1.
К примеру, результатом произведения чисел 56 и 65 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Пример 6Необходимо вычислить произведение положительных рациональных чисел 0,5 и 625.
Решение
Представим заданную десятичную дробь в виде обыкновенной 0,5 = 510= 12.
Далее произведем умножение обыкновенных дробей: 12 · 625= 650= 325.
Ответ: 0,5 ·625= 325
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Пример 7Необходимо вычислить произведение рациональных чисел 2,121 и 3,4.
Решение
Перемножим десятичные дроби столбиком:
Ответ: 2,121 · 3,4 = 7,2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Определение 10Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Пример 8Необходимо найти произведение чисел: -338и 212
Решение
Согласно вышеуказанному правилу получим: -338·212=-338·212=-338·212
Заменим смешанные дроби неправильными и найдем искомое произведение: -338·212=-278·52=-13516=-8716
Ответ: -338·212=-8716
Умножение отрицательных рациональных чисел
Определение 11Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Пример 9Необходимо найти произведение отрицательных рациональных чисел -3,146 и -56.
Решение: модули заданных чисел соответственно равны 3,146 и 56.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Ответ: (-3,146) · (-56) = 176,176
Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b·c =a следует, что a:b =c и a:c=b. И наоборот: из равенств a:b=c и a:c=b следует, что b·c=a.
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Определение 12Разделить число а на число b, отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a·b-1.
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств (a·b-1)· b=a·(b-1·b)=a·1=a, которая и доказывает равенство a : b = a · b-1.
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Пример 10Необходимо выполнить действие деления 313:-116
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: -116= -76.
Число, обратное этой дроби, будет: -67. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 313-116=313·-67=103·(-67) =-(103·67)=-207= -267
Ответ: 313:-116=-267
правила, примеры, решения, арифметические действия с рациональными числами
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5+1 4возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Определение 1Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a.
Пара простых примеров: сумма рационального числа 2,1 и числа 0 равно 2,1 и: 645+0 = 645.
Сложение противоположных рациональных чисел
Определение 2Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a+(-a)=0 (для любого рационального числа a).
К примеру, числа 45,13 и -45,13 являются противоположными, т.е. их сумма равно нулю: 45,13+(-45,13) = 0.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Пример 1Необходимо произвести сложение рациональных чисел: 0,6 и 59.
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0,6 + 59 = 610 + 59.
Осуществим сложение дробей с разными знаменателями:
610+59= 5490+ 5090= 10490=1745
Ответ: 0,6 + 59= 1745.
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Определение 3Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Необходимо осуществить сложение рациональных чисел с разными знаками 8,2 и -234 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: |8,2| = 8,2 и|-234|=234. Проведя сравнение модулей — рациональных чисел, получим: 8,2 > 234 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8,2-234= 8210- 234= 59 20.
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8,2 +(-234)= 5920.
Сложение отрицательных рациональных чисел
Определение 4Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Пример 3Необходимо произвести сложение чисел: -4,0203 и -12,193.
Решение
Модули заданных чисел соответственно равны: 4,0203 и 12,193. Сложим их:
Полученному результату присваиваем знак минус: -16,2133.
Ответ: (-4,0203)+(-12,193) =-16,2133.
Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b=a следует, что a-b=c и a-c=b. И наоборот: из равенств a-b =c и a-c=b следует, что c+b=a.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Определение 5При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Пример 4Необходимо вычислить разность рациональных чисел: 4,(36)– 15.
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4,(36) = 4+(0,36 + 0,0036 +…)= 4+0,361-0,01=4 + 3699=4+ 411= 4411
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4, (36)-15= 4411- 15=4 + 411-15=4+2055- 1155=4+955=4955
Ответ: 4,(36)-15= 4955
Определение 6В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a–b=a+(-b).
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: (a+(-b))+b=a+((-b)+b)=a+0=a. Отсюда в силу смысла действия вычитания следует, что сумма a+(-b) есть разность чисел a и b.
Пример 5Необходимо из рационального числа 27 вычесть рациональное число 537
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. -537. Тогда: 27-537=27+-537
Далее произведем сложение рациональных чисел с разными знаками: 27+-537=-537-27=-537-27= -517
Ответ:27+-537=-517
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Определение 7Произведение любого рационального числа a на нуль есть нуль.
Т.е. a·0=0.
Используя переместительное свойство умножения, получим: 0·а=0.
К примеру, умножение рационального числа 713 на 0 даст 0. Перемножив отрицательное рациональное число -718и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0·0=0.
Умножение на единицу
Определение 8Умножение любого рационального числа a на 1 дает число a.
Т.е. a·1=a или 1 · a = a (для любого рационального a). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5,46 на 1 даст в итоге число 5,46.
Умножение взаимообратных чисел
Определение 9Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а·а-1=1.
Т.е. : а·а-1=1.
К примеру, результатом произведения чисел 56 и 65 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Пример 6Необходимо вычислить произведение положительных рациональных чисел 0,5 и 625.
Решение
Представим заданную десятичную дробь в виде обыкновенной 0,5 = 510= 12.
Далее произведем умножение обыкновенных дробей: 12 · 625= 650= 325.
Ответ: 0,5 ·625= 325
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Пример 7Необходимо вычислить произведение рациональных чисел 2,121 и 3,4.
Решение
Перемножим десятичные дроби столбиком:
Ответ: 2,121 · 3,4 = 7,2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Определение 10Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Пример 8Необходимо найти произведение чисел: -338и 212
Решение
Согласно вышеуказанному правилу получим: -338·212=-338·212=-338·212
Заменим смешанные дроби неправильными и найдем искомое произведение: -338·212=-278·52=-13516=-8716
Ответ: -338·212=-8716
Умножение отрицательных рациональных чисел
Определение 11Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Пример 9Необходимо найти произведение отрицательных рациональных чисел -3,146 и -56.
Решение: модули заданных чисел соответственно равны 3,146 и 56.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Ответ: (-3,146) · (-56) = 176,176
Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b·c =a следует, что a:b =c и a:c=b. И наоборот: из равенств a:b=c и a:c=b следует, что b·c=a.
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Определение 12Разделить число а на число b, отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a·b-1.
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств (a·b-1)· b=a·(b-1·b)=a·1=a, которая и доказывает равенство a : b = a · b-1.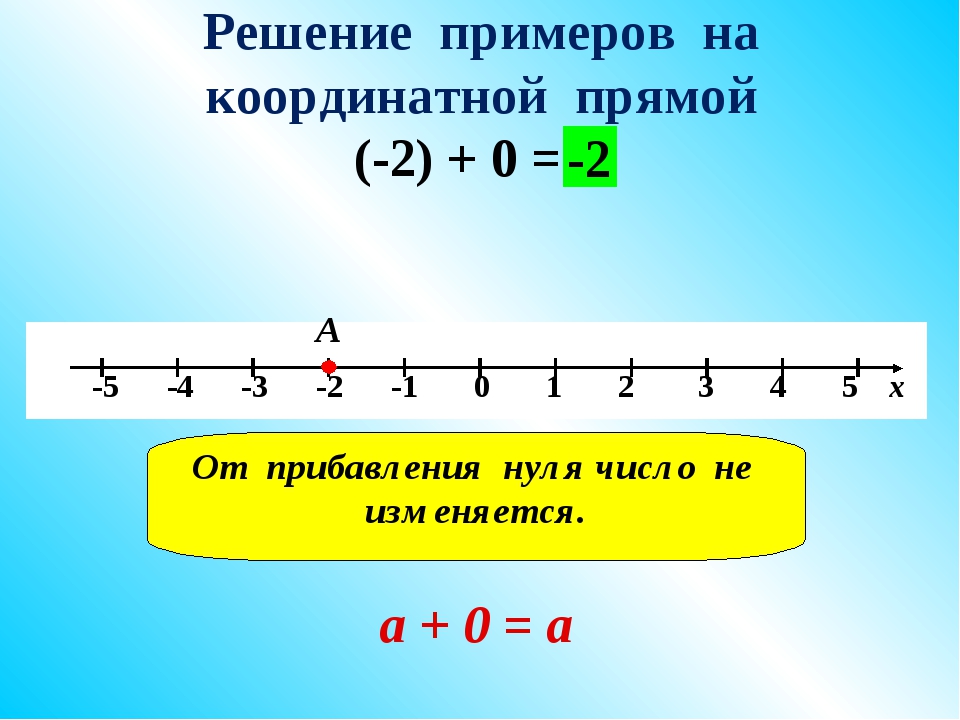
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Пример 10Необходимо выполнить действие деления 313:-116
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: -116= -76.
Число, обратное этой дроби, будет: -67. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 313-116=313·-67=103·(-67) =-(103·67)=-207= -267
Ответ: 313:-116=-267
Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.
При этом, b не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.
Пример 1. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .
Поэтому мы из вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .
Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами и является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Запишем решение данного примера покороче:
Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Пример 3. Найти значение выражения:
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Заключим каждое рациональное число в скобки вместе своими знаками:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Запишем решение данного примера покороче:
Пример 4. Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками:
Вычислим данное выражение в следующем порядке: слóжим рациональные числа и , затем из полученного результата вычтем рациональное число .
Первое действие:
Второе действие:
Таким образом, значение выражения равно
Пример 5. Найти значение выражения:
Представим целое число −1 в виде дроби , а смешанное число переведём в неправильную дробь:
Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Получили ответ .
Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.
Итак, вернёмся к изначальному выражению:
Заключим каждое число в скобки. Для этого смешанное число временно развернём:
Вычислим целые части:
(−1) + (+2) = 1
В главном выражении вместо (−1) + (+2) запишем полученную единицу:
Полученное выражение свернём. Для этого запишем единицу и дробь вместе:
Для этого запишем единицу и дробь вместе:
Запишем решение этим способом покороче:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальную часть перепишем без изменения:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Запишем решение данного примера покороче:
Пример 7. Найти значение выражение
Представим целое число −5 в виде дроби , а смешанное число переведём в неправильную дробь:
Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно .
Решим данный пример вторым способом. Вернемся к изначальному выражению:
Запишем смешанное число в развёрнутом виде. Остальное перепишем без изменений:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо запишем полученное число −7
Выражение является развёрнутой формой записи смешанного числа . Запишем число −7 и дробь вместе, образуя окончательный ответ:
Запишем это решение покороче:
Пример 8. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные и
Запишем это решение покороче:
Пример 9. Найти выражения выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число в скобки вместе своим знаком. Рациональное число в скобки заключать не нужно, поскольку оно уже в скобках:
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
После их приведения к общему знаменателю, они примут следующий вид:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.
В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Пример 10. Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:
Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:
Вычислим его любым удобным для нас способом:
Пример 11. Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Пример 12. Найти значение выражения
Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение , затем выражение Полученные результаты слóжим .
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Пример 13. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число в скобки вместе со своим знаком. Рациональное число заключать в скобки не нужно, поскольку оно уже в скобках:
Рациональное число заключать в скобки не нужно, поскольку оно уже в скобках:
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Таким образом, значение выражения равно
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.
Пример 14. Найти значение выражения −3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
Но мы его запишем для наглядности:
(−3,2) + (+4,3)
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
(−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1
Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2
Таким образом, значение выражения −3,2 + (+4,3) равно 1,1
Этот пример можно записать покороче:
−3,2 + (+4,3) = 1,1
Пример 15. Найти значение выражения 3,5 + (−8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:
Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:
3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8
Таким образом, значение выражения 3,5 + (−8,3) равно −4,8
Этот пример можно записать покороче:
3,5 + (−8,3) = −4,8
Пример 16. Найти значение выражения −7,2 + (−3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.
Запись с модулями можно пропустить, чтобы не загромождать выражение:
−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31
Таким образом, значение выражения −7,2 + (−3,11) равно −10,31
Этот пример можно записать покороче:
−7,2 + (−3,11) = −10,31
Пример 17. Найти значение выражения −0,48 + (−2,7)
Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18
Пример 18. Найти значение выражения −4,9 − 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
(−4,9) − (+5,9)
Заменим вычитание сложением:
(−4,9) + (−5,9)
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8
Таким образом, значение выражения −4,9 − 5,9 равно −10,8
Запишем решение этого примера покороче:
−4,9 − 5,9 = −10,8
Пример 19. Найти значение выражения 7 − 9,3
Найти значение выражения 7 − 9,3
Заключим в скобки каждое число вместе со своими знаками
(+7) − (+9,3)
Заменим вычитание сложением
(+7) + (−9,3)
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3
Таким образом, значение выражения 7 − 9,3 равно −2,3
Запишем решение этого примера покороче:
7 − 9,3 = −2,3
Пример 20. Найти значение выражения −0,25 − (−1,2)
Заменим вычитание сложением:
−0,25 + (+1,2)
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
−0,25 + (+1,2) = 1,2 − 0,25 = 0,95
Запишем решение этого примера покороче:
−0,25 − (−1,2) = 0,95
Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)
Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5
Первое действие:
4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0
Второе действие:
−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5
Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.
Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)
Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:
Первое действие:
3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6
Второе действие:
3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4
Третье действие
0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.
Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
(−3,8) + (+17,15) − (+6,2) − (+6,15)
Заменим вычитание сложением там, где это можно:
(−3,8) + (+17,15) + (−6,2) + (−6,15)
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:
Первое действие:
(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35
Второе действие:
13,35 + (−6,2) = 13,35 − −6,20 = 7,15
Третье действие:
7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1
Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.
Пример 24. Найти значение выражения
Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:
Далее вычисляем данное выражение, применяя ранее изученные правила:
Пример 25. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко
А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26. Найти значение выражения
Переведём смешанное число в неправильную дробь, а десятичную дробь −0,85 в обыкновенную дробь. Получим следующее выражение:
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
Пример 27. Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:
Пример 28. Найти значение выражения
Найти значение выражения
Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:
Пример 29. Найти значение выражения
Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.
Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного результата вычесть . Этим вариантом и воспользуемся.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 30. Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.
Первое действие:
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас
Второе действие:
Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:
Третье действие:
Ответ: значение выражения равно
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
сложение и вычитание, умножение и деление
Сложение
При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.
Пример 1. Найти сумму рациональных чисел 2,5 и 3,2.
Решение: Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:
2,5 + 3,2 = 5,7.
Пример 2. Найти сумму отрицательных чисел (-2,5) и (-3,2).
Решение: Сначала надо сложить модули слагаемых:
2,5 + 3,2 = 5,7.
Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:
(-2,5) + (-3,2) = -5,7.
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4,7) + (+12) = 7,3, так как 12 — 4,7 = 7,3;
9 + (-15) = -6, так как 15 — 9 = 6.
Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю.
Примеры:
125 + (-125) = 0;
-34 + (+34) = 0.
Вычитание
Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.
Примеры:
(+10) — (+3,4) = (+10) + (-3,4) = 6,6;
(+10) — (-3,4) = (+10) + (+3,4) = 13,4;
(-10) — (-3,4) = (-10) + (+3,4) = -6,6;
(-10) — (+3,4) = (-10) + (-3,4) = -13,4.
Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение
При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.
Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.
Примеры:
3 · 5 = 15;
3 · (-5) = -15;
-3 · 5 = -15;
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | — | = | — |
| — | · | + | = | — |
| — | · | — | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 · (-1) = 1,5;
2,5 · (-1) = -2,5.
Деление
При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3;
15 : (-5) = -3;
-15 : 5 = -3;
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | — | = | — |
| — | : | + | = | — |
| — | : | — | = | + |
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 : (-1) = 1,5;
2,5 : (-1) = -2,5.
Рациональные числа, формулы и онлайн калькуляторы
Содержание:
Определение
Рациональной дробью называется выражение вида $\frac{m}{n}$, где целое число $m$ называется числителем дроби, а натуральное число $n$ — знаменателем дроби.
Рациональные числа — это положительные и отрицательные числа (целые и дробные) и нуль.
Множество рациональных чисел обозначается $Q$.
Две рациональные дроби $\frac{m}{n}$ и $\frac{p}{q}$ называются эквивалентными, если $mq = np$.
Пример
Дроби $\frac{2}{3}$ и $\frac{4}{6}$ эквивалентные, так как $2 \cdot 6 = 3 \cdot 4$
Рациональным числом называется множество всех эквивалентных между собой дробей.
Сравниваются рациональные числа следующим образом:
- Всякое положительное рациональное число больше нуля.

- Всякое отрицательное рациональное число меньше нуля.
- Из двух отрицательных чисел больше то, у которого абсолютная величина меньше.
Слишком сложно?
Рациональные числа не по зубам? Тебе ответит эксперт через 10 минут!
Арифметические операции с рациональными числами
Сложение рациональных чисел. Чтобы сложить рациональные числа с одинаковыми знаками, складывают их абсолютные величины и перед суммой ставят их общий знак.
Чтобы сложить два рациональных числа с разными знаками, необходимо из числа с большей абсолютной величиной вычесть число с меньшей абсолютной величиной и поставить знак числа, большего по модулю.
Пример
Задание. Вычислить $4+\frac{5}{2} ;-4+\left(-\frac{5}{2}\right) ;(-4)+\frac{5}{2}$
$$\begin{array}{l} 4+\frac{5}{2}=+\left(|4|+\left|\frac{5}{2}\right|\right)=+\left(4+\frac{5}{2}\right)=\frac{8}{2}+\frac{5}{2}=\frac{13}{2} \\ -4+\left(-\frac{5}{2}\right)=-\left(|-4|+\left|-\frac{5}{2}\right|\right)=-\left(4+\frac{5}{2}\right)=-\left(\frac{8}{2}+\frac{5}{2}\right)=-\frac{13}{2} \\ -4+\frac{5}{2}=-\left(|-4|-\left|\frac{5}{2}\right|\right)=-\left(4-\frac{5}{2}\right)=-\left(\frac{8}{2}-\frac{5}{2}\right)=-\frac{3}{2} \end{array}$$Вычитание рациональных чисел. Чтобы вычесть одно рациональное число из другого, достаточно
к уменьшаемому прибавить число, противоположное вычитаемому.
Чтобы вычесть одно рациональное число из другого, достаточно
к уменьшаемому прибавить число, противоположное вычитаемому.
Пример
Задание. Вычислить $5-\frac{3}{2} ;-5-\left(-\frac{3}{2}\right) ;(-5)-\frac{3}{2}$
$$5-\frac{3}{2}=5+\left(-\frac{3}{2}\right)=+\left(|5|+-\left|-\frac{3}{2}\right|\right)=+\left(5-\frac{3}{2}\right)=\frac{10}{2}-\frac{3}{2}=\frac{7}{2}$$
$$-5-\left(-\frac{3}{2}\right)=-5+\frac{3}{2}=-\left(|-5|-\left|\frac{3}{2}\right|\right)=-\left(5-\frac{3}{2}\right)=-\left(\frac{10}{2}-\frac{3}{2}\right)=-\frac{7}{2}$$
$$-5-\frac{3}{2}=-5+\left(-\frac{3}{2}\right)=-\left(|-5|+\left|-\frac{3}{2}\right|\right)=-\left(5+\frac{3}{2}\right)=-\left(\frac{10}{2}+\frac{3}{2}\right)=-\frac{13}{2}$$
Умножение рациональных чисел. Чтобы перемножить два рациональных числа, надо перемножить их
абсолютные величины и перед результатом поставить знак плюс, если оба сомножителя имеют одинаковые знаки, или минус,
если сомножители разных знаков.
Пример
Задание. Вычислить $\frac{3}{4} \cdot\left(-\frac{7}{2}\right):\left(-\frac{3}{4}\right) \cdot\left(-\frac{7}{2}\right) ;\left(-\frac{3}{4}\right) \cdot \frac{7}{2}$
$$\frac{3}{4} \cdot\left(-\frac{7}{2}\right)=-\left|\frac{3}{4}\right| \cdot\left|-\frac{7}{2}\right|=-\frac{3}{4} \cdot \frac{7}{2}=-\frac{21}{8}$$ $$\left(-\frac{3}{4}\right) \cdot\left(-\frac{7}{2}\right)=+\left|-\frac{3}{4}\right| \cdot\left|-\frac{7}{2}\right|=\frac{3}{4} \cdot \frac{7}{2}=\frac{21}{8}$$ $$\left(-\frac{3}{4}\right) \cdot \frac{7}{2}=-\left|-\frac{3}{4}\right| \cdot\left|\frac{7}{2}\right|=-\frac{3}{4} \cdot \frac{7}{2}=-\frac{21}{8}$$Деление рациональных чисел. Частное от деления двух рациональных чисел с одинаковыми знаками равно частному их абсолютных величин, взятому со знаком плюс.
Частное от деления двух рациональных чисел с разными знаками равно частному их абсолютных величин, взятому со знаком минус.
Пример
Задание. Читать следующую тему: смешанные числа (дроби). Решения NCERT для математики класса 8 Глава 1 Упражнение по рациональным числам 1.1 Ex 1.1 Class 8 Maths Question 1. Пр. 1.1, класс 8, математика, вопрос 2. Пр. 1.1 Класс 8 по математике, вопрос 3. Пр. 1.1 Математика для класса 8, вопрос 4. Пр. 1.1 Математика, класс 8, вопрос 5. Пр. 1.1 Класс 8 по математике, вопрос 6. Пр. 1.1 Математика класса 8 Вопрос 7. Пр. 1.1 Математика для класса 8, вопрос 8. Пр. 1.1 Математика для класса 8, вопрос 9. Пр. 1.1 Математика для класса 8, вопрос 10. Пр. 1.1 Математика для класса 8, вопрос 11. Как складывать, вычитать, умножать и делить рациональные числа Рациональное число — это число, которое можно записать в виде простой дроби (т. Итак, рациональное число выглядит так: п кв Но q не может быть нулем, так как оно делится на ноль. Если рациональное число представляет собой что-то простое, например, 3 или 0,001 , тогда просто используйте мысленную арифметику или калькулятор! Но как насчет того, чтобы он был в форме p q ? Здесь мы увидим эти операции в более общем стиле алгебры. Вы также можете прочитать Дроби в алгебре. Начнем с умножения, так как это самый простой способ. Чтобы умножить два рациональных числа , умножьте вершины и основания отдельно , например: Вот пример: Чтобы разделить два рациональных числа, сначала переверните второе число (сделайте его обратным), а затем произведите умножение, как указано выше: Вот пример: Мы рассмотрим сложение и вычитание за один раз, поскольку это один и тот же метод. Перед тем, как мы добавим или вычтем, рациональные числа должны иметь то же самое нижнее число (называемое общим знаменателем). Проще всего это сделать на Умножьте обе части каждого числа на нижнюю часть другого Вот так (обратите внимание, что точка · означает умножение): Вот пример сложения: И пример вычитания (средний шаг пропущен для ускорения): Иногда бывает такое рациональное число: 10 15 Но это не так просто! Мы можем разделить верх и низ на 5, чтобы получить: Теперь он в «простейшей форме», как этого хочет большинство людей! У нас может возникнуть соблазн написать неправильную дробь (дробь с «тяжелым верхом», т.е.е. где верхнее число больше нижнего числа) в виде смешанной дроби: Например, 7 / 4 = 1 3 / 4 , здесь показано: Но для математики «неправильная» форма (например, 7 / 4 ) на самом деле лучше . , потому что смешанные дроби (например, 1 3 / 4 ) могут сбивать с толку, когда мы записываем их в формулу, так как это может выглядеть как умножение : Поэтому попробуйте использовать неправильную дробь при выполнении математических расчетов. Представьте каждое из следующих рациональных чисел в виде дробей. Стандарт 8.NS.1 требует от учащихся «преобразовать десятичное представление, которое в конечном итоге повторяется, в рациональное число». Несмотря на такой выбор формулировок, числа в этой задаче являются рациональными числами независимо от выбора представления.Например, $ 0.33 \ overline {3} $ и $ \ frac13 $ — это два разных способа представления одного и того же числа. Так что же такое рациональное число? Иногда люди определяют рациональное число как отношение целых чисел, но для согласованности с CCSSM нам нужно сказать, что рациональное число — это любое число, которое является значением отношения двух целых чисел. Иногда люди определяют рациональное число, исходя из того, как его можно представить; вот типичное определение: Рациональное число — это любое число, которое может быть представлено как $ \ frac {a} {b} $, где $ a $ и $ b $ — целые числа, а $ b \ neq 0 $. Более конструктивное определение рационального числа, которое не зависит от того, как мы его представляем: Итак, $ 0,33 \ overline {3} $ — рациональное число, потому что это результат, который мы получаем, когда делим 1 на 3, или, что эквивалентно, потому что это решение $ 1 = 3x $. Однако числа типа $ \ pi $ и $ \ sqrt {2} $ не являются рациональными, поскольку ни одно из них не удовлетворяет уравнению вида $ a = bx $, где $ a $ и $ b $ — целые числа. Это на самом деле сложно показать, и это упражнение осталось до школы или колледжа. Пример 1 — Решить: Пример 2 — Решить: Нажмите здесь для практических задач Пример 3 — Нажмите здесь для практических задач Пример 4 — Нажмите здесь для практических задач Пример 5 — Нажмите здесь для практических задач Пример 6 — Нажмите здесь для практических задач Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: Список пять
рациональные числа от: (я) —
1 и 0 (ii) — 2 и — 1 (iii) (iv) (я) -1
и 0 (ii) −2
и −1 Пять рациональных чисел — (iii) Пять рациональных чисел — (iv) Пять рациональных чисел — Напишите еще четыре рациональных числа в каждом из следующих шаблонов: (i) (ii) (iii) (iv) (я) Можно заметить, что числитель кратен 3, а знаменатель кратен 5, и по мере их дальнейшего увеличения эти кратные увеличиваются.Следовательно, следующие четыре рациональных числа в этом шаблоне — (ii) Следующие четыре рациональных числа в этом шаблоне — (iii) Следующие четыре рациональных числа в этом шаблоне — (iv) Следующие четыре рациональных числа в этом шаблоне — Решение NCERT для математики класса 7 — рациональные числа 182, вопрос 2 Дайте четыре
рациональные числа, эквивалентные: (i) (ii) (iii) (я) Четыре рациональных числа — (ii) Четыре рациональных числа — (iii) Четыре рациональных числа — Нарисуйте числовую линию и изобразите на ней следующие рациональные числа: (i) (ii) (iii) (iv) (я) Эта дробь представляет собой 3 части из 4 равных частей.Следовательно, каждое пробел между двумя целыми числами на числовой строке необходимо разделить на 4 равные части. можно представить как (ii) Эта дробь представляет 5 частей из 8 равных частей. Отрицательный знак означает, что он находится на отрицательной стороне числовой прямой. Следовательно, каждое пробел между двумя целыми числами на числовой строке необходимо разделить на 8 равных частей. можно представить как (iii) Эта дробь представляет собой 1 целую часть и 3 части из 4 равных частей.Отрицательный знак означает, что он находится на отрицательной стороне числовой прямой. Следовательно, каждое пробел между двумя целыми числами на числовой строке необходимо разделить на 4 равные части. можно представить как (iv) Эта дробь представляет собой 7 частей из 8 равных частей. Следовательно, каждое пробел между двумя целыми числами на числовой строке необходимо разделить на 8 равных частей. можно представить как Решение NCERT для математики класса 7 — рациональные числа 183, вопрос 4 Точки P, Q, R, S, T, U, A и B на числовой прямой таковы, что TR = RS = SU и AP = PQ = QB. Назовите рациональные числа, представленные буквами P, Q, R и S. Расстояние между U и T = 1 шт. Он разделен на 3 равные части. TR = RS = SU = R = S = Аналогично AB = 1 шт. Он разделен на 3 равные части. P = Q = Решение NCERT для математики класса 7 — рациональные числа 183, вопрос 5 (я) В виде,
следовательно, он не представляет одинаковые рациональные числа. (ii) Следовательно, он представляет собой те же рациональные числа. (iii) Следовательно, он представляет собой те же рациональные числа. (iv) Следовательно, он представляет собой те же рациональные числа. (в) Следовательно, он представляет собой те же рациональные числа. (vi) В виде,
следовательно, он не представляет одинаковые рациональные числа. (vii) Переписать
следующие рациональные числа в простейшем виде: (i) (ii) (iii) (iv) (я) (ii) (iii) (iv) (я) Поскольку -15 <14, Следовательно, (ii) Поскольку -28 <-25 Следовательно, (iii) Здесь, Следовательно, (iv) Поскольку −32> −35, Следовательно, (в) Поскольку -4 <-3, Следовательно, (vi) (vii) (я) Преобразуя их в одинаковые дроби, Поскольку 15> 4, следовательно,
является
больше. (ii) (iii) Преобразуя их в одинаковые дроби, (iv) (в) Преобразуя их в одинаковые дроби, Запишите следующие рациональные числа в порядке возрастания: (i) (ii) (iii) (я) As −3 <−2 <−1, (ii) Преобразуя их в одинаковые дроби, As −12 <−3 <−2, (iii) Преобразуя их в одинаковые дроби, Как -42 <-21 <-12, Решение NCERT для математики класса 7 — рациональные числа 184, вопрос 10 (i) 45 + -11 4 = 45-11 4 = 16-55 20 = -39 20 (ii) L.C.M 3 и 5 равно 15. (iii) L.C.M 10 и 15 равно 30. (iv) Л.C.M 11 и 9 — это 99. (в) L.C.M 19 и 57 равно 57. (vi) (vii) = L.C.M 3 и 5 равно 15. Решение NCERT для математики класса 7 — рациональные числа 190, вопрос 1 (я) Л.C.M 24 и 36 равно 72. (ii) L.C.M из 63 и 7 — это 63. (iii) L.C.M 13 и 15 — это 195. (iv) L.C.M 8 и 11 равно 88. (в) L.C.M 9 и 1 равно 9. (я) (ii) (iii) (iv) (в) (vi) (я) (ii) (iii) (iv) (в) (vi) (vii) Решение NCERT для математики класса 7 — рациональные числа 190, вопрос 4 Просмотреть решения NCERT для всех глав класса 7 Используя соответствующие свойства найти: (я) (ii) (я) (ii) (По коммутативности) (я) Аддитивная инверсия = (ii) Аддитивная инверсия = (iii) Аддитивная инверсия = (iv) Противоположное число (в) Противоположное число Проверить
что — (- x ) = x для. (i) (ii) (я) −13 Мультипликативный обратный знак = — (ii) Мультипликативный обратный = (iii) Мультипликативный обратный знак = 5 (iv) Мультипликативный обратный (в) Мультипликативный обратный (vi) -1 Мультипликативный обратный знак = −1 Назовите
свойство умножения используется в каждом из следующих случаев: (я) (ii) (iii) (я) 1 — мультипликативное тождество. (ii) Коммутативность (iii) Мультипликативный
обратный Умножить
от
обратная величина. Скажите, что
свойство позволяет вычислить. Является ли мультипликатив обратной величиной? Почему или почему нет? Если это обратное умножение, то произведение должно быть 1. Однако здесь продукт не 1, а Решение NCERT для математики класса 8 — рациональные числа 14, вопрос 8 Is
0,3 мультипликативная обратная величина?
Почему или почему нет? 0,3 × = 0,3 × Здесь
продукт 1.Следовательно, 0,3 является мультипликативной обратной величиной. Запись: (i)
рациональное число, не имеющее обратного. (ii)
рациональные числа, равные своим обратным величинам. (iii)
рациональное число, равное своему отрицательному. (i) 0 — это
рациональное число, но его обратная величина не определена. (ii) 1 и
−1 — рациональные числа, равные их
взаимные. (iii) 0 — это
рациональное число, равное его отрицательному. Заполнить
заготовки. (i) ноль
имеет __________ взаимно. (ii)
числа __________ и __________ являются собственными обратными (iii)
обратная величина — 5 __________. (iv) Взаимный
из,
где
является
__________. (v)
произведение двух рациональных чисел всегда __________. (vi)
обратное положительное рациональное число __________. (и) № (ii) 1,
−1 (iii) (iv) x (v) Рациональный
номер (vi) Положительно
рациональное число Изобразите эти числа в числовой строке. (i) (ii) (i) можно представить в числовой строке следующим образом. (ii) можно представить на числовой прямой следующим образом. Решение NCERT для математики класса 8 — рациональные числа 20, вопрос 1 Обозначьте на числовой строке. можно представить в числовой строке следующим образом. Решение NCERT для математики класса 8 — рациональные числа 20, вопрос 2 Напишите пять рациональных чисел, меньших 2. 2 можно представить как. Следовательно, пять рациональных чисел меньше 2 равны Решение NCERT для математики класса 8 — рациональные числа 20, вопрос 3 Найти
десять рациональных чисел между
а также. Найди пять
рациональные числа от (я) (ii) (iii) Написать
пять рациональных чисел больше — 2. -2
можно представить как -. Следовательно,
пять рациональных чисел больше −2 равны Найдите десять рациональных чисел между и. Просмотреть решения NCERT для всех глав класса 8 {4}=\frac{16}{81}$$
{4}=\frac{16}{81}$$ Решения NCERT для математики класса 8 Глава 1 Рациональные числа
Решения NCERT для математики класса 8 Глава 1 Рациональные числа
Используя соответствующие свойства найдите:
Solution:
Запишите аддитивное обратное для каждого из следующих значений:
(i) \ (\ frac {2} {8} \)
(ii) \ (\ frac {-5} {9 } \)
(iii) \ (\ frac {-6} {-5} \)
(iv) \ (\ frac {2} {-9} \)
(v) \ (\ frac {19} { -6} \)
Решение:
Убедитесь, что — (- x) = x для
(i) x = \ (\ frac {11} {5} \)
(ii) x = \ (\ frac {-13} {17} \)
Раствор: 
Найдите обратное умножение следующего:
Решение:
Назовите свойство при умножении, используемое в каждом из следующих пунктов:
Решение:
(i) Коммутативное свойство умножения
(ii) Коммутативное свойство умножения
(iii) Мультипликативное обратное свойство
Умножьте \ (\ frac {6} {13} \) на величину, обратную \ (\ frac {-7} {16} \).
Решение:
Скажите, какое свойство позволяет вам вычислить
Решение:
Поскольку a × (b × c) = (a × b) × c показывает ассоциативное свойство умножения.
Является ли \ (\ frac {8} {9} \) мультипликативным обратным значением -1 \ (\ frac {1} {8} \)? Почему или почему нет?
Решение:
Здесь -1 \ (\ frac {1} {8} \) = \ (\ frac {-9} {8} \).
Поскольку мультипликативная обратная величина к \ (\ frac {8} {9} \) равна \ (\ frac {9} {8} \), но не \ (\ frac {-9} {8} \)
\ (\ frac {8} {9} \) не является мультипликативным обратным к -1 \ (\ frac {1} {8} \)
Если 0,3 — мультипликативная обратная величина 3 \ (\ frac {1} {3} \)? Почему или почему нет?
Решение:
Мультипликативная обратная величина 0,3 или \ (\ frac {3} {10} \) равна \ (\ frac {10} {3} \).
Таким образом, 0,3 является мультипликативным обратным 3 \ (\ frac {1} {3} \).
Напишите:
(i) Рациональное число, не имеющее обратной величины.
(ii) Рациональные числа, равные своим обратным величинам.
(iii) Рациональное число, равное отрицательному.
Решение:
(i) 0 — рациональное число, не имеющее обратной величины.
[∵ \ (\ frac {1} {0} \) не определено]
(ii) Взаимно с 1 = \ (\ frac { 1} {1} \) = 1
Взаимно с -1 = \ (\ frac {1} {-1} \) = -1
Таким образом, 1 и -1 — требуемые рациональные числа.
(iii) 0 — рациональное число, равное своему отрицательному.
Заполните пропуски.
(i) Ноль имеет ……… .. обратный.
(ii) Числа ……… .. и ……… .. являются обратными.
(iii) Обратное значение -5 равно ………
(iv) Обратно \ (\ frac {1} {x} \), где x ≠ 0 равно ……….
(v) Произведение двух рациональных чисел всегда …………
(vi) Обратная величина положительного рационального числа равна ……….
Решение:
(i) нет
(ii) -1 и 1
(iii) \ (\ frac {-1} {5} \)
(iv) x
(v) рациональное число
(vi) положительное Дополнительные учебные материалы по классу 8 CBSE
Использование рациональных чисел
 е. как отношение ).
е. как отношение ). Примеры:
Номер В виде фракции 5 1/5 1,75 7/4 .001 1/1000 0,111 … 1/9 В целом …
Как сложить, вычесть, умножить и разделить

Умножение
Отдел
Сложение и вычитание
Самая простая форма

÷ 5 10 15 = 2 3 ÷ 5 Будьте осторожны с «смешанными дробями»
Смешанная фракция: Что такое: 1 + 2 1 4 ? Это: 1 + 2 + 1 4 = 3 1 4 ? Или это: 1 + 2 × 1 4 = 1 1 2 ? Неправильная фракция: Что такое: 1 + 9 4 ? Это: 4 4 + 9 4 = 13 4 
Иллюстративная математика
Задача
Комментарий IM
 Интересно сравнить это с определением рационального числа, данным в Глоссарии CCSSM (а также с более тонким значением, разработанным в самих стандартах, начиная с 3 класса и выше).
Интересно сравнить это с определением рационального числа, данным в Глоссарии CCSSM (а также с более тонким значением, разработанным в самих стандартах, начиная с 3 класса и выше). Число является рациональным, если оно является частным $ a \ div b $ двух целых чисел $ a $ и $ b $, где $ b \ neq 0 $.
или, что то же самое, Рациональное число — это число, удовлетворяющее уравнению вида $ a = bx $, где $ a $ и $ b $ — целые числа, а $ b \ neq 0 $.

Решение рациональных уравнений
Решение рациональных уравнений
Вот шаги, необходимые для решения рациональных уравнений: Шаг 1 : Удалите все дроби.При решении рациональных уравнений у вас есть выбор из двух способов исключить дроби. Опция 1; умножьте всю проблему на наименьший общий знаменатель или ЖКД. Вариант 2; вы можете крестить умножение. Вариант 1 подойдет для любой задачи, но вы можете выполнить перекрестное умножение только в том случае, если у вас одна дробь равна одной дроби, то есть если дроби пропорциональны. Щелкните ссылку, чтобы просмотреть шаги по поиску ЖК-дисплея. Обратите внимание, что при решении рациональных уравнений все дроби должны исчезнуть после первого шага. Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. 
Шаг 3 : Решите упрощенное уравнение. Если упрощенное уравнение имеет более высокие степени, например x 2 или x 3 , вы можете решить уравнение, приравняв его к нулю и разложив на множители. Если упрощенная задача не содержит более высоких степеней, тогда решите для x, получив x с одной стороны и числа с другой. Шаг 4 : Проверьте каждое решение. Подставьте каждое решение в знаменатель исходного вопроса и отклоните любые решения, которые приводят к тому, что знаменатель становится равным нулю, потому что это делает проблему неопределенной. Этот шаг не гарантирует правильного ответа; это только гарантирует, что ответ приемлем. Шаг 1 : Удалите все дроби. 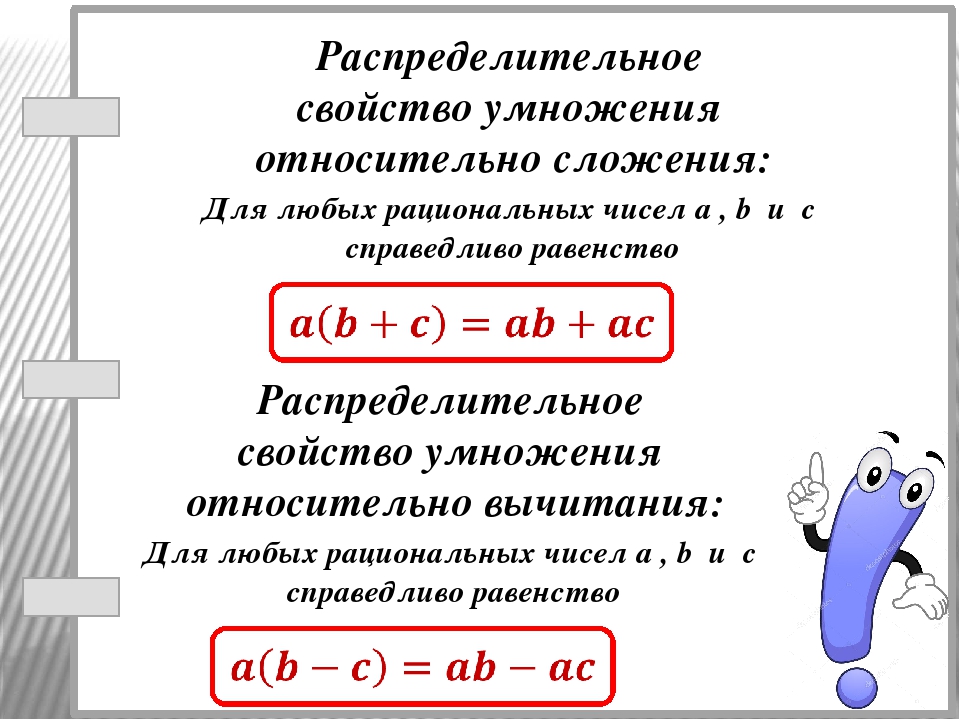 В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби.
В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби. Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне. Шаг 4 : Проверьте каждое решение.В этом случае единственное число, которое сделало бы проблему неопределенной, — 0. Поскольку наш ответ не равен 0, ответ принимается. Шаг 1 : Удалите все дроби. В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби. 
Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне. Шаг 4 : Проверьте каждое решение. В этом случае единственными числами, которые могут сделать проблему неопределенной, являются 3 или –3. Поскольку наш ответ не равен 3 или –3, ответ принят. Шаг 1 : Удалите все дроби.В этом случае мы можем либо умножить на ЖК-дисплей, либо крест-накрест, чтобы исключить дроби. 
Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне, потому что члены x 2 будут сокращаться. Шаг 4 : Проверьте каждое решение. В этом случае единственные числа, которые делают проблему неопределенной, — это 2 или 5. Поскольку наш ответ — не 2 или 5, ответ принимается. Шаг 1 : Удалите все дроби. В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби. 
Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне. Шаг 4 : Проверьте каждое решение. В этом случае единственные числа, которые делают проблему неопределенной, — это 1 или 4.Поскольку наш ответ равен 4, ответ не принимается, что означает: Шаг 1 : Удалите все дроби. В этом случае мы можем либо умножить на ЖК-дисплей, либо крест-накрест, чтобы исключить дроби. Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить уравнение, равное нулю, и решить его путем факторизации. Шаг 4 : Проверьте каждое решение. В этом случае единственные числа, которые делают проблему неопределенной, — это 0 или –12/5. Поскольку наши ответы не равны 0 или –12/5, ответы принимаются. Шаг 1 : Удалите все дроби.В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби. Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины. Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить уравнение, равное нулю, и решить его путем факторизации. Шаг 4 : Проверьте каждое решение.В этом случае единственными числами, которые могут сделать проблему неопределенной, являются 1, –1 или –2. Поскольку наши ответы не равны 1, –1 или –2, ответы принимаются. Как найти решение Набор
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105 NCERT для математики класса 7 Глава 9
Страница № 182:
Вопрос 1:
Ответ:
Страница № 182:
Вопрос 2:
Ответ:
Видео Решение для рациональных чисел (Страница: 182, В.№: 2)
Страница № 183:
Вопрос 3:
Ответ:
Страница № 183:
Вопрос 4:
Ответ:
Видео решение для рациональных чисел (Страница: 183, В.№: 4)
Страница № 183:
Вопрос 5:
Ответ:
Видео решение для рациональных чисел (Страница: 183, Вопрос №: 5)
Страница № 183:
Ответ:
Страница № 183:
Вопрос 7:
Ответ:
Страница № 183:
Ответ:
Страница № 184:
Ответ:
Страница № 184:
Вопрос 10:
Ответ:
Видео Решение для рациональных чисел (Страница: 184, В.№: 10)
Страница № 190:
Ответ:
Видео решение для рациональных чисел (Страница: 190, Вопрос №: 1)
Страница № 190:
Ответ:
Страница № 190:
Ответ:
Страница № 190:
Ответ:
Видео Решение для рациональных чисел (Страница: 190, В.№: 4)
NCERT для математики класса 8 Глава 1
Страница № 14:
Вопрос 1:
Ответ:
Страница № 14:
Ответ:
Страница № 14:
Вопрос 3:
Страница № 14:
Ответ:
Страница № 14:
Вопрос 5:
Ответ:
Страница № 14:
Вопрос 6:
Ответ:
Страница № 14:
Вопрос 7:
Страница № 14:
Вопрос 8:
Ответ:
Видео Решение для рациональных чисел (Стр .: 14, В.№: 8)
Страница № 14:
Вопрос 9:
Ответ:
Страница № 15:
Вопрос 10:
Ответ:
Страница № 15:
Вопрос 11:
Ответ:
Страница № 20:
Вопрос 1:
Ответ:
Видео решение для рациональных чисел (Страница: 20, Вопрос №: 1)
Страница № 20:
Вопрос 2:
Ответ:
Видео решение для рациональных чисел (Страница: 20, Вопрос №: 2)
Страница № 20:
Вопрос 3:
Ответ:
Видео решение для рациональных чисел (Страница: 20, Вопрос №: 3)
Страница № 20:
Вопрос 4:
Страница № 20:
Вопрос 5:
Страница № 20:
Вопрос 6:
Ответ:
Страница № 20:
Вопрос 7:

