НОУ ИНТУИТ | Лекция | Решение систем линейных уравнений
Аннотация: В лекции рассматривается задача решения систем линейных уравнений. Приводятся необходимые определения и постановка задачи. Описывается последовательный и параллельный варианты одного из прямых методов решения линейных систем общего вида – метода Гаусса. Далее дается описание последовательного и параллельного алгоритмов, реализующих итерационный метод сопряженных градиентов
Ключевые слова: система линейных уравнений, Трансцендентное уравнение, линейное уравнение, решение системы линейных уравнений, алгоритм Гаусса, балансировка вычислений, операции передачи данных, топология сети передачи данных, MPI, вычислительный эксперимент, EM64T, computer cluster, итерационные методы решения систем линейных уравнений, итерационный алгоритм, метод сопряженных градиентов, горизонтальное разделение, программная реализация
Системы линейных уравнений возникают при решении ряда
прикладных задач, описываемых дифференциальными, интегральными
или системами нелинейных (трансцендентных) уравнений.
Матрицы коэффициентов систем линейных уравнений могут иметь различные структуру и свойства. Матрицы решаемых систем могут быть плотными, и их порядок может достигать несколько тысяч строк и столбцов. При решении многих задач могут появляться системы, обладающие симметричными положительно определенными ленточными матрицами с порядком в десятки тысяч и шириной ленты в несколько тысяч элементов. И, наконец, при рассмотрении большого ряда задач могут возникать системы линейных уравнений с разреженными матрицами с порядком в миллионы строк и столбцов.
8.1. Постановка задачи
Линейное уравнение с n неизвестными x0, x1, ѕ, xn-1 может быть определено при помощи выражения (
8.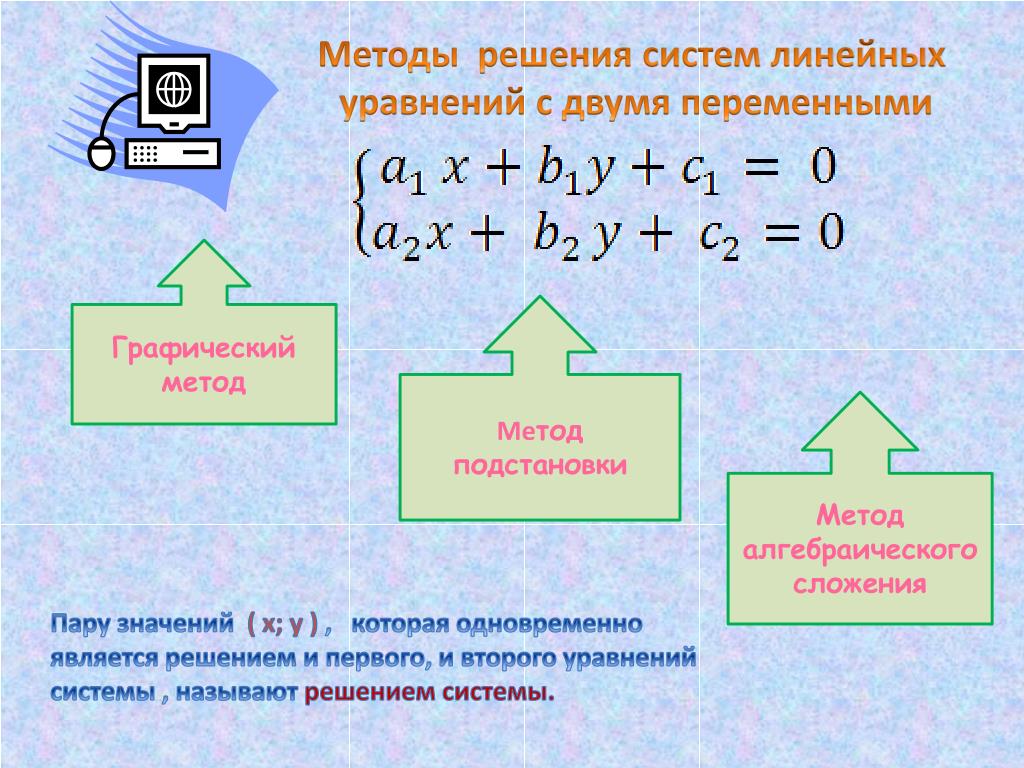 1) 1) |
где величины a0,a1,…,an-1 и b представляют собой постоянные значения.
Множество из n линейных уравнений
| ( 8.2) |
называется системой линейных уравнений или
Ax = b,
где A=(ai,j) есть вещественная матрица размера nxn, а векторы b и x состоят из n элементов.
Под задачей решения системы линейных уравнений для заданных
матрицы А и вектора b обычно понимается нахождение значения
вектора неизвестных x, при котором выполняются все уравнения
системы.
8.2. Алгоритм Гаусса
Метод Гаусса – широко известный прямой алгоритм решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными. Если система линейных уравнений невырожденна, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы (8.2)) к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.
В подразделе дается общая характеристика метода Гаусса,
достаточная для начального понимания алгоритма и позволяющая
рассмотреть возможные способы параллельных вычислений при решении
систем линейных уравнений. Более полное изложение алгоритма со
строгим обсуждением вопросов точности получаемых решений может
быть получено, например, в работах [
[
6
]
,
[
22
]
,
[
47
]
] и др.
8.2.1. Последовательный алгоритм
Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных ). К числу таких преобразований относятся:
- умножение любого из уравнений на ненулевую константу;
- перестановка уравнений;
- прибавление к уравнению любого другого уравнения системы.
Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду
где матрица коэффициентов получаемой системы имеет вид
intuit.ru/2010/edi»>На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1, после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д.8.2.1.1. Прямой ход алгоритма Гаусса
Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0<=i<n-1, метода производится исключение неизвестной i для всех уравнений с номерами k, большими i (т.е. i<k<=n-1 ). Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу ( aki/aii ), с тем чтобы результирующий коэффициент при неизвестной xi в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:
(следует отметить, что аналогичные вычисления выполняются и над
вектором b ).
Поясним выполнение прямого хода метода Гаусса на примере системы линейных уравнений вида:
На первой итерации производится исключение неизвестной x0 из второй и третьей строки. Для этого из этих строк нужно вычесть первую строку, умноженную соответственно на 2 и 1. После этих преобразований система уравнений принимает вид:
В результате остается выполнить последнюю итерацию и исключить неизвестную x1 из третьего уравнения. Для этого необходимо вычесть вторую строку, и в окончательной форме система имеет следующий вид:
На рис. 8.1 представлена общая схема состояния данных на i -й
итерации прямого хода алгоритма Гаусса. Все коэффициенты при
неизвестных, расположенные ниже главной диагонали и левее столбца i, уже являются нулевыми. На i -й итерации прямого хода метода
Гаусса осуществляется обнуление коэффициентов столбца i,
расположенных ниже главной диагонали, путем вычитания строки i,
умноженной на нужную ненулевую константу. После проведения (n-1)
подобной итерации матрица, определяющая систему линейных
уравнений, становится приведенной к верхнему треугольному
виду.
После проведения (n-1)
подобной итерации матрица, определяющая систему линейных
уравнений, становится приведенной к верхнему треугольному
виду.
Рис. 8.1. Итерация прямого хода алгоритма Гаусса
При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование
Возможный способ избежать подобной проблемы может состоять в
следующем: при выполнении каждой очередной итерации прямого хода
метода Гаусса следует определить коэффициент с максимальным
значением по абсолютной величине в столбце, соответствующем
исключаемой неизвестной, т. е.
е.
и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).
Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O(n3).
8.2.1.2. Обратный ход алгоритма Гаусса
После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1, после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д. В общем виде выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:
Поясним, как и ранее, выполнение обратного хода метода Гаусса
на примере рассмотренной в п.
Из последнего уравнения системы можно определить, что неизвестная x2 имеет значение 3. В результате становится возможным разрешение второго уравнения и определение значение неизвестной x1=13, т.е.
На последней итерации обратного хода метода Гаусса определяется значение неизвестной x0, равное -44.
С учетом последующего параллельного выполнения можно отметить, что вычисление получаемых значений неизвестных может выполняться сразу во всех уравнениях системы (и эти действия могут выполняться в уравнениях одновременно и независимо друг от друга). Так, в рассматриваемом примере после определения значения неизвестной x2 система уравнений может быть приведена к виду
Вычислительная сложность обратного хода алгоритма Гаусса
составляет O(n2).
Решение системы линейных уравнений
При помощи рассмотренного ранее инструмента Поиск решения можно также легко решать системы линейных равнений.
Системой n линейных уравнений с m неизвестными называется система вида:
где: aij и bi (i = 1, … , m; b = 1, … , n) – некоторые известные числа, x1, … , xn – неизвестные.
В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй индекс j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных часто записывают в виде матрицы, которая называется матрицей системы:
Числа, стоящие в правых частях уравнений, b1, … , bm называются свободными членами.
Совокупность n чисел c1, … , cn называется решением данной системы уравнений, если каждое уравнение обращается в равенство после подстановки в него чисел c1, … , cn вместо соответствующих неизвестных x1, … , xn.
Наша задача найти решение системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений.
- И третий случай, когда система вообще не имеет решения.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Существуют различные способы нахождения решений системы:
- Матричный метод решения систем линейных уравнений.

- Метод Крамера.
- Метод Гаусса.
Создадим новый метод решения системы линейных уравнений, используя инструмент Поиск решения.
В качестве примера рассмотрим систему 3-х линейных уравнений с 3-мя неизвестными:
Коэффициенты при неизвестных и свободные члены запишем в виде таблицы:
В ячейках A7:C7 находятся будущие корни системы уравнений. Сначала присвоим им нулевые значения:
В ячейку D2 запишем формулу для вычисления свободного члена первого уравнения =СУММПРОИЗВ($A$7:$C$7;A2:C2). Эта функция перемножает соответствующие элементы заданных массивов одинаковой размерности и возвращает сумму произведений. Затем сделаем автозаполнение формулы для двух других ячеек в столбце D:
Вот так выглядят наши таблички в режиме значений:
Наша задача добиться попарного совпадения значений в соседних ячейках столбцов D и E, изменяя значения в ячейках A7:C7. Для этого будем использовать Поиск решения (на вкладке Данные → в группе Анализ → кнопка Поиск решения):
Для этого будем использовать Поиск решения (на вкладке Данные → в группе Анализ → кнопка Поиск решения):
В диалоговом окне
Поиск решения устанавливаем следующие параметры:- Установить целевую ячейку: тут должно быть пусто (стираем все значения, если они там были).
- Равной: значению: 0.
- Изменяя ячейки: $A$7:$C$7 (подбираем корни системы уравнений).
- Ограничения: $D$2:$D$4=$E$2:$E$4.
Нажимаем кнопку Выполнить:
Оставляем пункт Сохранить найденное решение → кнопка OK.
Теперь в ячейках A7, B7 и С7 будут записаны точные значения корней системы уравнений:
В противном случае в окне Результаты поиска решения получим сообщение Поиск не может найти подходящего решения:
« Назад
Вперед »
Системы линейных уравнений с бесконечными решениями (3 способа сказать) – JDM Educational
При работе с системами линейных уравнений мы часто видим единственное решение или вообще не видим решения. Однако также возможно, что линейная система будет иметь бесконечно много решений.
Однако также возможно, что линейная система будет иметь бесконечно много решений.
Итак, когда система линейных уравнений имеет бесконечные решения? Система двух линейных уравнений с двумя переменными имеет бесконечные решения, если две линии совпадают. С алгебраической точки зрения мы получаем уравнение, которое всегда верно, если мы решаем систему. Визуально линии имеют одинаковый наклон и одинаковую точку пересечения по оси Y (они пересекаются в каждой точке линии).
Конечно, система из трех уравнений с тремя переменными имеет бесконечные решения, если плоскости пересекаются по прямой (или по всей плоскости, если все 3 уравнения эквивалентны).
В этой статье мы поговорим о том, как можно сказать, что система линейных уравнений имеет бесконечные решения. Мы также рассмотрим некоторые примеры линейных систем с бесконечными решениями с двумя и тремя переменными.
Начнем.
Системы линейных уравнений с бесконечными решениями
Система линейных уравнений может иметь бесконечные решения, если уравнения эквивалентны. Это означает, что одно из уравнений кратно другому.
Это означает, что одно из уравнений кратно другому.
Это также означает, что каждая точка на прямой удовлетворяет всем уравнениям одновременно.
На изображении ниже показаны 3 возможных случая решения системы из 2 линейных уравнений с 2 переменными.
Решите систему уравнений 2 на 2 с помощью…
Включите JavaScript
Решите систему уравнений 2 на 2 методом исключения
Система из 2 линейных уравнений с 2 переменными имеет бесконечно много решений, если две линии имеют одинаковый наклон и одинаковую точку пересечения по оси Y (то есть эти два уравнения эквивалентны и представляют собой одной и той же прямой, поэтому они пересекаются в каждой точке этой прямой).Система уравнений с 2, 3 и более переменными может иметь бесконечное число решений. Начнем с линейных уравнений с двумя переменными и бесконечным решением.
Когда линейная система имеет бесконечные решения? (Система линейных уравнений с 2 переменными)
Есть несколько способов узнать, когда линейная система с двумя переменными имеет бесконечное число решений:
- Решите систему — если вы решите систему и получите уравнение, которое всегда истинно, независимо от значения переменной (например, 1 = 1), то существуют бесконечные решения.

- Посмотрите на график – если две линии одинаковы (они перекрываются или пересекаются везде на линии), то существует бесконечное число решений системы.
- Посмотрите на наклон и точку пересечения с ординатой — решить оба уравнения для y, чтобы получить форму пересечения наклона, y = mx + b. Если два уравнения имеют одинаковый наклон и одинаковую точку пересечения по оси Y, то линии эквивалентны и существует бесконечное число решений (вы можете узнать, как определить, что две линии параллельны, в моей статье здесь).
Рассмотрим несколько примеров для каждого случая, начиная с решения системы.
Решение линейной системы с бесконечными решениями
Когда мы попытаемся решить линейную систему с бесконечными решениями, в результате мы получим уравнение, которое всегда верно. Например, после того, как мы упростим и объединим подобные термины, мы получим что-то вроде 1 = 1 или 5 = 5.
Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.
Пример 1. Использование исключения для демонстрации того, что линейная система имеет бесконечные решения
Допустим, мы хотим решить следующую систему линейных уравнений:
Мы будем использовать исключение для решения. Попробуем исключить переменную «x».
Начнем с умножения первого уравнения на 3, чтобы получить:
- 3(2x + 4y) = 3(3) [умножить первое уравнение на 3 с обеих сторон]
- 6x + 12y = 9 [распределить 3 через круглые скобки]
Теперь добавляем это изменение Уравнение ко второму:
6x + 12y = 9
+
-6x -12y = -9
___________
0x + y = 0
. , что всегда верно — независимо от того, какие значения x или y мы выбираем. Это означает, что оба уравнения представляют одну и ту же прямую.
Это также означает, что каждая точка на этой прямой является решением этой линейной системы. Итак, система имеет бесконечные решения.
Итак, система имеет бесконечные решения.
На приведенном ниже графике показана линия, полученная из обоих уравнений этой системы.
Два уравнения 2x + 4y = 3 и -6x — 12y = -9 имеют одинаковый наклон и одинаковую точку пересечения по оси y, поэтому они представляют собой одну и ту же прямую и пересекаются во всех точках на прямой, а это означает, что существует бесконечное число решений уравнения линейная система.Пример 2. Использование подстановки для демонстрации того, что линейная система имеет бесконечные решения
Допустим, мы хотим решить следующую систему линейных уравнений:
- y = 2x + 5
- 10x – 5y = -25
Для решения воспользуемся подстановкой. Подставим y из первого уравнения в y во втором уравнении:
- 10x – 5y = -25 [начнем со второго уравнения]
- 10x – 5(2x + 5) = -25 [подставьте y = 2x + 5 из первого уравнения]
- 10x – 10x – 25 = -25 [распределить 5 через круглые скобки]
- 0x = 0 [объединить одинаковые члены на противоположных сторонах]
Отсюда следует, что 0 = 0, что всегда верно – независимо от значений х или у мы выбираем. Это означает, что оба уравнения представляют одну и ту же прямую.
Это означает, что оба уравнения представляют одну и ту же прямую.
Это также означает, что каждая точка на этой прямой является решением этой линейной системы. Итак, система имеет бесконечные решения.
На приведенном ниже графике показана линия, полученная из обоих уравнений этой системы.
Два уравнения y = 2x + 5 и 10x – 5y = -25 имеют одинаковый наклон и одинаковую точку пересечения по оси y, поэтому они представляют собой одну и ту же прямую и пересекаются во всех точках на прямой, а это означает, что существует бесконечное число решений уравнения линейная система.Глядя на график линейной системы с бесконечными решениями
Когда мы рисуем линейную систему с бесконечными решениями, мы получаем две перекрывающиеся линии. То есть они пересекаются в каждой точке прямой, так как два уравнения эквивалентны и дают нам одну и ту же прямую.
Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.
Пример 1. График двух эквивалентных уравнений из линейной системы с бесконечными решениями
Построим график следующей системы линейных уравнений:
- y = 2x + 4
Линии имеют одинаковый наклон (m = 2) и одинаковую точку пересечения по оси y (b = 4), как вы можете видеть на графике ниже:
Два уравнения y = 2x + 4 и -2y = -4x – 8 имеют одинаковый наклон и одинаковую точку пересечения по оси Y, поэтому они представляют собой одну и ту же прямую и пересекаются во всех точках на прямой, а это означает, что линейная система имеет бесконечные решения.
Поскольку наклоны одинаковы и точки пересечения с осью y одинаковы, уравнения представляют одну и ту же прямую. Значит, они пересекаются в каждой точке прямой.
Это означает, что существует бесконечное число решений линейной системы, с которой мы начали.
Пример 2. График двух эквивалентных уравнений из линейной системы с бесконечными решениями
Построим график следующей системы линейных уравнений:0038
Линии горизонтальны, поэтому они обе имеют одинаковый наклон (m = 0). Они также имеют одинаковую точку пересечения по оси y (b = 4), как вы можете видеть на графике ниже:
Два уравнения y = 4 и 3y = 12 имеют одинаковый наклон и одинаковую точку пересечения по оси y, поэтому они одинаковы. прямой, и они пересекаются во всех точках прямой, что означает, что линейная система имеет бесконечные решения. Поскольку наклоны одинаковы и точки пересечения с осью y одинаковы, уравнения представляют одну и ту же прямую. Значит, они пересекаются в каждой точке прямой.
Это означает, что существует бесконечное количество решений линейной системы, с которой мы начали.
Глядя на наклон и пересечение Y линейной системы с бесконечными решениями
Когда мы решаем линейное уравнение относительно y, мы получаем форму наклона и пересечения. Если мы сделаем это для обоих уравнений в линейной системе, мы сможем сравнить наклон и точку пересечения по оси y.
Если два наклона одинаковы и точки пересечения с осью Y одинаковы, то две прямые эквивалентны, т. е. пересекаются во всех точках на прямой, и линейная система имеет бесконечные решения.
Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.
Пример 1. Сравнение наклона и точки пересечения Y для демонстрации существования бесконечных решений системы двух линейных уравнений
Допустим, у нас есть следующая система линейных уравнений: 7y = -14x + 28
Мы найдем y в обоих уравнениях, чтобы получить форму пересечения наклона, y = mx + b.
Решая первое уравнение относительно у, получаем:
- 4x = -2y + 8
- 4x + 2y = 8 [Добавить 2y к обеим сторонам]
- 2y = -4x + 8 [Снижение 4x с обеих сторон]
- y = — 2x + 4 [разделить на 2 с обеих сторон]
Решив второе уравнение относительно y, получим:
- 7y = -14x + 28
- y = -2×0 на 6 900de с обеих сторон]
Итак, два уравнения в форме пересечения наклона:
- y = -2x + 4
- y = -2x + 4
Поскольку эти два уравнения имеют одинаковый наклон (m = -2) и одинаковую точку пересечения с координатой y (b = 4), мы знаем, что они представляют одну и ту же линию.
Поскольку прямые пересекаются во всех точках прямой, система имеет бесконечное число решений.
Два уравнения 4x = -2y + 8 и 7y = -14x + 28 имеют одинаковый наклон и одинаковую точку пересечения по оси y, поэтому они представляют собой одну и ту же прямую и пересекаются во всех точках на прямой, а это означает, что существует бесконечное число решений уравнения линейная система.
Пример 2. Сравнение наклона и точки пересечения Y для демонстрации существования бесконечности решений системы двух линейных уравнений
Допустим, у нас есть следующая система линейных уравнений: – 20x + 10 = 22
Мы найдем y в обоих уравнениях, чтобы получить форму пересечения наклона, y = mx + b.
Решив первое уравнение относительно y, получим:
- 30x = 6y – 18
- 30x + 18 = 6y [прибавьте по 18 к обеим частям]
- 5x + 3 = y [делите на 6 с обеих сторон]
Решив второе уравнение относительно y, получим:
Таким образом, два уравнения в форме пересечения наклона имеют вид: ) и один и тот же y-отрезок (b = 4), мы знаем, что они представляют одну и ту же прямую.
Поскольку прямые пересекаются во всех точках прямой, система имеет бесконечное число решений.
Два уравнения 30x = 6y – 18 и 4y – 20x +10 = 22 имеют одинаковый наклон и одинаковую точку пересечения по оси y, поэтому они представляют собой одну и ту же прямую и пересекаются во всех точках на прямой, а это означает, что существует бесконечное число решений уравнения линейная система.Как создать систему линейных уравнений с бесконечными решениями
Чтобы создать систему линейных уравнений с бесконечными решениями, мы можем использовать следующий метод:
- Сначала напишите линейное уравнение вида ax + by = c . Затем выберите ненулевое число d. Затем умножьте обе части уравнения на d, чтобы получить adx + bdy = cd. Это второе уравнение эквивалентно первому, и у нас есть наша система.
Пример. Создание системы линейных уравнений с бесконечными решениями
Сначала мы выбираем любые значения для a, b и c, какие пожелаем. Это дает нам наше первое уравнение:
Это дает нам наше первое уравнение:
- 2x + 5y = 9 [мы выбрали a = 2, b = 5, c = 9]
Затем мы выбираем ненулевое значение d: d = 4,
Теперь умножим обе части первого уравнения на d = 4:
- 2x + 5y = 9 [первое уравнение]
- 4(2x + 5y) = 4(9) [умножьте обе части на d = 4]
- 8x + 20y = 36 [распределите 4 через скобки]
Теперь у нас есть второе уравнение.
Наша система двух уравнений:
- 2x + 5y = 9
- 8x + 20y = 36
Поскольку эти два уравнения эквивалентны, они представляют одну и ту же линию на графике. Таким образом, существует бесконечное количество решений этой системы.
Два уравнения 2x + 5y = 9 и 8x + 20y = 36 имеют одинаковый наклон и одинаковую точку пересечения по оси y, поэтому они представляют собой одну и ту же прямую и пересекаются во всех точках на прямой, что означает наличие бесконечных решений линейной система.
Система линейных уравнений с тремя переменными с бесконечными решениями
Система уравнений с тремя переменными будет иметь бесконечные решения, если плоскости пересекаются по всей прямой или по всей плоскости.
Последний случай имеет место, если все три уравнения эквивалентны и представляют одну и ту же плоскость.
Вот пример второго случая:
- x + y + z = 1
- 2x + 2y + 2z = 2
- 3x + 3y + 3
Обратите внимание, что второе уравнение — это первое уравнение, умноженное на 2 с обеих сторон. Также обратите внимание, что третье уравнение — это первое уравнение, умноженное на 3 с обеих сторон.
Поскольку все уравнения кратны друг другу, они эквивалентны. Это означает, что все они представляют один и тот же план.
Итак, их пересечение представляет собой всю плоскость, описываемую уравнением x + y + z = 1.
Это означает, что существует бесконечное число решений приведенной выше системы: каждая точка плоскости x + y + z = 1,
Когда система линейных уравнений имеет решение?
Система линейных уравнений с двумя переменными имеет решение, если две прямые пересекаются хотя бы в одном месте.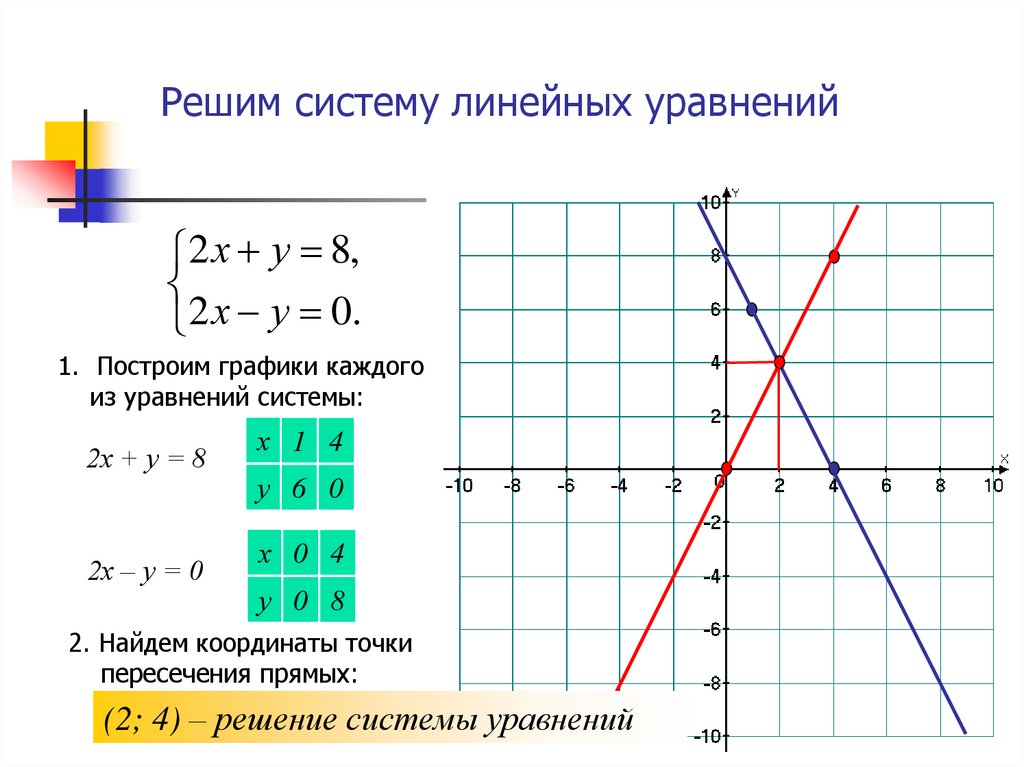
- Если две линии имеют одинаковый наклон и одинаковую точку пересечения по оси Y, то эти два уравнения эквивалентны и представляют одну и ту же прямую (поэтому существует бесконечно много решений, поскольку каждая точка на прямой является решением) .
- Если две линии имеют разные наклоны, то они пересекаются ровно в одной точке.
Когда система линейных уравнений не имеет решения?
Система двух линейных уравнений с двумя переменными не имеет решения, если две прямые параллельны.
С точки зрения алгебры это означает, что мы получаем ложное уравнение при решении системы.
Визуально линии никогда не пересекаются на графике, так как они имеют одинаковый наклон, но разные точки пересечения по оси Y.
Подробнее об этом случае (и некоторых примерах) можно узнать из моей статьи здесь.
Заключение
Теперь вы знаете, когда система линейных уравнений имеет бесконечные решения. Вы также знаете, на что обращать внимание с точки зрения наклона, точки пересечения по оси Y и графика линий в этих системах.
Вы также знаете, на что обращать внимание с точки зрения наклона, точки пересечения по оси Y и графика линий в этих системах.
Вы можете узнать о системах линейных уравнений с одним решением в моей статье здесь и системах линейных уравнений без решений в моей статье здесь.
Подробнее о наклоне можно узнать в этой статье.
Здесь вы можете узнать о других уравнениях с бесконечными решениями.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~Джонатон
Решение системы линейных уравнений: Решаемые системы: вторичное
Содержание этой страницы:
Введение
0005 linear system ) представляет собой группу (линейных) уравнений, которые имеют более одного неизвестного фактора . Неизвестные факторы появляются в различных уравнениях, но не обязательно во всех. Эти уравнения связывают между собой все неизвестные факторы. Например,
Неизвестные факторы появляются в различных уравнениях, но не обязательно во всех. Эти уравнения связывают между собой все неизвестные факторы. Например,
$$\слева\{ \begin{выравнивание} 3х+2у=1 \\ х-5у=6 \end{эквнаррай} \Правильно. $$
— это система уравнений с двумя уравнениями с двумя неизвестными факторы ( х и х ).
Решение этого типа задач (система) состоит в том, чтобы найти значение для каждого неизвестного фактор таким образом, чтобы он применялся ко всем уравнения в система. Решение примера системы:
$$ \begin{выравнивание} х=1 \\ у=-1 \end{eqnarray}$$
Не всегда есть решение и даже может быть бесконечное множество решений . Если существует только одно решение (по одному значению для каждого неизвестного фактора, как в предыдущем примере), говорят, что система является согласованной зависимой системой . Мы не будем говорить о других видах систем.
Мы не будем говорить о других видах систем.
Чтобы решить последовательно зависимую систему, нам нужно не менее столько же уравнений, сколько и неизвестных факторов. В этом разделе мы решим линейные системы из двух уравнений и двух неизвестных факторов с помощью методов, описанных далее, которые основаны на получении уравнения первой степени (линейного уравнения).
Методы
Подстановка (исключение переменных): Заключается в выделении один из неизвестных факторов (например, x ) и подставьте это выражение в другое уравнение. Таким образом получается уравнение первой степени с неизвестным множителем y . После решения получаем значение x , используя значение y , которое мы знаем.
Исключение: Состоит в эксплуатации уравнения, например, сложение или вычитание обоих уравнений, поэтому один из неизвестных факторов исчезает.




