Решение системы уравнений 9 класс примеры и их решение: Методы решения систем рациональных уравнений. Алгебра, 9 класс: уроки, тесты, задания.

Содержание

Решение систем уравнений второй степени и решение задач с помощью таких систем 9 класс онлайн-подготовка на Ростелеком

Тема 8.

Решение систем уравнений второй степени и решение задач с помощью таких систем.

Какие основные способы решения систем уравнений вы знаете? (методы сложения, подстановки, графический)

Каким способом можно решить систему, одно из уравнений которой – уравнение второй степени?

Такие системы всегда можно решить способом подстановки. Для этого поступают следующим образом:

Выражают из уравнения первой степени одну переменную через другую;
Подставляют полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;
Решают получившееся уравнение с одной переменной;
Находят соответствующие значения второй переменной.

Рассмотрим пример:

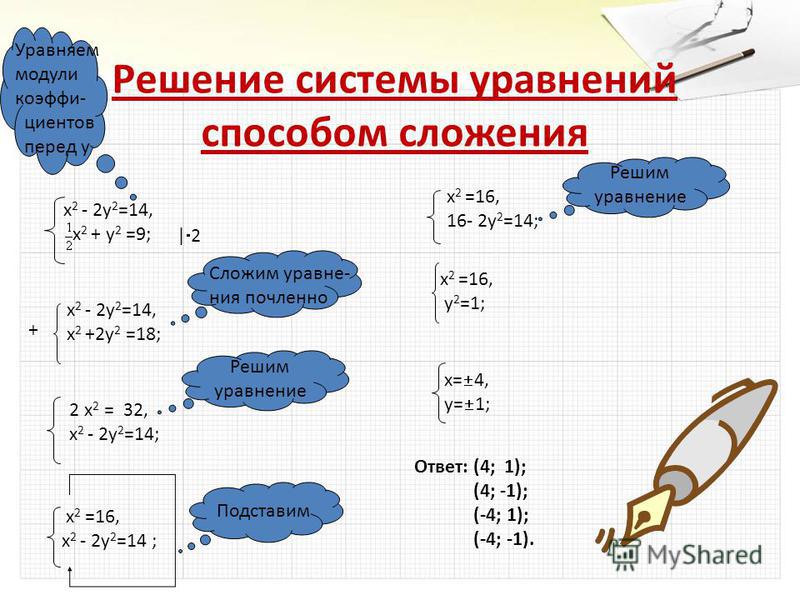
Решим систему уравнений:

x2+y=14,y-x=8;

Выразим из первого уравнения переменную y и подставим во второе:

y=14-x2,14-x2-x=8;

Решим второе уравнение, относительно х:

x² + x — 6 = 0, корни которого равны (– 3) и 2.

Вернемся к системе:

x1=-3,y1=14—32;

x1=-3,y1=5;

x2=2,y2=10;

Рассмотрим еще один пример, решим систему

x2-y2=17,x-y=2;

Эту систему так же можно решить методом подстановки, выразив переменную x, но можно упростить первое уравнение.

Заметим, что левую часть первого уравнения можно разложить на множители по формуле разности квадратов, получим:

x-yx+y=17,x-y=2;

Из второго уравнения разность x — y = 2.

Поэтому вместо первой скобки в первое уравнение подставим число 2, получим:

2x+y=17,x-y=2;

Разделим обе части первого уравнения на 2, получим:

x+y=8,5,x-y=2;

А эту систему давай решим методом сложения, сложим два уравнения, а затем из первого уравнения вычтем второе, получим:

2x=10,5,2y=6,5;

x=5,25,y=3,25.

А теперь решим несколько задач с помощью систем: уравнений второй системы:

Сумма двух чисел равна 12, а их произведение равно 35. Найдите эти числа.

Пусть число x – первое число, а y – второе число. Тогда получим:

x+y=12,x∙y=35;

Выразим из первого уравнения переменную х и подставим во второе, получим:

x=12-y,x∙y=35;

x=12-y,12-yy=35;

Решим уравнение:

12y — y² — 35 = 0

y² — 12y + 35 = 0

Получим корни 5 и 7.

Возвращаемся к нашей системе:

y1=55x=35

y2=7,7x=35;

y1=5×1=7

y2=7×2=5

Ответ: (7;5) и (5;7)

Рассмотрим еще одну задачу:

Площадь прямоугольного треугольника равен 24 см², а его гипотенуза равна 10 см. Каковы катеты треугольника?

Пусть a – длина одного катета, а b – длина второго катета.

Вспомним формулу площади прямоугольного треугольника и теорему Пифагора:

Итак, площадь равна половине произведения катетов.

А квадрат гипотенузы равен сумме квадратов катетов:

12ab=24a2+b2=100

Решим эту систему, первое уравнение домножим на 2, получим:

ab=48a2+b2=100

Выразим переменную а из первого уравнения и подставим во второе, получим:

a=48b48b2+b2=100

Решим второе уравнение системы:

2304b2+b2-100=0,

b4-100b2+2304=0, решим это биквадратное уравнение:

Пусть b² = t, тогда получим:

t² — 100t + 2304 = 0, отсюда

t₁ = 64, t₂ = 36

Возвращаемся к нашей замене, получим:

b1,2=±8,b3,4=±6, так как b – это длина катета, то она не может быть отрицательной, следовательно, b равно 6 или 8, тогда второй катет равен 8 или 6 соответственно.

определение, виды, примеры решения, что это такое

Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.

Определение системы уравнений

Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.

Например, возьмем два уравнения 2·x+y=−3 и x=5, после чего объединим фигурной скобкой такого плана:

2·x+y=-3,x=5.

Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.

Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.

Определение 1

Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.

Основные виды систем уравнений

Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.

Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.

Другая классификация затрагивает число переменных. Когда количество переменных 1, говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример

x+y=5,2·x-3·y=1

Очевидно, что система уравнений включает в себя две переменные х и у.

При записи таких уравнений считается число всех переменных, имеющихся в записи.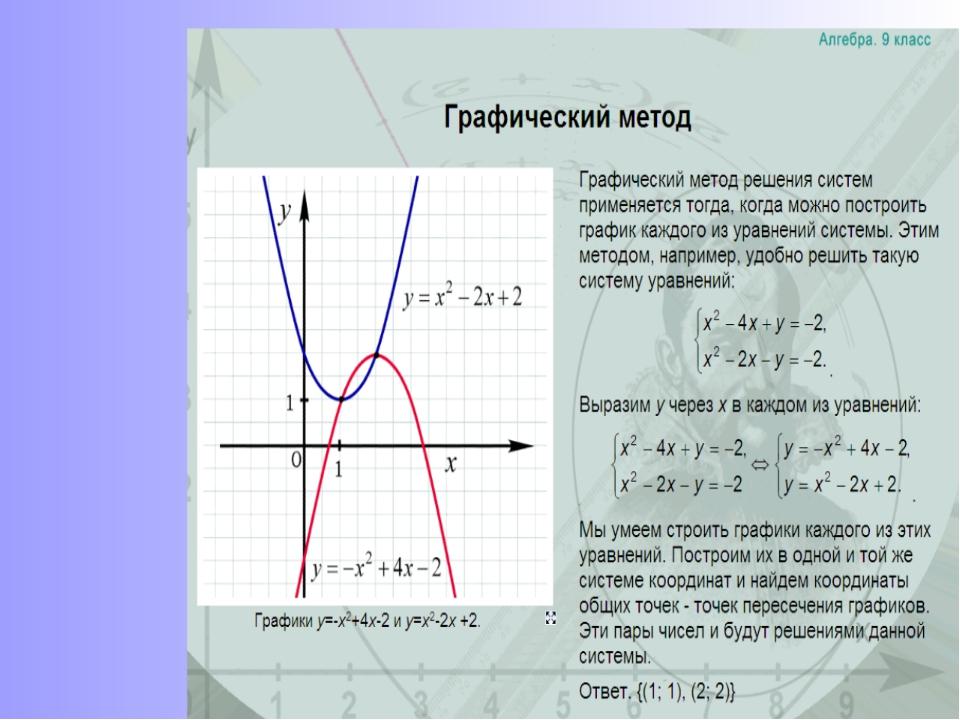 Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений

2x=11,x-3·z2=0,27·x+y-z=-3

Данная система имеет 3 переменные х, у, z. Первое уравнение имеет явный х и неявные у и z. Неявные переменные – это переменные, имеющие 0 в коэффициенте. Второе уравнение имеет х и z, а у неявная переменная. Иначе это можно записать таким образом

2x+0·y+0·z=11

А другое уравнение x+0·y−3·z=0.

Третья классификация уравнений – это вид. В школе проходят простые уравнения и системы уравнений, начиная с систем двух линейных уравнений с двумя переменными. Имеется в виду, что система включает в себя 2 линейных уравнения. Для примера рассмотрим

2·x-y=1,x+2·y=-1и -3·x+y=0.5,x+223·y=0

Это основные простейшие линейные уравнения. Далее можно столкнуться с системами, содержащими 3 и более неизвестных.

В 9 классе решают уравнения с двумя переменными и нелинейные. В целых уравнениях повышается степень для увеличения сложности. Такие системы называют системами нелинейных уравнений с определенным количеством уравнений и неизвестных. Рассмотрим примеры таких систем

x2-4·x·y=1,x-y=2 и x=y3x·y=-5

Обе системы с двумя переменными и обе являются нелинейными.

При решении можно встретить дробно-рациональные уравнения. Например

x+y=3,1x+1y=25

Могут называть просто системой уравнений без уточнения, каких именно. Редко уточняют сам вид системы.

Старшие классы переходят к изучению иррациональных, тригонометрических и показательных уравнений. Например,

x+y-x·y=5,2·x·y=3, x+y=5·π2,sin x+cos 2y=-1,y-log3x=1,xy=312.

Высшие учебные заведения изучают и исследуют решения систем линейных алгебраических уравнений (СЛАУ). Левая часть таких уравнений содержит многочлены с первой степенью, а правая – некоторые числа. Отличие от школьных в том, что количество переменных и количество уравнений может быть произвольным, чаще всего несовпадающим.

Решение систем уравнений

Определение 2

Решение системы уравнений с двумя переменными – это пара переменных, которая при подстановке обращает каждое уравнение в верное числовое неравенство, то есть является решением для каждого уравнения данной системы.

К примеру, пара значений х=5 и у=2 являются решением системы уравнений x+y=7,x-y=3. Потому как при подстановке уравнения обращаются в верные числовые неравенства 5+2=7 и 5−2=3. Если подставить пару х=3 и у=0, тогда система не будет решена, так как подстановка не даст верное уравнение, а именно, мы получим 3+0=7.

Сформулируем определение для систем, содержащих одну и более переменных.

Определение 3

Решение системы уравнений с одной переменной – это значение переменной, которая является корнем уравнений системы, значит, все уравнения будут обращены в верные числовые равенства.

Рассмотрим на примере системы уравнений с одной переменной t

t2=4,5·(t+2)=0

Число -2 – решение уравнения, так как (−2)·2=4, и 5·(−2+2)=0 являются верными числовыми равенствами. При t=1 система не решена, так как при подстановке получим два неверных равенства 12=4 и 5·(1+2)=0.

Определение 4

Решение системы с тремя и более переменными называют тройку, четверку и далее значений соответственно, которые обращают все уравнения системы в верные равенства.

Если имеем значения переменных х=1, у=2, z=0, то подставив их в систему уравнений 2·x=2,5·y=10,x+y+z=3, получим 2·1=2, 5·2=10 и 1+2+0=3. Значит, эти числовые неравенства верные. А значения (1, 0, 5) не будут решением, так как, подставив значения, второе из них будет неверное, как и третье: 5·0=10, 1+0+5=3.

Системы уравнений могут не иметь решений вовсе или иметь бесконечное множество. В этом можно убедиться при углубленном изучении данной тематики. Можно прийти к выводу, что системы уравнений – это пересечение множеств решений всех ее уравнений. Раскроем несколько определений:

Определение 5

Несовместной называют систему уравнений, когда она не имеет решений, в противном случае ее называют совместной.

Определение 6

Неопределенной называют систему, когда она имеет бесконечное множество решений, а определенной при конечном числе решений либо при их отсутствии.

Такие термины редко применяются в школе, так как рассчитаны для программ высших учебных заведений. Знакомство с равносильными системами углубит имеющиеся знания по решению систем уравнений.

Решения систем уравнений: объяснение, обзор и примеры

Решение — это слово, которое мы часто используем в математике, но оно может означать разные вещи в зависимости от контекста. Однако в общем случае решение представляет собой значение или набор значений, которые делают уравнения верными. Хотя идея истины может показаться чем-то более подходящим для таких дисциплин, как наука и философия, чем математика, мы ищем истину, когда ищем решения систем уравнений.

Что такое решение системы уравнений?

Чтобы понять, что такое решение системы уравнений, давайте начнем с рассмотрения некоторых уравнений и их решений.

Equation	Solution
5+4=s	s=9
n+7=9	n=2

What do the two общего между уравнениями и их решениями? Решения делают уравнения верными. Когда с=9, то 5+4=с. Когда n=2, то n+7=9.

Система уравнений включает два или более уравнений. Каждое из уравнений должно иметь как минимум две переменные, например, x и y.

Чтобы узнать, что такое система уравнений, ознакомьтесь с нашим постом: Написание систем уравнений .

набор решений системы уравнений будет координатами упорядоченной пары (пар), которые удовлетворяют всем уравнениям в системе. Другими словами, эти значения x и y сделают уравнения верными. Соответственно, при построении системы уравнений решением будут все точки пересечения графиков.

Заинтересованы в лицензии школы Альберта?

Количество решений системы уравнений

Количество решений системы уравнений зависит от самих уравнений. Системы могут иметь одно решение, несколько решений, бесконечно много решений или даже не иметь решения.

Системы линейных уравнений классифицируются по количеству решений, которые они имеют. Существуют две основные категории систем уравнений:

An несовместная система, не имеющая решений
непротиворечивая система, имеющая одно или несколько решений

непротиворечивые системы могут быть дополнительно подразделены на:

независимая система, имеющая ровно одно решение
Зависимая система , с бесконечным числом решений

Начните практиковать Алгебру 1 на Альберте прямо сейчас!

Системы уравнений без решения (пример)

Давайте начнем с рассмотрения несовместимых систем, как мы это называем, когда у систем уравнений нет решений. Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, если наша система уравнений состоит из двух или более параллельных прямых, то не будет мест пересечения графиков прямых, а значит, не будет и решений.

Обзор параллельных линий см. в нашем обзорном руководстве Параллельные и перпендикулярные линии .

Прямые y=x+3 и y=x-2 параллельны. Их графики показаны справа.

Из графика видно, что линии никогда не пересекаются с , а значит, у этой системы уравнений нет решений. Таким образом, хотя каждое линейное уравнение в системе имеет бесконечное число решений, система уравнений, состоящая из обоих этих линейных уравнений, не имеет решений. Мы можем классифицировать систему как несовместимую.

Системы нелинейных уравнений также могут не иметь решений. Ниже приведен график системы двух квадратных уравнений, которые никогда не пересекаются. Вместе эти уравнения составляют систему, не имеющую решений.

Как насчет систем с более чем двумя уравнениями? Решения должны удовлетворять всем уравнениям системы. Графически только точки пересечения всех графов в системе считаются решениями.

Например, на приведенном ниже графике показана система из трех уравнений: две параллельные прямые и одна прямая, пересекающая параллельные прямые. Эта система уравнений не имеет решения, потому что нет места, где все три прямые пересекаются друг с другом одновременно.

Заинтересованы в лицензии школы Альберта?

Система уравнений с бесконечными решениями (пример)

Теперь давайте впадем в противоположную крайность и рассмотрим системы уравнений, которые являются одновременно непротиворечивыми и зависимыми, что происходит, когда существуют бесконечные решения систем уравнений. Графически мы ищем систему уравнений, которая пересекается в бесконечном числе точек. Как это может случиться? Это происходит всякий раз, когда два уравнения на самом деле являются одним и тем же уравнением.

Например, рассмотрим систему:

y=x+3

х=у-3

Хотя второе уравнение не записано в форме точки пересечения, мы можем видеть, что уравнение имеет тот же наклон, 1, и ту же точку пересечения по оси y, 3, что и y=x+3.

Краткий обзор форм линейных уравнений можно найти в нашем блоге Форма пересечения наклонов .

Тот факт, что два уравнения идентичны, станет очевидным, если мы перепишем x=y-3 в форме пересечения наклона:

х=у-3
x{\color{red}{-y}}=y-3{\color{red}{-y}}
х-у=-3
х-у {\ цвет {красный} {-x}} = -3 {\ цвет {красный} {-x}}
-у=-х+-3
{\ color {красный} {(-1)}} (-y) = {\ color {красный} {(-1)}} (-x + -3)
у=х+3
Таким образом, мы также можем записать эту систему как:
y=x+3
у=х+3
Графики этих двух уравнений показаны справа.
Как видно из графика, эти уравнения представляют собой одну и ту же прямую на координатной плоскости. Поскольку все точки на одной прямой находятся и на другой прямой, у этой системы существует бесконечное число решений.
Обратите внимание: это не означает, что каждый набор координат является решением этого уравнения. Например, координаты (0,5) не являются решением системы уравнений, так как эта точка не лежит на прямых. Однако, поскольку линия простирается до бесконечности в обоих направлениях, на каждой линии существует бесконечное количество точек и, следовательно, бесконечное количество решений системы уравнений.

Другие системы уравнений, которые являются как непротиворечивыми, так и зависимыми, включают любые комбинации уравнений, такие как уравнения для окружностей, парабол и других фигур, где графики уравнений полностью перекрываются.
Начните практиковать Алгебру 1 на Альберте прямо сейчас!
Система уравнений с одним решением (пример)
Сколько решений системы уравнений существует для системы, которая одновременно независима и непротиворечива? Такая система имеет ровно одно решение, что означает, что она имеет один набор значений, который делает все уравнения в системе верными.
Линейные уравнения в приведенной ниже системе соответствуют этому описанию:
y=x+3
y=-x-1
Линии, представляющие эти уравнения на координатной плоскости, будут пересекаться ровно в одной точке, как показано ниже.
Поскольку эти прямые пересекаются в точке (-2,1), эта точка является единственным решением системы. Мы можем использовать алгебру, чтобы убедиться, что координаты (\color{red}{-2},\color{blue}{1}) превращают каждое уравнение в истинное утверждение.
Начнем с первого уравнения:
y=x+3
{\color{синий}{1}}={\color{красный}{-2}}+3
1=1
А теперь давайте проверим второе уравнение:
y=-x-3
{\color{синий}{1}}=-({\color{красный}{-2}})-1
1=2-1
1=1
Обратите внимание: мы могли бы определить, что эта система уравнений имеет одно решение, просто взглянув на сами уравнения, если бы заметили, что они имеют разные наклоны. Наклон y=x+3 равен 1, а наклон y=-x-1 равен -1. Линии с разным наклоном никогда не бывают параллельными, а прямые, лежащие в одной плоскости, но не параллельные, всегда пересекаются ровно в одной точке.
Заинтересованы в лицензии школы Альберта?
Как найти решение системы уравнений
Существует несколько методов решения систем уравнений, в том числе: Такие инструменты, как Desmos и Geogebra, предлагают графические онлайн-калькуляторы, помогающие в этом процессе.
Использование алгебраических стратегий, таких как замена или исключение, для нахождения значений переменных, которые делают все уравнения в системе верными.
Каждый из этих методов может помочь нам найти не только количество решений систем уравнений, но и то, что это за решения.
Когда мы находим решение или решения системы уравнений, мы можем подставить значения обратно в уравнения, чтобы убедиться, что они верны.
Начните практиковать Алгебру 1 на Альберте прямо сейчас!
Решения систем уравнений: ключи для запоминания
Решение систем уравнений — это набор координат, который делает все уравнения в системе верными.
Системы уравнений могут иметь любое количество решений от нуля до бесконечности.
Мы можем классифицировать системы уравнений как несовместные, зависимые или независимые и непротиворечивые в зависимости от количества решений.
Системы уравнений без решений несовместны, а системы с бесконечными решениями зависимы. Системы уравнений, имеющие ровно одно решение, называются независимыми и непротиворечивыми.
Решения систем уравнений можно найти графически или алгебраически.
Заинтересованы в школьной лицензии?
Пригласите Альберта в свою школу и предоставьте всем учителям лучший в мире банк вопросов для:
➜ SAT® и ACT®
➜ AP®
➜ ELA, математика, естественные науки и социальные науки
➜ State Assessments
Варианты для учителей, школы, районы.
УЗНАТЬ О ВАРИАНТАХ
4.3 Решение систем уравнений методом исключения – Бизнес/Техническая математика
4. Системы уравнений
Линн Маречек и МэриЭнн Энтони-Смит
Ожидается, что к концу этого раздела вы сможете:
Решать систему уравнений методом исключения
Решение приложений систем уравнений методом исключения
Выберите наиболее удобный способ решения системы линейных уравнений
Мы решили системы линейных уравнений с помощью графиков и подстановок. Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему подстановкой, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добраться туда.
Метод исключения основан на свойстве сложения равенства. Свойство сложения равенства говорит о том, что, когда вы добавляете одно и то же количество к обеим частям уравнения, вы все равно получаете равенство. Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Для любых выражений a , b , c и d ,
Чтобы решить систему уравнений методом исключения, мы начинаем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет проще всего исключить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
и прибавляются к нулю, и мы получаем одно уравнение с одной переменной.
Давайте попробуем еще один:
На этот раз мы не видим переменную, которую можно сразу исключить, если мы добавим уравнения.
Но если мы умножим первое уравнение на -2, мы сделаем коэффициенты x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2.
Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будет устранено, когда мы добавим эти два уравнения.
Сложите уравнения самостоятельно — результат должен быть −3 y = −6. И это кажется легко решить, не так ли? Вот как это будет выглядеть.
Сделаем еще один:
Не похоже, чтобы коэффициенты одной переменной были противоположны, если умножить одно из уравнений на константу, если только мы не используем дроби. Поэтому вместо этого нам придется умножить оба уравнения на константу.
Мы можем сделать коэффициенты x противоположными, если умножим первое уравнение на 3, а второе на -4, так что мы получим 12 x и -12 x . Это дает нам два новых уравнения: всего одна переменная, мы ее решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы посмотрим, как использовать исключение для решения той же системы уравнений, которую мы решали с помощью графика и подстановки.
Как решить систему уравнений методом исключения
Решить систему методом исключения.
Решение
Решите систему методом исключения.
Показать ответ
Шаги перечислены ниже для удобства.
Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
Сделайте коэффициенты одной переменной противоположными.
Решите, какую переменную вы удалите.
Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
Найдите оставшуюся переменную.
Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
Запишите решение в виде упорядоченной пары.
Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Сначала мы сделаем пример, в котором мы можем сразу исключить одну переменную.
Решить систему методом исключения.
Раствор
x – y = 12 becomes 11 – (-1) = 12 and 12 = 12. The figure then states, “The solution is (11, -1).» data-label=»»>
Оба уравнения имеют стандартную форму.
Коэффициенты y уже противоположны.
Добавьте два уравнения, чтобы исключить y .
Полученное уравнение содержит только 1 переменную x .
Найдите x оставшуюся переменную.
Подставьте x = 11 в одно из исходных уравнений.
Найдите другую переменную, y .
Запишите решение в виде упорядоченной пары. Упорядоченная пара (11, −1).
Убедитесь, что упорядоченная пара является решением
до обоих исходных уравнений.
Решение (11, −1).
Решите систему методом исключения.
Показать ответ
В следующем примере мы сможем сделать коэффициенты одной переменной противоположными, умножив одно уравнение на константу.
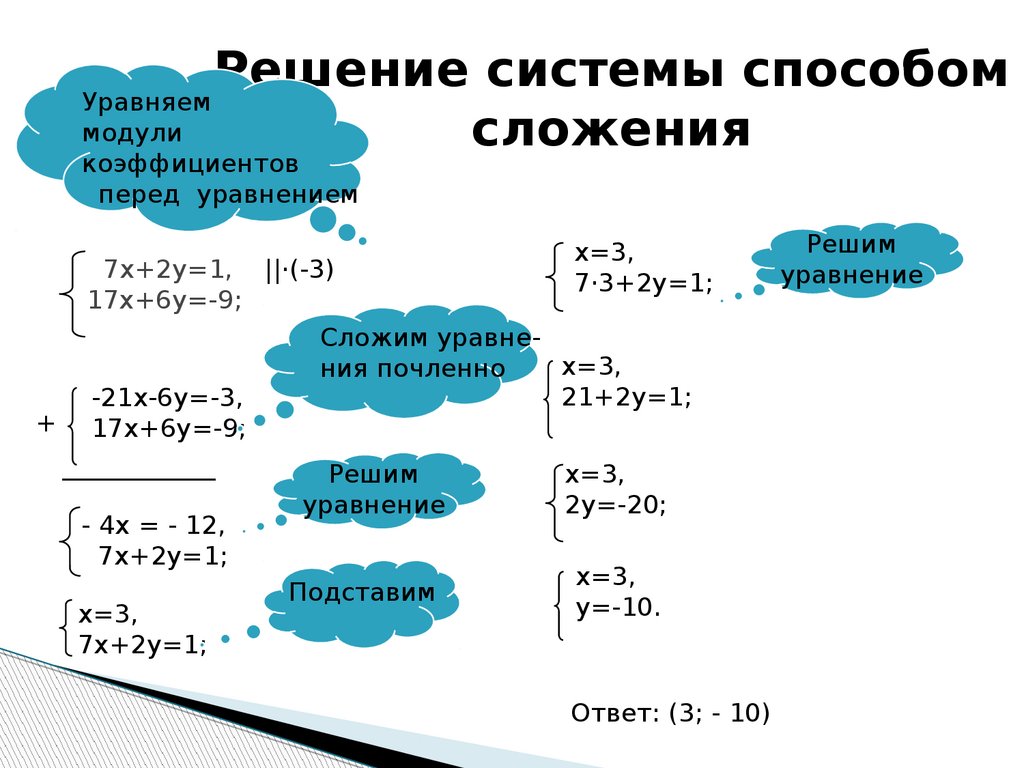
Решить систему методом исключения.
Раствор
” The figure then shows the equations. The first is -3 times (3x – 2y) = -3 times -2, and the second is 5x – 6y = 10. The figure then instructs, “Simplify.” The two equations are -9x + 6y = 6 and 5x – 6y = 10. The figure then says, “Add the two equations in eliminate y.” The two equations added together becomes -4x = 16. The figure then says, “Solve for the remaining variable x.” Thus x = -4. The figure then instructs, “Substitute x = -4 into one of the original equations. Thus 3x – 2y = -2 becomes 3 times -4 – 2y = -2. The figure then instructs, “Solve for y.” The equation becomes -12 — 2y = 2 or -2y = 10. Thus y = -5. The figure then says, “Write the solution as an ordered pair. The ordered pair is (-4, -5).” The figure then says, “Check that the ordered pair is a solution to both original equations.” Thus 3x -2y = -2 becomes 3 times -4 — 2 times -5 = -2 or -12 +10 = -2 or -2y = -2. It also shows that 5x – 6y = 10 becomes 3 times -4 – 6 times -5 = 10 or -20 + 30 = 10. Thus 10 = 10. The figure then says, ‘The solutions is (-4, -5). » data-label=»»>
Оба уравнения имеют стандартную форму.
Ни один из коэффициентов не является противоположным.
Мы можем сделать коэффициенты y противоположными, умножив
первое уравнение на −3.
Упрощение.
Добавьте два уравнения, чтобы исключить y .
Решите для оставшейся переменной, x .
Подставьте x = −4 в одно из исходных уравнений.
Найдите y .

Запишите решение в виде упорядоченной пары. Упорядоченная пара (−4, −5).
Убедитесь, что упорядоченная пара является решением
обоих исходных уравнений.
Решение (−4, −5).
Решите систему методом исключения.
Показать ответ
Теперь сделаем пример, где нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Решить систему методом исключения.
Решение
В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на константу, чтобы получить противоположности.
The figure then says, “Both equations are in standard form. To get opposite coefficients of y, we will multiply the first equation by 2 and the second equation by 3.” It then shows the equations as 2 times (4x – 3y) = 2 times 9 and 3 times (7x + 2y) = 3 times -6. The figure then says, “Simplify.” The equations then become 8x – 6y = 18 and 21x + 6y = -18. The figure then says, “Add the two equations to eliminate y. After adding, the answer is 39x = 0. The figure then says, “Solve for x.” Thus, x = 0. The figure then reads, “Substitute x = 0 into one of the original equations.” Thus 7x +2y = -6 becomes 7 times 0 + 2y = -6. The figure then says, “Solve for y.” It then says, 2y = -6 and thus 2y = -3. The figure then reads, “Write the solution as an ordered pair. The ordered pair is (0, -3).” The figure then instructs, “Check that the ordered pair is a solution to both original equations. Thus 4x – 3y = 9 becomes 4 times 0 – 3 times -3 = 9 or 9 = 9. Thus 7x + 2y = -6 becomes 7 times 0 + 2 times -3 = -6 or -6 = -6. 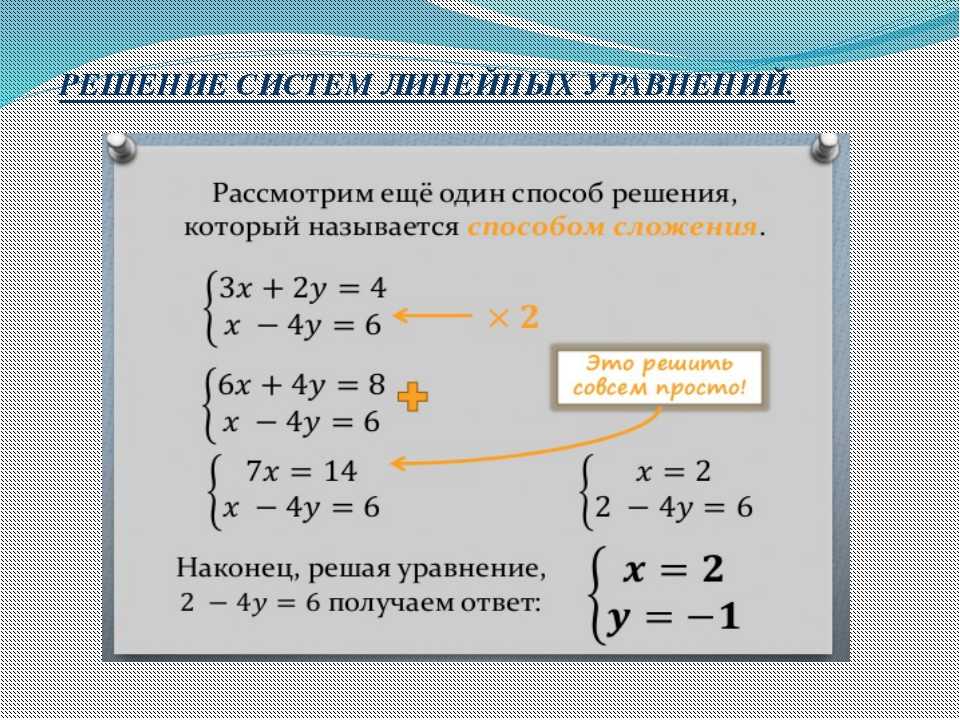The figure then says, “The solution is (0, -3).”» data-label=»»> .
Оба уравнения имеют стандартную форму. Чтобы получить противоположные
коэффициенты y , умножим первое уравнение на 2
, а второе уравнение на 3
Упрощение.
Добавьте два уравнения, чтобы исключить y .
Найдите x .
Подставьте x = 0 в одно из исходных уравнений.
Найдите y .
Запишите решение в виде упорядоченной пары. Упорядоченная пара (0, −3).
Убедитесь, что упорядоченная пара является решением
обоих исходных уравнений.
Решение равно (0, −3).
Какие еще константы мы могли бы выбрать, чтобы исключить одну из переменных? Решение будет таким же?
Решить систему методом исключения.
Показать ответ
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на его ЖК-дисплей.
Решить систему методом исключения.
Решение
В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на его ЖК-дисплей, чтобы очистить дроби.
” It then shows the equations as 2 times (x + (1/2)y) = 2 times 6 and 6 times ((3/2)x + (2/3)y) = 6 times (17/2). The figure then says, “Simplify.” The equations then become 2x + y = 12 and 9x + 4y = 51. The figure then says, “Now we are ready to eliminate one of the variables. Notice that both equations are in standard form. We can eliminate y multiplying the top equation by -4.” It then shows -4 times (2x + y) = -4 times 12 and 9x + 4y = 51. The figure then says, “Simplify and add.” The equations added are thus -8x – 4y = -48 plus 9x + 4y = 51 which gives x = 3. The figure then says, “Substitute x = 3 into one of the original equations. Solve for y.” Thus x + (1/2)y = 6 becomes 3 + (1/2)y = 6. This becomes (1/2)y = 3 or y = 6. The figure then says, “Write the solution as an ordered pair. The ordered pair is (3, 6). The figure then says, “Check the ordered pair is a solution to both original equations. Thus x + (1/2)y = 6 becomes 3 + (1/2) times 6 = 6 or 3 + 6 = 6. Thus 6 = 6. The second equation is (3/2)x + (2/3)y = 17/2 or (3/2) times 3 + (2/3) times 6 = 17/2. This becomes 9/2 + 4 = 17/2 or 9/2 + 8/2 = 17/2. Thus 17/2 = 17/2. The figure then says, “The solution is (3, 6).”» data-label=»»>
Чтобы очистить дроби, умножьте каждое уравнение на его ЖК-дисплей.
Упрощение.
Теперь мы готовы удалить одну из переменных. Обратите внимание, что
оба уравнения имеют стандартную форму.
Мы можем исключить y , умножив первое уравнение на −4.
Упростить и добавить.
Подставьте x = 3 в одно из исходных уравнений.
Найдите y .
Запишите решение в виде упорядоченной пары. Заказанная пара (3, 6).
Убедитесь, что упорядоченная пара является решением
до обоих исходных уравнений.
Решение (3, 6).
Решите систему методом исключения.
Показать ответ
Когда мы решали системы линейных уравнений графически, мы увидели, что не все системы линейных уравнений имеют в качестве решения одну упорядоченную пару. Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
Решите систему путем устранения:
A)
B)
C)
D)
Решение
A)
Запишите второе уравнение в стандартной форме.
Очистите дроби, умножив второе уравнение на 4.
Упрощение.
Чтобы исключить переменную, мы умножаем второе уравнение на .
Упростить и добавить.
Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, вы заметили, что эти два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии.
б)
бесконечно много решений
в)
бесконечно много решений
г)
Уравнения в стандартной форме.
Умножьте второе уравнение на 3, чтобы исключить переменную.
Упростить и добавить.
Это утверждение неверно. Уравнения несовместимы, поэтому их графики будут параллельными линиями.
Система не имеет решения.
Решите систему методом исключения.
Показать ответ
нет решения
Некоторые прикладные задачи переводятся непосредственно в уравнения в стандартной форме, поэтому для их решения мы будем использовать метод исключения. Как и прежде, мы используем нашу Стратегию решения проблем, чтобы оставаться сосредоточенными и организованными.
Сумма двух чисел равна 39. Их разница равна 9. Найдите числа.
Решение
Шаг 1. Прочтите проблему.
Шаг 2. Определите что мы ищем. Ищем два числа.
Шаг 3. Назовите то, что мы ищем.
Выберите переменную для представления этого количества. Пусть первое число.
второй номер.
Шаг 4. Переведите в систему уравнений.
Система:
Сумма двух чисел равна 39.

Их разница равна 9.
Шаг 5. Решить систему уравнений.
Чтобы решить систему уравнений, используйте исключение.
Уравнения имеют стандартный вид, а коэффициенты противоположны. Добавлять.
Решите для .
Подставьте в одно из исходных уравнений и найдите .
Шаг 6. Проверьте ответ. Так как и , ответы проверяются.
Шаг 7. Ответьте на вопрос. Цифры 24 и 15.
Сумма двух чисел равна 42. Их разница равна 8. Найдите числа.
Показать ответ
Числа 25 и 17.
Каждый день по пути на работу Джо останавливается в бургерной. В понедельник он заказал один средний картофель фри и две маленькие газированные напитки, в которых было в общей сложности 620 калорий. Во вторник у него было два заказа картофеля фри среднего размера и одна маленькая газировка, всего 820 калорий. Сколько калорий в одном заказе картофеля фри среднего размера? Сколько калорий в одной маленькой газировке?
Решение
2f + s = 820. Our syste is f + 2s = 620 and 2f + s = 820. Step 5. Solve the system of equations. To solve the system of equations, use elimination. The equations are in standard form. To get opposite coefficients of f, multiply the top equation by -2.” The equations are -2(f + 2s) = -2 times 620 and 2f + s =820. The figure then says, “Simplify and add.” Thus -2f – 4s = -1240 plus 2f + s = 820 equals -3s = -420. The figure then says, “Solve for s.” Thus s = 140. The figure then reads, “Substitute s = 140 into one of the original equations and then solve for f. Thus, f + 2s = 620 becomes f + 2 times 140 = 620 or f +280 = 620. Thus f = 340. The figure then reads, “Step 6. Check the answer. Verify that these numbers make sense in the problem and that they are solutions to both equations. We leave this to you! Step 7. Answer the question. The small soda has 140 calories and the fries have 340 calories.”» data-label=»»>
Шаг 1. Прочтите проблему.
Шаг 2. Определите что мы ищем. Ищем количество калорий
в одном заказе среднего картофеля фри
и в одной маленькой газировке.
Шаг 3. Назовите то, что мы ищем. Пусть f = количество калорий в
1 порции картофеля фри среднего размера.
s = количество калорий в
1 маленькой газировке.
Шаг 4. Переведите в систему уравнений: один средний картофель фри и две маленькие газированные напитки содержали
всего 620 калорий
два средних картофеля фри и одна маленькая газировка содержали
в общей сложности 820 калорий.
Наша система:
Шаг 5. Решите систему уравнений.
Чтобы решить систему уравнений, используйте исключение
. Уравнения представлены в стандартной форме
. Чтобы получить противоположные коэффициенты f ,
умножьте верхнее уравнение на -2.
Упростить и добавить.
Найдите s .
Подставьте s = 140 в одно из исходных
уравнений, а затем найдите 9.0296 ф .
Шаг 6. Проверьте ответ. Убедитесь, что эти числа имеют смысл
в задаче и что они являются
решениями обоих уравнений.
Мы оставляем это вам!
Шаг 7. Ответьте на вопрос. Маленькая газировка содержит 140 калорий, а
картофель фри — 340 калорий.
Малик останавливается в продуктовом магазине, чтобы купить пакет подгузников и 2 банки детского питания. Всего он тратит 37 долларов. На следующей неделе он останавливается и покупает 2 пакета подгузников и 5 банок со смесью на общую сумму 87 долларов. Сколько стоит мешок подгузников? Сколько стоит банка смеси?
Показать ответ
Пакет с подгузниками стоит 11 фунтов, а банка со смесью — 13 фунтов.
Когда вам нужно будет решить систему линейных уравнений на последнем уроке математики, вам обычно не говорят, какой метод использовать. Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением. Поясните свой ответ.
а)
б)
Решение
а)
Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет метод исключения.
б)
Поскольку одно уравнение уже решено для y , наиболее удобным будет использование подстановки.
Для каждой системы линейных уравнений решите, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.
а)
б)
Показать ответ
а) Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование исключения.
б) Так как одно уравнение уже решено для , наиболее удобным будет использование подстановки.
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения систем линейных уравнений методом исключения.
Учебное видео по решению систем уравнений методом исключения
Обучающее видео-решение путем исключения
Обучающие видеосистемы решения от Elimination
Решение системы уравнений методом исключения
Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
Сделайте коэффициенты одной переменной противоположными.
Решите, какую переменную вы исключите.
Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
Найдите оставшуюся переменную.
Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
Запишите решение в виде упорядоченной пары.
Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
В следующих упражнениях решите системы уравнений методом исключения.
В следующих упражнениях переведите систему уравнений и решите.
Сумма двух чисел равна 65. Их разница равна 25. Найдите числа.
Сумма двух чисел равна −27. Их разница составляет −59. Найдите числа.
Андреа покупает новые рубашки и свитера. Она может купить 3 рубашки и 2 свитера за 114 долларов или 2 рубашки и 4 свитера за 164 доллара. Сколько стоит рубашка? Сколько стоит свитер?
Общее количество натрия в 2 хот-догах и 3 чашках творога составляет 4720 мг. Общее количество натрия в 5 хот-догах и 2 чашках творога составляет 6300 мг. Сколько натрия в хот-доге? Сколько натрия в чашке творога?
В следующих упражнениях решите, будет ли удобнее решать систему уравнений путем замены или исключения.
Норрис может прогрести 3 мили вверх по течению за то же время, что и 5 миль вниз по течению по течению. Решите систему.
для , его скорость гребли в стоячей воде.
Затем найдите , скорость течения реки.
Ответы:
(6, 9)
(6, 1)
(2, 3)
(9, 5)
бесконечно много решений
бесконечно много решений
бесконечно много решений
противоречиво, нет решения
противоречиво, нет решения
Цифры 20 и 45.
No related posts.