Решение системы уравнений методом гаусса онлайн с решением: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Содержание

Решение системы линейных уравнений. Методы решения системы линейных уравнений

Похожие презентации:

Системы линейных уравнений и методы их решения. (Тема 2)

Решение систем линейных алгебраических уравнений по правилу Крамера, матричным методом, методом Гаусса

Методы решения системы трёх линейных уравнений с тремя неизвестными

Алгоритмы решения систем линейных алгебраических уравнений

Метод Гаусса решения систем линейных уравнений. Ранг матрицы. Исследование систем линейных уравнений

Численные методы линейной алгебры

Системы линейных уравнений

Решение систем линейных уравнений методом Гаусса

Системы из n линейных уравнений с n неизвестными. Метод Гаусса решения систем линейных уравнений

1. Занятие 12

Решение системы линейных уравнений

2. Методы решения системы линейных уравнений

Метод обратной матрицы
1. Для нахождения решений системы методом обратной матрицы надо
умножить обратную матрицу на столбец свободных членов (предварительно
выбрав массив ячеек для столбца решений).

2. Для вычисления обратной матрицы используйте функцию
МОБР(диапазон исходной матрицы).
2 x1 x 2 3x 3 9
x 1 2 x 2 x 3 2
3×1 2 x 2 2 x 3 7

3. Методы решения системы линейных уравнений

Метод Крамера
1. Для решения системы линейных уравнений методом Крамера,
нужно найти определитель матрицы исходного уравнения (D), а также
определители новых матриц (d1, d2, d3), которые получаются путем замены
1-го, 2-го и 3-го столбцов (по-очереди) исходной матрицы столбцом
свободных членов исходной системы уравнений.
2. Для нахождения решений используйте формулу: xk = dk / D, где dk
– определитель, получающийся из определителя D при замене k-го столбца
соответствующими свободными членами, т.е., к примеру, x1 = d1 / D, где d1
– определитель матрицы с замененным 1-ым столбцом исходной матрицы
столбцом свободных членов.
2 x1 x 2 3x 3 9
x 1 2 x 2 x 3 2
3×1 2 x 2 2 x 3 7
Проверка показывает, что решение
найдено правильно

4.

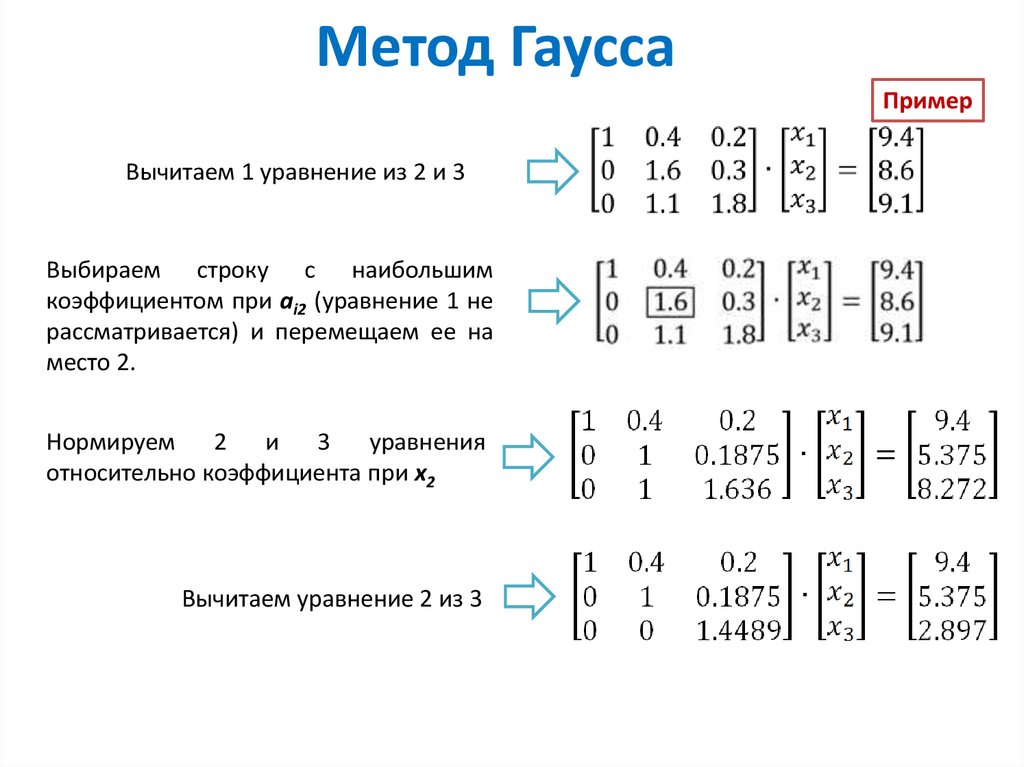
Методы решения системы линейных уравненийМетод Гаусса
Метод Гаусса основан на том, чтобы при помощи эквивалентных
преобразований получить трапециевидную систему уравнений (у которой в
левой нижней части остаются единицы по диагонали, а остальные – нули, см.
пример), поэтому от исходной матрицы нужно получить новую. Будем делать
это поэтапно.
6х1-6х2+2х3+8х4=12
2х1+2х2-х3+4х4=13
8х1+6х2+4х3-2х4=5
-3х1+х2+7х3-4х4=56
Шаг 1. Деление элементов
первой строки на
коэффициент при Х1.
Шаг 2. Вычитание значений
первой строки из
последующих строк
Шаг 3. Деление элементов
второй строки на
коэффициент при Х2
Шаг 4. Вычитание значений
второй строки из
последующих строк
Шаг 5. Деление элементов
третьей строки на
коэффициент при Х3
Шаг 6. Вычитание значений
третьей строки из значений
четвертой строки
Шаг 5. Деление элементов третьей строки на
коэффициент при Х3
Шаг последний. Вычисление значений
неизвестных

7.

Самостоятельно решить следующие системы уравнений каждую всеми тремя способами

English Русский Правила

уникальная серия-матрикс-калькулятор-Google Suce

AllebildershoppingVideOsmapsNewsbücher

Sucoptionen

Решающие системы линейных уравнений-Матрикс. Метод обратной матрицы или правило Крамера. Также вы можете вычислить ряд …

Исключение Гаусса-Жордана — Калькулятор матриц — Решиш

matrix.reshish.com › gauss-jordanElimination

Наш калькулятор способен решать системы с единственным единственным решением, а также неопределенные системы, которые имеют бесконечно много решений.

Ähnliche Fragen

Как найти единственное решение матрицы?

Какова формула уникального решения?

Как найти единственное решение расширенной матрицы?

Может ли матрица MXN иметь единственное решение?

9- Найдите значение h,k, для которого система уравнений .

Калькулятор матриц — Решатель систем Онлайн — Mathstools

www.mathstools.com › section › main › system_equations_solver

Решатель линейных систем — это Калькулятор линейных систем линейных уравнений и матричный калькулятор для квадратных матриц. Он вычисляет собственные значения и …

Комплексные матрицы и линейные системы — Калькулятор матриц

калькуляторы-math.com › калькулятор комплексных матриц

1,99 $

Калькулятор матриц для выполнения матричной алгебры и решения систем линейных уравнений методом исключения Гаусса-Жордана . Все матрицы могут быть комплексными матрицами.

Общее решение системы линейных уравнений с помощью …

planetcalc.com › …

Этот онлайн-калькулятор решает систему линейных алгебраических уравнений методом исключения Гаусса. Это дает результат, есть ли у вас уникальный …

Калькулятор матриц — Symbolab

www.symbolab.com › . .. › Матрицы и векторы

Бесплатный калькулятор матриц — решение матричных операций и функций … Чтобы перемножить две матрицы вместе, внутренние размеры матриц должны совпадать .

Online Systems of Equations Solver — Wolfram|Alpha

www.wolframalpha.com › system-equation-calculator

Wolfram|Alpha способен решать самые разные системы уравнений. Он может решать системы линейных уравнений или системы, включающие нелинейные уравнения, …

Калькулятор системы линейных уравнений — eMathHelp

www.emathhelp.net › калькуляторы › алгебра-2 › система… метод исключения Гаусса-Жордана, обратная матрица.

Калькулятор исключения Гаусса-Жордана — eMathHelp

www.emathhelp.net › калькуляторы › линейная алгебра

Калькулятор выполнит исключение Гаусса для заданной расширенной матрицы с показанными шагами. Полная редукция доступна опционально.

ähnliche suceanfragen

Калькулятор элиминации GAUSS с переменными

Решение линейного уравнения Матрица

Solver Linear System System

Solation Solation Solation Solation levation Solation Solation Solation Solation Solation Solation

Solve Solve Linear Solation Solation Solation

Решение матричного уравнения

scipy.

optimize.fsolve — SciPy v1.10.1 Manual

scipy.optimize.fsolve( Func , x0 , args = () , FPRIME = None , FULL_OUTPUT = 0 , COL_DERIV = 0 , xtol = 1.49012E-08 , xtol = 1.49012E-08 , xtol = 1.49012E-08 , xtol = 1.49012E-08 , . =Нет , epsfcn=Нет , factor=100 , diag=Нет )[источник]

Найдите корни функции.

Возвращает корни (нелинейных) уравнений, заданных формулой func(x) = 0 при начальной оценке.

Параметры:

func callable f(x, *args): Функция, которая принимает хотя бы один (возможно, векторный) аргумент, и возвращает значение той же длины.
x0 ndarray: Начальная оценка корней func(x) = 0 .
args кортеж, необязательный: Любые дополнительные аргументы для func .
fprime
callable f(x, *args) , необязательный: Функция для вычисления якобиана func с производными по рядам. По умолчанию будет оцениваться якобиан.
full_output bool, необязательный: Если True, вернуть необязательные выходные данные.
col_deriv bool, необязательный: Укажите, вычисляет ли функция Якоби производные вниз столбцы (быстрее, потому что нет операции транспонирования).
xtol float, необязательный: Вычисление будет прекращено, если относительная ошибка между двумя последовательных итераций не более xtol .
maxfev int, необязательный: Максимальное количество вызовов функции. Если ноль, то 100*(N+1) — максимум, где N — количество элементов в x0 .
полоса кортеж, необязательный: супердиагонали внутри полосы матрицы Якоби, Матрица Якоби считается ленточной (только для fprime=Нет ).
epsfcn float, опционально: Подходящая длина шага для прямой разницы приближение якобиана (для fprime=None ). Если epsfcn меньше машинной точности, предполагается что относительные ошибки в функциях порядка точность станка.
factor float, необязательный: Параметр, определяющий границу начального шага ( коэффициент * || диаг * х|| ). Должен быть в промежутке (0,1, 100) .
diag последовательность, необязательная: N положительных записей, которые служат коэффициентами масштабирования для переменные.

Возвраты:

x ndarray

Решение (или результат последней итерации для неудачный вызов).

infodict dict

Словарь дополнительных выходов с ключами:

nfev: количество вызовов функций
njev: номер вызова Якобиана
fvec: функция оценивается на выходе
fjac: ортогональная матрица q, созданная QR факторизация окончательного приближенного якобиана матрица, хранимая по столбцам
r: верхняя треугольная матрица, полученная QR-факторизацией той же матрицы
qtf: вектор (транспонирование(q) * fvec)

ier int

Целочисленный флаг.