Решение сложных иррациональных уравнений: Иррациональные уравнения на примерах

Содержание

Сложные преобразования перед введением новой переменной. Пример решения иррационального уравнения.

В записи данного иррационального уравнения (при необходимости смотрите что такое иррациональное уравнение) аж три отдельных корня, более того, есть и переменная не под знаком корня. Из этого сразу понятно, что не стоит прибегать к решению уравнения по определению корня. Также понятно, что и использование метода возведения обеих частей уравнения в квадрат будет не лучшим выбором, так как приведет к уравнению высокой степени. Так что же, вводить новую переменную? Может быть, но сразу не видно, как это сделать. Попробуем провести некоторые преобразования, возможно, они что-то прояснят.

Давайте поработаем с корнем . Проверим, имеет ли квадратный трехчлен 2·x²+5·x+3 корни, для этого нам нужно решить квадратное уравнение 2·x²+5·x+3:

Найденные корни дают нам возможность разложить квадратный трехчлен на множители:
2·x²+5·x+3=2·(x+3/2)·(x+1)= =(2·x+3)·(x+1).

Следовательно, . Учитывая этот результат, исходное уравнение можно записать в следующем виде .

Уже лучше — проявились одинаковые выражения 2·x+3 и x+1. Что дальше? Несложно заметить, что выражение на ОДЗ для исходного уравнения в силу свойства корня из произведения можно представить как . А это не что иное, как удвоенное произведения корней из левой части уравнения и . Это в свою очередь навевает на мысль: нельзя ли выражение в правой части уравнения свернуть в квадрат . Если это так, то мы сможем ввести новую переменную . Проверим эту догадку.

А в правой части уравнения находится выражение , которое можно представить как и дальше в силу последнего полученного результата как .

Итак, от исходного уравнения мы перешли к равносильному уравнению , которое в свою очередь равносильно уравнению .

Полученное уравнение можно решить методом введения новой переменной. Выбранный метод решения предполагает следующую последовательность действий:

Осуществить введение новой переменной.
Решить уравнение с новой переменной. Если оно не имеет решений, то сделать вывод об отсутствии корней решаемого уравнения со старой переменной. Если оно имеет корни, то перейти к следующему шагу.
Возвратиться к старой переменной, составив в зависимости от количества найденных на предыдущем шаге корней, одно уравнение, совокупность нескольких уравнений или совокупность уравнений и/или неравенств.
Наконец, решить составленное уравнение или совокупность.

Принимаем , это от уравнения со старой переменной x приводит нас к уравнению t=t²−20 с новой переменной t.

Решаем уравнение с новой переменной. Оно равносильно квадратному уравнению t

2−t−20=0, которое имеет два корня t₁=−4 и t₂=5 (они легко находятся через дискриминант или по теореме Виета).

Возвращаемся к старой переменной. Мы принимали и нашли t₁=−4, t₂=5, поэтому имеем совокупность двух уравнений .

Осталось решить совокупность. Первое уравнение решений не имеет, так как сумма двух корней не может быть отрицательным числом (при необходимости смотрите метод оценки для решения иррациональных уравнений). Для решения второго уравнения воспользуемся методом возведения обеих частей уравнения в квадрат:

Таким образом, первое уравнение совокупности не имеет корней, а второе уравнение совокупности имеет единственный корень 3. Следовательно, совокупность имеет единственный корень 3. Это означает, что и уравнение имеет единственный корень 3. Следовательно, равносильное ему исходное иррациональное уравнение имеет тот же единственный корень 3.

При желании можно сделать контрольную проверку найденного корня уравнения:

Решение иррациональных уравнений и неравенств 11 класс

Решение иррациональных уравнений и неравенств

Рекомендации выпускникам

школ и абитуриентам технических вузов

Учитель математики СОШ № 8

Погорелая О. И.

Содержание.

I. Введение

II. Основные правила

III. Иррациональные уравнения:

· Решение иррациональных уравнений стандартного вида.

· Решение иррациональных уравнений смешанного вида.

· Решение сложных иррациональных уравнений.

IV. Иррациональные неравенства:

· Решение иррациональных неравенств стандартного вида.

· Решение нестандартных иррациональных неравенств.

· Решение иррациональных неравенств смешанного вида.

V. Вывод

VI. Список литературы

I. Введение

Я, Погорелая О.И., составила рекомендации для выпускников по теме: «Иррациональные уравнения и неравенства».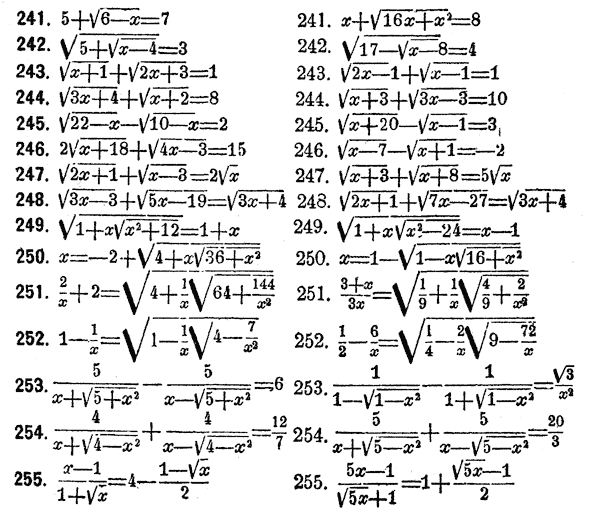

Особенностью моей работы является то, что в школьном курсе на решение иррациональных уравнений отводится очень мало времени, а ВУЗовские задания вообще не решаются. Решение иррациональных неравенств в школьном курсе не рассматривают, а на вступительных экзаменах эти задания часто встречаются.

В данной работе показаны решения как иррациональных уравнений и неравенств стандартного типа, так и повышенной сложности. Поэтому мои рекомендации можно использовать как учебное пособие для подготовки в ВУЗ, также ими можно пользоваться при изучении этой темы на факультативных занятиях.

II. Иррациональные уравнения

Иррациональным называется уравнение, в котором переменная содержится под знаком корня.

Решаются такие уравнения возведением обеих частей в степень. При возведении в четную степень возможно расширение области определения заданного уравнения.

Поэтому при решении таких иррациональных уравнений обязательны проверка или нахождение области допустимых значений уравнений. При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется.

Иррациональные уравнения стандартного вида можно решить пользуясь следующим правилом:

Решение иррациональных уравнений стандартного вида:

а) Решить уравнение = x – 2,

Решение.

= x – 2,

2x – 1 = x² – 4x + 4, Проверка:

x² – 6x + 5 = 0, х = 5, = 5 – 2,

x₁ = 5, 3 = 3

x₂ = 1 – постор. корень х = 1, 1 – 2 ,

Ответ: 5 пост. к. 1 -1.

б) Решить уравнение = х + 4,

Решение.

= х + 4,

Ответ: -1

в) Решить уравнение х – 1 =

Решение.

х – 1 =

х³ – 3х² + 3х – 1 = х² – х – 1,

х³ – 4х² + 4х = 0,

х(х² – 4х + 4) = 0,

х = 0 или х² – 4х + 4 = 0,

(х – 2)

2 = 0,

х = 2

Ответ: 0; 2.

г) Решить уравнение х – + 4 = 0,

Решение.

х – + 4 = 0,

х + 4 = , Проверка:

х² + 8х + 16 = 25х – 50, х = 11, 11 – + 4 = 0,

х² – 17х + 66 = 0, 0 = 0

х₁ = 11, х = 6, 6 – + 4 = 0,

х₂ = 6. 0 = 0.

Ответ: 6; 11.

Решение иррациональных уравнений смешанного вида:

· Иррациональные уравнения, содержащие знак модуля:

а) Решить уравнение =

Решение.

= , _{–
+}

Учитывая ноль подкоренного выражения, данное уравнение равносильно двум системам:

или

Ответ:

б) Решить уравнение

Решение.

, _{– +}

Учитывая ноль подкоренного выражения, данное уравнение равносильно двум системам:

или

Ответ: .

· Иррациональные показательные уравнения:

а) Решить уравнение

Решение.

ОДЗ:

Пусть = t, t > 0

Сделаем обратную замену:

= 1/49, или = 7,

= ,

– (ур-ние не имеет решений) x = 3.

Ответ: 3

б) Решить уравнение

Решение.

Приведем все степени к одному основанию 2:

данное уравнение равносильно уравнению:

Ответ: 0,7

· Иррациональное уравнение, содержащее иррациональность четной степени:

Решить уравнение

Решение.

возведем обе части уравнения в квадрат

3x – 5 – 2

2x – 2 = 2

x –1 =

x Проверка:

x x = 3,

4x 1 = 1.

x = 1,75
Ответ: 3.

· Иррациональное уравнение, содержащее иррациональность нечетной степени:

Решить уравнение

Решение.

возведем обе части уравнения в куб

но , значит:

возведем обе части уравнения в куб

(25 + x)(3 – x) = 27,

Ответ: –24; 2.

· Иррациональные уравнения, которые решаются заменой:

а) Решить уравнение

Решение.

Пусть = t, тогда = , где t > 0

t –

Сделаем обратную замену:

= 2, возведем обе части в квадрат

Проверка: x = 2,5

Ответ: 2,5.

б) Решить уравнение

Решение.

Пусть = t, значит = , где t > 0

t+ t – 6 = 0,

Сделаем обратную замену:

= 2, возведем обе части уравнения в четвертую степень

x + 8 = 16, Проверка:

x = 8, x = 2,

x = 2. 6 = 6

Ответ: 2.

в) Решить уравнение

Решение.

Пусть = t, где t > 0

Сделаем обратную замену:

= 2, возведем обе части уравнения в квадрат

Проверка:

Ответ: –5; 2.

Решение сложных иррациональных уравнений:

· Иррациональное уравнение, содержащее двойную иррациональность:

Решить уравнение

Решение.

возведем обе части уравнения в куб

возведем обе части уравнения в квадрат

Пусть = t

t ²– 11t + 10 = 0,

Сделаем обратную замену: Проверка:

= 10, или = 1, x = ,

x = -пост. корень 0

Ответ: 1. x = 1,

1 = 1

· Иррациональные логарифмические уравнения:

а) Решить уравнение lg3 + 0,5lg(x – 28) = lg

Решение.

lg3 + 0,5lg(x – 28) = lg,

lg(3 = lg,

Учитывая ОДЗ, данное уравнение равносильно системе:

Ответ: 32,75

б) Решить уравнение

Решение.

Ответ: ; – 2; 3.

IV. Иррациональные неравенства

Неравенства называются иррациональными, если его неизвестное входит под знак корня (радикала).

Иррациональное неравенство вида равносильно системе неравенств:

Иррациональное неравенство вида равносильно совокуп-ности двух систем неравенств:

Решение иррациональных неравенств стандартного вида:

а) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

_{+ – +}

Ответ: [1; 2). 1 3 x

б) Решить неравенство

Решение.

Данное неравенство равносильно двум системам неравенств:

Ответ:

в) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ: нет решений

Решение иррациональных неравенств нестандартного вида:

а) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ:

б) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ:

· Решение иррациональных неравенств с помощью правила знаков при умножении и делении:

а) Решить неравенство

Решение.

Учитывая то, что и правило знаков при делении данное неравенство равносильно системе неравенств:

Ответ:

б) Решить неравенство (2x – 5)

Решение.

(2x – 5)

Учитывая то, что и правило знаков при делении данное неравенство равносильно системе неравенств:

Ответ:

· Решение иррациональных неравенств способом группировки:

Решить неравенство

Решение.

сгруппируем по два слагаемых

вынесем общий множитель за скобку

учитывая, что > 0 и правило знаков при умножении данное неравенство равносильно системе неравенств:

Ответ: ( 0; 1 )

· Иррациональное неравенство, содержащее два знака иррациональности:

Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ:

· Решение иррациональных неравенств заменой:

Решить неравенство

Решение.

Пусть = t, тогда = , t > 0

Сделаем обратную замену:

возведем в квадрат обе части неравенства

Ответ:

Решение иррациональных неравенств смешанного вида:

· Иррациональные показательные неравенства:

а) Решить неравенство

Решение.

т.к. y = 0,8^t , то

0,5x(x – 3) < 2,

0,5x² – 1,5x – 2 < 0,

x² – 3x – 4 < 0,

f(x) = x² – 3x – 4,

ОДЗ, _{+
– +}

Нули функции: x₁ = 4; x₂ = – 1. _{–1 4} x

Ответ: х

б) Решить неравенство 4– 2 < 2– 32

Решение.

4– 2 < 2– 32, ОДЗ: x > 0

2– 2 2 < 2 2⁴ – 2⁵, выполним группировку слагаемых

2(2– 2) – 2⁴(2–2) < 0,

(2– 2) (2– 2⁴) < 0, учитывая правило знаков и ОДЗ данное неравенство равносильно 2-м системам:

или

т.к. y = 2^t, то т.к. y = 2^t, то

Ответ: х

· Решение иррациональных логарифмических неравенств:

Решить неравенство

Решение.

уч. ОДЗ данное нер-во равносильно системе нер-ств

Ответ:

V. Вывод

Данные рекомендации помогут выпускникам средней школы научиться решать иррациональные уравнения и неравенства следующих типов: стандартные, показательные, содержащие знак модуля, логарифмические, повышенного уровня.

Примеры взяты и подробно разобраны не только из школьной программы, но и из вступительных экзаменов в школу А.Н. Колмогорова при МГУ, из сборника задач по математике под редакцией М.И. Сканави.

Этот материал может быть интересен и полезен выпускникам школ и абитуриентам технических вузов.

VI. Список литературы

1) Алгебра и начала анализа. Под редакцией А.Н. Колмогорова

2) 3000 конкурсных задач по математике. Авторы: Е.Д. Куланин, В.П. Норин

3) Справочные материалы по математике. Авторы: В.А. Гусев, А.Г. Мордкович

4) Сборник задач по математике. Под редакцией М.И. Сканави

5) Справочный материал

Радикальные уравнения и комплексные числа

Радикальные уравнения и комплексные числа

Радикальные уравнения

Если у нас есть уравнение с одним радикалом, мы следуем процедуре:

Шаг 1. Изолируйте радикал так, чтобы радикал был один с левой стороны. уравнения со всем остальным на другой стороне уравнения.
Шаг 2 Возведите в квадрат обе части уравнения.
Шаг 3. Математика 152A (старый материал).
Шаг 4. Проверьте свой ответ на наличие посторонних решений.

Пример

Решать

— 2 = 5

Раствор

= 7
7x + 4 = (7) ²
7x + 4 = 49
7x = 45
x = 45/7
Теперь подключите и проверьте:
«=» 7 — 2 = 5 ок.

Упражнения

Решать

+ 3 = 6
+ 5 = 2

Комплексные числа (Определения)

Напомним, что мы определили Естественное, Целое, Целое, Рациональное, Иррациональное, и действительные числа. Мы также сказали, что не является реальным числом.

Определение комплексных чисел

Мы определяем

я = (так что i ² = -1)

и пусть Комплексные числа ( C ) быть числами вида

а + би

где а и б являются действительными числами. Мы называем реальная часть и b мнимая часть . Комплексное число называется чистым . мнимый если а = 0.

Пример

2+ = 2 + = 2 + 3i

Упражнение

Представим в комплексной форме следующее:

Сложение и вычитание комплексных чисел

Пусть a + bi и c + di — комплексные числа, тогда

(а + би) + (в + ди) = (а + в) + (б + г) я

Примеры

(2 — 3и) + (5 + 6и) = (2 + 5) + (-3 + 6) i = 7 + 3i

(4 + 2и) — (3 — i) = (4 — 3) + (2 + 1) i = 1 + 3i

Умножение комплексных чисел

Чтобы умножить два комплексных числа, мы в шутку используем FOIL и помним, что

я ² = -1

Пример

(2 — 3и)(5 + я) = 10 + 2i — 15i — 3i ²

«=» 10 — 13i — 3(-1) = 13 — 13i

Упражнения

Умножьте комплексные числа.

(3 + 2и)(3 — 2и)
(5 — я) (2 — 3я)
(4 — и) ²

Отдел комплексных чисел

Пусть a + bi будет комплексным числом, тогда мы определим комплексное сопряжение будет а — би

У нас есть

(а + би) (а — би) = а ² + b ²

Для деления комплексных чисел надо умножить числитель и знаменатель на комплекс сопряженный.

Пример

Разделять

5 — 3i

4 + 2и

Решение

Умножьте верх и низ на 4 — 2i:

(5 — 3и)(4 — 2и)

(4 + 2i)(4 — 2и)

20 — 10i — 12i + 6i ²
«=»
16 + 4

14 — 22i 7–11i
«=» =
20 10

7 11
«=» — я
10 10

Упражнения

Разделите следующее:

1

я
3 — я

3 + я
1 + 2i

3 — 5и

Назад на страницу Экспоненты и радикалы

Назад на страницу «Основная алгебра, часть II»

Назад к математике Домашняя страница отдела

электронная почта Вопросы и предложения

3.

1: Комплексные числа — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 1343

OpenStax
OpenStax

Цели обучения

Выражение квадратных корней из отрицательных чисел в виде кратных \(i\).
Нанесение комплексных чисел на комплексную плоскость.
Сложение и вычитание комплексных чисел.
Умножать и делить комплексные числа.

Изучение математики постоянно саморазвивается. Отрицательные целые числа, например, заполняют пустоту, оставленную набором положительных целых чисел. Множество рациональных чисел, в свою очередь, заполняет пустоту, оставленную множеством целых чисел. Множество действительных чисел заполняет пустоту, оставленную множеством рациональных чисел. Неудивительно, что множество действительных чисел также имеет пустоты. Например, у нас до сих пор нет решения таких уравнений, как 92+4=0\]

Наши лучшие предположения могут быть +2 или -2. Но если мы проверим +2 в этом уравнении, это не сработает. Если мы проверим -2, это не сработает. Если мы хотим получить решение этого уравнения, нам придется пойти дальше, чем мы до сих пор. В конце концов, до сих пор мы описывали квадратный корень из отрицательного числа как неопределенный. К счастью, есть другая система чисел, которая обеспечивает решение подобных проблем. В этом разделе мы рассмотрим эту систему счисления и то, как в ней работать.

Выражение квадратных корней из отрицательных чисел в виде кратных

Мы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренного числа отрицательное, корень называется мнимым числом. Мнимое число i определяется как квадратный корень из минус 1.

\[\sqrt{-1}=i\]

Итак, используя свойства радикалов, 92=−1\]

Мы можем записать квадратный корень любого отрицательного числа как кратное i. Возьмем квадратный корень из –25.

\[\begin{align} \sqrt{-25}&=\sqrt{25 {\cdot} (-1)}\\ &=\sqrt{25}\sqrt{-1} \\ &= 5i \end{align}\]

Мы используем 5 i , а не −5 i , потому что главный корень из 25 является положительным корнем.

Комплексное число представляет собой сумму действительного числа и мнимого числа. Комплексное число выражается в стандартной форме при записи \(a+bi\), где \(a\) — действительная часть, а \(bi\) — мнимая часть. Например, \(5+2i\) — комплексное число. То же самое и с \(3+4\sqrt{3}i\).

Рисунок \(\PageIndex{1}\)

Мнимые числа отличаются от действительных чисел, поскольку возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел.

Мнимые и комплексные числа

Комплексное число — это число вида \(a+bi\), где

\(a\) — действительная часть комплексного числа.
\(bi\) — мнимая часть комплексного числа.

Если \(b=0\), то \(a+bi\) — действительное число. Если \(a=0\) и \(b\) не равно 0, комплексное число называется мнимым числом . Мнимое число – это четный корень из отрицательного числа.

Стандартная форма

Дано мнимое число, выразить его в стандартной форме.

Запишите \(\sqrt{-a}\) как \(\sqrt{a}\sqrt{-1}\).
Выразите \(\sqrt{−1}\) как \(i\) .
Напишите \(\sqrt{a}{\cdot}i\) в простейшей форме.

Пример \(\PageIndex{1}\): Выражение мнимого числа в стандартной форме

Выражение \(\sqrt{−9}\) в стандартной форме.

Решение

\[\sqrt{−9}=\sqrt{9}\sqrt{−1}=3i \nonnumber\]

В стандартной форме это \(0+3i\).

Упражнение \(\PageIndex{1}\)

Экспресс \(\sqrt{−24}\) в стандартной форме.

Ответить: \(\sqrt{−24}=0+2i\sqrt{6}\)

Нанесение комплексного числа на комплексную плоскость

Мы не можем наносить комплексные числа на числовую прямую, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар \((a,b)\), где \(a\) представляет координату по горизонтальной оси, а \(b\) представляет координату по вертикальной оси.

Рассмотрим число \(−2+3i\). Действительная часть комплексного числа равна −2, а мнимая часть равна \(3i\). Мы построили упорядоченную пару \((−2,3)\) для представления комплексного числа \(−2+3i\), как показано на рисунке \(\PageIndex{2}\)

Комплексная плоскость

На комплексной плоскости горизонтальная ось — это действительная ось, а вертикальная ось — воображаемая ось, как показано на рисунке \(\PageIndex{3}\).

How To …

Дан комплексный номер, представить его компоненты на комплексной плоскости.

Определите действительную и мнимую части комплексного числа.
Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
Перемещение параллельно вертикальной оси для отображения мнимой части числа.
Нанесите точку.

Пример \(\PageIndex{2}\): построение комплексного числа на комплексной плоскости

Нанесение комплексного числа \(3−4i\) на комплексную плоскость.

Решение

Действительная часть комплексного числа равна 3, а мнимая часть равна \(−4i\). Наносим упорядоченную пару \((3,−4)\), как показано на рисунке \(\PageIndex{4}\).

Упражнение \(\PageIndex{1}\)

Постройте комплексное число \(−4−i\) на комплексной плоскости.

Ответить: Рисунок \(\PageIndex{5}\)

Сложение и вычитание комплексных чисел

Как и с действительными числами, мы можем выполнять арифметические операции над комплексными числами. Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части и объединяем мнимые части.

Комплексные числа: сложение и вычитание

Сложение комплексных чисел:

\[(a+bi)+(c+di)=(a+c)+(b+d)i\]

Вычитание комплексных чисел:

\[(a+bi) −(c+di)=(a−c)+(b−d)i\]

Как…

Даны два комплексных числа, найдите их сумму или разность.

Определите действительную и мнимую части каждого числа.
Добавьте или вычтите действительные части.
Сложите или вычтите мнимые части.

Пример \(\PageIndex{3}\): добавление комплексных чисел

Добавить \(3−4i\) и \(2+5i\).

Решение

Складываем действительные части и складываем мнимые части.

\[\begin{align*} (a+bi)+(c+di)&=(a+c)+(b+d)i \\ (3−4i)+(2+5i)&= (3+2)+(−4+5)i \\ &=5+i \end{align*}\]

Упражнение \(\PageIndex{3}\)

Вычесть \(2+5i\) из \(3–4i\).

Ответить: \((3−4i)−(2+5i)=1−9i\)

Умножение комплексных чисел

Умножение комплексных чисел очень похоже на умножение биномов. Основное отличие состоит в том, что мы работаем с реальной и мнимой частями отдельно.

Умножение комплексного числа на вещественное число

Начнем с умножения комплексного числа на вещественное число. Мы распределяем действительное число так же, как и биномиальное. Так, например,

Как…

Даны комплексное и действительное числа, умножьте их, чтобы найти произведение.

Использовать свойство дистрибутива.
Упростить.

Пример \(\PageIndex{4}\): умножение комплексного числа на действительное число

Найдите произведение \(4(2+5i).\)

Решение

Распределите 4.

\[\begin{align*} 4(2+5i)&=(4⋅2)+(4⋅5i) \\ &=8+20i \end{align*}\]

Упражнение \(\PageIndex{ 4}\)

Найдите произведение \(−4(2+6i)\).

Ответить

Решение сложных иррациональных уравнений: Иррациональные уравнения на примерах

Сложные преобразования перед введением новой переменной. Пример решения иррационального уравнения.

Решение иррациональных уравнений и неравенств 11 класс

Радикальные уравнения и комплексные числа

3.

Выражение квадратных корней из отрицательных чисел в виде кратных

Нанесение комплексного числа на комплексную плоскость

Сложение и вычитание комплексных чисел

Умножение комплексных чисел

Умножение комплексного числа на вещественное число

Деление комплексных чисел

Упрощающие степени \(i\)

Ключевые понятия

Глоссарий

Добавить комментарий Отменить ответ