Разработка урока по математике 5 класс «Решение текстовых задач с помощью сложения и вычитания»
Автор: Трушина Н.В.
МБОУ «Краснопоймовская СОШ»
Учитель: Трушина Наталья Вячеславовна
Класс: 5 класс
Предмет: математика
Конспект урока на тему: «Решение текстовых задач с помощью сложения и вычитания»
Продолжительность: 45 минут
Тип урока: комбинированный
Форма урока: урок-сказка
Цели урока:
Образовательные цели: создать условия для углубления навыков решения текстовых задач арифметическим способом.
Развивающие цели: создать условия для развития логического мышления, поисково-познавательной активности обучающихся, смекалки, настойчивости и математической речи.
Воспитательные цели: создать условия для воспитания трудолюбия, чувства ответственности за свои знания, за успехи своего коллектива.
План урока:
Организационный момент (1 мин)
Актуализация знаний и умений (устный счет – 10 мин)
Формирование умений и навыков (25 мин)
Физкультминутка (4 мин)
Итоги урока (3 мин)
Постановка домашнего задания (2 мин)
Организационный момент (1 мин)
Приветствие, постановка темы и цели урока.
-Здравствуйте, ребята! Сегодня 19 сентября и тема нашего урока «Решение текстовых задач»
Как вы думаете, чему мы должны с вами сегодня научиться?
А кто мне скажет, какую задачу мы называем текстовой?
Открываем свои тетради, записываем число, классная работа и тема урока. Как вы правильно сказали, целью нашего сегодняшнего урока будет углубление навыков решения текстовых задач. А помогут нам в этом сказочные герои. Ну, что ж, начнем!
— В мире много сказок
Грустных и смешных.
И прожить на свете
Нам нельзя без них!
Пусть герои сказок
Дарят нам тепло,
Пусть добро навеки
Побеждает зло!
2. Актуализация знаний и умений (10 мин)
Устный счет
Помогите Золушке вовремя вернуться домой. Вычислите устно:
а) 23+8+11-12=31+11-12=32-12-8=12
б) 59-56+29-14=3+29-14=32-14-6=12
в) 90-16/2+23/5=12
г) 60-22/2+46/5=12
Помогите Иа найти ошибку и исправить ее:
а) 90+81+9=180
б) 18*4+28*3=156
в) 223+3*9=252
г) 20+16+42=77
3. Формирование умений и навыков (25мин)
Формирование умений и навыков (25мин)
А теперь давайте попробуем решить такую задачу:
Задача №1
В окрестностях пруда четыре болота. В каждом болоте по 58 кочек, а на каждой кочке живет по шесть лягушек. Каждая лягушка мечтает стать лягушкой – путешественницей.
Сколько нужно уток, чтобы осуществилась их мечта?
Надеюсь, вы не забыли способ передвижения лягушки – путешественницы по воздуху!?
Решение:
4*58*6*2=2784 (ут)
Ответ: нужно 2784 утки
Задача №2
Узнав о дне рождения ослика Иа, Винни – Пух решил подарить ему несколько горшочков меда. Придя домой, он обнаружил, что у него есть 25 горшочков. Мед из 15 горшочков он тут же съел, а остальные захватил с собой. По дороге он съел мед еще из 3 горшочков. Сколько горшочков с медом все – таки получил в подарок ослик Иа?
Решение:
25-15-3=7 (г)
Ответ: Иа получил 7 горшочков с медом.
4. Физкультминутка
Раз – подняться, потянуться.
Два – нагнуться, разогнуться.
Три – в ладоши три хлопка.
Головою три кивка.
На четыре – руки шире,
Пять – руками помахать,
Шесть – на место тихо сесть.
Семь и восемь – лень отбросим!
Пока мы с вами отдыхали, наши герои тоже решили попить чай. И вот, что у них произошло…
Задача №3
Белоснежка, Золушка и Спящая Красавица решили попить чай. Белоснежка и Золушка выпили вдвоем 11 чашек, Белоснежка и Спящая Красавица выпили вдвоем 15 чашек, а Золушка и Спящая Красавица выпили вдвоем 14 чашек. Вопрос: сколько чашек чая выпили все три девушки вместе?
Решение:
(11+15+14)/2=20 (ч)
Ответ: вместе они выпили 20 чашек чая.
Решите задачу из учебника:
С. 20 № 74
Первая бригада собрала за смену 52 прибора, вторая – на 9 приборов меньше, чем первая, а третья – на 12 приборов больше, чем вторая. Сколько всего приборов собрали три бригады за смену?
1 бригада – 52 прибора
2 бригада — ? приборов, на 9 приборов меньше, чем первая
3 бригада — ? приборов, на 12 приборов больше, чем вторая
Решение:
52-9=43 (пр) – собрала 2 бригада;
43+12=55 (пр) – собрала 3 бригада;
52+43+55=150 (пр) – собрали три бригады вместе.

Ответ: всего три бригады собрали 150 приборов за смену.
5. Итоги урока (3 мин)
Итак, ребята, сегодня на уроке мы с вами вспомнили, что такое текстовая задача; повторили методы решения текстовых задач, которые вы уже знали и научились новым методам.
6. Постановка домашнего задания:
№68 – на оценку «3»
№72 – на оценку «4»
№75 – на оценку «5»
Карта сайта
Муниципальное бюджетное общеобразовательное учреждение
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА ИМ. Н.С.ПРОКИНА С. НИКОЛО — БАРНУКИПензенская область, Сосновоборский район , с. Николо — Барнуки, ул. Центральная 49а
- Сведения об общеобразовательной организации
- Основные сведения
- Структура и органы управления образовательной организацией
- Документы
- Правоустанавливающие документы
- Локальные акты
- Финансовая деятельность
- Об оказании платных услуг
- Результаты проверок
- О защите ПДн
- Общие документы
- Методическая копилка
- Правоустанавливающие документы
- Локальные акты
- Финансовая деятельность
- Отчеты о результатах самообследования
- Об оказании платных услуг
- Результаты проверок
- О защите ПДн
- Общие документы
- Образование
- Образовательные стандарты РФ
- Руководство.
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав - Материально-техническое обеспечение и оснащённость образовательного процесса
- Стипендии и иные виды материальной поддержки
- Финансово-хозяйственная деятельность
- Вакантные места для приёма (перевода)
- Доступная среда
- Международное сотрудничество
- Дистанционное обучение
- «Я помню и горжусь…
- Food
- Каникулы
- Школьный спортивный клуб
- ГТО
- Здоровьесбережение
- Физическая культура и спорт
- Школьное питание
- Медицинское обслуживание
- Профилактика
- Питание
- Центр «ТОЧКА РОСТА»
- Общая информация о центре «Точка роста»
- Документы
- Образовательные программы
- Педагоги
- Материально-техническая база
- Режим занятий
- Мероприятия
- Дополнительная информация
- Обратная связь (контакты, социальные сети)
- Организация питания в образовательной организации
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Личный кабинет
Выйти
Тесты с ответами, МАТЕМАТИКА, 5 класс
Что проходят в 5 классе по математике?
Математика
Тесты по математике тут…
- Тест по математике 5 класс (Имеет ли точка размерность …)
- Тест по математике Отрезок, Длина отрезка, 5 класс (Что такое …)
- Тест по математике Сравнение натуральных чисел 5 класс (Что означает …)
- Тест Сложение натуральных чисел, Свойства сложения, 5 (В выражении …)
- Тест по математике Вычитание натуральных чисел, 5 класс (В выражении …)
- Тест Числовые и буквенные выражения, Формулы, 5 (Как найти периметр …)
- Тест по математике Уравнение, 5 класс (Что ищут в уравнениях …)
- Тест по математике Понятие обыкновенной дроби, 5 (Число, записанное …)
- Тест Цифры.
 Десятичная запись натуральных чисел, 5 (Знаки, с помощью которых …)
Десятичная запись натуральных чисел, 5 (Знаки, с помощью которых …) - Тест математика 5 класс ( Вычислите: 3,34 + 28,7 …)
- Тест по математике Шкала. Координатный луч, 5 (Одно деление на линейке …)
- Тест Уравнения с ответами, 5 класс, математика (Решите уравнения …)
Вариант программы для 5 класса
Урок 1. Повторение тем 1-4 классов. Нумерация. Разряды. Сравнение чисел. Текстовые задачи разных видов
Урок 2. Геометрические фигуры. Геометрические тела
Урок 3. Ряд натуральных чисел. Десятичная система записи натуральных чисел
Урок 4. Сравнение натуральных чисел
Урок 5. Сложение натуральных чисел. Законы сложения
Урок 6. Вычитание
Урок 7. Решение текстовых задач с помощью сложения и вычитания
Урок 8. Умножение. Законы умножения
Урок 9. Распределительный закон
Урок 10. Сложение и вычитание чисел столбиком
Урок 11. Обобщение и систематизация знаний по теме «Сложение и вычитание натуральных чисел»
Урок 12. Умножение чисел столбиком
Умножение чисел столбиком
Урок 13. Степень с натуральным показателем
Урок 14. Деление нацело
Урок 15. Решение текстовых задач с помощью умножения и деления
Урок 16. Задачи «на части»
Урок 17. Деление с остатком
Урок 18. Числовые выражения
Урок 19. Задачи на нахождение двух чисел по их сумме и разности
Урок 20. Обобщение и систематизация знаний по теме «Натуральные числа и нуль»
Урок 21. Прямая, луч, отрезок
Урок 22. Измерение отрезков
Урок 23. Метрические единицы длины
Урок 24. Представление натуральных чисел на координатном луче
Урок 25. Обобщение и систематизация знаний по теме «Наглядные представления о геометрических фигурах»
Урок 26. Окружность и круг. Сфера и шар
Урок 27. Углы. Измерение углов
Урок 28. Треугольники
Урок 29. Четырёхугольники
Урок 30. Площадь прямоугольника. Единицы площади
Урок 31. Прямоугольный параллелепипед
Урок 32. Объём прямоугольного параллелепипеда. Единицы
объёма
Единицы
объёма
Урок 33. Единицы массы
Урок 34. Единицы времени
Урок 35. Задачи на движение
Урок 36. Обобщение и систематизация знаний по теме «Измерение величин»
Урок 37. Многоугольники
Урок 38. Занимательные задачи по теме «Измерение величин»
Урок 39. Свойства делимости
Урок 40. Признаки делимости
Урок 41. Простые и составные числа
Урок 42. Делители натурального числа
Урок 43. Наибольший общий делитель (НОД)
Урок 44. Наименьшее общее кратное (НОК)
Урок 45. Обобщение и систематизация знаний по теме «Делимость натуральных чисел»
Урок 46. Занимательные задачи по теме «Делимость натуральных чисел»
Урок 47. Понятие дроби
Урок 48. Равенство дробей
Урок 49. Задачи на дроби (нахождение части целого)
Урок 50. Нахождение целого по его части
Урок 51. Приведение дробей к общему знаменателю
Урок 52. Приведение дробей к общему знаменателю. Сокращение дробей
Урок 53. Сравнение дробей
Урок 54. Сравнение дробей. Сравнение с единицей. Сравнение
остатков до единицы
Сравнение дробей. Сравнение с единицей. Сравнение
остатков до единицы
Урок 55. Сложение дробей с одинаковым знаменателем
Урок 56. Сложение дробей с разными знаменателями
Урок 57. Законы сложения
Урок 58. Законы сложения. Решение задач с использованием законов сложения
Урок 59. Вычитание дробей
Урок 60. Решение задач с использованием вычитания дробей
Урок 61. Обобщение и систематизация знаний по теме «Сложение и вычитание дробей»
Урок 62. Умножение натурального числа на дробь
Урок 63. Решение задач на применение умножения дроби на натуральное число и умножение дробей
Урок 64. Законы умножения. Распределительный закон
Урок 65. Деление дробей
Урок 66. Решение задач с использованием деления дробей
Урок 67. Нахождение части целого и целого по его части
Урок 68. Обобщение и систематизация знаний по теме «Умножение и деление дробей»
Урок 69. Задачи на совместную работу
Урок 70. Задачи на совместную работу и движение навстречу друг другу
Урок 71. Понятие смешанной дроби
Понятие смешанной дроби
Урок 72. Сложение смешанных дробей
Урок 73. Вычитание смешанных дробей
Урок 74. Решение задач с применением свойств вычитания смешанных дробей
Урок 75. Умножение смешанных дробей
Урок 76. Деление смешанных дробей
Урок 77. Решение задач с применением правил умножения и деления смешанных дробей
Урок 78. Обобщение и систематизация знаний по теме «Смешанные дроби»
Урок 79. Координатный луч
Урок 80. Представление дробей на координатном луче
Урок 81. Площадь прямоугольника
Урок 82. Объём прямоугольного параллелепипеда
Урок 83. Занимательные задачи по теме «Смешанные дроби»
Урок 84. Итоговое обобщение и систематизация знаний по темам «Делимость натуральных чисел»
Урок 85. Итоговое обобщение и систематизация знаний по темам «Обыкновенные дроби и смешанные дроби»
Онлайн уроки по математике за 5 класс
Учить урок
Цифры и числа. Множество натуральных чисел. Классы и разряды. Большие числа. Порядок действий
Множество натуральных чисел. Классы и разряды. Большие числа. Порядок действий
Учить урок
Составление выражений при решении задач. Знакомство с комбинаторными методами (размещение с повторениями)
Учить урок
Точка и отрезок. Обозначение и построение отрезков. Расположение точек по отношению к отрезку. Сравнение и измерение длин отрезков. Меры длины. Основные свойства измерения отрезков. Ломаная линия. Многоугольники и их основные элементы и характеристики. Треугольник, периметр треугольника.
Учить урок
Отрезок. Обозначение отрезков. Измерение длин. Точки. Расположение точек по отношению к геометрическим фигурам. Сравнение длин отрезков, нахождение/построение отрезков, равных данным
Обозначение отрезков. Измерение длин. Точки. Расположение точек по отношению к геометрическим фигурам. Сравнение длин отрезков, нахождение/построение отрезков, равных данным
Учить урок
Измерение различных величин. Измерительные инструменты. Шкалы. Деления, цена деления
Учить урок
Измерительные инструменты. Шкалы. Деления, цена деления
Учить урок
Координаты. Координатный луч. Измерение расстояний между точками с помощью координатного луча. Сравнение длин отрезков
Учить урок
Составление выражений при решении задач. Знакомство с комбинаторными методами (размещение)
Знакомство с комбинаторными методами (размещение)
Учить урок
Сравнение чисел с одинаковым количеством знаков. Сравнение чисел по расположению на координатной прямой. Двойные неравенства. Сортировка по возрастанию и убыванию. Текстовые задачи, содержащие условия «меньше на..» или «больше на…»
Учить урок
Сложение натуральных чисел. Иллюстрация операции сложения натуральных чисел с помощью координатного луча. Переместительное и сочетательное свойство сложения. Сложение натуральных чисел с нулем. Демонстрация свойств сложения с помощью координатного луча. Группировка слагаемых. Округление натуральных чисел при сложении
Учить урок
Разряды и классы. Разрядные слагаемые. Сумма разрядных слагаемых. Таблица сложения натуральных чисел. Поразрядное сложение натуральных чисел. Сложение натуральных чисел столбиком. Округление и группировка натуральных чисел при сложении.
Разрядные слагаемые. Сумма разрядных слагаемых. Таблица сложения натуральных чисел. Поразрядное сложение натуральных чисел. Сложение натуральных чисел столбиком. Округление и группировка натуральных чисел при сложении.
Учить урок
Вычитание натуральных чисел. Иллюстрация операции вычитания натуральных чисел с помощью координатного луча. Свойства вычитания натуральных чисел. Демонстрация свойств вычитания с помощью координатного луча. Сравнение двух натуральных чисел с помощью вычитания.
Учить урок
Правила нахождения компонентов вычитания. Таблица сложения/вычитания натуральных чисел. Поразрядное вычитание натуральных чисел. Вычитание натуральных чисел «столбиком». Округление натуральных чисел при вычитании.
Учить урок
Задачи, решаемые с помощью сложения. Задачи, решаемые с помощью вычитания. Решение составных текстовых арифметических задач на сложение и вычитание. Округление натуральных чисел
Учить урок
Числовые выражения. Значение числового выражения. Буквенные выражения. Значение выражения при заданном значении переменной. Применение числовых и буквенных выражений в математике
Учить урок
Выражения с переменной. Тождества. Тождественные преобразования числовых и буквенных выражений. Буквенная запись свойств сложения натуральных чисел. Буквенная запись свойств вычитания натуральных чисел
Буквенная запись свойств вычитания натуральных чисел
Учить урок
Уравнение. Корень уравнения. Запись уравнений. Равносильные уравнения. Решение уравнений. Решение задач с помощью уравнений
Учить урок
Смысл умножения. Компоненты умножения. Буквенная запись свойств умножения. Упрощение буквенных выражений с использованием свойств умножения
Учить урок
Компоненты деления. Свойства деления. Алгоритм проверки правильности решения. Деление «уголком». Упрощение буквенных выражений и решение уравнений, содержащих действие деления
Учить урок
Деление натуральных чисел с остатком. Компоненты математической операции деления с остатком: делимое, делитель, неполное частное, остаток. Нахождение компонентов деления с остатком. Решение текстовых задач
Компоненты математической операции деления с остатком: делимое, делитель, неполное частное, остаток. Нахождение компонентов деления с остатком. Решение текстовых задач
Учить урок
Свойства умножения натуральных чисел. Свойства деления натуральных чисел
Учить урок
Виды простых арифметических задач на умножение и деление. Примеры решения задач арифметическим способом на умножение и деление. Правило проверки правильности вычислений умножения и деления натуральных чисел. Решение задач на умножение и деление алгебраическим способом
Учить урок
Упрощение выражения. Основные способы упрощения математического выражения. Упрощение математических выражений при решении уравнений и текстовых задач
Основные способы упрощения математического выражения. Упрощение математических выражений при решении уравнений и текстовых задач
Учить урок
Действия первой и второй ступени. Порядок выполнения действий в выражениях без скобок. Порядок выполнения действий в выражениях со скобками
Учить урок
Степень числа. Основание и показатель степени. Квадрат и куб числа. Таблицы квадратов и кубов первого десятка натуральных чисел. Порядок выполнения действий в выражениях, содержащих степень. Примеры нахождения значения выражений, содержащих квадраты и кубы чисел. Стандартный вид числа
Учить урок
Понятие формулы. Выражение одной величины через другие известные величины. Общие правила оформления и решения задач с использованием формул. Примеры зависимостей между величинами. Решение текстовых задач с помощью формул
Выражение одной величины через другие известные величины. Общие правила оформления и решения задач с использованием формул. Примеры зависимостей между величинами. Решение текстовых задач с помощью формул
Учить урок
Прямоугольник и квадрат. Понятие площади и ее единицы измерения. Свойства площади. Равные фигуры. Формулы площади прямоугольника и квадрата. Примеры решение текстовых задач по теме.
Учить урок
Единицы измерения длины и площади. Взаимосвязь единиц измерения площади между собой, правило перевода из одной единицы измерения в другую. Правила и способы измерения площадей. Примеры решение текстовых задач по теме
Учить урок
Прямоугольный параллелепипед и его элементы. Измерения прямоугольного параллелепипеда. Куб. Площадь поверхности прямоугольного параллелепипеда. Примеры решение текстовых задач по теме
Измерения прямоугольного параллелепипеда. Куб. Площадь поверхности прямоугольного параллелепипеда. Примеры решение текстовых задач по теме
Учить урок
Объем. Единицы измерения объема. Правило перевода из одной кубической единицы измерения в другую. Объем прямоугольного параллелепипеда. Объем куба. Основные свойства объема. Решение задач с использованием формулы объема прямоугольного параллелепипеда
Учить урок
Окружность и круг. Основные характеристики окружности и круга. Круговая диаграмма. Длина окружности. Циркуль. Построение окружности (круга) с заданным радиусом
Учить урок
Доли. Сравнение долей. Обыкновенные дроби. Числитель и знаменатель дроби. Чтение и запись обыкновенных дробей. Изображение дробных чисел на координатном луче
Сравнение долей. Обыкновенные дроби. Числитель и знаменатель дроби. Чтение и запись обыкновенных дробей. Изображение дробных чисел на координатном луче
Учить урок
Нахождение части от целого. Нахождение целого по его части. Алгоритм и примеры решения задач на нахождение части от целого и целого по его части
Учить урок
Сравнение дробей с одинаковым числителем. Сравнение дробей с одинаковым знаменателем. Сравнение дробей с различными числителями и знаменателями. Приведением дробей к общему знаменателю
Учить урок
Правильная дробь. Неправильная дробь. Сравнение правильных и неправильных дробей. Расположение правильных и неправильных дробей на координатном луче. Примеры решения задач на нахождение части от целого и целого по части
Неправильная дробь. Сравнение правильных и неправильных дробей. Расположение правильных и неправильных дробей на координатном луче. Примеры решения задач на нахождение части от целого и целого по части
Учить урок
Правила сложения и вычитания обыкновенных дробей с одинаковыми знаменателями. Иллюстрация операции сложения и вычитания дробей с помощью координатного луча. Решение уравнений и простых текстовых задач с использованием правил сложения и вычитания дробей с одинаковыми знаменателями
Учить урок
Запись частного в виде дроби. Решение уравнений, содержащих дроби. Решение текстовых задач с использованием обыкновенных дробей
Учить урок
Смешанное число. Целая и дробная часть смешанного числа. Правило перевода смешанного числа в неправильную дробь. Правило выделения целой части из неправильной дроби. Изображение смешанных чисел на координатном луче
Целая и дробная часть смешанного числа. Правило перевода смешанного числа в неправильную дробь. Правило выделения целой части из неправильной дроби. Изображение смешанных чисел на координатном луче
Учить урок
Сравнение смешанных чисел. Правила сложения смешанных чисел. Правила вычитания смешанных чисел. Решение текстовой задачи на сложение и вычитание смешанных чисел
Учить урок
Десятичные дроби. Правила записи и чтения десятичных дробей. История возникновения десятичных дробей. Перевод обыкновенной дроби в десятичную дробь и обратно
Учить урок
Разряды десятичных дробей. Разложение десятичной дроби по разрядам. Изображение десятичных дробей на координатном луче. Правила сравнения десятичных дробей
Разложение десятичной дроби по разрядам. Изображение десятичных дробей на координатном луче. Правила сравнения десятичных дробей
Учить урок
Правила сложения десятичных дробей. Правила вычитания десятичных дробей. Правила сложения и вычитания десятичных дробей столбиком. Решение текстовой задачи на сложение и вычитание десятичных дробей
Учить урок
Приближенные значения с избытком. Приближенные значения с недостатком. Правило округления чисел до заданного разряда. Примеры округления чисел
Учить урок
Умножение десятичных дробей на натуральное число. Умножение десятичных дробей на 10, 100, 1000 и т.д. Примеры решение текстовых задач по теме
Умножение десятичных дробей на 10, 100, 1000 и т.д. Примеры решение текстовых задач по теме
Учить урок
Деление десятичных дробей на натуральное число. Деление натуральных чисел без остатка. Деление десятичных дробей на 10, 100, 1000 и т.д. Примеры решения текстовых задач по теме
Лэйдл предлагает пройти уроки математики за 5 класс в режиме онлайн. Дополнительные занятия позволят подтянуть знания по той или иной теме, разобраться в точных науках и значительно повысить успеваемость в школе.
Программа 5 класса включает в себя информацию о натуральных числах и арифметических операциях с ними, начальные знания о геометрических фигурах и вычислении их площади, а также сведения о дробях и остатках. Все это – база, без которой невозможно дальнейшее изучение математики. Вот почему дополнительные онлайн-уроки просто необходимы школьникам, испытывающим проблемы с точными науками.
3 причины выбрать Лэйдл
- Готовая программа.
Команда опытных преподавателей собрала самую важную информацию за 5 класс и представила ее в простой и структурированной форме, значительно облегчив процесс обучения. - Мультимедийные материалы.
Красочные фото и детальные видео помогают освоить арифметику и геометрию – ребенок легче воспринимает теорию и учится применять полученные знания на практике. - Задачи и уравнения.
На сайте представлены не только теоретические уроки, но и многочисленные задачи и уравнения, которые полностью соответствуют школьной программе. После прохождения такого «испытания» вызов к доске будет не страшен.
Решите проблему с изучением математики раз и навсегда – зарегистрируйтесь на Лэйдл и радуйтесь успехам своего ребенка!
Этапы урока | время | Деятельность учащихся | Деятельность учителя | УУД |
I. Организационная часть. | 1 мин | Приветствие, | ||
II. Выборочное краткое домашней работы | до 10 минут | Анализируют ошибки допущенные, при решение заданий. Выполняют вычисления с натуральными числами | Организует работу учащихся | Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Познавательные: умения формулировать вопросы к тексту, самостоятельно формулировать ответы с опорой на текст. |
Самоопределение к деятельности. Этап работы с информацией. | 5 мин | Разбирают решение задачи рабочей тетради стр13. № 44 | Организует и контролирует обсуждение вопросов. | |
IV. Постановка учебной задачи | 1-2 мин | Устанавливаем цели урока. | Организует работу по целеполаганию и мотивации | Регулятивные: целеполагание. Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение-формулирование |
V. Этап тренинга | 10 мин | Обсуждаем, что это за этап, производим целеполагание, планирование, распределение времени, задаём необходимость самооценки и коррекции результатов. Решают в парах задачи 45 – 47. По истечении отведённого для выполнения заданий времени производим самооценку и коррекцию результатов. | Организует и контролирует работу учащихся. Организует обсуждение и итоги работ. | Познавательные УУД: формирование умений по использованию математических знаний для решения различных математических задач и оценки полученных результатов; – по использованию доказательной математической речи; – по работе с информацией, в том числе и с различными математическими текстами; – регулятивные УУД (формирование умений ставить личные цели деятельности, планировать свою работу, действовать по плану, оценивать полученные результаты; – коммуникативные УУД формирование умений совместно с другими детьми в группе находить решение задачи и оценивать полученные результаты. |
VI. Физкультминутка. | 1-2 мин | Ученики выполняют упражнение. | Сядьте равно. Руки положите за спины. Не поворачивая головы, посмотрите на окно, на стенд на противоположной стороне, наверх, на парту, на доску. Закройте глаза, представьте голубое небо. Откройте глаза. Руки положите на стол. Продолжим… | |
VII. Этап закрепления нового материала. Работа с самопроверкой по эталону | 20 мин | Выполняют самостоятельно с взаимопроверкой задания на стр. 20. № 71(а), 72(а), 74 По истечении времени, отведённого для выполнения работы, её результаты выносятся для обсуждения в классе: | Организует выполнение учащимися самостоятельной работы, самопроверку, самооценку. | познавательные УУД формирование умений по использованию математических знаний для решения различных математических задач и оценки полученных результатов; регулятивные УУД формирование умений ставить личные цели деятельности, планировать свою работу, действовать по плану, оценивать полученные результаты; коммуникативные УУД формирование умений совместно с другими детьми в группе сверять полученные результаты с образцом. |
VI. Домашнее задание | 1 мин | Записывают домашнее задание | Комментирует дом задание: Стр.21 Информационный блок . № 74, 75 | |
VII. Рефлексия Подведение итогов урока | 1 мин | Участвуют в рефлексии, выражают свое настроение. устно оценивают содержание урока. | Организует рефлексию.. Я предлагаю вам закончить предложения: Мне на уроке понравилось… Мне показалось трудным… Я бы ещё хотел выполнить … Главным результатом считаю… | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Регулятивные: оценка, самооценка |
Подборка по базе: Рбочая программа (ID 4690901) 7 класс история.  docx, Разработка занятия по финансовой грамотности _Как накопить, чтоб, Методика организации мастер класса.pdf, 10 класс онегин.docx, Разработка урока на тему_ %22Холодная война%22 (11 класс).docx, Итоговый тест по обществознанию 9 класс.docx, местоимения 3 класс.docx, конспектГероическая тема в русской музыке 7 класс.docx, конспект по музыке 5 класс фольклор.docx, Об утверждении классификации видов работ, выполняемых при содерж docx, Разработка занятия по финансовой грамотности _Как накопить, чтоб, Методика организации мастер класса.pdf, 10 класс онегин.docx, Разработка урока на тему_ %22Холодная война%22 (11 класс).docx, Итоговый тест по обществознанию 9 класс.docx, местоимения 3 класс.docx, конспектГероическая тема в русской музыке 7 класс.docx, конспект по музыке 5 класс фольклор.docx, Об утверждении классификации видов работ, выполняемых при содержТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ 5 класс МАТЕМАТИКА (34 час)
|
Как преподавать задачи на сложение и вычитание
Мои ученики мучились с тем, как решать задачи на сложение и вычитание , казалось, целую вечность. Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа вместе, не понимая смысла задачи.
Тьфу.
Вы можете рассказать?
Я большой сторонник НЕ преподавания списков ключевых слов. Это просто не работает последовательно во всех проблемах. Это короткий путь, ведущий к сбоям в математическом мышлении. Я более подробно рассказываю о том, почему это не работает, в статье «Проблема с использованием ключевых слов для решения текстовых задач».
Это просто не работает последовательно во всех проблемах. Это короткий путь, ведущий к сбоям в математическом мышлении. Я более подробно рассказываю о том, почему это не работает, в статье «Проблема с использованием ключевых слов для решения текстовых задач».
Вы можете узнать больше о ресурсе задач на сложение и вычитание, который я использую в своем классе, в этой записи блога.
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении словесным задачам с использованием любого ресурса.
Итак, как мне учить текстовые задачи? Это довольно сложно, но так весело, как только вы войдете в него.
Основные компоненты обучения задачам на сложение и вычитание включают:
- Обучение связи числа s — Как учитель, знайте тип задачи и помогайте учащимся решать действия в задаче
- Дифференцируйте числа — Дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязая в вычислениях
- Используйте академический словарь — и будьте последовательны в том, что вы используете.

- Хватит искать «Ответ» — дело не в ответе; речь идет о процессе
- Различия между моделями и стратегиями — один связан с отношениями между числами, а другой — с тем, как учащиеся «решают» или вычисляют задачу.
Обучаю соотношению чисел в задачах со словами
Я обучаю задачам со словами, удаляя числа. Звучит странно, верно? Удаление отвлекающих факторов помогает учащимся сосредоточиться на проблемной ситуации и понять действие или взаимосвязь чисел. Это также удерживает учащихся от решения задачи до того, как мы поговорим о взаимосвязи чисел.
Когда я преподаю текстовые задачи, я даю ученикам задачи с пробелами и без чисел. Сначала поговорим о действии в задаче. Мы определяем, добавляется ли что-то к чему-то другому или отнимается от чего-то другого. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.
___ + ___ = неизвестно
Хотите бесплатный образец текстовых задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже. БЕСПЛАТНЫЙ образец текстовых задач по типу задачи
БЕСПЛАТНЫЙ образец текстовых задач по типу задачи
Различие чисел в задачах Word
Только после того, как мы обсудили задачу, я даю ученикам числа. Я различаю числа в зависимости от потребностей учащихся. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что ученики понимают процесс.
После того, как учащиеся ознакомятся с процессом, я начинаю давать разным учащимся разные числа в зависимости от их уровня математического мышления. Я также меняю числа в течение года с однозначных на двузначные числа. Прелесть пустых мест в том, что я могу вставить в задачу любые числа, которые захочу, чтобы попрактиковаться в стратегиях, над которыми мы работали в классе.
В какой-то момент мы создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, соединяют ли эти действия что-то или разделяют. Сколько вы можете придумать? Вот несколько идей:
Присоединяйтесь: положил, получил, взял, купил, сделал
Раздельно: съел, потерял, положил, уронил, использовал
Не бойтесь использовать академическую лексику
Я учу своих учеников определять начало проблемы, изменение в задаче и результат в задаче. Я учу их искать неизвестных . Это все слова, которые мы используем при решении задач, и мы изучаем структуру словесной задачи через словарный запас и взаимосвязь чисел.
Я учу их искать неизвестных . Это все слова, которые мы используем при решении задач, и мы изучаем структуру словесной задачи через словарный запас и взаимосвязь чисел.
На самом деле, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.
Возьмите эти примеры, можете ли вы определить начало , изменение и результат в каждой задаче?
Подсказка: посмотрите на код, используемый для типа задачи, в правом нижнем углу.
Для задач сравнения мы используем термины больше , меньше , больше и меньше . Попробуйте решить эти задачи и посмотрите, сможете ли вы определить компоненты словесных задач.
Перестаньте искать «ответ»
Это заблуждение труднее всего разрушить. Студенты не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, я хочу, чтобы ученики могли объяснить свой процесс и понять глубину текстовых задач.
Итак, это первоклассники и второклассники. Я знаю.
Мои ученики все еще могут объяснить после обучения, что они начинают ed с одного числа. Проблема результат ед в другом другом номере. Затем учащиеся узнают, что они ищут замену на между этими двумя числами.
Все дело в отношениях.
Различие между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь учащимся разработать адекватные модели для понимания взаимосвязи чисел в задаче.
У меня в голове взорвалась лампочка. Мне нужно было провести различие между моделями, которые студенты используют для понимания связи чисел в задаче, и стратегиями решения вычислений в задаче. Эти две вещи работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми учащийся решает задачу, складывая и разбирая числа.
Самое главное в моделях — отойти от них. Я знаю, это звучит странно.
Я знаю, это звучит странно.
Вы так долго обучаете студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели. Ну, на самом деле, вы хотите, чтобы студенты двигались к эффективности.
Младшие школьники разыгрывают задачи, рисуют задачи с изображениями и рисуют задачи с кругами или линиями. Направьте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять отношение чисел
Это яркий пример перехода от модели перевернутой v к модели столбцов.
Ученик переходит от рисования кругов к использованию перевернутой буквы v.
Учащиеся должны полностью использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока выясняют сходство между моделями.
Студенты также должны иметь возможность создавать свои собственные модели. Вы увидите, как я иногда давал ученикам копии модели, которые они могли вклеить в свои тетради, а иногда ученики рисовали свою собственную модель. Они должны нести ответственность за выбор того, что лучше всего подходит для них. Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них для использования. Всегда подталкивайте учащихся к более эффективным моделям.
Они должны нести ответственность за выбор того, что лучше всего подходит для них. Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них для использования. Всегда подталкивайте учащихся к более эффективным моделям.
То же самое касается стратегий для вычислений. Сначала обучайте стратегиям с помощью математических фактов, а затем применяйте их к текстовым задачам, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них для использования. При обучении сосредоточьтесь на одной или двух стратегиях. Как только учащиеся овладеют некоторыми стратегиями, попросите их выбрать стратегии, которые работают для решения различных задач.
Будьте целеустремленны в числах, которые вы выбираете для своих словесных задач. Разные наборы чисел подходят для разных стратегий и разных моделей. Используйте числовые наборы, которые учащиеся уже использовали в вычислениях. Если вы научились делать 10, используйте числа, которые составляют 10. Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислениями и решением задачи, тем лучше.
Чем больше связей вы сможете установить между вычислениями и решением задачи, тем лучше.
Приведенные выше примеры в основном предназначены для задач объединения и разделения. Неудивительно, что у наших студентов такие трудности с задачами на сравнение, поскольку мы не учим их в той же степени, что и задачи на соединение и разделение. Нашим ученикам нужно еще больше практиковаться в подобных задачах, потому что отношения между числами более абстрактны. Однако я собираюсь оставить это для другого поста в блоге.
Хотите БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения задачам на сложение и вычитание по типу задач 9?0005 ? Нажмите на эту ссылку или изображение ниже.
Полный ресурс также доступен в моем магазине для покупки и на сайте Teachers Pay Teachers.
Дополнительные идеи для обучения словесным задачам
Ключевые слова словесных задач на сложение и вычитание
Словесные задачи на сложение и вычитание обычно преподаются во втором классе (ключевой этап 1 в Великобритании) или во втором классе (в США).
Стратегия решения текстовых задач состоит в том, чтобы, во-первых, выписать соответствующие числа, а во-вторых, решить, какую операцию использовать, прочитав ключевые слова в вопросе.
Чтобы решить задачи на сложение и вычитание, мы пытаемся прочитать вопрос и найти ключевые слова. Приведенный ниже список ключевых слов поможет определить, есть ли у нас задача на сложение или вычитание слов.
Некоторые общие ключевые слова добавления:
- Добавить
- Плюс
- Подробнее
- Всего
- Увеличение
- Вместе / Всего
- Комбинированный
- Сумма
- Расти
Если мы видим эти слова, у нас, вероятно, есть проблема со сложением слов.
Некоторые общие ключевые слова вычитания:
- Вычесть
- Минус
- Забрать
- Меньше / Меньше
- Разница
- Уменьшение
- Сколько осталось/осталось?
- Сдача – в денежных вопросах
- Слова, оканчивающиеся на «эр», например, короче, длиннее, быстрее.

Вот наш первый пример словесной задачи.
У Уильяма 20 жетонов, и ему дается еще 7 .
Сколько у него в всего ?
Мы видим, что у нас есть два дополнительных ключевых слова: « больше » и « всего ».
При обучении словесным задачам полезно сначала выписывать числа, которые есть в тексте вопроса.
У нас есть 20 и 7.
Слова « больше » и « всего » говорят нам, что это задача на сложение слов. Начинаем с 20 фишек и добавляем еще 7.
Как только мы узнаем, что у нас есть задача на сложение слов, мы можем складывать числа.
20 + 7 = 27
Всего у Уильяма 27 жетонов.
Вот еще один пример словесной задачи.
У Фиби 12 см ленты, а у Джека 23 см.
Сколько у них всего ?
Наша стратегия состоит в том, чтобы сначала выписать числа, участвующие в вопросе.
Мы записываем 12, а затем 23. Мы можем писать числа друг над другом и выстраивать цифры в каждом числе.
В этом вопросе есть только одно ключевое слово — , всего .
Это ключевое слово добавления, которое говорит нам, что мы хотим объединить две суммы, чтобы получить общую сумму.
Мы хотим сложить числа 12 и 23.
На этом этапе дети обычно записывают единицы, участвующие в вопросе. Однако проще всего просто записать сами числа, а затем вставить единицы измерения в конце вопроса, чтобы проверить результат.
Добавляем столбец единиц, 2 + 3 = 5.
Складывая цифры в столбце десятков, 1 + 2 = 3.
Следовательно, 12 + 23 = 35 и, следовательно, у нас всего 35 см ленты.
Мы измеряем длину ленты в см, поэтому в конце ответа пишем «см».
Вот еще один пример словесной задачи.
Я покупаю 2 конфеты по 43 пенса каждая.
Сколько они стоят в итого ?
Каждая конфета стоит 43 пенса и их две.
В этом вопросе дважды пишем 43.
Ключевое слово « всего » говорит нам, что это задача на сложение слов.
Мы добавим две суммы 43, написав их цифры непосредственно друг над другом, не написав «пенс» в конце.
Складывая единицы, 3 + 3 = 6.
Складываем десятки, 4+4=8.
Две конфеты стоят в общей сложности 86 пенсов.
Мы можем написать пенсы или «п» в окончательном ответе теперь, когда расчет сделан.
В этой формулировке вопроса у нас есть только одно число в самом тексте. Написано только одно «43».
При обучении детей словесным задачам может помочь нарисовать диаграмму, чтобы помочь представить ситуацию.
Вот еще одна проблема слов, связанная с деньгами.
У Мэтью 35 пенсов.
Он тратит 13 пенсов.
Сколько у него осталось ?
Записываем задействованные числа, а именно 35 и 13.
В этой текстовой задаче ключевое слово слева .
Нахождение того, сколько осталось , является ключевым словом для задачи на вычитание слов.
Это означает, что мы вычитаем меньшее число из большего числа.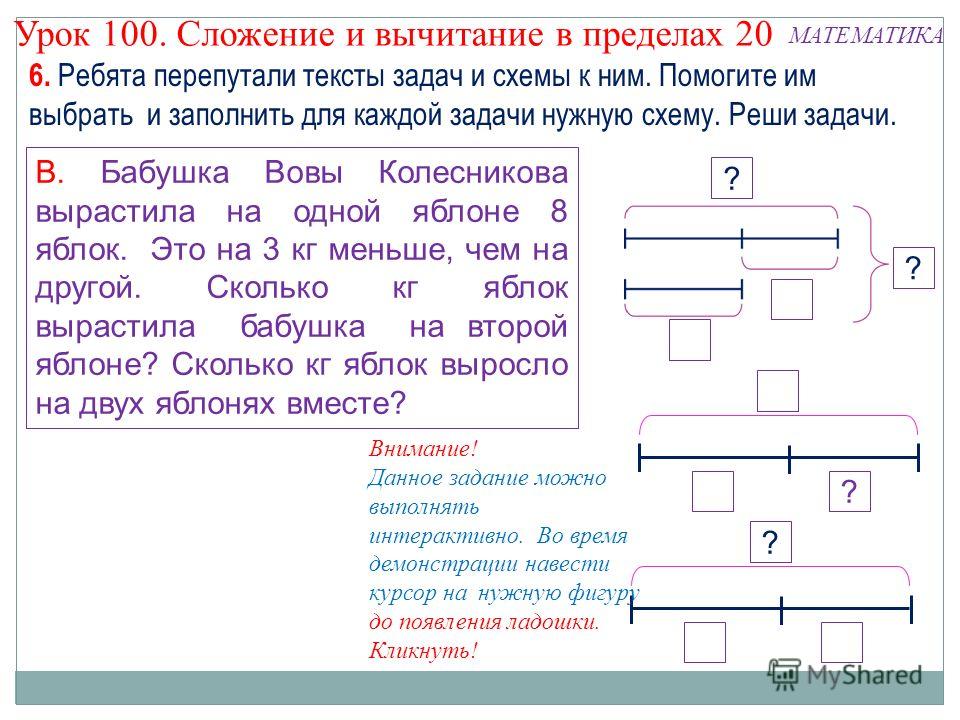
Чтобы вычесть 13 из 35, мы записываем большее число над меньшим числом и выстраиваем цифры.
Вычитая столбец единиц, 5 – 3 = 2.
Вычитая столбец десятков, 3 – 1 = 2.
35 – 13 = 22
Это была проблема, связанная с поиском сдачи деньгами.
Трата денег, а затем получение сдачи также, скорее всего, указывает на то, что проблема со словами связана с вычитанием.
В следующей сформулированной задаче у Адама есть 59 граммов шоколада.
Он съедает 49 грамм.
Сколько у него осталось ?
Первый шаг стратегии словесных задач состоит в том, чтобы выписать оба числа, участвующие в вопросе.
У нас есть 59 и 49.
Второй шаг — определение ключевых слов. Слово оставило — ключевое слово вычитания.
Мы хотим увидеть, сколько осталось от после того, как 49 граммов были вычтены из из .
Мы записываем вычитание с большим числом над меньшим числом.
Вычитая цифры столбца единиц, 9 – 9 = 0.
Вычитая цифры столбца десятков, 5 – 4 = 1.
59 – 49= 10.
Шоколада осталось 10 грамм.
Вот еще один пример словесной задачи.
У меня есть свеча длиной 38 см.
После того, как я зажигаю, 11 см тает .
Какой длины сейчас свеча?
Эта проблема со словами сложнее, поскольку в вопросе нет прямых ключевых слов.
Однако фраза « тает » говорит нам, что мы удаляем или вычитаем.
Опять же, при обучении текстовым задачам полезным приемом является рисование диаграммы.
Если нет диаграммы или рисунка, полезно нарисовать ситуацию в начале, а также ситуацию в конце.
Вычитая цифры в столбце единиц, 8 – 1 = 7.
Если вычесть цифры в столбце десятков, 3 – 1 = 2.
38 – 11 = 27
Осталось 27 см свечи.
В этом примере свеча уменьшилась в размере, потому что мы удаляли длину по мере ее плавления.
Свеча стала короче . Shorter — это слово, оканчивающееся на «er», что также может указывать на то, что у нас есть проблема с вычитанием слов.
Слова «э-э» часто ищут разницу между двумя значениями, а поиск разницы — это вычитание.
Опять же, это может помочь нарисовать ситуацию с помощью диаграммы, чтобы помочь понять, какой у нас тип словесной задачи.
Fifth Grade Math – обучение и практика математики для 5-го класса
[«`#», «Моя учетная запись»]Описание класса: Учащиеся более глубоко изучают закономерности и операции разрядного значения. Их понимание расширяется и включает десятичные дроби в сотых и тысячных, операции с дробями и десятичными дробями, многозначное умножение и деление с остатками, модели площади, свойства умножения и деления, оценку и измерение объема. Введем координатную плоскость (квадрант I), которую учащиеся используют для решения задач.
Дошкольный классДетский сад1 класс 2 класс 3 класс 4 класс 5
Pre-kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 5
МОДУЛЬ 1.
 Разрядное значение и десятичные дроби
Разрядное значение и десятичные дробиТема A: Мультипликативные закономерности на таблице разрядного значения и разделить для решения задач с десятичным числом в качестве множителя или частного.
Умножение на 10 с таблицей разрядных значений и без нее
Узнайте, как быстро умножить число на 10. Используйте таблицу разрядных значений, чтобы облегчить перестановку цифр с использованием концепции разрядных значений. Затем примените полученные знания, чтобы умножить на 10, не имея таблицы разрядности 9.0007
Умножение на 100 с таблицей стоимостей и без нее
Узнайте, почему умножение на 100 равносильно двукратному умножению на 10. Используйте таблицу разрядных значений, чтобы умножить число (до 4 цифр) на 100 путем сдвига цифр с использованием концепции разрядного значения. Затем примените полученные знания, чтобы умножить на 100
Умножить на 1000 с таблицей стоимостей и без нее
Узнайте, что умножение на 1000 равносильно трехкратному умножению на 10. Используйте диаграмму разрядности, чтобы умножить число (до 4 цифр) на 1000 путем сдвига цифр с использованием концепции разрядности 9.0007
Используйте диаграмму разрядности, чтобы умножить число (до 4 цифр) на 1000 путем сдвига цифр с использованием концепции разрядности 9.0007
Умножение на 10, 100 и 1000
Потренируйтесь умножать число на 10, 100 или 1000. Используйте понимание разрядности, чтобы переместить цифры в нужное место и добавить соответствующее количество нулей в конце числа. product
Завершите схему умножения на 10 или 100
Изучите схему чисел и вставьте число, которое правильно завершает схему. Используйте понимание умножения на 10, 100 или 1000, чтобы определить, какой фактор создает шаблон
Деление на 10 с таблицей разрядов и без нее
Научитесь быстро делить число на 10. Определите число, показанное на таблице разрядов. Затем используйте диаграмму, чтобы помочь в смещении цифр, чтобы смоделировать деление. Наконец, примените полученные знания, чтобы разделить на 10
Разделить на 100 с таблицей стоимостей и без нее
Узнайте, почему деление на 100 равносильно двойному делению на 10.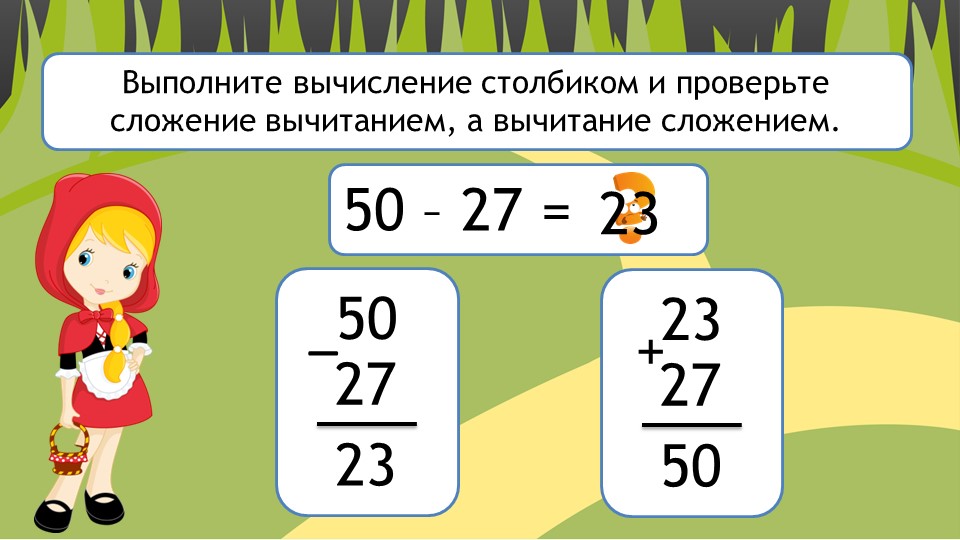 Используйте диаграмму разряда, чтобы разделить число на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания для деления на 100 без таблицы 9.0007
Используйте диаграмму разряда, чтобы разделить число на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания для деления на 100 без таблицы 9.0007
Деление на 1000 с таблицей разрядных значений и без нее
Попрактикуйтесь в делении числа, состоящего из 4 и более цифр, на 1000. Сначала вы можете выбрать использование таблицы разрядных значений для моделирования трехкратного деления на 10. Затем примените полученные знания, чтобы удалить правильное количество нулей из частного. значение, чтобы переместить цифры в соответствующее место и удалить правильное количество нулей с конца
Найдите и завершите образец деления на 10 или 100
Изучите образец чисел и вставьте число, которое правильно завершает образец. Используйте понимание деления на 10, 100 или 1000, чтобы определить, какой делитель образует закономерность
Выносите на множители степени 10, чтобы умножать числа с одной ненулевой цифрой
Узнайте, как умножать два числа, кратные 10.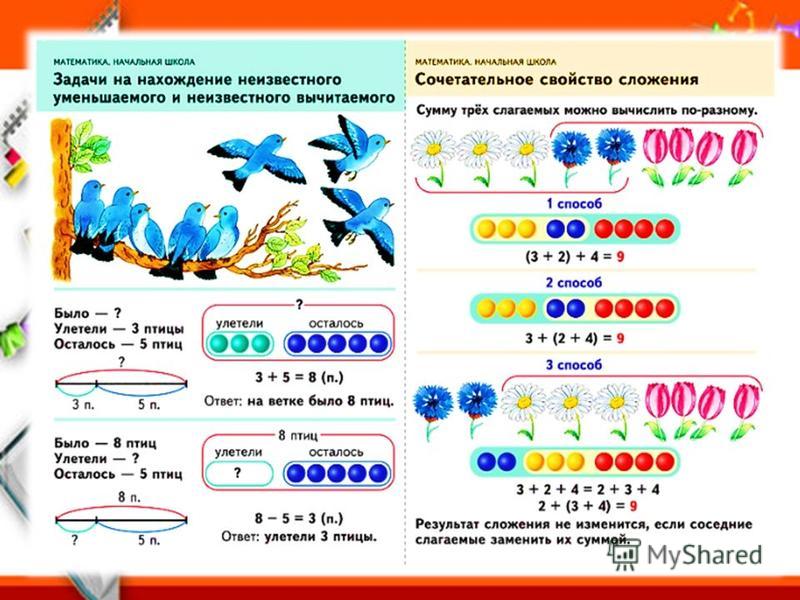 Во-первых, распознавать ненулевые цифры и практиковаться в написании до 6-значных чисел с одной ненулевой цифрой. Затем научитесь умножать два числа, разлагая на множители и переставляя ненулевые цифры
Во-первых, распознавать ненулевые цифры и практиковаться в написании до 6-значных чисел с одной ненулевой цифрой. Затем научитесь умножать два числа, разлагая на множители и переставляя ненулевые цифры
Умножение чисел с одной ненулевой цифрой
Практика умножения двух чисел, кратных степеням 10
Запись соотношения между сотыми и тысячными долями с помощью таблицы разрядных значений
Изучение соотношения между сотыми и тысячными разрядными значениями десятичных знаков. Используйте десятичные счетчики и эквивалентные им дроби для сокращения дробей
Умножение десятичного числа на 10 с таблицей разрядов и без нее
Быстрое умножение десятичного числа на 10. Используйте диаграмму разряда, чтобы помочь в смещении цифр, используя концепцию разряда. Затем примените полученные знания, чтобы умножить на 10, не имея таблицы разрядности 9.0007
Умножение десятичного числа на 100 с таблицей разрядов и без нее
Узнайте, почему умножение на 100 равносильно двойному умножению на 10.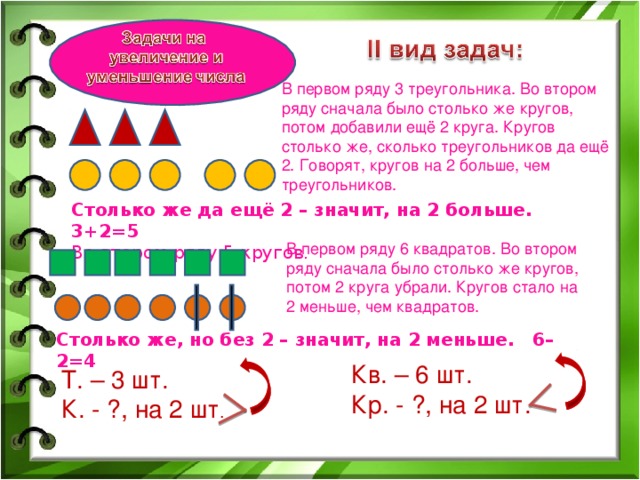 Используйте диаграмму разряда, чтобы умножить десятичную дробь на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания, чтобы умножить на 100 без таблицы
Используйте диаграмму разряда, чтобы умножить десятичную дробь на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания, чтобы умножить на 100 без таблицы
Умножить десятичное число на 1000 с таблицей разрядных значений и без нее
Узнайте, что умножение на 1000 равносильно умножению на 10 три раза. Первоначально вы можете использовать диаграмму разряда для моделирования умножения десятичного числа на 1000 путем сдвига цифр, используя концепцию разряда 9.0007
Умножение десятичного числа на 10, 100 и 1000
Потренируйтесь умножать десятичное число на 10, 100 или 1000. Используйте понимание разрядности, чтобы переместить цифры в нужное место. Кроме того, изучите взаимосвязь между нулями множителя и движением десятичной точки.
Заполните образец умножения на 10, 100 и 1000
Изучите образец десятичных чисел и вставьте число, которое правильно завершает образец. Используйте понимание умножения десятичной дроби на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Преобразование единиц, десятых, сотых и тысячных в задачах на деление.

Используйте названия мест, чтобы помочь в задачах на деление. Создавайте эквивалентные выражения, вводя правильные термины
Разделите десятичное число на 10 с таблицей разрядов и без нее
Быстро разделите десятичное число на 10. Используйте диаграмму разряда, чтобы помочь в смещении цифр, используя концепцию разряда. Затем примените полученные знания, чтобы разделить на 10, не имея при себе таблицы стоимостей 9.0007
Разделить десятичное число на 100 с таблицей разрядов и без нее
Узнайте, почему деление на 100 равносильно двойному делению на 10. Используйте диаграмму разряда, чтобы разделить десятичную дробь на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания для деления на 100 без таблицы
Разделите десятичное число на 1000 с таблицей разрядов и без нее
Узнайте, что деление на 1000 равнозначно трехкратному умножению на 10. Первоначально вы можете использовать диаграмму разряда для моделирования деления десятичной дроби на 1000 путем сдвига цифр с использованием концепции разряда.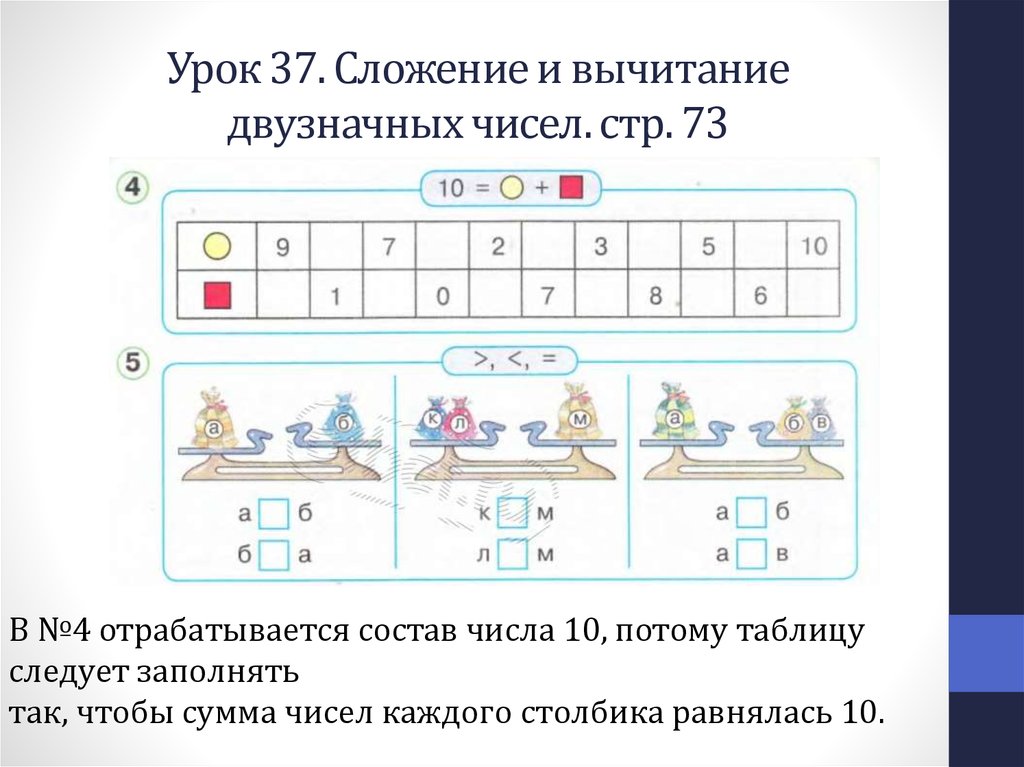 Затем примените понимание
Затем примените понимание
Разделите число на 10, 100 и 1000
Попрактикуйтесь в делении десятичной дроби на 10, 100 или 1000. Используйте понимание разрядности, чтобы переместить цифры в нужное место. Кроме того, изучите соотношение между нулями делителя и движением десятичной точки.
Заполните образец деления на 10, 100 и 1000
Изучите образец десятичных чисел и вставьте число, которое правильно завершает образец. Используйте понимание деления десятичной дроби на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Представление многократного умножения 10 в виде 10 с показателем степени
Изучите взаимосвязь между повторным умножением на 10 и количеством нулей в произведении. Представление повторяющихся множителей 10 в виде показателей степени 10
Представление числа 10 с показателем степени в виде повторного умножения
Узнайте взаимосвязь между экспоненциальным выражением и его выражением умножения. Определите показатель степени в выражении. Разверните показатель степени 10 в выражение умножения. Кроме того, потренируйтесь переписывать число как показатель степени 10 9.0007
Определите показатель степени в выражении. Разверните показатель степени 10 в выражение умножения. Кроме того, потренируйтесь переписывать число как показатель степени 10 9.0007
Умножение десятичного числа на 10 с показателем степени
Узнайте, как разложить числа, умноженные на степень 10. Используйте понимание степени 10 и умножения десятичных дробей, чтобы разложить числа. Этот навык часто используется в науке для записи очень больших чисел в экспоненте
Деление числа на 10 с показателем степени
Расширение чисел, которые делятся на степень 10. Используйте понимание показателей степени 10 и деления десятичных дробей для расширить числа
Тема B: Десятичные дроби и модели разрядов
Учащиеся используют знакомые символы (<, =, >) для сравнения чисел до тысячных. Они определяют, составляют и упорядочивают числа равной и неравной длины.
Запишите десятичное число в расширенной системе счисления
Узнайте, как преобразовать десятичное число в сумму его разрядных компонентов.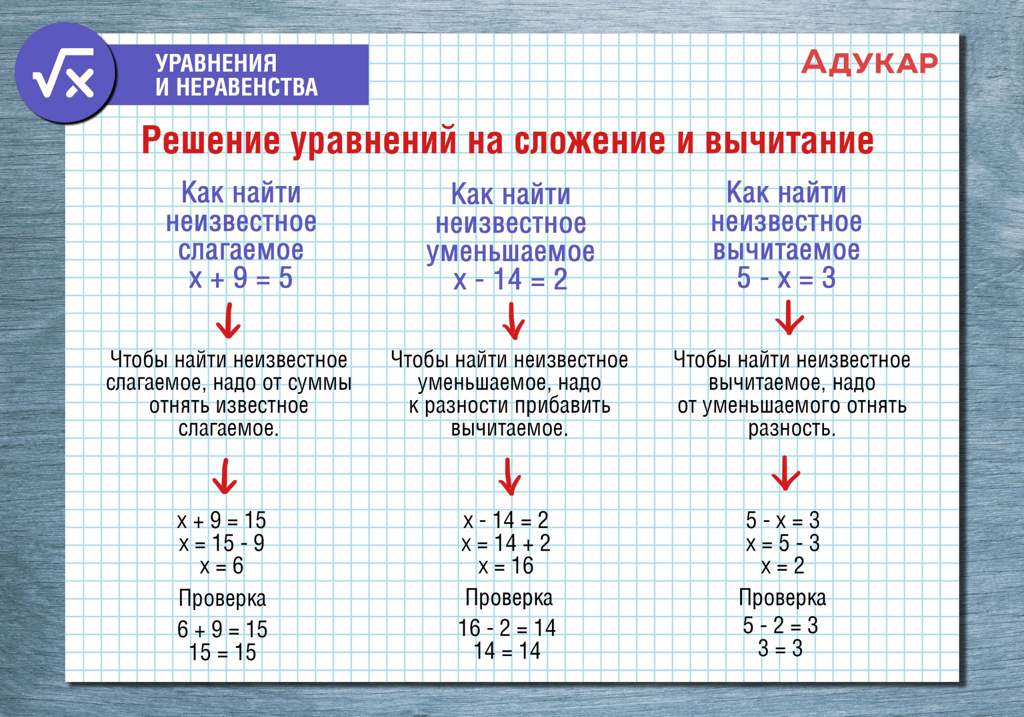 Определите разрядное значение каждой цифры в десятичной дроби. Затем покажите развернутую сумму, из которой получилось число
Определите разрядное значение каждой цифры в десятичной дроби. Затем покажите развернутую сумму, из которой получилось число
Сравнение чисел с точностью до сотых с таблицей разрядов и без нее
Научитесь сравнивать десятичные дроби. Используйте диаграмму стоимости мест, чтобы сравнить каждый набор значений мест слева направо. Затем используйте полученные знания для сравнения двух десятичных дробей без помощи таблицы.
Завершите неравенства, сравнивающие числа до сотых долей.
Потренируйтесь сравнивать десятичные дроби. Сначала вставьте правильный символ неравенства, чтобы сравнить два числа. Затем выберите правильное число, чтобы создать истинное утверждение о неравенстве. Затем проверьте свое понимание, вставив цифру, чтобы сделать утверждение о неравенстве
Расположите десятичные числа в порядке от наименьшего к наибольшему (Уровень 1)
Научитесь расставлять десятичные числа в порядке от наименьшего к наибольшему. Расставь три числа по порядку, поставив между ними правильный знак неравенства. Кроме того, потренируйтесь расставлять числа так, чтобы они были в правильном порядке.
Кроме того, потренируйтесь расставлять числа так, чтобы они были в правильном порядке.
Расположите десятичные числа в порядке от наименьшего к наибольшему (уровень 2)
Потренируйтесь расставлять десятичные числа по порядку. Переставить 4 числа от наименьшего к наибольшему
Расставить десятичные числа в порядке от наименьшего к наибольшему (уровень 3)
Потренируйтесь упорядочивать десятичные числа. Переставьте 4 числа от наименьшего к наибольшему
Тема C: Разрядное значение и округление десятичных дробей
Используя числовую прямую для предоставления контекста, учащиеся сначала определяют среднюю точку между двумя десятичными числами. Затем они переходят к округлению, используя числовую прямую и среднюю точку. Наконец, учащиеся округляют десятичные числа до любого заданного разряда без использования числовой строки.
Определить среднюю точку между двумя десятичными числами на числовой прямой
Узнайте, как легко определить середину между двумя десятичными знаками. Во-первых, используйте числовую строку, чтобы определить среднюю точку между двумя десятичными числами, отмеченными на этой числовой строке. Затем определите среднюю точку между двумя десятичными знаками, представленными в словесных выражениях
Во-первых, используйте числовую строку, чтобы определить среднюю точку между двумя десятичными числами, отмеченными на этой числовой строке. Затем определите среднюю точку между двумя десятичными знаками, представленными в словесных выражениях
Определите, находится ли десятичное число больше или больше половины расстояния между двумя точками на числовой прямой
Узнайте, как определить, находится ли десятичное число меньше или больше половины между два заданных числа на числовой прямой. Сначала найдите десятичную дробь на числовой прямой. Затем найдите точку на полпути между двумя числами в строке чисел 9.0007
Составьте и примените правило округления чисел
Изучите правила округления десятичных дробей. Используйте числовую строку, чтобы определить, следует ли округлить данное десятичное число в большую или меньшую сторону, а затем выберите правильный ответ. Завершите предложения правил округления
Определите, округляется ли десятичное число вверх или вниз
Практика округления десятичных чисел.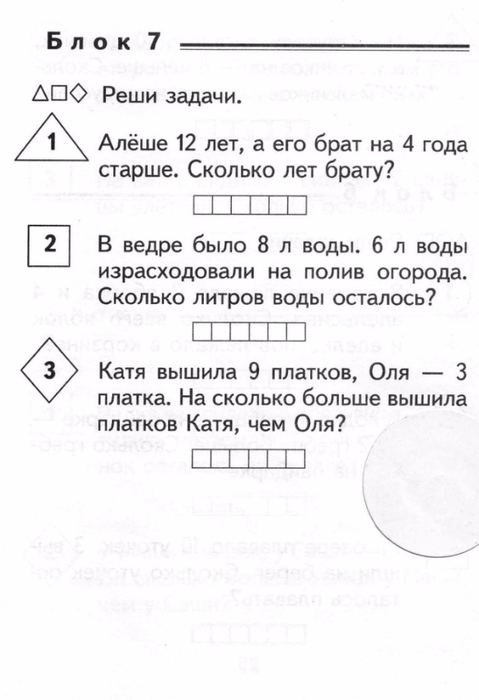 Учитывая десятичное число на баскетбольном мяче, выберите, в какую корзину должен попасть мяч, чтобы правильно округлить число
Учитывая десятичное число на баскетбольном мяче, выберите, в какую корзину должен попасть мяч, чтобы правильно округлить число
Округлить заданное число, сначала определив его ближайшие десятые доли
Научитесь округлять десятичное число, определяя ближайшие числа, до которых можно округлить данное десятичное число. Затем определите среднюю точку между ближайшими числами. Определите, меньше или больше заданное число средней точки, и округлите соответственно
Округлите данное число до сотых, десятых и единиц
Потренируйтесь округлять одно и то же число до ближайших сотых, десятых и единиц. Введите правильное значение, округленное до соответствующего разряда
Округлите десятичное число до заданного разряда (уровень 1)
Практика округления чисел. Выберите правильный ответ на вопросы с округлением, чтобы решить головоломку с картинками
Округлите десятичное число до заданного разрядного значения (Уровень 2)
Узнайте, как проверить разрядные значения для правильного округления. Определите разрядное значение, до которого вы хотите округлить, и разрядное значение справа от него. Затем определите, округляется ли значение вверх или вниз, и введите правильное округленное значение
Определите разрядное значение, до которого вы хотите округлить, и разрядное значение справа от него. Затем определите, округляется ли значение вверх или вниз, и введите правильное округленное значение
Округлите десятичное число до заданного разряда (уровень 3)
Узнайте, как округлить до указанного разряда. Определите разрядное значение справа от значения, до которого следует округлить, затем определите, следует ли округлить в большую или меньшую сторону, и введите правильное округленное значение
Округлите десятичное число до заданного разрядного значения (уровень 4)
Практика округления чисел к заявленной стоимости места. Используйте свое понимание правил округления
Тема D: Сложение и вычитание десятичных знаков
На основе знакомой модели диска учащиеся складывают и вычитают числа до разряда тысяч. Они складывают и вычитают в уравнениях, требующих перегруппировки, и учатся использовать стандартный алгоритм (сложение столбцов и вычитание столбцов).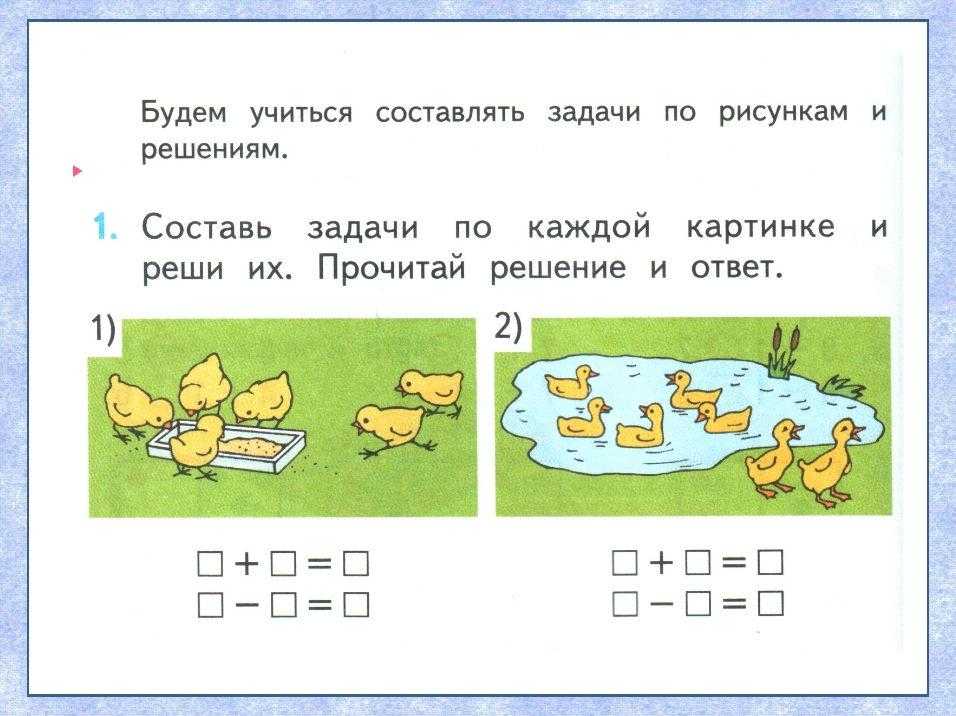
Сложение чисел до сотых с перегруппировкой с использованием модели диска
Научитесь складывать два десятичных числа (до сотых). Представьте каждое число моделью дисков для каждого разряда. Затем соедините диски с одинаковым разрядом двух чисел, чтобы получить сумму
Сложите числа до тысячных с перегруппировкой с помощью модели диска
Узнайте, как складывать два десятичных числа (до тысячных). Представьте каждое число моделью дисков для каждого разряда. Затем объедините диски с одинаковыми разрядами двух чисел, чтобы получить сумму 9.0007
Сложение чисел до разряда тысячных с перегруппировкой с использованием сложения столбцов и модели диска
Сложение двух десятичных чисел (до разряда тысяч). Перепишите задачу на сложение в виде столбцов и используйте модели дисков, чтобы помочь найти сумму с любой необходимой перегруппировкой
Добавление чисел до тысячных с перегруппировкой с использованием сложения столбцов
Узнайте, как складывать два десятичных числа (до разряда тысяч). Перепишите задачу на сложение в виде столбца, чтобы лучше визуализировать любую необходимую перегруппировку при нахождении суммы
Перепишите задачу на сложение в виде столбца, чтобы лучше визуализировать любую необходимую перегруппировку при нахождении суммы
Вычитание чисел до сотых с перегруппировкой с использованием модели диска
Вычитание двух десятичных чисел (до сотых). Смоделируйте задачу на вычитание с помощью дисков, включая необходимую перегруппировку
Вычитание чисел до тысячных с перегруппировкой с использованием модели диска
Вычитание двух десятичных чисел (до сотых). Смоделируйте задачу на вычитание с помощью дисков, включая любую необходимую перегруппировку
Вычитание чисел до тысячных с перегруппировкой, используя вычитание столбцов и модель диска
Научитесь вычитать два десятичных числа (до разряда тысяч). Перепишите задачу на вычитание в виде столбцов и используйте модели дисков, чтобы помочь найти разницу с любой необходимой перегруппировкой
Вычитание чисел разной длины до тысячных с перегруппировкой, используя вычитание столбцов и модель диска
Научитесь вычитать два десятичных числа разной длины. Перепишите задачу на вычитание в виде столбцов и используйте модели дисков, чтобы помочь найти разницу с любой необходимой перегруппировкой
Перепишите задачу на вычитание в виде столбцов и используйте модели дисков, чтобы помочь найти разницу с любой необходимой перегруппировкой
Вычитание чисел до тысячных с перегруппировкой с использованием вычитания столбцов
Научитесь вычитать два десятичных числа (до тысячных). Перепишите задачу на вычитание в виде столбца, чтобы лучше визуализировать любую необходимую перегруппировку при поиске разницы
Тема E: Умножение десятичных чисел
Учащиеся делают первые шаги в понимании умножения десятичных чисел. Работая с однозначным целым числом и десятичным числом, учащиеся шаг за шагом выполняют процесс, используя знакомую модель диска. Они обмениваются дисками, чтобы смоделировать перегруппировку и изучить важность размещения десятичной точки.
Умножение десятичного числа с перегруппировкой с использованием модели диска
Узнайте, как умножить целое число на десятичную. Используйте модель диска для представления десятичной дроби и ее умножения.
Умножьте десятичное число с перегруппировкой, используя модель диска и стандартный алгоритм.
Умножьте целое число на десятичную дробь. Используйте модель диска, чтобы представить десятичную дробь и ее умножение, и перепишите задачу в виде столбца
Сравните умножение целого числа с умножением числового числа с теми же цифрами
Узнайте, как использовать умножение целых чисел, чтобы помочь с умножением десятичной дроби на целое число. Определите, используют ли десятичное и связанное с ним целое одни и те же цифры. Сравните произведение десятичного числа и целого числа с произведением
Умножьте десятичное число, преобразовав его в целое число, а произведение обратно в десятичное число
Преобразуйте десятичное число в целое, чтобы помочь в решении задачи на умножение. Определите соответствующий коэффициент, чтобы преобразовать десятичную дробь в целое число. Затем найти продукт. Наконец, преобразуйте ответ обратно в десятичную цифру 9. 0007
0007
Тема F: Деление десятичных дробей
Учащиеся полагаются на знакомые модели и процедуры, чтобы применить свои знания о делении десятичных дробей. Шаг за шагом они учатся правильно работать с помощью перегруппировки, использования нового разряда, использования нулей и добавления десятичной дроби в частное.
Разделение десятичного числа на однозначное число на основе модели
Узнайте, как разделить десятичное число на целое число. Используйте модель диска, чтобы физически найти частичные частные каждого разрядного значения. Может потребоваться перегруппировка
Деление десятичного числа на однозначное число с перегруппировкой и без нее на основе модели
Деление десятичной дроби на целое число. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Разделение десятичного числа на однозначное число с перегруппировкой и без нее на основе модели
Научитесь делить десятичную дробь на целое число. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Деление десятичного числа на однозначное число с перегруппировкой в новое разрядное значение на основе модели
Узнайте, как делить десятичное число на целое число, если в частном больше десятичных разрядов, чем в делимом. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Перегруппировка на новое разрядное значение будет
Деление десятичного числа на однозначное число с перегруппировкой и без нее с использованием деления в большую сторону и модели
Используйте длинное деление с делением десятичной дроби на целое число. Перепишите задачу на деление в длинном формате деления. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Может потребоваться перегруппировка
Деление в длинное для деления десятичного числа на однозначное число с перегруппировкой и без нее
Научитесь делить десятичное число на целое с помощью деления в длинное. Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разряда и запишите их в длинном делении. Может потребоваться перегруппировка
Используйте длинное деление, чтобы разделить десятичное число на однозначное число с частными, которые включают 0
Разделите десятичное число на целое, используя длинное деление. Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разряда и запишите их в длинном делении. Иногда частичное частное может быть равно 0, поэтому перегруппировка может
Использовать длинное деление для деления десятичного числа на однозначное число с перегруппировкой до нового разрядного значения
Деление десятичной дроби на целое в длинное деление и что делать, если последняя цифра не делится нацело. Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разрядного значения и запишите их в длинном делении
Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разрядного значения и запишите их в длинном делении
МОДУЛЬ 2. Операции с многозначными целыми числами и десятичными дробями
Тема A: Умственные стратегии для умножения многозначных целых чисел
Учащиеся работают с круглыми числами в десятках, сотнях и тысячах, чтобы увидеть, как факторизация может облегчить умственное умножение. При этом они применяют свойства умножения.
Уменьшить 10, 100 или 1000 из заданного числа
Уменьшить 10, 100 или 1000 из числа. Сначала умножьте число на 10, 100 или 1000, а затем изучите, как эти два фактора формируют произведение. Затем назовите множители для данных кратных 10, 100 или 1000
Решите задачи на умножение, используя ассоциативные и коммутативные свойства
Изучите ассоциативные и коммутативные свойства умножения. Изучите наборы факторов, чтобы определить, меняет ли их расположение ответ. Этот навык может помочь вам упростить задачи на умножение, чтобы иметь возможность быстро находить произведение с помощью меня
Решите задачу на умножение нескольких цифр, используя факторизацию и свойства умножения (Уровень 1)
Узнайте, как использовать факторизацию 10, 100 и 1000 и свойства умножения для умножения больших чисел. Вынесите на множители 10,100 или 1000, а затем сгруппируйте вместе однозначные числа и степени 10
Вынесите на множители 10,100 или 1000, а затем сгруппируйте вместе однозначные числа и степени 10
Решите в уме задачу на умножение многозначных чисел
Попрактикуйтесь в использовании ментальной арифметики для умножения больших чисел. Этот навык позволит вам быстрее решать проблемы
Решите задачу на умножение нескольких цифр, используя факторизацию и свойства умножения (уровень 2)
Используйте факторизацию 10, 100 и 1000 и свойства умножения для умножения больших чисел. Вынесите на множители 10 100 или 1000, а затем сгруппируйте вместе однозначные числа и степени 10. Перестановка множителей позволяет быстро умножать
Круглые многозначные числа для оценки площади прямоугольника
Узнайте, как оценить площадь прямоугольника. Округлите измерения длины и ширины, а затем умножьте их, чтобы оценить площадь. Это позволяет быстро рассчитать примерную площадь
Округлите многозначные числа для оценки произведения.
Оцените ответ на задачу на умножение слов. Округлите большие числа до крайнего левого разряда. Затем используйте понимание степеней 10 и свойств умножения, чтобы быстро найти оценку ответа
Округлите большие числа до крайнего левого разряда. Затем используйте понимание степеней 10 и свойств умножения, чтобы быстро найти оценку ответа
Тема B: Стандартный алгоритм умножения многозначных целых чисел
работа с многозначными числами. Они осваивают использование перегруппировки и работу с нулями. Для дальнейшего концептуального понимания стандартный алгоритм представлен вместе с другими стратегиями, такими как модель площади и факторизация степеней числа 10.
Определение суммы, разности, произведения и частного в уравнениях
Изучите определения слов сумма, разность и частное. Выберите правильное слово для типа показанного уравнения. Затем сопоставьте тип задачи со словом ее результата
Составьте простые числовые выражения из текста
Научитесь преобразовывать словесные выражения в математические выражения. Из данного утверждения напишите математическое выражение, которое представляет слова. Этот навык поможет вам решать текстовые задачи, используя правильные операции
Составление выражений сложения и умножения с несколькими слагаемыми или множителями
Научитесь преобразовывать словесные выражения, содержащие более двух чисел, в математические выражения. Из данного утверждения напишите выражение сложения или умножения, которое представляет слова
Из данного утверждения напишите выражение сложения или умножения, которое представляет слова
Составьте сложные числовые выражения на основе модели (Часть 1)
Преобразуйте словесное выражение с тремя числами в математическое выражение. Используя диаграмму, вы выберете правильные действия и расставите числа в соответствующем порядке, чтобы образовать выражение
Составление сложных числовых выражений на основе модели (Часть 2)
Узнайте, как преобразовать словесное выражение с тремя числами в математическое выражение. Используя диаграмму, вы будете выбирать правильные операции и располагать числа в соответствующем порядке, чтобы образовать выражение
Составление сложных числовых выражений на основе модели (часть 3)
Преобразование словесного выражения с тремя числами в математическое выражение. Используя диаграмму, вы выберете правильные действия и расставите числа в соответствующем порядке, чтобы образовать выражение
Умножение по стандартному алгоритму (1 цифра на 3 цифры)
Узнайте, как умножить однозначное число на трехзначное. Перепишите задачу в виде столбца с большим числом вверху. Понимать, как умножать справа налево, переводя десятки частичного произведения в разрядное значение слева
Перепишите задачу в виде столбца с большим числом вверху. Понимать, как умножать справа налево, переводя десятки частичного произведения в разрядное значение слева
Умножать по стандартному алгоритму (1 цифра на 4 цифры)
Умножать однозначное число на четыре -цифровое число. Перепишите задачу в виде столбца с большим числом вверху. Понять, как умножать справа налево, переводя десятки частичного произведения в разрядное значение слева
Вынесение на множители степеней 10 для упрощения выражений умножения
Упрощение выражений умножения путем вынесения на множители степеней 10. Применение свойств умножения для перестановки множителей, чтобы иметь возможность использовать ментальную арифметику для быстрого завершения умножения
Решить связанные выражения умножения после разложение на множители степени числа 10
Узнайте, как быстро умножать большие числа. Умножьте на соответствующую однозначную цифру, а затем используйте понимание степеней 10 и их количество нулей, чтобы найти конечный продукт
Умножение в уме числа степени 10
Практикуйте математические методы в уме, чтобы быстро умножать большие числа. Используйте понимание степеней 10. Вы можете использовать форму столбца для умножения связанной задачи перед добавлением соответствующего количества нулей к конечному результату
Используйте понимание степеней 10. Вы можете использовать форму столбца для умножения связанной задачи перед добавлением соответствующего количества нулей к конечному результату
Умножьте на число со степенью 10, используя стандартный алгоритм
Узнайте, как умножить двузначное число на кратное 10, используя умножение в столбик. Используйте пошаговые инструкции, чтобы найти частичные продукты, которые формируют окончательный ответ
Умножение с использованием модели площади и стандартного алгоритма
Нахождение площади прямоугольника. Узнайте, как разбить прямоугольник на части с площадью, которую легче вычислить. Обратите внимание, как площади частей представлены в частичных произведениях стандартного алгоритма
Умножение по стандартному алгоритму (3 цифры на 3 цифры) (Часть 1)
Узнайте, как умножать два трехзначных числа. Перепишите задачу в виде столбца. Поймите, как умножать справа налево, чтобы найти частичные произведения. Затем добавьте частичные произведения, чтобы найти окончательный ответ
Умножение по стандартному алгоритму (3 цифры на 3 цифры) (Часть 2)
Умножение двух трехзначных чисел. Перепишите задачу в виде столбца. Поймите, как умножать справа налево, чтобы найти частичные произведения, включая эффект цифры 0. Затем сложите частичные произведения, чтобы получить окончательный ответ.
Перепишите задачу в виде столбца. Поймите, как умножать справа налево, чтобы найти частичные произведения, включая эффект цифры 0. Затем сложите частичные произведения, чтобы получить окончательный ответ.
Умножьте, используя стандартный алгоритм (3 цифры на 4 цифры) (Часть 1)
Узнайте, как умножить 3-значное число на 4-значное число. Перепишите задачу в виде столбца. Понять, как умножать справа налево, чтобы найти частичные произведения, и как найти сумму этих произведений для окончательного ответа
Умножение по стандартному алгоритму (3 цифры на 4 цифры) (Часть 2)
Умножение 3-значного числа на 4-значное число. Перепишите задачу в виде столбца. Понять, как умножать справа налево, чтобы найти частичные произведения, включая влияние цифры 0
Умножать по стандартному алгоритму (2 цифры на 5 цифр)
Научиться умножать 5-значное число на 2-значный номер. Перепишите задачу в виде столбца. Понять, как умножать справа налево, чтобы найти частичные произведения, и как найти сумму этих произведений для окончательного ответа
Тема C: Десятичное многозначное умножение
Учащиеся расширяют свое понимание умножения десятичных чисел, увеличивая количество цифр в множителях. Работая с 2- или 3-значным целым числом и десятичным числом в десятых или сотых долях, учащиеся шаг за шагом выполняют процесс, используя стандартный алгоритм. Они узнают, как поставить десятичную дробь в своем ответе и как оценить, чтобы проверить обоснованность своего ответа.
Работая с 2- или 3-значным целым числом и десятичным числом в десятых или сотых долях, учащиеся шаг за шагом выполняют процесс, используя стандартный алгоритм. Они узнают, как поставить десятичную дробь в своем ответе и как оценить, чтобы проверить обоснованность своего ответа.
Умножение 2-значного десятичного числа на 2-значное целое с использованием частичных произведений с моделью площади
Умножение 2-значного десятичного числа на 2-значное целое число. Используйте сегментированный прямоугольник для представления частичных произведений в соответствующем умножении целого числа на целое число. Применить понимание разряда, чтобы найти произведение десятичных чисел
Умножить двузначное десятичное число на двузначное целое число, используя стандартный алгоритм (уровень 1)
Использовать родственное умножение двух целых чисел для обучения как умножить двузначное десятичное число на двузначное целое число. Умножьте десятичную дробь на 10, затем используйте стандартный алгоритм, чтобы найти произведение целых чисел 9. 0007
0007
Умножение трехзначного десятичного числа на двузначное целое с использованием стандартного алгоритма (уровень 1) числа. Умножьте десятичную дробь на 100, затем используйте стандартный алгоритм, чтобы найти произведение целых чисел. Преобразование произведения целых чисел
Умножение 2- или 3-значного десятичного числа на 2-значное целое число с использованием стандартного алгоритма (уровень 2)
Умножить 2-значное или 3-значное десятичное число на 2-значное целое число, используя связанное умножение двух целых чисел. Временно игнорируйте десятичную точку и используйте стандартный алгоритм для нахождения произведения целых чисел
Умножьте 2- или 3-значное десятичное число на 2-значное целое число, используя стандартный алгоритм (уровень 3) 2-значное или 3-значное десятичное число на 2-значное целое число. Используйте стандартный алгоритм для поиска произведения и определения положения десятичной точки на основе понимания десятичного умножения
Умножение десятичного числа на круглое путем вынесения на множители степени 10
Узнайте, как использовать круглые числа при умножении десятичного числа на целое число. Фактор степени 10 из целого числа. Переставьте множители, чтобы упростить умножение
Фактор степени 10 из целого числа. Переставьте множители, чтобы упростить умножение
Умножение десятичного числа на круглое число
Практика умножения десятичного числа на круглое число
Оценка произведения десятичного числа и трехзначного целого числа (Часть 1)
Используйте округление для оценки произведения десятичного и трехзначного целого числа. Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизительно получить ответ.
Оцените произведение десятичного числа и трехзначного целого числа (Часть 2)
Потренируйтесь оценивать произведение десятичного числа и трехзначного целого числа. Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизительно получить ответ
Оцените произведение десятичного числа и трехзначного целого числа, затем решите с помощью стандартного алгоритма
Оцените произведение десятичного числа и трехзначного целого числа, а затем сравните оценку с фактическим произведением. Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизить ответ. Затем используйте стандарт
Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизить ответ. Затем используйте стандарт
Тема D: Умственные стратегии для деления многозначных целых чисел
Учащиеся полагаются на свое понимание степеней 10, деления, разрядности и округления, чтобы мысленно разделить многозначные целые числа.
Деление круглых чисел на степень 10
Научитесь быстро делить круглое число на степень 10. Уменьшить количество нулей в частном на количество нулей в делителе
Разделить, вынеся из делителя степени 10
Упростить задачи деления, вынеся из множителя степени 10. Вынести из делителя степень десяти. Затем разделите делимое сначала на эту степень 10, а затем на другой множитель
Разделите мысленно многозначные круглые числа
Попрактикуйтесь в делении многозначных круглых чисел с помощью математических вычислений в уме. Соберите головоломку с картинками, правильно решив задачи
Округлите многозначное число до заданного разряда (Уровень 1)
Узнайте, как округлить многозначное число до заданного разряда. Выберите значение справа от места, до которого вы хотите округлить, затем определите, следует ли округлять в большую или меньшую сторону.
Выберите значение справа от места, до которого вы хотите округлить, затем определите, следует ли округлять в большую или меньшую сторону.
Округление многозначного числа до заданного разряда (уровень 2) данное место
Список кратных заданному двузначному круглому числу
Пропустить счет путем перечисления нескольких кратных данному числу. Этот навык может помочь в решении задач на деление
Округление 3-значного числа до ближайшего кратного заданному 2-значному округленному числу (Уровень 1)
Научитесь округлять 3-значное число до ближайшего кратного заданного числа 2 -цифровое число. Назовите кратные двузначного числа. Определите, какое из кратных имеет наименьшую разницу с трехзначным числом
Округление 3-значного числа до ближайшего кратного заданному 2-значному округленному числу (Уровень 2)
Округление 3-значного числа до ближайшего кратного заданного 2-значного числа. Найдите кратные двузначного числа, которые стоят по обе стороны от трехзначного числа. Определите, какое из кратных имеет наименьшую разницу с трехзначным числом
Определите, какое из кратных имеет наименьшую разницу с трехзначным числом
Оцените частное, найдя ближайшее кратное
Узнайте, как вычислить частное. Округлите делитель до крайнего левого места. Затем округлить делимое до ближайшего кратного округленному делителю. Найдите приблизительное частное
Оценка частного уравнения многоразрядного деления (Уровень 1)
Оценка частного уравнения многоразрядного деления. Округлите и делитель, и делимое до крайнего левого места. Используйте степени 10, чтобы упростить задачу. Разделите округленное значение, чтобы найти приблизительное частное
Оцените частное уравнения многоразрядного деления (уровень 2)
Оцените частное уравнения многоразрядного деления. Округлите и делитель, и делимое до крайнего левого места. Используйте степени 10 и разместите значения, чтобы упростить задачу. Разделите округленное значение, чтобы найти приблизительное частное
Тема E: Неполные частные и деление многоразрядных целых чисел
Учащиеся заглянут под капот деления, чтобы действительно понять концепцию остатка, а также шаги, связанные с делением на большие числа. Учащиеся работают с одно-, дву- и трехзначными делимыми и одно- и двузначными делителями. Они используют стандартный алгоритм деления в большую сторону, но по-разному подходят к нему, чтобы добиться математической гибкости.
Учащиеся работают с одно-, дву- и трехзначными делимыми и одно- и двузначными делителями. Они используют стандартный алгоритм деления в большую сторону, но по-разному подходят к нему, чтобы добиться математической гибкости.
Разделить группу объектов на группы заданного размера с остатком
Научитесь делить с остатком. Переведите словесную задачу в математическое выражение. Используйте модель для создания необходимых групп. Определите частное и остаток
Найдите частное и остаток, используя кратные делителя
Научитесь делить с остатком. Используйте ближайшее кратное делителя, которое меньше делимого, чтобы найти частное. Затем определите остаток
Найдите частное и остаток, вычитая делитель из делимого (Часть 1)
Используйте повторное вычитание, чтобы найти остаток от задачи деления. Оцените частное, затем вычтите делитель из делимого столько раз, сколько возможно, чтобы найти остаток
Найдите частное и остаток, вычитая делитель из делимого (Часть 2)
Определите частное и остаток задачи деления через многократное вычитание. Вычтите делитель как можно больше раз. Посчитайте, сколько раз его вычли, чтобы найти частное. Число, оставшееся после вычитания, равно 9.0007
Вычтите делитель как можно больше раз. Посчитайте, сколько раз его вычли, чтобы найти частное. Число, оставшееся после вычитания, равно 9.0007
Оцените частное, затем решите, используя деление в длинное с однозначным частным (Часть 1)
Используйте оценку, чтобы научиться выполнять деление в длинное число. Округлите дивиденд до ближайшего кратного делителю, затем используйте коэффициенты 10, чтобы упростить оценку деления. Используйте оценку для завершения деления в большую сторону, включая нахождение остатка
Оцените частное, затем решите делением в большую сторону с однозначным частным (Часть 2)
Используйте оценку, чтобы научиться выполнять деление в большую сторону. Округлите делимое до ближайшего кратного делителя, чтобы получить частное. Перепишите задачу деления в длинной форме деления. Используйте оценку, чтобы завершить длинное деление, включая нахождение
Решите, используя деление в большую сторону с однозначным частным
Найдите частное, используя деление в прямую. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные произведения в длинном делении. При необходимости можно использовать столбцовое умножение и вычитание.
Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные произведения в длинном делении. При необходимости можно использовать столбцовое умножение и вычитание.
Решите, используя деление в большую сторону с однозначным частным (завышение)
Узнайте, что делать, если оценочное частное слишком велико. Перепишите задачу деления в длинной форме деления. Округлите делитель и делимое. Если частичное произведение в длинном делении слишком велико, чтобы его можно было вычесть, уменьшите оценку на 1. Умножение столбца
Решите, используя деление в большую сторону с однозначным частным (занижение)
Распознайте, когда предполагаемое частное слишком мало. Перепишите задачу деления в длинной форме деления. Округлите делитель и делимое. Если остаток после вычитания в длинном делении больше или равен делителю, увеличьте оценку на
Решите, используя деление в длинное с однозначным частным
Попрактикуйтесь в делении в длинное с однозначным частным. Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Решите, используя деление в большую сторону с двузначным частным (Часть 1)
Найдите двузначное частное, используя деление в прямую. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичное частное в длинном делении. При необходимости можно использовать столбцовое умножение и вычитание
Решите, используя деление в большую сторону с двузначным частным (переоценка и занижение)
Узнайте, что делать, если расчетное частное слишком велико или слишком мало. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные частные в длинном делении. Пересмотрите оценки, если вычитание не может быть завершено или
Решите, используя деление в большую сторону с двузначным частным (Часть 2)
Практика деления в большую сторону с двузначным частным. Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного проведет вас через проблему
Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного проведет вас через проблему
Решите, используя деление в длинное с 3-значным частным
Найдите частное из 3-х цифр, используя деление в длинное число. Перепишите задачу деления в длинной форме деления. Используйте оценку, чтобы найти частичные частные. При необходимости можно использовать умножение и вычитание в столбик
Решите, используя деление в большую сторону с трехзначным частным (переоценка и занижение) (Часть 1)
Узнайте, что делать, если предполагаемое частное слишком высокое или слишком низкое. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные частные в длинном делении. Пересмотрите оценки, если вычитание не может быть завершено, или
Решите, используя деление в длинное число с 3-значным частным (переоценка и занижение) (Часть 2)
Попрактикуйтесь в делении в длинное число с 2-значным частным. Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Тема F: Неполные частные и многоразрядное десятичное деление
Учащиеся заглянут под капот деления, чтобы действительно понять концепцию остатка, а также шаги, связанные с делением на большие числа. Учащиеся работают с одно-, дву- и трехзначными делимыми и одно- и двузначными делителями. Они используют стандартный алгоритм деления в большую сторону, но по-разному подходят к нему, чтобы добиться математической гибкости.
Переименование десятичных чисел в единицах измерения
Переименование десятичных чисел в виде десятых, сотых или тысячных долей. Сначала заполните пропуск количеством заданных единиц. Затем выберите правильную единицу для данного числа
Переименовать число в формате единиц в десятичное число
Записать число в единицах разряда в виде десятичного числа. Данные числа имеют возрастающее количество цифр
Переименовать целое число в форме единиц и десятичной форме
Переименовать целое число в форме разряда единиц. Добавьте соответствующее количество нулей к каждому целому числу, чтобы записать его в виде десятых или сотых долей. Напишите правильное количество нулей после запятой, чтобы заменить целое число на заданное разрядное значение
Добавьте соответствующее количество нулей к каждому целому числу, чтобы записать его в виде десятых или сотых долей. Напишите правильное количество нулей после запятой, чтобы заменить целое число на заданное разрядное значение
Деление десятичной дроби на целое число (с использованием формы единиц и без нее)
Деление десятичной дроби на целое число с использованием разрядных значений. Во-первых, десятичная дробь указывается в форме единицы разряда. Затем выберите единицу стоимости места. Разделите и запишите ответ в виде десятичного числа. Наконец, попрактикуйтесь в делении десятичной дроби на целое число
Деление десятичной дроби на 10 или 100
Деление десятичной дроби на 10-ю степень. Узнайте, как сдвинуть десятичную точку в зависимости от количества нулей в делителе. Затем попрактикуйтесь в этом навыке деления 9.0007
Деление десятичного числа на кратное 10 или 100
Используйте коэффициенты 10 для деления десятичного числа на двузначное или трехзначное круглое число. Вынесите из делителя степень числа 10. Затем разделите в два этапа, упростив деление
Вынесите из делителя степень числа 10. Затем разделите в два этапа, упростив деление
Оцените частное деления десятичного числа на двузначное число (Уровень 1)
Оцените частное деления десятичного числа на двузначное целое число. Округлите каждое число до крайнего левого разряда. Затем определите кратное делителя, ближайшего к делимому, и определите приблизительное частное. Этот навык поможет вам
Оценить частное деления десятичного числа на двузначное число (Уровень 2)
Оценить частное десятичного числа, разделенного на двузначное целое число. Округлите делитель до крайнего левого разряда, а делимое — до ближайшего кратного округленному делителю. Затем определите приблизительное частное. Этот навык поможет вам в lon
Решить длинное деление до десятых разрядов
Научитесь находить частное двух целых чисел до десятых разрядов вместо записи остатка. Перепишите задачу в длинной форме деления, затем выполните деление. Увеличьте делимое, добавив десятичную точку, за которой следует 0, чтобы продолжить деление
Решить длинное деление с точностью до сотых
Найти частное двух целых чисел с точностью до сотых вместо записи остатка. Перепишите задачу в длинной форме деления, затем выполните деление. Увеличьте делимое, добавив десятичную точку, за которой следуют нули, чтобы продолжить деление
Перепишите задачу в длинной форме деления, затем выполните деление. Увеличьте делимое, добавив десятичную точку, за которой следуют нули, чтобы продолжить деление
Решение деления десятичного числа в длинное число (Уровень 1)
Практика деления десятичного числа в длинное на двузначное целое число. Оцените частичные частные, корректируя оценки по мере необходимости. Добавление нулей не требуется для этих задач. Умножение столбцов и вычитание могут использоваться, если требуется
Деление десятичного числа в длинное (Уровень 2)
Практика деления десятичного числа в длинное на двузначное целое число. Оцените частичные частные, корректируя оценки по мере необходимости. Возможно, потребуется добавить нули для дополнительных разрядов, чтобы расширить деление. Умножение столбцов и вычитание
Решение деления десятичного числа в длинное число (сверх- и заниженно)
Использование деления в длинное деление десятичной дроби на двузначное целое число. Перепишите задачу на деление в длинном формате деления. Оцените частичные частные, узнав, когда корректировать оценки
Перепишите задачу на деление в длинном формате деления. Оцените частичные частные, узнав, когда корректировать оценки
Деление десятичного числа в длинное (Уровень 3)
Практика деления десятичного числа в длинное на двузначное целое число. На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного. При необходимости можно использовать столбцовое умножение и вычитание.
Использование длинного деления для решения словесной задачи с десятичным частным
Решение словесной задачи с использованием длинного деления. Используйте модель, чтобы представить ситуацию, и запишите задачу на деление в длинную сторону. На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного. Нули, возможно, придется добавить для
Используйте длинное деление для решения задач на площади с десятичным частным.
Решите задачи на площади с использованием длинного деления. Обозначьте диаграмму полученной информацией и напишите задачу на деление в длинную сторону. На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного.
На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного.
МОДУЛЬ 3. Сложение и вычитание дробей
Тема A: Эквивалентные дроби
Учащиеся знакомятся с основами эквивалентности дробей. Они учатся умножать, чтобы найти эквивалентную дробь, и делить, чтобы уменьшить дробь. Также вводятся и применяются понятия общих множителей и наибольшего общего множителя.
Обозначьте числитель и знаменатель дроби.
Запишите дробь, представленную моделью. Выучить названия частей дроби
Записать эквивалентную дробь (большего размера) на основе заданного множителя или знаменателя
Научиться записывать эквивалентные дроби. Во-первых, используйте модель. Затем используйте умножение, чтобы создать эквивалентные дроби. Наконец, дополните недостающую часть набора эквивалентных дробей
Напишите эквивалентную дробь (меньшую) на основе заданного делителя, числителя или знаменателя
Запишите уменьшенные эквивалентные дроби. Во-первых, используйте модель. Затем используйте деление, чтобы создать эквивалентные дроби. Наконец, дополните недостающую часть набора эквивалентных дробей
Во-первых, используйте модель. Затем используйте деление, чтобы создать эквивалентные дроби. Наконец, дополните недостающую часть набора эквивалентных дробей
Полные эквивалентные дроби
Практика эквивалентных дробей. во-первых, определите операцию, создавшую эквивалентные дроби. Затем дополните недостающую часть пары эквивалентных дробей. Наконец, сопоставьте эквивалентные дроби в игре на память
Определите общие делители двух заданных чисел
Найдите общие делители двух чисел. Перечислите все пары факторов обоих чисел, затем выберите общие факторы. Затем научитесь определять общие делители двух чисел, не перечисляя все пары делителей обоих чисел.
Определите общий делитель двух заданных чисел и разделите их на общий делитель
Определите общий делитель пары чисел. Разделите оба числа на этот множитель и проанализируйте, есть ли у этих частных еще общий множитель. Этот навык может помочь вам найти наибольший общий множитель и полностью сократить дроби
Приведение дроби к простейшей форме путем деления на наибольший общий множитель
Приведение дроби к простейшей форме. Выберите число, которое можно разделить как на числитель, так и на знаменатель. Выполните деление и определите, имеют ли части дроби еще один общий множитель. Продолжайте до тех пор, пока дробь не станет самой простой
Выберите число, которое можно разделить как на числитель, так и на знаменатель. Выполните деление и определите, имеют ли части дроби еще один общий множитель. Продолжайте до тех пор, пока дробь не станет самой простой
Тема B: Создание одинаковых единиц в картинках
Учащиеся полагаются на свои знания эквивалентности дробей, чтобы работать со всеми аспектами сложения и вычитания с дробями и смешанными числами. Благодаря большому количеству визуальной поддержки и пошаговым подсказкам они работают с одинаковыми и разными знаменателями. Учащиеся учатся преобразовывать смешанные числа в дроби для решения задач, писать ответы в простейшей форме и решать текстовые задачи.
Сложение дробей с одинаковыми знаменателями
Узнайте, как складывать дроби с одинаковыми знаменателями. Используйте модель, чтобы выполнить сложение, а затем введите ответ. Затем найдите сумму без модели
Перепишите неправильную дробь в виде смешанного числа
Перепишите неправильную дробь в виде смешанного числа. Запишите неправильную дробь, изображенную на модели. Затем используйте модель, чтобы найти целое число и дробь. Запишите неправильную дробь в виде суммы целого числа и дроби. Переход к написанию m
Запишите неправильную дробь, изображенную на модели. Затем используйте модель, чтобы найти целое число и дробь. Запишите неправильную дробь в виде суммы целого числа и дроби. Переход к написанию m
Сложите дроби с одинаковыми знаменателями и запишите сумму как смешанное число
Потренируйтесь складывать две дроби с одинаковыми знаменателями. Сумма должна быть переписана в виде смешанного числа
Разделить фигуры на равное количество частей (прекурсор нахождения общего знаменателя)
Разделить два прямоугольника на равное количество равных частей. Перетащите две разделенные фигуры друг на друга, чтобы найти общее количество частей. Этот навык поможет вам найти общие знаменатели дробей
Сложение дробей с разными знаменателями (умножение знаменателей для нахождения общего знаменателя)
Узнайте, как складывать дроби с разными знаменателями. Используйте модель прямоугольников, разделенных на равные части, чтобы помочь найти одинаковый знаменатель. Умножьте, чтобы получить эквивалентные дроби с одинаковым знаменателем
Умножьте, чтобы получить эквивалентные дроби с одинаковым знаменателем
Переименуйте дроби с разными знаменателями (Уровень 1)
Переименуйте две дроби, чтобы они имели общий знаменатель. Умножьте знаменатели вместе, затем запишите эквивалентные дроби с этими знаменателями
Переименование дробей с разными знаменателями (Уровень 2)
Определение общего знаменателя двух дробей. Перепишите эквивалентные дроби с общим знаменателем
Сложите дроби с разными знаменателями и запишите сумму в виде смешанного числа
Узнайте, как складывать дроби с разными знаменателями. Перемножьте знаменатели вместе, чтобы найти общий знаменатель, затем создайте эквивалентные дроби с тем же знаменателем. Добавьте переименованные дроби. Если сумма представляет собой неправильную дробь, перепишите ее на 9.0007
Сложите дроби с разными знаменателями и перепишите сумму в простейшей форме (Часть 1)
Сложите дроби с разными знаменателями. Составьте равнозначные дроби с одинаковыми знаменателями. Добавьте переименованные дроби. Уменьшите сумму, если она не выражена простым языком. Перепишите сумму как смешанное число, если это неправильная дробь
Добавьте переименованные дроби. Уменьшите сумму, если она не выражена простым языком. Перепишите сумму как смешанное число, если это неправильная дробь
Сложите дроби с разными знаменателями и запишите сумму в простейшей форме (Часть 2)
Потренируйтесь складывать дроби с разными знаменателями. Перемножьте знаменатели вместе, чтобы найти общий знаменатель, затем создайте эквивалентные дроби с тем же знаменателем. Добавьте переименованные дроби. Если сумма неправильная дробь, перепишите ее как
Вычитание дробей с одинаковыми знаменателями
Научитесь вычитать дроби с одинаковыми знаменателями. Используйте модель для выполнения вычитания, а затем введите ответ. Затем найдите разность без модели
Вычтите дроби с разными знаменателями (перемножьте знаменатели, чтобы найти общий знаменатель)
Используйте модели прямоугольников с равными частями, чтобы научиться вычитать дроби с разными знаменателями. Умножьте знаменатели, а затем создайте эквивалентные дроби с тем же знаменателем. Затем вычтите дроби
Затем вычтите дроби
Вычитание дробей с разными знаменателями
Вычитание дробей с разными знаменателями. Составьте равнозначные дроби с одинаковыми знаменателями. Вычитание переименованных дробей
Преобразование смешанного числа в неправильную дробь
Узнайте, как преобразовать смешанное число в неправильную дробь. Запишите целое число в виде дроби и прибавьте к дробной части. Затем отработайте этот навык, не выполняя шаги
. Вычтите дробь из смешанного числа с одинаковыми знаменателями (переименуйте смешанное число в дробь)
Потренируйтесь вычитать дробь из смешанного числа. Дроби имеют одинаковые знаменатели, но смешанные числа, возможно, придется переписать как неправильные дроби
Вычесть дробь из смешанного числа с разными знаменателями (переименовать смешанное число в дробь)
Вычесть дробь из смешанного числа с разными знаменатели. Перепишите дроби с общими знаменателями. При необходимости замените смешанное число неправильной дробью. Затем вычтите
Затем вычтите
Вычтите дробь из смешанного числа с разными знаменателями и запишите разницу в простейшей форме
Потренируйтесь вычитать дробь из смешанного числа. Найдите общий знаменатель и перепишите смешанное число в виде неправильной дроби, если это необходимо. Напишите ответ в простейшей форме
Вычтите дробь из смешанного числа с разными знаменателями, чтобы решить задачку со словами
Решите задачу со словами, включающую разность смешанного числа и дроби. Пометьте диаграмму, чтобы идентифицировать части проблемы и помочь составить выражение для решения. Найдите общий знаменатель и перепишите смешанное число как неправильное fra
Вычтите дробь из 1 целого, чтобы решить задачку со словами
Узнайте, как решать задачи со словами, в которых часть целого уже завершена или использована. Пометьте диаграмму, чтобы идентифицировать части проблемы и помочь составить выражение для решения. Затем вычтите, чтобы ответить на вопрос.
Вычтите две дроби из одного целого, чтобы решить задачу со словами
Решите задачи со словами на вычитание двух дробей из целого. Используйте схему для систематизации информации. Найдите общий знаменатель и сложите две дроби. Вычтите эту сумму из 1
Используйте схему для систематизации информации. Найдите общий знаменатель и сложите две дроби. Вычтите эту сумму из 1
Сложение дробей для решения задач со словами
Решение задач со словами на сложение дробей. Используйте схему для систематизации информации. Найдите общий знаменатель, а затем сложите две дроби
Тема C: Численное создание одинаковых единиц
Учащиеся усложняют операции сложения и вычитания, которые они могут решать, используя смешанные числа. Они закрепляют и применяют свое понимание эквивалентности чисел, переименовывая числа для решения задач.
Сложите смешанное число и целое число с одинаковыми знаменателями
Найдите сумму смешанного числа и целого числа. Сложите целые части числа вместе. Затем добавьте дробную часть
Вычтите дробь или смешанное число из целого числа с одинаковыми знаменателями с числовой линией и без нее
Найдите разность целого числа и дроби или смешанного числа. Во-первых, используйте числовую линию, чтобы помочь с вычитанием. Затем потренируйтесь без помощи числовой линии 9.0007
Затем потренируйтесь без помощи числовой линии 9.0007
Сложите смешанное число и дробь с одинаковыми знаменателями
Сложите смешанное число и дробь. Сначала найдите сумму дробных частей, а затем прибавьте их к целому числу. Для этих задач не требуется упрощение
Сложение смешанных чисел с одинаковыми знаменателями
Узнайте, как сложить два смешанных числа. Сначала сложите целые части числа, а затем добавьте дробные части. Переименуйте сумму дробных частей, если она равна 1 или если это неправильная дробь
Сложение смешанных чисел с разными знаменателями (Уровень 1)
Найдите сумму двух смешанных чисел с разными знаменателями. Сложите целые части числа. Затем найдите общий знаменатель для дробных частей и переименуйте их перед сложением
Сложите смешанные числа с разными знаменателями (Уровень 2)
Сложите два смешанных числа с разными знаменателями. Сложите целые части числа. Затем найдите общий знаменатель для дробных частей и переименуйте их перед добавлением. Если сумма дробных частей представляет собой неправильную дробь, перепишите ее как смешанное число 9.0007
Если сумма дробных частей представляет собой неправильную дробь, перепишите ее как смешанное число 9.0007
Вычитание смешанных чисел с одинаковыми знаменателями
Вычитание двух смешанных чисел с одинаковыми знаменателями. Вычтите целые части числа друг из друга, затем вычтите дробные части друг из друга. Для этих задач не требуется перегруппировка или упрощение.
Вычитание смешанных чисел с разными знаменателями (Уровень 1)
Вычитание двух смешанных чисел с разными знаменателями. Вычтите целые части числа друг из друга. Затем найдите общий знаменатель для дробных частей и переименуйте их перед вычитанием. Для этих 9 не требуется перегруппировка или упрощение.0007
Вычитание дроби из смешанного числа с одинаковыми знаменателями (переименование смешанного числа)
Научитесь вычитать дробь из смешанного числа, если дробь больше дробной части смешанного числа. Переименуйте смешанное число, переназначив 1 из целой части числа в дробную часть. Затем вычтите дроби
Вычтите смешанные числа с разными знаменателями (Уровень 2)
Вычтите смешанные числа с разными знаменателями. Сначала вычтите целые числа. Затем переименуйте дробные части смешанных чисел с общими знаменателями. При необходимости переименуйте смешанный номер, переназначив 1 из целой части номера на f
Сначала вычтите целые числа. Затем переименуйте дробные части смешанных чисел с общими знаменателями. При необходимости переименуйте смешанный номер, переназначив 1 из целой части номера на f
Вычитание смешанных чисел с разными знаменателями (Уровень 3)
Потренируйтесь вычитать смешанные числа с разными знаменателями. Сначала вычтите целые числа. Затем переименуйте дробные части смешанных чисел с общими знаменателями. При необходимости переименуйте смешанное число, переназначив 1 из целого числа p
Тема D: Дальнейшие приложения
Для поддержки более сложного понимания операций с дробями учащимся помогают визуальные модели, числовая линия и диаграммы. Они применяют свои знания о дробях для вычисления сумм и разностей и решения многошаговых задач со смешанными числами.
Сравните дроби с разными знаменателями с 1/2, чтобы вычислить сумму
Определите, является ли каждая дробь больше, меньше или равна 1/2. Затем определите, является ли сумма двух дробей больше, меньше или равна 1. Сначала используйте модели, чтобы визуализировать дроби. Затем потренируйтесь без моделей
Сначала используйте модели, чтобы визуализировать дроби. Затем потренируйтесь без моделей
Сравните дроби с разными знаменателями с отсутствующей единицей, чтобы оценить сумму.
Оцените сумму двух дробей с разными знаменателями. Сначала используйте числовую прямую для представления большей дроби и определите, насколько она близка к 1. Затем сравните разницу с другой дробью, чтобы определить, будет ли сумма больше или меньше 9.0007
Сравните дроби с разными знаменателями, чтобы оценить разность смешанного числа за вычетом дроби.
Оцените разность двух дробей с разными знаменателями. Сначала определите, какую дробь нужно вычесть из смешанного числа, чтобы получить 1. Затем сравните эту дробь с дробью, которую предполагается вычесть из смешанного числа
Сложите несколько смешанных чисел и дробей
Потренируйтесь складывать несколько дробей и смешанные числа вместе. Переставьте члены так, чтобы дроби с общими знаменателями стояли рядом друг с другом, и сначала найдите эти частичные суммы. Затем сложите частичные суммы вместе
Затем сложите частичные суммы вместе
Решите многошаговую задачу со смешанными числами с разными знаменателями (Часть 1)
Узнайте, как решать задачи со словами, включающие несколько дробей с разными знаменателями. Используйте диаграмму, чтобы систематизировать информацию, данную в задаче. Затем напишите и решите выражение для каждого шага задачи
Решите многоэтапную задачу со смешанными числами с разными знаменателями (Часть 2)
Решите задачу со словами, включающую несколько дробей с разными знаменателями. Используйте диаграмму, чтобы систематизировать информацию, данную в задаче. Затем напишите и решите выражение для каждого шага задачи
МОДУЛЬ 4. Умножение и деление дробей и десятичных дробей
Тема A: Линейные графики измерений дробей
Учащиеся объединяют свои знания об измерениях, округлении и смешанных числах для создания линейных графиков. Затем они анализируют данные, требуя от них выполнения операций со смешанными числами.
Округлите по линейке до ближайшего полудюйма
Используйте линейку для измерения до ближайшего полудюйма. Определите приращения на линейке. Затем используйте промежуточные точки между приращениями, чтобы определить, следует ли округлять длину объекта в большую или меньшую сторону. Выберите правильную округленную длину на линейке
Округлите по линейке до ближайшего полудюйма, чтобы построить линейный график и проанализировать данные.
Создайте линейный график на основе измерений длины нескольких объектов с округлением до ближайшего полудюйма. Проанализируйте данные для минимального и максимального измерения. Определите наиболее частое измерение, а также диапазон
Округлите по линейке до четверти дюйма
Используйте линейку для измерения до четверти дюйма. Определите приращения на линейке. Затем используйте промежуточные точки между приращениями, чтобы определить, следует ли округлять длину объекта в большую или меньшую сторону. Выберите правильную округленную длину на
Округлите по линейке до четверти дюйма, чтобы построить линейный график и проанализировать данные.

Измерьте длину нескольких объектов с точностью до четверти дюйма, создав линейный график измерений. Проанализируйте данные для минимального и максимального измерения. Определите наиболее частое измерение, а также разницу между двумя измерениями
Округлите до ближайшей восьмой фута по линейке
Используйте линейку для измерения до ближайшей восьмой фута. Определите приращения на линейке. Затем используйте промежуточные точки между приращениями, чтобы определить, следует ли округлять длину объекта в большую или меньшую сторону. Выберите правильную округленную длину на ру
Округлите линейку до ближайшей восьмой дюйма, чтобы построить линейный график и проанализировать данные.
Измерьте длину нескольких объектов с точностью до восьмой дюйма, создав линейный график измерений. Проанализируйте данные для минимального и максимального измерения. Определите наиболее частое измерение, а также разницу между двумя измерениями
Тема B: Дроби как деление
Чтобы закрепить свое понимание дробей как деления, учащиеся работают над преобразованием между ними, используя дроби больше и меньше единицы. Затем они работают шаг за шагом, чтобы понять оставшуюся часть задачи деления как дробь. Вооружившись этим пониманием, учащиеся решают все более сложные задачи на деление слов.
Затем они работают шаг за шагом, чтобы понять оставшуюся часть задачи деления как дробь. Вооружившись этим пониманием, учащиеся решают все более сложные задачи на деление слов.
Перепишите деление целых чисел в виде дроби на основе модели
Узнайте взаимосвязь между делением количества и записью количества в виде дроби. Представьте деление как целое количество продуктов, разделенных между большим целым числом тарелок. Продукты будут разрезаны на количество частей, представленное pla
Перепишите деление целых чисел в виде дроби и сопоставьте дробь с соответствующим уравнением деления
Перепишите деление двух целых чисел в виде дроби. Делимое становится числителем, а делитель становится знаменателем. Практикуйте концепцию, сопоставляя дроби с соответствующим им выражением деления
Свяжите деление с дробями
Потренируйтесь записывать выражения деления как дроби. Вставьте пропущенное число в уравнение
Связать деление с дробями больше единицы
Представление деления в виде неправильной дроби. Во-первых, модель еды и тарелок используется для визуализации частного. Затем потренируйтесь переписывать выражения деления в виде дробей. Заполните пропущенное число в уравнении
Во-первых, модель еды и тарелок используется для визуализации частного. Затем потренируйтесь переписывать выражения деления в виде дробей. Заполните пропущенное число в уравнении
Разделите и сообщите остаток в виде дроби на основе модели
Научитесь делить два целых числа с остатком дроби. Модель еды и тарелок используется для физического представления разделения. Запишите частное в виде неправильной дроби и смешанного числа
Переименуйте дробь больше единицы в смешанное число (Уровень 1)
Перепишите неправильную дробь в смешанное число. Запишите дробь в виде выражения деления. Затем найдите частное и остаток задачи на деление, чтобы записать ответ в виде смешанного числа
Переименовать дробь больше единицы в смешанное число (уровень 2)
Используйте длинное деление, чтобы преобразовать неправильную дробь в смешанное число. Запишите дробь в виде длинного деления, затем выполните деление. Частное становится целой частью числа, а остаток становится числителем дробной части
Решение задач со словами на основе модели (Уровень 1)
Научитесь решать задачи со словами на дроби. Определите часть полосы, которая заштрихована. Затем с помощью линейки смоделируйте текстовую задачу и ответьте на вопрос 9.0007
Определите часть полосы, которая заштрихована. Затем с помощью линейки смоделируйте текстовую задачу и ответьте на вопрос 9.0007
Решение задач со словами на дроби на основе модели (уровень 2)
Использование модели для представления задачи со словами, включающей дроби. Обозначьте схему полученной информацией. Запишите нужное деление в виде дроби. Затем измените его на смешанное число и ответьте на вопрос
Решите задачи на дроби на основе модели (уровень 3)
Представьте задачу на дроби, используя модель. Обозначьте схему полученной информацией. Перепишите искомое деление в виде смешанного числа в простейшем виде и ответьте на вопрос 9.0007
Решение задач со словами на дроби на основе модели (уровень 4)
Решение задач со словами на дроби с использованием модели. Обозначьте схему полученной информацией. Запишите нужное деление в виде дроби. Затем используйте длинное деление, чтобы преобразовать дробь в смешанное число, и ответьте на вопрос
Решите задачи со словами на основе модели (Уровень 5)
Попрактикуйтесь в решении задач со словами на дроби. Запишите соответствующее выражение деления для задачи. Затем перепишите его в виде дроби или смешанного числа, если необходимо
Запишите соответствующее выражение деления для задачи. Затем перепишите его в виде дроби или смешанного числа, если необходимо
Тема C: Умножение целого числа на дробь
Учащиеся начинают с нахождения единичной дроби целого числа и других дробей целого числа, используя знакомые модели. Затем они связывают этот процесс с умножением. Чтобы умножить целое число на дробь, учащиеся учатся находить общие множители и сокращать до или после умножения.
Определение частей целого числа на основе модели (уровень 1)
Найдите число, являющееся частью целого числа. Используйте модель, чтобы найти ответ. Затем сопоставьте дробь с моделью
Определение частей целого числа на основе модели для решения задачи со словами
Представление задачи со словами с помощью модели. Выберите, на сколько групп разделить целое число, исходя из информации в задаче. Найдите часть целого числа с помощью модели, затем ответьте на вопросы
Определите части целого числа на основе модели (Уровень 2)
Найдите часть целого числа с помощью модели. Представьте информацию, данную в задаче с моделью, выбрав количество частей. Затем напишите выражение для модели и решите. Если решение представляет собой неправильную дробь, перепишите
Представьте информацию, данную в задаче с моделью, выбрав количество частей. Затем напишите выражение для модели и решите. Если решение представляет собой неправильную дробь, перепишите
Определение долей целого числа на основе модели (уровень 3)
Вычисление доли целого числа с помощью модели. Представьте информацию, данную в задаче с моделью, выбрав количество частей. Вычислите значение одной части, затем выделите, сколько частей представлено дробями
Определите целое число по дробной части этого числа на основе модели
Найдите целое число, если вы знаете дробную часть этого числа. Используйте модель для представления данной информации. Определите стоимость одной части, а затем используйте эту информацию для расчета общей суммы
Умножение целого числа на дробь
Узнайте, как умножить целое число на дробь. Запишите умножение как многократное сложение дроби. Обратите внимание на эти отношения повторного сложения и частей дроби. Затем отработайте эту концепцию, не переписывая ее как additio
Свяжите часть целого числа с умножением и решите
Найдите часть целого числа путем умножения. Используйте модель для представления одной части целого числа, затем напишите необходимое выражение умножения. Затем найдите произведение
Используйте модель для представления одной части целого числа, затем напишите необходимое выражение умножения. Затем найдите произведение
Определить долю измерения путем преобразования единиц измерения и умножения
Определить долю измерения. Во-первых, преобразовать измерение в более мелкие единицы. Затем умножьте на дробь и упростите ответ
Определите общие делители двух целых чисел
Найдите общие делители двух чисел. Перечислите все пары факторов обоих чисел, затем выберите общие факторы. Затем определите общие множители двух чисел, не перечисляя все пары множителей обоих чисел.0007
Деление целых чисел на общий делитель
Определение общего делителя пары чисел. Разделите оба числа на этот множитель и проанализируйте, есть ли у этих частных еще общий множитель. Этот навык поможет вам найти наибольший общий множитель и полностью сократить дроби.
Сократить дробь путем деления на общий делитель
Научитесь приводить дробь к простейшим терминам. Найдите общий делитель числителя и знаменателя. Затем разделите оба числа на общий множитель. Продолжайте делить на общие множители до тех пор, пока в числителе и знаменателе не останется комм
Найдите общий делитель числителя и знаменателя. Затем разделите оба числа на общий множитель. Продолжайте делить на общие множители до тех пор, пока в числителе и знаменателе не останется комм
Уменьшение коэффициентов перед умножением целого числа на дробь (Уровень 1)
Умножение дроби на целое число. Изучите, как уменьшение общего множителя перед умножением может упростить умножение. Выберите числа, которые имеют общий множитель, и определите этот множитель. Затем разделите общий множитель и умножьте
Сократите множители перед умножением целого числа на дробь (Уровень 2)
Потренируйтесь уменьшать общие множители перед умножением в знаменателе дроби. Выберите два числа, которые имеют общий делитель, и разделите их на общий делитель. При необходимости повторите. Затем умножьте оставшиеся числа в числителе. Если т
Умножение целого числа на дробь путем уменьшения до или после умножения
Выберите, следует ли уменьшать до или после умножения в числителе дроби. Научитесь делать правильный выбор, чтобы иметь возможность использовать арифметику в уме
Научитесь делать правильный выбор, чтобы иметь возможность использовать арифметику в уме
Тема D: Выражения дробей и задачи со словами
Учащиеся обобщают свое понимание дробей и операций для построения и решения выражений. Знакомые модели поддерживают их обучение, а словесные задачи помещают навыки в контекст.
Сопоставьте операции с терминами сумма, разность, произведение и частное
Попрактикуйтесь в словарных терминах, используемых для сложения, вычитания, умножения и деления. Сопоставьте словесное выражение с правильным математическим выражением
Составьте выражение на основе текста
Напишите математическое выражение для данного словесного выражения. Выберите правильную операцию для использования между двумя числами. Также расставьте цифры в правильном порядке, если необходимо
Составление составного выражения на основе текста (Часть 1)
Составление математического выражения, включающего три значения, сложение и умножение. Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильными операциями, вставив круглые скобки
Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильными операциями, вставив круглые скобки
Составьте составное выражение на основе текста (Часть 2)
Составьте математическое выражение, включающее три значения и умножение целых чисел на дробь. Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильными операциями, ins
Составление составного выражения на основе текста (часть 3)
Напишите математическое выражение, включающее три значения, а также умножение и вычитание целых чисел и дробей. Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильным
Составьте сложное уравнение на основе модели и решите (Часть 1)
Напишите и решите составное уравнение на основе показанной модели. Определите часть стержня, который помечен, и выражение, представляющее полную длину стержня. Затем организуйте числа и необходимые операции в выражении. Найдите с
Затем организуйте числа и необходимые операции в выражении. Найдите с
Составьте сложное уравнение на основе модели и решите (Часть 2)
Напишите и решите сложное уравнение на основе показанной модели. Определите количество разделов на панели и выражение, которое представляет каждый раздел. Затем организуйте числа и необходимые операции в выражении. Найдите решение, переписав i
Решите сложные уравнения с дробями и скобками
Найдите решение составного уравнения с дробями и скобками. Перепишите выражения деления в виде дробей. Следуйте порядку операций для решения. Запишите решение в виде упрощенных дробей или смешанных чисел
Решите задачу на умножение целого числа на дробь (Уровень 1)
Решите задачу на умножение целого числа на дробь. Составьте выражения, отвечающие на каждый вопрос. Затем решите выражения, упрощая перед умножением. Ответьте на все вопросы
Решите задачу на умножение целого числа на дробь (Уровень 2)
Решите задачу на умножение целого числа на дробь. Используйте схему для моделирования проблемы. Составьте выражения, отвечающие на каждый вопрос. Затем решите выражения, упрощая перед умножением на 9.0007
Используйте схему для моделирования проблемы. Составьте выражения, отвечающие на каждый вопрос. Затем решите выражения, упрощая перед умножением на 9.0007
Тема E: Умножение дроби на дробь
Учащиеся учатся умножать дроби, начиная с единичных дробей и используя модель площади. Затем они переходят к умножению, которое включает в себя смешанные числа, сокращение и единицы измерения.
Умножение долей единиц с использованием модели площади
Использование площади прямоугольника для моделирования произведения двух долей единиц. Обозначьте на схеме длины сторон прямоугольников. Затем найдите уравнение площади и свяжите его с произведением дробей
Умножение дробей с использованием модели площади
Моделирование произведения двух дробей с использованием площади прямоугольника. Обозначьте на схеме длины сторон прямоугольников. Затем найдите уравнение площади и свяжите его с умножением дробей
Умножьте дроби (уменьшите перед умножением)
Потренируйтесь умножать две дроби. Сократите общие все множители из числителя и знаменателя перед умножением, если это возможно. Кроме того, потренируйтесь писать выражения дробей и упрощайте их, прежде чем находить произведение 9.0007
Сократите общие все множители из числителя и знаменателя перед умножением, если это возможно. Кроме того, потренируйтесь писать выражения дробей и упрощайте их, прежде чем находить произведение 9.0007
Умножение дробей (уменьшение до или после умножения)
Умножение двух дробей. Решите, умножать или уменьшать на каждом шаге. Найдите упрощенный продукт
Решите текстовые задачи, умножив дроби, используя модель площади
Решите текстовые задачи, моделируя произведение двух дробей, используя площадь прямоугольника. Обозначьте диаграмму информацией, данной в задаче. Затем запишите полученное выражение и решите его, чтобы ответить на вопрос 9.0007
Преобразование смешанного числа в дробь для умножения на дробь
Преобразование смешанного числа в неправильную дробь перед умножением. Затем уменьшите общие множители от умножения, прежде чем найти произведение
Преобразование измерений путем умножения целого числа на дробь
Преобразование единиц измерения. Определить соотношение между меньшими и большими единицами. Затем умножьте целое число и дробь, чтобы преобразовать единицы. Запишите ответ в простейшей форме или в виде смешанного числа, в зависимости от ситуации
Определить соотношение между меньшими и большими единицами. Затем умножьте целое число и дробь, чтобы преобразовать единицы. Запишите ответ в простейшей форме или в виде смешанного числа, в зависимости от ситуации
Преобразование измерений путем умножения дробей
Преобразование единиц измерения. Определить соотношение между меньшими и большими единицами. Затем умножьте, чтобы преобразовать единицы. Смешанные числа, возможно, придется переписать в виде неправильных дробей, а общие множители следует разделить перед умножением
Преобразовать умножение на десятичную дробь в умножение на дробь и решить
Изучить взаимосвязь между умножением на 0,1 или 0,01 и умножением на эквивалентную дробь . Преобразование между десятичными дробями и дробями. Обратите внимание, что умножение на десятичную дробь можно переписать как деление на 9.0007
Умножение на 0,1 с использованием таблицы разрядных значений
Использование таблицы разрядных значений для умножения числа на 0,1. Определите число, изображенное на графике. Затем переместите цифры в правильное место для данного умножения. Узнайте, как перемещать десятичную точку для быстрого вычисления в уме
Определите число, изображенное на графике. Затем переместите цифры в правильное место для данного умножения. Узнайте, как перемещать десятичную точку для быстрого вычисления в уме
Умножение на 0,01 с помощью таблицы разрядных значений
Используйте таблицу разрядных значений для умножения числа на 0,01. Определите число, изображенное на графике. Затем переместите цифры в правильное место для данного умножения. Научитесь перемещать десятичную точку для быстрого счета в уме
Умножение на 0,1 или 0,01
Практика умножения числа на 0,1 или 0,01
Разложение десятичного числа для умножения
Разложение десятичного числа для простого умножения. Запишите десятичную дробь как произведение целого числа и 0,1 или 0,01. Затем переставьте множители, чтобы упростить умножение. Найти произведение
Определить место запятой в произведении двух десятичных чисел
Узнайте, как найти место запятой в произведении двух десятичных чисел. Перетащите десятичную дробь в нужное место
Умножение двух десятичных чисел с помощью умножения столбцов (Часть 1)
Использование умножения столбцов для нахождения произведения двух десятичных чисел. Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Сложите частичные произведения и вставьте десятичную точку в нужное место для fina
Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Сложите частичные произведения и вставьте десятичную точку в нужное место для fina
Умножьте два десятичных числа, используя умножение столбца (Часть 2)
Найдите произведение двух десятичных чисел, используя умножение столбца. Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Добавьте частичные произведения и вставьте десятичную точку в правильном месте для последних
Умножение двух десятичных чисел с помощью умножения столбцов (часть 3)
Использование умножения столбцов для нахождения произведения двух десятичных чисел. Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Сложите частичные произведения и вставьте десятичную точку в правильном месте для fina
Тема F: Умножение с дробями и десятичными дробями как масштабирование и текстовые задачи
Учащиеся изучают эффекты умножения на меньше, равно и больше 1 , Они решают задачи на умножение, вводят недостающие множители и дополняют неравенства, чтобы закрепить свое понимание.
Умножение дроби на дробь, равную 1
Найдите эквивалентные дроби, умножив дробь на дробь, равную 1. Узнайте, что дробь с одинаковым числом в числителе и знаменателе равна 1. Этот навык полезен при переименовании дроби с общими знаменателями для сложения o
Определите недостающий множитель как дробь, равную 1
Потренируйтесь умножать дробь на другую дробь, равную 1. Сначала составьте дроби, равные 1, заполнив пропущенный числитель или знаменатель. Затем выберите правильную дробь, равную 1. Наконец, напишите любую дробь
Определить закономерности умножения на дроби меньше, равно и больше 1
Изучить эффект умножения на дроби меньше, равно или больше 1. Определить дробь как меньше, равно или больше чем 1. Затем определите, является ли произведение этой дроби и целого числа меньше, равно или больше
Используйте
<, = и > для сравнения результата умножения на дроби меньше, равно и больше 1 Используйте символы неравенства, чтобы сравнить дробь с 1. Затем сравните произведение этой дроби и другой дроби со значением второй дроби
Затем сравните произведение этой дроби и другой дроби со значением второй дроби
Найдите дробь, которая завершает неравенство умножения.
Потренируйтесь определять связь между произведением двух дробей и значением одной из этих дробей. Во-первых, имея выбор из трех дробей, выберите ту, которая делает утверждение о неравенстве верным. Затем заполните недостающую часть
Преобразование дроби меньше единицы в десятичную форму (Уровень 1)
Узнайте, как преобразовать дробь в десятичную. Определите, какой множитель изменит знаменатель до степени 10, а затем умножьте, чтобы получить эквивалентную дробь. Затем запишите эту дробь как десятичную
Преобразование дроби больше единицы в десятичную форму
Преобразование неправильной дроби в десятичную. Определите, какой множитель изменит знаменатель до степени 10, а затем умножьте, чтобы получить эквивалентную дробь. Затем запишите эту дробь как десятичную
Преобразуйте дробь меньше единицы в десятичную форму (уровень 2)
Перепишите дробь как десятичную. Дополните множитель, который составит эквивалентную дробь с заданной степенью 10 в знаменателе. Затем умножьте числители и запишите дробь как десятичную 9.0007
Дополните множитель, который составит эквивалентную дробь с заданной степенью 10 в знаменателе. Затем умножьте числители и запишите дробь как десятичную 9.0007
Преобразование дроби меньше единицы в десятичную форму с помощью деления
Используйте длинное деление, чтобы преобразовать дробь в десятичную. Разделите числитель на знаменатель, добавив нули, чтобы продолжить деление без остатка
Преобразование дроби больше единицы в десятичную форму с помощью деления
Используйте длинное деление, чтобы преобразовать неправильную дробь в десятичную. Разделить числитель на знаменатель, добавив нули, чтобы продолжить деление без остатка
Определить результат умножения с помощью
<, = или > (Часть 1)Изучить эффект умножения на десятичное число меньше, равное или большее 1. Определить десятичное число как меньшее, равное или большее 1. Затем определить, является ли произведение этого десятичного числа и целого числа меньше, равно или больше th
Полное неравенство с умножением на десятичное число
Попрактиковаться в определении отношения между произведением двух десятичных знаков и значением одного из этих десятичных знаков. Во-первых, имея выбор из трех десятичных знаков, выберите тот, который делает утверждение о неравенстве верным. Затем заполните недостающую часть де
Во-первых, имея выбор из трех десятичных знаков, выберите тот, который делает утверждение о неравенстве верным. Затем заполните недостающую часть де
Определите результат умножения с помощью
<, = или > (Часть 2)Умножьте на дробь или десятичную дробь, большую 1. Определите, меньше или больше произведение одного из множителей, используя символы неравенства. Демонстрация понимание концепции путем помещения правильного неравенства в выражение формулы
Определите результат умножения с помощью
<, = или > (Часть 3)Умножьте дробь или десятичную дробь меньше 1. Определите, меньше ли произведение или больше, чем один из факторов, используя символы неравенства. Продемонстрируйте понимание концепции, поместив правильное неравенство в выражение формулы
Тема G: Деление дробей и десятичных дробей
Учащиеся полагаются на свое понимание умножения дробей, чтобы научиться делить дроби. С помощью знакомых моделей, таких как ленточные диаграммы и модели с площадями, они изучают различные подходы к делению дробей. На этом этапе они используют единичные дроби с целыми числами и единичные дроби с единичными дробями.
На этом этапе они используют единичные дроби с целыми числами и единичные дроби с единичными дробями.
Переписать уравнение с умножением на дробь как уравнение деления на основе модели
Изучите взаимосвязь между умножением на дробь и делением. Используя данную модель, разрезанную на равные части, укажите, сколько частей составляет целое. Затем завершите выражения умножения и деления по модели
Составьте уравнение деления с дробью на основе модели
Напишите выражения деления на основе модели. Используя данную модель, разрезанную на равные части, укажите, сколько частей составляет целое. Затем завершите выражение деления о модели
Разделите целое число на дробную часть на основе ленточной диаграммы
Используйте ленточную диаграмму для деления целого числа на дробную часть. Обозначьте на схеме целые числа и дробные части. Используйте числовую строку, чтобы пропустить подсчет частей дроби. Затем определите общее количество разделов
Соотнесите деление на единичную дробь с умножением на знаменатель
Изучите взаимосвязь между делением на единичную дробь и умножением на знаменатель. Используя ленточную диаграмму, обозначьте на диаграмме целые числа и дробные части. Используйте числовую строку, чтобы пропустить подсчет частей дроби. Затем напишите мю
Используя ленточную диаграмму, обозначьте на диаграмме целые числа и дробные части. Используйте числовую строку, чтобы пропустить подсчет частей дроби. Затем напишите мю
Разделить целое число на дробную часть путем умножения на знаменатель
Переписать деление на дробь как умножение. Умножьте целое число на знаменатель дроби и запишите полученное произведение
Разделите целое число на дробную единицу
Разделите целое число на дробную единицу в контексте текстовой задачи. Перепишите деление как умножение и найдите произведение
Разделите дробную единицу на целое число на основе ленточной диаграммы (Часть 1)
Научитесь делить дробь на целое число. Используйте ленточную модель, чтобы представить дробь как равные части. Затем разделите каждую часть на количество частей, указанное целым числом. Ответьте, сколько всего секций
Разделите дробную часть на целое число на основе ленточной диаграммы (Часть 2)
Разделите дробную часть на целое число с помощью ленточной диаграммы. Используйте модель, чтобы представить дробь как равные части. Затем разделите каждую часть на количество частей, указанное целым числом. Перепишите дробь так, чтобы она представляла все части, показанные на цифре 9.0007
Используйте модель, чтобы представить дробь как равные части. Затем разделите каждую часть на количество частей, указанное целым числом. Перепишите дробь так, чтобы она представляла все части, показанные на цифре 9.0007
Разделить дробную часть на целое число
Попрактиковаться в делении дробной части на целое число. Переименуйте дробь, вставив пропущенный знаменатель. Затем разделите и приведите дробь к простейшей форме
Умножьте единичную дробь на единичную дробь с моделью площади и без нее (Часть 1)
Умножьте две единичные дроби вместе. Используйте модель площади для представления обеих дробей на одном прямоугольнике. Найдите заштрихованную площадь, представляющую произведение двух дробей. Затем примените эту концепцию к задачам на умножение без использования режима площади 9.0007
Умножение единичной дроби на единичную дробь с моделью площади и без нее (Часть 2)
Используйте модель площади для представления деления дроби единицы на целое число. Перепишите деление как умножение на дробь. Используйте получившуюся заштрихованную область, чтобы найти произведение двух дробей
Перепишите деление как умножение на дробь. Используйте получившуюся заштрихованную область, чтобы найти произведение двух дробей
Свяжите деление на целое число с умножением на единичную дробь
Используйте ленточную диаграмму, чтобы обнаружить взаимосвязь между делением на целое число и умножением на единичную дробь. Разделите диаграмму на участки в соответствии со значениями, указанными в задаче. Перепишите полученное выражение деления как множитель
Решите уравнения деления с дробями и целыми числами.
Попрактикуйтесь в делении дробей на целые числа. Перепишите выражение деления как умножение и найдите произведение
Умножьте десятичное число на десятую степень
Найдите произведение десятичного числа на десятую степень. Узнайте, как сдвинуть десятичную точку для быстрого вычисления в уме.
Упростите дробь, используя основное свойство дробей
Используйте основное свойство дробей, чтобы упростить дроби. Сначала выведите из дроби общий множитель. Затем выберите уравнения дробей, которые показывают основное свойство дробей. Наконец, дополните пропущенное число в основном свойстве дробей eq 9.0007
Затем выберите уравнения дробей, которые показывают основное свойство дробей. Наконец, дополните пропущенное число в основном свойстве дробей eq 9.0007
Преобразуйте дробь в заданный знаменатель, используя основное свойство дробей.
Напишите эквивалентные уравнения, используя основное свойство дробей. Учитывая дробь и новое значение знаменателя, определите, на какое число нужно умножить, чтобы получить этот знаменатель. Затем запишите эквивалентную дробь
Преобразование между выражениями деления и дробями
Перепишите выражение деления как дробь. Запишите делимое как числитель, а делитель как знаменатель. Также потренируйтесь писать выражение деления из дроби
Завершение выражений дробей с использованием основного свойства дробей
Использование основного свойства дробей для упрощения дробей. Сначала выведите из дроби общий множитель. Затем дополните пропущенное число в уравнении основного свойства дробей
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (Уровень 1)
Используйте основное свойство дробей для преобразования дробей, содержащих десятичные числа, в дроби, содержащие только целые числа. Превратите выражение деления в дробь. Затем выберите правильный множитель, который делает знаменатель целым числом. Упростить фр
Превратите выражение деления в дробь. Затем выберите правильный множитель, который делает знаменатель целым числом. Упростить фр
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (Уровень 2)
Преобразование дробей, содержащих десятичные числа, в дроби, содержащие только целые числа. Превратите выражение деления в дробь. Затем выберите правильный множитель, который делает знаменатель целым числом. Упростить дробь
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (уровень 3)
Преобразование дробей, содержащих десятичные дроби, в дроби, содержащие только целые числа. Перепишите выражение деления в виде дроби. Затем выберите правильный множитель, который делает знаменатель целым числом. Найдите частное, при необходимости используя длинное деление
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (Уровень 4)
Используйте основное свойство дробей для преобразования дробей, содержащих десятичные дроби, в дроби, содержащие только целые числа. Выберите правильный множитель, который делает знаменатель целым числом. Затем умножьте и упростите дробь
Выберите правильный множитель, который делает знаменатель целым числом. Затем умножьте и упростите дробь
Преобразование выражений деления с десятичными делителями в выражения с делителями целых чисел (Уровень 1)
Узнайте, как преобразовать деление десятичных дробей в выражение деления, содержащее целые числа. Сдвиньте запятую делителя вправо на столько знаков, сколько необходимо, чтобы он стал целым числом. Сдвиньте запятую делимого на то же число
Преобразование выражений деления с десятичными делителями в выражения с делителями целых чисел (уровень 2)
Преобразование деления десятичных дробей в выражение деления, содержащее целые числа. Сдвиньте запятую вправо на столько разрядов, сколько необходимо, чтобы получилось целое число. Сдвиньте запятую делимого на такое же количество знаков. Затем найдите
МОДУЛЬ 5: Алгебраические выражения
Тема A: Решение сложных уравнений с отсутствующими слагаемыми
Описание темы: Учащиеся решают все более сложные уравнения с отсутствующими слагаемыми. В этих предварительных алгебраических уравнениях проблема заключается не в числовых значениях, а в логике того, как числа и уравнения могут быть объединены для решения чисел, представленных символами.
В этих предварительных алгебраических уравнениях проблема заключается не в числовых значениях, а в логике того, как числа и уравнения могут быть объединены для решения чисел, представленных символами.
Решите отсутствующие уравнения слагаемых
Найдите отсутствующий член в уравнении сложения или вычитания. Каждое уравнение имеет символ вместо одного из членов. Найдите пропущенное число
Решите многошаговые уравнения с отсутствующими слагаемыми
Решите уравнения с более чем одним пропущенным членом. Каждое уравнение будет иметь один и тот же символ вместо двух или трех членов. Найдите пропущенное число
Найдите пропущенные слагаемые в парных уравнениях (Уровень 1)
Найдите два пропущенных члена в паре уравнений. Каждое уравнение имеет один или два символа вместо члена. Найдите пропущенные числа
Найдите пропущенные слагаемые в системе из трех уравнений.
Найдите три пропущенных члена в системе из трех уравнений. Каждое уравнение имеет один или два символа вместо члена. Найдите пропущенные числа
Найдите пропущенные числа
Найдите пропущенные слагаемые в парных уравнениях (уровень 2)
Найдите пропущенные члены в паре уравнений. Каждое уравнение имеет один или два символа вместо члена. Узнайте, как заменить набор терминов, если общее значение известно. Найдите недостающие числа
Решите отсутствующие уравнения слагаемых, содержащие 0
Решите два отсутствующих члена в паре уравнений. Каждое уравнение имеет символы вместо термина. Найдите недостающие числа. Изучите эффект добавления 0 в уравнение
Найдите пропущенные слагаемые в парных уравнениях, содержащих 0
Попрактикуйтесь в решении уравнений с более чем одним пропущенным членом. Каждое уравнение имеет символы вместо двух или трех членов. Найдите пропущенные числа
Типы задач на сложение и вычитание
Словесные задачи часто являются самой большой проблемой для учителей математики. Говорили ли вы что-то вроде «Дети их не понимают». и «Они берут числа и выполняют случайную операцию». Мы пробуем так много разных методов, чтобы попытаться помочь, и они терпят неудачу. Потому что часто мы не концентрируемся на обучении студентов операциям в явном виде. И учить их явно — это то, что нам нужно делать! Стандарты Common Core State излагают различные типы задач на сложение и вычитание, которые должны знать учащиеся. Обучая их явно, мы даем им инструменты, необходимые им для успешного решения проблем. Мы связываем то, как математика, которую они изучают, имеет отношение к их реальной жизни. Мы помогаем им по-настоящему понять математическую операцию и то, как и когда она используется. Сосредоточив внимание на текстовых задачах и их типах, мы сосредоточимся на том, что делает сложение и вычитание тем, чем они являются.
Мы пробуем так много разных методов, чтобы попытаться помочь, и они терпят неудачу. Потому что часто мы не концентрируемся на обучении студентов операциям в явном виде. И учить их явно — это то, что нам нужно делать! Стандарты Common Core State излагают различные типы задач на сложение и вычитание, которые должны знать учащиеся. Обучая их явно, мы даем им инструменты, необходимые им для успешного решения проблем. Мы связываем то, как математика, которую они изучают, имеет отношение к их реальной жизни. Мы помогаем им по-настоящему понять математическую операцию и то, как и когда она используется. Сосредоточив внимание на текстовых задачах и их типах, мы сосредоточимся на том, что делает сложение и вычитание тем, чем они являются.
В этом посте подробно рассматриваются все типы задач на сложение и вычитание. Я также даю несколько полезных ссылок внизу, в которых обсуждаются когнитивно-управляемые инструкции или типы задач CGI. Они используют несколько иную лексику, чем CCSS, но имеют тот же набор навыков. Важное замечание: когда я говорю об обучении типов задач на сложение и вычитание в явном виде, я не имею в виду, что они отрабатываются только во время определенного раздела или что мы обучаем определенным ключевым словам для каждого типа задач. Учащиеся должны прочитать задачу и понять контекст. Распознавание типа проблемы может поддержать эту работу, но оно не сосредоточено на ключевых словах. Кроме того, я ежедневно решаю задачи со словами вне нашей основной работы. Я твердо верю в спираль стандартов в текстовых задачах, чтобы учащиеся должны были сосредоточиться на контексте для решения. Для получения дополнительной помощи в решении проблем ознакомьтесь с моей публикацией «Почему ваши ученики борются с задачами в Word и что вы можете с этим поделать».
Важное замечание: когда я говорю об обучении типов задач на сложение и вычитание в явном виде, я не имею в виду, что они отрабатываются только во время определенного раздела или что мы обучаем определенным ключевым словам для каждого типа задач. Учащиеся должны прочитать задачу и понять контекст. Распознавание типа проблемы может поддержать эту работу, но оно не сосредоточено на ключевых словах. Кроме того, я ежедневно решаю задачи со словами вне нашей основной работы. Я твердо верю в спираль стандартов в текстовых задачах, чтобы учащиеся должны были сосредоточиться на контексте для решения. Для получения дополнительной помощи в решении проблем ознакомьтесь с моей публикацией «Почему ваши ученики борются с задачами в Word и что вы можете с этим поделать».
ЧАСТЬ-ЧАСТЬ-ЦЕЛОЕ
Вероятно, наиболее распространенным типом сложения и вычитания в умах большинства учителей является часть части целого. Мы используем числовые связи и линейчатые модели для моделирования и представления отношений часть/целое. Мы моделируем сложение как объединение двух наборов объектов. Мы вводим вычитание как разделение нашего общего количества объектов на более мелкие части. И это основа для будущей работы с дробями, умножением и делением. Часть-часть-целое — такое важное понятие для понимания математики нашими студентами. Важно, чтобы мы связали эту работу с нашим языком в текстовых задачах. Многие задачи со словами можно рассматривать как сценарии «часть-часть-целое» (даже многие из описанных ниже типов «начало-изменение-конец»).
Мы моделируем сложение как объединение двух наборов объектов. Мы вводим вычитание как разделение нашего общего количества объектов на более мелкие части. И это основа для будущей работы с дробями, умножением и делением. Часть-часть-целое — такое важное понятие для понимания математики нашими студентами. Важно, чтобы мы связали эту работу с нашим языком в текстовых задачах. Многие задачи со словами можно рассматривать как сценарии «часть-часть-целое» (даже многие из описанных ниже типов «начало-изменение-конец»).
| ВСЕГО НЕИЗВЕСТНО | ЧАСТЬ НЕИЗВЕСТНО | ОБЕ ЧАСТИ НЕИЗВЕСТНО | |
| На дереве было 5 синих птиц и 3 кардинала. Сколько птиц всего? 5 + 3 = 8 | На дереве 8 птиц. 5 — синие птицы, а остальные — кардиналы. Сколько кардиналов? 8 – 5 = ? | На дереве 8 птиц. Некоторые из них — синие птицы, а некоторые — кардиналы. ? + ? = 8 |
Всего неизвестных задач являются типичными задачами на сложение. Есть два комплекта, которые идут вместе. Часто это не один и тот же предмет. Например, это могут быть красные яблоки и зеленые яблоки вместе. Или кошек и собак. Когда это один и тот же объект, это часто, но не всегда, сценарий «начало-изменение-конец», потому что изменение заключается в соединении этих двух наборов. Словесная проблема ниже демонстрирует полное неизвестное, имеющее тот же предмет — людей.
Часть неизвестна задач на вычитание. Мы знаем общее количество предметов, но не знаем их количество в одном из наборов. Работая с частично неизвестными задачами, мы усиливаем обратную связь между сложением и вычитанием. Мы можем написать аналогичное уравнение 5 + ? = 8, чтобы соединить две операции. Важно работать с неизвестными в любом положении, и часть неизвестных задач — это то место, где я предпочитаю работать над обратными операциями и семействами фактов.
Обе части неизвестны Проблемы встречаются реже. Это сценарии с несколькими решениями. Учащиеся знают общее количество предметов и дают возможную схему распределения этих предметов. Обе части неизвестных сценариев — мой любимый способ ввести неизвестные справа от знака равенства 8 = ? + ?. Это помогает учащимся понять, что они не просто решают слева направо и что означает знак равенства.
Для получения дополнительной информации о Части Части Целого у меня есть подробный пост в блоге, в котором показаны практические стратегии, которые я использую, чтобы представить и отработать отношения часть/целое.
НАЧАТЬ-ИЗМЕНИТЬ-КОНЕЦ
Хотя часть-часть-целое является наиболее распространенным типом задачи на сложение и вычитание, по мнению многих учителей, она, вероятно, не самая распространенная в задачах на рассказы. В реальных сценариях сложение и вычитание чаще всего демонстрируются через начало-изменение-результат. В сценариях результатов изменения запуска что-то присоединяется к другим или покидает их. Это типы проблем, когда кто-то что-то получил больше или что-то сломалось. Если мы не преднамеренно решаем задачи со словами, мы склонны по умолчанию решать задачи с неизвестным результатом. Эти типы задач часто имеют такие вопросы, как «сколько осталось?» и «сколько их сейчас?». Действие уже произошло.
Это типы проблем, когда кто-то что-то получил больше или что-то сломалось. Если мы не преднамеренно решаем задачи со словами, мы склонны по умолчанию решать задачи с неизвестным результатом. Эти типы задач часто имеют такие вопросы, как «сколько осталось?» и «сколько их сейчас?». Действие уже произошло.
Я использую термин «конец» вместо «результат», потому что «конец» противоположен «началу», и я думаю, что у учащихся более четкое понимание, чем с результатом. Это также тот же язык, который я использую для решения проблем с прошедшим временем в 3-м классе, и мне нравится, чтобы мой язык был как можно более последовательным.
В таблице ниже приведены примеры для каждого из 6 типов проблем начала изменения конца. Они довольно просты, поэтому я не буду подробно объяснять каждый из них. Будь то сложение или вычитание, язык указывает местонахождение неизвестного: субъекты в начале, субъекты, которые изменились, или субъекты в конце.
| НАЧАЛО НЕИЗВЕСТНО | ИЗМЕНЕНИЕ НЕИЗВЕСТНО | КОНЕЦ НЕИЗВЕСТНО | |
Дополнение | Несколько птиц сидели на дереве. На ветку прилетело еще 3 птички и теперь на дереве 8 птичек. Сколько птиц было на дереве в начале? На ветку прилетело еще 3 птички и теперь на дереве 8 птичек. Сколько птиц было на дереве в начале?? + 3 = 8 | 5 птиц сидели на дереве. На ветку летело несколько птиц и теперь на дереве их 8. Сколько птиц прилетело на ветку? 5 + ? = 8 | 5 птиц сидели на дереве. На ветку летят 3 птицы. Сколько птиц сейчас на дереве?
5 + 3 = ? |
| Вычитание | Несколько птиц сидели на дереве. 3 птицы улетели и теперь на дереве 8 птиц. Сколько птиц было на дереве в начале? ? – 3 = 8 | 11 птиц сидели на дереве. Некоторые птицы улетели и теперь на дереве 8 птиц. Сколько птиц улетело? 11 – ? = 8 | 11 птиц сидели на дереве. Улетели 3 птицы. Сколько птиц сейчас на дереве? 11 – 3 = ? |
Важно, чтобы мы давали студентам возможность попрактиковаться с неизвестными во всех позициях. Студенты видят, что именно через эти типы задач «начало-изменение-конец» их можно попросить определить, сколько чего-то было в начале. Или, что изменение/действие было. С задачами «начало-изменение-конец» учащиеся получают возможность понять, что неизвестные находятся во всех позициях, и развить свою компетентность в отношении сложения и вычитания, являющихся обратными операциями. Через неизвестные в любом месте учащиеся моделируют и решают, используя обратную операцию.
Студенты видят, что именно через эти типы задач «начало-изменение-конец» их можно попросить определить, сколько чего-то было в начале. Или, что изменение/действие было. С задачами «начало-изменение-конец» учащиеся получают возможность понять, что неизвестные находятся во всех позициях, и развить свою компетентность в отношении сложения и вычитания, являющихся обратными операциями. Через неизвестные в любом месте учащиеся моделируют и решают, используя обратную операцию.
Если начало-изменение-окончание для вас новая концепция, я дам вам инструменты и стратегии в подробном посте об обучении Начать Изменить Завершить.
СРАВНЕНИЯ
Сравнения — самые сложные текстовые задачи для учащихся. Они, естественно, не то, о чем мы думаем, когда думаем об операциях. По этой причине нам нужно учить их и практиковать их. Много!
| РАЗНИЦА НЕИЗВЕСТНО | БОЛЬШЕ НЕИЗВЕСТНО | МЕНЬШИЙ НЕИЗВЕСТНЫЙ | |
| Сравнить | Сколько еще? У Сары 3 птицы. На сколько меньше? У Сары 3 птицы. У Райны 5 птиц. На сколько меньше птиц у Сары, чем у Райны? 5 – 3 = ? 3 + ? = 5 | Подробнее У Сары 3 птицы. У Райны на 2 птицы больше, чем у Сары. Сколько птиц у Райны? Меньше У Сары 3 птицы. У нее на 2 птицы меньше, чем у Райны. Сколько птиц у Райны? 3 + 2 = ? ? – 2 = 3 | Подробнее У Райны 5 птиц. У нее на 2 птицы больше, чем у Сары. Сколько птиц у Сары? Меньше У Райны 5 птиц. У Сары на 2 птицы меньше, чем у Райны. Сколько птиц у Сары? 5 – 2 = ? 2 + ? = 5 |
Разница Неизвестно задач обычно решают с помощью вычитания. Независимо от вопроса, на сколько больше или на сколько меньше, вопрос хочет знать сумму между ними. Слово «больше» может сбить учащихся с толку, потому что они хотят добавить. Вы можете использовать уравнение сложения, чтобы продемонстрировать его в представленном виде, но, в конечном счете, вычитание — самый простой способ решить его. Мой любимый способ моделирования этих задач — числовая прямая, потому что я могу продемонстрировать оба типа вопросов, считая в прямом или обратном порядке.
Слово «больше» может сбить учащихся с толку, потому что они хотят добавить. Вы можете использовать уравнение сложения, чтобы продемонстрировать его в представленном виде, но, в конечном счете, вычитание — самый простой способ решить его. Мой любимый способ моделирования этих задач — числовая прямая, потому что я могу продемонстрировать оба типа вопросов, считая в прямом или обратном порядке.
В вопросах Большое неизвестное и Меньшее неизвестное все становится немного сложнее. Что касается меня, то, как и в случае с любой проблемой, я прошу студентов начать с сосредоточения внимания на неизвестном в вопросе. С этими проблемами, я думаю, лучше всего работать над ними вместе, потому что их легко запутать.
В моих плакатах типа задачи на сложение и вычитание я комбинирую по известной информации. В обеих описанных выше ситуациях нам говорят, что у кого-то больше, и у них обоих один и тот же вопрос. Сосредоточив внимание на том, что означает «больше», мы показываем учащимся различия в типах вопросов и тонкости между ними. Вы можете скачать мои плакаты с задачами на сложение и вычитание, подписавшись ниже.
Вы можете скачать мои плакаты с задачами на сложение и вычитание, подписавшись ниже.
Большие Неизвестные задач в таблице содержат вопрос «Сколько птиц у Райны?». Из-за расположения стола мы понимаем, что у Райны больше птиц, чем у Сары. Но давайте подробнее рассмотрим проблемы.
У Сары 3 птицы. У Райны на 2 птицы больше, чем у Сары. Сколько птиц у Райны?
В этой задаче говорится, что у Райны больше, чем у Сары. Это довольно простая задача на сложение: сложить число Сары и еще одно число — сравнение — чтобы найти общее число Райны.
У Сары 3 птицы. У нее на 2 птицы меньше, чем у Райны. Сколько птиц у Райны?
Эта проблема не так проста. Это говорит нам о том, что у Райны больше, говоря нам, что 3 у Сары на 2 меньше, чем у Райны. Когда учащиеся видят «меньше», они хотят вычесть, но большее число неизвестно. Мы можем смоделировать это уравнение на вычитание как неизвестное — 2 дает нам 3 для Сары.
Меньшие неизвестные Обе задачи спрашивают, сколько у Сары в таблице, поскольку у Сары меньшее количество. Опять же, давайте подробнее рассмотрим проблемы.
У Райны 5 птиц. У нее на 2 птицы больше, чем у Сары. Сколько птиц у Сары?
В этой задаче слово «больше» может заставить учащихся почувствовать, что им нужно добавить. Но вычитание — лучшая операция. Если у Райны на 2 больше, чем у Сары, мы можем вычесть 2 из суммы Сары и суммы Райны. Или, как дополнение, Сара + 2 = Райна 5.
У Райны 5 птиц. У Сары на 2 меньше, чем у Райны. Сколько птиц у Сары?
Эта задача более проста, чем предыдущая. У Сары на 2 меньше, чем у Райны, поэтому ученики, естественно, будут вычитать.
Для этих сценариев я считаю наиболее полезным начать с вопроса. Неизвестный. Если мне нужно знать, сколько птиц у Сары, я держу это в уме, возвращаясь к задаче со словами во второй раз и переформулируя ее. 5 у Райны на 2 больше, чем у Сары. У Сары на 2 меньше, чем у Райны 5. Начав с неизвестного, которое я решаю, я могу лучше понять, что вопрос просит меня сделать, связав его с известным.
5 у Райны на 2 больше, чем у Сары. У Сары на 2 меньше, чем у Райны 5. Начав с неизвестного, которое я решаю, я могу лучше понять, что вопрос просит меня сделать, связав его с известным.
Я учу своих учеников внимательно читать каждое слово-задачу. Я связываю это с внимательным чтением, которое мы делаем на уроках ELA. Потому что на самом деле и то, что мы читаем в ELA, и задачи, которые мы решаем, являются сложными текстами. Я использую программу 3 чтения. Первое чтение должно получить общее понимание — суть — контекст. В следующем читается прохождение словесной проблемы с упором на неизвестные и вопрос. Вы можете прочитать больше о моей рутине 3 чтения в этом сообщении в блоге.
Типы задач на сложение и вычитание
У меня есть плакаты для всех типов задач на сложение и вычитание. Вы можете использовать их как часть якорной таблицы, когда вы пишете свои собственные текстовые задачи вместе для каждого типа задач. Вы можете отображать их по мере того, как вводите их. Вы можете распечатать несколько на странице и дать учащимся свои собственные в качестве справочных материалов.
Вы можете распечатать несколько на странице и дать учащимся свои собственные в качестве справочных материалов.
У меня также есть справочный лист типов задач на сложение и вычитание для вас. Этот одностраничный печатный лист — хороший справочный лист, который вы всегда будете иметь под рукой. Или учащиеся могут сохранить копию в своей папке с математическими справочниками, если она у вас есть. Включенные словесные задачи такие же, как и на этом сайте, а не те, что на плакатах, ссылки на которые приведены выше.
Заполните форму ниже, чтобы подписаться на получение плакатов с задачами на сложение и вычитание.
Информационный бюллетень
Подпишитесь, чтобы получать бесплатные плакаты с задачами на сложение и вычитание! После подтверждения электронной почты вы получите файл и будете подписаны на мою еженедельную рассылку.
Загрузка…
У меня также есть цифровые карточки с задачами на сложение и вычитание. Они организованы по типам текстовых задач и тренируются на сложении и вычитании в пределах 20. В наборах «Часть-Часть-Целое» и «Начало-Изменить-Конец» есть особая практика, позволяющая различать их, когда учащиеся сопоставляют неизвестное и заданное уравнение с заданными сценариями.
Они организованы по типам текстовых задач и тренируются на сложении и вычитании в пределах 20. В наборах «Часть-Часть-Целое» и «Начало-Изменить-Конец» есть особая практика, позволяющая различать их, когда учащиеся сопоставляют неизвестное и заданное уравнение с заданными сценариями.
Каждый из наборов дает учащимся определенную практику по каждому типу задач на сложение и вычитание. Учащиеся используют встроенные инструменты для написания уравнений с переменными или символами для неизвестных. После написания уравнения учащиеся используют манипуляторы для моделирования задачи на числовой прямой и десятках кадров. Формат позволяет учащимся практиковать несколько стандартов математической практики, моделируя и решая задачу, а также проверяя свою работу.
В дополнение к типам задач «часть-часть-целое», «начало-изменение-конец» и «сравнение» существует также набор задач «Сложение 3 чисел». Этот набор представлен в сценариях часть/целое или часть-часть-часть-целое. Набор бесплатный, и его можно загрузить из моего магазина TpT, нажав на обложку ниже.
Набор бесплатный, и его можно загрузить из моего магазина TpT, нажав на обложку ниже.
Я надеюсь, что этот пост дал вам идеи и ресурсы для обучения ваших студентов каждому типу задач на сложение и вычитание. Чем больше практики и опыта получают студенты, тем успешнее они будут. Вас также может заинтересовать мой пост «Игры для сложения и вычитания фактов».
Для получения дополнительной информации о типах задач CGI Word, этот пост от Langford Math довольно подробный, и в этой вики есть куча примеров задач Word.
IXL | Учим математику в 5 классе
IXL | Изучайте математику в 5 классе.1
Преобразование между стандартной и расширенной формой
2
Значение места
3
Сравните числа до миллиардов
4
Запись чисел словами: переводим слова в цифры
5
Запись чисел словами: переводим цифры в слова
6
Названия слов по буквам для чисел до миллиона
7
римские цифры
8
Округление
9
Чет или нечет: правила арифметики
10
Научная нотация
1
Складывать и вычитать целые числа до миллиардов
2
Складывать и вычитать целые числа: текстовые задачи
3
Полное сложение и вычитание предложений
4
Вставьте недостающие цифры
5
Выберите числа с определенной суммой или разностью
6
Свойства добавления
7
Добавить с помощью свойств
8
Оценивать суммы и разности целых чисел
9
Оценить суммы и разности: текстовые задачи
1
Умножение на однозначные числа
2
Умножение на однозначные числа: текстовые задачи
3
Образцы умножения по возрастанию разрядных значений
4
Умножение чисел, заканчивающихся нулями
5
Умножение чисел, оканчивающихся на нули: текстовые задачи
6
Свойства умножения
7
Умножение с использованием свойств
8
Выберите номера с конкретным продуктом
9
Оценить продукты
10
Оценка продуктов: текстовые задачи
11
Коробочное умножение
12
Умножение решетки
13
Умножение на двузначные числа: выполните недостающие шаги
14
Умножение двузначных чисел на двузначные числа
15
Умножение двузначных чисел на трехзначные числа
16
Умножение двузначных чисел на большее число
17
Умножение на двузначные числа: текстовые задачи
18
Умножение трех и более чисел до 2 цифр каждое
19
Умножение на трехзначные числа
20
Умножьте три числа до 3 цифр каждое
21
Умножение трех и более чисел: текстовые задачи
22
Неравенства с умножением
23
Таблицы ввода/вывода умножения
24
Таблицы ввода/вывода умножения: найти правило
1
Факты о делении на 12
2
Разделение фактов на 12: словесные задачи
3
Разделить многозначные числа на однозначные числа
4
Деление многозначных чисел на однозначные: текстовые задачи
5
Разделить на однозначные числа: интерпретировать остатки
6
Шаблоны деления по возрастанию разрядных значений
7
Разделить числа, заканчивающиеся нулями
8
Разделить числа, оканчивающиеся на нули: текстовые задачи
9
Оценка частных: двузначные делители
10
Оцените коэффициенты
11
Оценить коэффициенты: текстовые задачи
12
Разделите на двузначные числа, используя модели
13
Разделить на двузначные числа, используя неполные частные
14
Разделить двузначные и трехзначные числа на двузначные числа
15
Деление двузначных и трехзначных чисел на двузначные числа: задачи со словами
16
Разделить четырехзначное число на двузначное
17
Делим четырехзначные числа на двузначные: текстовые задачи
18
Отрегулируйте коэффициенты
19
Многоступенчатые текстовые задачи: мультипликативное сравнение
20
Связать умножение и деление
21
Завершите предложение деления: 2-значные делители
22
Выберите числа с определенным частным
1
Понимание степени десяти
2
Оцените степени десяти
3
Напишите степени десяти с показателями
4
Умножение целого числа на степень десяти: с показателями
5
Умножение десятичной дроби на степень десяти: с показателями
6
Разделить на степень десяти: с показателями
7
Умножение и деление на степень десяти: с показателями
8
Понимание показателей
9
Оценить показатели
10
Найдите пропущенный показатель или основание
1
Определите факторы
2
Простые и составные числа
3
простые множители
4
Простая факторизация с показателями
5
Правила делимости
6
Правила делимости: текстовые задачи
7
Найдите все пары множителей числа
8
Наибольший общий делитель
9
Наибольший общий делитель трех чисел
10
Наименьший общий множитель
11
Наименьшее общее кратное трех или четырех чисел
1
Какое десятичное число изображено?
2
Модель десятичных дробей и дробей
3
Модели разрядного значения для десятичных чисел
4
Понимание десятичных дробей, выраженных словами
5
Поместите значения в десятичные числа
6
Связь между значениями десятичных разрядов
7
Преобразование десятичных знаков между стандартной и расширенной формой
8
Составление и разложение десятичных дробей несколькими способами
9
Эквивалентные десятичные дроби
10
Круглые десятичные дроби
11
Десятичные числовые строки
12
Сравните десятичные числа, используя сетки
13
Сравните десятичные дроби в числовых рядах
14
Сравните десятичные числа
15
Расположи десятичные числа по порядку
16
Сравнить, упорядочить и округлить десятичные дроби: текстовые задачи
17
Преобразование дробей в десятичные
18
Преобразование смешанных чисел в десятичные
19
Преобразование десятичных дробей в дроби
20
Преобразование десятичных дробей в смешанные числа
21
Преобразование десятичных знаков между стандартной и расширенной формой с использованием дробей
22
Сравните десятичные дроби и дроби в числовых рядах
23
Сравните десятичные дроби и дроби
24
Последовательности чисел, включающие десятичные дроби
25
Повторяющиеся десятичные дроби
26
Расположи десятичные дроби и дроби по порядку
27
Расположите смесь десятичных дробей, дробей и смешанных чисел по порядку
1
Сложите десятичные числа с помощью блоков
2
Добавить десятичные числа
•
Новинка! Вычитание десятичных чисел с помощью блоков
3
Вычитание десятичных чисел
4
Сложение и вычитание десятичных чисел
5
Сложение и вычитание десятичных дробей: текстовые задачи
6
Выберите десятичные дроби с определенной суммой или разницей
7
Завершите десятичное сложение или вычитание предложения
8
Неравенства с десятичным сложением и вычитанием
9
Оцените суммы и разности десятичных знаков с помощью округления
10
Оцените суммы и разности десятичных знаков, используя эталоны
1
Оценка произведений целых чисел и десятичных дробей
2
Оценить произведения десятичных дробей
3
Умножить десятичную дробь на степень десяти
4
Умножить на 0,1 или 0,01
5
Умножение на степень десяти с десятичными знаками: найди пропущенное число
6
Умножение десятичной дроби на целое однозначное число с помощью блоков
7
Умножить десятичную дробь на целое однозначное число, используя распределительное свойство
8
Умножение десятичной дроби на однозначное целое число
9
Умножение десятичной дроби на двузначное целое число с использованием площадных моделей
10
Умножение десятичной дроби на многозначное целое число
11
Умножение десятичных и целых чисел: текстовые задачи
12
Умножение трех и более чисел, одно из которых десятичное
13
Завершите предложение десятичного умножения, используя сетки
14
Умножение десятичных дробей с помощью сетки
15
Умножение двух знаков после запятой: куда идет десятичная точка?
16
Умножение двух десятичных знаков: произведения до сотых
17
Умножение двух десятичных знаков: произведения до тысячных
18
Неравенства с десятичным умножением: произведения до сотых
19
Неравенства с десятичным умножением: произведения до тысячных
1
Разделить на десять
2
Шаблоны десятичного деления по возрастанию разрядных значений
3
Разделить на десять с десятичной дробью: найти недостающее число
4
Разделите десятичные дроби с помощью блоков: завершите уравнение
5
Разделите десятичные дроби, используя модели площади: завершите уравнение
6
Деление с десятичными частными
7
Деление с десятичными частными и округлением
8
Деление с десятичными частными: текстовые задачи
9
Оцените десятичные частные
10
Разделить на 0,1 или 0,01
11
Разделить на десятичные дроби без добавления нулей
12
Разделить на десятичные дроби
1
Обзор фракций
2
Дроби целого: текстовые задачи
3
Дроби группы: текстовые задачи
4
Эквивалентные дроби
5
Запишите дроби в меньших терминах
6
Преобразование между неправильными дробями и смешанными числами
7
Наименьший общий знаменатель
8
График и сравнение дробей на числовых линиях
9
Сравните дроби, используя эталоны
10
Сравните дроби и смешанные числа
11
Расставь дроби по порядку
12
Шаблоны сложения и вычитания с дробями
13
Образцы умножения с дробями
14
Круглые смешанные числа
15
Взаимные
16
Соотнесите деление и дроби
17
Понять дроби как деление: текстовые задачи
1
Разложите дроби несколькими способами
2
Сложите и вычтите дроби с одинаковыми знаменателями, используя числовые линии
3
Складывать и вычитать дроби с одинаковыми знаменателями
4
Складывать и вычитать дроби с одинаковыми знаменателями: текстовые задачи
5
Складывать и вычитать смешанные числа с одинаковыми знаменателями
6
Сложите дроби с разными знаменателями, используя модели
7
Сложите до 4 дробей со знаменателями 10 и 100.

8
Сложите дроби с разными знаменателями
9
Вычитание дробей с разными знаменателями с использованием моделей
10
Оцените суммы и разности дробей, используя эталоны
11
Вычитание дробей с разными знаменателями
12
Складывать и вычитать дроби с разными знаменателями: текстовые задачи
13
Сложите 3 или более дроби с разными знаменателями
14
Сложите 3 и более дроби: текстовые задачи
15
Сравните суммы и разности единичных дробей
16
Завершите предложения сложения и вычитания с дробями
17
Неравенства со сложением и вычитанием дробей
18
Оценить суммы и разности смешанных чисел
19
Сложите смешанные числа с разными знаменателями
20
Вычитание смешанных чисел с разными знаменателями
21
Сложение и вычитание смешанных чисел: текстовые задачи
22
Складывать и вычитать дроби в рецептах
23
Завершите предложения на сложение и вычитание со смешанными числами.

24
Неравенства со сложением и вычитанием смешанных чисел
1
Умножение единичных дробей на целые числа с помощью числовых рядов
2
Умножайте единичные дроби на целые числа с помощью моделей
3
Кратные единичные дроби: найти пропущенные числа
4
Умножение единичных дробей и целых чисел: сортировка
5
Умножение дробей на целые числа с помощью массивов
6
Умножение дробей на целые числа с помощью числовых рядов
7
Умножение дробей на целые числа: выбираем модель
8
Умножайте дроби на целые числа, используя модели: завершите уравнение
9
Кратные дроби: найти недостающие числа
10
Умножение дробей и целых чисел: сортировка
11
Умножать дроби на целые числа I
12
Умножение дробей на целые числа II
13
Умножение дробей на целые числа: текстовые задачи
14
Умножение дробей на целые числа: таблицы ввода/вывода
15
Доли числа I
16
Доли числа: текстовые задачи
17
Доли числа II
18
Умножьте две единичные дроби, используя модели
19
Умножьте две дроби с помощью моделей: вставьте недостающий множитель
20
Умножьте две дроби, используя модели
21
Умножить две дроби
22
Умножение двух дробей: текстовые задачи
23
Масштабирование целых чисел дробями: обоснуйте свой ответ
24
Масштабирование целых чисел дробями
25
Масштабирование дробей дробями
26
Масштабирование смешанных чисел дробями
•
Новинка! Масштабирование по дробям и смешанным числам
27
Умножение трех и более дробей и целых чисел
28
Завершите предложение умножения дроби I
29
Завершите предложение умножения дроби II
30
Знать умножение дробей и площадь
31
Умножьте дроби, чтобы найти площадь
32
Оцените произведения смешанных чисел
33
Умножение смешанного числа на целое по модели I
34
Умножение смешанного числа на целое по модели II.

35
Умножение на смешанные числа с использованием площадных моделей
36
Умножение смешанного числа на целое число
37
Умножить смешанное число на дробь
38
Умножить два смешанных числа
•
Новинка! Умножение смешанных чисел, дробей и целых чисел
39
Умножение трех и более смешанных чисел, дробей и целых чисел
40
Умножение со смешанными числами: текстовые задачи
41
Умножение дробей и смешанных чисел в рецептах
1
Разделите единичные дроби на целые числа с помощью моделей
2
Разделить дробные единицы на целые числа
3
Разделите целые числа на единичные дроби, используя модели
4
Разделить целые числа на дроби единиц
5
Разделите единичные дроби и целые числа, используя модели площадей
6
Разделите единичные дроби и целые числа
7
Разделить единичные дроби и целые числа: текстовые задачи
8
Разделить дроби на целые числа
9
Делить целые числа на дроби
10
Разделить две дроби
11
Разделите дроби и смешанные числа
12
Разделить дроби и смешанные числа: текстовые задачи
1
Складывать, вычитать, умножать и делить целые числа
2
Складывать, вычитать, умножать и делить целые числа: текстовые задачи
3
Запись числовых выражений: одна операция
4
Запись числовых выражений: две операции
5
Вычислить числовые выражения
6
Вычислять числовые выражения со скобками
7
Вычислять числовые выражения со скобками и квадратными скобками
8
Выявление ошибок, связанных с порядком операций
9
Вычислять числовые выражения со скобками в разных местах
10
Отсутствующие операторы
11
Сложение, вычитание, умножение и деление десятичных дробей
12
Сложение, вычитание, умножение и деление десятичных дробей: текстовые задачи
13
Уравнения со смешанными операциями: правда или ложь
14
Складывать, вычитать, умножать и делить дроби и смешанные числа
15
Складывать, вычитать, умножать и делить дроби и смешанные числа: текстовые задачи
1
Сделайте максимально возможное частное
2
Напишите числовые выражения для текстовых задач
3
Многоступенчатые текстовые задачи
4
Многошаговые словесные задачи с остатками
5
Многоступенчатые текстовые задачи: определите разумные ответы
6
Проблемы со словами с лишней или отсутствующей информацией
7
Проблемы с угадыванием и проверкой
8
Найти заказ
9
Используйте диаграммы Венна для решения задач
1
Какой процент изображен?
2
Преобразование между процентами, дробями и десятичными дробями
3
Процент числа
1
Складывать и вычитать денежные суммы
2
Складывать и вычитать деньги: словесные задачи
3
Прибавляй и вычитай деньги: многоступенчатые словесные задачи
4
Умножение денежных сумм
5
Умножение денежных сумм: словесные задачи
6
Умножение денежных сумм: многошаговые словесные задачи
7
Разделите денежные суммы
8
Разделить денежные суммы: текстовые задачи
9
Прайс-листы
10
Цены за единицу
11
Найдите количество монет каждого вида.

1
Использование правила для завершения числовой последовательности
2
Сравните шаблоны
3
Заполните возрастающую числовую последовательность
4
Заполните геометрическую числовую последовательность
5
Числовые последовательности: проблемы со словами
6
Номерные серии: смешанный обзор
1
Опишите координатную плоскость
2
Объекты на координатной плоскости
3
График точек на координатной плоскости
4
График точек из таблицы
5
Используйте правило для заполнения таблицы и графика
6
Анализ графических отношений
7
Координатные плоскости как карты
8
Следуйте указаниям на координатной плоскости
1
Напишите переменные выражения
2
Напишите переменные выражения: текстовые задачи
3
Вычислить переменные выражения
4
Напишите уравнения с переменными: текстовые задачи
5
Решайте уравнения с целыми числами
6
Решайте уравнения с десятичными дробями
7
Найдите значение, используя уравнения с двумя переменными
8
Заполните таблицу для связи с двумя переменными
9
Заполнить таблицу по графику
10
Графические шаблоны с использованием правил
11
График отношения с двумя переменными
12
Напишите уравнение с двумя переменными
1
Читать таблицу
2
Интерпретировать линейные графики
3
Создание линейных графиков
4
Интерпретация гистограмм
5
Интерпретация гистограмм: многошаговые задачи
6
Создание гистограмм
7
Интерпретировать пиктограммы
8
Создание пиктограмм
9
Интерпретировать линейные графики
10
Создание линейных графиков
11
Создание и интерпретация линейных графиков с дробями
12
Интерпретация частотных диаграмм: одношаговые задачи
13
Интерпретация частотных диаграмм: многошаговые задачи
14
Создание частотных диаграмм
15
Интерпретация сюжетов «стебель-листья»
16
Создание участков стебля и листьев
1
Найдите режим
2
Найдите среднее
3
Найдите медиану
4
Найдите диапазон
5
Означает: найти пропущенное число
6
Медиана: найти пропущенное число
7
Диапазон: найти недостающее число
8
Интерпретируйте диаграммы и графики, чтобы найти моду
9
Интерпретируйте диаграммы и графики, чтобы найти среднее значение
10
Интерпретируйте диаграммы и графики, чтобы найти медиану
11
Интерпретируйте диаграммы и графики, чтобы найти диапазон
12
Понимание вероятности
13
Найдите вероятность
14
Делать предсказания
15
Комбинации
1
Преобразование единиц времени
2
Сложение и вычитание смешанных единиц времени
3
Часовые пояса
4
Пройденное время
5
Найти время начала и окончания: текстовые задачи
6
Расписания и сроки
1
Выберите подходящую общепринятую единицу измерения
2
Сравнивайте и конвертируйте общепринятые единицы длины
3
Сравнивайте и конвертируйте обычные единицы веса
4
Сравните и конвертируйте обычные единицы объема
5
Сравните и конвертируйте обычные единицы
6
Таблицы преобразования — общепринятые единицы
7
Сравните обычные единицы, умножив
8
Преобразование обычных единиц, включающих дроби
9
Преобразовать смешанные обычные единицы
10
Сложение и вычитание смешанных обычных единиц
11
Многошаговые задачи с обычными преобразованиями единиц измерения
12
Выберите подходящую метрическую единицу измерения
13
Сравните и конвертируйте метрические единицы длины
14
Сравните и конвертируйте метрические единицы веса
15
Сравните и конвертируйте метрические единицы объема
16
Сравните и конвертируйте метрические единицы
17
Преобразование метрических единиц с использованием десятичных знаков
18
Таблицы преобразования — метрические единицы
19
Преобразование метрических смешанных единиц
20
Сложение и вычитание метрических смешанных единиц
21
Многоэтапные проблемы с преобразованием метрических единиц
22
Многоэтапные проблемы с обычными или метрическими преобразованиями единиц
23
Понимание кубических единиц
24
Разумная температура — по Цельсию и по Фаренгейту
1
Это полигон?
2
Количество сторон в многоугольниках
3
Правильные и неправильные многоугольники
4
Точки, прямые, отрезки, лучи и углы
5
Параллельные, перпендикулярные и пересекающиеся прямые
6
Виды углов
7
Углы 90, 180, 270 и 360 градусов
8
Измерьте углы транспортиром
9
Сортировка полигонов в диаграммы Венна
10
Свойства полигонов
11
Части круга
1
Остроугольные, тупоугольные и прямоугольные треугольники
2
Разносторонние, равнобедренные и равнобедренные треугольники
3
Классифицировать треугольники
4
Параллельные стороны в четырехугольниках
5
Определите параллелограммы
6
Определить трапеции
7
Определить прямоугольники
8
Определите ромбы
9
Классифицировать четырехугольники
10
Нарисуйте четырехугольники
11
Определите отношения между четырехугольниками
12
Опишите отношения между четырехугольниками.

1
Линейная симметрия
2
Вращательная симметрия
3
Вращательная симметрия: величина вращения
4
Отражение, вращение и перевод
5
Назовите равные и подобные фигуры
1
Определять трехмерные фигуры
2
Подсчет вершин, ребер и граней
3
Сетки трехмерных фигур
4
Трехмерные фигуры, рассматриваемые с разных точек зрения
1
Периметр с целыми числами длин сторон
2
Периметр с десятичными длинами сторон
3
Периметр с дробными длинами сторон
4
Периметр фигур на сетке
5
Площадь квадратов и прямоугольников
6
Площадь квадратов и прямоугольников с дробями
7
Площадь треугольников
8
Площадь параллелограммов и трапеций
9
Площадь сложных фигур
10
Площадь между двумя прямоугольниками
11
Площадь фигур на сетке
12
Площадь и периметр: текстовые задачи
13
Объем прямоугольных призм из единичных кубов
14
Объем неправильных фигур из единичных кубов
15
Объем кубов и прямоугольных призм
16
Объем составных фигур
17
Соотношение между объемом и площадью основания: текстовые задачи
18
Объем кубов и прямоугольных призм: текстовые задачи
19
Сравни объемы и размеры прямоугольных призм: текстовые задачи
20
Объем кубов и прямоугольных призм с десятичными длинами сторон
21
Площадь поверхности
1
Налоги на прибыль и фонд заработной платы: понимание платежных квитанций
2
Налог на прибыль и фонд заработной платы: текстовые задачи
3
Налоги с продаж и имущества: текстовые задачи
4
Назовите виды налогов.

5
Понимание валовой и чистой прибыли
6
Рассчитать валовую и чистую прибыль
7
Выявление преимуществ и недостатков способов оплаты
8
Оцените способы оплаты
9
Чтение финансовых отчетов
10
Ведение финансовой отчетности
11
Сбалансировать бюджет
12
Изменить бюджет
Смысл числа
- Значение места
- Простые и составные числа
- простые множители
- Факторы
- Наибольший общий делитель
- Мультипликаторы
- Наименьший общий множитель
Умножение
- Умножение кратных 10
- Оценка продуктов
- Умножение модели площади
- Частичные продукты
- Умножение решетки
- Умножение на однозначные числа
- Умножение на двузначные числа
- Умножение на трехзначные числа
- Длинное умножение
Отдел
- Деление кратных 10
- Оценка частных
- Частичные частные
- Районный модельный отдел
- Деление на однозначные числа
- Деление на двузначные числа
- Длинное деление
Показатели и степени числа 10
- Экспоненты
- Степени 10
Недвижимость и смешанные операции
- Распределительная собственность
- Порядок операций
- ПЕМДАС
Дроби
- Обзор фракций
- Понимание дробей
- Модели фракционной площади
- Дроби на числовой прямой
- Фракции набора
- Эквивалентные дроби
- Сравнение дробей
- Наименьший общий знаменатель
- Простейшая форма
- Смешанные числа и неправильные дроби
- Дроби как деление
Сложение дробей
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Добавление смешанных чисел
Вычитание дробей
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
- Вычитание смешанных чисел
Умножение дробей
- Умножение дробей и целых чисел
- Умножение дробей
- Умножение смешанных чисел
- Умножение как масштабирование
Разделение дробей
- Деление дробей и смешанных чисел
- Деление дробей на целые числа
- Деление целых чисел на дроби
- Взаимные
Десятичные числа
- Дроби и десятичные дроби
- Преобразование между дробями, десятичными знаками и процентами
- Десятичное разрядное значение
- Запись десятичных дробей в расширенной форме
- Написание десятичных дробей в словесной форме
- Эквивалентные десятичные дроби
- Сравнение десятичных дробей
- Округление десятичных знаков
Сложение и вычитание десятичных дробей
- Добавление десятичных знаков
- Вычитание десятичных знаков
Умножение десятичных дробей
- Умножение десятичных дробей на степени 10
- Умножение десятичных дробей на целые числа
- Умножение десятичных дробей
Деление десятичных дробей
- Деление десятичных дробей на степени 10
- Деление десятичных дробей на целые числа
- Разделение десятичных дробей
Геометрия
- Параллельные и перпендикулярные линии
- Виды углов
- Измерение углов транспортиром
- Типы треугольников
- Виды четырехугольников
- Параллелограммы
- ромбы
- прямоугольники
- Квадраты
- Трапеции
- Воздушные змеи
- Правильные многоугольники
- Площадь прямоугольников
- Площадь сложных фигур
- Объем прямоугольных призм
Данные и измерения
- Линейные графики
- Метрические единицы измерения
- Преобразование метрических единиц
- Привычные единицы измерения
- Преобразование обычных единиц
- Таблицы частот
Стратегии решения текстовых задач
Простое добавление этих слов увеличивает сложность (а иногда и математическую тревогу) примерно в 100 раз!
Как вы можете помочь своим ученикам научиться уверенно решать текстовые задачи? Обучая своих учеников решать текстовые задачи поэтапно и организованно, вы дадите им инструменты, необходимые для решения текстовых задач гораздо более эффективным способом.
Вот семь стратегий, которые я использую, чтобы помочь учащимся решать текстовые задачи.
1. Прочтите задачу целиком
Прежде чем учащиеся будут искать ключевые слова и пытаться понять, что делать, им нужно немного замедлиться и прочитать задачу целиком один раз (а еще лучше, дважды). Это помогает детям получить более широкую картину, чтобы понять ее немного лучше.
2. Подумайте о задаче со словами
Учащиеся должны задавать себе три вопроса каждый раз, когда они сталкиваются с задачей со словами. Эти вопросы помогут им составить план решения проблемы.
Вот вопросы:
А. В чем именно вопрос?
В чем проблема? Часто составители учебных программ включают в задачу дополнительную информацию, казалось бы, без уважительной причины, разве что для того, чтобы научить детей игнорировать эту постороннюю информацию (грррр!). Студенты должны быть в состоянии оставаться сосредоточенными, игнорировать эти лишние детали и выяснять, в чем заключается настоящий вопрос в конкретной задаче.
B. Что мне нужно, чтобы найти ответ?
Учащимся необходимо еще больше сузить круг, чтобы понять, что нужно для решения задачи, будь то сложение, вычитание, умножение, деление или их комбинация. Им потребуется общее представление о том, какая информация будет использоваться (или не использоваться) и что они будут делать.
Здесь очень помогают ключевые слова. Когда учащиеся учатся распознавать, что одни слова означают сложение (например, в сумме, вместе взятые ), а другие означают вычитание, умножение или деление, это помогает им решить, как поступить немного лучше
Вот таблица ключевых слов, которую я люблю использовать для обучения словесным задачам. Раздаточный материал можно было бы скопировать в меньшем размере и вклеить в интерактивные математические тетради. Его можно поместить в папки по математике или в папки под математическим разделом, если ваши учащиеся используют папки.
Однажды я сделал огромные математические знаки (символы сложения, вычитания, умножения и деления) и написал вокруг них ключевые слова. Они служили постоянным напоминанием о ключевых словах для текстовых задач в классе.
Они служили постоянным напоминанием о ключевых словах для текстовых задач в классе.
Если вы хотите загрузить этот БЕСПЛАТНЫЙ раздаточный материал по ключевым словам, нажмите здесь:
C. Какая информация у меня уже есть?
Здесь учащиеся сосредоточатся на числах, которые будут использоваться для решения задачи.
3. Напишите в Word Задача
Этот шаг укрепляет размышления, которые были сделаны на шаге номер два. Учащиеся используют карандаш или цветные карандаши, чтобы записывать информацию на рабочих листах (конечно, не в книгах, если только они не расходные материалы). Есть много способов сделать это, но вот что я люблю делать:
- Обведите любые цифры, которые вы будете использовать.
- Слегка зачеркните ненужную информацию.
- Подчеркните фразу или предложение, в котором точно указано, что вам нужно найти.
4. Нарисуйте простое изображение и подпишите его
Рисование изображений с использованием простых форм, таких как квадраты, круги и прямоугольники, помогает учащимся визуализировать проблемы. Добавление номеров или имен в качестве меток также помогает.
Добавление номеров или имен в качестве меток также помогает.
Например, если в словесной задаче сказано, что было пять коробок и в каждой коробке было 4 яблока, дети могут нарисовать пять квадратов с числом четыре в каждом квадрате. Мгновенно дети могут увидеть ответ намного проще!
5. Оцените ответ перед решением
Имея общее представление о примерном ответе на задачу, учащиеся узнают, является ли их фактический ответ разумным или нет. Эта быстрая приблизительная оценка — хорошая математическая привычка. Это помогает учащимся по-настоящему задуматься о точности своего ответа, когда проблема будет окончательно решена.
6. Проверка выполненной работы
Эта стратегия дополняет пятую стратегию. Одна из фраз, которые я постоянно использую во время занятий по математике, звучит так: Ваш ответ разумен ? Я хочу, чтобы учащиеся делали больше, чем просто считали, но действительно думали о том, что означают эти цифры.
Кроме того, когда учащиеся привыкают проверять работу, они более склонны выявлять ошибки по невнимательности, которые часто являются причиной неправильных ответов.
7. Часто тренируйтесь решать словесные задачи
Точно так же, как требуется практика, чтобы научиться играть на кларнете, вести мяч в футболе и реалистично рисовать, нужна практика, чтобы стать мастером решения словесных задач.
Когда учащиеся решают текстовые задачи, часто происходит несколько вещей. Словесные задачи становятся менее страшными (нет, правда).
Они начинают замечать сходство в типах проблем и способны быстрее понять, как их решать. Они приобретут уверенность даже при работе с новыми типами текстовых задач, зная, что они успешно решали многие текстовые задачи в прошлом.
Если вам нужны карточки с текстовыми задачами, у меня их довольно много для учащихся 3-5 классов. В этом наборе карточек с заданиями по математике для 3-го класса есть задачи со словами почти в каждом из 30 наборов карточек с заданиями.


 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав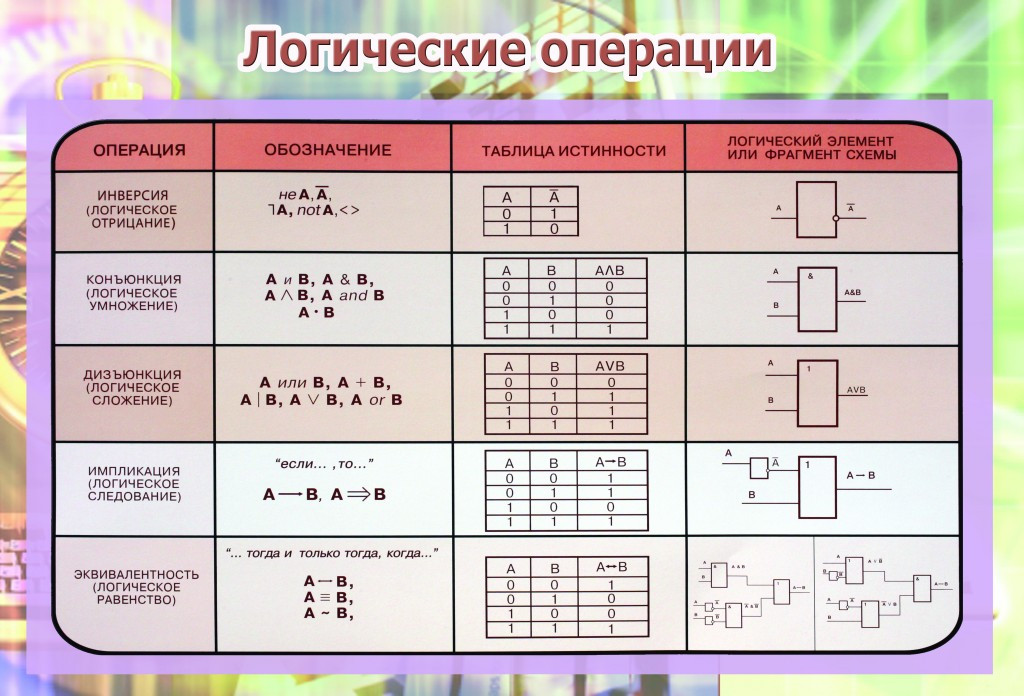 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав ..
.. Десятичная запись натуральных чисел, 5 (Знаки, с помощью которых …)
Десятичная запись натуральных чисел, 5 (Знаки, с помощью которых …) Решать задачи с помощью сложения и вычитания.
Решать задачи с помощью сложения и вычитания.


 Законы сложения»
Законы сложения» edu.ru/subject/lesson/7743/main/234700/
edu.ru/subject/lesson/7743/main/234700/ Линии на плоскости (12 ч)
Линии на плоскости (12 ч) Правильные и неправильные дроби. Основное свойство дроби. Сравнение дробей.
Правильные и неправильные дроби. Основное свойство дроби. Сравнение дробей. edu.ru/subject/lesson/7761/start/288262/
edu.ru/subject/lesson/7761/start/288262/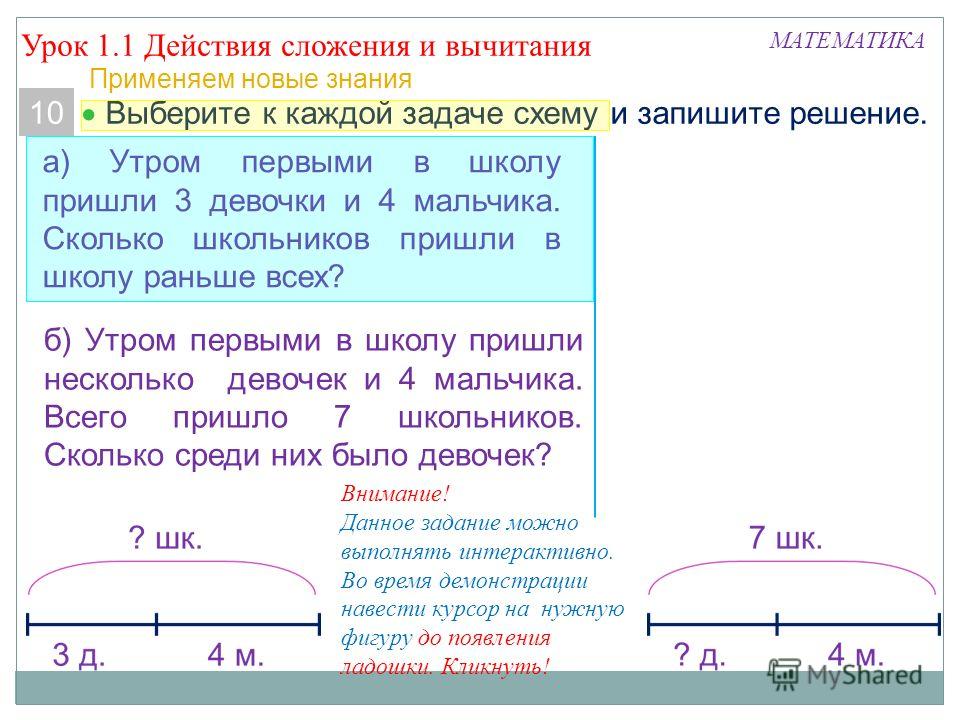 edu.ru/subject/lesson/7780/main/287892/
edu.ru/subject/lesson/7780/main/287892/ edu.ru/subject/lesson/7727/start/325306/
edu.ru/subject/lesson/7727/start/325306/ sdamgia.ru/
sdamgia.ru/
 edu.ru/subject/lesson/7745/main/313661/
edu.ru/subject/lesson/7745/main/313661/
