Построить параллелограмм на векторах онлайн. Векторное произведение векторов. Смешанное произведение векторов
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах.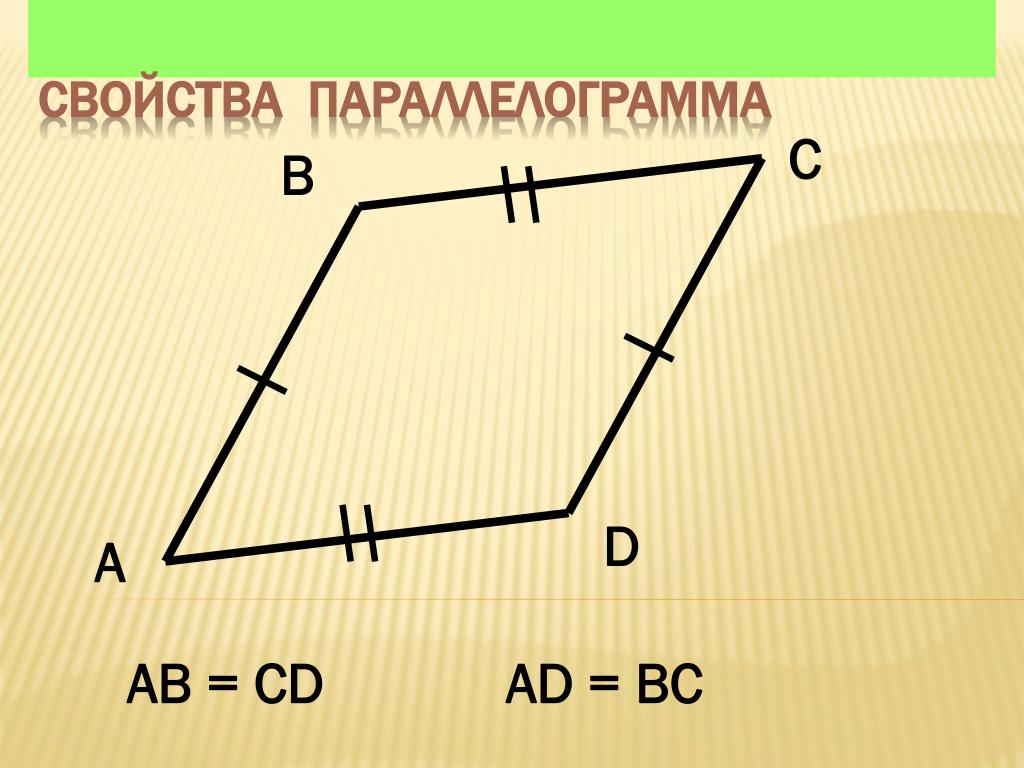 Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор.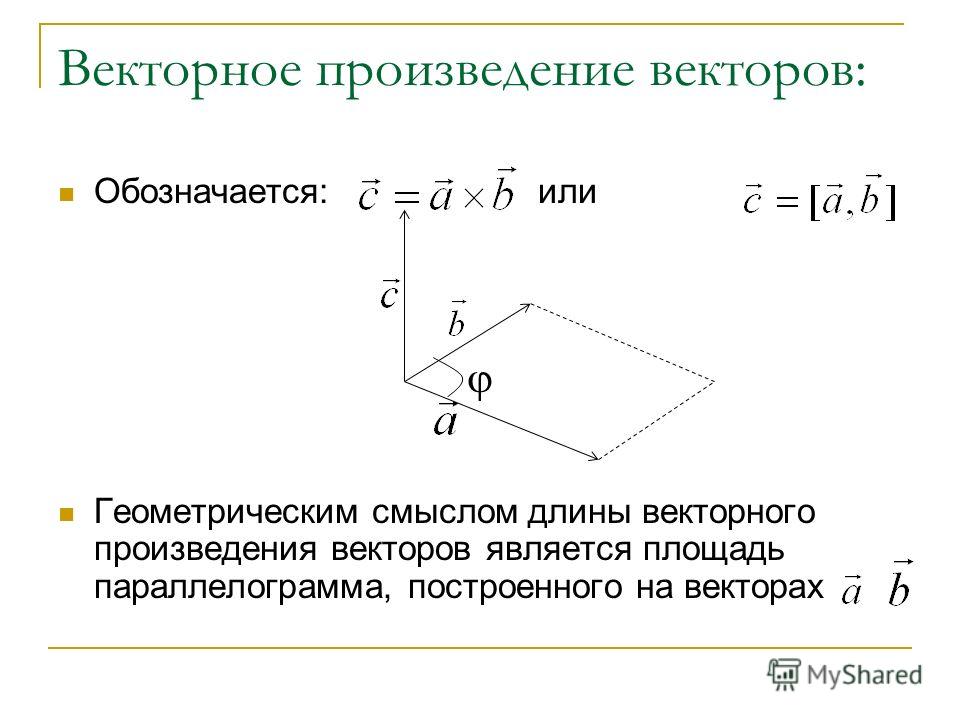 Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони.
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми.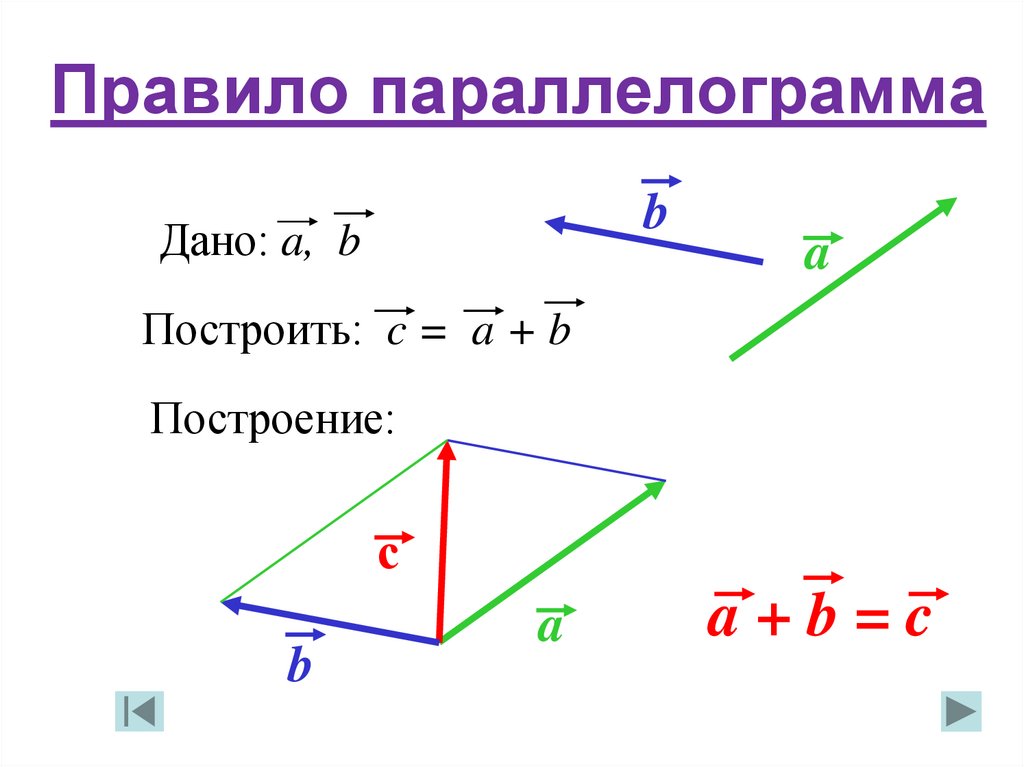 Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле .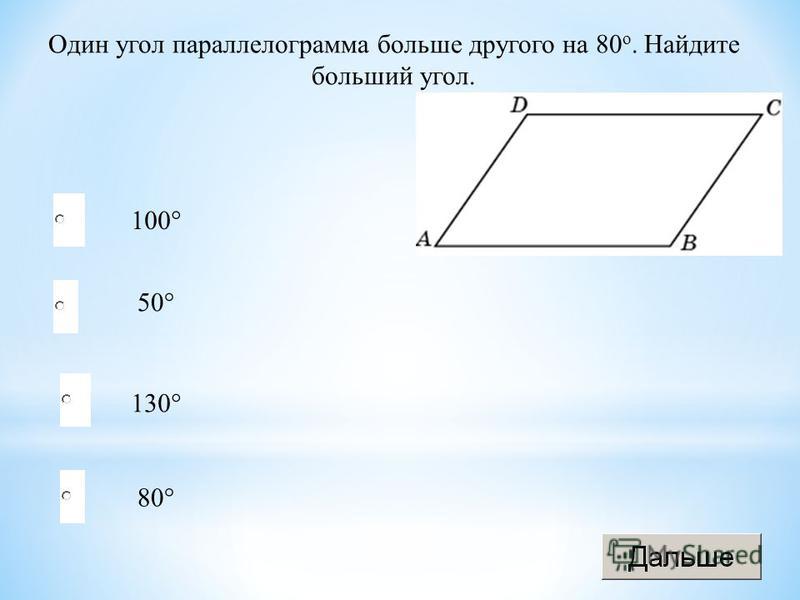 Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения.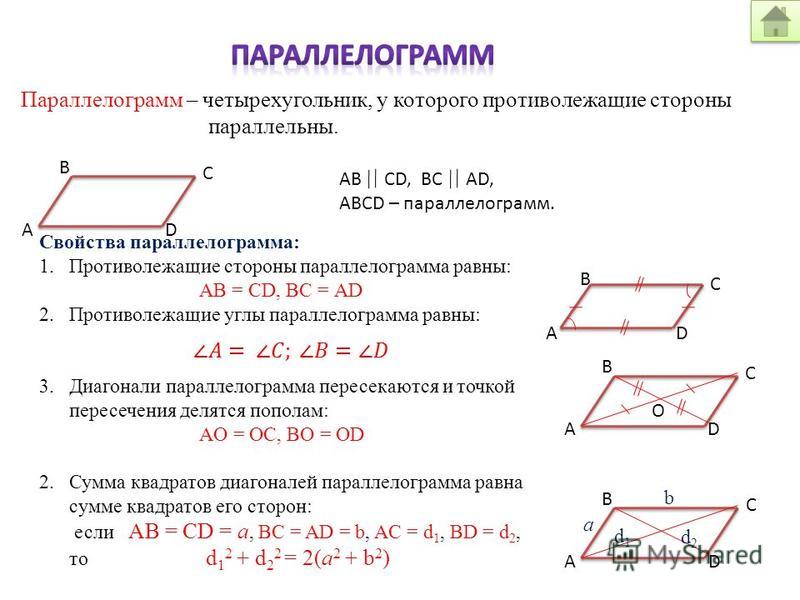 Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
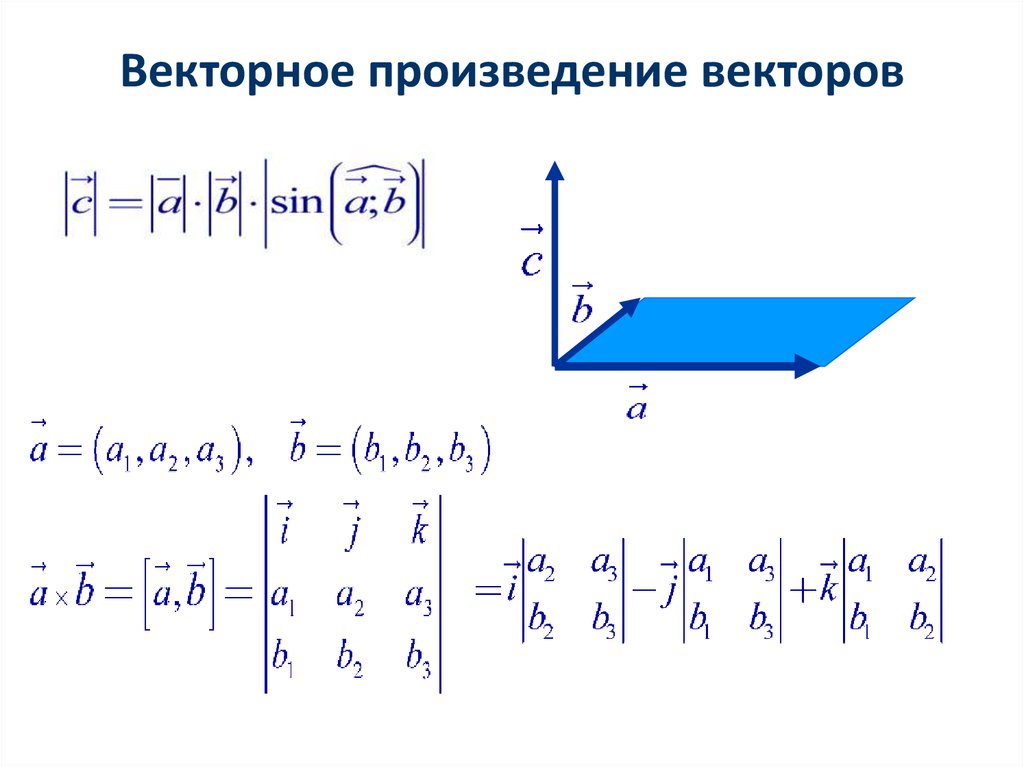
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .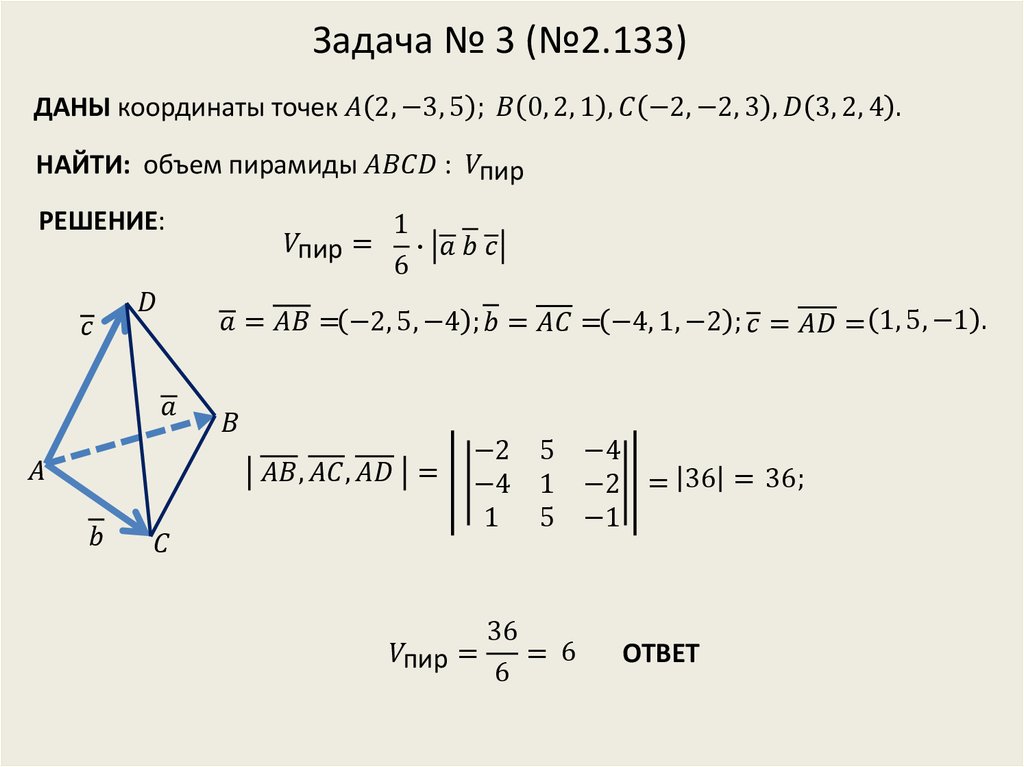
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7).
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). - Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
- Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.
 5.
5. - В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.
Смешанное произведение калькулятор. Смешанное произведение векторов. Онлайн калькулятор
Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a на векторное произведение b x c , т. е. число a(b x c), или, что то же, (b x c)a.
Обозначение: abc .
Назначение . Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word . Дополнительно создается шаблон решения в Excel .
a (; ; )b (; ; )
c (; ; )
При вычислении определителя использовать правило треугольников
Признаки компланарности векторов
Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трех векторов – нулевой, то три вектора тоже считаются компланарными.
Признак компланарности . Если система a, b, c – правая, то abc>0 ; если левая, то abcГеометрический смысл смешанного произведения . Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c , взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая.
Свойства смешанного произведения
- При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный: abc=bca=cab=-(bac)=-(cba)=-(acb)
Вытекает из геометрического смысла. - (a+b)cd=acd+bcd (распределительное свойство). Распространяется на любое число слагаемых.
Вытекает из определения смешанного произведения. - (ma)bc=m(abc) (сочетательное свойство относительно скалярного множителя).
Вытекает из определения смешанного произведения. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения. - Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: aab=0 .
Пример №1 . Найти смешанное произведение. ab(3a+2b-5c)=3aba+2abb-5abc=-5abc .
Пример №2 . (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca . Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc . Поэтому (a+b)(b+c)(c+a)=2abc .
Пример №3
. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k .
Решение . Чтобы вычислить смешанное произведение векторов, необходимо найти определитель системы, составленной из координат векторов. Запишем систему в виде.
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение.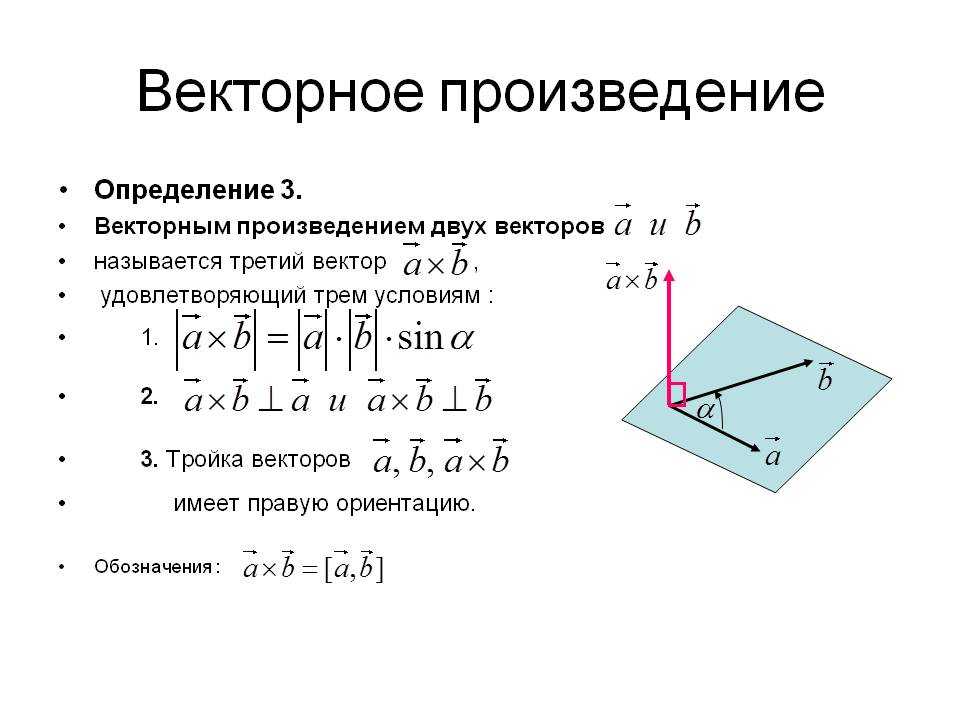 В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Yandex.RTB R-A-339285-1
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Определение 1
Смешанным произведением a → , b → и d → является та величина, которая равняется скалярному произведению a → × b → и d → , где a → × b → — умножение a → и b → . Операцию умножения a → , b → и d → зачастую обозначают a → · b → · d → . Можно преобразовать формулу так: a → · b → · d → = (a → × b → , d →) .
Умножение в системе координат
Мы можем умножить вектора, если они указаны на координатной плоскости.
Возьмем i → , j → , k →
Произведение векторов в данном конкретном случае будет иметь следующий вид: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Определение 2
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Из этого следует:
a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
a → × b → = (a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → , d x · i → + d y · j → + d z · k →) = = a y a z b y b z · d x — a x a z b x b z · d y + a x a y b x b y · d z = a x a y a z b x b y b z d x d y d z
Таким образом, можно сделать вывод, что:
a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z
Определение 3
Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z .
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение.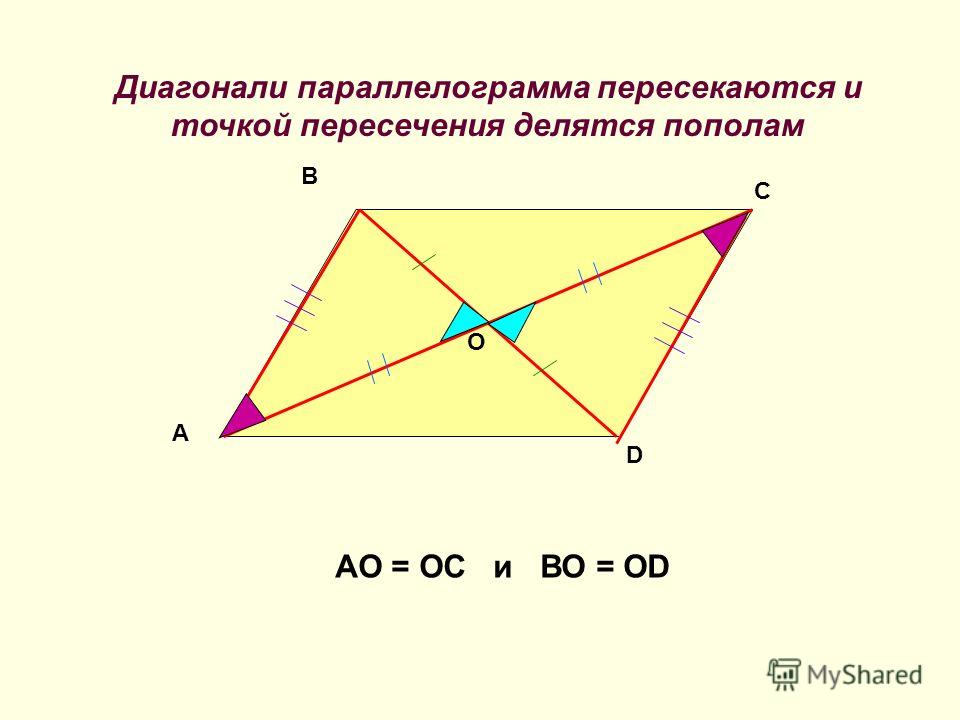 Ниже мы приведем основные свойства.
Ниже мы приведем основные свойства.
- (λ · a →) · b → · d → = a → · (λ · b →) · d → = a → · b → · (λ · d →) = λ · a → · b → · d → λ ∈ R ;
- a → · b → · d → = d → · a → · b → = b → · d → · a → ; a → · d → · b → = b → · a → · d → = d → · b → · a → ;
- (a (1) → + a (2) →) · b → · d → = a (1) → · b → · d → + a (2) → · b → · d → a → · (b (1) → + b (2) →) · d → = a → · b (1) → · d → + a → · b (2) → · d → a → · b → · (d (1) → + d (2) →) = a → · b → · d (2) → + a → · b → · d (2) →
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.
Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Действительно, если a → = b → , то, следуя определению векторного произведения [ a → × b → ] = a → · b → · sin 0 = 0 , следовательно, смешанное произведение равно нулю, так как ([ a → × b → ] , d →) = (0 → , d →) = 0 .
Если же a → = b → или b → = d → , то угол между векторами [ a → × b → ] и d → равен π 2 . По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Пример 1
Докажите равенство ([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) , где λ — некоторое действительное число.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →)
Мы разобрали, что (([ a → × b → ] , b →) = 0 . Из этого следует, что
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →) = = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + 0 = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →)
Согласно первому свойству ([ a ⇀ × b ⇀ ] , λ · a →) = λ · ([ a ⇀ × b ⇀ ] , a →) , а ([ a ⇀ × b ⇀ ] , a →) = 0 . , d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
, d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
Неравенство доказано.
Разбор типовых задач
Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z .
Пример 3
В прямоугольной системе координат представлены 3 вектора с такими координатами: a → = (1 , — 2 , 3) , b → (- 2 , 2 , 1) , d → = (3 , — 2 , 5) . Необходимо определить, чему равно произведение указанных векторов a → · b → · d → .
Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z = 1 — 2 3 — 2 2 1 3 — 2 5 = = 1 · 2 · 5 + (- 1) · 1 · 3 + 3 · (- 2) · (- 2) — 3 · 2 · 3 — (- 1) · (- 2) · 5 — 1 · 1 · (- 2) = — 7
Пример 4
Необходимо найти произведение векторов i → + j → , i → + j → — k → , i → + j → + 2 · k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i → + j → = (1 , 1 , 0) i → + j → — k → = (1 , 1 , — 1) i → + j → + 2 · k → = (1 , 1 , 2)
Используем формулу, которая использовалась выше
i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 1 1 0 1 1 — 1 1 1 2 = 0 i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 0
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
Пример 5
В прямоугольной системе координат расположены три вектора a → , b → и d → , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4 , 2 и 3 . Необходимо умножить вектора.
Обозначим c → = a → × b → .
Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a → · b → · d → = ([ a → × b → ] , d →) = c → , d → = c → · d → · cos (c → , d → ^) . ) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
Абсолютная величина n p c → d → равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a → , b → и d → в качестве сторон. Исходя из этого, следует уточнить, что c → = [ a → × b → ] перпендикулярен a → и вектору и вектору согласно определению умножения векторов. Величина c → = a → x b → равняется площади параллелепипеда, построенного на векторах a → и b → .
Делаем вывод, что модуль произведения a → · b → · d → = c → · n p c → d → равен результату умножения площади основания на высоту фигуры, которая построена на векторах a → , b → и d → .
Определение 4
Абсолютная величина векторного произведения является объемом параллелепипеда : V п а р а л л е л е п и п и д а = a → · b → · d → .
Данная формула и является геометрическим смыслом.
Определение 5
Объем тетраэдра , который построен на a → , b → и d → , равняется 1 / 6 объема параллелепипеда Получаем, V т э т р а э д а = 1 6 · V п а р а л л е л е п и п и д а = 1 6 · a → · b → · d → .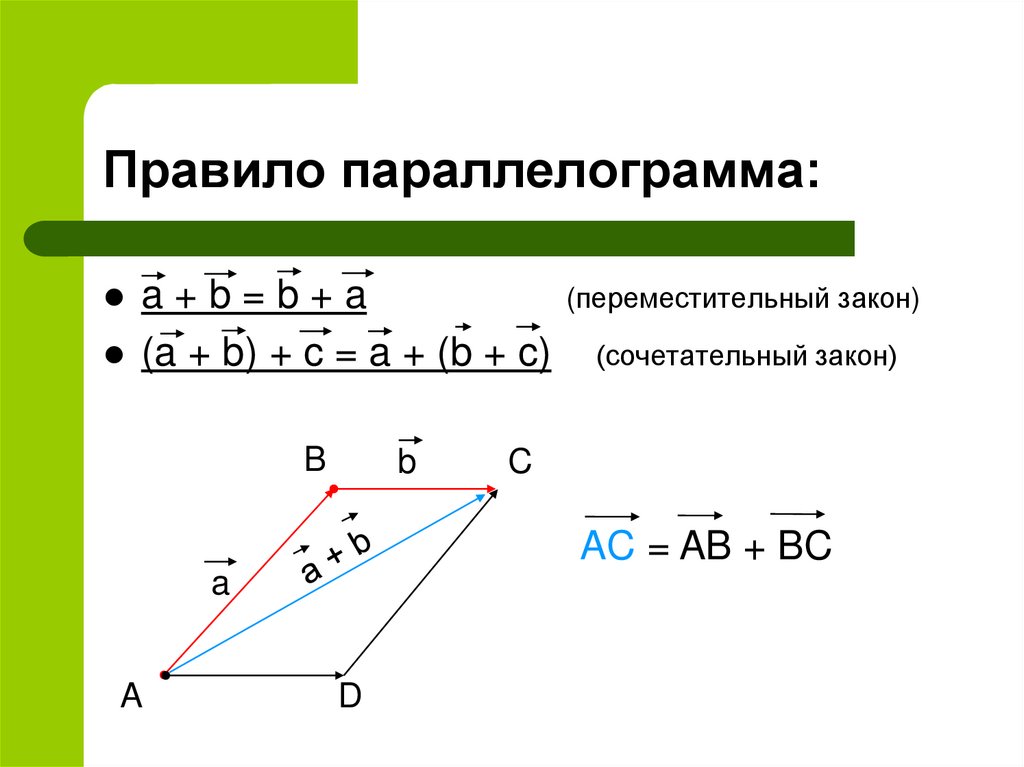
Для того, чтобы закрепить знания, разберем несколько типичных примеров
Пример 6
Необходимо найти объем параллелепипеда, в качестве сторон которого используются A B → = (3 , 6 , 3) , A C → = (1 , 3 , — 2) , A A 1 → = (2 , 2 , 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: A B → · A C → · A A 1 → = 3 6 3 1 3 — 2 2 2 2 = 3 · 3 · 2 + 6 · (- 2) · 2 + 3 · 1 · 2 — 3 · 3 · 2 — 6 · 1 · 2 — 3 · (- 2) · 2 = — 18
Тогда, V п а р а л л е л е п и п е д а = — 18 = 18 .
V п а р а л л е л е п и п и д а = 18
Пример 7
В системе координат заданы точки A (0 , 1 , 0) , B (3 , — 1 , 5) , C (1 , 0 , 3) , D (- 2 , 3 , 1) . Следует определить объем тетраэдра, который расположен на этих точках.
Воспользуемся формулой V т э т р а э д р а = 1 6 · A B → · A C → · A D → . Мы можем определить координаты векторов по координатам точек: A B → = (3 — 0 , — 1 — 1 , 5 — 0) = (3 , — 2 , 5) A C → = (1 — 0 , 0 — 1 , 3 — 0) = (1 , — 1 , 3) A D → = (- 2 — 0 , 3 — 1 , 1 — 0) = (- 2 , 2 , 1)
Дальше определяем смешанное произведение A B → · A C → · A D → по координатам векторов: A B → · A C → · A D → = 3 — 2 5 1 — 1 3 — 2 2 1 = 3 · (- 1) · 1 + (- 2) · 3 · (- 2) + 5 · 1 · 2 — 5 · (- 1) · (- 2) — (- 2) · 1 · 1 — 3 · 3 · 2 = — 7 Объем V т э т р а э д р а = 1 6 · — 7 = 7 6 .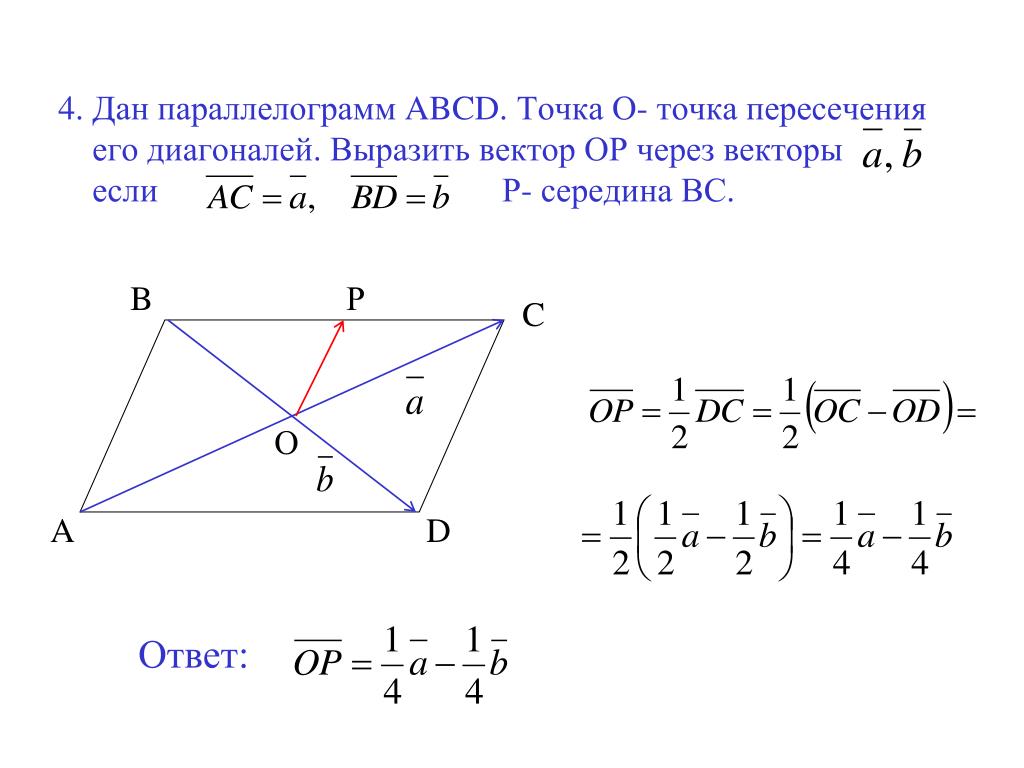
V т э т р а э д р а = 7 6 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны.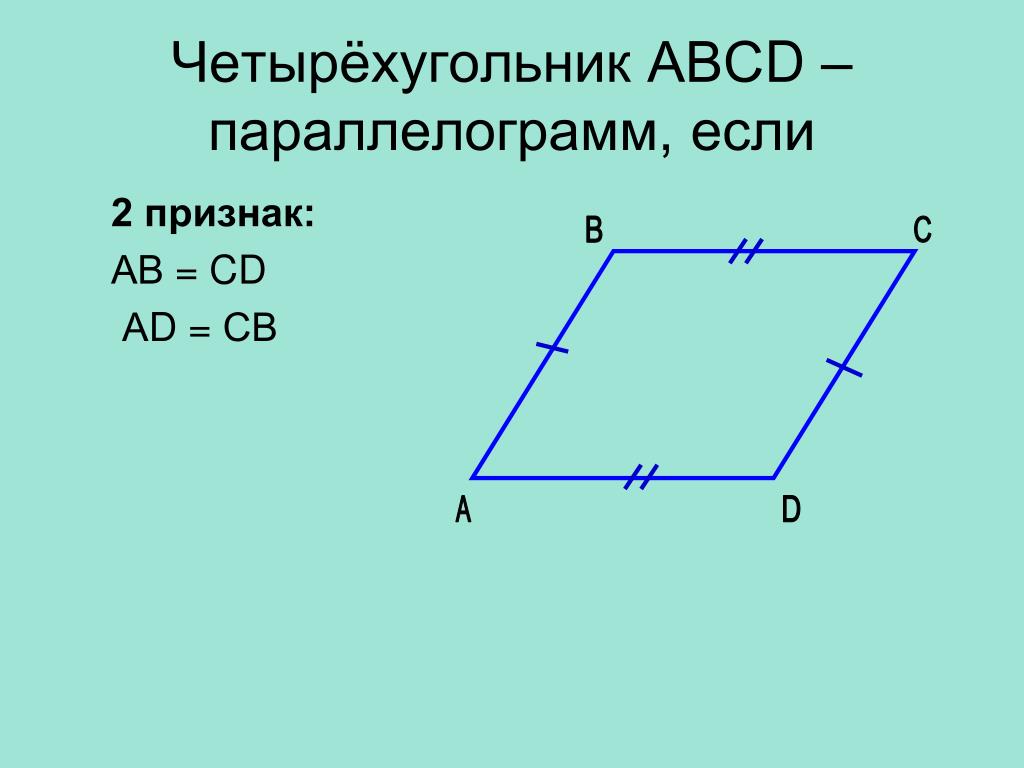 Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане.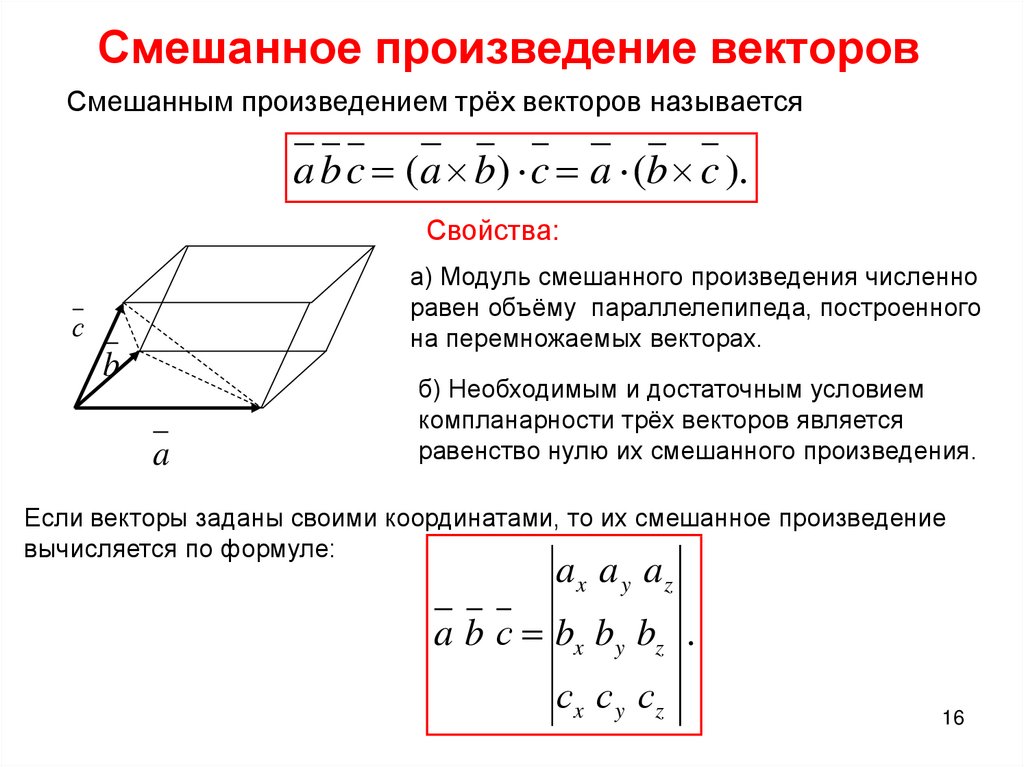 Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.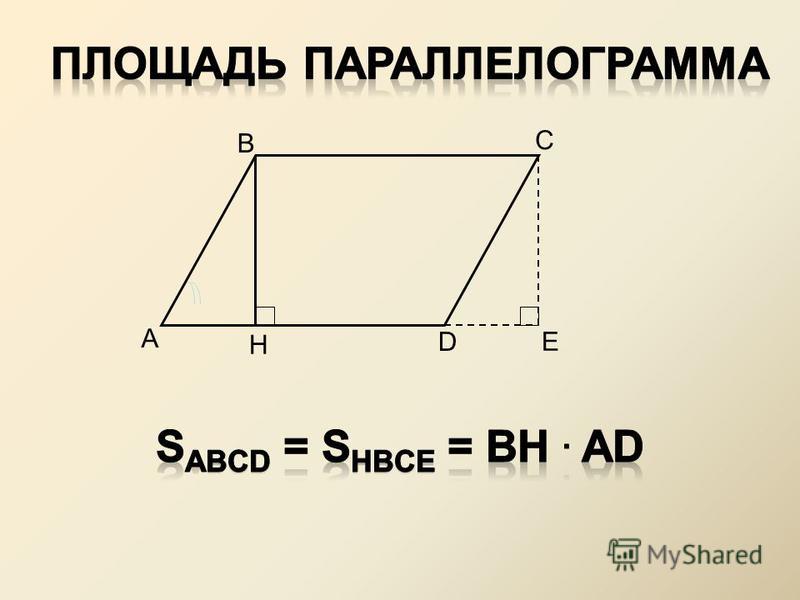
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Смешанное произведение векторов (теория)
Смешанное произведение
трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c , то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab ] скалярно умножается на вектор c .
Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c ). Тогда можно записать:
| abc =([ab ],c ) |
Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2″ и 3 на странице векторное произведение векторов онлайн).
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Теорема 1. Смешанное произведение векторов ([ab ],c ) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c , взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab ],c ) равно нулю.
Следствие 1. Имеет место следующее равенство:
Следовательно нам достаточно доказать, что
| ([ab ],c )=([bc ],a ) | (3) |
Из выражения (3) видно, что левая и правая часть равны объему параллелипеда.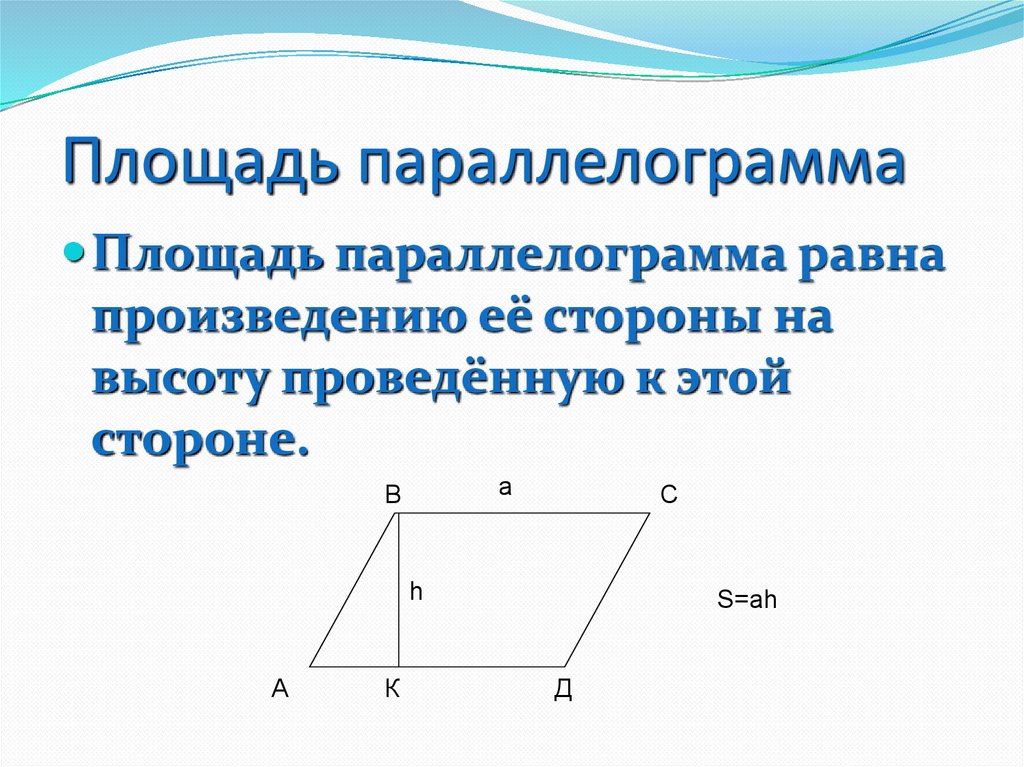 Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc , не указывая, какие именно два вектора перемножаются векторно первые два или последние два.
Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.
Смешанное произведение векторов в декартовых координатах
Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами
Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab ] и c . Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой ():
Последнее выражение можно записать, используя определители второго порядка:
необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:
| . | (7) |
Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.
Смешанное произведение векторов на примерах
Пример 1. Найти смешанное произведение векторов abс , где
Смешанное произведение векторов a, b, c равен определителю матрицы L . Вычислим определитель матрицы L , разложив определитель по строке 1:
Конечная точка вектора a .
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решите уравнение x²-5x=14.
Решено
В треугольнике ABC известно что AB=3 BC=8 AC=7. Найдите косинус (COS) угла ABC. Помогите пожалуйста с решением-очень очень нужно. Спасибо.
Составьте таблицу «Международные отношения в 1920-1930-е гг.» Дата | События | Последствия для фашисткого блока | Последствия для стран запада
В треугольнике abc прямая ad является биссектрисой угла bac, причём точка d лежит на стороне bc. найти разложение вектора ad по векторам ac=b и ab=c
Решено
В контуре,индуктивность которого 0,5Гн,при изменении силы тока в течении 0,4с возникла ЭДС самоиндукции 5В.а) на сколько изменилась сила тока в контуре?
Пользуйтесь нашим приложением
Сайт репетитора по математике Фроловой Л.А.
Решение систем уравнений — http://ru.onlinemschool.com/math/assistance/equation/matr/
http://ru. onlinemschool.com/math/assistance/
onlinemschool.com/math/assistance/
Онлайн калькуляторы. Конвертеры величин.
- Онлайн калькулятор. Конвертер единиц массы и веса
- Онлайн калькулятор. Конвертер единиц расстояния и длины.
- Онлайн калькулятор. Конвертер единиц площади
- Онлайн калькулятор. Конвертер единиц объема
- Онлайн калькулятор. Конвертер единиц времени
- Онлайн калькулятор. Преобразование скоростей (метры в секунду, километры в час)
Онлайн калькуляторы. Теория чисел
- Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.
- Онлайн калькулятор. Сложение и вычитание в столбик.
- Онлайн калькулятор. Умножение в столбик.
- Онлайн калькулятор. Деление в столбик.
- Онлайн калькулятор. НОД и НОК двух чисел
- Онлайн калькулятор. Разложение числа на множители
Онлайн калькуляторы с дробями
- Онлайн калькулятор дробей. Вычисления с двумя дробями. Сложение, вычитание, умножение и деление дробей.

- Онлайн калькулятор. Вычисления с обыкновенной и десятичной дробями.
Онлайн калькулятор. Преобразование десятичной дроби в обыкновенную дробь.
- Онлайн калькулятор. Преобразование неправильных дробей в смешанные числа.
- Онлайн калькулятор. Преобразование смешанных чисел в неправильные дроби.
- Онлайн калькулятор. Сокращение дробей.
- Онлайн калькулятор. Сравнение дробей.
- Онлайн калькуляторы. Калькуляторы с процентами
Онлайн калькулятор. Найти X процентов от числа Y.
- Онлайн калькулятор. Найти число X зная его Y процентов.
- Онлайн калькулятор. Добавить или вычесть X процентов от числа.
- Онлайн калькулятор. Найти сколько процентов составляет число X от числа Y.
- Онлайн калькулятор. Калькулятор сложных процентов. Депозитный калькулятор.
- Онлайн калькуляторы. Решение уравнений
- Онлайн калькулятор.
 Решение квадратных уравнений.
Решение квадратных уравнений.
Онлайн калькулятор. Решение биквадратных уравнений.
- Онлайн калькулятор. Решение систем линейных уравнений.
- Онлайн калькулятор. Решение систем линейных уравнений. Метод Гауса.
- Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера.
- Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод.
Онлайн калькуляторы. Прогрессии
- Онлайн калькулятор. Значение n-того члена арифметической прогрессии.
- Онлайн калькулятор. Сумма арифметической прогрессии.
Онлайн калькуляторы. Пределы и производные функций
- Онлайн калькулятор. Решение пределов онлайн.
- Онлайн калькулятор. Решение производных онлайн.
Онлайн калькуляторы. Интегралы онлайн
- Онлайн калькулятор. Решение интегралов онлайн.
- Онлайн калькулятор. Решение определенных интегралов онлайн.
- Онлайн калькуляторы.
 Комбинаторика. Теория вероятности.
Комбинаторика. Теория вероятности.
Онлайн калькулятор. Вычисление числа перестановок из n элементов.
- Онлайн калькулятор. Вычисление числа размещений из n по k.
- Онлайн калькулятор. Вычисление числа сочетаний из n по k.
- Онлайн калькулятор. Вычисление математического ожидания дискретного распределения.
- Онлайн калькулятор. Вычисление дисперсии дискретного распределения.
Онлайн калькуляторы с комплексными числами
- Онлайн калькулятор. Сложение, вычитание, умножение и деление комплексных чисел.
- Онлайн калькулятор. Модуль комплексного числа.
- Онлайн калькулятор. Конвертер алгебраической формы комплексного числа в тригонометрическую и показательную.
Онлайн калькуляторы с векторами
- Онлайн калькулятор. Определение вектора по двум точкам.
- Онлайн калькулятор. Длина вектора. Модуль вектора.
- Онлайн калькулятор. Направляющие косинусы вектора.
- Онлайн калькулятор.
 Сложение и вычитание двух векторов.
Сложение и вычитание двух векторов. - Онлайн калькулятор. Умножение вектора на число.
- Онлайн калькулятор. Скалярное произведение векторов.
- Онлайн калькулятор. Угол между векторами.
- Онлайн калькулятор. Проекция вектора на вектор.
- Онлайн калькулятор. Векторное произведение векторов.
- Онлайн калькулятор. Смешанное произведение векторов.
- Онлайн калькулятор. Коллинеарность векторов.
- Онлайн калькулятор. Ортогональность векторов.
- Онлайн калькулятор. Компланарность векторов.
- Онлайн калькулятор. Площадь треугольника построенного на векторах.
- Онлайн калькулятор. Площадь параллелограмма построенного на векторах.
- Онлайн калькулятор. Объем пирамиды построенной на векторах.
- Онлайн калькулятор. Проверить являются ли векторы базисом.
- Онлайн калькулятор. Разложение вектора по базису.
Онлайн калькуляторы с матрицами
- Онлайн калькулятор. Сложение и вычитание матриц.

- Онлайн калькулятор. Транспонированная матрица.
- Онлайн калькулятор. Умножение матрицы на число.
- Онлайн калькулятор. Умножение матриц.
- Онлайн калькулятор. Возведение матрицы в степень.
- Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.
- Онлайн калькулятор. Ранг матрицы.
- Онлайн калькулятор. Обратная матрица.
- Онлайн калькулятор. Обратная матрица методом алгебраических дополнений.
Векторное произведение векторов калькулятор
Результатом векторного произведения двух векторов будет являться вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора
Задайте координаты первого вектора
a̅ =
{
;
;
}
Задайте координаты второго вектора
b̅ =
{
;
;
}
Векторное произведение векторов
Векторным произведением двух векторов a и b в трехмерном евклидовом пространстве – называется вектор c. Модуль вектора c, численно равен площади параллелограмма OABQ, построенного на векторах a и b, то есть |c| = |a||b| sin(∠a, b).
Модуль вектора c, численно равен площади параллелограмма OABQ, построенного на векторах a и b, то есть |c| = |a||b| sin(∠a, b).
Векторное произведение векторов a и b обозначается как: [a b], [a, b], a × b, a ∧ b
Параллелограмм OABQНаправление получившегося вектора c будет перпендикулярно плоскости параллелограмма OABQ.
В правом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
Формула для координат векторного произведения вычисляется из определителя третьего порядка, где первая строка – векторы i, j, k (i = (1 0 0), j(0 1 0), k = (0 0 1)), а вторая и третья строки – координаты векторов a и b:
[a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axby — k̅ aybx = ax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то в правом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ ((By — Ay)(Dz — Cz) — (Dy — Cy)(Bz — Az)) - j̅ ((Bx — Ax)(Dz — Cz) — (Dx — Cx)(Bz — Az)) + k̅ ((Bx — Ax)(Dy — Cy) — (Dx — Cx)(By — Ay))
Векторное произведение не обладает переместительным свойством, поэтому при перестановке множителей векторное произведение изменит знак: b × a = -(a × b)
Векторное произведение равно нулю, когда векторы a и b коллинеарны (параллельны, т. е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.
е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.
В левом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ (azby — bzay) + j̅ (axbz — bxaz) + k̅ (aybx — byax)
Примеры векторного произведения векторов
Пример 1. Найдем векторное произведение векторов. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
N̅ = [AB × CD] =
= i̅i̅ j̅ k̅ ABx ABy ABz CDx CDy CDz
— j̅ABy ABz CDy CDz
+ k̅ABx ABz CDx CDz
= i̅ AByCDz — i̅ ABzCDy — j̅ ABxCDz + j̅ ABzCDx + k̅ ABxCDy — k̅ AByCDx = ABx ABy CDx CDy
i̅ (AByCDz — CDyABz) — j̅ (ABxCDz — CDxABz) + k̅ (ABxCDy — CDxABy)
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay; Bz — Az} = {-1 — 7 ; 0 — 0. 2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy; Dz — Cz} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
ABx = -8
ABy = -1/5
ABz = -275/4
CDx = 7
CDy = 6
CDz = 7
N̅ = [AB × CD] = i̅ (-1/5 ⋅ 7 — 6 ⋅ (-275/4)) — j̅ (-8 ⋅ 7 — 7 ⋅ (-275/4)) + k̅ (-8 ⋅ 6 — 7 ⋅ (-1/5)) = i̅ (-7/5 — (-825/2)) — j̅ (-56 — (-1925/4)) + k̅ (-48 — (-7/5)) = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = [AB × CD] = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = {4111/10 ; -1701/4 ; -233/5}
N̅ = {411.1 ; -425.25 ; -46.6}
Пример 2.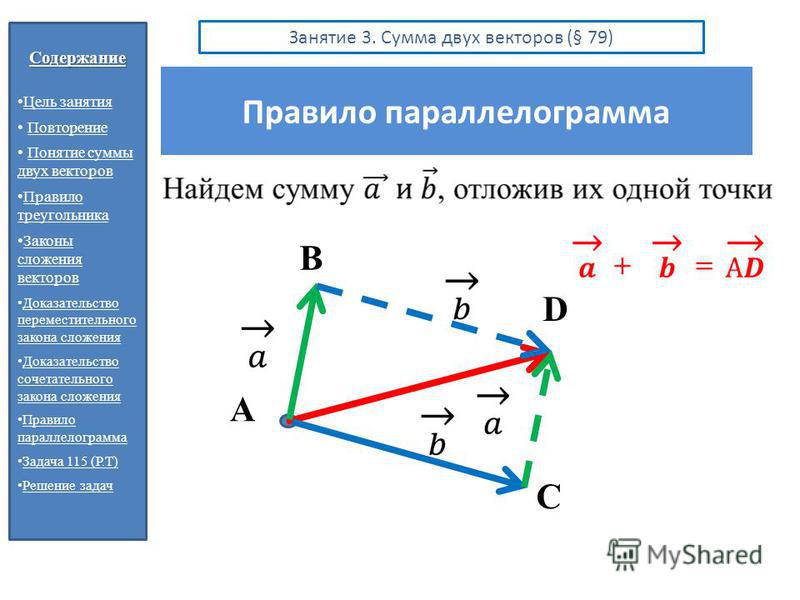 Найдем векторное произведение векторов.
Найдем векторное произведение векторов.
Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)
N̅ = [a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axby — k̅ aybx = ax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
ax = 5
ay = 1
az = 7
bx = 2
by = 4
bz = 6
N̅ = [a × b] = i̅ (1 ⋅ 6 — 4 ⋅ 7) — j̅ (5 ⋅ 6 — 2 ⋅ 7) + k̅ (5 ⋅ 4 — 2 ⋅ 1) = i̅ (6 — 28) — j̅ (30 — 14) + k̅ (20 — 2) = -22i̅ -16j̅ +18k̅
N̅ = [a × b] = -22i̅ -16j̅ +18k̅
N̅ = {-22 ; -16 ; 18}
Площадь параллелограмма, построенного на векторах, заданных своими координатами на плоскости
Предположим, что заданы координаты векторов :
. Тогда
Тогда
Можно доказать, что , если пара векторов — правая, и , если пара векторов — левая.
Аналог смешанного произведения для векторов плоскости
Для векторов на плоскости операция, аналогичная смешанному произведению, будет операцией над двумя векторами.
Если два вектора на плоскости имеют координаты: , то естественно определить аналог смешанного произведения как число равное определителю:
Ввиду доказанной формулы для , получим геометрический смысл этой операции: , если пара векторов — правая и , если эта пара левая.
Аналогия простирается и дальше на пространство любой размерности.
Задача
Докажите, что аналог векторного произведения для векторов плоскости – это операция, совершаемая над одним вектором (результат обозначим). Она сводится к повороту этого вектора на против часовой стрелки.
Указание
Определите координаты вектора из условия:
для любого вектора
То
есть мы как бы «делим» скалярно «смешанное
произведение» на вектор
.
ЗАДАНИЯ УПРАЖНЕНИЙ
1. Даны координаты точек на плоскости . Найти
а) координаты вектора ,
б) координаты точки — середины отрезка,
в) координаты точки , если,
г) координаты точки , если,
д) координаты точки , если.
2. Даны координаты векторов
Найти а) координаты ,
б) координаты ,
в) координаты .
3. Даны длины векторов и угол между ними
Найти а) скалярное произведение ,
б) скалярное произведение ,
в) длину вектора ,
г) проекцию вектора на направление другого вектора ,
д) угол между векторами и.
4. Даны координаты векторов
Выполнить задания пунктов а) — д) предыдущей задачи.
5. При каком значении параметра векторыибудут перпендикулярны?
6. При каких значениях ивекторыибудут параллельны?
7. Даны длины векторов и угол между ними
Найти а) длину векторного произведения ,
б)
длину векторного произведения
.
8. Даны координаты векторов
Найти координаты векторного произведения .
9. Даны координаты вершин треугольника на плоскости
. Найти площадь треугольника .
10. Даны координаты вершин треугольника в пространстве
. Найти площадь треугольника .
11. Даны координаты векторов в пространстве
Найти смешанное произведение .
12. Даны координаты вершин пирамиды в пространстве
. Найти а) объём пирамиды ,
б) длину высоты .
13. При каком значении параметра векторы,,будут компланарны?
14. При каком значении параметра точкибудут лежать в одной плоскости?
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Московский государственный университет
приборостроения и информатики
кафедра высшей математики
Головешкин
В.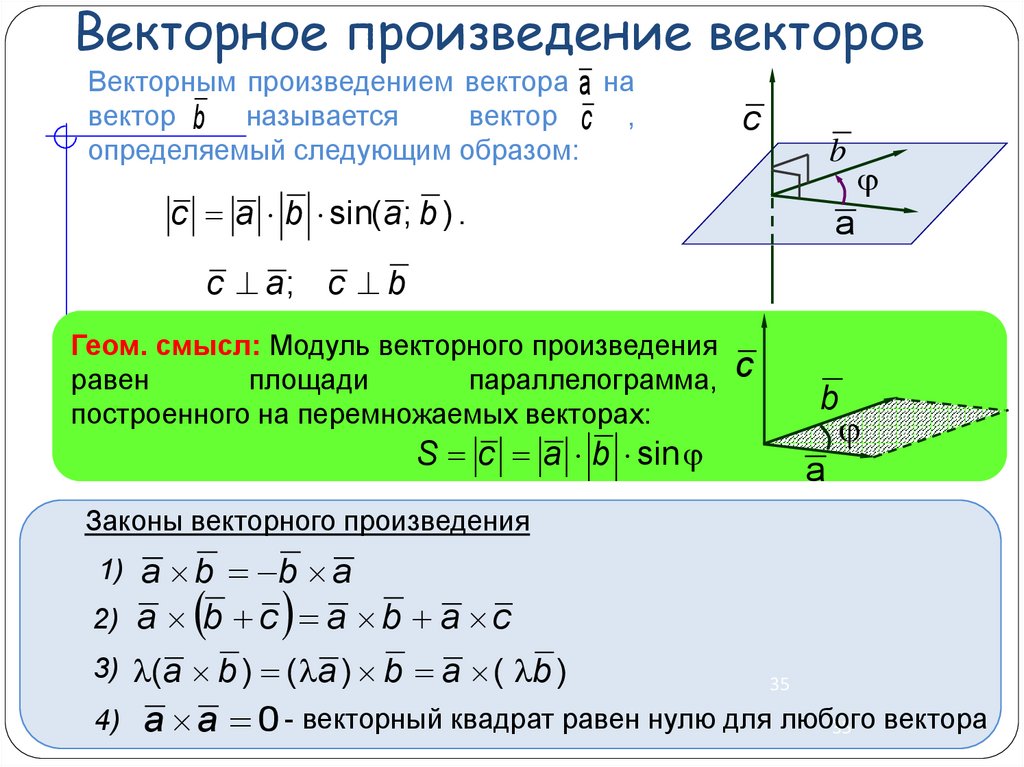 А.
А.
аналитическая геометрия прямой и плоскости, линии и поверхности второго порядка, основы теории линейных операторов и квадратичных форм
Редакция для дистанционного обучения:
Выборнов А.Н.
Москва 2011
Тема 1. Понятие об уравнении линии на плоскости. Уравнение окружности. Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору. Общее уравнение прямой и его исследование. Уравнение прямой, проходящей через данную точку параллельно данному вектору. Параметрические уравнения прямой. Уравнения прямой, проходящей через две данные точки. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Уравнение прямой, проходящей через данную точку с данными угловыми коэффициентами. Расстояние от точки до прямой.
Вначале
дадим определение понятия уравнения
линии на плоскости.
Пусть на плоскости задана некоторая линия.
Уравнение называется уравнением линии, если выполнены два условия:
1.для любой точки с координатами, лежащей на линии, выполнено, то есть ее координаты удовлетворяют уравнению линии;
2. любая точка , координаты которой удовлетворяют уравнению, лежит на линии.
Приведем пример.
Из курса элементарной математики известно уравнение биссектрисы первого и третьего координатного угла: , или то же самое.
Зададимся вопросом, будет ли уравнение уравнением данной прямой? Очевидно, что любая точка прямойбудет удовлетворять и уравнению. С другой стороны, точкаудовлетворяет уравнению, но не лежит на прямой. Следовательно, уравнениене будет уравнением исследуемой линии.
линейная алгебра — Площадь параллелограмма, вершины $(-1,-1), (4,1), (5,3), (10,5)$.
спросил
Изменено 4 года, 10 месяцев назад
Просмотрено 66 тысяч раз
$\begingroup$
Мне нужно найти площадь параллелограмма с вершинами $(-1,-1), (4,1), (5,3), (10,5)$.
Если я обозначу $A=(-1,-1)$, $B=(4,1)$, $C=(5,3)$, $D=(10,5)$, то я вижу что $\overrightarrow{AB}=(5,2)=\overrightarrow{CD}$. Точно так же $\overrightarrow{AC}=\overrightarrow{BD}$. Итак, я вижу, что эти точки действительно образуют параллелограмм.
Это задание из класса линейной алгебры. Я не был уверен, должен ли я использовать матрицу или что-то в этом роде.
- линейная алгебра
- геометрия
- определитель
- площадь
- перекрестное произведение
$\endgroup$
8
$\begingroup$
Подсказка: площадь параллелограмма (см. крайнее левое изображение) равна определителю матрицы $2\times 2$, образованной векторами-столбцами, представляющими вектор-компоненты, определяемые заданными точками. $$A = \text{det}\,\left(\vec u \;\; \vec v\right)$$
Площадь параллелограмма также равна величине векторного произведения составляющих векторов $\vec u, \vec v$ = $$|\vec u\times \vec v| = |\vec u|\,|\vec v|\sin \theta$$
где $\theta$ — мера угла, образованного векторами компонент $\vec u, \vec v$.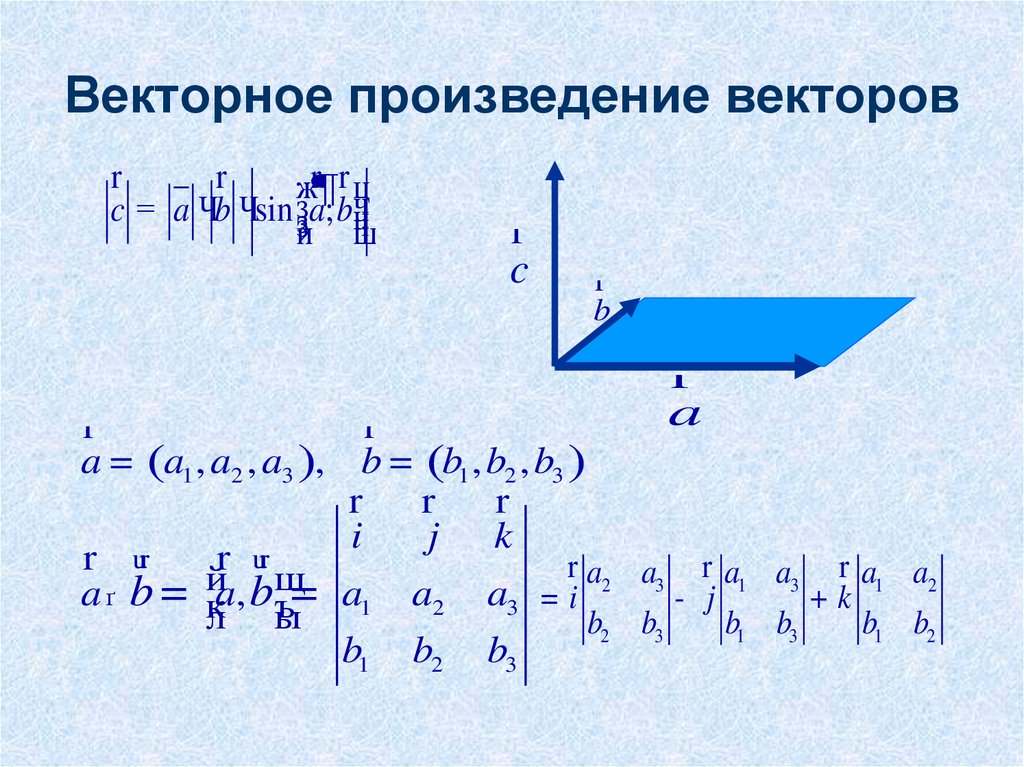
Используйте свои точки для определения компонент векторов $\vec u, \vec v$.
Для параллелограмма, образованного $p_1, p_2, p_3, p_4$, положим $\vec u = p_2 — p_1$, $\vec v = p_3 — p_1$ (где $p_4$ — точка, противоположная $p_1$, $ p_2$ точка напротив $p_3$): $$\vec u = \langle 4 -(- 1), 1-(-1)\rangle = \langle 5, 2\rangle$$ $$\vec v = \langle 5 — (-1), 3 — (-1)\rangle = \langle 6, 4\rangle$$
Итак, вычислите $$A = \det \begin{pmatrix} 5 & 6 \\ 2 & 4 \end{pmatrix},\;\;\text{or}\;\; A = \vert \vec u\times \vec v\vert$$
См. параллелограмм, площадь которого определяется векторами компонент $\vec u, \vec v\;\;$ (слева на изображении):
$\endgroup$
1
$\begingroup$
Подсказки:
- Площадь параллелограмма с боковыми векторами $\bf a$ и $\bf b$ равна $\det(\bf a\ \bf b)$.

- Для параллелограмма $A,B,C,D$ его боковые векторы равны, например, $B-A$ и $C-A$.
$\endgroup$
$\begingroup$
Поскольку диагональ параллелограмма $A(-1,-1),B(4,1),C(5,3),D(10,5)$ делится на два конгруэнтных треугольника, это означает, что треугольники имеют тот же район.
Таким образом, площадь параллелограмма будет равна $2\cdot$ площади любого из $\треугольника ABC,\треугольника ADC, \треугольника ABD, \треугольника BCD$
Например, площадь $$\треугольника ABC =\frac12\left|\det\begin{pmatrix} -1&-1&1 \\ 4&1&1 \\ 5&3&1\end{pmatrix}\right|$$
$$=\frac12\left|\det\begin{pmatrix} -1&-1&1 \\ 5&2&0 \\ 6&4&0\end{pmatrix}\right|\text{ применение} R_2’=R_2-R_1,R_3’= R_3-R_1$$
$$=\frac12\left|5\cdot4-6\cdot2\right|=4$$
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Площадь формулы параллелограмма
Овладейте семью столпами школьной успеваемости
Улучшите свои оценки и снизьте стресс
Что, если вы знаете площадь параллелограмма, сможете ли вы найти его высоту?
Формула для нахождения площади параллелограмма: основание, умноженное на высоту , но есть небольшой нюанс.
Высота — это не длина стороны, как в прямоугольнике, а высота.
Высота (высота) определяется путем проведения перпендикулярной линии от основания к самой высокой точке фигуры.
Теорему Пифагора также можно использовать для нахождения высоты параллелограмма, если высота не задана. Чтобы использовать этот метод, вам нужно знать длину основания прямоугольного треугольника. В задаче ниже это расстояние от a до b. 92
Шаг 2. Сторона параллелограмма становится гипотеновой в правом треугольнике
Следовательно, 6 = 2x
Разделите обе стороны на 2
6/2 = 2x/x
6/2 = 2x/x
6/2 = 2x/x
6/2 = 2x/x
. =3
=3
Шаг 3. Теперь, когда я знаю x , я могу найти высоту, используя правила 30-60-90. Высота параллелограмма — это длина длинной ноги.
Длинная ветвь=3√x
3√3
Площадь Параллелограмма без высоты, указанная
A B C
3
можно рассчитать область параллелеграммы с использованием векторов.
Площадь параллелограмма равна величине перекрестного произведения.
Перейдите по ссылке, чтобы посмотреть очень полезное видео, в котором объясняется, как найти площадь по двум векторам
Площадь параллелограмма из двух векторов
Площадь параллелограмма с заданными диагоналями
Диагонали параллелограмма не определяют площадь параллелограмма * d2
Common Core Standard 6.G.1 , 7.G.6 Математика 6-го класса Математика 7-го класса
Задача 1. Какова площадь параллелограмма с основанием из 8 единиц и сторонами из 5 единиц и высотой 4 единицы?
Какова площадь параллелограмма с основанием из 8 единиц и сторонами из 5 единиц и высотой 4 единицы?
Эта задача проста, потому что указана высота. Просто умножьте основание на высоту
. Шаг 1. Умножьте основание 8 единиц на высоту 4 единиц.
Шаг 2. 8*4 = 32 единицы в квадрате
Задача 2. Какова площадь параллелограмма, длина стороны которого равна 6 единицам, основанию — 10 единицам, а угол равен 60 градусам?
Эта задача немного сложна, потому что высота не задана. Поскольку параллелограмм имеет угол 60 градусов, вы можете создать 30-60-9.0 треугольник, чтобы найти высоту.
Шаг 1. Найти высоту. Если вы рисуете вершину прямо вниз, она создает треугольник. См. рисунок ниже. Треугольник — это треугольник 30-60-90. Я могу использовать правила 30-60-90, чтобы найти высоту параллелограмма.
Правила 30-60-90 следующие:
Формула площади параллелограмма равна b x h (основание x высота)
youtube.com/embed/cyW-_QSXgiM?autoplay=0&color1=0x999999&color2=0xe8e8e8&wmode=transparent» allowfullscreen=»»>Как найти площадь параллограмма
Объяснение нахождения площади параллелограмма
Существует как минимум два способа найти высоту (высоту) параллелограмма.
Первый метод: используйте теорему Пифагора, длину стороны параллелограмма и расстояние от основания до высоты.
Метод второй: если вам дана мера угла, образующая особый прямоугольный треугольник, вы можете использовать правила особого прямоугольного треугольника, чтобы найти высоту.
В этом случае мера угла создает 30-60-92 = высота (высота)
Видео работы «Как найти высоту параллелограмма по заданной площади».
Проведение линии от угла к основанию создает треугольник
. Вы также можете насладиться ……
Вы также можете насладиться ……
Площадь Формулы Диаграмма
Формулы базовой площади
Область нахождения треугольника
Геометрические шипы
Geometric Shapes
.
Long leg = x√3
Hypotenuse = 2x
Area/Perimeter Formulas
Perimeter Paralleogram
Что такое паралеограмма?
векторный анализ | математика | Британика
векторный анализ
Посмотреть все СМИ
- Ключевые люди:
- Герман Гюнтер Грассманн
- Связанные темы:
- анализ вектор вектор
Просмотреть весь связанный контент →
векторный анализ , раздел математики, который имеет дело с величинами, имеющими как величину, так и направление. Некоторые физические и геометрические величины, называемые скалярами, можно полностью определить, указав их величину в подходящих единицах измерения. Таким образом, массу можно выразить в граммах, температуру в градусах по некоторой шкале, а время в секундах. Скаляры могут быть представлены графически точками на некоторой числовой шкале, такой как часы или термометр. Существуют также величины, называемые векторами, для которых необходимо указать не только величину, но и направление. Скорость, сила и перемещение являются примерами векторов. Векторная величина может быть представлена графически направленным отрезком линии, обозначенным стрелкой, указывающей в направлении векторной величины, причем длина отрезка представляет величину вектора.
Некоторые физические и геометрические величины, называемые скалярами, можно полностью определить, указав их величину в подходящих единицах измерения. Таким образом, массу можно выразить в граммах, температуру в градусах по некоторой шкале, а время в секундах. Скаляры могут быть представлены графически точками на некоторой числовой шкале, такой как часы или термометр. Существуют также величины, называемые векторами, для которых необходимо указать не только величину, но и направление. Скорость, сила и перемещение являются примерами векторов. Векторная величина может быть представлена графически направленным отрезком линии, обозначенным стрелкой, указывающей в направлении векторной величины, причем длина отрезка представляет величину вектора.
Векторная алгебра.
Прототипом вектора является направленный отрезок A B ( см. рис. 1), который можно представить как перемещение частицы из ее исходного положения A в новое положение B . Для отличия векторов от скаляров принято обозначать векторы жирным шрифтом. Таким образом, вектор A B на рисунке 1 может быть обозначен как a , а его длина (или величина) как | и |. Во многих задачах положение начальной точки вектора не имеет значения, поэтому два вектора считаются равными, если они имеют одинаковую длину и одно и то же направление.
Для отличия векторов от скаляров принято обозначать векторы жирным шрифтом. Таким образом, вектор A B на рисунке 1 может быть обозначен как a , а его длина (или величина) как | и |. Во многих задачах положение начальной точки вектора не имеет значения, поэтому два вектора считаются равными, если они имеют одинаковую длину и одно и то же направление.
Britannica Quiz
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Равенство двух векторов a и b обозначается обычным символическим обозначением a = b , а полезные определения элементарных алгебраических операций над векторами подсказаны геометрией. Таким образом, если A B = a на рисунке 1 представляет собой смещение частицы от A до B и впоследствии частица перемещается в положение C , так что B C = b , видно, что перемещение с А на С может быть осуществлено за одно перемещение А С = с . Таким образом, логично записать a + b = c . Эта конструкция суммы c , a и b дает тот же результат, что и закон параллелограмма, в котором результирующая c задается диагональю A C параллелограмма, построенного на векторах A B и A D в качестве сторон. Поскольку расположение начальной точки B вектора B C = b несущественно, отсюда следует, что B C = A D . На рис. 1 показано, что A D + D C = A C , так что закон коммутативности выполняется для сложения векторов. Кроме того, легко показать, что ассоциативный закон выполняется, и, следовательно, скобки в (2) можно опустить без каких-либо неясностей.
Таким образом, логично записать a + b = c . Эта конструкция суммы c , a и b дает тот же результат, что и закон параллелограмма, в котором результирующая c задается диагональю A C параллелограмма, построенного на векторах A B и A D в качестве сторон. Поскольку расположение начальной точки B вектора B C = b несущественно, отсюда следует, что B C = A D . На рис. 1 показано, что A D + D C = A C , так что закон коммутативности выполняется для сложения векторов. Кроме того, легко показать, что ассоциативный закон выполняется, и, следовательно, скобки в (2) можно опустить без каких-либо неясностей.
Если с является скаляром, s или s определяется как вектор, длина которого равна | с || и | и чье направление совпадает с направлением и , когда s положительно, и противоположно направлению s , если s отрицательно. Таким образом, a и — a являются векторами, равными по модулю, но противоположными по направлению. Приведенные выше определения и хорошо известные свойства скалярных чисел (представленных s и t ) показывают, что
Таким образом, a и — a являются векторами, равными по модулю, но противоположными по направлению. Приведенные выше определения и хорошо известные свойства скалярных чисел (представленных s и t ) показывают, что
Поскольку законы (1), (2) и (3) идентичны законам, встречающимся в обычной алгебре, вполне уместно использовать знакомые алгебраические правила для решения систем линейные уравнения, содержащие векторы. Этот факт позволяет вывести чисто алгебраическими средствами многие теоремы синтетической евклидовой геометрии, требующие сложных геометрических построений.
Произведения векторов.
Умножение векторов приводит к двум типам произведений: точечному произведению и перекрестному произведению.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Скалярное произведение двух векторов a и b , записанное как a · b , является действительным числом | и || б | cos( a , b ), где ( a , b ) обозначает угол между направлениями a и b . Геометрически
Геометрически
Если а и b находятся под прямым углом, тогда a · b = 0, и если ни a , ни b не являются нулевым вектором, то исчезновение скалярного произведения показывает, что векторы перпендикулярны. Если a = b , то cos ( a , b ) = 1, и a · a = | и | 2 дает квадрат длины .
Ассоциативные, коммутативные и распределительные законы элементарной алгебры справедливы для точечного умножения векторов.
Перекрестное или векторное произведение двух векторов a и b , записанное как a × b , представляет собой вектор, где n представляет собой вектор единичной длины, перпендикулярный плоскости a и b и направлен так, чтобы правосторонний винт, вращающийся от a к b , продвигался в направлении n ( см. рис. 2). Если a и b параллельны, a × b = 0. Величина a × b может быть представлена площадью параллелограмма, имеющего a и b в качестве смежных сторон. Кроме того, поскольку вращение от b до a противоположно вращению от a до b ,
2). Если a и b параллельны, a × b = 0. Величина a × b может быть представлена площадью параллелограмма, имеющего a и b в качестве смежных сторон. Кроме того, поскольку вращение от b до a противоположно вращению от a до b ,
Это показывает, что векторное произведение является не коммутативным, а ассоциативным законом ( s a ) b = s ( a × b ), и закон распределения справедлив для перекрестных произведений.
Системы координат.
Поскольку эмпирические законы физики не зависят от специального или случайного выбора систем отсчета, выбранных для представления физических отношений и геометрических конфигураций, векторный анализ представляет собой идеальный инструмент для изучения физической вселенной. Введение специальной системы отсчета или системы координат устанавливает соответствие между векторами и наборами чисел, представляющими компоненты векторов в этой системе отсчета, и индуцирует определенные правила действий над этими наборами чисел, которые следуют из правил действий над прямой сегменты.
Если выбран определенный набор из трех неколлинеарных векторов (называемых базовыми векторами), то любой вектор A может быть однозначно выражен как диагональ параллелепипеда, ребра которого являются компонентами A в направлениях основных векторов . Обычно используется набор из трех взаимно ортогональных единичных векторов ( т. е. векторов длины 1) i , j , k , направленных вдоль осей знакомой нам декартовой системы отсчета ( см. рис. 3). В этой системе выражение принимает вид, где х , y и z — проекции A на оси координат. Если представить два вектора A 1 и A 2 в виде, то применение законов (3) дает для их суммы
. A 2 — это вектор, определяемый формулой ( x 1 + y 1 , x 2 + Y 2 , x 3 + 696969696969696969696969696969696969696969,9696969 2 . Кроме того, скалярное произведение может быть записано как
Кроме того, скалярное произведение может быть записано как
. Использование закона (6) приводит к тому, что перекрестное произведение является вектором, определяемым тройкой чисел, входящих в число коэффициентов i , j и k в (9).
Если векторы представлены матрицами 1 × 3 (или 3 × 1), состоящими из компонентов ( x 1 , x 2 , x 3 ) векторов можно перефразировать формулы с (7) по (9) на языке матриц. Такая перефразировка предполагает обобщение понятия вектора на пространства размерности выше трех. Например, состояние газа вообще зависит от давления p , объема v , температуры T и времени t . Четверка чисел ( р , v , T , t ) не могут быть представлены точкой в трехмерной системе отсчета. Но поскольку геометрическая визуализация не играет никакой роли в алгебраических вычислениях, образный язык геометрии все же можно использовать, вводя четырехмерную систему отсчета, определяемую набором базовых векторов a 3 , a 4 с компонентами, определяемыми строками матрицы
Вектор х затем представляется в виде, так что в четырехмерном пространстве каждый вектор определяется четверкой компонентов 3 , x 4 ).
Расчет векторов.
Частица, движущаяся в трехмерном пространстве, может быть определена в каждый момент времени t вектором положения r , проведенным из некоторой фиксированной точки отсчета О . Поскольку положение конечной точки r зависит от времени, r является векторной функцией t . Его компоненты в направлениях декартовых осей, введенные при O , являются коэффициентами i , j и k в представлении
. Если эти компоненты являются дифференцируемыми функциями, производная r с относительно t определяется формулой, которая представляет собой скорость v частицы. Декартовы компоненты v появляются как коэффициенты i , j и k в (10). Если эти компоненты также дифференцируемы, то ускорение a = d v / d t получается дифференцированием (10):
Правила дифференцирования произведений скалярных функций остаются в силе для производных скалярные и векторные произведения вектор-функций, а также подходящие определения интегралов вектор-функций позволяют построить векторное исчисление, ставшее основным аналитическим инструментом в физических науках и технике.
Найдите векторное произведение. Перекрестное произведение двух векторов. Онлайн калькулятор. Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника найдем выражение векторного произведения векторов
Прежде чем дать понятие векторного произведения , обратимся к вопросу об ориентации упорядоченной тройки векторов a →, b →, c → в трехмерном пространстве.
Отложим для начала векторы a →, b →, c → из одной точки. Ориентация тройки a →, b →, c → может быть правой или левой, в зависимости от направления самого вектора c →. По тому направлению, в котором совершается кратчайший поворот от вектора а → к b → от конца вектора с →, будет определен вид тройки а →, b →, с →.
Если кратчайший поворот против часовой стрелки, то тройка векторов a →, b →, c → называется вправо , если по часовой стрелке — влево .
Далее возьмем два неколлинеарных вектора a → и b →. Отложим тогда векторы A B → = a → и A C → = b → из точки A. Построим вектор A D → = c →, перпендикулярный одновременно и к AB →, и к A C →. Таким образом, при построении самого вектора A D → = c → мы можем сделать две вещи, придав ему либо одно направление, либо противоположное (см. иллюстрацию).
Построим вектор A D → = c →, перпендикулярный одновременно и к AB →, и к A C →. Таким образом, при построении самого вектора A D → = c → мы можем сделать две вещи, придав ему либо одно направление, либо противоположное (см. иллюстрацию).
Упорядоченная тройка векторов a →, b →, c → может быть, как мы выяснили, правой или левой, в зависимости от направления вектора.
Исходя из вышесказанного, мы можем ввести определение перекрестного произведения. Это определение дано для двух векторов, заданных в прямоугольной системе координат трехмерного пространства.
Определение 1
Векторное произведение двух векторов a → и b → будем называть такой вектор, заданный в прямоугольной системе координат трехмерного пространства, что:
- если векторы a → и b → коллинеарны, то будет равен нулю;
- он будет перпендикулярен как вектору a →, так и вектору b →, т. е. ∠ a → c → = ∠ b → c → = π 2;
- его длина определяется по формуле: c → = a → b → sin ∠ a →, b →;
- тройка векторов a →, b →, c → имеет ту же ориентацию, что и данная система координат.

Векторное произведение векторов a → и b → имеет следующие обозначения: a → × b →.
Координаты векторного произведения
Поскольку любой вектор имеет определенные координаты в системе координат, можно ввести второе определение векторного произведения, которое позволит найти его координаты по заданным координатам векторов.
Определение 2
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов a → = (a x; a y; a z) и b → = (b x; b y; b z) назвал вектор c → = a → × b → = (ay bz — az by) i → + (az bx — ax bz) j → + (ax by — ay bx) k →, где i →, j →, k → — координатные векторы.
Векторное произведение можно представить в виде определителя квадратной матрицы третьего порядка, где первая строка — векторы ортов i →, j →, k →, вторая строка содержит координаты вектора a →, а третья содержит координаты вектора b → в заданной прямоугольной системе координат, этот определитель матрицы имеет вид: c → = a → × b → = i → j → k → axayazbxbybz
Разлагая этот определитель над элементами первой строки получаем равенство: c → = a → × b → = i → j → k → axayazbxbybz = ayazbybz i → — axazbxbz j → + axaybxby k → = = a → × b → = ( ay bz — az by) i → + (az bx — ax bz) j → + (ax by — ay bx) k →
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется в виде определителя матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z, то на основании свойств определителя матрицы отображает следующие свойств векторного произведения:
- антикоммутативность a → × b → = — b → × a →;
- дистрибутивность a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → или a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) →;
- ассоциативность λ a → × b → = λ a → × b → или a → × (λ b →) = λ a → × b →, где λ — произвольное действительное число.

Эти свойства нетрудно доказать.
В качестве примера мы можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативности
По определению, a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z. А если переставить две строки матрицы, то значение определителя матрицы должно измениться на противоположное, следовательно, a → × b → = i → j → k → axayazbxbybz = — i → j → k → bxbybzaxayaz = — b → × a →, что и доказывает антикоммутативность векторного произведения.
Векторный продукт — примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно задаются длины двух векторов и угол между ними, но нужно найти длину векторного произведения. В этом случае используйте следующую формулу c → = a → b → sin ∠ a →, b →.
Пример 1
Найдите длину векторного произведения векторов a → и b →, если известны a → = 3, b → = 5, ∠ a →, b → = π 4.
Решение
Определив длину векторного произведения векторов a → и b →, решим эту задачу: a → × b → = a → b → sin ∠ a →, b → = 3 5 sin π 4 = 15 2 2.
Ответ: 15 2 2 .
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов а → = (а х; а у; а z) и b → = (b x; b y; b z) .
Для данного типа задач можно решить массу вариантов задач. Например, могут быть заданы не координаты векторов a → и b →, а их разложения по координатным векторам вида b → = b x i → + b y j → + b z k → и c → = a → × b → = (ay bz — az by) i → + (az bx — ax bz) j → + (ax by — ay bx) k →, или векторы a → и b → могут быть определяется координатами их начальной и конечной точек.
Рассмотрим следующие примеры.
Пример 2
В прямоугольной системе координат заданы два вектора a → = (2; 1; — 3), b → = (0; — 1; 1). Найдите их векторное произведение.
Найдите их векторное произведение.
Раствор
По второму определению находим векторное произведение двух векторов в заданных координатах: a → × b → = (ay bz — az by) i → + (az bx — ax bz) j → + (ax by — ay Bx) k → = = (1 1 — (- 3) (- 1)) i → + ((- 3) 0 — 2 1) j → + (2 (- 1) — 1 0) k → = = — 2 i → — 2 j → — 2 k →.
Если векторное произведение записать через определитель матрицы, то решение этого примера будет выглядеть так: a → × b → = i → j → k → axayazbxbybz = i → j → k → 2 1 — 3 0 — 1 1 = — 2 i → — 2 j → — 2 k →.
Ответ: a → × b → = — 2 i → — 2 j → — 2 k →.
Пример 3
Найдите длину векторного произведения векторов i → — j → и i → + j → + k →, где i →, j →, k → — единичные векторы прямоугольной декартовой системы координат.
Решение
Сначала найдем координаты данного векторного произведения i → — j → × i → + j → + k → в заданной прямоугольной системе координат.
Известно, что векторы i → — j → и i → + j → + k → имеют координаты (1; — 1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения с помощью определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → …
Найдем длину векторного произведения с помощью определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → …
Следовательно, векторное произведение i → — j → × i → + j → + k → имеет координаты (- 1; — 1; 2) в данной системе координат.
Длину векторного произведения находим по формуле (см. раздел о нахождении длины вектора): i → — j → × i → + j → + k → = — 1 2 + — 1 2 + 2 2 = 6.
Ответ: i → — j → × i → + j → + k → = 6. …
Пример 4
В прямоугольной декартовой системе координат координаты трех точек A (1, 0, 1), B ( 0, 2, 3), С (1, 4, 2). Найдите какой-нибудь вектор, перпендикулярный к A B → и AC → одновременно.
Решение
Векторы AB → и A C → имеют следующие координаты (- 1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB → и AC →, очевидно, что это вектор, перпендикулярный по определению и к AB →, и к AC →, то есть является решением нашей задачи. Найдем A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k →.
Найдем A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k →.
Ответ: — 6 i → + j → — 4 k →. — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. Применив которые, мы получим решение поставленной задачи.
Пример 5
Векторы a → и b → перпендикулярны, их длины равны 3 и 4 соответственно. Найдите длину векторного произведения 3 a → — b → × a → — 2 b → = 3 a → × a → — 2 b → + — b → × a → — 2 b → = = 3 a → × a → + 3 а → × — 2 б → + — б → × а → + — б → × — 2 б →.
Решение
По свойству дистрибутивности векторного произведения мы можем написать 3 a → — b → × a → — 2 b → = 3 a → × a → — 2 b → + — b → × a → — 2 b → = = 3 a → × a → + 3 a → × — 2 b → + — b → × a → + — b → × — 2 b →
По свойству ассоциативности выносим числовые коэффициенты за знак векторных произведений в последнем выражении: 3 a → × a → + 3 a → × — 2 b → + — b → × a → + — b → × — 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → — 6 a → × b → — b → × а → + 2 б → × б →
Векторные произведения a → × a → и b → × b → равны 0, поскольку a → × a → = a → a → sin 0 = 0 и b → × b → = b → b → sin 0 = 0, тогда 3 a → × a → — 6 a → × b → — b → × a → + 2 b → × b → = — 6 a → × b → — b → × a →. …
…
Из антикоммутативности векторного произведения следует — 6 a → × b → — b → × a → = — 6 a → × b → — (- 1) a → × b → = — 5 a → × b →. …
Используя свойства векторного произведения, получаем равенство 3 a → — b → × a → — 2 b → = = — 5 a → × b →.
По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2. Теперь осталось только подставить найденные значения в соответствующие формулы: 3 a → — b → × a → — 2 b → = — 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a →, b →) = 5 · 3 · 4 · sin π 2 = 60.
Ответ: 3 a → — b → × a → — 2 b → = 60.
Длина векторного произведения векторов по порядку равна a → × b → = a → b → sin ∠ a →, b →. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон на синус угла между этими сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a → и b →, проведенных из одной точки, на синус угол между ними sin ∠ a →, b →.
Это геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Определение 3
Моментом силы F →, приложенной к точке B относительно точки A, мы понимаем следующее векторное произведение AB → × F →.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Очевидно, что в случае перекрестного произведения порядок, в котором берутся векторы, имеет значение; кроме того,
Также непосредственно из определения следует, что для любого скалярного фактора k (числа) верно следующее:
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, перекрестное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (Если один из них является нулевым вектором, помните, что нулевой вектор коллинеарен любому вектору по определению).
Векторное произведение имеет свойство распределения , то есть
Выражение векторного произведения через координаты векторов.
Пусть заданы два вектора
(как найти координаты вектора по координатам его начала и конца — см. статью Скалярное произведение векторов, параграф Альтернативное определение скалярного произведения, или вычисление скалярного произведение двух векторов, заданных их координатами.)
Почему перекрестное произведение?
Существует множество способов использования векторного произведения, например, как уже писалось выше, вычислив векторное произведение двух векторов, можно узнать, коллинеарны ли они.
Или его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина полученного вектора и есть площадь этого параллелограмма.
Существует также огромное количество приложений в области электричества и магнетизма.
Он-лайн калькулятор векторного произведения.
Чтобы найти скалярное произведение двух векторов с помощью этого калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую — второго. Координаты векторов можно вычислить по координатам их начала и конца (см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения или вычисление скалярного произведения двух векторов, заданных их координатами. )
Угол между векторами
Для того, чтобы нам ввести понятие векторного произведения двух векторов, мы должны сначала понять такое понятие, как угол между этими векторами.
Пусть даны два вектора $\overline(α)$ и $\overline(β)$. Возьмем некоторую точку $O$ в пространстве и отложим от нее векторы $\overline(α)=\overline(OA)$ и $\overline(β)=\overline(OB)$, тогда угол $AOB$ будет называется углом между этими векторами (рис. 1).
Обозначение: $ ∠ (\overline (α), \ overline (β)) $
Понятие векторного произведения векторов и формула нахождения
Определение 1
Векторное произведение двух векторов есть вектор перпендикулярен обоим заданным векторам, а его длина будет равна произведению длин этих векторов на синус угла между этими векторами, и этот вектор с двумя инициалами имеет ту же ориентацию, что и декартова система координат.
Обозначение: $ \ overline (α) x \ overline (β) $.
Математически это выглядит так:
- $ | \ сверху (α) х \ сверху (β) | = | \ надчеркнуть (α) || \ зачеркнут (β) | sin∠ (\надчеркивание (α), \ надчеркивание (β)) $
- $ \ overline (α) x \ overline (β) ⊥ \ overline (α) $, $ \ overline (α) x \ overline (β) ⊥ \ overline (β) $
- $ (\ overline (α) x \ overline (β), \ overline (α), \ overline (β)) $ и $ (\ overline (i), \ overline (j), \ overline (k)) $ одинаково ориентированы (рис. 2)
Очевидно, что внешнее произведение векторов будет равно нулевому вектору в двух случаях: 9\circ$ (поскольку в этом случае синус равен нулю).
Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решений.
Пример 1
Найдите длину вектора $\overline(δ)$, который будет результатом векторного произведения векторов, с координатами $\overline(α)=(0,4,0)$ и $ \ зачеркнутый (β) = (3,0,0) $.
Решение .
Представим эти векторы в декартовом координатном пространстве (рис. 3): 9\circ=4\cdot 3\cdot 1=12$
Ответ:$12$.
Вычисление векторного произведения по координатам векторов
Из определения 1 сразу следует метод нахождения векторного произведения двух векторов. Так как вектор, кроме своего значения, имеет еще и направление, найти его только с помощью скалярной величины невозможно. Но кроме него есть еще способ поиска векторов по координатам векторов.
Заданы векторы $\overline(α)$ и $\overline(β)$, которые будут иметь координаты $(α_1, α_2, α_3)$ и $(β_1, β_2, β_3)$ соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:
$ \ overline (α) x \ overline (β) = \ begin (vmatrix) \ overline (i) & \ overline (j) & \ overline (k) \\ α_1 & α_2 & α_3 \\ β_1 & β_2 & β_3 \ end (vmatrix) $
Иначе, разложив определитель, получим следующие координаты
$ \ overline (α) х \ overline (β) = (α_2 β_3-α_3 β_2, α_3 β_1-α_1 β_3, α_1 β_2 -α_2 β_1)$
Пример 2
Найти вектор векторного произведения коллинеарных векторов $\overline(α)$ и $\overline(β)$ с координатами $(0,3,3)$ и $( — 1,2,6)$.
Решение .
Воспользуемся приведенной выше формулой. Получаем
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\0&3&3\- 1 & 2 & 6 \ end (vmatrix) = (18 -6) \ overline (i) — (0 + 3) \ overline (j) + (0 + 3) \ overline (k) = 12 \ overline (i) — 3 \ надчертание (j) +3 \ надчертание (k ) = (12, -3,3) $
Ответ: $ (12, -3,3) $.
Свойства векторного продукта
Для произвольных смешанных трех векторов $\overline(α)$, $\overline(β)$ и $\overline(γ)$, а также $r∈R$ выполняются следующие свойства:
Пример 3
Найдите площадь параллелограмма, вершины которого находятся в координатах $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8, 0) $.
Решение .
Сначала изобразим этот параллелограмм в координатном пространстве (рис. 5):
Рисунок 5. Параллелограмм в координатном пространстве. Author24 — онлайн обмен студенческими работами
Мы видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $ \ overline (α) = (3,0,0) $ и $ \ overline (β) = (0,8,0) $. Используя четвертое свойство, получаем:
Используя четвертое свойство, получаем:
$ S = | \ сверху (α) х \ сверху (β) | $
Найдите вектор $ \ overline (α) x \ overline (β) $:
$ \ overline (α) x \ overline (β) = \ begin (vmatrix) \ overline (i) & \ overline (j ) & \ overline (k) \\ 3 & 0 & 0 \\ 0 & 8 & 0 \ end (vmatrix) = 0 \ overline (i) -0 \ overline (j) +24 \ overline (k) = (0 ,0,24) $ 9б;
2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т.е.
3. Векторы a, b и c образуют правую тройку.
Перекрестное произведение обозначается a x b или [a, b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между векторами i, j и k (см. рис. 18):
i x j = k, j x k = i, k x i = j.
Докажем, например, что i хj = k. 9дж;
2) | к | = 1, но | я х j | = | я | | Дж | sin (90°) = 1;
3) векторы i, j и k образуют правую тройку (см. рис. 16).
7. 2. Свойства векторного произведения
2. Свойства векторного произведения
1. При перестановке множителей векторное произведение меняет знак; a xb = (b xa) (см. рис. 19).
Векторы a xb и b коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположные направления (тройки a, b, a xb и a, b, b x a противоположной ориентации). Это а xb = -(b xa).
2. Векторное произведение обладает комбинаторным свойством по отношению к скалярному множителю, т. е. l (а хb) = (l а) х b = а х (l b).
Пусть l > 0. Вектор l (a xb) перпендикулярен векторам a и b. Вектор ( l a) x b также перпендикулярен векторам a и b (векторы a, l и лежат в одной плоскости). Следовательно, векторы l(a xb) и ( l a) x b коллинеарны. Очевидно, что их направления совпадают. Имеют одинаковую длину:
Поэтому l(a хb) = l a xb. Аналогично доказывается для l
3. Два ненулевых вектора a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. a || ba xb = 0,
е. a || ba xb = 0,
В частности, i * i = j * j = k * k = 0,
4. Векторное произведение обладает свойством распределения:
(a + b) xc = a xc + б хс.
Мы примем его без доказательств.
7.3. Выражение векторного произведения через координаты
Воспользуемся таблицей векторного произведения векторов i, j и k:
если направление кратчайшего пути от первого вектора ко второму совпадает с направлением стрелки, то произведение равно третьему вектору, если нет, то третий вектор берется со знаком минус.
Пусть даны два вектора a = a x i + a y j+ a z k и b = b x i+ b y j+ b z k . Найдем векторное произведение этих векторов, умножив их как многочлены (по свойствам векторного произведения) :
Полученную формулу можно записать еще короче:
, так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки. Равенство (7.2) легко запомнить.
Равенство (7.2) легко запомнить.
7.4. Некоторые приложения векторной работы
Установление коллинеарных векторов
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов a и b | хб | = | а | * | б | sin g, то есть S пар = | а х б |. И, следовательно, D S = 1/2 | а х б |.
Определение момента силы относительно точки
Пусть в точке A приложена сила F = AB отпустить O — некоторая точка пространства (см. рис. 20).
Из физики известно, что момент силы F относительно точки О называется вектором М, , проходящим через точку О и:
1) перпендикулярно плоскости, проходящей через точки О, А, В;
2) численно равен произведению силы на плечо
3) образует правую тройку с векторами ОА и АВ.
Следовательно, M = OA x F.
Нахождение линейной скорости вращения
Скорость v точки M твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется по формуле Эйлера v = w хr, где r = ОМ, где О — некоторая неподвижная точка оси (см. рис. 21).
рис. 21).
Using the vector product of VECTORS
to calculate the area
some geometric shapes
Research work in mathematics
Pupil 10 B grade
MOU SOSH №73
Perevoznikov Mikhail
Leaders:
Assistant на кафедру математического анализа механико-математического факультета СумГУ им. Н.Г. Чернышевский Бердников Глеб Сергеевич
Саратов, 2015
Введение.
1. Теоретический обзор.
1.1. Векторы и расчеты с векторами.
1.2. Использование скалярного произведения векторов в решении задач
1.3 Скалярное произведение векторов в координатах
1.4. Векторное произведение векторов в трехмерном евклидовом пространстве: определение понятия.
1.5. Векторные координаты произведений векторов.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма. Вывод формулы и геометрический смысл векторного произведения векторов.
2.2. Зная только координаты точек, найдите площадь треугольника. Доказательство теоремы
2.3. Проверка правильности формулы на примерах.
2.4. Практическое использование векторной алгебры и векторного произведения.
Заключение
Введение
Как известно, многие геометрические задачи имеют два основных способа решения — графический и аналитический. Графический метод связан с построением графиков и рисунков, а аналитический предполагает решение задач преимущественно с помощью алгебраических действий. В последнем случае алгоритм решения задач связан с аналитической геометрией. Аналитическая геометрия — это область математики, а точнее линейная алгебра, рассматривающая решение геометрических задач средствами алгебры на основе метода координат на плоскости и в пространстве. Аналитическая геометрия позволяет анализировать геометрические изображения, линии и поверхности, важные для практических приложений. Более того, в этой науке для расширения пространственного понимания фигур, кроме того, иногда используется векторное произведение векторов.
В связи с широким распространением трехмерных пространственных технологий актуальным представляется изучение свойств некоторых геометрических фигур с помощью векторного произведения.
В связи с этим была указана цель данного проекта — использование векторного произведения векторов для вычисления площади некоторых геометрических фигур.
В связи с поставленной целью решались следующие задачи:
1. Теоретически изучить необходимые основы векторной алгебры и определить векторное произведение векторов в системе координат;
2. Проанализировать связь между векторным произведением и площадью треугольника и параллелограмма;
3. Вывести формулы площади треугольника и параллелограмма в координатах;
4. Проверить на конкретных примерах правильность полученной формулы.
1. Теоретический обзор.
Векторы и вычисления с векторами
Вектор – это направленный отрезок, для которого указаны его начало и конец:
В этом случае начало отрезка точка A , конец отрезка точка V . .. Сам вектор обозначается
.. Сам вектор обозначается
или … Чтобы найти координаты вектора
, зная координаты его начальной точки А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:
= { Б х — А х ; Б и — А и }
Коллинеарные векторы — это векторы, лежащие на параллельных прямых или на одной прямой. В этом случае вектор представляет собой отрезок, характеризующийся длиной и направлением.
Длина сегмента направления определяет числовое значение вектора и называется длиной вектора или модулем вектора.
Длина вектора || в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат.
Вы можете выполнять различные действия с векторами.
Например, доп. Для их сложения необходимо сначала провести второй вектор из конца первого, а затем соединить начало первого с концом второго (рис. 1). Сумма векторов — это еще один вектор с новыми координатами.
1). Сумма векторов — это еще один вектор с новыми координатами.
Сумма векторов = { a x ; a y ) и = { b x ; б г ) можно найти по следующей формуле:
+ = (а х + б х ; и + б и }
Рис. 1. Действия с векторами
Вычитая векторы, нужно провести их сначала из одной точки, а затем соединить конец второй с концом первой.
Разность векторов = { a x ; a y ) и = { b x ; б г } можно найти по формуле:
— знак равно и х — б х ; и — б и }
Также векторы можно умножать на число. Результатом также будет вектор в k раз больше (или меньше) заданного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном — противоположно.
Произведение вектора = { a x ; а у } и числа k можно найти по следующей формуле:
k = (k A х ; к а и }
Можно ли умножить вектор на вектор? Конечно, и даже два варианта!
Первый вариант — скалярное произведение.
Рис. 2. Скалярное произведение в координатах
Для нахождения произведения векторов можно использовать угол между этими векторами, показанный на рисунке 3.
Из формулы следует, что скалярное произведение равно произведению длин этих векторов на косинус угла между ними, его результатом является число. Важно, что если векторы перпендикулярны, то их скалярное произведение равно нулю, потому что косинус прямого угла между ними равен нулю.
В координатной плоскости вектор тоже имеет координаты. V Векторы, их координаты и скалярное произведение являются одними из самых удобных методов для вычисления угла между прямыми линиями (или их отрезками), если введена система координат. А если координаты
А если координаты
, то их скалярное произведение равно:
В трехмерном пространстве 3 оси и соответственно точки и векторы в такой системе будут иметь 3 координаты, а скалярное произведение векторов вычисляется по формуле формула:
1.2. Векторное произведение векторов в трехмерном пространстве.
Второй вариант вычисления произведения векторов — перекрестное произведение. Но для его определения требуется уже не плоскость, а трехмерное пространство, в котором начало и конец вектора имеют 3 координаты.
В отличие от скалярного произведения векторов в трехмерном пространстве, операция «векторное умножение» над векторами приводит к другому результату. Если в предыдущем случае скалярного умножения двух векторов результатом было число, то в случае векторного умножения векторов результатом будет другой вектор, перпендикулярный обоим векторам, входящим в произведение. Поэтому это произведение векторов называется векторным произведением.
Очевидно, что при построении результирующего вектора , перпендикулярного двум, вошедшим в работу — и, можно выбрать два противоположных направления. При этом направление результирующего вектора определяется правилом правой руки или правилом карданного подвеса. Если нарисовать векторы так, чтобы их начала совпадали, и повернуть первый вектор-фактор кратчайшим образом ко второму вектору-фактору, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора произведения (рис. 7).
Рис. 7. Правило правой руки
1.3. Свойства векторного произведения векторов.
Длина результирующего вектора определяется по формуле
.
Где
перекрестное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен
, а его направление определяется по правилу правой руки.
Векторное произведение зависит от порядка множителей, а именно:
Векторное произведение ненулевых векторов равно 0, если они коллинеарны, то синус угла между ними будет 0.
Координаты векторов в трехмерном пространстве выражаются следующим образом:. Затем координаты результирующего вектора находятся по формуле
Длина результирующего вектора находится по формуле:
.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма на плоскости. Геометрический смысл векторного произведения векторов.
Дан треугольник ABC (рис. 8). Известно, что .
Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника найдем выражение векторного произведения векторов:
Из вышеприведенного, можно определить геометрический смысл векторного произведения (рис. 9):
длина векторного произведения векторов равна удвоенной площади треугольника, имеющего векторы и стороны, если их отложить от одной точки .
Другими словами, длина векторного произведения векторов и равна площади параллелограмма, построенного на векторах и , при этом стороны и и угол между ними равны.
Рис. 9. Геометрический смысл векторного произведения векторов
В связи с этим можно дать еще одно определение векторного произведения векторов :
Векторным произведением вектора на вектор называется вектор, длина которого численно равна площади параллелограмма, построенного на векторах и, перпендикулярного плоскости этих векторов и направленного так, чтобы наименьший поворот от k вокруг вектора осуществляли против часовой стрелки, если смотреть с конца вектора (рис. 10).
Рис. 10. Определение векторного произведения векторов
с помощью параллелограмма
2.2. Вывод формулы нахождения площади треугольника в координатах.
Итак, нам дан треугольник ABC на плоскости и координаты его вершин. Найдем площадь этого треугольника (рис. 11).
Рис. 11. Пример решения задачи на нахождение площади треугольника по координатам его вершин
Раствор.
Для начала рассмотрим координаты вершин в пространстве и вычислим координаты векторов АВ и АС.
Используя приведенную выше формулу, вычисляем координаты их векторного произведения. Длина этого вектора равна 2 площадям треугольника ABC. Площадь треугольника равна 10.
При этом, если рассматривать треугольник на плоскости, то первые 2 координаты векторного произведения всегда будут равны нулю, поэтому можно сформулировать следующую теорему.
Теорема: Пусть задан треугольник ABC и координаты его вершин (рис. 12).
Тогда .
Рис. 12. Доказательство теоремы
Доказательство.
Рассмотрим точки в пространстве и вычислим координаты векторов BC и VA. … По приведенной ранее формуле вычисляем координаты векторного произведения этих векторов. Обратите внимание, что все термины, содержащие z 1 или z 2, равны 0, потому что z 1 и z 2 = 0. УДАЛИТЬ !!!
Итак, поэтому
2.3. Проверка правильности формулы на примерах
Найти площадь треугольника, образованного векторами a = (-1; 2; -2) и b = (2; 1; -1).
Решение: Найдем векторное произведение этих векторов:
a × b =
I (2 (-1) — (-2) 1) — j ((- 1) (-1) — (-2 ) 2) + k ((- 1) 1 — 2 2) =
I (-2 + 2) — j (1 + 4) + k (-1 — 4) = -5 j — 5 k = (0 ;-5;-5)
Из свойств векторного произведения:
SΔ =
| а × б | =
√ 02 + 52 + 52 =
√ 25 + 25 =
√ 50 =
5√ 2
Ответ: SΔ = 2,5√2.
Заключение
2.4. Приложения векторной алгебры
и скалярное и векторное произведение векторов.
Где нужны векторы? Векторное пространство и векторы имеют не только теоретическое, но и вполне реальное практическое применение в современном мире.
В механике и физике многие величины имеют не только числовое значение, но и направление. Такие величины называются векторными. Наряду с использованием элементарных механических понятий, исходя из их физического смысла, многие величины рассматриваются как скользящие векторы, а их свойства описываются как аксиомами, как это принято в теоретической механике, так и посредством математических свойств векторов. Наиболее яркими примерами векторных величин являются скорость, импульс и сила (рис. 12). Например, угловой момент и сила Лоренца математически записываются с использованием векторов.
Наиболее яркими примерами векторных величин являются скорость, импульс и сила (рис. 12). Например, угловой момент и сила Лоренца математически записываются с использованием векторов.
В физике важны не только сами векторы, но и их произведения, которые помогают вычислить определенные величины. Векторное произведение полезно для определения коллинеарности векторов, модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправлены или противоположно направлены.
Другой пример: скалярное произведение используется для расчета работы по приведенной ниже формуле, где F — вектор силы, а s — вектор смещения.
Одним из примеров использования произведения векторов является момент силы, равный произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
Многое из того, что вычисляется в физике по правилу правой руки, является векторным произведением. Найдите подтверждение, приведите примеры.
Найдите подтверждение, приведите примеры.
Также стоит отметить, что двумерное и трехмерное пространство не исчерпывает возможных вариантов векторных пространств. Высшая математика рассматривает пространства большей размерности, в которых также определены аналоги формул скалярного и векторного произведений. Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание не способно представить визуально, они удивительным образом находят применение во многих областях науки и производства.
При этом результатом векторного произведения векторов в трехмерном евклидовом пространстве является не число, а результирующий вектор с его координатами, направлением и длиной.
Направление результирующего вектора определяется правилом правой руки, которое является одним из самых удивительных моментов аналитической геометрии.
Векторное произведение векторов можно использовать для нахождения площади треугольника или параллелограмма при заданных координатах вершин, что было подтверждено выводом формулы, доказательством теоремы и решением практических задач.
Векторы широко используются в физике, где такие показатели, как скорость, импульс и сила, могут быть представлены в виде векторных величин и вычислены геометрически.
Список использованных источников
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 7-9 классы: учебник для организаций образования. М.:, 2013. 383 с.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10-11 классы: учебник для организаций образования: базовый и профильный уровни. М.:, 2013. 255 с.
Бугров Ю.С., Никольский С.М. Высшая математика. Том первый: Элементы линейной алгебры и аналитической геометрии.
Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, Физматлит, 1998.
Аналитическая геометрия.
Матем. Клевер.
Изучайте математику онлайн.
http://ru.onlinemschool.com/math/library/vector/multiply1/
Сайт В. Глазнева.
http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7. htm
htm
Википедия.
https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5 %ED % E8% E5
Калькулятор площади параллелограмма
Создано Ханной Памула, докторантом
Отредактировано Богной Шик и Стивеном Вудингом
Последнее обновление: 14 сентября 2022 г. Как пользоваться этим калькулятором площади параллелограмма?
Если у вас возникли проблемы с геометрией параллелограмма, проверьте этот калькулятор площади параллелограмма (а также его брат-близнец, калькулятор периметра параллелограмма).
Хотите ли вы вычислить площадь, зная основание и высоту, стороны и угол, или диагонали параллелограмма и угол между ними, вы попали по адресу. Не спрашивайте, как найти площадь параллелограмма; просто попробуйте калькулятор!
Ниже вы можете узнать, как работает инструмент — формулы площади параллелограмма и четкое объяснение — все, что вам нужно, чтобы понять тему.
Формулы площади параллелограмма
Параллелограмм — это простой четырехугольник с двумя парами параллельных сторон. Каждый прямоугольник является параллелограммом, так же как каждый ромб и квадрат. Помните, это не работает наоборот!
Какие формулы использует калькулятор площади параллелограмма?
Площадь с учетом основания и высоты
площадь = основание × высотаВы что-то заметили? Формула площади параллелограмма почти такая же, как и для прямоугольника! Почему это так? Взгляните на рисунок: параллелограмм можно разделить на трапецию и прямоугольный треугольник и превратить в прямоугольник.
Узнайте больше о площади прямоугольника с помощью нашего калькулятора площади прямоугольника.
Площадь с учетом сторон и угла между ними
площадь = a × b × sin(угол)
Это звонит в колокольчик? Эта формула пришла из тригонометрии и используется, например, в нашем калькуляторе площади треугольника — параллелограмм можно рассматривать как два конгруэнтных треугольника. Смежные углы в параллелограмме являются дополнительными, поэтому вы можете выбрать любой угол, который вы хотите, потому что
Смежные углы в параллелограмме являются дополнительными, поэтому вы можете выбрать любой угол, который вы хотите, потому что sin(угол) = sin(180° - угол) .
Площадь данных диагоналей параллелограмма и угла между ними
площадь = ½ × e × f × sin(угол)Формула тоже взята из тригонометрии. Хотите знать, откуда оно?
Разделите параллелограмм на два треугольника и предположите, что наша диагональ
иявляется «базой» для обоих новых треугольников.Какова высота этого треугольника? Используйте функцию синуса. Это
(f/2) × sin(угол)!Площадь треугольника равна нашему «основанию»
eумножить на высоту:e × (f/2) × sin(угол)Параллелограмм состоит из двух таких треугольников, поэтому его площадь равна
e × f × sin(angle).
Как пользоваться этим калькулятором площади параллелограмма?
Вы все еще не уверены, что наш калькулятор площади параллелограмма работает? Мы покажем вам шаг за шагом:
Посмотрите на свое упражнение.
 Что дано, что неизвестно? Выберите нужную часть калькулятора для ваших нужд . Предположим, что мы хотим вычислить площадь, зная диагонали параллелограмма и угол между диагоналями.
Что дано, что неизвестно? Выберите нужную часть калькулятора для ваших нужд . Предположим, что мы хотим вычислить площадь, зная диагонали параллелограмма и угол между диагоналями.Введите указанные значения в правые поля . Примите 5 дюймов, 13 дюймов и 30° для первой диагонали, второй диагонали и угла между ними соответственно.
Калькулятор отображает площадь параллелограмма значением . В нашем случае это 32,5 дюйма².
Ознакомьтесь с нашими калькуляторами площади для других форм, таких как калькулятор площади ромба, калькулятор площади круга и калькулятор площади трапеции.
Часто задаваемые вопросы
Как найти площадь параллелограмма, зная его смежные стороны?
Чтобы определить площадь по смежным сторонам параллелограмма, вам также необходимо знать угол между сторонами . Тогда можно применить формулу: площадь = a × b × sin(α) , где а и b — стороны, а α — угол между ними.
Как найти площадь параллелограмма по диагоналям?
Площадь параллелограмма можно определить по его диагоналям, при условии, что вы также знаете угол между диагоналями .
Если e и f — длины диагоналей и φ — угол между ними, то площадь можно вычислить следующим образом: площадь = ½ × e × f × sin(φ) .
Как найти площадь параллелограмма без высоты?
Можно найти площадь параллелограмма без высоты! Например, достаточно знать одну из следующих вещей:
- Длина смежных сторон и угол между ними — пользуйтесь тригонометрией.
- Длину диагоналей и угол между ними по формуле – использовать тригонометрию.
- Длина диагоналей и одной стороны – по формуле Герона.
Какова площадь параллелограмма с перпендикулярными диагоналями длиной 10 и 15?
Ответ: 75 . Мы используем формулу, которая говорит, что площадь равна ½ , умноженных на произведение длин диагоналей на синус угла между ними. Поскольку наши диагонали перпендикулярны, угол между ними равен
Поскольку наши диагонали перпендикулярны, угол между ними равен 90° и sin 90° = 1 . Следовательно, вычисление, которое нам нужно выполнить, равно ½ × 10 × 15 = 75 .
Ханна Памула, кандидат наук
Основание (b)
Высота (h)
Посмотреть 21 похожий калькулятор 2d геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 18
Построить параллелограмм из векторов онлайн. Векторное произведение векторов. Смешанное произведение векторов
Площадь параллелограмма, построенного на векторах, равна произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда длины этих самых векторов даны по условиям. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах, можно только после вычислений по координатам.
Если вам повезло, и длины векторов даны по условиям, то нужно просто применить формулу, которую мы уже подробно разбирали в статье. Площадь будет равна произведению модулей на синус угла между ними:
Площадь будет равна произведению модулей на синус угла между ними:
Рассмотрим пример вычисления площади параллелограмма, построенного на векторах.
Задача: Параллелограмм строится на векторах и . Найдите площадь, если , а угол между ними равен 30°.
Выразим векторы через их значения:
Возможно у вас возник вопрос — откуда взялись нули? Стоит помнить, что мы работаем с векторами, и для них. также обратите внимание, что если в результате мы получим выражение, то оно будет преобразовано в . Теперь проведем окончательные расчеты:
Вернемся к задаче, когда в условиях не указаны длины векторов. Если ваш параллелограмм лежит в декартовой системе координат, то вам нужно сделать следующее.
Вычисление длин сторон фигуры, заданной координатами
Для начала найдем координаты векторов и из конечных координат вычтем соответствующие начальные координаты. Примем координаты вектора a (x1;y1;z1) и вектора b (x3;y3;z3).
Теперь найдем длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, затем сложить результаты и извлечь корень из конечного числа. По нашим векторам будут произведены следующие расчеты:
Для этого каждую координату необходимо возвести в квадрат, затем сложить результаты и извлечь корень из конечного числа. По нашим векторам будут произведены следующие расчеты:
Теперь вам нужно найти скалярное произведение наших векторов. Для этого их соответствующие координаты перемножаются и складываются.
Зная длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь мы можем найти синус того же угла:
Теперь у нас есть все необходимые величины, и мы легко можем найти площадь параллелограмма, построенного на векторах, по уже известной формуле.
В этом уроке мы рассмотрим еще две операции с векторами: перекрестное произведение векторов и смешанное произведение векторов (прямая ссылка для тех кому нужно) . Ничего страшного, иногда бывает так, что для полного счастья помимо скалярного произведения векторов нужно еще и еще. Такая вот векторная зависимость. Может сложиться впечатление, что мы попадаем в дебри аналитической геометрии. Это неправда. В этом разделе высшей математики дров вообще мало, разве что на Буратино хватит. На самом деле материал очень распространенный и простой — вряд ли сложнее того же скалярное произведение , даже типовых задач будет меньше. Главное в аналитической геометрии, как многие увидят или уже видели, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Это неправда. В этом разделе высшей математики дров вообще мало, разве что на Буратино хватит. На самом деле материал очень распространенный и простой — вряд ли сложнее того же скалярное произведение , даже типовых задач будет меньше. Главное в аналитической геометрии, как многие увидят или уже видели, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молния на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или заново приобрести базовые знания о векторы. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, часто встречающихся в практической работе
Что сделает тебя счастливым? Когда я был маленьким, я мог жонглировать двумя и даже тремя мячами. Это сработало хорошо. Теперь вообще не нужно жонглировать, так как мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами будут опущены. Почему? Так родились эти действия — вектор и смешанное произведение векторов определены и работают в трехмерном пространстве. Уже проще!
Почему? Так родились эти действия — вектор и смешанное произведение векторов определены и работают в трехмерном пространстве. Уже проще!
В этой операции так же, как и в скалярном произведении, два вектора . Пусть это будут нетленные буквы.
Само действие обозначало следующим образом: . Есть и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь еще и перемножаются два вектора, то чем отличается ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом перекрестного произведения векторов является ВЕКТОР : , то есть мы перемножаем векторы и снова получаем вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения также могут различаться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : векторное произведение неколлинеарных векторов, взятых в таком порядке , называется ВЕКТОР, длина которая численно равна площади параллелограмма , построенного на этих векторах; вектор ортогонален векторам , и направлен так, чтобы основание имело правильную ориентацию:
Разбираем определение по костям, там много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , указанные красными стрелками, по определению не коллинеарны . Возникающие коллинеарные векторы будет уместно рассмотреть несколько позже.
2) Векторы взяты в строгом порядке : – «а» умножается на «будь» , а не «будь» на «а». Результатом векторного умножения является VECTOR , который обозначен синим цветом. Если векторы перемножить в обратном порядке, то получится вектор равный по длине и противоположный по направлению (малиновый цвет). То есть равенство.
То есть равенство.
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный момент! ДЛИНА синего вектора (и, следовательно, малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке этот параллелограмм заштрихован черным цветом.
Примечание : рисунок схематичен, и, разумеется, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышеизложенного, справедлива формула расчета ДЛИНЫ векторного произведения:
Подчеркну, что в формуле речь идет о ДЛИНЕ вектора, а не о самом векторе. Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находится через понятие векторного произведения:
Получаем вторую важную формулу. Диагональ параллелограмма (красная пунктирная линия) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важным фактом является то, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам.
5) Вектор направлен так, что основа Имеет правую ориентацию. В уроке о переходе на новую основу я подробно рассказал о плоскостной ориентации , а теперь разберемся, что такое ориентация пространства. объясню на пальцах правой руки . Мысленно соедините указательных пальцев с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате thumb — векторное произведение будет искать вверх. Это правоориентированный базис (он на рисунке). Теперь поменяйте местами векторы ( указательный и средний пальцы ) в некоторых местах, в результате большой палец развернется, а векторное произведение уже будет смотреть вниз. Это тоже правильная основа. Возможно у вас возник вопрос: какой базис имеет левую ориентацию? «Назначить» тем же пальцам левой руки вектора, и получить левое основание и левую пространственную ориентацию (в этом случае большой палец будет располагаться в направлении нижнего вектора) . Образно говоря, эти основания «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным — например, самое обычное зеркало меняет ориентацию пространства, а если «вытащить из зеркала отражаемый предмет», то вообще невозможно будет совместите его с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение 😉
Это тоже правильная основа. Возможно у вас возник вопрос: какой базис имеет левую ориентацию? «Назначить» тем же пальцам левой руки вектора, и получить левое основание и левую пространственную ориентацию (в этом случае большой палец будет располагаться в направлении нижнего вектора) . Образно говоря, эти основания «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным — например, самое обычное зеркало меняет ориентацию пространства, а если «вытащить из зеркала отражаемый предмет», то вообще невозможно будет совместите его с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение 😉
… как хорошо, что вы теперь знаете о право- и левоориентированных основаниях, ведь заявления некоторых лекторов о смене ориентации ужасны =)
Векторное произведение коллинеарных векторов Определение Детально проработано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь таких, как говорят математики, вырожденный параллелограмм равен нулю. То же следует из формулы — синус нуля или 180 градусов равен нулю, значит площадь равна нулю
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь таких, как говорят математики, вырожденный параллелограмм равен нулю. То же следует из формулы — синус нуля или 180 градусов равен нулю, значит площадь равна нулю
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частным случаем является векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверить коллинеарность трехмерных векторов, и эту задачу среди прочих мы тоже разберем.
Для решения практических примеров может понадобиться тригонометрическая таблица для нахождения по ней значений синусов.
Что ж, разожжем огонь:
Пример 1
а) Найдите длину векторного произведения векторов, если
б) Найдите площадь параллелограмма, построенного на векторах, если
Решение : Нет, это не опечатка, я намеренно сделал исходные данные в пунктах условий одинаковыми. Потому что дизайн решений будет другим!
Потому что дизайн решений будет другим!
а) По условию требуется найти длины вектор (векторное произведение). По соответствующей формуле:
Ответ :
Раз спрашивали о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти квадратов параллелограммов, построенных на векторах . Площадь этого параллелограмма численно равна длине перекрестного произведения:
Ответ :
Обратите внимание, что в ответе про векторное произведение речи вообще не идет, нас спрашивали про площадь фигуры , соответственно размерность квадратные единицы.
Мы всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем четкий ответ. Это может показаться буквализмом, но буквалистов среди учителей хватает, и задание с хорошими шансами будет возвращено на доработку. Хотя это не особо натянутая придирка — если ответ неверный, то складывается впечатление, что человек не понимает простых вещей и/или не вникал в суть задачи. Этот момент нужно всегда держать под контролем, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент нужно всегда держать под контролем, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда делась большая буква «ан»? В принципе, можно было бы дополнительно прилепить к раствору, но для того, чтобы сократить запись, я этого не сделал. Надеюсь, все это понимают и обозначают одно и то же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах, если
Формула нахождения площади треугольника через векторное произведение приведена в комментарий к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространенная, треугольники вообще можно замучить.
Для решения других задач нам потребуются:
Свойства векторного произведения векторовМы уже рассмотрели некоторые свойства векторного произведения, тем не менее, я включу их в этот список.
Для произвольных векторов и произвольного числа следующие свойства:
1) В других источниках информации этот пункт обычно не выделяется в свойствах, но в практическом плане он очень важен. Так пусть будет.
Так пусть будет.
2) — свойство также обсуждалось выше, иногда его называют антикоммутативность . Другими словами, порядок векторов имеет значение.
3) — комбинация или ассоциативное векторное произведение законов. Константы легко выносятся за пределы векторного произведения. Действительно, что они там делают?
4) — распределение или распространение законов векторного произведения. С открытием скобок тоже проблем нет.
В качестве демонстрации рассмотрим короткий пример:
Пример 3
Найти
Решение: По условию снова требуется найти длину векторного произведения. Раскрасим нашу миниатюру:
(1) По ассоциативным законам выносим константы за пределы векторного произведения.
(2) Выносим константу из модуля, при этом модуль «съедает» знак минус. Длина не может быть отрицательной.
(3) Дальнейшее понятно.
9Пример 4 используя формулу. Загвоздка в том, что векторы «ce» и «te» сами представляются как суммы векторов. Алгоритм здесь стандартный и чем-то напоминает примеры №3 и 4 урока. Скалярное произведение векторов . Давайте разобьем его на три этапа для ясности:
Алгоритм здесь стандартный и чем-то напоминает примеры №3 и 4 урока. Скалярное произведение векторов . Давайте разобьем его на три этапа для ясности:1) На первом шаге векторное произведение выражаем через векторное произведение, фактически выражаем вектор через вектор . О длине пока ничего не сказано!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскройте скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, мы выносим все константы за пределами векторных произведений. При небольшом опыте действия 2 и 3 можно выполнять одновременно.
(4) Первый и последний члены равны нулю (нулевой вектор) в силу приятного свойства . Во втором члене мы используем свойство антикоммутативности векторного произведения:
(5) Приведем аналогичные члены.
В итоге вектор получился выраженным через вектор, чего и требовалось добиться:
2) На втором шаге находим длину нужного нам векторного произведения. Это действие аналогично примеру 3:
Это действие аналогично примеру 3:
3) Найдите площадь искомого треугольника:
Шаги 2-3 решения можно расположить в одну строку.
Ответ :
Рассматриваемая задача достаточно распространена в контрольной работе, вот пример решения своими руками:
Пример 5
Найти если
Быстрое решение и ответ в конце урока. Посмотрим, насколько внимательными вы были при изучении предыдущих примеров 😉
Перемножение векторов в координатах, приведенное в ортонормированном базисе, выражается формулой :
Формула действительно проста: записываем координатные векторы в верхнюю строку определителя, «упаковываем» координаты векторов во вторую и третью строки, а ставим в строгом порядке — первую, координаты вектора «ve», затем координаты вектора «double-ve». Если векторы нужно перемножать в другом порядке, то строки тоже следует поменять местами:
Пример 10
Проверить коллинеарность следующих пространственных векторов:
a)
b)
Решение : Тест основан на одном из утверждений этого урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевой вектор): .
а) Найдите векторное произведение:
Значит, векторы не коллинеарны.
б) Найдите векторное произведение:
Ответ : а) не коллинеарно, б)
Вот, пожалуй, и вся основная информация о векторном произведении векторов.
Этот раздел будет не очень большим, так как мало задач, где используется смешанное произведение векторов. На самом деле все будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов это произведение трех векторов :
Вот так выстроились как поезд и ждут, не могут дождаться пока их вычислят.
Сначала опять определение и картинка:
Определение : Смешанное произведение некомпланарных векторов , взятых в таком порядке , называется объемом параллелепипеда , построенного на этих векторах, снабженного «+ знак «, если основание правое, и знак «-«, если основание левое.
Давайте нарисуем. Пунктиром проведены невидимые для нас линии:
Пунктиром проведены невидимые для нас линии:
Углубимся в определение:
2) Векторы взяты в определенном порядке , то есть перестановка векторов в произведении, как нетрудно догадаться, не проходит без последствий.
3) Прежде чем комментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов есть ЧИСЛО : . В учебной литературе оформление может быть несколько иным, я привык обозначать смешанный продукт сквозным, а результат вычислений буквой «пэ».
А-приора смешанное произведение объем параллелепипеда , построенный по векторам (рисунок нарисован красными векторами и черными линиями). То есть число равно объему данного параллелепипеда.
Примечание : Чертеж схематический.
4) Не будем лишний раз заморачиваться понятием ориентации базиса и пространства. Смысл заключительной части в том, что к громкости можно добавить знак минус. Проще говоря, смешанный продукт может быть отрицательным: .
Формула вычисления объема параллелепипеда, построенного на векторах, следует непосредственно из определения.
Квадрат параллелограмм построен на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для расчета необходимо использовать координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — концепция вектора;
- — свойства векторов;
- — Декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов) , синусом угла между ними S=│a│ │ b│ sin(α).
- Если векторы даны в декартовой системе координат, то для нахождения площади параллелограмм построен на них, делаем следующее:
- Найти координаты векторов, если они не заданы сразу, вычитая координаты начал из соответствующих координат концов векторов.
 Например, если координаты начальной точки вектора (1;-3;2), а конечной точки (2;-4;-5), то координаты вектора будут (2-1 ;-4+3;-5-2)=(1 ;-1;-7). Пусть координаты вектора a(x1;y1;z1), вектора b(x2;y2;z2).
Например, если координаты начальной точки вектора (1;-3;2), а конечной точки (2;-4;-5), то координаты вектора будут (2-1 ;-4+3;-5-2)=(1 ;-1;-7). Пусть координаты вектора a(x1;y1;z1), вектора b(x2;y2;z2). - Найдите длины каждого из векторов. Возведя в квадрат каждую из координат векторов, найдите их сумму x1²+y1²+z1². Возьмите квадратный корень из результата. Для второго вектора проделайте ту же процедуру. Таким образом, вы получаете │a│ и │b│.
- Найдите скалярное произведение векторов. Для этого умножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определить косинус угла между ними, для чего разделить скалярное произведение векторов, полученных на шаге 3, на произведение длин векторов, вычисленных на шаге 2 (Cos(α)= │a b│/(│a │ │ б│)).
- Синус полученного угла будет равен квадратному корню из разницы между числом 1 и квадратом косинуса того же угла, вычисленного на шаге 4 (1-Cos²(α)).
- Вычислить площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в пункте 2, и умножить результат на число, полученное после вычислений в пункте 5.


 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). 5.
5.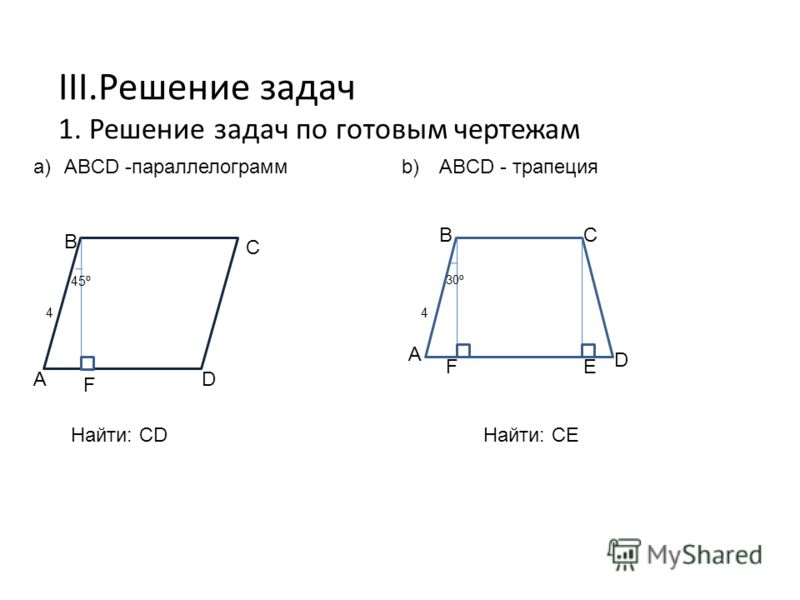 Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения. 10.17
10.17
 Решение квадратных уравнений.
Решение квадратных уравнений.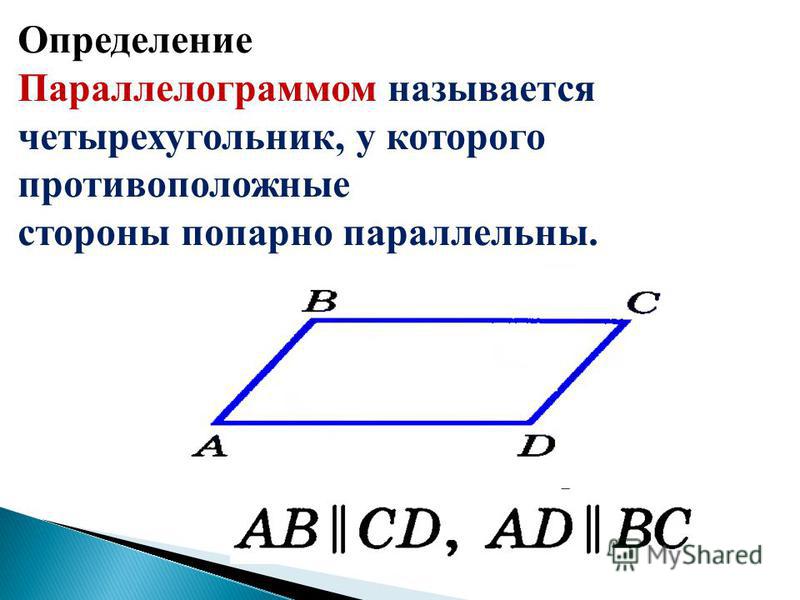 Комбинаторика. Теория вероятности.
Комбинаторика. Теория вероятности. Сложение и вычитание двух векторов.
Сложение и вычитание двух векторов.
