6 умножить на 8: сколько 6 умножить на 8 — Спрашивалка

alexxlab / / Разное

Содержание

Mathway | Популярные задачи

1Найти объемсфера (5)
2Найти площадьокружность (5)
3Найти площадь поверхностисфера (5)
4Найти площадьокружность (7)
5Найти площадьокружность (2)
6Найти площадьокружность (4)
7Найти площадьокружность (6)
8
Найти объем		сфера (4)
9Найти площадьокружность (3)
10Вычислить(5/4(424333-10220^2))^(1/2)
11Разложить на простые множители741
12Найти объемсфера (3)
13Вычислить3 квадратный корень из 8*3 квадратный корень из 10
14Найти площадьокружность (10)
15Найти площадьокружность (8)
16Найти площадь поверхностисфера (6)
17Разложить на простые множители1162
18Найти площадьокружность (1)
19Найти длину окружностиокружность (5)
20Найти объемсфера (2)
21Найти объемсфера (6)
22Найти площадь поверхностисфера (4)
23Найти объемсфера (7)
24Вычислитьквадратный корень из -121
25Разложить на простые множители513
26Вычислитьквадратный корень из 3/16* квадратный корень из 3/9
27Найти объемпрямоугольный параллелепипед (2)(2)(2)
28Найти длину окружностиокружность (6)
29Найти длину окружностиокружность (3)
30Найти площадь поверхностисфера (2)
31Вычислить
2 1/2÷22000000
32Найти объемпрямоугольный параллелепипед (5)(5)(5)
33Найти объемпрямоугольный параллелепипед (10)(10)(10)
34Найти длину окружностиокружность (4)
35Перевести в процентное соотношение1. 2-4*-1+2
45Разложить на простые множители228
46Вычислить0+0
47
Найти площадь		окружность (9)
48Найти длину окружностиокружность (8)
49Найти длину окружностиокружность (7)
50Найти объемсфера (10)
51Найти площадь поверхностисфера (10)
52Найти площадь поверхностисфера (7)
53Определить, простое число или составное5
54
Перевести в процентное соотношение		3/9
55Найти возможные множители8
56Вычислить(-2)^3*(-2)^9
57Вычислить35÷0. 2
60Преобразовать в упрощенную дробь2 1/4
61Найти площадь поверхностисфера (12)
62Найти объемсфера (1)
63Найти длину окружностиокружность (2)
64Найти объемпрямоугольный параллелепипед (12)(12)(12)
65Сложение2+2=
66Найти площадь поверхностипрямоугольный параллелепипед (3)(3)(3)
67Вычислитькорень пятой степени из 6* корень шестой степени из 7
68Вычислить7/40+17/50
69Разложить на простые множители1617
70Вычислить27-( квадратный корень из 89)/32
71Вычислить9÷4
72Вычислить2+ квадратный корень из 21
73Вычислить-2^2-9^2
74Вычислить1-(1-15/16)
75Преобразовать в упрощенную дробь8
76Оценка656-521
77Вычислить3 1/2
78Вычислить-5^-2
79Вычислить4-(6)/-5
80Вычислить3-3*6+2
81Найти площадь поверхностипрямоугольный параллелепипед (5)(5)(5)
82Найти площадь поверхностисфера (8)
83Найти площадьокружность (14)
84Преобразовать в десятичную форму11/5
85Вычислить3 квадратный корень из 12*3 квадратный корень из 6
86Вычислить(11/-7)^4
87Вычислить(4/3)^-2
88Вычислить1/2*3*9
89Вычислить12/4-17/-4
90Вычислить2/11+17/19
91Вычислить3/5+3/10
92Вычислить4/5*3/8
93Вычислить6/(2(2+1))
94Упроститьквадратный корень из 144
95Преобразовать в упрощенную дробь725%
96Преобразовать в упрощенную дробь6 1/4
97Вычислить7/10-2/5
98Вычислить6÷3
99Вычислить5+4
100Вычислитьквадратный корень из 12- квадратный корень из 192

Как научить ребёнка умножению и быстро выучить таблицу

Рано или поздно в каждой семье наступает этот день, когда ребёнку задают выучить таблицу умножения. В большинстве школ это случается во втором классе. Но учителя, понимая, в какую драму может превратиться жизнь ученика в этот период, предлагают начинать ещё на летних каникулах. Ведь постижение новой науки в короткие сроки – огромный стресс. А постепенное продвижение к цели даёт время понять принцип умножения и научиться находить искомые значения разными способами, не прибегая к формальному заучиванию.

Но всё это выглядит простым только в теории. На практике изучение умножения оказывается едва ли не переломным моментом в жизни детей. Почему так происходит и как всё-таки научить ребенка, чтобы просто и быстро выучить таблицу умножения – расскажет эта статья.

Таблица умножения – неприступная стена

Первое знакомство малышей с математикой в большинстве случаев проходит успешно. «Было три апельсина, один съели – осталось два», – дошкольники и первоклассники считают знакомые предметы, людей и животных, ловко прибавляют и вычитают. Это просто, понятно, и даже кажется занятным. Но вот ученику говорят: «За лето нужно выучить таблицу умножения», и с этого момента всё меняется.

Неудачи на этом пути обещаны каждому: и тем, кто «зубрит» без понимания, и тем, кому растолковали суть этой арифметической операции и как она пригодится в жизни. Запомнить 100 примеров с их значениями – это серьёзная задача. Детей пугают объемы и необходимость тратить на это своё свободное время – много времени. И каждая новая попытка заканчивается слезами, капризами или настоящим протестом. А затем закономерно перерастает в нелюбовь к предмету и так называемую «математическую тревожность».

Как показывает статистика, даже многие ученики средней и старшей школы не знают полностью таблицы умножения. Неумение перемножать числа до 10 крайне осложняет учебный процесс ещё в начальной школе. И с каждым годом проблемы с математикой накапливаются, как снежный ком, а затем распространяются и на другие связанные с ней предметы.

Как помочь ребёнку выучить таблицу умножения?

Некоторые взрослые всерьёз полагают, что именно период усвоения таблицы умножения делит детей на «гуманитариев» и «технарей». В действительности же отсутствие такой взаимосвязи было доказано не одним десятком исследований. Любой человек может добиться успеха в любой науке, если приложит к этому достаточно усилий и не окажется под давлением ярлыка «неспособный», навешенного окружением. Точно так же малыши учатся ходить, говорить, писать: у них не всё получается с первого раза, но это не означает, что им «не дано» и стоит оставить попытки.

В изучении таблицы умножения главное – заинтересовать ученика и найти подходящий именно ему способ. В отличие от этапов, когда ребёнок постигает базовые навыки, на мотивацию к обучению влияет и психологический настрой. Вот, что родители могут сделать, чтобы поддержать ребёнка:

  • позвольте ему придерживаться собственного темпа. Пусть сначала хорошо выучит примеры с одним множителем, затем переходите к следующему;
  • регулярно повторяйте пройденное, чередуя методики. Игры вызовут интерес к процессу и отвлекут от ощущения учебной обязанности, а разные виды дидактических материалов помогут систематизировать знания;
  • не сравнивайте его с другими и не добавляйте негативных эмоций угрозами, а также не нервничайте сами;
  • поощряйте успехи: угостите мороженым за освоение очередного столбика или разрешите лечь спать немного позже;
  • напоминайте, что все ошибаются, и это нормально; иногда нарочно демонстрируйте это сами.

Самые простые способы выучить таблицу умножения

Поколение современных родителей в большинстве своём учили умножение чисел по таблице с 10 столбиками примеров. Этот способ популярен и до сих пор, но педагоги почти единогласны в том, что для изучения он совсем не подходит. Но есть много других способов, и разным детям могут подойти разные из них.

   1. Зрительное запоминание: квадрат Пифагора

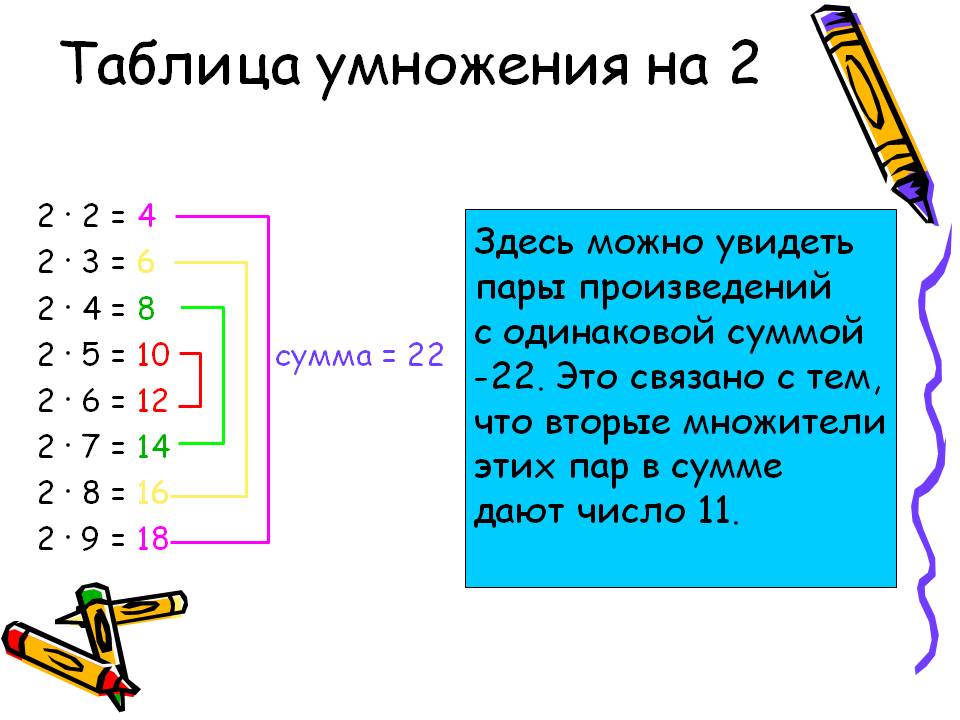
Этому варианту таблицы уже более 4 тысяч лет. Её преимущество заключается в симметрии: значения по обе стороны диагонального ряда квадратов чисел дублируются. То есть учить придётся не 100 примеров, а в два раза меньше. Мозг человека ищет симметрию во всём, поэтому такие таблицы – особенно яркие и разноцветные – хорошо отпечатываются в памяти детей. Когда ученик многократно обращается к квадрату Пифагора при решении примеров, он активизирует зрительную память и запоминает его визуально.

Перед изучением таблицы ребёнок должен отчетливо понимать, как с ней работать: числа из левого столбца умножаются на множители из верхней строчки, а на месте их пересечения находится искомое произведение. Объясните ребёнку, как связано умножение и сложение, то есть, что 3х3 = 3+3+3. Продемонстрируйте, что «от перестановки множителей произведение не меняется» или что при умножении на 1 получается то же самое число, а также известные хитрости для каждого множителя.

   2. Наглядные примеры

При объяснении сути умножения этот метод первичен. Дети должны понимать, откуда что берётся, и что числа и операции с ними – не просто абстрактные знаки, которые превращаются в другие знаки. Сначала дети видят, как 2 группы палочек по 3 штуки в каждой становятся 6 палочками. Потом учатся считать клеточки в прямоугольнике 5х5. Вычисляют количество колёс у машин перед подъездом или количество ног у всех кукол дома, визуализируют подсчёт апельсинов в нескольких коробках. Для подтверждения правильности счёта можно использовать любые подручные предметы: карандаши, кубики и т.д.

   3. Стихотворения или рифмованные фразы

Существует множество уже сочинённых двустиший или четверостиший про каждый пример из таблицы.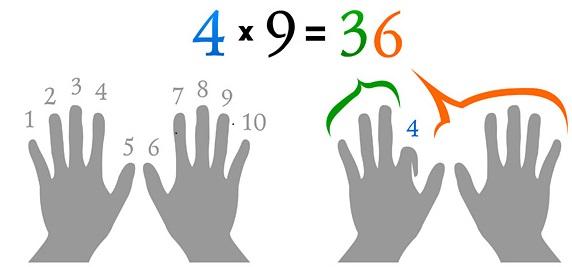 Предложите ребёнку выучить их или сочините свои. Ритм и рифма отлично помогают с запоминанием сложных вещей и являются одними из основных мнемотехник. Хорошо, если взрослые тоже выучат такие стихотворения – тогда повторять их можно будет где угодно. Родители могут иногда поддаваться ребенку, будто забыли, как правильно. Малышам же будет вдвойне интересно и самим вспомнить ответ, а затем поделиться им с мамой и папой.

   4. Карточки

Этот способ очень распространён для заучивания иностранных слов или толкований. Так же успешно его можно использовать для запоминания примеров из таблицы умножения. Карточки можно вырезать из бумаги/картона или купить в канцелярском магазине.

С одной стороны пишется пример, с другой – значение. Ребёнок пытается дать верный ответ по памяти и переворачивает карточку для проверки себя. Угаданные карточки откладываются, а те, с которыми возникли затруднения, прорабатываются снова, пока ученик не запомнит правильный ответ. Начать можно с одного множителя, потом смешать карточки примеров с двумя разными множителями и т. д. Главное, тренироваться регулярно. Использовать карточки можно и наоборот, особенно при переходе к изучению деления: ребёнок видит перед собой число и должен ответить, какие примеры из таблицы умножения ему соответствуют.

   5. Счёт на пальцах

Такой счёт скорее помогает не заучить таблицу, а вспомнить забытые ответы. Детям процесс складывания и загибания пальцев напоминает фокусы, потому нравится уже сам по себе. А то, что так можно найти решение примера, и вовсе кажется магией.

Если положить на стол обе ладони и загнуть любой палец, получится результат умножения номера пальца на 9. Количество пальцев перед загнутым – это десятки, а после – единицы. А на схеме ниже представлен лайфхак, как выучить таблицу умножения чисел 6, 7, 8 и 9 друг на друга, если уже запомнил её от 1 до 5.

   6. Онлайн-тренажеры и приложения для смартфона

Сегодня ассортимент обучающих программ и приложений безграничен. Среди них можно выбрать подходящие для любого вкуса и целей – выучить таблицу или закрепить её. В более сложных программах есть и теоретические материалы – справка, и возможность практиковаться в счёте; есть подсказки, ведётся статистика, внедрена система поощрений и наград и так далее. И очень удобно, если можно поставить напоминание о необходимости потренироваться.

Современные дети проводят много времени в гаджетах. Значит, такой способ может оказаться для них понятнее и интереснее: это как игра, только еще и полезная.

   7. Настольные игры

Как и с пунктом выше, настольных игр, созданных специально для запоминания таблицы, очень много. Быстрые, долгие, с историей, в дорогу, карточные или с игровой доской – существуют сотни вариантов. Можно найти игру, задействующую почти любую из известных игровых механик. А можно и создать такую самостоятельно.

Выбирая варианты, как проще учить таблицу умножения с ребенком, учитывайте его индивидуальные особенности восприятия. «Аудиалы» лучше запоминают на слух – им подойдут заучивание стихов, проговаривание, ассоциативные рассказы. «Визуалы» быстрее освоят её с помощью ярких плакатов, карточек, раскрасок «по номерам», где вместо чисел – примеры. «Кинестетикам» нужно всё трогать и много двигаться: им понравятся настольные игры, счёт на предметах или на пальцах.

Как научиться быстро умножать в уме

Когда таблица уже выучена и все примеры из неё многократно отработаны, школьников ждёт умножение многозначных чисел. На уроке можно вычислять в столбик или по китайскому методу пересекающихся линий. Сложные подсчёты разрешают делать на калькуляторе. Но умножать приходится не только в школе. И одна из самых удобных методик для устного счёта – ментальная арифметика.

Эта техника помогает производить все вычисления в уме, равно как и быстро умножать любые числа. В начале обучения дети используют специальные счёты – абакус, но постепенно учатся обходиться без них, просто представляя инструмент перед собой. Уже через пару месяцев занятий дети бегло считают в уме, могут выполнять одновременно несколько разных действий. Визуализация подсчёта активирует сразу оба полушария мозга, что положительно влияет на все сферы жизни ребёнка. А, освоив ментальный счёт, ему больше не придётся ничего заучивать, и таблица умножения в школе не будет препятствием ни во всестороннем развитии, ни в выборе профессии. И вопрос, как проще выучить таблицу умножения – лишь один из многих, на который способна дать ответ ментальная арифметика.

Помогите решить уравнение с дробями (8:x-2,6)умножить на(… -reshimne.ru

Новые вопросы

Ответы

Похожие вопросы


Найдете х пропорциях:#3,5…

Выполните тождественные преобразования 6(1-3-3с)+7(3в-5с )-4(-11+2в)…

Запиши все двузначные числа от 30 до 100 в которых число десятков на 2 больше числа единиц
. ..

Сформулируйте как найти неизвестный компонент действия и найдите его
456 + с = 1362
р + 207 = 1451
2045 — х = 15
b — 45 = 96…

Вычислить приближенных значения выражений округлые числа до тысяч.7.810-4.287, 5079-1200, 6905-2089, 17 456+7645, 28450-14568,32478+2098…

Для одной из фирм куплены телефон и факс на сумму 147 р. телефон стоил на 23 р. дешевле чем факс. сколько стоил факс?…

Математика

Литература

Алгебра

Русский язык

Геометрия

Английский язык

Химия

Физика

Биология

Другие предметы

История

Обществознание

Окружающий мир

География

Українська мова

Українська література

Қазақ тiлi

Беларуская мова

Информатика

Экономика

Музыка

Право

Французский язык

Немецкий язык

МХК

ОБЖ

Психология

Урок 5.

Опорное число при умножении чисел до 100

Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. В прошлом уроке, когда показывался способ умножения чисел до 20, по сути мы использовали опорное число 10.

Также стоит отметить, что подробнее вы можете ознакомиться с методикой использования опорного числа в книге «Считайте в уме как компьютер» Билла Хэндли.

Общие правила использования опорного числа

Опорное число полезно при перемножении чисел, находящихся близко и при возведении в квадрат. Как можно использовать метод опорного числа вы уже поняли из прошлого урока, теперь давайте обобщим все сказанное.

Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.

Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.

Оба числа меньше опорного (под опорным)

Допустим, мы хотим умножить 48 на 47. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.

Чтобы умножить 48 на 47, используя опорное число 50, нужно:

47*48

  1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или из 48 вычесть 3 – это всегда одно и то же)
  2. Дальше 45 умножаем на 50 = 2250
  3. Затем прибавляем 2*3 к этому результату и вуа ля – 2 256!

Схематично в уме удобно представлять приведенную ниже табличку.

50

(опорное число)

48

*

47

(48-3)*50 = 45*50 = 2 250

(или (47-2)*50  = 45*50 вспомните, что умножение на 5 – это тоже самое что деление на 2)

 

2

*

3

+6

Ответ:

 

 

 

2 250 + 6 = 2 256

Опорное число пишем слева от произведения.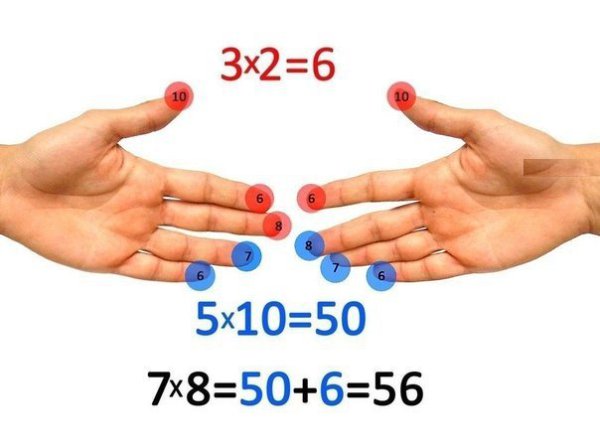 Если числа меньше опорного, то разница между ними и опорным пишется ниже этих чисел. Справа от 48*47 пишем расчет с опорным числом, справа от остатков 2 и 3 пишем их произведение.

Если использовать упрощенную схему, то решение выглядит так: 47*48=45*50 + 6= 2 256

Посмотрим другие примеры:

Умножить 18*19

20

(опорное число)

18

*

19

(18-1)*20 = 340

 

 

2

*

1

+2

Ответ:

 

 

 

342

Короткая запись: 18*19 = 20*17+2 = 342

Умножить 8*7

10

(опорное число)

8

*

7

(8-3)*10 = 50

 

 

2

*

3

+6

Ответ:

 

 

 

56

Короткая запись: 8*7 = 10*5+6 = 56

Умножить 98*95

100

(опорное число)

98

*

95

(95-2)*100 = 9300

 

 

2

*

5

+10

Ответ:

 

 

 

9310

Короткая запись: 98*95 = 100*93 + 10 = 9 310

Умножить 98*71

100

(опорное число)

98

*

71

(71-2)*100 = 6900

 

 

2

*

29

+58

Ответ:

 

 

 

6958

Короткая запись: 98*71 = 100*69 + 58 = 6 958

Оба числа больше опорного (над опорным)

Допустим, мы хотим умножить 54 на 53. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа. Но в отличие от предыдущих примеров, эти числа больше опорного. По сути, модель их умножения не меняется, но теперь нужно не вычитать остатки, а прибавлять.

  1. К 54 прибавить столько, на сколько 53 превышает 50, то есть 3. Получается 57 (или к 53 прибавить 4 – это всегда одно и то же)
  2. Дальше 57 умножаем на 50 = 2 850 (умножение на 50 – схоже с делением на 2)
  3. Затем прибавляем 4*3 к этому результату. Ответ: 2862

 

4

*

3

+12

50

(опорное число)

54

*

53

(54+3)*50 = 2 850

или (53+4)*50  = 57*50 (вспомните, что умножение на 5 – это тоже самое что деление на 2)

Ответ:

 

 

 

2 862

Короткое решение выглядит так: 50*57+12 = 2 862

Для наглядности еще ниже приведены примеры:

Умножить 23*27

 

3

*

7

+21

20

(опорное число)

23

*

27

(23+7)*20 = 600

 

Ответ:

 

 

 

621

Короткая запись: Короткая запись: 23*27 = 20*30 + 21 = 621

Умножить 51*63

 

1

*

13

+13

50

(опорное число)

51

*

63

(63+1)*50 = 3 200

 

Ответ:

 

 

 

3 213

Короткая запись: Короткая запись: 51*63 = 64*50 + 13 = 3 213

Одно число под опорным, а другое над

Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие.

Умножить 45*52

Произведение 45*52 считается так:

  1. Из 52 вычитаем 5 или к 45 прибавляем 2. В любом обоих случая получается: 47
  2. Дальше 47 умножаем на 50 = 2 350 (умножение на 50 – схоже с делением на 2)
  3. Затем вычитаем (а не прибавляем, как раньше!) 2*5. Ответ: 2 340

 

 

 

2

 

50

(опорное число)

45

*

52

(45+2)*50 = 2 350

 

 

5

 

 

-10

Ответ:

 

 

 

2 340

Короткая запись: 45*52 = 47*50-10 = 2 340

Также поступаем с подобными примерами:

Умножить 91*103

 

 

 

3

 

100

(опорное число)

91

*

103

(91+3)*100 = 9400

 

 

9

 

 

-27

Ответ:

 

 

 

9 373

Только одно число близко к опорному, а другое нет

Как вы уже видели из примеров, опорным числом удобно пользоваться, если даже только одно число близко к опорному. Желательно, чтобы разница этого числа с опорным составляла не более 2-x или 3-х или была равна числу, на которое удобно умножать (например, 5, 10, 25 – см. второй урок)

Умножить 48*73

 

 

 

23

 

50

(опорное число)

48

*

73

(73-2)*50 = 3 550

 

 

2

 

 

-46

Ответ:

 

 

 

3 504

Короткое решение: 48*73 = 71*50 – 23*2 = 3 504

Умножить 23*69

 

3

 

49

147

20

(опорное число)

23

*

69

(3+69)*20 = 1440

 

Ответ:

 

 

 

1 587

Короткая запись: Короткое решение: 23*69 = 72*20 + 147 = 1 587 — чуть сложнее

Умножить 98*41

100

(опорное число)

98

*

41

(41-2)*100 = 3900

 

 

2

*

59

+118

Ответ:

 

 

 

4018

Короткая запись: Короткая запись: 98*41 = 100*39 + 118 = 4 018

Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Если у вас получается хорошо умножать на 30, 40, 60, 70 или 80 – тогда, вы сможете с помощью этой методики умножать любые числа (до 100 и даже больше).

Использование нескольких опорных чисел

Методика двух опорных чисел заключается в том, что мы сначала делим 88 на 4 и получаем 22, производим умножение 23 на 22 и произведение умножаем снова 4. То есть, мы сначала делим произведение на 4, а потом умножаем на 4. Получается: 23*22 = 250*2+6= 506, а 506*4 = 2024 – это и есть ответ!

Для визуализации можно использовать уже привычную схему. Произведение23*88 считается так:

  1. Записываем удобное опорное число «20» и рядом приписываем множитель 4, с помощью которого можно выразить 80 через 20.
  2. Дальше делаем, как и раньше, пишем, на сколько 23 превышает 20 (3), а 88 превышает 80 (8).
  3. Выше тройки пишем произведение 3 на 4 (то есть 3 на множитель опорного).
  4. К 88 прибавляем произведение 3 на 4 и умножаем на опорное (20), получается 100*20 = 2000
  5. Прибавляем к 2000 произведением 3-х и 8-и. Результат: 2024

 

3*4=12

 

 

 

 

3

*

8

+24

20*4

(опорное число)

23

*

88

(88+12)*20 = 2 000

 

Ответ:

 

 

 

2 024

Короткая запись: 23*88 = (88+3*4)*20 + 24 = 2024

Теперь давайте попробуем умножить 23*88, используя опорное число 100 для 88 и 25 для 23. В этом случае главным опорным числом является 100. А 25 можно записать, как 100:4=25

100:4

(опорное число)

23

*

88

(23-3)*100 = 2 000

 

 

2

 

12

+24

 

 

 

12:4=3

 

Ответ:

 

 

 

2 024

Короткая запись: 23*88 = (23-12:4)*100 + 24 = 2024

Как видим, ответ получается один и тот же.

Способ с использованием двух опорных чисел несколько сложнее, и требует дополнительных действий. Во-первых, вы должны понять, какие 2 опорных числа вам удобно использовать. Во-вторых, нужно совершить дополнительное действие, для поиска числа, которое нужно умножать на опорное.

Эту методику применяйте лучше тогда, когда вы уже достаточно хорошо усвоили умножение с одним опорным числом.

Тренировка

Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.

Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.

1. Таблица умножения 8
2. Советы для 8-кратного стола
3. Часто задаваемые вопросы о таблице умножения на 8

Таблица умножения на 8 до 10
8 × 1 = 8 8 × 6 = 48
8 × 2 = 16 8 × 7 = 56
8 × 3 = 24 8 × 8 = 64
8 × 4 = 32 8 × 9 = 72
8 × 5 = 40 8 × 10 = 80

8 × 11 = 88 8 × 16 = 128
8 × 12 = 96 8 × 17 = 136
8 × 13 = 104 8 × 18 = 144
8 × 14 = 112 8 × 19 = 152
8 × 15 = 120 8 × 20 = 160