Математическая индукция vs полная математическая индукция : Вопросы преподавания
| Padawan |
| |||
13/12/05 |
| |||
| ||||
| venco |
| |||
04/05/09 |
| |||
| ||||
| Padawan |
| |||
13/12/05 |
| |||
| ||||
| Dandan |
| ||
24/03/07 |
| ||
| |||
| bot |
| |||
21/12/05 |
| |||
| ||||
| Doil-byle |
| ||
05/09/11 |
| ||
| |||
| LaTeXScience |
| |||
24/06/11 |
| |||
| ||||
| Padawan |
| |||
13/12/05 |
| |||
| ||||
| epros |
| |||
28/09/06 |
| |||
| ||||
| Padawan |
| ||
13/12/05 | |||
| |||
| epros |
| |||
28/09/06 |
| |||
| ||||
| Doil-byle |
| ||
05/09/11 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы, Супермодераторы
Математика в деталях: how to математическая индукция
Начнем с того, что такое математическая индукция.
Математическая индукция – метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел, согласно Wikipedia. Говоря простыми словами, у нас есть какое-то математическое высказывание о натуральных числах, и мы хотим доказать/опровергнуть его истинность.
Разные источники дают разное определение натуральных чисел. В моем университете один профессор включает ноль во множество N, а по определению другого натуральные числа начинаются с единицы. Дело вкуса 😉 Но очень важно понять, с каким именно множеством вы работаете. Позже узнаете, почему.
Конечно, если наше математическое высказывание (формула) относится к маленькому множеству чисел, то гораздо легче просто высчитать ответ в уме или ввести данные в Wolfram – на этом всё, пускайте титры.
Например, вы, убивая время в интернете, где-то прочли, что сумма положительных натуральных чисел от 1 до n, то есть, 1+2+3+., вычисляется по формуле  ..+n
..+nn*(n+1)/2. Допустим, у вас проблемы с доверием, и вы хотите проверить, работает ли эта формула на самом деле, или это просто часть всемирного заговора?
Эту формулу можно применить к маленьким множествам, так как вы можете легко вычислить сумму чисел от 1 до 10, от 1 до 20, от 1 до 50, а если вас замучила бессонница, то попробуйте посчитать не овечек, а сумму чисел от 1 до 100. Помогает. Иногда.
Потом остается только подставить значения в формулу и сравнить.
Но если мы говорим о множестве с большим количеством элементов или о бесконечном множестве, то именно тут и пригодится индукция.
Проверка высказывания для наименьшего числа – это начало индукции.
Мы начинаем с базиса (база, base case) – нам дано наименьшее число, для которого нужно проверить истинность высказывания. Обычно это 1, но могут быть и другие варианты, которые обязательно указываются в условии. Например, можно начать с 4 или 5. Это не так важно. Но иногда этот базис не указывается эксплицитно. В этом случае вы начинаете с наименьшего числа вашего множества. Поэтому важно знать, с чего начать. Уточните, включается ноль в N или нет. В примерах в этой статье множество натуральных чисел начинается с единицы.
Затем мы утверждаем, что выражение истинно для любого n>=1. Мы не знаем этого наверняка, конечно. Но мы предполагаем, что если утверждение истинно для любого n, то оно будет верно и для n+1. Это называется шагом индукции. А так как n – это любое число из множества N, то мы можем проверить математическое высказывание для очень-очень-очень больших чисел.
Итак, вернёмся к нашей формуле вычисления суммы чисел от 1 до n.
Начало индукции: проверяем, верна ли формула для n=1: n*(n+1)/2=> 1*(1+1)/2=1*(2)/2=1
Так как сумма чисел от 1 до 1 равна 1, то высказывание истинно для n=1.
Затем мы утверждаем, что математическое высказывание истинно для любого n>=1. То есть 1+2+3+...+n = n*(n+1)/2.
Переходим к шагу индукции – если высказывание верно для n, то оно истинно и для n + 1. 1+2+3+...+n + (n+1) = (n+1)(n+1 + 1)/2.
Левая часть уравнения – это сумма чисел от 1 до n+1. Мы заменили все n в правой части на n+1, так как мы больше не рассматриваем n, а доказываем, что высказывание истинно именно для n+1.
Если вы помните, то сумма чисел от 1 до n вычисляется по формуле n*(n+1)/2. Поэтому часть выражения справа (а именно 1+2+3+...+n) можно заменить на n*(n+1)/2.
У нас остается n*(n+1)/2 + (n+1) = (n+1)(n+1 + 1)/2. Нам нужно доказать или опровергнуть равенство этих двух выражений.
Всё, что происходит дальше – это чистая алгебра. Нам надо всего лишь упростить эти выражения, так как немного трудно что-либо сказать об их равенстве, просто посмотрев на них. Даже если вы своими эльфийскими глазами можете рассмотреть, чему равны обе части, с вас всё равно потребуют формальное доказательство.
Немного упрощаем правую сторону:
n*(n+1)/2 + (n+1) = (n+1)(n+2)/2
Затем раскрываем скобки справа (умножаем n*(n+1)) и слева (умножаем (n+1)(n+2)).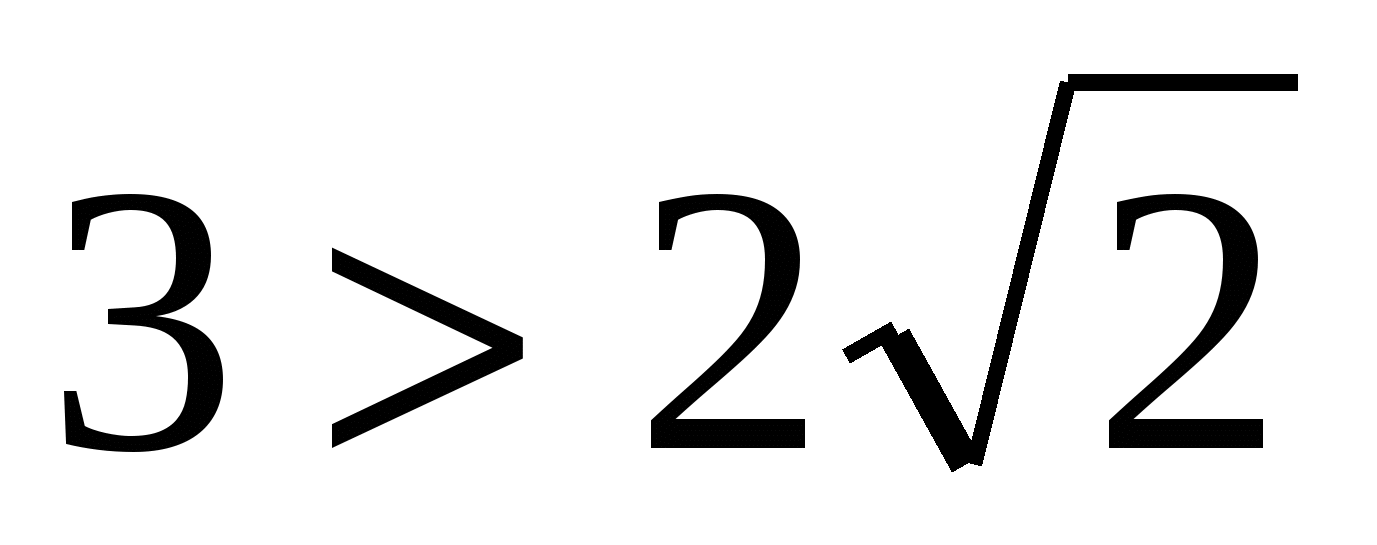 2 + 2n + 1
2 + 2n + 1
Правая и левая часть уравнения совпадают. Значит, математическое высказывание истинно.
Математическую индукцию еще сравнивают с эффектом домино. Если косточки домино выстроены в ряд, и какая-то упадёт, приложившись к следующей и опрокинув её, то та, в свою очередь, опрокинет следующую, и за ней последуют все остальные. А если мы опрокинем первую косточку, то упадёт весь ряд.
В индукции, если высказывание истинно для натурального числа, с которого мы начинаем, например, 8, то оно истинно для 9. Если оно истинно для 9, то оно верно для 10. И так далее. До бесконечности. Это мы и пытаемся доказать. Есть задачи, которые имею несколько базисов. Например, вам надо проверить какое-то высказывание для n=4, n=5, n=6 в начале индукции.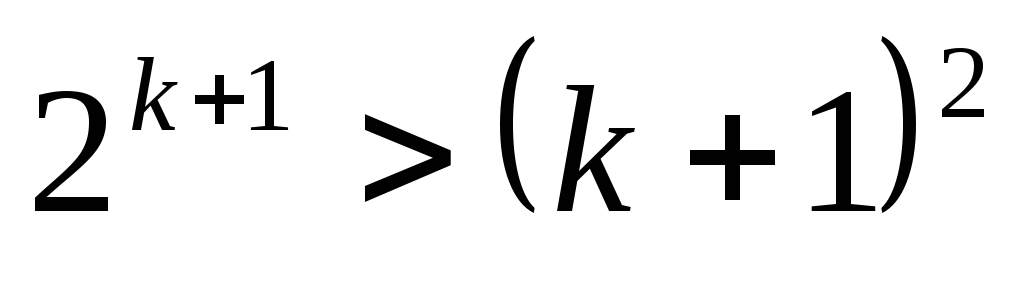 Попадаются и задачи, где база дана в рекурсивной форме.
Попадаются и задачи, где база дана в рекурсивной форме.
Потренируйтесь на других примерах. Основным скилом для решения подобных задач является умение находить паттерны. Вы также должны понимать, что именно вы хотите доказать? Что описывает формула? Очень важно знать и уметь применять некоторые формулы, которые помогут вам упростить выражения. Например, те же самые формулы сокращённого умножения. Они очень часто встречаются в математической индукции. Очень многие допускают ошибки именно в конце, когда надо подключить свои знания алгебры.
Помните, что математическая индукция применяется только к высказываниям с натуральными числам. Ваш n не может равняться -10 или 8.5. Дискриминация по отношению к действительным и комплексным числам? Вполне может быть.
Для чего же это всё?
Во-первых, решая подобные задачи, вы развиваете логику и алгоритмическое мышление, что играет не последнюю роль в программировании. Вы учитесь распознавать всякого рода паттерны.
Вы учитесь распознавать всякого рода паттерны.
Во-вторых, если вы внимательнее посмотрите на принцип математической индукции, вы заметите, что это чистейшая рекурсия. Предполагаю, что вы знакомы с рекурсией, если вы хотя бы немного программируете. Есть base case – условие завершения алгоритма. Также есть правило перехода. И чтобы проверить высказывание для n, нужно решить что-то для n-1, а потом с помощью алгебры дойти до n.
Рекурсию можно или любить, или люто ненавидеть. Но если ее понять и правильно использовать, она может сделать код элегантнее.
Математическая индукция в математике с примерами решения и образцами выполнения
Оглавление:
Дедукцией называется переход от общего утверждения к частному. Приведем пример.
Площадь всякого треугольника равна
это утверждение общее.
От этого общего утверждения можно сделать переход к частному утверждению, например такому:
площадь равностороннего треугольника равна
т.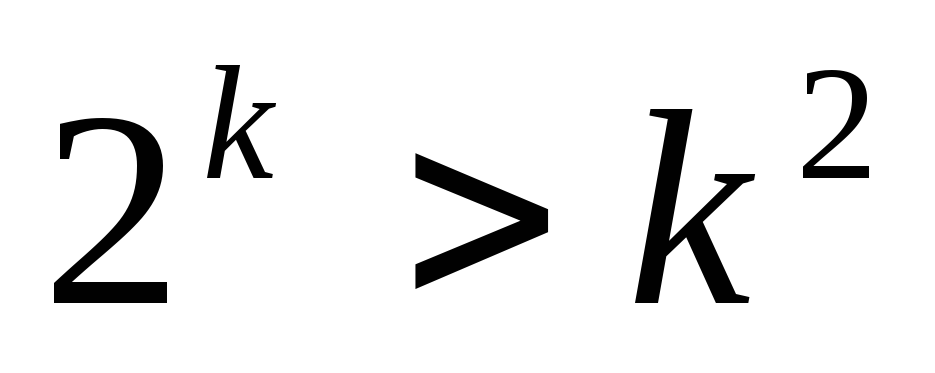 е. равна , где а — длина стороны равностороннего треугольника.
е. равна , где а — длина стороны равностороннего треугольника.
Дедукция есть одна из форм умозаключения. (Дедукция происходит от латинского слова «deductio» — выведение.)
Индукцией называется переход от частного утверждения к общему. Индукция есть также одна из форм умозаключения, применяя которую от знания отдельного факта идут к обобщению, к общему положению. (Индукция происходит от латинского слова «inductio» — наведение, побуждение.)
Все формы умозаключения связаны между собой, а потому связаны между собой дедукция и индукция. Одна дедукция (или одна индукция) никогда не может обеспечить познания объективной действительности.
Легкомысленное применение индукции может привести к неправильным выводам. Приведем пример.
Рассмотрим выражение
Подставив в это выражение вместо п нуль, получим простое число 41. Подставив вместо п единицу, получим 43, т. е. опять простое число. Продолжая подставлять вместо п последовательно 2; 3; 4; 5; 6; 7; 8; 9; 10; 11, получим соответственно 47, 53; 61; 71; 83; 97; 113; 131 151; 173, т. е. опять же числа простые. Можем ли мы теперь быть уверенными в справедливости такого утверждения:
е. опять же числа простые. Можем ли мы теперь быть уверенными в справедливости такого утверждения:
«Выражение принимает значение, равное простому числу при любом целом положительном значении буквы п»?
Быть уверенными в справедливости этого утверждения мы не можем, так как полученные выше результаты не являются достаточным основанием для такого утверждения. Они являются лишь основанием для предположения о верности этого утверждения. В действительности более полное исследование выражения показывает, что значение этого выражения не при всяком целом значении п является простым числом. Например, при п= 40 получается число 1681, которое уже не является простым. (Число 1681 делится на 41.)
Этот пример показывает, что утверждение может быть верным при одних значениях натурального числа п и неверным при других.
Математическая индукция есть весьма общий метод, позволяющий во многих случаях исследовать законность перехода от частного утверждения к утверждению общему.
Принцип математической индукции можно сформулировать следующим образом.
Теорема о математической индукцииПусть S(n)—некоторое утверждение, в формулировку которого входнт натуральное число п. Пусть, во-первых, утверждение справедливо и пусть, во-вторых, из справедливости утверждения S(k), где k есть тоже любое натуральное число, не меньшее следует справедливость утверждения S(k + 1). Тогда утверждение S(n) справедливо при любом
Доказательство:
Допустим, что утверждение S(n) не справедливо при некотором т. е. что утверждение S(N) ложно. Тогда должно быть ложным и утверждение S(N — 1), так как в противном случае из справедливости S(N — 1) по второму условию теоремы следовала бы справедливость и утверждения S(N). Точно так же убеждаемся, что из ложности S(N— 1) следует ложность S(N — 2), а из этого ложность
S(N —3) и т. д.
д.
Таким образом (каким бы большим ни было число N), мы рано или поздно, отнимая от этого числа по единице, дойдем до числа и получим, что утверждение ложно, что противоречит первому условию теоремы. Полученное противоречие доказывает справедливость теоремы.
Приведенное доказательство теоремы о математической индукции может показаться некоторым читателям труднопонимаемым. Поэтому ниже приводится несколько упрощенная схема метода математической индукции.
Если в утверждении некоторой теоремы фигурирует целое положительное число п и если из справедливости этой теоремы для какого угодно частного значения п = k следует справедливость ее для значения k + 1, то, коль скоро это утверждение справедливо для п — 1, оно будет справедливо для любого целого положительного числа п.
Здесь дело обстоит так. Сначала мы убеждаемся в том, что теорема верна при п = 1. Затем, предполагая, что она верна для какого угодно частного значения п = k, доказываем ее справедливость для п = k + 1.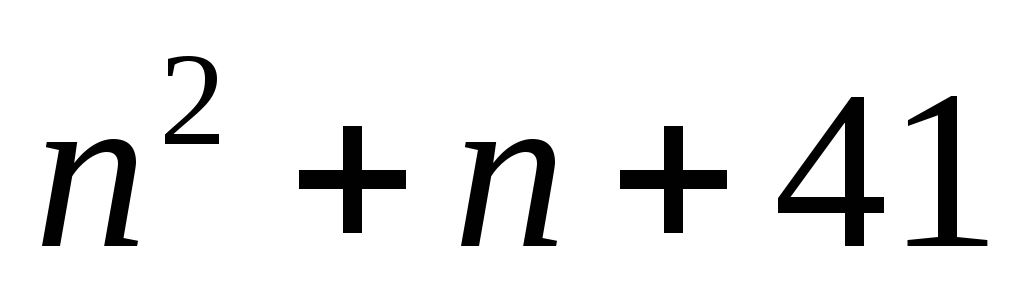
После этого рассуждаем так: поскольку теорема верна для п = 1, значит, она будет верной и для п — 1 + 1, т. е. для п = 2. Поскольку она верна для п = 2, она будет верной и для п = 2 + 1, т. е. для п = 3 и т. д.
Применение метода математической индукции
Примеры:
1. Доказать, что
Этой формулой утверждается следующее: для того чтобы найти сумму кубов нескольких первых натуральных чисел, надо последнее из них умножить на число, большее его на единицу, полученное произведение разделить на 2 и возвести в квадрат.
Доказательство:
1. При п = 1 утверждение справедливо,
так как
2. Допустим, что утверждение справедливо при п = k, т. е
Тогда
Утверждение оказалось верным и для п =k+1. Следовательно, теорема верна при всяком целом положительном значении п.
Доказать, что
Доказательство:
1.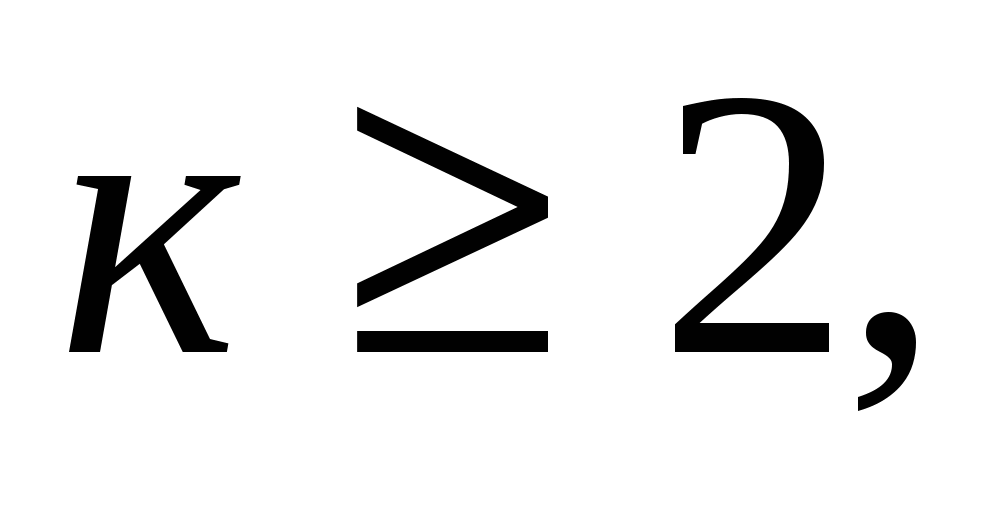 При п = 1 утверждение справедливо, так как
При п = 1 утверждение справедливо, так как
2. Допустим, что утверждение справедливо при п = k, т. е.
Тогда
Утверждение оказалось верным и для п = k + 1. Следовательно, формула верна при всяком целом положительном значении п.
3. Доказать, что при п > 1
Доказательство:
При п = 2 утверждение справедливо.
Действительно,
Итак, оказалось, что
Но а потому
Следовательно,
Пусть
Докажем, что тогда будет справедливым и неравенство:
К обеим частям неравенства (I) прибавим по . Тогда получим:
или
или
Но Поэтому и подавно
что и требовалось доказать,
Теперь мы видим, что утверждение (А) оказалось верным и для n=k+1. Следовательно, это утверждение справедливо при всяком целом положительном значении n, большем двух.
Существует очень много и других теорем, которые успешно доказываются с помощью метода математической индукции. Некоторые из таких теорем встретятся нам в последующих главах.
Некоторые из таких теорем встретятся нам в последующих главах.
Доказательство неравенства
Иногда приходится применять метод математической индукции в несколько усложненной форме. Покажем это на примере. Пусть требуется доказать следующее неравенство:
где — положительные числа.
(Выражение называется средним геометрическим чисел , выражение — их средним арифметическим.)
Во-первых, покажем справедливость неравенства (А) при n = 2.
Очевидно,что
Отсюда
Значит, при n = 2 неравенство (А) справедливо. Теперь докажем следующую лемму.
Лемма:
Если неравенство (А) верно при п = k, то оно будет верно при n=2k.
Доказательство:
Пользуясь свойствами арифметических корней, получим:
Но
(Мы здесь воспользовались доказанным выше неравенством:
Следовательно,
Поскольку мы предположили неравенство (А) верным при n = k, постольку
Учитывая эти два последних неравенства и неравенство (В), получим:
Итак, предполагая, что неравенство (А) справедливо при п = 2k, мы доказали, что оно будет справедливым и при п = 2k.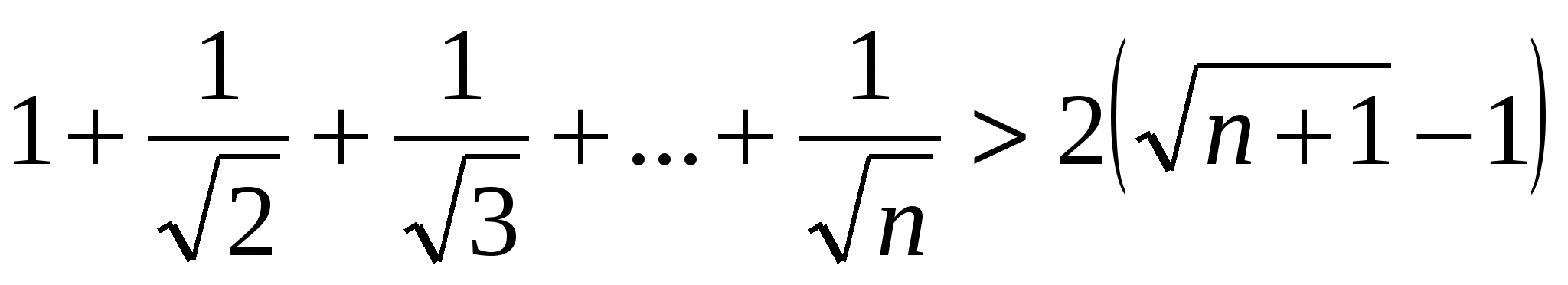 Но ранее было доказано, что неравенство (А) справедливо при п = 2. Следовательно, оно будет справедливым и при п = 4,8,16, 32,…, т. е. при где m — любое натуральное число.
Но ранее было доказано, что неравенство (А) справедливо при п = 2. Следовательно, оно будет справедливым и при п = 4,8,16, 32,…, т. е. при где m — любое натуральное число.
Теперь перейдем к доказательству неравенства (А) для любого натурального числа п.
Пусть п есть любое натуральное число. Если окажется, что п есть целая степень числа 2, то для такого п, как это уже было доказано, неравенство (А) справедливо. Если же п не есть целая степень числа 2, то к n всегда можно прибавить такое число q, что п+ q станет целой степенью числа 2. Итак, положим, что
Тогда получим неравенство:
справедливое при любых положительных где
Это следует из того, что число п + q есть целая степень числа 2. Положим, что
Тогда получим последовательно:
или
и, наконец,
что и требовалось доказать.
Значит, неравенство (А) справедливо при всяком натуральном п.
Метод доказательства, называемый методом математической индукции, основан на следующем принципе, который является одной из аксиом арифметики натуральных чисел.
Предложение , зависящее от натуральной переменной , считается истинным для всех , если выполнены следующие два условия:
а) предложение истинно для ;
б) из предположения, что истинно для (где — любое натуральное число), следует, что оно истинно и для следующего значения, т.е. для .
Этот принцип называется принципом математической индукции.
Под методом математической индукции понимают следующий способ доказательства: во-первых, проверяют истинность высказывания , и, во-вторых, предположив истинность высказывания , пытаются доказать, что истинно высказывание . Если это удается доказать (при любом натуральном ), то предложение считается истинным для всех значений .
Пример:
Методом математической индукции доказать равенство
Доказательство:
При равенство (1) является верным . Нужно доказать, что из предположения о том, что является верным равенство (1), следует справедливость равенства
Нужно доказать, что из предположения о том, что является верным равенство (1), следует справедливость равенства
полученного из (1) заменой на
Прибавляя к обеим частям (1) слагаемое , имеем
Преобразуя правую часть (3), получаем
Таким образом, равенство (2) является верным, и поэтому формула (1) доказана для любого
Дадим другое доказательство формулы (1), используя символ которым обозначается сумма т.е. Воспользуемся тождеством
Полагая в (4) и складывая получаемые равенства, находим
Левая часть (5) равна а Поэтому из (5) получаем
откуда следует равенство (1).
Пример:
Доказать, что для любых и при любом справедлива формула бинома Ньютона
где
Правую часть формулы (6) называют разложением бинома, числа — биномиальными коэффициентами, слагаемое членом разложения бинома.
Доказательство. Воспользуемся методом математической индукции. При формула (6) верна, так как ее правая часть равна левой:
Предполагая справедливым равенство (6), докажем, что верна формула
Умножая обе части равенства (6) на получаем
где
Следовательно,
Сравнивая правые части равенств (8) и (9), заключаем, что для доказательства формулы (8) достаточно показать, что
Используя (7), находим
Поэтому
Равенство (10) доказано и поэтому справедливо равенство (8). Итак, формула (6) верна при любом . Отметим, что
Итак, формула (6) верна при любом . Отметим, что
т.е.
Поэтому формулу (6) можно записать в виде
Из (11) следует, что .
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
§ 6.
 Математическая индукция. Введение в логику и научный метод § 6. Математическая индукция. Введение в логику и научный метод
Математическая индукция. Введение в логику и научный метод § 6. Математическая индукция. Введение в логику и научный методВикиЧтение
Введение в логику и научный метод
Коэн Моррис
Содержание
§ 6. Математическая индукция
«Но не забываете ли вы, что в математике также имеет место индукция?» – может возразить читатель. «Вы описывали математику как типичную дедуктивную науку, в которой все теоремы являются необходимыми следствиями аксиом. Однако вы ведь не упустите из вида такой метод доказательства, как математическая индукция?».
Читатель, без сомнения, находится в ловушке слов. Действительно, существует метод математической индукции, однако это название не вполне удачно, поскольку подразумевает некое сходство с методом проведения экспериментов и подтверждения гипотез, использующимся в естественных науках. Однако такого сходства на самом деле нет, а математическая индукция является чисто доказательным методом.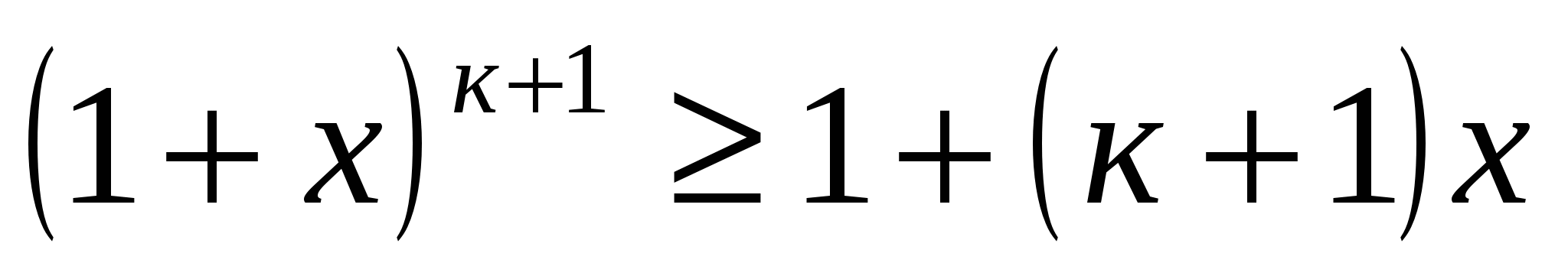
Однако следует ли еще раз предостерегать читателя от распространенной ошибки спутывания временного порядка, в котором мы обнаруживаем те или иные суждения науки, и порядка их логической зависимости? Любой, кто когда-либо решал задачу по геометрии, знает, что существует подготовительная «стадия прощупывания», во время которой мы строим догадки, размышляем, строим вспомогательные линии и т. д. до тех пор, пока мы, как говорится, не наткнемся на доказательство. При этом никто не станет спутывать данную предварительную стадию, какой бы существенной она ни была, с достигаемым в итоге доказательством. Такая начальная стадия «прощупывания», действительно, обладает большим сходством с тем, как люди осуществляют исследования в какой бы то ни было сфере. Процесс проверки путем догадок характерен и для математического исследования, так же как и для исследования в естественных науках.
Принцип математической индукции может быть сформулирован следующим образом: если некоторое свойство принадлежит числу 1 и если, когда оно принадлежит числу п, можно доказать, что оно принадлежит и п + 1, то оно принадлежит всем числам. Докажем с помощью данного принципа следующую теорему для всех целочисленных значений п:
Докажем с помощью данного принципа следующую теорему для всех целочисленных значений п:
1 + 3 + 5 + 7 +… (2п – 1) = n2.
Очевидно, что это истинно для rt = 1. Теперь покажем, что, если то же самое имеет место и для числа п, то оно имеет место и для (п + 1).
a. 1 + 3 + 5 +… (2 n – 1) = n2.
Прибавив (2 n – 1) + 2 или (2 n + 1) к обеим сторонам уравнения, мы получим:
b. 1 + 3 + 5 +… (2 n – 1) + (2 n + 1) = n2 + (2 n + 1) = (n +1)2.
Однако Ь имеет ту же форму, что и а. Таким образом, мы показали, что если теорема истинна для числа п, то она истинна и для (n + 1). Она истинна для n = 1. Следовательно, она истинна для n = 1 + 1, т. е. для 2; следовательно, она истинна для n = 2 + 1, т. е. для 3, и т. д. для каждого целого числа, которого можно достигнуть путем последовательного прибавления 1. Таким образом, получившееся доказательство является абсолютно строгим, дедуктивным и всецело формальным. В нем нет никакой апелляции к эксперименту. А принцип математической индукции, как показывают современные исследователи, является частью самого значения конечных, или «индуктивных», чисел.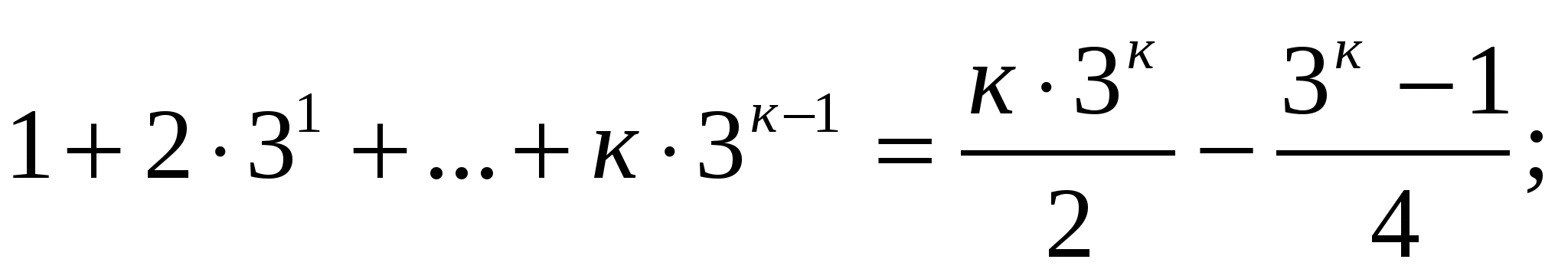
Данный текст является ознакомительным фрагментом.
7.5. Математическая модель внутрифирменного СТ-управления
7.5. Математическая модель внутрифирменного СТ-управления * Еще во времена плановой социалистической экономики ставилась задача интеграции производства и управления. Так, в основных положениях коренной перестройки управления экономикой, утвержденных июньским (1987 г.)
3.4. Математическая структура как модель актуальной действительности
3.4. Математическая структура как модель актуальной действительности
Что такое познание? Полезно вспомнить высказывания В.И. Ленина, записанные им по поводу учения о понятии в «Науке логики» Гегеля: «Познание есть отражение человеком природы. Но это не простое, не
Но это не простое, не
§ 3. НАУЧНАЯ ИНДУКЦИЯ
§ 3. НАУЧНАЯ ИНДУКЦИЯ Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.В зависимости от способов исследования различают: (1) индукцию методом отбора (селекции) и (2) индукцию методом
Глава V. Индукция
Глава V. Индукция Другой, кроме дедукции, наиболее общий тип умозаключений — это индукция. В ней заключено глубокое своеобразие, и она находится в тесных взаимоотношениях с дедукцией. В реальной практике мышления ее сущность проявляется тоже в многообразных
2. Полная индукция
2. Полная индукция
Полной индукция получается в том случае, если, во-первых, исследованы все элементы класса предметов и, во-вторых, если установлено, что каждому из них принадлежит (или не принадлежит) одно и то же общее свойство (отношение). В простейшем случае это выглядит
В простейшем случае это выглядит
3. Неполная индукция
3. Неполная индукция Неполной индукцией называется умозаключение обо всем классе предметов в целом на основе изучения лишь части предметов данного класса.Формула неполной индукции:S1 — PS2 — P…..Sn — PS1, S2 … Sn … составляют часть класса S. Следовательно, все S — Р.В
Глава V. Индукция
Глава V. Индукция 1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется,
1. Индукция как тип умозаключения
1. Индукция как тип умозаключения
Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода:
«Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется, была мысль связать
Сначала у него, как кажется, была мысль связать
Глава VI. Обобщенная, или математическая, логика
Глава VI. Обобщенная, или математическая, логика § 1. Логика как наука о типах порядка В предыдущих главах мы видели, что обоснованность доказательства зависит не от истинности или ложности посылок, а от их формы, или структуры. В качестве фундаментальной задачи логики мы
Глава VI. Обобщенная или математическая логика
Глава VI. Обобщенная или математическая логика 1. Укажите, какое отношение имеет место в каждом из следующих примеров: транзитивное, интранзитивное, симметричное, асимметричное, одно?однозначное, одно?многозначное или много?многозначное.a. Он самый низкорослый в
НЕПОЛНАЯ ИНДУКЦИЯ
НЕПОЛНАЯ ИНДУКЦИЯ
Индуктивное умозаключение, результатом которого является общий вывод обо всем классе предметов на основании знания лишь некоторых предметов данного класса, принято называть неполной или популярной индукцией. Например, из того, что инертные газы
Например, из того, что инертные газы
Математическая модель человека
Математическая модель человека В начале XVIII века стала очевидной победа механистического мышления. Человека понимали, как замечательную машину, сделанную из чудных деталей, созданных, конечно, Богом, — несомненное чудо, идеальный и точный инструмент.Декарт считал себя
Математическая интуиция
Математическая интуиция Обратите внимание, что мы здесь сталкиваемся с одной примечательной особенностью. Часто думают, что теорема Геделя имеет, в некотором роде, отрицательный смысл, поскольку она указывает на принципиальные ограничения в применении формальных
Популярная индукция
Популярная индукция
Популярная, она же народная индукция — это индукция через перечисление. Та самая, про которую мы говорили вчера. «Если три моих знакомых еврея хитры, то и все евреи хитры».Популярная индукция — одно из любимых орудий демагогов. Например:
Василий
Та самая, про которую мы говорили вчера. «Если три моих знакомых еврея хитры, то и все евреи хитры».Популярная индукция — одно из любимых орудий демагогов. Например:
Василий
Научная индукция
Научная индукция Научная индукция работает иначе. Научная индукция объясняет свои выводы. Вернёмся к нашему примеру с хитрыми евреями. Научная индукция для этого примера может выглядеть так:«Мозг этих трёх евреев имеет особый отдел мозга, отвечающий за хитрость, и этот
Индукция (Induction)
Индукция (Induction) Вид доказательства, в классическом понимании определяемый как переход от частного к общему, или от фактов к закону. Тем самым противостоит дедукции, которая обычно идет от общего к частному, от принципа к следствиям.Нетрудно догадаться, что индукция,
Шень А.
 Математическая индукция
Математическая индукция- формат pdf
- размер 225.68 КБ
- добавлен 21 ноября 2010 г.
М.: МЦНМО, 2007. — 32 с. 3-е изд., дополн.
В брошюре рассказывается (для школьников 7 — 11 классов) о методе
математической индукции на примере 46 задач, из которых 19 снабжены
подробными решениями. Предыдущее издание книги вышло в 2004 г.
Читать онлайн
Похожие разделы
- Академическая и специальная литература
- Математика
- Задачники и решебники
Смотрите также
- формат pdf
- размер 1.
 81 МБ
81 МБ - добавлен 23 октября 2010 г.
Московские математические регаты / Сост. А. Д. Блинков, Е. С. Горская, В. М. Гуровиц. М.: МЦНМО, 2007. 360 с. Математическая регата — соревнование для школьных команд, проводящееся ежегодно. В данном сборнике представлены материалы всех московских математических регат по 2005/06 учебный год. Приведены также правила проведения регаты, описана технология ее проведения и особенности подготовки. В приложение включены материалы школьных математически…
- формат djvu
- размер 923.8 КБ
- добавлен 15 октября 2011 г.
М.: Физико-математическая школа № 1180 при MГТУ имени Н.Э. Баумана. Специализированный учебно-научный центр. 1997, 29 с. Целью настоящего сборника является ознакомление учащихся с уровнем требований, предъявляемых на вступительных экзаменах в СУНЦ при МГТУ им. Н.Э. Баумана и порядком их проведения. В сборнике приведены типовые варианты экзаменационных заданий по математике.
Н.Э. Баумана и порядком их проведения. В сборнике приведены типовые варианты экзаменационных заданий по математике.
- формат djvu
- размер 2.14 МБ
- добавлен 11 февраля 2011 г.
12-е изд., стер. — М.: Мнемозина, 2010 — 224с. Учебник содержит завершающий теоретический материал курса алгебры основной общеобразовательной школы. Он базируется на принципиально новой концепции, ключевыми понятиями которой являются математический язык и математическая модель, а приоритетной содержательно-методической линией — функционально — графическая. Включено большое число примеров с детальными и обстоятельными решениями. Упражнения для сам…
- формат pdf
- размер 93.58 КБ
- добавлен 14 сентября 2011 г.
Всероссийская отраслевая физико-математическая олимпиада «Росатом» (до 2005 года олимпиада Минатома РФ) является традиционным мероприятием и имеет многолетний опыт проведения (проводится в существующем формате более 10 лет).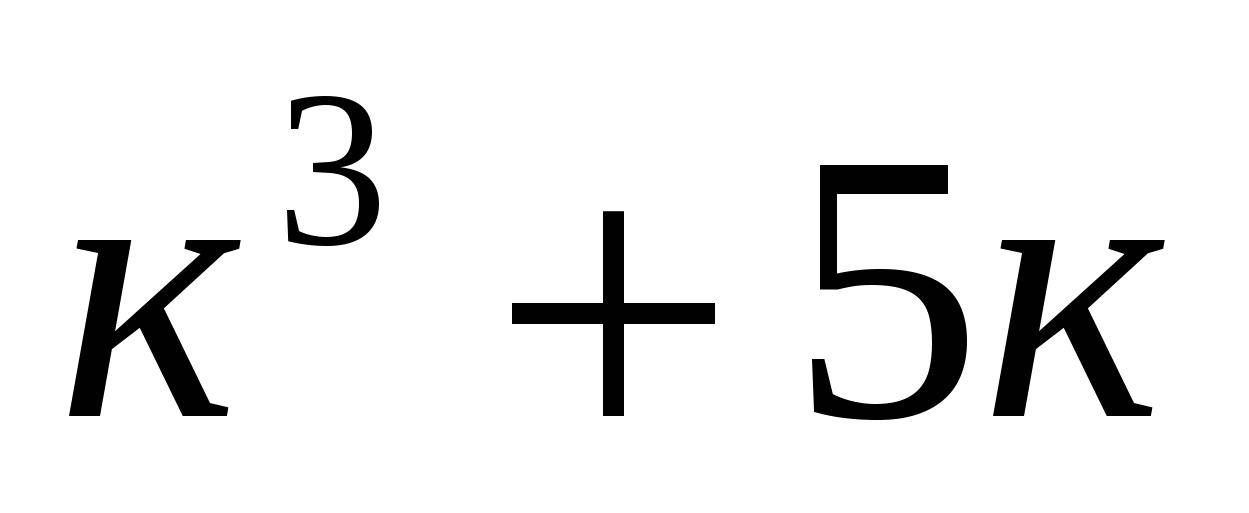 За истекший многолетний период олимпиада подтвердила статус Всероссийской олимпиады, которая позволяет выявить и поддержать наиболее способную молодежь страны и подготовить абитуриентов для поступления в ведущие технические в…
За истекший многолетний период олимпиада подтвердила статус Всероссийской олимпиады, которая позволяет выявить и поддержать наиболее способную молодежь страны и подготовить абитуриентов для поступления в ведущие технические в…
- формат djvu
- размер 2.84 МБ
- добавлен 20 ноября 2011 г.
Учеб. пособие. — М.: Изд-во «Наука», 1967. — 144 с. Книга рассчитана на учащихся старший классов средней школы, а также на студентов младших курсов. Книга состоит из двух частей: Индукция в арифметике и алгебре, где рассматриваются доказательства тождеств, тригонометрические и алгебраические задачи, задачи на доказательство неравенств, представлены доказательства некоторых теорем элементарной алгебры методом математической индукции, и индукция…
- формат pdf
- размер 907 КБ
- добавлен
07 октября 2010 г.

М.: Посев, 2003. 128 с. В книге широко представлены задачи по математике, предлагавшиеся школьникам 6-7 классов на занятиях математических кружков и олимпиадах. Основное ее содержание — классические арифметические задачи. Кроме них, есть геометрические задачи, требующие фантазии и изобретательности, и просто шутки. Книга предназначена для учащихся 6-7 классов, но будет интересна и полезна как более старшим, так и более младшим школьникам, а так…
- формат pdf
- размер 1.09 МБ
- добавлен 08 марта 2011 г.
М.: МЦНМО, 2000. — 272 с. Книга содержит учебные материалы, составлявшие содержание курса «математического анализа» в математическом классе 57 школы (выпуск 2000 года, класс «В»). В неё включены задачи вечерней математической школы и собеседований, задачи всех четырёх лет обучения (включая контрольные работы и экзамены), а также список тем лекций, читавшихся школьникам.
- формат pdf
- размер 201.25 КБ
- добавлен 21 ноября 2010 г.
М.: МЦНМО, 2005. — 24 с. Начиная с рассуждения Галилея о том, что скорость падения тела не может быть пропорциональна пройденному пути, мы приходим к определению логарифма как площади под гиперболой и экспоненты как обратной (к логарифму) функции. Брошюра написана по материалам лекции для школьников 10-11 классов, прочитанной автором по приглашению А. В. Спивака.
- формат pdf
- размер 871.74 КБ
- добавлен 08 октября 2010 г.
М.: МЦНМО, 2006. 72 с. Математики традиционно гордятся «математической строгостью», точностью и полнотой доказательств теорем на основе определений и аксиом. Насколько этот идеал достигнут в школьном курсе математики? Можно ли его достигнуть? В брошюре разбираются несколько вопросов школьного курса математики (в чём проблема, как её пытаются решить в школьных учебниках и как её можно было бы решать). Изложение рассчитано на любознательных школ…
Изложение рассчитано на любознательных школ…
- формат pdf
- размер 230.79 КБ
- добавлен 02 февраля 2012 г.
Александр Шень. Простые и составные числа. | М.: МЦНМО, 2005. | 16 с.: ил. В книге приведено доказательство «основной теоремы арифметики» о единственности раз- ложения целых чисел на простые множители, а также несколько доказательств бес- конечности множества простых чисел.
Метод математической индукции
Математическая индукция лежит в основе одного из самых распространенных методов математических доказательств. С его помощью можно доказать большую часть формул с натуральными числами n, например, формулу нахождения суммы первых членов прогрессии Sn=2a1+n-1d2·n, формулу бинома Ньютонаa+bn=Cn0·an·Cn1·an-1·b+…+Cnn-1·a·bn-1+Cnn·bn.
В первом пункте мы разберем основные понятия, потом рассмотрим основы самого метода, а затем расскажем, как с его помощью доказывать равенства и неравенства.
Понятия индукции и дедукции
Для начала рассмотрим, что такое вообще индукция и дедукция.
Определение 1Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному.
Например, у нас есть утверждение: 254 можно разделить на два нацело. Из него мы можем сделать множество выводов, среди которых будут как истинные, так и ложные. Например, утверждение, что все целые числа, которые имеют в конце цифру 4, могут делиться на два без остатка – истинное, а то, что любое число из трех знаков делится на 2 – ложное.
В целом можно сказать, что с помощью индуктивных рассуждений можно получить множество выводов из одного известного или очевидного рассуждения. Математическая индукция позволяет нам определить, насколько справедливы эти выводы.
Допустим, у нас есть последовательность чисел вида 11·2, 12·3, 13·4, 14·5,…, 1n(n+1), где n обозначает некоторое натуральное число. В таком случае при сложении первых элементов последовательности мы получим следующее:
S1=11·2=12, S2=11·2+12·3=23, S3=11·2+12·3+13·4=34,S4=11·2+12·3+13·4+14·5=45,. ..
..
Используя индукцию, можно сделать вывод, что Sn=nn+1. В третьей части мы докажем эту формулу.
В чем заключается метод математической индукции
В основе этого метода лежит одноименный принцип. Он формулируется так:
Определение 2Некое утверждение будет справедливым для натурального значения n тогда, когда 1) оно будет верно при n=1 и 2) из того, что это выражение справедливо для произвольного натурального n=k, следует, что оно будет верно и при n=k+1.
Применение метода математической индукции осуществляется в 3 этапа:
- Для начала мы проверяем верность исходного утверждения в случае произвольного натурального значения n (обычно проверка делается для единицы).
- После этого мы проверяем верность при n=k.
- И далее доказываем справедливость утверждения в случае, если n=k+1.
Как применять метод математической индукции при решении неравенств и уравнений
Возьмем пример, о котором мы говорили ранее.
Пример 1Докажите формулу Sn=11·2+ 12·3+.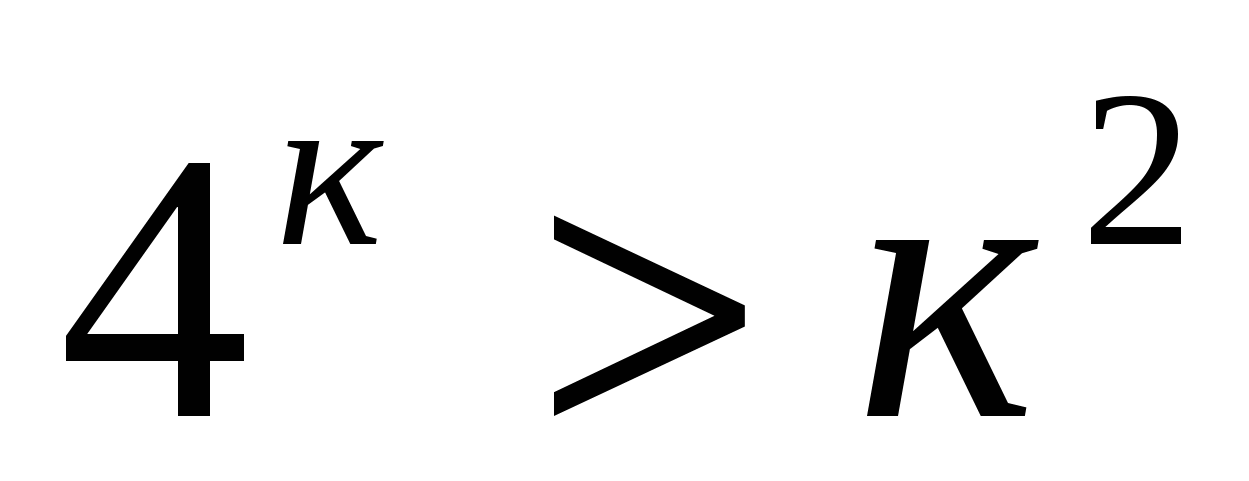 ..+1n(n+1)=nn+1.
..+1n(n+1)=nn+1.
Решение
Как мы уже знаем, для применения метода математической индукции надо выполнить три последовательных действия.
- Для начала проверяем, будет ли данное равенство справедливым при n, равном единице. Получаем S1=11·2=11+1=12. Здесь все верно.
- Далее делаем предположение, что формула Sk=kk+1 верна.
- В третьем шаге нам надо доказать, что Sk+1=k+1k+1+1=k+1k+2, основываясь на справедливости предыдущего равенства.
Мы можем представить k+1 в качестве суммы первых членов исходной последовательности и k+1:
Sk+1=Sk+1k+1(k+2)
Поскольку во втором действии мы получили, что Sk=kk+1, то можно записать следующее:
Sk+1=Sk+1k+1(k+2).
Теперь выполняем нужные преобразования. Нам потребуется выполнить приведение дроби к общему знаменателю, приведение подобных слагаемых, применить формулу сокращенного умножения и сократить то, что получилось:
Sk+1=Sk+1k+1(k+2)=kk+1+1k+1(k+2)==k(k+2)+1k+1(k+2)=k2+2k+1k+1(k+2)=(k+1)2k+1(k+2)=k+1k+2
Таким образом, мы доказали равенство в третьем пункте, выполнив все три шага метода математической индукции.
Ответ: предположение о формуле Sn=nn+1 является верным.
Возьмем более сложную задачу с тригонометрическими функциями.
Пример 2Приведите доказательство тождества cos2α·cos4α·…·cos2nα=sin 2n+1α2nsin 2α.
Решение
Как мы помним, первым шагом должна быть проверка верности равенства при n, равном единице. Чтобы это выяснить, нам надо вспомнить основные тригонометрические формулы.
cos 21=cos 2αsin 21+1α21sin 2α=sin 4α2sin 2α=2sin 2α·cos 2α2sin 2α=cos 2α
Следовательно, при n, равном единице, тождество будет верным.
Теперь предположим, что его справедливость сохранится при n=k, т.е. будет верно, что cos 2α·cos 4α·…·cos 2kα=sin 2k+1α2ksin 2α.
Доказываем равенство cos 2α·cos 4α·…·cos 2k+1α=sin 2k+2α2k+1sin 2α для случая, когда n=k+1, взяв за основу предыдущее предположение.
Согласно тригонометрической формуле,
sin 2k+1α·cos 2k+1α==12(sin(2k+1α+2k+1α)+sin(2k+1α-2k+1α))==12sin(2·2k+1α)+sin 0=12sin 2k+2α
Следовательно,
cos 2α·cos 4α·. ..·cos 2k+1α==cos 2α·cos 4α·…·cos 2kα·cos 2k+1α==sin 2k+1α2k sin 2α·cos 2k+1α=12·sin 2k+1α2ksin 2α=sin 2k+2α2k+1sin 2α
..·cos 2k+1α==cos 2α·cos 4α·…·cos 2kα·cos 2k+1α==sin 2k+1α2k sin 2α·cos 2k+1α=12·sin 2k+1α2ksin 2α=sin 2k+2α2k+1sin 2α
Ответ: На этом тождество можно считать доказанным. Мы успешно применили для этого метод математической индукции. Точно так же мы можем доказать справедливость формулы бинома Ньютона.
Пример решения задачи на доказательство неравенства с применением этого метода мы привели в статье о методе наименьших квадратов. Прочтите тот пункт, в котором выводятся формулы для нахождения коэффициентов аппроксимации.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Медикаментозное лечение (МАТ) | САМХСА
Узнайте, как медикаментозное лечение (МПТ) используется для лечения расстройств, связанных с употреблением психоактивных веществ, а также для поддержания выздоровления и предотвращения передозировки.
Медикаментозное лечение (МПТ) — это использование медикаментов в сочетании с консультированием и поведенческой терапией для обеспечения комплексного подхода к лечению расстройств, связанных с употреблением психоактивных веществ. Лекарства, используемые в ОЗТ, одобрены Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA), а программы ОЗТ разработаны с учетом клинических требований и адаптированы для удовлетворения потребностей каждого пациента.
Исследования показывают, что сочетание лекарств и терапии может успешно лечить эти расстройства, а некоторым людям, борющимся с зависимостью, МПТ может способствовать выздоровлению. MAT также используется для предотвращения или уменьшения передозировки опиоидов.
Узнайте о многих расстройствах, связанных с употреблением психоактивных веществ, для лечения которых разработана программа MAT.
МАТ в основном используется для лечения зависимости от опиоидов, таких как героин, и отпускаемых по рецепту болеутоляющих средств, содержащих опиаты. Назначенное лекарство нормализует химический состав мозга, блокирует эйфорические эффекты алкоголя и опиоидов, снимает физиологическую тягу и нормализует функции организма без негативного и эйфорического воздействия употребляемого вещества.
Назначенное лекарство нормализует химический состав мозга, блокирует эйфорические эффекты алкоголя и опиоидов, снимает физиологическую тягу и нормализует функции организма без негативного и эйфорического воздействия употребляемого вещества.
Эффективность МПТ
По оценкам, в 2018 г. около 2 миллионов человек страдали расстройством, связанным с употреблением опиоидов, включая рецептурные обезболивающие, содержащие опиаты и героин.
МПТ оказалась клинически эффективной и значительно снизила потребность в стационарных услугах по дезинтоксикации для этих лиц. MAT предлагает более комплексную, индивидуально подобранную программу медикаментозной и поведенческой терапии, отвечающую потребностям большинства пациентов.
Конечной целью ОЗТ является полное выздоровление, включая способность вести самостоятельную жизнь. Было показано, что этот подход к лечению:
- Повышение выживаемости пациентов
- Увеличить удержание при лечении
- Снижение незаконного употребления опиатов и другой преступной деятельности среди людей с расстройствами, связанными с употреблением психоактивных веществ
- Повышение способности пациентов получить и сохранить работу
- Улучшение исходов родов у беременных женщин с расстройствами, связанными с употреблением психоактивных веществ
Исследования также показывают, что эти лекарства и методы лечения могут способствовать снижению риска заражения ВИЧ или гепатитом С за счет снижения вероятности рецидива. Узнайте больше о злоупотреблении психоактивными веществами и о том, как это связано с ВИЧ, СПИДом и вирусным гепатитом.
Узнайте больше о злоупотреблении психоактивными веществами и о том, как это связано с ВИЧ, СПИДом и вирусным гепатитом.
Узнайте больше о сопутствующих заболеваниях и других состояниях здоровья.
Лекарства для ЗГТ
FDA одобрило несколько различных препаратов для лечения расстройств, связанных с употреблением алкоголя и опиоидов. Лекарства для ЗГТ облегчают симптомы отмены и психологические пристрастия, вызывающие химический дисбаланс в организме. Лекарства, используемые для МПТ, являются вариантами лечения, основанными на фактических данных, и не просто заменяют один препарат другим.
Лекарства от алкогольной зависимости
Акампросат, дисульфирам и налтрексон являются наиболее распространенными препаратами, используемыми для лечения расстройств, связанных с употреблением алкоголя. Они не излечивают расстройство, но наиболее эффективны у людей, которые участвуют в программе МПТ. Узнайте больше о влиянии злоупотребления алкоголем.
Узнайте больше о МПТ при расстройствах, связанных с употреблением алкоголя, и просмотрите «Лекарства для лечения расстройств, связанных с употреблением алкоголя: краткое руководство», 2015 г.
Лекарства от опиоидной зависимости
Бупренорфин, метадон и налтрексон используются для лечения расстройств, связанных с употреблением опиоидов, опиоидов короткого действия, таких как героин, морфин и кодеин, а также полусинтетических опиоидов, таких как оксикодон и гидрокодон. Эти препараты МАТ безопасны для использования в течение месяцев, лет или даже на протяжении всей жизни. Как и с любым лекарством, проконсультируйтесь с врачом перед прекращением использования.
Узнайте больше о МПТ при расстройствах, связанных с употреблением опиоидов.
Препарат для предотвращения передозировки опиоидами
Налоксон используется для предотвращения передозировки опиоидов путем устранения токсических эффектов передозировки. По данным Всемирной организации здравоохранения (ВОЗ), налоксон является одним из ряда лекарств, которые считаются необходимыми для функционирования системы здравоохранения.
Лекарства MAT и безопасность детей
Важно помнить, что если лекарства разрешено хранить дома, они должны быть заперты в безопасном месте, недоступном для детей. Метадон в жидкой форме окрашен и иногда его принимают за безалкогольный напиток. Дети, принимающие лекарства, используемые при МПТ, могут получить передозировку и умереть.
Метадон в жидкой форме окрашен и иногда его принимают за безалкогольный напиток. Дети, принимающие лекарства, используемые при МПТ, могут получить передозировку и умереть.
Find MAT Treatment
MAT Лекарства вводятся, выдаются и назначаются в различных учреждениях, таких как аккредитованная и сертифицированная SAMHSA программа лечения опиоидов (OTP) или сертифицированные практикующие врачи, в зависимости от лекарства.
- Каталог программ лечения опиоидов
- Поиск услуг по лечению поведенческих заболеваний SAMHSA
- Поиск врача по лечению бупренорфином SAMHSA
- Национальная горячая линия SAMHSA; Звоните: 1-800-662-ПОМОЩЬ (4357); Текст: 435748
- Поиск лечения от наркозависимости (FindTreatment.gov)
ОЗТ и права пациентов
SAMHSA выпустила брошюру, предназначенную для помощи пациентам с ОЗТ, а также для обучения и информирования других (PDF | 415 КБ). В соответствии с Положением о конфиденциальности, 42 Свода федеральных правил (CFR) 2, личная информация о состоянии здоровья, связанная с употреблением психоактивных веществ и лечением алкоголизма, должна обрабатываться с более высокой степенью конфиденциальности, чем другая медицинская информация.
Свяжитесь с нами
Для получения информации об отказе от бупренорфина обращайтесь в Центр лечения злоупотребления психоактивными веществами (CSAT) SAMHSA по телефону 866-BUP-CSAT (866-287-2728) или по электронной почте [email protected].
Для получения информации о другом медикаментозном лечении (MAT) или сертификации программ лечения опиоидами (OTP) обращайтесь в Отдел фармакологической терапии SAMHSA по телефону 240-276-2700. [email protected].
Чтобы получить помощь в отношении Экстранета Программы лечения опиоидов, обратитесь в службу поддержки OTP по адресу [email protected] или по телефону 1-866-348-5741.
Обратитесь к региональным специалистам SAMHSA по соблюдению требований OTP, чтобы определить, имеет ли OTP право предоставлять лечение расстройств, связанных с употреблением психоактивных веществ.
Бупренорфин | SAMHSA
Сертификат отказа от бупренорфина
Чтобы получить сертификат отказа от бупренорфина для введения, отпуска и назначения бупренорфина:
- Врачи, работающие в офисе, должны уведомить Центр лечения злоупотребления психоактивными веществами (CSAT) SAMHSA, Отдел фармакологической терапии (DPT) о своих намерение практиковать эту форму медикаментозного лечения (МПТ).

- NOI должен быть представлен в SAMHSA до первоначальной выдачи или назначения лекарств для лечения OUD.
- Недавно опубликованные Практические рекомендации создали гибкость обучения для Уведомлений о намерениях (NOI) для назначения бупренорфина.
- Найдите практикующих, освобожденных от бупренорфина, в вашем районе.
Для подачи заявки на последующее увеличение числа клиентов, имеющих право на лечение бупренорфином:
- Поставщики медицинских услуг в офисе обязаны проводить необходимое обучение. Завершение необходимого обучения сопровождает NOI.
- Этот подход признает важность специализированного обучения ведению большей группы пациентов, которым может потребоваться лечение бупренорфином.
- Подходящий поставщик услуг может пройти обучение или отказаться от него до назначения бупренорфина. Те, кто отказывается от обучения, могут лечить не более 30 пациентов одновременно.
Чтобы расширить доступ к бупренорфину, Практическое руководство по применению бупренорфина для лечения расстройств, связанных с употреблением опиоидов , освобождает правомочных врачей, фельдшеров, практикующих медсестер, клинических медсестер-специалистов, сертифицированных зарегистрированных медсестер-анестезиологов и сертифицированных медсестер-акушерок от сертификационных требований. связанные с обучением, консультированием и другими вспомогательными услугами (например, психосоциальными услугами) в соответствии с 21 U.S.C. § 823(g)(2)(B)(i)-(ii) Закона о контролируемых веществах (CSA). Практикующие, использующие это освобождение, могут лечить не более 30 пациентов одновременно (время, проведенное в соответствии с этим освобождением, не дает практикующему врачу право на более высокий лимит пациентов). Это исключение применяется только к назначению препаратов Списка III, IV и V или комбинаций таких препаратов, подпадающих под действие CSA, таких как бупренорфин.
связанные с обучением, консультированием и другими вспомогательными услугами (например, психосоциальными услугами) в соответствии с 21 U.S.C. § 823(g)(2)(B)(i)-(ii) Закона о контролируемых веществах (CSA). Практикующие, использующие это освобождение, могут лечить не более 30 пациентов одновременно (время, проведенное в соответствии с этим освобождением, не дает практикующему врачу право на более высокий лимит пациентов). Это исключение применяется только к назначению препаратов Списка III, IV и V или комбинаций таких препаратов, подпадающих под действие CSA, таких как бупренорфин.
Программа оплаты услуг сельских клиник, прошедших курс обучения бупренорфину . В июне 2021 года Управление ресурсов и услуг здравоохранения (HRSA) предприняло усилия по улучшению доступа к лекарствам для лечения расстройств, связанных с употреблением опиоидов, заплатив поставщикам, которые не могут назначать бупренорфин, лекарство, используемое для лечения расстройств, связанных с употреблением опиоидов. Сельские поликлиники (RHC) по-прежнему имеют возможность подать заявку на выплату в размере 3000 долларов США от имени каждого поставщика медицинских услуг, прошедшего обучение для получения отказа, необходимого для назначения бупренорфина после 1 января 2019 г.. Приблизительно 1,2 миллиона долларов США в виде программного финансирования остаются доступными для RHC и будут выплачиваться в порядке очереди до тех пор, пока средства не будут исчерпаны. Информация и регистрация на бесплатное обучение отказу доступны. По любым вопросам обращайтесь по адресу [email protected].
Сельские поликлиники (RHC) по-прежнему имеют возможность подать заявку на выплату в размере 3000 долларов США от имени каждого поставщика медицинских услуг, прошедшего обучение для получения отказа, необходимого для назначения бупренорфина после 1 января 2019 г.. Приблизительно 1,2 миллиона долларов США в виде программного финансирования остаются доступными для RHC и будут выплачиваться в порядке очереди до тех пор, пока средства не будут исчерпаны. Информация и регистрация на бесплатное обучение отказу доступны. По любым вопросам обращайтесь по адресу [email protected].
Некоторые федеральные законы и постановления разрешают врачам и другому медицинскому персоналу вводить лекарства, одобренные Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) для лечения расстройств, связанных с употреблением опиоидов (OUD), при особых обстоятельствах без отказа от бупренорфина. Узнайте об этих особых обстоятельствах.
Кроме того, бупренорфин также вводят в рамках сертифицированных SAMHSA программ лечения опиоидов (OTP).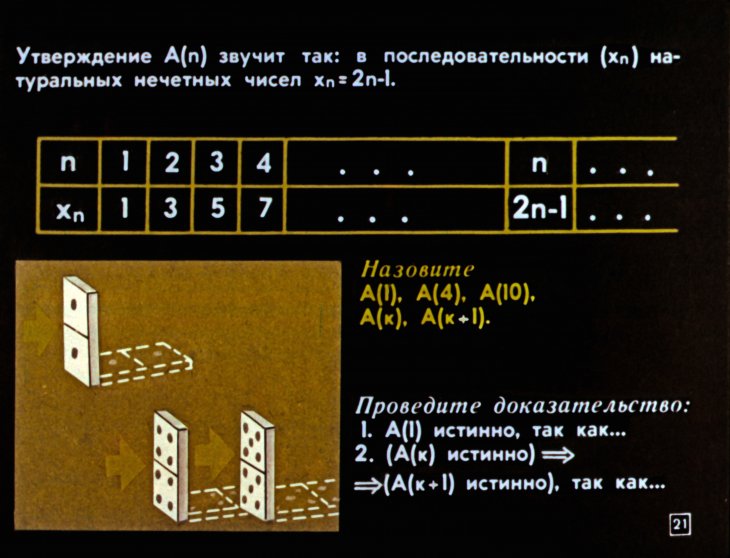 Найдите OTP, сертифицированного SAMHSA, в вашем регионе.
Найдите OTP, сертифицированного SAMHSA, в вашем регионе.
Как действует бупренорфин
Бупренорфин является частичным агонистом опиоидов. Он вызывает такие эффекты, как эйфория или угнетение дыхания при низких и умеренных дозах. Однако у бупренорфина эти эффекты слабее, чем у полных опиоидных агонистов, таких как метадон и героин.
При соблюдении предписаний бупренорфин безопасен и эффективен. Бупренорфин обладает уникальными фармакологическими свойствами, которые помогают:
- Уменьшают последствия физической зависимости от опиоидов, такие как абстинентный синдром и тяга к наркотикам
- Повышение безопасности при передозировке
- Снижение вероятности неправильного использования
Бупренорфин при расстройствах, связанных с употреблением опиоидов
- Чтобы начать лечение, пациент с OUD должен воздерживаться от употребления опиоидов в течение как минимум 12–24 часов и находиться на ранних стадиях синдрома отмены опиоидов.
 У пациентов с опиоидами в кровотоке или у тех, кто не находится на ранних стадиях абстиненции, может возникнуть острая абстиненция.
У пациентов с опиоидами в кровотоке или у тех, кто не находится на ранних стадиях абстиненции, может возникнуть острая абстиненция. - После того, как пациент прекратил или значительно сократил употребление опиоидов, больше не испытывает тяги к наркотикам и почти не испытывает побочных эффектов, при необходимости доза бупренорфина может быть скорректирована. Из-за пролонгированного действия бупренорфина, как только состояние пациентов стабилизируется, можно будет перейти с ежедневного приема на прием через день.
- Продолжительность приема бупренорфина зависит от потребностей каждого пациента, и в некоторых случаях лечение может быть бессрочным. Чтобы предотвратить возможный рецидив, люди могут продолжать лечение — с МПТ или без нее.
Перед началом приема бупренорфина
Пациенты с диагнозом OUD должны поговорить со своим лечащим врачом перед началом лечения бупренорфином, чтобы полностью понять лекарство и другие доступные варианты лечения.
Распространенные и серьезные побочные эффекты бупренорфина
Это не все побочные эффекты бупренорфина. Для получения дополнительной информации пациенты должны поговорить со своим лечащим врачом или фармацевтом. Пациенты должны сообщать своему лечащему врачу о любых побочных эффектах, которые беспокоят или не проходят.
Для получения дополнительной информации пациенты должны поговорить со своим лечащим врачом или фармацевтом. Пациенты должны сообщать своему лечащему врачу о любых побочных эффектах, которые беспокоят или не проходят.
Пациентам и практикующим врачам рекомендуется сообщать обо всех побочных эффектах через Интернет в MEDWatch, программу отчетности FDA о безопасности медицинских продуктов для медицинских работников, пациентов и потребителей, или по телефону 1-800-FDA-1088.
МПТ Лекарства, консультирование и сопутствующие состояния
Медикаментозное лечение (МПТ) — это использование лекарств в сочетании с консультированием и поведенческой терапией для обеспечения комплексного подхода к лечению расстройств, связанных с употреблением психоактивных веществ. Также важно учитывать другие состояния здоровья во время лечения.
Лекарства для ЗГТ
Управление по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) одобрило несколько различных лекарств для лечения расстройств, связанных с употреблением алкоголя и опиоидов. Лекарства, используемые для МПТ, являются вариантами лечения, основанными на фактических данных, и не просто заменяют один препарат другим.
Лекарства, используемые для МПТ, являются вариантами лечения, основанными на фактических данных, и не просто заменяют один препарат другим.
Метадон, используемый для лечения лиц с подтвержденным диагнозом расстройства, связанного с употреблением опиоидов, может выдаваться только через OTP, сертифицированный SAMHSA. Некоторые из лекарств, используемых в МПТ, являются контролируемыми веществами из-за возможности их неправильного использования. Наркотики, вещества и некоторые химические вещества, используемые для изготовления наркотиков, классифицируются Управлением по борьбе с наркотиками (DEA) по пяти отдельным категориям или спискам, в зависимости от приемлемого медицинского применения и возможности неправильного использования. Узнайте больше о списках препаратов DEA.
Лекарства от алкогольной зависимости — Акампросат, дисульфирам и налтрексон являются наиболее распространенными препаратами, используемыми для лечения алкогольной зависимости. Они не излечивают расстройство, но наиболее эффективны у людей, которые участвуют в программе МПТ.
- Акампросат — для выздоравливающих, которые больше не употребляют алкоголь и хотят воздержаться от употребления алкоголя. Он помогает предотвратить употребление алкоголя людьми, но не предотвращает абстинентный синдром после употребления алкоголя. Не было показано, что он работает у людей, которые продолжают употреблять алкоголь, потребляют запрещенные наркотики и / или злоупотребляют отпускаемыми по рецепту лекарствами. Использование акампросата обычно начинается на пятый день воздержания, достигая полной эффективности через пять-восемь дней. Он предлагается в форме таблеток и принимается три раза в день, желательно в одно и то же время каждый день. Побочные эффекты лекарства могут включать диарею, расстройство желудка, потерю аппетита, беспокойство, головокружение и проблемы со сном.
- Дисульфирам – лечит хронический алкоголизм и наиболее эффективен у людей, уже прошедших дезинтоксикацию или находящихся на начальной стадии абстиненции.
 Предлагаемый в форме таблеток и принимаемый один раз в день, дисульфирам никогда не следует принимать в состоянии алкогольного опьянения и не следует принимать в течение как минимум 12 часов после употребления алкоголя. Неприятные побочные эффекты (тошнота, головная боль, рвота, боли в груди, затрудненное дыхание) могут проявиться уже через десять минут после употребления даже небольшого количества алкоголя и могут продолжаться в течение часа и более.
Предлагаемый в форме таблеток и принимаемый один раз в день, дисульфирам никогда не следует принимать в состоянии алкогольного опьянения и не следует принимать в течение как минимум 12 часов после употребления алкоголя. Неприятные побочные эффекты (тошнота, головная боль, рвота, боли в груди, затрудненное дыхание) могут проявиться уже через десять минут после употребления даже небольшого количества алкоголя и могут продолжаться в течение часа и более. - Налтрексон — блокирует эйфорические эффекты и чувство опьянения и позволяет людям с расстройствами, связанными с употреблением алкоголя, сократить употребление алкоголя и сохранять мотивацию продолжать прием лекарств, продолжать лечение и избегать рецидивов.
Чтобы узнать больше о МПТ при расстройствах, связанных с употреблением алкоголя, просмотрите раздел «Лекарства для лечения расстройств, связанных с употреблением алкоголя: краткое руководство — 2015» и СОВЕТ 49: Внедрение алкогольной фармакотерапии в медицинскую практику.
Лекарства от опиоидной зависимости . Бупренорфин, метадон и налтрексон используются для лечения расстройств, связанных с употреблением опиоидов, таких как опиоиды короткого действия, такие как героин, морфин и кодеин, а также полусинтетические опиоиды, такие как оксикодон и гидрокодон. Эти препараты МАТ безопасны для использования в течение месяцев, лет или даже на протяжении всей жизни. Как и с любым лекарством, проконсультируйтесь с врачом перед прекращением использования.
- Бупренорфин – подавляет и уменьшает тягу к опиоидам. Узнайте больше о бупренорфине.
- Метадон – уменьшает тягу к опиоидам и синдром отмены, а также притупляет или блокирует действие опиоидов. Узнайте больше о метадоне.
- Налтрексон – блокирует эйфорический и седативный эффекты опиоидов и предотвращает чувство эйфории. Узнайте больше о налтрексоне.
Узнайте больше о МПТ при расстройствах, связанных с употреблением опиоидов, и загрузите СОВЕТ 63: Лекарства от расстройств, связанных с употреблением опиоидов — 2021.
Лекарства для профилактики передозировки опиоидами – Налоксон спасает жизни, обращая вспять токсические эффекты передозировки. По данным Всемирной организации здравоохранения (ВОЗ), налоксон является одним из ряда лекарств, которые считаются необходимыми для функционирования системы здравоохранения.
- Налоксон – используется для предотвращения передозировки опиоидов, налоксон устраняет токсические эффекты передозировки. Узнайте больше о налоксоне.
Лекарства MAT и безопасность детей
Важно помнить, что если лекарства разрешено хранить дома, они должны быть заперты в безопасном месте, недоступном для детей. Метадон в жидкой форме окрашен и иногда его принимают за безалкогольный напиток. У детей, принимающих лекарства, используемые при МПТ, может возникнуть передозировка или побочные реакции.
Предотвратите случайное проглатывание детьми и домашними животными, храня его в недоступном месте. Для получения дополнительной информации посетите образовательную кампанию CDC Up and Away. Для получения информации о том, как утилизировать лекарства в вашем доме, обратитесь к информации FDA «Как безопасно утилизировать неиспользованные или просроченные лекарства» или на веб-страницах DEA по утилизации лекарств.
Для получения информации о том, как утилизировать лекарства в вашем доме, обратитесь к информации FDA «Как безопасно утилизировать неиспользованные или просроченные лекарства» или на веб-страницах DEA по утилизации лекарств.
Консультирование и поведенческая терапия
Согласно федеральному закону 42.CFR 8.12, пациенты с МПТ, проходящие лечение в OTP, должны получать консультации, которые могут включать различные формы поведенческой терапии. Эти услуги необходимы наряду с медицинскими, профессиональными, образовательными и другими услугами по оценке и лечению. Узнайте больше об этих методах лечения расстройств, связанных с употреблением психоактивных веществ.
Вне зависимости от того, в каких условиях проводится МПТ, она более эффективна, когда в нее включены консультирование и другие поведенческие методы лечения, обеспечивающие пациентам комплексный подход.
Сопутствующие расстройства и другие состояния здоровья
Сосуществование как расстройства, связанного с употреблением психоактивных веществ, так и психического заболевания, известного как сопутствующее расстройство, распространено среди людей с МПТ. Кроме того, у людей могут быть другие состояния, связанные со здоровьем, такие как гепатит, ВИЧ и СПИД. Узнайте больше о сопутствующих заболеваниях и других состояниях здоровья.
Кроме того, у людей могут быть другие состояния, связанные со здоровьем, такие как гепатит, ВИЧ и СПИД. Узнайте больше о сопутствующих заболеваниях и других состояниях здоровья.
Обучение и ресурсы
SAMHSA предлагает инструменты, обучение и техническую помощь практикующим специалистам в области психического здоровья и расстройств, связанных с употреблением психоактивных веществ. Найдите информацию об обучении и ресурсах SAMHSA.
Сертификация программ лечения опиоидов (OTP)
Как стать аккредитованной и сертифицированной программой лечения опиоидов (OTP)
В Соединенных Штатах использование медикаментозного лечения (MAT) для расстройств, связанных с употреблением опиоидов (OUD) при лечении опиоидами программ (OTP) регулируется Сертификацией программ лечения опиоидов, 42 Свода федеральных правил (CFR) 8. Постановление создало систему для сертификации и аккредитации OTP, что позволяет им вводить и выдавать одобренные FDA препараты MAT. Кроме того, пациенты с расстройством, связанным с употреблением опиоидов (OUD), получающие препараты MAT, также должны получать консультации и другие виды поведенческой терапии, чтобы предоставить пациентам индивидуальный подход.
OTP также должны консультировать по вопросам профилактики аутоиммунного вируса человека (ВИЧ). SAMHSA рекомендует OTPS также проводить скрининг и обучение пациентов с высоким риском других инфекционных заболеваний.
Узнайте больше об используемых лекарствах и консультациях по лечению расстройств, связанных с употреблением психоактивных веществ.
Чтобы предоставить MAT для пациентов с OUD, OTP должны успешно пройти процесс сертификации и аккредитации и соответствовать другим требованиям, изложенным в 42 CFR 8. Требования включают:
- OTP должны быть как сертифицированы, так и аккредитованы;
- Лицензия штата, в котором они работают; и
- Зарегистрировано в Управлении по борьбе с наркотиками (DEA) через местное отделение DEA.
Программы, подающие заявки на аккредитацию или сертификацию, также должны соответствовать применимым законам и правилам своих штатов. Дополнительную информацию о нормативных актах отдельных штатов можно получить, обратившись в Управление штата по лечению опиоидов.
Чтобы помочь OTP добиться соответствия нормативным требованиям как для сертификации, так и для аккредитации, SAMHSA разработала Федеральное руководство для программ лечения опиоидов – 2015 г.
Аккредитация OTP
Аккредитация — это процесс экспертной оценки, в ходе которого OTP оценивается на соответствие стандартам лечения опиоидов SAMHSA и стандартам аккредитации аккредитационных органов, утвержденных SAMHSA. Процесс аккредитации включает выезд на место специалистов, имеющих опыт работы с препаратами для лечения опиоидов и связанной с ними лечебной деятельностью. Цель посещений объектов состоит в том, чтобы убедиться, что одноразовые одноразовые программы соответствуют определенным, принятым на национальном уровне стандартам для МПТ. Аккредитация ОТП:
- Повышает доверие сообщества
- Улучшает набор медицинского персонала
- Удовлетворяет большинству государственных лицензионных требований
- Соответствует определенным сертификационным требованиям Medicare
- Влияет на взносы по страхованию ответственности
Узнайте больше о законодательных актах, положениях и рекомендациях, применимых к OTP и MAT.
Сертификация OTP
Прежде чем получить сертификацию SAMHSA, OTP должны пройти процесс аккредитации и соответствовать другим требованиям, изложенным в Сертификации программ лечения опиоидов, 42 Свода федеральных правил (CFR). подать заявку на OTP и медикаментозное лечение (MAT).
Отдел фармакологической терапии (DPT) SAMHSA, входящий в состав Центра лечения наркозависимости (CSAT) SAMHSA, отвечает за сертификацию того, что программа лечения опиоидов (OTP) соответствует федеральным нормам, регулирующим лечение расстройств, связанных с употреблением психоактивных веществ.
Положения 42 CFR 8 позволяют DPT SAMHSA сосредоточить свои надзорные усилия на улучшении лечения, а не только на обеспечении того, чтобы OTP соответствовали нормативным критериям. Регламент также сохраняет за штатами право регулировать OTP. Надзор за лечебными препаратами, используемыми при ОЗТ, остается многосторонней системой с участием штатов, SAMHSA, Министерства здравоохранения и социальных служб (HHS) и DEA.
Предварительная сертификация
Программа может подать заявку на предварительную (первоначальную) сертификацию, поскольку она работает над получением аккредитации органом по аккредитации OTP, утвержденным SAMHSA. Предварительная сертификация — это временная сертификация, предоставляемая новому OTP на срок до одного года, в течение которого он должен пройти аккредитацию.
После того, как программа с предварительной сертификацией получает аккредитацию, она должна подать заявку в SAMHSA на получение полной сертификации через заявку на продление. После сертификации OTP должны продлевать сертификацию ежегодно или каждые три года в зависимости от срока выдачи аккредитации.
- OTP могут подать заявку в SAMHSA на предварительную (первоначальную) сертификацию и должны подать заявку в утвержденный SAMHSA орган по аккредитации для аккредитации.
- Временная сертификация носит временный характер и действует только один год.
OTP - также могут запросить предварительную сертификацию, пока они работают над получением разрешений штата и DEA.

- Однако SAMHSA не выдает предварительную сертификацию без одобрения штата и DEA.
- В течение одного года предварительной сертификации OTP должен получить свою аккредитацию.
- После того, как OTP получит аккредитацию, он должен подать заявку на продление/повторную сертификацию своей сертификации SAMHSA. Сотрудник по соблюдению требований OTP SAMHSA рассмотрит всю документацию, чтобы подтвердить, что OTP имеет право на сертификацию для предоставления лечения в соответствии с 42 CFR 8.
Программы, претендующие на предварительную сертификацию в качестве OTP, должны использовать онлайн-форму SMA-162: Заявление на сертификацию для использования опиоидных препаратов в программе лечения.
Для каждого приложения требуется разная сопроводительная документация. Эту документацию можно загрузить вместе с формой SMA-162. Допустимые файлы для загрузки могут быть в любом из следующих форматов:
- Текстовые файлы
- Файлы изображений TIFF
- PDF-файлы
- Документы Word (.
 doc или .docx)
doc или .docx)
Новые заявители должны подготовить следующие подтверждающие документы:
- Копия заявки на сертификацию, включая дату подачи заявки на аккредитацию, даты любых предыдущих проведенных или запланированных аккредитационных исследований и предполагаемый график завершения процесса аккредитации.
- Описание и диаграмма организационной структуры программы с указанием ключевых сотрудников OTP, включая их должность и звание, а также имя и полный адрес любой центральной администрации или более крупной организационной структуры, перед которой отвечает программа.
- Описание помещений, схема и описание, демонстрирующие адекватность помещений для выдачи лекарств и индивидуального и группового консультирования. В описании должно быть указано, как КО будет предоставлять адекватные медицинские, консультационные, профессиональные, образовательные и оценочные услуги в первичном учреждении, если только спонсор программы не заключил официальное документально оформленное соглашение с другой организацией.

- Название, адрес и описание каждой больницы, учреждения, клинической лаборатории или другого учреждения, используемого КО для предоставления необходимых медицинских и реабилитационных услуг.
- Название и адрес любого учреждения, кроме основного пункта выдачи, где метадон будет выдаваться либо на регулярной основе, либо по выходным, а также в качестве услуги в рамках программы лечения.
- Копия регистрации медицинского директора Управления по борьбе с наркотиками (DEA), государственной лицензии и биографических данных. Если медицинский директор также является медицинским директором другой лечебной программы, приложите письменное обоснование возможности такой договоренности. Эта возможность должна учитывать часть времени медицинского директора, затрачиваемого на лечение неродственных медицинских пациентов, и членство в советах и комитетах, которые конкурируют за время, выделенное на программы лечения.
- Имя и номер лицензии штата всех сотрудников OTP (кроме врачей программы), имеющих по закону лицензию на отпуск наркотических средств, даже если в настоящее время они не несут ответственности за прием или отпуск метадона в рамках программы.
 К ним относятся фармацевты, дипломированные медсестры и лицензированные практические медсестры.
К ним относятся фармацевты, дипломированные медсестры и лицензированные практические медсестры. - Предварительное расписание, показывающее часы выдачи лекарств, часы консультирования и часы работы врачей, медсестер и консультантов. Любая работа, которая будет выполняться за пределами основного места раздачи, также должна быть указана. Программа должна быть открыта для отпуска не менее шести дней в неделю. Кроме того, опишите, насколько часы выдачи являются адекватными и обеспечивают качество ухода за пациентами в соответствии с 42 CFR 8.12 (b).
- Список источников финансирования программы, включая название и адрес каждого государственного учреждения, предоставляющего средства.
- Описание количества пациентов, подлежащих лечению при действующей мощности.
- Утвердительное заявление о том, что программа лечения будет использовать контейнеры для всех лекарств, выдаваемых амбулаторным пациентам на дом, с защитными крышками.
- Подтверждение того, что медицинский директор и/или врач программы должны зарегистрировать учетную запись на веб-сайте SAMHSA OTP Extranet, чтобы подавать федеральные запросы пациентов на исключение (форма SMA-168) онлайн.
 Кандидаты могут зарегистрировать учетную запись в экстрасети на веб-сайте SAMHSA OTP Extranet. После проверки запроса заявитель получит электронное письмо с именем пользователя и паролем для использования веб-сайта.
Кандидаты могут зарегистрировать учетную запись в экстрасети на веб-сайте SAMHSA OTP Extranet. После проверки запроса заявитель получит электронное письмо с именем пользователя и паролем для использования веб-сайта.
Продление сертификации и другие виды использования формы SMA-162
OTP должны продлевать свою сертификацию ежегодно или каждые три года в зависимости от срока предоставленной аккредитации.
Для получения инструкций по доступу к учетной записи вашей программы обратитесь в службу поддержки SAMHSA OTP Extranet:
- 1-866-348-5741
- [email protected]
Для получения дополнительной информации о сертификации OTP и открытии программы лечения обратитесь к специалисту по соблюдению OTP в вашем штате.
Услуги OTP через пункты приема лекарств
Блок приема лекарств — это компонент OTP, географически отделенный от OTP. Медицинские подразделения могут быть мобильными или стационарными, и они могут предоставлять те же услуги, что и OTP, если пространство позволяет оказывать качественную помощь пациентам. Необходимые услуги, не предоставляемые в медицинских отделениях, должны оказываться в OTP, включая медицинские, консультационные, профессиональные, образовательные и другие услуги по оценке и лечению. Медикаментозные отделения позволяют пациентам МАТ установить режим и поддерживать продуктивную жизнь. Это может быть особенно полезно для людей, живущих в сельской местности с ограниченным доступом. Даже в крупных городах медицинские пункты могут быть ценным ресурсом и способствовать расширению доступа к лечению.
Необходимые услуги, не предоставляемые в медицинских отделениях, должны оказываться в OTP, включая медицинские, консультационные, профессиональные, образовательные и другие услуги по оценке и лечению. Медикаментозные отделения позволяют пациентам МАТ установить режим и поддерживать продуктивную жизнь. Это может быть особенно полезно для людей, живущих в сельской местности с ограниченным доступом. Даже в крупных городах медицинские пункты могут быть ценным ресурсом и способствовать расширению доступа к лечению.
Лекарственные единицы должны соответствовать тем же правилам и рекомендациям для OTP, которые изложены SAMHSA и штатом, в котором они находятся, и должны подавать заявки и обновляться для сертификации. Чтобы получить сертификацию SAMHSA для лекарственного препарата, используйте форму онлайн-заявки SMA-162.
Для получения дополнительной информации см. Руководство по OTP.
Часто задаваемые вопросы об OPT доступны для получения дополнительной информации.
Медикаментозное лечение расстройств, связанных с употреблением опиоидов, в сельской семейной врачебной практике
- Список журналов
- Общественное здравоохранение J Prim Care
- т.
 11; Январь-декабрь 2020 г.
11; Январь-декабрь 2020 г. - PMC7278292
J Prim Care Community Health. 2020 январь-декабрь; 11: 2150132720931720.
Published online 2020 Jun 6. doi: 10.1177/2150132720931720
, 1 , 1 , 1 , 1 , 2 and 3
Author information Article notes Copyright and Информация о лицензии Отказ от ответственности
Расстройство, связанное с употреблением опиоидов (OUD), является причиной значительной заболеваемости и смертности в Соединенных Штатах. Хотя предпринимаются усилия по ограничению доступа к опиоидам, отпускаемым по рецепту, потребление героина и синтетических опиоидов, а также смертность от передозировки опиоидов увеличились. Медикаментозное лечение (MAT) представляет собой сочетание психосоциального вмешательства с одобренными Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) лекарствами (метадон, бупренорфин плюс налтрексон) для лечения OUD. МПТ привела к снижению смертности от передозировки, преступной деятельности и передачи инфекционных заболеваний. Доступ к ОЗТ в сельской местности ограничен из-за нехватки специалистов, прошедших подготовку в области лечения зависимости, отсутствия доступа к комплексным программам лечения зависимости, транспорта и проблем, связанных с затратами. Сельские врачи выражают озабоченность по поводу отсутствия наставничества и утечки лекарств как причин, по которым следует избегать ОЗТ. Для назначения МП с бупренорфином требуется разрешение Агентства по борьбе с наркотиками (DEA), которое может быть легко получено поставщиками услуг семейной медицины. МПТ может быть включена в амбулаторную практику, где частота последующего наблюдения за пациентами и количество, необходимое для лечения, чтобы добиться изменений, аналогичны таковым при других хронических заболеваниях. Мы описываем случай передозировки опиоидов и предлагаемый протокол для индукции МАТ бупренорфином/налоксоном (субоксоном) для ОУД в амбулаторной практике сельской семейной медицины.
МПТ привела к снижению смертности от передозировки, преступной деятельности и передачи инфекционных заболеваний. Доступ к ОЗТ в сельской местности ограничен из-за нехватки специалистов, прошедших подготовку в области лечения зависимости, отсутствия доступа к комплексным программам лечения зависимости, транспорта и проблем, связанных с затратами. Сельские врачи выражают озабоченность по поводу отсутствия наставничества и утечки лекарств как причин, по которым следует избегать ОЗТ. Для назначения МП с бупренорфином требуется разрешение Агентства по борьбе с наркотиками (DEA), которое может быть легко получено поставщиками услуг семейной медицины. МПТ может быть включена в амбулаторную практику, где частота последующего наблюдения за пациентами и количество, необходимое для лечения, чтобы добиться изменений, аналогичны таковым при других хронических заболеваниях. Мы описываем случай передозировки опиоидов и предлагаемый протокол для индукции МАТ бупренорфином/налоксоном (субоксоном) для ОУД в амбулаторной практике сельской семейной медицины. Доступ к лечению облегчается за счет использования протокола, позволяющего офисному персоналу работать в той мере, в какой это разрешено их лицензией, способствуя командной работе и сводя к минимуму затраты времени врача. Мы пришли к выводу, что улучшенный доступ к ОЗТ может быть обеспечен в сельской амбулатории семейной медицины персоналом, который поддерживает и наставляет друг друга посредством использования протокола ОЗТ.
Доступ к лечению облегчается за счет использования протокола, позволяющего офисному персоналу работать в той мере, в какой это разрешено их лицензией, способствуя командной работе и сводя к минимуму затраты времени врача. Мы пришли к выводу, что улучшенный доступ к ОЗТ может быть обеспечен в сельской амбулатории семейной медицины персоналом, который поддерживает и наставляет друг друга посредством использования протокола ОЗТ.
Ключевые слова: опиаты, наркотики, вещества, наркомания, терапия, бупренорфин, первичная помощь, клиника
Расстройство, связанное с употреблением опиоидов (OUD), определяется как проблемная модель употребления опиоидов, которая приводит к серьезным нарушениям или дистрессу. 1 В конце 1990-х годов потребление отпускаемых по рецепту опиоидов увеличилось во всех регионах США, включая сельские районы. 2,3 Свободное использование опиоидов, отпускаемых по рецепту, в значительной степени поощрялось фармацевтической промышленностью, которая ранее заверяла поставщиков и пациентов в том, что как пролонгированные формы опиоидов, так и опиоиды, назначаемые при соматической боли, не вызывают привыкания. 3 Злоупотребление этими лекарствами и их утечка стали широко распространены; к 2017 г. примерно 1,7 миллиона человек в Соединенных Штатах страдали расстройствами, связанными с употреблением психоактивных веществ, связанными с рецептурными опиоидными обезболивающими препаратами, и 652 000 человек страдали расстройствами, связанными с употреблением героина (не исключая друг друга). 4 OUD является причиной значительной заболеваемости и смертности, и почти 47 000 человек умерли от передозировки опиоидов в Соединенных Штатах в 2018 году. угнетение дыхания, 6 , риск которых повышается при одновременном применении бензодиазепинов. 7 Злоупотребление новыми опиоидами, которые основаны главным образом на сильнодействующем опиоиде фентаниле и смешанном с героином, в последние годы увеличилось. 8
3 Злоупотребление этими лекарствами и их утечка стали широко распространены; к 2017 г. примерно 1,7 миллиона человек в Соединенных Штатах страдали расстройствами, связанными с употреблением психоактивных веществ, связанными с рецептурными опиоидными обезболивающими препаратами, и 652 000 человек страдали расстройствами, связанными с употреблением героина (не исключая друг друга). 4 OUD является причиной значительной заболеваемости и смертности, и почти 47 000 человек умерли от передозировки опиоидов в Соединенных Штатах в 2018 году. угнетение дыхания, 6 , риск которых повышается при одновременном применении бензодиазепинов. 7 Злоупотребление новыми опиоидами, которые основаны главным образом на сильнодействующем опиоиде фентаниле и смешанном с героином, в последние годы увеличилось. 8
Опиоиды вызывают сильное привыкание, и злоупотребление ими может привести к смертельным последствиям, что в большей степени затрагивает сельские районы. Скорость роста смертности из-за употребления опиоидов в сельской местности превышает таковую в несельских районах США. с 19С 1999 по 2015 год число случаев передозировки наркотиков в сельской местности увеличилось на 325% по сравнению с 198%-ным ростом среди городского населения. 9 Центры по контролю и профилактике заболеваний (CDC) сообщили в октябре 2017 года, что «постоянный ограниченный доступ к услугам по лечению наркомании в сельской местности» способствовал повышенному риску в сельской местности и что меры вмешательства должны включать лучшее просвещение о роли опиоиды в лечении хронической боли, а также улучшение доступа к медикаментозной терапии (МПТ). 9
Скорость роста смертности из-за употребления опиоидов в сельской местности превышает таковую в несельских районах США. с 19С 1999 по 2015 год число случаев передозировки наркотиков в сельской местности увеличилось на 325% по сравнению с 198%-ным ростом среди городского населения. 9 Центры по контролю и профилактике заболеваний (CDC) сообщили в октябре 2017 года, что «постоянный ограниченный доступ к услугам по лечению наркомании в сельской местности» способствовал повышенному риску в сельской местности и что меры вмешательства должны включать лучшее просвещение о роли опиоиды в лечении хронической боли, а также улучшение доступа к медикаментозной терапии (МПТ). 9
МПТ обладает значительным потенциалом для компенсации последствий для пациентов с ОУД, если бы только она была более широко доступна. Заболеваемость, связанная с OUD, измеряемая использованием ЭД, составляет 20,1% в месяц. 10 MAT снижает коэффициент использования ЭД на 51%. 10 Кроме того, было показано, что МПТ приводит к снижению преступной активности, а также снижению вируса иммунодефицита человека и гепатита С. 11 Долгосрочные данные об эффективности MAT для OUD ограничены; рандомизированное исследование пациентов с OUD, назначенных либо на метадон, либо на бупренорфин/налоксон (субоксон), продемонстрировало 5-летнее воздержание от героина на уровне 33,2% (число, необходимое для лечения = 3) и 20,7% от всех опиоидов. 12 Несмотря на признание важности МПТ, по оценкам, только 11% пациентов получают рецепт на лекарство, одобренное Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) для лечения OUD. 13
11 Долгосрочные данные об эффективности MAT для OUD ограничены; рандомизированное исследование пациентов с OUD, назначенных либо на метадон, либо на бупренорфин/налоксон (субоксон), продемонстрировало 5-летнее воздержание от героина на уровне 33,2% (число, необходимое для лечения = 3) и 20,7% от всех опиоидов. 12 Несмотря на признание важности МПТ, по оценкам, только 11% пациентов получают рецепт на лекарство, одобренное Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) для лечения OUD. 13
Доступ к ОЗТ является общенациональной проблемой, но сельские сообщества сталкиваются с уникальными и значительными препятствиями на пути к лечению опиоидной зависимости. Меньше учреждений, ограниченные услуги и большие расстояния, необходимые для поездки, чтобы получить помощь. 14 В целом в 88,6% сельских округов отсутствует достаточное количество программ лечения опиоидов. 15 Амбулаторные службы первичной медико-санитарной помощи, предлагающие ОЗТ, исключительно редко встречаются в сельской местности; почти 30% сельских жителей живут в округе, где нет поставщика бупренорфина, по сравнению с 2,2% городских жителей. 16 Опрос сельских врачей показал, что отсутствие наставничества, опасения по поводу вмешательства Управления по борьбе с наркотиками (DEA) в их практику и неправильное использование пациентами лекарств были препятствиями для предложения МПТ. 17
16 Опрос сельских врачей показал, что отсутствие наставничества, опасения по поводу вмешательства Управления по борьбе с наркотиками (DEA) в их практику и неправильное использование пациентами лекарств были препятствиями для предложения МПТ. 17
Краеугольным камнем программ первичной медико-санитарной помощи при ОЗТ является использование бупренорфина/налоксона (субоксона) в сочетании с тщательной оценкой состояния пациента. Стать врачом, выписывающим рецепты, не обошлось без барьеров и ограничений. Врачи первичной медико-санитарной помощи должны иметь действующую лицензию DEA и пройти 8-часовой курс, одобренный Управлением по борьбе со злоупотреблением психоактивными веществами и психическим здоровьем (SAMHSA), прежде чем подавать заявку на отказ DEA для назначения бупренорфина. Помощники врача (PA) и практикующие медсестры (NP) должны пройти 24-часовой утвержденный курс обучения. Медицинские работники также должны уметь пользоваться такими инструментами, как Клиническая шкала отмены опиатов (COWS), для информирования своих пациентов. 18 В первый год отказа поставщик может лечить не более 100 пациентов. В последующие годы поставщик услуг может подать заявку в SAMHSA на получение разрешения на лечение до 275 пациентов. 19
18 В первый год отказа поставщик может лечить не более 100 пациентов. В последующие годы поставщик услуг может подать заявку в SAMHSA на получение разрешения на лечение до 275 пациентов. 19
Наша система здравоохранения предоставляет первичную помощь 77 000 пациентов в 11 сельских клиниках на Среднем Западе США. Из 64 поставщиков первичной медико-санитарной помощи только 3 имеют разрешение DEA на назначение бупренорфина и в совокупности лечили 20 пациентов. Следуя простому процессу для завершения индукции и последующих посещений, пациенты могут получать МПТ в обычном рабочем процессе нашей сельской семейной медицины.
Наш пациент был в остальном здоровым 43-летним мужчиной, который в течение 14 лет периодически принимал метадон, фентанил и оксикодон, отпускаемые по рецепту, по поводу хронической боли в пояснице. В последние 2-3 года он употреблял героин после прихода домой с работы в ночную смену; он вводил героин внутривенно, чтобы расслабиться и заснуть, а позже присоединялся к своей супруге и дочери за ужином, прежде чем вернуться к работе. Зная о серьезности и прогрессировании своей проблемы, пациент обратился в несколько местных программ лечения зависимости. Предварительные расходы, необходимость поездки в лечебный центр и невозможность отсутствовать на работе не позволили ему участвовать в какой-либо программе лечения.
Зная о серьезности и прогрессировании своей проблемы, пациент обратился в несколько местных программ лечения зависимости. Предварительные расходы, необходимость поездки в лечебный центр и невозможность отсутствовать на работе не позволили ему участвовать в какой-либо программе лечения.
Однажды добытый им героин оказался сильнее, чем ожидалось. Он сделал себе укол и уснул. Когда он не отвечал на звонки своей супруги, она пришла домой с работы и обнаружила, что он не отвечает и у него одышка; это было всего за несколько минут до того, как их дочь-подросток пришла бы домой из школы. Его супруга, непрофессионалка, не смогла найти дома налоксон и провела сердечно-легочную реанимацию до прибытия спасателей, хотя сама она не работает в системе здравоохранения. Сотрудники службы экстренного реагирования ввели 2 дозы налоксона интраназально, когда пациент был доставлен в отделение неотложной помощи (ED) больницы критического доступа в том же городе. Там он был стабилизирован с медицинской точки зрения и находился под наблюдением в течение ночи. Так совпало, что его семейный врач, который заботился обо всей его семье и был знаком с пациентом, в ту ночь работал в отделении неотложной помощи. Он знал о том, что его коллеги в амбулаторной практике предлагали терапию субоксоном для OUD, и срочно направил к поставщику МПТ. На следующее утро пациент был осмотрен в клинике семейной медицины. Он активно находился в состоянии абстиненции с оценкой COWS 16, что указывает на умеренную абстиненцию. Терапия субоксоном была начата в соответствии с протоколом МАТ, 2 мг вначале и 2 мг каждый час после этого, всего 4 дозы. Его состояние стабилизировалось в течение нескольких дней наблюдения при дозе 8 мг субоксона два раза в день. Последующее наблюдение состояло из частых еженедельных посещений в течение первых 4 недель, ежемесячных посещений в течение 6 месяцев, а затем продолжалось посещение офиса каждые 3 месяца.
Так совпало, что его семейный врач, который заботился обо всей его семье и был знаком с пациентом, в ту ночь работал в отделении неотложной помощи. Он знал о том, что его коллеги в амбулаторной практике предлагали терапию субоксоном для OUD, и срочно направил к поставщику МПТ. На следующее утро пациент был осмотрен в клинике семейной медицины. Он активно находился в состоянии абстиненции с оценкой COWS 16, что указывает на умеренную абстиненцию. Терапия субоксоном была начата в соответствии с протоколом МАТ, 2 мг вначале и 2 мг каждый час после этого, всего 4 дозы. Его состояние стабилизировалось в течение нескольких дней наблюдения при дозе 8 мг субоксона два раза в день. Последующее наблюдение состояло из частых еженедельных посещений в течение первых 4 недель, ежемесячных посещений в течение 6 месяцев, а затем продолжалось посещение офиса каждые 3 месяца.
При последующем посещении через 6 месяцев МП пациент был мотивирован поделиться своим положительным опытом с другими и направил 2 человек для МП в нашу практику. Через год после начала МПТ он все еще принимал субоксон по 8 мг два раза в день и чувствовал, что готов начать отлучение от груди до более низкой дозы. Он работал, получил повышение, активно участвовал в семейных мероприятиях и взял за правило посещать все школьные мероприятия дочери. Он и его семья остаются в нашей практике семейной медицины и в остальном физически и эмоционально здоровы.
Через год после начала МПТ он все еще принимал субоксон по 8 мг два раза в день и чувствовал, что готов начать отлучение от груди до более низкой дозы. Он работал, получил повышение, активно участвовал в семейных мероприятиях и взял за правило посещать все школьные мероприятия дочери. Он и его семья остаются в нашей практике семейной медицины и в остальном физически и эмоционально здоровы.
Представленный случай иллюстрирует, как сельская семейная врачебная практика может повысить доступность лечения МПТ. Раньше доступ к МПТ был ограничен из-за отсутствия гибкости нескольких других вариантов, существующих в этой сельской местности. Альтернативные программы ОЗТ либо требуют госпитализации в стационар с риском для пациентов потерять работу, либо требуют ежедневных поездок продолжительностью более часа в близлежащий более крупный город для регистрации в метадоновой программе. Эти барьеры помешали пациенту в данном случае получить лечение МАТ раньше. Этот пациент выразил искреннюю уверенность в том, что он не был бы жив, если бы не простота немедленного обращения из отделения неотложной помощи в амбулаторную клинику для начала лечения МПТ.
МАТ может быть предложена пациентам в нескольких формах, включая метадон, бупренорфин с налоксоном или без него и налтрексон, но субоксон является наиболее эффективным и практичным вариантом включения МАТ в амбулаторную практику семейной медицины. Большое сравнительное исследование эффективности, в котором приняли участие 40 885 взрослых с OUD, рассмотрело 6 различных путей лечения и показало, что только лечение бупренорфином или метадоном было связано со снижением риска как передозировки, так и серьезного обращения за неотложной помощью, связанной с опиоидами, по сравнению с отсутствием лечения в 3 и 12 месяцев наблюдения. 20 Между этими двумя вариантами существуют дополнительные препятствия для амбулаторного лечащего врача при назначении метадона по сравнению с субоксоном. Чтобы практикующий врач мог вводить и распределять метадон для OUD, он должен получить отдельную регистрацию DEA в качестве программы лечения наркомании. Этот вид деятельности требует дополнительного одобрения и регистрации Центра лечения наркомании (CSAT) в рамках SAMHSA Министерства здравоохранения и социальных служб (HHS), а также соответствующего государственного органа по метадону. 21 Учитывая его относительную эффективность и практичность, Suboxone является лечением MAT, используемым в нашем протоколе сельской семейной медицины.
21 Учитывая его относительную эффективность и практичность, Suboxone является лечением MAT, используемым в нашем протоколе сельской семейной медицины.
Предлагаемый клинический протокол, разработанный и внедренный в нашей сельской амбулаторной семейной врачебной практике, чтобы предоставить пациентам с OUD путь к получению MAT с Suboxone, показан в приложении. У персонала, ответственного за планирование, и дипломированной медсестры бригады (RN) есть список конкретных задач по подготовке пациента к первичной консультации с врачом. К моменту осмотра пациентки были завершены соответствующие лабораторные анализы, в том числе тесты функции печени, скрининг на вирус иммунодефицита человека и гепатита С, на инфекции, передающиеся половым путем, и тест на беременность, где это уместно. База данных Государственной программы мониторинга рецептурных препаратов (PDMP) запрашивается, и пациент получает согласие на получение записей от предыдущих поставщиков лечения. Свяжитесь с медицинской страховой компанией пациента, чтобы определить, есть ли предпочтительная форма бупренорфина, и стоимость этого лекарства для пациента. Предварительное разрешение получено от страховой компании, чтобы убедиться, что рекомендуемый продукт доступен во время первичной консультации в клинике. Кроме того, выясняются поведенческие и социальные услуги, покрываемые медицинской страховой компанией пациента.
Предварительное разрешение получено от страховой компании, чтобы убедиться, что рекомендуемый продукт доступен во время первичной консультации в клинике. Кроме того, выясняются поведенческие и социальные услуги, покрываемые медицинской страховой компанией пациента.
Пациенты обычно включаются в расписание медработников за неделю до их первоначальной консультации, предоставляя время для выполнения предварительных мероприятий, описанных выше. Предпочтительны встречи в начале дня и в начале недели, чтобы обеспечить мониторинг в рабочее время и последующее наблюдение в течение рабочей недели. Срочные назначения назначаются, когда произошла острая детоксикация и пациент готов немедленно начать терапию.
КОУВ вводится при поступлении пациента в клинику. Оценка по шкале COWS от 13 до 24 указывает на то, что пациент находится в состоянии отмены опиоидов, и дальнейшие симптомы отмены, скорее всего, не будут спровоцированы началом МП. 18 Если пациент недавно употреблял опиоиды и еще не достиг синдрома отмены, о чем свидетельствует оценка по шкале COWS менее 13, его просят вернуться в клинику или начать лечение на следующий день. Пациенты, которые воздерживались от опиоидов в течение многих дней и больше не находятся в состоянии абстиненции, могут немедленно начать лечение или быть выписаны домой для индукции в домашних условиях. Те пациенты, которых отправляют домой, принимают лекарство самостоятельно, и медсестра связывается с ними по телефону в течение 1–2 часов после ранее согласованного времени начала МП. Начало лечения в домашних условиях следует тому же режиму дозирования, что и при назначении в офисе (приложение).
Пациенты, которые воздерживались от опиоидов в течение многих дней и больше не находятся в состоянии абстиненции, могут немедленно начать лечение или быть выписаны домой для индукции в домашних условиях. Те пациенты, которых отправляют домой, принимают лекарство самостоятельно, и медсестра связывается с ними по телефону в течение 1–2 часов после ранее согласованного времени начала МП. Начало лечения в домашних условиях следует тому же режиму дозирования, что и при назначении в офисе (приложение).
В нашей практике инициация МПТ в кабинете требуется для лиц с функциональным статусом <4 MET (метаболических эквивалентов), атеросклеротической болезнью коронарных артерий, сахарным диабетом, множественными сопутствующими заболеваниями, переходом на метадон (текущая доза метадона <40 мг ежедневно) и хронические болевые расстройства. МАТ начинают с 2–4 мг компонента бупренорфина, вводимого каждый час, пока пациент не почувствует себя комфортно и тяга к опиоидам не исчезнет. Дозировка рассчитывается с использованием эквивалентной морфину дозы 1 мг бупренорфина на 10 мг перорального морфина для тех пациентов, которые принимают лекарства, отпускаемые по рецепту. Пациентам, употребляющим героин или с неизвестным употреблением опиоидов, начинают с первой дозы 4 мг. В течение начального периода RN и врач поочередно осматривают пациента каждые 15–30 минут, что позволяет врачу продолжать обычно запланированную практику. Поскольку многие пациенты имеют коморбидный болевой синдром, а отмена опиоидов может включать выявление некоторой хронической боли, посещение РН включает оценку общего самочувствия пациента, основных показателей жизнедеятельности, COWS и оценку боли. Когда пациент чувствует себя комфортно, обычно после приема 2–3 доз бупренорфина, его выписывают. С пациентом связываются по телефону в течение 24 часов после индукции и снова осматривают в течение 1 недели для последующего наблюдения. После этого пациент наблюдается в клинике еженедельно в течение месяца и ежемесячно в течение 6 месяцев. Пациенты, которые стабильны в долгосрочной перспективе, продолжают наблюдаться каждые 3 месяца. Скрининг мочи на наркотики проводится в начале и случайным образом и завершается не реже одного раза в 6 месяцев во время лечения МПТ.
Пациентам, употребляющим героин или с неизвестным употреблением опиоидов, начинают с первой дозы 4 мг. В течение начального периода RN и врач поочередно осматривают пациента каждые 15–30 минут, что позволяет врачу продолжать обычно запланированную практику. Поскольку многие пациенты имеют коморбидный болевой синдром, а отмена опиоидов может включать выявление некоторой хронической боли, посещение РН включает оценку общего самочувствия пациента, основных показателей жизнедеятельности, COWS и оценку боли. Когда пациент чувствует себя комфортно, обычно после приема 2–3 доз бупренорфина, его выписывают. С пациентом связываются по телефону в течение 24 часов после индукции и снова осматривают в течение 1 недели для последующего наблюдения. После этого пациент наблюдается в клинике еженедельно в течение месяца и ежемесячно в течение 6 месяцев. Пациенты, которые стабильны в долгосрочной перспективе, продолжают наблюдаться каждые 3 месяца. Скрининг мочи на наркотики проводится в начале и случайным образом и завершается не реже одного раза в 6 месяцев во время лечения МПТ.
В первые 2 года нашей программы 16 из 20 пациентов продолжали воздержание, 4 пациента не продолжали прием бупренорфина, и ни один из них не был потерян для последующего наблюдения. 4 пациентам, которые не продолжали прием бупренорфина, ранее назначали метадон (n = 1), трамадол (n = 1) или гидрокодон (n = 2) для лечения хронических болевых синдромов. Трое из этих пациентов были направлены на МПТ из-за неудачных договоренностей о опиоидной терапии, и каждый пациент ранее принимал более 50 мг эквивалентов морфина в день. Эти пациенты были переведены с бупренорфина и в настоящее время принимают опиоиды, отпускаемые по рецепту, в дозе 10 мг, эквивалентной морфину, или меньше. Программа все еще относительно новая и находится в стадии разработки. Поскольку неэффективность лечения МАТ может наступить через месяцы или даже годы терапии, мы ожидаем, что большее количество пациентов не смогут поддерживать воздержание в будущем.
Важным фактором успеха нашей программы является то, что пациенты могут быть зарегистрированы, когда они просят о приеме, в течение недели, а не только в то время, которое отведено специально для МПТ. Это означает, что пациенты могут быть осмотрены в срочном порядке, когда они активно находятся в состоянии отмены или готовы к терапии на своих условиях. Поскольку процесс индукции не отнимает времени у поставщика медицинских услуг в клинике, срочно направленные пациенты могут быть включены в график поставщика медицинских услуг в соответствии с теми же заранее установленными процедурами для любого пациента с любым состоянием здоровья, будь то осмотр для первичной консультации, индукции или для последующего наблюдения. Удаленные телемедицинские встречи могут быть предложены пациентам после того, как их план лечения МПТ будет надлежащим образом разработан.
Это означает, что пациенты могут быть осмотрены в срочном порядке, когда они активно находятся в состоянии отмены или готовы к терапии на своих условиях. Поскольку процесс индукции не отнимает времени у поставщика медицинских услуг в клинике, срочно направленные пациенты могут быть включены в график поставщика медицинских услуг в соответствии с теми же заранее установленными процедурами для любого пациента с любым состоянием здоровья, будь то осмотр для первичной консультации, индукции или для последующего наблюдения. Удаленные телемедицинские встречи могут быть предложены пациентам после того, как их план лечения МПТ будет надлежащим образом разработан.
В заключение, улучшенный доступ к ОЗТ для OUD может быть обеспечен в сельской местности группами поставщиков услуг семейной медицины и обученным персоналом путем включения ОЗТ в регулярное оказание первичной медицинской помощи в их практике и в сообществе.
Протокол бупренорфина/налоксона
Направление пациента (только постоянный пациент в системе здравоохранения клиники или новый пациент из соседних округов)
Если пациент звонит в клинику: электронная медицинская карта (ЭМК) на время ухода с запросом на прием
Медсестра связывается с поставщиком услуг из списка поставщиков, отказавшихся от приема бупренорфина/налоксона, чтобы записаться на прием
Предпочтительное время приема рано утром и в начале недели
Предпочтительно 40-минутное время приема
Доступ в тот же день предоставляется для пациентов, принимающих незаконные наркотики, которые уже прошли детоксикацию и находятся в состоянии абстиненции
Внутреннее направление поставщика медицинских услуг: поставщик отправляет безопасное сообщение через электронную медицинскую карту поставщику с отказом от бупренорфина, чтобы инициировать процесс записи на прием /поставщики обезболивающих или другие поставщики, ранее назначавшие пациенту опиоиды
Медсестра определяет, находится ли пациент на консультации по поводу расстройства, связанного с употреблением опиоидов (OUD)
Врач запрашивает лабораторные анализы: тесты функции печени, вирус иммунодефицита человека, гепатит С, инфекции, передающиеся половым путем, тест на беременность (если женщина) аптека
Критерии присутствия дипломированной медсестры для осмотра во время введения:
Функциональный статус <4 MET, атеросклеротическая болезнь коронарных артерий, сахарный диабет, множественные сопутствующие заболевания, переход на метадон (текущая доза метадона менее более 40 мг в день) и хронические болевые расстройства.

День 1 (День консультации)
Пациент Заполняет форму оценки использования веществ A
. соглашение a
Пациент предоставляет образец мочи для проверки на наркотики
Медсестра получает доступ к Программе мониторинга рецептурных препаратов (PDMP) и отправляет защищенное сообщение через EHR с результатами поставщику.
Поставщик отправляет в аптеку рецепт на недельный запас лекарств
Вводный курс пациента (обычно в тот же день, что и консультация)
Previsit 5a, выше
Пациент получает рецепт в аптеке непосредственно перед приемом до прибытия в клинику
Персонал палаты регистрирует жизненно важные признаки: артериальное давление, пульс, дыхание и температуру
Пациент заполняет шкалу клинической оценки синдрома отмены опиатов (COWS) b
Медицинский работник дает пациенту 2–4 мг бупрелиноринфина сублингвально в клинику
Персонал палаты через 15-30 минут повторяет жизненные показатели: кровяное давление и частоту сердечных сокращений
Пациент снова проходит оценку COWS, и жизненные показатели снова получают через 1 час
Через 1 час после первой дозы врач дает вторую дозу 1-4 мг бупренорфина
Персонал в палате через 15-30 минут повторяет основные показатели жизнедеятельности: артериальное давление и частоту сердечных сокращений
Если пациент со стабильными показателями жизненно важных функций и приемлемой оценкой COWS, они могут быть выписаны из клиники
Через 2 часа после первой дозы и с 2-часовыми интервалами при необходимости вводят дополнительный бупренорфин
Последующее наблюдение за пациентом
Пациент должен быть осмотрен или связаться с клиникой в течение 24 часов
Пациент должен повторно наблюдаться еженедельно в течение одного месяца, ежемесячно в течение 6 месяцев, затем минимум каждые три месяца.
 Скрининг мочи на наркотики проводится в начале и случайным образом, но в последующем не реже одного раза в 6 месяцев.
Скрининг мочи на наркотики проводится в начале и случайным образом, но в последующем не реже одного раза в 6 месяцев.
a Средства скрининга доступны через SAMHSA-HRSA. https://www.integration.samhsa.gov. 22
b Клиническая шкала отмены опиатов (COWS). J Психоактивные препараты . 2003;35:253-259. 18
Согласие пациента: Пациент предоставил разрешение на использование своей медицинской информации в исследовательских целях.
Декларация о конфликте интересов: Автор(ы) заявили об отсутствии потенциального конфликта интересов в отношении исследования, авторства и/или публикации этой статьи.
Финансирование: Авторы раскрыли получение следующей финансовой поддержки для исследования, авторства и/или публикации этой статьи: Д-р Мансухани был главным исследователем исследовательского гранта, финансируемого ResMed Foundation в 2016-2019 гг. что не имеет отношения к текущей работе. Доктор Мансухани является лауреатом премии Пола и Руби Цай и семейного фонда за развитие карьеры в 2017–2020 годах в клинике Майо.
что не имеет отношения к текущей работе. Доктор Мансухани является лауреатом премии Пола и Руби Цай и семейного фонда за развитие карьеры в 2017–2020 годах в клинике Майо.
ORCID iD: Марк Дейо-Свендсен https://orcid.org/0000-0001-6446-630X
Мегна П. Мансухани https://orcid.org/0000-0003-2351-5640
1. Американская психиатрическая ассоциация. Диагностическое и Статистическое Руководство по Психическим Расстройствам. 5-е изд. Американская психиатрическая ассоциация; 2013. doi: 10.1176/appi.books.97808
596 [CrossRef] [Google Scholar]2. Мороне Н.Е., Вайнер Д.К. Боль как пятый жизненный признак: выявление жизненной потребности в обучении боли. Клин Тер. 2013;35:1728-1732. doi: 10.1016/j.clinthera.2013.10.001 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
3.
Ван Зи А.
Продвижение и маркетинг ОксиКонтина: коммерческий триумф, трагедия общественного здравоохранения. Am J Общественное здравоохранение. 2009;99:221-227. doi: 10. 2105/AJPH.2007.131714 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2105/AJPH.2007.131714 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
4. Центр статистики и качества поведенческого здоровья. Результаты Национального исследования по употреблению наркотиков и здоровью 2017 года: подробные таблицы. Опубликовано 7 сентября 2018 г. По состоянию на 18 мая 2020 г. https://www.samhsa.gov/data/sites/default/files/cbhsq-reports/NSDUHDetailedTabs2017/NSDUHDetailedTabs2017.pdf
5. Центры по контролю и профилактике заболеваний. ЧУДО ЦКЗ; По состоянию на 18 мая 2020 г. http://wonder.cdc.gov [Google Scholar]
6. Рамачандран С.К., Хайдер Н., Саран К.А. и др. Угрожающие жизни критические респираторные события: ретроспективное исследование послеоперационных пациентов, не реагирующих на обезболивающую терапию. Джей Клин Анест. 2011;23:207-213. doi: 10.1016/j.jclinane.2010.09.003 [PubMed] [CrossRef] [Google Scholar]
7.
Эрнандес И., Хе М., Брукс М.М., Чжан Ю.
Связь воздействия и реакции между одновременным употреблением опиоидов и бензодиазепинов и риском передозировки, связанной с опиоидами, у участников программы Medicare, часть D. JAMA Сеть открыта. 2018;1:e180919. doi: 10.1001/jamanetworkopen.2018.0919 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
JAMA Сеть открыта. 2018;1:e180919. doi: 10.1001/jamanetworkopen.2018.0919 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
8. Барабанщик О. Смертельные случаи, вызванные новыми опиоидами: обзор. Судебно-медицинская экспертиза. 2019;4:95-110. дои: 10.1080/20961790.2018.1460063 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
9. Мак К.А., Джонс К.М., Баллестерос М.Ф. Незаконное употребление наркотиков, расстройства, связанные с употреблением запрещенных наркотиков, и смерти от передозировки наркотиков в городских и других районах — США. Ам Джей Трансплант. 2017;17:3241-3252. doi: 10.1111/ajt.14555 [PubMed] [CrossRef] [Google Scholar]
10.
Шах А., Поуп Дж., Ласиджан-Дрю К.
Понимание наших участников: инициирование МПТ и вовлечение в каскадную структуру ухода. Документ представлен на: DATA-Informed Expansion of MAT Services: Process, Framework, and Clinical Transformation; 29 мая-31, 2019; Бенд, Орегон
По состоянию на 18 мая 2020 г.
https://www. linesforlife.org/wp-content/uploads/5_30_19-10-am-Cascade-B-Data-Informed-Expansion-of-MAT-Services-Brewster-et-al.pdf [Google Scholar]
linesforlife.org/wp-content/uploads/5_30_19-10-am-Cascade-B-Data-Informed-Expansion-of-MAT-Services-Brewster-et-al.pdf [Google Scholar]
11. Кребс Э., Урада Д., Эванс Э., Хуанг Д., Хсер Ю.И., Носик Б. Стоимость преступлений во время и после финансируемого государством лечения расстройств, связанных с употреблением опиоидов: исследование на уровне населения в штате Калифорния: расходы на преступления во время и после лечения OUD. Зависимость. 2017;112:838-851. doi: 10.1111/доп.13729[Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
12. Zhu Y, Evans EA, Mooney LJ, et al. Корреляты длительного воздержания от опиоидов после рандомизации на метадон по сравнению с бупренорфином/налоксоном в многоцентровом исследовании. J Нейроиммунная Фармакол. 2018;13:488-497. doi: 10.1007/s11481-018-9801-x [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
13.
Остерле Т.С., Тусиус Н.Дж., Румманс Т.А., Голд М.С.
Медикаментозное лечение расстройств, связанных с употреблением опиоидов. Мэйо Клин Proc. 2019;94:2072-2086. doi: 10.1016/j.mayocp.2019.03.029 [PubMed] [CrossRef] [Google Scholar]
Мэйо Клин Proc. 2019;94:2072-2086. doi: 10.1016/j.mayocp.2019.03.029 [PubMed] [CrossRef] [Google Scholar]
14. Пуллен Э., Озер С. Препятствия для лечения наркомании в сельских и городских общинах: точки зрения консультанта. Неправильное использование Subst. 2014;49:891-901. doi: 10.3109/10826084.2014.891615 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
15. Дик А.В., Пакула Р.Л., Гордон А.Дж. и др. Увеличение отказов от бупренорфина для врачей увеличило потенциальный доступ к лечению опиоидными агонистами, 2002–2011 годы. Health Aff (Миллвуд). 2015;34:1028-1034. doi: 10.1377/hlthaff.2014.1205 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
16.
Андрилла ЧА, Мур Т.Э., Паттерсон Д.Г., Ларсон Э.Х.
Географическое распределение поставщиков с отказом от DEA для назначения бупренорфина для лечения расстройств, связанных с употреблением опиоидов: 5-летнее обновление: распределение поставщиков с отказом от DEA. J Сельское здоровье. 2019;35:108-112. doi: 10.1111/jrh.12307 [PubMed] [CrossRef] [Google Scholar]
doi: 10.1111/jrh.12307 [PubMed] [CrossRef] [Google Scholar]
17. Андрилла ЧА, Мур Т.Э., Паттерсон Д.Г. Преодоление препятствий к назначению бупренорфина для лечения расстройств, связанных с употреблением опиоидов: рекомендации сельских врачей: рекомендации сельских врачей по бупренорфину. J Сельское здоровье. 2019;35:113-121. doi: 10.1111/jrh.12328 [PubMed] [CrossRef] [Google Scholar]
18. Вессон Д.Р., Линг В. Клиническая шкала отмены опиатов (COWS). J Психоактивные препараты. 2003;35:253-259. doi: 10.1080/02791072.2003.10400007 [PubMed] [CrossRef] [Google Scholar]
19. Управление по борьбе со злоупотреблением психоактивными веществами и психиатрическими услугами. Подать заявление на освобождение от практики. Подайте заявление об отказе практикующего врача от назначения или отпуска бупренорфина в соответствии с Законом о лечении наркозависимости от 2000 г. (DATA 2000). По состоянию на 18 мая 2020 г. https://www.samhsa.gov/medication- Assistance-treatment/training-materials-resources/apply-for-practitioner-waiver
20. Уэйкман С.Е., Ларошель М.Р., Амели О. и др.
Сравнительная эффективность различных способов лечения расстройств, связанных с употреблением опиоидов. JAMA Сеть открыта. 2020;3:e1920622. doi: 10.1001/jamanetworkopen.2019.20622 [PubMed] [CrossRef] [Google Scholar]
Уэйкман С.Е., Ларошель М.Р., Амели О. и др.
Сравнительная эффективность различных способов лечения расстройств, связанных с употреблением опиоидов. JAMA Сеть открыта. 2020;3:e1920622. doi: 10.1001/jamanetworkopen.2019.20622 [PubMed] [CrossRef] [Google Scholar]
21. Раннаццизи Дж.Т., Каверли М.В. Руководство для практикующих: информационный очерк Закона о контролируемых веществах. Опубликовано в 2006 г. По состоянию на 18 мая 2020 г. https://www.deadiversion.usdoj.gov/pubs/manuals/pract/pract_manual012508.pdf
22. Центр интегрированных решений для здравоохранения SAMHSA-HRSA. Инструменты скрининга. По состоянию на 18 мая 2020 г. https://www.integration.samhsa.gov/clinical-practice/screening-tools
Статьи из Journal of Primary Care & Community Health предоставлены здесь SAGE Publications
Ознакомление с MAT в учебном сообществе отделения неотложной помощи
- О нас
- Карьера
- Сообщество
- Образование
- Предоставление
- Новости
- Исследовательская работа
- Моя карта
Заголовок
Введение в MAT в учебном сообществе отделения неотложной помощи
Свидание
понедельник, 11 января 2021 г. , 16:00 — понедельник, 13 сентября 2021 г., 18:00
, 16:00 — понедельник, 13 сентября 2021 г., 18:00
Адрес
Двенадцатинедельные сессии будут проводиться через платформу телеконференций MetroHealth WebEx
Map & Directions.
Контактное лицо
Мэри Роуленд
Почта для связи
[электронная почта защищена]
Представлено Управлением по безопасности опиоидов MetroHealth
Учебное сообщество будет включать двенадцатинедельную учебную программу по два часа каждый, включающую структурированные образовательные занятия; постоянная техническая помощь (ТА), оказываемая нашими сертифицированными экспертами по неотложной помощи и наркологии, а также лицензированным вспомогательным персоналом, доступным для всех больничных систем по всему Огайо.
Мероприятие бесплатное. Требуется регистрация.
Как принять участие
- Зарегистрируйтесь ниже
- Двенадцатинедельные сеансы будут проводиться через платформу телеконференций MetroHealth WebEx.
- Тематический опрос об удовлетворенности каждым дидактическим и интерактивным сеансом будет отправлен каждому участнику по электронной почте в течение 72 часов после каждого сеанса через электронную платформу MetroHealth MyEvaluations.com.
- Для получения кредитов CME/CEU необходимо будет пройти опросы, а результаты опросов будут использоваться для постоянного совершенствования процессов.
- Каждое 2-часовое занятие дает два кредита, всего можно заработать 24 часа CME/CEU.
Зарегистрированные лица, принявшие участие в 10 двухчасовых вебинарах в прямом эфире из этой серии и в одном звонке в службу технической поддержки, могут иметь право на получение стипендии в размере 500 долларов США. Это поощрение будет доступно для 2 человек в учреждении. Другие поощрения будут доступны во время и после завершения учебных занятий.
Другие поощрения будут доступны во время и после завершения учебных занятий.
Цели сессии учебного сообщества:
- Определите, как включить поддержку коллег в настройку ED
- Оценка стратегий индукции бупренорфина или снижения вреда на основе потребностей пациента
- Распознать симптомы расстройства, связанного с употреблением опиоидов, у пациентов со сложной ЭД
Темы сессий
Регистрация
Финансирование этой инициативы частично стало возможным благодаря Департаменту психического здоровья и наркологии штата Огайо (OhioMHAS).
Представленная учебная программа согласуется с обучением, предусмотренным в учебной программе Providers Clinical Support System (PCSS) MAT, и охватывает основные элементы, уникальные для лечения опиоидной зависимости с помощью MAT в отделении неотложной помощи.
Если у вас есть вопросы или дополнительная информация, свяжитесь с Мэри Роуленд по адресу [email protected].
Вспомогательные ресурсы:
Американское общество медицины зависимостей (ASAM), полуторадневные онлайн-тренинги
Калифорнийский мост к лечению — Модель моста: расстройство, связанное с употреблением психоактивных веществ, в учреждениях неотложной помощи
Система клинической поддержки поставщиков медицинских услуг: предоставляет основанное на фактических данных обучение и ресурсы, чтобы дать медицинским работникам знания о необходимости лечения OUD (расстройства, связанного с употреблением опиоидов)
Финансирование этого тренинга стало возможным (частично) благодаря гранту штата Огайо по борьбе с опиатами — 1H79T1081684-01 от SAMHSA. Мнения, выраженные в письменных материалах или публикациях конференции, а также докладчиками и модераторами, не обязательно отражают официальную политику Министерства здравоохранения и социальных служб; упоминание торговых наименований, коммерческой практики или организаций также не означает одобрения со стороны правительства США.


 Просто должны быть такие индукционные переходы, чтобы по ним можно было добраться до любого числа.
Просто должны быть такие индукционные переходы, чтобы по ним можно было добраться до любого числа.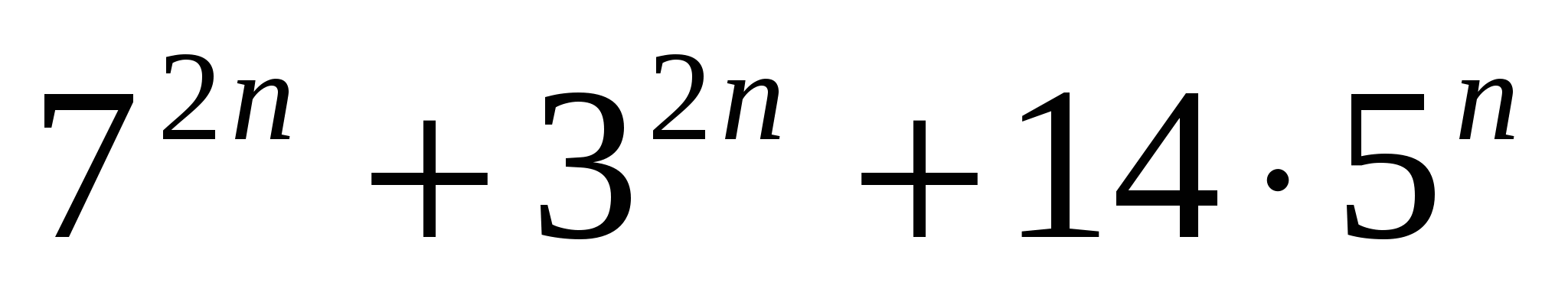 wikipedia.org/wiki/Ramsey’s_theorem
wikipedia.org/wiki/Ramsey’s_theorem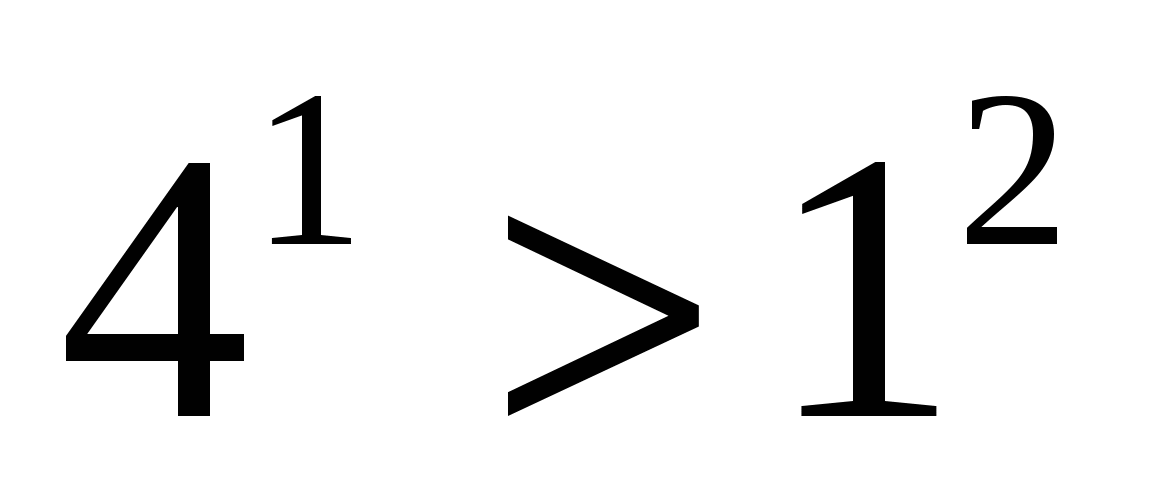
 Видимо это должно быть какое-то неравенство.
Видимо это должно быть какое-то неравенство.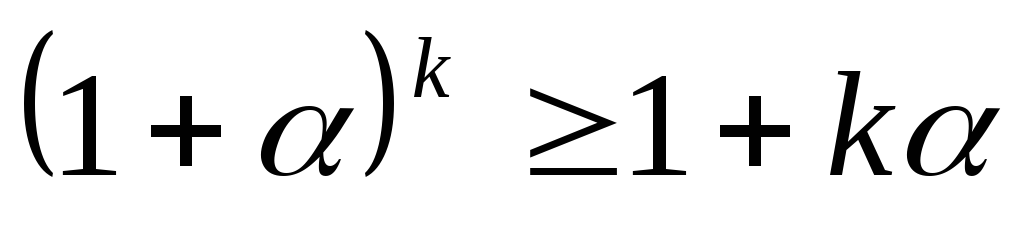
 04.2012, 00:33
04.2012, 00:33 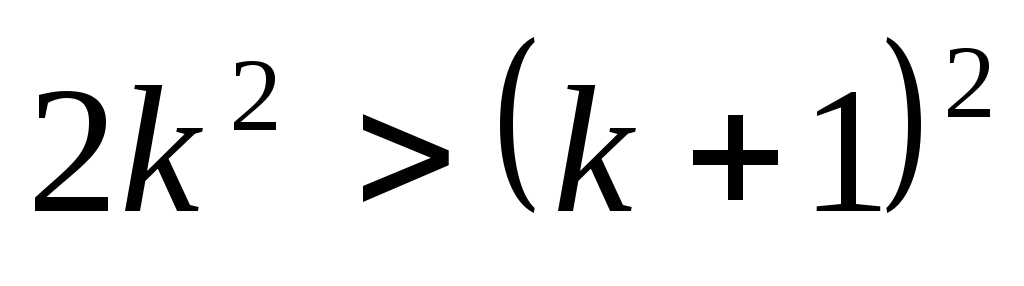 04.2012, 00:37
04.2012, 00:37 
 04.2012, 09:40
04.2012, 09:40 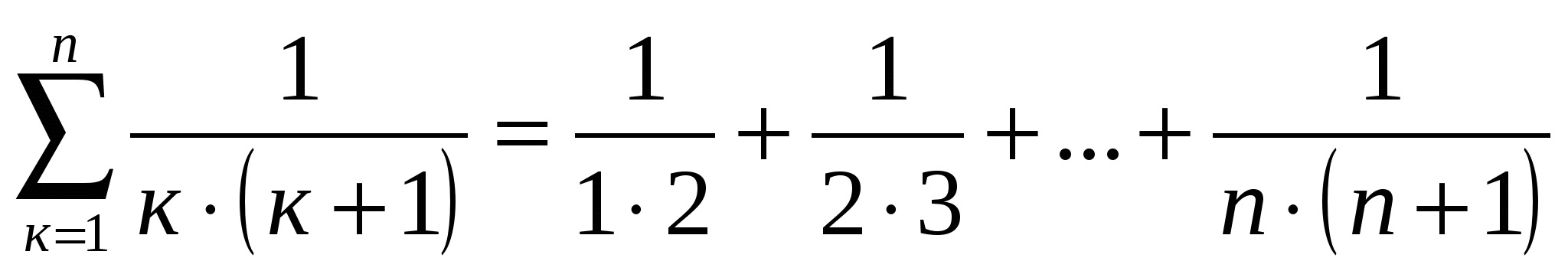 Например, насколько я понимаю, то, что последовательности Гудстейна упорядочены таким образом, что любое их множество имеет минимальный элемент, недоказуемо в арифметике первого порядка. И именно это не позволяет доказать теорему Гудстейна в арифметике первого порядка.
Например, насколько я понимаю, то, что последовательности Гудстейна упорядочены таким образом, что любое их множество имеет минимальный элемент, недоказуемо в арифметике первого порядка. И именно это не позволяет доказать теорему Гудстейна в арифметике первого порядка.
 81 МБ
81 МБ
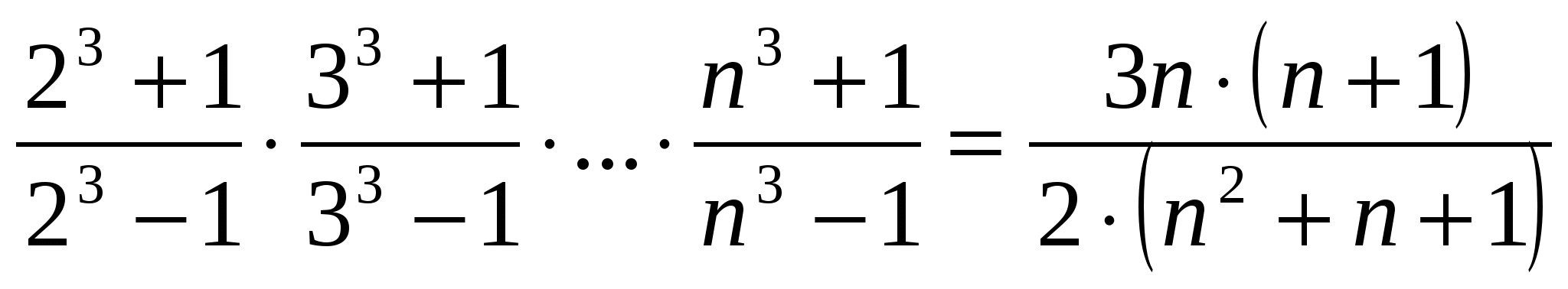
 У пациентов с опиоидами в кровотоке или у тех, кто не находится на ранних стадиях абстиненции, может возникнуть острая абстиненция.
У пациентов с опиоидами в кровотоке или у тех, кто не находится на ранних стадиях абстиненции, может возникнуть острая абстиненция. Предлагаемый в форме таблеток и принимаемый один раз в день, дисульфирам никогда не следует принимать в состоянии алкогольного опьянения и не следует принимать в течение как минимум 12 часов после употребления алкоголя. Неприятные побочные эффекты (тошнота, головная боль, рвота, боли в груди, затрудненное дыхание) могут проявиться уже через десять минут после употребления даже небольшого количества алкоголя и могут продолжаться в течение часа и более.
Предлагаемый в форме таблеток и принимаемый один раз в день, дисульфирам никогда не следует принимать в состоянии алкогольного опьянения и не следует принимать в течение как минимум 12 часов после употребления алкоголя. Неприятные побочные эффекты (тошнота, головная боль, рвота, боли в груди, затрудненное дыхание) могут проявиться уже через десять минут после употребления даже небольшого количества алкоголя и могут продолжаться в течение часа и более.
 doc или .docx)
doc или .docx)
 К ним относятся фармацевты, дипломированные медсестры и лицензированные практические медсестры.
К ним относятся фармацевты, дипломированные медсестры и лицензированные практические медсестры. Кандидаты могут зарегистрировать учетную запись в экстрасети на веб-сайте SAMHSA OTP Extranet. После проверки запроса заявитель получит электронное письмо с именем пользователя и паролем для использования веб-сайта.
Кандидаты могут зарегистрировать учетную запись в экстрасети на веб-сайте SAMHSA OTP Extranet. После проверки запроса заявитель получит электронное письмо с именем пользователя и паролем для использования веб-сайта. 11; Январь-декабрь 2020 г.
11; Январь-декабрь 2020 г.
 Скрининг мочи на наркотики проводится в начале и случайным образом, но в последующем не реже одного раза в 6 месяцев.
Скрининг мочи на наркотики проводится в начале и случайным образом, но в последующем не реже одного раза в 6 месяцев.