ЕСЛИ (функция ЕСЛИ)
Формулы и функции
Формулы и функции
Формулы и функции
Функция ЕСЛИ
-
Общие сведения о формулах в Excel
Статья -
ПРОСМОТРX
Статья -
ВПР
Статья -
Функция СУММ
Статья -
Функция СЧЁТЕСЛИ
Статья -
Функция ЕСЛИ
-
ЕСЛИМН
Статья -
СУММЕСЛИ
Статья -
СУММЕСЛИМН
Статья -
ПОИСКПОЗ
Статья
Далее: Использование функций
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще.
Функция ЕСЛИ — одна из самых популярных функций в Excel. Она позволяет выполнять логические сравнения значений и ожидаемых результатов.
Поэтому у функции ЕСЛИ возможны два результата. Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.
Например, функция =ЕСЛИ(C2=»Да»;1;2) означает следующее: ЕСЛИ(С2=»Да», то вернуть 1, в противном случае вернуть 2).
Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие.
ЕСЛИ(лог_выражение; значение_если_истина; [значение_если_ложь])
Например:
|
Имя аргумента |
|
|---|---|
|
лог_выражение (обязательно) |
Условие, которое нужно проверить. |
|
значение_если_истина (обязательно) |
Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА. |
|
значение_если_ложь (необязательно) |
Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ. |
Простые примеры функции ЕСЛИ
-
=ЕСЛИ(C2=»Да»;1;2)
В примере выше ячейка D2 содержит формулу: ЕСЛИ(C2 = Да, то вернуть 1, в противном случае вернуть 2)
В этом примере ячейка D2 содержит формулу: ЕСЛИ(C2 = 1, то вернуть текст «Да», в противном случае вернуть текст «Нет»). Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.
Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.
В примере выше функция ЕСЛИ в ячейке D2 означает: ЕСЛИ(C2 больше B2, то вернуть текст «Превышение бюджета», в противном случае вернуть текст «В пределах бюджета»)
На рисунке выше мы возвращаем не текст, а результат математического вычисления. Формула в ячейке E2 означает: ЕСЛИ(значение «Фактические» больше значения «Плановые», то вычесть сумму «Плановые» из суммы «Фактические», в противном случае ничего не возвращать).
В этом примере формула в ячейке F7 означает: ЕСЛИ(E7 = «Да», то вычислить общую сумму в ячейке F5 и умножить на 8,25 %, в противном случае налога с продажи нет, поэтому вернуть 0)
Примечание: Если вы используете текст в формулах, заключайте его в кавычки (пример: «Текст»).
Распространенные неполадки
|
Проблема |
Возможная причина |
|---|---|
|
0 (ноль) в ячейке |
Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ. |
|
#ИМЯ? в ячейке |
Как правило, это указывает на ошибку в формуле. |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Операторы вычислений и их приоритеты в Excel
Использование вложенных функций в формуле
Использование функции ЕСЛИ для проверки ячейки на наличие символов
Видео: расширенное применение функции ЕСЛИ
Функция ЕСЛИМН (Microsoft 365, Excel 2016 и более поздние версии)
Усложненные функции ЕСЛИ: как работать с вложенными формулами и избежать ошибок
Обучающие видео: усложненные функции ЕСЛИ
Подсчет значений на основе одного условия с помощью функции СЧЁТЕСЛИ
Подсчет значений на основе нескольких условий с помощью функции СЧЁТЕСЛИМН
Суммирование значений на основе одного условия с помощью функции СУММЕСЛИ
Суммирование значений на основе нескольких условий с помощью функции СУММЕСЛИМН
Функция И
Функция ИЛИ
Функция ВПР
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Логические функции
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Шкала температуры.
 Шкала Цельсия, Фаренгейта, Кельвина, Реомюра
Шкала Цельсия, Фаренгейта, Кельвина, РеомюраИстория
Слово «температура» возникло в те времена, когда люди считали, что в более нагретых телах содержится большее количество особого вещества — теплорода, чем в менее нагретых. Поэтому температура воспринималась как крепость смеси вещества тела и теплорода. По этой причине единицы измерения крепости спиртных напитков и температуры называются одинаково — градусами.
Из того, что температура — это кинетическая энергия молекул, ясно, что наиболее естественно измерять её в энергетических единицах (т.е. в системе СИ в джоулях). Однако измерение температуры началось задолго до создания молекулярно-кинетической теории, поэтому практические шкалы измеряют температуру в условных единицах — градусах.
Шкала Кельвина
В термодинамике используется шкала Кельвина, в которой температура отсчитывается от абсолютного нуля (состояние, соответствующее минимальной теоретически возможной внутренней энергии тела), а один кельвин равен 1/273. 16 расстояния от абсолютного нуля до тройной точки воды (состояния, при котором лёд, вода и водяной пар находятся в равновесии). Для пересчета кельвинов в энергетические единицы служит постоянная Больцмана. Используются также производные единицы: килокельвин, мегакельвин, милликельвин и т.д.
16 расстояния от абсолютного нуля до тройной точки воды (состояния, при котором лёд, вода и водяной пар находятся в равновесии). Для пересчета кельвинов в энергетические единицы служит постоянная Больцмана. Используются также производные единицы: килокельвин, мегакельвин, милликельвин и т.д.
Шкала Цельсия
В быту используется шкала Цельсия, в которой за 0 принимают точку замерзания воды, а за 100° точку кипения воды при атмосферном давлении. Поскольку температура замерзания и кипения воды недостаточно хорошо определена, в настоящее время шкалу Цельсия определяют через шкалу Кельвина: градус Цельсия равен кельвину, абсолютный ноль принимается за −273,15 °C. Шкала Цельсия практически очень удобна, поскольку вода очень распространена на нашей планете и на ней основана наша жизнь. Ноль Цельсия — особая точка для метеорологии, поскольку замерзание атмосферной воды существенно всё меняет.
Шкала Фаренгейта
В Англии и, в особенности, в США используется шкала Фаренгейта. В этой шкале на 100 градусов раздёлен интервал от температуры самой холодной зимы в городе, где жил Фаренгейт, до температуры человеческого тела. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия.
В этой шкале на 100 градусов раздёлен интервал от температуры самой холодной зимы в городе, где жил Фаренгейт, до температуры человеческого тела. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия.
В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 °F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F — 32), то есть изменение температуры на 1 °F соответствует изменению на 5/9 °С. Предложена Г. Фаренгейтом в 1724.
Шкала Реомюра
Предложенна в 1730 году Р. А. Реомюром, который описал изобретённый им спиртовой термометр.
Единица — градус Реомюра (°R), 1 °R равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °R) и кипения воды (80 °R)
1 °R = 1,25 °C.
В настоящее время шкала вышла из употребления, дольше всего она сохранялась во Франции, на родине автора.
|
Пересчёт температуры между основными шкалами |
|||
|
|
Кельвин |
Цельсий |
Фаренгейт |
|
Кельвин (K) |
= K |
= С + 273,15 |
= (F + 459,67) / 1,8 |
|
Цельсий (°C) |
= K − 273,15 |
= C |
= (F − 32) / 1,8 |
|
Фаренгейт (°F) |
= K · 1,8 − 459,67 |
= C · 1,8 + 32 |
= F |
Сравнение температурных шкал
|
Описание |
Кельвин | Цельсий |
Фаренгейт |
Ньютон | Реомюр |
|
Абсолютный ноль |
0 |
−273. |
−459.67 |
−90.14 |
−218.52 |
|
Температура таяния смеси Фаренгейта (соли и льда в равных количествах) |
255.37 |
−17.78 |
0 |
−5.87 |
−14.22 |
| Температура замерзания воды (нормальные условия) |
273.15 |
0 |
32 |
0 |
0 |
|
Средняя температура человеческого тела¹ |
310.0 |
36.8 |
98.2 |
12. |
29.6 |
|
Температура кипения воды (нормальные условия) |
373.15 |
100 |
212 |
33 |
80 |
| Температура поверхности Солнца |
5800 |
5526 |
9980 |
1823 |
4421 |
¹ Нормальная температура человеческого тела — 36.6 °C ±0.7 °C, или 98.2 °F ±1.3 °F. Приводимое обычно значение 98.6 °F — это точное преобразование в шкалу Фаренгейта принятого в Германии в XIX веке значения 37 °C. Поскольку это значение не входит в диапазон нормальной температуры по современным представлениям, можно говорить, что оно содержит избыточную (неверную) точность.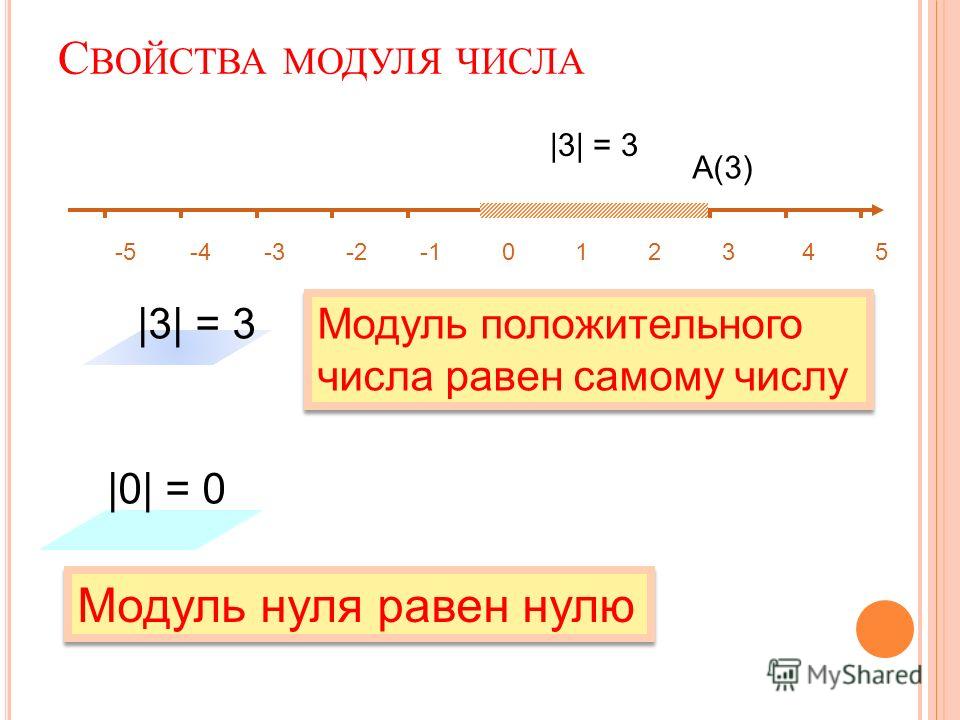 Некоторые значения в этой таблице были округлены.
Некоторые значения в этой таблице были округлены.
Сопоставление шкал Фаренгейта и Цельсия
(oF — шкала Фаренгейта, oC — шкала Цельсия)
|
oF |
oC |
|
oF |
oC |
|
oF |
oC |
|
oF |
oC |
|
-459. |
-273.15 |
|
-60 |
-51.1 |
|
-4 |
-20.0 |
|
20 |
-6.7 |
Для перевода градусов цельсия в кельвины необходимо пользоваться формулой T=t+T0 где T- температура в кельвинах, t- температура в градусах цельсия, T0=273.15 кельвина. По размеру градус Цельсия равен Кельвину.
Конспект урока «Знаки > (больше),
Конспект урока по математике в 1 классе
« Знаки > (больше), < (меньше), = (равно) »
УМК «Школа России», автор учебника М.И. Моро
Тип урока: изучение нового материала.
Цель урока: в ходе практической работы и наблюдений познакомить
со знаками >, <, =; научить выполнять записи с этими знаками; закреплять
знания состава чисел, развивать умение рассуждать.
Планируемые результаты: учащиеся научатся сравнивать любые два
числа и записывать результат сравнения, используя знаки >, <, =; читать
записи; выполнять мыслительные операции анализа и синтеза и делать
умозаключения; применять полученные ранее знания в измененных
условиях; слушать собеседника и вести диалог; слушать учителя и выполнять
его требования; оценивать себя, границы своего знания и незнания; работать
в паре и оценивать товарища.
Познавательные УУД:
1. Ориентироваться в учебнике.
2. Понимать информацию, представленную в виде текста, рисунка,
схем.
3. Сравнивать предметы, объекты: находить общее и различие.
4. Классифицировать предметы, объекты по заданным критериям.
Регулятивные УУД:
1. Организовывать свое рабочее место.
2. Осуществлять контроль в форме сличения своей работы с
заданным эталоном..
3. Вносить дополнения, исправления в свою работу.
Коммуникативные УУД:
1. Соблюдать нормы речевого этикета.
2. Вступать в диалог.
3. Сотрудничать с товарищами при выполнении заданий в паре:
устанавливать и соблюдать очередность действий, корректно
сообщать товарищу об ошибках.
4. Участвовать в коллективном обсуждении учебной проблемы.
Оборудование: для учителя — интерактивная доска или проектор;
магнитный набор цифр и знаков, геометрических фигур; учебник
«Математика, 1 класс»; рабочая тетрадь с печатной основой;
для учащихся – геометрический набор; большие карточки с цифрами;
учебник; рабочая тетрадь, пенал.
Ход урока
1. Организационный момент
2. Актуализация знаний
1. Логическая разминка.
— Сколько хвостов у четырех щенят?
— Сколько месяцев длится лето?
— Что лишнее: ручка, карандаш, отрезок? Почему?
— Прошли четыре дня после воскресенья. Какой наступил день?
— Сколько букв в слове «книга»?
2. Устный счет.
— Сегодня мы отправимся в математическое путешествие, но сначала нам
нужно выбрать транспортное средство. Путешествие сказочное, поэтому,
прибывать на станции мы будем всегда одновременно.
Приготовьте счетный набор, выполните задание.
Задание:
Выбрать рисунок и выложить такой же на парте.
— Какое кол-во фигур вы использовали? Положите карточку
соответствующую кол-ву. ( На доске также.)
— На каких рисунках столько же фигур? (Корабль, легковая машина.)
— На каких рисунках меньше всего? (Маленький грузовик.)
— На каких больше 6, но меньше 9? (Ракета. )
)
— Внимание! Путешествие начинается. Чтобы попасть на математическую
станцию, необходимо хором вести отсчет. Закрыли глаза. Считаем от1 до 5.
• Станция «Быстрый счет»
— Мы прибываем на станцию ( Чтение хором, на доске появляется
запись.)
1 задание (Работа с большими карточками, цифры от 1 до 5.)
— Дети, получившие карточки, выходят к доске и строятся по порядку.
(Проверка.)
— Делайте шаг вперед, если ответом является число на карточке и
называйте его.
1) Какое число следует за числом 3? 4?
2) Какое число стоит между числами 1 и 3? 3 и 5?
3) Какое число предшествует числу 4? 5? 2?
4) Назовите соседей числа 3? 2?
2 задание (Задачи в стихах. Дети показывают карточку с ответом.)
1) Карандаш один у Миши,
Карандаш один у Гриши.
Сколько всего карандашей у малышей?
2) Четыре краски есть у Сани,
Одна у маленького брата.
Все краски посчитайте сами.
Ну, постарайтесь-ка, ребята!
3) Четыре сороки пришли на уроки.
Одна из сорок не знала урок.
Сколько прилежно трудилось сорок?
4) Два щенка – баловника бегают, резвятся.
К шалунишкам три дружка с громким лаем мчатся.
Вместе лучше – веселей.
Сколько будет всех друзей?
— Вы справились с заданиями, и мы отправляемся на следующую
станцию.
• Станция «Спортивная»
— Закрываем глаза, путешествие продолжается.
— Хором считаем от 3 до 8.
(Дети встают и выполняют зарядку.)
Мы читали, мы считали,
А теперь тихонько встали.
Раз – присели, два – нагнулись,
На носочках потянулись.
Руки ставим на бочок:
На носочках скок, скок, скок.
А теперь все тихо сели,
Продолжаем наш урок.
• Станция «Числовые домики»
— Закрыли глаза. Считаем от 7 до 3.
— Вы должны зажечь окошки в домиках. (Работа ведется около доски и
с места, ответ дети показывают карточками.)
— Закрыть глаза – продолжить состав чисел.
2 – это 1 и ?
3 – это 2 и ?
4 – это 2 и ?
4 – это 1 и ?
5 – это 4 и ?
5 – это 2 и ?
3. Работа по теме урока
Работа по теме урока
1) Фронтальная работа
• Станция «Математические знаки»
— Закрыли глаза. Считаем от 10 до 5.
— Перечислите знаки, которые вы знаете. (Дети выходят к доске и берут
карточки со знаками +, -, =. )
Дети выкладывают на парте примеры (счетный набор)
2 3=5 — Какие карточки перевернуты? Выйти к доске и заполнить
пропуски.
5 1=4
3 1 4
Физкультминутка на внимание.
Покажите, что вы готовы к работе.
— левую руку вверх
— 3 вращения кистью
— правую руку вверх
— 2 хлопка
— правую руку вперед
— 3 вращения кистью
— левую руку вперед
— 2 хлопка
— Сложили руки на столе.
(Вернуться к изображениям транспортных средств. Индивидуальная работа
(дети используют счетный набор) и фронтальная (на доске – магнитные
цифры).
— Сравните количество фигур корабля и легковой машины. Как это
записать? (10=10)
— А теперь сравните по количеству фигуры грузовиков. Где фигур
Где фигур
больше? Как же мы запишем сравнение? (Ответы детей.)
— Мы не можем воспользоваться знаком =. Нужен новый знак. В
математике этот знак называется больше >.
9 > 6
(Читает учитель. Читают все дети.)
— На каком рисунке фигур меньше? Значит, какое число меньше 6 или
9? В записи мы будем использовать знак меньше <.
6 < 9
(Читает учитель. Читают все дети.)
— Что вам напоминают эти знаки? (уголки, клювики, ротики)
Открытый ротик направлен к большему числу, уголочек – к меньшему.
Физкультминутка
2) Работа по учебнику
— Откройте учебник на с. 46. Как называются знаки вверху страницы?
(Больше, меньше, равно.)
— Прочитайте, что мы будем делать сегодня на уроке.
— Что мы уже узнали? (Как обозначаются слова «больше», «меньше»,
«равно».)
— Как вы думаете, для чего нужны эти знаки? (Чтобы экономить время
при записи.)
— Посмотрите на левый верхний рисунок. Какие фигуры вы видите?
Какие фигуры вы видите?
(Два зеленых квадрата и три синих круга)
— Чего больше? Как это записать? Чего меньше? Прочитайте запись.
(По аналогии разбираются картинки справа, иллюстрирующие записи 5>4,
4<5 и 5=5.)
— Посмотрите на рисунок с птицами. Составьте рассказ по записи.
(Было 3 птицы, прилетела еще 1. Птиц стало 4.)
— Птиц стало больше или меньше? Как это записали?
— Составьте рассказ по второй записи. (Было 4 птицы, одна птица
улетела. Осталось 3 птицы.)
— Птиц стало больше или меньше? Прочитайте запись. (Три меньше
четырех.)
Работа в паре.
— Вместе с соседом по парте составьте записи к картинкам с вишнями.
(Проверка. Записи приведены на доске: 3+1=4, 4>1, 4-3=1, 1<4.)
4. Закрепление изученного материала
1) Работа в тетради с печатной основой.
— Откройте тетрадь на с. 18. Прочитайте первое задание.
Самостоятельно запишите, какое время показывают часы.
(Фронтальная проверка.)
— Посмотрите на знаки, приведенные ниже. Как называется знак,
который записан первым? Вторым?
(Объяснение, показ, запись знаков в тетради.)
— Посмотрите на рисунок с мячами.
(Записать количество, заполнить пропуски рисунками, с помощью новых
знаков составить запись 5>3, 3<5.)
2) Работа по учебнику.
— Рассмотрите рисунок на с. 47. вспомните сказку В. Сутеева «Мешок
яблок». За что звери принесли зайцу столько подарков? (За доброту.)
Работа в паре.
— Пользуясь рисунком, расскажите соседу по парте, как можно
получить число 5.
(Проверка. Выходит к доске пара для ответа. Спросить несколько пар.)
— Посмотрите на следующий рисунок. Сколько желтых полосок нужно
положить, чтобы накрыть розовую? А сколько зеленых? Почему получили
разные ответы? (Полоски разной длины.) Каких полосок нужно больше?
5. Рефлексия
— Наше путешествие заканчивается.
— Оцените, как вы поняли новую тему, с помощью «Светофора».
6. Подведение итогов урока
— С какими знаками мы сегодня познакомились?
— Покажите знак «больше».
— Покажите знак «меньше».
1 Биткоин в долларах, чему равен, сколько стоит 1 Bitcoin, BTC в долларах
- Главная
- Курсы валют
- Курсы криптовалют
- Курс Биткоина
- 1 Биткоин в долларах
Динамика стоимости 1 Биткоина в долларах
| Дата | USD | Изменения | Изменения % |
|---|---|---|---|
21. 09.2022 09.2022 | 19238.8 $ | +284.8 $ | +1.4803 % |
| 20.09.2022 | 18954 $ | -563.2 $ | -2.9714 % |
| 19.09.2022 | 19517.2 $ | -170.9 $ | -0.8756 % |
18. 09.2022 09.2022 | 19688.1 $ | -403.3 $ | -2.0484 % |
| 17.09.2022 | 20091.4 $ | +371.7 $ | +1.85 % |
| 16.09.2022 | 19719.7 $ | -113.2 $ | -0.574 % |
15. 09.2022 09.2022 | 19832.9 $ | -93.8 $ | -0.473 % |
| Валюта | Стоимость | Капитализация | Объём (24ч.) | Изменение (24 ч.) | ||
|---|---|---|---|---|---|---|
Bitcoin | 19238.8$ +111.23 | 368 554 457 841$ | 1 027 300 000$ | +0. 5815% 5815% | ||
Ethereum | 1349.66$ -0.25 | 165 282 513 030$ | 1 224 810 000$ | -0.0185% | ||
Ripple | 0.4028$ +0.0168 | 40 275 687 999$ | 182 128 000$ | +4.3523% | ||
Litecoin | 53. 48$ +1.9 48$ +1.9 | 3 808 735 737$ | 28 867 600$ | +3.6836% | ||
Monero | 143.4$ +2.38 | 2 606 613 989$ | 27 876 700$ | +1.6877% | ||
Bitcoin Cash / BCC | 114.21$ +1.29 | 2 190 518 521$ | 9 629 260$ | +1. 1424% 1424% | ||
EOS | 1.311$ +0.04 | 1 397 322 440$ | 28 308 100$ | +3.1471% | ||
DigitalCash | 40.77$ +0.17 | 445 447 689$ | 12 508 300$ | +0.4187% |
| Биржа | Курс | Мин. (24ч.) (24ч.) | Макс. (24ч.) | Изменения | Объём |
|---|---|---|---|---|---|
Coinbase 21.09.2022 14:20 | 19083.3$ | 18722$ | 19319.1$ | -132.98 -0.692% | 26587Ƀ |
CoinsBit 21.09.2022 07:13 | 18998.9$ | 18782.3$ | 19565.3$ | -378.066 -1.9511% | 21068.4Ƀ |
Bitfinex 21.09.2022 14:20 | 19108$ | 18754$ | 19319$ | -124 -0.6448% | 7223.08Ƀ |
Kraken 21.09.2022 15:38 | 19239.2$ | 18731.1$ | 19318.1$ | 116.1 +0.6071% | 3954.17Ƀ |
Bitstamp 21.09.2022 14:54 | 19170$ | 18717$ | 19310$ | -56 -0.2913% | 2813.85Ƀ |
P2PB2B 21.09.2022 09:31 | 18854.6$ | 18739.2$ | 19580$ | -525.19 -2.71% | 2349.3Ƀ |
Gemini 21. | 19111.9$ | 18733.6$ | 19340.1$ | -110.74 -0.5761% | 1133.14Ƀ |
OKCoin 21.09.2022 15:37 | 19258.9$ | 18737.1$ | 19319.9$ | 117.6 +0.6144% | 645.359Ƀ |
itBit 21.09.2022 15:08 | 19173.8$ | 18741.2$ | 19301.5$ | 38.25 +0.1999% | 262.025Ƀ |
Exmo 21.09.2022 14:01 | 21088.5$ | 20729$ | 21271.3$ | -147.14 -0.6929% | 112.715Ƀ |
Курс Биткоина по отношению к доллару
Урок математики. (1-й класс): «Знаки «меньше», «больше», «равно»
Цели урока:
- Образовательная: познакомить со знаками меньше «<», больше « >», равно «=» и записями вида 2<3, 3>2, 4=4, повторить геометрический материал, состав чисел;
- Развивающая: развитие коммуникативных качеств личности (умение работать в паре, вести учебный диалог, проводить самооценку)
- Воспитательная: воспитание чувства сопереживания, взаимопомощи.

1. Орг. момент
Внимание, проверь дружок,
Готов ли ты начать урок?
Всёли на месте, всёли в порядке
Книга, ручка и тетрадки?
И цветные карандаши
Ты на парту положи,
И линейку не забудь
В математику держим путь!А сейчас, ребята, поудобнее садитесь,
Не шумите, не вертитесь,
И внимательно считайте
А спрошу вас – отвечайте.
Вам условие понятно?
– Да!
Это слышать мне приятно
Путешествие зовёт
Первоклашек на урок!
2. Основная часть:
Учитель: А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?
Ученики: Решаем, считаем, пишем, думаем…
Учитель: А как вы думаете, что мы будем делать сегодня?
Ученики: Считать, решать, отвечать, думать, чертить…
Учитель: Чтобы полёт прошёл удачно, необходимо быть:
- Внимательными
- Точно и правильно выполнять задания
- Не допускать ошибок, иначе ракета может потерпеть аварию.

В расчётное время, стартуя с Земли,
К загадочным звёздам
Летят корабли
Представим: чуть-чуть помечтали –
И все космонавтами стали.
Учитель: Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)
- Счёт цепочкой до 10.
- Начинает учитель, дети продолжают.
- Отсчёт в обратном направлении.
- Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!
Учитель: Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?
Ученики: геометрические фигуры.
Учитель: Что это за фигуры, назовите.
Ученики: отрезок, прямая, точки, ломаная, кривая.
Учитель: Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.
Рисуй глазами треугольник,
Теперь его переверни
Вершиной вниз
И вновь глазами
Ты по периметру веди.
Рисуй восьмёрку вертикально
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води
И на бочок её клади.
Теперь следи горизонтально.
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец
Зарядка окончилась.
Ты молодец!
Учитель: Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.
1*34**7*910
- Какое число идёт при счёте за числом 3, 6, 9?
- Какое число стоит перед числом 2, 5, 8, 10?
- Назовите соседей числа 2, 7?
Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)
| 2 3=5 | 4 =2 | |
| 5 1=4 | 1+ =4 | |
| 3+ =5 | 5- =4 |
Молодцы! Пульт исправен.
Учитель: Пока наша ракета поднимается ввысь, поиграем в игру «Сложи фигуру».
Нужно из палочек сложить фигуру, состоящую из четырёх квадратов.
Посчитай сколько здесь квадратов? (фигура состоит из 4 квадратов)
Переложи 2 палочки так, чтобы получилось 5 одинаковых квадратов.
Наша ракета всё дальше и дальше удаляется от Земли, как приятно вспомнить всё, что связано с землёй. Представьте, что мы на большой лесной полянке.
Физминутка: (негромко звучит весёлая музыка)
На зарядку солнышко поднимает нас,
Поднимаем руки мы по команде раз,
А над нами весело шелестит листва,
Опускаем руки мы по команде два.
Соберём в корзину ягоды, грибы –
Дружно наклоняемся по команде три.
На четыре и на пять
Будем дружно мы скакать.
Ну, а по команде шесть
Всем за парты тихо сесть!
Учитель: А сейчас приготовьте свои квадраты. Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.
Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.
Каких квадратов меньше?
Какое число меньше 2 или 3?
В математике есть специальная запись. Это записывают так: 2<3
< – знак меньше
Каких квадратов больше? (синих)
Какое число больше? (3)
Кто догадался, как это записать? 3>2
> – знак больше
Знак ставится так, чтобы к большему числу «клювик» был открыт.
Давайте отдохнём и посмотрим телевизор, что у нас сегодня показывают (работа с учебником, выполнение задания).
- Сколько было птичек на первой картинке
- Сколько прилетело
- Сколько стало
- Их стало больше или меньше
- Как это записали, прочитайте
- Сколько ягод на кисточке
- Что произошло с ягодами
- Как это записать
- Какое число больше, меньше?
Учитель: Наша ракета стремительно несётся ввысь. Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.
Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.
У кого можно попросить помощи, если очень трудно? (соседа по парте)
| 2+2 | 1+2 | 4-2 | ||
| 3+2 | 3-1 | 5-3 |
– Мы победили, корабль удаляется. Заполним ботржурналы. Проверьте рабочее место, сядьте поудобнее, чтобы бортжурналы лежали правильно, записи были чёткими и аккуратными. Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)
Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)
– Перед вами знаки. Как называется первый знак? (больше)
Как называется второй знак? (меньше)
Напишите знак по точкам, допишите до конца строки.
Учитель: Перед стартом ракеты я предлагаю вам поработать в паре. У вас на столах карточки, нужно вставить недостающие знаки «больше» или «меньше».
Карточка.
| 2*3 | 5*7 | 8*5 | ||
| 5*3 | 10*7 | 6*2 | ||
| 3*9 | 7*1 | 6*9 |
3.
 Рефлексия:
Рефлексия:Благодаря дружной работе наша ракета совершила мягкую посадку. Во время полёта мы провели большую работу.
– Скажите, что вы для себя узнали нового?
– Чем мы сегодня занимались?
– Что вам помогло хорошо работать на уроке?
У вас на столах лежат мордочки, нарисуйте на них выражения лица весёлое или грустное, кому на уроке было хорошо поднимите весёлую мордочку. А у кого что-то не получилось и было грустно? (таких может не быть)
Полёт завершён, всем спасибо!
Глава 11. Механические колебания и волны
Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где — некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде
Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде
(11.1) |
где , и — некоторые числа.
Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний — это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус — периодическая функция с периодом .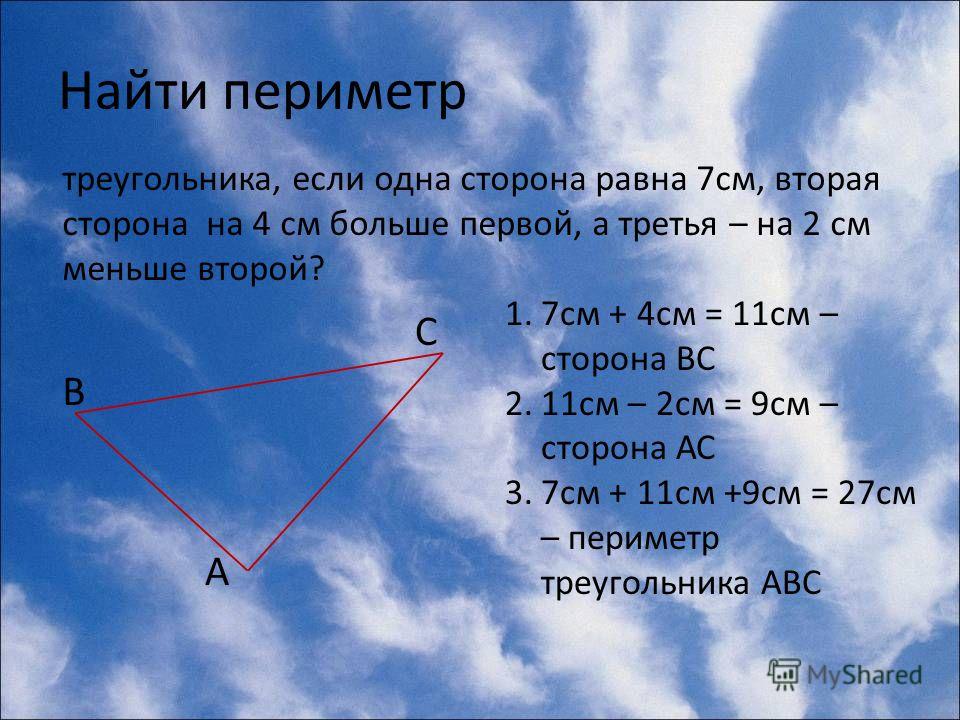 Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем
Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем
(11.2) |
Частотой колебаний тела называется число колебаний, совершаемых в единицу времени. Очевидно, что частота колебаний связана с периодом колебаний по формуле
(11.3) |
Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).
Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.
Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.
В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника
Для пружинного маятника
(11.4) |
где — коэффициент жесткости пружины, — масса груза. Период колебаний математического маятника определяется следующим соотношением
(11.5) |
где — длина нити, — ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.
Чтобы найти циклическую частоту колебаний груза в задаче 11.1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с-1 (ответ 1).
Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11. 1.3), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия — одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону — вторая, назад в положение равновесия — третья, из положения равновесия в начальную точку — четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода — две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4).
1.3), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия — одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону — вторая, назад в положение равновесия — третья, из положения равновесия в начальную точку — четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода — две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4).
Величина перемещения тела — расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3).
По определению фаза колебаний — это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 — 3.
Поэтому правильный ответ в задаче 11.1.5 — 3.
Период — это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6) тело затрачивает четвертую часть периода (ответ 3).
Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2. Функция же — тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4).
Функция же — тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4).
При гармонических колебаниях скорость тела изменяется по закону , где — амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени (задача 11.1.8). Используя далее известную тригонометрическую формулу, получаем
Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2).
За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2).
Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2).
Амплитуду колебаний скорости (задача 11.1.10) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где — коэффициент жесткости пружины, — амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где — масса тела, — скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим
Приравнивая эти энергии, находим
(ответ 1), где использовано выражение для круговой частоты колебаний груза на пружине:
По формуле (11.4) получаем в задаче 11.2.1
(ответ 4).
Из формулы (11.5) заключаем (задача 11.2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).
Часы — это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3).
Чтобы найти амплитуду колебаний в задаче 11. 2.4, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим
2.4, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим
где — такой угол, что . Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).
В задаче 11.2.5 имеем при см. Откуда см (ответ 2).
Задачи 11.2.6 и 11.2.7 посвящены механическим волнам. Волна – некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка среды совершает колебания около определенного положения и в среднем не перемещается в пространстве. Волна характеризуется периодом (или связанной с ним частотой ), скоростью и длиной волны , которая определяется как минимальное расстояние между точками, колеблющимися в одинаковой фазе. Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны
Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны
(11.6) |
которую легко запомнить, поскольку эта связь имеет такой же вид как обычное соотношение между расстоянием, скоростью и временем. Например, в задаче 11.2.6 по формуле (11.6) находим длину волны м (ответ 2).
Как следует из рисунка в задаче 11.2.7 длина волны, распространяющейся по шнуру, равна м. Поэтому по формуле (11.6) имеем Гц (ответ 4).
Поскольку в момент максимального отклонения пружинного маятника, механическая энергия системы равна потенциальной энергии пружины, то
где — амплитуда колебаний, — жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличилась в раз (задача 11.2.8 – ответ 1).
Используя известную тригонометрическую формулу, получим в задаче 11.2.9
Эта зависимость представляет собой гармоническую функцию, но колеблющуюся вокруг точки . Амплитудой этих колебаний является множитель перед косинусом — (так как сам косинус меняется в интервале от -1 до 1). Циклической частотой — величина (ответ 4).
Вертикальный пружинный маятник отличается от горизонтального (задача 11.2.10) наличием силы тяжести. Однако сила тяжести приводит только к сдвигу положения равновесия маятника, а возвращающая сила по прежнему будет зависеть от смещения маятника от положения равновесия по закону (так как возвращающей силой будет разность силы упругости и постоянной силы тяжести). Поэтому период колебаний груза на вертикальной и горизонтальной пружине — одинаков (конечно, при условии, что и сам груз и пружины одинаковы). Правильный ответ в задаче — 3.
Подкаст о здоровье Калифорнийского университета в Сан-Диего
N Equals One — это подкаст о науке и открытиях, созданный и размещенный Центром здравоохранения Калифорнийского университета в Сан-Диего. Коммуникационная команда. В каждом выпуске мы представляем вам историю одного проекта, одного открытия или одного ученого.
Коммуникационная команда. В каждом выпуске мы представляем вам историю одного проекта, одного открытия или одного ученого.
Вы также можете найти N Equals One в iTunes, SoundCloud или использовать наш RSS-канал, чтобы добавить нас в свое любимое приложение для подкастов.
Все последние новости о COVID-19 и фертильности, беременности и грудном вскармливании
Несмотря на настоятельные рекомендации Центра по контролю и профилактике заболеваний, у беременных в США по-прежнему низкий уровень вакцинации против COVID-19. Это был трудный выбор для многих родителей или будущих родителей, поэтому в этом выпуске мы углубимся в детали. Эксперты по здравоохранению Калифорнийского университета в Сан-Диего Синтия Гьямфи-Баннерман, доктор медицины, Кристина Чемберс, доктор философии, магистр здравоохранения, и Ларс Боде, доктор философии, все оценивают последние исследования и рекомендации. Мы также поговорили с мамой из Сан-Диего Жасмин Фаниель о ее проблемах и о том, каково было столкнуться с этим выбором во время ее беременности. Узнайте больше о безопасности воздействия при беременности и кормлении грудью на сайте mothertobaby.org.
Узнайте больше о безопасности воздействия при беременности и кормлении грудью на сайте mothertobaby.org.
Слушайте сейчас
Справедливость финансирования: расовые различия в грантовом финансировании исследований
Академические ученые полагаются на гранты для финансирования своих исследований, а крупнейшим спонсором биомедицинских исследований является Национальный институт здравоохранения США (NIH). К сожалению, многие проявления расового неравенства в академической науке просочились в этот процесс финансирования грантов. В нынешнем виде заявки от афроамериканских или чернокожих ученых с меньшей вероятностью будут финансироваться NIH, чем заявки, поданные белыми учеными. В этом выпуске Майкл Таффе, доктор философии, профессор Калифорнийского университета в Сан-Диего, объясняет сложные первопричины этого несоответствия и то, что ученые и Национальный институт здравоохранения могут сделать для его устранения.
Слушайте сейчас
От ландшафтного дизайна к лаборатории: путешествие Дэвида Гонсалеса по академическим кругам
Дэвид Гонсалес, доктор философии, доцент Калифорнийского университета в Сан-Диего, где его лаборатория изучает, как бактерии влияют на наше здоровье. Он также американец мексиканского происхождения в первом поколении из округа Сан-Диего. Гонсалес, как и его братья и сестры, бросил школу, устроился на работу и создал семью. Но когда он обнаружил, что косит газоны напротив местного колледжа, что-то внутри него изменилось. В этом эпизоде Гонсалес рассказывает о своем уникальном путешествии по академическим кругам и чествует наставников, которые вдохновляли его на этом пути.
Он также американец мексиканского происхождения в первом поколении из округа Сан-Диего. Гонсалес, как и его братья и сестры, бросил школу, устроился на работу и создал семью. Но когда он обнаружил, что косит газоны напротив местного колледжа, что-то внутри него изменилось. В этом эпизоде Гонсалес рассказывает о своем уникальном путешествии по академическим кругам и чествует наставников, которые вдохновляли его на этом пути.
Слушайте сейчас
Экологическая справедливость: где COVID-19 встречается с изменением климата
Изменение климата и COVID-19, возможно, являются двумя величайшими кризисами нашего времени. Еще одна их общая черта — это то, что они непропорционально сильно влияют на одних и тех же людей — в первую очередь на малообеспеченные слои населения и цветные сообщества. В этом выпуске мы поговорим с Тариком Бенмарниа, доктором философии, о его работе в области экологической справедливости и о том, как она влияет на здоровье общества, будь то инфекционное заболевание, загрязняющие вещества, жара или лесные пожары. Если мы сможем устранить структурные фундаментальные причины этих проблем и неравенства, говорит он, мы сможем построить более устойчивые сообщества.
Если мы сможем устранить структурные фундаментальные причины этих проблем и неравенства, говорит он, мы сможем построить более устойчивые сообщества.
Слушайте сейчас
Правительство отрицает COVID-19
Несмотря на политический риск для исследователей и участников, новое исследование дает первое представление о влиянии пандемии COVID-19 на работников здравоохранения в Никарагуа, стране, где правительство отказывается признать существование пандемия, или сделать что-нибудь с этим. Исследователь Джеймс МакКерроу, доктор медицинских наук, обсуждает свою работу с коллегой Хорхе Уэте-Пересом, доктором философии. Ричард Файнберг, доктор философии, делится своим мнением в качестве эксперта по американо-латиноамериканским отношениям.
Слушайте сейчас
Защитите свое здоровье
Более 5 миллионов человек во всем мире умирают по причинам, связанным с недостатком физической активности. Новости приходят, когда многие люди перешли на работу из дома, сталкиваются с закрытием местных спортивных залов и могут укрываться на месте, поскольку мы сталкиваемся с пандемией COVID-19. Две исследовательские группы из Медицинской школы Калифорнийского университета в Сан-Диего стремились понять сидячий образ жизни: одна обнаружила, что даже легкая физическая активность, в том числе простое стояние, может принести пользу здоровью, а другая обнаружила, что американцы все еще слишком много сидят.
Новости приходят, когда многие люди перешли на работу из дома, сталкиваются с закрытием местных спортивных залов и могут укрываться на месте, поскольку мы сталкиваемся с пандемией COVID-19. Две исследовательские группы из Медицинской школы Калифорнийского университета в Сан-Диего стремились понять сидячий образ жизни: одна обнаружила, что даже легкая физическая активность, в том числе простое стояние, может принести пользу здоровью, а другая обнаружила, что американцы все еще слишком много сидят.
Слушайте сейчас
Вакцины против COVID-19: наш шанс на иммунитет от SARS-CoV-2
Во всем мире по крайней мере 53 вакцины против COVID-19 в настоящее время проходят клинические испытания. Четыре самых крупных и перспективных проекта вышли на финальный этап Фазы III. Калифорнийский университет в Сан-Диего является испытательным полигоном для трех компаний из большой четверки: Moderna, AstraZeneca и Janssen/Johnson & Johnson. Мы разговариваем со Сьюзен Литтл, доктором медицинских наук, главным исследователем двух клинических испытаний COVID-19 в Сан-Диего, которые сосредоточены на поиске вакцины против SARS-CoV-2. Литтл обсуждает науку, стоящую за вакцинами, как они будут работать для борьбы с текущей пандемией и когда потенциальный COVID-19вакцина будет готова.
Литтл обсуждает науку, стоящую за вакцинами, как они будут работать для борьбы с текущей пандемией и когда потенциальный COVID-19вакцина будет готова.
Слушайте сейчас
Как предотвратить твиндемию (подсказка: сделайте прививку от гриппа!)
У нас пока нет вакцины для предотвращения заражения SARS-CoV-2, новым коронавирусом, вызывающим COVID-19, но у нас есть вакцина против другого респираторного вируса: гриппа. В этом выпуске врач-инфекционист Мишель Риттер, доктор медицинских наук, рассказывает о разнице между гриппом и COVID, о том, можно ли заразиться и тем, и другим, и почему сделать прививку от гриппа в этом году как никогда важно.
Слушайте сейчас
Что мини-легкие в тарелке могут рассказать нам о COVID-19? Карлин изучает такие вирусы, как вирус Зика, а Лейбель разработала «мини-легкие» — органоиды на основе стволовых клеток, которые растут в чашке Петри в лаборатории, где она может изучать заболевания, поражающие легкие новорожденных.
 Во всяком случае, это то, чем они занимались полгода назад. Затем SARS-CoV-2, новый коронавирус, вызвавший COVID-19.пандемия вошла в нашу жизнь. Карлин и Лейбель быстро объединились, чтобы изучить, что происходит с легкими, когда они заражены SARS-CoV-2, и как мы можем уменьшить этот ущерб.
Во всяком случае, это то, чем они занимались полгода назад. Затем SARS-CoV-2, новый коронавирус, вызвавший COVID-19.пандемия вошла в нашу жизнь. Карлин и Лейбель быстро объединились, чтобы изучить, что происходит с легкими, когда они заражены SARS-CoV-2, и как мы можем уменьшить этот ущерб.Слушайте сейчас
Фармацевт встретится с вами сейчас
В этом выпуске Кандис Морелло, PharmD, фармацевт и преподаватель Школы фармации и фармацевтических наук Skaggs в Калифорнийском университете в Сан-Диего, рассказывает о своей карьере, вдохновленной персиковым деревом ее бабушки. — и объясняет, как фармацевты стали неотъемлемой частью медицинской команды пациента. Ее клиника по коррекции диабета является примером того, как фармацевты могут улучшить результаты лечения пациентов и помочь снизить расходы на здравоохранение.
Слушайте сейчас
Наука встречается с искусством — на платье
Днем научный сотрудник Беата Мирзва, доктор философии, изучает клеточное деление. Ночью она делает одежду — платья, брюки, обувь, рюкзаки — покрытые разноцветными делящимися ячейками. В этом эпизоде она рассказывает о своей любви как к науке, так и к искусству, о том, как ее уникальные проекты помогают людям увлекаться наукой, и о своей новой роли посла IF/THEN Американской ассоциации содействия развитию науки (AAAS). Узнайте больше о Мирзве и ее проектах на
beatascienceart.com и
www.ifthenshecan.org/ambassadors.
Ночью она делает одежду — платья, брюки, обувь, рюкзаки — покрытые разноцветными делящимися ячейками. В этом эпизоде она рассказывает о своей любви как к науке, так и к искусству, о том, как ее уникальные проекты помогают людям увлекаться наукой, и о своей новой роли посла IF/THEN Американской ассоциации содействия развитию науки (AAAS). Узнайте больше о Мирзве и ее проектах на
beatascienceart.com и
www.ifthenshecan.org/ambassadors.
Слушайте сейчас
Медицинский ДНК-тест и потребительский генетический анализ
Лиза Мадленски, доктор философии, директор программы семейной генетики рака в Онкологическом центре Мура при Калифорнийском университете в Сан-Диего, объясняет разницу между медицинскими тестами ДНК и потребительским генетическим анализом, таким как 23andMe. Она рассказывает о самородках, которые можно получить из потребительских товаров, и о том, что может не применяться. Она предостерегает нас от использования потребительских товаров для принятия медицинских решений. Вместо этого, если вас беспокоит риск для вашего здоровья, поговорите с консультантом по генетике.
Вместо этого, если вас беспокоит риск для вашего здоровья, поговорите с консультантом по генетике.
Слушайте сейчас
Совмещая докторскую степень, докторскую степень и адвокатскую деятельность с Алеком Калаком
В детстве Алек Калак знал, что хочет стать врачом, следуя по стопам своего отца, но не раньше, чем он поступил в колледж в другом штате и оставил свое сообщество позади, что он обнаружил свою вторую страсть: защиту интересов. Теперь, будучи студентом второго курса MD/PhD в Медицинской школе Калифорнийского университета в Сан-Диего, Алек рассказал нам о том, как он заполняет свое «свободное» время, выступая за большую известность и поддержку коренных американцев в STEM и медицинской карьере.
Слушайте сейчас
Ваши легкие, высокогорье и спортивная подготовка
Сьюзен Хопкинс, доктор медицинских наук, профессор медицины и радиологии, работает над тем, чтобы выяснить, как работают легкие, и, в частности, что происходит с легкими при стрессе. После извилистого пути, который привел ее из семейной медицины в маленьком горном городке в Канаде в Медицинскую школу Калифорнийского университета в Сан-Диего, где она исследует влияние низкого содержания кислорода и физических упражнений на функцию легких, интересы Хопкинс возвращаются к ее любви к вычислениям. как все работает. Она изучает высотный отек легких (ВОЛЭ), уникальное состояние, возникающее только на больших высотах и вызывающее внезапное наполнение легких жидкостью, и пытается понять, почему ВОЛ легко обратим, в то время как другие подобные состояния в клинике могут быть настолько обратимыми. смертельный. В этом выпуске она беседует с нашим стажером Ноем Лоуи о своих исследованиях и делится некоторыми мыслями о том, как взаимосвязаны спортивные тренировки и функция легких.
После извилистого пути, который привел ее из семейной медицины в маленьком горном городке в Канаде в Медицинскую школу Калифорнийского университета в Сан-Диего, где она исследует влияние низкого содержания кислорода и физических упражнений на функцию легких, интересы Хопкинс возвращаются к ее любви к вычислениям. как все работает. Она изучает высотный отек легких (ВОЛЭ), уникальное состояние, возникающее только на больших высотах и вызывающее внезапное наполнение легких жидкостью, и пытается понять, почему ВОЛ легко обратим, в то время как другие подобные состояния в клинике могут быть настолько обратимыми. смертельный. В этом выпуске она беседует с нашим стажером Ноем Лоуи о своих исследованиях и делится некоторыми мыслями о том, как взаимосвязаны спортивные тренировки и функция легких.
Слушайте сейчас
Бесплатная клиника, управляемая студентами: обучение состраданию, забота о нуждающихся для недостаточно обслуживаемых в Сан-Диего и предоставляет уникальный практический опыт для врачей-стажеров.
 Одно из самых заветных воспоминаний Смит за более чем 20 лет работы в клинике — это время, когда студенты собирали средства, чтобы помочь незастрахованному мужчине получить протез ноги, который ему был нужен, чтобы вернуться к работе. По ее словам, одна из лучших вещей в клинике — это возможность быть частью жизни пациентов в течение многих лет, знакомясь с ними и их семьями. Клиника является частью нового Института эмпатии и сострадания Т. Денни Сэнфорда Калифорнийского университета в Сан-Диего. Узнать больше об институте можно на
сострадание.ucsd.edu
Одно из самых заветных воспоминаний Смит за более чем 20 лет работы в клинике — это время, когда студенты собирали средства, чтобы помочь незастрахованному мужчине получить протез ноги, который ему был нужен, чтобы вернуться к работе. По ее словам, одна из лучших вещей в клинике — это возможность быть частью жизни пациентов в течение многих лет, знакомясь с ними и их семьями. Клиника является частью нового Института эмпатии и сострадания Т. Денни Сэнфорда Калифорнийского университета в Сан-Диего. Узнать больше об институте можно на
сострадание.ucsd.eduСлушайте сейчас
Присоединяйтесь ко всем нам
На протяжении большей части истории научные и медицинские исследования в основном касались белых людей, и в основном белых мужчин. Теперь мы знаем, что эти результаты не всегда применимы к людям с разным генетическим и экологическим происхождением. Вот почему цель Исследовательской программы «Все мы» — ускорить медицинские открытия путем сбора данных о здоровье, привычках, семейной истории, генетике и окружающей среде от миллиона или более участников, особенно участников из исторически недопредставленных сообществ. В UC San Diego Health проект All of Us возглавляет Люсила Оно-Мачадо, доктор медицинских наук, профессор и заведующая кафедрой биомедицинской информатики. В этом выпуске она рассказывает о программе, о том, что ее волнует и что будет дальше. Узнайте больше на
В UC San Diego Health проект All of Us возглавляет Люсила Оно-Мачадо, доктор медицинских наук, профессор и заведующая кафедрой биомедицинской информатики. В этом выпуске она рассказывает о программе, о том, что ее волнует и что будет дальше. Узнайте больше на
Слушайте сейчас
Спортивный врач направляется на чемпионат мира среди женщин
В этом эпизоде мы поговорим с Аланом Шахтаджи, DO, врачом семейной и спортивной медицины в UC San Diego Health и врачом команды женской национальной сборной США по футболу. Мы встретились с Шахтаджи утром перед его отъездом, чтобы присоединиться к команде и отправиться с ними на чемпионат мира 2019 года во Францию. Он рассказывает о том, чем занимается, что ему в этом нравится и что сложного в оказании медицинской помощи элитной команде за границей. Он также дает несколько советов всем, кто заинтересован в том, чтобы оставаться здоровым и хорошо выступать в футболе, в том числе родителям детей, которые занимаются спортом.
Слушайте сейчас
Соревнования по краудсайсингу в классе
Трей Идекер и Самсон Фонг читают курс в Медицинской школе Калифорнийского университета в Сан-Диего под названием «Биологические сети и биомедицина». Он предназначен для того, чтобы познакомить аспирантов с концепцией сетевой биологии — живых систем как взаимосвязанного целого, а не с отдельными клетками, белками или генами — и с инструментами биоинформатики, используемыми для изучения этих систем. Но вместо стандартного итогового экзамена Идекер и Фонг устроили соревнование. Студенты работали в группах, чтобы проанализировать базу данных генетической информации пациентов и определить гены, наиболее тесно связанные с шизофренией. Ведущие команды не только составили список известных генов, связанных с шизофренией, они провели анализ менее чем за пять минут и превзошли ранее опубликованные подходы.
Слушайте сейчас
Все об эндометриозе
«Крошечные конькобежцы на вашей матке» — так одна пациентка с эндометриозом описывает боль, с которой она жила в течение девяти лет, прежде чем ей поставили диагноз. В этом выпуске пациентка Моника Кейн рассказывает о своем личном пути к изнурительному заболеванию, а Санджай Агарвал, доктор медицинских наук, рассказывает обо всем, что связано с эндометриозом, в том числе о первом новом лекарстве за десятилетие, которое меняет правила игры.
В этом выпуске пациентка Моника Кейн рассказывает о своем личном пути к изнурительному заболеванию, а Санджай Агарвал, доктор медицинских наук, рассказывает обо всем, что связано с эндометриозом, в том числе о первом новом лекарстве за десятилетие, которое меняет правила игры.
Слушайте сейчас
Следующий шаг в лечении рака: персонализированная вакцина?
Тамара Штраус, первая пациентка, принявшая участие в первом в своем роде клиническом испытании в Онкологическом центре Мура в Калифорнийском университете в Сан-Диего для тестирования персонализированной вакцины с использованием ее уникальных раковых мутаций для усиления противоопухолевого иммунного ответа, присоединяется Эзра Коэн, доктор медицинских наук, заместитель директора по трансляционным наукам в Онкологическом центре Мурса, и Стивен Шенбергер, доктор медицинских наук, профессор иммунологии в Институте аллергии и иммунологии Ла-Хойя, рассказывают о надежде на новую персонализированную противораковую вакцину. доктора Коэн и Шенбергер разработали новую технологию, которая определяет уникальные цели пациента, которые можно использовать для создания вакцины, специфичной для каждого отдельного человека. В пилотном исследовании на первом этапе принимают участие 10 пациентов с солидными опухолями. Чтобы узнать больше об этом исследовательском визите
рак.ucsd.edu
доктора Коэн и Шенбергер разработали новую технологию, которая определяет уникальные цели пациента, которые можно использовать для создания вакцины, специфичной для каждого отдельного человека. В пилотном исследовании на первом этапе принимают участие 10 пациентов с солидными опухолями. Чтобы узнать больше об этом исследовательском визите
рак.ucsd.edu
Слушайте сейчас
Выживание после рака, часть 2: Рак не определяет вас
В нашем предыдущем выпуске о выживании после рака Мишель Брубейкер рассказала о своем недавнем пути к раку. В этом выпуске Лори Найт, лицензированный клинический социальный работник, и Сесилия Касперик, медсестра-навигатор по лечению рака молочной железы, из Комплексного центра здоровья груди Калифорнийского университета в Сан-Диего, рассказывают о том, как Мишель может двигаться вперед после лечения, не определяя свою жизнь раком. . Они дают советы друзьям и членам семьи, чтобы помочь пациентам перейти к выживанию и дальше. Чтобы узнать больше о путешествии Мишель, посмотрите ее видео на
health.ucsd.edu/cancerstories
Чтобы узнать больше о путешествии Мишель, посмотрите ее видео на
health.ucsd.edu/cancerstories
Слушайте сейчас
Выживание после рака, часть 1: история выжившего
Когда у человека нет признаков рака, он переходит в фазу, известную как «выживание». «Хотя это радостный момент, он также может быть эмоциональным», — говорит Мишель Брубейкер. Только недавно Мишель превратилась из больной раком груди в выжившую, и она решает множество вопросов и чувств. Пока Мишель делится своей историей, Лори Найт, лицензированный клинический социальный работник, и Сесилия Касперик, медсестра-навигатор по лечению рака молочной железы из Комплексного центра здоровья груди при Калифорнийском университете в Сан-Диего, объясняют выживаемость. Чтобы узнать больше о путешествии Мишель, посмотрите ее видео на health.ucsd.edu/cancerstories
Слушайте сейчас
Клинические испытания 101
В этом выпуске мы поговорим с Кэтрин Голд, доктором медицинских наук, онкологом, специализирующимся на лечении рака головы, шеи и легких, о клинических испытаниях — что это такое и зачем кому-то может понадобиться принять участие в одном, и как они могли бы начать работу.
Послушайте
Истории обмена медсестрами отделения интенсивной терапии на пенсии
Мы беседуем с Мэри Хаким и Яном Хеберт об их 37-летней карьере медсестер в UC San Diego Health. Они выполняли различные функции в Службе помощи женщинам и младенцам, специализируясь в отделении интенсивной терапии новорожденных (ОИТН). Узнайте об их личном опыте, проблемах и всех технологических достижениях, сделанных за эти годы, которые теперь дают шанс выжить детям, рожденным менее чем за фунт.
Слушайте сейчас
Разговор о нейробиологии и #scicomm с Эли Астроцит
В этом выпуске мы поговорим с аспиранткой нейробиологии Элисон Колдуэлл, известной в Интернете как Alie_Astrocyte в Твиттере и Neuro Transmissions на YouTube, о ее исследованиях, жизни аспиранта и почему она думает о науке. общение (#scicomm) очень важно.
Слушай сейчас
Нерассказанная история врожденного сифилиса
По данным Центров по контролю и профилактике заболеваний, врожденный сифилис растет с 2001 г. , причем в 2014 г. он резко увеличился в Соединенных Штатах. Хотя многие могут не думать о сифилисе как о текущей проблеме общественного здравоохранения, он по-прежнему представляет реальную угрозу для матерей и их будущих детей. Недавно получившая грант в размере 150 000 долларов США для дальнейшего изучения основных причин этой вспышки, Дженнифер Вагман, доктор медицинских наук, доцент кафедры инфекционных заболеваний и глобального здравоохранения Медицинской школы Калифорнийского университета в Сан-Диего, обсуждает некоторые мысли о том, почему мы можем наблюдать рост врожденного сифилиса и какие шаги можно предпринять для борьбы с этой эпидемией.
, причем в 2014 г. он резко увеличился в Соединенных Штатах. Хотя многие могут не думать о сифилисе как о текущей проблеме общественного здравоохранения, он по-прежнему представляет реальную угрозу для матерей и их будущих детей. Недавно получившая грант в размере 150 000 долларов США для дальнейшего изучения основных причин этой вспышки, Дженнифер Вагман, доктор медицинских наук, доцент кафедры инфекционных заболеваний и глобального здравоохранения Медицинской школы Калифорнийского университета в Сан-Диего, обсуждает некоторые мысли о том, почему мы можем наблюдать рост врожденного сифилиса и какие шаги можно предпринять для борьбы с этой эпидемией.
Слушайте сейчас
Медицинские работники помогают выявить торговлю людьми
Согласно последним данным Национальной горячей линии по борьбе с торговлей людьми, количество случаев торговли людьми в Соединенных Штатах выросло более чем на 35 процентов в 2016 году. Мысль о торговле людьми может вызывать в воображении образы правоохранительных органов приходят на помощь, но часто помощь приходит из других мест. Большинство жертв попадают в больницу для лечения состояний, связанных с торговлей людьми. В этом эпизоде мы беседуем с сотрудниками Калифорнийского университета в Сан-Диего, доктором медицинских наук Региной Ванг, Сарой Уильямсон, RN, и Карен Митчелл-Килс, RN, которые сформировали комитет, чтобы помочь информировать медицинских работников о признаках, которые могут указывать на то, что пациент жертва торговли людьми.
Большинство жертв попадают в больницу для лечения состояний, связанных с торговлей людьми. В этом эпизоде мы беседуем с сотрудниками Калифорнийского университета в Сан-Диего, доктором медицинских наук Региной Ванг, Сарой Уильямсон, RN, и Карен Митчелл-Килс, RN, которые сформировали комитет, чтобы помочь информировать медицинских работников о признаках, которые могут указывать на то, что пациент жертва торговли людьми.
Слушайте сейчас
«Особое мнение» о раке
В научно-фантастическом фильме 2002 года «Особое мнение» персонаж Тома Круза возглавляет футуристическое полицейское подразделение, которое предотвращает преступления, основанные на мутировавших людях, называемых «предсказателями», которые «превизуализируют» преступления с помощью видений будущего. Другими словами, предсказатели предсказывают, где и когда произойдет что-то плохое. Неправдоподобно? Возможно, нет, по крайней мере, когда речь идет о «предварительной визуализации» рака. Здесь мы беседуем с биологом-компьютерщиком Ханной Картер, доктором философии, которая может использовать данные из унаследованного генома человека, чтобы помочь предсказать, где может появиться его будущая опухоль, как она будет себя вести и как ее лучше всего лечить.
Здесь мы беседуем с биологом-компьютерщиком Ханной Картер, доктором философии, которая может использовать данные из унаследованного генома человека, чтобы помочь предсказать, где может появиться его будущая опухоль, как она будет себя вести и как ее лучше всего лечить.
Слушай сейчас
Powered by chemo
Несмотря на диагноз рака поджелудочной железы IV стадии и продолжающуюся химиотерапию, Майк Левин участвовал в одном из самых изнурительных физических соревнований: чемпионате мира Ironman. Когда у Майка рак распространился на легкие, он начал планировать уход из жизни, но второе мнение в Онкологическом центре Мура при Калифорнийском университете в Сан-Диего дало ему еще один шанс поучаствовать в любимом виде спорта. В этом выпуске мы поговорим с Майком, его женой, партнером по тренировкам и врачом о том, как он это делает.
Послушайте
Вы больше, чем то, что закодировано в вашей ДНК
Ваш геном похож на книгу рецептов со всеми рецептами, которые нужны клетке вашего тела для производства белков, необходимых для ее функционирования. В каждой из ваших 10 триллионов клеток есть полная копия полной книги рецептов. Но это проблема — как каждая клетка узнает, какие рецепты использовать, а какие игнорировать? Например, только клеткам кожи нужен рецепт для производства пигмента, и им не нужен рецепт инсулина. Вот где в дело вступает эпигеномика, предоставляющая «заметки» в книге рецептов, чтобы каждая клетка использовала только те рецепты, которые ей нужны. В этом выпуске мы поговорим обо всем этом с Дейвом Горкиным, заместителем директора нового Центра эпигеномики в Медицинской школе Калифорнийского университета в Сан-Диего. Он также рассказывает нам, как наша эпигенетика может меняться со временем под влиянием факторов окружающей среды и, в свою очередь, влияет на нашу восприимчивость к болезням.
В каждой из ваших 10 триллионов клеток есть полная копия полной книги рецептов. Но это проблема — как каждая клетка узнает, какие рецепты использовать, а какие игнорировать? Например, только клеткам кожи нужен рецепт для производства пигмента, и им не нужен рецепт инсулина. Вот где в дело вступает эпигеномика, предоставляющая «заметки» в книге рецептов, чтобы каждая клетка использовала только те рецепты, которые ей нужны. В этом выпуске мы поговорим обо всем этом с Дейвом Горкиным, заместителем директора нового Центра эпигеномики в Медицинской школе Калифорнийского университета в Сан-Диего. Он также рассказывает нам, как наша эпигенетика может меняться со временем под влиянием факторов окружающей среды и, в свою очередь, влияет на нашу восприимчивость к болезням.
Слушайте сейчас
Как старое лекарство от астмы может стать новым средством лечения диабета
В недавнем клиническом исследовании у некоторых пациентов с диабетом 2 типа было продемонстрировано клинически значимое снижение уровня глюкозы в крови после приема противоастматического препарата в течение 12 недель. Здесь мы поговорим с Аланом Салтиэлем, доктором философии, который руководил исследованием, о том, что это за препарат, почему он помогает некоторым диабетикам, но не другим, и как его команда работает над персонализацией лечения диабета.
Здесь мы поговорим с Аланом Салтиэлем, доктором философии, который руководил исследованием, о том, что это за препарат, почему он помогает некоторым диабетикам, но не другим, и как его команда работает над персонализацией лечения диабета.
Слушайте сейчас
Микробы как лекарство
Мы беседуем с Ричардом Галло, доктором медицинских наук, дерматологом и исследователем, чья команда недавно испытала крем «трансплантация микробиома» на небольшой группе пациентов с экземой. У людей с экземой, как правило, больше бактерий Staphylococcus aureus на их коже, чем те, у кого их нет, что может усугубить зуд и воспаление. В отличие от традиционных антибиотиков, которые без разбора уничтожают как вредные, так и полезные бактерии, подход Галло использует хорошие бактерии для борьбы с плохими.
Слушайте сейчас
Препарат вековой давности испытан на мальчиках с аутизмом
В ходе небольшого клинического испытания одна внутривенная доза препарата сурамина вековой давности привела к измеримым, но временным улучшениям у пяти мальчиков с расстройствами аутистического спектра (РАС). Здесь ведущий исследователь Роберт К. Навио, доктор медицинских наук, беседует с Майлзом Макинерни, подростком с РАС, который участвовал в исследовании, но не получал сурамин, и его матерью Ким Кеннеди. Они обсуждают судебный процесс, почему Майлз хотел участвовать и его опасения по поводу изменения того, что делает его тем, кто он есть.
Здесь ведущий исследователь Роберт К. Навио, доктор медицинских наук, беседует с Майлзом Макинерни, подростком с РАС, который участвовал в исследовании, но не получал сурамин, и его матерью Ким Кеннеди. Они обсуждают судебный процесс, почему Майлз хотел участвовать и его опасения по поводу изменения того, что делает его тем, кто он есть.
Слушай сейчас
Экспериментальная фаговая терапия спасла Тому жизнь
Том Паттерсон, доктор философии, и его жена отдыхали в Египте, когда он заразился полирезистентной инфекцией. Его доставили в UC San Diego Health, где его жизнь была спасена экспериментальной внутривенной терапией фагами — вирусами, убивающими бактерии. Хотя это только один пациент, опыт Паттерсона открывает новое направление исследований, направленных на поиск альтернатив традиционным антибиотикам на фоне растущей проблемы устойчивости к противомикробным препаратам.
Слушайте сейчас
Количественная хирургия: 3D-модели персонализируют процедуры задолго до первого разреза что его хирург Соня Рамамурти, доктор медицинских наук, могла исследовать задолго до того, как ей сделали первый разрез.
 Успешная процедура Смарра была настоящим экспериментом «N равно одному», но также, возможно, и взглядом в будущее хирургии.
Успешная процедура Смарра была настоящим экспериментом «N равно одному», но также, возможно, и взглядом в будущее хирургии.Слушайте сейчас
Изменение того, как ваш мозг воспринимает боль
В нашем последнем выпуске мы говорили о плюсах и минусах опиоидов для обезболивания. Здесь мы говорим с Марком Уоллесом, доктором медицинских наук, об альтернативном методе лечения хронической боли — типе нейромодуляции, называемом стимуляцией спинного мозга. Мы также слышали от пациента, которому имплантировали стимулятор спинного мозга в спину, чтобы помочь ему справиться с хронической болью в руке.
Слушайте сейчас
История двух кризисов: хроническая боль и злоупотребление опиоидами
Не проходит и дня, чтобы мы не слышали об эпидемии опиоидной зависимости в США в новостях. Но хроническая боль — это тоже эпидемия, и иногда опиоиды — лучшее лечение. Мы беседуем с экспертами, работающими на передовой с обеих сторон — фармацевтом по паллиативной помощи Рабией Атайи, PharmD, о трудностях лечения хронической боли и психиатром Карлой Мариенфельд, доктором медицины, о лечении опиоидной зависимости.
Слушайте сейчас
Что делать с электронными сигаретами?
Что такое электронные сигареты? Чем они отличаются от обычных сигарет? Они лучше для вас? В этом выпуске Лора Кротти Александер, доктор медицинских наук, пульмонолог и научный сотрудник Медицинской школы Калифорнийского университета в Сан-Диего и службы здравоохранения Сан-Диего по делам ветеранов, отвечает на эти вопросы и развеивает несколько мифов. Мы также говорим о мышах для вейпинга, блогах с рецептами и советах, как сделать эту привычку менее опасной.
Слушайте сейчас
Опухоли головного мозга — что старое может снова стать новым
До недавней защиты докторской диссертации Тиффани Тейлор изучала клетки глиобластомы и то, как они растут, работая в лаборатории Фрэнка Фурнари, доктора философии, в Школе Калифорнийского университета в Сан-Диего. Медицина и исследование рака Людвига. Здесь она рассказывает о том, как ее результаты могут помочь врачам лучше использовать уже имеющиеся у них методы лечения глиобластомы. Она также делится своими карьерными планами и надеется на увеличение разнообразия в следующем поколении ученых.
Она также делится своими карьерными планами и надеется на увеличение разнообразия в следующем поколении ученых.
Послушайте
Здоровое питание с научной точки зрения
Кажется, что каждый день появляется новое исследование продуктов питания, которое противоречит предыдущему: яйца вредны, яйца полезны; глютен — это яд, никакой красный краситель не яд — просто ешьте капусту! Где наука и что на самом деле означает «здоровое питание»? Мы беседуем с Кристин Зумас, MS, RD, старшим диетологом и директором программы здорового питания в Онкологическом центре Мура в Калифорнийском университете в Сан-Диего, о том, чему она учит больных раком и выживших после рака на своих уроках питания и кулинарии.
Слушайте сейчас
Иммунотерапия рака, часть 2: На пороге чего-то великого
В эпизоде 8 мы услышали от рок-звезды Рикки Рокетта о его опыте лечения рака и иммунотерапии. Здесь мы углубимся в этот передовой подход, который борется с раком, укрепляя собственную иммунную систему пациента. Сандип Патель, доктор медицинских наук, онколог Онкологического центра Мурса, который проводит клинические испытания Рикки, рассказывает, почему он в восторге от иммунотерапии, и о проблемах, связанных с предоставлением этих методов лечения большему количеству пациентов.
Сандип Патель, доктор медицинских наук, онколог Онкологического центра Мурса, который проводит клинические испытания Рикки, рассказывает, почему он в восторге от иммунотерапии, и о проблемах, связанных с предоставлением этих методов лечения большему количеству пациентов.
Слушайте сейчас
Иммунотерапия рака, часть 1: Рок-звезда Рикки Рокетт делится своим опытом
В этом специальном выпуске Хизер беседует с Рикки Рокеттом, барабанщиком группы Poison, в тот день, когда он был в онкологическом центре Мура в Калифорнийском университете в Сан-Диего. для сканирования, которое скажет ему, сработала ли его экспериментальная иммунотерапия. Узнайте о путешествии Рикки через диагностику, рекомендацию удалить ему весь язык и, наконец, о клиническом испытании.
Слушайте сейчас
Исследование вируса Зика набирает обороты
Скотт и Хизер рассказывают трем исследователям обо всей новой информации о вирусе Зика, которая появилась всего за последние несколько месяцев — доказательство того, что вирус вызывает микроцефалию, потенциальное объяснение того, как это происходит, и усилия по открытию новых лекарств в сотрудничестве с краудсорсинговым проектом IBM World Community Grid OpenZika.
Слушайте сейчас
Что делает грудное молоко таким особенным? Интервью с «молочником»
Мишель и Мелани изучают науку о том, что «грудь лучше всего», от Ларса Боде, доктора медицинских наук, доцента педиатрии Медицинской школы Калифорнийского университета в Сан-Диего и преданного спортсмена, ставшего мировым лидером в исследованиях состава грудного молока. Они говорят о пользе грудного молока и о том, как кормящие матери могут иметь ключ к разработке лекарств от хронических заболеваний взрослых.
Слушайте сейчас
СЛЕДУЮЩАЯ БОЛЬШАЯ ВЕЩЬ может быть очень, очень маленькой
Ядира и Хизер обсуждают наномедицину — использование крошечных частиц для диагностики и лечения — и то, как этот подход помогает решить самую большую проблему современного здравоохранения: людей. Они разговаривают с Адой Альмутаири, доктором философии, доцентом и директором Центра передового опыта в области наномедицины в Школе фармации и фармацевтических наук Скаггса в Калифорнийском университете в Сан-Диего.
Слушайте сейчас
Редактирование генов болезни Альцгеймера с помощью CRISPR/Cas9
Скотт и Хизер узнают о CRISPR/Cas9, новейшем методе редактирования генов. Они беседуют с Джоном Стилом, научным сотрудником лаборатории Ларри Гольдштейна в Медицинской школе Калифорнийского университета в Сан-Диего, о том, как работает CRISPR/Cas9 и как он использует его, а также другой передовой метод — индуцированные плюрипотентные стволовые клетки (ИПСК) — для изучить болезнь Альцгеймера и другие неврологические расстройства.
Слушайте сейчас
Когда антибиотики перестанут работать, что дальше?
Мишель и Хизер рассказывают о молодом спортсмене, который недавно потерял ногу из-за бактериальной инфекции, устойчивой к антибиотикам. Как это происходит? Почему антибиотики иногда не помогают? Какие еще варианты лечения у нас есть? В этом выпуске рассказывается о Россе Корридене, ученом проекта из Медицинской школы Калифорнийского университета в Сан-Диего, который обнаружил в лаборатории и экспериментах на мышах, что препарат тамоксифен от рака молочной железы помогает стимулировать иммунную систему.
Послушайте
Стволовые клетки ведут себя плохо
Мишель и Хизер обсуждают хорошие, плохие и уродливые аспекты стволовых клеток — от регенеративной медицины и туризма стволовых клеток до рака. С участием Лесли Крюс, старшего научного сотрудника лаборатории Катрионы Джеймисон в Медицинской школе Калифорнийского университета в Сан-Диего и Сэнфордского консорциума регенеративной медицины.
Слушай сейчас
Что живет в твоих какашках?
В этом выпуске Скотт и Хизер рассказывают о кишечном микробиоме — уникальном созвездии микробов, живущих внутри вас. Мы также узнаем об инициативе гражданской науки под названием American Gut Project и о том, как вы можете принять в ней участие. С участием Дэниела Макдональда, бывшего менеджера проекта American Gut, и Эмбриетт Хайд, нынешнего менеджера проекта American Gut и исследователя с докторской степенью в лаборатории Роба Найта в Калифорнийском университете в Сан-Диего.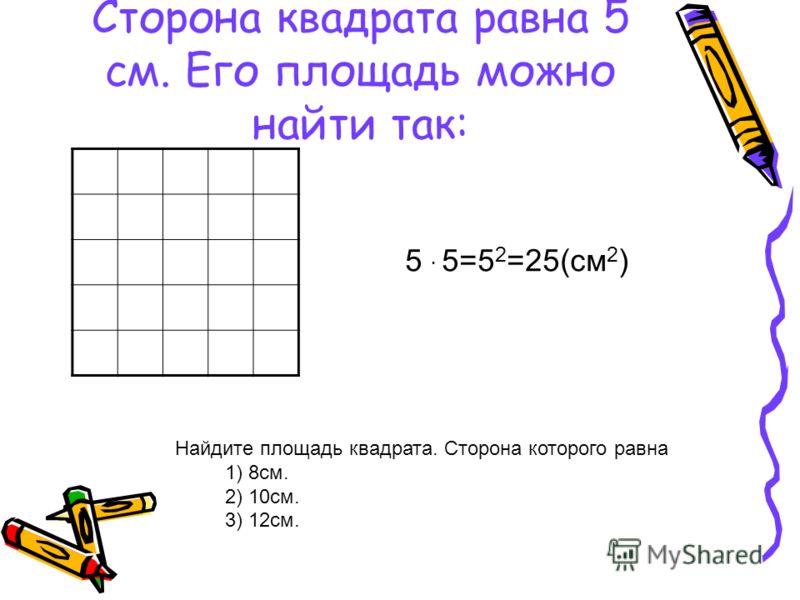
Слушайте сейчас
Доказательство: почему вероятность дополнения A равна единице минус вероятность A [ P(A’) = 1-P(A) ]
Вероятность относится к степени возникновения событий. Когда происходит событие, такое как бросок мяча, выбор карты из колоды и т. д., то с этим событием должна быть связана некоторая вероятность.
Основные термины:
- Случайное событие-
Если эксперимент повторяется несколько раз в одинаковых условиях, если он не дает каждый раз один и тот же результат, но результат в испытании является одним из несколько возможных исходов, то такой эксперимент называется случайным событием или вероятностным событием. - Пространство выборки –
Пространство выборки относится к набору всех возможных исходов случайного события. Например, когда подбрасывается монета, возможны исходы «орёл» и «решка».
- Событие –
Под событием понимается подмножество выборочного пространства, связанное со случайным событием. - Возникновение события –
Говорят, что событие, связанное со случайным событием, произошло, если любое из принадлежащих ему элементарных событий является исходом. - Дополнение –
В наборах дополнение к набору, А – это набор всех элементов, которые не присутствуют в А. Он обозначается А’ или А c . Например, в эксперименте с броском игральной кости, если А — это набор всех четных результатов, то А’ — это набор всех нечетных результатов. - Взаимоисключающие события –
Два или более события, связанные со случайным событием, называются взаимоисключающими событиями. Если происходит одно из событий, оно предотвращает возникновение всех остальных событий. Это означает, что никакие два или более события не могут произойти одновременно.
Если А и В являются взаимоисключающими событиями, то А ∩ В = ∅ Кроме того, P(A ∩ B) = 0
Аксиомы вероятности:
- Для любого множества A вероятность A всегда будет больше или равна нулю, т.е. P(A) >=0
- Вероятность Sample Space(S) всегда будет равна единице, то есть P(S) = 1,
- . взаимоисключающих событий, то вероятность объединения этих взаимоисключающих событий будет равна сумме вероятностей этих взаимоисключающих событий, т. е. P(A 1 ∪ А 2 ∪ А 3 ∪ А 4 ∪ …. А N ) = Р(А 1 ) + Р(А 2 ) + Р(А 3 ) + Р(А 4 ) + …. + P(A N )
Постановка задачи:
Почему вероятность дополнения A равна единице минус вероятность A?
Решение:
Давайте начнем с доказательства приведенной выше постановки задачи. Ниже приведены шаги для доказательства. 0005
0005
1. Рассмотрим событие A. Поскольку выборочное пространство эксперимента содержит все возможные исходы эксперимента, а объединение A и A’ содержит все возможные исходы эксперимента. Таким образом, выборочное пространство можно записать как
S = A ∪ A'. Кроме того, P(S) = P(A ∪ A') --- (1)
2. Поскольку пересечение A и A’ равно ∅, можно сказать, что A и A’ — взаимоисключающие события. Итак, согласно аксиоме 3,
Так как A ∩ A' = ∅ P(A ∪ A') = P(A) + P(A') --- (2)
3. Теперь из уравнения (1) и (2) это можно записать как
P(S) = P(A) + P(A')
4. Из аксиомы 2 известно что вероятность выборочного пространства всегда равна 1, т.е.
P(S) = 1 P(A) + P(A') = 1 --- (3)
5. После преобразования уравнения (3) получается следующее уравнение:
P(A') = 1 - P(A )
т. е. вероятность дополнения A равна единице минус вероятность A. Следовательно, Доказано.
Примеры:
Давайте посмотрим на некоторые решенные примеры, связанные с приведенным выше доказательством-
1. Кость подбрасывается один раз.
Кость подбрасывается один раз.
Событие A- Появляется четное число
Пространство выборки, S- {1, 2, 3, 4, 5, 6}
P(S) = 1
A = {2, 4, 6}, т. е. P(A) = 3/6 = 1/2
A’ = {1, 3, 5}, т. е. P(A’) = 3/6 = 1/2
Теперь мы можем легко заметим, что S = A ∪ A’, и поскольку A ∩ A’ = ∅,
A и A’ являются взаимоисключающими событиями, откуда следуетP(S) = P(A ∪ A’)
P(S) = P(A) + P(A’)
P(S) = 1/2 + 1/2
= 1
P(A’) = 1 – P(A)
P(A’) = 1 – 1/2
P(A’) = 1/2
2. Подбрасываются две монеты.
Событие A- Появление двух головок =1/4
A’ = {HT, TH, TT}, т.е. P(A’) =3/4
т. е. S = A ∪ A’, и поскольку A ∩ A’ = ∅, мы можем сказать, что A и A’ являются
взаимоисключающими событиями, откуда следует, что –P(S) = P(A ∪ A’)
P(S) = P(A) + P(A’)
P(S) = 1/4 + 3/4
P(S) = 1
P(A’) = 1 – P (A)
P(A’) = 1 – 1/4
P(A’) = 3/4
Равен единице | Набор с фиксированной оплатой – Лидс
Простой и легкий процесс
Реклама на национальных досках объявлений премиум-класса не может быть проще. Все вакансии рекламируются в течение 2 часов, и вы можете получить доступ к своим кандидатам через нашу уникальную систему отслеживания кандидатов, или мы можем отправить их прямо на ваш почтовый ящик.
Все вакансии рекламируются в течение 2 часов, и вы можете получить доступ к своим кандидатам через нашу уникальную систему отслеживания кандидатов, или мы можем отправить их прямо на ваш почтовый ящик.
Платите «единую фиксированную плату» независимо от роли, зарплаты или местоположения.
Читать всеЧто говорят наши клиенты
Филиппа дала отличный совет, где разместить объявление о вакансии специалиста. Она разместила рекламу в нескольких местах без проблем. Она провела первоначальный отбор и отправила пакет вакансий только тем кандидатам, которые соответствовали спецификациям. Спасибо за то, что так легко найти хорошего кандидата.
Кэролайн — заземление HRВ декабре один из моих клиентов попросил меня помочь им с набором на вакансию менеджера по продажам. Я провел 30-минутные телефонные интервью с шестью кандидатами из резюме, которое мне прислала Филиппа, а затем мой клиент провел собеседование с пятью через зум при моей поддержке.
Трейси – Практичные люди Они были очень впечатлены…
Они были очень впечатлены…С Equals One очень легко работать. Они очень отзывчивы, и мы всегда чувствуем, что кандидаты, которых мы получаем, соответствуют нашим критериям. Мы полностью рекомендуем их.
Софи, Кертис Контракт Мебель«Мы небольшая компания, и подход Equals One к найму позволил нам найти нужных кандидатов по низкой цене. Это также было невероятно эффективно, поскольку Equals One брал на себя трудоемкую работу администратора, освобождая нас для продвижения нашего набора. Мы очень впечатлены…
Директор, Mystery Eyes LtdBigChange — это технологический бизнес, который вырос за последние 5 лет. В настоящее время в компании работает 60 человек, и компания Deloitte занимает 25-е место среди самых быстрорастущих технологических компаний Великобритании. В течение следующих 5 лет продажи BigChange вырастут до 40 миллионов фунтов стерлингов и будут работать в Великобритании, континентальной…
Мартин Порт – генеральный директор BigChange«Куда мне обратиться, чтобы найти лучших людей для должности, которую мне нужно заполнить? В каком издании лучше разместить объявление? В какой день выходит? Должен ли я использовать агентство? Сколько стоит!!!» Вопросы, которые я задавал при поиске новых сотрудников…
Крис Лайтфут (партнер @ Co-ownership Solutions LLP и управляющий директор Futurelight Ltd)Мы использовали Equals One для выполнения ряда задач и убедились, что их внимание к деталям, быстрое реагирование и профессиональное отношение не имеют себе равных.
Иннсерв Фиксированная структура вознаграждения позволяет мне контролировать наши расходы на подбор персонала, а их широкий охват приводит к хорошему выбору…
Фиксированная структура вознаграждения позволяет мне контролировать наши расходы на подбор персонала, а их широкий охват приводит к хорошему выбору…Equals One предложили помощь в наборе нашего нового сотрудника. Благодаря их высококвалифицированному и систематическому подходу в тот же день была подготовлена наша должностная инструкция и объявлена вакансия. Мы рассмотрели полученные резюме, провели собеседование, и в течение двух недель к нам присоединился новый участник…
Carl – PQS Survey LtdУслуги по сантехнике и отоплению Clarke охватывают все аспекты сантехнических и отопительных работ в Западном Йоркшире. Мы гордимся нашими высокими стандартами работы и профессионализмом. Ключом к сохранению нашей репутации уважаемой фирмы является процесс отбора новых сотрудников и…
Мэтью – Кларк СантехникМы работаем с Филиппой и командой Equals One более 5 лет и получаем отличный сервис. Их понимание потребностей нашего бизнеса и культуры нашей организации позволяет им предоставлять нам подходящих кандидатов.
Демса От оценки задания до назначения новой команды…
От оценки задания до назначения новой команды…Качество услуг, предлагаемых Equals One, просто фантастическое. Если мне нужно набрать сотрудников для нашей компании, Equals One — это наш первый порт захода, проверка приложений имеет неоценимое значение и означает, что мы получаем только те приложения, которые соответствуют нашим критериям. Спасибо Equals One за все, и мы…
Саманта — Деревня ДенегМы просто хотели написать и сказать, что вы сделали это снова! Мы получили отличный отклик на объявление, которое вы помогли нам создать. Кандидаты были исключительно талантливы, и ваш процесс отбора помог мне найти двух очень подходящих кандидатов, которые принесут…
Лоррейн, Color Heroes Ltd«Мы использовали Equals One в течение нескольких лет и обнаружили, что эта услуга профессиональна, экономична, эффективна и проста. Как малый бизнес, мы чувствуем себя неловко платить комиссионные агентству по подбору персонала, и эта услуга хорошо подходит для наших нужд.
Мэтт – UK Workspace Ltd С помощью этой услуги мы набрали сотрудников всех уровней и…
С помощью этой услуги мы набрали сотрудников всех уровней и…Последние два года я работал с Philippa and Equals one, в течение которых она оказывала исключительную помощь в подборе персонала для Moda в Пелле. Филиппа помогала с подбором персонала на ряд вакансий в компании и всегда профессиональна, дружелюбна и чрезвычайно полезна. Все наши вакансии…
Мода в ПеллеB38Group использует Philippa at Equals one в течение нескольких лет, и мы были впечатлены скоростью и скоростью отклика кандидатов на наши рекламные запросы
B38 ГруппаЯ работал с Equals one в течение нескольких лет как в предыдущей, так и в нынешней компании. Equals one выделяется среди других поставщиков демонстрацией выполненной работы и ценности, которую она добавляет для сотрудников, нуждающихся в поддержке при найме, и тех, кто ищет работу. Открытость и…
Руки – руководитель практики Ридли и адвокаты ХоллаЯ использую Equals One для подбора персонала уже много лет и не могу придумать лучшего сервиса по подбору персонала.
Стабильная компания Мы наняли всех сотрудников от руководства до рабочей силы, используя услуги, предоставляемые Equals One Recruitment. Я очень рекомендую их услуги.”
Мы наняли всех сотрудников от руководства до рабочей силы, используя услуги, предоставляемые Equals One Recruitment. Я очень рекомендую их услуги.”В Autohorn Fleet Services мы понимаем важность предоставления исключительного обслуживания клиентов по самым лучшим ценам. Я рад сообщить, что Equals One разделяет нашу философию. Экономия времени и денег просто колоссальная. Сотрудники Equals One знают свою работу наизнанку и пишут лаконично…
Autohorn Fleet ServicesЯ использую Equals One Recruitment уже много лет и всегда был очень впечатлен их эффективным и профессиональным подходом. Благодаря Филиппе я быстро нашел отличных кандидатов, идеально соответствующих описанию вакансии. Уровень заботы, внимания к деталям и приверженности компании Equals One…
Сью — управляющий директор, Apollo Lighting LtdКомпания Equals One очень помогла Sutcliffe Play в недавнем найме нового управляющего директора. Их полностью профессиональные услуги в сочетании с простым и экономичным подходом к ценообразованию очень приветствовались на очень конкурентном рынке подбора персонала.
Игра Сатклифф Они сыграли значительную роль в очень успешном исходе.
Они сыграли значительную роль в очень успешном исходе.
1 доллар равен 1 центу – помните о своих решениях
Если вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.
Опубликовано 1 апреля 2018 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .
.
.
«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.
.
.
Я знаю, о чем ты думаешь. Вы собираетесь сказать мне, что 1 доллар равен 100 центам. Но математически 1 доллар на самом деле равен 1 центу, как демонстрирует доказательство в видео.
Но математически 1 доллар на самом деле равен 1 центу, как демонстрирует доказательство в видео.
Шокирующее новое доказательство: 1 доллар равна 1 цент
Текстовая версия:
$ 1
= 100 ¢
= (10 ¢) 2
= (0,10 долл.
Так вот, 1 доллар на самом деле равен 1 центу!
И хорошие новости для Verizon; наконец-то у него есть доказательство того, что 0,002 доллара равняется 0,002 цента. Теперь ты меня слышишь?
(И, конечно же, все это просто первоапрельская шутка. Неверный шаг состоит в том, чтобы сказать (0,10 доллара США) 2 = 0,01 доллара США, потому что в этом случае единицы измерения были бы долларами в квадрате, что не имеет того же значения, что и доллары. Или как Ананд указывает в комментариях, что даже более ранний шаг = 100 центов
= (10 центов) 2 имеет неправильные размеры.)
Источники
://www.youtube.com/watch?v=MShv_74FNWU
http://verizonmath.blogspot.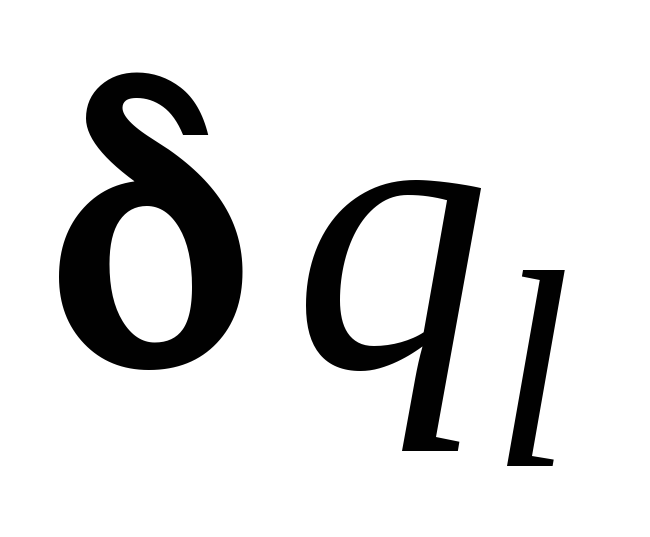 com/2006/12/response-from-verizon-100-refund.htm
com/2006/12/response-from-verizon-100-refund.htm
http://www.math.vanderbilt.edu/~schectex/commerrs/
https:// www.physics.umd.edu/courses/Phys374/fall05/hw/sol_hw01/G06-S.htm
http://volokh.com/2013/04/24/a-new-and-useful-proof-that- 1-1%C2%A2/
https://www.futilitycloset.com/2005/06/19/dollars-equal-cents/
Как доказать, что один доллар равен одному центу (видео Нареша Сабниса, комментарий Verizon от MicrowaveMeShow)
https://www.youtube.com/watch?v=5j9kZqY0-RA
МОИ КНИГИ
Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
Рейтинги книг по состоянию на январь 2022 г. 1) Радость теории игр: введение в стратегическое мышление
(2) 40 парадоксов в логике, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения
(4) Лучшие математические приемы в уме
(5) Умножение чисел путем рисования линий
Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 отзывах)
(оценка 4,2/5 звезд в 224 отзывах)
40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд по 38 отзывам)
Иллюзия иррациональности: как принимать обдуманные решения и преодолевать предубеждения — это справочник, в котором объясняется, как мы предвзято относимся к принятию решений, и предлагаются методы принятия обдуманных решений. (рейтинг 4/5 звезд в 24 обзорах)
Лучшие приемы ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (рейтинг 4,2/5 звезд в 76 обзорах)
Умножить Числа, рисуя линии Эта книга является справочным руководством для моего видео, которое набрало более 1 миллиона просмотров, о геометрическом методе умножения чисел. (рейтинг 4,3/5 звезд в 30 обзорах)
Размышляйте над головоломками представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.
Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.
Математические головоломки, том 2 — это продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)
Math Puzzles Volume 3 — третья книга в серии. (рейтинг 4,2/5 звезд по 22 отзывам)
KINDLE UNLIMITED
Учителя и студенты со всего мира часто пишут мне по электронной почте о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.
В настоящее время вы можете читать большинство моих электронных книг через программу Amazon «Kindle Unlimited». Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)
ТОВАРЫ
Возьмите кружку, футболку и многое другое на официальном сайте товаров: Следите за своими решениями в Teespring .
Часто задаваемые вопросы (FAQ) — Управление энергетической информации США (EIA)
Перейти к поднавигации На этой странице нет вложенной навигации. Перейти к содержимому страницы.
Перейти к содержимому страницы.
Уголь
- Имеются ли в EIA данные о производстве энергии на уровне уездов?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Публикует ли EIA цены на коксующийся уголь?
- Как преобразовать короткие тонны в метрические?
- Насколько велики запасы угля в США?
- Сколько электростанций в США?
- Сколько угля США экспортируют и куда?
- Сколько угля импортируют США и откуда?
- Сколько угля, природного газа или нефти используется для производства киловатт-часа электроэнергии?
- Сколько стоит выработка электроэнергии на различных типах электростанций?
- Какая часть выбросов углекислого газа в США связана с производством электроэнергии?
- Какие цены на уголь публикует EIA?
- Что такое производство электроэнергии в США по источникам энергии?
- Какова теплоемкость американского угля?
- Какие виды и количества энергии производятся в каждом штате?
- Какие штаты производят больше всего угля?
Преобразование и эквиваленты
- Как сравнить стоимость топлива для отопления?
- Как преобразовать короткие тонны в метрические?
- Как преобразовать данные в одной единице измерения в другую единицу измерения?
- Сколько галлонов бензина и дизельного топлива производится из одного барреля нефти?
- Что такое Ccf, Mcf, Btu и термы? Как преобразовать цены на природный газ в долларах за кубический фут или тысячу кубических футов в доллары за БТЕ или терм?
- Каковы коэффициенты выбросов парниковых газов и загрязнителей воздуха для топлива и электроэнергии?
- Каков КПД различных типов электростанций?
Дизельное топливо
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Публикует ли EIA цены на бензин и дизельное топливо с поправкой на инфляцию?
- Публикует ли EIA цены на дизельное топливо для бездорожья?
- Как рассчитать надбавку за дизельное топливо?
- Сколько галлонов бензина и дизельного топлива производится из одного барреля нефти?
- Сколько дизельного топлива на основе биомассы производится, импортируется, экспортируется и потребляется в Соединенных Штатах?
- Сколько углекислого газа образуется при потреблении бензина и дизельного топлива в США?
- Сколько налогов мы платим за галлон бензина и галлон дизельного топлива?
- Каковы прогнозы цен на бензин и дизельное топливо в США?
- За что я плачу галлоном бензина и дизельного топлива?
- Когда в США был построен последний НПЗ?
- Почему цены на дизельное топливо выше цен на бензин?
Электричество
- Могут ли потребители электроэнергии выбирать поставщика электроэнергии?
- Имеются ли в EIA данные о производстве энергии на уровне уездов?
- Имеются ли в EIA данные о затратах на передачу и распределение электроэнергии?
- Есть ли у EIA данные о каждой электростанции в США?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA информация о незапланированных отключениях или отключениях энергетической инфраструктуры США?
- Публикует ли EIA данные о пиковой или почасовой выработке электроэнергии, спросе и ценах?
- Публикует ли EIA данные о тарифах на электроэнергию, тарифах и сборах по требованию?
- Публикует ли EIA данные о продажах электроэнергии и ценах по штатам и коммунальным предприятиям?
- Публикует ли EIA данные о потреблении энергии и ценах по городам, округам или по почтовым индексам?
- Публикует ли EIA расположение электростанций, линий электропередачи и подстанций?
- Как электричество используется в домах США?
- Сколько альтернативных видов топлива и гибридных автомобилей в Соединенных Штатах?
- Сколько атомных электростанций в США и где они расположены?
- Сколько электростанций в США?
- Сколько интеллектуальных счетчиков установлено в США и у кого они есть?
- Сколько угля, природного газа или нефти используется для производства киловатт-часа электроэнергии?
- Сколько стоит строительство различных типов электростанций в США?
- Сколько стоит выработка электроэнергии на различных типах электростанций?
- Сколько электроэнергии вырабатывает атомная электростанция?
- Сколько электроэнергии потребляет американский дом?
- Сколько электроэнергии теряется при передаче и распределении электроэнергии в США?
- Сколько электроэнергии используется для охлаждения в Соединенных Штатах?
- Сколько электроэнергии используется для освещения в США?
- Сколько энергии потребляет мир в каждом секторе конечного потребления энергии?
- Какая часть выбросов углекислого газа в США связана с производством электроэнергии?
- Какая часть потребления энергии и производства электроэнергии в США приходится на возобновляемые источники энергии?
- Какая часть мирового потребления и производства энергии приходится на возобновляемые источники энергии?
- Сколько лет атомным электростанциям США и когда была построена самая новая?
- Что такое производство электроэнергии в США по источникам энергии?
- В чем разница между мощностью производства электроэнергии и производством электроэнергии?
- Каков КПД различных типов электростанций?
- Каков прогноз цен на топливо для отопления домов этой зимой?
- Какие виды и количества энергии производятся в каждом штате?
Окружающая среда
- Есть ли в EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Как преобразовать короткие тонны в метрические?
- Сколько углекислого газа образуется при потреблении бензина и дизельного топлива в США?
- Сколько углекислого газа производится на киловатт-час производства электроэнергии в США?
- Сколько углекислого газа образуется при сжигании различных видов топлива?
- Какая часть выбросов углекислого газа в США связана с производством электроэнергии?
- Является ли озон парниковым газом?
- Каковы выбросы углекислого газа в США, связанные с энергетикой, по источникам и секторам?
- Что такое парниковые газы и как они влияют на климат?
- Каковы связанные с энергетикой выбросы углекислого газа от ископаемого топлива в Соединенных Штатах и во всем мире?
- Каковы коэффициенты выбросов парниковых газов и загрязнителей воздуха для топлива и электроэнергии?
- Почему выбросы углекислого газа весят больше, чем исходное топливо?
Бензин
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA исторические цены на бензин для каждого штата?
- Публикует ли EIA данные о потреблении энергии и ценах по городам, округам или по почтовым индексам?
- Публикует ли EIA цены на бензин по городам, округам или почтовым индексам?
- Публикует ли EIA цены на бензин и дизельное топливо с поправкой на инфляцию?
- Сколько галлонов бензина и дизельного топлива производится из одного барреля нефти?
- Сколько углекислого газа образуется при потреблении бензина и дизельного топлива в США?
- Сколько этанола содержится в бензине и как это влияет на экономию топлива?
- Сколько бензина потребляют США?
- Сколько налогов мы платим за галлон бензина и галлон дизельного топлива?
- Каковы прогнозы цен на бензин и дизельное топливо в США?
- За что я плачу галлоном бензина и дизельного топлива?
- Когда в США был построен последний НПЗ?
General Energy
- Имеются ли в EIA данные о производстве энергии на уровне округов?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA информация о газо- и нефтепроводах США?
- Есть ли у EIA информация о незапланированных отключениях или отключениях энергетической инфраструктуры США?
- Публикует ли EIA данные о потреблении энергии и ценах по городам, округам или по почтовым индексам?
- Публикует ли EIA расположение электростанций, линий электропередачи и подстанций?
- Как сравнить стоимость топлива для отопления?
- Сколько интеллектуальных счетчиков установлено в США и у кого они есть?
- Сколько стоит строительство различных типов электростанций в США?
- Сколько электроэнергии используется для охлаждения в Соединенных Штатах?
- Сколько энергии расходует человек в год?
- Сколько энергии потребляет каждый сектор конечного потребления энергии в мире?
- Сколько энергии потребляется в зданиях США?
- Сколько природного газа потребляется в США?
- Какая часть потребления энергии и производства электроэнергии в США приходится на возобновляемые источники энергии?
- Какая часть мирового потребления и производства энергии приходится на возобновляемые источники энергии?
- Что такое производство электроэнергии в США по источникам энергии?
- Какова доля США в мировом потреблении энергии?
- Какие виды и количества энергии производятся в каждом штате?
- Где я могу получить помощь в оплате счетов за коммунальные услуги?
Природный газ
- Имеются ли в EIA данные о производстве энергии на уровне округов?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA информация о газо- и нефтепроводах США?
- Есть ли у EIA информация о незапланированных отключениях или отключениях энергетической инфраструктуры США?
- Публикует ли EIA данные о потреблении энергии и ценах по городам, округам или по почтовым индексам?
- Публикует ли EIA данные о добыче и запасах сланцевого газа и метана угольных пластов?
- Как EIA рассчитывает годовые и пятилетние средние значения в Еженедельном отчете о хранении природного газа?
- Сколько альтернативных видов топлива и гибридных автомобилей в Соединенных Штатах?
- Сколько угля, природного газа или нефти используется для производства киловатт-часа электроэнергии?
- Сколько стоит выработка электроэнергии на различных типах электростанций?
- Сколько природного газа есть в США и как долго его хватит?
- Сколько природного газа потребляется в США?
- Какая часть выбросов углекислого газа в США связана с производством электроэнергии?
- Сколько сланцевого газа добывается в США?
- Что такое Ccf, Mcf, Btu и термы? Как преобразовать цены на природный газ в долларах за кубический фут или тысячу кубических футов в доллары за БТЕ или терм?
- Каковы основные факторы, влияющие на цены на природный газ?
- На что я могу рассчитывать за отопление этой зимой?
- Что такое производство электроэнергии в США по источникам энергии?
- Каков прогноз цен на топливо для отопления домов этой зимой?
- Какова цена или стоимость природного газа для производителей электроэнергии в США?
- Каков объем мировых запасов природного газа?
- Какие виды и количества энергии производятся в каждом штате?
- Какие штаты потребляют и производят больше всего природного газа?
- Почему за мазут или пропан с меня берут больше, чем цена, указанная на веб-сайте EIA?
Атомная
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA информация о незапланированных отключениях или отключениях энергетической инфраструктуры США?
- Сколько атомных электростанций в США и где они расположены?
- Сколько электростанций в США?
- Сколько стоит выработка электроэнергии на различных типах электростанций?
- Сколько электроэнергии вырабатывает атомная электростанция?
- Какая часть выбросов углекислого газа в США связана с производством электроэнергии?
- Сколько лет атомным электростанциям США и когда была построена самая новая?
- Что такое производство электроэнергии в США по источникам энергии?
Нефть/нефть
- Имеются ли в EIA данные о производстве энергии на уровне округов?
- Есть ли у EIA данные о нефтеперерабатывающих заводах США и их местоположении?
- Имеются ли у EIA данные о перемещении (перевозке) сырой нефти, нефтепродуктов, топливного этанола и биодизеля по железной дороге?
- Имеются ли у EIA данные о типе или качестве сырой нефти?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA информация о газо- и нефтепроводах США?
- Есть ли у EIA информация о незапланированных отключениях или отключениях энергетической инфраструктуры США?
- Достаточно ли в мире нефти для удовлетворения наших будущих потребностей?
- Сколько альтернативных видов топлива и гибридных автомобилей в Соединенных Штатах?
- Сколько галлонов бензина и дизельного топлива производится из одного барреля нефти?
- Сколько угля, природного газа или нефти используется для производства киловатт-часа электроэнергии?
- Сколько сырой нефти, добываемой в США, потребляется в США?
- Сколько нефти, потребляемой Соединенными Штатами, поступает из других стран?
- Сколько нефти потребляется в США?
- Сколько масла используется для производства пластика?
- Сколько нефти импортируют и экспортируют США?
- Сколько сланцевой (плотной) нефти добывается в США?
- Что такое нефтепродукты и для чего используется нефть?
- Какие страны являются ведущими производителями и потребителями нефти?
- За что я плачу галлоном бензина и дизельного топлива?
- Что такое производство электроэнергии в США по источникам энергии?
- В чем разница между сырой нефтью, нефтепродуктами и нефтью?
- Каков прогноз цен на топливо для отопления домов этой зимой?
- Какие виды и количества энергии производятся в каждом штате?
- Когда в США был построен последний НПЗ?
Цены
- Цены, опубликованные EIA, скорректированы с учетом инфляции?
- Есть ли у EIA данные о ценах на этанол?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA исторические цены на бензин для каждого штата?
- Публикует ли EIA цены на коксующийся уголь?
- Публикует ли EIA данные о пиковой или почасовой выработке электроэнергии, спросе и ценах?
- Публикует ли EIA данные о тарифах на электроэнергию, тарифах и сборах по требованию?
- Публикует ли EIA данные о продажах электроэнергии и ценах по штатам и коммунальным предприятиям?
- Публикует ли EIA данные о потреблении энергии и ценах по городам, округам или по почтовым индексам?
- Публикует ли EIA цены на бензин по городам, округам или почтовым индексам?
- Публикует ли EIA цены на бензин и дизельное топливо с поправкой на инфляцию?
- Публикует ли EIA цены на дизельное топливо для бездорожья?
- Как рассчитать надбавку за дизельное топливо?
- Как сравнить стоимость топлива для отопления?
- Сколько стоит выработка электроэнергии на различных типах электростанций?
- Сколько налогов мы платим за галлон бензина и галлон дизельного топлива?
- Что такое Ccf, Mcf, Btu и термы? Как преобразовать цены на природный газ в долларах за кубический фут или тысячу кубических футов в доллары за БТЕ или терм?
- Какие цены на уголь публикует EIA?
- Каковы прогнозы цен на бензин и дизельное топливо в США?
- На что я могу рассчитывать за отопление этой зимой?
- За что я плачу галлоном бензина и дизельного топлива?
- Каков прогноз цен на топливо для отопления домов этой зимой?
- Какова цена или стоимость природного газа для производителей электроэнергии в США?
- Где я могу получить помощь в оплате счетов за коммунальные услуги?
- Почему за мазут или пропан с меня берут больше, чем цена, указанная на веб-сайте EIA?
- Почему цены на дизельное топливо выше цен на бензин?
Возобновляемые источники энергии
- Есть ли у EIA данные о перемещении (транспортировке) сырой нефти, нефтепродуктов, топливного этанола и биодизеля по железной дороге?
- Есть ли у EIA данные о ценах на этанол?
- Есть ли у EIA прогнозы или прогнозы производства, потребления и цен на энергию для отдельных штатов?
- Есть ли у EIA информация о незапланированных отключениях или отключениях энергетической инфраструктуры США?
- Сколько альтернативных видов топлива и гибридных автомобилей в Соединенных Штатах?
- Сколько дизельного топлива на основе биомассы производится, импортируется, экспортируется и потребляется в Соединенных Штатах?
- Сколько стоит выработка электроэнергии на различных типах электростанций?
- Сколько этанола содержится в бензине и как это влияет на экономию топлива?
- Сколько топливного этанола производится, импортируется, экспортируется и потребляется в Соединенных Штатах?
- Какая часть выбросов углекислого газа в США связана с производством электроэнергии?
- Какая часть потребления энергии и производства электроэнергии в США приходится на возобновляемые источники энергии?
- Какая часть мирового потребления и производства энергии приходится на возобновляемые источники энергии?
- Что такое производство электроэнергии в США по источникам энергии?
- Какие виды и количества энергии производятся в каждом штате?
верхний
На этой странице:
- Уголь
- Преобразование и эквиваленты
- Дизель
- Электричество
- Окружающая среда
- Бензин
- Дженерал Энерджи
- Природный газ
- Ядерный
- Масло/нефть
- Цены
- Возобновляемые источники энергии
- Полный список предстоящих отчетов
- Подпишитесь на уведомления по электронной почте
Пункт девять повторяющихся равен одному @ Вещи, представляющие интерес
(Эта страница полностью соответствует фактам.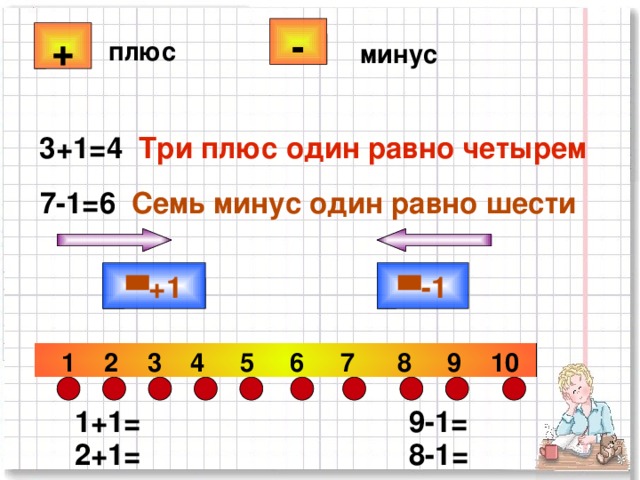 Это не шутка, не сатира и не набор ложных доказательств. Все эти доказательства подлинны, а результаты верны. Спасибо.)
Это не шутка, не сатира и не набор ложных доказательств. Все эти доказательства подлинны, а результаты верны. Спасибо.)
Предварительное примечание
ВСЕ числа являются бесконечными десятичными расширениями.
Например, всякий раз, когда вы пишете «1», вы используете это как удобное сокращение для «1,0000…» точно так же, как «1,0000…» является удобным сокращением для 1, десятичной точки и бесконечно много нулей.
Точно так же «13556» — это сокращение от «13556,0000…», «1/3» — это сокращение от «0,3333…», а «пи» — это сокращение от «3,14159265…». Более короткие формы — это просто полезная запись, потому что утомительно / невозможно записывать бесконечно много десятичных цифр всякий раз, когда вы хотите написать число.
Хотите верьте, хотите нет, но так было всегда, с того момента, как вы начали заниматься математикой. Это также часть фундаментальной основы математики, а не то, с чем можно спорить или спорить.
Теперь читаем дальше:
Аргумент от ассоциативности сложения
0,9999... = 0,9999... + 0 = 0,9999... + (0,9999... - 0,9999...) = (0,9999... + 0,9999...) - 0,9999... = 1,9999... - 0,9999... = 1.0000...
Аргумент от непрерывности действительных чисел
Для любых двух различных действительных чисел можно выбрать третье число, которое находится между ними.
Кроме того, любое действительное число можно записать в виде десятичной записи по крайней мере одним способом.
Итак, если бы 0,9999… и 1,0000… были разными числами, то можно было бы найти число, которое находится между ними, и записать его.
Но невозможно записать десятичное расширение числа между 0,9999… и 1.0000… .
Следовательно, они не могут быть разными номерами.
Следовательно, это один и тот же номер.
«Этот аргумент не работает с целыми числами. Между 3 и 4 нет целых чисел, но
и не равны.» Различные наборы чисел имеют разные свойства. Мы рассматриваем реальные числа, а не целые числа. Между 3 и 4 существует множество действительных чисел.
Между 3 и 4 существует множество действительных чисел.
Аргумент от промежуточного значения
Set x до 0,9999… и и до 1,0000… .
Предположим, x < y . Тогда есть значение на полпути между ними, x < ( x + y ) / 2 < y .
Находим, что ( x + y ) / 2 = (0,9999… + 1,0000…) / 2 = 1,9999… / 2 = 0,9999… = x . Это не «половина между x и y «, это точно равно x .
Это противоречие. Таким образом, наше первоначальное предположение, x < y , должно быть ложным. Вместо этого x = y , то есть 0,9999… = 1,0000… .
Аргумент от вычитания
Если разница между двумя числами равна нулю, то они равны. Например, если x — 5 = 0, то x = 5.
Разница между 1,0000… и 0,9999… составляет:
1,0000... - 0,9999... = 0,0000... = 0
Следовательно, они равны.
«На этом первом шаге вы уже принимаете 1 = 0,9999…»
Нет, я просто делаю простое вычитание. Разработайте сами, если хотите.
«Но 0.0000… должна иметь 1 в конце.»
Нет, не должно. Нет конца. «0,0000…1» не имеет смысла. «…» означает «каждая десятичная цифра равна 0».
Доказательство умножения
Пусть
х = 0,9999...
Умножьте обе части на десять:
10х = 9.9999...
Вычесть x с обеих сторон:
10х - х = 9,9999... - 0,9999...
9х = 9.0000...
Разделить на девять:
х = 1,0000...
«Но во второй строке 9,9999… должно быть 9,9999…0, потому что вы умножили на десять.»
«9.9999…0» бессмысленно. «…» означает «каждая десятичная цифра равна 9».
Аргумент геометрического ряда
0,9999... = 0,9 + 0,09 + 0,009 + 0,0009 +... п =∞ = Σ 0,9 * 0,1 n n =0 n =∞ = ? н =0 = a / (1 - r ) = 0,9 / (1 - 0,1) = 0,9 / 0,9 = 1
Используется формула S = a / (1 — r ) для суммы геометрического ряда с начальным членом a и отношением r , доказательство которого предоставляется читателю.
Настоящее доказательство
Большая часть причин, по которым люди не понимают, почему повторяющаяся точка девять равна единице, заключается в том, что они не до конца понимают, что на самом деле означает десятичное представление . Взгляните на определение 0,9999… и все станет предельно ясно:
0,9999... = 0,9 + 0,09 + 0,009 + 0,0009 + ...
= 9·0,1 + 9·0,01 + 9·0,001 + 9·0,0001 + ...
= 9·10 -1 + 9·10 -2 + 9·10 -3 + 9·10 -4 + . ..
n =∞
= Σ 9·10 - n n =1
н = н
:= lim Σ 9·10 - n N →∞ n =1
= лим ( 9·10 -1 + 9·10 -2 + ... + 9·10 - N )
С →∞
= lim ( 9·0,1 + 9·0,01 + ... + 9·0,000...0001 )
N →∞ \________/
N цифры
= lim ( 0,9 + 0,09 + ... + 0,000 ... 0009 )
N →∞ \________/
N цифры
= lim (0,999...999)
N →∞ \_______/
N девятки
= lim ( 1 - 0,000...0001 )
N →∞ \________/
N цифры
= lim ( 1 - 10 - N )
С →∞
= lim 1 - lim 10 - N N →∞ с.
..
n =∞
= Σ 9·10 - n n =1
н = н
:= lim Σ 9·10 - n N →∞ n =1
= лим ( 9·10 -1 + 9·10 -2 + ... + 9·10 - N )
С →∞
= lim ( 9·0,1 + 9·0,01 + ... + 9·0,000...0001 )
N →∞ \________/
N цифры
= lim ( 0,9 + 0,09 + ... + 0,000 ... 0009 )
N →∞ \________/
N цифры
= lim (0,999...999)
N →∞ \_______/
N девятки
= lim ( 1 - 0,000...0001 )
N →∞ \________/
N цифры
= lim ( 1 - 10 - N )
С →∞
= lim 1 - lim 10 - N N →∞ с. ш. →∞
= 1 - 0
= 1
ш. →∞
= 1 - 0
= 1
Подробное строгое доказательство от противного
Если ваши рассуждения верны, но вывод, к которому вы пришли, определенно неверен, значит, что-то не так с вашими предположениями.
Четко
0,9999... ≤ 1.
Предположим,
0,9999... ≠ 1 (*).
Затем
0,9999... < 1,
, значит должно быть какое-то положительное число P такой, что
0,9999... + P = 1.
Но для ЛЮБОГО положительного P ,
0,9999... + Р > 1,
, что является противоречием и определенно неправильным. Поэтому мы вынуждены заключить, что предположение (*) было неверным, то есть:
0,9999... = 1
По многочисленным просьбам
1/3 = 0,3333...
1 = 3/3
= 3 * 1/3
= 3 * 0,3333...
= 0,9999...
Доказательство того, что 1/3 = 0,3333. .. предоставляется читателю.
.. предоставляется читателю.
Это может показаться вам убедительным
Используйте длинное деление, чтобы найти 9 / 9, но вместо 90/9 = 10 каждый раз подставляйте 81 в остатке 9 и смотрите, что получится.
0,9999...
-----------
9 | 9.0000...
8.1
---
90
81
--
90
81
--
9...
Или как насчет этого?
Следите за повторяющимся узором.
1/11111 = 0,0000
9... 1/1111 = 0,000
000... 1/111 = 0,0009009... 1/11 = 0,0
09... 1/1 = 0,9999... = 1
Аргумент ограничения
Последовательность может иметь только одно ограничение.
Обратите внимание, что предел последовательности
0,9 0,99 0,999 0,9999 0,99999 ...
это
0,9999...
То есть последовательность все ближе и ближе к 0,9999... на самом деле бесконечно близко.
Но последовательность все ближе и ближе к 1. 0000... фактически бесконечно близко. Итак, 1.0000... также является пределом этой последовательности.
0000... фактически бесконечно близко. Итак, 1.0000... также является пределом этой последовательности.
Но у последовательности может быть только один предел, поэтому 0,9999... и 1,0000... должны совпадать.
Наконец, рассмотрим это
НЕТ доказательств того, что 0,9999... и 1 - разные числа.
Куда угодно.
Общие контраргументы и мои ответы
"0,9999... и 1 - явно разные числа."
В математике "очевидный" означает "доказательство сразу же приходит на ум". Если вы не имеете в виду доказательство, то, к сожалению, никакое математическое утверждение, которое вы делаете, не имеет никакого веса.
"1 и 0,9999... пишутся по-разному, поэтому это разные числа."
Любое число можно записать разными способами. Вы можете написать 1/1, или 3-2, или 1,0, или 1,00, или 1,0000... или любое количество других выражений, и все они в конечном итоге будут иметь одно и то же значение «один».
"0,9999... это понятие, а не число.
 "
"Все числа являются понятиями.
"0,9999... не может существовать в реальности, а 1 может, поэтому они разные."
- То, что число не может «существовать в реальности», не означает, что оно не может существовать в математике.
- Поскольку 1 = 0,9999..., это означает, что 0,9999... "существует в действительности" точно в той же степени, что и 1.
"Ошибка округления. 0,9999... и 1 примерно равны."
Ошибки округления возникают только тогда, когда мы усекаем десятичное расширение после конечного числа цифр. Во всех приведенных выше доказательствах на каждом шаге используется обозначение «...», что означает, что мы всегда учитываем все бесконечное количество десятичных цифр. Округления нет, значит нет ошибки.
"0,9999... все ближе и ближе к 1, но никогда не достигает ее."
0,9999... это одно число. Он не двигается, поэтому не может приблизиться к чему-либо. Это там, где оно есть.
"0,9999.
 .. это десятичное представление бесконечности, а не число."
.. это десятичное представление бесконечности, а не число."0,9999... определенно меньше 2, поэтому оно не может быть бесконечно большим.
"Люди не могут постичь бесконечность, а неспособность постичь бесконечность означает, что с ней нельзя делать математику."
- Люди могут постичь бесконечность. Математики делают это постоянно.
Бесконечность подчиняется правилам. Если что-то последовательно подчиняется правилам, то с этим можно делать математические операции. Хорошим примером является порядковая арифметика.
В случае, если связь не ясна, то, что верно для бесконечных значений, в равной степени верно и для бесконечных десятичных разложений. Есть правила и процедуры, и они работают и дают значимые результаты. См. «Настоящее доказательство» выше, чтобы получить относительно скромное представление об этом, что на самом деле представляет собой обширную область математики, известную как «анализ», естественно основанную на незыблемых фундаментальных аксиомах.

"Бесконечность не определена четко."
Конечно.
"Мой приятель/мой папа/мой учитель математики/профессор Стивен Хокинг сказал мне, что 0,9999... и 1 были разными числами."
Они ошибались.
"Но они это тоже доказали." Я до сих пор в это не верю и имею право на собственное мнение."
В обычной науке есть теории. Теория выдвигается для объяснения наблюдений и может быть опровергнута в свете новых, необъяснимых наблюдений. Несколько теорий и мнений могут конкурировать друг с другом.Есть мода.Есть место для дебатов.
В математике у нас есть теоремы вместо теорий. Теорема — это результат математического доказательства . Теорема - это факт. Теорема не может быть опровергнута и не является вопросом мнения. Однажды доказанная теорема означает вечность. Математика не идеологична.
Благодаря многочисленным доказательствам, приведенным выше, «повторяющаяся точка девять равна единице» является именно такой теоремой.


 15
15 21
21 67
67 6
6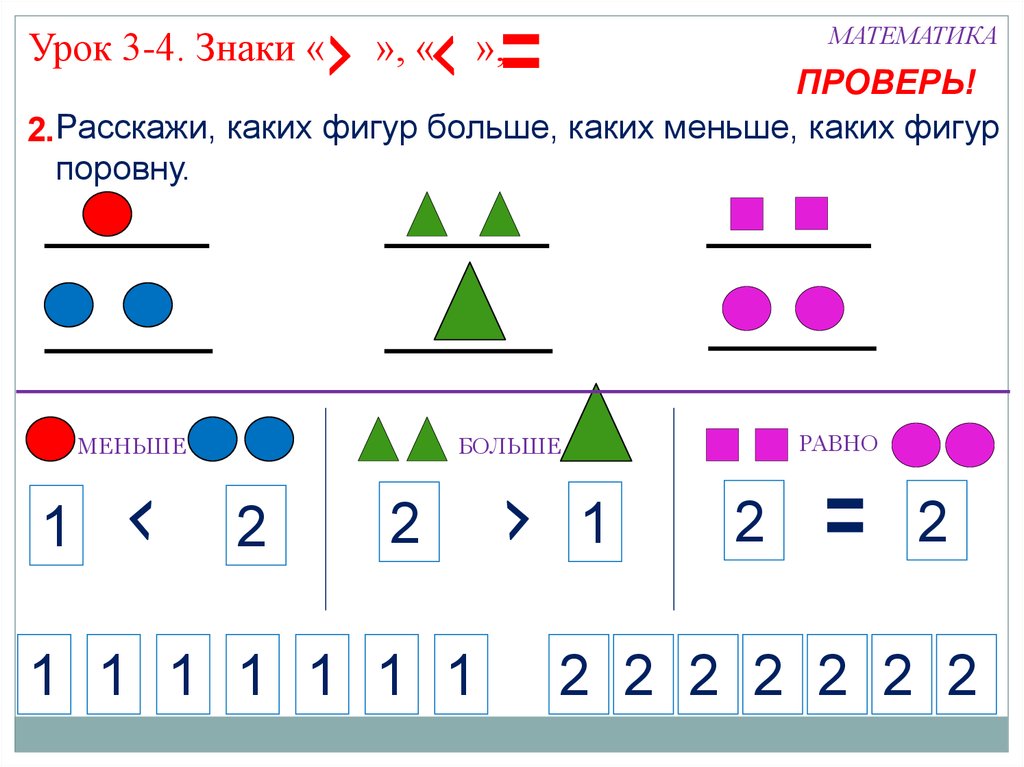 3
3 09.2022 14:01
09.2022 14:01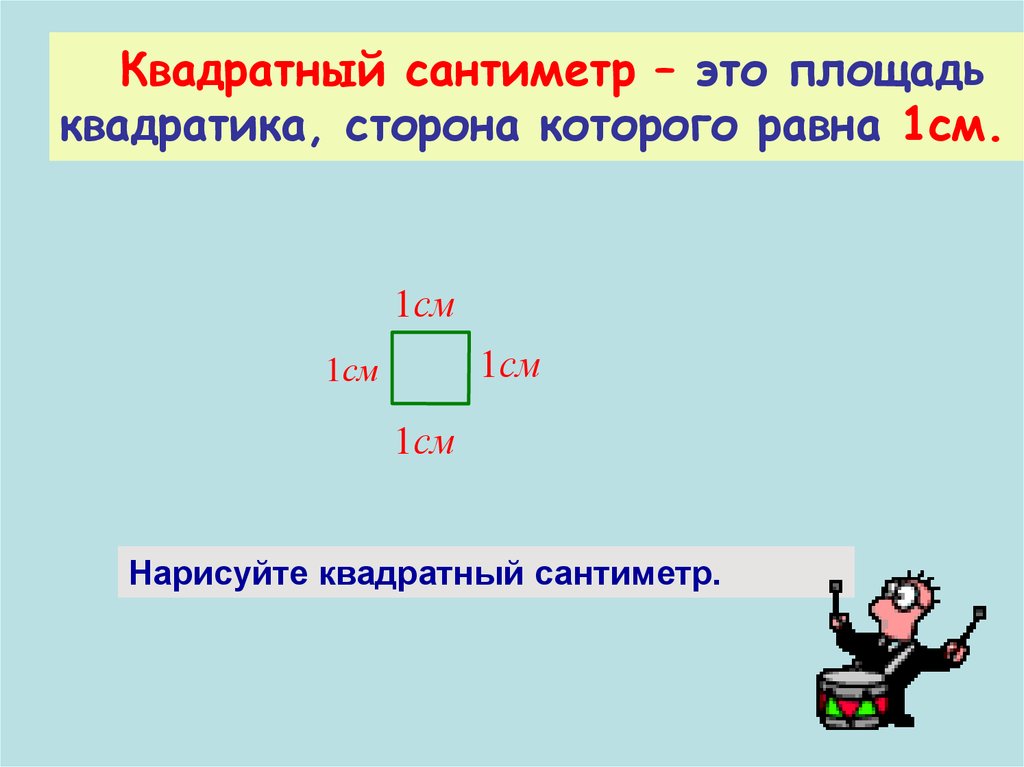



 Они были очень впечатлены…
Они были очень впечатлены… Фиксированная структура вознаграждения позволяет мне контролировать наши расходы на подбор персонала, а их широкий охват приводит к хорошему выбору…
Фиксированная структура вознаграждения позволяет мне контролировать наши расходы на подбор персонала, а их широкий охват приводит к хорошему выбору… От оценки задания до назначения новой команды…
От оценки задания до назначения новой команды… С помощью этой услуги мы набрали сотрудников всех уровней и…
С помощью этой услуги мы набрали сотрудников всех уровней и… Мы наняли всех сотрудников от руководства до рабочей силы, используя услуги, предоставляемые Equals One Recruitment. Я очень рекомендую их услуги.”
Мы наняли всех сотрудников от руководства до рабочей силы, используя услуги, предоставляемые Equals One Recruitment. Я очень рекомендую их услуги.” Они сыграли значительную роль в очень успешном исходе.
Они сыграли значительную роль в очень успешном исходе. .. = 0,9999... + 0
= 0,9999... + (0,9999... - 0,9999...)
= (0,9999... + 0,9999...) - 0,9999...
= 1,9999... - 0,9999...
= 1.0000...
.. = 0,9999... + 0
= 0,9999... + (0,9999... - 0,9999...)
= (0,9999... + 0,9999...) - 0,9999...
= 1,9999... - 0,9999...
= 1.0000...
 .. - 0,9999... = 0,0000...
= 0
.. - 0,9999... = 0,0000...
= 0
 ..
п =∞
= Σ 0,9 * 0,1 n n =0
n =∞
= ?
н =0
= a / (1 - r )
= 0,9 / (1 - 0,1)
= 0,9 / 0,9
= 1
..
п =∞
= Σ 0,9 * 0,1 n n =0
n =∞
= ?
н =0
= a / (1 - r )
= 0,9 / (1 - 0,1)
= 0,9 / 0,9
= 1
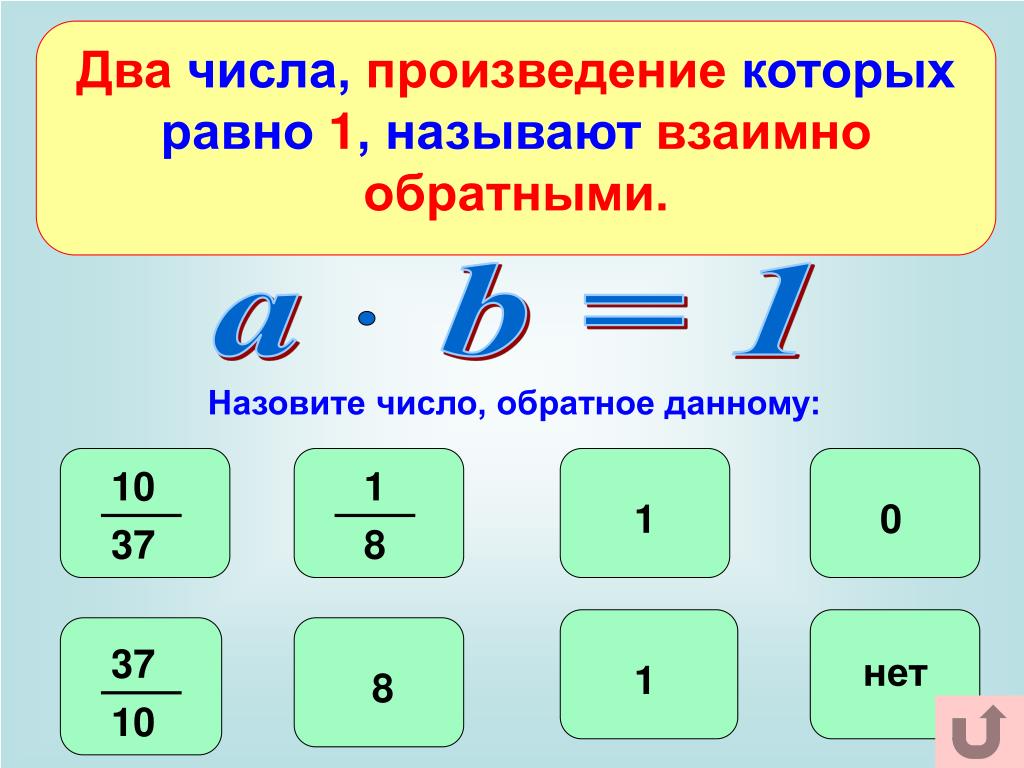 ..
n =∞
= Σ 9·10 - n n =1
н = н
:= lim Σ 9·10 - n N →∞ n =1
= лим ( 9·10 -1 + 9·10 -2 + ... + 9·10 - N )
С →∞
= lim ( 9·0,1 + 9·0,01 + ... + 9·0,000...0001 )
N →∞ \________/
N цифры
= lim ( 0,9 + 0,09 + ... + 0,000 ... 0009 )
N →∞ \________/
N цифры
= lim (0,999...999)
N →∞ \_______/
N девятки
= lim ( 1 - 0,000...0001 )
N →∞ \________/
N цифры
= lim ( 1 - 10 - N )
С →∞
= lim 1 - lim 10 - N N →∞ с.
..
n =∞
= Σ 9·10 - n n =1
н = н
:= lim Σ 9·10 - n N →∞ n =1
= лим ( 9·10 -1 + 9·10 -2 + ... + 9·10 - N )
С →∞
= lim ( 9·0,1 + 9·0,01 + ... + 9·0,000...0001 )
N →∞ \________/
N цифры
= lim ( 0,9 + 0,09 + ... + 0,000 ... 0009 )
N →∞ \________/
N цифры
= lim (0,999...999)
N →∞ \_______/
N девятки
= lim ( 1 - 0,000...0001 )
N →∞ \________/
N цифры
= lim ( 1 - 10 - N )
С →∞
= lim 1 - lim 10 - N N →∞ с. ш. →∞
= 1 - 0
= 1
ш. →∞
= 1 - 0
= 1
