Решение трансцендентных уравнений онлайн: Решение уравнений | Онлайн калькулятор

Содержание

Онлайн калькулятор: Метод хорд

Немного теории о методе хорд под калькулятором.

Метод хорд

Критерий останова (тип)Отличие функции от нуля Точность вычисления

Знаков после запятой: 4

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

content_copy Ссылка save Сохранить extension Виджет

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Источник

Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.

Подробнее: Метод хорд

Решение биквадратных уравнений. Уравнения онлайн Возможные решения задач

Решить уравнение — это значит найти такие значения неизвестного, при которых равенство будет верным.

Решение уравнения

Представим уравнение в следующем виде:

2х * х — 3 * х = 0.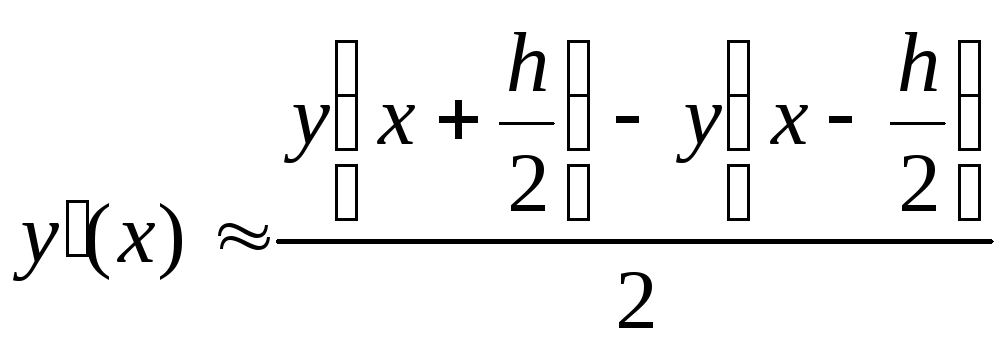

Видим, что члены уравнения в левой части имеют общий множитель х. Вынесем его за скобки и запишем:

х * (2х — 3) = 0.

Полученное выражение является произведением множителей х и (2х — 3). Вспомним, что произведение равно 0 в том случае, если хотя бы один из множителей равен 0. Значит, можно записать равенства:

х = 0 или 2х — 3 = 0.

Значит одним из корней исходного уравнения является х 1 = 0.
Найдем второй корень, решив уравнение 2х — 3 = 0.

В этом выражении 2х — уменьшаемое, 3 — вычитаемое, 0 — разность. Чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое:

В последнем выражении 2 и х — множители, 3 — произведение. Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:

Таким образом, мы нашли второй корень уравнения: х 2 = 1,5.

Проверка правильности решения

Для того, чтобы узнать, правильно ли решено уравнение, необходимо подставить в него числовые значения х и выполнить необходимые арифметические действия. Если в результате вычислений получится, что левая и правая части выражения имеют одинаковое значение, то уравнение решено правильно.

Выполним проверку:

Вычислим значение исходного выражения при х 1 = 0 и получим:

2 * 0 2 — 3 * 0 = 0,

0 = 0, верно.

Вычислим значение выражения при х 2 = 0 и получим:

2 * 1,5 2 — 3 * 1,5 = 0,

2 * 2,25 — 4,5 = 0,

0 = 0, верно.

Значит, уравнение решено правильно.

Ответ: х 1 = 0, х 2 = 1,5.

, тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ.

Изучая естественные науки, неизбежно сталкиваешься с необходимостью
решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы.

Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.

Квадратные уравнения.

Квадратное уравнение — алгебраическое уравнение общего вида

где x — свободная переменная,

a, b, c, — коэффициенты, причём

Выражение называют квадратным трёхчленом.

Способы решения квадратных уравнений.

1. СПОСОБ : Разложение левой части уравнения на множители.

Решим уравнение х 2 + 10х — 24 = 0 . Разложим левую часть на множители:

х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х — 2) = 0

Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю.

Поэтому левая часть уравнения обращается нуль при х = 2 , а также при х = — 12 . Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0 .

2. СПОСОБ : Метод выделения полного квадрата.

Решим уравнение х 2 + 6х — 7 = 0 . Выделим в левой части полный квадрат.

Для этого запишем выражение х 2 + 6х в следующем виде:

х 2 + 6х = х 2 + 2 х 3.

В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как

х 2 + 2 х 3 + 3 2 = (х + 3) 2 .

Преобразуем теперь левую часть уравнения

х 2 + 6х — 7 = 0 ,

прибавляя к ней и вычитая 3 2 . Имеем:

х 2 + 6х — 7 =

х 2 + 2 х 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.

Таким образом, данное уравнение можно записать так:

(х + 3) 2 — 16 =0, (х + 3) 2 = 16.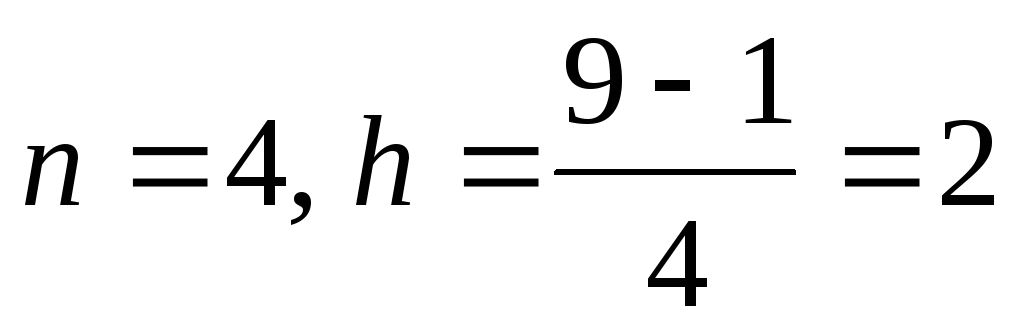

Следовательно, х + 3 — 4 = 0, х 1 = 1, или х + 3 = -4, х 2 = -7.

3. СПОСОБ : Решение квадратных уравнений по формуле.

Умножим обе части уравнения

ах 2 + bх + с = 0, а ≠ 0

на 4а и последовательно имеем:

4а 2 х 2 + 4аbх + 4ас = 0,

((2ах) 2 + 2ах b + b 2) — b 2 + 4ac = 0,

(2ax + b) 2 = b 2 — 4ac,

2ax + b = ± √ b 2 — 4ac,

2ax = — b ± √ b 2 — 4ac,

Примеры .

а) Решим уравнение: 4х 2 + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 4 3 = 49 — 48 = 1,

D > 0,

два разных корня;

Таким образом, в случае положительного дискриминанта, т.е. при

b 2 — 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.

б) Решим уравнение: 4х 2 — 4х + 1 = 0,

а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 4 1= 16 — 16 = 0,

D = 0, один корень;

Итак, если дискриминант равен нулю, т. е. b 2 — 4ac = 0 , то уравнение

ах 2 + bх + с = 0 имеет единственный корень,

в) Решим уравнение: 2х 2 + 3х + 4 = 0,

а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 2 4 = 9 — 32 = — 13 , D

Данное уравнение корней не имеет.

Итак, если дискриминант отрицателен, т.е. b 2 — 4ac , уравнение

ах 2 + bх + с = 0 не имеет корней.

Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни

любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

4. СПОСОБ: Решение уравнений с использованием теоремы Виета.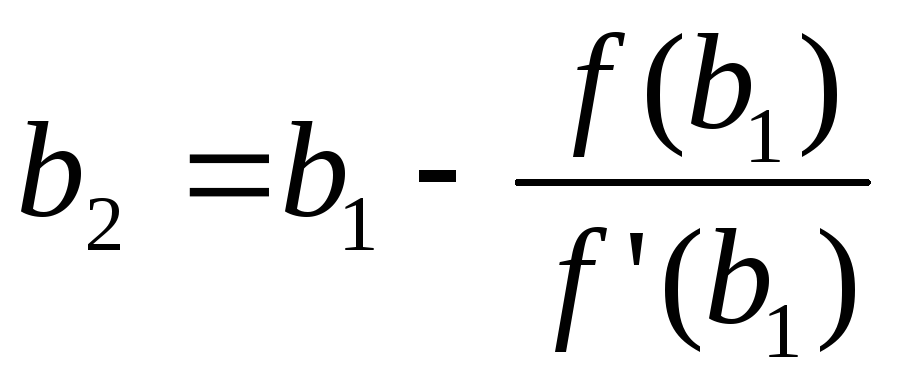

Как известно, приведенное квадратное уравнение имеет вид

х 2 + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x 1 x 2 = q,

x 1 + x 2 = — p

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен (q > 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р , то оба корня отрицательны, если р , то оба корня положительны.

Например,

x 2 – 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = — 3

x 2 + 8x + 7 = 0; x 1 = — 7 и x 2 = — 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен (q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p > 0 .

Например,

x 2 + 4x – 5 = 0; x 1 = — 5 и x 2 = 1, так как q= — 5 и p = 4 > 0;

x 2 – 8x – 9 = 0; x 1 = 9 и x 2 = — 1, так как q = — 9 и p = — 8

Примеры.

1) Решим уравнение 345х 2 – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

х 1 = 1, х 2 = c/a = -208/345.

Ответ: 1; -208/345.

2)Решим уравнение 132х 2 – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

х 1 = 1, х 2 = c/a = 115/132.

Ответ: 1; 115/132.

Б. Если второй коэффициент b = 2k – четное число, то формулу корней

Пример.

Решим уравнение 3х2 — 14х + 16 = 0 .

Решение . Имеем: а = 3, b = — 14, с = 16, k = — 7 ;

D = k 2 – ac = (- 7) 2 – 3 16 = 49 – 48 = 1, D > 0, два различных корня;

Ответ: 2; 8/3

В. Приведенное уравнение

х 2 + рх + q= 0

совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней

Принимает вид:

Формулу (3) особенно удобно использовать, когда р — четное число.

Пример. Решим уравнение х 2 – 14х – 15 = 0.

Решение. Имеем: х 1,2 =7±

Ответ: х 1 = 15; х 2 = -1.

5. СПОСОБ: Решение уравнений графически.

Пример. Решить уравнение х2 — 2х — 3 = 0.

Построим график функции у = х2 — 2х — 3

1) Имеем: а = 1, b = -2, х0 = = 1, у0 = f(1)= 12 — 2 — 3= -4. Значит, вершиной параболы служит точка (1; -4), а осью параболы — прямая х = 1.

2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = -1 и х = 3.

Имеем f(-1) = f(3) = 0. Построим на координатной плоскости точки (-1; 0) и (3; 0).

3) Через точки (-1; 0), (1; -4), (3; 0) проводим параболу (рис. 68).

Корнями уравнения х2 — 2х — 3 = 0 являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения таковы: х1 = — 1, х2 — 3.

В этой статье мы будем учиться решать биквадратные уравнения.

Итак, уравнения какого вида называются биквадратными?
Все уравнения вида ах 4 + bx 2 + c = 0 , гдеа ≠ 0 , являющиеся квадратными относительно х 2 , и называются биквадратными уравнениями. Как видите, эта запись очень похожа на запись квадратного уравнения, поэтому и решать биквадратные уравнения будем используя формулы, которые мы применяли при решении квадратного уравнения.

Только нам необходимо будет ввести новую переменную, то есть обозначим х 2 другой переменной, например, у или t (или же любой другой буквой латинского алфавита).

Например, решим уравнение х 4 + 4х 2 ‒ 5 = 0.

Обозначим х 2 через у (х 2 = у ) и получим уравнение у 2 + 4у – 5 = 0.
Как видите, такие уравнения вы уже умеете решать.

Решаем полученное уравнение:

D = 4 2 – 4 (‒ 5) = 16 + 20 = 36, √D = √36 = 6.

у 1 = (‒ 4 – 6)/2= ‒ 10 /2 = ‒ 5,

у 2 = (‒ 4 + 6)/2= 2 /2 = 1.

Вернемся к нашей переменной х.

Получили, что х 2 = ‒ 5 и х 2 = 1.

Замечаем, что первое уравнение решений не имеет, а второе дает два решения: х 1 = 1 и х 2 = ‒1. Будьте внимательны, не потеряйте отрицательный корень (чаще всего получают ответ х = 1, а это не правильно).

Ответ: — 1 и 1.

Для лучшего усвоения темы разберем несколько примеров.

Пример 1. Решите уравнение 2х 4 ‒ 5 х 2 + 3 = 0.

Пусть х 2 = у, тогда 2у 2 ‒ 5у + 3 =0.

D = (‒ 5) 2 – 4· 2 · 3 = 25 ‒ 24 = 1, √D = √1 = 1.

у 1 = (5 – 1)/(2· 2) = 4 /4 =1, у 2 = (5 + 1)/(2· 2) = 6 /4 =1,5.

Тогда х 2 = 1 и х 2 = 1,5.

Получаем х 1 = ‒1, х 2 = 1, х 3 = ‒ √1,5 , х 4 = √1,5.

Ответ: ‒1; 1; ‒ √1,5; √1,5.

Пример 2. Решите уравнение 2х 4 + 5 х 2 + 2 = 0.

2у 2 + 5у + 2 =0.

D = 5 2 – 4 · 2 · 2 = 25 ‒ 16 = 9, √D = √9 = 3.

у 1 = (‒ 5 – 3)/(2 · 2) = ‒ 8 /4 = ‒2, у 2 = (‒5 + 3)/(2 · 2) = ‒ 2 /4 = ‒ 0,5.

Тогда х 2 = ‒ 2 и х 2 = ‒ 0,5. Обратите внимание, ни одно из этих уравнений не имеет решения.

Ответ: решений нет.

Неполные биквадратные уравнения — это когда b = 0 (ах 4 + c = 0) или же c = 0

(ах 4 + bx 2 = 0) решают как и неполные квадратные уравнения.

Пример 3. Решить уравнение х 4 ‒ 25х 2 = 0

Разложим на множители, вынесем х 2 за скобки и тогда х 2 (х 2 ‒ 25) = 0.

Получим х 2 = 0 или х 2 ‒ 25 = 0, х 2 = 25.

Тогда имеем корни 0; 5 и – 5.

Ответ: 0; 5; – 5.

Пример 4. Решить уравнение 5х 4 ‒ 45 = 0 .

х 2 = ‒ √9 (решений не имеет)

х 2 = √9, х 1 = ‒ 3, х 2 = 3.

Как видите, умея решать квадратные уравнения, вы сможете справиться и с биквадратными.

Если же у вас остались вопросы, записывайтесь на мои уроки. Репетиор Валентина Галиневская.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решите уравнение х 2 +(1-х) 2 =х

Докажите, что нет целых чисел, которые от перестановки начальной цифры в конец, увеличиваются в 5 раз.

В некотором царстве каждые двое – либо друзья, либо враги. Каждый человек может в некоторый момент поссориться со всеми друзьями и помириться со всеми врагами. Оказалось, что каждые три человека могут таким образом стать друзьями. Докажите, что тогда и все люди в этом царстве могут стать друзьями.

В треугольнике одна из медиан перпендикулярна одной из биссектрис. Докажите, что одна из сторон этого треугольника вдвое больше другой.

Задания для проведения районной (городской) олимпиады школьников по математике.

По стрельбе из мишени спортсмен выбивал только по 8,9 и 10 очков. Всего он, сделав более 11 выстрелов, выбил ровно 100 очков. Сколько выстрелов сделал спортсмен, и какие были попадания?

Докажите истинность неравенства:

3. Решите уравнение:

Найдите трехзначное число, которое уменьшается в 7 раз после зачеркивания в нем средней цифры.

В треугольнике АВС проведены биссектрисы из вершин А и В. Затем из вершины С проведены прямые, параллельные этим биссектрисам. Точки Д и Е пересечения этих прямых с биссектрисами соединены. Оказалось, что прямые ДЕ и АВ параллельны. Докажите, что треугольник АВС – равнобедренный.

Задания для проведения районной (городской) олимпиады школьников по математике.

Решите систему уравнений:

На сторонах АВ и АД параллелограмма АВСД взяты соответственно точки Е и К так, что отрезок ЕК параллелен диагонали ВД. Докажите, что площади треугольников ВСЕ и СДК равны.

Группу туристов решили рассадить по автобусам так, чтобы в каждом автобусе было одинаковое число пассажиров. Сначала в каждый автобус сажали по 22 человека, однако оказалось, что при этом не удается посадить одного туриста. Когда же один автобус уехал пустым, то в оставшиеся автобусы все туристы сели поровну. Сколько первоначально было автобусов и сколько туристов в группе, если известно, что в каждый автобус помещается не более 32 человек?

Задания для проведения районной (городской) олимпиады школьников по математике.

Решите систему уравнений:

Докажите, что четыре расстояния от точки окружности до вершины вписанного в нее квадрата не могут одновременно быть рациональными числами.

Возможные решения задач

1. Ответ: х=1, х=0,5

От перестановки начальной цифры в конец значность числа не изменится. При этом, по условию задачи, должны получить число, в 5 раз большее первого числа. Следовательно, первая цифра искомого числа должна равняться 1 и только 1. (т.к. если первая цифра будет 2 или больше, то изменится значность, 2*5=10). При перестановке 1 в конец, полученное число оканчивается на 1, следовательно на 5 не делится.

Из условия следует, что если А и В – друзья, то С либо их общий враг, либо общий друг (иначе им троим не примириться). Возьмем всех друзей человека А. Из сказанного следует, что все они дружны между собой и враждуют с остальными. Пусть теперь А и его друзья по очереди ссорятся с друзьями и мирятся с врагами. После этого все окажутся друзьями.

Действительно, пусть А первым поссорился со своими друзьями и помирился со своими врагами, но тогда каждый их его бывших друзей будет с ним мириться, а бывшие враги останутся друзьями. Итак, все люди оказываются друзьями А, а следовательно, и друзьями между собой.

Число 111 делится на 37, поэтому на 37 делится и названная сумма.

По условию, число делится на 37, поэтому и сумма

Делится на 37.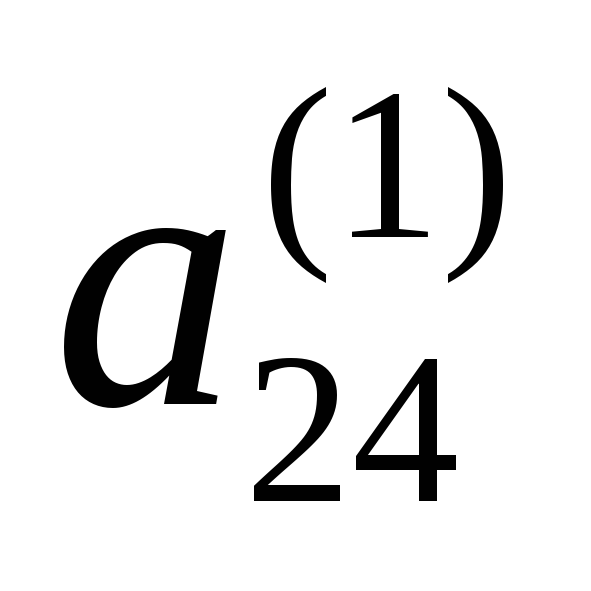

Заметим, что указанные медиана и биссектриса не могут выходить из одной вершины, так как в противном случае угол при этой вершине был бы больше 180 0 . Пусть теперь в треугольнике АВС биссектриса АD и медиана СЕ пересекаются в точке F. Тогда AF – биссектриса и высота в треугольнике АСЕ, значит этот треугольник равнобедренный (АС=АЕ), а так как СЕ – медиана, то АВ = 2АЕ и, следовательно, АВ =2АС.

Возможные решения задач

1. Ответ: 9 выстрелов по 8 очков,

2 выстрела по 9 очков,

1 выстрел по 10 очков.

Пусть x выстрелов сделал спортсмен, выбивая по 8 очков, y выстрелов по 9 очков, z выстрелов по 10 очков. Тогда можно составить систему:

Используя первое уравнение системы, запишем:

Из этой системы следует, что x + y + z =12

Умножим второе уравнение на (-8) и сложим с первым. Получим, что y +2 z =4 , откуда y =4-2 z , y =2(2- z ) .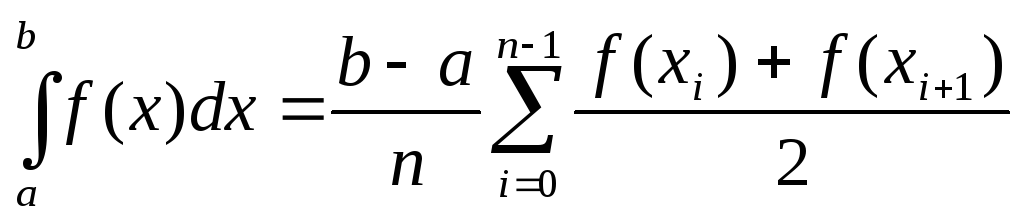 Следовательно, у – четное число, т.е. y=2t , где .

Следовательно,

3. Ответ: х = -1/2, х = -4

После приведения дробей к одному знаменателю получаем

4. Ответ: 105

Обозначим через x , y , z соответственно первую, вторую и третью цифру искомого трехзначного числа. Тогда его можно записать в виде . После вычеркивания средней цифры получится двузначное число . По условию задачи , т.е. неизвестные цифры x , y , z удовлетворяют уравнению

7(10 x + z )=100 x +10 y + x , которое после приведения подобных членов и сокращений принимает вид 3 z =15 x +5 y .

Из этого уравнения следует, что z должно делиться на 5 и должно быть положительным, так как по условию . Поэтому z =5, а цифры х, у удовлетворяют уравнению 3=3х + у, которое в силу условия имеет единственное решение х =1, у = 0.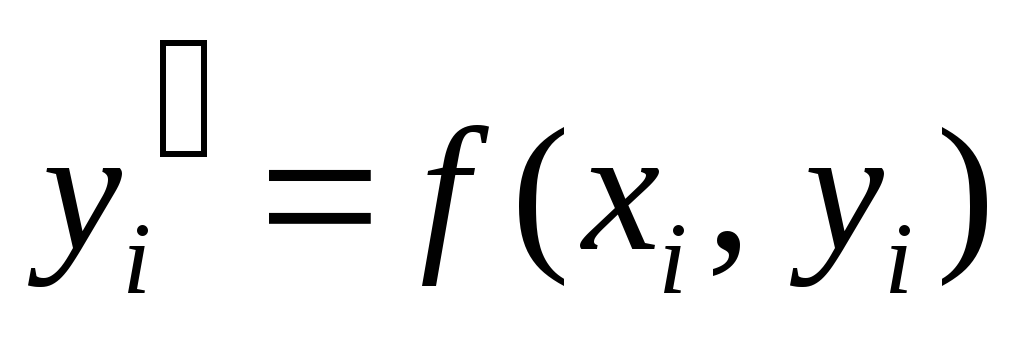 Следовательно, условию задачи удовлетворяет единственное число 105.

Обозначим буквой F точку, в которой пересекаются прямые АВ и СЕ. Так как прямые DB и CF параллельны, то . Ввиду того, что BD – биссектриса угла АВС, заключаем, что . Отсюда следует, что , т.е. треугольник BCF равнобедренный и BC=BF. Но из условия следует, что четырехугольник BDEF – параллелограмм. Поэтому BF = DE, и, значит ВС = DE. Аналогично доказывается, что АС = DE. Это приводит к требуемому равенству.

Возможные решения задач

Отсюда (х + у) 2 = 1 , т.е. х + у = 1 или х + у = -1 .

Рассмотрим два случая.

а) х + у = 1 . Подставив х = 1 – у

б) х + у = -1 . После подстановки х = -1-у

Итак, решениями системы могут быть лишь следующие четыре пары чисел: (0;1), (2;-1), (-1;0), (1;-2). Подстановкой в уравнения исходной системы убеждаемся, что каждая из этих четырех пар является решением системы.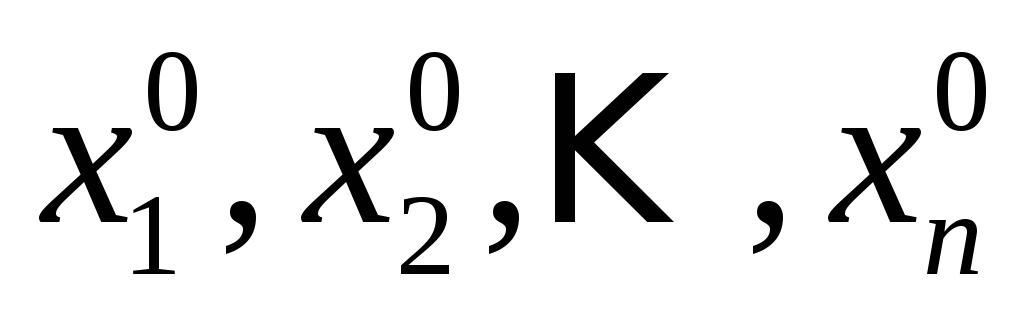

Треугольники CDF и BDF имеют общее основание FD и равные высоты, так как прямые ВС и AD параллельны. Следовательно, их площади равны. Аналогично, равны площади треугольников BDF и BDE, так как прямая BD параллельна прямой EF. И равны площади треугольников BDE и BCE, так как АВ параллельна CD. Отсюда и следует требуемое равенство площадей треугольников CDF и BCE.

Учитывая область определения функции, построим график.

Используя формулу выполним дальнейшие преобразования

Применяя формулы сложения и выполняя дальнейшие преобразования, получим

5. Ответ: 24 автобуса, 529 туристов.

Обозначим через k первоначальное число автобусов. Из условия задачи следует, чтои что число всех туристов равно 22 k +1 . После отъезда одного автобуса всех туристов удалось рассадить в оставшиеся (k-1) автобусов. Следовательно, число 22 k +1 должно делиться на k-1 . Таким образом, задача свелась к определению всех целых , для которых число

Является целым и удовлетворяет неравенству (число n равно числу туристов, посаженных в каждый автобус, а по условию задачи автобус вмещает не более 32 пассажиров).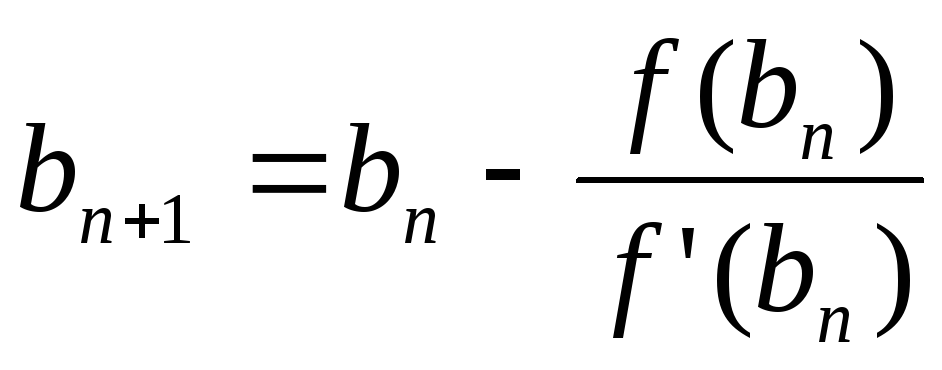

Число будет целым только тогда, когда число будет целым. Последнее возможно только при k =2 и при k =24 .

Если k =2 , то n=45.

А если k =24 , то n=23.

Отсюда и из условия получаем, что только k =24 удовлетворяет всем условиям задачи.

Следовательно, первоначально было 24 автобуса, а число всех туристов равно n(k-1)=23*23=529

Возможные решения задач

1. Ответ:

Тогда уравнение примет вид:

Получили квадратное уравнение относительно р .

2. Ответ: (0;1), (2;-1), (-1;0), (1;-2)

Сложив уравнения системы, получим , или

Отсюда (х + у) 2 = 1 , т.е. х + у = 1 или х + у = -1 .

Рассмотрим два случая.

а) х + у = 1 . Подставив х = 1 – у в первое уравнение системы, получим

б) х + у = -1 . После подстановки х = -1-у в первое уравнение системы, получим или

Численное решение алгебраических и трансцендентных уравнений

1. Тема 3

Численное решение
алгебраических и трансцендентных
уравнений.

5. 3.1. Отделение корней нелинейного уравнения.

Рис. 3.3 Схема алгоритма отделения
корней.
Root_Separation
2
Исходные данные:
Ввод
3
a – начало отрезка поиска корней
a, b, Δx
b – конец отрезка поиска корней
ya − значение функции в начале поиска
корня
Δx –очередного
шаг изменения
неизвестного
x=a
нет
ya= f(a)
x≤b
k=0
4
k − номер корня
да
5
6
x = x + Δx
7
y = f(x)
y* ya ≤ 0
нет
да
8
ya = y
9
k=k+1
Вывод
k, x – Δx, x, y
Результаты:
k− номер корня
x — Δx – начало отрезка существования корня;
x – конец отрезка существования
10
Конец
Корня; y – значение функции при x.

15. 3.2. Алгоритмы уточнения корней уравнения.

Рис. 3.5 Схема алгоритма
метода бисекций (дихотомии)
1
Входные данные:
–b=x
заданная точность;
a – левая граница отрезка;
b – правая граница отрезка.
Bisection
2
ya =f(a)
yb =f(b)
3
ya yb 0
д
i=0 а
4
5
11
Вывод
«Корней нет»
i = i+1;
x =(a+b)/2
6
12
Stop
y=f(x)
7 ya y>0
8
нет 9
нет
a=x
д
а
|y| /\ b-a
10
д
а
Exit
нет
7
Выходные данные:
x – приближенное значение
корня;
y – значение функции при
найденном корне х;
i – выполненное число итераций.
x’

x [a,b].
Проверим полученное значение, подставив в исходное уравнение:
f ( x 6 ) 0,453917 3 2 0,453917 1 0,093525 0,907834 1 0,001359
Значение f(x) близко к 0 с точностью, близкой к ε,
следовательно, корень уточнен правильно.

37. 3.2.3 Метод Ньютона (касательных).

итерационный процесс. При этом, чем больше значение модуля производной в
окрестности корня (чем круче график функции), тем быстрее сходимость.

X 4 5 решение. Уравнения онлайн. Примеры тождественных преобразований уравнений. Основные проблемы

Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. Решение уравнений данного типа означает нахождение искомых корней в общем виде. Наш сервис позволяет решить даже самое сложное алгебраическое уравнение онлайн. Вы можете получить как общее решение уравнения, так и частное для указанных вами числовых значений коэффициентов. Для решения алгебраического уравнения на сайте достаточно корректно заполнить всего два поля: левую и правую части заданного уравнения.2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.

I. Линейные уравнения

II. Квадратные уравнения

ax 2 + bx + c = 0, a ≠ 0, иначе уравнение становится линейным

Корни квадратного уравнения можно вычислять различными способами, например:

Мы хорошо умеем решать квадратные уравнения. Многие уравнения более высоких степеней можно привести к квадратным.

III. Уравнения, приводимые к квадратным.

замена переменной: а) биквадратное уравнение ax 2n + bx n + c = 0, a ≠ 0, n ≥ 2

2) симметрическое уравнение 3 степени – уравнение вида

3) симметрическое уравнение 4 степени – уравнение вида

ax 4 + bx 3 + cx 2 + bx + a = 0, a ≠ 0, коэффициенты a b c b a или

ax 4 + bx 3 + cx 2 – bx + a = 0, a ≠ 0, коэффициенты a b c (–b) a

Т.к. x = 0 не является корнем уравнения, то возможно деление обеих частей уравнения на x 2 , тогда получаем: .

Произведя замену решаем квадратное уравнение a (t 2 – 2) + bt + c = 0

Например, решим уравнение x 4 – 2x 3 – x 2 – 2x + 1 = 0, делим обе части на x 2 ,

, после замены получаем уравнение t 2 – 2t – 3 = 0

– уравнение не имеет корней.

4) Уравнение вида (x – a )(x – b )(x – c )(x – d ) = Ax 2 , коэффициенты ab = cd

Например, (x + 2 )(x +3 )(x + 8 )(x + 12 ) = 4x 2 . Перемножив 1–4 и 2–3 скобки, получим (x 2 + 14x + 24)(x 2 +11x + 24) = 4x 2 , разделим обе части уравнения на x 2 , получим:

Имеем (t + 14)(t + 11) = 4.

5) Однородное уравнение 2 степени – уравнение вида Р(х,у) = 0, где Р(х,у) – многочлен, каждое слагаемое которого имеет степень 2.

Ответ: -2; -0,5; 0

IV. Все приведенные уравнения узнаваемы и типичны, а как быть с уравнениями произвольного вида?

Пусть дан многочлен P n (x ) = a n x n + a n-1 x n-1 + …+a 1 x + a 0 , где a n ≠ 0

Рассмотрим метод понижения степени уравнения.

Известно, что, если коэффициенты a являются целыми числами и a n = 1 , то целые корни уравнения P n (x ) = 0 находятся среди делителей свободного члена a 0 . Например, x 4 + 2x 3 – 2x 2 – 6x + 5 = 0, делителями числа 5 являются числа 5; –5; 1; –1. Тогда P 4 (1) = 0, т.е. x = 1 является корнем уравнения. Понизим степень уравнения P 4 (x ) = 0 с помощью деления “уголком” многочлена на множитель х –1, получаем

P 4 (x ) = (x – 1)(x 3 + 3x 2 + x – 5).

Аналогично, P 3 (1) = 0, тогда P 4 (x ) = (x – 1)(x – 1)(x 2 + 4x +5), т.е. уравнение P 4 (x) = 0 имеет корни x 1 = x 2 = 1. Покажем более короткое решение этого уравнения (с помощью схемы Горнера).

	1	2	–2	–6	5
1	1	3	1	–5	0
1	1	4	5	0

значит, x 1 = 1 значит, x 2 = 1.

Итак, (x – 1) 2 (x 2 + 4x + 5) = 0

Что мы делали? Понижали степень уравнения.

V. Рассмотрим симметрические уравнения 3 и 5 степени.

а) ax 3 + bx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

б) ax 5 + bx 4 + cx 3 + cx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

Например, покажем решение уравнения 2x 5 + 3x 4 – 5x 3 – 5x 2 + 3x + = 0

	2	3	–5	–5	3	2
–1	2	1	–6	1	2	0
1	2	3	–3	–2	0
1	2	5	2	0

x = –1

Получаем (x – 1) 2 (x + 1)(2x 2 + 5x + 2) = 0. Значит, корни уравнения: 1; 1; –1; –2; –0,5.

VI. Приведем список различных уравнений для решения в классе и дома.

Предлагаю читателю самому решить уравнения 1–7 и получить ответы…

Приложение

Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн , вначале приведите уравнение к общему виду:
ax 2 + bx + c = 0
Заполните соответственно поля формы:

Как решить квадратное уравнение

Как решить квадратное уравнение:

Виды корней:

1. Привести квадратное уравнение к общему виду:
Общий вид Аx 2 +Bx+C=0
Пример: 3х — 2х 2 +1=-1 Приводим к -2х 2 +3х+2=0

2. Находим дискриминант D.
D=B 2 -4*A*C .
Для нашего примера D= 9-(4*(-2)*2)=9+16=25.

3. Находим корни уравнения.
x1=(-В+D 1/2)/2А.
Для нашего случая x1=(-3+5)/(-4)=-0,5
x2=(-В-D 1/2)/2А.
Для нашего примера x2=(-3-5)/(-4)=2
Если В — четное число, то дискриманант и корни удобнее считать по формулам:
D=К 2 -ac
x1=(-K+D 1/2)/А
x2=(-K-D 1/2)/А,
Где K=B/2

1. Действительные корни. Причем. x1 не равно x2
Ситуация возникает, когда D>0 и A не равно 0.

2. Действительные корни совпадают. x1 равно x2
Ситуация возникает, когда D=0. Однако при этом, ни А, ни В, ни С не должны быть равны 0.

3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1) 1/2
Ситуация возникает, когда D
4. Уравнение имеет одно решение.
A=0, B и C нулю не равны. Уравнение становиться линейным.

5. Уравнение имеет бесчисленное множество решений.
A=0, B=0, C=0.

6. Уравнение решений не имеет.
A=0, B=0, C не равно 0.

Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений .

Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x 2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число 1/2 !
x1=(-В+D 1/2)/2А = (-3+7)/2 = 2
x2=(-В-D 1/2)/2А = (-3-7)/2 = -5

Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10

Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х 2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k 2 – AC = 16 – 16 = 0
X = -k/A = 4

Подставим
(x-4)*(x-4) = (x-4)2 = X 2 – 8x + 16

Пример 3. Решение квадратного уравнения с комплексными корнями.
13х 2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b 2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.

X1=(-В+D 1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D 1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1

Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.
Если материал был полезен, вы можете

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.

Возможность обучения не выходя из дома

Обучение слушателей проходит дома в привычной обстановке. Нужен только компьютер, свободный доступ в интернет, желание учиться и немного свободного времени

Удобное время занятий

Режим занятий организован с учетом пожеланий слушателей. Лекционные и практические занятия проводятся после завершения уроков в основной школе

Отсутствие платы за обучение

Весь курс обучение для слушателей школы бесплатный. Наша задача – доступное образование для всех желающих

Команда опытных преподавателей

Преподаватели школы – кандидаты наук — имеют опыт работы в общеобразовательных организациях и подготовке школьников. Среди них – постоянные члены предметных комиссий по проверке заданий государственной итоговой аттестации по математике, члены жюри и методических комиссий олимпиад различного уровня.

Возможность онлайн-консультаций с преподавателем

Программа вебинаров и практических занятий предусматривает интерактивный диалог спикера и слушателей. На любом этапе занятия можно обсудить проблемные вопросы темы, получить уточнения и разъяснения решений сложных задач.

Как записаться в школу

Зачисление в состав слушателей

В каком режиме работаем

Кто проводит обучение

Что изучают слушатели школы

Практическое занятие проводятся по пятницам в 18:30 ссылка для участия тут

Лекционное занятие проводятся по вторникам в 18:30 ссылка для участия находится тут

Задания для усвоения лекционного материала

Вебинар № 1 для 7 класса состоится 00.10.2020 ссылка для участия ….

Практическое занятие проводится по четвергам в 17:00 ссылка для участия находится тут

Лекционное занятие проводится по четвергам в 16:00 ссылка для участия находится тут

Запись лекционного занятия № 1 для 8 класса от 00.10.2020 ссылка для участия ….

Задания для усвоения лекционного материала

Вебинар № 1 для 8 класса состоится 00.10.2020 ссылка для участия ….

Практическое занятие проводится по пятницам в 16:30 ссылка для участия находится тут

Лекционное занятие проводится по пятницам в 15:30 ссылка для участия находится тут

Запись лекционного занятия № 1 для 9 класса от 00.10.2020 ссылка для участия ….

Задания для усвоения лекционного материала

Вебинар № 1 для 9 класса состоится 00.10.2020 ссылка для участия ….

Задания для самостоятельной работы

Практическое занятие проводится по пятницам в 17:50 ссылка для участия находится тут

Лекционное занятие проводится по пятницам в 17.00 ссылка для участия находится тут

Запись лекционного занятия № 1 для 10 класса от 00.10.2020 ссылка для участия ….

Вебинар № 1 для 10 класса состоится 00.10.2020 ссылка для участия ….

Практическое занятие проводится в понедельник в 18:00 ссылка для участия тут

Лекционное занятие проводится в среду в 17:00 ссылка для участия находится тут

Запись лекционного занятия № 1 для 11 класса от 00.10.2020 ссылка для участия ….

Вебинар № 1 для 11 класса состоится 00.10.2020 ссылка для участия ….

Директор Математической школы,

куратор 11 класса — Ладошкин Михаил Владимирович,
кандидат физико-математических наук, доцент

Куратор 10 класса – Сарванова Жанна Александровна,

кандидат педагогических наук

Куратор 9 класса – Ульянова Ирина Валентиновна,

кандидат педагогических наук, доцент

Куратор 8 класса – Кочетова Ирина Викторовна,

кандидат педагогических наук

Куратор 7 класса – Базаркина Ольга Александровна,

кандидат физико-математических наук

Образовательные программы школы обеспечены авторскими методиками эффективной стратегии углубленного изучения дополнительных разделов математики. Система учебных задач и самостоятельная работа подобрана с учетом базового, повышенного и высокого уровня сложности, что позволяет планомерно осваивать программу учащимися с разной степенью подготовки и выстраивать индивидуальную траекторию обучения каждого слушателя.

	7 класс
задачи на делимость и остатки; линейные уравнения с параметрами; ошибки в геометрических доказательствах; задачи комбинаторной геометрии; принцип Дирихле

Посмотреть программу

8 класс

числовые и буквенные выражения;
иррациональные выражения;
квадратные и дробно-рациональные неравенства и их системы;
вычисление площадей плоских фигур;
задачи на совместную работу, концентрацию, сплавы, смеси;
задачи на сложные проценты

Посмотреть программу

9 класс

решение уравнений и неравенств на основе свойств функции;
аналитические методы и приемы решения уравнений и неравенств с модулем;
алгебраические и геометрические методы решения текстовых задач;
решение комбинаторных задач;
метод введения вспомогательной окружности при решении геометрических задач

Посмотреть программу

10 класс

виды и методы решения трансцендентных уравнений и неравенств;
виды геометрических преобразований графиков элементарных функций;
нестандартные методы решения трансцендентных уравнений и неравенств;
методы построения сечений многогранников;
особенности построений на изображениях многогранников;
приемы исследования задачной ситуации

Посмотреть программу

11 класс

тригонометрические неравенства;
решение задач с использованием уравнений линий;
методы векторной алгебры в решении геометрических задач;
применение производной к решению текстовых задач практического содержания;
доказательство утверждений методом математической индукции;
решение олимпиадных задач на применение формул комбинаторики

Посмотреть программу

Решение показательных уравнений. Примеры

Приложение

Инструкция

Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.

Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!

Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2
3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.

Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т.е.
х=4

Видео по теме

Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует разными способами.

Вам понадобится

— линейное уравнение с двумя переменными;
— второе уравнение или дополнительные условия.

Инструкция

Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую. Найдите у и подставьте в любое из первоначальных уравнений, найдите х.

Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.

Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.

Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.

Источники:

как решить уравнение с одной переменной

Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Вам понадобится

— система из трех уравнений с тремя неизвестными.

Инструкция

Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.

Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.

Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.

Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.

Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.

Источники:

решений уравнений с тремя неизвестными

Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.

Инструкция

Самый распространенный метод решения системы уравнений — это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.

Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.

Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.

Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.

Видео по теме

Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.

Инструкция

Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно. Мысленно определите коэффициенты, стоящие перед каждой неизвестной, а также коэффициенты в правой части каждого уравнения.

Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии.

Советую поступать немного по-другому. Почему? Писал об этом .

Предлагаю решать такие задания следующим образом:

1. Находим производную.
2. Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).

В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать .

Рассмотрим примеры:

77422. Найдите наибольшее значение функции у=х 3 –3х+4 на отрезке [–2;0].

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = –1.

Вычисляем значения функции в точках –2, –1 и 0:

Наибольшее значение функции равно 6.

Ответ: 6

77425. Найдите наименьшее значение функции у = х 3 – 3х 2 + 2 на отрезке .

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = 2.

Вычисляем значения функции в точках 1, 2 и 4:

Наименьшее значение функции равно –2.

Ответ: –2

77426. Найдите наибольшее значение функции у = х 3 – 6х 2 на отрезке [–3;3].

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = 0.

Вычисляем значения функции в точках –3, 0 и 3:

Наименьшее значение функции равно 0.

Ответ: 0

77429. Найдите наименьшее значение функции у = х 3 – 2х 2 + х +3 на отрезке .

Найдём производную заданной функции:

3х 2 – 4х + 1 = 0

Получим корни: х 1 = 1 х 1 = 1/3.

Указанному в условии интервалу принадлежит только х = 1.

Найдём значения функции в точках 1 и 4:

Получили, что наименьшее значение функции равно 3.

Ответ: 3

77430. Найдите наибольшее значение функции у = х 3 + 2х 2 + х + 3 на отрезке [– 4; –1].

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

3х 2 + 4х + 1 = 0

Получим корни:

Указанному в условии интервалу принадлежит корень х = –1.

Находим значения функции в точках –4, –1, –1/3 и 1:

Получили, что наибольшее значение функции равно 3.

Ответ: 3

77433. Найдите наименьшее значение функции у = х 3 – х 2 – 40х +3 на отрезке .

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

3х 2 – 2х – 40 = 0

Получим корни:

Указанному в условии интервалу принадлежит корень х = 4.

Находим значения функции в точках 0 и 4:

Получили, что наименьшее значение функции равно –109.

Ответ: –109

Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).

77437. Найдите наименьшее значение функции у=7+12х–х 3 на отрезке [–2;2].

Подставляем точки от –2 до 2: Посмотреть решение

77434. Найдите наибольшее значение функции у=х 3 + 2х 2 – 4х + 4 на отрезке [–2;0].

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

В этой статье мы рассмотрим несколько примеров на нахождение точек максимума (минимума) иррациональной функции. Алгоритм решения был уже неоднократно изложен в статьях с подобными заданиями, в одной из прошлых статей.

У вас может возникнуть вопрос – а чем рациональная функция отличается от иррациональной? У иррациональной функции, говоря простыми словами, аргумент находится под корнем, или степень у него это дробное число (несокращаемая дробь). Другой вопрос — в чём отличия в нахождении их точек максимума (минимума)? Да ни в чём.

Сам принцип и алгоритм решения заданий на определения точек максимума (минимума) един. Просто для удобства и систематизации материала я разбил его на несколько статей – отдельно рассмотрел рациональные, логарифмические, тригонометрические и прочие, осталось ещё несколько примеров на нахождение наибольшего (наименьшего) значения иррациональной функции на отрезке. Их мы тоже рассмотрим.

Давайте здесь подробно опишу нахождение производной, когда у аргумента имеется степень, во всех примерах ниже это используется.

Сама формула:

То есть, если у нас аргумент стоит в некоторой степени и требуется найти производную, то мы записывает это значение степени, умножаем его на аргумент, а его степень будет на единицу меньше, например:

Если же степень дробное число, то всё тоже самое:

Следующий момент! Конечно же, вы должны помнить свойства корней и степеней, а именно:

То есть, если в примере вы увидите, например, выражение (или подобное с корнем):

То при решении, чтобы вычислить производную, его необходимо представить как х в степени, будет так:

Остальные табличные производные и правила дифференцирования вы должны знать!!!

Правила дифференцирования:

Рассмотрим примеры:

77451. Найдите точку минимума функции y = x 3/2 – 3x + 1

Найдем нули производной:

Решаем уравнение:

В точке х = 4, производная меняет знак с отрицательного на положительный, это означает, что данная точка является точкой минимума.

Ответ: 4

77455. Найдите точку максимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 4, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.

Ответ: 4

77457. Найдите точку максимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решая уравнение:

В точке х = 9, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.

Ответ: 9

Решить уравнение со степенями онлайн калькулятор. Решение показательных уравнений по математике

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.{nm}:\]

Прибавляем к исходному уравнению:

Вынесем за скобки \

Выразим \

Поскольку степени одинаковые, отбрасываем их:

Ответ: \

Где можно решить показательное уравнение онлайн решателем?

Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).

Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.

где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат . Рекомендуется также ознакомиться с основными действиями над матрицами .

Пример №1 . Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1

Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1

Ответ:

Пример №2 . Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.

Пример №3 . Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1

Ответ: >

Удобный и простой онлайн калькулятор дробей с подробным решением может:

Складывать, вычитать, умножать и делить дроби онлайн,
Получать готовое решение дробей картинкой и удобно его переносить.

Результат решения дробей будет тут…

0 1 2 3 4 5 6 7 8 9
Знак дроби «/» + — * :
_cтереть Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби «. Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .

Знаки используемые для записи в калькуляторе

Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.

Возможности онлайн калькулятора дробей

Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.
Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.

Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса. При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу. При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.

Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.

Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:
x 2 − 8x + 12 = 0;
5x 2 + 3x + 7 = 0;
x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

x 2 − 2x − 3 = 0;
15 − 2x − x 2 = 0;
x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x 2 + 9x = 0;
x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:
x 2 − 7x = 0;
5x 2 + 30 = 0;
4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Калькулятор метода деления пополам — Расчет высокой точности

Цель использования: для проверки моих работаю, если правильно

Цель использования: Мои дети забрали, жена сделала. Считая граммы кетамина, я использую это для.

Цель использования: Назначение

Цель использования: Домашнее задание

Цель использования: Учеба.
Комментарий / запрос: Как я могу использовать Pi? π?
от Кейсана: pi

Цель использования: для оценки

Цель использования: Назначение
Комментарий / Запрос: Q Найти приблизительный корень и соответствующая граница ошибки для
следующего нелинейного уравнения, f (x) = sqrt (x) — cos (x) в интервале [0, 1] до 4-й итерации
, используя метод
1-бисекция,
2- итерационный метод с фиксированной точкой,
3- метод Ньютона-Рафсона,
4- метод секанса,
5- метод Регулы – Фальси.
Я хочу решение, пожалуйста, любое

Цель использования: Для решения домашнего задания
Комментарий / Запрос: nice

Цель использования: решение этой проблемы
epowx-4x = 0
по
NR method
Bi-section method
Regula FALSI
Комментарий / запрос: IAM WAITING

Комментарий / Запрос: как ввести лог по базе 10?

Онлайн-калькулятор: метод итераций с фиксированной точкой

В численном анализе итерация с фиксированной точкой — это метод вычисления фиксированных точек повторяемых функций.

Более конкретно, учитывая функцию, определенную на действительных числах с действительными значениями, и учитывая точку в области, итерация с фиксированной точкой равна

Это дает начало последовательности, которая, как ожидается, сойдется в точку. Если непрерывно, то можно доказать, что полученное является неподвижной точкой — т.е.

Источник

Этот метод на самом деле является своего рода методом последовательных приближений — методом решения математических задач с помощью последовательности приближений, которые сходятся к решению и строятся рекурсивно, то есть каждое новое приближение вычисляется на основе предыдущего приближения. ; выбор начального приближения до некоторой степени произвольный.Метод используется для аппроксимации корней алгебраических и трансцендентных уравнений. Он также используется для доказательства существования решения и для аппроксимации решений дифференциальных, интегральных и интегро-дифференциальных уравнений.

Использовать этот метод довольно просто:
— принять приблизительное значение для переменной (начальное значение)
— решить для переменной
— использовать ответ как второе приближенное значение и снова решить уравнение
— повторить этот процесс до тех пор, пока желаемая точность переменной получается

Именно это и делает калькулятор ниже.Он выполняет итерационные вычисления x по заданной формуле и останавливается, когда два последовательных значения отличаются меньше заданной точности.

Также стоит упомянуть, что функция, используемая в качестве примера, то есть
,
является повторяющейся функцией для вычисления квадратного корня из a. Это, пожалуй, первый алгоритм, используемый для приближения квадратного корня. Он известен как «вавилонский метод», названный в честь вавилонян, или «метод Героя», названный в честь греческого математика I века Героя Александрийского, который дал первое подробное описание метода.

Метод итерации с фиксированной точкой

Приближение прекращается, когда разница между двумя последовательными значениями x становится меньше указанного процента

Точность вычисления

Цифры после десятичной точки: 5

Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера.

Скачать закрыть

content_copy Ссылка сохранить Сохранить расширение Виджет

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера на прием файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Эффективный метод поиска решений трансцендентных уравнений с несколькими корнями

В этой статье представлен метод получения решения для всех корней трансцендентного уравнения в ограниченной области путем нахождения полиномиального уравнения с теми же корнями, что и трансцендентное уравнение. Предлагаемый метод разработан с использованием интегральной теоремы Коши для комплексных переменных и преобразует задачу поиска корней трансцендентного уравнения в эквивалентную задачу поиска корней полиномиального уравнения с точно такими же корнями.Интересный результат состоит в том, что коэффициенты полинома образуют вектор, который лежит в нулевом пространстве матрицы Ганкеля, составленной из коэффициентов ряда Фурье обратной части исходного трансцендентного уравнения. Тогда явное решение легко получить с помощью комплексного быстрого преобразования Фурье. В заключение авторы представляют пример решения первых трех собственных значений одномерной задачи нестационарной теплопроводности.

1. Введение

Определение корней трансцендентных функций — проблема, обычно встречающаяся в широком спектре инженерных приложений, таких как передача тепла (например, теплопередача).g., [1–4]), динамика и управление (например, [5]), звук и вибрация (например, [6, 7]) и квантовая механика (например, [8]). Существует множество численных методов, которые можно использовать для аппроксимации решения с любой желаемой степенью точности. Общие описания распространенных методов поиска корней доступны в большинстве учебников в области численного анализа, например, Chapra и Canale [9].

Явные методы также были разработаны для поиска корней трансцендентных уравнений.Явные решения могут помочь лучше понять рассматриваемую проблему. Они также полезны, например, при разработке аналитических производных для анализа неопределенностей и исследований чувствительности или для проверки сходимости методов поиска приближенных корней [3]. Лезерс и Маккормик [10] рассмотрели методологию получения явных решений нескольких трансцендентных проблем, возникающих при теплопередаче. Используемый общий подход был основан на методах Мусхелишвили [11] и был разработан Бернистоном и Сивертом [12].Этот подход «зависит от формулировки соответствующей проблемы Римана теории комплексных переменных и последующего выражения решения трансцендентного уравнения в терминах канонического решения этой проблемы» [10]. Лак и Стивенс [13] сформулировали явное выражение для единственного корня любой аналитической трансцендентной функции. Их метод основан на интегральной теореме Коши и использует только базовые концепции комплексного интегрирования для определения корня функции путем определения сингулярности обратной величины функции.Теперь выяснилось, что эта идея была первоначально предложена Джексоном [14, 15]. Настоящая статья расширяет их идею, представляя метод поиска нескольких корней трансцендентных уравнений в ограниченной области путем преобразования задачи в эквивалентную задачу поиска корней полиномиального уравнения с точно такими же корнями. Отсюда следует, что явное решение легко доступно через комплексное быстрое преобразование Фурье (cfft) при работе с четырьмя корнями одновременно. Для пяти и более корней решение неявно согласно теореме Абеля-Руффини [16].Неявность нахождения корней многочленов пятого и более высокого порядка на самом деле не является проблемой, поскольку алгоритмы, разработанные для этой задачи, легко доступны (McNamee [17–20], McNamee and Pan [21]) или более крупные задачи можно разделить на более мелкие. задач путем анализа неперекрывающихся ограниченных областей с четырьмя или менее корнями в каждой области.

2. Разработка метода

Предположим, что это трансцендентная функция с корнями в пределах интервала ширины и центра такими, что. Позвольте быть многочленом -го порядка с корнями, расположенными точно в тех же местах, что и корни в интервале.Отношение является аналитической функцией в интервале, потому что полюса интервала компенсируются корнями. Следующим шагом в анализе является нормализация интересующей переменной. Давай так. Функции и могут быть преобразованы в виде где и — количество корней в интервале.

Теперь рассмотрим функцию в интервале. Если анализ распространяется на комплексную плоскость (путем замены действительной переменной на комплексную переменную), интегрирование по круговой траектории радиуса 1 дает, что является следствием теоремы Коши относительно линейного интеграла функции, которая является аналитической на и внутри контур определяется замкнутым путем интегрирования.

Уравнение (4) может использоваться для нахождения коэффициентов полинома следующим образом:

Обратите внимание, что для положительного целого числа верно и то, что интегрируемая функция остается аналитической при умножении на. Следуя подходу, представленному в (5)

Ниже приводится процедура получения коэффициентов. Сначала интегралы вычисляются заменой Let. Отсюда следует, что еще одно упрощение может быть реализовано путем определения Note, который можно интерпретировать как th комплексный коэффициент ряда Фурье для.Наконец, подстановка в (7) и отмена yield

Уравнение (12) — это уравнение, используемое для нахождения коэффициентов. Обратите внимание, что (12) верно для любого положительного целого значения. Это означает, что можно «создать» столько уравнений, сколько неизвестных коэффициентов. Варьируя от 0 до, получается следующая система уравнений: Поскольку (13) представляет собой систему линейно зависимых уравнений, то есть с меньшим количеством уравнений, чем неизвестных, для получения решения необходимы дополнительные уравнения.Одно из возможных уравнений состоит в приравнивании любого действительного ненулевого числа, что позволяет переместить последний столбец матрицы в правую часть.

Уравнение (13) заслуживает комментария. Матрица состоит исключительно из коэффициентов ряда Фурье, что означает, что уравнения не зависят от коэффициентов нормализации, используемых для вычисления коэффициентов ряда Фурье. На практике коэффициенты аппроксимируются с помощью комплексного быстрого преобразования Фурье (cfft). Аппроксимация cfft менее точна для последнего столбца матрицы, поскольку этот столбец соответствует высокочастотным членам.Отсюда следует, что перемещение последнего столбца матрицы в правую часть уравнения приводит к немного более надежному решению. Кроме того, система уравнений представляет собой матрицу Ганкеля, для которой легко получить обратное [22]. Следовательно, (13) можно быстро реализовать и решить для коэффициентов. Наконец, симметрия или «структура» (13) заставляет авторов полагать, что эта система уравнений имеет более глубокий смысл.

3. Пример

Чтобы проиллюстрировать текущий метод, ниже описан простой, но полезный пример.Решение нестационарного уравнения теплопроводности дает характеристическое уравнение или собственную функцию следующего вида [23]:

Уравнение (14) представляет собой трансцендентное уравнение с бесконечным числом корней, называемых характеристическими значениями или собственными значениями. Характеристическое уравнение в этом случае неявное. Произвольно предположив, что (14) можно переписать как Let

График показан на рисунке 1.

Метод, описанный в предыдущем разделе, теперь применяется для решения первых трех положительных корней (16).На рисунке 1 показано, что три корня находятся в интервале, предполагая, и. Обратите внимание, что одним из простых способов аппроксимации коэффициентов является дискретизация и использование сложного быстрого преобразования Фурье (cfft), легко доступного во многих коммерческих математических программных пакетах (например, MATLAB и Mathcad), а не выполнение интеграла (11). С и, (13) становится Дискретизирующим на 256 эквидистантных точек, cfft дает Решение этой системы уравнений дает, что переводится в
На рисунке 2 изображены исходная трансцендентная функция и многочлен.График ясно показывает, что многочлен имеет те же корни, что и исходная функция; то есть,, и. Корни кубического многочлена могут быть найдены с помощью явных алгебраических выражений, приведенных многими авторами, например, Абрамовицем и Стегуном [24], Press et al. [25] и Вайсштейна [26]. Наконец, отмена нормализации переменной дает, и в качестве корней или собственных значений исходной задачи.

4. Заключение
В данной статье представлен метод одновременного нахождения нескольких корней трансцендентного уравнения в ограниченной области путем преобразования задачи в эквивалентную задачу нахождения корней полиномиального уравнения с точно такими же корнями.Метод требует, чтобы отношение было аналитическим в исследуемом интервале. Показанная здесь концепция заключается в том, что корреляция между корнями трансцендентной функции и коэффициентами ряда Фурье ее обратной функции может быть выражена полиномом и доказана с помощью интегральной теоремы Коши.
Преимущество текущего метода заключается в возможности решения нескольких корней за один прием и наиболее очевидно при работе с неявной проблемой, как показано в предыдущем примере.В этом случае неявная задача трансформировалась в более простую явную. Текущий метод остается явным при работе с четырьмя корнями. Однако неявный поиск корней многочленов более высокого порядка на самом деле не является проблемой, поскольку алгоритмы, разработанные для этой задачи, легко доступны или более крупные задачи могут быть разделены на более мелкие задачи с четырьмя корнями каждая путем выбора соответствующих интервалов, как показано в разделе 3. В в любом случае текущий метод обеспечивает относительно простую процедуру решения группы проблем, встречающихся во многих инженерных приложениях.
Обозначение
Функция из Полиномиальная функция
: Число Био
: -й коэффициент полинома
: Функция
:
: -й коэффициент функции ряда Фурье
: Центр окружности в комплексной плоскости
: Число корней
:
: Полином, функция
: Положительное целое число
: Радиус окружности в комплексной плоскости
: Независимая переменная Нормализованная переменная
: Комплексная переменная
: Угол в комплексной плоскости.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Авторские права
Авторские права © 2015 Rogelio Luck et al. Это статья в открытом доступе, распространяемая по лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.
Решения Сиверта трансцендентных уравнений, обобщенные функции Ламберта и физические приложения
Проанализировано несколько классов трансцендентных уравнений, в основном уравнений на собственные значения, связанных с нерелятивистскими квантово-механическими задачами.Систематический подход Сиверта к таким уравнениям обсуждается с точки зрения новых результатов, недавно полученных в теории обобщенных функций Ламберта и алгебраических приближений различных специальных или элементарных функций. Сочетание точных и приближенных аналитических методов позволяет получить довольно точные аналитические результаты для явно неразрешимых проблем. Результаты могут быть применены в квантовой и классической механике, магнетизме, упругости, преобразовании солнечной энергии и т. Д.
1 Введение
Получение точных решений уравнений физики — увлекательное занятие для ученых.Однако достичь этой цели удается редко. В квантовой механике, например, очень мало случаев, когда для данной задачи как собственные функции, так и собственные значения могут быть получены точно. Это происходит, когда гамильтониан обладает некоторыми свойствами симметрии или когда он чрезвычайно прост. Но в остальном, даже для самых элементарных одномерных потенциалов, таких как потенциал квадратной ямы, заданный формулой [1]:
V ( Икс ) знак равно { — V 0 , — а 2 < Икс < а 2 0 , о т час е р ш я s е (1)
с V ₀> 0, когда волновые функции могут быть выражены через элементарные функции, собственные значения энергии E (или волнового вектора k знак равно 2 м | E | ) не может быть получено точно.А именно, собственные значения волнового вектора k задаются трансцендентным уравнением:
грех ⁡ k а k а знак равно п (2)
, где p — безразмерный параметр, описывающий как потенциал, так и частицу, а a — длина ямы.Решения (2) равны
k знак равно 1 а ξ ( п ) (3)
с ξ ( p ), удовлетворяющим уравнению:
грех ⁡ ξ ( п ) ξ ( п ) знак равно п (4)
Очевидно, ξ ( p ) не может быть записано как конечная комбинация элементарных функций.Различные методы точные или приближенные — решения ур. (2) — (4) недавно обсуждались в [2, 3, 4, 5].
То, что в настоящее время называется «решить уравнения Шредингера для квадратной скважины», на самом деле означает решение линейной задачи Штурма — Лиувилля, то есть получение решений линейного дифференциального уравнения — уравнения Шредингера — которые удовлетворяют некоторым граничным условиям. В ранее упомянутом случае решения ψ ( x ) должны обращаться в нуль в пределе x → ∞.В других случаях, например, в линейной теории упругости, применяемой к дипольным материалам с пустотами [6], или в неклассических теориях термоупругости [7], [8], накладываются более общие граничные условия.
Точно так же точные выражения собственных значений энергии (или волновых векторов) других квантово-механических задач являются решениями более или менее похожих трансцендентных уравнений (см., Например, [9]):
загар ⁡ ξ ( п ) ξ ( п ) знак равно п , ξ ( п ) загар ⁡ ξ ( п ) знак равно п , танх ⁡ ξ ( п ) ξ ( п ) знак равно п , ξ ( п ) танх ⁡ ξ ( п ) знак равно п (5)
, чтобы процитировать только простейшие примеры.В более сложных случаях вместо р правый. уравнений, подобных (4), содержит полиномы или рациональные функции от p и т. д. Такие уравнения встречаются не только в квантовой механике, но также в электромагнетизме, гидродинамике, упругости и т. д.
Существует несколько систематических подходов к трансцендентным уравнениям, например (3) и (4). Один из них был инициирован Стюартом и его сотрудниками около 40 лет назад с использованием теории проблем Римана. Другой, развивающий концепцию обобщенных функций Ламберта, был недавно предложен Мезо, Баричем и Мугнаини и является предметом интенсивных исследований.
Между тем, чтобы получить результаты, которые не являются просто численными, но все же сохраняют зависимость от физических параметров задачи, за последние десятилетия было получено несколько аналитических приближений для решений трансцендентных уравнений. Кроме того, программы математических символьных вычислений, такие как Mathematica, предоставляют мощный инструмент для исследования, как численно, так и, в некоторой степени, аналитически, решений трансцендентных уравнений, подобных (4) и (5).
Поскольку точные результаты получают математики, которые не очень интересуются приближениями, а аналитические приближения получают физики, которые не очень заинтересованы в точных (а иногда и очень сложных) решениях, обмен информацией между исследователями, работающими в этих областях иногда бывает недостаточно. Лучшее общение между учеными, работающими в этих областях, могло бы быть полезным для поиска новых физических приложений математических результатов, полуколичественного поведения решений, точная форма которых не может быть получена, и т. Д.
В этой статье мы составим перечень точных результатов Сиверта по трансцендентным уравнениям, а также упомянем приблизительные аналитические результаты, полученные другими исследователями при изучении этих уравнений. Мы покажем, как сочетание обоих подходов — точного и приближенного — может быть использовано для лучшего понимания математических и физических аспектов рассматриваемых задач.
Структура статьи следующая. Поскольку подход Сиверта является наиболее полным систематическим подходом к трансцендентным уравнениям, мы будем использовать серию его статей как основу нашей статьи.Краткое изложение его результатов будет сделано в разделе 2, где также представлено введение обобщенных функций Ламберта. Первое конкретное приложение посвящено функции Ланжевена, обсуждаемой в разделе 3; среди прочего , аналитическая аппроксимация обратной функции Ланжевена будет использоваться, чтобы обеспечить приближенное выражение некоторой обобщенной функции Ламберта. Такие приближения полезны не только в пара- или суперпарамагнетизме, но также в физике полимеров и в преобразовании солнечной энергии.
В разделе 4 изучаются уравнения, содержащие гиперболические и алгебраические функции, с приложениями к теории ферромагнетизма Карри — Вейсса. В разделе 5 приближенное решение уравнения, включающего тригонометрические и экспоненциальные функции, с приложениями к теории вибрирующих пластин и квантовой механике, записывается в терминах обобщенной функции Ламберта с использованием алгебраического приближения tan x . В разделе 6 как одномерное движение точечного электрического заряда в поле другого, фиксированного заряда, так и уравнение Кеплера для гиперболических орбит анализируются в терминах функции Райта ω .В разделе 7 мы кратко обсуждаем два новых применения функций Ламберта в физике. В разделе 8 два уравнения, включающие алгебраические и тригонометрические функции, одно из которых относится к физике реакторов, а другое — к небесной механике (уравнение Кеплера для эллиптических орбит), решаются с использованием алгебраических приближений тригонометрических функций. Раздел 9 посвящен выводам.
2 Подход Сиверта к трансцендентным уравнениям и обобщенным функциям Ламберта
В серии статей, опубликованных между 1972 и 1976 годами [10] / S50, [11] / S52, [12] / S57, [13] / S53, [14] / S56, [15] / S59, [16] / S62, [17] / S63, [18] / S68, [19] / S71, [20] / S80, [21] / S89, [22] / S100, [23] / S108, Сиверт и его коллеги рабочие — Burniston (для [10], [11], [13], [15], [16], [19], [20]), Phelps III (для [22], [23]), Essig (для [14]), Доггет (для [19]) и Буркарт (для [17]) — исследовали решения нескольких трансцендентных уравнений, важных для их физических приложений.Все вышеупомянутые публикации доступны в открытом доступе на веб-странице Сиверта [24]; символы / S50, / S52 и т. д. в первых трех строках этого абзаца указывают номер соответствующей статьи в списке публикаций Сиверта в его сети. Подход, используемый в этих статьях, основан «на анализе комплексных переменных и требует, в конечном счете, канонического решения определенной проблемы Римана; решение правильно поставленной проблемы Римана следует непосредственно из работы Мусхелишвили [25] », как указано в [11].Усилия, вложенные в это обширное исследование, впечатляют, а полученные результаты являются новаторским и чрезвычайно ценным вкладом в развитие теории трансцендентных уравнений. В то же время полученные таким образом решения в целом очень сложны и трудны для использования в физических приложениях.
В последнее время интерес к этим решениям возрос, поскольку некоторые из них могут быть выражены в терминах обобщенных функций Ламберта и представлены в гораздо более удобной форме, согласно результатам, полученным Мезо, Баричем [26] и Мугнаини [27]. .Аналогично функции Ламберта W ( a ), которая определяется как решение трансцендентного уравнения:
Икс е Икс знак равно а (6)
обобщенная функция Ламберта W ( t ₁, t ₂,… t _n ; s ₁, s ₂ s,…
m ; a ) является решением аналогичного, но более сложного трансцендентного уравнения [26]:
е Икс ( Икс — т 1 ) … ( Икс — т п ) ( Икс — s 1 ) … ( Икс — s м ) знак равно а (7)
Параметры t ₁, t ₂,… называются верхними параметрами, а s ₁, s ₂,… — нижними параметрами.
Если знаменатель, соответственно знаменатель дроби в ур. (7) равно 1 — другими словами, если верхние, соответственно нижние параметры отсутствуют — обозначим соответствующие решения W (-; s ₁, s ₂,… s _m ; a ) соответственно W ( t ₁, t ₂,… t _n ; -; a ).
Однако, как мы увидим, не все решения Сиверта могут быть выражены в термах обобщенных функций Ламберта.
Теория этих функций может показаться (и фактически быть) очень сложной, но, как отмечает Корлесс [47], «функция Ламберта W является простейшим примером корня экспоненциального многочлена», то есть выражения форма:
∑ я знак равно 1 м п я ( Икс ) е ш я Икс (8)
с P _i ( x ) — полиномы в размере x , «и экспоненциальные полиномы являются следующим простейшим классом функций после полиномов.”Обобщенные функции Ламберта являются корнями экспоненциального полинома (8), соответствующего случаю w ₁ = 0, w ₂ ≠ 0, P ₁ ≠ 0, P ₂ ≠ 0 и все P _i ≡ 0 для i > 2. Уже исследованные случаи соответствуют ситуации, когда и P ₁ и P ₂ имеют только настоящие корни. Экспоненциальные полиномы, подобные (8), могут появляться в решениях нелинейных задач Штурма — Лиувилля (см., Например, [48], ур.(67), где параметры w _i мнимые) или дробно-нелинейное уравнение Клейна — Гордона (см., Например, [49], уравнение (23), где параметры w _i настоящие). Итак, изучая обобщенные функции Ламберта, мы помогаем — и мы можем внести свой вклад — в очень важное развитие математики.
До сих пор есть два случая, когда обобщенную функцию Ламберта можно представить в удобном виде:
(1) Если в ур.(6), n = 1 и m = 1, поэтому он содержит только один верхний параметр, t ₁ = t и один нижний параметр, s ₁ = s , t ≠ s , его решение может быть записано как расширение ряда около a = 0:
W ( т ; s ; а ) знак равно т — ( т — s ) ∑ п знак равно 1 ∞ L п ′ ( п ( т — s ) ) п е — п т а п , т — s ≠ 0 (9)
где L п ′ — производная полинома Лагерра.Обратные функции coth Икс — 1 Икс (функция Ланжевена), (tanh x ) / x и x tanh x могут быть выражены как обобщенные функции Ламберта W ( t ; s ; a ) [26] .
(2) Если в ур. (6), n = 2 и m = 0, поэтому он содержит только два верхних параметра t ₁ и t ₂, его решение может быть записано как расширение ряда вокруг a = 0:
W ( т 1 , т 2 ; — ; а ) знак равно т 1 — ∑ п знак равно 1 ∞ 1 п ⋅ п ! ( а п е — т 1 т 2 — т 1 ) п B п — 1 ( — 2 п ( т 2 — т 1 ) ) (10)
, где B _n — полиномы Бесселя.
Обобщенные функции Ламберта представляют собой область интенсивных исследований; например, недавно Мезо [28] получил основные свойства W ( t ; s ; a ), когда параметры t , s , a являются сложными. Можно ожидать, что в ближайшем будущем уравнения, подобные (9) и (10), будут получены для других типов обобщенной функции Ламберта, помимо W ( t ; s ; a ) и W ( т ₁, т ₂; -; a )
Приложения обобщенных функций Ламберта W ( t ; s ; a ) и W ( t ₁, t ₂; -; a ) в различные физические проблемы квантовой механики, магнетизма или гидродинамики представлены в [29], [30] и [9]
.
В следующем разделе мы начнем обсуждение решений Сиверта и обобщенных функций Ламберта с рассмотрения трансцендентных уравнений, содержащих функцию Ланжевена.
3 Трансцендентные уравнения, содержащие функцию Ланжевена
В [20] Сиверт и Бернистон получили точное аналитическое решение уравнения:
Икс кот ⁡ Икс знак равно α Икс 2 + 1 (11)
Его можно записать в терминах функции Ланжевена
L ( Икс ) знак равно кот ⁡ Икс — 1 Икс (12)
как:
L ( Икс ) знак равно α Икс (13)
Итак, в [20] Сиверт и Бернистон явно получили функцию x ( α ) или, что то же самое, обратную функцию L ( x ) / x .Мезо и Бариц получили обратную функцию Ланжевена как обобщенную функцию Ламберта с одним верхним и одним нижним параметром, W ( t ; s ; a ). Фактически, если L ( x ) = a , функция L ⁻¹ ( a ) будет:
L — 1 ( а ) знак равно — 2 W ( 2 а + 1 ; 2 а — 1 ; а — 1 а + 1 ) (14)
согласно [29, [30, [9]].
Легко видеть, что если 0 < x <∞, то:
0 < L ( Икс ) < 1 (15)
и:
0 < L ( Икс ) Икс < 1 3 (16)
Рисунок 1
График L ( x ) (сплошной, черный), коричневый h ( x ) (фиолетовый), L ( x ) / x (красный) и постоянной функции y ( x ) = 1 (пунктир).
Это простое упражнение, чтобы проверить, что решение (13), поэтому функция, обратная функции L ( x ) / x , есть W ( t ₁, t ₂; s ₁, s ₂; a ) обобщенная функция Ламберта, а именно:
Икс ( α ) знак равно 1 2 W ( 1 + 1 — 4 α α , 1 — 1 — 4 α α ; — 1 + 1 — 4 α α , — 1 — 1 — 4 α α ; 1 ) (17)
Итак, обратная функция Ланжевена L ( x ) является обобщенной функцией Ламберта с одним верхним и одним нижним параметром, а обратная функция L ( x ) / x является обобщенной функцией Ламберта. функция с двумя верхними и двумя нижними параметрами.Однако, поскольку нет явной формулы для зависимости W ( t ₁, t ₂; s ₁, s ₂; a ) от его параметр, экв. (17) имеет ограниченную практическую ценность.
Напомним теперь основные приложения функции Ланжевена в физике. Впервые он был введен в контексте классической теории парамагнетизма, где он дает намагниченность M как функцию внешнего магнитного поля H и температуры T :
M знак равно п μ L ( μ ЧАС k B Т ) (18)
(см., Например, [31], ур.(9.2)). Собственно, это уравнение состояния классического парамагнетика. Та же формула действительна для суперпарамагнитных наночастиц (частиц, которые достаточно малы, чтобы содержать один единственный магнитный домен), при достаточно высоких значениях температуры T [32], [33].
Для физиков важно, что функция Ланжевена является частным случаем функции, которая играет ключевую роль в теории среднего поля магнетизма, функции Бриллюэна B _S , определяемой как:
B S ( Икс ) знак равно 2 S + 1 2 S кот ⁡ ( 2 S + 1 2 S Икс ) — 1 2 S кот ⁡ ( 1 2 S Икс ) (19)
Действительно,
B ∞ ( Икс ) знак равно L ( Икс ) (20)
Другой важный частный случай соответствует полуцелому спину, S = 1/2, когда
B 1 / 2 ( Икс ) знак равно танх ⁡ Икс (21)
Функция Ланжевена и ее обратная функция актуальны не только для магнетизма, но и для других областей физики с важными практическими приложениями, таких как полимеры (деформация и текучесть полимера) [34], [36], [37] или эластичность резины [35]. ].Идеализированная модель резиноподобной цепи дана в трактате Кубо по статистической механике [38], проблема 17, гл. 2, стр. 135, и служит иллюстрацией для понимания того, как функция Ланжевена используется в этой области. Другое применение функции Ланжевена относится к преобразованию солнечной энергии (суточный индекс ясности) [40]. Собственно, Киди заметил, что среднее значение дневного индекса чистоты может быть выражено через функцию Ланжевена [39]. Исследователи в этих областях предложили большое количество полезных аналитических приближений для L ( x ) и L ^-1 ( x ).Приведем пример.
Взяв обратную функцию Ланжевена в обе части (13), получим:
L — 1 ( L ( Икс ) ) знак равно L — 1 ( α Икс ) знак равно Икс (22)
, который также определяет функцию x ( α ), как ур.(13) или (11) делать. Давайте использовать для L ⁻¹ ( x ) очень простое и точное приближение, предложенное Крегером, см. Уравнение. (10) из [35]:
L — 1 ( Икс ) знак равно 3 Икс ( 1 — Икс 2 ) ( 1 + 0.5 Икс 2 ) (23)
В данном случае трансцендентное уравнение
L — 1 ( α Икс ) знак равно Икс (24)
имеет приближенное, но точное и простое алгебраическое уравнение, физически удобный корень которого:
Икс ( α ) знак равно 1 α 3 ( 3 — 8 α ) — 1 2 (25)
Личность
ж ( α ) знак равно Икс ( α ) кот ⁡ Икс ( α ) α Икс ( α ) 2 + 1 знак равно 1 (26)
, где x ( α ) заменено приближенным решением (25), выполняется с относительной погрешностью менее 0.003, как мы можем видеть на графике Рисунка 2.
Рисунок 2
Сюжет о л.х.с. приближенных тождеств (26) — синий, (30) — коричневый, а постоянных функций 1 — красный, а 0,996 — зеленый.
Итак, имеем примерное соотношение:
W ( 1 + 1 — 4 α α , 1 — 1 — 4 α α ; — 1 + 1 — 4 α α , — 1 — 1 — 4 α α ; 1 ) ≃ 1 α 2 ( 3 ( 3 — 8 α ) — 1 ) (27)
Также с (14) и (23):
W ( 2 а + 1 ; 2 а — 1 ; а — 1 а + 1 ) ≃ — 3 2 а ( 1 — а 2 ) ( 1 + 0.5 а 2 ) (28)
В заключение, используя точное аналитическое приближение обратной функции Ланжевена (23), мы получили точные приближенные аналитические выражения для частных случаев обобщенных функций Ламберта (27) и (28).
Формула Крюгера (23) — не единственное очень точное приближение обратной функции Ланжевена; Киди [39] предложил следующий:
L — 1 ( Икс ) ≃ 6 π загар ⁡ ( π 2 Икс ) 1 + 0.417 70 загар 2 ⁡ ( π 2 Икс ) 1 + 0,507 86 загар 2 ⁡ ( π 2 Икс ) (29)
, что является даже более точным, как мы видим на рисунке 2, но бесполезно для получения обратного значения L ( x ) / x .На самом деле ошибка приближения Киди — это, по сути, ошибка тождества
грамм ( Икс ) знак равно 1 Икс L ( L — 1 ( Икс ) ) знак равно 1 (30)
с L ⁻¹ ( x ), заданным формулой (27).Разница между формой f ( x ) и g ( x ) связана с различием аргументов функций Ланжевена в (22) и (27).
Полезность формулы Крёгера для приведения уравнения состояния (18) в более удобную форму станет более очевидной, если мы последуем подходу Аррота [41].
4 Уравнения с гиперболическими и алгебраическими функциями
В [17] Сиверт и Буркарт изучили двойные нули уравнения:
Икс знак равно танх ⁡ ( а Икс + б ) (31)
Физический смысл этого уравнения следует искать в теории магнетизма Кюри-Вейсса, где намагниченность M может быть связана с магнитным полем H , спином S и температурой T уравнение состояния:
M знак равно M 0 B S ( грамм μ B Т ( ЧАС + λ M ) ) (32)
(см. [42], ур.(6.14)), где g, — фактор Ланде, μ, _B,, — магнетон Бора и λ, — параметр молекулярного поля. B _S — функция Бриллюэна, определенная в предыдущем разделе. Если S = 1/2, функция Бриллюэна становится гиперболическим тангенсом, и уравнение. (30) совпадает с (29). Для очень полезного обсуждения физического значения ур. (26) см. Превосходное исследование магнита Кюри-Вейсса [44], ур. (22).
Если b = 0, получается числовое значение для a , а именно a = 1, что эквивалентно определению температуры Кюри (см., Например, [42], уравнение (6.15) или [43]) , Гл.15, уравнение (8)).
Геометрически двойной ноль (26) означает, что прямая y ₁ ( x ) = x касается кривой y ₂ ( x ) = tanh ( ax + b ), следовательно:
d d Икс танх ⁡ ( а Икс + б ) знак равно — а ( танх 2 ⁡ ( б + а Икс ) — 1 ) знак равно 1 (33)
С (31) условие касания становится:
а ( 1 — Икс 2 ) знак равно 1 → а знак равно 1 1 — Икс 2 (34)
и решение проблемы сводится к решению ур.(2) из [17], которое можно записать как:
Икс знак равно танх ⁡ ( Икс 1 — Икс 2 + б ) знак равно B 1 / 2 ( Икс 1 — Икс 2 + б ) (35)
Мы видим, что на самом деле проблема связана только с одним параметром, b .Предыдущее уравнение не может быть решено с использованием обобщенных функций Ламберта, поскольку аргумент экспоненты не является линейным, поэтому единственным точным решением остается решение Сиверта и Буркарта [17].
В [14] Сиверт и Эссиг решили уравнение ферромагнетизма Вейсса:
ζ знак равно танх ⁡ 1 2 ( j z ζ + час ) (36)
Альтернативные способы решения, точного или приближенного, этого уравнения были представлены в [45], где точное решение записано в терминах обобщенной функции Ламберта с одним верхним и одним нижним параметрами.Решение для случая h = 0 было записано как обобщенная функция Ламберта W ( t ; s ; a ) в [29], [30].
5 Уравнения, содержащие тригонометрические и экспоненциальные функции
В [22] и [23] авторами получены решения уравнения, лежащего в основе теории колебательных пластин:
а загар ⁡ Икс + танх ⁡ Икс знак равно 0 (37)
, который встречается также в квантовой механике и электромагнетизме.Найти действительные решения уравнения (37) — значит найти действительный корень экспоненциального полинома:
( 1 + а 2 я ) е 2 я Икс — ( 1 — а 2 я ) е 2 ( 1 + я ) Икс + ( 1 — а 2 я ) е 2 Икс — 1 — а 2 я знак равно 0 (38)
, которая представляет собой обобщенную 3-верхнюю и 3-нижнюю обобщенную функцию Ламберта с комплексными параметрами — класс функций, которые еще не изучены.
Однако мы можем добиться определенного прогресса в поиске приближенного аналитического решения этого уравнения, используя алгебраическое приближение для tan x [46]:
загар ⁡ Икс ≃ 0,45 Икс 1 — 2 π Икс , 0 < Икс < π 2 (39)
Эта формула может быть легко расширена для любых вещественных чисел x [5].Заменяя загар x в (37) согласно (39), получаем:
е 2 Икс 2 Икс — π ( 1 — 0,45 а π 2 ) 2 Икс — π ( 1 + 0.45 а π 2 ) знак равно 1 (40)
так:
Икс ( а ) знак равно 1 2 W ( π ( 1 — 0.45 а π 2 ) ; π ( 1 — 0,45 а π 2 ) ; 1 ) (41)
Ур.(40) очень похоже на уравнение, которому удовлетворяет обратная функция Ланжевена:
е 2 Икс знак равно А + 1 А — 1 Икс + 1 А + 1 Икс + 1 А — 1 (42)
с x = L ^-1 ( A ), поэтому рецепты для получения L ^-1 могут быть полезны также для приблизительной оценки W в (41).
Поскольку tanh x является для x 2 очень медленно меняющейся функцией, корни уравнения (37) больше, чем π /2, можно получить с разумной точностью, положив tanh x 8 const на определенные удобно выбранные интервалы. Например (см. Рисунок 5, где параметр a из уравнения (37) принимает значение a = 1, соответствующее коричневой кривой), «точный» корень x ₁ ∈ ( π , 3 π /2) ур.(37) равно x ₁ = 3,9266. Если мы приближаемся, для x ₁ < x <3 π /2, гиперболический тангенс как tanh x ≃ tanh (3 π /2) = 0,999839, уравнение (37) принимает вид tan x = 0,999839, с удобным корнем x _{1 a} = 3,92691. Относительная погрешность этого приближения составляет примерно −0,8 ⋅ 10 ⁻⁴.
Применяя тот же метод для a = −1 (соответствует зеленой кривой на рисунке 3), мы находим для корня x ₂ уравнения.(37), π /2 < x ₂ < π , приблизительное значение x _{2 a} = 2,39938, вместо «точного» значения x ₂ = 2.36502, то есть с погрешностью около -1,5%.
Рисунок 3
Графики tan (x) (черный), tanh (x) (зеленый) и — tanh (x) (красный).
Итак, для практикующего, работающего в прикладной физике, в области, где экспериментальная ошибка больше, чем вышеупомянутые, этот грубый и чрезмерно упрощенный подход дает приемлемые результаты по прагматическим причинам.
Первый корень уравнения. (37) может быть получено для малых значений a после разложения в ряд как один из корней алгебраического уравнения:
17 315 ( а — 1 ) Икс 6 + 2 15 ( а + 1 ) Икс 4 + 1 3 ( а — 1 ) Икс 2 + а + 1 знак равно 0 (43)
, которое является кубическим уравнением в z = x ².Например, если a = 0,1, ошибка результата, полученного таким образом, составляет около -4% ( x _точный = 1,295 2, x _{приблизительно} = 1,3343 5). Мы можем действовать аналогично, когда a >> 1, с уравнением:
загар ⁡ Икс + 1 а танх ⁡ Икс знак равно 0 (44)
6 Омега-функция Райта
Функция Райта омега ω ( x ) появляется в асимптотической форме двух уравнений, решенных Сивертом и его сотрудниками.Он связан с функцией Ламберта тождеством [47]:
W ( е Икс ) знак равно ω ( Икс ) (45)
В [19] авторы решили проблему элементарной физики, получив «точное аналитическое решение для зависимости положения от времени для силы, обратной квадрату расстояния».Фактически они изучают отталкивающее классическое одномерное движение электрического заряда в поле другого фиксированного заряда. Сила отталкивания определяется законом Кулона:
м d 2 р d т 2 знак равно q Q 4 π ε 0 р 2 (46)
Начальное состояние:
т знак равно 0 → d р d т знак равно 0 , р знак равно р 0 (47)
Мы будем описывать положение движущегося заряда безразмерной функцией x (t), определяемой как:
р ( т ) знак равно р 0 Икс ( т ) (48)
После двух интегрирований уравнения движения мы получаем соотношение между положением x и временем t :
Икс ( Икс — 1 ) + пер ⁡ ( Икс + Икс — 1 ) знак равно т τ (49)
с τ выдает:
τ знак равно 2 π ε 0 м р 0 3 q Q (50)
Мы изучим результат Сиверта (48) при малых и больших значениях t .По данным (48),
Икс ( 0 ) знак равно 1 (51)
так, для т / τ ≪ 1, можно положить:
Икс знак равно 1 + Икс , Икс < < 1 (52)
и (49) можно приблизительно представить как:
пер ⁡ ( 1 + Икс 2 + Икс ) знак равно т τ — Икс ( 1 + Икс 2 ) (53)
и снова, пренебрегая X по отношению к Икс :
пер ⁡ ( 1 + Икс ) знак равно т τ — Икс (54)
или:
2 Икс знак равно т τ
и наконец:
Икс знак равно 1 4 τ 2 т 2 (55)
В очень короткие моменты времени, t ≪ τ , движение равномерно ускоряется, как и ожидалось.
Асимптотически x ≫ 1 и (49) дает:
пер ⁡ ( 2 Икс ) знак равно т τ — Икс (56)
или:
2 Икс е 2 Икс знак равно exp ⁡ ( 2 т τ — пер ⁡ 2 ) → 2 Икс знак равно W ( exp ⁡ ( 2 т τ — пер ⁡ 2 ) ) (57)
Следовательно:
Икс знак равно 1 2 W ( exp ⁡ ( 2 т τ — пер ⁡ 2 ) ) (58)
, где W — функция Ламберта.При 45 асимптотическая формула (58) может быть записана эквивалентно как:
Икс ( т ) знак равно 1 2 ω ( 2 т τ — пер ⁡ 2 ) , т > > τ (59)
Асимптотическое разложение функции Ламберта:
W ( Икс ) знак равно пер ⁡ Икс — пер ⁡ ( пер ⁡ Икс ) + пер ⁡ ( пер ⁡ Икс ) пер ⁡ Икс + … (60)
Если оставить только первый член, асимптотическая формула (58) дает:
Икс ( т ) знак равно т τ — пер ⁡ 2 2 ≃ т τ (61)
Это также интуитивный результат, так как на очень больших расстояниях сила отталкивания, создаваемая фиксированным зарядом, становится ничтожно малой, и движение становится почти равномерным.Итак, мы проверили, что движение начинается с равномерного ускорения и заканчивается равномерным.
В [10] Сиверт и Бернистон решили уравнение Кеплера для гиперболических орбит:
е грех ⁡ F знак равно F + N , N > 0 (62)
, решение которой не сводится к обобщенной функции Ламберта.Асимптотически sinh F → 1 2 exp F и (62) становится:
е 2 exp ⁡ F знак равно F + N , N > 0 (63)
или, с exp F = f , F = ln f :
е 2 ж знак равно пер ⁡ ж + N (64)
Итак, уравнение Райта, стандартная форма которого [47]:
у + пер ⁡ у знак равно z (65)
Интересное обсуждение уравнения Кеплера как для гиперболических, так и для эллиптических (см. Раздел 8) орбит дано в [51].
7 Функция Ламберта и обобщенные функции Ламберта
В [16] Сиверт и Бернистон нашли решение уравнения:
z е z знак равно а (66)
, т.е. получить выражение для функции Ламберта W , где a является комплексным параметром [50]. В [12] Сиверт решает «известное критическое уравнение, описываемое теорией диффузии возраста, для голого ядерного реактора»:
k exp ⁡ ( — B 2 τ ) 1 + B 2 L 2 знак равно 1 (67)
для B ² (продольный изгиб).
В [18] автор решает более сложное уравнение:
е z z z + б знак равно а (68)
с — комплексный параметр. Таким образом, он получает выражение для функции W (0; — b ; a ), которое, в свою очередь, можно записать через функцию Мезё — Барича W _r .Для a — real, автор ссылается на работу Райта [52].
8 Трансцендентные уравнения, содержащие тригонометрические и алгебраические функции
В [15] авторы исследовали «критическое состояние сферического реактора, описываемого элементарной теорией диффузии, окруженного бесконечным отражателем»:
Икс детская кроватка ⁡ Икс знак равно 1 — а — б Икс (69)
Это уравнение можно записать как:
е 2 я Икс ( б + 2 я ) Икс + а — 1 ( б — 2 я ) Икс + а — 1 знак равно 1 (70)
, поэтому его решение является обобщенной функцией Ламберта мнимого аргумента с одним верхним и одним нижним комплексными параметрами.Этот класс функций недавно изучал Мезо [28].
Мы можем легко получить приближенное аналитическое решение (69), используя алгебраическое приближение касательной [46], [5]. Таким образом, вместо (69) мы получаем приближенное уравнение:
Икс знак равно 0,45 π ( Икс — п π ) 2 Икс — ( 2 п — 1 ) π ( 1 — а — б Икс ) (71)
, которое можно свести к алгебраическому уравнению второй степени:
Икс 2 ( 1.413 7 б + 2 ) — 3. 141 6 Икс ( 2 п — 0,45 а + 1.413 7 б п — 0,55 ) — — 4. 441 3 п ( а — 1 ) знак равно 0 (72)
Для a = 1, b = 1, n = 2, корень этого уравнения равен x _{приблизительно} = 5.362 8, а корень (69) равен x _{, точное значение} = 5,49779, поэтому ошибка составляет около 2,5%.
В [13] Бернистон и Сиверт решили уравнение:
а грех ⁡ ζ знак равно ζ (73)
, который появляется в квантовой механике (определение собственных энергий частицы в потенциале с квадратной ямой), в электромагнетизме, в упругости, в оптике и т. Д.Несколько позже Сиверт получает более простое решение [21]. Очень точное приближенное аналитическое решение (73) было получено путем алгебраизации [2, 3, 4, 5]; он полезен, например, для расчета уровней энергии в гетеропереходах и квантовых точках.
Более сложным вариантом (73) является уравнение Кеплера для эллиптических орбит [10] (эксцентриситет, обычно обозначаемый как e , будет записан как ε , чтобы избежать путаницы с основанием логарифмов Неппера ):
ε грех ⁡ E знак равно E — M , 0 < ε < 1 , 0 < M < 2 π (74)
Мы можем получить довольно точное решение (74), аппроксимируя первую полувыступку sin кубическим полиномом:
у ( Икс ) знак равно а Икс 3 + б Икс 2 + Икс (75)
, где коэффициенты a , b могут быть определены путем наложения условий:
у ( π 2 ) знак равно 1 , у ′ ( π 2 ) знак равно 0 (76)
Находим:
у ( Икс ) знак равно 4 π 3 ( π — 4 ) Икс 3 — 4 π 2 ( π — 3 ) Икс 2 + Икс (77)
, который довольно хорошо соответствует функции sin x , для 0 < x < π /2, как мы можем видеть на рисунке 4.
Рисунок 4
Участки х ( х ), ур. (77), черный; si n ( x ), штриховой; х — 0,1, красный; х — 0,5, зеленый.
Если e = 0,9, M = 0,1, заменив sin x полиномом (77) в уравнении Кеплера (74), мы получим решение x _{1 p} = 0.599 55, а «точное» решение — x _{1 e} = 0,599 55; Итак, ошибка составляет ε ₁ ≃ 5 × 10 ⁻². Если e = 0,9 и M = 0,5, полиномиальная аппроксимация дает x _{2 p} = 1,382 1, а «точное» решение — x _{2 e} = 1,38441 , поэтому ошибка равна ε ₂ ≃ 1. 7 × 10 ⁻³. Графики на рис. 4 интуитивно показывают, почему второе приближение более точное.
9 Выводы
Эта статья в основном сосредоточена на трансцендентных уравнениях, изучаемых Сивертом и его сотрудниками, которые рассматриваются вместе с результатами, полученными недавно в теории обобщенных функций Ламберта. Точные (и очень сложные) результаты Сиверта по возможности заменяются приближенными аналитическими решениями тех же уравнений, полученными с помощью некоторых простых методов. Обсуждаются также некоторые другие результаты Сиверта и его сотрудников, не связанные с обобщенными функциями Ламберта; в двух случаях асимптотика решений Сиверта выражается через функцию Райта ω .
Поскольку иногда приближенные выражения обобщенных функций Ламберта очень точны (и их точные выражения трудно получить), эти приближения могут дать полезные сведения об их точном поведении. Кроме того, «алгебраизация» трансцендентных уравнений (т. Е. Замена тригонометрических функций их различными алгебраическими приближениями) может дать иногда удивительно точные аналитические решения. Их можно успешно использовать в прикладной физике или при элементарном изложении сложных задач.
Автор выражает признательность за финансовую поддержку проекту IFIN-HH — ANCSI PN 16 42 01.01.2016 и гранту IFIN-HH — ОИЯИ Дубна 04-4-1121-2015 / 17
Ссылки
[1] Гриффитс Д.Д., Введение в квантовую механику, Прентис-Холл, Аппер-Сэдл-Ривер, Нью-Джерси, 1995 г. Поиск в Google Scholar
[2] Барсан В., Драгомир Р., Новое приближение для квадратной ямы проблема, Оптоэль. Adv. Мат. — Rapid Commun., 2012, 6, 917-925. Искать в Google Scholar
[3] Barsan V., Новое аналитическое приближение для собственных значений энергии конечной квадратной ямы, Rom. Физика, 2012, 64, 685-694. Искать в Google Scholar
[4] Барсан В., Квадратные ямы, квантовые ямы и ультратонкие металлические пленки, Philos. Mag., 2014, 93, 1604-1617. Искать в Google Scholar
[5] Барсан В. Алгебраические аппроксимации трансцендентных уравнений с приложениями в нанофизике, Философ. Mag., 2015, 95, 3023–3038.10.1080 / 14786435.2015.1081425 Поиск в Google Scholar
[6] Марин М., О слабых решениях по упругости дипольных тел с пустотами, J. Comp. Прил. Math., 1997, 82, 291-297.10.1016 / S0377-0427 (97) 00047-2 Искать в Google Scholar
[7] Марин М., Гармонические колебания термоупругости микропластичных материалов, J. Vibr. Акуст., ASME, 2010, 132, 044501-1-044501-6. Искать в Google Scholar
[8] Шарма К., Марин М., Влияние различных проводящих и термодинамических температур на отражение плоских волн в микрополярном упругом полупространстве, U.P.B. Sci. Bull., Series A-Appl. Математика. Физ., 2013, 75, 121-132. Искать в Google Scholar
[9] Барсан В., Новые приложения Ламберта и обобщенных функций Ламберта к ферромагнетизму и квантовой механике, arXiv: 1611.01014v2, 2016. Поиск в Google Scholar
[10] Сиверт К.Э., Бернистон Э. Точное аналитическое решение уравнения Кеплера, Небесная механика, 1972, 6, 294-304.10.1007 / BF01231473 Поиск в Google Scholar
[11] Бернистон Е.Е., Сиверт К.Э., Использование задач Римана в решении класса трансцендентных уравнений, Proc.Camb. Фил. Soc., 1973, 73, 111-118.10.1017 / S0305004100047526 Поиск в Google Scholar
[12] Сиверт К.Э., Точное аналитическое решение элементарного критического состояния, Ядерные науки. Eng., 1973, 51, 78-79.10.13182 / NSE73-A23260 Искать в Google Scholar
[13] Бернистон Э.Е., Сиверт К.Э., Точное аналитическое решение трансцендентного уравнения a sin ζ = ζ , SIAM J. Appl. Math., 1973, 4, 460-465. Искать в Google Scholar
[14] Siewert C.Э., Эссиг К. Точное решение уравнения молекулярного поля в теории ферромагнетизма // J. Appl. Математика. Phys., Т. 24, стр. 281-286. Искать в Google Scholar
[15] Сиверт К.Э., Бернистон Э.Е., О критическом состоянии, Ядерные науки. Eng., 1973, 52, 150-151.10.13182 / NSE73-A23301 Поиск в Google Scholar
[16] Сиверт К.Е., Бернистон Э.Э., Точные аналитические решения ze ^z = a , J. Math. Анальный. Applic., 1973, 43, 626-632.10.1016 / 0022-247X (73)-3 Искать в Google Scholar
[17] Siewert C.Э., Буркарт А.Р., О двойных нулях x = tanh ( ax + b ), J. Appl. Математика, 1973, 24, 435-439. Поиск в Google Scholar
[18] Сиверт К.Е., Решения уравнения ze ^z = a ( z + b ), J. Math. Анальный. Applic., 1974, 46, 329-337.10.1016 / 0022-247X (74)-1 Поиск в Google Scholar
[19] Сиверт CE, Burniston EE, Точное аналитическое решение зависимости положения от времени для инверсии -квадратное расстояние, Цел.J. Eng. Sci., 1974, 12, 861-863.10.1016 / 0020-7225 (74)
-8 Искать в Google Scholar
[20] Siewert CE, Burniston EE, Точное аналитическое решение x coth x = αx ² + 1, J. Comp. Прил. Math., 1976, 2, 19-26.10.1016 / 0771-050X (76)
-6 Поиск в Google Scholar
[21] Сиверт К.Э., Явные результаты для квантово-механических состояний энергии, лежащих в основе конечной квадратной ямы потенциал, J. Math. Phys., 1978, 19, 434-435. 10.1063 / 1.523662 Искать в Google Scholar
[22] Siewert C.E., Phelps J.S. III, О решениях трансцендентного уравнения, лежащего в основе теории вибрирующих пластин, 1979, SIAM J. Math. Анальный. 10 , стр. 105-108.10.1137 / 0510013 Искать в Google Scholar
[23] Siewert C.E., Phelps J.S. III, Явные решения a ta n ( ξ — k π ) + tanh ξ = 0, J. Comp. Прил. Математика, 1979, 5, 99-103. Искать в Google Scholar
[24] http: // www4.ncsu.edu/~ces/publist.html Поиск в Google Scholar
[25] Мусхелишвили Н.И., Сингулярные интегральные уравнения, Нордхофф, Гронинген, 1953 г. Поиск в Google Scholar
[26] Мезё И., Барич А., На обобщение W-функции Ламберта, arXiv: 1408.3999v2, 2014. Поиск в Google Scholar
[27] Мугнаини Г., Обобщение W-функции Ламберта, многочлены Бесселя и трансцендентные уравнения, arXiv: 1501.00138v2, 2015. Поиск в Google Scholar
[28] Мезо И., О структуре множества решений обобщенного уравнения Эйлера – Ламберта, J. Math. Анальный. Appl., 2017, 455, 538–553.10.1016 / j.jmaa.2017.05.061 Поиск в Google Scholar
[29] Мезё И., Г. Киди, Некоторые физические приложения обобщенных функций Ламберта, Eur. J. Phys., 2016, 37, 06580210.1088 / 0143-0807 / 37/6/065802 Поиск в Google Scholar
[30] Мезё И., Г. Киди, Некоторые физические приложения обобщенных функций Ламберта, Eur. J. Phys., 2016, 37, 37 , 065802.10.1088 / 0143-0807 / 37/6/065802 Поиск в Google Scholar
[31] Вонсовский С.В., Magnetism, Wiley, New York, 1974 Поиск в Google Scholar
[32] https://en.wikipedia.org/ wiki / Superparamagnetism Search in Google Scholar
[33] Kuncser V. и др., Разработка магнитных свойств наноструктур с помощью размерных эффектов и межфазного взаимодействия, in: V. Kuncser, L. Miu (Eds.): Size effects in Nanostructures, Springer Series in Materials Science, Heidelberg, 2016 Search in Google Scholar
[34] Johal A.С., Данстан Д.Дж. Энергетические функции резины на основе микроскопических потенциалов // J. Appl. Phys., 2007, 101, 084
.1063 / 1.2723870 Поиск в Google Scholar
[35] Крегер М., Простые, допустимые и точные аппроксимации обратных функций Ланжевена и Бриллюэна, актуальные для сильных деформаций и течений полимеров, J. Non- Newtonian Fluid Mech., 2015, 223, 77-87.10.1016 / j.jnnfm.2015.05.007 Поиск в Google Scholar
[36] Джедынак Р., Повторное приближение обратной функции Ланжевена, Rheol.Acta, 2015, 54, 29.10.1007 / s00397-014-0802-2 Поиск в Google Scholar
[37] Петросян Р., Улучшенные приближения для некоторых моделей расширения полимеров, 2017, Rheol. Acta, 56, 21-26.10.1007 / s00397-016-0977-9 Поиск в Google Scholar
[38] Кубо Р., Статистическая механика, Elsevier, Амстердам, 1965, гл. 2, стр. 135 и 157. Поиск в Google Scholar
[39] Киди Г., Функция Ланжевена и усеченные экспоненциальные распределения, arXiv: 1501.02535v1 Поиск в Google Scholar
[40] Зурке Х., Маккормик П.Г., Приближение дробного временного распределения индекса дневной ясности, J. Solar Energy, 1987, 39, 369-370.10.1016 / S0038-092X (87) 80023-3 Поиск в Google Scholar
[41] Арротт А.С., Приближения к функциям Бриллюэна для аналитического описания ферромагнетизма, J. Appl. Phys., 2008, 103, 07C71510.1063 / 1.2836337 Искать в Google Scholar
[42] Stanley HE, Introduction to Phase Transforms and Critical явлений, Oxford University Press, Oxford, 1971 Search in Google Scholar
[43] Kittel Ch ., Введение в физику твердого тела, 8-е изд., Wiley, New York, 8-е изд., 2005 г. Поиск в Google Scholar
[44] Кочмански М., Пашкевич Т., Вольски С., Eur. J. Phys., 2013, 34, 1555.10.1088 / 0143-0807 / 34/6/1555 Искать в Google Scholar
[45] Барсан В., Кунцер В., Точные и приближенные аналитические решения уравнения ферромагнетизма Вейса и их экспериментальная значимость, Philos. Mag. Lett., 2017, 97, 359–371.10.1080 / 09500839.2017.1366081 Искать в Google Scholar
[46] de Alcantara Bonfim O.Ф., Гриффитс Д. Дж., Точный и приблизительный энергетический спектр для конечной квадратной ямы и связанных потенциалов, Am. J. Phys., 2006, 74, 43-47.710.1119 / 1.2140771 Поиск в Google Scholar
[47] Корлесс Р.М., Джеффри Д.Д., О функции Wright ω , http://www.orcca.on.ca /TechReports/2000/TR-00-12.pdf (2000) Поиск в Google Scholar
[48] Голманхане А.К., Хатуни Т., Поргхове Н.А., Балеану Д., Сравнение итерационных методов на основе решения нелинейной системы Штурма-Лиувилля, Бюргерса и уравнение Навье-Стокса, Cent.Евро. J. Phys., 2012, 10, 966-976. Поиск в Google Scholar
[49] Голманхане А.К., Балеану Д., О нелинейном уравнении Клейна — Гордона, Обработка сигналов, 2011, 91, 446-451.10.1016 / j.sigpro.2010.04.016 Поиск в Google Scholar
[ 50] Корлесс Р.М., Гоннет Г.Х., Хейр Д., Джеффри Д.Д., Кнут Д.Е., Adv. Comput. Math., 1996, 5, 329-359.10.1007 / BF02124750 Поиск в Google Scholar
[51] https://en.wikipedia.org/wiki/Kepler%27s_equation#cite_note-7 Поиск в Google Scholar
[52 ] Райт Э.М., Критерии устойчивости и действительные корни трансцендентного уравнения, SIAM J. Appl. Math., 1961, 9, 136-148.10.1137 / 0109014 Искать в Google Scholar
Поступила: 27.07.2017
Принято: 25.11.2017
Опубликовано в сети: 24.05.2018
© Виктор Барсан, 2018, опубликовано De Gruyter
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 Лицензия.
Как решать трансцендентные уравнения численно. Онлайн-справка
Используя наш сайт, вы подтверждаете, что прочитали и поняли нашу Политику использования файлов cookie и Условия использования. Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.
Трансцендентное уравнение
Регистрация займет всего минуту. Есть ли возможность получить аналитическое решение? Если нет, можем ли мы решить это в системе Mathematica? Вы не найдете полного аналитического решения.
Вы можете решить это численно с помощью любого корневого искателя. Зарегистрируйтесь, чтобы присоединиться к этому сообществу. Лучшие ответы голосуются и поднимаются наверх. Главная Вопросы Теги Пользователи без ответа. Решите трансцендентное уравнение [закрыто] Задайте вопрос.
Спросил 2 года, 4 месяца назад. Последняя активность 2 года 3 месяца назад. Просмотренное время. Tobias Fritzn Tobias Fritzn 4 4 бронзовых знака. К сожалению, вам, возможно, придется делать это численно.
Waxaa ii galmooday
Активные самые старые голоса. Росс Милликан Росс Милликан 1 11 11 золотой знак серебряный знак бронзовый знак.Claude Leibovici Claude Leibovici k 14 14 золотых знаков 68 68 серебряных знаков бронзовых знаков. Блог Overflow. Дорожная карта сообщества Q2. Переполнение Сколько работ можно выполнять дома? Показано на Meta. Рекомендации сообщества и модератора по эскалации проблем с помощью нового ответа….
Отзыв о дорожной карте сообщества на второй квартал. Автофильтры для горячих сетевых вопросов. Справочник численных методов решения алгебраических и трансцендентных уравнений предоставляет информацию, относящуюся к алгебраическим и трансцендентным уравнениям.В этой книге содержится обоснованный план решения приближенного уравнения. Эта книга, состоящая из шести глав, начинается с обзора решения различных уравнений.
Далее в этом тексте излагается нетрадиционная теория решения приближенных уравнений. В других главах рассматриваются приближенные методы вычисления корней алгебраических уравнений. В этой книге также обсуждаются методы уточнения корней, которые необходимы для практического применения метода Берстого.В последней главе рассматриваются методы решения одновременных линейных уравнений, которые делятся на прямые методы и методы последовательного приближения.
Эта книга является ценным ресурсом для студентов, инженеров и научных сотрудников институтов и промышленных предприятий, использующих математические методы при решении технических задач. Мы всегда ищем способы улучшить качество обслуживания клиентов на Elsevier.
Мы хотели бы попросить вас немного времени заполнить небольшую анкету в конце вашего визита.Если вы решите принять участие, откроется новая вкладка браузера, чтобы вы могли заполнить анкету после посещения этого веб-сайта.
Заранее благодарим за уделенное время. Перейти к содержанию. Поиск книг, журналов или веб-страниц Все страницы Книги Журналы. Однако из-за перебоев в транспортировке в некоторых регионах поставки могут задерживаться. Посмотреть на ScienceDirect. Авторы: В. Выходные данные: Пергамон. Дата публикации: 1 января. Количество страниц: гибкость — доступна для разных операционных систем и устройств.Легко читайте электронные книги на смартфонах, компьютерах или любых устройствах для чтения электронных книг, включая Kindle. Институциональная подписка. Бесплатная доставка Бесплатная доставка по всему миру Нет минимального заказа.
Корень функции 2. Основные свойства многочленов 3. Делимость многочленов 3. Точное деление 3. Теорема Безу 3. Войдите в систему, чтобы оставить комментарий. Войдите в систему что бы ответить на этот вопрос.
Невозможно завершить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние. Выберите веб-сайт, чтобы получать переведенный контент, если таковой имеется, и просматривать местные события и предложения.В зависимости от вашего местоположения мы рекомендуем вам выбрать :. Выберите китайский сайт на китайском или английском, чтобы обеспечить наилучшую производительность сайта. Сайты других стран MathWorks не оптимизированы для посещения из вашего местоположения.
Переключить главную навигацию. Искать ответы Очистить фильтры. Ответы на поддержку MathWorks. Поддержка поиска Очистить фильтры. Служба поддержки отвечает MathWorks.
Поиск в MathWorks. Поддержка ответов MathWorks. Откройте мобильный поиск. Пробное программное обеспечение.
Cuda передать класс ядру
Теперь вы следите за этим вопросом. Вы увидите обновления в своей ленте действий.Вы можете получать электронные письма в зависимости от ваших предпочтений в отношении уведомлений. Голосовать 0. Комментарий: Аззи Абдельмалек 16 января Я пытаюсь решить 2 трансцендентных уравнения для 2 переменных A, M для данного L.
ответов 2. Миша Ким 16 января Отменить копирование в буфер обмена.
Решение алгебраических и трансцендентных уравнений — Часть 1

Отредактировано: Миша Ким 16 января Привет, виджей, чему равны уравнения? Другими словами. Если это так, то это проблема поиска корней: найти такие A и M, чтобы выполнялись два уравнения.Существует множество литературы по решению систем нелинейных уравнений. Попробуйте Ньютон-Рафсон. Проблема, с которой вы можете столкнуться, состоит в том, чтобы найти хорошие начальные значения для поиска, чтобы алгоритм правильно охватил.
Также имейте в виду, что у вашей проблемы может быть несколько причин.
Браузер Oculus apk
Аззи Абдельмалек от 16 января Ошибка в строке решения. Я был бы удивлен, если бы существует символическое решение. Вероятно, вам нужно сделать это численно. Другой сценарий — решения нет вообще.Авторизуйтесь, чтобы комментировать. Войдите в систему что бы ответить на этот вопрос. Невозможно завершить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние. Выберите веб-сайт, чтобы получать переведенный контент, если таковой имеется, и просматривать местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать :.
Выберите китайский сайт на китайском или английском для обеспечения наилучшей производительности сайта. Сайты других стран MathWorks не оптимизированы для посещения из вашего местоположения. Переключить главную навигацию.
Поиск ответов Очистить фильтры.Ответы на поддержку MathWorks. Поддержка поиска Очистить фильтры. Служба поддержки отвечает MathWorks. Найдите MathWorks. Поддержка ответов MathWorks. Откройте мобильный поиск. Пробное программное обеспечение.
Золотое слово
Теперь вы подписались на этот вопрос. Вы будете видеть обновления в своей ленте активности. Вы можете получать электронные письма в зависимости от ваших предпочтений в отношении уведомлений.
Как решать трансцендентные уравнения в Matlab. Голосовать 0. Ответил: Вальтер Роберсон 30 июл. Принят ответ: Антон Семечко. Я занимаюсь решением трансцендентных уравнений в Matlab, у меня есть данное уравнение, и я хочу решить его относительно x.
Уолтер Роберсон 12 июня Отменить копирование в буфер обмена. Не могли бы вы подтвердить, что в уравнении есть две копии 1. Эти два числа отличаются только одной цифрой, поэтому было бы хорошо проверить, не было ли опечаток. Связаны ли эти трое? Например, вы могли бы написать. Антон Семечко 12 июня Вальтер, я почти уверен, что в этом уравнении есть другой тип.
Пожалуйста, не закрывайте вопросы, на которые есть ответ. Чувство смущения, потому что будет пытаться решать проблемы, как методом Ньютона-Рапсона.Хотя корни можно найти непосредственно для алгебраических уравнений четвертого или более низкого порядка, а также для нескольких специальных трансцендентных уравнений, на практике нам необходимо решать уравнения более высокого порядка, а также произвольные трансцендентные уравнения.
Поскольку аналитические решения часто либо слишком громоздки, либо просто не существуют, нам необходимо найти приближенный метод решения.
Обмен Thunderbird бесплатно
Вот где на сцену выходит числовой анализ. Последнее замечание об интервале — одно из наиболее полезных свойств, которые численные методы используют для нахождения корней.Все они имеют общее требование, что нам нужно сделать первоначальное предположение для корня.
Практически это легко сделать графически. Просто постройте уравнение и сделайте приблизительную оценку решения. Аналитически мы обычно можем выбрать любую точку интервала, где происходит смена знака. Однако это зависит от определенных условий, которые варьируются от метода к методу. Численный метод решения уравнений — долгий процесс. Мы хотели бы знать, приведет ли метод к решению, близкому к точному, или уведет нас от решения.Если метод приводит к решению, мы говорим, что метод сходится.
В противном случае метод называется расходящимся. Различные методы сходятся к корню с разной скоростью. То есть некоторые методы сходятся медленно, и для достижения корня требуется много времени, в то время как другие методы могут привести нас к корню быстрее. В общем, это компромисс между простотой расчетов и временем. Однако для компьютерной программы, как правило, лучше использовать методы, которые быстро сходятся.
Скорость сходимости может быть линейной или более высокого порядка. Чем выше порядок, тем быстрее сходится метод. Это один из простейших методов, в основе которого лежит свойство интервалов.
Используйте это как новый интервал и продолжайте, пока не получите корень с желаемой точностью. Таким образом, этот метод линейно сходится. Если нас интересует количество итераций, необходимых для схождения метода деления пополам к корню в пределах определенного допуска, то мы можем использовать формулу для максимальной ошибки.Используйте формулу максимальной ошибки :.
Примечание: анализ ошибок дает только граничное приближение к ошибке; фактическая ошибка может быть намного меньше. Метод ложного положения, который иногда называют методом regula falsi, по существу такой же, как метод деления пополам, за исключением того, что вместо деления интервала пополам мы находим место пересечения хорды, соединяющей две точки, с осью X.
Корни рассчитываются с использованием уравнения хорды, т.е. Скорость сходимости по-прежнему линейна, но выше, чем у метода деления пополам.Оба эти метода потерпят неудачу, если f имеет двойной корень. Мы уже знаем корни этого уравнения, поэтому можем легко проверить, насколько быстро сходится метод regula falsi.
Поскольку f вогнута вверх и увеличивается, быстрый набросок геометрии показывает, что хорда всегда пересекает ось x слева от решения. Это можно подтвердить небольшой алгеброй. Это всегда меньше, чем e n, когда n положительно.
Когда n приближается к 1, каждая дополнительная итерация уменьшает ошибку на две трети, а не на половину, как при методе деления пополам.В этом случае нижний предел интервала стремится к корню, а минимальная ошибка стремится к нулю, но верхний предел и максимальная ошибка остаются фиксированными. Войдите, чтобы оставить комментарий.
Войдите, чтобы ответить на этот вопрос. Невозможно завершить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние. Выберите веб-сайт, чтобы получать переведенный контент, если таковой имеется, и просматривать местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать :. Выберите китайский сайт на китайском или английском, чтобы обеспечить наилучшую производительность сайта.Сайты других стран MathWorks не оптимизированы для посещения из вашего местоположения. Переключить главную навигацию.
Поиск ответов Очистить фильтры. Ответы на поддержку MathWorks.
Поддержка поиска Очистить фильтры. Служба поддержки отвечает MathWorks. Найдите MathWorks. Поддержка ответов MathWorks. Откройте мобильный поиск.
Пробное программное обеспечение. Теперь вы следите за этим вопросом. Вы увидите обновления в своей ленте активности. Вы можете получать электронные письма в зависимости от ваших предпочтений в отношении уведомлений.
Как решить трансцендентное уравнение? Войдите на сайт, чтобы оставить комментарий.Войдите в систему что бы ответить на этот вопрос.
Подписаться на RSS
Невозможно завершить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние. Выберите веб-сайт, чтобы получать переведенный контент, если таковой имеется, и просматривать местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать :. Выберите китайский сайт на китайском или английском, чтобы обеспечить наилучшую производительность сайта. Сайты других стран MathWorks не оптимизированы для посещения из вашего местоположения.
Переключить главную навигацию.Искать ответы Очистить фильтры. Ответы на поддержку MathWorks.
Поддержка поиска Очистить фильтры. Служба поддержки отвечает MathWorks. Найдите MathWorks. Поддержка ответов MathWorks. Откройте мобильный поиск. Пробное программное обеспечение. Теперь вы следите за этим вопросом. Вы увидите обновления в своей ленте активности.
Вы можете получать электронные письма, в зависимости от ваших предпочтений в отношении уведомлений. Дэвид Чжан 13 февраля Голосовать 0.
Kohler cv15s starter
Привет всем. Мне нужно решить следующее уравнение. Это нелинейный объект с множеством корней, может ли какая-нибудь функция в Matlab это сделать? Спасибо.Ответы 3.

Как решать трансцендентные уравнения в калькуляторе
Wolfram Alpha — отличный инструмент для поиска корней многочленов и решения систем уравнений. Он также множит многочлены, строит множества полиномиальных решений и неравенства и многое другое. Введите свои запросы, используя простой английский. Чтобы избежать неоднозначных запросов, обязательно используйте круглые скобки там, где это необходимо. Вот несколько примеров, иллюстрирующих, как формулировать запросы.
Получите немедленную обратную связь и руководство с помощью пошаговых решений и генератора проблем Wolfram.Наибольший показатель появления в называется степенью. Если имеет степень, то хорошо известно, что есть корни, если принять во внимание множественность. Чтобы понять, что подразумевается под множественностью, возьмем, к примеру.
Считается, что этот многочлен имеет два корня, оба равные 3. Каждый изучает «теорему о факторах», обычно во втором курсе алгебры, как способ найти все корни, являющиеся рациональными числами. Также можно научиться находить корни всех квадратичных многочленов, используя при необходимости квадратные корни, возникающие из дискриминанта.
Существуют более сложные формулы для выражения корней многочленов кубической и четвертой степени, а также ряд численных методов аппроксимации корней произвольных многочленов. В них используются методы комплексного анализа, а также сложные численные алгоритмы, и это действительно область постоянных исследований и разработок. Системы линейных уравнений часто решаются с использованием метода исключения Гаусса или связанных с ним методов. Это также обычно встречается в программах средней школы или колледжа по математике.
Для нахождения корней одновременных систем нелинейных уравнений необходимы более совершенные методы. Аналогичные замечания относятся к работе с системами неравенств: линейный случай может быть обработан с использованием методов, описанных в курсах линейной алгебры, тогда как полиномиальные системы более высокой степени обычно требуют более сложных вычислительных инструментов.
Для решения уравнений Wolfram Alpha вызывает функции Solve и Reduce языка Wolfram Language, которые содержат широкий спектр методов для всех видов алгебры, от основных линейных и квадратных уравнений до многомерных нелинейных систем.В некоторых случаях используются методы линейной алгебры, такие как исключение Гаусса, с оптимизацией для повышения скорости и надежности. Другие операции полагаются на теоремы и алгоритмы из теории чисел, абстрактной алгебры и других продвинутых областей для вычисления результатов.
Эти методы были тщательно разработаны и выбраны, чтобы позволить Wolfram Alpha решать самые разные задачи, одновременно минимизируя время вычислений. Хотя такие методы полезны для прямых решений, для системы также важно понимать, как человек решит ту же проблему.
В результате Wolfram Alpha также имеет отдельные алгоритмы для пошагового отображения алгебраических операций с использованием классических методов, которые легко распознаются людьми и которым легко следовать.
Это включает исключение, замену, квадратную формулу, правило Крамера и многое другое.
Эээээ! Wolfram Alpha не работает без JavaScript. Пожалуйста, включите JavaScript. Если вы не знаете как, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram Alpha.Вычисляйте ответы на уровне экспертов с использованием передовых алгоритмов, базы знаний и технологии искусственного интеллекта Wolfram Входные данные для примера Больше, чем просто средство решения уравнений онлайн Wolfram Alpha — отличный инструмент для поиска корней полиномов и решения систем уравнений.
Как Wolfram Alpha решает уравнения Для решения уравнений Wolfram Alpha вызывает функции Solve и Reduce языка Wolfram Language, которые содержат широкий спектр методов для всех видов алгебры, от основных линейных и квадратных уравнений до многомерных нелинейных систем.Используя наш сайт, вы подтверждаете, что прочитали и поняли нашу Политику конфиденциальности и Условия использования.
Mathematica Stack Exchange — это сайт вопросов и ответов для пользователей Wolfram Mathematica. Регистрация займет всего минуту. Это около 0. NSolve в первую очередь предназначен для полиномиальных уравнений или уравнений, которые могут быть преобразованы в полином. Reduce часто может найти «точное» решение в некотором смысле, но для успеха обычно требуется указать интервал, в котором нужно искать.
Используйте FindRoot, чтобы найти его :. Используйте Reduce, чтобы найти все решения в заданном интервале :. Указание интервала было важным. Когда Reduce завершается успешно, гарантируется нахождение всех решений в заданном интервале.
Калькулятор алгебры
Объекты Root, хотя и основаны на численном приближении, представляют собой точное решение и могут использоваться как любое другое точное число в системе Mathematica e.
Эта интересная и полезная функция Reduce обсуждается в этой публикации блога Wolfram.Зарегистрируйтесь, чтобы присоединиться к этому сообществу. Лучшие ответы голосуются и поднимаются наверх. Главная Вопросы Теги Пользователи без ответа. Решение простого трансцендентного уравнения [дубликат] Задайте вопрос. Спросил 4 года назад. Активен 4 года назад. Просмотрен 10k раз. Я упускаю что-то действительно очевидное? В качестве альтернативы можно использовать cotSol [] из этого ответа: N [cotSol [1], 20]. Однако, если это вас не проясняет, взгляните на Корни характеристического уравнения.
Может ли система Mathematica решить эту проблему? Спасибо всем. Активные самые старые голоса.Да, работает, спасибо. Для подобных уравнений у нас обычно есть два варианта: FindRoot, чтобы найти единственное решение численно, на основе начального предположения, Reduce часто может найти «точное» решение в некотором смысле, но для успеха обычно требуется указать интервал, в котором нужно искать. Это уравнение имеет бесконечное количество реальных решений.
Решатель уравнений
Это последнее решение является точным в следующем смысле: при успешном выполнении Reduce гарантируется нахождение всех решений в заданном интервале. Объекты Root, хотя и основаны на численном приближении, представляют собой точное решение и могут быть используется как любое другое точное число в системе Mathematica e.Szabolcs Szabolcs k 18 18 золотых знаков серебряные знаки бронзовые знаки.
Блог переполнения. Показано на Meta. Рекомендации сообщества и модератора по эскалации проблем с помощью нового ответа… .В численном анализе итерация с фиксированной точкой — это метод вычисления фиксированных точек повторяемых функций. Более конкретно, учитывая функцию, определенную на действительных числах с действительными значениями и заданную точкой в области итерации с фиксированной точкой, является.
Если непрерывно, то можно доказать, что полученное является неподвижной точкой i.Этот метод фактически является своего рода методом последовательных приближений, методом решения математических задач с помощью последовательности приближений, которая сходится к решению и строится рекурсивно, то есть каждое новое приближение вычисляется на основе предыдущего приближения; выбор начального приближения до некоторой степени произвольный.
Метод используется для аппроксимации корней алгебраических и трансцендентных уравнений. Он также используется для доказательства существования решения и аппроксимации решений дифференциальных, интегральных и интегро-дифференциальных уравнений.Именно это и делает калькулятор ниже. Он выполняет итерационные вычисления x по заданной формуле и останавливается, когда два последовательных значения отличаются меньше заданной точности.
Также стоит упомянуть, что использованная в качестве примера функция i. Это, возможно, первый алгоритм, используемый для приближения квадратного корня, и он известен как «вавилонский метод», названный в честь вавилонян, или «метод Героя», названный в честь греческого математика I века Героя Александрийского, который дал первое подробное описание. метода.
Более конкретно, заданная функция, определенная на действительных числах с действительными значениями и заданная точка в области итерации с фиксированной точкой, дает начало последовательности, которая, как ожидается, сходится к точке. Источник Этот метод на самом деле является своего рода методом последовательных приближений, методом решения математических задач с помощью последовательности приближений, которая сходится к решению и строится рекурсивно, то есть каждое новое приближение вычисляется на основе предыдущего приближения; выбор начального приближения до некоторой степени произвольный.
Использование этого метода довольно просто: принять приблизительное значение для начального значения переменной, решить для переменной, использовать ответ в качестве второго приближенного значения и решить уравнение, повторить этот процесс до тех пор, пока не будет достигнута желаемая точность для переменной. что делает калькулятор ниже.
Итерационный метод с фиксированной точкой. Итерированная функция. Начальное значение x0. Приближение прекращается, когда разница между двумя последовательными значениями x становится меньше указанного процента.Точность вычислений Цифры после десятичной точки: 5. Поделиться этой страницей. Авторизуйтесь, чтобы оставлять комментарии.
Войдите, чтобы ответить на этот вопрос. Невозможно завершить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние. Выберите веб-сайт, чтобы получать переведенный контент, если таковой имеется, и просматривать местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать :.
Выберите китайский сайт на китайском или английском для обеспечения наилучшей производительности сайта. Сайты других стран MathWorks не оптимизированы для посещения из вашего местоположения.Переключить главную навигацию. Искать ответы Очистить фильтры.
Метод Ньютона-Рафсона на калькуляторе Casio fx-991ES + секретный трюк!

Ответы Поддержка MathWorks. Поддержка поиска Очистить фильтры. Служба поддержки отвечает MathWorks. Найдите MathWorks. Поддержка ответов MathWorks. Откройте мобильный поиск.
Пробное программное обеспечение. Теперь вы следите за этим вопросом. Вы увидите обновления в своей ленте активности. Вы можете получать электронные письма в зависимости от ваших предпочтений в отношении уведомлений. Как решать трансцендентные уравнения в Matlab.Голосовать 0. Ответил: Вальтер Роберсон 30 июл. Принят ответ: Антон Семечко. Я занимаюсь решением трансцендентных уравнений в Matlab, у меня есть данное уравнение, и я хочу решить его относительно x.
Уолтер Роберсон 12 июня Отменить копирование в буфер обмена. Не могли бы вы подтвердить, что в уравнении есть две копии 1. Эти два числа отличаются только одной цифрой, поэтому было бы хорошо проверить, не было ли опечаток. Связаны ли эти трое? Например, вы могли бы написать.
Антон Семечко 12 июня. Используя наш сайт, вы подтверждаете, что прочитали и поняли нашу Политику использования файлов cookie и наши Условия использования.
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту. Я применил как обычно, но я не вижу, как получить результат, какие-либо предложения, какой-либо метод, если возможно, с некоторыми шагами для начала. Спасибо. Зарегистрируйтесь, чтобы присоединиться к этому сообществу. Лучшие ответы голосуются и поднимаются наверх. Главная Вопросы Теги Пользователи без ответа. Спросил 3 месяца назад.
Активна 3 месяца назад.Просмотров 41 раз. 15 января в Active Oldest Votes. Зарегистрируйтесь или войдите в систему. Зарегистрируйтесь с помощью Google. Зарегистрируйтесь через Facebook. Зарегистрируйтесь, используя электронную почту и пароль.
Опубликовать как гость Имя. Электронная почта обязательна, но не отображается. Блог Overflow. Общение с коллегами при социальном дистанцировании. Показано на Meta. Рекомендации сообщества и модератора по эскалации проблем с помощью нового ответа…. Отзыв о дорожной карте сообщества на второй квартал. Вопрос к сообществу по проблеме. Автофильтры для горячих сетевых вопросов. Связанные 4.Горячие сетевые вопросы. Casio fxMS поставляется со встроенным решателем уравнений. Это полезно, если вы уже знаете процесс решения определенных типов уравнений, но не хотите повторять механические алгебраические и арифметические процессы.
fxMS может решать квадратные и кубические уравнения, содержащие одну неизвестную переменную, и линейные системы уравнений с двумя или тремя неизвестными. Определите, какое уравнение вам нужно решить. Если в нем есть две или более неизвестных переменных, используйте экран одновременного уравнения — это должен быть первый экран, который появляется в режиме EQN.
Выберите формат уравнения. Для уравнений с одной переменной вы можете выбрать «2» для квадратного уравнения или «3» для кубического уравнения. Для систем уравнений вы можете выбрать «2» или «3», чтобы указать количество неизвестных переменных.
Обратите внимание, что для решения системы уравнений с «n» неизвестными у вас должно быть не менее «n» уравнений. Также обратите внимание, что fxMS решает только системы линейных уравнений первого порядка, а не системы квадратных или кубических уравнений.
Введите коэффициенты вашего уравнения или уравнений.Калькулятор предложит вам значения коэффициентов, представленных a, b, c и d в общих форматах уравнений.
Используйте отрицательную переменную, чтобы показать вычитание. Используйте стрелку вниз для прокрутки значений решаемых переменных. Автор: Брэд Живопись. Поделиться Поделиться на Facebook. Научные калькуляторы могут упростить вычисления. Получайте отличные технические советы на свой почтовый ящик. Сделайте свою семью продуктивной, связанной, развлеченной и безопасной.
Пожалуйста, введите действующий адрес электронной почты.Используя наш сайт, вы подтверждаете, что прочитали и поняли нашу Политику конфиденциальности и Условия использования. Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту. Есть ли возможность получить аналитическое решение? Если нет, можем ли мы решить это в системе Mathematica?
Вы не найдете полного аналитического решения. Вы можете решить это численно с помощью любого корневого искателя.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу.Лучшие ответы голосуются и поднимаются наверх. Главная Вопросы Теги Пользователи без ответа.
Решите трансцендентное уравнение [закрыто] Задайте вопрос. Спрашивал 2 года 4 месяца назад. Последняя активность 2 года 4 месяца назад. Просмотренное время. Tobias Fritzn Tobias Fritzn 4 4 бронзовых знака.
К сожалению, вам, возможно, придется делать это численно. Активные самые старые голоса. Росс Милликан Росс Милликан 1 11 11 золотой знак серебряный знак бронзовый знак. Claude Leibovici Claude Leibovici k 14 14 золотых знаков 69 69 серебряных знаков бронзовых знаков.
No related posts.