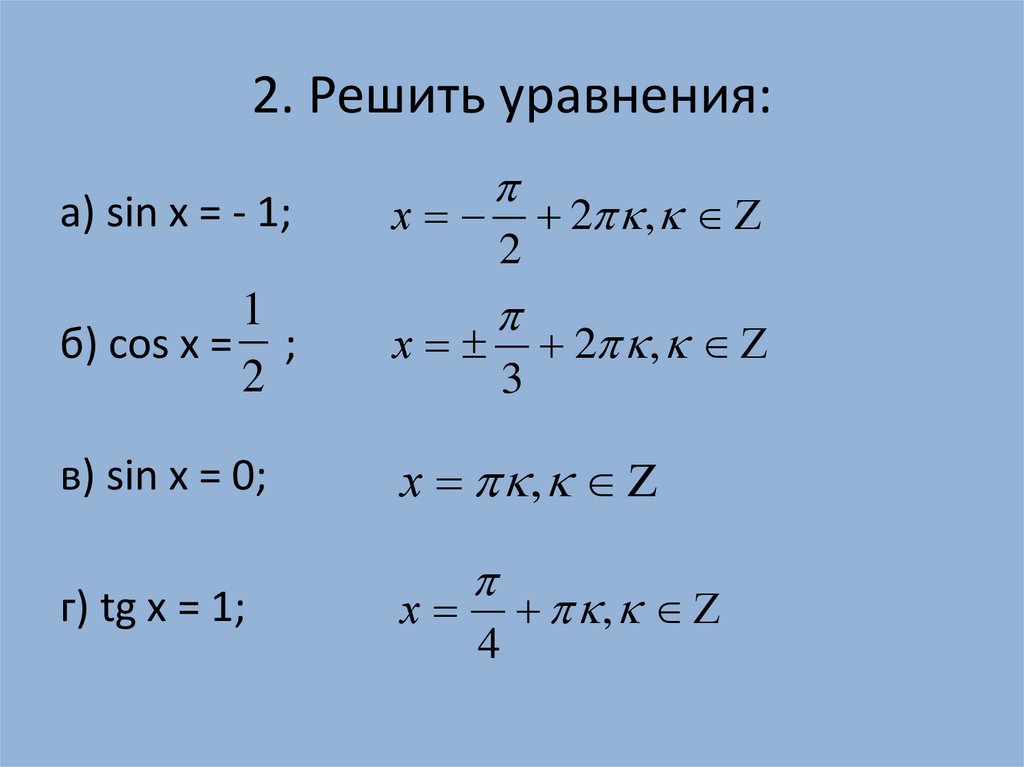РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ В СРЕДНЕЙ ШКОЛЕ,
1. Ананченко К.О. Общая методика преподавания математики в школе. — Минск.: Университецкае, 1997. — 190 с.
2. Алгебра и начала математического анализа.10 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень)/ А.Г. Мордкович, П.В.Семенов. — 6-е изд.,стер. — М.: Мнемозина, 2009. — 424 с.
3. Алгебра и начала математического анализа.10 класс: учеб. для
общеобразоват. учреждений: базовый и профил. уровни)/ [С.М.Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. — 8-е изд. — М.:
Просвещение, 2009. — 430 с.
4. Алгебра и начала математического анализа.10 кл.: учеб. для общеобразоват. учреждений/ Г.К. Муравин. — 6-е изд.,стер. — М.: Дрофа,
2013. — 287 с.
5. Алгебра и начала математического анализа.10-11 классы. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень)/ А.Г. Мордкович. — 14-е изд.,стер. — М.: Мнемозина, 2013. — 400 с.
— 14-е изд.,стер. — М.: Мнемозина, 2013. — 400 с.
— М.: Советская педагогика. №7, 1965. — с. 83
7. Глейзер Г.И. История математики в школе.: пособие для учителей/ под ред. Молодшего В.Н. — М.: Просвещение, 1964. — 376 с.
8. Горнштейн П.И. Тригонометрия помогает алгебре /Горнштейн П.И. — М.: Квант. №5, 1989. — с. 68-70
9. Гилемханов Р.Г. О преподавании тригонометрии в 10 классе / Гилемханов Р.Г. — М.: Математика в школе. №6, 2001. — с. 26-28
10. Колягин Ю.М. Методика преподавания математики в средней школе. — М.: Просвещение, 1999. — 462 с.
11. Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной
математике: Алгебра. Тригонометрия: Учеб. Пособие для студентов
67
физ.мат.спец.пед.ин-тов. — 2-е изд., перераб. и доп. — М.: Просвещение, 1991.
— 352с.
12. Марасанов А.Н. О методологическом подходе в обучении тригонометрии /Н.
 И. Попов, А.Н. Марасанов// (Марийский государственный университет): Знание и понимание. Умение. № 4, 2008. — с. 139-141
И. Попов, А.Н. Марасанов// (Марийский государственный университет): Знание и понимание. Умение. № 4, 2008. — с. 139-14113. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровни/ [Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.]. — 3-е изд. — М.: Просвещение, 2016. — 463 с.
14. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Углубленный уровень. 10 класс.: учебник/ Г.К. Муравин, О.В. Муравина. — М.: Дрофа, 2013. — 318 с.
15. Математический энциклопедический словарь./ Гл.ред. Прохоров Ю.В.
— М.: Сов. энциклопедия,1988. — 847 с.
16. Министерство образования и науки Российской Федерации//Приказ от
31.03.2014 №253 (ред.от 29.12.2016)// «Об утверждении федерального

17. Мордкович А.Г. Беседы с учителями: Учеб. — метод. пособие/ А.Г. Мордкович. — 2-е изд., доп. и перераб. — М.: ООО «Издательский дом «ОНИКС 21 век»»: ООО «Издательство «Мир и Образование»», 2005. — 336 с.
18. Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной школе /Мордкович А.Г. М.: Математика в школе. №6, 2002. — с. 32-33
19. Нахман А.Д. Тригонометрия: учебно-методическое пособие/
утверждено Методическим советом ТГТУ (протокол №7 от 23.09.14). — Тамбов,2014. — 87 с.
20. Нестандартные методы решения тригонометрических неравенств: учебно-методическое пособие/ Е.Р. Садыкова, О.В. Разумова. — Казань: Казан.ун-т, 2013. — 69 с.
21. Репьев В.В. Методика тригонометрии. — М.: Государственное учебно-педагогическое издательство, 1937. — 152 с.
22. Решетников Н.Н. Тригонометрия в школе. — М.: Педагогический университет «Первое сентября», 2006. — лк 1
23. Рогановский Н.М. Методика преподавания в средней школе.
 — Минск: Высшая школа, 1990. — 388 с.
— Минск: Высшая школа, 1990. — 388 с.24. Тригонометрия: учебное пособие /Ю.Ю. Громов, Н,А. Земской, О.Г. Иванова и др. Тамбов: Изд-во Тамб.гос.техн.ун-та, 2003. — 104 с.
25. Цейтен Г.Г. История математики в XVI и XVII веках. /изд. 2-е, исп.и доп. — М.Л.:ОНТИ,1938. — 470с.
26. Шаталов В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии /Шаталов В.Ф. — М.: Новая школа, 1993. — 83 с.
27. Шатов В.Ф. Быстрая тригонометрия. — М: ГУП ЦРП «Москва-Санкт- Петербург», 2002. — 72 с.
Презентация к обобщающему уроку «Решение тригонометрических уравнений и неравенств» | Учебно-методический материал по алгебре (10 класс):
Слайд 1
Тригонометрические уравнения и неравенства Обобщающий урок Алгебра-10 Луценко Ольга Александровна, учитель математики МБОУ «Средняя школа №23 г. Йошкар-Олы »
Йошкар-Олы »
Слайд 2
Как работать Сегодня весь урок ты будешь работать самостоятельно. Ты сможешь обобщить и систематизировать знания по решению тригонометрических уравнений и неравенств. В ходе урока ты сможешь проверить степень своей готовности к предстоящей контрольной работе. К концу урока постарайся зафиксировать свои ошибки (сколько, какие). В дальнейшем вместе с учителем ты сможешь разобрать эти ошибки. Удачи!
Слайд 3
План урока Устная разминка Решение уравнений базового уровня Решение неравенств Решение уравнений повышенного уровня Дополнительное задание Подведение итогов
Слайд 4
Вспомни формулы arcsin(- a ) = -arcsin a для любого а [-1,1] arctg(- a ) = -arctg a для любого а arc с tg(- a ) = π -arc с tg a для любого а arccos(- a ) = π -arcos a для любого а [0,1]
Слайд 5
Устная разминка Вычисли и запиши в столбик ответы в тетради: 1 . arcsin 2 . arccos 3 . arctg 5. arcsin (– ) 4. arctg ( — ) 6 . arccos (- 1 ) 7 arc со s( — ) Проверь ответы: 6) π
Слайд 6
Вспомни и запиши формулы для решения уравнений 1.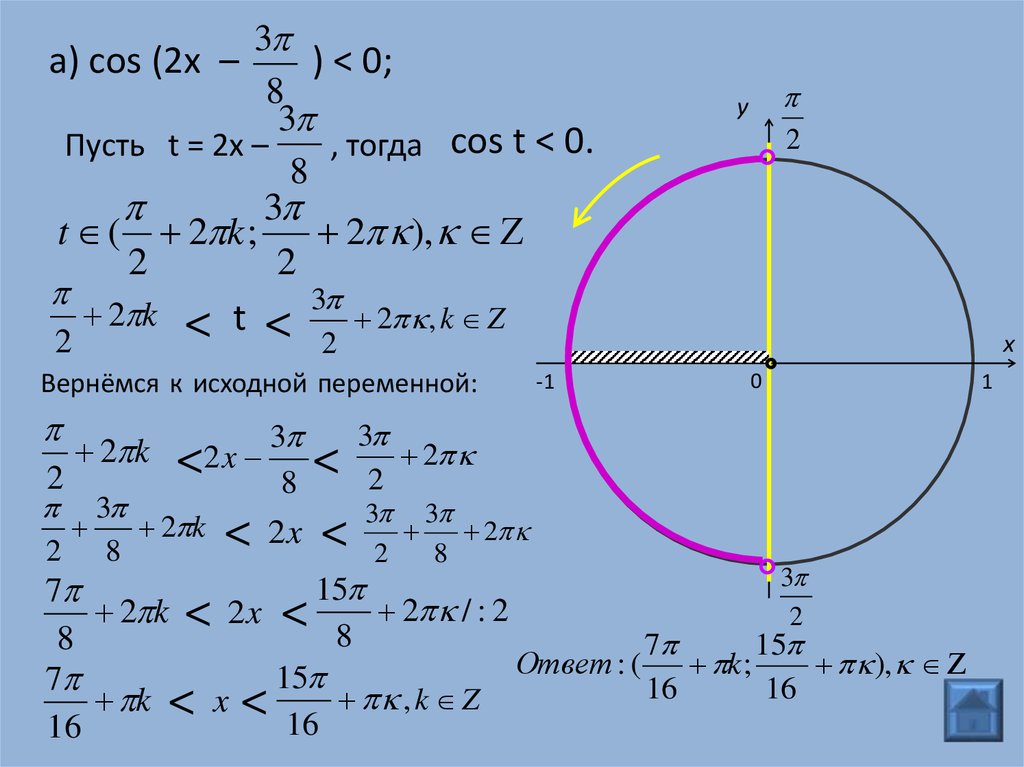 с os x= a , | a |≤1 х = 2. sinx= a , | a | ≤ 1 х= 3. tgx= a х = 4. с tgx= a х = ±arccos a +2 π k (-1) ·arcsin a + π п а rctg a + π k arcctg a + π k
с os x= a , | a |≤1 х = 2. sinx= a , | a | ≤ 1 х= 3. tgx= a х = 4. с tgx= a х = ±arccos a +2 π k (-1) ·arcsin a + π п а rctg a + π k arcctg a + π k
Слайд 7
Реши уравнения базового уровня 1) 2со sx — = 0 2) sin2x =- 3) 2со s ( x — ) = -1 4) tg²x — 6 tg х+5=0 5) (2 sinx – 1)( cos х-1) =0 Проверь ответы: х= ± π /6+2 π k . х= (-1) · (- π /6 ) + π n/2 . 3) х= +2 π k , х= — + 2 π k . х= π /4+ π n , х= arctg5+ π k . х= (-1) · π /6 + π n , х= 2 π k . Если не верно Если верно К слайду 9 К слайду 10
Слайд 8
Решение некоторых уравнений базового уровня со s ( x — ) = -1/2, 3) 2со s ( x — ) = -1, х — = ±arccos (-1/2) +2 π k , х= ± +2 π k , х- = ± +2 π k , х= +2 π k , х= — + 2 π k 4) tg²x — 6 tg х+5=0 Обозначим tg х=а. тогда а ² -6а+5=0 Отсюда а = 5, а = 1 , tg х=5 и tg х=1 х= ar с tg 5 + π k , х= arctg 1 + π k , х= + π k 5) (2 sinx – 1)( cos х-1)=0 Подсказка : произведение равно 0, если…
Слайд 9
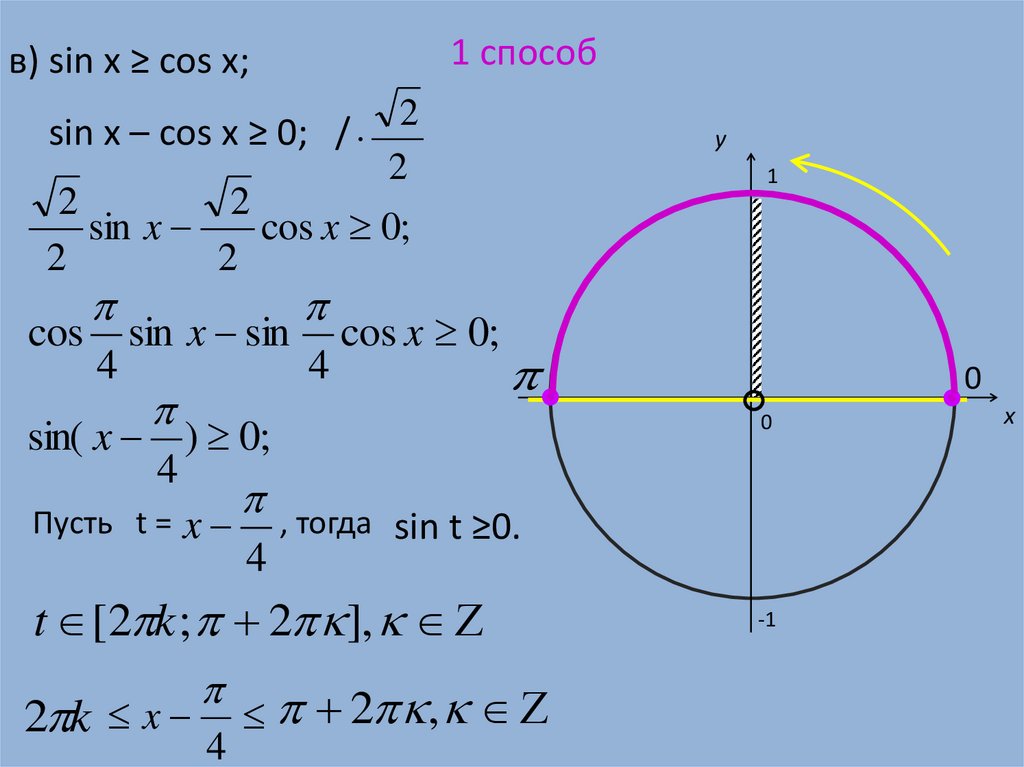
Решение неравенств Реши неравенства: 1 ) cos х > 2) sin х ≥0 3) cos х Проверь ответы: Если не верно Если верно К слайду 11 К слайду 12 1 )- π /6 +2 π k
Слайд 10
Проверь решения неравенств º º 1) cos х > у х 2) sin х ≥0 у х — π /6 +2 π k · º º π /4+ 2 π k
Слайд 11
Реши уравнения повышенного уровня 1.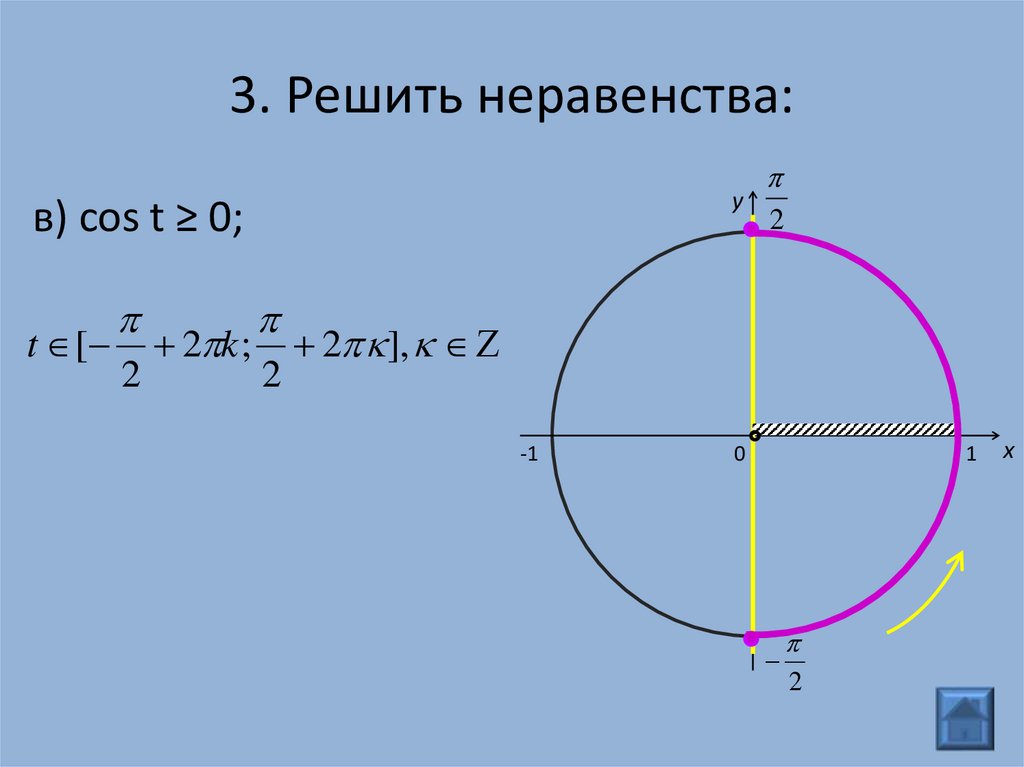 sin5 х = cos5 х 2. sin² х +cos ( π /2- х )sin( π /2- х )-2cos² х =0 3. tg(2 π + х )+ 2 tg( π /2+ х )= -1 Проверь ответы: 1. х = + 2. х= + π k , х= — arctg2+ π k 3. х= + π k , х= — arctg2+ π k Если не верно Если верно К слайду1 3 К слайду 1 4
sin5 х = cos5 х 2. sin² х +cos ( π /2- х )sin( π /2- х )-2cos² х =0 3. tg(2 π + х )+ 2 tg( π /2+ х )= -1 Проверь ответы: 1. х = + 2. х= + π k , х= — arctg2+ π k 3. х= + π k , х= — arctg2+ π k Если не верно Если верно К слайду1 3 К слайду 1 4
Слайд 12
Решение уравнений повышенного уровня 1. sin5 х =cos5 х ( однородное 1-й степени ) Разделим обе части на cos5 х. Получим: tg5x=1 , 5х= arctg1+ π k , 5х= π /4+ π k , х = + 2. sin² х +cos ( π /2- х )sin( π /2- х )-2cos² х =0 (однородное 2-й степени). Упростим левую часть по формулам приведения: sin² х +s in х ·cos х -2cos² х =0 . Разделим обе части на со s²x : tg²x + tgx -2=0, отсюда: tgx =1 и t gx =-2 х= + π k , х= — arctg2+ π k 3. tg(2 π + х )+ 2 tg( π /2+ х )= -1 , tg х- 2/ tg х = -1 . Умножим обе части на tg х, при условии tgx≠ 0.Получим: tg²x- 2 =-tgx , tg²x + tgx -2=0, отсюда: tgx =1, tgx =-2. х= + π k , х= -acrctg2+ π k
Слайд 13
Дополнительно 1. Реши уравнение: 2 sin( -х )= и найди: а) наименьший положительный корень; б) корни, принадлежащие промежутку [ 0 , π ] 2. Реши уравнение: sin² 2 x -3=2 sin2 х cos2x
Реши уравнение: sin² 2 x -3=2 sin2 х cos2x
Слайд 14
Подведение итогов Итак, мы закончили изучение очень важной темы « Тригонометрические уравнения и неравенства». К этой теме мы вернёмся при изучении следующей главы «Преобразование тригонометрических выражений». Сегодня на уроке повторили общие формулы решений простейших тригонометрических уравнений, а также частные формулы. На уроке также были рассмотрены основные виды и способы решения тригонометрических уравнений: разложение на множители; замена переменной; однородные тригонометрические уравнения 1-й и 2-й степени. Если было что-то непонятно, обратись к учителю.
Методы решения тригонометрических уравнений и неравенств
Прежде чем приступить к изучению тригонометрических уравнений, прочтите и узнайте все о радикалах и показателях степени. Не зная об этом всего, вы не будете знать метода решения тригонометрических уравнений и неравенств.
Хорошо, начнем.
Тригонометрические уравнения — это уравнения, имеющие форму $f(x) = a$, где a — действительное число, а $f(x)$ — некоторая тригонометрическая функция.
Каждое тригонометрическое уравнение будет иметь бесконечно много решений, но, поскольку тригонометрические функции являются периодическими, мы можем относительно красиво записать их в виде набора решений.
1. Тригонометрическое уравнение $ cos x = a$, $ \mid a \mid \le 1$
Множество решений B будет: $ B = (\pm x + 2k\pi, k \in \mathbb{Z})$, где x — одно из решений этого уравнения.
Пример 1. : Найдите $ x$ в $ cos(x) = 1$
$ Cos(x) = 1$ говорит нам, что значение косинуса. Это верно только для $ 0 +2 k\pi$. Ничего запоминать не надо, просто нарисуйте единичный круг и сделайте из него вывод.
Пример 2. : Найти $ x$ в $ cos(x) = \frac{1}{2}$
Из этого можно сделать вывод, что существуют два угла, значение синуса которых равно $\frac{1}{2}$. $X$ и $-X$.
Как бы вы его нашли?
Если $ cos(x) = \frac{1}{2}$, это означает, что $ x = Arc Cos(\frac{1}{2})$, и если мы вспомним нашу базовую таблицу тригонометрических значений, то увидим, что x равно $\frac{\pi}{3}$. Теперь мы нашли только одно решение, окончательный набор решений будет:
Теперь мы нашли только одно решение, окончательный набор решений будет:
$ B = ( \pm \frac{\pi}{3} + 2k\pi, k \in \mathbb{Z} )$
2 , Тригонометрическое уравнение $ sin(x) = a$, $ \mid a \mid \le 1$
Множество решений B будет следующим: $ B = ( x + 2k\pi, k \in \mathbb{Z})$ $\bigcup$ $(\pi – x + 2k\pi, k \in \mathbb{Z})$, где $x$ — одно из решений этого уравнения.
Почему эта форма решения. Если вы посмотрите на единичный круг и изучите, для каких углов равны значения синусов, вы заметите, что у вас также есть два угла:
Пример 1: Найдите $ x$ в $sin x = \frac {\ sqrt {2}} {2} $
$ arc sin (\ frac {\ sqrt {2}} {2}) = x $, $ x = \ frac {\ pi} {4} $, это одно решение, которое мы получили. И записать его как целый набор решений:
$ B = (\frac{\pi}{4} + 2k\pi, k \in \mathbb{Z})$ U $(\frac{3 \pi}{4} + 2k\pi, k \ в \mathbb{Z})$
3. Тригонометрические уравнения $ tan x = a$, $ a \epsilon R$
Множество решений B будет $ B = (x + k\pi, k \in \mathbb{Z})$
Пример 1. : решить $ tan x = 1 \rightarrow x = \frac{\pi}{4} \rightarrow B = (\frac{\pi}{4} + k \pi, k \in \mathbb{Z})$
: решить $ tan x = 1 \rightarrow x = \frac{\pi}{4} \rightarrow B = (\frac{\pi}{4} + k \pi, k \in \mathbb{Z})$
4. Тригонометрические уравнения $ cot x = a$, $ a \in \mathbb{R}$
Множество решений B будет $ B = ( x + k\pi , k \in \mathbb{Z} )$
У каждого тригонометрического уравнения есть один метод, который лучше всего подходит для нахождения решения. Чтобы знать, какой метод использовать, вам нужно узнать о каждом методе, а затем решить, какой из них вы будете использовать для конкретного уравнения.
Метод решения тригонометрических уравнений с использованием подстановки
Когда аргумент любой тригонометрической функции больше, чем просто неизвестное, мы можем подставить это выражение целиком. Когда мы находим значения для нашей замены, мы возвращаемся к исходной замене и находим наш главный угол.
Сначала кое-что простое:
$ sin(2x) = 1$. Здесь мы пытаемся в основном не найти угол, значение синуса которого равно 1, а найти x.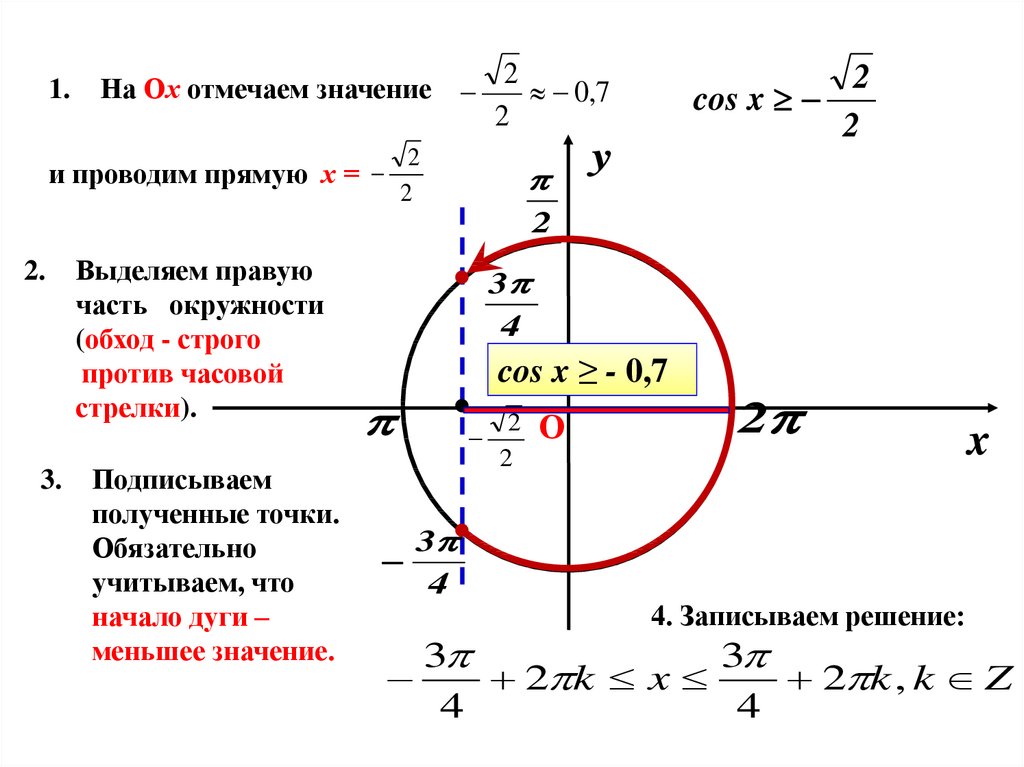
Замена должна помочь нам, упростив эту задачу до чего-то, что мы знаем, как решить, например, $ sin t = 1$. Это означает, что мы будем использовать замену $ t = 2x$.
Теперь у нас есть совершенно новое уравнение:
$ Sin t = 1 \rightarrow t = Arcsin(1)$. Это табличное значение, отсюда $ t = \frac{\pi}{2}$. Если вы не уверены в своих знаниях решения табличных значений, вы можете проверить это на своих калькуляторах. Чтобы добраться до дуги синуса, вы должны нажать SHIFT, а затем sin и ввести значение. Значение должно быть равно полученному углу. Если вы хотите перевести его в радианы, вам придется разделить на π. Когда вы вычислите $ arcsin(1)$, вы получите 1,5707, а когда вы разделите это на $ \pi$, вы получите $\frac{\pi}{2}$, просто убедитесь, что ваш калькулятор настроен на радианы. Если вам проще сначала считать в градусах, то можно, но потом проще считать в радианах (мы научились переводить градусы в радианы и наоборот в отрезки и углы).
Решения для уравнений $sin t = 1$ будем обозначать знаком $B_t$, а для $sin(2x) = 1$ знаком $B_x$.
Опять же, решение не только в этом одном угле, но и в наборе.
$ B_t = ( \frac{\pi}{2} + 2k\pi, k \in \mathbb{Z}) \bigcup (\pi – \frac{\pi}{2} + 2k\pi, k \in \mathbb{Z})$$ = ( \frac{\pi}{2}+ 2k\pi, k \in \mathbb{Z})$ $\bigcup$ $(\frac{\pi}{2 } + 2k\pi, k \in \mathbb{Z})$
Эти два множества совпадают, поэтому мы можем написать только $ B_t = ( \frac{\pi}{2} + 2k\pi, k \in \mathbb{Z} )$.
Мы еще не закончили. Не забывайте, что вы ищете. Нам нужно найти x и окончательный набор решений.
$ 2 B_x = B_t$, теперь каждое слагаемое в $B_t$ нужно разделить на 2.
$ B_x = ( \frac{\pi}{4} + \frac{k\pi}{2}, k \in \mathbb{Z})$, что является нашим окончательным решением.
Преобразование тригонометрических уравнений в полиномиальные
Форма $P(f(x))$, где P — полином, а $f(x)$ — тригонометрическая функция.
Задачи такого рода решаются с помощью подстановки и превращения нашего уравнения в известный нам многочлен. Будьте осторожны, такие замены можно использовать только в том случае, если в вашем уравнении используется только один тип тригонометрической функции: синус, косинус, тангенс или котангенс. 92 – 3t + 1 = 0$ и мы получили уравнение, которое умеем решать.
92 – 3t + 1 = 0$ и мы получили уравнение, которое умеем решать.
Мы получили два решения для t и теперь вернемся к подстановке:
Для $ x_1 = 1$:
$ t = sin(x) \rightarrow sin(x) = 1$
$ B_1 = (\frac{\pi}{2} + 2k\pi, k \in \mathbb{Z} )$.
А для $ x_2 = \frac{1}{2}$
$ t = sin(x) -> sin(x) = \frac{1}{2}$
$ B_2 = (\frac{ \pi}{6}+ 2k\pi) U (\frac{5 \pi}{6}+ 2k\pi)$
Окончательное решение $ B_1 U B_2$:
$( \frac{\pi}{2} + 2k\pi, k \in \mathbb{Z}) \bigcup (\frac{\pi}{6} + 2k\pi) U (\frac{5 \pi}{6}+ 2k\pi)$.
Преобразование тригонометрических уравнений к sin(x) + b cos(x) = c (универсальная замена)
До сих пор в каждом уравнении была только одна тригонометрическая функция, и это было просто, мы использовали простую замену и получали наше решение. Теперь мы не можем использовать эту замену, потому что x связан с другими функциями.
Мы знаем, что синус и косинус могут быть связаны одной функцией — тангенсом tan $ x = \frac{sin x}{cos x}$, и мы можем использовать это, чтобы получить только одну функцию для нашей подстановки. 2 = 0 \rightarrow t = \frac{1 {3}$
2 = 0 \rightarrow t = \frac{1 {3}$
И вернемся к нашей подстановке:
$ B = (0,105\pi +2k\pi : k \in \mathbb{Z})$
Мы получим два значения для t, подставим их оба в подстановку и объединим решения.
Метод решения систем тригонометрических уравнений
Система тригонометрических уравнений – это любая система уравнений, в которой хотя бы одно из них является тригонометрическим.
Решение этих уравнений обычно основано на тригонометрических тождествах или простой настройке.
Пример: решить систему $ sin(x)sin(y) = 1$, $cos(y)cos(x) = 0$
Если мы сложим эти два уравнения, то получим $ sin(x)sin( y) + cos(y)cos(x) = 1$
И это выглядит знакомо. Здесь мы можем использовать нашу формулу сложения $ sinx siny + уютный уютный = cos (x – y)$
Что приводит нас к $ cos(x – y) = 1 \rightarrow x – y = arc cos1 \rightarrow x – y = 0 + 2k\pi$
Если вычесть эти два уравнения, мы получим $ sinx \cdot sin(y) – cos(y) \cdot cos(y) = 1$, но это не какое-либо тригонометрическое тождество. Мы знаем, что $ cos(x + y) = cos(x)cos(y) – sin(x)sin(y)$, чтобы получить это, мы умножим это уравнение на – 1 и получим $ cos (x + y) = -1 \rightarrow x + y = arccos(-1) \rightarrow x + y = \pi + 2n\pi$.
Мы знаем, что $ cos(x + y) = cos(x)cos(y) – sin(x)sin(y)$, чтобы получить это, мы умножим это уравнение на – 1 и получим $ cos (x + y) = -1 \rightarrow x + y = arccos(-1) \rightarrow x + y = \pi + 2n\pi$.
Мы получили другую систему: $ x + y = \pi + 2n\pi$, $ x – y = 2k\pi$
если сложить эти два вместе: $ 2x = \pi + 2n\pi + 2k\ pi \rightarrow x = \frac{\pi}{2} + (n + k)\pi \rightarrow \frac{\pi}{2} + (n + k)\pi + y = \pi + 2n\pi $
$ y = \frac{\pi}{2} + 2n\pi – n\pi – k\pi \rightarrow y = \frac{\pi}{2} + (n – k)\pi$
Это очень простой пример системы тригонометрических уравнений, но все остальные системы решаются аналогично. Единственная сложность, которая может возникнуть, заключается в том, что для каждого уравнения, которое у вас есть, у вас есть 2 значения (положительное и отрицательное), которые дадут вам четыре решения для одной переменной.
Например, если мы получили:
Теперь вы’ Получим четыре системы линейных уравнений.
$ x – y = \frac{\pi}{6}$ и $ x + y = \frac{\pi}{2}$
$ x – y = -\frac{\pi}{6} $ и $ x + y = \frac{\pi}{2}$
$ x – y = \frac{\pi}{6}$ и $ x + y = -\frac{\pi}{2} $
$ x – y = -\frac{\pi}{6}$ и $ x + y = -\frac{\pi}{2}$, просто решите их, и вы получите четыре решения для x , и четыре для y.
Тригонометрические неравенства
Каждое тригонометрическое неравенство решается сначала решением его тригонометрического уравнения и выводом из единичной окружности. Как и в любом другом неравенстве, у нас будет один или несколько интервалов для решения.
Пример 1. Решить неравенство $ cos(x) \le \frac{1}{2}$
Первый шаг – решить уравнение $ cos(x) = \frac{1}{2}$, чтобы получить до концов нашего интервала.
Это $ B = (\pm \frac{\pi}{3} + 2k\pi, k \in \mathbb{Z})$.
Начертите единичную окружность и обозначьте углы $\frac{\pi}{3}$ и $ -\frac{\pi}{3} = \frac{5 \pi}{3}$.
Вы хотите найти все углы, значение косинуса которых меньше или равно $\frac{1}{2}$. Это означает, что мы идем по единичной окружности влево от точки $\frac{\pi}{3}$ и переходим к $\frac{5 \pi}{3}$. И мы берем все эти углы, потому что их значение косинуса меньше $\frac{1}{2}$. Если мы продолжим от $\frac{5\pi}{3}$ до $\frac{\pi}{3}$, их значение косинуса будет больше, чем $\frac{1}{2}$. Это означает, что нашим единственным решением будет $ [\frac{\pi}{3}, \frac{5 \pi}{3}]$.
Это означает, что мы идем по единичной окружности влево от точки $\frac{\pi}{3}$ и переходим к $\frac{5 \pi}{3}$. И мы берем все эти углы, потому что их значение косинуса меньше $\frac{1}{2}$. Если мы продолжим от $\frac{5\pi}{3}$ до $\frac{\pi}{3}$, их значение косинуса будет больше, чем $\frac{1}{2}$. Это означает, что нашим единственным решением будет $ [\frac{\pi}{3}, \frac{5 \pi}{3}]$.
Но так как это будет справедливо и для других углов, удаленных от них на всю окружность.
Это приводит нас к окончательному решению frac{5\pi}{3} + 2k\pi]$.
Это означает только то, что мы объединяем все сегменты с этим свойством.
Пример 2 :
Решить неравенство $ tan(x) \le 1$
Первый $ tan x = 1$: решения на первом круге: $\frac{\pi}{4} + k\pi$ и $\frac{\pi}{2} + k\pi$.
Теперь ищем все углы, значение тангенса которых меньше или равно 1. Это углы от 0 до $\frac{\pi}{4}$ и от $\pi$ до $\frac {5 \pi}{4}$. Это приводит нас к окончательному решению:
Это приводит нас к окончательному решению:
Таблицы тригонометрических уравнений и неравенств
Найдите недостающую сторону x (230,6 КиБ, 821 совпадение)
Найдите площадь треугольника (272,8 КиБ, 727 совпадений)
Тригонометрические уравнения (184,3 КиБ, 1169 совпадений)
Тригонометрические уравнения и неравенства
Обучающие цели
Распространить процесс обратных операций на тригонометрические уравнения и неравенства.
Поймите, что использование единичного круга даст бесконечные решения тригонометрического уравнения, которые, возможно, придется ограничить в зависимости от контекста, и что обратная тригонометрическая функция дает только одно решение, которое, возможно, потребуется расширить с помощью симметрии.
Краткий план урока
Первый опыт:
Сегодня мы вернемся к контексту урока 6. 7, где учащиеся построили модель температуры снаружи дома Кариссы. Сегодня учащиеся получают модель и должны найти моменты, когда температура достигает определенного значения. По сути, они решают триггерные уравнения.
7, где учащиеся построили модель температуры снаружи дома Кариссы. Сегодня учащиеся получают модель и должны найти моменты, когда температура достигает определенного значения. По сути, они решают триггерные уравнения.
Как всегда, мы хотим подчеркнуть множественность представлений и разную степень точности. К вопросу 1 можно подойти с интуитивной точки зрения (температура начинается с минимального значения, максимальное должно произойти в середине цикла) или аналитического (максимальное значение F достигается, когда cos(πt/12)=-1) подхода.
Теперь мы представляем интуитивный подход к решению уравнений, который выходит за рамки простого «действия наоборот». Сначала учащиеся используют график для оценки решений, что затем также позволяет им проверить обоснованность своих аналитических решений. Затем учащиеся обдумывают выражение для F(t) по частям и изолируют влияние переменной t. Другими словами, если F(t)=75˚, каким должно быть выражение 10cos(πt/12), чтобы при вычитании его из 80 я получил 75? Каким же тогда должно быть выражение cos(πt/12)? Вопрос 3d может быть сложным для учащихся, потому что они должны думать о πt/12 как об одной величине, представляющей угол. Может быть полезно использовать изображение или символ, например, маленькую черную коробку, для представления πt/12. Накладывая это на уравнение, учащиеся могут сначала выяснить, какой должна быть «коробка», а затем определить значение t.
Может быть полезно использовать изображение или символ, например, маленькую черную коробку, для представления πt/12. Накладывая это на уравнение, учащиеся могут сначала выяснить, какой должна быть «коробка», а затем определить значение t.
В вопросе 3 значения представляют собой целые числа, и их можно найти с помощью единичного круга. В вопросах 4–8 учащиеся должны вычислить обратную триггерную функцию с помощью своего калькулятора. На основе вчерашнего урока учащиеся должны понять, почему калькулятор выдает только одно значение. В ключе для ответов вы заметите, что поиск другого угла является примечанием на полях, потому что учащиеся могут или не могут добраться туда самостоятельно. Однако учащиеся должны понимать, что им не хватает решения, поскольку на графике есть две точки пересечения. При разборе аналитических ответов обязательно подчеркните, что учащиеся могут проверить обоснованность своих ответов, сравнив свои решения со своими оценками в вопросе 4. Поскольку t=7,16 очень близко к t=7, а t=16,84 близко к t=17 решения кажутся разумными.
Контрольные вопросы:
Сколько раз температура будет ровно 83°, согласно этой модели?
Предположим, что ввод — это «ящик». Какой должна быть коробка?
(Вопрос 7) Можно ли найти это значение, используя круг единиц измерения?
Почему ваш калькулятор дает вам только одно значение, когда мы видим, что есть два решения?
Где еще cos(theta)=-0,3? Как наличие одного решения помогает найти другое?
Формализовать Позже:
В этом уроке учащиеся должны понять, что решение тригонометрического уравнения ничем не отличается от решения любого другого уравнения; это требует выделения влияния независимой переменной. Мы рекомендуем вам избегать таких выражений, как «перейти на другую сторону» и «получить х само по себе», поскольку они иногда могут скрыть математическую концепцию отмены уравнения и точного определения эффекта одной переменной.