Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375581 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Наталья Борисовна Карасева
«
Мы восторге от репетитора. Наталья Борисовна грамотный педагог, она любит свою профессию, любит учеников. Занятия с сыном (2 класс), он находится на домашнем обучении, проходят по скайпу в комфортной обстановке. Репетитор умеет заинтересовать ребенка и выстраивает занятие с учетом его способностей, доступно объясняя предметы русский язык и математику.
По результатам занятий можно сразу заметить повышение уровня успеваемости ученика. Наталья Борисовна хороший педагог, умеет быстро найти общий язык с ребенком, внимательная, легко передающая знания ученику. С большим удовольствием будем продолжать наши занятия, т.к. мы всем довольны.
«
Елена Васильевна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
RU
«Решение тригонометрических уравнений, сводящихся к квадратным». 11-й класс
Цели и задачи урока.- Образовательные:
- повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения
- сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к квадратным.
- уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к квадратным и решать их.
- Развивающие:
- развивать логическое мышление учащихся, память,
внимание, речь; умения рассуждать и выделять
главное; умение самостоятельно приобретать
знания и применять их на практике, развивать
навыки самоконтроля и взаимоконтроля.
- развивать логическое мышление учащихся, память,
внимание, речь; умения рассуждать и выделять
главное; умение самостоятельно приобретать
знания и применять их на практике, развивать
навыки самоконтроля и взаимоконтроля.
- Воспитательные:
- воспитывать уважительное отношение к одноклассникам, самостоятельность, ответственность, эстетический вкус, аккуратность, интерес к математике.
Оборудование: мультимедийный проектор, экран, лист самооценки.
Организационные формы общения: фронтальная, групповая, индивидуальная.
Тип урока: усвоения новых знаний.
Образовательные технологии: ИКТ, проектная.
План урока.
- Организационный момент, формирование мотивации работы учащихся.
- Формулирование темы, цели урока.
- Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала.
- Этап усвоения новых знаний и способов действий.
- Этап активной релаксации и активизации.
- Этап первичной проверки понимания изученного.
- Этап рефлексии и оценивания. Подведение итогов урока.
- Этап информирования учащихся о домашнем задании, инструктаж по его выполнению.
Подготовительная работа
Учащихся класса необходимо заранее поделить на
группы. Принцип деления учащихся на группы
учитель вправе выбрать самостоятельно.
Один из вариантов – группы, в которые вошли бы
учащиеся с разным уровнем математической
подготовки: от «базового» до «продвинутого».
Каждая группа предварительно получает задание
изучить алгоритм решения одного из типов
тригонометрических уравнений (используются
предложенные учителем источники информации и
самостоятельно найденные). Результаты своей
работы члены каждой группы представляют на одном
из уроков по теме «Тригонометрические
уравнения». В зависимости от объёма
предлагаемого материала и его сложности одном
уроке могут успеть выступить 1-2 группы,
представив результаты своей работы.
Предлагаем вашему вниманию урок, на котором рассматривается решение тригонометрических уравнений, сводящихся к квадратным.
Из дома реальности легко забрести в лес математики, но лишь немногие способны вернуться обратно.
Х. Штейнхаус
Чем больше человек будет становиться человеком, тем меньше он согласится на что-либо иное, кроме бесконечного и неистребимого движения к новому.
Пьер Шарден
ХОД УРОКА
1. Организационный момент, формирование мотивации работы учащихся (3 мин.)
Приветствие. Фиксация отсутствующих, проверка
готовности учащихся к уроку. Далее каждому
ученику выдаётся оценочный лист. Учитель
кратко комментирует правила заполнения
оценочного листа и предлагает заполнить 1-3
строки. Приложение 1.
Организация внимания учащихся: учитель цитирует
учащимся Пьера Шардена, предлагает пояснить, как
они поняли смысл слов (можно выслушать 2-3
человека), предлагает сделать слова девизом
урока и интересуется, знают ли они, кто является
их автором.
Краткая историческая справка
(Слайд 3).
*Инструкция по использованию Презентации – Приложение 2.
2. Формулирование темы, цели урока
Учитель просит сформулировать тему
предыдущего урока (Решение простейших
тригонометрических уравнений). Интересуется у
учащихся, как они думают, существуют ли другие
типы тригонометрических уравнений? (Да. Если есть
«простейшие», то значит, есть более сложные,
иначе нет необходимости вводить термин
«простейшие», если это единственный тип
тригонометрических уравнений). Исходя из выше
сказанного, предлагает сформулировать тему
сегодняшнего урока (Решение
сложных/других/различных типов
тригонометрических уравнений).
После корректировки темы, предлагает учащимся
записать в их тетрадях: дату проведения урока,
фразу «Классная работа» и тему урока «Решение
различных типов тригонометрических уравнений:
уравнения, сводящиеся к квадратным».
На столе у каждого из учащихся находятся шаблоны
яблок и фломастеры. Предлагается написать на
«яблоках» свои ожидания от предстоящего урока,
тему которого уже сформулировали. После этого
все шаблоны яблок прикрепляются, например, с
помощью скотча на заранее приготовленный плакат
с изображением дерева. Получается «Дерево
ожиданий».
По мере достижения того или иного ожидания соответствующее яблоко можно считать созревшим и собирать в корзину. Использование этого активного метода обучения – наглядный способ отслеживания продвижения учащихся на уроке. [1]
Возможен другой вариант: учитель ставит песочные часы перед учениками класса и предлагает ответить на вопрос о том, чему они хотят научиться на уроке, тема которого уже сформулирована (достаточно 1-2 варианта).
3. Актуализация знаний и подготовка
учащихся к активному и сознательному усвоению
нового материала (10 мин.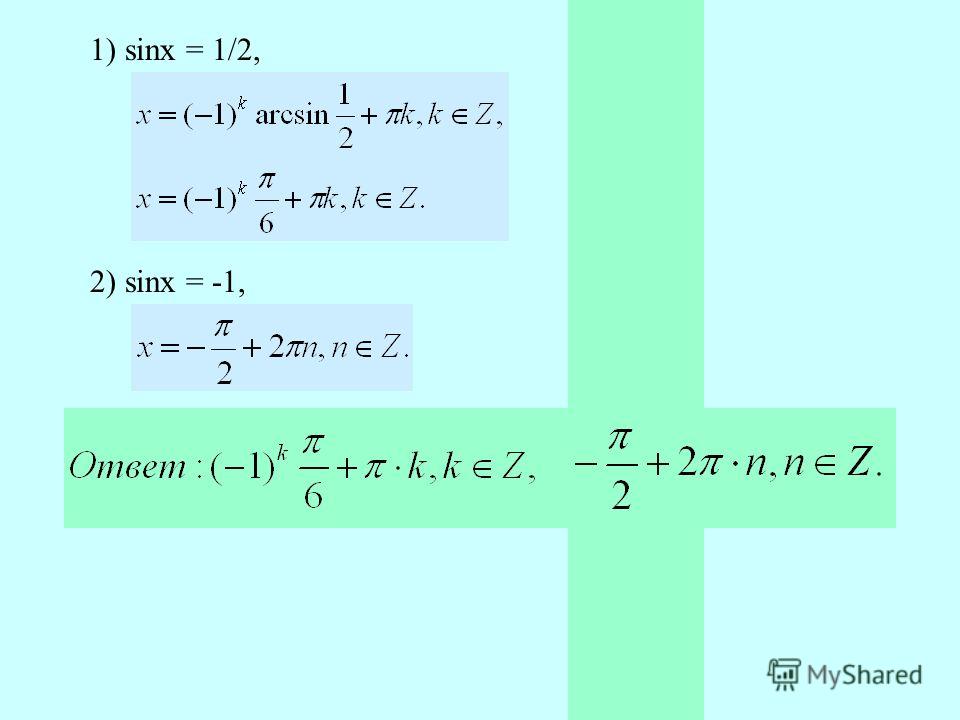
).
Учитель. Герберт Спенсер говорил, что если знания человека в беспорядочном состоянии, то чем больше их у него, тем сильнее расстраивается его мышление. Последуем совету этого известного британского философа (информация для общего развития личности – краткая историческая справка. (Слайд 5) Прежде чем перейти к изучению нового материала, давайте вспомним, что мы знаем из раздела «Тригонометрия».
Фронтальная работа (устно)
– Дайте определение тригонометрического
уравнения.
– Сколько корней может иметь тригонометрическое
уравнение?
– Что такое простейшие тригонометрические
уравнения?
– Что значит решить простейшее
тригонометрическое уравнение?
– Какие способы решения тригонометрических
уравнений вы знаете? (2 варианта: формулы;
единичная окружность).
а) Заполните таблицу:
б) Поставьте в соответствие уравнениям их решения, представленные на единичных окружностях (с комментарием)
Самостоятельная работа (Приложение 3)
С последующей взаимопроверкой/самопроверкой
(правильность ответов проверяется с помощью
презентации) на умение решать простейшие
тригонометрические уравнения.
Демонстрируется
(Слайд 12). При необходимости решения некоторых
уравнений коротко комментируются.
Заполняется пункт №4 Приложения 1.
4. Этап усвоения новых знаний и способов действий (15 мин.).
Учащиеся класса предварительно были поделены
на группы, каждая из которых самостоятельно
рассмотрела, используя материал рекомендуемый
учителем и найденный самостоятельно, один из
типов тригонометрических уравнений.
Результаты работы оформляются в виде некой
рекомендации/алгоритма/схемы решения в формате
презентации Power Point. Учитель в случае
необходимости консультирует учащихся групп и
предварительно проверяет итоговый продукт их
работы.
Для презентации результатов того или иного
способа решения на уроке выбирается один из
представителей группы, остальные на уроке
помогают отвечать на возникающие вопросы по
решению данного типа тригонометрического
уравнения.
Учащиеся заранее знакомятся с
критериями оценивания своей работы в группе.
Мне приходится делить время
между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важней.
Политика существует только для данного момента,
а уравнения будут существовать вечно.
Альберт Эйнштейн
Возможные варианты выполнения задания группой. (Слайды 14-18)
1 группа. Решение тригонометрических уравнений, сводящихся к квадратным.
Отличительные признаки уравнений, сводящихся к квадратным:
1. В уравнении присутствуют тригонометрические
функции от одного аргумента или они легко
сводятся к одному аргументу.
2. В уравнении присутствует только одна
тригонометрическая функция или все функции
можно свести к одной.
Алгоритм решения:
– Используются ниже приведённые тождества; с их помощью необходимо выразить одну тригонометрическую функцию через другую:
– Выполняется подстановка.
– Выполняется преобразование выражения.
– Вводится обозначение (например, sinx = y).
– Решается квадратное уравнение.
– Подставляется значение обозначенной величины,
и решается тригонометрическое уравнение.
Пример 1
6cos2 x + 5 sin x – 7 = 0.
Решение.
Пример 2
Пример 3
Заполняется пункт №5 Приложения 1.
5. Этап активной релаксации и активизации (2 мин.).
Авторы метода: С. Казаков, Ю. Долинова. Приложение 4 (текст), слайды 20-25.
6. Этап первичной проверки понимания изученного (8 мин.)
Самостоятельная работа (Приложение 5)
Работа дифференцированная, каждый уровень
сложности заданий представлен в двух вариантах.
I уровень – «3», II уровень – «4», III уровень – «5» в
случае полного правильного решения. Работа будет
проверена учителем к следующему уроку, отметки
будут выставлены за урок.
7. Этап рефлексии и оценивания. Подведение итогов урока (2 мин.).
Заполнить пункт №6,7 листа самооценки – Приложение 1.
8. Этап информирования учащихся о домашнем задании, инструктаж по его выполнению (2 мин.).
Дифференцированное (раздаётся каждому ученику на отдельных листах) – Приложение 6
Список литературы:
- Корнилов С.В., Корнилова Л.Э. Методический ларец. – Петрозаводск: ПетроПресс, 2002. – 12 с.
Методы решения тригонометрических уравнений
Методы решения
тригонометрических уравнений
1.
Решение
простейших тригонометрических уравнений
2. Решение тригонометрических уравнений разложением на множители
3. Решение тригонометрических уравнений сводящихся к квадратным уравнениям
4. Решение тригонометрических уравнений преобразованием суммы тригонометрических функций в произведение
5. Решение тригонометрических уравнений преобразованием произведения тригонометрических функций в сумму
6. Решение тригонометрических уравнений с применением формул понижения степени
7. Решение тригонометрических уравнений как однородное
8. Решение тригонометрических уравнений с помощью введения вспомогательного аргумента
9. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки
10.
Решение
тригонометрических уравнений с помощью замены неизвестного
11. Решение тригонометрических уравнений с помощью оценки левой и правой частей уравнения (метод оценок)
12. Решение тригонометрических уравнений содержащих тригонометрические функции под знаком радикала
1. Решение простейших тригонометрических уравнений
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
Ответ:
2. Решение тригонометрических уравнений разложением на множители
или
или решений нет
Отметим полученные решения и
область определения на тригонометрическом круге.
Решением уравнения является:
Ответ:
3. Решение тригонометрических уравнений
сводящихся к квадратным уравнениям
Пусть , тогда
или
Т.к.
при , то корней нет.
Ответ:
4. Решение тригонометрических уравнений преобразованием
суммы тригонометрических функций в произведение
или
Ответ: ;
5. Решение тригонометрических уравнений преобразованием
произведения тригонометрических функций в сумму
а) Найдем область определения
функции.
Областью определения данного уравнения является:
б) Решим данное уравнение.
Ответ:
6. Решение тригонометрических уравнений с
применением формул понижения степени
Пусть , тогда
или
Т.к.
при , то корней нет.
Ответ:
7. Решение тригонометрических уравнений как однородное
Однородное уравнение – это уравнение, в котором каждое слагаемое имеет одну и туже степень.
, где
— действительные числа. — показатель однородности.
Если , то и , что противоречит основному тригонометрическому тождеству, значит . Разделим обе части на , получим
Ответ:
8. Решение тригонометрических уравнений с помощью
введения вспомогательного аргумента
Т. к. , то корни есть.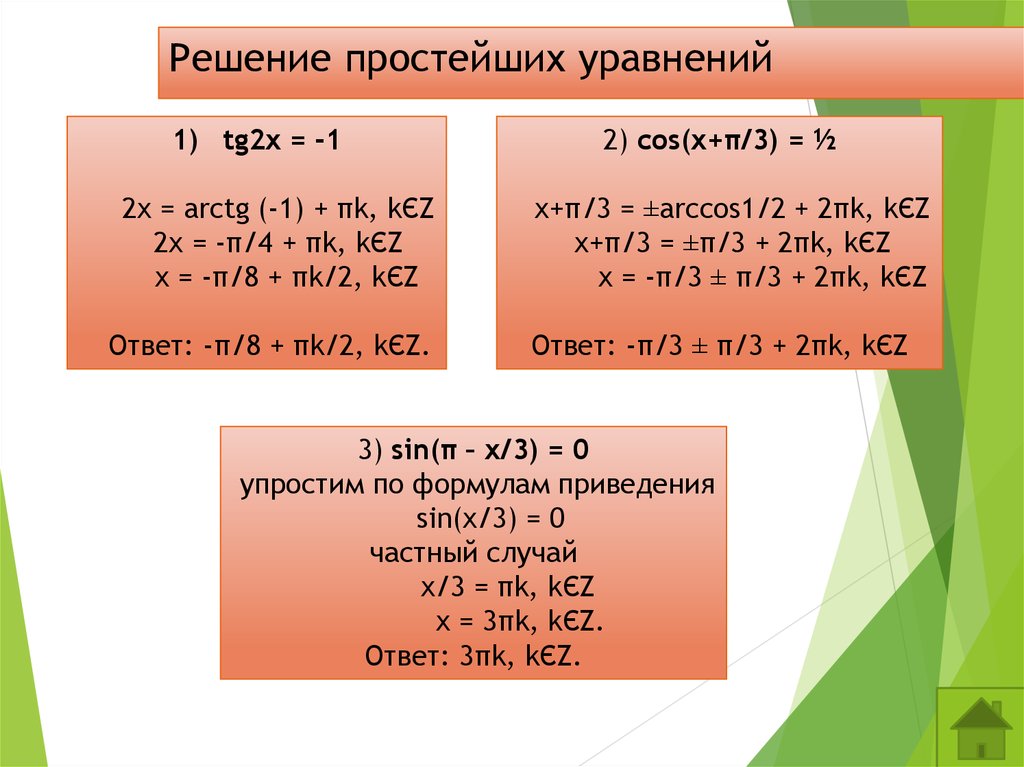
Разделим обе части уравнения на , получим
Т. к. и , то существует такой угол , что , а , тогда получим
Ответ:
Теория.
1) если , то уравнение однородное.
2) если и (то есть хотя бы одно из чисел или не равно 0), то разделим обе части уравнения на , получим
Т. к. и , то существует такой угол , что , тогда
а) если, т. е. , то корней нет.
в) если, т. е. , тогда
Т. к. , то корней нет.
9.
Решение
тригонометрических уравнений с помощью
универсальной тригонометрической подстановки
(1)
(2)
При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения корнями данного уравнения.
Проверка.
Если , тогда
— не верно, значит , не является корнями исходного уравнения.
Ответ:
10. Решение тригонометрических уравнений
с помощью замены неизвестного
Уравнение вида решается следующей заменой , , ,
Способ I
Пусть , , , , получим
или
(3)
Разделим на , получим
Т.
к. , при , то корней нет.
Ответ:
Теория.
, при
Доказательство:
Шесть способов решения уравнения (3).
1. применение формулы .
2. через .
3. привести к однородному уравнению второй степени.
4. способ введения вспомогательного аргумента.
5. с помощью неравенства , при .
6. метод оценки левой и правой частей уравнения.
Способ II
или
Разделим на , получим
Т.
к. , при , то корней нет.
Ответ:
11. Решение тригонометрических уравнений с помощью оценки
левой и правой частей уравнения (метод оценок)
12. Решение тригонометрических уравнений содержащих
тригонометрические функции под знаком радикала
Пример №1
Решим уравнение 2.
или
Отметим поученные решения и условие 1 на тригонометрическом круге.
Ответ: ,
Пример №2
Решим уравнение 2.
Решим квадратное уравнение относительно.
и то корней нет.
Отметим поученные решения и условие 1 на тригонометрическом круге.
Ответ:
7.6 Решение квадратных тригонометрических уравнений
Тригонометрические тождества и уравнения > 7.6 Решение квадратных тригонометрических уравнений
Квадратные тригонометрические уравнения В некоторых случаях тригонометрическое уравнение можно сократить или преобразовать в квадратное уравнение относительно тригонометрической функции. Эти уравнения обычно содержат только тригонометрические функции одного угла или их можно легко преобразовать в одну переменную. Кроме того, в уравнения такого типа входит только одна триггерная функция, либо все функции могут быть сведены к одной функции. 92} — 4 \cdot \left( { — 4} \right) = 25,\;{t_{1,2}} = \frac{{3 \pm \sqrt {25} }}{2} = — 1 ,4.\] Возвращаясь к переменной \(x,\), мы получаем следующие решения: \[\tan x = {t_1} = — 1, \Rightarrow x_1 = \arctan \left( { — 1} \right) + \pi n = — \arctan 1 + \pi n = — \frac{\pi }{4} + \pi n,\;n \in \mathbb{Z};\] \[\tan x = {t_2} = 4, \Rightarrow {x_2} = \arctan 4 + \pi k,\;k \in \mathbb{Z}.\] Ответ: \[{x_1} = — \frac{\pi }{4} + \pi n,\;{x_2} = \arctan 4 + \pi k,\;n,k \in \mathbb{Z}.\ ] 92}х — \sin х = 0.\] У нас есть неполное квадратное уравнение, которое можно решить с помощью разложения. \[\sin x\left( {\sin x — 1} \right) = 0.\] Решение \(1\text{st}\) равно нулю функции синуса: \[\sin x = 0, \Rightarrow {x_1} = \pi n,\;n \in \mathbb{Z}. Решение \(2\text{nd}\) дается числом \[\sin x = 1, \Rightarrow {x_2} = \frac{\pi }{2} + 2\pi k,\;k \in \mathbb{Z}.\] Основные решения уравнения включают следующие значения: 92} + t — 1 = 0, \Rightarrow {t_{1,2}} = \frac{{ — 1 \pm \sqrt 9 }}{4} = — 1,\frac{1}{2}.\ ] Первое значение \({t_1} = -1\) дает следующее решение: \[\cos 2x = {t_1} = — 1, \Rightarrow 2x = \pi + 2\pi n, \Rightarrow {x_1} = \frac{\pi }{2} + \pi n,\;n \ в \mathbb{Z}.\] Корень \({t_2} = \frac{1}{2}\) определяет другой набор решений: \[\cos 2x = {t_2} = \frac{1}{2}, \Rightarrow 2x = \pm \arccos \frac{1}{2} + 2\pi k = \pm \frac{\pi } {3} + 2\pi k, \Rightarrow {x_2} = \pm \frac{\pi }{6} + \pi k,\;k \in \mathbb{Z}.\] Следовательно, ответ равен .\[{x_1} = \frac{\pi }{2} + \pi n,\;{x_2} = \pm \frac{\pi }{6} + \pi k,\;n,k \in \mathbb{Z}.\] Пример 4.Решить уравнение \[\tan x + \cot x = 2.\] Раствор. Это уравнение включает функции тангенса и котангенса, которые имеют точки разрыва. Поэтому сначала рассмотрим область определения этого уравнения: \[\left\{ \begin{массив}{l} \cos х \ne 0\\ \sin х \ne 0 \end{массив} \right., \Rightarrow \left\{ \begin{массив}{l} х \ ne \ frac {\ pi } {2} + \ pi n \\ х \ne \pi n \end{array} \right., \Rightarrow x \ne \frac{{\pi n}}{2},\;n \in \mathbb{Z}.\] 92}2x = {t_2} = \frac{1}{4}, \Rightarrow \cos 2x = \pm \frac{1}{2}.\] У нас есть два основных уравнения: \[\cos 2x = \frac{1}{2}, \Rightarrow 2x = \pm \arccos \frac{1}{2} + 2\pi n = \pm \frac{\pi }{3} + 2\pi n, \Rightarrow {x_1} = \pm \frac{\pi }{6} + \pi n,\;n \in \mathbb{Z}.\] \[\cos 2x = — \frac{1}{2}, \Rightarrow 2x = \pm \arccos \left( { — \frac{1}{2}} \right) + 2\pi k = \pm \left( {\pi — \arccos \frac{1}{2}} \right) + 2\pi k = \pm \frac{{2\pi}}}{3} + 2\pi k, \Rightarrow { x_2} = \pm \frac{\pi }{3} + \pi k,\;k \in \mathbb{Z}.\] 92}2x = {t_1} = \frac{3}{4}, \Rightarrow \cos 2x = \pm \frac{{\sqrt 3}}{2}, \Rightarrow 2x = \pm \arccos \left( { \pm \frac{{\sqrt 3}}{2}} \right) + 2\pi n,\;n \in \mathbb{Z}. Это выражение содержит два семейства решений. В первом случае имеем \[2x = \pm \arccos \frac{{\sqrt 3}}{2} + 2\pi n = \pm \frac{\pi }{6} + 2\pi n, \Rightarrow {x_1} = \pm \frac{\pi }{{12}} + \pi n,\;n \in \mathbb{Z}.\] Второе семейство решений задается \[2x = \pm \arccos \left( { — \frac{{\sqrt 3}}{2}} \right) + 2\pi k = \pm \left( {\pi — \arccos \frac{ {\sqrt 3}}{2}} \right) + 2\pi k = \pm \frac{{5\pi}}{6} + 2\pi k, \Rightarrow {x_2} = \pm \frac{ {5\pi }}{{12}} + \pi k,\;k \in \mathbb{Z}.\] Рисунок 2.Мы можем объединить оба этих множества и описать их одной формулой: \[x = \pm \frac{\pi }{{12}} + \frac{{\pi n}}{2} = \frac{\pi }{{12}}\left( {6n \pm 1} \right),\;n \in \mathbb{Z}.\] 92}x = 1, \Rightarrow \tan x = \pm 1, \Rightarrow {x_{1,2}} = \arctan \left( { \pm 1} \right) + \pi n = \pm \frac{ \pi }{4} + \pi n,\;n \in \mathbb{Z}.\]Мы можем описать оба этих решения одной формулой \[x = \frac{\pi }{4} + \frac{{\pi n}}{2},\;n \in \mathbb{Z}. Квадратичная формула с тригонометрией — ТригонометрияВсе ресурсы по тригонометрии6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Учитесь по концепции ← Предыдущая 1 2 3 Следующая → Справка по тригонометрии » Тригонометрические уравнения » Решение тригонометрических уравнений » Квадратичная формула с тригонометрией Решите следующее уравнение для . Возможные ответы: Решения не существует Объяснение: ; Используйте тождество двойного угла для косинуса. ; Переместите все в левую часть уравнения. ; Это квадратичное выражение, которое нельзя разложить на множители. Мы должны использовать квадратичную формулу. Это может быть полезно, если заменить на , чтобы получилось:
Вспомните квадратную формулу подключите . Теперь у нас есть ; Разделите это на два уравнения и возьмите арксинус. или Первое уравнение дает нам . Используя единичный круг, как мы это делали в предыдущих задачах, мы можем найти второй ответ, который равен . Второе уравнение не даст нам решения. Сообщить об ошибке Каковы нули вышеперечисленной функции для интервала . Возможные ответы: Правильный ответ: Объяснение: Когда к функции применяется квадратичная формула, она дает Итак, это нули для синуса, но синус имеет минимум -1, поэтому -2 отсутствует. Для -1/2 синус достигает этого дважды за цикл, при π+π/6 и 2π-π/6. Таким образом, хотя -π/6 верно, это неверно, поскольку оно не находится в данном интервале. Therefore on the given interval the zeros are: Report an Error Solve the following trigonometric equation: for Possible Answers: The equation does not есть решение. Правильный ответ: Пояснение: Поскольку можно записать как: . Мы не можем иметь. Поэтому . Это означает, что где k — целое число. с . Имеем x=0 — единственное число, удовлетворяющее этому свойству. Сообщить об ошибке Решить каждое уравнение в домене (ответ в градусах). Возможные ответы: Правильный ответ: Объяснение: Переставьте задачу, В интервале от 0 до 360 градусов cosx = 1/2 при 60 градусах и 300 градусах. Сообщить об ошибке Решить уравнение на интервале Объяснение: Сначала составим уравнение в терминах одной триггерной функции. Мы можем сделать это, заменив на Пифагорейское тождество . Тогда у нас есть . Сложите все термины в одну сторону, чтобы найти . Мы можем разложить это квадратичное число на . Это означает, что . Единственным значением угла, для которого это верно, является . Отчет о ошибке Решайте, предоставив ваш ответ в качестве положительного угла меры: Возможные ответы: Нет решения  w3.org/1999/xhtml» cellspacing=»0″> |
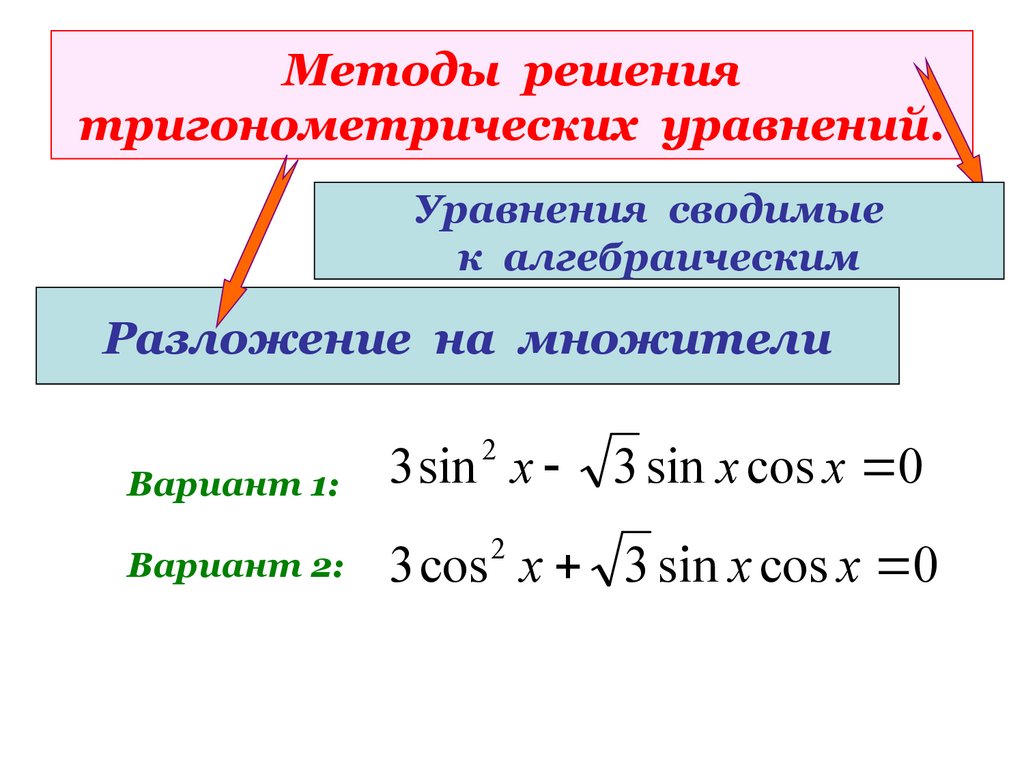
0 или tan x +1=0
В случаях, когда уравнение
нельзя разложить на множители, используйте формулу квадратного уравнения, а затем решите полученное
линейные тригонометрические уравнения.
com/embed/HHFtLmRXceg?rel=0&wmode=opaque» frameborder=»0″ allowfullscreen=»true»> 
\]
\]
\]
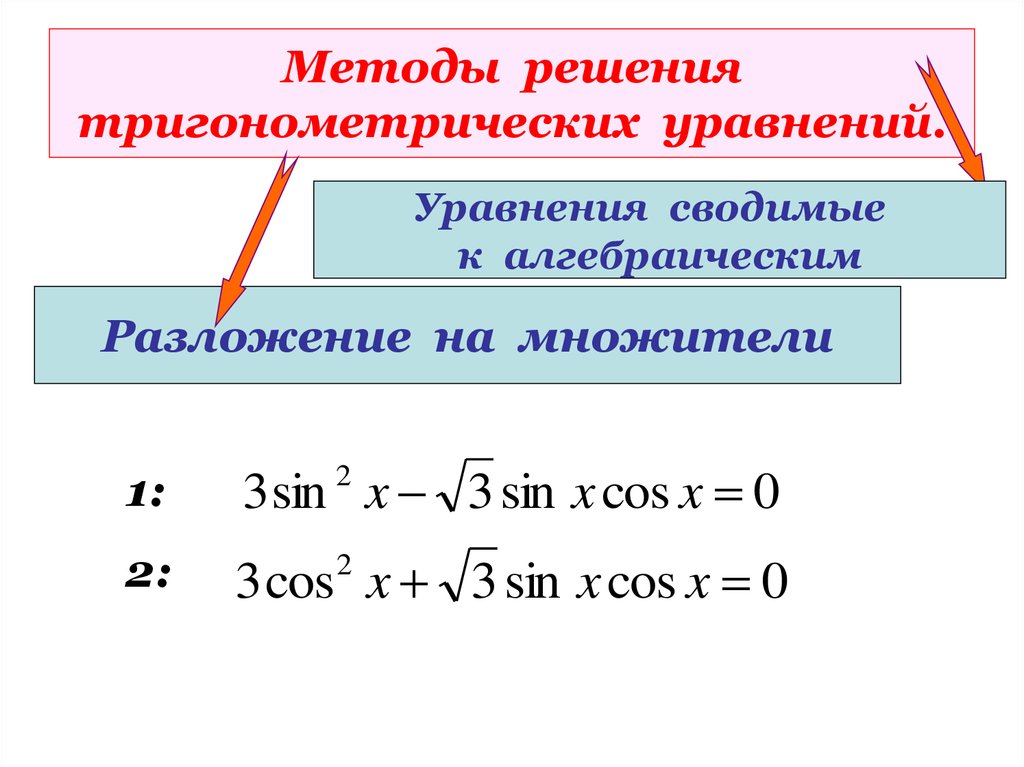
В этом случае коэффициенты a, b и c равны a=4, b=1 и c=-1: