VI.2. Вычисление тройного интеграла — МАТЕМАТИКА для обучающихся в агротехнологических вузах
(схема 41) Для функции трех переменных имеет место обобщение определенного интеграла — тройной интеграл (также кратный интеграл). Его теория аналогична теории двойного интеграла. Пусть непрерывная функция u=f (x,y,z) задана в некоторой ограниченной замкнутой пространственной области V (рис. 6.4). Разобьем эту область на пространственные ячейки . В каждой ячейке выберем произвольную точку и умножим значение функции f в этой точке на объем ∆νi ячейки Vi. Сумма таких произведений по всем ячейкам называется интегральной суммой. Обозначим через d(Vi) диаметр ячейки Vi, то есть расстояние между наиболее удаленными точками этой ячейки, и max  Тройным интегралом от функции f(M) по области V называется предел интегральной суммы при условии max d(Vi)→0, то есть при неограниченном увеличении числа ячеек, когда все ячейки стягиваются в точку: . Если такой предел существует, то функция f(M) называется интегрируемой в области V; всякая непрерывная в ограниченной замкнутой области V функция f(M) интегрируема в ней. В дальнейшем мы будем рассматривать только непрерывные функции. В декартовых координатах элемент объема обычно записывают в виде dν=dxdydz, а тройной интеграл обозначают . (6. 9) 9)Тройной интеграл (6.9) выражает массу неоднородного тела объема V, с плотностью в каждой точке γ=f (x,y,z) посредством формулы: . (6.10) Координаты центра тяжести тела вычисляются по формулам: . (6.11) Если плотность γ=1, то тройной интеграл (6.9) будет выражать собой объем области
1. Вычисление тройного интеграла в декартовой системе координат Пусть V проектируется в область D на плоскости x0y так, что всякая прямая, параллельная оси 0z и
проходящая внутри области D, пересекает границу области V ровно в
двух точках. . (6.12) Здесь
внутренний интеграл берется по z при фиксированных, но
произвольных в D значениях x и y, от нижней границы области V до ее
верхней границы, то есть по отрезку KL (рис. Наиболее простой вид формула (6.12) принимает в случае, когда V есть прямоугольный параллелепипед, ограниченный плоскостями : . (6.13) Если область V имеет более сложную форму, то ее разбивают на конечное число областей , каждая из которых удовлетворяет условиям, изложенным выше. Примечание. Аналогичные определения и формулы могут быть получены и тогда, когда область V проектируется в область D, лежащую или в плоскости x0z, или в плоскости y0z Пример 6.4. Вычислить тройной интеграл , где область V ограничена координатными плоскостями и плоскостью x+y+z=1 (рис. Решение. Область V – треугольная пирамида – ограничена снизу плоскостью z=0, сверху – плоскостью z=1–x–y. Область V проектируется на плоскость x0y в виде прямоугольного треугольника, который определяется неравенствами . Следовательно, используя (6.5) и (6.12), получим: Пример 6.5. Найти объём тела ограниченного параболоидом z=x2+y2+2 и плоскостями z=1, x=0, y=0, x+y=2 (рис. 6.6).
Решение. По условию область V задана неравенствами: . Следовательно,
(единиц объема) Пример 6.6.  Решение. По условию область V совпадает с той областью, которая была рассмотрена в примере 6.4 (см. рис. 6.5). Искомая масса M согласно формуле (6.11) равна интегралу . Следовательно, . Чтобы вычислить полученный интеграл, положим 1–x=t; тогда dx= – dt; при этом t=1 при x=0 и t=0 при x=1. (единиц массы) Пример 6.7. Вычислить координаты центра тяжести куба , если плотность в каждой его точке равна произведению координат этой точки. Решение. По условию плотность γ=x y z. Вычислим массу M куба по (6.10): . Из соображений симметрии следует xc = yc = zc. Поэтому достаточно найти только одну координату xc.
2. Вычисление тройного интеграла в цилиндрических координатах Для упрощения вычисления тройного интеграла часто бывает целесообразным перейти к цилиндрическим координатам. Точка M(x;y;z) в пространстве 0xyz может быть определена заданием трех величин r; φ; (6. . В этом случае тройной интеграл вычисляется по формуле . (6.15) После применения (6.15) вычисление тройного интеграла сводится к трехкратному по r, по φ и по z согласно формуле (6.12). Пример 6.8. Вычислить , где V – область, ограниченная частью конуса и плоскостью z=2. Решение. Заданная область V – часть конуса, вершина которого расположена в начале координат. Его уравнение в цилиндрических координатах (6.14) имеет вид или z=r. Граница области V – окружность x2+y2 =4 запишется как r=2. Новые переменные изменяются в следующих пределах: , (прямая, параллельная
оси 0z, пересекающая область D, входит в конус z=r и выходит
из него на высоте z=2). С учетом формулы замены (6.15) можем вычислить заданный тройной интеграл: Обратим внимание на то, что, не переходя к цилиндрическим координатам, мы получили бы достаточно сложное трехкратное интегрирование согласно формуле (6.12) Примечание. Переход к цилиндрическим координатам рационален, когда область интегрирования образована цилиндрической или конической поверхностью
3. Вычисление тройного интеграла в сферических координатах Если область интегрирования V представляет собой шар или его часть (граница шара x2+y2+z2=R2 в сферических координатах имеет очень простой вид ρ=R), то удобно переходить к сферическим координатам. Сферическими координатами точки M(x;y;z) пространства 0xyz называется тройка чисел ρ; φ; θ (рис. . (6.16) В этом случае тройной интеграл вычисляется по формуле . (6.17) Примечание. Переход к сферическим координатам целесообразен также в том случае, когда подынтегральная функция имеет вид f(x2+y2+z2) Вопросы для самопроверки |
34. Тройные интегралы
Определение тройного интеграла
Определение
тройного интеграла аналогично определениям
определенного и двойного интегралов.
П
Рис. 34.1
усть на пространственном компактом теле ТÌ R3 задана функция
f: T®R. Рассмотрим разбиение {Tк} тела Т с диаметрами dk и объемами DVк (к = 1, …, n) (рис. 34.1). Наибольший из диаметров dk назовем диаметром произведенного разбиения и обозначим через d.
В каждом частичном теле Tк выберем произвольную точку () и составим сумму
Jn = DVк. (34.1)
Суммы
вида (34.1) называются трехмерными
интегралами. Суммами Римана функции f(x, y, z), соответствующими разбиению {Tк} с отмеченными точками ( ).
Определение 1. Предел трехмерных интегральных сумм вида (34.1) при d ® 0 (если он существует) называется тройным интегралом (по Риману) от функции f(x, y, z) по области Т и обозначается . Таким образом
= DVк. (34.2)
В этом случае функция f(x, y, z) называется интегрируемой (по Риману) в области Т, переменные x, y, z — переменными интегрирования; f(x, y, z) — подынтегральной функцией; dV = dxdydz — элементом объема в декартовых прямоугольных координатах, Т – областью интегрирования.
Геометрический и физический смысл
тройного интеграла
Тройной
интеграл по области Т от функции f(x, y, z) º 1 на Т равен объему этого тела. В декартовых
прямоугольных координатах получим
В декартовых
прямоугольных координатах получим
= . (34.3)
В этом состоит геометрический смысл тройного интеграла. Доказательство этого утверждения непосредственно следует из определения тройного интеграла.
Тройной интеграл по области Т от плотности r(x, y, z) материального тела Т равен массе этого тела
m = . (34.4)
Эта формула выражает физический смысл тройного интеграла. Доказательство этого утверждения аналогично доказательству подобного утверждения в двумерном случае.
Свойства тройных интегралов
Можно доказать, что если подынтегральная функция непрерывна на компактном теле Т с кусочно-гладкой границей, то тройной интеграл (34.2) всегда существует.
Свойства
тройных интегралов аналогичны свойствам
двойных интегралов. Ограничимся
перечислением этих свойств. Предполагаем
непрерывность подынтегральных функций
в рассматриваемых областях.
Предполагаем
непрерывность подынтегральных функций
в рассматриваемых областях.
1. Тройной интеграл по области Т равен объему этого тела.
2. Свойство аддитивности
Если пространственная область Т разбита на две непересекающиеся области T1 и T2, то
= + .
3. Свойство линейности
Если функции f1 и f2 интегрируемы в области Т, то и функция c1f1 + c2f2, где c1 и c2 – любые вещественные константы, также интегрируема в области Т, причем
=c1+
+c2 .
4. Свойство монотонности
Если всюду в области Т выполняется неравенство f1(x, y, z) £ f2(x, y, z), то
£ .
5. Абсолютная величина тройного интеграла не превосходит тройного интеграла от абсолютной величины подынтегральной функции, т.е.
│ │ £ .
6. Теорема о среднем. Если функция f(x, y, z) непрерывна в замкнутой ограниченной области ТÌR3, то в этой области найдется точка ( )ÎT, что =
=V f( ), где V – объем области Т.
7. Если функция f(x, y, z) непрерывна в замкнутой ограниченной области ТÌ R3, то mV ≤ £ MV, где m и M – наименьшее и наибольшее значение функции f(x, y, z) в области V.
Вычисление тройного интеграла в декартовых
прямоугольных координатах
В
прямоугольных координатах элемент
объема dV вычисляется по формуле: dV
= dxdydz.
Тройной интеграл от функции f(x, y, z) трех независимых переменных, в области V (риc. 34.1) имеет вид:
и вычисляется по формуле:
. (34.5)
Рис. 34.2
Рис. 1.10
Под областью V, на которую распространен тройной интеграл, понимается пространственная область, ограниченная снизу и сверху поверхностями, определяемыми уравнениями z=1(x,y) и z=2(x,y) (1(x,y) 2(x,y)), а с боков цилиндрической поверхностью с образующими, параллельными от OZ.
Переменные, Х и У изменяются в плоской области Dхоу, которая является проекцией на плоскость ХОУ, пространственной
области V.
Область Dхоу ограниченна непрерывными кривыми, определяемыми уравнениями у=1(x) и у=2(x) и прямыми х = а и х =b (а b, 1(x) 2(x))
Таким образом, вычисление тройного интеграла сводится к трем последовательным интегралам по формуле (34.5). При, вычислении внутреннего интеграла переменные Х и У следует рассматривать как постоянные. В результате получится функция двух независимых переменных Х и У.
Таким образом, мы сведем вычисление тройного интеграла к двойному интегралу, с вычислением которого мы уже знакомы.
Отметим,
что порядок интегрирования может быть
изменен, но при этом пределы интегрирования
во внешнем интеграле всегда величины
постоянные.
Пример 1 . Вычислить интеграл: , где V – тетраэдр, ограниченный координатными плоскостями и плоскостью 2х + 2у + z – 6 = 0.
Решение. Тетраэдр, ограниченный снизу плоскостью z = 0, сверху плоскостью z = 6 – 2х – 2у. Поэтому в области интегрирования V переменная z изменяется от z = 0, до z = 6 – 2х – 2у (рис. 34.3).
Рис. 34.3
Проекцией области V на плоскость ХОУ является треугольник ОАВ.
Уравнение прямой АВ получим, решая совместно уравнения плоскостей:
Отсюда, уравнение прямой АВ имеет вид: х + у – 3 = 0.
В
области Dхоу переменная х изменяется в пределах 0 х 3, а переменная у изменяется 0 у 3 – х.
Поэтому:
.
Вычислим внутренний интеграл в тройном интеграле
.
Следовательно: .
Вычислим внутренний интеграл в двойном интеграле:
. Получим
.
Тройной интеграл в цилиндрических и сферических
координатах
а) Цилиндрические координаты
В цилиндрических координатах положение точки М в пространстве определяется следующим образов:
Точка М проектируется на плоскость ХОУ и определяются полярные координаты r и ее проекции.
Третьей цилиндрической координатой является расстояние точки М от плоскости ХОУ, т.е. ее аппликата z (рис. 34.4). Область изменения цилиндрических координат определяется неравенствами: z > 0, .
Рис. 34.4
Формулы, обязывающие прямоугольные координаты и цилиндрические координаты точки имеют вид:
x
= r cos ,
y = r sin ,
z = z (34. 6)
6)
В цилиндрических координатах элемент объема:
dV = r dz d dz (34.7)
Для того, чтобы тройной интеграл
преобразовать к цилиндрическим координатам, надо х, у и z
в подынтегральной функции заменить по формулам (34.6), а
элемент объема dxdydz по формуле (34.7). После этого тройной интеграл вычислить тремя последовательными интегрированиями.
б) Сферические координаты
В сферических координатах положение точки М в пространстве, определяется тремя числами , , ,
где — расстояние точки М от начала координат
Точка М проектируется на плоскость ХОУ в точку М1.
Угол , составленный ОМ1 и осью ОХ является второй сферической координатой
точки М. Он отсчитывается от оси ОХ против часовой стрелки может изменяться
от 0 до 2.
Он отсчитывается от оси ОХ против часовой стрелки может изменяться
от 0 до 2.
Третьей сферической координатой является угол между осью OZ и ОМ (0 ).
Рис. 34.5
Формулы, связывающие прямоугольные координаты точки и ее сферические координаты имеют вид:
(34.8)
В сферических координатах элемент объема:
. (34.9)
Для
того, чтобы тройной интеграл преобразовать
к сферическим координатам надо x, y и z заменить в
подынтегральной функции по формулам
(34.8), а элемент объема dxdydz по формуле (34.9). После того вычислить
его тремя последовательными интегралами
(порядок интегрирования безразличен).
Заметим, что переход к сферическим
координатам особенно удобен в том
случае, когда областью интегрирования
является шар (или часть шара) или
подынтегральная функция содержит в
себе выражение вида x2 + y2 + z2, так как в сферических координатах x2 + y2 + z2 = 2.
Применение тройных интегралов в геометрии и механике
а) Вычисление объема тела
Объем тела, ограниченного областью V, в прямоугольных координатах вычисляется по формуле:
. (34.10)
В цилиндрических координатах объем тела:
. (34.11)
В сферических координатах объем тела:
. (34.12)
Пример 2. Вычислить объем тела, ограниченного поверхностями: x2 + y2 + z2 – 2z = 0 и x2 + y2 = 2 – z.
Решение. Первая
поверхность сфера. Преобразуем уравнение
сферы к виду x2 + y2 + (z – 1)2 = 1. Откуда
видно, что центр сферы находится на оси OZ в точке (0, 0,
1), а ее радиус
равен 1. Вторая поверхность – параболоид
вращения (рис. 34.6).
Откуда
видно, что центр сферы находится на оси OZ в точке (0, 0,
1), а ее радиус
равен 1. Вторая поверхность – параболоид
вращения (рис. 34.6).
Найдем уравнение линии, по которой пересекаются эти поверхности. Этой линией является окружность. Определим, на какой высоте над плоскостью ХОУ расположена эта линия.
Р ис. 34.6
Для этого из второго уравнения подставим значение
x2 + y2 =2 – z в первое уравнение, получим (2
– z)2 + z2 – 2z = 0 или z2 – 3z + 2 = 0. Решая
его получим z1 = 1, z2 = 2. Точка, в
которой z = 2 – это
вершина параболоида, поэтому линия
пересечения поверхностей находится на
высоте z = 1 над
плоскостью ХОУ. Уравнение этой линии получим, подставляя z = 1 в уравнение
любой из этих поверхностей.
Уравнение этой линии получим, подставляя z = 1 в уравнение
любой из этих поверхностей.
Оно имеет вид .
Это окружность, она проектируется на плоскость ХОУ в окружность x2 + y2 = 1, а все тело проектируется в круг DХОУ, ограниченный этой окружностью.
По формуле (34.6) объем тела равен .
Внутреннее интегрирование проведем по переменной z. Определим пределы изменения переменной в области интегрирования: из уравнения сферы получим на нижней полусфере , а из уравнения параболоида z = 2 – (x2 + y2). Таким образом, в области интегрирования
.
Поскольку
под знаком интеграла имеется выражение x2 + y2, а область интегрирования круг, удобно
перейти к полярным координатам, в которых x2 + y2 = r2, а элемент площади dxdy = rdrd. Так как в круге DХОУ , то
Так как в круге DХОУ , то
.
б) Вычисление массы тела
Если дано некоторое тело с объемной плотностью (х, у, z), представляющий собой непрерывную функцию, то масса m этого тела, равна тройному интегралу от функции плотности (х, у, z), распространенному на объем V, занимаемый этим телом:
. (34.13)
Пример 3 . Вычислить массу тела, ограниченного сферой х2 + у2 + z2 = 4 и параболоидом х2 + у2 = 3z, если плотность в каждой точке тела равна аппликате точки (т.е. = z).
Решение. В этой задаче
удобно перейти к цилиндрическим
координатам, так как в уравнении
параболоида содержится сумма х2 + у2, а в цилиндрических координатах х2 + у2 = r2.
Запишем уравнения поверхностей, ограничивающих тело, в цилиндрических координатах.
Уравнение сферы примет вид: r2 + z2 = 4; r2 = 4 – z2.
Уравнение параболоида: r2 = 3z.Из этих уравнений следует, что на параболоиде: , а на сфере .
Спроектируем это тело на плоскость ХОУ. Проекцией будет круг. Найдем радиус этого круга. Для этого определим, при каком значении z пересекаются поверхности, т.е. определим z из системы:
;
Получим z2 + 3z – 4 = 0; z1 = 1; z2 = – 4.
Смыслу задачи удовлетворяет только z = 1.
Подставим
это значение в любое из уравнений
системы, получим r2 = 3, .
Итак, радиус круга, в который проектировалось тело
равен ; переменные r,, z в теле изменяются в пределах:
0 r , 0 2 , .
Масса тела вычисляется по формуле (34.13), в которой элемент объема .
Таким образом,
.
Тройной интеграл (объемный интеграл): Определение, пример
Интегралы >
Содержание:
- Что такое тройной интеграл?
- Рабочий пример
- Теорема о расходимости
Тройной интеграл (также называемый трехмерным определенным интегралом или объемным интегралом ) ∫∫∫ D f(x, y, z) dV является расширением «обычного» интеграла до трех -размеры. Часто это предпочтительный выбор для решения трехмерных задач, таких как определение центра масс, моментов инерции или объема твердого тела.
Формальное определение тройного интеграла
Определение тройного интеграла очень похоже на определение двойного интеграла. Функция трех переменных f ( x , y , z ) над трехмерной областью V может быть записана как (Бронштейн и др., 2013):
Это не так сложно, как это выглядит, пока вас устраивают правила интеграции. Это потому, что это повторяющихся интегралов : все, что вам нужно сделать, это интегрировать три раза, работая слоями изнутри наружу.
Пример задачи : Найдите центр масс деревянного бруска со стороной 4 м. Один угол куба расположен в начале координат, а соседние углы лежат на положительных осях x, y и z. Предположим, что плотность ящика пропорциональна расстоянию от плоскости x-y и что k = 1 кг на кубический м на м.
Решение
Шаг 1: Настройте тройной интеграл.
Здесь W представляет куб, f ( x , y , z ) = kz плотность куба; k — константа.
Шаг 2: Вычислите интеграл. Вам нужно будет сделать это три раза (по одному разу для каждого интеграла по x, y и затем по z). Примечание : Для кубической формы интеграл не зависит от порядка интегрирования, если f(x,y,z) является непрерывной функцией.
- Сначала проинтегрируем по x (рассматривая y и z как константы):
Поскольку нижний предел равен «0», это упрощает интеграцию. Обычно вам придется оценивать функцию в нижнем и верхнем пределах интегрирования, вычитая два, чтобы получить вашу площадь. Однако, поскольку нижняя граница (x = 0) всегда будет равна нулю, вы можете пропустить этот шаг и просто подставить найденное значение верхнего предела. - Оценить следующий слой (относительно y):
- Оцените еще раз, и интеграция завершена!
Вам сказали, что блок измеряется в метрах и что k равно 1 кг на кубический метр на м. Значит масса блока 128 кг.
Исчисление 3. Тройные интегралы (1 из 25) Что такое тройной интеграл?
Тройные интегралы (1 из 25) Что такое тройной интеграл?
Посмотрите это видео на YouTube.
Теорема о дивергенции (иногда называемая теоремой Гаусса или Остроградского ) представляет собой связь между тройными интегралами и поверхностными интегралами. В нем говорится, что при определенных условиях некоторые объемные интегралы равны поверхностным интегралам. Это может привести к более простой интеграции.
В качестве простого примера, чтобы выполнить интегрирование фигуры, подобной пирамиде, вам потребуются четыре поверхностных интеграла: по одному для каждой стороны. Но можно, если форма удовлетворяет нескольким основным требованиям, вместо этого использовать один тройной интеграл.
Формальное определение теоремы о дивергенции
Теорема верна для замкнутой поверхности S , что означает, что S образует полную границу твердого тела. К закрытым поверхностям относятся области, ограниченные кубами, эллипсоидами, сферами, тетраэдрами или комбинациями этих поверхностей.
Формальное определение теоремы о дивергенции
Две части этой сплошной области Q ориентированы одним восходящим единичным вектором нормали N (S 1 ) и одним нисходящим (S 2 ).
На изображении выше показан пример формы, которую охватывает теорема о дивергенции; Сплошная область, которую мы назовем Q , ограниченная замкнутой поверхностью S и ориентированная одним или несколькими единичными векторами нормалей, направленными наружу от Q.
If F — векторное поле с составляющими функциями, которые имеют непрерывные первые частные производные в Q, тогда [1]:
Теорема получила свое название от дивергенции векторного поля F = M i + N j + P k . Это определяется как:
Где ∂ — частная производная.
Пример
Изображение выше ограничено четырьмя плоскостями: координатными плоскостями x, y и плоскостью 2x + 2y + z = 6 с
F = x i + y 2 j + z k .
Вместо вычисления поверхностного интеграла для четырех разных плоскостей мы можем использовать тройной интеграл.
Нам нужно найти делений F , прежде чем мы сможем решить тройной интеграл. Имеем:
- = 1 + 2у + 1
- = 2 + 2г.
Я использовал калькулятор Symbolab для вычисления тройного интеграла. Решение:
Теорема о дивергенции: ссылки
[1] Ларсон Р. и Эдвардс Б. (2016). Исчисление, 10-е издание. Cengage Learning.
Другие ссылки
Бронштейн И. и др. Справочник по математике. 2013. Springer Berlin Heidelberg.
Зилл, Д. и Райт, В. Исчисление: ранние трансцендентальные. 2009. Обучение Джонса и Бартлетта.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Тройной интеграл (объемный интеграл): определение, пример» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www. statisticshowto.com/triple-integral-volume-integral/
statisticshowto.com/triple-integral-volume-integral/
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Тройные интегралы
Тройные интегралы
Определение тройного интеграла
Мы видели, что геометрия двойного интеграла включает в себя разрезание двух размерную область на крошечные прямоугольники, умножая площади прямоугольников по значению функции там, суммируя площади и беря предел как размер прямоугольников приближается к нулю. Мы также видели, что это эквивалентно нахождению дважды повторенного повторного интеграла.
Теперь мы перенесем эту идею в следующее измерение. Вместо региона
в плоскости xy мы будем рассматривать твердое тело в xyz-пространстве. Вместо того, чтобы резать
область на прямоугольники, мы разрежем твердое тело на прямоугольные
твердые вещества. И вместо умножения значения функции на площадь
прямоугольник, умножим значение функции на объем прямоугольника
твердый.
И вместо умножения значения функции на площадь
прямоугольник, умножим значение функции на объем прямоугольника
твердый.
Мы можем определить тройку интеграл как предел суммы произведения функции, умноженной на объем прямоугольных тел.
Вместо двойного интеграла, эквивалентного двойному повторению интеграл, тройной интеграл эквивалентен тройному повторному интегралу.
Определение тройного интеграла Пусть f(x,y,z) быть непрерывной функцией трех переменные, определенные над сплошным Q. Тогда тройной интеграл по Q определяется как где сумма берется по прямоугольным телам, входящим в тело Q а под lim понимается предел как длины сторон прямоугольного твердый. |
Это определение применимо только для оценки тройного интеграла, когда
дан набор данных. Когда у нас есть символически определенная функция, мы используем
расширение основной теоремы исчисления, которая является просто теоремой Фубини
для тройных интегралов.
Когда у нас есть символически определенная функция, мы используем
расширение основной теоремы исчисления, которая является просто теоремой Фубини
для тройных интегралов.
Теорема для вычисления тройки Интегралы Пусть f(x,y,z) — непрерывная функция над твердым Q определяется а < х < б h 1 (x) < у < ч 2 (х) g 1 (x, y) < z < g 2 (x, y) Тогда тройной интеграл равен тройной повторный интеграл. |
Примечание: Как и в случае двойных интегралов, порядок интеграции может быть изменен с осторожностью.
Примеры
Пример
Оценить
Где
f(x,y,z) = 1 — x
и Q — это тело, лежащее в первом октанте, а ниже равнины
3x + 2y + z = 6
Раствор
фото региона
задача здесь состоит в том, чтобы найти пределы. Сначала мы работаем над самым внутренним пределом
что соответствует переменной «z».
Представьте, что вы стоите вертикально. Ваши ноги будут опираться на нижний предел и
ваша голова коснется верхнего предела. Нижний предел — это плоскость xy или
Сначала мы работаем над самым внутренним пределом
что соответствует переменной «z».
Представьте, что вы стоите вертикально. Ваши ноги будут опираться на нижний предел и
ваша голова коснется верхнего предела. Нижний предел — это плоскость xy или
г = 0
верхний предел – заданная плоскость. Решая для z, мы получаем
г = 6 — 3x — 2y
Сейчас мы работаем над средними пределами, которые соответствуют переменной «y». Смотрим на проекцию поверхности на xy-плоскость. Это показано ниже.
Сейчас мы находим пределы так же, как находили пределы двойных интегралов. нижний предел всего
у = 0
Если мы устанавливаем z = 0 и решаем для y, получаем для верхнего предела
у = 3 — 3/2 х 90 003
Далее находим внешние пределы, соответствующие переменной «х». Наименьшее значение x равно 0, а наибольшее значение x равно 2. Отсюда
0 < х < 2
таким образом, интеграл равен
Пример
Переключатель
порядок интегрирования из предыдущего примера, чтобы dydxdz
появляется.
Раствор
Это время, когда мы работаем над переменной «y» первый. Нижний предел для переменной y равен 0. Для верхнего предела мы решаем для y на плоскости получить
у = 3 — 3/2 x – 1/2 z
Кому находим пределы «x», проецируем на плоскость xz как показано ниже
нижний предел для x равен 0. Чтобы найти верхний предел, мы устанавливаем y = 0 и решаем для x чтобы получить
х = 2 — 1/3 z
Наконец, чтобы получить пределы для z, мы видим, что наименьшее z получит 0 и самый большой z будет равно 6. Получаем
0 < z < 6
Мы можем написать
Масса, центр масс и моменты инерции
Для трехмерного твердого тела с постоянной плотностью масса равна плотности
раза больше объема. Если плотность не постоянная, а непрерывная
функцией x, y и x, то мы можем разрезать тело на очень маленькие прямоугольные
тел так, чтобы на каждом прямоугольном теле плотность была примерно
постоянный. Объем прямоугольника
Объем прямоугольника
Д Масса = (Плотность)(DОбъем) = f(x,y,z) DxDyDz
Теперь сделайте как обычно. Складываем все малые массы и берем ограничение по мере того, как прямоугольные тела становятся маленькими. Это даст нам тройку интеграл
Мы часто интересует центр масс твердого тела. Например, когда спутник NEAR вращался вокруг астероида Эрос, ученым НАСА нужно было вычислить центр масс астероида. Кеплер сказал нам, что стабильное орбита всегда будет вращаться по эллиптической орбите с центром масс в качестве одного из фокусы.
Спутник NEAR на орбите Эроса
Мы находим центр масс твердого тела так же, как нашли центр массы пластинки. Поскольку мы находимся в трех измерениях, вместо моменты относительно осей, находим моменты относительно координатных плоскостей. Мы сформулируем определения из физики ниже.
Определение: Моменты и центр масс Пусть г (х, у, г)
— плотность твердого вещества Q. и центр масс дано |
Обратите внимание, что если функция плотности будет тождественно равна 1, это даст объем
Упражнение
Найти центр масс твердого тела, лежащего ниже параболоида
г = 4 — х 2 — у 2
, лежащий над плоскостью xy, если плотность области определяется как
.r(x,y,z) = x 2 + 2y 2 + z
Вы можете использовать свой калькулятор или компьютер для вычисления интегралов.
Так же, как и в случае пластинки, существуют формулы для моментов инерции относительно
три оси. Они включают умножение функции плотности на квадрат
расстояние от осей.

 В общем случае такая область ограничена сверху поверхностью z=ψ2(x,y), снизу –
поверхностью z=ψ1(x,y) и с боков – цилиндрической поверхностью с
образующими, параллельными оси 0z (рис. 52). Такая область V называется правильной. В частных случаях
боковая поверхность цилиндра может превратиться в линию. Функции ψ1(x,y) и ψ2(x,y) мы будем считать непрерывными. Тройной интеграл по
такой области вычисляется по формуле
В общем случае такая область ограничена сверху поверхностью z=ψ2(x,y), снизу –
поверхностью z=ψ1(x,y) и с боков – цилиндрической поверхностью с
образующими, параллельными оси 0z (рис. 52). Такая область V называется правильной. В частных случаях
боковая поверхность цилиндра может превратиться в линию. Функции ψ1(x,y) и ψ2(x,y) мы будем считать непрерывными. Тройной интеграл по
такой области вычисляется по формуле 6.4). В
результате получается некоторая функция двух переменных x и y, которая
интегрируется затем по области D с помощью формул (6.5) или (6.6). Таким образом,
вычисление тройного интеграла сводится к трехкратному интегрированию.
6.4). В
результате получается некоторая функция двух переменных x и y, которая
интегрируется затем по области D с помощью формул (6.5) или (6.6). Таким образом,
вычисление тройного интеграла сводится к трехкратному интегрированию.
 Вычислим числитель для xc в формуле (6.11).
Вычислим числитель для xc в формуле (6.11).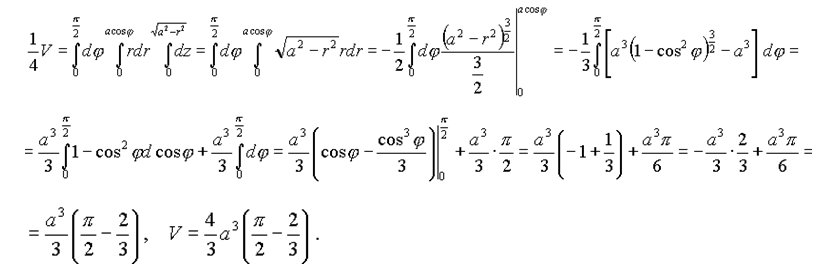 14)
14)
 6.8), где ρ – длина радиус-вектора точки M, φ – угол, образованный проекцией радиус-вектора на плоскость x0y и осью 0x, θ – угол отклонения радиус-вектора от оси 0z. Эти координаты связаны с декартовыми координатами
точки M соотношениями:
6.8), где ρ – длина радиус-вектора точки M, φ – угол, образованный проекцией радиус-вектора на плоскость x0y и осью 0x, θ – угол отклонения радиус-вектора от оси 0z. Эти координаты связаны с декартовыми координатами
точки M соотношениями: Затем первые мгновения о координатных плоскостях
Затем первые мгновения о координатных плоскостях