Примеры решения квадратных и биквадратных уравнений
Пример 1. Решить квадратное уравнение x2 — 3x = 0.
Решение.
Уравнение x2 — 3x = 0 неполное квадратное, поэтому будем решать его методом разложения на множители:
x2 — 3x = 0 x(x-3)=0
x = 0, x = 0,
x — 3 = 0 x = 3.
Ответ: 0, 3.
Пример 2. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть уравнения:
Умножим на 4 обе части уравнения:
x2 — 4 = 0 x2 = 4 x = ± 2.
Ответ: ± 2.
Пример 3. Решить квадратное уравнение x2 + 3x + 10 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 3, c = 10.
D = b2 — 4ac = 32 — 4*1*10 = 9 — 40 = -31
Ответ: корней нет.
Лучшие математические приложения для школьников и их родителей, студентов и учителей.
Пример 4. Решить квадратное уравнение x2 + 12x + 36 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 12, c = 36.
Так как b = 12 — четное число, то вычислим дискриминант D1 :
D1 = (b/2)2 — ac = 62 — 1*36 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = (-6)/1 = -6.
Это уравнение можно решить и без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
x2 + 12x + 36 = 0 (x+6)2 = 0 x = -6.
Ответ: -6.
Пример 5. Решить квадратное уравнение 4x2 -28x + 49 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.
Так как b = -28 — четное число, то вычислим дискриминант D1 :
D1 = (b/2)2 — ac = (-14) 2 — 4*49 = 196-196 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = 14/4 = 7/2.
Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
4x2 -28x + 49 = 0 (2x-7)2 = 0 2x = 7 x = 7/2.
Ответ: 7/2.
Пример 6. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть уравнения:
Умножив обе части уравнения на -4, получим x2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
x2 + 3x = 0 x(x+3) = 0
x = 0, x = 0,
x — 3 = 0 x = 3.
Ответ: 0, 3.
Пример 7. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:
Получим 6x2
Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10,
D = b2 — 4ac = (-17)2 — 4*6*10 = 289 — 240 = 49 > 0, следовательно, уравнение имеет два действительных корня.
Ответ: 5/6, 2.
Пример 8. Решить уравнение .
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.
Так как b = 2√2, то есть b делится на 2 (b/2 = √2), вычислим дискриминант D1:
D1 = (b/2)2 — ac = (√2)2 — 1*1 = 1 > 0. Cледовательно, уравнение имеет два действительных корня.
Ответ: -√2-1, -√2+1.
Пример 9. Решить уравнение .
Решение.
Умножим левую и правую части уравнения на 6:
Вычислим дискриминант полученного квадратного трехчлена. У нас a = 3, b = -6, c = 2.
Так как b = -6, то есть b делится на 2 (b/2=3), вычислим дискриминант D1:
D1 = (b/2)2 — ac = 32 — 3*2 = 3 > 0. Cледовательно, уравнение имеет два действительных корня.
Ответ: (3-√3)/3, (3+√3)/3.
Пример 10. Решить уравнение x4 — 17x2 + 16 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
x4 — 17x2 + 16 = 0 => t2 — 17t + 16 = 0.
Вычислим дискриминант квадратного трехчлена: a = 1, b = -17, c = 16,
D = b2 — 4ac = (-17)2 — 4*1*16 = 289-64 = 225 > 0, следовательно, уравнение имеет два действительных корня.
По найденным значениям t, решая уравнения x
Таким образом, исходное уравнение имеет 4 действительных корня.
Ответ: ±1, ±4.
Пример 11. Решить уравнение 9x4 + 32x2 — 16 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
9x4 + 32x2 — 16 = 0 => 9t2 + 32t — 16 = 0
Вычислим дискриминант квадратного трехчлена. У нас a = 9, b = 32, c = -16.
У нас a = 9, b = 32, c = -16.
Так как b = 32, то есть b делится на 2 (b/2=16), вычислим дискриминант D1:
D1 = (b/2)2 — ac = 162 — 9*(-16) = 400 >0. Cледовательно, уравнение имеет два действительных корня.
По найденным значениям t, решая уравнения x 2 = t, найдем корни исходного биквадратного уравнения:
Первое уравнение x2 = -4 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x= ±2/3.
Ответ: ±2/3.
Пример 12. Решить уравнение x4 + 3x2 — 10 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
x4 + 3x2 — 10 = 0 => t2 + 3t — 10 = 0
Вычислим дискриминант полученного квадратного трехчлена: a = 1, b = 3, c = -10,
D = b2 — 4ac = 32 — 4*1*(-10) = 9+40 = 49 > 0, следовательно, уравнение имеет два действительных корня.
По найденным значениям t, решая уравнения x2 = t, найдем корни исходного биквадратного уравнения:
Первое уравнение x2 = -5 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x = ±√2.
Ответ: ±√2.
10 квадратных уравнений
10 квадратных уравненийВы искали 10 квадратных уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 ac, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «10 квадратных уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни.

Решить задачу 10 квадратных уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решение квадратных уравнений в форме
Общие рекомендации по решению квадратных уравнений
Используйте коэффициенты квадратного уравнения, чтобы решить, какой метод наиболее подходит для его решения. Хотя квадратичная формула работает всегда, иногда это не самый эффективный метод. Если задано любое квадратное уравнение в стандартной форме,
Хотя квадратичная формула работает всегда, иногда это не самый эффективный метод. Если задано любое квадратное уравнение в стандартной форме,
ax2+bx+c=0 где c = 0, то лучше всего вынести GCF и решить факторингом.
Пример 1
Решите: 12×2−3x=0.
Решение:
В этом случае c = 0, и мы можем решить, выделив GCF 3 x .
12×2−3x=03x(4x−1)=0
Затем примените свойство нулевого произведения и установите каждый множитель равным нулю.
3x=0или 4x−1=0x=04x=1x=14
Ответ: Решения равны 0 и 14.
Если b = 0, то мы можем решить путем извлечения корней.
Пример 2
Решите: 5×2+8=0.
Решение:
В этом случае b = 0 и мы можем решить путем извлечения корней. Начните с выделения квадрата.
5×2+8=05×2=-8×2=-85
Затем примените свойство квадратного корня. Не забудьте включить ±.
x=±−85Обоснуйте знаменатель.=±−4⋅25⋅55Упростите. =±2i2⋅55=±2i105
=±2i2⋅55=±2i105
Ответ: Решения равны ±2i105.
Если задано квадратное уравнение в стандартной форме, где a , b и c отличны от нуля, определите значение дискриминанта по формуле b2−4ac.
- Если дискриминант — полный квадрат, то решить с помощью факторизации.
- Если дискриминант не является полным квадратом, решите его по формуле квадрата.
Напомним, что если дискриминант не является полным квадратом и положителен, квадратное уравнение будет иметь два иррациональных решения. А если дискриминант отрицателен, квадратное уравнение будет иметь два комплексно-сопряженных решения.
Пример 3
Решите: (3x+5)(3x+7)=6x+10.
Решение:
Начните с перезаписи квадратного уравнения в стандартной форме.
(3x+5)(3x+7)=6x+109×2+21x+15x+35=6x+109×2+36x+35=6x+109×2+30x+25=0
Замена a = 9, b = 30 и c = 25 в дискриминантную формулу.
b2−4ac=(30)2−4(9)(25)=900−900=0
Поскольку дискриминант равен 0, решите факторингом и ожидайте одно действительное решение, двойной корень.
9×2+30x+25=0(3x+5)(3x+5)=03x+5=0или3x+5=03x=-53x=-5x=-53x=-53
Ответ: Решение равно −53.
Приятно знать, что квадратичная формула поможет найти решения для всех примеров в этом разделе. Однако это не всегда лучшее решение. Если уравнение можно решить разложением на множители или извлечением корней, следует использовать этот метод.
Решение квадратных уравнений в форме
В этом разделе мы описываем алгебраический метод, который широко используется в математике для преобразования уравнений в знакомые формы. Начнем с определения квадратичной формы уравнения вида au2+bu+c=0, где a , b и c — действительные числа, а u представляет собой алгебраическое выражение. Вот несколько примеров:
(t+2t)2+8(t+2t)+7=0⇒u = t+2tu2+8u+7=0x2/3−3×1/3−10=0⇒u = x1/ 3u2−3u−10=03y−2+7y−1−6=0⇒u = y−13u2+7u−6=0
Если мы можем выразить уравнение в квадратичной форме, то мы можем использовать любой из используемых методов решать квадратные уравнения. Например, рассмотрим следующее полиномиальное уравнение четвертой степени:
Например, рассмотрим следующее полиномиальное уравнение четвертой степени:
x4−4×2−32=0
Если мы допустим u=x2, то u2=(x2)2=x4, и мы можем записать
x4−4×2−32=0⇒(x2)2−4(x2)− 32=0↓↓u2−4u−32=0
Эта замена превращает уравнение в известное квадратное уравнение относительно u , которое в этом случае можно решить с помощью факторизации.
u2−4u−32=0(u−8)(u+4)=0 u=8 или u=−4
Поскольку u=x2 x 908, можно выполнить обратную замену, а затем найти 90,08.
u=8oru=−4↓ ↓x2=8×2=−4x=±8x=±−4x=±22x=±2i
Следовательно, уравнение x4−4×2−32=0 имеет четыре решения {±22,±2i}, два действительных и два комплексных. Этот метод, часто называемый u -подстановкой. Метод в алгебре, использующий замену для преобразования уравнений в знакомые формы, также может быть использован для решения некоторых неполиномиальных уравнений.
Пример 4
Решите: x−2x−8=0.
Решение:
Это радикальное уравнение, которое можно записать в квадратичной форме. Если мы допустим u=x, то u2=(x)2=x, и мы можем написать
Если мы допустим u=x, то u2=(x)2=x, и мы можем написать
x−2x−8=0 ↓ ↓ u2− 2u − 8=0
Найти u .
u2−2u−8=0(u−4)(u+2)=0u=4 или u=−2
Обратно подставьте u=x и найдите x .
x=4orx=−2(x)2=(4)2(x)2=(−2)2x=16x=4
Напомним, что возведение в квадрат обеих частей уравнения приводит к возможности появления посторонних решений. Поэтому мы должны проверить наши потенциальные решения.
Проверка x=16Проверка x=4x−2x−8=016−216−8=016−2⋅4−8=016−8−8=00=0✓x−2x−8=04−24−8= 04−2⋅2−8=04−4−8=0−8=0✗
Поскольку x=4 является лишним, существует только одно решение, x=16.
Ответ: Решение: 16.
Пример 5
Решите: x2/3−3×1/3−10=0.
Решение:
Если мы позволили u = x1/3, то U2 = (x1/3) 2 = x2/3, и мы можем написать
x2/3×1/3–10 = 0 ↓ ↓ U2 — 3U − 10=0
Найдите u .
u2−3u−10=0(u−5)(u+2)=0u=5 или u=−2
Обратно подставьте u=x1/3 и найдите x .
x1/3=5orx1/3=−2(x1/3)3=(5)3(x1/3)3=(−2)3x=125x=−8
Проверить.
Проверка x=125Проверка x=−8×2/3−3×1/3−10=0(125)2/3−3(125)1/3−10=0(53)2/3−3(53)1 /3−10=052−3⋅5−10=025−15−10=00=0✓x2/3−3×1/3−10=0(−8)2/3−3(−8)1/3 −10=0[(−2)3]2/3−3[(−2)3]1/3−10=0(−2)2−3⋅(−2)−10=04+6−10 =00=0✓
Ответ: Решение: −8, 125.
Пример 6
Решите: 3y−2+7y−1−6=0.
Решение:
Если мы позволим u = y — 1, то U2 = (y — 1) 2 = y — 2, и мы можем написать
3y — 2+7y — 1 = 0 ↓ ↓ 3U2+7U − 6=0
Найдите u .
3u2+7u−6=0(3u−2)(u+3)=0u=23 или u=−3
Обратно подставить u=y−1 и найти y .
y-1=23ory-1=-31y=231y=-3y=32y=-13
Исходное уравнение на самом деле является рациональным уравнением, где y≠0. В этом случае решения не являются ограничениями; они решают исходное уравнение.
Ответ: решения равны −13, 32
Пример 7
Решите: (t+2t)2+8(t+2t)+7=0.
Решение:
Если мы допустим u=t+2t, то u2=(t+2t)2 и мы можем записать
(t+2t)2+8(t+2t)+7=0 ↓↓u2+8u+7 =0
Найдите u .
u2+8u+7=0(u+1)(u+7)=0u=−1 или u=−7
Обратно подставить u=t+2t и найти t .
t+2t=-1ort+2t=-7t+2=-tt+2=-7t2t=-28t=-2t=-1t=-14
Ответ: Решения равны -1, -14. Чек остается читателю.
Попробуйте! Решите: 12x−2−16x−1+5=0
Ответ: Решение: 65, 2,
(щелкните, чтобы посмотреть видео)
До сих пор все примеры были уравнениями с коэффициентом. Как известно, не все квадратные уравнения факторные. В этом случае используем квадратичную формулу.
Пример 8
Решите: x4−10×2+23=0. Приблизительно с точностью до сотой.
Решение:
Если принять u=x2, то u2=(x2)2=x4, и мы можем написать
фактор; поэтому используйте квадратичную формулу, чтобы найти решения для и . Здесь a=1, b=-10 и c=23.u=−b±b2−4ac2a=−(−10)±(−10)2−4(1)(23)2(1)=10±82=10±222=5±2
Следовательно, и=5±2. Теперь снова подставьте u=x2 и найдите x .
u=5−2oru=5+2↓↓x2=5−2×2=5+2x=±5−2x=±5+2
Округлите четыре решения следующим образом.
x=−5−2≈−1,89x=−5+2≈−2,53x=5−2≈1,89x=5+2≈2,53
Ответ: Решения приблизительно равны ±1,89, ±2,53.
Если подсчитать кратные и комплексные корни, то основная теорема алгебры Если подсчитать кратные и комплексные корни, то каждый многочлен с одной переменной будет иметь столько корней, сколько его степени. подразумевает, что каждый полином с одной переменной будет иметь столько корней, сколько его степени. Например, мы ожидаем, что f(x)=x3−8 будет иметь три корня. Другими словами, уравнение
х3-8=0 должно иметь три решения. Чтобы найти их, можно сначала попытаться извлечь кубические корни так же, как мы это делали с квадратными корнями:
x3−8=0x3=8x=83x=2
кубический корень. Там должно быть два других; попробуем найти их.
Пример 9
Найдите множество всех корней: f(x)=x3−8.
Решение:
Обратите внимание, что выражение x3−8 представляет собой разность кубов, и вспомним, что a3−b3=(a−b)(a2+ab+b2). Здесь a=x и b=2, и мы можем написать
x3-8=0(x-2)(x2+2x+4)=0
Затем примените свойство нулевого произведения и установите каждый множитель равным нулю. Установив коэффициенты равными нулю, мы можем решить полученное уравнение, используя соответствующие методы.
Установив коэффициенты равными нулю, мы можем решить полученное уравнение, используя соответствующие методы.
x−2=0orx2+2x+4=0x=2x=−b±b2−4ac2a=−(2)±(2)2−4(1)(4)2(1)=−2±−122 =−2±2i32=−1±i3
Используя этот метод, мы смогли получить множество всех трех корней {2,−1±i3}, одного действительного и двух комплексных.
Ответ: {2,−1±i3}
Иногда корни функции встречаются несколько раз. Например, g(x)=(x−2)3 имеет третью степень, где корни можно найти следующим образом:
(x-2)3=0(x-2)(x-2)(x-2)=0x-2=0orx-2=0orx-2=0x=2x=2x=2
Хотя g имеет степень 3, существует только один действительный корень {2}; это происходит 3 раза.
Ключевые выводы
- Квадратная формула может решить любое квадратное уравнение. Однако иногда это не самый эффективный метод.
- Если квадратное уравнение можно решить разложением на множители или извлечением квадратных корней, следует использовать этот метод.
- Иногда мы можем преобразовать уравнения в квадратичные по форме, сделав соответствующие и — замена.
 После решения эквивалентного уравнения вернитесь к исходной переменной и решите ее.
После решения эквивалентного уравнения вернитесь к исходной переменной и решите ее. - При подсчете кратных и комплексных корней основная теорема алгебры гарантирует столько корней, сколько степени полиномиального уравнения с одной переменной.
Тематические упражнения
х2-9х=0
х2+10х=0
15×2+6x=0
36×2−18x=0
x2−90=0
х2+48=0
2×2+1=0
7×2−1=0
6×2−11x+4=0
9×2+12x−5=0
х2+х+6=0
х2+2х+8=0
4т2+28т+49=0
25т2-20т+4=0
и2-4и-1=0
и2-2и-11=0
2(х+2)2=11+4х−2х2
(2x+1)(x−3)+2×2=3(x−1)
(3x+2)2=6(2x+1)
(2x−3)2+5×2=4(2−3x)
4(3x−1)2−5=0
9(2x+3)2−2=0
Часть A: Решение квадратных уравнений
Решить.
х4+х2-72=0
х4-17х2-18=0
х4-13х2+36=0
4×4−17×2+4=0
х+2х-3=0
х-х-2=0
х-5х+6=0
х-6х+5=0
х2/3+5х1/3+6=0
х2/3-2х1/3-35=0
4×2/3−4×1/3+1=0
3×2/3-2×1/3-1=0
5x−2+9x−1−2=0
3x−2+8x−1−3=0
8x−2+14x−1−15=0
9x−2−24x−1+16=0
(х-3х)2-2(х-3х)-24=0
(2x+1x)2+9(2x+1x)−36=0
2(хх+1)2−5(хх+1)−3=0
3(x3x−1)2+13(x3x−1)−10=0
4г-2-9=0
16у-2+4у-1=0
30y2/3−15y1/3=0
у2/3-9=0
81y4−1=0
5(1x+2)2−3(1x+2)−2=0
12(х2х-3)2-11(х2х-3)+2=0
10x−2−19x−1−2=0
х1/2-3х1/4+2=0
х+5х-50=0
8×2/3+7×1/3−1=0
х4/3-13х2/3+36=0
y4−14y2+46=0
х4/3-2х2/3+1=0
2у-2-у-1-1=0
2x-2/3-3x-1/3-2=0
4x−1−17x−1/2+4=0
3x−1−8x−1/2+4=0
2×1/3−3×1/6+1=0
х1/3-х1/6-2=0
х4-6х2+7=0
х4-6х2+6=0
х4-8х2+14=0
х4-12х2+31=0
4×4−16×2+13=0
9×4−30×2+1=0
f(x)=x3−1
г(х)=х3+1
f(x)=x3−27
г(х)=х4−16
ч(х)=х4−1
ч(х)=х6−1
f(x)=(2x−1)3
г(х)=х2(х-4)2
f(x)=x3−q3, q>0
f(x)=x3+q3, q>0
х6+7х3-8=0
х6-7х3-8=0
х6+28х3+27=0
х6+16х3+64=0
|x2+2x−5|=1
|x2−2x−3|=3
|2×2−5|=4
|3×2−9x|=6
{±3i}
{±i5}
{±3}
{±26}
{1±3}
{2±32}
{1±6i}
{2±3i}
Часть B: Решение квадратных уравнений в форме
Найдите все решения.
Найдите все решения. Округлите ответы до сотых.
Округлите ответы до сотых.
Найдите множество всех корней.
Найдите все решения.
Найдите квадратичную функцию с целыми коэффициентами и заданным набором корней. (Подсказка: если r1 и r2 — корни, то (x−r1)(x−r2)=0.)
Напишите на карточке свою стратегию решения квадратного уравнения.
 Поделитесь своей стратегией на доске обсуждений.
Поделитесь своей стратегией на доске обсуждений.Составьте собственное квадратичное уравнение. Поделитесь этим и решением на доске обсуждений.
Часть C: Дискуссионная доска
Ответы
0, 9
−25, 0
±310
±22i
12,43
−12±232i
−72
2±5
−32,12
±23
2±56
±22, ±3i
±2, ±3
1
4, 9
−27, −8
18
−12, 5
−25,43
±35
−32,−13
±23
0, 18
±13,±i3
−32, 6
1, 16
−1, 1512
±7−3, ±7+3
−2, 1
116, 16
164, 1
±1,26, ±2,10
±1,61, ±2,33
±1,06, ±1,69
{1,−12±32i}
{3,−32±332i}
{±1,±i}
{12}
{q,−q2±q32i}
-2, 1, 1±i3, -12±32i
−3, −1, 32±332i, 12±32i
−1±7, −1±5
±22, ±322
f(x)=x2+9
f(x)=x2−3
f(x)=x2−2x−2
f(x)=x2−2x+37
Ответ может отличаться
Квадратные уравнения: резюме
Онлайн-заметки Пола
Главная
/
Алгебра
/
Решение уравнений и неравенств
/ Квадратные уравнения: резюме
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.7: Квадратные уравнения: Краткий обзор
В предыдущих двух разделах мы довольно много говорили о решении квадратных уравнений. На этом этапе возникает логичный вопрос: какой метод следует использовать для решения заданного квадратного уравнения? К сожалению, ответ таков: это зависит.
Если ваш инструктор указал метод для использования, то, конечно же, вы должны использовать именно его. Однако, если ваш инструктор НЕ указал метод для использования, мы должны будем сами принять решение. Вот общий набор рекомендаций, которые могут быть полезны при определении того, какой метод следует использовать.
- Явно ли это проблема свойства квадратного корня? Другими словами, состоит ли уравнение ТОЛЬКО из чего-то квадрата и константы. Если это так, то свойство квадратного корня, вероятно, является самым простым методом для использования.
- Фактор? Если да, то это, вероятно, путь. Обратите внимание, что вам не следует тратить много времени на то, чтобы определить, влияет ли квадратное уравнение на факторы. Посмотрите на уравнение, и если вы можете быстро определить, что оно влияет, тогда используйте его. Если вы не можете быстро определить, что это влияет, не беспокойтесь об этом.
- Если вы достигли этой точки, значит, вы определили, что уравнение имеет неправильную форму для свойства квадратного корня и что оно не учитывается (или что вы не можете быстро увидеть, что оно учитывается). Итак, на данный момент единственным реальным вариантом для вас является квадратичная формула.
Как только вы решите достаточное количество квадратных уравнений, приведенный выше набор рекомендаций станет для вас почти второй натурой, и вы обнаружите, что выполняете их почти не задумываясь.
Обратите также внимание, что нигде в наборе указаний не было заполнения упомянутого квадрата. Причина этого просто в том, что это долгий метод, который подвержен ошибкам, когда вы спешите. Квадратичная формула также всегда будет работать, и ее метод намного короче. Как правило, вы должны использовать заполнение квадрата только в том случае, если ваш инструктор потребовал от вас его использования.
В качестве решающей техники заполнение квадрата всегда должно быть вашим последним выбором. Однако это не означает, что это не важный метод. Мы увидим, как процесс завершения квадрата возникает в нескольких разделах последующих глав. Интересно, что когда мы увидим этот процесс в последующих разделах, мы не будем решать уравнения! Этот процесс очень полезен во многих ситуациях, решение которых — только одна из них.
Перед тем, как покинуть этот раздел, у нас есть еще одна тема для обсуждения. В предыдущих парах разделов мы видели, что при решении квадратного уравнения в стандартной форме 92} + Ьх + с = 0\]
мы получим один из следующих трех возможных наборов решений.
- Два действительных различных ( т.е. не равных) решения.
- Двойной корень. Вспомните, это возникает, когда мы можем разложить уравнение на идеальный квадрат.
- Два комплексных решения.
Это ЕДИНСТВЕННЫЕ возможности решения квадратных уравнений в стандартной форме. Обратите внимание, однако, что если мы начнем с рационального выражения в уравнении, мы можем получить разные наборы решений, потому что нам может потребоваться избежать одного из возможных решений, чтобы мы не получили ошибки деления на ноль. 92} — 4ас > 0\). В этом случае мы будем брать квадратный корень из положительного числа, поэтому квадратный корень будет действительным числом. Следовательно, числитель в квадратной формуле будет равен -\(b\) плюс-минус действительное число. Это означает, что в числителе будут два разных действительных числа. Разделение любого из них на 2\(a\) не изменит того факта, что они реальны, и не изменит того факта, что они различны.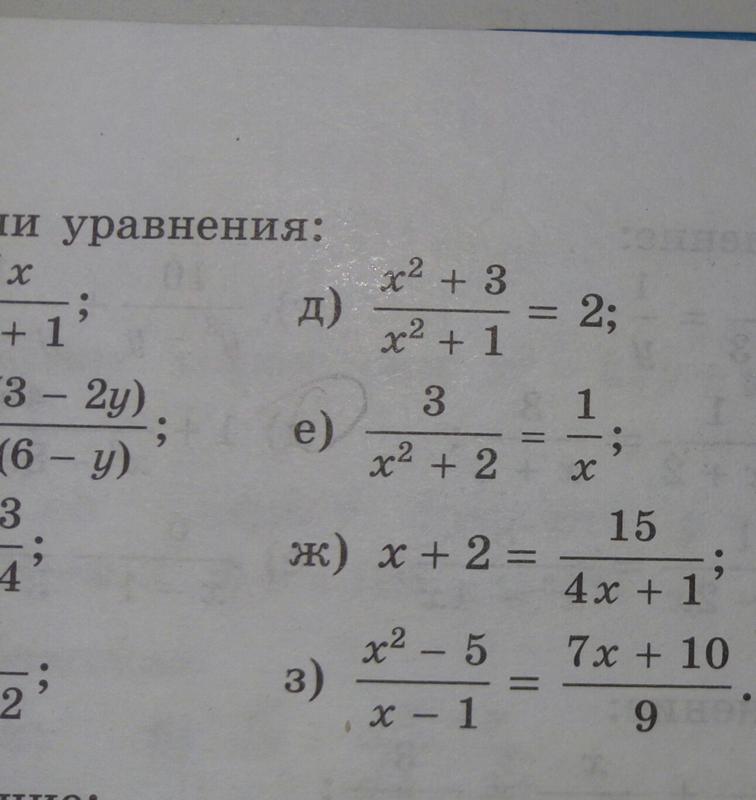

 После решения эквивалентного уравнения вернитесь к исходной переменной и решите ее.
После решения эквивалентного уравнения вернитесь к исходной переменной и решите ее.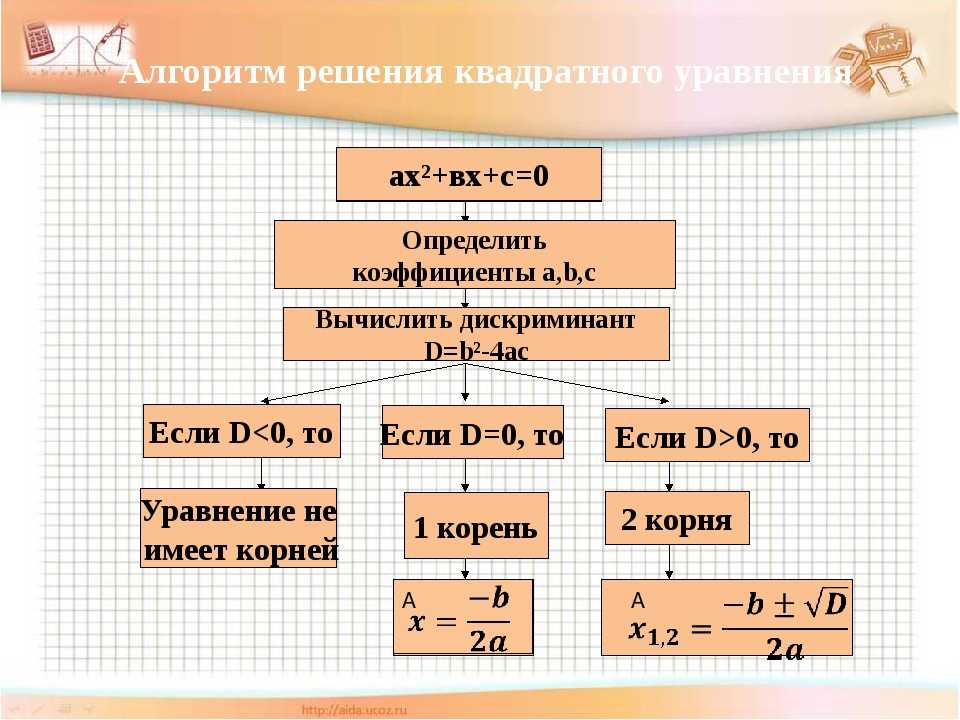 Поделитесь своей стратегией на доске обсуждений.
Поделитесь своей стратегией на доске обсуждений.