Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12), для ввода обыкновенных дробей воспользуйтесь знаком «/» (например, 1/2 или 3/4).
Что такое квадратное уравнение и как его решать
Уравнение вида ax2 + bx + c = 0 называется квадратным.
Решить квадратное уравнение означает найти его корни, а миненно x1 и x2, либо установить, что корней нет.
Числа a, b, c — называются коэфициентами квадратного уравнения, где a ≠ 0.
Каждый коэфициент квадратного уравнения имеет название:
a — старший коэфициент
b — средний коэфициент
c — свободный член
Если коэфициент b или c или оба этих коэфициента равны нулю, то такое уравнение называется неполным.
Дискриминант квадратного уравнения D выражается следующей формулой D = b2 — 4ac.
Прежде всего при решении квадратного уравнения необходимо найти его дискрименант.
Если D > 0, то уравнение имеет два действительных корня, которые можно найти по формуле:
Если D = 0, то корни квадратного уравнения равны, по сути уравнение имеет один корень, например 9x2=0. При D = 0 необходимо воспользоваться формулой:
Если D , например, 5x2 + 6x + 7 = 0, 20x2 + 2x + 3 = 0.
При D
Примеры решения квадратных уравнений
Пример 1
7x2 + 14x — 3 = 0
Найдем дискриминант D квадратного уравнения 7x2 + 14x — 3 = 0.В данном уравнении a = 7; b = 14; c = -3, тогда
D = b2 — 4ac = 142 — 4 · 7 · (-3) = 280
Дискриминант уравнения больше нуля, следовательно, уравнение имеет два корня.
При D > 0 корни x1 и x2
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
ОТВЕТ
Пример 2
35x2 — 47x = 0
Найдем дискриминант D квадратного уравнения 35x2 — 47x = 0.В данном уравнении a = 35; b = -47; c = 0, тогда
D = b2 — 4ac = (-47)2 — 4 · 35 · 0 = 2209
Дискриминант уравнения больше нуля, следовательно, уравнение имеет два корня.
При D > 0 корни x1 и x2 квадратного уравнения ax2 + bx + c = 0 находятся по формуле
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
ОТВЕТ
Пример 3
35x2 + x + 9 = 0
Найдем дискриминант D квадратного уравнения 35x2 + x + 9 = 0.В данном уравнении a = 35; b = 1; c = 9, тогда
D = b2 — 4ac = 1
Дискриминант меньше нуля, следовательно, уравнение не имеет действительных корней. Корнями уравнения могут быть только комплексные числа.
При D < 0 корни x1 и x2 квадратного уравнения ax2 + bx + c = 0 находятся по формуле
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
ОТВЕТ
| -17.5 + (620.941824972356)i | ||
| -17.5 — (620.941824972356)i | ||
Пример 4
x2 + x — 6 = 0
Найдем дискриминант D квадратного уравнения x2 + x — 6 = 0.В данном уравнении a = 1; b = 1; c = -6, тогда
D = b2 — 4ac = 12 — 4 · 1 · (-6) = 25
Дискриминант уравнения больше нуля, следовательно, уравнение имеет два корня.
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
ОТВЕТ
Механика
Электричество и магнетизм
Конденсаторы
Решить уравнение с корнем онлайн калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Довольно часто в уравнениях встречается знак корня и многие ошибочно считают, что такие уравнения сложные в решении. Для таких уравнений в математике существует специальный термин, которым и именуют уравнения с корнем — иррациональные уравнения.
Главным отличием в решении уравнений с корнем от других уравнений, например, квадратных, логарифмических, линейных, является то, что они не имеют стандартного алгоритма решения. Поэтому чтобы решить иррациональное уравнение необходимо проанализировать исходные данные и выбрать более подходящий вариант решения.

Так же читайте нашу статью «Решить уравнения онлайн решателем»
В большинстве случаев для решения данного рода уравнений используют метод возведения обеих частей уравнения в одну и ту же степень
Допустим, дано следующее уравнение:
\[\sqrt{(5x-16)}=x-2\]
Возводим обе части уравнения в квадрат:
\[\sqrt{(5х-16))}^2 =(x-2)^2\], откуда последовательно получаем:
\[5x-16=x^2-4х+4\]
\[x^2-4x+4-5x+16=0\]
\[x^2-9x+20=0\]
Получив квадратное уравнение, находим его корни:
\[x=(9\pm\sqrt{(81-4\cdot1\cdot20)\div(2\cdot1)}\]
\[x=(9\pm1)\div 2\]
Ответ: \[x1=4, x2=5\]
Если выполнить подстановку данных значений в уравнение, то получим верное равенство, что говорит о правильности полученных данных.
Где можно решить уравнение с корнями онлайн решателем?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Калькулятор корней с решением онлайн
Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12), для ввода обыкновенных дробей воспользуйтесь знаком «/» (например, 1/2 или 3/4).
Корень в математике
Операция извлечения корня из числа, является обратной операцией к операции возведения в степень.
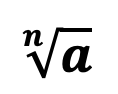
Обозначение: корень обозначается при помощи символа, который называется знаком корня. Число a, которое находится под корнем называется подкоренным выражением, а число n, расположенное слева от символа корня, называется – степенью корня.
Степень корня – должна быть выражена натуральным числом (1, 2, 3, 4, 5…), т.е. не может быть отрицательной, нулем или дробным числом.
По сути, как уже было сказано выше извлечь корень из числа а означает возведение числа a в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня.
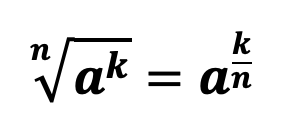
Следует заметить, что если степень корня равна 2, то число два как правило не пишут, а такой корень называется – квадратным.
Приведем примеры:
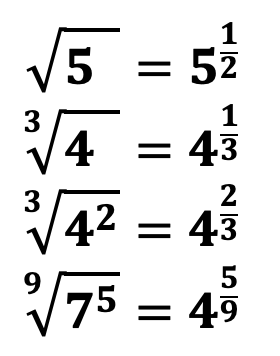
Приведем примеры извлечения корня:
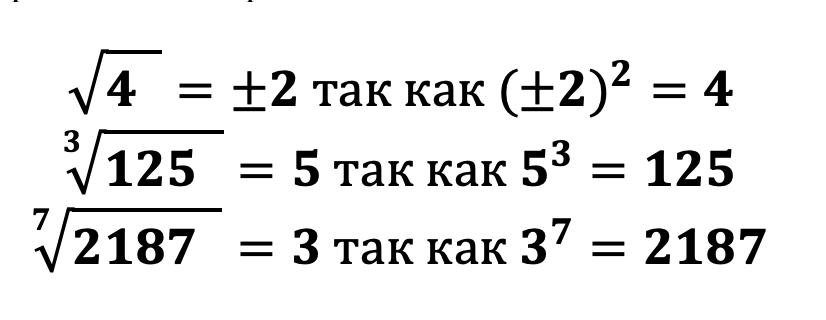
Исходя из вышенаписанных примеров можно сделать вывод, что когда мы хотим извлечь корень, к примеру 2-й степени, то нам необходимо найти такое число, что при возведении во 2-ю степень мы получим подкоренное выражение. То есть под корнем всегда находится число, уже возведенное в степень равную степени корня!
Четная и нечетная степень корня
Корень нечетной степени
При извлечении корня нечетной степени из положительного числа будем всегда получать положительное число, например:
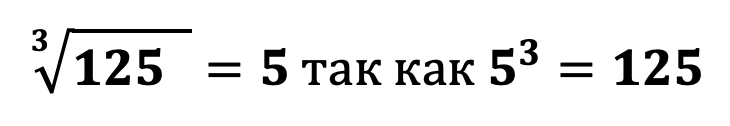
При извлечении корня нечетной степени из отрицательного числа будем всегда получать отрицательное число, например
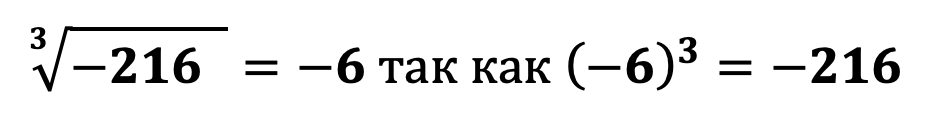
В данном примере можно легко увидеть почему при извлечении корня нечетной степени из отрицательного числа всегда будет получаться отрицательно число. Как известно чтобы возвести число в степень необходимо его умножить само на себя в количестве показателя степени : если (-6) умножить на (-6) получится положительное число 36 (мы знаем, что при умножении двух отрицательных чисел будет получаться положительное число), затем если умножить число 36 на (-6) получим -216, так как при умножении отрицательного числа на положительное всегда будет получаться отрицательное число.
Корень четной степени
При извлечении корня четной степени из положительного числа всегда будет получать два значения с противоположенными знаками. Это связанно с тем, что если представить, к примеру функцию квадратного корня y= √x и посмотреть на ее график, то мы увидим, что каждому значению xсоответствует два значения корня, одно положительное, а другое отрицательное.
Для понимания данного факта, нет необходимости строить график, рассмотрим на примере извлечение квадратного корня из числа 4:

Квадратный корень из 4 равен 2 так как = 4 и . Проверим 2 ⋅ 2 = 4 и -2 ⋅(-2) = 4.
Приведем еще пример с четной степенью корня для положительного числа.

Корень степени 4 за числа 81 равен 3 так как = 81 и . Проверим 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81 и -3 ⋅ (-3) ⋅ (-3) ⋅ (-3) = 81
Теперь рассмотрим ситуацию, когда под корнем четной степени стоит отрицательное число.
Допустим, мы ходим извлечь квадратный корень из отрицательного числа, например, √-4 теперь подумаем есть ли вообще такое число, которое при возведении в квадрат давало бы -4? Ответ – нет! Любое число при возведении в четную степень всегда будет положительным. Поэтому корня чётной степени из любого отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число.
Тем не менее извлечь корень четной степени всё-таки можно, но результатом будет всегда комплексное число, например:
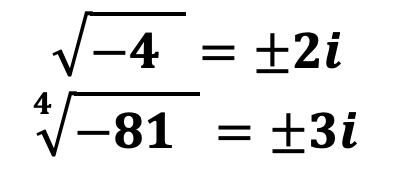
Арифметический и алгебраический корни
Для упрощения записи корня четной степени из положительного числа, в калькуляторах, школьных учебниках и т.д. было введено понятие арифметического корня, значение которого, представляется всегда положительным числом. Алгебраический корень в свою очередь для корня четной степени из положительного числа является полным ответом и содержит как положительные, так и отрицательные значения.
Арифметический корень – упрощенная запись корня четной степени из положительного числа, всегда положительный. Например:
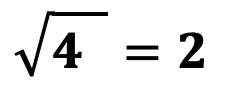
Алгебраический корень – полная запись корня четной степени из положительного числа. Например:
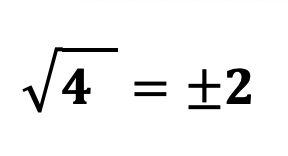
Как упростить корень
Для того, чтобы упростить любой корень, необходимо разложить подкоренное выражение на простые множители (для разложения числа на простые множители можно воспользоваться калькулятором разложения числа на простые множители) и вынести за знак корня тот множитель, который повторяется равное степени корня число раз. Например:
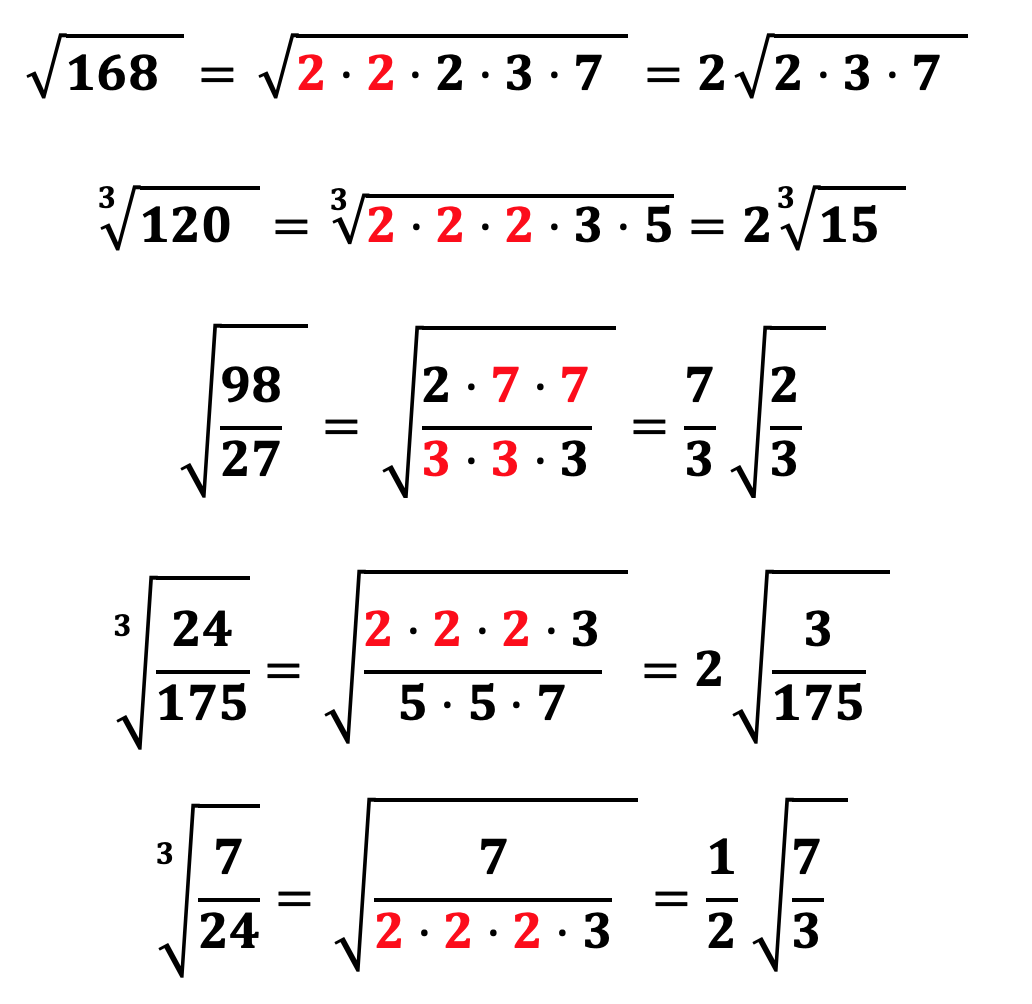
Как мы уже разобрали извлечь корень из числа а означает возведение числа a в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня, поэтому следуя данному правилу мы легко выносим множители из под корня. Распишем предыдущие два примера еще раз:
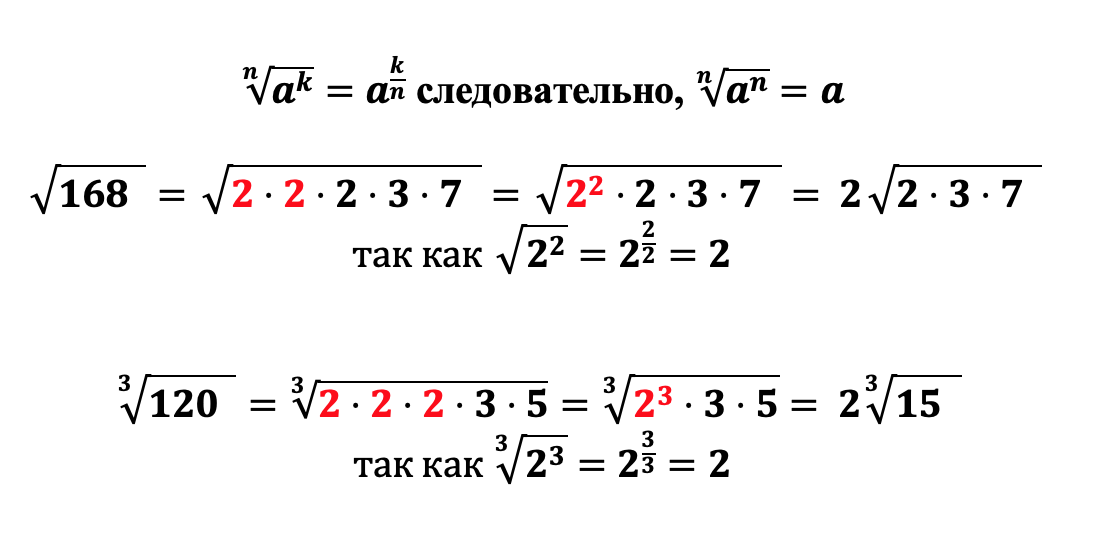
Решение квадратных уравнений онлайн
С помощю этого онлайн калькулятора можно найти решение (корни) квадратного уравнения. Дается подробное решение с пояснениями. Для нахождения решений квадратного уравнения введите коэффициенты уравнения и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Корни квадратного уравнения − теория примеры и решения
Квадратным уравнением называется уравнение следующего вида:
где x−переменная, а a, b, c некоторые числа (a≠0). Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.
Если a=1, то квадратное уравнение называется приведенным. Заметим, что любое квадратное уравнение можно привести к приведенному виду, разделив обе части уравнения на a. Действительно:
Если в квадратном уравнении (1) один из коэффициентов b, c равен нулю или оба коэффициента b, c равны нулю, то квадратное уравнение называется неполным.
Рассмотрим разные виды неполных квадратных уравнений.
1. При b=0 имеем:
Для решения этого уравнения свободный член перенесем в правую часть уравнения:
Решая последнее уравнение относительно x получим корни квадратного уравнения (3):
Если  , то квадратное уравнение не имеет действительных корней.
, то квадратное уравнение не имеет действительных корней.
2. При c=0 имеем:
Разложим левую часть последнего уравнения на множители:
Из (4) следует x=0 или ax+b=0. Следовательно имеем следующие решения:
 |
3. При b=0, c=0 имеем:
и, следовательно
Рассмотрим, далее, алгоритм решения квадратных уравнений общего вида (1). Разделим обе части уравнения на a:
Сделаем эквивалентные преобразования уравнения (5):
Легко догадаться, что первые три слагаемые уравнения (6) образуют квадрат следующей суммы:
 |
Тогда
Обозначим
D− называется дискриминантом квадратного уравнения (1). Так как a≠0, то 4a2>0. Знак правой части уравнения (7) определяется знаком дискриминанта D.
Учитывая (8) запишем (7) в следующем виде:
При решении последнего уравнения возможны следующие варианты:
1. При D>0, имеем
Таким образом, при D>0, квадратное уравнение (1) имеет две корни:
2.При D=0, имеем
 |
То есть, при D=0 квадратное уравнение (1) имеет единственный корень:
 |
3. При D<0, правая часть уравнения (9) отрицательна, а так как квадрат числа не может быть отрицательным числом, то квадратное уравнение (1) не имеет корней.
Пример 1. Решить квадратное уравнение
 . . | (10) |
Решение. Запишем коэффициенты квадратного уравнения (10):
 |
Вычислим дискриминант квадратного уравнения:
 . . |
Дискриминант положительное число. Следовательно квадратное уравнение (10) имеет два решения.
Найдем решение квадратного уравнения используя следующую формулу:
 . . | (11) |
Подставляя значения коэффициентов a, b, c, D в (11), получим:
 , , |
 . . |
Ответ:
Пример 2. Решить следующее квадратное уравнение:
 . . | (12) |
Решение. Запишем коэффициенты квадратного уравнения (12):
 |
Вычислим дискриминант квадратного уравнения:
 . . |
Дискриминант равен нулю. Следовательно квадратное уравнение (12) имеет единственное решение. Найдем решение квадратного уравнения используя следующую формулу:
 . . | (13) |
Подставляя значения коэффициентов a, b, c, D в (13), получим:
 , , |
Ответ:
 . . |
Пример 3. Решить следующее квадратное уравнение:
 . . | (14) |
Решение. Запишем коэффициенты квадратного уравнения (14):
 |
Вычислим дискриминант квадратного уравнения:
 . . |
Дискриминант отрицательное число. Следовательно квадратное уравнение (14) не имеет действительных корней.
Ответ: Квадратное уравнение не имеет действительных корней.
Применение квадратных уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Квадратные уравнения человек использовал еще в древности и с тех пор их применение только возрастает.

— без корней:
— с 1 корнем;
— с 2 корнями.
Это самое главное отличие квадратных уравнений от линейных. Для определения корней используют дискриминант: \[D=b^2-4ac\]. По знаку дискриминанта определяется количество корней:
— \[D
— \[D = 0\] — 1 корень;
— \[D > 0\] — 2 корня.
Все это позволит быстро найти правильный путь в решении квадратного уравнения, онлайн можно найти огромное количество решенных разными способами примеров.
Так же читайте нашу статью «Решить систему рациональных уравнений онлайн «
Допустим, нам даны следующие квадратные уравнения:
\[1 — x^2-7x = 0;\]
\[2 — 5x^2+ 30 = 0;\]
\[3 — 4x^2- 9 = 0\]
Решение:
\[1: x^2 — 7x = 0\]
\[x · (x — 7) = 0\]
\[x_1 = 0; x_2= -(-7)/1 = 7\]
\[2: 5 x^2 + 30 = 0\]
\[5 x^2 = -30\]
\[x^2 = -6\] — здесь нет корней, поскольку отрицательное число, а квадрат отрицательным быть не может.
\[3: 4 x^2 — 9 = 0 \]
\[4 x^2 = 9 \]
\[x^2 = 9/4 \]
\[x_1 = 3/2 = 1,5; x_2 = -1,5\] — нет корней.
Где можно решить квадратное уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Решить квадратное уравнение онлайн
Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.Чтобы произвести решение квадратного уравнения онлайн, вначале приведите уравнение к общему виду:
ax2 + bx + c = 0
Заполните соответственно поля формы:
Как решить квадратное уравнение
| Как решить квадратное уравнение: | Виды корней: |
| 1. Привести квадратное уравнение к общему виду: Общий вид Аx2+Bx+C=0 Пример : 3х — 2х2+1=-1 Приводим к -2х2+3х+2=0 2. Находим дискриминант D. 3. Находим корни уравнения. | 1. Действительные корни. Причем. x1 не равно x2 Ситуация возникает, когда D>0 и A не равно 0. 2. Действительные корни совпадают. x1 равно x2 3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1)1/2 4. Уравнение имеет одно решение. 5. Уравнение имеет бесчисленное множество решений. 6. Уравнение решений не имеет. |
Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений.
Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B2-4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число1/2!
x1=(-В+D1/2)/2А = (-3+7)/2 = 2
x2=(-В-D1/2)/2А = (-3-7)/2 = -5
Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10
Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k2 – AC = 16 – 16 = 0
X = -k/A = 4
Подставим
(x-4)*(x-4) = (x-4)2 = X2 – 8x + 16
Пример 3. Решение квадратного уравнения с комплексными корнями.
13х2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.
x1=(-В+D1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1
Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Иррациональные уравнения бывают от простых до сложных — и всех их можно решить онлайн и с подробным решением с помощью калькулятора онлайн.
Итак:
Простые иррациональные уравнения
Будем считать, что простые уравнения будут содержат только одну часть иррациональности. Тогда рассмотрим пример:
2*x + sqrt(-x + 3) = 3
Введём это уравнение в форму калькулятора

Тогда, вы получите подробное решение:
Дано уравнение
_______ \/ 3 - x + 2*x = 3
_______ \/ 3 - x = 3 - 2*x
Возведём обе части ур-ния в(о) 2-ую степень
Перенесём правую часть уравнения левую часть уравнения со знаком минус
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то
(11)^2 - 4 * (-4) * (-6) = 25
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
Т.к.
_______ \/ 3 - x = 3 - 2*x
и
то
или
Тогда, окончательный ответ:
Средние иррациональные уравнения
Средними же будем считать уравнения, которые содержат две иррациональные части в уравнении.
Например,
sqrt(4*x + 1) + sqrt(3*x — 2) = 2
надо ввести в форму в калькуляторе

Результат будет таким:
Дано уравнение
_________ __________ \/ 1 + 4*x + \/ -2 + 3*x = 2
Возведём обе части ур-ния в(о) 2-ую степень
2
/ _________ __________\
\\/ 1 + 4*x + \/ -2 + 3*x / = 4или
2 _____________________ 2 1 *(3*x - 2) + 2*\/ (3*x - 2)*(4*x + 1) + 1 *(4*x + 1) = 4
или
__________________
/ 2
-1 + 2*\/ -2 - 5*x + 12*x + 7*x = 4преобразуем:
__________________
/ 2
2*\/ -2 - 5*x + 12*x = 5 - 7*xВозведём обе части ур-ния в(о) 2-ую степень
2 2
-8 - 20*x + 48*x = (5 - 7*x)
2 2
-8 - 20*x + 48*x = 25 - 70*x + 49*x Перенесём правую часть уравнения левую часть уравнения со знаком минус
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то
(50)^2 - 4 * (-1) * (-33) = 2368
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
Т.к.
__________________
/ 2 5 7*x
\/ -2 - 5*x + 12*x = - - ---
2 2 и
__________________ / 2 \/ -2 - 5*x + 12*x >= 0
то
или
проверяем:
__________ ___________
-2 + \/ 1 + 4*x1 + \/ -2 + 3*x1 = 0=
_______________________ ________________________ / / ____\ / / ____\ \/ 1 + 4*\25 - 4*\/ 37 / + \/ -2 + 3*\25 - 4*\/ 37 / - 2 = 0
=
— тождество
Тогда, окончательный ответ:
Сложные иррациональные уравнения
Самыми сложными же будут уравнения с тремя частями иррациональностями, значит будет такой пример:
sqrt(x + 5) — sqrt(x — 1) = sqrt(2*x + 4)
В форме калькулятора это будет выглядеть так:

Тогда получите подробное объяснение
Дано уравнение
_______ ________ _________ \/ 5 + x - \/ -1 + x = \/ 4 + 2*x
Возведём обе части ур-ния в(о) 2-ую степень
2
/ _______ ________\
\\/ 5 + x - \/ -1 + x / = 4 + 2*xили
2 _________________ 2 1 *(x + 5) - 2*\/ (x + 5)*(x - 1) + (-1) *(x - 1) = 4 + 2*x
или
_______________
/ 2
4 - 2*\/ -5 + x + 4*x + 2*x = 4 + 2*xпреобразуем:
_______________
/ 2
-2*\/ -5 + x + 4*x = 0преобразуем
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то
(4)^2 - 4 * (1) * (-5) = 36
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
проверяем:
________ _________ __________ \/ 5 + x1 - \/ -1 + x1 - \/ 4 + 2*x1 = 0
=
_______ ________ _______ \/ 5 + 1 - \/ -1 + 1 - \/ 4 + 2 = 0
=
— тождество
________ _________ __________ \/ 5 + x2 - \/ -1 + x2 - \/ 4 + 2*x2 = 0
=
_______ ________ ____________ \/ 5 - 5 - \/ -1 - 5 - \/ 4 + 2*(-5) = 0
=
— Нет
Тогда, окончательный ответ:
Purplemath
Давайте еще раз посмотрим на эту последнюю проблему на предыдущей странице:
На предыдущей странице я решил это квадратное уравнение, разложив разность квадратов в левой части уравнения, а затем установив каждый коэффициент равным нулю и т. Д. И т. Д.Решение было « x = ± 2». Однако —
Я также могу попытаться выделить член с квадратом переменной в левой части уравнения (то есть, я могу попытаться получить сам термин x 2 на одной стороне знака «равно»), переместив числовую часть (то есть 4) в правую часть, например:
MathHelp.ком
Когда я решаю уравнение, я знаю, что я могу делать с этим уравнением все, что мне нравится, если я делаю одно и то же с обеими сторонами этого уравнения . С левой стороны этого конкретного уравнения у меня есть x 2 , и я хочу простой старый x .Чтобы превратить x 2 в x , я могу взять квадратный корень с каждой стороны уравнения, например:
x = ± 2
Тогда решение будет x = ± 2, точно так же, как это было, когда я решил с помощью разности квадратов.
Зачем мне нужен знак «±» (то есть «плюс-минус») на 2, когда я взял квадратный корень из 4? Потому что я пытаюсь найти всех значений переменной, которые делают исходное утверждение истинным, и это могло быть либо положительное 2, либо отрицательное 2, которое было возведено в квадрат, чтобы получить это 4 в исходном уравнении.
Эта двойственность похожа на то, как у меня было два фактора, один «плюс» и один «минус», когда я использовал формулу разности квадратов для решения этого же уравнения на предыдущей странице.
«Нахождение решения уравнения» — это процесс, очень отличающийся от , от «вычисления квадратного корня числа». Находя квадратный корень числа, мы имеем дело исключительно с положительным значением. Зачем? Потому что так определяется квадратный корень числа.Значение квадратного корня числа может быть только положительным, потому что именно так определяется «квадратный корень числа».
Решение уравнения, с другой стороны, то есть поиск всех возможных значений переменной, с которой может работать в уравнении, отличается от простой оценки выражения, которое уже определило как имеющее только одно значение.
Держи этих двоих прямо! Квадратное число имеет только одно значение, а уравнение с квадратными корнями имеет два значения из-за переменной.
В математике нам нужно уметь получать один и тот же ответ, независимо от того, какой правильный метод мы использовали для получения этого ответа. Таким образом, сравнивая ответ, который я получил выше, с ответом, который я получил на предыдущей странице, подтверждает, что мы должны использовать «±», когда принимаем квадратные корни для решения.
(Возможно, вы сомневаетесь в моей работе выше на шаге, где я взял квадратный корень с любой стороны, потому что я поставил знак «±» только на одной стороне уравнения.Разве я не должен добавить этот символ к обеим сторонам уравнения? Вроде да. Но если бы я поместил это в обе части уравнения, что-нибудь действительно изменилось бы? Нет. Попробуйте все случаи, если вы не уверены.)
Преимущество этого процесса с квадратным корнем состоит в том, что он позволяет нам решать некоторые квадратики, которые мы не могли бы решить раньше при использовании только факторинга. Например:
Этот квадрат имеет квадратную и числовую части.Я начну с добавления числового термина к другой стороне уравнения (таким образом, квадратная часть будет сама по себе), а затем получу квадратный корень с обеих сторон. Мне нужно запомнить, чтобы упростить квадратный корень:
x 2 — 50 = 0
x 2 = 50
Тогда мое решение:
Хотя мы могли бы получить предыдущее целочисленное решение с помощью факторинга, мы никогда не смогли бы получить это радикальное решение с помощью факторинга.Факторинг явно полезен для решения некоторых квадратных уравнений, но дополнительные виды методов позволяют нам находить решения дополнительных видов уравнений.
Решить ( x — 5) 2 — 100 = 0.
Этот квадрат имеет квадратную и числовую части.Я начну с добавления строго числового члена в правую часть уравнения, чтобы квадратное биномиальное выражение, содержащее переменную, само находилось в левой части. Затем я получу квадратный корень с обеих сторон, вспомнив «±» на числовой стороне, а затем упросту:
( x — 5) 2 — 100 = 0
( x — 5) 2 = 100
x — 5 = ± 10
x = 5 ± 10
x = 5 — 10 или x = 5 + 10
x = –5 или x = 15
Это уравнение, после получения квадратного корня с любой стороны, не содержало радиальных значений.Благодаря этому я смог упростить свои результаты, вплоть до простых значений. Мой ответ:
Предыдущее уравнение является примером уравнения, в котором неосторожный ученик при решении опускает знак «±», а затем понятия не имеет, как книга получила ответ « x = –5, 15».
Эти студенты имеют плохую привычку не беспокоиться о том, чтобы писать знак «±», пока они не проверят свои ответы в конце книги и внезапно не «вспомнят», что они «хотели» вставить «±», когда они d взял квадратный корень с любой стороны уравнения.
Но эта «магия» работает только тогда, когда у вас есть ответ сзади (чтобы напомнить вам) и когда решение содержит радикалы (что не всегда происходит). В остальных случаях не будет «напоминания». Особенно на тестах, ошибка опускания «±» может быть смертельной. Не будь этим учеником. Всегда не забывайте вставлять «±».
Кстати, поскольку решение предыдущего уравнения состояло из целых чисел, этот квадратик также можно было бы решить путем умножения квадрата, факторинга и т. Д .:
( x — 5) 2 — 100 = 0
x 2 — 10 x + 25 — 100 = 0
x 2 — 10 x — 75 = 0
( x — 15) ( x + 5) = 0
x — 15 = 0, x + 5 = 0
x = 15, –5
Решить ( x — 2) 2 — 12 = 0
Этот квадрат имеет квадратную и числовую части.Я добавлю числовую часть на другую сторону, так что квадрат с переменной будет сам по себе. Затем я получу квадратный корень с обеих сторон, не забывая добавить «±» к числовой стороне, а затем я упросту:
( x — 2) 2 — 12 = 0
( x — 2) 2 = 12
Я не могу упростить это больше.В моем ответе будут радикалы. Мое решение:
Это квадратное уравнение, в отличие от предыдущего, также не могло быть решено с помощью факторинга. Но как бы я решил это, если бы они имели , а не , дав мне квадратик, уже введенный в форму «(квадратная часть) минус (числовая часть)»? Эта проблема приводит к следующей теме: решение путем заполнения квадрата.
URL: https://www.purplemath.com/modules/solvquad2.htm
,Решение радикальных уравнений
Как решать уравнения с квадратными корнями, кубическими корнями и т. Д.
Радикальные уравнения
Решение радикальных уравнений
Мы можем избавиться от квадратного корня, возведя в квадрат. (Или кубиками, кубами и т. Д.)
Но Предупреждение: это может иногда создавать «решения», которые на самом деле не работают, когда мы помещаем их в исходное уравнение. Так что нам нужно проверить!
Выполните следующие действия:
- изолировать квадратный корень на одной стороне уравнения
- квадратных обе стороны уравнения
Тогда продолжайте с нашим решением!
Пример: решить √ (2x + 9) — 5 = 0
изолировать квадратный корень: √ (2x + 9) = 5
квадрат с обеих сторон: 2x + 9 = 25
Теперь это должно быть проще решить!
Переместить 9 вправо: 2x = 25 — 9 = 16
Разделите на 2: x = 16/2 = 8
Ответ: х = 8
Проверка: √ (2 · 8 + 9) — 5 = √ (25) — 5 = 5 — 5 = 0
Тот работал отлично.
Больше чем один квадратный корень
Что если есть два или более квадратных корня? Легко! Просто повторите процесс для каждого.
Это будет дольше (намного больше шагов) … но ничего сложного.
Пример: решить √ (2x − 5) — √ (x − 1) = 1
изолировать один из квадратных корней: √ (2x − 5) = 1 + √ (x − 1)
квадрат с обеих сторон: 2x − 5 = (1 + √ (x − 1)) 2
Мы удалили один квадратный корень.
расширить правую часть: 2x − 5 = 1 + 2√ (x − 1) + (x − 1)
Упрощение: 2x − 5 = 2√ (x − 1) + x
отнимите x с обеих сторон: x − 5 = 2√ (x − 1)
Теперь снова сделайте «квадратный корень»:
изолировать квадратный корень: √ (x − 1) = (x − 5) / 2
квадрат с обеих сторон: x − 1 = ((x − 5) / 2) 2
Мы успешно удалили оба квадратных корня.
Давайте продолжим с решением.
Расширить правую часть: x − 1 = (x 2 — 10x + 25) / 4
Это квадратное уравнение! Итак, давайте изложим это в стандартной форме.
Умножьте на 4, чтобы удалить деление: 4x − 4 = x 2 — 10x + 25
Принесите все влево: 4x — 4 — x 2 + 10x — 25 = 0
Объединить аналогичные термины: −x 2 + 14x — 29 = 0
Поменяйте местами все знаки: x 2 — 14x + 29 = 0
Использование квадратичной формулы (a = 1, b = −14, c = 29) дает решения:
2.53 и 11,47 (до 2 десятичных знаков)
Давайте проверим решения:
2,53: √ (2 × 2,53−5) — √ (2,53−1) ≈ −1 Упс! Должно быть плюс 1.
11,47: √ (2 × 11,47−5) — √ (11,47−1) ≈ 1 Да, это работает.
Существует действительно только одно решение :
Ответ: 11,47 (до 2 десятичных знаков)
Видите? Этот метод может иногда производить решения, которые на самом деле не работают!
Корень, который, казалось, работал, но не был прав, когда мы проверили его, называется «Посторонний корень»
Итак: проверка важна.
,Purplemath
Квадратное уравнение в последнем примере предыдущей страницы было:
Выражение в левой части этого уравнения можно умножить и упростить до:
Но мы все равно не смогли бы решить уравнение, даже если квадратик отформатирован таким образом, потому что он не учитывает и не готов к квадратному корню.
MathHelp.com
Единственная причина, по которой мы смогли решить эту проблему на предыдущей странице, заключалась в том, что они уже поместили весь материал x в квадрат, чтобы мы могли переместить строго числовую часть уравнения на другую сторону от «равно» знак, а затем квадратный корень с обеих сторон.Они не всегда будут форматировать вещи так хорошо, как это. Итак, как нам перейти от регулярного квадратика, подобного приведенному выше, к уравнению, готовому к квадратным корням?
Нам нужно будет «завершить квадрат».
Вот как мы решили бы последнее уравнение на предыдущей странице, если бы они не отформатировали его для нас.
Используйте завершение квадрата для решения x 2 — 4 x — 8 = 0.
Как отмечалось выше, это квадратичное значение не учитывается, поэтому я не могу решить уравнение с помощью факторинга. И они не дали мне уравнение в форме, которая готова к квадратному корню. Но у меня есть способ манипулировать квадратиком, чтобы поместить его в форму, готовую для квадратного корня, чтобы я мог решить.
Сначала я поставил число с другой стороны уравнения:
x 2 — 4 x — 8 = 0
x 2 — 4 x = 8
Затем я смотрю на коэффициент x , который в данном случае равен –4.Я беру половину этого числа (, включая знак ), что дает мне -2. (Мне нужно отслеживать это значение. Это упростит мою работу позже.)
Затем я возводю это значение в квадрат, чтобы получить +4, и добавляю это квадратное значение к обеим сторонам уравнения:
x 2 — 4 x + 4 = 8 + 4
x 2 — 4 x + 4 = 12
Этот процесс создает квадратное выражение, представляющее собой идеальный квадрат в левой части уравнения.Я могу учесть, или я могу просто заменить квадратичную форму квадратом-биномом, которая является переменной, x , вместе с половиной числа, которое я получил раньше (и отметил, что мне нужно будет позже), которое было -2. В любом случае, я получаю квадратное уравнение:
(я знаю, что это «–2» в скобках, потому что половина –4 была –2. Отмечая знак, когда я нахожу половину коэффициента, я помогаю себе не запутаться в знаке позже, когда Я перехожу в квадратно-биномиальную форму.)
(Кстати, этот процесс называется «завершением квадрата», потому что мы добавляем термин для преобразования квадратного выражения в нечто, что считается квадратом бинома; то есть мы «завершили» выражение для создания бином идеального квадрата.)
Теперь я могу получить квадратный корень с обеих сторон уравнения, упростить и решить:
( x — 2) 2 = 12
Используя этот метод, я получаю тот же ответ, что и раньше; а именно:
Решите 2 x 2 — 5 x + 1 = 0, заполнив квадрат.
Существует один дополнительный шаг для решения этого уравнения, поскольку старший коэффициент не равен 1; Сначала мне нужно разделить, чтобы преобразовать ведущий коэффициент в 1. Вот мой процесс:
2 x 2 — 5 x + 1 = 0
x 2 — (5/2) x + 1/2 = 0
x 2 — (5/2) x = — (1/2)
Теперь, когда у меня есть все слагаемые с переменными на одной стороне, а на другой стороне строго числовой, я готов заполнить квадрат с левой стороны.Сначала я беру коэффициент линейного члена (вместе со знаком), — (5/2) и умножаю на половину, а квадрат:
(1/2) × [- (5/2)] = — (5/4)
(- (5/4)) 2 = 25/16
Затем я добавляю это новое значение в обе стороны, преобразую в квадратно-биномиальную форму слева и решаю:
x 2 — (5/2) x + 25/16 = — (1/2) + 25/16
( x — 5/4) 2 = 17/16
кв.м. [( x — 5/4) 2 ] = ± кв.м. [17/16]
x — 5/4 = ± sqrt [17] / 4
x = 5/4 ± sqrt [17] / 4
Два термина в правой части последней строки выше могут быть объединены по общему знаменателю, и это часто («обычно»?), Как ответ будет написан, особенно если инструкции для упражнения включали условие «упростить» окончательный ответ:
В другом месте у меня есть урок только по решению квадратного уравнения путем заполнения квадрата.Этот урок (повторно) объясняет шаги и дает (больше) примеров этого процесса. Это также показывает, как квадратичная формула может быть получена из этого процесса. Если вам нужны дальнейшие инструкции или практика по этой теме, прочитайте урок по приведенной выше гиперссылке.
Между прочим, если вам не сказали, что у вас есть , чтобы использовать для завершения квадрата, вы, вероятно, никогда не будете использовать этот метод в реальной практике при решении квадратных уравнений. Либо какой-то другой метод (например, факторинг) будет очевидным и более быстрым, иначе будет проще использовать Квадратичную формулу (рассмотренную далее).Однако, если ваш класс покрыл завершение квадрата, вам следует ожидать, что вы должны показать, что вы можете заполнить квадрат, чтобы решить квадратик в следующем тесте.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении квадратных уравнений, заполнив квадрат. Попробуйте введенное упражнение или введите собственное упражнение. Затем нажмите кнопку и выберите «Решить, заполнив квадрат», чтобы сравнить свой ответ с Mathway.(Или пропустите виджет и перейдите на следующую страницу.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvquad3.htm
,Purplemath
Кто-то (возможно, в седьмом веке в Индии) решал множество квадратных уравнений, заполняя квадрат. В какой-то момент он (и да, тогда это был бы парень) заметил, что он всегда делал одни и те же шаги в одном и том же порядке для каждого уравнения.
Великая сила алгебры в том, что она дает нам возможность работать с абстракциями, такими как формулы, которые всегда работают. Это может избавить нас от бремени и беспорядка, связанного с тем, чтобы разбираться с числами каждый раз, когда мы делаем одно и то же. Используя эту силу в отношении решения квадратиков путем заполнения квадрата, он составил формулу из того, что он делал; а именно, квадратичная формула, которая гласит:
MathHelp.ком

Квадратичная формула: дано квадратное уравнение в следующем виде:
… где a , b и c являются числовыми коэффициентами членов квадратичного, значение переменной x определяется следующим уравнением:
Хорошая вещь в квадратичной формуле состоит в том, что квадратичная формула всегда работает.Есть некоторые квадратики (большинство из них на самом деле), которые мы не можем решить с помощью факторинга. Но Квадратичная Формула всегда выдаст ответ, независимо от того, было ли квадратичное выражение факториальным.
Давайте попробуем эту первую проблему с предыдущей страницы еще раз, но на этот раз мы будем использовать Квадратичную формулу вместо кропотливого процесса заполнения квадрата:
Используйте Квадратичную формулу для решения x 2 — 4 x — 8 = 0
Квадратичная формула требует, чтобы у меня было квадратичное выражение на одной стороне знака «равно», а «ноль» — на другой.Они дали мне уравнение уже в этой форме. Также Формула задается в терминах числовых коэффициентов членов квадратичного выражения. Глядя на коэффициенты в этом уравнении, я вижу, что a = 1, b = –4 и c = –8. Я вставлю эти цифры в формулу и упросту. (Я должен получить тот же ответ, что и раньше.)
Это тот же ответ, который я получил раньше, который подтверждает, что Квадратичная формула работает как задумано.Еще раз, мой окончательный ответ:
Хорошая вещь в квадратичной формуле (по сравнению с завершением квадрата) состоит в том, что мы просто подключаемся к формуле. Нет «шагов» для запоминания, и, следовательно, меньше ошибок. Как говорится:
Старайтесь не опускать знак «±» перед радикалом.
Не рисуйте линию дроби как находящуюся только под квадратным корнем, потому что она также находится под начальной частью «- b «.
Не забывайте, что знаменатель формулы — «2 и », а не просто «2». То есть, когда начальный термин имеет вид «5 x 2 », вам нужно помнить, чтобы в знаменателе было указано значение « a = 5».
Используйте круглые скобки вокруг коэффициентов при первом включении их в формулу, особенно когда любой из этих коэффициентов является отрицательным, чтобы вы не потеряли знаки «минус».
Решить 4 x 2 + 3 x — 2 = 0 с использованием квадратичной формулы.
Сначала я зачитаю значения коэффициентов, которые буду вставлять в формулу:
Теперь все, что мне нужно сделать, это вставить эти значения в формулу и упростить, чтобы получить мой ответ:
x = [- (3) ± sqrt {(3) 2 — 4 (4) (- 2}] / [2 (4)]
= [–3 ± sqrt {9 + 32}] / [8]
= [–3 ± sqrt {41}] / [8]
Абсолютно ничего здесь не упростит, так что я закончил.Мой ответ:
x = [–3 ± sqrt {41}] / [8]
Вы должны обязательно запомнить Квадратичную формулу. Мне все равно, если ваша учительница скажет, что собирается дать ее вам на следующем тесте; все равно запомни это, потому что оно тебе понадобится позже. Это не так долго, и есть даже песня, которая поможет вам вспомнить ее, настроенная на мелодию «Pop Goes the Weasel»:
X равно отрицательному B
Плюс или минус квадратный корень
Из B в квадрате минус четыре A C
Всего более двух A
(Эта песня не оригинальна для меня.Я узнал об этом в другом месте.)
При использовании формулы, не торопитесь, потому что, пока вы аккуратно выполняете свою работу, Квадратичная формула будет давать вам правильный ответ каждый раз.
У меня есть урок по квадратичной формуле, который предоставляет проработанные примеры и показывает связь между дискриминантом (часть « b 2 — 4 ac » внутри квадратного корня), числом и типом решений квадратное уравнение и график связанной параболы.Если вам нужна дополнительная помощь по формуле, изучите урок по приведенной выше гиперссылке.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении квадратных уравнений с помощью квадратичной формулы. Попробуйте введенное упражнение или введите собственное упражнение. Затем нажмите кнопку и выберите «Решить, используя квадратичную формулу», чтобы сравнить свой ответ с Mathway. (Или пропустите виджет и продолжайте на следующей странице.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvquad4.htm
,