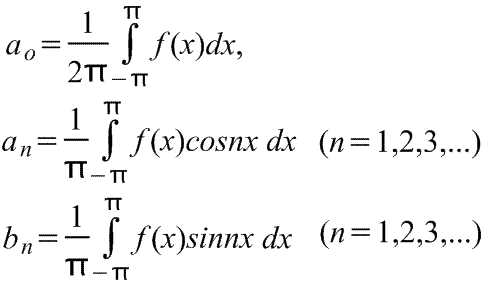Разложение функции у=1-х в ряды фурье по синусам и косинусам
Типовой расчёт (вар. 4)
Задача 5.
А) Разложить функцию , заданную па полупериоде , в ряд Фурье по косинусам. Построить графики второй, третьей частичных сумм. Записать равенство Парсеваля для полученного ряда
Б) Разложить функцию , заданную на полупериоде , в ряд Фурье по синусам. Построить графики второй, третьей частичных сумм.
В) Разложить функцию в ряд Фурье, продолжая ее па полупериод функцией, равной 0. Построить графики второй, четвертой частичных сумм.
Решение
а) Доопределим функцию на промежутке чётным образом и продолжим её на всю числовую ось как периодическую с периодом, равным 8. — чётная функция. Тригонометрический ряд Фурье содержит только косинусы. Вычислим коэффициенты Фурье этой функции.
, следовательно
Так как рассматриваемая функция непрерывна всюду, то сумма её ряда Фурье равна данной функции при всех х и
.
Равенство Парсеваля:
, так как , то
Б) Доопределим функцию на промежутке нечётным образом, а значение в т : и продолжим её на всю числовую ось как периодическую с периодом, равным 8. Согласно теореме Дирихле тригонометрический ряд Фурье такой функции будет сходиться к этой функции во всех точках непрерывности. Вычислим коэффициенты Фурье этой функции.
Так как рассматриваемая функция непрерывна всюду, то сумма её ряда Фурье равна данной функции при всех х и .
В) Разложим в ряд Фурье функцию
Т=8
Вычислим коэффициенты Фурье этой функции
, следовательно
Ряд Фурье имеет вид:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
лекция№60
Лекция №60
6.21. Ряды Фурье для чётных и нечётных функций.
Теорема: Для любой чётной функции её ряд Фурье состоит только из косинусов.
Для любой нечётной
функции: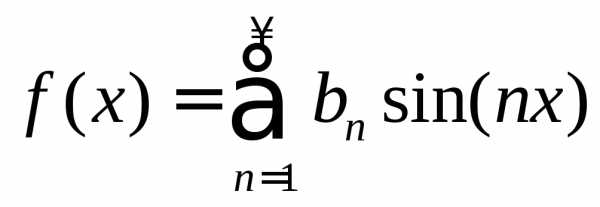 
Доказательство: Из определения четной и нечетной функции следует, что если ψ(x) – четная функция, то
.
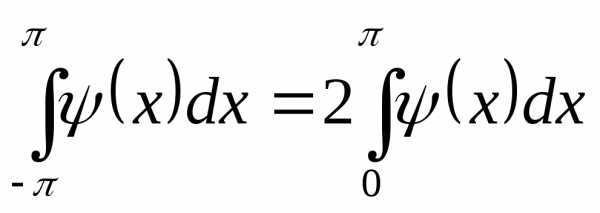Действительно,
так как по определению четной функции ψ(- x) = ψ(x).
Аналогично можно доказать, что если ψ(x) – нечетная функция, то
Если в ряд Фурье разлагается нечетная функция ƒ(x), то произведение ƒ(x) ·coskxесть функция также нечетная, а ƒ(x) ·sinkx– четная; следовательно,
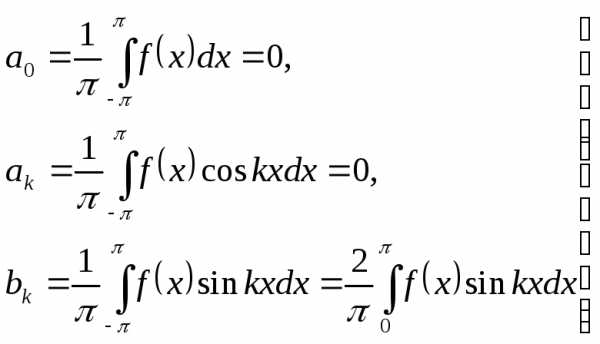(21)
т. е. ряд Фурье нечетной функции содержит «только синусы».
Если в ряд Фурье разлагается четная функция, то произведение ƒ(x)·sinkxесть функция нечетная, а ƒ(x) ·coskx– четная, то:
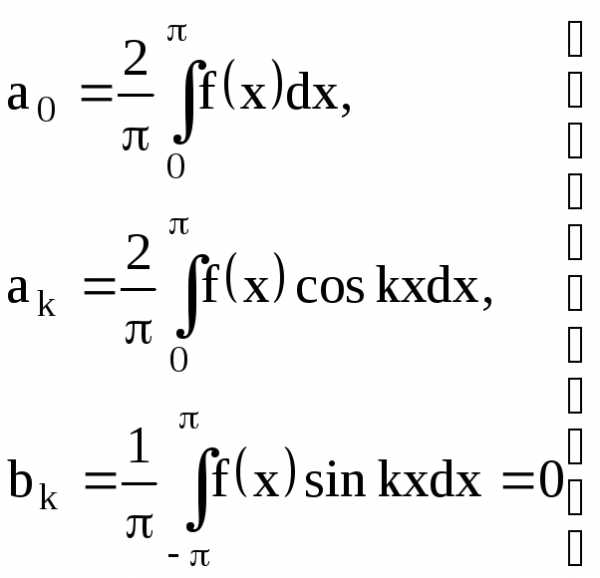(22)т. е. ряд Фурье четной функции содержит «только косинусы».
Полученные формулы позволяют упрощать вычисления при разыскании коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной, а также получать разложение в ряд Фурье функции, заданной на части промежутка .
Во многих задачах
функция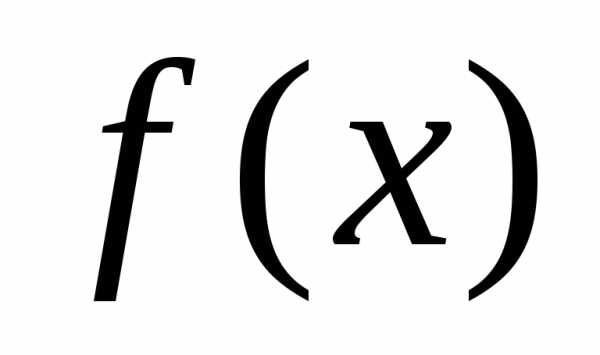 
задается в интервале 
.
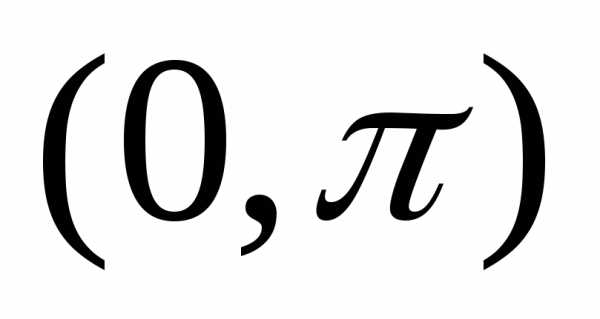Требуется представить данную функцию
в виде бесконечной суммы синусов и
косинусов углов, кратных числам
натурального ряда, т.е. необходимо
произвести разложение функции в ряд
Фурье. Обычно в таких случаях поступают
следующим образом.
Чтобы разложить
заданную функцию по косинусам, функцию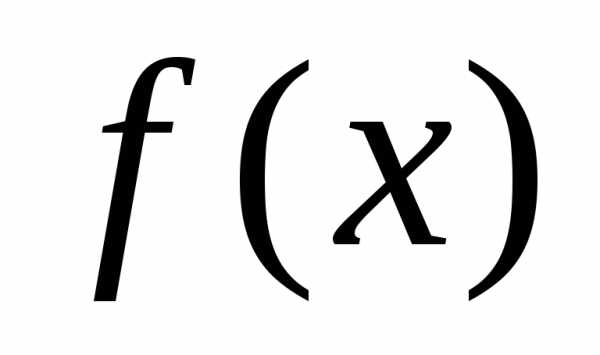 
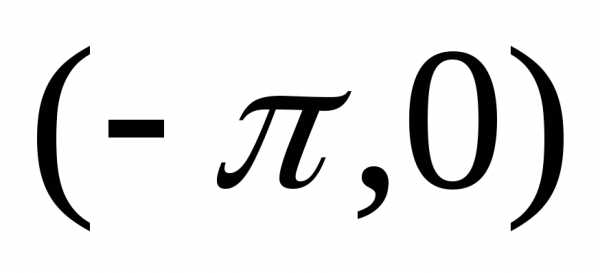четным образом, т.е. так, что в интервале 
.
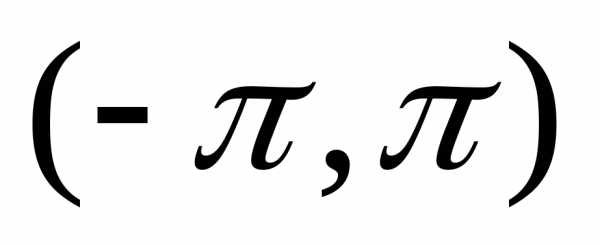Тогда для «продолженной» четной функции
справедливы все рассуждения предыдущего
параграфа, и, следовательно, коэффициенты
ряда Фурье определяются по формулам,
.
В этих формулах,
как видим, фигурируют значения функции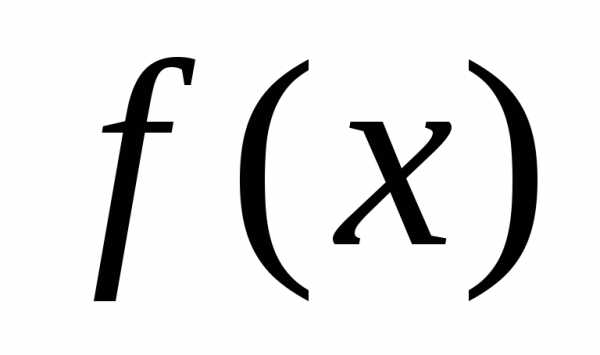 
,
лишь заданные в интервале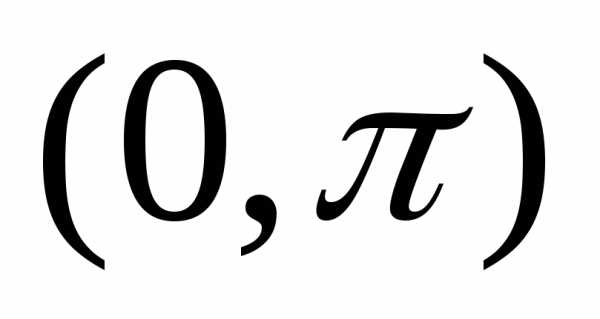
.
Чтобы разложить функцию
,
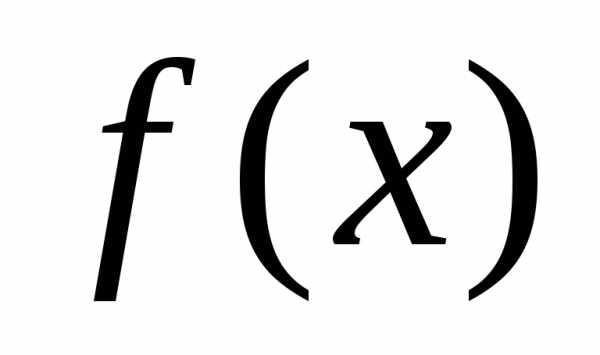заданную в интервале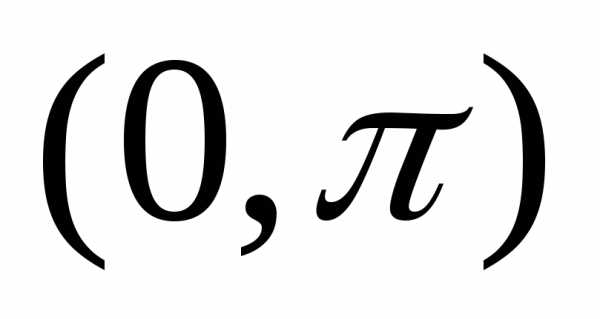
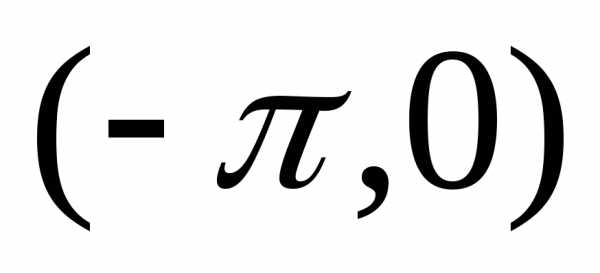нечетным образом, т.е. так, что в интервале
.Тогда вычисление коэффициентов ряда Фурье нужно вести по формулам
,
.
Теорема 1.Функцию заданную на промежуткеможно бесконечным числом способов разложить в тригонометрический ряд Фурье, в частности по cos или по sin.
Замечание.Функция
,
заданная в интервале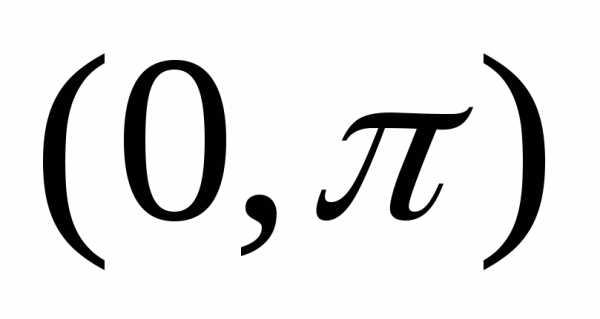
может быть доопределена в интервале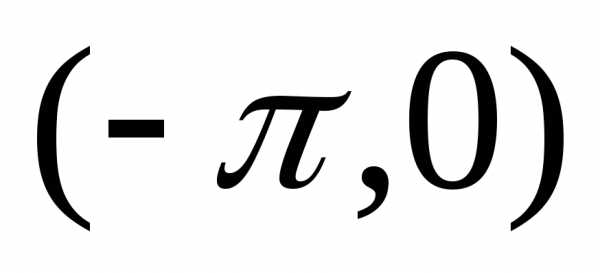
Пример.Разложить в ряд Фурье по косинусам
функцию,
заданную в интервале
(рис.2а).
Решение.Доопределим функцию
в интервале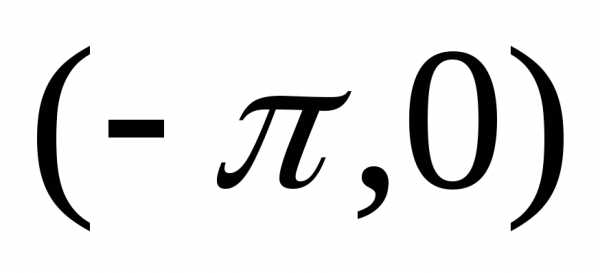
четным образом (график симметричен
относительно оси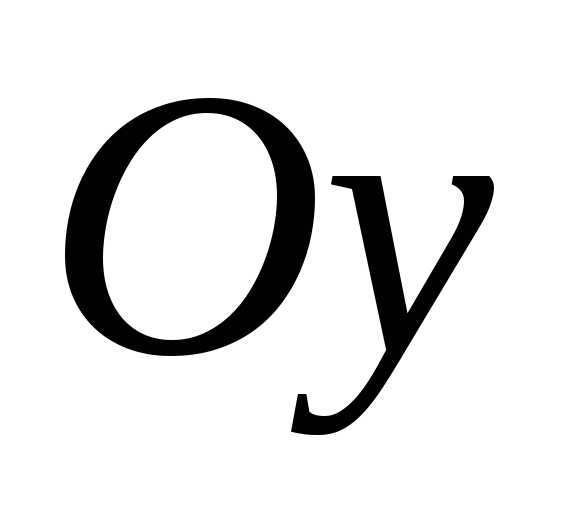
)
а б
Рис.2
,
.
Так как , то при 
,
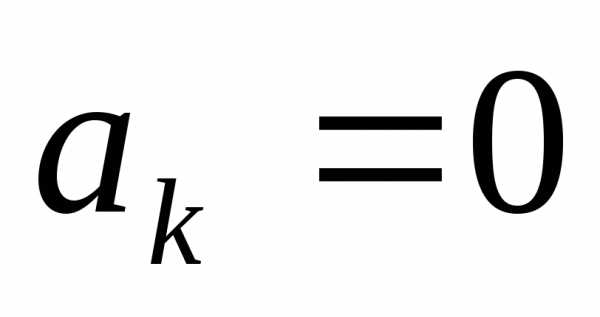при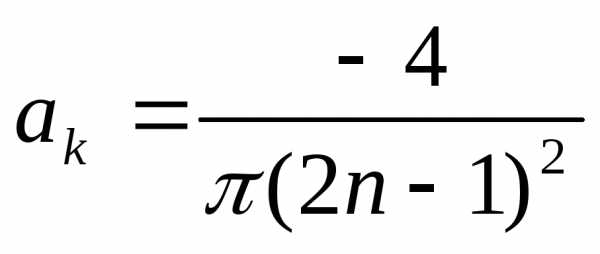 
и
6.22. Ряд Фурье для функции, заданной на произвольном промежутке
До
сих пор мы рассматривали функцию,
заданную в интервале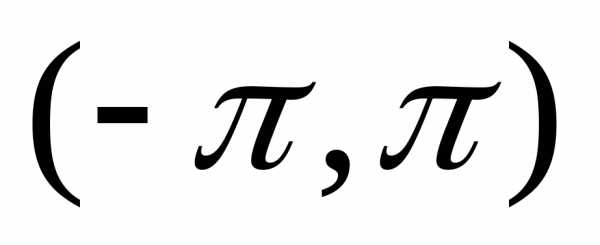 
,
считая ее вне этого интервала периодической,
с периодом
.
Рассмотрим
теперь функцию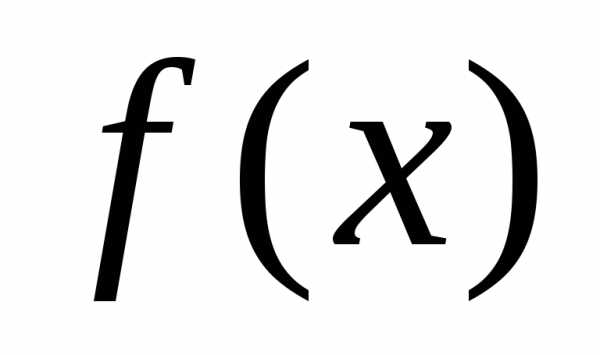 
,
период которой равен 2l,
т.е.на интервале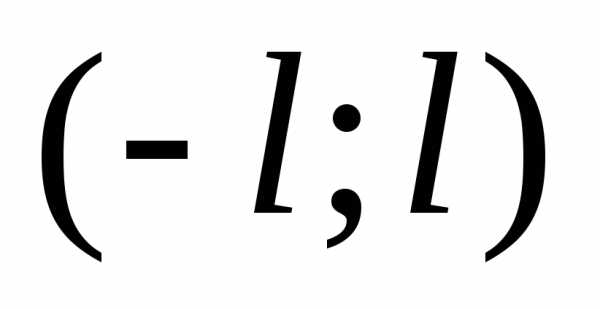
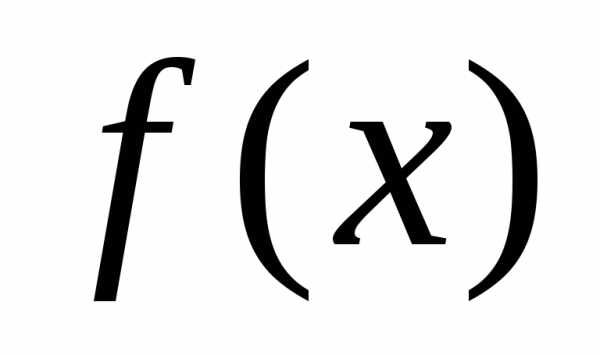может быть разложена в ряд Фурье. Положим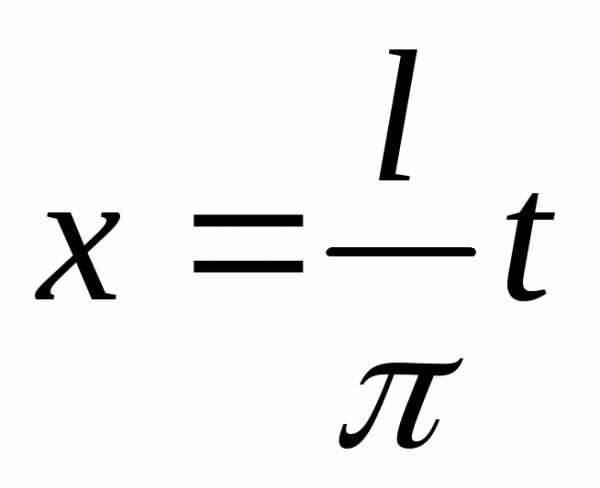 
,
или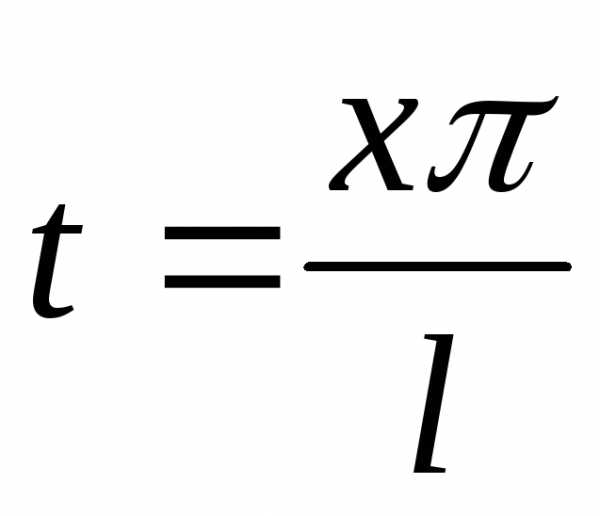
.
Тогда при изменении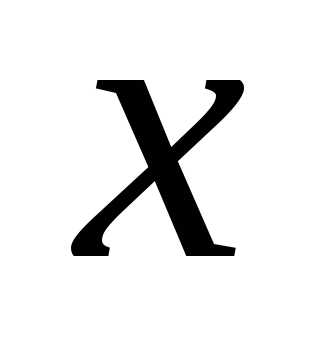
от –lдоlновая переменная
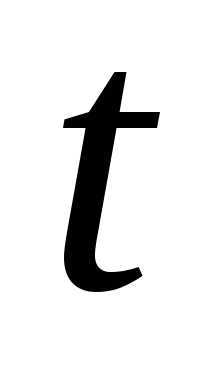изменяется от
до
и, следовательно, функцию
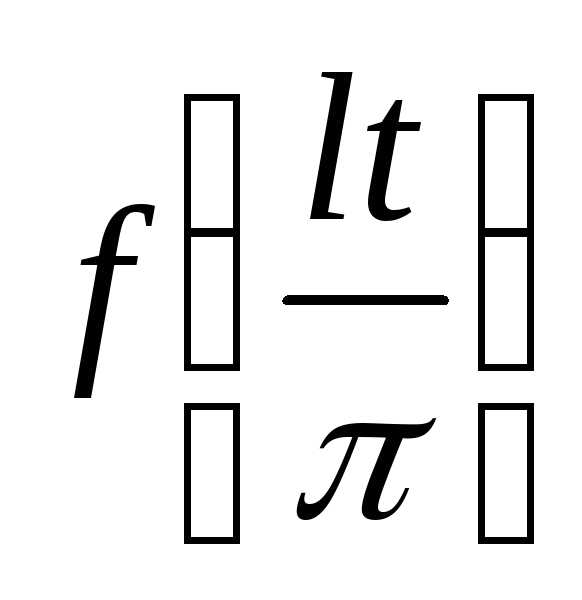можно рассматривать как функцию, заданную
в интервале от
и периодическую вне этого промежутка,
с периодом
.Итак, .
Разложив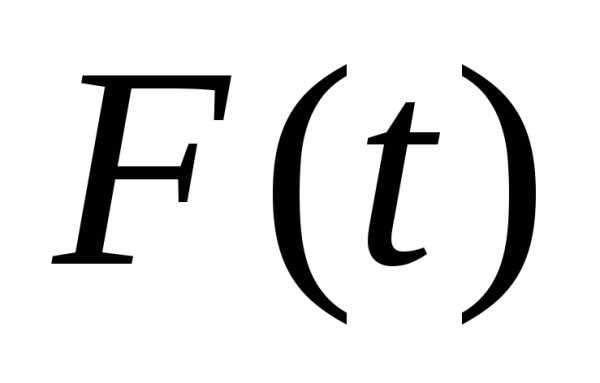 
в ряд Фурье, получим
,
где
.
Переходя
к старым переменным, т.е. полагая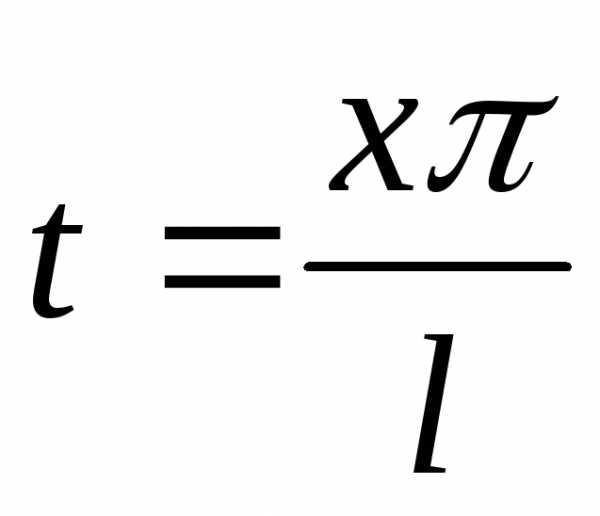 
,
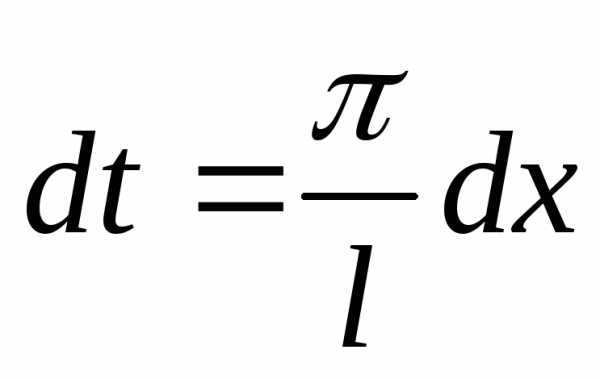получим,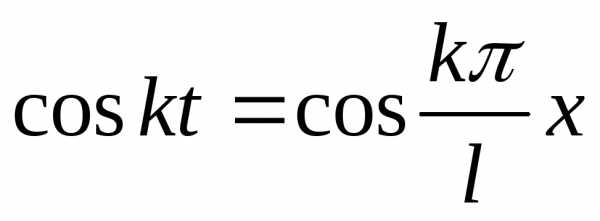
и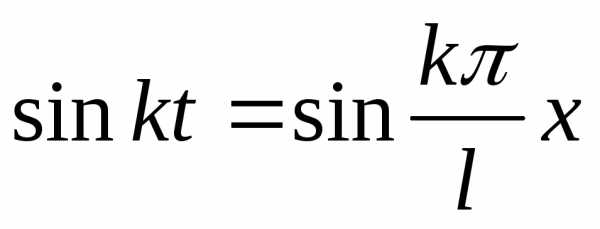
То
есть ряд Фурье для функции 
,
заданной в интервале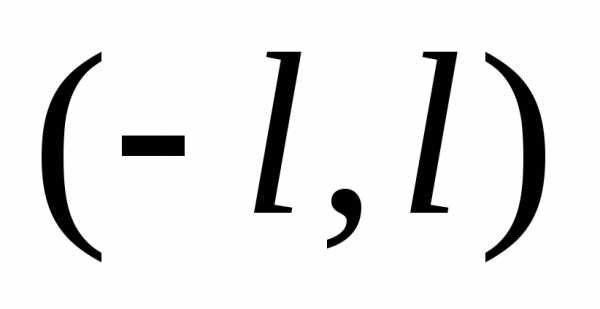
,
будет иметь вид:
,
где
,
,
.
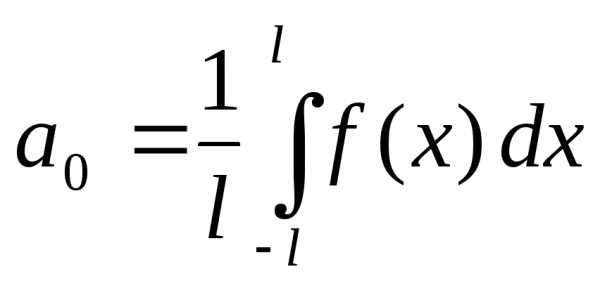Если
функция 
четная, то формулы для определения
коэффициентов ряда Фурье упрощаются:
,
,
.
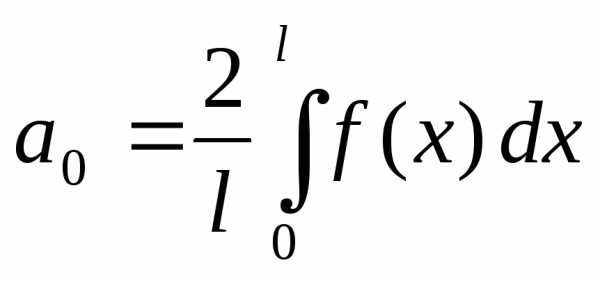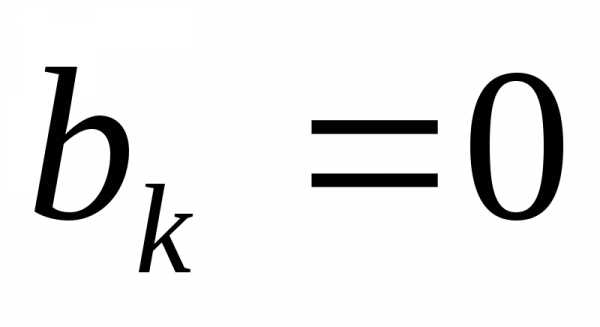В
случае, если функция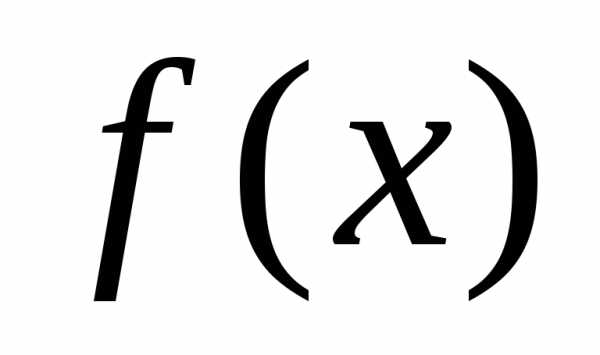 
нечетная:
,
,
.
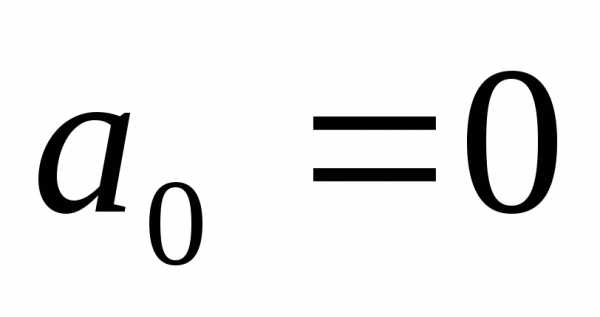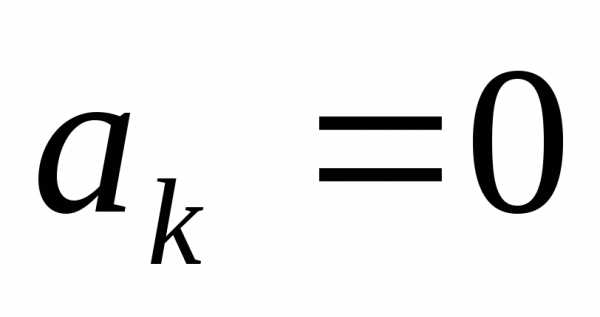Если
функция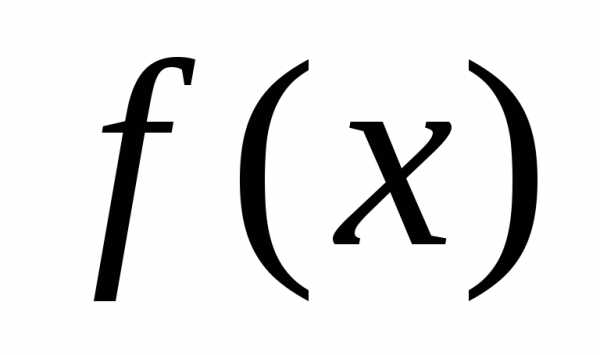 
задана в интервале
,
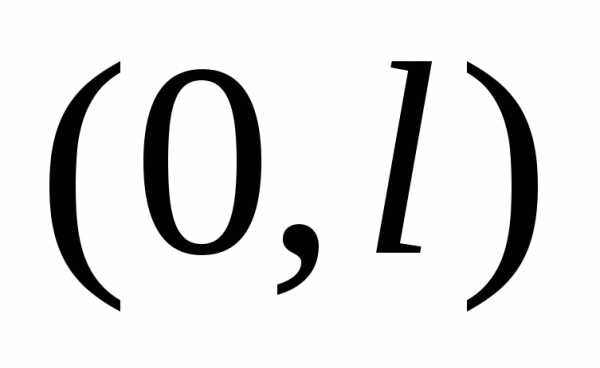то ее можно продолжить в интервале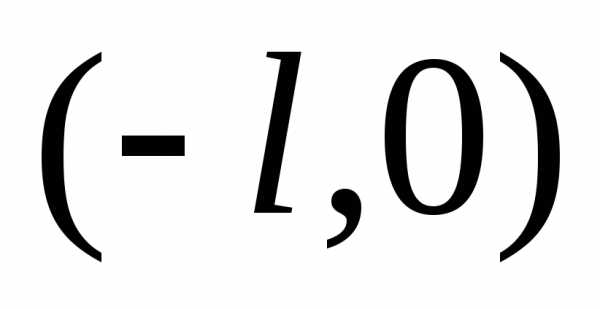
либо четным, либо нечетным образом. В
случае четного продолжения функции в
интервалекоэффициенты ряда Фурье находятся по
формулам
,
.
В
случае нечетного доопределения функции
в интервале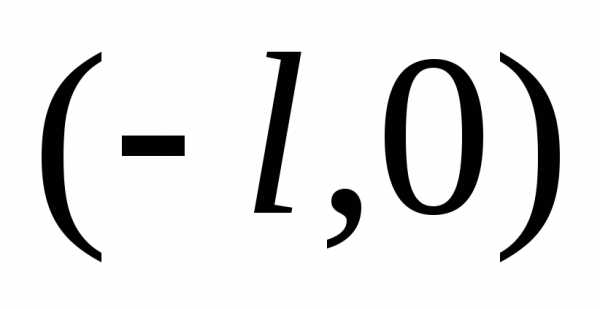 
коэффициенты ряда Фурье находятся по
формулам
,
.
Пример. Разложить в ряд Фурье функцию
по синусам кратных дуг.
Решение. График заданной функции представлен на рис.3. Продолжим функцию нечетным образом (рис.4), т.е. будем вести разложение по синусам.
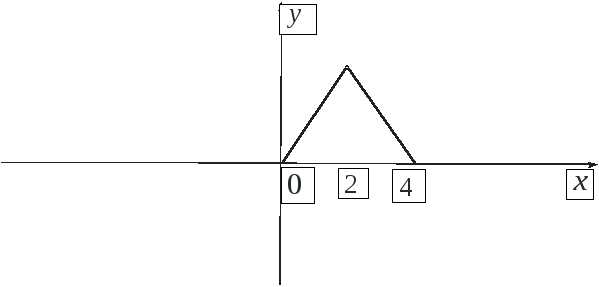
Рис.3
Рис.4
Все
коэффициенты 
,
Введем
замену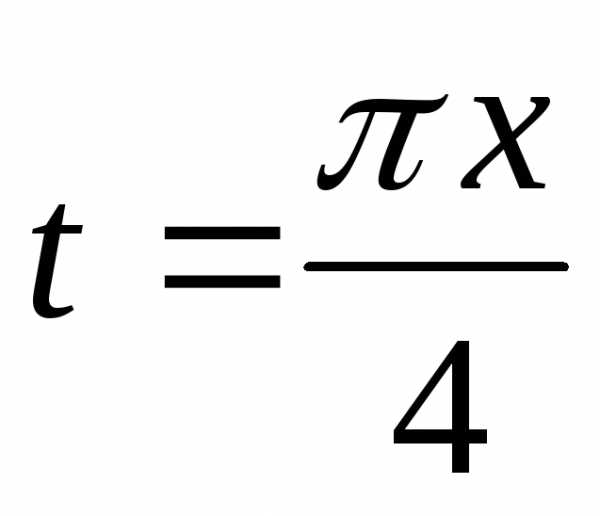 
.
Тогда при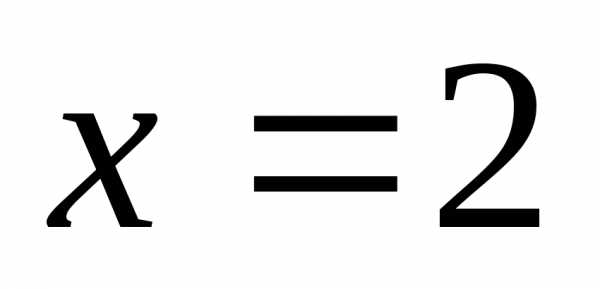
получим
,
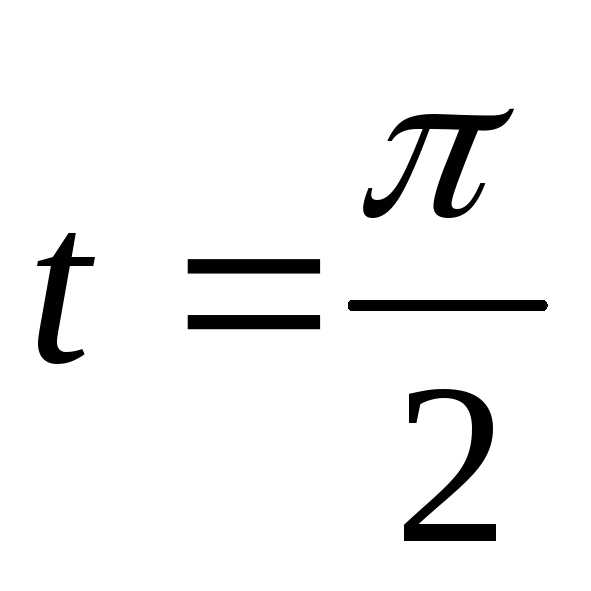при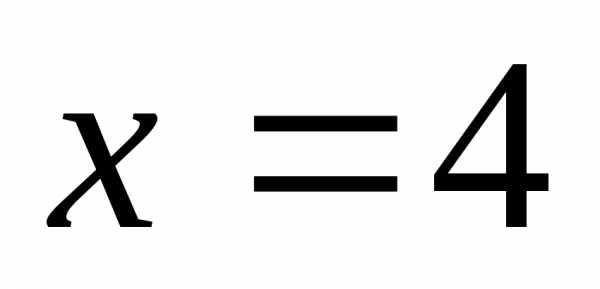
имеем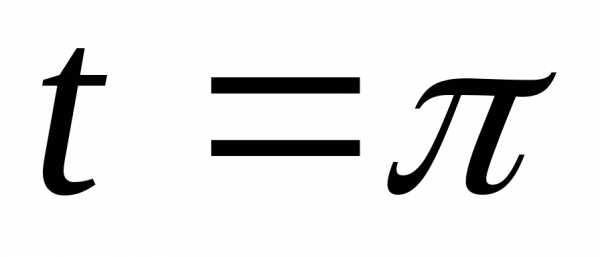
.
Таким образом
.
6.23..Понятие о разложении в ряд Фурье непериодических функций
Функцию, заданную в основной области (-ℓ, ℓ), можно периодически продолжить за основную область с помощью функционального соотношения ƒ(x+2 ℓ) = ƒ(x).
Для непериодической функции ƒ(x) (-∞ <x< +∞) можно выделить участок (-ℓ <x< ℓ), а затем взять периодическую функцию φ(x) с периодом Т=2 ℓ, которая в промежутке (-ℓ, ℓ) равна ƒ(x). Периодическую функцию φ(x) можно разложить в ряд Фурье
φ(x)=(2.18)
Формула (2.18) будет верна на всей оси -∞ < x< ∞ . Можно написать подобное разложение для функции
ƒ(x)=(2.19)
Формула (2.19) будет верна только на конечном промежутке (-ℓ, ℓ), так как на этом промежутке ƒ(x) и φ(x) совпадают.
Таким образом, непериодическую функцию можно разложить в ряд Фурье на конечном промежутке.
studfiles.net
1.5. Разложение в ряд Фурье функции f(X), определённой на отрезке [0, l]
Функцию f(x), определëнную на отрезке [0, l] и являющуюся на этом отрезке кусочно-монотонной и ограниченной, можно разложить в ряд Фурье двумя способами. Для этого достаточно представить продолжение функции на промежуток [–l, 0]. Если продолжение f(x) на [–l, 0] чётное (симметричное относительно оси ординат), то ряд Фурье можно записать по формулам (1.12–1.13), то есть по косинусам. Если продолжить функцию f(x) на [–l, 0] нечётным образом, то разложение функции в ряд Фурье будет представлено формулами (1.14–1.15), то есть по синусам. При этом оба ряда будут иметь в интервале (0, l) одну и ту же сумму.
Пример. Разложить в ряд Фурье функцию y = x, заданную на промежутке [0, 1] (см. рис.1.4).
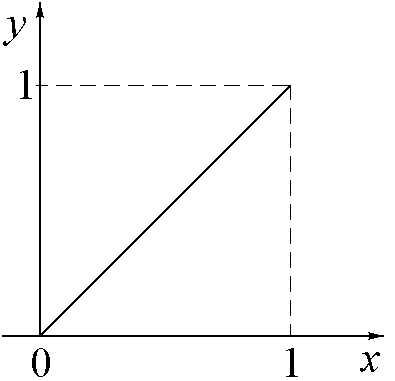
Рис.1.4.
Решение.
a). Разложение в ряд по косинусам. Строим чётное продолжение функции в соседний промежуток [–1, 0]. График функции вместе с её чётным продолжением на [–1, 0 ] и последующим продолжением (по периоду T = 2) на всю ось 0x показан на рис.1.5.
Рис.1.5.
Так как l = 1, то ряд Фурье для данной функции при чётном разложении будет иметь вид
(1.18)
при этом
,
.
В результате получим при
. (1.19)
На всей оси 0x ряд сходится к функции, изображенной на рис.1.4.
2). Разложение в ряд по синусам. Строим нечётное продолжение функции в соседний промежуток [–1, 0]. График функции вместе с её нечётным продолжением на [–1, 0] и последующим периодическим продолжением на всю числовую ось 0x показан на рис.1.6.
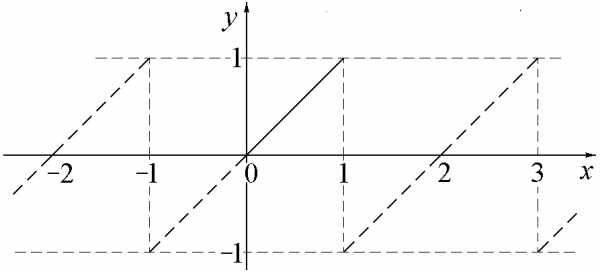
Рис.1.6.
При нечëтном разложении
,
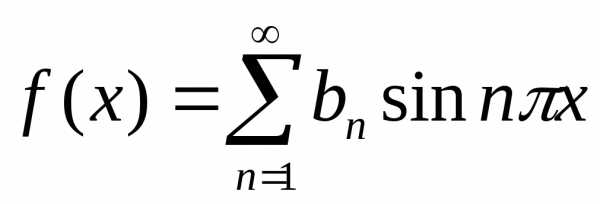(1.20)
где
.
Поэтому ряд Фурье по синусам для данной функции при будет иметь вид
. (1.21)
В точке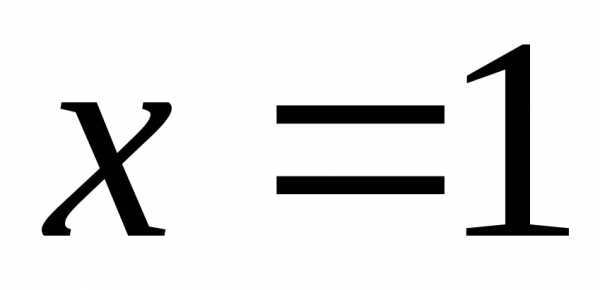 
сумма ряда будет равна нулю, хотя исходная
функция равна 1. Это обусловлено тем,
что при таком периодическом продолжении
точкаx = 1 становится точкой разрыва.
Из сравнения
выражений (1.19) и (1.21) следует, что скорость
сходимости ряда (1.19) выше, чем ряда
(1.21): она определяется в первом случае
множителем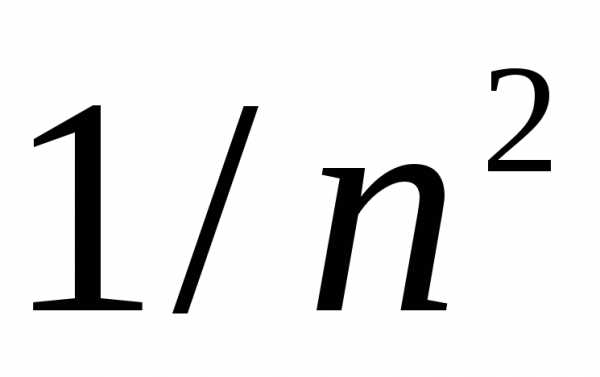 
,
а во втором случае множителем 1/n.
Поэтому разложение в ряд по косинусам
в данном случае предпочтительнее.
В общем случае
можно показать, что если функция f(x)
не обращается в нуль хотя бы на одном
из концов промежутка [0, l],
то предпочтительнее еë разложение в
ряд по косинусам. Это обусловлено тем,
что при чётном продолжении в соседний
промежуток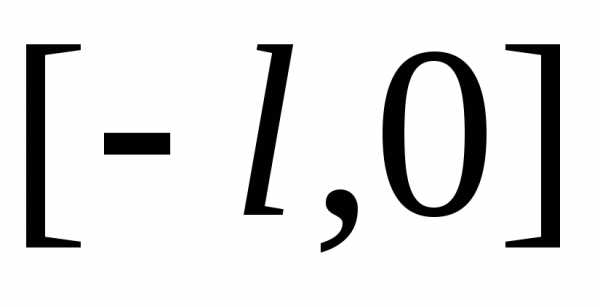 
функция будет непрерывной (см. рис.1.5),
и скорость сходимости получающегося
ряда будет выше, чем ряда по синусам.
Если функция, заданная на [0,l],
обращается в нуль на обоих концах
интервала, то предпочтительнее её
разложение в ряд по синусам, так как при
этом будет непрерывной не только сама
функция f(x),
но и её первая производная.
1.6. Обобщённый ряд Фурье
Функци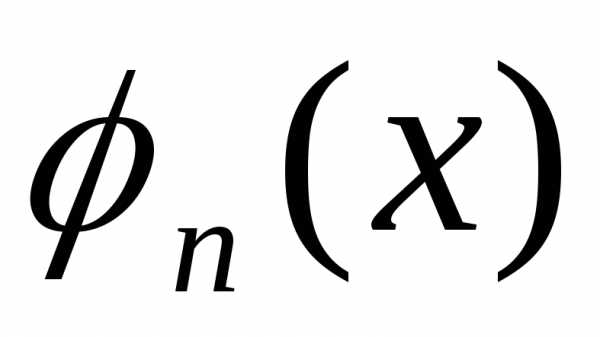и 
и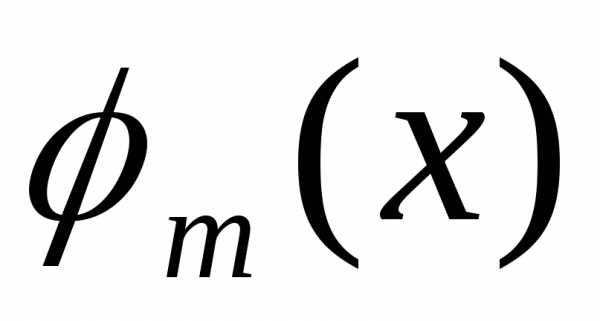
(n, m = 1, 2, 3,…) называются ортогональными на отрезке [a, b],
если при n ≠ m
.
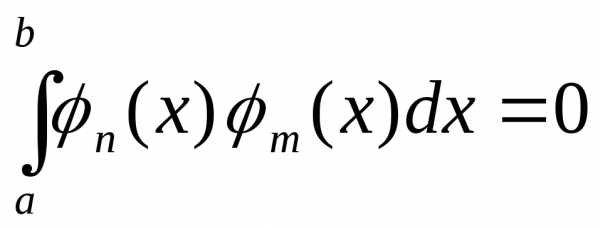(1.22)
При этом предполагается, что
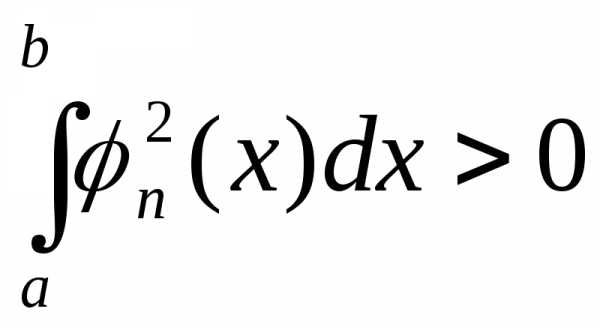и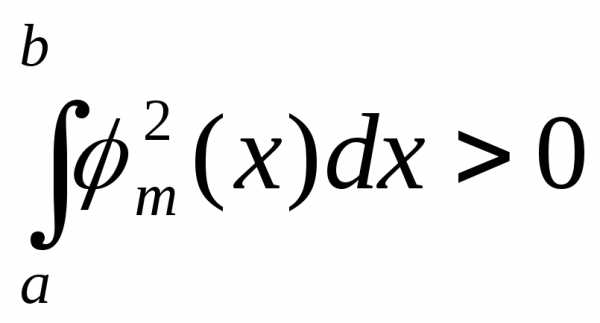 
.
Рассмотрим
разложение функции f(x),
которая определена на отрезке [a, b],
в ряд по системе ортогональных функций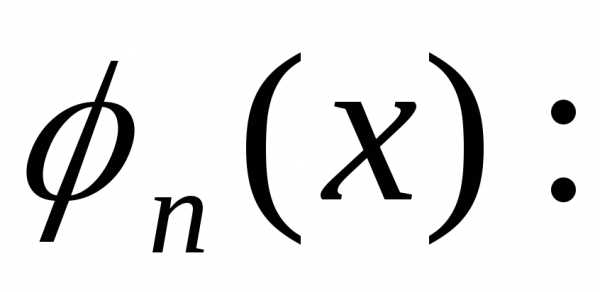 
, (1.23)
где коэффициенты 
(i = 0,1,2…) являются постоянными числами.
Для определения
коэффициентов разложения 
умножим равенство (1.23) на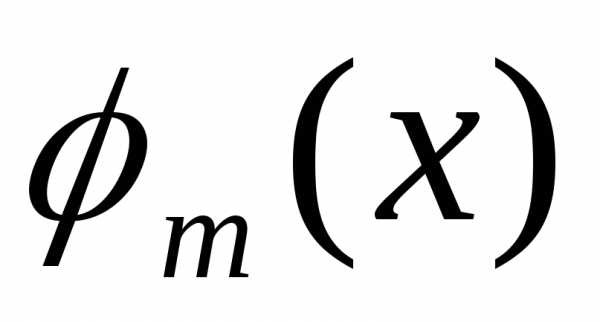 
и проинтегрируем почленно на отрезке
[a, b].
Получим равенство
В силу ортогональности
функций 
все интегралы в правой части равенства
будут равны нулю, кроме одного (при).
Отсюда следует, что
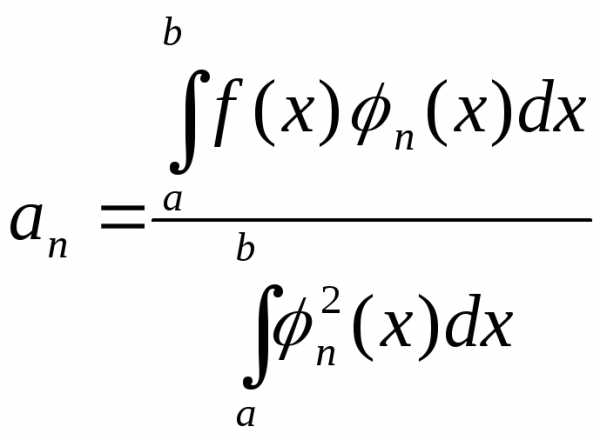(1.24)
Ряд (1.23) по системе ортогональных функций, коэффициенты которого определяются по формуле (1.24), называется обобщённым рядом Фурье для функции f(x).
Для упрощения формул для коэффициентов применяют, так называемое, нормирование функций. Система функций φ0(x), φ1(x),…, φn(x),… называется нормированной на промежутке [a, b], если
.
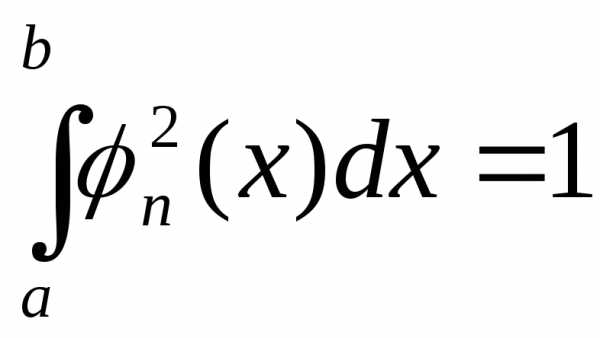(1.25)
Справедлива теорема: всякую ортогональную систему функций можно нормировать. Это означает, что можно подобрать постоянные числа μ0, μ1,…, μn,… так, чтобы система функций μ0φ0(x), μ1φ1(x),…, μnφn(x),… была не только ортогональной, но и нормированной. Действительно, из условия
получим, что
.
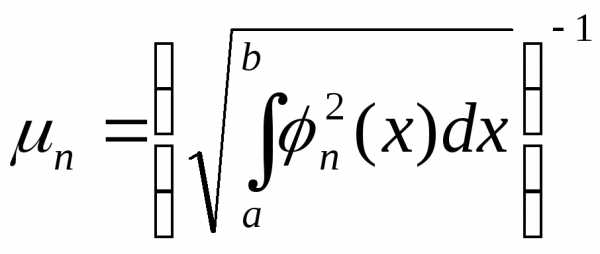Число
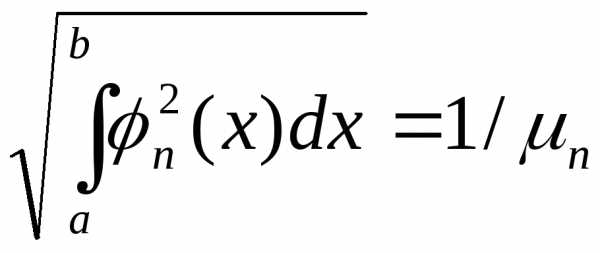
называется нормой функции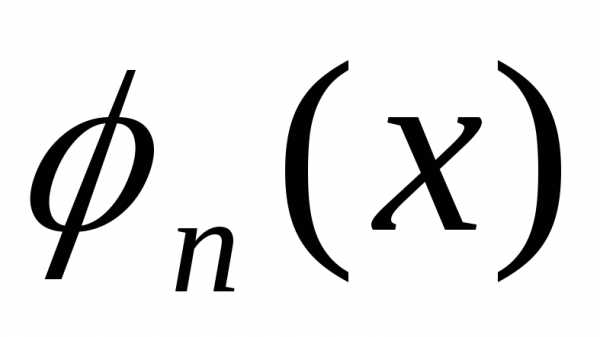 
и обозначается через 
.
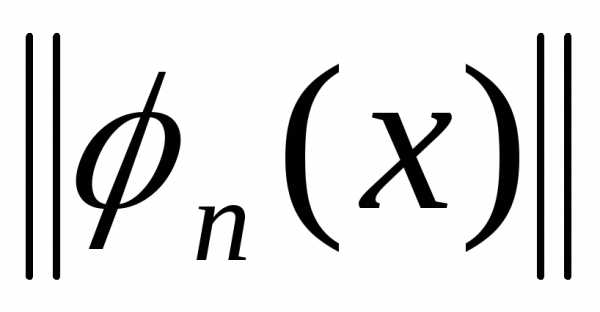Если система
функций нормирована, то, очевидно,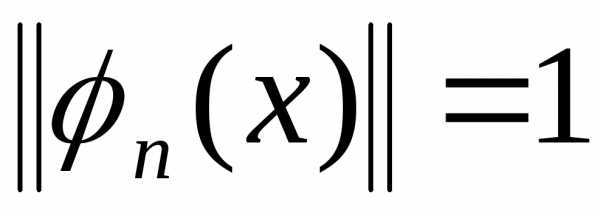 
.
Последовательность функцийφ0(x), φ1(x),…, φn(x),…,
определённых на отрезке [a, b],
является ортонормированной на этом отрезке, если все функции
нормированы и взаимно ортогональны на
[a, b].
Для ортонормированной системы функций коэффициенты обобщённого ряда Фурье равны
.
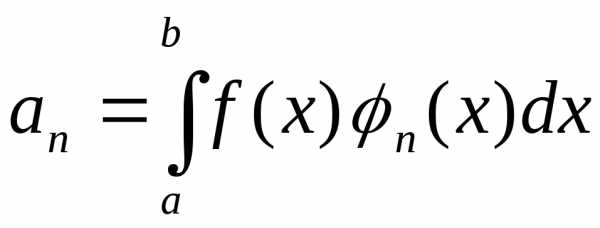(1.26)
Пример. Разложить функцию y = 2 – 3x на отрезке в обобщëнный ряд Фурье по системе ортогональных на этом отрезке функций, в качестве которых взять собственные функции задачи на собственные значения
,
предварительно проверив их на квадратичную интегрируемость и ортогональность.
Замечание. Говорят, что функция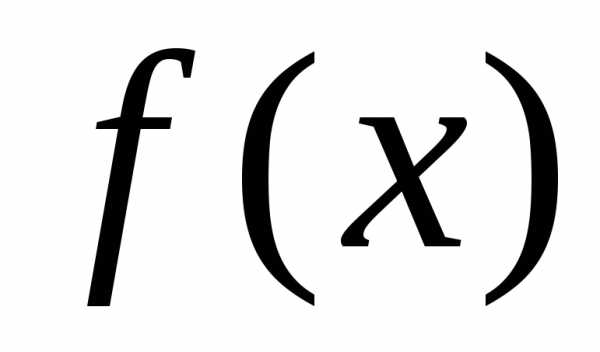 
,
заданная на отрезке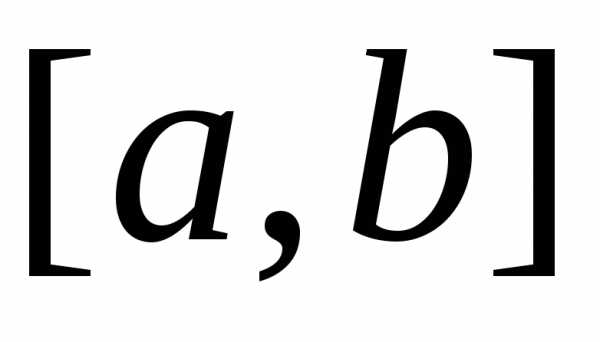
,
есть функция с интегрируемым квадратом,
если она сама и еë квадрат интегрируемы
на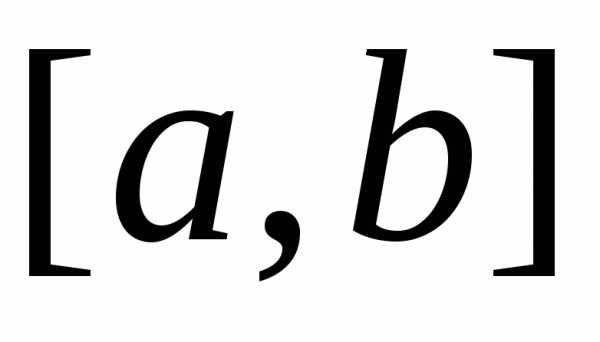
,
то есть, если существуют интегралы
и
.
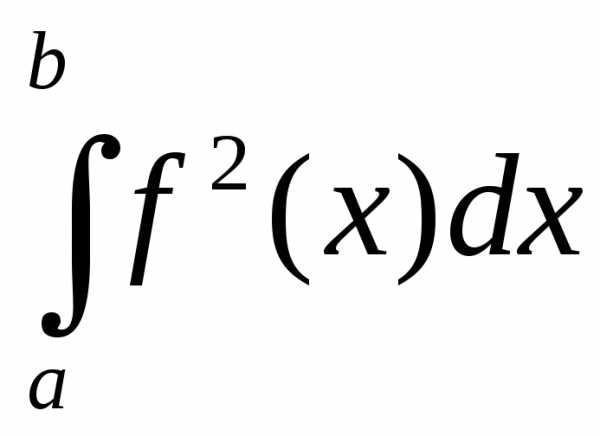Решение. Сначала решаем задачу на собственные значения. Общее решение уравнения этой задачи будет
,
а его производная запишется в виде
.
Поэтому из граничных условий следует:
Для существования нетривиального решения необходимо принять
,
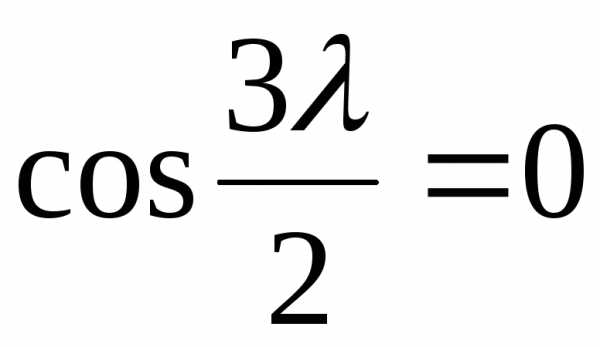откуда
следует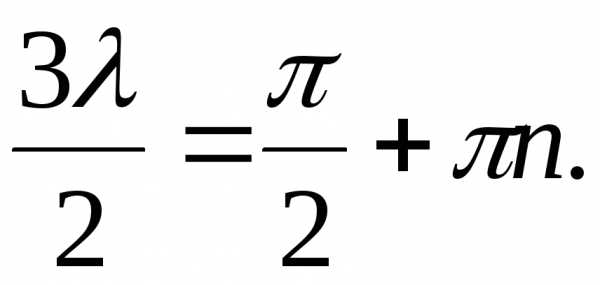 
Поэтому собственные значения параметра 
равны
,
а соответствующие им собственные функции с точностью до множителя будут
. (1.27)
Проверим полученные собственные функции на ортогональность на отрезке [0, 3/2]:
так
как
при целых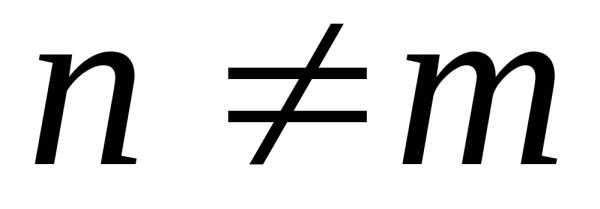
.При
этом
.
Следовательно, найденные собственные функции ортогональны на отрезке [0, 3/2].
Разложим заданную функцию в обобщëнный ряд Фурье по системе ортогональных собственных функций (1.27):
, (1.28)
коэффициенты которого вычисляются по (1.24):
. (1.29)
Подставляя (129) в (1.28), окончательно получим
.
studfiles.net
Разложение в ряд Фурье — Калькулятор Онлайн
Введите функцию, которую будете разложить в ряд Фурье
Выполним разложение функции f(x)
в ряд Фурье на отрезке [a, b]
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
www.kontrolnaya-rabota.ru
Ряд и преобразование Фурье методичка
Ряд Фурье
Ряд Фурье функции x(t) представляется в виде :
где коэффициенты Фурье a0, an и bn определяются формулами
При расчете коэффициентов ряда Фурье необходимо выбрать начальный момент времени t0 периода интегрирования. Как правило, значение t0 выбирают так, чтобы упростить вычисления. Обычно, исходя из этого условия, принимают
t0=-Т/2 . Формулы приобретают следующий вид:
Разложение в ряд Фурье четных и нечетных функций
Если функция x(t), описывающая сигнал, является четной, то есть
x(t)=x(-t), то коэффициенты an=0, n=0,1,2,…, и в разложении остаются только постоянная и косинусоидальные составляющие:
Если функция x(t), описывающая сигнал, является нечетной, то есть
x(t)=-x(t), то коэффициенты an=0, n=0,1,2,…, и в разложении остаются только синусоидальные составляющие:
Получила распространение и другая форма записи тригонометрического ряда Фурье:
где амплитуда An и фаза n-ой гармонической составляющей связаны с коэффициентами an и bn соотношениям:
или
Пример 1.
Найти разложение в ряд Фурье для функции
заданной в интервале [−π, π].
Решение.
Найдем сначала a0:
Далее вычислим коэффициенты an:
Заметим, что
Поскольку cos (n − 1)π = (−1)n −1, то для коэффициентов an получаем выражение
Видно, что an = 0 для нечетных n. Для четных n, когда n = 2k (k = 1,2,3,…), мы имеем
Вычислим теперь коэффициенты bn. Начнем с b1:
Остальные коэффициенты bn при n > 1 равны нулю. Действительно,
Таким образом, формула разложения заданной функции в ряд Фурье имеет вид
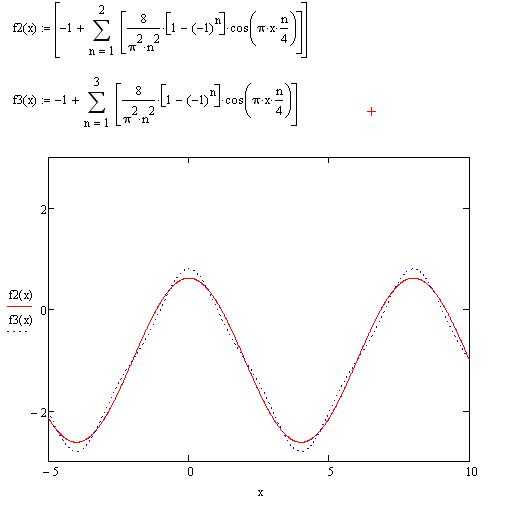
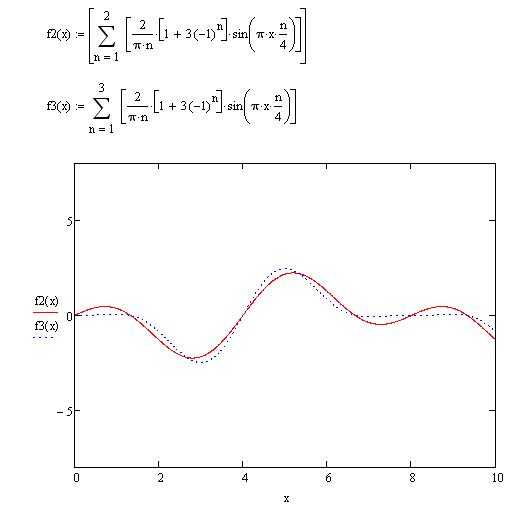
График функции и варианты разложения для n = 2 и n = 8 показаны на рисунке 1.
Рисунок 1.
Пример 2.
Разложить
в ряд Фурье функцию с периодом 
,
заданную на интервале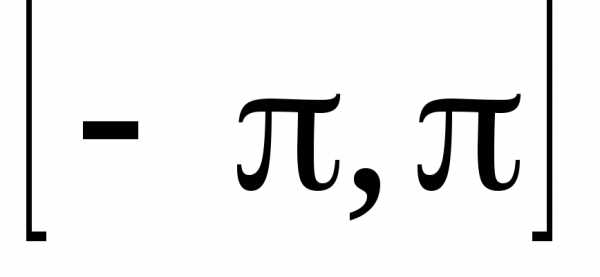
формулой
.
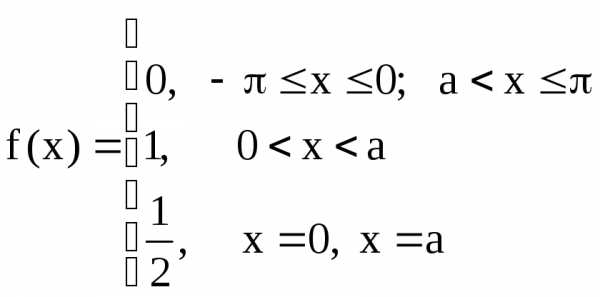Построим график функции (рис. 2).
y
1
-3 -2 - 2 3 x
Рисунок 2
Решение. Функция удовлетворяет условиям Дирихле. Применяя формулы (2) и (3), находим коэффициенты Фурье
,
,
.
Разложение
в ряд Фурье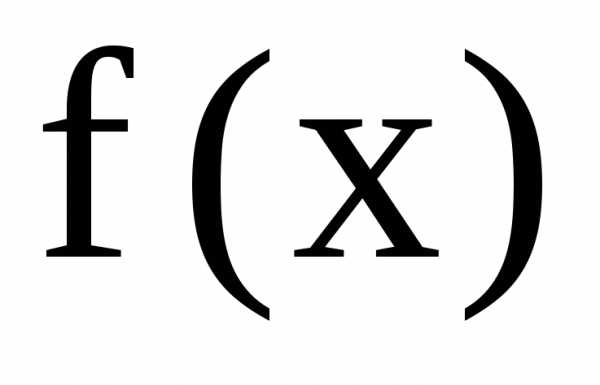 
имеет вид
.
Индивидуальное задание.
Разложить в ряд Фурье функцию, построить график функции.
На отрезке разложить в ряд Фурье функции:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
Разложить функцию в тригонометрический ряд Фурье на отрезке [-1;1] ;
21. Разложить функцию в тригонометрический ряд Фурье на отрезке [-1/2;1/2] ;
22. Разложить функцию в тригонометрический ряд Фурье на отрезке [-/2;/2] ;
23. Разложить функцию в тригонометрический ряд Фурье на отрезке [-1/2;1/2] ;
24. Разложить функцию в тригонометрический ряд Фурье на отрезке
[-1;1] в комплексной форме;
25. Разложить функцию в тригонометрический ряд Фурье на отрезке [-3;3] в комплексной форме;
26. Разложить функцию в тригонометрический ряд Фурье на отрезке [1;3] ;
27. Разложить функцию в тригонометрический ряд Фурье на отрезке [5;15] ;
28. Разложить функцию в тригонометрический ряд Фурье на отрезке [0;1] ;
29. Разложить функцию заданную на отрезке и продолженную на отрезок четным образом в тригонометрический ряд Фурье
Преобразование Фурье
Представим интеграл Фурье
в виде:
(1)
(2)
Функция F(), определенная формулой (1), называется косинусом-преобразованием Фурье дляf(x).
Формула (2) задает обратное косинус – преобразование Фурье, позволяющее по F(a ) находить f(x).
Аналогично, если f(x) – нечетная функция, то A(a ) = 0, тогда формулы (3) и (4) задают соответственно прямое и обратное синус-преобразование Фурье
(3)
(4)
Если интеграл Фурье в комплексной форме представить в виде
(5)
то функция S(a ) также называется спектральной и S(a ) = 2p C(a ).
Преобразованием Фурье называется функция определенная формулой (6)
(6)
а функция f(x) , определенная формулой (7) называется обратным преобразованием Фурье
(7)
Преобразование Фурье отличается от спектральной функции только множителем
(также называется спектральной функцией).
Если функция f(x) – оригинал с показателем роста , то функция g(x), определенная формулой, гденазывается затухающим оригиналом. Тогда для функции g(x) существует и преобразование Фурье и преобразование Лапласа и они связаны между собой формулой
(8)
Пример 1.
Для функции найти косинус преобразование Фурье.
Решение
Тогда косинус — преобразование Фурье функции имеет вид
Пример 2
Найти преобразование Фурье для функции
Решение.
Данная функция является затухающим оригиналом, т.к. функция — оригинал с показателем ростаигде
Воспользуемся формулой (8), связывающей преобразование Фурье с преобразованием Лапласа. Найдем для функции преобразование Лапласа по таблице
Тогда
Получили преобразование Фурье заданной функции:
Индивидуальные задания.
Найти синус и косинус – преобразование Фурье для функции:
Найти преобразование Фурье следующих функций:
на отрезке [ 0;6];
на отрезке [0;4];
на отрезке [0;10];
на отрезке [0;9];
на отрезке [0;10];
на отрезке [0;9];
на отрезке [0;8];
на отрезке [0;9].
и)
к) ;
л) ;
м) ;
н) ;
о)
п)
р)
с)
т)
у) ф)
studfiles.net
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов. Вариант для печати.Ряд Фурье периодических функций с периодом 2π.Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах. Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов): Стандартная (=обычная) запись через сумму sinx и cosxf(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…, где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е. (1) Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой, Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn) Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен a |
dpva.ru
Использование методов численного интегрирования при разложении функции в ряд Фурье
Разложение функции в ряд Фурье, или гармонический анализ, оказывается нужным во многих чисто практических вопросах машиноведения, электротехники и пр. Но в этих случаях очень редко приходится непосредственно пользоваться формулами Эйлера-Фурье:
для вычисления коэффициентов разложения. Дело в том, что функции, которые нужно подвергнуть гармоническому анализу, обыкновенно задаются таблицей своих значений или графиком. Таким образом, аналитического выражения функции в нашем распоряжении нет; иногда к самому гармоническому анализу прибегают именно для того, чтобы таким путем получить хотя бы приближенное аналитическое выражение для функции. В этих условиях для вычисления коэффициентов Фурье нужно обратиться к приближенным методам. Разумеется, на практике приходится пользоваться лишь немногими первыми членами тригонометрического разложения. Коэффициенты ряда Фурье в большинстве случаев убывают, а с ними быстро падает и влияние далеких гармоник.
Обычно дается (или снимается с графика) ряд равноотстоящих ординат, т.е. ряд значений функции , отвечающих равноотстоящим значениям аргумента x. По этим ординатам коэффициенты можно приближенно вычислить, пользуясь методами изложенными выше. Но вычисления здесь оказываются довольно громоздкими, и для того чтобы упростить и, так сказать, автоматизировать их, придумано много различных приемов, один из которых мы и предлагается.
Можно сделать вывод, что ряды Фурье широко применяются в инженерно-технических расчетах. Они часто встречаются при рассмотрении ряда задач измерительной техники, особенно при исследовании колебательных процессов в измерительных системах, а также при анализе результатов измерений нестационарных параметров. Пример буден приведен при решении нулевого варианта контрольной работы.
Вопросы для самопроверки
1. Запишите формулу средних прямоугольников для вычисления определенного интеграла
Примерный вариант и образец выполнения
Контрольной работы по теме
«Ряды Фурье»
Задача 1. Разложить в ряд Фурье функцию , имеющую период .
Решение. Построим график функции
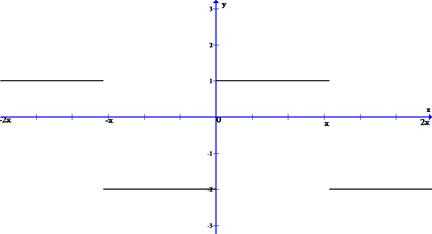
Эта функция f(x) имеет период , одну точку разрыва первого рода x=0 на отрезке , отрезок можно разбить на два отрезка так, что внутри каждого из них функция f(x) монотонна.
По формуле (2) найдем коэффициент этого ряда.
.
Найдем по формуле (3)
По формуле (4) найдем аналогичным образом
.
Подставляя коэффициенты в формулу (1), получаем или .
Это равенство справедливо во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее предельных значений изнутри отрезка, то есть в точке x=0.
= , а на концах отрезка в точках и = .
Ответ.
Построим график S4(x)
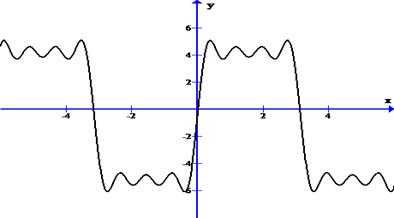
Задача 2. Разложить в ряд Фурье функцию , заданную на отрезке сначала по синусам, затем по косинусам.
Решение.Построим график
1. Продолжая эту функцию на промежуток нечетным образом, получим функцию, ряд Фурье для которой составлен в §2, пример 2.
Ряд для такого разложения
Построим S5(x)
2. Продолжая эту функцию на промежуток четным образом. Построим график
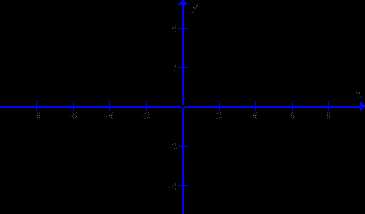
Эта функция f(x) имеет период , четная, продолжена непрерывно.
. Найдем =
Это равенство справедливо во всех точках числовой прямой.
Построим график S4(x)
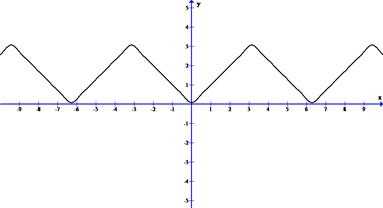
Задача3.Разложить в ряд Фурье периодическую функцию , с периодом Т=6.
Решение. Построим эскиз графика функции
Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. Заданная функция общего вида с периодом Т=6, l=3, поэтому в разложении ее ряд Фурье имеет вид: .
Подставляя коэффициенты в формулу ряда, получаем или . Это равенство имеет место во всех точках, кроме точек -3 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть .
Построим график S5 (x)
Можно совместить оба графика на одном чертеже
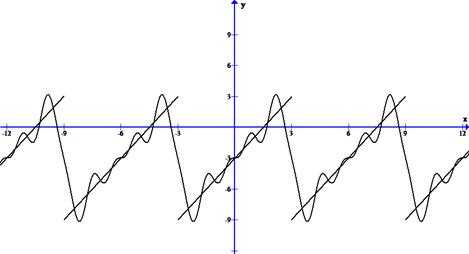
Отметим близость этих графиков.
Задача4. Разложить в ряд Фурье функцию . Построить график S5(x).
Решение. Будем считать функцию периодической с периодом T=3-1=2, l=1 т.е. , T=2, l=1. Построим эскиз графика этой функции
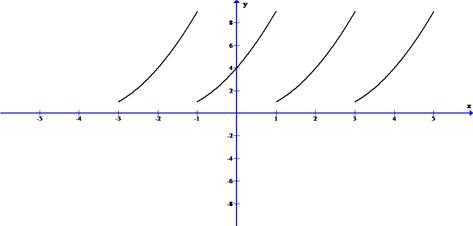
Ряд Фурье для этой функции будет иметь следующий вид: .
Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. .
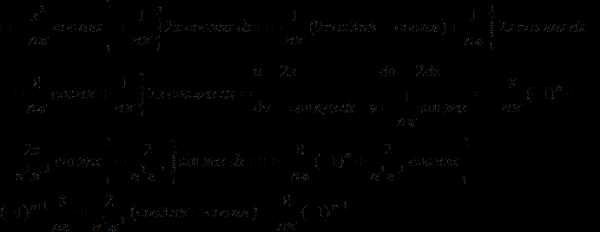Подставляя коэффициенты в формулу ряда, получаем или Это равенство имеет место во всех точках, кроме точек 1 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть .
Построим график S5 (x)
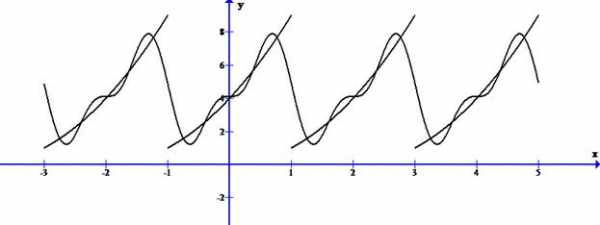
Задача 5. Разложить в комплексный ряд Фурье периодическую функцию с периодом , определенную следующим образом: . Построить амплитудно-частотный спектр.
Решение. Будем считать функцию периодической с периодом Т =2. Построим график.
Проверив выполнение условий Дирихле для функции , переходим к вычислению коэффициентов Фурье по формуле .
Интеграл, стоящий в правой части последнего равенства, определяется по частям:
;
Если , то полученные формулы не дают результата. Поэтому коэффициент надо вычислить иначе׃ , так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим
Это равенство имеет место лишь в точках непрерывности функции . В точках разрыва , где k— любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр
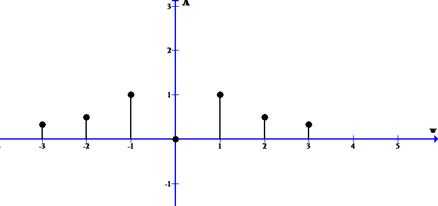
Задача 6. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 2] (получить первые 4 гармоники разложения).
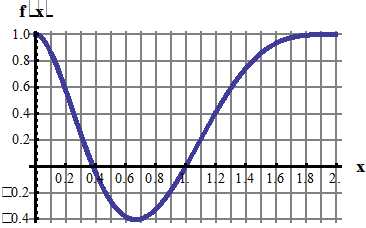
Решение. По условию функция – четная, задана на отрезке [0; 2] = [0; l], следовательно, ее график на промежутке [–2; 0] симметричен заданному графику относительно оси ординат и период функции T = 2l =4 (длина промежутка [–2; 2]).
Ряд Фурье для четной периодической функции с периодом 2l имеет вид:
, (1)
где , . (2)
Поскольку вид функции ) неизвестен, для вычисления интегралов используем одну из квадратурных формул – формулу средних прямоугольников:
,
где – середина k-го отрезка разбиения промежутка интегрирования [a; b], k = 1, 2, …, m, h – длина шага разбиения промежутка интегрирования: .
Возьмем m = 10, , т.е. разобъем отрезок [0; 2] на 10 равных частей точками и считаем с графика значения функции в серединах полученных отрезков. Чтобы вычислить коэффициенты a0, a1, a2, a4 для первых 4 гармоник разложения функции в ряд Фурье по формулам (2), построим таблицу значений функции f(x) и в полученных точках:
| k | xk-1/2 | f(xk-1/2) | |||
| 0,1 | 0,9 | 0,89 | 0,86 | 0,80 | |
| 0,3 | 0,25 | 0,22 | 0,15 | 0,04 | |
| 0,5 | – 0,25 | – 0,18 | 0,18 | ||
| 0,7 | – 0,4 | – 0,18 | 0,24 | 0,40 | |
| 0,9 | – 0,2 | – 0,03 | 0,19 | 0,09 | |
| 1,1 | 0,2 | – 0,03 | – 0,19 | 0,09 | |
| 1,3 | 0,6 | – 0,27 | – 0,35 | 0,59 | |
| 1,5 | 0,85 | – 0,60 | 0,60 | ||
| 1,7 | 0,9 | – 0,80 | 0,53 | – 0,14 | |
| 1,9 | – 0,99 | 0,95 | – 0,89 | ||
| 3,85 | – 1,97 | 2,38 | 1,76 |
Вычислим коэффициенты ряда a0, a1, a2, a4.
;
Подставляем найденные коэффициенты в формулу (1) и получаем аппроксимацию функции частичной суммой ряда s3(x):
Для сравнения с функцией f(x) построим на промежутке [0; 2] график заданной функции f(x) и график полученной аппроксимации :
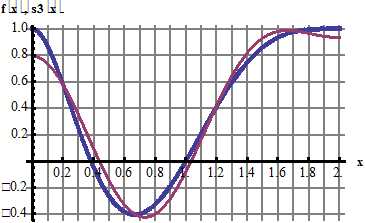
Если в аппроксимацию sn(x) включить сумму большего числа гармоник, например, 5, то графики s5(x) и функции f(x) практически совпадают:
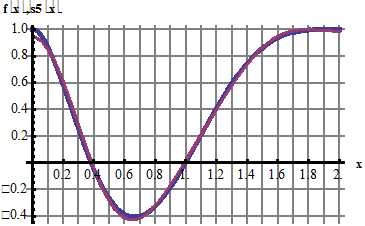
Ответ: , .
Варианты контрольной работы по теме «Ряды Фурье»
Задача 1.
Построить эскиз графика, разложить в ряд Фурье следующие функции, периодические с периодом , определить сумму в точках разрыва. Построить график частичной суммы Фурье для n=4.
Задача 2. Разложить в ряд Фурье функцию , заданную формулой на отрезке , сначала по синусам, затем по косинусам. Построить график и частичных сумм для n=4.
| № | Функция | № | Функция |
| f(x)=2x-1 | f(x)=x-4 | ||
| f(x)=x2-1 | f(x)=x2+2 | ||
| f(x)=-x-1 | f(x)=-x-3 | ||
| f(x)=x2+1 | f(x)=x2-3 | ||
| f(x)=3x-2 | f(x)=0.5x-1 |
Задача3.Разложить в ряд Фурье периодическую функцию , с периодом Т=2l. Построить график частичной суммы при n=5.
| № | Функция | T | № | Функция | T |
| f(x)=x+4 | f(x)=2x+1 | ||||
| f(x)=-x+4 | f(x)=2x-1 | ||||
| f(x)=2x+4 | f(x)=3x+4 | ||||
| f(x)=x+1 | f(x)=3x-2 | ||||
| f(x)=-x+2 | f(x)=-3x-1 |
Задача4Разложить в ряд Фурье функцию . Построить график частичной суммы S4(x).
Задача 5. Разложить в комплексный ряд Фурье периодическую функцию с периодом , определенную следующим образом: , . Построить амплитудно-частотный спектр.
Задача 6. Разложить в ряд Фурье функцию f(x), графически заданную на промежутке [0; l] (получить первые гармоники разложения).
Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).
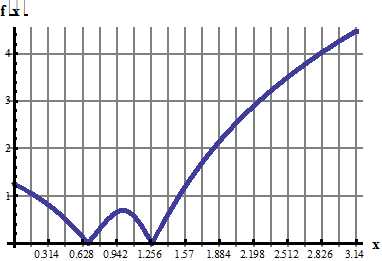
1. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 1] (получить первые 4 гармоники разложения).
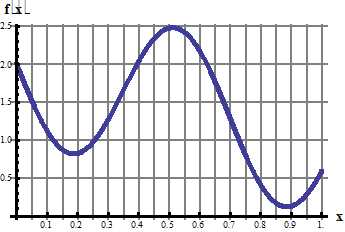
2. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 2] (получить первые 4 гармоники разложения).
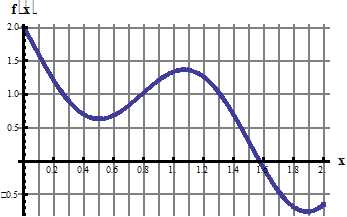
3. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 2,5] (получить первые 4 гармоники разложения).
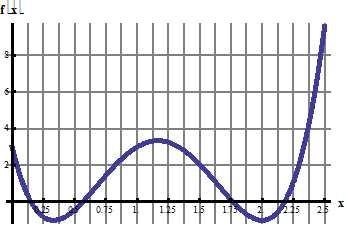
4. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 3] (получить первые 4 гармоники разложения).
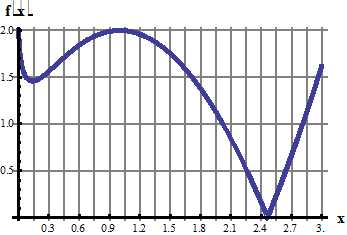
5. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).
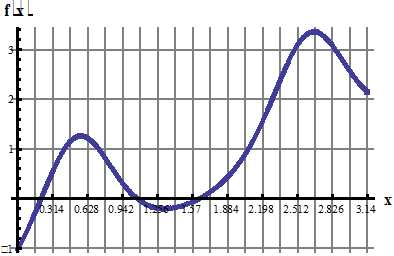
6. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 4] (получить первые 4 гармоники разложения).
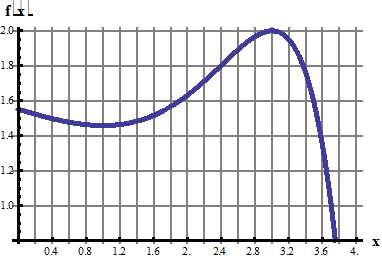
7. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 5] (получить первые 4 гармоники разложения).
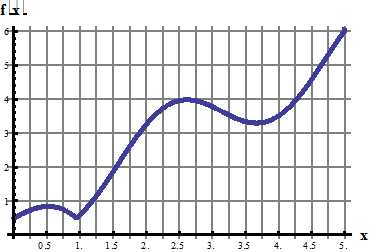
8. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).
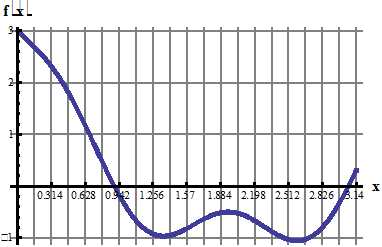
9. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 1] (получить первые 4 гармоники разложения).
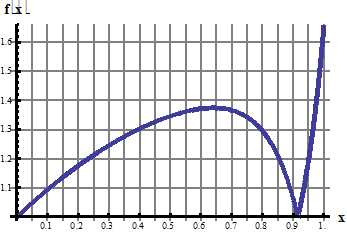
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с.
2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М.: Высш. шк., 1998.– 479 с.
3.Берман Г.Н. Сборник задач по курсу математического анализа: Уч. пособие.- 22-изд., перераб.- СПб., Изд-во «Профессия», 2005.-432с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев.– М.: Высш. шк., 2001.– 304 с.
infopedia.su