Решение уравнений простых: Ошибка 403 — доступ запрещён

Содержание

Решение простых уравнений — intmag24.ru

Решение простых уравнений — одна из базовых тем для усвоения, при этом они являются достаточно мощным инструментом для решения большинства задач. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.

Уравнение — это равенство, содержащее в себе переменную. Значение данной переменной требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.

Переменную, входящую в уравнение, еще называют неизвестным.

Примеры:

выражение 3+2=5 является равенством, так как при вычислении получаем 5=5
выражение 3+х=5 является уравнением, так как содержит переменную х, значение которой можно найти.

Решить уравнение — значит найти такое значение х, чтобы равенство было верным.

То есть, в уравнении 3+х=5 значение будет равно 2 (х=2), чтобы получилось верное равенство.
При этом говорят, что 2 — это корень уравнения или решение уравнения 3+х=5.

Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.

Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.

Компоненты

Компонентами называются числа и переменные, которые входят в равенство:

компоненты сложения — слагаемые и сумма;
компоненты вычитания — уменьшаемое, вычитаемое и разность;
компоненты умножения — множители и произведение;
компоненты деления — делимое, делитель и частное.

Правила нахождения неизвестных

Чтобы выразить переменную через другие числа, нужно переменную оставить (или перенести) в левой части выражения, а все числа перенести в правую часть.

Решение простых уравнений подразумевает применение следующих правил:

чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
чтобы найти неизвестное делимое, нужно частное умножить на делитель;
чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Примеры:

3+х=5.
Нужно задать вопрос: что сделать с числами 5 и 3, чтобы получить переменную х.
Чтобы найти слагаемое, нужно из суммы вычесть известное слагаемое: х=5-3.
х-3=7
Нужно задать вопрос: что сделать с числами 3 и 7, чтобы получить переменную х.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое: х=7+3.
8-х=6
Нужно задать вопрос: что сделать с числами 8 и 6, чтобы получить переменную х.
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность: х=8-6.
3×а=6 (а-переменная)
Нужно задать вопрос: что сделать с числами 3 и 6, чтобы получить переменную а.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель
а:4=3
(а-переменная)
Нужно задать вопрос: что сделать с числами 4 и 3, чтобы получить переменную а.
Чтобы найти неизвестное делимое, нужно частное умножить на делитель: а=3*4
12:а=3(а-переменная)
Нужно задать вопрос: что сделать с числами 12 и 3, чтобы получить переменную а.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное: а=12:3.

Если неизвестное имеет коэффициент

Решение простых уравнений сводится к тому, что неизвестное нужно выразить через другие числа. Но чаще всего задаются уравнения, в которых неизвестное имеет коэффициент, например: 2х, 5х и т.д. В таких случаях неизвестное нельзя выразить сразу, поскольку оно содержит коэффициент. Поэтому нужно привести это уравнение к виду, в котором переменная будет выражена.

Рассмотрим пример: 2х+4=8.
В данном примере: 2x — первое слагаемое, 4 — второе слагаемое, 8 — сумма.

Принимает слагаемое 2х за неизвестное слагаемое. Применяем правило нахождения неизвестного слагаемого: вычитаем из суммы известное слагаемое. Получаем: 2х=8-4 или 2*х=4.
Мы получили новое уравнение . Теперь мы имеем дело с умножением. Применяем правило нахождения неизвестного множителя: произведение делим на известный множитель. Получаем: х=4:2; х=2
Вычислим правую часть, получим значение переменной х.
Проверяем: 2*2+4=8. Равенство верное.

Если уравнение имеет неизвестные с разными коэффициентами

Рассмотрим пример: a+2a+3a=30.
Cразу выразить неизвестное нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить. Для этого нужно сложить все неизвестные величины с коэффициентами: 1а+2а+3а=6а (а — это переменная с коэффициентом 1. который не пишется).
Получаем уравнение вида: 6*а=30. Его можно решить как простое уравнение. Получаем корень: а=5.

Равносильные уравнения

Уравнения называют равносильными, если их корни совпадают.

Из предыдущего примера: уравнение a+2a+3a=30 и уравнение 6а=30 являются равносильными.
Проверим это. Подставим корень сначала в уравнение a+2a+3a=30, а затем в уравнение 6а=30, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения.

Мы должны получить верные числовые равенства.

Для удобства решения можно любое уравнение преобразовать в равносильное. Для этого можно применить законы математики и свойства уравнений.

Свойства уравнений

Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.

Пример. Решить уравнение 5х-10=20.
Вычтем из обеих частей уравнения число 10, получим: 5х=20-10 или 5х=10.
В результате получилось равносильное уравнение , корень которого равен 2.

Пример. Решить уравнение 4(х+3)=20.
Раскроем скобки: 4х+12=20.
Вычтем из обеих частей уравнения число 12, получим: 4х=20-12 или 4х=8.

В результате получилось равносильное уравнение , корень которого равен 2.

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.

Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные числа.

Пример. Решить уравнение (1/4)х+5=6,5

При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
Для упрощения обе части уравнения можно умножить на 4: 4*(1/4)х+4*5=4*6,5 или х+20=26.
В результате останется простейшее уравнение. Получаем, что корень равен 6.
Вернемся к исходному уравнению и подставим вместо
x найденное значение. Получается верное числовое равенство. Значит уравнение решено правильно.

Пример. Решить уравнение 8х+16=56

Для упрощения обе части уравнения можно разделить на 8: 8х:8+16:8=56:8 или х+2=7.
В результате останется простейшее уравнение. Получаем, что корень равен 5.
Вернемся к исходному уравнению и подставим вместо x найденное значение. Получается верное числовое равенство. Значит уравнение решено правильно.

Если обе части уравнения умножить на минус единицу (поменять знаки), то получится уравнение равносильное данному.

Это правило следует из того, что если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю, то получится равносильное уравнение. Иногда это нужно для того, чтобы получить равносильное уравнение, которое проще решать.

Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.

При этом минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать.

Пример. Решить уравнение: 2х-5х+10=4.

Приведем подобные слагаемые: -3х+10=4
Перенесем второе слагаемое в правую часть: -3х=-6
Для удобства умножим обе части на (-1). получим: 3х=6.
Корень: х=2.

Уравнение имеет несколько корней

Уравнение может иметь несколько корней.

Рассмотрим уравнение: x(x + 9) = 0.
Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из множителей равен нулю.
То есть в уравнении x(x + 9) = 0 равенство будет выполняться, если x будет равен нулю или (x + 9) будет равно нулю. Таким образом, уравнение имеет два корня: 0 и −9.

Уравнение имеет бесконечно много корней

Уравнение может иметь бесконечно много корней, когда при подстановке подставив в такое уравнение любого числа, мы получим верное равенство.

Например: рассмотрим простое уравнение 6*(х+2)=6х+12. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 6х+12= 6х+12. Это равенство будет выполняться при любом х.

Уравнение не имеет корней

Бывает и так, что уравнение совсем не имеет корней.

Например: уравнение х+2=х.
Данное уравнение не имеет корней, так как при любом значении х, левая часть уравнения всегда будет больше правой на 2.

Таким образом, мы рассмотрели в статье решение разных видов простых уравнений. Решение более сложных уравнений без знания данного материала практически невозможно.

Далее вы можете переходить к решению квадратных уравнений и решению систем линейных уравнений.

Для решения уравнений вам также могут понадобится темы: раскрытие скобок и порядок действий в примерах.

Решение простых уравнений

Уравнения

Презентацию подготовила

учитель начальных классов

Казимирская Ирина Валентиновна

Реши примеры и прочитай тему урока

Р —

19*5 =

Е —

100:25=

Н —

80:16=

15*4=

Ш —

В —

60:5 =

И —

45*2=

У —

11*5 =

А —

70:2=

Й —

75:3=

№ 9 стр. 75

а) 81-х= 6 в) m+15=80 д) k-17= 45

б) 2∙у=18 г) t: 9=60 e) 48: n=12

Х= 75

m= 65

k= 62

у = 9

t=540

n= 4

Названия компонентов действия

Названия результатов действия

СУММА

СЛАГАЕМОЕ

УМЕНЬШАЕМОЕ

РАЗНОСТЬ

ВЫЧИТАЕМОЕ

МНОЖИТЕЛЬ

ПРОИЗВЕДЕНИЕ

ДЕЛИМОЕ

ЧАСТНОЕ

РАВЕНСТВО

ДЕЛИТЕЛЬ

УРАВНЕНИЕ

Уравнением называется равенство, содержащее переменную , значение которой надо найти.

Значение переменной , при котором из уравнения получается верное равенство, называет корнем уравнения.

Решить уравнение – значит найти все его корни (или убедиться, что их нет.)

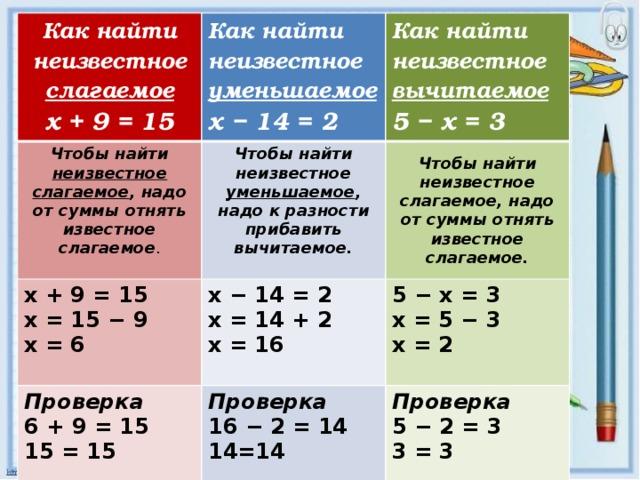
х + 28 = 53 Неизвестно слагаемое. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

у – 34 = 26 Неизвестно уменьшаемое . Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

35 – Z + 19 Неизвестно вычитаемое . Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

7 x а = 56 Неизвестен множитель. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

в : 23 = 4 Н еизвестно делимое . Чтобы найти неизвестное делимое, надо делитель умножить на частное.

90 : с = 5 Неизвестен делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Чтобы найти неизвестное слагаемое , надо

Чтобы найти неизвестное уменьшаемое, надо

из суммы вычесть известное слагаемое

из уменьшаемого вычесть разность.

Чтобы найти неизвестное вычитаемое, надо

к разности прибавить вычитаемое.

Что найти неизвестный множитель, надо

частное умножить на делитель.

Чтобы найти неизвестное делимое, надо

произведение разделить на другой множитель.

Чтобы найти неизвестный делитель, надо

делимое разделить на частное.

Алгоритм решения уравнения

Вспомнить компоненты действия

данного уравнения

Определить неизвестный компонент

Вспомнить правило нахождения

неизвестного компонента

Применить правило и найти

корень уравнения

Делаю проверку

Называю ответ

№ 1 стр. 78

17 + х =304

х = 304 — 17

х =287

17 + 287 = 304

304 = 304

Простые уравнения: учитесь и практикуйтесь на решенных примерах

Автор Мадхурима дас
Последнее изменение 13-03-2023

Простые уравнения: Концепция уравнения в алгебре очень похожа на концепцию балансировки. Уравнение может состоять из переменных, констант или знака равенства, знак равенства (=) можно рассматривать как точку опоры или центр при решении простого уравнения. Следовательно, если вы измените одну часть уравнения, вы должны изменить и другую часть. Баланс поддерживается добавлением одинакового количества к обеим частям уравнения (скажем, по 7 в каждую сторону).

В приборе для взвешивания принцип работы символа равенства такой же, как и у весов. Простое уравнение считается линейным уравнением с одной переменной. Это означает, что он включает полином первой степени и только с одной переменной. Решение простого уравнения означает, что мы узнаем значение неизвестной переменной. В этой статье вы найдете простое определение уравнения и изучите различные методы его решения.

Переменная — это величина, которая может меняться в зависимости от контекста математической задачи. Когда переменная используется в алгебраическом выражении, известно, что это не постоянное число, но оно может представлять множество чисел. Алфавиты, такие как \(x,\,y,\,z\), являются общим типом переменных и используются большую часть времени, но иногда мы выбираем букву, которая напоминает нам о величине, которую она представляет, например, \( v\) для скорости, \(t\) для времени, \(s\) для скорости, \(d\) для расстояния и т. д. 92}\, + \,5 = 0\) — уравнения.

Простые линейные уравнения

Уравнение, в котором самая высокая степень задействованных переменных равна единице, называется линейным уравнением. Линейное уравнение может включать различные переменные. Когда оно состоит из двух разных переменных, оно известно как линейное уравнение с двумя переменными. Если оно состоит из трех переменных, оно известно как линейное уравнение с тремя переменными и так далее.
Например,
Линейное уравнение с одной переменной, \(3x + 2 = 9,x = 7\)
Линейное уравнение с двумя переменными, \(x\, + \,2y = 0\)
Линейное уравнение с тремя переменными, \(a\, + 3b + c = 0\)

Простое Уравнение

Линейное уравнение, которое включает только одну переменную, известно как простое уравнение или линейное уравнение с одной переменной.

Например, \(3x + 2 = 23,x = 7,2x + 6 = 3x – 4,\) и т. д. – это простые уравнения.

Методы решения простых уравнений

Мы можем решить простое уравнение, используя три метода. Методы

Метод проб и ошибок
Систематический метод
Метод перестановки

Метод проб и ошибок

В этом методе мы угадываем решение уравнения. Находим значения левой и правой сторон данного уравнения при различных значениях переменной. Значение переменной, для которой \({\rm{LHS = RHS}}\) является решением уравнения.
Возьмем пример \(x + 7\, = \,10\)
Имеем \({\rm{LHS}}\, = x + 7\, = \,10\) и \({\ rm{RHS}} = 10.\)

Следовательно, \({\rm{LHS}}\,{\rm{ = }}\,{\rm{RHS}}\) для \({\rm{x}}\,{\rm{ = }}\,{\rm{3}}\)

Систематический метод

Уравнение можно сравнить с весами. Две стороны уравнения — это две кастрюли, и знак равенства говорит нам, что две кастрюли уравновешены. Если в две кастрюли положить одинаковые гири, то две кастрюли будут уравновешены. Если мы удалим или добавим равные веса к обеим чашам, мы все равно увидим, что чаши находятся в равновесии.

Возьмем несколько примеров простых уравнений,

Уравнение, включающее сложение

\(x – 7 = 6\)
Тогда, добавляя \(7\) с обеих сторон, мы имеем \({\rm{x}}\, – 7 + 7 = 6 + 7 \)
Следовательно, \(x = 13\)

Уравнение с вычитанием

\(x + 3 = 5\)
Тогда, вычитая \(3\) с обеих сторон, мы имеем \(x + 3 – 3 = 5 – 3\)
Следовательно, \(x = 2,\)

Уравнение, включающее деление

\(15x = 45\)
Тогда, разделив на \(15\) с обеих сторон, мы получим,
\(\ frac{{15x}}{{15}} = \frac{{45}}{{15}}\)

Следовательно, \(x = 3\)

Уравнение, включающее более одного правила

\(3x\, + 2 = 5\)
Вычитая \(2\) из обеих частей, которые у нас есть, + 2 – 2 = 5 – 2 \Rightarrow 3x = 3\)

Разделив обе части на \(3\), получим \(\frac{{3x}}{3} = \frac{3}{3} \)

Следовательно, \(x = \,1\)

Метод перестановки

В этом методе любой член уравнения переводится в другую сторону с изменением знака, не затрагивая равенства. Когда мы сдвигаем один член уравнения с левой стороны на правую или наоборот, знак плюс сдвинутого члена меняется на знак минус, а знак минус меняется на знак плюс.

Например, \(3(x – 1) = 2x – 11\)
Раскрывая скобки в \({\rm{LHS}}\) , мы имеем, \(3x – 3 = 2x – 11\)
Теперь, транспонируя \(3\) из \({\rm{LHS}}\) в \({\rm{RHS}}\), мы имеем, \(3x = 2x — 11 + 3\)
Транспонирование \(2x\) из \({\rm{RHS}}\), мы получаем, \(3x\, – 2x = – 8\)

Следовательно, \(x = – 8\)

Составляя уравнение из Решение

Теперь мы знаем, как решить простое уравнение. Давайте посмотрим, как мы составим простое уравнение, используя решение. Например,

Данное решение, \(x = 5\)
Сложить \(3\) с обеих сторон,
\( \Стрелка вправо x + 3 = 5 + 3\)
Умножить \(4\) с обеих сторон,
\ ( \Стрелка вправо 4(x + 3) = 4 \times 8\)
\( \Стрелка вправо 4x + 12 = 48\)
Аналогичным образом можно составить больше уравнений.

Применение простых уравнений в реальной жизни

Значение неизвестной величины можно определить, если можно составить простое уравнение, используя информацию, относящуюся к неизвестной величине. Неизвестная величина может рассматриваться как \(x\) или любая другая переменная, такая как \(a,\,b,\,c,\,d\) и т. д. Процедура составления уравнения из реальной задачи с использованием данной информации (известных и неизвестных величин) известна как постановка задачи. Таким образом, процесс решения реальной проблемы состоит из двух частей, таких как постановка и решение.

Например, добавление \(6\) к числу дает число \(6\). Найдите число.

Здесь число, которое мы хотим найти, является неизвестной величиной.
\(6\) и \(10\) — известные величины, связанные с неизвестной величиной.
Примем число (неизвестное количество) за \(x\).

Согласно утверждению, \(x\, + 6 = 10\)
Теперь, вычитая \(6\) с обеих сторон, мы имеем

\(x\, + 6 – 6\,\, = 10 – 6 \Rightarrow x = 4\)
Следовательно, неизвестное число равно \(4\)

Решенные примеры – простые уравнения

Q.1: Решить уравнение )
Преобразовать \(9\) в \({\rm{RHS}}\)
\( \Стрелка вправо 2x\, = 19 – 9\)
\( \Стрелка вправо 2x\, = 10\)
Теперь разделим с обеих сторон на \(2\)
\( \Стрелка вправо \frac{{2x}}{2} = \frac{{10}}{2}\)
\( \Стрелка вправо x\,\, = \,5 \)
Следовательно, решение уравнения \(2x\, + \,9\, = 19\) равно \(x = \,5\)

Q. 2 : Решите уравнение \(x – 4\, = \,0\) используя метод проб и ошибок.
Ответ:

Следовательно, решением уравнения \(x – 4\, = \,0\) является \(x\,\, = \,\,4\)

Q.3: Сумма двух последовательных четных чисел равна \(86\) Найдите числа.
Ответ: Рассмотрим последовательные четные числа как \(x\) и \(x + 2\).
Учитывая, что сумма двух последовательных четных чисел равна \(86\).
\( \Стрелка вправо x + (x + 2) = 86\)
\( \Стрелка вправо x + x + 2 = 86\)
Переставляя \(2\) из левой стороны в правую, мы получаем
\( \Стрелка вправо 2x + 86 – 2\)
\( \Стрелка вправо 2x = 84\)
Разделив обе части на \(2\), получим
\( \Стрелка вправо \frac{{2x}}{2} = \frac{{84} {2}\)
\( \Стрелка вправо x = 42\)
Следовательно, два последовательных числа равны \(42\) и \(44\).

Q.4: Отец Прии в три раза старше Прии. Предположим, что сумма их возрастов равна \(56\) лет. Найдите их возраст.
Ответ: Допустим, возраст Прии составляет \(x\) лет.
Возраст отца Прии составляет \(3x\) лет.
Согласно данному утверждению,
\(3x + x\, = 56\)
\( \Rightarrow 4x = 56\)
\( \Rightarrow \frac{{4x}}{4} = \frac{{56 }}{4}\)
\( \Стрелка вправо x\, = 14\)
Возраст Прии — \(14\) лет, а возраст ее отца — \(3 \умножить на 14 = 42\) лет.

Q.5: Разница между двумя числами \(7\) . Сумма шести произведений меньшего и большего равна \(77\) . Найдите числа.
Ответ: Учитывая, что разница между двумя числами равна \(7\), допустим, что меньшее число равно \(х\), а большее равно \(х\, + 7\).
Теперь меньшее число в шесть раз равно \(6x\)
Согласно данному утверждению,
\(6x\, + (x + 7) = 77\)
\( \Rightarrow 6x\, + x + 7 = 77\)(раскрытие скобок в левой части)
\( \Стрелка вправо 7x\, = 77 – 7\) (перенос \(7\) из левой стороны в правую)
\( \Стрелка вправо 7x\, = 70\)
\( \Rightarrow \frac{{7x}}{7}\, = \frac{{70}}{7}\)
\( \Rightarrow x = 10\)
Следовательно, меньшее число равно \(x = 10\), а большее число равно \(x + 7 = 10 + 7 = 17\)
Учащиеся могут делать заметки по простым уравнениям из решенных примеров, чтобы быстро повторить концепцию.

Простые уравнения: резюме

В этой статье мы узнали о простых уравнениях и методах их решения, таких как метод проб и ошибок, систематический метод и метод транспонирования. Кроме того, мы обсудили применение простых уравнений в реальной жизни.

Часто задаваемые вопросы о простых уравнениях Класс 7

Некоторые из часто задаваемых вопросов о простых уравнениях приведены ниже:

Q. 1: Как вы решаете простые уравнения?
Ответ: Когда дается простое уравнение, мы сохраняем переменные члены слева от знака равенства, а постоянные члены — справа, используя систематический метод или метод транспонирования. Затем мы найдем неизвестную переменную.

Q.2: Объясните простые уравнения на примерах.
Ответ: Линейное уравнение, которое включает только одну переменную, известно как простое уравнение или линейное уравнение с одной переменной.
Например, \(x + 5 = 4,2x – 6 = 8x + 2,\) и т. д. являются простыми уравнениями.

Q.3: Какие существуют \(3\) методы решения простых уравнений?
Ответ: Три метода решения простых уравнений:
1. Метод проб и ошибок
2. Систематический метод
3. Метод перестановки

Q.4: Что такое алгебраическое выражение?
Ответ: Комбинация констант и переменных, связанных знаком основных операций сложения, вычитания, умножения и деления, называется алгебраическим выражением. 92}\, + \,5,\) и т. д. — алгебраические выражения.

Q.5: Приведите три реальных примера простых уравнений.
Ответ: Мы используем простые уравнения,
1. Задачи на возраст
2. Задачи на нахождение неизвестных чисел
3. Задачи на прибыль и убыток

Q.6: Как писать уравнения ?
Ответ: В уравнении всегда есть знак равенства. Знак равенства показывает, что значение выражения слева от него равно значению выражения справа от него. Таким образом, мы можем написать уравнение, используя переменные и алгебраические выражения со знаком равенства.

Мы надеемся, что эта подробная статья о простых уравнениях помогла вам в учебе. Если у вас есть какие-либо сомнения или вопросы, вы можете задать их нам в разделе комментариев ниже. Приятного обучения!

Как решать простые уравнения?

Концепция школьной математики. Черная доска с деревянной рамой, слово, текстовая математика красочными буквами, красный фон стены
Математика — неотъемлемая часть жизни, а уравнения — фундаментальная концепция математического мира. Решение простых уравнений может быть пугающим для некоторых людей, но это не обязательно! Обладая необходимыми знаниями и практикой, любой может научиться быстро и точно решать простые уравнения. В этой статье приведены советы по решению основных уравнений с пошаговыми инструкциями, чтобы вы стали более уверенными в своих арифметических способностях.

Как решать простые уравнения?
Уравнения бывают разных форм и уровней сложности, от простых цифр до сложных алгебраических выражений. Хотя поначалу они могут показаться пугающими, разбиение уравнения на более мелкие компоненты значительно упрощает их понимание и решение.
Понимая, что означает каждый компонент и как они взаимодействуют друг с другом, вы сможете определить закономерности, упрощающие поиск решения. Научиться решать простые уравнения полезно не только для школьных занятий или экзаменов, но и для развития навыков решения задач, которые бесценны в повседневной жизни.
Нанять репетитора
Что такое простые уравнения?
Простые уравнения — это алгебраические уравнения, включающие одну переменную и операцию. Например, уравнение может быть выражено как «x+3=5». Это простое уравнение с переменным членом, равным «x». Линейные уравнения, уравнения деления и уравнения вычитания могут быть классифицированы как типы простых уравнений.
Независимо от того, с каким уравнением вы имеете дело, вашей конечной целью всегда должно быть упрощение его до исходной формы. С практикой и терпением вы в конечном итоге научитесь лучше распознавать закономерности в каждом типе вопросов и станете более искусными в быстром поиске решений!

Этапы решения простых уравнений
Решение простых уравнений является неотъемлемой частью базовой алгебры. Уравнения с переменными можно решить всего за несколько шагов.
Рассмотрим обратное
Важно помнить, что решение простых уравнений требует использования обратных операций. Это означает, что вам нужно будет использовать сложение/вычитание и умножение/деление при работе с числовыми терминами. Эти основные операции необходимы для того, чтобы исключить любые дополнительные данные или символы в уравнении и изолировать переменную.
Решить обе части уравнения
После выделения переменной можно найти ее значение, выполнив соответствующие арифметические операции с обеими частями уравнения. Также важно перепроверить свой ответ, прежде чем переходить к более сложным уравнениям, так как это гарантирует, что все значения, введенные в уравнение, были правильными.
Как решить математическое уравнение
Понимание свойства распределения
При работе с уравнениями любого типа важно понимать свойство распределения. Этот принцип гласит, что при умножении числа на другое с более чем одним термином вы можете разбить его на части и распределить число по каждому из этих терминов отдельно. Например, если у нас есть 4x(x + 2), то это будет равно 4×2+8x из-за распределительного свойства. Вы распределяете то, что находится внутри скобки поровну с обеих сторон.
Полезность распределительного свойства заключается в его способности упрощать уравнения. Применяя эту концепцию, вы можете взять любое заданное уравнение и переписать его в более удобной для решения форме без изменения его значения. Кроме того, этот процесс позволяет изолировать определенные переменные от других, чтобы решать их самостоятельно.

Решение одновременных уравнений
Одновременные уравнения состоят из двух или более алгебраических уравнений, которые имеют общие переменные, такие как x и y. Они требуют одновременного решения двух или более уравнений с несколькими неизвестными и могут помочь вам получить ответ быстрее, чем если бы вы решали их по отдельности.
Ниже приведено пошаговое руководство по решению одновременных уравнений:
Определите коэффициенты при x и y в обоих уравнениях;
Используйте метод подстановки или метод исключения, чтобы изолировать одну переменную в любом уравнении;
Замените это новое уравнение другим исходным уравнением, чтобы найти оставшуюся переменную;
Проверьте свои ответы, подставив их обратно в оба исходных уравнения.

Решение квадратных уравнений
Решение квадратных уравнений может быть сложным, но это полезный навык. Существует два основных подхода к решению этих типов уравнений: разложение на множители и использование квадратичной формулы.
Факторинг
Факторинг включает в себя разбиение уравнения на множители, которые при умножении равны выражению слева от знака равенства. Этот метод лучше всего работает с простыми уравнениями, где есть только одно решение или ответ.
Квадратная формула
Использование квадратной формулы требует от вас использования алгебраической формулы для определения решений любого заданного квадратного уравнения. Квадратичная формула выглядит следующим образом:
ax ² + bx + c = 0
Этот метод, как правило, работает лучше, чем факторинг, если требуется несколько решений, а также более сложные уравнения, которые не могут быть легко решены с помощью одного факторинга. Независимо от того, какой подход вы выберете, хорошее понимание обоих методов облегчит вашу жизнь, когда придет время заняться квадратикой!

Решение линейных уравнений
Линейные уравнения проще квадратных, поскольку имеют только одно решение или корень.
No related posts.