Решение уравнений с корнями кубическими – Иррациональные уравнения с кубическими радикалами

Содержание

Решение кубического уравнения по формулам Кардано.

1. Приведение уравнения к каноническому виду.

Сделаем замену переменного по формуле:

Получим уравнение:

Раскроем скобки:

Получим уравнение:

или

Уравнение приведено к каноническому виду

Дискриминантом уравнения

называется число:

2. Решение уравнения

Ищем решение в виде:

Получили равенство:

Число

удовлетворяет этому равенству, если числа m и n удовлетворяют системе из двух уравнений:

Находим числа m и n

2.1. Дискриминант меньше нуля:

Уравнение имеет три различных действительных корня.

Найдём модуль комплексных чисел:

Модуль этих комплексных чисел равен:

Аргумент числа

равен:

Для k=0, k=1, k=2 получаем решение:

Итак, если дискриминант меньше нуля, то уравнение имеет три различных действительных корня:

2.2. Дискриминант больше нуля:

Уравнение имеет один действительный корень и два комплексно-сопряжённых корня.

При этом для любых комплексных значений кубических корней необходимо выполнение условия:

Примем аргумент F обоих действительных чисел, стоящих под знаком кубического корня, равным нулю. При этом модули этих чисел могут принимать отрицательное значение. Это упростит задачу. (Если бы мы выдвигали требование неотрицательности модуля этих чисел, то, если бы под знаком кубического корня находилось отрицательное число, его аргументу нужно было бы присваивать значение F=Pi, а не F=0)

При извлечении кубического корня из отрицательного модуля получим отрицательный модуль. Аргумент же кубического корня будет принимать 3 значения:

0, 2*Pi/3, 4*Pi/3

Каждое решение y=y1, y=y2, y=y3 будет состоять из суммы двух комплексных чисел:

Число z1 находится в группе из трёх чисел:

Число z2 находится в группе из трёх чисел:

Для действительных значений кубических корней выполняется условие:

Поэтому действительный корень уравнения:

Учитывая равенство

получим два комплексно сопряжённых корня:

Итак, если дискриминант больше нуля, то уравнение имеет один действительный корень и два комплексно-сопряжённых корня:

2.3. Дискриминант равен нулю:

Уравнение имеет три действительных корня, и два корня из трёх обязательно совпадают друг с другом.

Рассуждая точно так же, как в случае с положительным дискриминантом, учитывая равенство

из формул корней уравнения с положительным дискриминантом получим:

Итак, если дискриминант равен нулю, то уравнение имеет три действительных корня, и два корня из трёх обязательно совпадают друг с другом:

3. Решение кубического уравнения:

Это уравнение получается из уравнения

путём замены переменной

Дискриминант этого уравнения равен:

где

Программа «Решение кубического уравнения Ax³+B*x²+Cx+D=0» на javaScript Программа «Решение кубического уравнения Ax³+B*x²+Cx+D=0» Код программы «Решение кубического уравнения Ax³+B*x²+Cx+D=0» На главную страницу.

ateist.spb.ru

Решение кубических уравнений с рациональными корнями.

Начнем с простейшего случая, когда х=0 является корнем кубического уравнения .

В этом случае свободный член D равен нулю, то есть уравнение имеет вид . Если вынести х за скобки, то в скобках останется квадратный трехчлен, корни которого легко найти либо через дискриминант, либо по теореме Виета . http://intelmath.narod.ru/kangaroo-problems_1_5.html

Найти действительные корни уравнения . x=0 является корнем уравнения. Найдем корни квадратного трехчлена . Так как его дискриминант меньше нуля, то действительных корней трехчлен не имеет. Если коэффициенты кубического уравнения являются целыми числами, то уравнение может иметь рациональные корни. При , домножим обе части уравнения на и проведем замену переменных y = Ax:
Пришли к приведенному кубическому уравнению. Оно может иметь целые корни, которые являются делителями свободного члена. Так что выписываем все делители и начинаем их подставлять в полученное уравнение до получения тождественного равенства. Тот делитель , при котором тождество получено, является корнем уравнения. Следовательно, корнем исходного уравнения является . Далее делим многочлен на и находим корни полученного квадратного трехчлена. Найти корни кубического уравнения . .

Замечание.

По такому алгоритму можно решать возвратные уравнения. Так как -1 является корнем всякого возвратного кубического уравнения, то можно разделить левую часть исходного уравнения на х+1 и найти корни полученного квадратного трехчлена.

matematika-2014elena-viktorovna.blogspot.com

Кубическое уравнение — Википедия

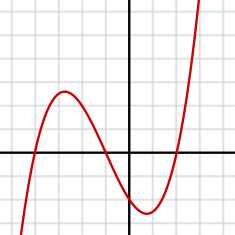График кубической функции , у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0). Имеются 2 критические точки

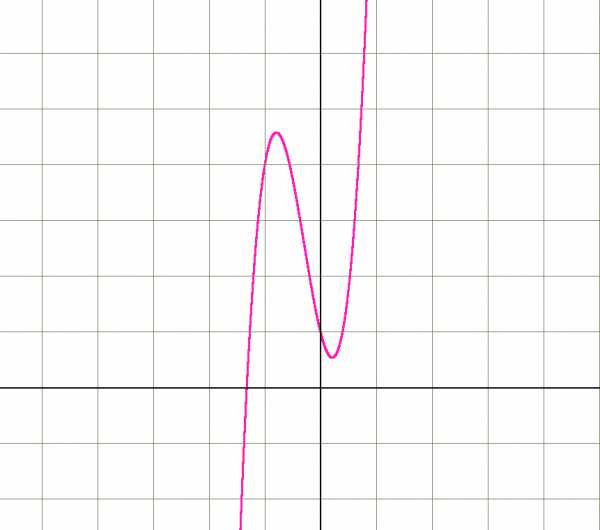Уравнение имеет один действительный и два мнимых корня.

Куби́ческое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий:

Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.

Кубическое уравнение общего вида может быть приведено к каноническому виду заменой переменной приводящей уравнение к виду:

где

Кубические уравнения были известны ещё в древнем Вавилоне, древним грекам, китайцам, индийцам и египтянам^[1]^[2]^[3]. Были найдены клинописные таблички времён вавилонского царства (20—16 век до нашей эры), содержащие таблицы вычисления кубов и кубических корней^[4]^[5]. Вавилоняне могли использовать эти таблицы для решения кубических уравнений, но не существует никаких свидетельств, что они это делали^[6].

Задача удвоения куба использует простейшее и наиболее старое из кубических уравнений, и древние египтяне не верили, что решение его существует

[7]. В пятом веке до нашей эры Гиппократ свёл эту задачу к нахождению двух средних пропорциональных между одним отрезком и другим, вдвое большим его, но не смог решить её с помощью циркуля и линейки^[8], что, как теперь известно, невозможно сделать.

В III веке нашей эры древнегреческий математик Диофант нашёл целые и рациональные решения для некоторых кубических уравнений с двумя неизвестными (диофантовых уравнений)^[3]^[9]. Считается, что Гиппократ, Менехм и Архимед подошли ближе к решению задачи об удвоении куба с помощью конических сечений^[8], хотя некоторые историки, такие как Ревиль Нетц (Reviel Netz), говорят о том, что неизвестно, думали ли греки о кубических уравнениях, или просто о задачах, которые могут привести к кубическим уравнениям. Другие, как, например, Хит (T. L. Heath), переведший все труды Архимеда, не соглашаются, указывая на свидетельства, что Архимед действительно решал кубические уравнения с помощью пересечения двух конусов

[10].

Методы решения кубических уравнений появляются в китайском математическом тексте Математика в девяти книгах, составленном около второго столетия до нашей эры и прокомментированном китайским математиком Лю Хуэем в третьем столетии^[2].

В VII веке во времена династии Тан астроном и математик Ван Сяотун в своём математическом трактате, озаглавленном Цзигу Суаньцзин, изложил и решил 25 кубических уравнений вида , в 23 из которых , и в двух уравнениях ^[11].

В XI веке персидский поэт и математик Омар Хайям (1048—1131) сделал существенный прогресс в теории кубических уравнений. В ранних работах, посвящённых кубическим уравнениям, он обнаружил, что кубическое уравнение может иметь более одного решения, и утверждал, что уравнение не может быть решено с помощью циркуля и линейки. Он также нашёл геометрическое решение^[12]^[13]. В его более позднем труде, Трактат о демонстрации задач алгебры

, он описал полную классификацию кубических уравнений с их общими геометрическими решениями, использующими пересечения конических сечений^[14]^[15].

В двенадцатом столетии индийский математик Бхаскара II пытался решать кубические уравнения без особых успехов. Однако он привёл один пример решения кубического уравнения^[16]:

В том же столетии другой, персидский, математик, Шараф ад-Дин (1135—1213), написал Al-Mu’adalat (Трактат об уравнениях), в котором говорится о восьми типах кубических уравнений с положительными решениями и о пяти типах, не имеющих положительных решений. Он использовал подход, который позднее стал известен как метод «Руффини — Горнера» для численной аппроксимации корня кубического уравнения. Он разработал также концепцию производной функции и экстремумов кривой для решения кубических уравнений, которые могут не иметь положительных значений^[17]. Он понял важность дискриминанта кубического уравнения для нахождения алгебраического решения некоторых специальных видов кубических уравнений

[18].

Леонардо Пизанский, известный также как Фибоначчи (1170—1250), умел находить положительные решения кубического уравнения x³ + 2x² + 10x = 20 с помощью вавилонских цифр. Он указал решение 1,22,7,42,33,4,40 (что эквивалентно 1 + 22/60 + 7/60² + 42/60³ + 33/60⁴ + 4/60⁵ + 40/60⁶)^[19], что отличается от точного решения только на три триллионных.

В начале XVI века итальянский математик Сципион дель Ферро (1465—1526) нашёл общий метод решения важного класса кубических уравнений, а именно, уравнений вида с неотрицательными n и m. Фактически все кубические уравнения можно свести к такому виду, если допустить возможность для и быть отрицательными, но отрицательные числа в то время ещё не были известны. Дель Ферро держал своё открытие в секрете, пока не рассказал о нём перед своей смертью своему ученику Антонио Фиоре (Antonio Fiore).

Никколо Фонтана Тарталья.

В 1530 Никколо Тарталья (1500—1557) получил две задачи в виде кубических уравнений от Дзуанне да Кои (Zuanne da Coi) и объявил, что он их может решить. Он вскоре получил вызов от Фиоре на математическое соревнование, которое после его завершения стало знаменитым. Каждый из них должен был предложить определённое число задач сопернику для решения. Оказалось, что все задачи, полученные Тартальей, сводились к кубическим уравнениям типа . Незадолго до истечения срока Тарталье удалось разработать общий метод решения кубических уравнений этого типа (переоткрыв метод дель Ферро), а также обобщить его на два других типа ( и ). После этого он быстро решил все предложенные ему задачи. Фиоре же получил от Тартальи задачи из различных разделов математики, многие из которых оказались ему не под силу; в результате Тарталья выиграл соревнование.

Позднее Джероламо Кардано (1501—1576) неоднократно пытался убедить Тарталья раскрыть секрет решения кубических уравнений. В 1539 году ему это удалось: Тарталья сообщил свой метод, но при условии, что Кардано никому его не откроет до выхода книги самого Тартальи о кубических уравнениях, над которой он работал и где собирался опубликовать метод. Спустя шесть лет Тарталья так и не опубликовал свою книгу, а Кардано, узнав к тому времени о работах Ферро, счёл возможным опубликовать метод дель Ферро (с упоминанием имени Тартальи, как независимо его открывшего) в своей книге Ars Magna^[en] в 1545 году. Кардано оправдывался тем, что обещал не сообщать никому результаты Тартальи, а не дель Ферро. Тем не менее, Тарталья считал, что Кардано нарушил обещание и послал тому вызов на соревнование, который Кардано не принял. Вызов, в конце концов, принял ученик Кардано Лодовико Феррари (1522—1565), и оказался победителем^[20].

Кардано заметил, что метод Тарталья иногда (а именно — при наличии трех действительных корней) требует извлечения квадратного корня из отрицательного числа. Он даже включил вычисления с этими комплексными числами в Ars Magna, но, на самом деле, до конца проблему не понял. Рафаэль Бомбелли изучал эту проблему детально, а потому считается первооткрывателем комплексных чисел.

Франсуа Виет (1540—1603) независимо вывел решение кубического уравнения с тремя действительными корнями. Его решение было основано на тригонометрической формуле

В частности, подстановка приводит уравнение

к виду

Позднее, Рене Декарт (1596—1650) углубил работу Виета ^[21].

Корни уравнения[править]

Число , обращающее уравнение в тождество, называется корнем или решением уравнения. Оно является также корнем многочлена третьей степени, стоящего в левой части канонической записи.

Над полем комплексных чисел, согласно основной теореме алгебры, кубическое уравнение

всегда имеет 3 корня (с учётом кратности).

Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже. Эти случаи легко различаются с помощью дискриминанта

Итак, возможны только три случая:

Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть, когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо все три корня совпадают, образуя корень кратности 3. Разделить эти два случая помогает результант кубического уравнения и его второй производной: у многочлена есть корень кратности 3 тогда и только тогда, когда указанный результант также равен нулю.

По теореме Виета корни кубического уравнения связаны с коэффициентами следующими соотношениями^[22]:

Делением указанных тождеств друг на друга можно получить ещё несколько справедливых соотношений:

Методы решения[править]

Точные методы решения:

Также можно применять численные методы решения уравнений.

Подстановка Виета[править]

Как указывалось выше, любое кубическое уравнение можно привести к виду:

Сделаем подстановку, известную как подстановка Виета:

В результате получим уравнение:

Умножив на , получим уравнение шестой степени от , которое, на самом деле, является квадратным уравнением от :

Решая это уравнение, получим . Если , и являются тремя кубическими корнями , то корни исходного уравнения можно получить по формулам

Решение Омара Хайяма[править]

Геометрическое решение Омара Хайяма кубического уравнения для случая a=2, b=16, дающее корень 2. То, что вертикальная прямая пересекает ось в центре круга специфично для данного конкретного примера.

Как показано на графике, для решения уравнения третьей степени , где Омар Хайям построил параболу окружность, имеющую в качестве диаметра отрезок положительной полуоси , и вертикальную прямую, проходящую через пересечение параболы и окружности. Решение определяется длиной горизонтального отрезка от начала координат до пересечения вертикальной прямой с осью .

Простое современное доказательство построения: умножаем на x уравнение и группируем члены

Левая часть — это значение y² на параболе. Уравнение окружности — совпадает с правой частью уравнения и даёт значение y² на окружности.

↑ Британский музей BM 85200
↑ ^2,0^2,1 John Crossley, Anthony W.-C. Lun. The Nine Chapters on the Mathematical Art: Companion and Commentary. — Oxford University Press, 1999. — С. 176. — ISBN 978-0-19-853936-0.
↑ ^3,0^3,1 Van der Waerden. Geometry and Algebra of Ancient Civilizations. — Zurich, 1983. — С. chapter 4.
↑ Roger Cooke. The History of Mathematics. — John Wiley & Sons, 2012. — P. 63. — ISBN 978-1-118-46029-0.
↑ Karen Rhea Nemet-Nejat. Daily Life in Ancient Mesopotamia. — Greenwood Publishing Group, 1998. — P. 306. — ISBN 978-0-313-29497-6.
↑ Roger Cooke. Classical Algebra: Its Nature, Origins, and Uses. — John Wiley & Sons, 2008. — P. 64. — ISBN 978-0-470-27797-3.
↑ Guilbeau 1930 утверждает, что «египтяне полагали, что решение невозможно, но греки подошли к решению ближе.»
↑ ^8,0^8,1 Guilbeau 1930
↑ Thomas L. Heath. Diophantus of Alexandria: A Study in the History of Greek Algebra. — Martino Pub, 2009. — ISBN 978-1578987542.
↑ Archimedes (translation by T. L. Heath). The works of Archimedes. — Rough Draft Printing, 2007. — ISBN 978-1603860512.
↑ Yoshio Mikami. The Development of Mathematics in China and Japan. — 2nd ed. — New York: Chelsea Publishing Co., 1974. — С. 53—56. — ISBN 978-0-8284-0149-4.
↑ Работа Омара Хайама, Scripta Math. 26 (1963), стр. 323—337
↑ в книге О’Коннора и Робертсона «Omar Khayyam», MacTutor History of Mathematics archive, University of St Andrews, можно прочитать Эта задача привела Хайама к кубическому уравнению x³ + 200x = 20x² + 2000 и он нашёл положительный корень этого уравнения как пересечение равнобочной гиперболы и окружности. Приближённое численное решение было затем найдено путём интерполяции тригонометрических таблиц.
↑ J. J. O’Connor и E. F. Robertson (1999), Omar Khayyam, в архиве истории математики MacTutor^[en], утверждают, «Хайям, похоже, был первым, кто задумался об общей теории кубических уравнений.»
↑ Guilbeau 1930 утверждает, «Омар Аль Хей Хорасан около 1079 года сделал много по пути продвижения методов решения алгебраических уравнений с помощью пересекающихся конических сечений.»
↑ Datta, Singh. History of Hindu Mathematics. — Delhi, India, 2004. — С. 76,. стр. 76, Equation of Higher Degree; Bharattya Kala Prakashan
↑ O’Connor, John J.; Robertson, Edmund F., «Sharaf al-Din al-Muzaffar al-Tusi», MacTutor History of Mathematics archive, University of St Andrews.
↑ J. L. Berggren Innovation and Tradition in Sharaf al-Din al-Tusi’s Muadalat // Journal of the American Oriental Society. — 1990. — Vol. 110. —. — P. 304—309. — DOI:10.2307/604533.
↑ R. N. Knott and the Plus Team The life and numbers of Fibonacci // Plus Magazine. — 2013.
↑ Victor Katz. A History of Mathematics. — Boston: Addison Wesley, 2004. — С. 220. — ISBN 9780321016188.
↑ R. W. D. Nickalls Viète, Descartes and the cubic equation // Mathematical Gazette. — July 2006. —. — P. 203—208.
↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 139.

Бронштейн И. Н., Семендяев К. А. Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 138—139.