Решение уравнений система линейных уравнений: Страница не найдена

Содержание

Решение систем линейных уравнений

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Способ подстановки

2. Способ сложения

3. Графический способ

4. Пример решения систем линейных уравнений с двумя переменными

Напомним для начала определение решения системы линейных уравнений с двумя переменными.

Определение 1

Пара чисел называется решением линейного уравнения с двумя переменными, если при их подстановки в уравнение получается верное равенство.

В дальнейшем будем рассматривать системы из двух линейных уравнений с двумя переменными.

Рисунок 1.

Существуют три способа решения систем линейных уравнений: способ подстановки, способ сложения и графический способ.

Рассмотрим его на следующем примере:

Рисунок 2.

Способ подстановки

Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$

Рисунок 3.

Выразим из второго уравнения $y$ через $x$:

Подставим в первое уравнение, найдем $x$:

Найдем $y$:

Ответ: $(-2,\ 3)$

Способ сложения

Рассмотрим данный способ на примере:

Рисунок 4.

Умножим второе уравнение на $3$, получим:

Рисунок 5.

Теперь сложим оба уравнения между собой:

Найдем $y$ из второго уравнения:

Ответ: $(-2,\ 3)$

!!! Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».

Графический способ

Графический способ заключается в следующем: Оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

Рисунок 6.

Выразим из обоих уравнений $y$ через $x$:

Рисунок 7.

Изобразим оба графика на одной плоскости:

Рисунок 8.

Ответ: $(-2,\ 3)$

Пример решения систем линейных уравнений с двумя переменными

Пример 1

Решить систему уравнений тремя способами:

Рисунок 9.

Решение:

1) Способ подстановки.

Выразим $x$ через $y$:

\[x=y\]

Подставим в второе уравнение, найдем $y$:

\[2y+3y=-5\] \[y=-1\]

Найдем $x$:

\[x=-1\]

Ответ: $(-1,-1)$

2) Способ сложения.

Умножим первое уравнение на $3$, получим:

Рисунок 10.

сложим оба уравнения между собой:

\[5x=-5\] \[x=-1\]

Найдем $y$ из первого уравнения:

\[-1-y=0\] \[y=-1\]

Ответ: $(-1,\ -1)$

3) Графический способ.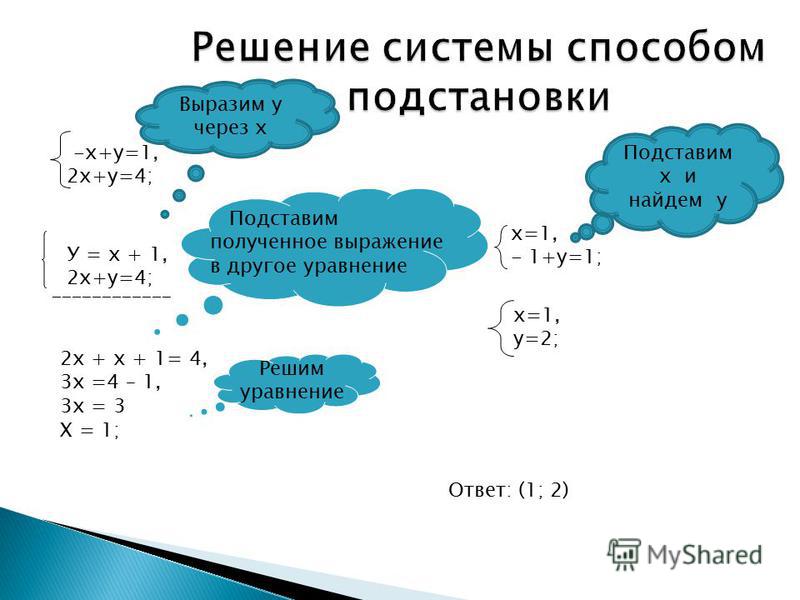

Выразим из обоих уравнений $y$ через $x$:

Рисунок 11.

Изобразим оба графика на одной плоскости:

Рисунок 12.

Ответ: $(-1,\ -1)$

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 04.03.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Механизм решения систем линейных алгебраических уравнений

10. 08.2018

Данная статья является анонсом новой функциональности.
Не рекомендуется использовать содержание данной статьи для освоения новой функциональности.

Полное описание новой функциональности будет приведено в документации к соответствующей версии.
Полный список изменений в новой версии приводится в файле v8Update.htm.

Реализовано в версии 8.3.14.1565.

В сложных прикладных решениях 1С:Предприятия существует прикладной функционал расчета себестоимости товаров. Это достаточно сложная задача и мы решили сделать встроенный в платформу механизм, который будет максимально простым в использовании и, при этом, весьма производительным.

Проанализировав работу прикладных решений, мы пришли к выводу, что один из наиболее трудозатратных этапов представляет собой, по сути, решение системы линейных алгебраических уравнений (СЛУ). В результате в платформе, во встроенном языке, мы реализовали новый объект, позволяющий находить решение СЛУ.

Существуют классические алгоритмы решения СЛУ, однако в платформе мы использовали собственный алгоритм с дополнительной оптимизацией. В случае разреженной матрицы СЛУ, что как раз соответствует задаче расчета себестоимости, наш алгоритм работает существенно быстрее классических алгоритмов. В случае плотной матрицы СЛУ он показывает результаты, близкие к классическим (гарантированно не хуже).

По нашим оценкам использование этого нового объекта в задаче расчета себестоимости позволит увеличить производительность в десятки раз.

Помимо этой задачи вы можете использовать новый объект и в других прикладных областях, которые автоматизируются решениями 1С:Предприятия:

Задачи планирования;
Взаиморасчеты между некоторым множеством юридических лиц, предприятий или отраслей;
Балансовые модели;

Прогнозирование;
Задачи поиска экстремумов, в том числе условных экстремумов.

Задача решения системы линейных алгебраических уравнений

В общем виде система линейных алгебраических уравнений выглядит следующим образом:

где это известные коэффициенты уравнений.

Решение системы линейных уравнений заключается в нахождении таких значений , при которых все равенства выполняются.

Новый объект РасчетСистемЛинейныхУравнений

Объект РасчетСистемЛинейныхУравнений обладает рядом свойств, которые позволяют гибко настраивать необходимую точность решения через численные значения и количество итераций алгоритма. Кроме этого они позволяют устанавливать границу изменения алгоритма решения для получения оптимальной скорости вычислений.

Объект содержит конструктор и два метода:

РассчитатьСистемыЛинейныхУравнений() — решает систему линейных уравнений и возвращает решение в виде объекта ТаблицаЗначений;
ПолучитьКомпонентыСвязности() — находит компоненты связности и возвращает результат в виде объекта ТаблицаЗначений. Вы можете использовать этот метод для выделения нескольких подмножеств данных и распределённой работы с ними.

Особенностью нового функционала является то, что он поддерживает параллельное использование вычислительных ресурсов. Вы можете регулировать количество используемых потоков вычисления. Функционал доступен на сервере, в толстом клиенте и в COM-соединении.

Схема использования механизма

Для решения системы линейных уравнений необходимо подготовить две таблицы с коэффициентами системы линейных уравнений – ИсточникДанныхУзлов и ИсточникДанныхСвязей

. Эти таблицы могут быть объектами типа ТаблицаЗначений или РезультатЗапроса.

ИсточникДанныхУзлов — должен содержать колонку с номерами уравнений и множество колонок, хранящих свободные коэффициенты уравнений;
ИсточникДанныхСвязей — так же содержит колонку с номерами уравнений, колонку номеров переменных и множество колонок, хранящих коэффициенты, с которыми переменные входят в уравнения.

Далее нужно дать описание этих таблиц, выставив определенные свойства объекта РасчетСистемЛинейныхУравнений: КолонкаУравненияВУзлах, КолонкаУравненияВСвязях, КолонкаПеременныеВСвязях.

Следующим шагом является описание систем линейных уравнений, которые требуется решить. Для этого существует специальный объект

ОписаниеСистемыЛинейныхУравнений. В нем нужно указать свойства КолонкаКоэффициентовВСвязях и КолонкаКоэффициентовВУзлах, соответствующие данной системе.

Полученные описания следует добавить в коллекцию ОписанияСистемЛинейныхУравнений (свойство ОписанияСистем объекта РасчетСистемЛинейныхУравнений). Для корректной работы нужно добавить в коллекцию как минимум одно ОписаниеСистемыЛинейныхУравнений.

Далее можно указать дополнительные (необязательные) свойства объекта РасчетСистемЛинейныхУравнений, которые позволяют тонко настроить механизм решения.

Финальный этап — вызов метода РассчитатьСистемыЛинейныхУравнений().

Отметим, что механизм позволяет рассчитывать сразу несколько систем линейных уравнений за один вызов метода

РассчитатьСистемыЛинейныхУравнений().

Теги: 8.3.14 разработка

Возврат к списку

Рассказать друзьям:

Системы линейных уравнений — задачи с решениями

Задача 1

Является ли точка на плоскости $(0,\frac{5}{2})$ решением следующей системы уравнений?

$\begin{array}{|l}5x +2y =1 \\ -3x +3y = 5\end{array}$

Задача 2

Является ли точка $(1; 3)$ решением следующей системы уравнений?

$\begin{array}{|l}2x -y = -1 \\ 3x +y =6\end{array}$

Задача 3

Следующий график представляет систему уравнений
$\begin{array}{|l}3x -4y = -6 \\ 2x +4y =16\end{array}$

Система имеет бесконечное количество решений.

Система не имеет решения.

Система имеет единственное решение.

Система имеет два возможных решения.

Задача 4

Следующий график представляет систему уравнений
$\begin{array}{|l}x +y =1 \\ 2x +2y =2\end{array}$

Система имеет бесконечное количество решений.

Система не имеет решения.

Система имеет единственное решение.

Система имеет два возможных решения.

Задача 5

Следующий график представляет систему уравнений
$\begin{array}{|l}x +y =3 \\ 2x +2y =2\end{array}$

Система имеет бесконечное количество решений.

Система не имеет решения.

Система имеет единственное решение.

Система имеет два возможных решения.

Задача 6

Какие из следующих точек на плоскости являются решениями?
Сколько решений у системы?

$\begin{array}{|l}y -2x =1 \\ 6x -3y = -3\end{array}$

(0; 0) и (1; 1)

(0; 1) и (1; 0)

(1; 3) и (-1; -1)

(1; -2) и (6; -3)

Задача 7

Система имеет бесконечное количество решений, означает ли это, что любая точка на плоскости является решением системы?

(Подсказка: возьмите любую точку (a; b) и подставьте эти значения в систему, которую нужно решить)

$\begin{array}{|l}x +2y =1 \\ 3x +6y =3\end{array}$

Задача 8

Решите следующую систему, построив график

$\begin{array}{|l}4x +y =4 \\ 3x +\frac{1}{2}y =2\end{array}$

Задача 9

Какая из следующих систем уравнений представлена на изображении?

A) $\begin{array}{c}2x -y = -1 \\ 3x +y =6\end{array}$

B) $\begin{array}{c}6\mathbf{y} -4\mathbf{x} =8 \\ 2x +y =12\end{array}$

C) $\begin{array}{c}\mathbf{y} -2\mathbf{x} =1 \\ x +3y =5\end{array}$

D) $\begin{array}{c}2\mathbf{y} -\mathbf{x} =10 \\ -2x +8y =6\end{array}$

Задача 10

Решите системы, используя метод подстановки
$\begin{array}{|l} -10x -5y =0 \\ 21x -7y =28\end{array}$

$(\frac{5}{4} , -\frac{5}{8})$

$(\frac{4}{5} , \frac{8}{5})$

$(\frac{4}{5} , -\frac{8}{5})$

$(1, -1)$

Задача 11

Решить систему уравнений с помощью подстановки
$\begin{array}{|l}x +y =3 \\ 2x -y =0\end{array}$

$x =1\ \ y =2$

$x =1\ \ y =1$

$x =2\ \ y =1$

$x =3\ \ y =2$

Задача 12

Решите следующую систему:
$\begin{array}{|l}5x -\frac{1}{2}y = -1 \\ 3x -2y =1\end{array}$

$x = -\frac{5}{17} \ \ y = -\frac{16}{17}$

$x = \frac{5}{17} \ \ y = \frac{16}{17}$

$x = -\frac{5}{17} \ \ y = -1$

$x = -\frac{16}{17} \ \ y = \frac{16}{17}$

Задача 13

Решите следующую систему уравнений с помощью сложения

$\begin{array}{|l}\frac{1}{3}x +\frac{1}{5}y =\frac{2}{7} \\ \frac{1}{2}x +\frac{1}{10}y =\frac{3}{7}\end{array}$

$x =\frac{6}{7} \ \ y =1$

$x =1 \ \ y =\frac{6}{7}$

$x =0 \ \ y =0$

$x =\frac{6}{7} \ \ y =0$

Задача 14

Решите следующую систему линейных уравнений
$\begin{array}{|l}5x -\frac{1}{2}y = -1 \\ 3x -2y =1\end{array}$

$x =\frac{ -5}{17} \ \ y =\frac{16}{17}$

$x =\frac{ -5}{17} \ \ y =\frac{-16}{17}$

$x =\frac{-16}{17} \ \ y =\frac{-5}{17}$

$x =1 \ \ y =2$

Задача 15

Решите следующую систему уравнений, используя сложение.
$\begin{array}{|l}2x +3y = -1 \\ 3x +4y =0\end{array}$

x = 3, y = -3

x = -4, y = -3

x = 4, y = 3

x = 4, y = -3

Задача 16

Удвоенная сумма двух чисел равна 32, а их разность равна 0. Что это за числа?

9 и 9

7 и 8

-8 и 8

8 и 8

Задача 17

Пусть у нас есть два числа, сумма которых равна 0. Если мы добавим 123 к одному из них, мы получим значение, которое вдвое больше другого числа.
Что это за числа

-1 и 1

-55 и 55

-21 и 21

-41 и 41

Задача 18

На ферме есть свиньи и индейки. Всего 58 голов и 168 ног. Сколько всего свиней и индеек?

Свиней 20, а индеек 38.

Свиней 26, а индеек 32.

Свиней 25, а индеек 33.

Свиней 48, а индеек 10.

Задача 19

Джон сказал: «У меня вдвое больше денег, чем у тебя», а Питер ответил: «Если ты дашь мне шесть долларов, то у нас будет одинаковое количество денег». Сколько денег у каждого из них?

У Питера \$12, а у Джона \$24.

У Питера \$6, а у Джона \$12.

У Питера \$8, а у Джона \$16.

У Питера \$20, а у Джона \$10.

Прислать задачу

Правильный:

Неверный:

Неразрешенные задачи:

Решение систем линейных уравнений с параметрами

Цель:

повторить решение систем линейных уравнений с двумя переменными
дать определение системы линейных уравнений с параметрами
научит решать системы линейных уравнений с параметрами.

Ход урока

Организационный момент
Повторение
Объяснение новой темы
Закрепление
Итог урока
Домашнее задание

2. Повторение:

I. Линейное уравнение с одной переменной:

1. Дайте определение линейного уравнения с одной переменной

[Уравнение вида ax=b, где х – переменная, а и b некоторые числа, называется линейным уравнением с одной переменной]

2. Сколько корней может иметь линейное уравнение?

[- Если а=0, b0, то уравнение не имеет решений, х

— Если а=0, b=0, то х R

— Если а0, то уравнение имеет единственное решение, х =

3. Выясните, сколько корней имеет уравнение (по вариантам)

I ряд – I вариант

7х-(х+3)=3(2х-1)

Решение:

7х-х-3=6х-3

6х-6х=-3+3

0*х=0

х – любое

Ответ: много корней

II ряд – II вариант

6х-(2х-5)=2(2х+4)

Решение:

6х-2х+5=4х+8

4х-4х=8-5

0*х=3

корней нет

Ответ: корней нет

III ряд – III вариант

8х-(х+4)=2(3х-2)

Решение:

8х-х-4=6х-4

7х-6х=-4+4

х=0

Ответ: единственный корень

II. Линейное уравнение с 2 –мя переменными и система линейных уравнений с 2- мя переменными.

1. Дайте определение линейного уравнения с двумя переменными. Приведите пример.

[Линейным уравнением с двумя переменными называются уравнения вида ах +by=с, где х и у – переменные, а, b и с – некоторые числа. Например, х-у=5]

2. Что называется решением уравнения с двумя переменными?

[Решением уравнения с двумя переменными называются пара значений переменных, обращающие это уравнение в верное равенство.]

3. Является ли пара значений переменных х = 7, у = 3 решением уравнения 2х + у = 17?

[2*7+3=17]

4. Что называется графиком уравнения с двумя переменными?

[Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых является решениями этого уравнения.]

5. Выясните, что представляет собой график уравнения:

3х + 2у = 6

[Выразим переменную у через х: у=-1,5х+3

Формулой у=-1,5х+3 является линейная функция, графиком которой служит прямая. Так как, уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6]

6. Что является графиком уравнения ах+bу=с с переменными х и у, где а0 или b0?

[Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.]

7. Что называется решением системы уравнений с двумя переменными?

[Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство]

8. Что значит решить систему уравнений?

[Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.]

9. Выясните, всегда ли имеет такая система решения и если имеет, то сколько (графическим способом).

Приложение 1

10. Сколько решений может иметь система двух линейных уравнений с двумя переменными?

[Единственное решение, если прямые пересекаются; не имеет решений, если прямые параллельны; бесконечно много, если прямые совпадают]

11. Каким уравнением обычно задается прямая?

[y=kx+b]

12. Установите связь между угловыми коэффициентами и свободными членами:

I вариант:

у=-х+2
y= -x-3,

k₁= k₂, b₁_{b_2,нет решений;}

II вариант:

y=-х+8
y=2x-1,

k₁_{k₂,
одно решение;}

III вариант:

y=-x-1
y=-x-1,

k₁= k₂, b₁= b_2,много решений.

Вывод:

Если угловые коэффициенты прямых являющихся графиками этих функций различны, то эти прямые пересекаются и система имеет единственное решение.
Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью у различны, то прямые параллельны, а система не имеет решений.
Если угловые коэффициенты и точки пересечения с осью у одинаковы, то прямые совпадают и система имеет бесконечно много решений.

На доске таблица, которую постепенно заполняет учитель вместе с учениками.

Приложение 2

III. Объяснение новой темы.

Определение: Система вида

A₁x+B₁y=C
A₂x+B₂y=C₂

где A_1,A_2,B₁,B_2,C₁ C_2
–выражения_,зависящие от параметров, а х и у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.

Возможны следующие случаи:

1) Если , то система имеет единственное решение

2) Если , то система не имеет решений

3) Если , то система имеет бесконечно много решений.

IV. Закрепление

Пример 1.

При каких значениях параметра а система

2х — 3у = 7
ах — 6у = 14

а) имеет бесконечное множество решений;

б) имеет единственное решение

Решение:

а) , а=4

б) , а?4

Ответ:

а) если а=4, то система имеет бесконечное множество решений;

б) если а4, то решение единственное.

Пример 2.

Решите систему уравнений

x+(m+1)y=1
x+2y=n

Решение: а) , т.е. при m1 система имеет единственное решение.

б) , т.е. при m=1 (2=m+1) и n1 исходная система решений не имеет

в) , при m=1 и n=1 система имеет бесконечно много решений.

Ответ: а) если m=1 и n1, то решений нет

б) m=1 и n=1, то решение бесконечное множество

у — любое
x=n-2y

в) если m1 и n - любое, то

y= x=

Пример 3.

Для всех значений параметра а решить систему уравнений

ах-3ау=2а+3
х+ау=1

Решение: Из II уравнения найдем х=1-ау и подставим в I уравнение

а(1-ау)-3ау=2а+3

а-а²у-3ау=2а+3

-а²у-3ау=а+3

-а(а+3)у=а+3

Возможны случаи:

1) а=0. Тогда уравнение имеет вид 0*у=3 [у ]

Следовательно, при а=0 система не имеет решений

2) а=-3. Тогда 0*у=0.

Следовательно, у . При этом х=1-ау=1+3у

3) а0 и а-3. Тогда у=-, х=1-а(-=1+1=2

Ответ:

1) если а=0, то (х; у)

2) если а=-3, то х=1+3у, у

3) если а0 и а?-3, то х=2, у=-

Рассмотрим II способ решения системы (1).

Решим систему (1) методом алгебраического сложения: вначале умножим первое уравнение системы на В_2,второе на – В₁и сложим почленно эти уравнения, исключив, таким образом, переменную у:

Т. к. А₁В₂-А₂В₁0, то х =

Теперь исключим переменную х. Для этого умножим первое уравнение системы (1) на А₂, а второе на – А₁, и оба уравнения сложим почленно:

А₁А₂х +А₂В₁у=А₂С₁
-А₁А₂х-А₁В₂у=-А₁С₂
у(А₂В₁-А₁В₂)=А₂С₁-А₁С₂

т.к. А₂В₁-А₁В₂ 0 у =

Для удобства решения системы (1) введем обозначения:

_—главный определитель

Теперь решение системы (1) можно записать с помощью определителей:

х= ; у=

Приведенные формулы называют формулами Крамера.

— Если , то система (1) имеет единственное решение: х=; у=

— Если , или , , то система (1) не имеет решений

— Если , , , , то система (1) имеет бесконечное множество решений.

В этом случае систему надо исследовать дополнительно. При этом, как правило, она сводится к одному линейному уравнению. В случае часто бывает удобно исследовать систему следующим образом: решая уравнение , найдем конкретные значения параметров или выразим один из параметров через остальные и подставим эти значения параметров в систему. Тогда получим систему с конкретными числовыми коэффициентами или с меньшим числом параметров, которую надо и исследовать.

Если коэффициенты А₁, А₂, В₁, В₂, системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы.

Пример 4.

Для всех значений параметра а решить систему уравнений

(а+5)х+(2а+3)у=3а+2
(3а+10)х+(5а+6)у=2а+4

Решение: Найдем определитель системы:

= (а+5)(5а+6) – (3а+10) (2а+3)= 5а²+31а+30-6а²-29а-30=-а²+2а=а(2-а)

= (3а+2) (5а+6) –(2а+4)(2а+3)=15а²+28а+12-4а²-14а-12=11а²+14а=а(11а+14)

=(а+5) (2а+4)-(3а+10)(3а+2)=2а²+14а+20-9а²-36а-20=-7а²-22а=-а(7а+22)

1) Тогда

х= у=

2) или а=2

При а=0 определители

Тогда система имеет вид:

5х+3у=2 5х+3у=2
10х+6у=4

При а=2 Этого достаточно, чтобы утверждать, что система не имеет решений.

Ответ:

1) если а и а, то х= у=

2) если а=0, то х,

3) если а=2, то (х; у)

Пример 5.

Для всех значений параметров а и b решить систему уравнений

(а+1)х+2у=b

bx+y=3

Решение: = =а+1-2b

= = b -6; = 3a+3-b

1) . Тогда

х= у=

Подставив выражение параметра а в систему, получим:

2bx+2y=b 2bx+2y=b
bx+y=3 2bx+2y=6

Если b6, то система не имеет решений, т.к. в этом случае I и II уравнения системы противоречат друг другу.

Если b=6, а=2b-1=2*6-1=11, то система равносильна одному уравнению

12х+2у=6 у=3-6х

Ответ:

1) если , (а), то x=, y=

2) если b, a, то система не имеет решений

3) если b=6, а=11, то х, у=3-6х

Самостоятельная работа.

Приложение 3

Итог урока: Повторить по таблице и поставить оценки.

Задание на дом:

При каких значениях параметра система уравнений

3х-2у=5
6х-4у=b

а) имеет бесконечное множество решений

б) не имеет решений

Ответ:

а) b=10

б) b10

Error

Sorry, the requested file could not be found

More information about this error

Jump to… Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1. 1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1. 1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1. 2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsЗадачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2. 2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3. 5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)

Алгебра 7-9 классы.

11. Способы решения систем линейных уравнений

Подробности: Категория: Алгебра 7-9 классы

СПОСОБ ПОДСТАНОВКИ

Решим систему уравнений:

Выразим из первого уравнения у через х:

Подставив во второе уравнение вместо у выражение , получим систему:

Докажем, что системы (1) и (2) имеют одни и те же решения.

Пусть некоторая пара значений х и у является решением системы (1). При этих значениях х и у уравнение обращается в верное равенство. Заменив в нем значение у равным ему значением выражения , мы снова получим верное равенство. Значит, каждое решение системы (1) является решением системы (2).

Аналогично доказывается, что каждое решение системы (2) является решением системы (1).

Таким образом, системы (1) и (2) имеют одни и те же решения. Такие системы называются равносильными.

В системе (2) второе уравнение содержит только одну переменную. Решим это уравнение:

Соответствующее значение у можно найти, подставив вместо х число 1 в первое уравнение системы (1). Удобнее, однако, воспользоваться формулой

Пара (1; 4) — решение системы (1).

Способ, с помощью которого мы решили систему (1), называют способом подстановки. При решении этим способом сначала из какого-нибудь уравнения выражают одну переменную через другую. Полученное выражение подставляют в другое уравнение, в результате чего приходят к уравнению с одной переменной. Решают это уравнение. Затем находят соответствующее значение второй переменной.

На рисунке 66 построены графики уравнений и . Они пересекаются в точке (1; 4). Через эту точку проходит и график уравнения т. е. прямая х = 1. Мы видим, что системы (1) и (2) имеют одно и то же решение.

Покажем применение способа подстановки еще на одном примере. Решим систему:

Выразим из второго уравнения х через у:

Подставим в первое уравнение вместо х выражение

Решим полученное уравнение с одной переменной у:

Подставим в уравнение вместо у число 4,5:

Ответ: х=—3, у = 4,5.

СПОСОБ СЛОЖЕНИЯ

Рассмотрим еще один способ решения систем уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Пример 1. Решим систему:

В уравнениях системы коэффициенты при у — противоположные числа. Сложив почленно левые и правые части уравнения, получим уравнение с одной переменной:

Заменим одно из уравнений системы (1), например первое, уравнением . Получим систему:

Решим систему (2). Из уравнения находим, что . Подставив это значение х в уравнение , получим уравнение с переменной у:

Решим это уравнение:

Пара (11; —9) — решение системы (2). Она является также решением системы (1), так как системы (1) и (2) равносильны. В этом можно убедиться с помощью рассуждений, аналогичных тем, которые были проведены в предыдущем пункте при решении систем способом подстановки.

На рисунке 67 изображены графики уравнений 2x + 3у = — 5 и х — Зу = 38.

График уравнения , т. е. прямая , проходит через точку их пересечения. Из рисунка видно, что система (2) имеет то же решение, что и система (1).

Пример 2. Решим систему:

Почленное сложение уравнений системы не приводит к исключению одной из переменных. Однако если умножить все члены первого уравнения на — 2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами:

Теперь почленное сложение приведет к уравнению с одной переменной . Из этого уравнения находим, что . Подставив во второе уравнение вместо у число —2, найдем значение х:

Ответ: х = 6, у= — 2.

Пример 3. Решим систему

Подберем множители к уравнениям так, чтобы коэффициенты при у стали противоположными числами. С этой целью умножим каждый член первого уравнения на 3, а второго на 7. Получим систему:

Сложив уравнения почленно, получим:

Отсюда

Подставив это значение х в уравнение , найдем, что у = 19.

Ответ: х=—14, у —19.

Решения систем линейных уравнений

Результаты обучения

Поиск решений систем уравнений
Решение систем уравнений с помощью графика

Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.

В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, каждое из которых содержит две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс]\begin{array}{l}2x+y=\text{ }15\\3x-y=\text{ }5\end{array}[/latex]

Решение для Система линейных уравнений с двумя переменными — это любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара [латекс](4, 7)[/латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.

[латекс]\begin{array}{l}2\left(4\right)+\left(7\right)=15\text{ }\text{True}\hfill \\ 3\left(4\ right)-\left(7\right)=5\text{ }\text{True}\hfill \end{array}[/latex]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейные уравнения по количеству решений. непротиворечивая система уравнений имеет хотя бы одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, подобное только что рассмотренному нами примеру. Две линии имеют разные наклоны и пересекаются в одной точке плоскости. Непротиворечивая система считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые и -перехваты. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.

Другой тип системы линейных уравнений — это противоречивая система , в которой уравнения представляют две параллельные линии. Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решения.

A Общее примечание: Типы линейных систем

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

Независимая система имеет ровно одну пару решений [латекс]\лево(х,у\право)[/латекс]. Точка пересечения двух прямых является единственным решением.
Несовместимая система не имеет решения. Две прямые параллельны и никогда не пересекутся.
зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

Ниже приведены графические изображения каждого типа системы.

Независимая и зависимая системы также непротиворечивы, поскольку обе они имеют хотя бы одно решение.

Как: Имея систему линейных уравнений и упорядоченную пару, определить, является ли упорядоченная пара решением

Подставьте упорядоченную пару в каждое уравнение в системе.
Определить, верны ли утверждения в результате замены в обоих уравнениях; если да, то упорядоченная пара является решением.

Пример

Определить, является ли упорядоченная пара [латекс]\влево(5,1\вправо)[/латекс] решением заданной системы уравнений.

[латекс]\begin{array}{l}x+3y=8\hfill \\ 2x — 9=y\hfill \end{array}[/latex]

Показать решение

В следующем видео мы покажем еще один пример того, как проверить, является ли упорядоченная пара решением системы уравнений.

Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив график системы уравнений на одном и том же наборе осей.

Пример

Решите следующую систему уравнений с помощью графика. Определите тип системы.

[латекс]\begin{array}{c}2x+y=-8\x-y=-1\end{массив}[/latex]

Показать решение

Графики можно использовать, если система непоследовательна или зависима. В обоих случаях мы все еще можем построить систему, чтобы определить тип системы и решения. Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.

В следующем видео мы покажем еще один пример того, как определить, имеет ли графическая система решение, и определить, какой тип решения представлен.

В нашем последнем видео мы покажем, как решить систему уравнений, сначала нарисовав линии, а затем найдя решение системы.

Системы линейных уравнений без решения (3 способа сказать) – JDM Educational

При работе с системами линейных уравнений мы часто видим одно или бесконечно много решений. Однако также возможно, что линейная система не будет иметь решения.

Итак, когда система линейных уравнений не имеет решения? Система двух линейных уравнений с двумя переменными не имеет решения, если две прямые параллельны. С точки зрения алгебры это означает, что при решении системы мы получаем ложное уравнение. Визуально линии никогда не пересекаются на графике, так как они имеют одинаковый наклон, но разные точки пересечения по оси Y.

Конечно, система из трех уравнений с тремя переменными не имеет решения, если нет точки пересечения всех трех плоскостей.

В этой статье мы поговорим о том, как можно сказать, что система линейных уравнений не имеет решения. Мы также рассмотрим некоторые примеры линейных систем без решения с 2 переменными и с 3 переменными.

Начнем.

Системы линейных уравнений без решения

Система линейных уравнений не может иметь решения, если уравнения несовместимы. Это означает, что не существует точки, удовлетворяющей всем уравнениям одновременно.

На изображении ниже показаны 3 возможных случая решения системы из 2 линейных уравнений с 2 переменными.

Система из двух линейных уравнений с двумя переменными не имеет решения, если две линии имеют одинаковый наклон и разные точки пересечения по оси y (то есть они параллельны и никогда не пересекаются).

Система уравнений с 2, 3 и более переменными не может иметь решения. Мы начнем с линейных уравнений с двумя переменными без решения.

Когда линейная система не имеет решения? (Система линейных уравнений с двумя переменными)

Есть несколько способов определить, что линейная система с двумя переменными не имеет решения:

так как 0 = 1), то решения нет.
Посмотрите на график – если две прямые параллельны (никогда не соприкасаются), то система не имеет решения.
Посмотрите на наклон и точку пересечения с осью – решите оба уравнения для y, чтобы получить форму кривой с точкой пересечения, y = mx + b. Если два уравнения имеют одинаковый наклон, но разные точки пересечения по оси y, то линии параллельны и решения нет (вы можете узнать, как определить, что две линии параллельны, в моей статье здесь).

Рассмотрим несколько примеров для каждого случая, начиная с решения системы.

Решение линейной системы без решения

Когда мы пытаемся решить линейную систему без решения, в результате мы получим бессмысленное уравнение. Например, после того, как мы упростим и объединим одинаковые термины, мы получим что-то вроде 0 = 1 или 2 = 5.

Давайте рассмотрим несколько примеров, чтобы понять, как это может происходить.

Пример 1. Использование исключения для демонстрации того, что линейная система не имеет решений

Допустим, мы хотим решить следующую систему линейных уравнений:

3x + 4y = 9
-6x – 8y = 10

Для решения воспользуемся методом исключения. Попробуем исключить переменную «x».

Начнем с умножения первого уравнения на 2, чтобы получить:

2(3x + 4y) = 2(9) [умножить первое уравнение на 2 с обеих сторон]
6x + 8y = 18 [распределите 2 через круглые скобки]

Теперь мы добавляем это модифицированное уравнение ко второму:

6x + 8y = 18

-6x – 8y = 10

___________

0x – 0y = 28

0 = 28

Since this equation is nonsense (это никогда не может быть правдой), это говорит нам о том, что у этой системы линейных уравнений нет решения. График ниже подтверждает, что прямые параллельны и не имеют решений (никогда не пересекаются).

Две прямые 3x + 4y = 9 (синяя) и -6x – 8y = 10 (красная) параллельны, поэтому они никогда не пересекаются, и линейная система не имеет решения.
Пример 2.
Использование подстановки для демонстрации того, что линейная система не имеет решения
Допустим, мы хотим решить следующую систему линейных уравнений:
y = 2x + 5
y = 2x + 8
6
Мы будем использовать подстановку для решения. Подставим y из первого уравнения в y во втором уравнении:

y = 2x + 8 [начните со второго уравнения]

2x + 5 = 2x + 8 [подставьте y = 2x + 8 2x + 5 из первого уравнения]
2x – 2x = 8 – 5 [поставить одинаковые члены с обеих сторон]
0x = 3 [объединить одинаковые члены]
0 = 3

9 быть правдой), это говорит нам об отсутствии решения этой системы линейных уравнений. График ниже подтверждает, что прямые параллельны и не имеют решений (никогда не пересекаются).

Глядя на график линейной системы без решения

Когда мы рисуем линейную систему без решения, мы получаем две параллельные линии, которые никогда не пересекаются.

Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.

Пример 1. График двух параллельных линий из линейной системы без решения

Построим график следующей системы линейных уравнений:

y = -3x + 4
y = -3x – 2

Обе линии будут иметь наклон -3, но они имеют разные точки пересечения с осью y, как вы можете видеть на графике ниже:

Две линии y = -3x + 4 (синие) и y = -3x – 2 ( красные) параллельны, поэтому они никогда не пересекаются, и линейная система не имеет решения.
Поскольку прямые параллельны, они никогда не пересекутся. Это означает, что линейная система, с которой мы начали, не имеет решения (нет точек, лежащих на обеих прямых).
Пример 2. График двух параллельных вертикальных линий из линейной системы без решения
Давайте нарисуем следующую систему линейных уравнений:
y = 5
y = -3
Обе линии будут иметь наклон 0, но они имеют разные точки пересечения с осью y. см. на графике ниже:
Две линии y = 5 (синяя) и y = -3 (красная) параллельны, поэтому они никогда не пересекаются, и линейная система не имеет решения.
Поскольку прямые параллельны, они никогда не пересекутся. Это означает, что линейная система, с которой мы начали, не имеет решения (нет точек, лежащих на обеих прямых).
Пример 3. График двух параллельных горизонтальных линий из линейной системы без решения
Построим график следующей системы линейных уравнений:
x = 2
x = -4
6 9 Обе линии будет иметь неопределенный наклон, так как они являются вертикальными линиями. Они также не пересекаются по оси y, но они параллельны, как вы можете видеть на графике ниже:
Две линии x = 2 (синяя) и x = -4 (красная) параллельны, поэтому они никогда не пересекаются, и здесь не является решением линейной системы.
Поскольку прямые параллельны, они никогда не пересекутся. Это означает, что линейная система, с которой мы начали, не имеет решения (нет точек, лежащих на обеих прямых).
Глядя на наклон и пересечение Y линейной системы без решения
Когда мы решаем линейное уравнение относительно y, мы получаем форму пересечения наклона. Если мы сделаем это для обоих уравнений в линейной системе, мы сможем сравнить наклон и точку пересечения по оси y.
Если два наклона одинаковы, а точки пересечения с осью Y различны, то две прямые параллельны, а это означает, что они никогда не пересекаются, и линейная система не имеет решения.
Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.
Пример 1. Сравнение наклона и точки пересечения Y для демонстрации отсутствия решения системы двух линейных уравнений
Предположим, у нас есть следующая система линейных уравнений: 3y = -6x + 9
Мы найдем y в обоих уравнениях, чтобы получить форму пересечения наклона, y = mx + b.
Решая первое уравнение относительно у, получаем:

4x = -2y + 8
4x + 2y = 8 [добавить 2y к обеим сторонам]

2y = -4x + 8 2x + 4 [разделить на 2 с обеих сторон]

Решив второе уравнение относительно y, получим:

3y = -6x + 9
y = -2x + 3 разделить на 3 с обеих сторон]

Итак, два уравнения в форме пересечения наклона:

y = -2x + 4
y = -2x + 3

Поскольку эти два уравнения имеют одинаковый наклон (m = -2) и разные точки пересечения по оси y (4 и 3), мы знаем что две прямые параллельны. Поскольку прямые никогда не пересекаются, у системы нет решения (нет точки, лежащей на обеих прямых).

Пример 2. Сравнение наклона и точки пересечения с Y для демонстрации отсутствия решения системы двух линейных уравнений

Допустим, у нас есть следующая система линейных уравнений:

40x = 5y – 15
4y – 32x + 5 = 13

Мы решим оба уравнения для угла пересечения. форма, y = mx + b.

Решение первого уравнения для Y, мы получаем:

40x = 5y — 15
40x + 15 = 5y [Добавить 15 к обеим сторонам]
8x + 3 = y 5 с обеих сторон]

Решив второе уравнение относительно y, получим:

4y – 32x + 5 = 13
4y – 32x = 13 – 5 [вычесть 5 с обеих сторон]
6 90
[объединить подобные термины: константы]
4y = 32x + 8 [прибавить 32x к обеим частям]
y = 8x + 2 [разделить на 4 с обеих сторон]

Итак, два уравнения в форма пересечения наклона:

y = 8x + 3
y = 8x + 2

Поскольку эти два уравнения имеют одинаковый наклон (m = 8) и разные точки пересечения по оси y (3 и 2), мы знаем, что две прямые параллельны. Поскольку прямые никогда не пересекаются, у системы нет решения (нет точки, лежащей на обеих прямых).

Как создать систему линейных уравнений без решения

Чтобы создать систему линейных уравнений без решения, мы можем использовать несколько подходов:

Один из методов состоит в том, чтобы начать с «бессмысленного» уравнения и добавлять переменные, пока мы не получим два линейных выражения, по одному с каждой стороны. уравнения.
Другой метод состоит в том, чтобы написать две линии в форме наклона-пересечения y = mx + b, где наклоны одинаковы, а точки пересечения у разные.

Давайте попробуем каждый метод по очереди.

Пример 1. Создание системы линейных уравнений без решения

Начнем с бессмысленного уравнения

0 = 1

Теперь добавим x к обеим частям:

x = x + 1

Теперь умножим на 3 с обеих сторон:

3x = 3x + 3

y = 3x [из левой части приведенного выше уравнения]
y = 3x + 3 [из правой части приведенного выше уравнения]

Вы можете видеть, что эти линии параллельны из график ниже, что означает, что система не имеет решения.

Пример 2. Создание системы линейных уравнений без решения

Запишем уравнения двух прямых в форме наклон-пересечение (то есть y = mx + b) с одинаковым наклоном и разными y-пересечениями.

Мы будем использовать общий наклон 2 с точками пересечения по оси y, равными 5 и 7:

y = 2x + 5 [наклон 2, точка пересечения с осью 5]
y = 2x + 7 [наклон 2, точка пересечения 7]

На приведенном ниже графике видно, что эти линии параллельны, а это означает, что система не имеет решения.

Система линейных уравнений с тремя переменными без решения

Система уравнений с тремя переменными не будет иметь решения, если не существует точки пересечения всех трех плоскостей. Это может произойти, если:

Все плоскости «параллельны» (никогда не пересекаются).
Две плоскости могут пересекаться, но не все три одновременно.

Вот пример первого случая:

x + y + z = 1
x + y + z = 2
x + y + z = 3

Обратите внимание, что все эти уравнения плоскости имеют одно и то же выражение в левой части, но разные константы в правой части.

Точно так же, как x = 1 и x = 2 не могут быть истинными одновременно, мы также можем сказать, что x + y + z = 1 и x + y + z = 2 не могут быть истинными одновременно.

Это означает, что для вышеуказанной системы нет решения.

Когда система линейных уравнений имеет решение?

Система линейных уравнений с двумя переменными имеет решение, если две прямые пересекаются хотя бы в одном месте.

Если две линии имеют одинаковый наклон и одинаковую точку пересечения по оси Y, то два уравнения эквивалентны и представляют одну и ту же прямую (поэтому существует бесконечно много решений, поскольку каждая точка на прямой является решением) .
Если две линии имеют разные наклоны, то они пересекаются ровно в одной точке.

Заключение

Теперь вы знаете, когда система линейных уравнений не имеет решения. Вы также знаете, на что обращать внимание с точки зрения наклона, точки пересечения по оси Y и графика линий в этих системах.

О системах линейных уравнений с одним решением вы можете узнать в моей статье здесь.

Вам также может быть полезно прочитать мою статью о системах линейных уравнений с бесконечными решениями.

Подробнее о наклоне можно узнать в этой статье.

Надеюсь, эта статья была вам полезна. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!

Подпишитесь на наш канал на YouTube!

~Джонатон

Система линейных уравнений (одновременные уравнения)

Ниранджан Хандерия, Мэй Ли, Ариндам Кумар Пол, а также

способствовал

Содержимое

Типы
Метод замены
Метод исключения
Система линейных уравнений — больше переменных
Элементарная операция со строками или метод исключения Гаусса
Система линейных уравнений Словесные задачи — Основные
Система линейных уравнений Словесные задачи — средний уровень
Система линейных уравнений — решение задач

Система линейных уравнений показана на рисунке ниже:

Несовместная: Если система линейных уравнений не имеет решения, то она называется несовместимой.
Непротиворечивая: Если система линейных уравнений имеет хотя бы одно решение, то она называется непротиворечивой.
Однородная система уравнений: Если постоянный член системы линейных уравнений равен нулю, т.е. значение после знака «=» равно нулю, то такая система уравнений называется однородной.
Тривиальные и нетривиальные решения: Каждая однородная система уравнений имеет общее решение, и оно равно нулю, потому что они имеют общее решение для всех переменных, равное 0. Это решение называется тривиальным решением. Если есть другие решения, то они называются нетривиальными решениями.

Мы изучим, как решить систему линейных уравнений, используя методы замены и исключения.

В этом методе мы
найти отношение, которое изолирует одну из переменных, заменив подлежащее;
подставить соотношение в другое уравнение(я), чтобы уменьшить количество переменных на 1;
повторяем, пока не останется одна переменная, и находим ее;
подставить найденное значение обратно в отношения;
укажите полное решение.

Давайте выполним описанные выше шаги, чтобы решить следующую систему уравнений:

х+у=5х-у=3.\начало{выровнено} х+у &= 5 \\ х-у &= 3. \end{align}x+yx−y=5=3.

Шаг 1: Изолируйте переменную xxx, используя второе уравнение: x=3+y x = 3 + y x=3+y.
Шаг 2. Подставим соотношение в другое уравнение: (3+y)+y=5⇒3+2y=5 (3 + y ) + y = 5 \Rightarrow 3 + 2y = 5 (3+y)+ у=5⇒3+2у=5.
Шаг 3. Повторите и затем решите. Поскольку теперь у нас есть только 1 переменная, найдите ее: 3+2y=5⇒y=5−32=1 3 + 2y = 5 \Rightarrow y = \frac{5-3}{2} = 1 3+2y= 5⇒y=25−3=1.
Шаг 4. Подставляем обратно в соотношения: x=3+y=3+1=4 x = 3 + y = 3 + 1 = 4 x=3+y=3+1=4.
Шаг 5. Укажите полное решение: (x,y)=(4,1) (x,y) = (4,1) (x,y)=(4,1).

Решить систему уравнений
2х+у=102у=8. \begin{выровнено} 2х + у &= 10\\ 2г &= 8 . \end{выровнено}2x+y2y=10=8.
В этом примере, поскольку во втором уравнении мы уже получили 2y=8 2y = 8 2y=8, мы знаем, что y=4 y = 4 y=4. Подставляя это в первое уравнение, мы получаем 2x+4=10 2x + 4 = 10 2x+4=10, и, таким образом, x=3 x = 3 x=3. □_\квадрат□
Примечание. Важно, какое уравнение мы используем и какую переменную выделяем. В этом примере, даже если мы получили x=10−y2 x = \frac{ 10 — y } { 2 } x=210−y из первого уравнения, мы обнаружим, что не можем подставить его во второе уравнение как нет ххх термина.

Решить систему уравнений
2х+у=43х+2у=7. \begin{выровнено} 2х + у &= 4\\ 3x + 2y &= 7. \end{выровнено}2x+y3x+2y=4=7.
Решение первого уравнения относительно yyy дает y=4−2xy=4-2xy=4−2x. Подстановка этого во второе уравнение дает 3x+2(-2x+4)=73x-4x+8=7-x=-1x=1.\begin{выровнено} 3x + 2(-2x+4) &= 7\\ 3х -4х + 8 &= 7\\ -х & = -1\\ х & = 1. \end{выровнено}3x+2(−2x+4)3x−4x+8−xx=7=7=−1=1. Затем, подставляя это значение в первое уравнение, мы имеем y=−2x+4=−2(1)+4=−2+4=2.y=-2x + 4= -2(1) + 4 = -2 + 4 = 2.y=-2x+4=-2(1)+4=-2+4=2. Следовательно, решением системы уравнений является x=1,y=2x=1, y=2x=1,y=2. □_\квадрат□

Использование процесса подстановки может быть не самым быстрым и не самым простым подходом для данной системы линейных уравнений. Однако мы всегда гарантированно найдем решение, если проработаем весь процесс. Слово «система» указывает на то, что уравнения следует рассматривать в совокупности, а не по отдельности. Таким образом, решение не должно терять достоверности ни для одного из уравнений. Выберите свои параметры, чтобы ваши расчеты были простыми, и используйте любой метод, который вам подходит.

Метод исключения умножает данные nnn уравнений на подходящие константы, так что при добавлении модифицированных уравнений одна из переменных удаляется. Как только это будет сделано, система будет эффективно сокращена на одну переменную и одно уравнение. Этот процесс повторяется до тех пор, пока не останется одна переменная и одно уравнение (а именно, значение переменной). Оттуда полученное значение подставляется в уравнение с двумя переменными, что позволяет найти решение для второй переменной. Процесс повторяется до тех пор, пока не будут найдены значения всех переменных nnn.

Метод
Найдите два уравнения с одной и той же переменной. Умножьте каждое уравнение на такое число, чтобы их коэффициенты были равны.
Вычтите два уравнения.
Повторяйте, пока не останется одна переменная, и найдите ее.
Подставьте полученное значение обратно в исходные уравнения, чтобы найти оставшиеся переменные.

Давайте выполним описанные выше шаги, чтобы решить следующую систему уравнений:

3x−4y=09x−8y=12.\begin{выровнено} 3х — 4у &= 0 \\ 9х — 8 у &= 12. \end{align}3x−4y9x−8y=0=12.

Шаг 1: Умножьте каждое уравнение на такое число, чтобы коэффициенты переменной были одинаковыми.
Допустим, мы хотим удалить переменную xxx.
Умножаем первое уравнение на 3, а второе уравнение на 1, и получаем
9x−12y=0,9x−8y=12. 9 х — 12 у = 0, 9 х — 8 у = 12. 9х-12у=0,9х-8у=12.
Шаг 2: Вычтите два уравнения:
9x−12y=0−(9x−8y=12)−4y=−12.\begin{выровнено} 9х — 12у &= 0 \\ — (9x — 8 у &= 12) \\ \hline -4 y & = — 12. \end{align} 9x−12y−(9x−8y−4y=0=12)=−12.
Шаг 3: Повторите и решите.
Мы уже остановились на одной переменной. Его решение дает нам y=−12−4=3 y = \frac{-12}{-4} = 3 y=−4−12=3.
Шаг 4: Подставьте полученное значение обратно в отношения.
Подставляя в первое уравнение, получаем 3x−4×3=0⇒x=123=4 3x — 4 \times 3 = 0 \Rightarrow x = \frac{12}{3} = 4 3x−4×3= 0⇒х=312=4.

Когда у нас есть больше переменных для работы, нам просто нужно не забывать придерживаться определенного метода и продолжать сокращать количество уравнений или переменных.

Решим следующую систему уравнений, используя оба подхода:

x+3y-z=62x-y+2z=13x+2y-z=2. \begin{выровнено} х + 3у — г &= 6\\ 2x — y + 2z &= 1\\ 3x + 2y — z &= 2. \end{выровнено}x+3y-z2x-y+2z3x+2y-z=6=1=2.

Метод замены
Начнем с первого из трех приведенных выше уравнений:
Шаг 1: первое уравнение дает x+3y−z=6⇒x=6−3y+zx+3y-z=6 \Rightarrow x=6-3y+zx+3y−z=6⇒x=6− 3г+з.
Шаг 2: Подставляя xxx во второе уравнение, получаем 2(6−3y+z)−y+2z=112−6y+2z−y+2z=1−7y+4z=−11.(1) \begin{aligned} 2(6-3у+г) — у + 2г &= 1\\ 12 — 6у + 2з — у + 2з &= 1\\ -7y + 4z &= -11. \qquad (1) \end{выровнено}2(6−3y+z)−y+2z12−6y+2z−y+2z−7y+4z=1=1=−11.(1) Подставляя xxx в третье уравнение, получаем 3(6−3y+z)+2y−z=218−9y+3z+2y-z=22z-7y=-16.(2) \begin{выровнено} 3(6-3y+z) + 2y — z & = 2\\ 18 — 9у + 3з + 2у — з &= 2\\ 2z — 7y &= -16. \qquad (2) \end{выровнено}3(6−3y+z)+2y−z18−9y+3z+2y−z2z−7y=2=2=−16.(2)
Шаг 3. Нам нужно повторять, пока у нас не останется только одно уравнение.
Теперь начнем с (1)(1)(1) двух уравнений (1)(1)(1) и (2)(2)(2) выше:
Шаг 1: Уравнение (1)(1)(1) дает нам y=4z+117 y = \frac{ 4z+11}{7} y=74z+11.
Шаг 2: Замена yyy в (2)(2)(2) дает 2z−74z+117=−162z−(4z+11)=−16−2z=−5. \begin{выровнено} 2z — 7 \frac{ 4z+11}{7}&= -16\\ 2з — ( 4з + 11 ) & = — 16\ -2z & = -5. \end{align}2z−774z+112z−(4z+11)−2z=−16=−16=−5.
Шаг 3: Теперь у нас осталось одно уравнение. Его решение дает нам z=−5−2=52 z = \frac{-5}{-2} = \frac{5}{2} z=−2−5=25.
Шаг 4: Подставьте z=52 z = \frac{5}{2} z=25 в y=4z+117 y = \frac{ 4z + 11} { 7} y=74z+11, чтобы получить у=4z+117=4×52+117=217=3. y = \frac{ 4z+ 11}{ 7} = \frac{ 4 \times \frac{5}{2} + 11 } { 7} = \frac{ 21}{7} = 3. y=74z+11 =74×25+11=721=3. Теперь подставьте z=52 z = \frac{5}{2}z=25 и y=3y = 3 y=3 в x=6−3y+z x = 6 — 3y + z x=6−3y+z, чтобы получать х=6-3×3+52=-12. x = 6 — 3 \times 3 + \frac{5}{2} = — \frac{1}{2}. х=6−3×3+25=−21.
Шаг 5: Следовательно, решение (х, у, г) = (-12,3,52). □ (x,y,z) = \left( — \frac{1}{2}, 3, \frac{5}{2} \right). \_\квадрат (x,y,z)=(−21,3,25). □

Метод исключения
Нам дана та же система линейных уравнений, что и выше: х+3у-г=62х-у+2г=13х+2у-г=2. \begin{выровнено} х + 3у — г &= 6\\ 2x — y + 2z &= 1\\ 3x + 2y — z &= 2. \end{align}x+3y-z2x-y+2z3x+2y-z=6=1=2.
Шаг 1: Исключим xxx из уравнений.
Шаг 2. Удвоение первого уравнения минус второе равно 2(x+3y−z=6)−(2x−y+2z=1)7y−4z=11.(4) \begin{align} 2(х + 3у — z &= 6)\\ -(2x — y + 2z &= 1)\\ \hline 7y — 4z & = 11. \qquad (4) \\\end{aligned} 2(x+3y−z−(2x−y+2z7y−4z=6)=1)=11.(4) Трижды первое уравнение минус третье равно 3(x+3y−z=6)−(3x+2y−z=2)7y−2z=16.(5) \begin{align} 3(х + 3у — z &= 6)\\ -(3x + 2y — z &= 2)\\ \hline 7y — 2z & = 16. \qquad (5) \\ \end{aligned} 3(x+3y−z−(3x+2y−z7y−2z=6)=2)=16.(5)
Нам нужно повторять, пока у нас не будет только одна переменная.
Шаг 1. Исключим y y y из уравнений.
Шаг 2. Четвертое уравнение минус пятое равно 7y−4z=11−(7y−2z=16)−2z=−5.(6) \begin{align} 7у — 4з&=11\ — ( 7у — 2з & = 16 ) \\ \hline -2z & = — 5. \qquad (6) \\ \end{aligned} 7y−4z−(7y−2z−2z=11=16)=−5. (6)
Шаг 3. Мы остановились на одной переменной. Его решение дает нам z=−5−2=52 z = \frac{-5}{-2} = \frac{5}{2} z=−2−5=25.
Шаг 4. Подставим z=52 z = \frac{5}{2} z=25 в четвертое уравнение 7y−4z=11 7y — 4z = 11 7y−4z=11, чтобы получить у=4z+117=4×52+117=217=3. y = \frac{ 4z+ 11}{ 7} = \frac{ 4 \times \frac{5}{2} + 11 } { 7} = \frac{ 21}{7} = 3. y=74z+11 =74×25+11=721=3. Теперь подставьте z=52,y=3 z = \frac{5}{2} , y = 3 z=25,y=3 в первое уравнение x=6−3y+z x = 6 — 3y + z x= 6−3y+z, чтобы получить х=6-3×3+52=-12. x = 6 — 3 \times 3 + \frac{5}{2} = — \frac{1}{2}. х=6−3×3+25=−21.
Шаг 5. Следовательно, решение (х, у, г) = (-12,3,52). □ (x,y,z) = \left( — \frac{1}{2}, 3, \frac{5}{2} \right).\ _\square (x,y,z)=(− 21,3,25). □

Решите следующую систему уравнений:
x+2y-3z=-32x-5y+4z=135x+4y-z=5. \begin{выровнено} х + 2у — 3z &= -3\\ 2х — 5у + 4з &= 13\\ 5x + 4y — z&= 5. \\ \end{выровнено} x+2y-3z2x-5y+4z5x+4y-z=-3=13=5.
Начнем с последнего уравнения. Решая для zzz, получаем
z=5x+4y-5.z = 5x + 4y — 5.z=5x+4y-5.
Подставляя это во второе уравнение, получаем
2x−5y+4(5x+4y−5)=1322x+11y−33=02x+y−3=0. \begin{выровнено} 2х — 5у + 4(5х + 4у — 5) &= 13 \\ 22х + 11у — 33 &= 0 \\ 2х + у — 3 &= 0. \end{выровнено} 2x−5y+4(5x+4y−5)22x+11y−332x+y−3=13=0=0.
Подставляя это в первое уравнение, получаем
х+2у-3(5х+4у-5)=-3х+2у-15х-12у+15+3=0-14х-10у+18=0-7х-5у+9=0. \begin{выровнено} х + 2у — 3(5х + 4у — 5) &= -3 \\ х + 2у — 15х -12у + 15 + 3 &= 0 \\ -14х — 10у + 18 &= 0\\ -7x — 5y + 9&= 0. \end{выровнено} x+2y-3(5x+4y-5)x+2y-15x-12y+15+3-14x-10y+18-7x-5y+9=-3=0=0=0 .
Таким образом, мы свели нашу систему к паре уравнений с двумя переменными:
2x+y-3=0-7x-5y+9=0. \begin{выровнено} 2х + у — 3 &= 0\\ -7x — 5y + 9 &= 0. \end{выровнено} 2x+y-3-7x-5y+9=0=0.
Решая yyy в первом уравнении, получаем
у=3-2х. у = 3 — 2х. у=3-2х.
Подставляя это во второе уравнение, получаем
−7x−5(3−2x)+9=0-7x-15+10x+9=03x-6=0x=2. \begin{выровнено} -7х — 5(3-2х)+9&=0 \\ -7x-15 + 10x + 9 &= 0\\ 3x — 6 &= 0 \\ х &= 2. \end{выровнено} −7x−5(3−2x)+9−7x−15+10x+93x−6x=0=0=0=2.
Следовательно,
y=3−2⋅2=−1,z=5⋅2+4⋅(−1)−5=1.y = 3 — 2\cdot2 = -1, z = 5\cdot2 + 4\cdot( -1) -5 = 1. y=3−2⋅2=−1,z=5⋅2+4⋅(−1)−5=1.
Таким образом, значения x,y,x, y,x,y и zzz, удовлетворяющие данной системе уравнений, равны (2,−1,1). □(2,-1,1). \ _ \ квадрат (2,−1,1). □

Основная статья: Решение линейных систем с использованием матриц

Элементарная операция со строками или исключение Гаусса — популярный метод решения системы линейных уравнений. С помощью этого метода каждый может решить систему линейных уравнений только с помощью уже известных вам матричных операций со строками. Термины, которые нам нужно знать для этого раздела, объясняются ниже.

Расширенная матрица:
Расширенная матрица для системы уравнений — это матрица чисел, в которой каждая строка представляет константы из одного уравнения, а каждый столбец представляет все коэффициенты для одной переменной.
Предположим, что система линейных уравнений x1+2×2+5×3=23×1+x2+4×3=12×1−7×2+x3=5.\begin{выровнено} х_{1} + 2х_{2} + 5х_{3}&=2\\ 3x_{1} + x_{2} + 4x_{3}&=1\\ 2x_{1} — 7x_{2} + x_{3}&=5. \end{выровнено}x1+2×2+5×33×1+x2+4×32×1−7×2+x3=2=1=5.
Тогда расширенная матрица этой системы линейных уравнений равна (125231412−715).\begin{pmatrix} 1 и 2 и 5 &2 \\ 3 и 1 и 4 и 1\\ 2 и -7 и 1 и 5 \end{pmatrix}.⎝⎛13221−7541215⎠⎞.

Что такое эшелонированная форма строки, уменьшенная форма эшелона строки и ведущая 1?

Матрица имеет уменьшенную ступенчатую форму строк (100101020012).\begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 и 1 и 0 и 2\\ 0 и 0 и 1 и 2 \end{pmatrix}. \text{th}4th, то она называется ступенчатой формой редуцированной строки.

Преобразование матрицы в эшелонированную форму строки с помощью операции с элементарной строкой:

Матрица может быть преобразована в сокращенную ступенчатую форму строк или строка может быть преобразована в уменьшенную ступенчатую форму строк с помощью следующих элементарных операций над строками:
Поменять местами одну строку матрицы с другой строкой матрицы.
Умножить одну строку матрицы на ненулевую скалярную константу.
Заменить одну строку одной строкой плюс константа, умноженная на другую строку матрицы.
Предположим, что система линейных уравнений x1+2×2+2×3=4×1+3×2+3×3=52×1+6×2+5×3=6,\begin{выровнено} х_{1} + 2х_{2} + 2х_{3}&=4\\ х_{1} + 3х_{2} + 3х_{3}&=5\\ 2x_{1} + 6x_{2} + 5x_{3}&=6, \end{выровнено}x1+2×2+2×3x1+3×2+3×32×1+6×2+5×3=4=5=6,
и его расширенная матрица (122413352656). \begin{pmatrix} 1 и 2 и 2 и 4 \\ 1 и 3 и 3 и 5\\ 2 и 6 и 5 и 6 \end{pmatrix}.⎝⎛112236235456⎠⎞.
Теперь мы применим элементарную операцию со строками к этой матрице и преобразуем ее в сокращенную ступенчатую форму строк:
⇒(122401112656)−1R1+R2⇒(12240111021−2)−2R1+R3⇒(1224011100−1−4)−2R2+R3⇒(122401110014)−1R3.\begin{выровнено} &\стрелка вправо\begin{pmatrix} 1 и 2 и 2 и 4 \\ 0 и 1 и 1 и 1\\ 2 и 6 и 5 и 6 \end{pmatrix}-1R_{1}+R_{2}\\ \\ &\стрелка вправо \begin{pmatrix} 1 и 2 и 2 и 4 \\ 0 и 1 и 1 и 1\\ 0 и 2 и 1 и -2 \end{pmatrix}-2R_{1}+R_{3}\\ \\ &\стрелка вправо\begin{pmatrix} 1 и 2 и 2 и 4 \\ 0 и 1 и 1 и 1\\ 0 и 0 и -1 и -4 \end{pmatrix}-2R_{2}+R_{3}\\ \\ &\стрелка вправо\begin{pmatrix} 1 и 2 и 2 и 4 \\ 0 и 1 и 1 и 1\\ 0 и 0 и 1 и 4 \end{pmatrix}-1R_{3}. \end{выровнено}⇒⎝⎛102216215416⎠⎞−1R1+R2⇒⎝⎛10021221141−2⎠⎞−2R1+R3 ⇒⎝⎛10021021−141−4⎠⎞−2R2+R3⇒⎝⎛100210211414⎠⎞−1R3.

Наконец, матрица имеет форму эшелона строк: (122401110014). \begin{pmatrix} 1 и 2 и 2 и 4 \\ 0 и 1 и 1 и 1\\ 0 и 0 и 1 и 4 \end{pматрица}. ⎝⎛100210211414⎠⎞.

Итак, наконец, мы получили приведенную форму системы линейных уравнений, которая x1+2×2+2×3=4×2+x3=1×3=4.\begin{выровнено} x_{1} +2x_{2}+2x_{3} &= 4\\ х_{2}+х_{3}&=1 \\ х_{3} &= 4. \end{выровнено}x1+2×2+2×3x2+x3x3=4=1=4. Решая это, мы получаем x1=2×2=-3×3=4.\begin{выровнено} х_{1}&= 2\\ х_{2} &=-3 \\ х_{3} &= 4. \end{выровнено}x1x2x3=2=−3=4.

Мд Нур Уддин учится на факультете математики Университета Кхулна. Теперь вам нужно найти его студенческий билет, решив следующую систему линейных уравнений:

−3x+2y−6z=65x+7y−5z=6x+4y−2z=8.\begin{align} -3x+2y-6z &=6\\ 5x+7y-5z &=6\\ х+4у-2г &=8. \end{aligned}−3x+2y−6z5x+7y−5zx+4y−2z=6=6=8.

Если решение удовлетворяет x+y=z,x+y=z,x+y= z, каково значение x+y,x+y,x+y или, что то же самое, z?z?z?

Какой вес покажут четвертые весы?

Бутылка, полностью содержащая мед, весит 1500 грамм.
Бутылка с половинкой меда весит 900 грамм.
Каков вес пустой бутылки в граммах?

Сегодня в комитете из 10 человек старого члена сменил молодой член. Таким образом, средний возраст сегодня такой же, как и 4 года назад.

Какова (положительная) разница в возрасте между новым участником и замененным старым участником?

Братья Луис и Лусио купили землю, окруженную стеной в 340 метров340 \text{ метров} 340 метров. Они построили внутреннюю стену, чтобы разделить землю на две части. Теперь часть Луиса окружена стеной в 260 метров, 260\text{ метров} ,260 метров, а часть Лусио стеной в 240 метров240\text{ метров} 240 метров. Какова длина внутренней стены?

Сегодня до конца моих экзаменов осталось в 4 раза больше дней, чем до начала моих экзаменов. 907:35 Завтра до конца моих экзаменов осталось в 5 раз больше дней, чем до начала моих экзаменов.

Сколько дней длятся мои экзамены?

Был вор, который пошел в винный магазин, чтобы украсть вино. Он вошел в 22:00, украл 15 литров вина и добавил 15 литров воды, чтобы долить бочку. Он вернулся в час ночи, украл 15 литров смеси из той же бочки и долил 15 литров воды. Он вернулся в 4 часа утра, украл из той же бочки 15 литров смеси и долил 15 литров воды. Утром соотношение вина и воды в бочке было 343:169.. Найдите начальное количество вина в бочке.

Решения системы уравнений
3x−y=a,x+y=53x-y=a, \qquad x+y=53x−y=a,x+y=5 такие же, как и в системе уравнений 2x+y=24,x−3y=b.2x+y=24, \qquad x-3y=b.2x+y=24,x−3y=b.
Каково значение a+ba+ba+b?
Поскольку две системы уравнений имеют одни и те же решения, мы сначала используем подстановку, чтобы найти решения одновременных уравнений
х+у=5,2х+у=24.х+у=5, \qquad 2х+у=24.х+у=5,2х+у=24.
Решение первого уравнения для yyy дает y=5−xy=5-xy=5−x, а подстановка во второе уравнение дает 2x+(5−x)=242x + (5-x) = 242x+(5−x)= 24 или х=19х=19х=19. Подставив это в первое уравнение, мы получим 19+y=519+y=519+y=5 или y=-14y=-14y=-14. Таким образом, x=19x=19x=19 и y=-14. у=-14. у=-14. Подстановка этих значений в 3x-y=a3x-y=a3x-y=a дает
a=3x−y=3×19−(−14)=71.a=3x-y=3×19-(-14)=71.a=3x−y=3×19−(−14)= 71.
Аналогично, подстановка в x−3y=bx-3y=bx−3y=b дает
b=x−3y=19−3×(−14)=61.b=x-3y=19-3×(-14)=61.b=x−3y=19−3×(−14)= 61.
Следовательно, а+б=71+61=132. □а+б=71+61=132. \ _\квадрат+b=71+61=132. □

30 33 36 34

Если числа рядом с каждым столбцом и строкой представляют собой сумму значений символов в этом столбце и строке, то какое число должно заменить вопросительный знак?

−1,3-1, 3−1,3 1,51, 51,5 −2,4-2, 4−2,4 2,32, 32,3

Учитывая, что x=y=0x=y=0x=y=0 не является единственным решением следующей системы линейных уравнений, определить все возможные значения k:k:k: x+2y=kx2x+y=ky. \begin{выровнено} х+2у &= кх \\ 2x+y &= ky . \end{align}x+2y2x+y=kx=ky.

Цитировать как: Система линейных уравнений (одновременных уравнений). Brilliant.org . Извлекаются из https://brilliant.org/wiki/system-of-linear-equations/

Объяснение урока: Общее решение системы линейных уравнений

В этом объяснении мы научимся находить общее решение системы линейных уравнений независимо от того, имеет ли оно единственное решение, бесконечное число решений или не имеет решения.

При работе с системой линейных уравнений существует 3 возможных категории решений, которые можно найти. Наиболее знакомым случаем будет система линейных уравнений, имеющая единственное решение. Возьмем, к примеру, систему линейных уравнений 2𝑥+3𝑦=1,−4𝑥+𝑦=−9.

Решение этой системы линейных уравнений любым методом даст 𝑥=2 и 𝑦=−1. Учитывая, что обе переменные 𝑥 и 𝑦 имеют только одно возможное значение, мы бы сказали, что решение единственно.

Предположим, что вместо этого мы имеем систему линейных уравнений 𝑥−3𝑦=2,−3𝑥+9𝑦=−6.

В этом примере мы видим, что нижнее уравнение, по сути, является просто копией первого уравнения, где каждый член умножается на −3. На самом деле, мы можем умножить каждый член в левой части на −13. без изменения решения, и система станет 𝑥−3𝑦=2,𝑥−3𝑦=2.

Первое и второе уравнения идентичны, а это означает, что записывать их оба бесполезно. Мы не теряем информации, записывая систему линейных уравнений более кратко, как 𝑥−3𝑦=2.

Это показывает, что в отличие от предыдущего примера, где у нас было единственное решение, теперь возможно 𝑥 и 𝑦 принимать бесконечно много значений, при этом решая оригинальная система линейных уравнений. Если бы мы решили приведенное выше уравнение для 𝑥, то мы бы нашли 𝑥=2+3𝑦. Если бы мы выбрали значение примера 𝑦=1, то мы бы нашли 𝑥=5 и мы могли бы проверить, действительно ли эта пара значений решает исходную систему.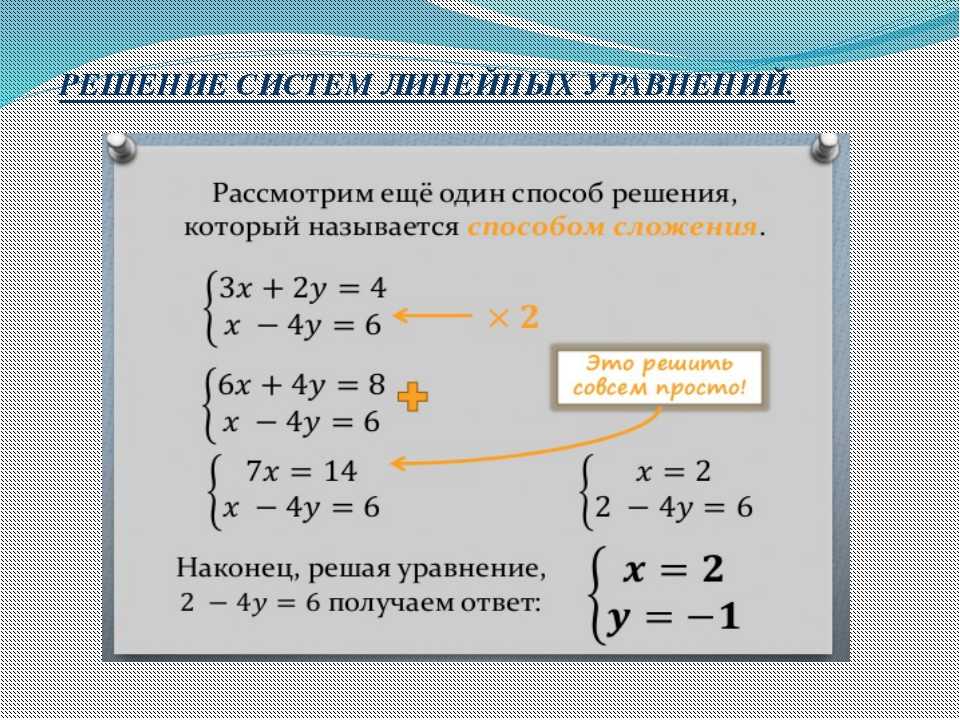 В равной степени мы бы выбрали 𝑦=−3, что дало бы 𝑥=−7. Это также тот случай, когда эта пара значений решает исходную система уравнений.

Учитывая, что мы можем выбрать любое значение 𝑦 и найти соответствующее значение 𝑥 из уравнения 𝑥=2+3𝑦, следовательно, у нас есть бесконечно много возможных решений. Именно этот тип решения мы обсудим в этом объяснении.

В завершение кратко упомянем окончательный возможный тип решения. Рассмотрим систему линейных уравнений 3𝑥+𝑦=−2,6𝑥+2𝑦=−6.

Мы видим, что второе уравнение очень похоже на первое уравнение. Умножаем все члены второго уравнения на 12, что дает 3𝑥+𝑦=−2,3𝑥+𝑦=−3.

Теперь у нас есть довольно любопытная пара уравнений с одинаковыми левыми частями, но разными правыми. Читая два приведенных выше уравнения, мы должны найти значения 𝑥 и 𝑦, которые при объединении вместе в точно так же, как-то дают разные результаты. Это заведомо смехотворно и недостижимо, т. е. данная система линейных уравнений не имеет решения. Мы бы сказали, что система несовместима или неразрешима. Естественно, мы не обычно интересуются такими типами систем линейных уравнений.

Способ и трудность решения системы уравнений с бесконечным числом решений не примечательны отличается от ситуации, когда существует единственное решение. Метод в основном такой же и не требует дополнительных знаний типа решения, опираясь на метод исключения Гаусса–Жордана для завершения вычислений. Это только наполовину через расчетов, когда тип решения определен, подход метода начинает отклоняться. Независимо от типа решения система линейных уравнений, мы всегда можем найти ее, используя тот же подход к группировке коэффициентов этой системы в конкретная матрица, которую мы затем манипулируем операциями со строками, чтобы найти решение.

Определение: расширенная матрица коэффициентов

Рассмотрим общую систему линейных уравнений с переменными 𝑥, 𝑥,…, 𝑥 и коэффициентами 𝑎: 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏.  

Тогда система линейных уравнений также описывается матричным уравнением ⎛⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠⎛⎜⎜⎝𝑥𝑥 ⋮ 𝑥⎞⎟⎟⎠ = ⎛⎜⎜⎜⎝𝑏𝑏 𝑏⎞⎟⎟⎟⎠. 

Расширенная матрица коэффициентов системы ⎛⎜⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎𝑏 ⋮⋮ ⋱ ⋮⋮ 𝑎𝑎 ⋯.

Предположим, что мы хотим решить систему линейных уравнений, определяемую как 𝑥−2𝑦=−3,5𝑥−10𝑦=−15.

К этому моменту уже очевидно, что второе уравнение совпадает с первым уравнением, за исключением того, что каждый член умножается на 5. Мы можем разумно предположить, что будет бесконечное количество решений, но сначала мы не будем исходить из таких предположений. Расширенная матрица коэффициентов этой системы уравнений имеет вид 1−2−35−10−15.

Вторая строка является копией первой строки после того, как каждая запись была умножена на 5. Причина записи системы линейных уравнений в этой форме заключается в том, что легче затем манипулировать матрицу в виде, представляющем решение системы. Это можно понять из следующей теоремы.

Теорема: расширенная матрица коэффициентов и редуцированная ступенчатая форма

Если система линейных уравнений имеет расширенную матрицу коэффициентов ⎛⎜⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎𝑏 ⋮⋮ ⋱ ⋮⋮ 𝑎𝑎 ⋯ 𝑎𝑏⎞⎟⎟⎟⎠,   то решение системы уравнений кодируется редуцированной ступенчатой формой этой матрицы.

Мы продемонстрируем эту теорему, используя систему линейных уравнений, которую мы имели выше: 𝑥−2𝑦=−3,5𝑥−10𝑦=−15, который имеет расширенную матрицу коэффициентов 1−2−35−10−15.

Мы выделили опорные точки в строке выше, потому что мы будем использовать их в качестве ориентира, чтобы начать процесс размещения матрица в уменьшенной эшелонированной форме. Для каждого поворота нам нужно убедиться, что все остальные записи в том же столбце имеют нулевое значение. Это означает, что мы можем удалить опорную точку в первой строке или опорную точку во второй строке. Наиболее разумно держать точку опоры в верхнюю строку, поэтому мы используем элементарную операцию строки 𝑟→𝑟−5𝑟, чтобы преобразовать матрицу в 1−2−3000.

Эта матрица теперь имеет редуцированную ступенчатую форму и по приведенной выше теореме дает нам решение исходной система линейных уравнений. Мы могли бы записать решение в виде 𝑥−2𝑦=−3, как мы сделали выше, но этого соглашения будет недостаточно, когда мы перейдем к системам линейных уравнений которые имеют более двух переменных, поэтому мы решили записать решение в определенном формате, который будет полезен нам позже.

При выражении решения системы линейных уравнений полезно идентифицировать все переменные, соответствующие опорной точке в сокращенную эшелонированную форму матрицы, а затем решить каждое полученное уравнение для этих переменных. В нашем случае у нас есть только одна сводная переменная, 𝑥, которое мы выражаем через неосевую переменную 𝑦 как 𝑥=−3+2𝑦.

Хотя это может показаться тривиальным, мы затем запишем несводные переменные в терминах самих себя: 𝑦=𝑦.

Выравнивание этих двух уравнений дает 𝑥=−3+2𝑦𝑦=𝑦.

Хотя это может показаться очень запутанным, это вполне адекватное изложение решения проблемы. оригинальная система уравнений. На самом деле мы можем пойти дальше и сгруппировать термины в векторной форме как 𝑥𝑦=−30+𝑦21.

Обычно считается лучшей практикой записывать любые переменные в правой части как независимый параметр, поэтому вместо этого мы записываем решение как 𝑥𝑦=−30+𝑡21.

Теперь, когда у нас есть все инструменты, необходимые для решения любой системы линейных уравнений, имеющей бесконечное множество решений, мы применим эти методы к ряду вопросов, которые включают в себя более крупные расширенные матрицы коэффициентов.

Пример 1. Система линейных уравнений с 3 переменными и 3 уравнениями

Найдите общее решение линейной системы 0−121011−25𝑥𝑦𝑧=1−11.

Ответ

Сначала составим расширенную матрицу коэффициентов данной системы линейных уравнений: ⎛⎜⎜⎝0−121101−11−251⎞⎟⎟⎠.

Мы будем использовать элементарные операции со строками, чтобы привести матрицу к редуцированному ступенчатому виду, тем самым дав решение к исходной системе уравнений. Чтобы помочь с этим, мы сначала выделяем опорные точки каждой строки, которые являются первыми ненулевыми элементами: ⎛⎜⎜⎝0−121101−11−251⎞⎟⎟⎠.

Будет легче достичь уменьшенной формы эшелона, если мы сможем сохранить значение 1 в верхнем левом элементе, поэтому мы сначала выполняем замену строк 𝑟↔𝑟, давая ⎛⎜⎜⎝1−251101−10−121⎞⎟⎟⎠.

Нам нужно удалить любую ненулевую запись, которая находится выше или ниже опорной точки в первой строке. Есть только одна такая запись, который является стержнем во втором ряду. Это можно устранить с помощью операции строки 𝑟→𝑟−𝑟, который производит матрицу ⎛⎜⎜⎝1−25102−4−20−121⎞⎟⎟⎠.

Всякий раз, когда это возможно, обычно разумнее всего удалять постоянные множители из целых строк, если мы можем сделать это, не вводя дроби в наши расчеты. В матрице каждый элемент во второй строке делится на 2, поэтому мы масштабируем эту строку с помощью операции 𝑟→12𝑟, что дает более простую матрицу ⎛⎜⎜⎝1−25101−2−10−121⎞⎟⎟⎠.

Теперь мы должны удалить ненулевую запись, которая находится ниже опорной точки во второй строке, с помощью операции строки 𝑟→𝑟+𝑟. Это дает матрицу ⎛⎜⎜⎝1−25101−2−10000⎞⎟⎟⎠, который теперь имеет нулевую строку в третьей строке, что означает, что будет бесконечно много решений системы, при условии, что это не противоречие. Чтобы удалить ненулевую запись над опорной точкой во второй строке, мы выполняем 𝑟→𝑟+2𝑟, что дает форму редуцированного эшелона ⎛⎜⎜⎝101−101−2−10000⎞⎟⎟⎠.

Теперь у нас есть решение исходной системы линейных уравнений. Обратите внимание, что переменные, соответствующие опорным точкам являются 𝑥 и 𝑦, а переменная, которая не соответствует ни одной опорной точке, — это 𝑧. Запишем матрицу в терминах исходных переменных, не включая нулевую строку: 𝑥+𝑧=−1𝑦−2𝑧=−1.

Решение обоих этих уравнений для опорных переменных дает 𝑥=−1−𝑧𝑦=−1+2𝑧.

У нас также есть несводная переменная 𝑧=𝑧. Запись этих 3 уравнений вместе дает 𝑥=−1−𝑧𝑦=−1+2𝑧𝑧=𝑧.

Мы могли бы эквивалентно выразить это решение в виде 𝑥𝑦𝑧=−1−10+𝑡−121, где 𝑡 — независимый параметр.

Пример 2. Система линейных уравнений с 3 переменными и 3 уравнениями

Найдите общее решение линейной системы 0−121−211−45𝑥𝑦𝑧=1−11.

Ответ

Сначала создадим расширенную матрицу коэффициентов системы линейных уравнений, выделив опорные элементы: ⎛⎜⎜⎝0−1211−21−11−451⎞⎟⎟⎠.

Нам нужно представить эту матрицу в виде сокращенного эшелона.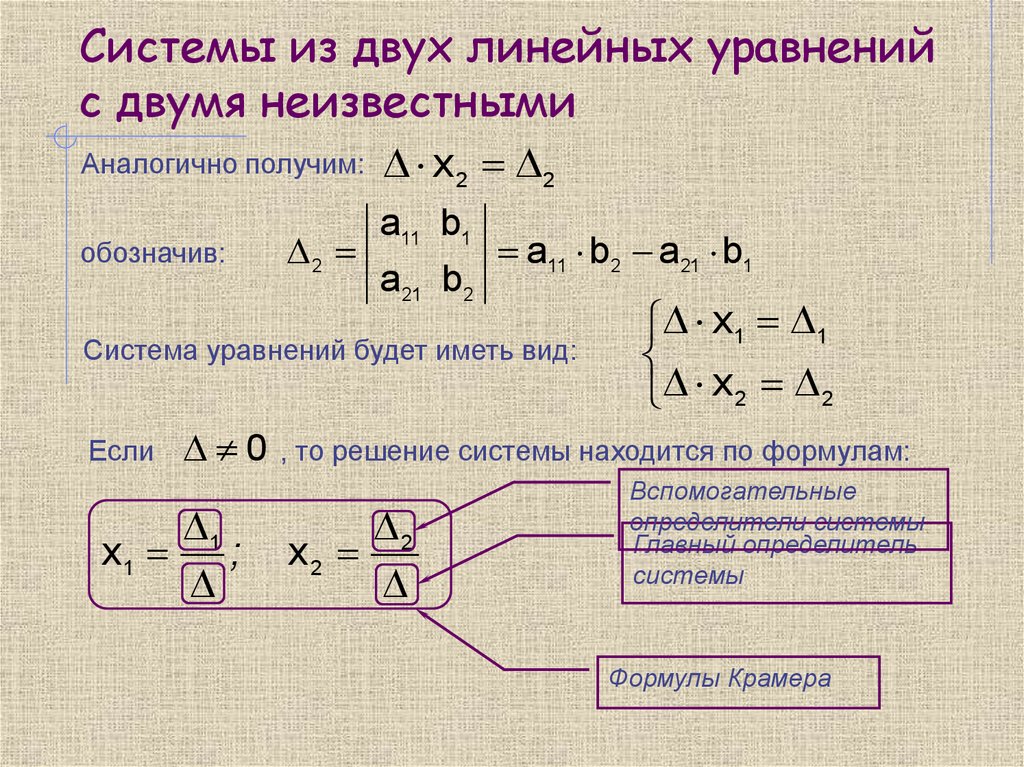 Чтобы поместить 1 в верхний левый элемент, мы сначала поменяем местами строки 𝑟↔𝑟: ⎛⎜⎜⎝1−4511−21−10−121⎞⎟⎟⎠.

Мы не можем представить матрицу в виде редуцированного эшелона, если есть какие-либо опорные точки ниже опорной в верхней строке, поэтому мы должны удалить опорную точку, которая в настоящее время отображается во второй строке. Элементарная операция строки 𝑟→𝑟−𝑟 добьется этого: ⎛⎜⎜⎝1−45102−4−20−121⎞⎟⎟⎠.

Будет полезно, если стержень во второй строке сделать равным 1, что в данном случае может быть достигнуто без введения дробей в строку, используя операцию строки 𝑟→12𝑟, чтобы получить ⎛⎜⎜⎝1−45101−2−10−121⎞⎟⎟⎠.

Теперь ясно, что третья строка является копией второй строки, за исключением изменения знака в каждой записи. Таким образом, мы можем удалить всю третью строку с помощью операции строки 𝑟→𝑟+𝑟: ⎛⎜⎜⎝1−45101−2−10000⎞⎟⎟⎠.

Уменьшенная форма эшелона затем достигается с помощью последней операции строки 𝑟→𝑟+4𝑟: ⎛⎜⎜⎝10−3−301−2−10000⎞⎟⎟⎠.

Переменные 𝑥 и 𝑦 относятся к двум столбцам, которые содержат опорные точки и переменную 𝑧 нет. Записав соответствующие уравнения 𝑥−3𝑧=−3𝑦−2𝑧=−1 и решение обоих для опорных переменных дает 𝑥=−3+3𝑧𝑦=−1+2𝑧.

В сочетании с неосевой переменной 𝑧=𝑧 дает 𝑥=−3+3𝑧𝑦=−1+2𝑧𝑧=𝑧.

Это полное решение, и мы также решили записать его в матричной форме как 𝑥𝑦𝑧=−3−10+𝑡321.

Все рассмотренные выше методы можно сразу же использовать с более крупной системой линейных уравнений. Пока мы опыт работы с строками и полное понимание формы сокращенного эшелона, метод немного отличается к любому из предыдущих примеров, которые мы практиковали. В следующем примере мы покажем, как точно такой же метод может быть применен, чтобы найти решение большей системы уравнений.

Пример 3. Система линейных уравнений с 4 переменными и 4 уравнениями

Найдите общее решение линейной системы ⎛⎜⎜⎝10111−1103−1323303⎞⎟⎟⎠𝑥𝑦𝑧𝑤=⎛⎜⎜⎝1243⎞⎟⎟⎠.

Ответ

Создадим расширенную матрицу коэффициентов и выделим опорные элементы: ⎛⎜⎜⎜⎝101111−11023−132433033⎞⎟⎟⎟⎠.

Нам нужно удалить все ненулевые записи ниже опорной точки в первой строке. Мы можем сделать это с помощью трех элементарных строк операции 𝑟→𝑟−𝑟, 𝑟→𝑟−3𝑟 и 𝑟→𝑟−3𝑟. Результирующая матрица ⎛⎜⎜⎜⎝101110−10−110−10−1103−300⎞⎟⎟⎟⎠.

Учитывая, что третья строка является копией второй строки, мы можем удалить всю строку с помощью операции 𝑟→𝑟−𝑟. Это дает матрицу, где третья строка является нулевой строкой: ⎛⎜⎜⎜⎝101110−10−110000003−300⎞⎟⎟⎟⎠, которую мы перемещаем в конец матрицы с помощью операции замены строк 𝑟↔𝑟, что дает ⎛⎜⎜⎜⎝101110−10−1103−30000000⎞⎟⎟⎟⎠.

Две нижние опорные переменные можно масштабировать, чтобы получить значение 1, с которым обычно удобнее работать, с помощью операций со строками 𝑟→−𝑟 и 𝑟→13𝑟. Это дает ⎛⎜⎜⎜⎝101110101−101−10000000⎞⎟⎟⎟⎠.

Теперь нам нужно удалить опорную запись в третьей строке, потому что она находится непосредственно под опорной точкой во второй строке. Операция строки 𝑟→𝑟−𝑟 достигает этого: ⎛⎜⎜⎜⎝101110101−100−1−1100000⎞⎟⎟⎟⎠.

На предпоследнем шаге мы масштабируем сводную запись в третьей строке с помощью 𝑟→−𝑟, что дает ⎛⎜⎜⎜⎝101110101−10011−100000⎞⎟⎟⎟⎠ и позволяет нам удалить оставшуюся ненулевую запись над опорной точкой в третьей строке с помощью операции строки 𝑟→𝑟−𝑟: ⎛⎜⎜⎜⎝100020101−10011−100000⎞⎟⎟⎟⎠.

Матрица теперь имеет уменьшенную эшелонированную форму с опорными точками, соответствующими переменным 𝑥, 𝑦 и 𝑧. Оставшаяся переменная 𝑤 представлен четвертым столбцом, который не содержит опорных точек. Выписывание соответствующих уравнений дает 𝑥=2𝑦+𝑤=−1𝑧+𝑤=−1.

Теперь мы решаем три уравнения для опорных переменных, что дает 𝑥=2𝑦=−1−𝑤𝑧=−1−𝑤.

Учитывая неосевую переменную 𝑤, полное решение 𝑥=2𝑦=−1−𝑤𝑧=−1−𝑤𝑤=𝑤.

Записанный в векторной форме, мы имеем 𝑥𝑦𝑧𝑤=⎛⎜⎜⎝2−1−10⎞⎟⎟⎠+𝑡⎛⎜⎜⎝0−1−11⎞⎟⎟⎠.

Хотя в этом не было строгой необходимости, мы решили представить вышеупомянутые решения в очень конкретной форме, с точки зрения векторов, а также с точки зрения некоторых произвольных параметров. Причины этого не совсем поверхностны, так как часто полезно иметь решение системы линейных уравнений, записанное в этой векторной форме, кодирующее ключевую информацию, которая определяет связанное векторное пространство. В отличие от решения, записанного в виде уравнений, гораздо легче понять ключевые компоненты векторного пространства, когда они представлены. в векторной форме.

До сих пор в этом объяснении мы не обсуждали, как мы будем записывать решение в терминах векторов, если имеется более одной опорной переменной. В качестве примера предположим, что нам дана система линейных уравнений, из которой мы уже создали расширенную матрицу коэффициентов и нашел редуцированную эшелонированную форму ⎛⎜⎜⎜⎝1−10220011−30000000000⎞⎟⎟⎟⎠.

Предполагая, что исходными переменными были 𝑥, 𝑦, 𝑧 и 𝑤, мы получили бы соответствующие уравнения 𝑥−𝑦+2𝑤=2,𝑧+𝑤=−3.

Сводные переменные будут 𝑥 и 𝑧, а несводные переменные будут 𝑦 и 𝑤. Мы решаем два приведенных выше уравнения для опорных переменных: 𝑥=2+𝑦−2𝑤,𝑧=−3−𝑤.

Теперь мы включаем два тривиальных уравнения 𝑦=𝑦 и 𝑤=𝑤 для неосевых переменных 𝑥=2+𝑦−2𝑤𝑦=𝑦𝑧=−3−𝑤𝑤=𝑤.

Сгруппируйте их вместе как векторы, и, используя два независимых параметра, мы получим полное решение 𝑥𝑦𝑧𝑤=⎛⎜⎜⎝20−30⎞⎟⎟⎠+𝑠⎛⎜⎜⎝1100⎞⎟⎟⎠+𝑡⎛⎜⎜⎝−20−11⎞⎟⎟⎠.

В приведенном выше примере нам потребовалось 3 вектора, чтобы полностью выразить решение. Конечно, векторов может быть больше 3. который необходимо использовать для выражения полного решения, а количество этих векторов связано с рангом и недействительностью матрицы, как из которых являются ключевыми понятиями линейной алгебры. Также возможно, что для выражения полного решения требуется только один вектор, хотя это означало бы, что решение уникально и что для выражения пространства решений не нужны никакие параметры.

Ключевые моменты

Над расширенной матрицей коэффициентов системы линейных уравнений можно работать, используя операции со строками. В редуцированном эшелонированном виде находится решение исходной системы.
Обычно бывает полезно выразить решение в терминах опорных переменных, т.е. соответствуют столбцам матрицы, которые содержат опорные точки, когда они представлены в виде сокращенного эшелона.
Если существует бесконечно много решений системы линейных уравнений, то эти решения обычно должны быть выражено через векторы с произвольными параметрами.

Введение в системы линейных уравнений

7.1 — Введение в системы линейных уравнений

Фон

Он состоит из нескольких частей, которые взаимодействуют и влияют друг на друга.
Производит эффект или вывод в результате какой-либо причины или ввод .

Линейная система — это система, в которой выход пропорционален входу. Например, если бизнес-организация представляет собой линейную систему, то если мы удвоим капитал, сотрудников, сырье и фабрики (входы), то мы ожидаем удвоить производство (выход).

Мы можем математически описать, как части линейной системы соотносятся с одной другой и на вход с помощью системы линейных уравнений . Если линейная система состоит из n частей (где n — некоторое число), то мы можем описать его системой из n линейных уравнений с n неизвестными или переменные. Неизвестными в этих уравнениях являются значения входных данных. Если мы сделали анализ правильно, то будет единственное решение для значения входов.

Вот пример системы двух линейных уравнений в двух неизвестные x и y :

Мы можем проверить, что { x = 3,6, y = 0,4} является решением уравнения систему, подставив ее в систему и получив пару уравнений 4 = 4 и 6 = 6. Теперь предположим, что мы удвоили выход (заменим 4 и 6 на 8 и 12):

выражения

нелинейными

Определения: Линейное уравнение в одном неизвестном есть уравнение вида a x = b , где a и b константы, а x — это неизвестное значение, которое мы хотим найти. Аналогично, линейное уравнение в n неизвестных x ₁ , x ₂ , …, x _n представляет собой уравнение вида:

a ₁ · x ₁ + a ₂ · x ₂ + … + a _n · x _n = b ,

где а ₁ , a ₂ , …, a _n и b являются константами. Название линейное происходит от того, что такое уравнение в двух неизвестные или переменные представляют собой прямую линию.

Набор таких уравнений называется системой линейных уравнений .

Методы решения систем линейных уравнений

Метод подстановки полезен, поскольку его можно применять к нелинейным а также линейные системы, но он вязнет для всего, кроме небольших систем. Тренер по алгебре может решить любую систему линейных уравнений, используя этот метод.

Метод устранения является хорошим методом для систем среднего размера, содержащие, скажем, от 3 до 30 уравнений. Его легко реализовать на компьютере. Тренер по алгебре может решить любую систему линейных уравнений, используя этот метод. Исключение Гаусса и Исключение Гаусса-Джордана являются двумя вариантами этого метода. На нем основаны другие методы, такие как метод разложения LU.

Правило Крамера (известное также как детерминантный метод) подходит для ручной расчет, потому что он позволяет избежать дробей. Однако это только практично для небольших систем (3 уравнения или меньше). Учитель алгебры не поясните этот метод.

Есть и другие методы, полезные при определенных обстоятельствах. Например, задача «предсказания погоды» на сетке 100×100 приводит к системе из 10 000 линейных уравнений. Такие большие системы решаются итерационным улучшением. В этом методе вы начинаете с любого предположения что угодно для решения. Затем вы повторяете (перерабатываете) это решение, улучшая его с каждой итерацией. Когда точность становится достаточно хорошей, вы останавливаетесь.

Другой метод, трехдиагональный матричный метод, полезен для систем, могут быть организованы в четко определенные этапы, и где каждый этап зависит непосредственно только на предыдущем этапе.

Некоторые уроки, которые можно извлечь из графического построения двух уравнений с двумя неизвестными

Любая точка на одной прямой является решением одного уравнения и любая точка на другая линия является решением другого уравнения. Точка пересечения линий { x = 3,6, y = 0,4} решение, удовлетворяющее обоим уравнениям одновременно. Заметим, что решение единственное. Это потому, что линии прямые и есть только одна точка, где они могут пересечься. Система линейных уравнений с единственным решением — «нормальная» ситуация.

Однако можно иметь систему уравнений с отсутствие решения или бесконечное множество решений. Такие системы уравнений называются несовместными и избыточными соответственно. Они являются результатом неточного или неправильного анализа физическая система, описываемая системой уравнений.

Рассмотрим следующую систему двух уравнений с двумя неизвестными:

несовместима,

избыточна,

Счет уравнений и неизвестных

Эти результаты можно обобщить на линейные системы уравнений с любое количество уравнений и любое количество неизвестных:

Линейная система уравнений с n неизвестные должны иметь по крайней мере n уравнений, чтобы получить единственное решение. Меньшего количества уравнений недостаточно; решение не будет единственным.
Достаточно иметь n уравнений, если только они не избыточно или непоследовательно.
Имея более n уравнений, Очень много; система будет либо избыточной, либо непоследовательной.

Оглавление

4.1 Решение систем линейных уравнений с двумя переменными — средний уровень алгебры 2e

Цели обучения

К концу этого раздела вы сможете:

Определить, является ли упорядоченная пара решением системы уравнений
Решите систему линейных уравнений, построив график
Решите систему уравнений подстановкой
Решите систему уравнений методом исключения
Выберите наиболее удобный способ решения системы линейных уравнений

Приготовься 4.

Прежде чем начать, пройдите этот тест на готовность.

Для уравнения y=23x−4,y=23x−4,
ⓐ Является ли (6,0)(6,0) решением? ⓑ Является ли (−3,−2)(−3,−2) решением?
Если вы пропустили эту проблему, просмотрите пример 3.2.

Приготовься 4.2

Найдите наклон и y -пересечение линии 3x−y=12.3x−y=12.
Если вы пропустили эту проблему, просмотрите пример 3.16.

Приготовься 4.3

Найдите точки пересечения x- и y линии 2x−3y=12,2x−3y=12.
Если вы пропустили эту проблему, просмотрите пример 3.8.

Определить, является ли упорядоченная пара решением системы уравнений

В разделе «Решение линейных уравнений» мы научились решать линейные уравнения с одной переменной. Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений.

Система линейных уравнений

Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений .

В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Мы будем решать более крупные системы уравнений позже в этой главе.

Ниже показан пример системы двух линейных уравнений. Мы используем фигурную скобку, чтобы показать, что два уравнения сгруппированы вместе, чтобы сформировать систему уравнений.

{2x+y=7x−2y=6{2x+y=7x−2y=6

Линейное уравнение с двумя переменными, например 2x+y=7,2x+y=7, имеет бесконечное число решений. Его график представляет собой линию. Помните, что каждая точка на прямой — это решение уравнения, а каждое решение уравнения — это точка на прямой.

Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями и уравнений. Другими словами, мы ищем упорядоченные пары (x,y)(x,y), которые делают оба уравнения верными. Они называются решениями системы уравнений.

Решения системы уравнений

решений системы уравнений являются значениями переменных, которые делают все уравнений верными. Решение системы двух линейных уравнений представлено упорядоченной парой (x,y).(x,y).

Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения верными, это решение системы.

Пример 4.1

Определить, является ли упорядоченная пара решением системы {x−y=−12x−y=−5.{x−y=−12x−y=−5.

ⓐ (−2,−1)(−2,−1) ⓑ (−4,−3)(−4,−3)

Решение

ⓐ

ⓑ

Попытайся 4.1

Определите, является ли упорядоченная пара решением системы {3x+y=0x+2y=-5. {3x+y=0x+2y=-5.

ⓐ (1,−3)(1,−3) ⓑ (0,0)(0,0)

Попытайся 4.2

Определить, является ли упорядоченная пара решением системы {x−3y=−8−3x−y=4.{x−3y=−8−3x−y=4.

ⓐ (2,−2)(2,−2) ⓑ (−2,2)(−2,2)

Решение системы линейных уравнений с помощью графика

В этом разделе мы будем использовать три метода для решения системы линейных уравнений. Первый метод, который мы будем использовать, — это построение графика.

График линейного уравнения представляет собой линию. Каждая точка на прямой является решением уравнения. Для системы двух уравнений мы начертим две линии. Тогда мы сможем увидеть все точки, являющиеся решениями каждого уравнения. И, найдя, что общего у линий, мы найдем решение системы.

Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, решениями являются все числа.

Аналогичным образом, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий на одной плоскости, возможны три случая, как показано.

Рисунок 4.2

Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его на одной и той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.

Пример 4.2

Как решить систему уравнений с помощью графика

Решите систему с помощью графика {2x+y=7x−2y=6.{2x+y=7x−2y=6.

Решение

Попытайся 4.3

Решите систему, построив график: {x−3y=−3x+y=5.{x−3y=−3x+y=5.

Попытайся 4.4

Решите систему, построив график: {−x+y=13x+2y=12.{−x+y=13x+2y=12.

Здесь показаны шаги, необходимые для решения системы линейных уравнений с помощью графика.

Как

Решите систему линейных уравнений с помощью графика.

Шаг 1. Нарисуйте первое уравнение.
Шаг 2. Начертите второе уравнение в той же прямоугольной системе координат.
Шаг 3. Определите, пересекаются ли прямые, параллельны или являются одной и той же прямой.
Шаг 4. Определите решение системы.
- Если линии пересекаются, определите точку пересечения. Это решение системы.
- Если прямые параллельны, система не имеет решения.
- Если линии одинаковые, система имеет бесконечное число решений.
Шаг 5. Проверьте решение в обоих уравнениях.

В следующем примере мы сначала перепишем уравнения в форме наклон-пересечение, так как это облегчит нам быстрое построение линий.

Пример 4.3

Решите систему, построив график: {3x+y=−12x+y=0.{3x+y=−12x+y=0.

Решение

Мы решим оба этих уравнения относительно yy, чтобы мы могли легко построить их график, используя их наклоны и y -пересечения.


Решите первое уравнение для y .
Найти наклон и у -пересечение.
Решите второе уравнение для y .
Найти наклон и у -пересечение.
Нарисуйте линии.
Определите точку пересечения.	Линии пересекаются в точке (−1,2).(−1,2).
Проверьте решение обоих уравнений.
	Решение: (−1,2).(−1,2).

Попытайся 4,5

Решите систему, построив график: {−x+y=12x+y=10.{−x+y=12x+y=10.

Попытайся 4.6

Решите систему, построив график: {2x+y=6x+y=1.{2x+y=6x+y=1.

Во всех системах линейных уравнений до сих пор линии пересекались, а решением была одна точка. В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, имеющую бесконечное число решений.

Пример 4.4

Решите систему, построив график: {y=12x−3x−2y=4.{y=12x−3x−2y=4.

Решение


Для построения графика первого уравнения мы будем использовать его наклон и точку пересечения и .
Для построения графика второго уравнения мы будем использовать точек пересечения.

Нарисуйте линии.
Определите точки пересечения.	Линии параллельны. Поскольку на обеих линиях нет точек, не существует упорядоченной пары, которая делает оба уравнения верными. У этой системы нет решения.

Попытайся 4.7

Решите систему, построив график: {y=-14x+2x+4y=-8.{y=-14x+2x+4y=-8.

Попытайся 4,8

Решите систему, построив график: {y=3x−16x−2y=6.{y=3x−16x−2y=6.

Иногда уравнения в системе представляют одну и ту же прямую. Поскольку каждая точка на прямой делает оба уравнения верными, существует бесконечно много упорядоченных пар, которые делают оба уравнения верными. Система имеет бесконечно много решений.

Пример 4,5

Решите систему, построив график: {y=2x−3−6x+3y=−9.{y=2x−3−6x+3y=−9.

Решение


Найдите наклон и y -пересечение первого уравнения.
Найдите точки пересечения второго уравнения.

Нарисуйте линии.
	Линии одинаковые! Поскольку каждая точка на прямой делает оба уравнения верными, существует бесконечно много упорядоченных пар, которые делают оба уравнения верными. У этой системы бесконечно много решений.

Если вы запишете второе уравнение в форме наклон-пересечение, вы можете заметить, что уравнения имеют один и тот же наклон и одно и то же y -пересечение.

Попытайся 4.9

Решите систему графически: {y=−3x−66x+2y=−12.{y=−3x−66x+2y=−12.

Попытайся 4.10

Решите систему, построив график: {y=12x−42x−4y=16.{y=12x−42x−4y=16.

Когда мы рисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две прямые совпадают. Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения y-.

Совпадающие линии

Совпадающие линии имеют одинаковый наклон и одинаковые г- перехват.

Каждая из систем уравнений в примере 4.2 и примере 4.3 имеет по две пересекающиеся прямые. Каждая система имела одно решение.

В примере 4.5 уравнения давали совпадающие прямые, поэтому система имела бесконечно много решений.

Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая хотя бы одно решение, называется -непротиворечивой -системой.

Система с параллельными прямыми, как в примере 4.4, не имеет решения. Мы называем такую систему уравнений не соответствует. Не имеет решения.

Непротиворечивые и непротиворечивые системы

Непротиворечивая система уравнений — это система уравнений, имеющая хотя бы одно решение.

Несовместимая система уравнений — это система уравнений, не имеющая решения.

Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, то каждое из них имеет собственный набор решений. Пересекающиеся прямые и параллельные прямые независимы.

Если два уравнения являются зависимыми, то все решения одного уравнения также являются решениями другого уравнения. Когда мы рисуем два зависимых уравнения, мы получаем совпадающие линии.

Подведем итоги, взглянув на графики трех типов систем. См. ниже и Таблицу 4.1.

Линии	Пересечение	Параллельный	Совпадение
Количество растворов	1 балл	Нет решения	Бесконечно много
Последовательный/непоследовательный	Последовательный	Несоответствие	Последовательный
Зависимый/ независимый	Независимый	Независимый	Зависимый

Стол 4. 1

Пример 4.6

Без построения графика определите количество решений, а затем классифицируйте систему уравнений.

ⓐ {y=3x−16x−2y=12{y=3x−16x−2y=12 ⓑ {2x+y=−3x−5y=5{2x+y=−3x−5y=5

Решение

ⓐ Сравним наклоны и точки пересечения двух линий.

Первое уравнение уже находится в форме пересечения наклона.	{y=3x−16x−2y=12y=3x−1{y=3x−16x−2y=12y=3x−1
Запишите второе уравнение в форме пересечения наклона.	6x−2y=12−2y=−6x+12−2y−2=−6x+12−2y=3x−66x−2y=12−2y=−6x+12−2y−2=−6x+12−2y =3x−6
Найдите наклон и точку пересечения каждой прямой.	y=3x-1y=3x-6m=3m=3b=-1b=-6y=3x-1y=3x-6m=3m=3b=-1b=-6
	Поскольку наклоны одинаковы, а точки пересечения и различны, линии параллельны.

Система уравнений, графики которой представляют собой параллельные прямые, не имеет решения, несовместна и независима.

ⓑ Сравним наклон и точки пересечения двух линий.

	{2x+y=-3x-5y=5{2x+y=-3x-5y=5
Запишите оба уравнения в форме наклона и точки пересечения.	2x+y=-3x-5y=5y=-2x-3-5y=-x+5-5y-5=-x+5-5y=15x-12x+y=-3x-5y=5y=-2x −3−5y=−x+5−5y−5=−x+5−5y=15x−1
Найдите наклон и точку пересечения каждой прямой.	y=-2x-3y=15x-1m=-2m=15b=-3b=-1y=-2x-3y=15x-1m=-2m=15b=-3b=-1
	Поскольку наклоны разные, линии пересекаются.

Система уравнений, графики которой пересекаются, имеет 1 решение, совместна и независима.

Попытайся 4.11

Без построения графика определите количество решений, а затем классифицируйте систему уравнений.

ⓐ {y=−2x−44x+2y=9{y=−2x−44x+2y=9 ⓑ {3x+2y=22x+y=1{3x+2y=22x+y=1

Попытайся 4.12

Без построения графика определите количество решений, а затем классифицируйте систему уравнений.

ⓐ {y=13x−5x−3y=6{y=13x−5x−3y=6 ⓑ {x+4y=12−x+y=3{x+4y=12−x+y=3

Решение систем линейных уравнений с помощью графика — хороший способ визуализировать типы решений, которые могут получиться. Однако во многих случаях решение системы с помощью графика неудобно или неточно. Если графики выходят за пределы небольшой сетки с размерами x и y в диапазоне от −10−10 до 10, построение графиков может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.

Решение системы уравнений путем замены

Теперь будем решать системы линейных уравнений методом подстановки.

Мы будем использовать ту же систему, которую использовали для построения графика.

{2x+y=7x−2y=6{2x+y=7x−2y=6

Сначала мы решим одно из уравнений либо для x , либо для y . Мы можем выбрать любое уравнение и найти решение для любой переменной, но мы постараемся сделать такой выбор, который облегчит нам работу.

Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение только с одной переменной, и мы знаем, как его решить!

После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной. Наконец, мы проверяем наше решение и убеждаемся, что оба уравнения верны.

Пример 4.7

Как решить систему уравнений подстановкой

Решить систему подстановкой: {2x+y=7x−2y=6.{2x+y=7x−2y=6.

Решение

Попытайся 4.13

Решите систему подстановкой: {−2x+y=−11x+3y=9. {−2x+y=−11x+3y=9.

Попытайся 4.14

Решите систему подстановкой: {2x+y=−14x+3y=3.{2x+y=−14x+3y=3.

Как

Решите систему уравнений подстановкой.

Шаг 1. Решите одно из уравнений для любой переменной.
Шаг 2. Подставьте выражение из шага 1 в другое уравнение.
Шаг 3. Решите полученное уравнение.
Шаг 4. Подставьте решение на шаге 3 в любое из исходных уравнений, чтобы найти другую переменную.
Шаг 5. Запишите решение в виде упорядоченной пары.
Шаг 6. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.

Будьте очень осторожны со знаками в следующем примере.

Пример 4,8

Решите систему подстановкой: {4x+2y=46x−y=8.{4x+2y=46x−y=8.

Решение

Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение для y .


Решите первое уравнение для y . Подставьте -2x+2-2x+2 вместо y во втором уравнении.
Замените y на −2x+2.−2x+2.
Решите уравнение для x .
Подставьте x=54x=54 в 4x+2y=44x+2y=4, чтобы найти y .
	Упорядоченная пара (54,−12). (54,−12).
Проверьте упорядоченную пару в обоих уравнениях.
	Решение: (54,−12).(54,−12).

Попытайся 4.15

Решите систему подстановкой: {x−4y=−4−3x+4y=0.{x−4y=−4−3x+4y=0.

Попытайся 4.16

Решите систему подстановкой: {4x-y=02x-3y=5.{4x-y=02x-3y=5.

Решение системы уравнений методом исключения

Мы решили системы линейных уравнений с помощью графиков и подстановок. Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.

Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему подстановкой, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добраться туда.

Метод исключения основан на свойстве сложения равенства. Свойство сложения равенства говорит о том, что, когда вы добавляете одно и то же количество к обеим частям уравнения, вы все равно получаете равенство. Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.

Для любых выражений a, b, c, и d .

ifa=bandc=dthena+c=b+d.ifa=bandc=dthena+c=b+d.

Чтобы решить систему уравнений методом исключения, мы начинаем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет проще всего исключить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.

Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:

{3x+y=52x−y=0—————5x=5{3x+y=52x−y=0—————5x=5

y прибавляются к нулю, и мы иметь одно уравнение с одной переменной.

Давайте попробуем еще:

{х+4у=22х+5у=-2{х+4у=22х+5у=-2

На этот раз мы не видим переменную, которую можно сразу исключить, если добавить уравнения.

Но если мы умножим первое уравнение на −2,−2, мы сделаем коэффициенты x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2,−2.

Тогда перепишите систему уравнений.

Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будет устранено, когда мы добавим эти два уравнения.

Как только мы получим уравнение с одной переменной, мы решим его. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.

Теперь мы посмотрим, как использовать исключение для решения той же системы уравнений, которую мы решали с помощью графика и подстановки.

Пример 4.9

Как решить систему уравнений методом исключения

Решите систему методом исключения: {2x+y=7x−2y=6.{2x+y=7x−2y=6.

Решение

Попытайся 4.17

Решите систему методом исключения: {3x+y=52x−3y=7.{3x+y=52x−3y=7.

Попытайся 4.18

Решите систему методом исключения: {4x+y=-5-2x-2y=-2.{4x+y=-5-2x-2y=-2.

Шаги перечислены здесь для удобства.

Как

Решите систему уравнений методом исключения.

Шаг 1. Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
Шаг 2. Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную вы исключите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
Шаг 3. Добавьте уравнения, полученные в результате шага 2, чтобы исключить одну переменную.
Шаг 4. Найдите оставшуюся переменную.
Шаг 5. Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
Шаг 6. Запишите решение в виде упорядоченной пары.
Шаг 7. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.

Теперь сделаем пример, где нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.

Пример 4.10

Решите систему методом исключения: {4x−3y=97x+2y=−6.{4x−3y=97x+2y=−6.

Решение

В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположные значения.


Оба уравнения имеют стандартную форму. Чтобы получить противоположные коэффициенты y , мы умножим первое уравнение на 2 и второе уравнение на 3.
Упрощение.
Добавьте два уравнения, чтобы исключить y .
Решить для x .
Подставьте x=0x=0 в одно из исходных уравнений.
Найдите y .
Запишите решение в виде упорядоченной пары.	Упорядоченная пара: (0,−3).(0,−3).
Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
	Решение: (0,−3).(0,−3).

Попытайся 4.19

Решите систему методом исключения: {3x−4y=−95x+3y=14.{3x−4y=−95x+3y=14.

Попытайся 4.20

Решите каждую систему методом исключения: {7x+8y=43x−5y=27.{7x+8y=43x−5y=27.

Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.

Пример 4.11

Решите систему методом исключения: {x+12y=632x+23y=172. {x+12y=632x+23y=172.

Решение

В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.


Чтобы очистить дроби, умножьте каждое уравнение на его ЖК-дисплей.
Упрощение.
Теперь мы готовы исключить одну из переменных. Обратите внимание, что оба уравнения имеют стандартную форму .
Мы можем исключить yy, умножив первое уравнение на −4,−4.
Упрости и добавь. Подставьте x=3x=3 в одно из исходных уравнений.
Решите для yy.
Запишите решение в виде упорядоченной пары.	Упорядоченная пара: (3,6).(3,6).
Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
	Решение (3,6).(3,6).

Попытайся 4.21

Решите каждую систему методом исключения: {13x−12y=134x−y=52.{13x−12y=134x−y=52.

Попытайся 4.22

Решите каждую систему методом исключения: {x+35y=−15−12x−23y=56.{x+35y=−15−12x−23y=56.

Когда мы решили систему с помощью графика, мы увидели, что не все системы линейных уравнений имеют в качестве решения одну упорядоченную пару. Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.

То же самое верно для замены или исключения. Если уравнение в конце подстановки или исключения является верным утверждением, мы имеем непротиворечивую, но зависимую систему, а система уравнений имеет бесконечно много решений. Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения.

Пример 4.12

Решите систему методом исключения: {3x+4y=12y=3−34x.{3x+4y=12y=3−34x.

Решение

	{3x+4y=12y=3−34x{3x+4y=12y=3−34x
Запишите второе уравнение в стандартной форме.	{3x+4y=1234x+y=3{3x+4y=1234x+y=3
Очистите дроби, умножив второе уравнение на 4.	{3x+4y=124(34x+y)=4(3){3x+4y=124(34x+y)=4(3)
Упрощение.	{3x+4y=123x+4y=12{3x+4y=123x+4y=12
Чтобы исключить переменную, мы умножаем второе уравнение на −1. Упростить и добавить.	{3x+4y=12−3x−4y=−12______________0=0{3x+4y=12−3x−4y=−12______________0=0

Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений.

После того, как мы очистили дроби во втором уравнении, вы заметили, что эти два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии.

Попытайся 4.23

Решите систему методом исключения: {5x−3y=15y=−5+53x.{5x−3y=15y=−5+53x.

Попытайся 4,24

Решите систему методом исключения: {x+2y=6y=−12x+3.{x+2y=6y=−12x+3.

Выберите наиболее удобный метод решения системы линейных уравнений

Когда вы решаете систему линейных уравнений в приложении, вам не сообщают, какой метод использовать. Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.

Выберите наиболее удобный метод для решения системы линейных уравнений Графическое изображение————Замена————— Исключение—————Используйте, когда вам нужноИспользовать, когда одно уравнениеИспользуйте, когда уравнения отражают ситуацию.Уже решены или могут быть в стандартной форме. легко решается для одной переменной. Выберите наиболее удобный метод решения системы линейных уравнений. ситуации. уже решена или может быть в стандартной форме. легко решается для одной переменной.

Пример 4.13

Для каждой системы линейных уравнений решите, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.

ⓐ {3x+8y=407x−4y=−32{3x+8y=407x−4y=−32 ⓑ {5x+6y=12y=23x−1{5x+6y=12y=23x−1

Решение

ⓐ

{3x+8y=407x−4y=−32{3x+8y=407x−4y=−32

Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование исключения.

ⓑ

{5x+6y=12y=23x−1{5x+6y=12y=23x−1

Поскольку одно уравнение уже решено для y , использование подстановки будет наиболее удобным.

Попытайся 4,25

ⓐ {4x−5y=−323x+2y=−1{4x−5y=−323x+2y=−1 ⓑ {x=2y−13x−5y=−7{x=2y−13x−5y=−7

Попытайся 4,26

ⓐ {y=2x−13x−4y=−6{y=2x−13x−4y=−6 ⓑ {6x−2y=123x+7y=−13{6x−2y=123x+7y=−13

Раздел 4.1 Упражнения

Практика ведет к совершенству

Определить, является ли упорядоченная пара решением системы уравнений

В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.

{2x−6y=03x−4y=5{2x−6y=03x−4y=5

ⓐ (3,1)(3,1) ⓑ (−3,4)(−3,4)

{−3x+y=8−x+2y=−9{−3x+y=8−x+2y=−9

ⓐ (−5,−7)(−5,−7) ⓑ (−5, 7)(−5,7)

{x+y=2y=34x{x+y=2y=34x

ⓐ (87,67)(87,67) ⓑ (1,34)(1,34)

{2x+3y=6y=23x+2{2x+3y=6y=23x+2
ⓐ (−6,2)(−6,2) ⓑ (−3,4)(−3,4)

Решение системы линейных уравнений с помощью графика

В следующих упражнениях решите следующие системы уравнений, построив график.

{3x+y=-32x+3y=5{3x+y=-32x+3y=5

{−x+y=22x+y=−4{−x+y=22x+y=−4

{у=х+2у=-2х+2{у=х+2у=-2х+2

{у=х-2у=-3х+2{у=х-2у=-3х+2

{y=32x+1y=-12x+5{y=32x+1y=-12x+5

10.

{y=23x−2y=−13x−5{y=23x−2y=−13x−5

11.

{х+у=-4-х+2у=-2{х+у=-4-х+2у=-2

12.

{−x+3y=3x+3y=3{−x+3y=3x+3y=3

13.

{−2x+3y=3x+3y=12{−2x+3y=3x+3y=12

14.

{2x−y=42x+3y=12{2x−y=42x+3y=12

15.

{х+3у=-6у=-43х+4{х+3у=-6у=-43х+4

16.

{−x+2y=−6y=−12x−1{−x+2y=−6y=−12x−1

17.

{−2x+4y=4y=12x{−2x+4y=4y=12x

18.

{3x+5y=10y=-35x+1{3x+5y=10y=-35x+1

19.

{4x−3y=88x−6y=14{4x−3y=88x−6y=14

20.

{х+3у=4-2х-6у=3{х+3у=4-2х-6у=3

21.

{х=-3у+42х+6у=8{х=-3у+42х+6у=8

22.

{4x=3y+78x−6y=14{4x=3y+78x−6y=14

23.

{2x+y=6-8x-4y=-24{2x+y=6-8x-4y=-24

24.

{5x+2y=7−10x−4y=−14{5x+2y=7−10x−4y=−14

Без построения графика определите количество решений, а затем классифицируйте систему уравнений.

25.

{у=23х+1-2х+3у=5{у=23х+1-2х+3у=5

26.

{у=32х+12х-3у=7{у=32х+12х-3у=7

27.

{5x+3y=42x−3y=5{5x+3y=42x−3y=5

28.

{у=-12х+5х+2у=10{у=-12х+5х+2у=10

29.

{5x−2y=10y=52x−5{5x−2y=10y=52x−5

Решение системы уравнений путем замены

В следующих упражнениях решите системы уравнений путем замены.

30.

{2x+y=-43x-2y=-6{2x+y=-43x-2y=-6

31.

{2x+y=-23x-y=7{2x+y=-23x-y=7

32.

{x−2y=−52x−3y=−4{x−2y=−52x−3y=−4

33.

{х-3у=-92х+5у=4{х-3у=-92х+5у=4

34.

{5x−2y=−6y=3x+3{5x−2y=−6y=3x+3

35.

{−2x+2y=6y=−3x+1{−2x+2y=6y=−3x+1

36.

{2x+5y=1y=13x−2{2x+5y=1y=13x−2

37.

{3x+4y=1y=-25x+2{3x+4y=1y=-25x+2

38.

{2x+y=5x−2y=−15{2x+y=5x−2y=−15

39.

{4x+y=10x−2y=−20{4x+y=10x−2y=−20

40.

{y=-2x-1y=-13x+4{y=-2x-1y=-13x+4

41.

{у=х-6у=-32х+4{у=х-6у=-32х+4

42.

{х=2у4х-8у=0{х=2у4х-8у=0

43.

{2x−16y=8−x−8y=−4{2x−16y=8−x−8y=−4

44.

{у=78х+4-7х+8у=6{у=78х+4-7х+8у=6

45.

{у=-23х+52х+3у=11{у=-23х+52х+3у=11

Решение системы уравнений методом исключения

В следующих упражнениях решите системы уравнений методом исключения.

46.

{5x+2y=2−3x−y=0{5x+2y=2−3x−y=0

47.

{6x−5y=−12x+y=13{6x−5y=−12x+y=13

48.

{2x−5y=73x−y=17{2x−5y=73x−y=17

49.

{5x−3y=−12x−y=2{5x−3y=−12x−y=2

50.

{3x−5y=−95x+2y=16{3x−5y=−95x+2y=16

51.

{4x−3y=32x+5y=−31{4x−3y=32x+5y=−31

52.

{3x+8y=-32x+5y=-3{3x+8y=-32x+5y=-3

53.

{11x+9y=-57x+5y=-1{11x+9y=-57x+5y=-1

54.

{3x+8y=675x+3y=60{3x+8y=675x+3y=60

55.

{2x+9y=-43x+13y=-7{2x+9y=-43x+13y=-7

56.

{13x−y=−3x+52y=2{13x−y=−3x+52y=2

57.

{х+12у=3215х-15у=3{х+12у=3215х-15у=3

58.

{х+13у=-113х+12у=1{х+13у=-113х+12у=1

59.

{13x−y=−323x+52y=3{13x−y=−323x+52y=3

60.

{2x+y=36x+3y=9{2x+y=36x+3y=9

61.

{х-4у=-1-3х+12у=3{х-4у=-1-3х+12у=3

62.

{−3x−y=86x+2y=−16{−3x−y=86x+2y=−16

63.

{4x+3y=220x+15y=10{4x+3y=220x+15y=10

Выберите наиболее удобный метод решения системы линейных уравнений

В следующих упражнениях решите, будет ли удобнее решать систему уравнений путем замены или исключения.

64.

ⓐ {8x−15y=−326x+3y=−5{8x−15y=−326x+3y=−5
ⓑ {x=4y−34x−2y=−6{x=4y−34x−2y= −6

65.

ⓐ {y=7x−53x−2y=16{y=7x−53x−2y=16
ⓑ {12x−5y=−423x+7y=−15{12x−5y=−423x+7y=−15

66.

ⓐ {y=4x+95x−2y=−21{y=4x+95x−2y=−21
ⓑ {9x−4y=243x+5y=−14{9х-4у=243х+5у=-14

67.

ⓐ {14x−15y=−307x+2y=10{14x−15y=−307x+2y=10
ⓑ {x=9y−112x−7y=−27{x=9y−112x−7y=−27

Письменные упражнения

68.

В системе линейных уравнений два уравнения имеют одинаковые точки пересечения. Опишите возможные решения системы.

69.

Решите систему уравнений подстановкой и объясните все свои действия словами: {3x+y=12x=y−8.{3x+y=12x=y−8.

70.

Решите систему уравнений методом исключения и объясните все свои шаги словами: {5x+4y=102x=3y+27.{5x+4y=102x=3y+27.

71.

Решите систему уравнений {x+y=10x−y=6{x+y=10x−y=6

Самопроверка

После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.

Если большинство ваших чеков было:

…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать.

Решение систем линейных уравнений

Способ подстановки

Способ сложения

Графический способ

Пример решения систем линейных уравнений с двумя переменными

Механизм решения систем линейных алгебраических уравнений

Задача решения системы линейных алгебраических уравнений

Новый объект РасчетСистемЛинейныхУравнений

Схема использования механизма

Системы линейных уравнений — задачи с решениями

Решение систем линейных уравнений с параметрами

Error

Алгебра 7-9 классы.

СПОСОБ ПОДСТАНОВКИ

СПОСОБ СЛОЖЕНИЯ

Решения систем линейных уравнений

Результаты обучения

A Общее примечание: Типы линейных систем

Как: Имея систему линейных уравнений и упорядоченную пару, определить, является ли упорядоченная пара решением

Пример

Пример

Системы линейных уравнений без решения (3 способа сказать) – JDM Educational

Системы линейных уравнений без решения

Когда линейная система не имеет решения? (Система линейных уравнений с двумя переменными)

Решение линейной системы без решения

Пример 1. Использование исключения для демонстрации того, что линейная система не имеет решений

Пример 2.

Глядя на график линейной системы без решения

Пример 1. График двух параллельных линий из линейной системы без решения

Пример 2. График двух параллельных вертикальных линий из линейной системы без решения

Пример 3. График двух параллельных горизонтальных линий из линейной системы без решения

Глядя на наклон и пересечение Y линейной системы без решения

Пример 1. Сравнение наклона и точки пересечения Y для демонстрации отсутствия решения системы двух линейных уравнений

Пример 2. Сравнение наклона и точки пересечения с Y для демонстрации отсутствия решения системы двух линейных уравнений

6 90

Как создать систему линейных уравнений без решения

Пример 1. Создание системы линейных уравнений без решения

Пример 2. Создание системы линейных уравнений без решения

Система линейных уравнений с тремя переменными без решения

Когда система линейных уравнений имеет решение?

Заключение

Система линейных уравнений (одновременные уравнения)

Содержимое

Решите следующую систему уравнений:

Решения системы уравнений

Объяснение урока: Общее решение системы линейных уравнений

Определение: расширенная матрица коэффициентов

Теорема: расширенная матрица коэффициентов и редуцированная ступенчатая форма

Пример 1. Система линейных уравнений с 3 переменными и 3 уравнениями

Ответ

Пример 2. Система линейных уравнений с 3 переменными и 3 уравнениями

Ответ

Пример 3. Система линейных уравнений с 4 переменными и 4 уравнениями

Ответ

Ключевые моменты

Введение в системы линейных уравнений

7.1 — Введение в системы линейных уравнений

Фон

Методы решения систем линейных уравнений

Некоторые уроки, которые можно извлечь из графического построения двух уравнений с двумя неизвестными

4.1 Решение систем линейных уравнений с двумя переменными — средний уровень алгебры 2e

Цели обучения

Приготовься 4.

Приготовься 4.2

Приготовься 4.3

Определить, является ли упорядоченная пара решением системы уравнений

Система линейных уравнений

Решения системы уравнений

Пример 4.1

Решение

Попытайся 4.1

Попытайся 4.2

Решение системы линейных уравнений с помощью графика

Пример 4.2

Как решить систему уравнений с помощью графика

Решение

Попытайся 4.3

Попытайся 4.4

Как

Решите систему линейных уравнений с помощью графика.