«Уравнения, содержащие переменную под знаком модуля»
Тип урока: урок обобщения и систематизации учебного материала.
Форма урока: урок-практикум.
Класс: 11.
Предмет: алгебра и начала анализа.
Тема: “Уравнения, содержащие переменную под знаком модуля”
Цели:
- Актуализировать знания: модуль числа и свойства модуля; совершенствовать умение при решении уравнений, содержащих переменную под знаком модуля, применять методы: раскрытие модуля по определению; возведение обеих частей уравнения в квадрат; метод разбиения на промежутки.
- Развивать интеллектуально-логические умения и математические способности;
- Воспитывать адаптивность к современным
условиям обучения, воспитывать личность,
интегрированную в современное общество.

ХОД УРОКА
I. Организационный момент.
II. Мотивация деятельности учащихся.
Сообщение целей и задач урока. Принятие учащимися целей урока.
III. Актуализация опорных знаний.
1. Определение модуля. Модулем (абсолютной величиной) действительного числа х называется само это число, если х > 0, и противоположное ему число –х, если х < 0.
Модуль х обозначается |х|. Итак,
2. Основные свойства модуля. (Запишите основные свойства модуля).
Для любых действительных х и у:
|x| > 0.
|-x| = |x|.
|x2| = x2.
-|x| < x < |x|.
|x·y| = |x|·|y|.
|x/y| = |x|/|y|, y 0.
При решении задач нужно помнить геометрический смысл модуля: |x-a| — это расстояние между точками х и а числовой оси. В частности, |x| — расстояние между точками х и 0.
IV. Совершенствование практических умений применять известные методы решения уравнений, содержащих переменную под знаком модуля.
Устная работа
При решении уравнений, содержащих переменную под знаком модуля, применяются чаще всего следующие методы:
1) раскрытие модуля по определению;
2) возведение обеих частей уравнения в квадрат;
3) метод разбиения на промежутки.
Решите уравнения:
|x| = 3; |x – 5| = 1; |x + 2| = 7; |x – 3| = |x + 1|.
Обменяйтесь тетрадями.
Отметьте в диагностических картах верно
выполненные задания знаком +, а неверно
выполненные задания знаком –.
Какой метод применяли при решении данных уравнений?
Алгоритм решения уравнения
Чтобы решить уравнение, содержащее переменную под знаком модуля, надо:
- Освободиться от знака модуля, используя его определение;
- Найти критические точки, то есть значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль;
- Разбить область допустимых значений переменной на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак;
- На каждом из найденных промежутков решить уравнение без знака модуля.
Объединение решений указанных промежутков и составляет все решения данного уравнения.
Решить уравнения, используя алгоритм решения уравнения и свойства модуля.
Уравнение вида |f(x)| = g(x).
|x – 7| = x3 – 15x2 + x + 7.
Решение
По определению модуля
Уравнение |x – 7| = x3 – 15x2 + x + 7 равносильно следующей совокупности двух смешанных систем:
Ответ: 0;
Уравнение вида |f(x)| = |g(x)|.
|x5-6x
Решение
|x5-6x2+9x-6| > 0 и |x5-2x3+6x2-13x+6| > 0.
Так как обе части уравнения неотрицательны, то данное уравнение равносильно совокупности двух уравнений:
Решив каждое из уравнений, получим:
х = 0; х = ± .
х = 1; х = 2; х = 3.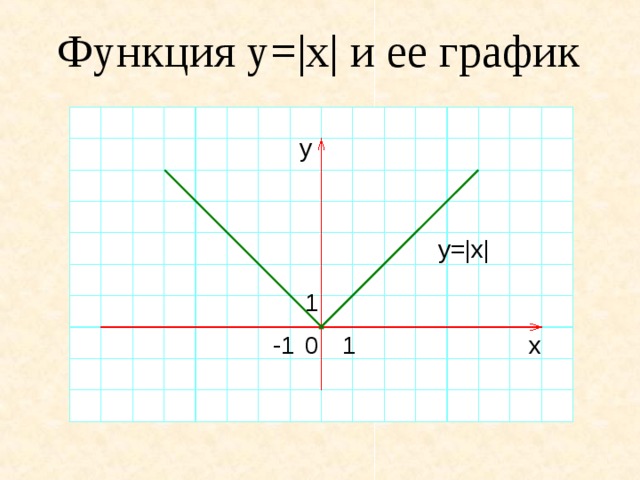
Ответ: 0; ± ; 1; 2; 3.
Найти сумму корней уравнения
|2x + 1| + |5 — 3x| + 1 — 4x = 0.
Решение
1. По определению модуля
2. Hайдём критические точки:
2х + 1 = 0; 5 — 3х = 0.
х = -?; х = 5/3.
3. Hули функции разбивают числовую ось на промежутки.
4. Решим уравнение на каждом из промежутков:
Уравнение, записанное без знака модуля на промежутках х, равносильно совокупности смешанных систем:
Ответ: ; 3.
Программированный контроль
Решение уравнений.
Ученик может выбрать любой из трёх уровней
примеров. Первый уровень оценивается оценкой
“3”, второй “4”, третий “5”. Решение в тетрадях с
последующим объяснением своего решения в
группах. Наиболее сложные задания решаются у
доски. Решения проверяются и записываются в
тетрадях. Оставшиеся задания выполняются дома.
Наиболее сложные задания решаются у
доски. Решения проверяются и записываются в
тетрадях. Оставшиеся задания выполняются дома.
V. Самостоятельная работа.
Самостоятельная письменная работа по
вариантам
Вариант 1 |
Вариант 2 |
|
|---|---|---|
А |
|x2-3x|=2x-4 ( МГУ 2000) | x2+|x-1|-5=0. (МФТИ 1999) |
Б |
|x2+2x-3|=|x+1|+2 (МФТИ) | |2x+8|-|x-5|=12 (МГУ 2000) |
В |
4|x+1|-1=3|2x+5|-2|x+5| (МГУ 1997) | |6x3-2x2+4x-33|=10x-35 (МФТИ) |
VI. Итог урока.
Итог урока.
Определение модуля.
Методы решения уравнений, содержащих переменную под знаком модуля.
Алгоритм решения уравнений, содержащих переменную под знаком модуля.
VII. Домашнее задание.
Решить три уравнения различного уровня.
Индивидуальные задания.
1. х2 = | 2 — х| ;
2. | | 3х + 2| — 5х| = 14;
3. | 2 — | 3х — 1| | = х2 + 1;
4. | 3х – 1| + | 2х — 4| = | х2 — 1| + 4;
5. | х + 2| — | 3х — 4| + | 2х + 7| — = | х + 5|.
Приложение
Решите уравнение √ x−3 4√ x−10=0
Алгебра
1) x=3; x=-3
2) x-3=2; x-3=-2
x=5; x=1
3) x-4=0
x=4
4) Корней нет
5)|х|=6
x=6; x=-6
Корней нет
7) 3|х|=1
|x|=1/3
x=1/3; x=-1/3
8) 2|x|=-3
|x|=-3/2
Корней нет
9)|3x+2|=4
3x+2=4; 3x+2=-4
3x=2; 3x=-6
x=2/3; x=-2
10)|2x-1|=1
2x-1=1; 2x-1=-1
2x=2; 2x=0
x=1: x=0
3- незнаю. …………………………..
…………………………..
Нету решений ибо модуль не может равняться отрицательному числу.
Нету решений ибо модуль не может равняться отрицательному числу.
Нету решений ибо модуль не может равняться отрицательному числу.
1) ответ +-6
2)ответ 0
3)ответ +-0,12
1)lxl=3
x=3 или x=-3
ответ: -3; 3
2) lx-3l=2
x-3=2 или х-3=-2
х=2+3 х=-2+3
х=5 х=1
ответ: 5; 1
3) lx-4l=0
x-4=0
x=4
ответ: 4
4) lx+3l=-4
корней нет, т.к. значение модуля всегда больше или равно 0.
5) lxl+1=7
lxl=7-1
lxl=6
x=6 или х=-6
ответ: 6; -6
6) lxl-2=-3
lxl=-3+2
lxl=-1
корней нет
7) 3*lxl -1 = 0
3*lxl=1
lxl=1/3
x=1/3 или х=-1/3
ответ: 1/3; -1/3
8) 2lxl+3=0
2lxl=-3
lxl=-3/2
корней нет
9) l3x+2l-4=0
l3x+2l=4
3x+2=4 или 3х+2=-4
3х=4-2 3х=-4-2
3х=2 3х=-6
х=2/3 х=-2
ответ: 2/3; -2
10) l2x-1l+7=8
l2x-1l=8-7
l2x-1l=1
2x-1=1 или 2х-1=-1
2х=1+1 2х=-1+1
2х=2 2х=0
х=1 х=0
ответ: 1; 0
1)х=3;х= -3 2)х-3=2/-2;х=5;х=1 3)х=4 4)х+3=-4/4;х=-7;1 5)х+1=7;х=7 6)х-2=3;х=-1 7)3х-1=0;3х=1;х=1/3 8)2х+3=0;2х=-3;х=-1,5 9)3х+2-4=0;3х=2;х=2/3 10)2х-1+7=8;2х-1+7-8=0;2х-2=0;х=1
4+|x|=10;x=10-4=6
9-|x|=9;x=9-9=0
0,8+|x|=0,92;x=0,92-0,8=0,12
|x|-0,6=1;x=1-0,6=0,4
|+0,042| : |x| = |-1,05|;x=1,05:0,042=25
|x| : |-3,5| = |+2,4|;x=2,4×3,5=8,4
1) x(x^2-4x+3)=0; x=0 или x^2-4x+3 = 0; x= 1 x=3
2) x^2(10-x^2-3x)=0; x^2=0: x=0 x^2+3x-10=0 x= -5 x=2
3) x(x^2+1-2x)=0 x=0 x^2-2x+1=0 x=1
4) (x-3)^2 * x=0 (x-3)^2=0 x-3=0 x=3 x=0
Відповідь:
1 задания
1) 25
2) 2
3) 0
4) -4,6
5) -11
6) -20
7) 38
8) -3,6
2 Задания
(3 — 12+6-12):9 = -1,6
(3 — 5,96 + 6 — 5,96) = -0. 2)
2)
Ответы:
Показать ответы
Алгебра, 09.03.2019 06:40, twv05355
Система уравнений: sin ((x+y)/2)*cos((x-y)/2)=1/2 2sin((x-y)/2)*cos((x+y)/2)=1/3
Ответы:
Показать ответы
Алгебра, 09.03.2019 11:50, ВероникаЛицей124
3синус(альфа +9пи)+4косинус(альфа+3пи/2)=
Ответы:
Показать ответы
Химия, 29.09.2022 10:12
Решить химию 10 класс…
Химия, 29.09.2022 09:59
Помогите срочно , ВПР сейчас…
Французский язык, 28.09.2022 22:37
Упр 5(см приложение) 1-7 поставить глаголы в Passé Composé Упр 6(см приложение) 1-2 поставить глаголы в Passé Composé
Экономика, 28.09.2022 17:11
На основании приведенных данных заполнить журнал регистрации хозяйственных операций и открыть счета бухгалтерского учета. Составить баланс на конец месяца. Исходные данные на карти…
Қазақ тiлi, 28.09.2022 16:47
2-тапсырма. Күрделі-құрама атаулардың әр тақырыптық тобына мысалдар
келтіріңдер. Келтірген мысалдарды катыстырып сөйлем құрандар. …
…
Английский язык, 26.05.2021 00:43
Insert Verbs (Conditionals)…
Математика, 26.05.2021 00:44
Результати 20 вимірів ємності конденсаторів приладом, що має рівень систематичної помилки (m = 2), склали такі відхилення від номіналу (пкФ): 3.42 0.34 1.97 5.20 -0.14 1.04 -1.71 -…
Физика, 26.05.2021 00:44
Площадь льдины 4м2, толщина 20см. Погрузится ли она полностью в пресную воду, если на неё встанет человек массой 80кг? Плотность льда 1000 кг/м3.…
Математика, 26.05.2021 00:44
Найдите значение производной функции cos3x в точке П/2 Найдите значение производной функции cos2x в точке П/4 Найдите значение производной функции х-3/х-1 в точке Хо=2…
Английский язык, 26.05.2021 00:46
с английским 5 и 6 зделать надо…
Lebih banyak pertanyaan tentang hal ini: Алгебра Вопросы без ответов
Решение простых уравнений с абсолютной величиной | Purplemath
HarderSpecial Case
Purplemath
Когда мы берем абсолютное значение числа, мы всегда получаем положительное число (или ноль). Независимо от того, был ли ввод положительным или отрицательным (или нулем), вывод всегда положительный (или нулевой). Например, | 3 | = 3 и | −3 | = 3 также.
Независимо от того, был ли ввод положительным или отрицательным (или нулем), вывод всегда положительный (или нулевой). Например, | 3 | = 3 и | −3 | = 3 также.
Это свойство — то, что и положительное, и отрицательное становятся положительными — делает решение уравнений с абсолютными значениями немного сложным. Но как только вы научитесь «трюку», они не так уж и плохи. Начнем с простого:
Содержание продолжается ниже
MathHelp.com
Решение уравнений с абсолютными значениями
Решить |
х | = 3
Я уже решил эту проблему в своем обсуждении выше:
| 3 | = 3
| −3 | = 3
Итак, x должно быть равно 3 или равно -3.
Но как мне это решить, если я разве уже не знает ответ? Я буду использовать положительное/отрицательное свойство абсолютного значения, чтобы разделить уравнение на два случая, и я буду использовать тот факт, что знак «минус» в отрицательном случае указывает на «противоположный знак», а не на «отрицательное число».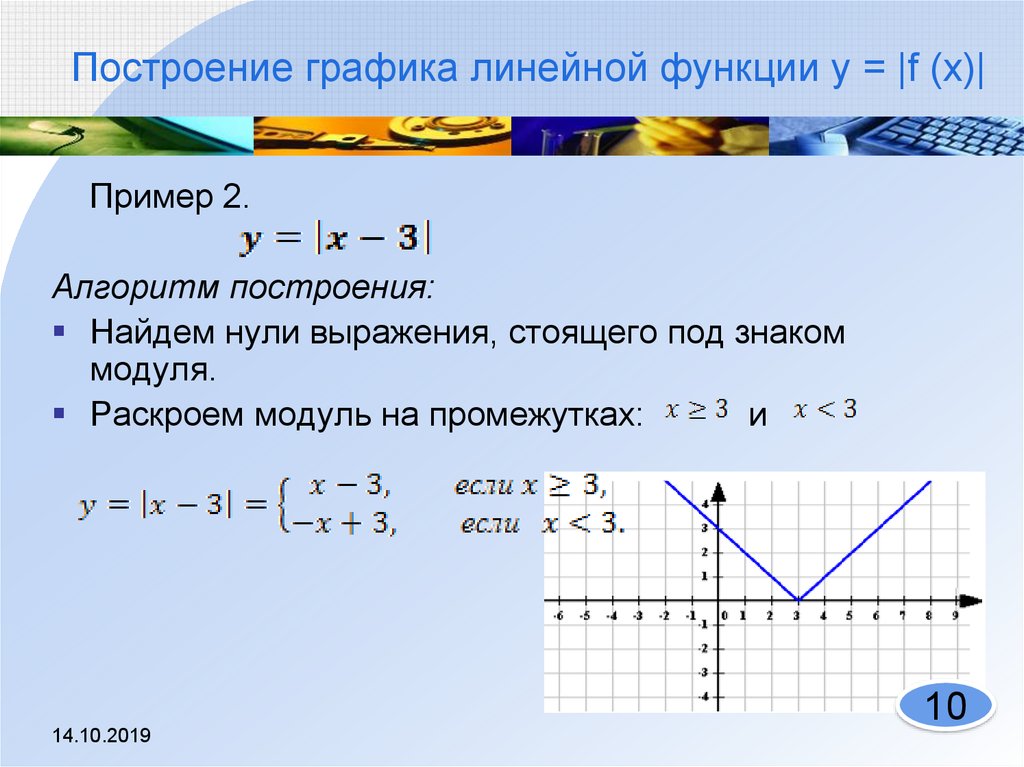
Например, если у меня x = -6, то «- x » означает «противоположное x » или, в данном случае, -(-6) = +6, положительное число. Знак «минус» в «− x » просто указывает, что я меняю знак на х . , а не означает отрицательное число. Это различие имеет решающее значение!
Каким бы ни было значение x , абсолютное значение x делает его положительным. Поскольку x изначально могло быть положительным, а могло быть отрицательным, я должен признать этот факт, когда удаляю столбцы абсолютного значения. Я делаю это, разбивая уравнение на два случая. Для этого упражнения эти случаи следующие:
a. Если значение x было неотрицательным (то есть, если оно было положительным или нулевым) для начала, тогда я могу вывести это значение из столбцов абсолютных значений, не меняя его знака, что даст мне уравнение x = 3.
б. Если значение x изначально было отрицательным, то я могу вывести это значение из столбцов абсолютных значений, изменив знак на x , что даст мне уравнение — x = 3, которое решается как х = -3.
Тогда мое решение
x = ±3
Между прочим, мы можем проверить приведенное выше решение графически. Когда мы пытаемся решить уравнение абсолютного значения | х | = 3, мы, по сути, устанавливаем два линейных уравнения равными друг другу и находим, где они пересекаются. Например:
Выше я построил график y 1 = | x | (это синяя линия, похожая на букву «V») и y 2 = 3 (это зеленая горизонтальная линия). Эти два графика пересекаются в x = -3 и x = +3 (две красные точки).
Если вы хотите проверить свои ответы на тесте (перед тем, как сдать его), может быть полезно ввести каждую часть исходного уравнения абсолютного значения в ваш калькулятор как свои собственные функции; затем запросите у калькулятора точки пересечения.
Конечно, любое решение также можно проверить, подключив его обратно к исходному упражнению и подтвердив, что левая часть (левая часть) уравнения упрощается до того же значения, что и правая часть (правая часть) уравнения. уравнение. Для уравнения выше, вот мой чек:
уравнение. Для уравнения выше, вот мой чек:
x = −3
Левая шкала: | х | = | −3 |
= 3 = RHS
x = +3
LHS: | х | = | +3 |
= 3 = RHS
Если вы когда-либо сомневались в своем решении уравнения, попробуйте построить график или попытаться снова включить свое решение в исходный вопрос. Проверка вашей работы всегда в порядке!
Вышеупомянутый шаг, когда уравнение абсолютного значения было переформулировано в двух формах, одна с «плюсом», а другая с «минусом», дает нам удобный способ упростить вещи: когда мы выделили абсолютное значение значение и перейти к снятию баров, мы можем разделить уравнение на два случая; мы обозначим эти случаи, поставив «минус» на противоположной стороне уравнения (для одного случая) и «плюс» на противоположной стороне (для другого). Вот как это работает:
Абсолютное значение изолировано в левой части уравнения, поэтому я уже подготовил разделение уравнения на два случая. Чтобы очистить столбцы абсолютного значения, я должен разделить уравнение на два возможных случая, по одному на случай, если содержимое столбцов абсолютного значения (то есть, если «аргумент» абсолютного значения) является отрицательным, и если он неотрицательный (то есть положительный или нулевой). Для этого я создаю два новых уравнения, единственная разница между которыми заключается в знаке в правой части. Во-первых, я сделаю «минус» случай:
Чтобы очистить столбцы абсолютного значения, я должен разделить уравнение на два возможных случая, по одному на случай, если содержимое столбцов абсолютного значения (то есть, если «аргумент» абсолютного значения) является отрицательным, и если он неотрицательный (то есть положительный или нулевой). Для этого я создаю два новых уравнения, единственная разница между которыми заключается в знаке в правой части. Во-первых, я сделаю «минус» случай:
x + 2 = -7
x + 2 = -7
x = -9
:
x + 2 = 7
x = 5
Теперь мне нужно проверить свои решения. Я сделаю это, подставив их обратно в исходное уравнение, поскольку оценщик не может видеть, как я проверяю графики на своем графическом калькуляторе.
x = −9:
Левая сторона: |(−9) + 2|
= |−7| = 7 = RHS
x = 5:
LHS: |(5) + 2|
= |7| = 7 = RHS
Оба решения проверяются, поэтому мой ответ таков:
x = −9, 5
Во-первых, я выделю абсолютную часть уравнения; то есть я получу выражение абсолютного значения с одной стороны знака «равно», а все остальное с другой стороны:
| 2 х — 3 | − 4 = 3
| 2 х − 3 | = 7
Теперь я уберу столбцы абсолютного значения, разделив уравнение на два случая, по одному для каждого знака аргумента. Сначала я возьму отрицательный случай:
Сначала я возьму отрицательный случай:
2 x — 3 = -7
2 x = -4
x = -2
:
2 x − 3 = 7
2 x = 10
x = 5
Упражнение не говорит мне проверять, поэтому я не буду. (Но если бы я захотел, я мог бы подставить «abs(2X−3)−4» и «3» в свой калькулятор (как Y1 и Y2 соответственно) и увидеть, что точки пересечения находятся на моих 9 точках.0019 x -значения.) Мой ответ:
x = −2, 5
Модуль для Can-Am Maverick X3 (с переключателем)
- Исследовать
- Характеристики
- Программное обеспечение Power Core
- Фурнитура
- загрузок
- Отзывы / Часто задаваемые вопросы
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ. Продажа или использование в Калифорнии запрещено законом. Одобренные в магазине детали
Продажа или использование в Калифорнии запрещено законом. Одобренные в магазине детали
УЗНАЙТЕ О ВОЗМОЖНОСТЯХ
Модуль управления запуском Dynojet (настоящий двухступенчатый) легко подключается к Can-Am Maverick X3, обеспечивая прилив мощности, когда вы впервые опускаете молот. Этот кнопочный модуль управления позволяет полностью открыть дроссельную заслонку во время запуска без ограничения крутящего момента. Требуется индивидуальная настройка.
Модуль управления запуском — это идеальный силовой стартер для Can-Am, который подходит для моделей Maverick X3 2017–2020 годов.
В этот комплект входит все необходимое для установки, что позволит вам получить тепло прямо из ворот. Установка проста благодаря конструкции plug-and-play, которая подключается к жгуту проводов OEM — не требуется обрезки или сращивания.
С помощью программного обеспечения Power Core у вас будет возможность отрегулировать скорость запуска, хотя мы рекомендуем установить скорость запуска так, чтобы она соответствовала скорости включения первичного сцепления, чтобы избежать потенциального повреждения ремня или сцепления.
Характеристики
- Позволяет полностью открыть дроссельную заслонку во время запуска
- Нет ограничений по крутящему моменту
- Настоящая двухступенчатая
- Стойкость к воздействию тепла, грязи и влаги
- Поставляется с переключателем активации2 и ремнями безопасности2
23
Программное обеспечение Power Core
Раскройте свой потенциал
- На базе ПК
- Соединяет участки динамометра с топливными настройщиками
- Настройка/создание калибровок и карт
Сравните ваши данные
Наше программное обеспечение для настройки C3 может сохранять все ваши данные с вашего топливного тюнера на ваш компьютер и сравнивать их, чтобы получить еще больше информации о вашей производительности.
Расширенные возможности настройки
Наше программное обеспечение PowerCore делает гораздо больше, чем просто сравнивает данные; это также поможет вам настроиться, как никогда раньше.
 Он может создавать карты с 30 положениями дроссельной заслонки, назначать целевые AFR для каждой ячейки карты и отображать несколько цилиндров одновременно.
Вы станете хозяином любой машины в мгновение ока.
Он может создавать карты с 30 положениями дроссельной заслонки, назначать целевые AFR для каждой ячейки карты и отображать несколько цилиндров одновременно.
Вы станете хозяином любой машины в мгновение ока.Clear Displays
Отображение и считывание данных в любой форме, необходимой для получения наилучшей возможной настройки. PowerCore может передавать данные в режиме реального времени и отображать их в виде ячеек питания или графиков для сравнения и легкой диагностики.
Комплектация
Can-Am
- Маверик Х3 2017
- Маверик Х3 Макс Турбо Р 2017, 2018, 2019
- Maverick X3 Max X ds Turbo R 2017, 2018, 2019
- Maverick X3 Max X RS Turbo R 2017, 2018, 2019
- Маверик Х3 Турбо Р 2017, 2018, 2019
- Maverick X3 X ds Turbo R 2017, 2018, 2019
- Маверик Х3 Х дс 2017
- Маверик X3 X рс 2017
- Maverick X3 X RS Turbo R 2017, 2018, 2019
- Маверик X3 900 HO 2018
- Маверик Х3 Макс Турбо 2018, 2019, 2020
- Маверик Х3 Турбо 2018, 2019, 2020
- Maverick X3 X мистер Турбо 2018, 2019, 2020, 2021
- Maverick X3 X Mr Turbo R 2018, 2019
- Maverick X3 X RC Турбо 2018, 2019, 2020, 2021
- Maverick X3 X RC Turbo R 2018, 2019
- Маверик X3 DS Турбо R 2020, 2021
- Maverick X3 Max DS Turbo R 2020, 2021
- Maverick X3 Max RS Turbo R 2020, 2021
- Maverick X3 Max X ds Turbo RR 2020, 2021
- Maverick X3 Max X Mr Turbo RR 2020, 2021
- Maverick X3 Max X RS Turbo RR 2020, 2021
- Маверик Х3 РС Турбо Р 2020, 2021
- Maverick X3 X ds Turbo RR 2020, 2021
- Maverick X3 X Mr Turbo RR 2020, 2021
- Maverick X3 X RC Turbo RR 2020, 2021
- Maverick X3 X RS Turbo RR 2020, 2021
- Маверик X3 DS Турбо 2021
- Maverick X3 Max DS Турбо 2021
- Maverick X3 Max X rs Turbo RR Smart-Shox 2021
- Maverick X3 X rs Turbo RR Smart-Shox 2021
Загрузки
Описание Размер Обновлено Скачать Руководство по установке — Модуль управления запуском для Can-Am Maverick X3 2017–2020 гг.  (1,70 МБ) (11 августа 2021 г.)
(1,70 МБ) (11 августа 2021 г.) 1,70 МБ 11 августа 2021 г. Отзывы клиентов и ответы на часто задаваемые вопросы
Подпишитесь на нашу рассылку новостей:
Подпишитесь на нашу рассылку:
Модуль 6 — Предел, когда x приближается к
Допуски
Первый допуск, который вы обнаружили в уроке 6.1, был ответом на вопрос:
- Насколько близко должно быть x к 3, чтобы находится в пределах 0,1 от 2?
x — Допуск
Процедура поиска решения поставленного выше вопроса может быть выражена с помощью двух составных неравенств.

- Найдите положительное число чтобы когда бы ни
Решение неравенства
Когда допуск и равен 0,1, x — допуск можно найти, решив
составное неравенство, , как показано ниже.Составное (или расширенное) неравенство — это неравенство, которое сравнивает более двух величин и содержит более одного символа неравенства. Смысл составного неравенства, приведенного выше, сохранялся, когда каждое выражение возводилось в квадрат, потому что каждое выражение представляло положительное число.

Решение составного неравенства примерно 2,87 < x < 3,136666667.
Обратите внимание, что решения те же, что и в уроке 6.1, когда вы использовали функцию «Пересечение» на экране «График».
Нахождение
Сравните приведенные ниже неравенства.
Это следует из того а также .
Решение двух уравнений для дает два разных значения: а также . Как и в уроке 6.1, правильным ответом является меньшее из двух значений: .
Меньше и -Допуск
Второй допуск x , который вы нашли в уроке 6.1, был получен при ответе на вопрос
- Насколько близко должно быть x к 3, чтобы гарантировать, что находится в пределах 0,01 от 2?
6.2.1 Переформулируйте вопрос выше, используя сложные неравенства. Щелкните здесь, чтобы получить ответ.
6.2.2 Решите первое сложное неравенство в ответе на 6.
 2.1. Щелкните здесь, чтобы получить ответ.
2.1. Щелкните здесь, чтобы получить ответ.6.2.3 Сравните ответ в 6.2.2 с неравенством 3 — < x < 3 + . Найдите значение , x -допуск. Щелкните здесь, чтобы получить ответ.
Поиск обобщенного решения
Предположим, вас попросили найти значения которые соответствуют все меньшим и меньшим y -допускам около y = 2. Вместо повторного выполнения одного и того же процесса для различных y -допуски, вы можете решить проблему один раз с обобщенным y -допуском.
Пусть общий y -толерантность представлен как , греческая буква «эпсилон». Дельта греческих букв, , и эпсилон, , используются для представления небольших положительных чисел.
Тогда вопрос толерантности становится
Насколько близко должно быть x к 3, чтобы внутри из 2?
Нахождение обобщенного x -допуска
Процедура, используемая для нахождения решения вопроса об обобщенной толерантности, выглядит следующим образом:
Учитывая положительное число , найти положительное число , чтобы когда бы ни
Решение обобщенного неравенства
Составное неравенство решается ниже.
 Метод решения предполагает, что меньше 2. Если больше 2, мы можем выбрать = 1.
Метод решения предполагает, что меньше 2. Если больше 2, мы можем выбрать = 1.Решением обобщенного сложного неравенства является
Сравнивая последнее неравенство с дает два уравнения:
а также Решения этих уравнений а также Если это небольшое положительное число будет положительным.
Меньшее из этих двух значений равно , что является общим решением.
При любом малом положительном значении для последнее уравнение можно использовать, чтобы найти соответствующее значение для . Например, когда = 0,01, это уравнение дает = 0,0133, то же значение, найденное ранее.
Ограничения
Когда значения на выходе могут быть сколь угодно близки к 2, взяв входные значения достаточно близко к 3, мы говорим
- Предел функции при приближении x к 3 равно 2.
То есть значение приближается к 2 по мере того, как x приближается к 3.
 Обозначение, используемое для обозначения этого,
Обозначение, используемое для обозначения этого,Лимит читается как «предел поскольку x приближается к 3, это 2».
В предыдущем примере мы обнаружили, что гарантирует, что
когда бы ни Потому что для любого положительного соответствующий положительный может быть найдено, удовлетворяющее вышеперечисленным условиям,
Это приводит к формальному определению предела.
Определение лимита
Значение функции при x = a не имеет значения при нахождении предела. Учитываются только значения функции, поскольку x приближается к и .
Формально, если для любого , существует такой, что
когда бы ни Концептуально f ( x ) приближается к L , поскольку x приближается к a , что также можно записать
Значение функции при x = a не имеет значения при нахождении предела.
 Учитываются только значения функции, когда x приближается к и .
Учитываются только значения функции, когда x приближается к и .6.2.4 Напишите оператор с составными неравенствами, представляющий условия, связанные с . Щелкните здесь, чтобы получить ответ. 93-8
9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 WSRD Модуль управления запуском Can-Am X3 | 2017-2022 QRSX+ Clutch — Whalen’s Speed R&D
WSRD Can-Am X3 Launch Control Module | 2017-2022 QRSX+ Clutch — исследования и разработки Whalen’s Speed | Уэлен Тюнинг перейти к содержаниюпо WSRD
Распродажа Распродажа
Первоначальная цена $ 384,00 — Первоначальная цена $ 505,00
Исходная цена 384,00 $
369,00 $
369,00 $ — $ 459.
 00
00Текущая цена $ 369,00
| /
Артикул
product.variants.choose_variant Can-Am X3 2-местный / WSRD Стандартная настройка 2200 об / мин / Нет, спасибо | У меня вариант поддерживающего сцепления — 369.00$ Can-Am X3 2-Seater / WSRD Enhanced 2600 RPM Setting / Нет, спасибо | У меня вариант поддерживающего сцепления — 369$.00 Can-Am X3 2-Seater / WSRD Enhanced 2600 RPM Setting / ADD | Розовая первичная пружина WSRD/KWI (зацепление 2900 об/мин) — $459,00 Can-Am X3 4-Seater / WSRD Standard 2200 RPM Setting / Нет, спасибо | У меня вариант поддерживающего сцепления — 369.00$ Can-Am X3 4-Seater / WSRD Enhanced 2600 RPM Setting / Нет, спасибо | У меня вариант поддерживающего сцепления — 369.00$ Can-Am X3 4-Seater / WSRD Enhanced 2600 RPM Setting / ADD | WSRD/KWI Розовая первичная пружина (2900 RPM Engagement) — $459.
 00
002-местный автомобиль Can-Am X3
4-местный автомобиль Can-Am X3
Стандартная настройка WSRD 2200 об/мин
Расширенная настройка WSRD 2600 об/мин
Нет, спасибо | У меня есть вариант поддерживающего сцепления
ДОБАВИТЬ | WSRD/KWI Розовая первичная пружина (2900 оборотов в минуту)
1 2 3 4 5 6 7 8 9 10+ Количество
Количество
Поделись этим: youtube.com/embed/he6yepLto8Q» allowfullscreen=»» allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» frameborder=»0″>Модуль управления запуском WSRD (LCM) предназначен для того, чтобы машина могла иметь контролируемую, постоянную скорость запуска, отключая зажигание на желаемых оборотах, а также увеличивая наддув за счет управления задержкой зажигания. Этот блок может быть добавлен к любой машине или к любой настройке и позволяет пользователю точно настроить скорость запуска и то, насколько агрессивной будет машина.
Операция управления запуском:
- LCM WSRD входят в стандартную комплектацию с задержкой операций
- Старые LCM поставлялись с трехсекундной задержкой между нажатием кнопки активации и фактической активацией LCM
- WSRD обновил это и теперь включает задержку в одну секунду с 1 февраля 2022 г.
- Для правильной работы нажмите кнопку мгновенного действия LCM, подождите одну секунду, а затем нажмите педаль газа для активации LCM
WSRD LCM имеет возможность замедления до 40*.
 Задержка зажигания позволяет больше нагревать выхлопные газы, что помогает скорости вращения вала турбины создавать больший наддув.
Задержка зажигания позволяет больше нагревать выхлопные газы, что помогает скорости вращения вала турбины создавать больший наддув.WSRD LCM будет отправлен с нашей стандартной настройкой 2200 об/мин с задержкой -30*. Мы также предлагаем настройку 2600 об/мин, которая может быть предварительно загружена. Это может быть изменено пользователем. С помощью нашего LCM Max Effort мы можем настроить и помочь пользователю с настройкой, а при использовании нашей настройки объединить как LCM, так и нашу настройку для достижения наилучших результатов.
- WSRD Стандартная настройка управления запуском 2200 об/мин
- Требуется синяя первичная пружина KWI (зацепление на 2500 об/мин), которая ранее использовалась в системах сцепления KWI AO (ПОЖАЛУЙСТА, ОБРАТИТЕ ВНИМАНИЕ: KWI теперь поставляет синюю/оранжевую первичную пружину со всеми системами сцепления, это НЕ поддерживает нашу конфигурацию управления запуском.
- Системы сцепления других производителей поддерживают это с аналогичными зацепляющими пружинами
- WSRD Расширенная настройка управления запуском 2600 об/мин
- Требуется WSRD | KWI Pink Primary Spring (2900 RPM Engagement), которая указана выше как НОВАЯ доступная опция .
- Системы сцепления других производителей поддерживают это с аналогичными зацепляющими пружинами
- WSRD Настройка управления запуском максимального усилия
- Перед покупкой проконсультируйтесь с Джоном
- Поддерживается сцеплением KWI Tapp Clutch и STM Powersports с высоким сцеплением

модулей Sage X3 | Топ 5 модулей | Основные характеристики
05 Авг Модули Sage X3 | Топ 5 модулей | Основные характеристики
Опубликовано в 19:39 в ERP, Сейдж от admin
0 Likes
Sage X3 — это самый продвинутый бухгалтерский пакет, предлагаемый Sage, поэтому имейте в виду, что каждый из этих модулей Sage X3 управляется процессами. Существует множество собственных и сторонних дополнительных модулей Sage X3. Здесь мы разбираем пять самых популярных модулей Sage ERP X3, чтобы дать вам лучшее представление о том, как они работают.
Список 5 лучших модулей Sage X3 Каждый из этих модулей отвечает за разные аспекты вашего бизнеса.
Каждый из этих модулей отвечает за разные аспекты вашего бизнеса.- Производственный модуль Sage X3
- Финансовый модуль Sage X3
- Инструмент для покупки Sage X3
- Сервисный модуль Sage X3
- Инструмент продаж Sage X3.
Производственный модуль Sage X3Производственный модуль Sage X3 — самый популярный встроенный модуль Sage X3, не включенный в базовую версию Sage X3. Модуль упрощает управление производственным процессом, позволяя пользователю фильтровать по заданию, заказу, инвентарю и т. д. Sage ERP X3 обеспечивает постоянный мониторинг запасов, планирование производства, функции планирования и общее управление; которые определяются прайс-листами, центрами затрат и станциями.
Этот модуль может упростить производственные процессы с помощью таких инструментов, как:
- Подробные технические данные
- Учет затрат
- Планирование
- Выпуск заказа на работу
- Инструменты для принятия решений
Финансовый модуль Sage ERP X3 включает основные финансовые функции Sage (GL, AR, AP и т.
 д.). Этот модуль может хранить информацию и отчеты в режиме реального времени между несколькими филиалами или даже несколькими компаниями. Вы можете сверять данные по всему миру в режиме реального времени благодаря мультивалютным, динамическим обменным курсам (обновляется ежедневно) и многоязычной поддержке. Финансовый модуль Sage X3 также может охватывать личный и финансовый бюджет, отчет о прибылях и убытках и т. д.
д.). Этот модуль может хранить информацию и отчеты в режиме реального времени между несколькими филиалами или даже несколькими компаниями. Вы можете сверять данные по всему миру в режиме реального времени благодаря мультивалютным, динамическим обменным курсам (обновляется ежедневно) и многоязычной поддержке. Финансовый модуль Sage X3 также может охватывать личный и финансовый бюджет, отчет о прибылях и убытках и т. д.Финансовый модуль поставляется с рядом готовых инструментов:
- Multi-Ledger (GL)
- Счета и финансовые календари
- Автоматические журналы
- Внутрифирменные операции
- Аналитические размеры
- Бюджетирование
- Запросы на учетную запись
- Отчетность
Инструмент для закупок Sage X3 является частью модуля распространения и берет на себя весь процесс закупок. Модуль включает в себя такие функции, как управление запросами предложений/запросами предложений, интеграция с прайс-листами, мониторинг доставки и прием поступающих товаров.

Поскольку модуль закупок встроен непосредственно в Sage X3, он обеспечивает пользователям более простой и быстрый контроль над бюджетом, запросами на покупку и выдачей заказов.
В модуле закупок доступны следующие процессы:
- Деловые партнеры и продукты
- Гибкие правила ценообразования
- Планирование закупок и оформление заказов
- Планирование доставки и получение
Потребности в сервисных модулях различны для всех компаний, поэтому важно тщательно изучить сервисный модуль с помощью sage X3, чтобы убедиться, что он соответствует вашим потребностям (если вы, скажем, подрядчик, вы можете поискать в другом месте).
Сервисный модуль Sage ERP X3 позволит вашей компании добиться большего за меньшее время и работать при этом удаленно. Сервисный модуль отлично смотрится на таких устройствах, как iPad, и улучшает реакцию на требования ваших клиентов. Редко можно найти сервисный модуль, который так хорошо связан с вашими финансами, как правило, он управляется через CRM.

Сервисный модуль Sage X3 предоставит организации следующие инструменты:
- Расчетные циклы и условия контрактов
- Расчет повторяющихся услуг и контактов
- Контроль интервалов технического обслуживания
- Автоматическая координация сервисных вызовов
- Управление арендными услугами
- Автоматический расчет стоимости и выставление счетов
Инструмент продаж Sage X3, как и инструмент закупок, сгруппирован в модуль распространения. Инструмент продаж Sage X3 позволяет пользователю предоставлять быструю информацию о продуктах, запасах, котировках, управлении контактами и подробной информации о каждой SKU. Вы можете создавать отчеты и изменять прайс-листы, скидки, дистрибьюторов, перевозчиков и многое другое на лету.
Другие процессы, включенные в модуль продаж Sage ERP X3:
- Деловые партнеры и продукты
- Гибкие правила ценообразования
- Гибкий прием и обработка заказов
- Распределение запасов и планирование доставки
- Подготовка заказа/отгрузки
Чтобы узнать больше о модулях Sage X3, нажмите здесь.




 Он может создавать карты с 30 положениями дроссельной заслонки, назначать целевые AFR для каждой ячейки карты и отображать несколько цилиндров одновременно.
Вы станете хозяином любой машины в мгновение ока.
Он может создавать карты с 30 положениями дроссельной заслонки, назначать целевые AFR для каждой ячейки карты и отображать несколько цилиндров одновременно.
Вы станете хозяином любой машины в мгновение ока. (1,70 МБ) (11 августа 2021 г.)
(1,70 МБ) (11 августа 2021 г.) 

 2.1. Щелкните здесь, чтобы получить ответ.
2.1. Щелкните здесь, чтобы получить ответ. Метод решения предполагает, что меньше 2. Если больше 2, мы можем выбрать = 1.
Метод решения предполагает, что меньше 2. Если больше 2, мы можем выбрать = 1. Обозначение, используемое для обозначения этого,
Обозначение, используемое для обозначения этого,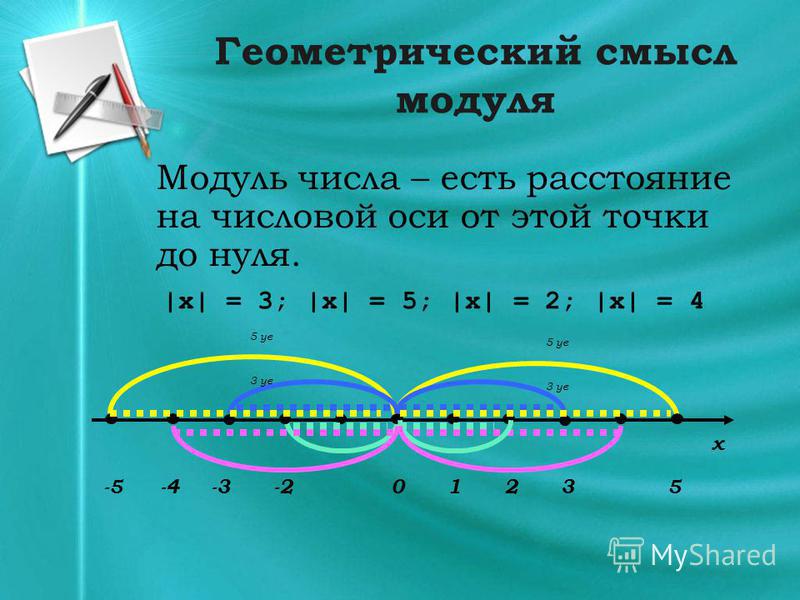 Учитываются только значения функции, когда x приближается к и .
Учитываются только значения функции, когда x приближается к и . 00
00 00
00 Задержка зажигания позволяет больше нагревать выхлопные газы, что помогает скорости вращения вала турбины создавать больший наддув.
Задержка зажигания позволяет больше нагревать выхлопные газы, что помогает скорости вращения вала турбины создавать больший наддув.
 Каждый из этих модулей отвечает за разные аспекты вашего бизнеса.
Каждый из этих модулей отвечает за разные аспекты вашего бизнеса. д.). Этот модуль может хранить информацию и отчеты в режиме реального времени между несколькими филиалами или даже несколькими компаниями. Вы можете сверять данные по всему миру в режиме реального времени благодаря мультивалютным, динамическим обменным курсам (обновляется ежедневно) и многоязычной поддержке. Финансовый модуль Sage X3 также может охватывать личный и финансовый бюджет, отчет о прибылях и убытках и т. д.
д.). Этот модуль может хранить информацию и отчеты в режиме реального времени между несколькими филиалами или даже несколькими компаниями. Вы можете сверять данные по всему миру в режиме реального времени благодаря мультивалютным, динамическим обменным курсам (обновляется ежедневно) и многоязычной поддержке. Финансовый модуль Sage X3 также может охватывать личный и финансовый бюджет, отчет о прибылях и убытках и т. д.

