Решение уравнений средствами MathCad — Mathcad (мат.задачи)
Решение одного уравнения
Для простейших уравнений вида f(x) = 0 решение в Mathcad находится с помощью функции root. root( f(х1, x2, …), х1, a, b ) Возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. Аргументы: f(х1, x2, …) — функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения. х1 — — имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня. a, b — необязательны, если используются, то должны быть вещественными числами, причем a < b. Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться. Рекомендации по использованию функции root:
.
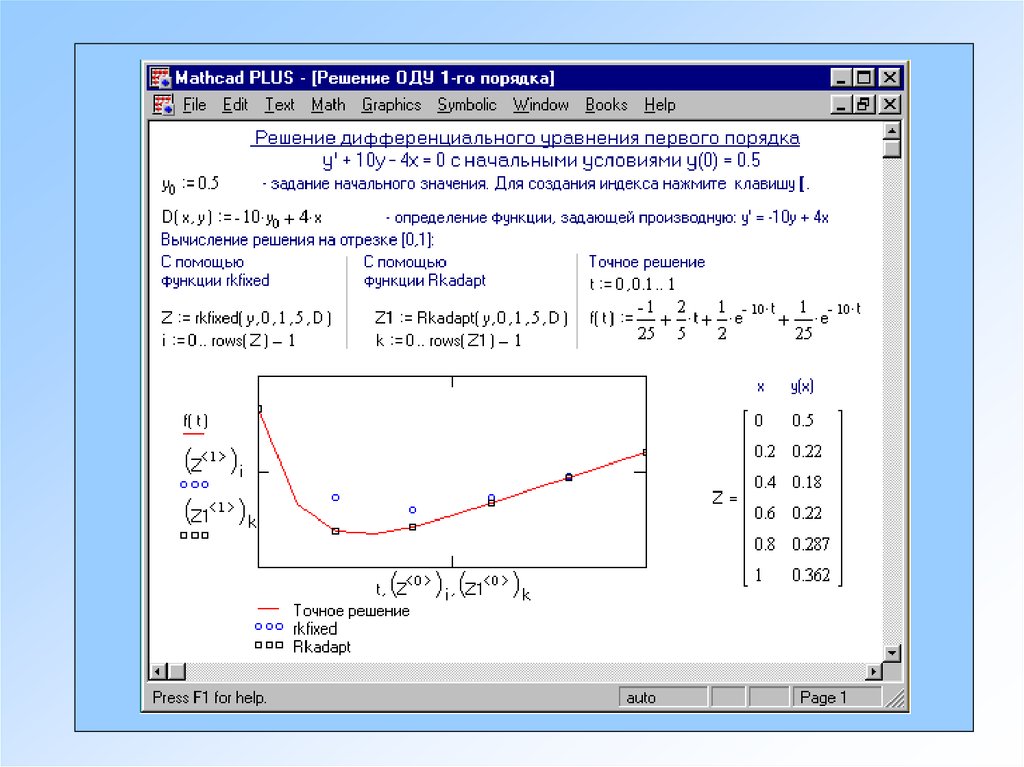
Рисунок 11.
Нахождение корней полинома Для нахождения корней выражения, имеющего вид vnxn + … + v2x2 + v1x + v0, лучше использовать функцию polyroots, нежели root. Polyroots(v) Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома. Аргументы: v — вектор, содержащий коэффициенты полинома. Рисунок 11 иллюстрирует решение уравнений средствами Mathcad. |
Решение уравнений и систем уравнений средствами Mathcad
Похожие презентации:
3D печать и 3D принтер
Системы менеджмента качества требования. Развитие стандарта ISO 9001
Операционная система. Назначение и основные функции
Adobe Photoshop
AutoCAD история и возможности
Microsoft Excel
Облачные технологии
Корпорация Microsoft и ее особенности
Веб-дизайн
Тема 2. Пакеты прикладных программ
Пакеты прикладных программ
Решение уравнений и
систем уравнений
средствами Mathcad
Для нахождения корней уравнения выделяют два
этапа:
1) отделение корней − определение интервала
нахождения каждого корня или определение
приблизительного значения корня. В Mathcad
наиболее наглядным является отделение корней
уравнения графическим способом;
2) уточнение корней − нахождение численного
значения корня с заданной точностью.
Точность нахождения корня устанавливается с помощью
Переопределить значение системной переменной TOL
можно:
• TOOLS – Worksheet Options –
перейти на вкладку Build-In Variables (Встроенные
переменные) и в поле TOL ввести новое значение,
например, 0.0001.
Это значение распространяется на весь документ
Mathcad.
• присваивание системной переменной TOL
непосредственно в документе Mathcad нового
значения, например, TOL:=0.0001
Для решения одного уравнения с одной неизвестной
предназначена встроенная функция root, формат обращения к
которой имеет вид:
root(f(x), x, [a, b]).
Данная функция возвращает значение переменной x, при котором
функция f(x) обращается в ноль.
Аргументы функции root:
f(x) – функция в левой части уравнения f(x) = 0;
x – переменная, относительно которой требуется решить
уравнение;
a, b – необязательные действительные числа, такие что a < b,
причем на интервале [a, b] находится только один корень.
Если функция root не может найти корни уравнения, то
рекомендуется уточнить начальное приближение, изменить
границы интервала [a, b] нахождения корня или увеличить
значение системной переменной TOL.
Поиск корней многочлена. Функция polyroots
Для решения полиномиальных уравнений вида
vn x vn 1 x
n
n 1
… v1 x v0 0
или нахождения всех корней полинома степени n,
используют функцию polyroots(v)
В общем виде нахождение корней полинома
сводится к выполнению следующих действий:
• Составляется вектор столбец v
a0
a1
из коэффициентов полинома
v
.
 …
… an
• Осуществляется непосредственный поиск корней
функцией polyroots(v)=
Пример 1. Решить уравнение:
2
f ( x) 2 x 8 x 25 x 64
0.395 3.132i
polyroots ( v ) 0.395 3.132i
3.211
v
25
8
2
64
Решение систем линейных уравнений
1) матричный способ
• задается матрица коэффициентов при неизвестных
системы A:=;
• задается столбец свободных членов b:=;
• вводится формула для нахождения решения
системы X:=A-1*b
• выводится вектор решений системы X=.
2) Использование функции lsolve(A, b)
Пакет Mathcad имеет встроенную функцию
lsolve(A, b)=
Решение систем нелинейных уравнений
Используются функции Find и Minerr.
Начальные условия
Given
Уравнения системы
Выражения с функциями
Find, Minerr
Пример. Найти точные решения системы
уравнений:
x y x y 7
x y x y 13
Решение :
x
1
y
1
Given
x y
x y 7
x y
x y 13
Find ( x y )
жирный знак равенства
CTRL+
5
2
Пример.
 Решить систему линейных уравнений
Решить систему линейных уравнений3x 4 y 5 z 1;
7 x 4 y z 2;
2 y 9 z 5.
РЕШЕНИЕ :
English Русский Правила
Решение символьных уравнений — MATLAB & Simulink
Основное содержимое
В этом примере используется:
Open Script
В этом примере показаны основы решения символьных уравнений.
Решить квадратное уравнение
Решить квадратное уравнение с помощью функции решить .
Решите квадратное уравнение без указания переменной для решения. Функция решить выбирает x для возврата решения. 92
Решение многомерных уравнений и присвоение выходных данных структуре
При решении для нескольких переменных удобнее хранить выходные данные в массиве структур, чем в отдельных переменных. Функция solve возвращает структуру, когда вы указываете один выходной аргумент и существует несколько выходов.
Решите систему уравнений, чтобы получить решения в массиве структур.
disp('Решите систему уравнений, чтобы получить решения в массиве структур')
disp('>> eqns = [2*u + v == 0, u - v == 1];')
disp('>> S = решить(eqns,[u v])')
Симс ты v
eqns = [2*u + v == 0, u - v == 1];
S = решить (уравнения, [u v])
Решите систему уравнений, чтобы найти решения в массиве структур
>> eqns = [2*u + v == 0, u - v == 1];
>> S = решить (уравнения, [u v])
С =
структура с полями:
у: 1/3
v: -2/3
Доступ к решениям путем обращения к элементам конструкции.
disp('Доступ к решениям внутри структуры')
disp('>> S.u')
Су
disp('>> S.v')
С.в
Доступ к решениям в структуре >> С.у. ответ = 1/3 >> С.в ответ = -2/3 92, С) е1 = 1/9 >> e2 = subs(3*v + u, S) е2 = -5/3
Если функция решить возвращает пустой объект, то решений не существует.
disp('Функция решения возвращает пустой объект, если решений не существует')
disp('> > решить([3*u+2, 3*u+1],u)')
S = решить([3*u+2, 3*u+1],u)
Функция решения возвращает пустой объект, если решений не существует >> решить([3*и+2, 3*и+1],и) С = Пустой символ: 0 на 1
Численное решение уравнений
Когда функция решить не может символически решить уравнение, она пытается найти числовое решение, используя функцию vpasolve . 2 — 1;
disp(‘>> решить (eqn,x)’)
S = решить (уравнение, х)
92 — 1;
>> решить (уравнение, х)
Предупреждение: невозможно решить символически. Возврат числового решения с помощью vpasolve.
С =
-0,636732650805282010887990828
2 — 1;
disp(‘>> решить (eqn,x)’)
S = решить (уравнение, х)
92 — 1;
>> решить (уравнение, х)
Предупреждение: невозможно решить символически. Возврат числового решения с помощью vpasolve.
С =
-0,636732650805282010887990828
Постройте левую и правую части уравнения. Заметим, что уравнение также имеет положительное решение.
disp('Постройте левую и правую части уравнения, чтобы увидеть, что уравнение также имеет положительное решение')
disp('>
> fplot([lhs(eqn) rhs(eqn)], [-2 2])')
fplot([lhs(eqn) rhs(eqn)], [-2 2])
Постройте левую и правую части уравнения, чтобы увидеть, что уравнение также имеет положительное решение >> fplot([lhs(eqn) rhs(eqn)], [-2 2])
Найдите другое решение, напрямую вызвав числовой решатель vpasolve и указав интервал.
disp('Найдите другое решение, вызвав числовой решатель vpasolve')
disp('>> V = vpasolve (eqn,x,[0,2])')
V = vpasolve(eqn,x,[0 2])
Найдите другое решение, вызвав числовой решатель vpasolve >> V = vpasolve (eqn,x,[0,2]) В = 1.4096240040025962492355939705895
У вас есть модифицированная версия этого примера. Хотите открыть этот пример со своими правками?
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
Solving quadratic equations matlab
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Решение
- График
- Система
- Математический решатель на вашем сайте
Связанные темы:
полиномиальный коэффициент в кубе | как выполнить обратную матрицу на калькуляторе ti84plus в дробях | калькуляторы упрощения рациональных выражений | неоднородное уравнение в частных производных первого порядка | тригонометрическое сложение и вычитание | алгебра 2 | калькулятор рациональных уравнений онлайн | план урока «Решение систем уравнений методом исключения» | решить за х.
 |2x + 2| = 14 |
решение полиномиальных уравнений факторингом |
соотношение решатель |
теряется в уравнении вычитания |
Калькулятор комбинирования похожих терминов
|2x + 2| = 14 |
решение полиномиальных уравнений факторингом |
соотношение решатель |
теряется в уравнении вычитания |
Калькулятор комбинирования похожих терминов| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| Дель Рови Дата регистрации: 05.04.2002 |
| ||||||
| Наверх | |||||||
| AllejHat Зарегистрирован: 16.07.2003 |
| ||||||
| Наверх | |||||||
| molbheus2matlih Зарегистрирован: 10.04.2002 |
| ||||||
| Наверх | |||||||
| мордгермкаундри Зарегистрирован: 18.04.2005 |
| ||||||
| Наверх | |||||||
| cmithy_dnl Зарегистрирован: 08. |
| ||||||
| Наверх | |||||||
| ТК Зарегистрирован: 25.09.2001 |
| ||||||



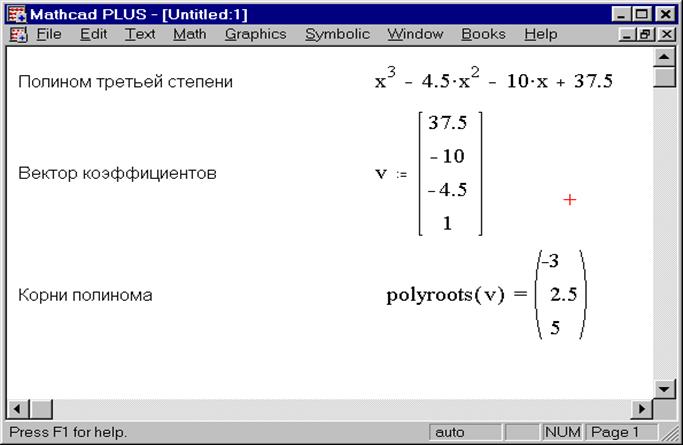 Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0
Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0 В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.
В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. 4096240040025962492355939705895
4096240040025962492355939705895
 Каждый день, когда я прихожу домой из школы, я трачу все свое время на домашнее задание по алгебре, и после всего потраченного времени я все еще получаю неправильные ответы. Однако я также не уверен, стоит ли того частный репетитор по алгебре, так как это действительно дорого, и кто знает, может быть, это даже не так полезно. Кто-нибудь знает что-нибудь о решении квадратных уравнений Matlab, что может мне помочь? Или, может быть, какие-то пояснения о факторинге полиномов, добавлении функций или добавлении функций? Любые идеи будут оценены.
Каждый день, когда я прихожу домой из школы, я трачу все свое время на домашнее задание по алгебре, и после всего потраченного времени я все еще получаю неправильные ответы. Однако я также не уверен, стоит ли того частный репетитор по алгебре, так как это действительно дорого, и кто знает, может быть, это даже не так полезно. Кто-нибудь знает что-нибудь о решении квадратных уравнений Matlab, что может мне помочь? Или, может быть, какие-то пояснения о факторинге полиномов, добавлении функций или добавлении функций? Любые идеи будут оценены. Какая часть сходства стороны-угла-стороны и вычисление формул создает больше проблем? Потому что я уверен, что вам действительно нужна хорошая программа, которая поможет вам понять основные понятия и способы решения упражнений. Вы когда-нибудь использовали такое программное обеспечение? Я пробовал несколько из них, но должен сказать, что Algebrator — лучший и самый простой в использовании. Она не похожа на другие программы, потому что учит решать, а не просто дает решения.
Какая часть сходства стороны-угла-стороны и вычисление формул создает больше проблем? Потому что я уверен, что вам действительно нужна хорошая программа, которая поможет вам понять основные понятия и способы решения упражнений. Вы когда-нибудь использовали такое программное обеспечение? Я пробовал несколько из них, но должен сказать, что Algebrator — лучший и самый простой в использовании. Она не похожа на другие программы, потому что учит решать, а не просто дает решения. Я использую его уже пару лет.
Я использую его уже пару лет.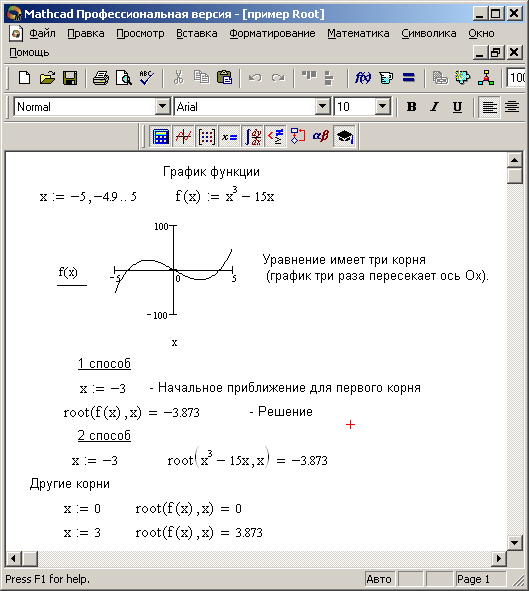 01.2002
01.2002 