Уравнение cos x = а
Мы знаем, что значения косинуса заключены в промежутке [-1; 1], т.е. -1 ≤ cos α ≤ 1. Поэтому если |а| > 1, то уравнение cos x = а не имеет корней. Например, уравнение cos x = -1,5 корней не имеет.
Рассмотрим несколько задач.
Задача 1.
Решить уравнение cos x = 1/2.
Решение.
Вспомним, что cos x – это абсцисса точки окружности с радиусом, равным 1, полученной в результате поворота точки Р (1; 0) на угол х вокруг начала координат.
Абсцисса 1/2 есть у двух точек окружности М1 и М2. Так как 1/2 = cos π/3, то точку М1 мы можем получить из точки Р (1; 0) путем поворота на угол х1 = π/3, а также на углы х = π/3 + 2πk, где k = +/-1, +/-2, …
Точка М2 получается из точки Р (1; 0) поворотом на угол х2 = -π/3, а также на углы -π/3 + 2πk, где k = +/-1, +/-2, …
Итак, все корни уравнения cos x = 1/2 можно найти по формулам
х = π/3 + 2πk
где k € Z.
Две представленные формулы можно объединить в одну:
х = +/-π/3 + 2πk, k € Z.
Задача 2.
Решить уравнение cos x = -1/2 .
Решение.
Абсциссу, равную – 1/2 , имеют две точки окружности М1 и М2. Так как -1/2 = cos 2π/3, то угол х1 = 2π/3, а потому угол х2 = -2π/3.
Следовательно, все корни уравнения cos x = -1/2 можно найти по формуле: х = +/-2π/3 + 2πk, k € Z.
Таким образом, каждое из уравнений cos x = 1/2 и cos x = -1/2 имеет бесконечное множество корней. На отрезке 0 ≤ х ≤ π каждое из этих уравнений имеет только один корень: х1 = π/3 – корень уравнения cos x = 1/2 и х1 = 2π/3 – корень уравнения cos x = -1/2.
Число π/3 называют арккосинусом числа 1/2 и записывают: arccos 1/2 = π/3, а число 2π/3 – арккосинусом числа (-1/2) и записывают: arccos (-1/2) = 2π/3.
Вообще уравнение cos x = а, где -1 ≤ а ≤ 1, имеет на отрезке 0 ≤ х ≤ π только один корень. Если а ≥ 0, то корень заключен в промежутке [0; π/2]; если а < 0, то в промежутке (π/2; π].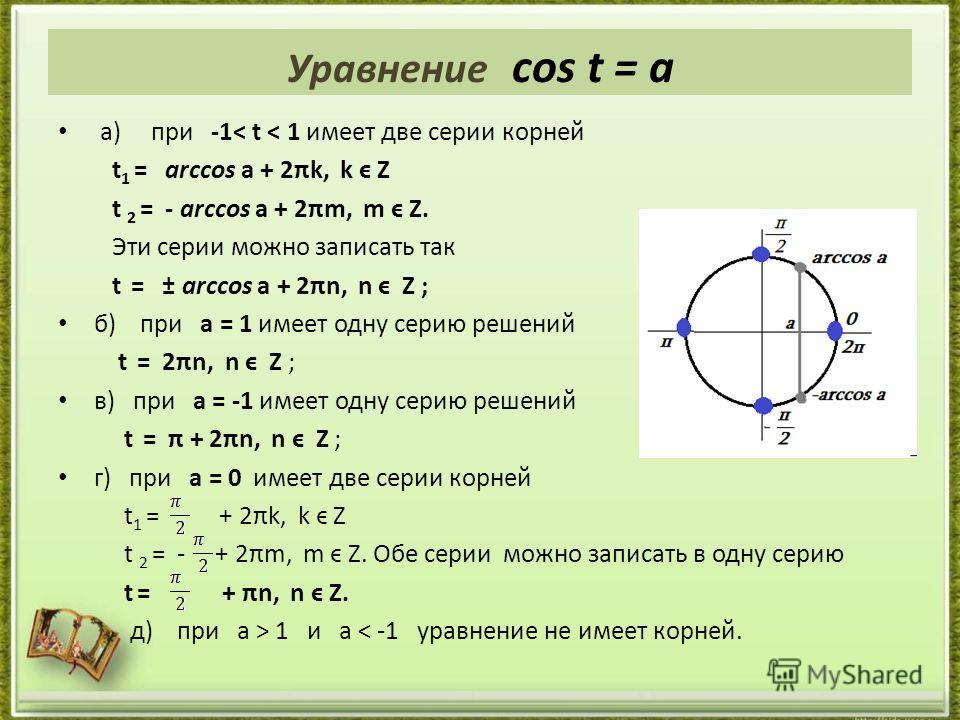
Таким образом, арккосинусом числа а € [-1; 1 ] называется такое число а € [0; π], косинус которого равен а:
arccos а = α, если cos α = а и 0 ≤ а ≤ π (1).
Например, arccos √3/2 = π/6, так как cos π/6 = √3/2 и 0 ≤ π/6 ≤ π;
arccos (-√3/2) = 5π/6, так как cos 5π/6 = -√3/2 и 0 ≤ 5π/6 ≤ π.
Аналогично тому, как это сделано в процессе решения задач 1 и 2, можно показать, что все корни уравнения cos x = а, где |а| ≤ 1, выражаются формулой
х = +/-arccos а + 2 πn, n € Z (2).
Задача 3.
Решить уравнение cos x = -0,75.
Решение.
По формуле (2) находим, х = +/-arccos (-0,75) + 2 πn, n € Z.
Значение arcos (-0,75) можно приближенно найти на рисунке, измерив угол при помощи транспортира. Приближенные значения арккосинуса также можно находить с помощью специальных таблиц (таблицы Брадиса) или микрокалькулятора. Например, значение arccos (-0,75) можно вычислить на микрокалькуляторе, получив приблизительное значение 2,4188583.
Ответ: arccos (-0,75) ≈ 139°.
Задача 4.
Решить уравнение (4cos x – 1)(2cos 2x + 1) = 0.
Решение.
1) 4cos x – 1 = 0, cos x = 1/4, х = +/-arcos 1/4 + 2 πn, n € Z.
2) 2cos 2x + 1 = 0, cos 2x = -1/2, 2х = +/-2π/3 + 2 πn, х = +/-π/3 + πn, n € Z.
Ответ. х = +/-arcos 1/4 + 2 πn, х = +/-π/3 + πn.
Можно доказать, что для любого а € [-1; 1] справедлива формула arccos (-а) = π – arccos а (3).
Эта формула позволяет выражать значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел. Например:
arccos (-1/2) = π – arccos 1/2 = π – π/3 = 2π/3;
arccos (-√2/2) = π – arсcos √2/2 = π – π/4 = 3π/4
из формулы (2) следует, что корни уравнения, cos x = а при а = 0, а = 1 и а = -1 можно находить по более простым формулам:
cos х = 0 х = π/2 + πn, n € Z (4)
cos х = 1 х = 2πn, n € Z (5)
cos х = -1 х = π + 2πn, n € Z (6).
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение тригонометрических уравнений
Модульный урок в 10 классе
Тема: «Решение тригонометрических уравнений»
Модульная педагогическая технология конструируется на основе ряда целей. Важнейшая из них – создание комфортного темпа работы для каждого ученика. Каждый ученик получает шанс определить свои возможности в учении и приспособиться к тем уровням изучения материала, которые предложены учителем.
Самым главным отличием технологии является применение принципа планирования совместной деятельности учителя и ученика.
Сначала определяются цели для учащегося, т.е. устанавливается, кто хочет знать не более того, что требуется государственным стандартом, а кто готов заниматься больше, поскольку планирует поступить в институт или просто хочет получить высокую оценку.
После того как учащиеся определились со своими целями, учитель выстраивает свое целеполагание, определяя содержание и объем педагогической помощи учащимся.
Исходя из целей проектируется итоговая диагностика. Она создается с учетом уровневой дифференциации, что позволяет учащимся осознанно определять то минимум знаний, который необходим для получения оценки «3».
На основании целеполагания и планируемой итоговой диагностики, отбирается предметное содержание (объяснение и задания из учебника, из дидактических материалов и т. д.).
На основе отобранного содержания выстраивается логика изучения темы (поурочное планирование), определяются время и место промежуточной и итоговой диагностик и учебной коррекции. Для каждого урока определяются микроцели учащихся и приемы обратной связи; создаются опорные конспекты для учащихся и задания к уроку.
В результате описанного процесса учитель создает:
- логическую структуру уроков с промежуточной диагностикой;
- разноуровневые материалы для диагностики знаний учащихся;
- дидактический материал ко всем урокам.
Модульная педагогическая технология помогает осуществлять индивидуальный подход к учащимся, включать каждого в осознанную учебную деятельность, мотивировать ее, формировать навыки самообучения и самоорганизации, обеспечивая тем самым постепенный переход от пассивно воспринимающей позиции ученика к его сотрудничеству с учителем.
Цели изучения этого модуля распределяются по трем уровням: I уровень – самый общий, т.е. знаниями этого уровня должны овладеть все учащиеся, II уровень включает все, что достигнуто на I уровне, но в более сложном виде, а III уровень – все, что достигнуто на I и на II уровнях, но теперь должно применяться в нестандартных ситуациях.
В результате овладения содержанием модуля учащиеся должны уметь:
I уровень — решать простейшие тригонометрические уравнения; решать тригонометрические уравнения по заданному алгоритму;
II уровень — Решать тригонометрические уравнения, самостоятельно выбирая метод решения;
III уровень — применять полученные знания в нестандартной ситуации.
Работа учащихся состоит из нескольких этапов, так называемых учебных элементов. Учебные элементы № 1 – 4 соответствуют I уровню подготовки, № 5 обеспечивает II уровень, № 6 – III уровень подготовки. Каждый учебный элемент содержит или указания учителя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, или ссылки на то, где в учебнике можно найти нужные пояснения, а также список заданий. Индивидуальный оценочный лист приведен ниже.
Оценочный лист учащегося
|
Фамилия |
|||
|
Имя |
|||
|
Учебные элементы |
Количество баллов за основные задания |
|
Общее количество баллов за этап |
|
№1 |
|
|
|
|
№2 |
|
|
|
|
№3 |
|
|
|
|
№4 |
|
|
|
|
№5 |
|
|
|
|
№6 |
|
|
|
|
Итоговое количество баллов |
(n) |
||
|
Оценка |
|
||
Прочитав указания учителя, ученик выполняет самостоятельные работы, которые включены в учебный элемент, и проверяет их по эталонам решений.
Эталон учитель демонстрирует ученику, когда тот объявляет о завершении самостоятельной работы. Ученик сравнивает свои ответы с эталонными и исправляет ошибки. Если он получил менее указанного в инструкции количества баллов, то должен набрать дополнительные баллы в корректирующих заданиях. Для этого ученик решает задания другого варианта, которые аналогичны тем, где он допустил ошибку. Оценка за весь модуль зависит от суммы n набранных баллов по всем учебным элементам. Если n ³ 32, то ученик получает «5», при 27 £ n £ 31 – оценка «4», при 21£ n £ 26 – оценка «3», при n £ 21 ученик получает «2».
Приведу теперь материалы, предлагаемые ученику в каждом учебном элементе.
Учебный элемент №1
Ц е л ь: Закрепить решение простейших тригонометрических уравнений.
Указания учителя
Вспомните основные правила решения тригонометрических уравнений.
Выполните письменно самостоятельную работу.
Задания самостоятельной работы (на 10 мин)
Решите уравнения (по вариантам по 7 уравнений) Каждое оценивается в 1 балл.
I вариант
cosx=1/2
sinx=-√3/2
tgx=1
cos(x+Π/3)=0
2cosx=1
3tgx=0
sin4x=1
II вариант
sinx=-1/2
cosx=√3/2
ctgx=-1
sin(x-Π/3)=0
4sinx=2
cos4x=0
5tgx=0
Список правильных ответов и критерии оценивания ученик получает от учителя. Учащийся исправляет ошибки и проставляет число заработанных баллов в свой оценочный лист. Если он набрал 6баллов или больше, то переходит к следующему учебному элементу. Если же набрано меньше 6 баллов, то следует прорешать задания другого варианта, аналогичные тем, в которых была допущена ошибка, и поставить набранные баллы в графу «Корректирующие задания».
Учебный элемент №2
Ц е л ь: закрепить умения решать тригонометрические уравнения методом сведения к квадратному.
Указания учителя
Прочитайте внимательно данные ниже пояснения.
Выполните самостоятельные работы.
Метод сведения к квадратному уравнению состоит в том, что, пользуясь изученными формулами ( они собраны в таблицу, которая вывешена в классе), надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x ) или комбинацию функций обозначить через у, получив при этом квадратное уравнение относительно у.
Пример. Решить уравнение 4 – cos2x = 4 sin x.
Р е ш е н и е. Вместо cos2x подставим тождественное ему выражение 1 – sin2x . Тогда исходное уравнение примет вид
4 – (1 –sin2x) = 4 sin x?
3 + sin2x =4 sin x
sin2x – 4 sin x + 3 = 0.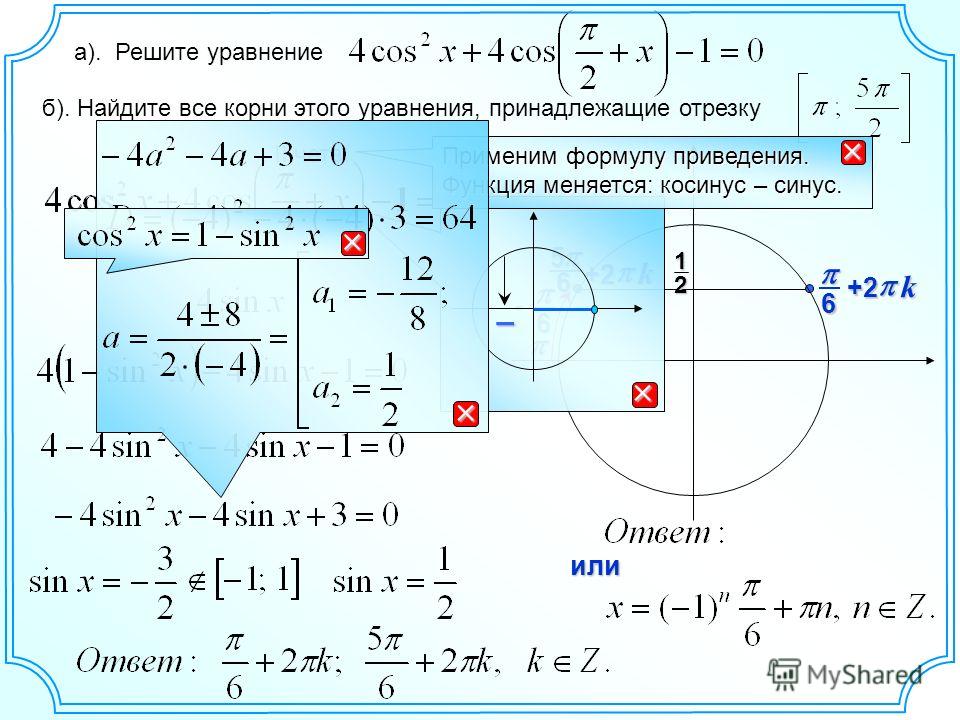
Если положить y = sin x, получим квадратное уравнение y2 – 4y + 3 = 0. Оно имеет корни 1 и 3. Значит, исходное уравнение равносильно совокупности уравнений
sin x = 1 или sin x = 3.
Уравнение sin x = 1 имеет решение
Уравнение sin x = 3 решений не имеет.
О т в е т:
Задания самостоятельной работы (на 10 мин)
Решите уравнения
I вариант
tg2 x – 3tg x + 2 = 0 (2 балла),
2cos2 x + 5sin x – 4 =0 (3 балла),
(3 балла).
II вариант
2+ cos2 x — 3 cos x = 0 (2 балла),
4 – 5 cos x – 2 sin2 x = 0 (3 балла),
(3 балла).
Указания учителя
Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, если они есть, поставьте количество баллов в оценочные листы.
Если вы набрали 5 баллов, то переходите к следующему этапу, если же меньше, то решайте задание другого варианта, аналогичное тому, в котором ошиблись.
Учебный элемент №3
Ц е л ь: закрепить навык решения тригонометрических уравнений методом разложения на множители.
Указания учителя
Внимательно прочитайте данные ниже пояснения и выполните задания.
Метод разложения на множители
Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит произведение нескольких множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, исходное уравнение можно представить в виде совокупности более простых уравнений.
К сожалению, нельзя указать единого способа разложения на множители любого выражения. Одними из самых популярных являются способы вынесения за скобки общего множителя, группировки, применения формул сокращенного умножения.
Пример. Решите уравнение 2 sin3 x – cos 2x – sin x = 0 .
Р е ш е н и е. Сначала сгруппируем первый член с третьим, а cos 2x представим в виде cos2 x – sin2 x. Получим
(2sin3 x- sin x) –(cos2 x- sin2 x) = 0
Из выражения, стоящего в первых скобках, вынесем sin x, а в выражении, стоящем во вторых скобках, вместо cos2 x запишем 1 – sin2x.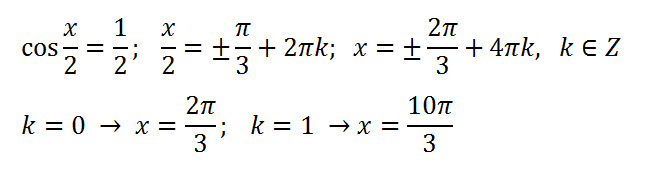
Уравнение примет вид
sin x (2sin2 x – 1) – (1 – 2sin2 x) = 0.
Выполним дальнейшие тождественные преобразования
sin x (2sin2 x – 1)+ (2sin2 x – 1) = 0,
(2sin2 x – 1)×(sin x + 1) = 0.
Отсюда следует, что исходное уравнение равносильно совокупности уравнений
2sin2 x – 1= 0 или sin x + 1= 0
Отсюда . Тогда
или sin x = -1.
О т в е т:
Задания самостоятельной работы (на 10 мин)
Решите уравнения
I вариант
sin2 x – sin x = 0 (2 балла),
3cos x + 2sin 2x = 0 (3 балла).
II вариант
ctg2 x – 4ctg x = 0 (2 балла),
5sin 2x – 2sin x = 0 (3 балла).
Указания учителя
Если набрано 5 баллов, то переходите к следующему элементу. Если меньше, то прорешайте соответствующее задание другого варианта.
Учебный элемент №4
Ц е л ь: закрепить навык решения однородных уравнений.
Указания учителя
Прочитайте пояснения и выполните задания.
Однородными называются уравнения вида
a sin x + b cos x = 0,
a sin2 x+ b sin x cos x + c cos2 x = 0
и т. д. Здесь a, b, c – числа.
Покажем сначала, как решать однородное уравнение первой степени, т. е. уравнение вида
a sin x + b cos x = 0.
Пример 1. Решить уравнение 5sin x – 2cos x = 0.
Р е ш е н и е. Поделим обе части уравнения cos x на sin x или.
Но предварительно надо доказать, что это выражение никогда не обращается в нуль. Итак, предположим, что cos x = 0. Тогда 5sin x – 2× 0 = 0 Û sin x = 0. Получается, что если sin x = 0, то и cos x = 0, чего быть не может ввиду равенства sin2 x + cos2 x = 1.
Значит, можно поделить уравнение на cos x:
.
Получим уравнение 5tg x – 2 = 0. Отсюда
Аналогично решаются однородные уравнения вида
a sin2 x+ b sin x cos x + c cos2 x = 0.
Их решение начинается с того, что обе части уравнения делят на cos2 x или sin2 x.
Пример 2. 12 sin2x + 3 sin 2x – 2 cos2 x = 2.
Р е ш е н и е. Данное уравнение не является однородным. Но его можно превратить в однородное, заменив 3 sin 2x на 6 sin x cos x и число 2 на 2sin2x+2cos2x.
Приведя подобные члены, получим уравнение
10 sin2 x+ 6 sin x cos x — 4 cos2 x = 0. (*)
Теперь надо доказать, что cos x¹ 0.
Пусть cos x = 0. Подставим это значение косинуса в уравнение (*). Получим 10sin2 x = 0 Û sin x = 0, чего быть не может ввиду равенства sin2 x + cos2 x = 1.
Значит, cos x¹ 0. Тогда можно поделить обе части уравнения (*) на cos2 x. Получим 10tg2 x+ 6tg x – 4 = 0 Û tg x = -1 или . Отсюда .
Задания самостоятельной работы (на 10 мин)
Решите уравнения
I вариант
sin x – cos x = 0 (2 балла)
sin2 x – sin 2x = 3cos2 x (3 балла)
II вариант
5sin x + 6cos x = 0 (2 балла)
3sin2 x – 2sin 2x + 5cos2 x = 2 (3 балла)
Указания учителя
Если набрано 5 баллов, то можно переходить к следующему учебному элементу.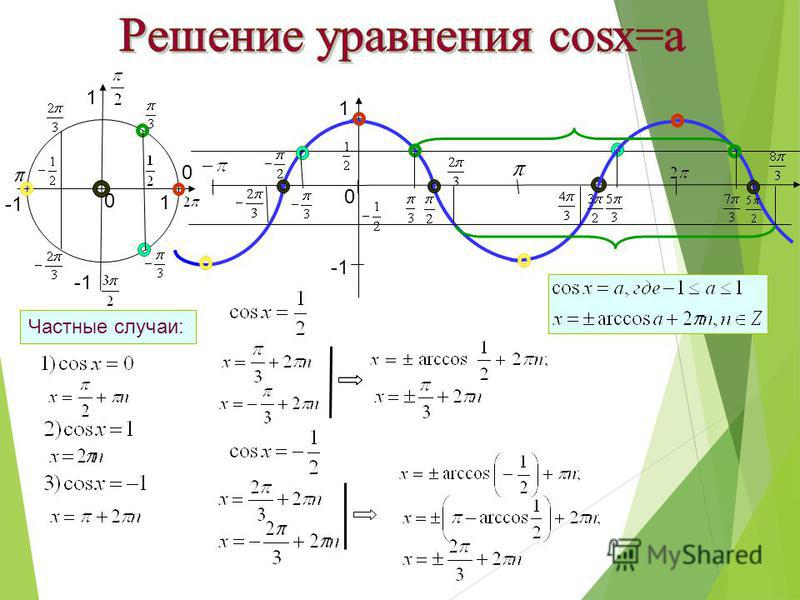
Если набрано менее 5 баллов, то нужно прорешать тот номер другого варианта, где допущена ошибка.
Учебный элемент №5
Указания учителя
Вы прошли I уровень усвоения материала. Теперь вам самостоятельно придется выбрать метод решения уравнений. Вспомните основные тригонометрические формулы.
Выполните письменно самостоятельную работу.
Задания самостоятельной работы (на 20 мин.)
Решите уравнения
I вариант
cos 2x – 5 sin x – 3 = 0 (1 балл),
sin 2x + cos 2x = 0 (1 балл),
cos2 x – cos 2x = sin x (2 балла).
sin 4x – cos 2x = 0 (2 балла),
(2 балла),
II вариант
cos 2x + 3 sin x = 2 (1 балл),
sin 2x — cos 2x = 0 (1 балл),
6 – 10 cos2 x + 4 cos 2x = sin 2x (2 балла),
cos x cos 2x = 1 (2 балла),
(2 балла).
Указания учителя
Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, если они есть. Проставьте баллы в оценочные листы.
Если набрано 5 баллов или больше, то переходите к следующему учебному элементу, если меньше, то решайте задания другого варианта аналогичные тем, в которых была допущена ошибка.
Учебный элемент №6
Указания учителя
Молодцы! Вы освоили решение уравнений II уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Задания самостоятельной работы
(Они даются в одном варианте и не ограничиваются временными рамками, так как их решают далеко не все учащиеся. А время, отводимое на эту работу, определяется ситуацией на уроке.)
- sin 6x + cos 6x = 1 – 2 sin 3x (2 балла),
- 29 – 36 sin2 (x – 2) – 36 cos (x – 2) = 0 (3 балла),
- (2 балла),
- sin 4x = 2 cos2 x – 1 (2 балла),
- sin x(sin x + cos x) = 1 (3 балла),
- (3 балла).
Указания учителя
В случае затруднений воспользуйтесь подсказками, Данными ниже.
Подсказки
- Воспользуйтесь формулой двойного угла для sin 6x, cos 6x.
- Обозначьте х – 2 = t, решите уравнение, сведя его к квадратному с помощью формулы sin2 t = 1 — cos2 t
- Сгруппируйте первое и третье слагаемые, примените разложение на множители.
- Воспользуйтесь формулой двойного угла для sin 4x, cos 4x, формулой понижения степени 2 cos2 x – 1 = cos 2x.
- Раскройте скобки, примените основное тригонометрическое тождество.
- Приведите дроби к общему знаменателю. А затем используйте основное тригонометрическое тождество sin2 x + cos2 x = 1, сведите уравнение к квадратному.
Указания учителя
Проверьте и оцените свои работы. Исправьте ошибки, если они есть, подсчитайте количество баллов. Проставьте количество баллов в оценочный лист. Оцените свои работы.
Домашнее задание
- Если вы получили оценку «4» или «5», то выполните любое задание из дополнительных глав учебника.
- Если вы получили «3» или»2», то выполните из учебника под редакцией А.Г. Мордковича №№ 18.4; 18.3; 21.24.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. |