Решение уравнений графическим способом — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Урок по теме
«Решение уравнений графическимспособом»
2. Цели данного урока
• Познакомить учащихся с графическимспособом решения уравнений
• Совершенствовать их умения и навыки в
построении графиков элементарных
функций
3. Этапы урока
12345-
Устная работа
Решение уравнений
Объяснение новой темы
Закрепление
Самостоятельная работа
4.
 Этап 1. Устная работа
Этап 1. Устная работаНа доске записаны фрагмент темы урока: «Решение уравнений…» и семь уравнений:
2х+3х+1=0
х+2х+3=0
-7х+х=0
х-9х+20=0
корень квадр-й из 5 *х=0
х-16=0
8х-14х+5=0 ученикам предлагаются следующие вопросы и задания:
1. какого типа записаны уравнения на доске?
2. какие квадратные уравнения называются полными, какие неполными?
3. Укажите среди данных квадратных уравнений : а) полные ;
б) неполные. Назовите коэффициенты каждого уравнения.
4.
Для каждого уравнения, имеющего корни, укажите их сумму и произведение.
5.
Решите те уравнения корни которых можно найти(подобрать) без вычислений.
5. 2 этап. Решение уравнений
• Далее учащимся предлагаются 4уравнения. Первые три из них ученики
решать умеют( решения записываются на
доске и в тетрадях), а четвёртое,
сводящееся к кубическому, пока нет( с его
помощью создаётся проблемная ситуация).
6. Задание 1. Решите уравнения
1.
 2х2+3х+11=0
2х2+3х+11=0решение: Д=1>0, х =-1/2 и х =-1
ответ: -1/2 и -1
2. 8х2-14х+5=0
решение: Д=9>0, х =1 ¼ и х =1/2
ответ: 1 ¼ и ½
3. х2-2/х+2=х+3/х-4
решение: одз: х не равен4 и -2, х= 2/11
4. х2 =6/х
решение: одз: х не равен 0,
х =6
как найти х ?
чтобы найти корни последнего уравнения, ученикам предлагается
рассмотреть функции у=х2 и у= 6/х и выполнить следующее задание.
7. Задание 2
• В одной координатной плоскостипостройте графики функций у= х2
и у= 6/х. Найдите абсциссы
координат точек пересечения
графиков функций.
8. 3 Этап. Объяснение темы
• После выполнения задания следует обратитьвнимание учащихся на то, что абсцисса точки
пересечения графиков есть значение
переменной х, при котором х =6/х, иначе
говоря, корень данного уравнения.
• Таким образом, при рассмотрении последнего
уравнения был применён новый способ
решения, основанный на построении графиков
функций.

• На доске дописывается тема «Решение
уравнений графическим способом»
9. Алгоритм решения уравнений графически(ученики его формулируют)
• Чтобы решить графически уравнение видаf(x)=q(x), нужно :
1) Построить в одной координатной
плоскости графики функций у =f(x) и у=q(x).
2) Найти точки пересечения этих графиков.
3) Указать абсциссу каждой из точек
пересечения.
4) Записать ответ.
• Для того, чтобы пользоваться графическим
способом решения уравнений , нужно уметь
строить графики различных функций и
«считывать» информацию с чертежа.
Преимуществом данного способа решения
уравнений является его наглядность,
возможность увидеть решение
непосредственно на рисунке. Стоит также
обратить внимание учеников на то, что при
решении уравнения графически часто
указывается приближённое значение корня,
что можно считать недостатком этого способа.
11. 4 этап. Закрепление
• Далее ученикам предлагается выполнитьследующее задание.

задание 3.
решите графически уравнение:
а) 8/х = -х+6 б) х2+2х-3=0
После выполнения задания 3 ещё раз
повторяется алгоритм решения уравнений
графическим способом.
12. 5 этап. Самостоятельная работа
• В конце урока проводится самостоятельная работа ( втрёх вариантах). Каждому ученику выдаётся листок с
заданием и рекомендациями по его выполнению:
1) Если есть необходимость, преобразуйте уравнение
таким образом, чтобы его в правой и левой частях
были функции f(x) и q(x), графики которых вы умеете
строить.
2) В одной координатной плоскости постройте графики
этих функций.
3) Найдите точки пересечения графиков.
4) В ответе запишите абсциссу каждой из точек
пересечения графиков. Если точек пересечения нет, то
…. (закончите предложение).
13. Задания к самостоятельным работам
• 1 вариантрешите графически уравнение х2+2х-3=0
ответ: х= -3 и х= 1.
• 2 вариант
решите графически уравнение х2+ 6/х =0
ответ: нет решений.

• 3 вариант
• решите графически уравнение х2 = 6 – х
ответ: х = 4.
14. рекомендации
• Проверку выполнения заданий можноосуществить, спроецировав их решения на
экран. Полезно обратить внимание учащихся
на то, что последнее уравнение ( х = 6 – х)
относится к иррациональным уравнениям,
которые изучаются в 11 классе, но уже в 8
классе несложные иррациональные уравнения
можно решить графически.
• В конце урока даётся домашнее задание.
English Русский Правила
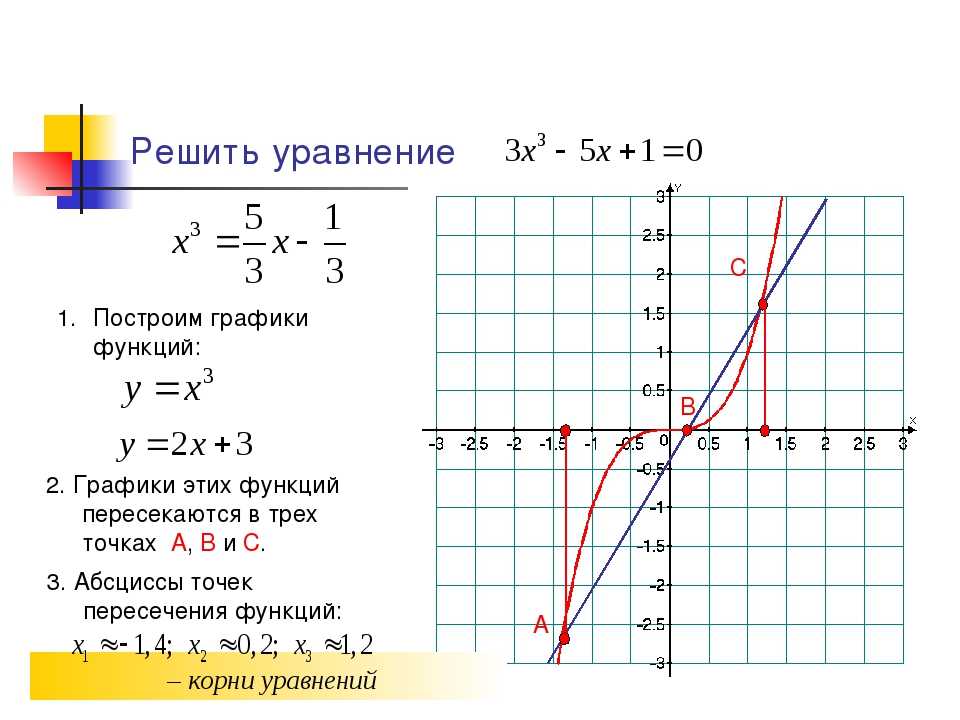
7. РЕШЕНИЕ УРАВНЕНИЙ
4×1 0,24×2 | 0,08×3 | 8; |
|
|
|
|
|
|
|
| 3×1 | x2 | 5; |
| ||||||||||||||||
3. 0,09×1 | 3×2 | 0,15×3 9; |
|
|
| 4. |
| 2×1 x2 | x3 | 0; | ||||||||||||||||||||
0,04x | 0,08x | 2 | 4x | 20. |
|
|
|
|
|
|
|
| 2x | x | 2 | 4x | 15. | |||||||||||||
|
|
|
|
| 1 |
|
| 3 |
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
| 3 |
| ||||
II. | ||||||||||||||||||||||||||||||
методом Крамера, | графическим способом и с помощью функции | |||||||||||||||||||||||||||||
solve: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. 2x y 4; |
|
|
| 3. 2x 3y 1; |
|
|
|
|
|
| ||||||||||||||||||||
3x 2y 3. |
|
|
|
| x 2y 4. |
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
и | 7x | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
С5x 2y 10; |
|
| 2y 2; |
|
|
|
|
|
| |||||||||||||||||||||
2. |
|
|
|
|
|
|
|
|
| 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
2x y 7. |
|
|
| x 4y 1. |
|
|
|
|
|
| ||||||||||||||||||||
III. Реш ть с стемы нелинейных уравнений графическим спосо- | ||||||||||||||||||||||||||||||
бом с помощью функции solve: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
2xy 16; |
|
|
| 2x |
|
| y 3; |
|
|
|
|
|
| |||||||||||||||||
1. |
| 2 y 8. |
|
|
| 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
x |
|
|
| x 2y 4. |
|
|
|
|
|
| ||||||||||||||||||||
| x | 3 | 2y 1; |
|
|
|
|
|
|
| 3 | 2x | 2 | y 5; |
|
| ||||||||||||||
2. |
|
|
|
|
| 3x |
|
|
|
|
|
| ||||||||||||||||||
| 2 |
|
|
|
|
|
|
| 4. |
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
| 3y 2. |
|
|
|
|
|
|
|
|
| 3x y 4. |
|
| ||||||||||||||||
x |
|
|
|
| 2x |
|
|
|
| |||||||||||||||||||||
IV. Решить системы нелинейных уравнений с помощью функ- | ||||||||||||||||||||||||||||||
ции solve: бА |
|
| ||||||||||||||||||||||||||||
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
| 2y 1; |
|
|
|
|
| x y |
| x y 8; |
|
| |||||||||||||||||||
x |
|
|
|
| 3. |
|
|
|
|
|
| |||||||||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
3x 3y2 2. |
|
|
| 4 |
| x | 3 | x | 2 | y xy | 2 | y | 3 | 12. | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uvx | 2 | 8; |
|
|
| Д3 2 | ||||||||||||||||||||||||
|
|
|
| x |
| 2x | 3y | z 2; |
| |||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
| 4. 2×2 |
| x y2 z2 | 1; |
| ||||||||||||||||||||||
x | 2 | wu 12; |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3z 1. |
|
|
| ||||||||||
|
|
|
| y3 2z2 |
|
|
| |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| И | ||||||
u v w x 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
Для решения уравнений вида f(x)=0 в MATLAB существует несколько способов.
35
| 7.1. Графический способ решения уравнений | |
Для решения уравнений графическим способом нужно: | ||
1. | Объявить символьные переменные (аргумент функции и саму | |
функцию). | ||
С | ||
2. | Задать функцию. | |
3. | Построить график функции. | |
4. | Добав ть на график линии сетки. | |
5. >> grid В результате получим следующийДграфик (рис. 11). 2×2–3x–1 И x Рис. 11. График функции f(x) 36 Используя кнопку Zoom In на панели инструментов и масштабируя график, можно достичь требуемой точности в определении корней уравнения. В результате получим приближенные значения корней уравне- ния: x1=–0,28; x2=1,78. СДля решен я уравнений, заданных символьными переменными, используется встроенная функция solve, позволяющая найти решение в анал ческой форме, и функция vpa для численной оценки с кон- 7.2. Решение уравнений с помощью функции solveтролируемой 1. ОбъявбАть с мвольные переменные (аргумент функции и саму точностью найденных решений. Для решен я уравнения вида f(x)=0 с помощью функции solve нужно: функц ю). 2. Задать функц ю. 3. Найти решен е в аналитической форме с помощью функции solve(функция, аргумент). 4. Вывести результат с заданной точностью с помощью функции vpa(переменная, число знаков). | ||
>> r=solve(f,x) |
| |
>> vpa(r,5) |
| |
В результате получим x1=–0,2808; x2=1,7808.
7.3. Нахождение корней полинома
Если функция f(x) является полиномом (многочленом n-й степени), то найти корни уравнения f(x)=0 можно с помощью функции roots. Для этого нужно:
37
1.Задать вектор коэффициентов полинома (начиная со старшего).
2.Вычислить корни с помощью функции roots(вектор).
Пример |
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
С |
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти корни полинома 2×2–3x–1=0. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Порядок ввода: |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получим |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
>> a=[2 –3 –1]; |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
>> x=roots(a) |
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
В результате |
|
| x1=–0,2808; x2=1,7808. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| бА | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 7.4. Нахождение минимума функции | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Нахожден е м нимума функции одной переменной на отрез- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ке [a; b]: |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
х=fminbnd(‘f ‘, a, b) |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример |
|
|
| Д | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти минимум функции на отрезке [0,2; 1]: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f (x) |
| 1 |
|
| 1 | 6. В результате получим x=0,6412. САМОСТОЯТЕЛЬН Я Р БОТА № 6 I. Решить уравнения графически и с помощью функции solve: 1) x 5 2 x 1 3; 2) 2x 1 1 0; Д 5)x3 2 x 1. И II. Решить уравнения графически, с помощью функции solve и с помощью функции roots:1) 2x 4)10x3x 3x 2×1; 0,5 0;3) ln(x 2) 2;
39 Графическое решение пары линейных уравнений | Решенные примерыLearnPracticeDownload Когда математические выражения переменных и констант вместе с математическими операциями образуют уравнение высшей степени один, оно называется линейным уравнением. Линейное уравнение — это алгебраическое уравнение между переменными, которое дает прямую линию при нанесении на график. Линейное уравнение одной переменной имеет вид ax + b = 0, где x — переменная.
Решение пары линейных уравнений графически Каждое линейное уравнение состоит из переменных. Решение уравнений зависит от положения линий. Обсудим решения, полученные в линейных уравнениях с двумя переменными. Типы решений
Посмотрите на таблицу ниже, в которой показаны условия для данных уравнений.
Как решить пару линейных уравнений графически? Решение линейного уравнения на графике зависит от переменных. Если это пара линейных уравнений с двумя переменными, то они представляются двумя линиями, а если это одна переменная, то они представляются одной линией. Даны уравнения:
Похожие статьи о графическом решении пары линейных уравнений
Давайте рассмотрим три разных примера, чтобы понять тему графического решения пары линейных уравнений в деталях с практическими иллюстрациями. Решенные примеры графического решения пары линейных уравнений
перейти к слайдуперейти к слайдуперейти к слайду Есть вопросы по основным математическим понятиям? Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду
Часто задаваемые вопросы о графическом решении пары линейных уравненийКак решить линейное уравнение графически? Для графического решения линейного уравнения необходимо найти не менее двух решений соответствующих уравнений. Каким будет решение двух пар линейных уравнений при графическом решении уравнений? Когда мы решаем две пары линейных уравнений графически, после геометрического построения точек нам нужно наблюдать за рисунком линий. В соответствии с уравнениями, основанными на их представлениях, может быть три соответствующих решения. Оно может быть последовательным, зависимым или непоследовательным. Если две прямые пересекаются в одной и той же точке, то эта точка дает единственное решение для обоих уравнений. Если две прямые совпадают, то в этом случае решений бесконечно много. Если две прямые параллельны, то в этом случае решения нет. Как решить линейное уравнение с двумя переменными?Для решения линейного уравнения с двумя переменными можно использовать множество методов. Ниже перечислены утвержденные математические методы решения уравнений:
Как вы описываете линейные уравнения?Линейные уравнения — это алгебраические уравнения первого порядка, имеющие вид y = mx + b (с двумя переменными). Как построить линейное уравнение с двумя переменными?
Скачать БЕСПЛАТНЫЕ учебные материалы Скачать рабочие листы для пары линейных уравнений с 2 переменными рабочие листы по графическому решению пары линейных уравнений Рабочие листы по математике и визуальный учебный план Графическое решение квадратных уравнений — GCSE Maths Revision GuideВведение Что такое корни квадратного? Как решать квадратные уравнения графически Рабочий лист квадратичных графиков Распространенные заблуждения Практика решения квадратных уравнений графически вопросы Решение квадратных уравнений графически вопросы GCSE Контрольный список обучения Следующие уроки Все еще застряли? Индивидуальные занятия по математике, созданные для успеха KS4 Еженедельные онлайн-уроки повторения математики GCSE теперь доступны Узнать больше Введение Что такое корни квадратного? Как решать квадратные уравнения графически Рабочий лист квадратичных графиков Распространенные заблуждения Практика решения квадратных уравнений графически вопросы Решение квадратных уравнений графически вопросы GCSE Контрольный список обучения Следующие уроки Все еще застряли? Здесь мы узнаем о графическом решении квадратных уравнений в том числе о том, как найти корни квадратной функции по графику, как использовать этот метод для решения любого квадратного уравнения, рисуя график, а затем как решить квадратное уравнение из графика, который уже нарисован для вас. На этой странице мы рассмотрим поиск корней, а затем поиск других решений с помощью графа. Как решать квадратные уравнения графическиЧтобы найти решения квадратного уравнения с помощью графика:
Объясните, как решать квадратные уравнения графическиРабочий лист с квадратичными графикамиПолучите бесплатный рабочий лист с квадратичными графиками, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы. СКАЧАТЬ БЕСПЛАТНО ИксРабочий лист с квадратичными графиками Получите бесплатный рабочий лист с квадратичными графиками, содержащий более 20 вопросов и ответов. СКАЧАТЬ БЕСПЛАТНО Связанные уроки по квадратичным графикамГрафическое решение квадратных уравнений является частью нашей серии уроков для поддержки пересмотра типов графиков . Возможно, вам будет полезно начать с основного урока по квадратичным графикам , чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства, приведенные ниже, для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||







 vx2w 24;
vx2w 24;
 2–3*x–1; >> ezplot(f)
2–3*x–1; >> ezplot(f) 2–3*x–1;
2–3*x–1;
 x-1′,[0,3])
x-1′,[0,3])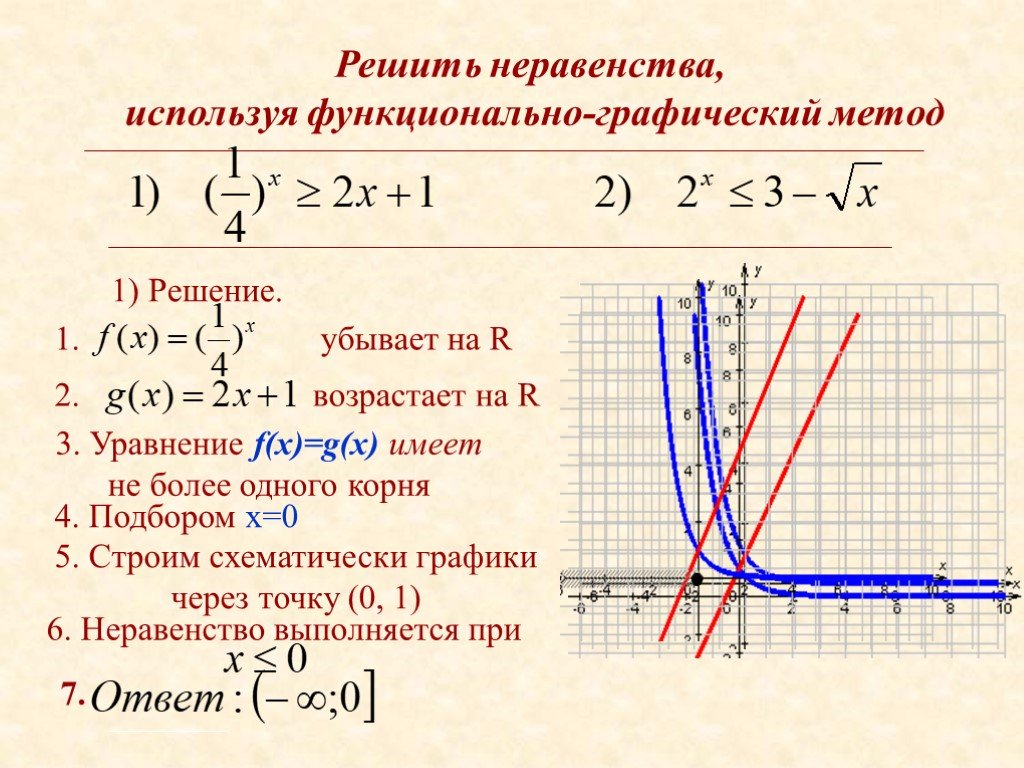 Линейные уравнения двух переменных имеют вид ax + by + c = 0, где x и y — две переменные, а c — константа. Пара линейных уравнений может быть решена и представлена двумя основными методами: графическим методом и алгебраическим методом. В этом мини-уроке мы рассмотрим решение системы двух линейных уравнений с использованием графического метода с помощью решенных примеров, листов линейных уравнений и интерактивных вопросов.
Линейные уравнения двух переменных имеют вид ax + by + c = 0, где x и y — две переменные, а c — константа. Пара линейных уравнений может быть решена и представлена двумя основными методами: графическим методом и алгебраическим методом. В этом мини-уроке мы рассмотрим решение системы двух линейных уравнений с использованием графического метода с помощью решенных примеров, листов линейных уравнений и интерактивных вопросов. Линейные уравнения имеют первый порядок и могут включать одну или две переменные. Когда дело доходит до решения линейных уравнений с использованием графического метода, основной подход состоит в том, чтобы представить их в виде прямых линий на графике и найти точки пересечения, если таковые имеются. Мы можем легко получить как минимум два решения, подставив значения x, найдя точки пересечения x и y и нанеся их геометрически на график. Давайте посмотрим на стандартную форму пары линейных уравнений здесь.
Линейные уравнения имеют первый порядок и могут включать одну или две переменные. Когда дело доходит до решения линейных уравнений с использованием графического метода, основной подход состоит в том, чтобы представить их в виде прямых линий на графике и найти точки пересечения, если таковые имеются. Мы можем легко получить как минимум два решения, подставив значения x, найдя точки пересечения x и y и нанеся их геометрически на график. Давайте посмотрим на стандартную форму пары линейных уравнений здесь. 
 Мы знаем, что решение уравнений зависит от положения линий. Давайте рассмотрим следующие шаги, чтобы решить пару линейных уравнений графически.
Мы знаем, что решение уравнений зависит от положения линий. Давайте рассмотрим следующие шаги, чтобы решить пару линейных уравнений графически.


 Они пересекаются в одной точке. Здесь на графике ось X обозначает переменные аттракционы на американских горках, а ось Y – катание на качелях-драконах.
Они пересекаются в одной точке. Здесь на графике ось X обозначает переменные аттракционы на американских горках, а ось Y – катание на качелях-драконах.
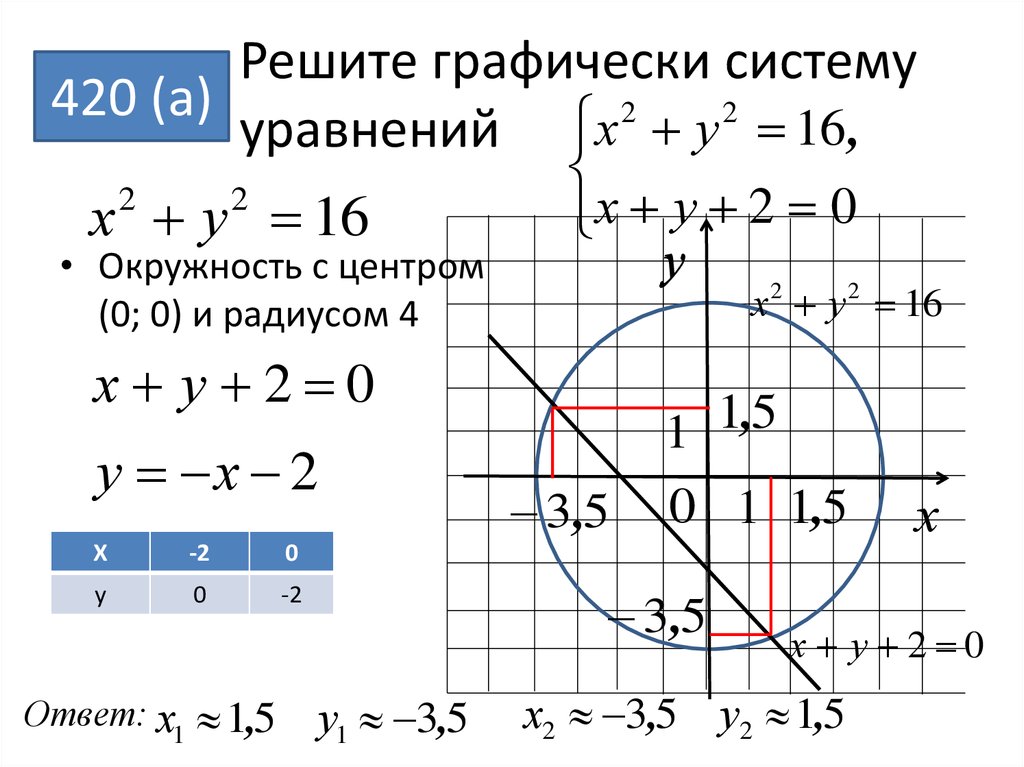 Это означает, что если две линии совпадают, то существует бесконечно много решений. Каждая точка на прямой становится решением.
Это означает, что если две линии совпадают, то существует бесконечно много решений. Каждая точка на прямой становится решением. Наблюдайте за образцом двух линий, сформированных для двух уравнений. Чтобы представить уравнения графически, у нас есть 4 соответствующие точки S (0, 2) и T (4, 0), нанесем эти точки на
Наблюдайте за образцом двух линий, сформированных для двух уравнений. Чтобы представить уравнения графически, у нас есть 4 соответствующие точки S (0, 2) и T (4, 0), нанесем эти точки на  После нанесения точек графически наблюдайте за рисунком линий, чтобы сделать вывод, является ли он последовательным, зависимым или противоречивым. Если две прямые пересекаются в одной и той же точке, то эта точка дает единственное решение для обоих уравнений. Если две прямые совпадают, то в этом случае решений бесконечно много. Если две прямые параллельны, то в этом случае решения нет.
После нанесения точек графически наблюдайте за рисунком линий, чтобы сделать вывод, является ли он последовательным, зависимым или противоречивым. Если две прямые пересекаются в одной и той же точке, то эта точка дает единственное решение для обоих уравнений. Если две прямые совпадают, то в этом случае решений бесконечно много. Если две прямые параллельны, то в этом случае решения нет.
 2+bx+c=0 , правая часть которого равна нулю, вы находите корни.
2+bx+c=0 , правая часть которого равна нулю, вы находите корни. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.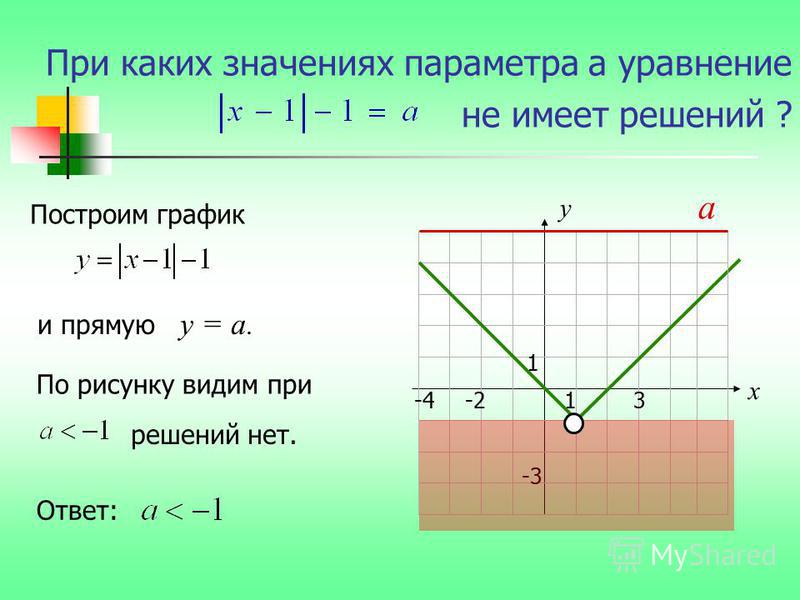 {2}=4x с точностью до одного десятичного знака.
{2}=4x с точностью до одного десятичного знака.
 92 и член +3x в обоих, но нам нужно изменить порядок так, чтобы постоянный член также был таким же, а левая часть уравнения соответствовала правой части функции.
92 и член +3x в обоих, но нам нужно изменить порядок так, чтобы постоянный член также был таким же, а левая часть уравнения соответствовала правой части функции. Чтобы решить когда вам дали график , перестройте так, чтобы одна часть уравнения соответствовала изображенной на графике функции.
Чтобы решить когда вам дали график , перестройте так, чтобы одна часть уравнения соответствовала изображенной на графике функции.  Приведите решения с точностью до 1 знака после запятой. 9{2}=3 , исправить до 1 десятичного знака.
Приведите решения с точностью до 1 знака после запятой. 9{2}=3 , исправить до 1 десятичного знака.