Параметры. Решение уравнений с параметрами.
Главная → Публикации → Математика → Факультативы → 8 класс → Параметры. Решение уравнений с параметрами.
Решение задач с параметрами является одним из самых трудных разделов школьной математики и требует большого количества времени на их изучение. При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить логические построения, аккуратность и внимательность для того, чтобы не потерять решение и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры.
Из опыта работы в выпускных классах, видно, что учащиеся, владеющие методами их решения, обычно успешно справляются и с другими задачами. Но в то же время задачи с параметрами, включенные в содержание ЕГЭ по математике, очень часто оказываются не по силам учащимся.
Поэтому наша цель – научить учащихся методам решения задач с параметром, помочь преодолеть психологический барьер, который обусловлен противоречивыми характеристиками параметра.
Содержимое публикации
Муниципальное автономное общеобразовательное учреждение гимназия №40 им. Ю.А. Гагарина г. Калининграда
Программа курса внеурочной деятельности
«Параметры. Решение задач с параметром»
для учащихся 7-8 класса
Малая Алла Александровна
учитель высшей категории
Г. Калининград
2020
Содержание.
Введение
Понятие уравнения с параметром
Линейные уравнения с параметрами
Линейные уравнения и приводимые к ним уравнения с параметрами
Графический метод решения уравнений c параметром
Системы линейных уравнений
Рациональные уравнения с параметрами
Квадратные уравнения с параметрами
Задачи на применение теорем Виета
Иррациональные уравнения с параметрами
Решение различных уравнений с параметрами.
Введение Решение задач с параметрами является одним из самых трудных разделов школьной математики и требует большого количества времени на их изучение. При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить логические построения, аккуратность и внимательность для того, чтобы не потерять решение и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры.
При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить логические построения, аккуратность и внимательность для того, чтобы не потерять решение и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры.
Из опыта работы в выпускных классах, видно, что учащиеся, владеющие методами их решения, обычно успешно справляются и с другими задачами. Но в то же время задачи с параметрами, включенные в содержание ЕГЭ по математике, очень часто оказываются не по силам учащимся.
Поэтому наша цель – научить учащихся методам решения задач с параметром, помочь преодолеть психологический барьер, который обусловлен противоречивыми характеристиками параметра.
Формировать умение учащихся видеть в выражении число, обозначенное буквой, необходимо на начальных ступенях обучения математике, а так же в 5-6 классах на простейших задачах — сравнение чисел, корень уравнения.
Продолжить работу по решению простейших линейных уравнений с параметрами и приводимых к ним можно в 7 классе при изучении темы: «Решение линейных уравнений». Задачи с параметрами можно и нужно использовать, уже начиная с линейных и квадратных уравнений и неравенств (7 – 9 классы).
Понятие уравнения с параметром
С параметрами учащиеся встречаются при введении некоторых понятий – функция прямая пропорциональность: y = kx ; линейная функция y=kx +b, где k — это параметр; а так же линейные и квадратные уравнения. К задачам с параметрами можно отнести задачи, например, поиск решений линейных и квадратных уравнений в общем виде, исследование количества их корней в зависимости от значений параметра.
Основное, что нужно усвоить при первом знакомстве с параметром – необходимость осторожного обращения с фиксированным, но неизвестным числом. Необходимость осторожного обращения с параметром хорошо видна на таких примерах, где замена параметра числом делает замену более простой. К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение и неравенство и т.д.
К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение и неравенство и т.д.
Рассмотрим примеры:
Сравнить: —a и 3a
Решение:
Если а 0, то -а 3а
Если а = 0, то -а = 3а
Если а, то -а 3а
Линейные уравнения и приводимые к ним уравнения с параметрами.
Линейным уравнением называется уравнение вида
2) Если
10. При каком значении
Точка В (5;) принадлежат прямой y = kx, значит 5к=
Найдем к, к= 3/2 и подставим , = 7,5
Ответ: = 7,5
5. Системы линейных уравнений
1. Подберите такие значения a и b, при которых система уравнений
имеет бесконечно много решений
единственное решение
не имеет решений
Решение:
1) a = -2 b = -6
2) a = 3 b = 7
3) a = -2 b =-12
2. При каком значении а имеет решение система уравнений:
Решение:
Решим систему 2-х уравнений
Умножим (1) уравнение на3, (2) уравнение на (-7)
Решим методом алгебраического сложения, получаем
= 63 — 140
-11 = — 77
= 7
Найдем ,
Подставим найденные значения в третье уравнение
Ответ: при
3. Графики функций y = ax + 12 и y = (3 – a)x + a пересекаются в точке с абсциссой 2. Найдите ординату точки пересечения.
Графики функций y = ax + 12 и y = (3 – a)x + a пересекаются в точке с абсциссой 2. Найдите ординату точки пересечения.
Решение:
получаем y = 2a + 12 и y = (3 – a)2 + a
получим
2a + 12 = (3 – a)2 + a
2а+ 12 = 6 – 2а + а
3а = -6
а = — 2
:
У = -2 * 2 + 12 = 8
Ответ: у = 8
Рациональные уравнения с параметром
Уравнение, левая и правая части которого являются рациональными выражениями, называются рациональными. Процесс решения заключается в построении алгоритма, позволяющего для любого значения параметра – найти множество корней уравнения.
Пример 1. Решите уравнение
Решение:
Приводим подобные и получаем
Уравнение равносильно системе ;
;
Исследуем на наличие решений:
1) если a =1 , то уравнение системы имеет вид 0x = 0 , с учетом ОДЗ, решением уравнения является любое число, кроме -2
2) если a1 , то получаем ;
Ответ: если a = 1 , то корнем уравнения является любое число, кроме -2; если a1, то x=1.
Мы видим, что при решении рационального уравнения с параметром, используем тот же алгоритм решения уравнения, как если бы вместо параметра было фиксированное число.
Пример 2. При каких значениях параметра a уравнение имеет единственное решение?
Решение:
Уравнение равносильно системе ;
;
1) При любом a уравнение имеет корень . Корень будет единственный, если или не удовлетворяет условию
Ответ: или
Пример 3. Для каждого значения параметра решите уравнение?
Решение:
1) если , то , то
2) если , то , то
3) если ; 1, то
Ответ:если, то если , то если ; 1, то
Примеры для самостоятельного решения:
4. Для каждого параметра решите уравнение:
1) ; 2) ; 3)
5. При каких значениях параметра уравнение имеет единственное решение
1) ; 2) ; 3)
7. Квадратные уравнения с параметрами
Квадратное уравнение
= 0Алгоритм решения уравнений:
Если a = 0, то получается линейное уравнениеbх + c=0.
Если a ≠ 0 и дискриминант уравнения D = b² – 4ac< 0, то уравнение не имеет действительных решений.
Если, a ≠ 0 и D = 0, то уравнение имеет единственное решение х =
Если a ≠ 0 и D > 0, то уравнение имеет два различных корня .
Пример 1. При каких значениях параметра a уравнение имеет единственный корень?
Решение: Уравнение имеет один корень, если его дискриминант равен нулю.
D = – 144
–144 = 0
Ответ: при
Пример 2. При каких значениях параметра b уравнение имеет два корня?
Решение: Уравнение имеет два корня, если его дискриминант больше нулю.
D = 9 – 4b
9 – 4b
– 4b
b
Ответ:Уравнение имеет два корня при b.
Пример 3. Для каждого параметра b решите уравнение:
Ответ: или = 4
Пример 4. При каких значениях параметра a сумма корней уравнения
равна 3?
Решение: По обратной т. Виета =3
Виета =3
+ — 3 = 0, отсюда = 1
Ответ: при = 1
Пример 5. При каких значениях параметра уравнение имеет единственный корень
Решение:
1) если , тогда получаем 15 = 0, решений нет;
2) если ≠ 0, ≠ 4, получаем квадратное уравнение. Уравнение имеет один корень, если дискриминант равен 0.
или Но при уравнение не имеет корней.
Ответ: = 19
Пример 6. При всех значениях параметра a решить уравнение
1) Решим квадратное уравнение по теореме обратной т. Виета, получаемили = 1;
2) уравнение равносильно системе
Исследуем на наличие корней: если а = 1, то ; если а = 7, то если а 1 и а 7, то .
Ответ: если а = 1, то ; если а = 7, то если а 1 и а 7, то .
Пример 7. При каких значениях параметра a уравнение имеет единственный корень?
Решение:
1)приполучаем 1 + 3 — + ;- 6 = 0,
если , то = 1 или , но так как по условию , то .
2) при получаем — + ;- 6 = 0,
если , получаем , = 3 или , но так как по условию , то – один корень;
3)если
ПолучаемD = , отсюда = 3,5.
Ответ: при = 3,5; 3; 4.
Примеры для самостоятельного решения:
Пример 8. При всех значениях параметра a решить уравнение
Пример 9. При каких значениях параметра a
Пример 10. При каких значениях параметра a уравнение имеет единственный корень
Заканчивая курс решения уравнений с параметрами для учащихся 7-8 классов, решим уравнение с модулем.
(ЕГЭ) Найдите все значения
Уравнение имеет ровно 3 корня при а = 1
Ответ: при а = 1
Подведение итога:
После того, как мои выпускники в 10-11 классах в рамках внеурочной деятельности изучали различные методы решения уравнений и неравенств с параметрами и успешно справились с заданием №18 ЕГЭ, то я решила разработать данный курс для учащихся 7-8 класса, чтобы они в дальнейшем не боялись заданий с параметрами, имели о них представления и умели их решать. В курсе 7-8 классов в основном рассматриваются две темы – Линейные уравнения и сводящиеся к ним и Квадратные уравнения и сводящиеся к ним. В дальнейшем я планирую разработать курс и для учащихся 9-х классов и применять в своей практике курс «Параметры» с 7-11 классы.
В курсе 7-8 классов в основном рассматриваются две темы – Линейные уравнения и сводящиеся к ним и Квадратные уравнения и сводящиеся к ним. В дальнейшем я планирую разработать курс и для учащихся 9-х классов и применять в своей практике курс «Параметры» с 7-11 классы.
Вам также может понравиться:
Конкурсы 169 работ
Всероссийский конкурс детско-юношеского творчества «ОТЕЦ – ЗВУЧИТ ГОРДО! » к Дню защитника Отечества
15 Января – 25 Марта
Конкурсы 1 работа
Международный творческий конкурс к Дню детской книги «КНИЖНАЯ КАРУСЕЛЬ »
01 Марта – 20 Мая
Конкурсы 148 работ
Всероссийский конкурс детско-юношеского творчества к Дню китов «ПУТЕШЕСТВИЕ В МОРСКИЕ ГЛУБИНЫ »
10 Января – 25 Марта
Свидетельство участника экспертной комиссии
Оставляйте комментарии к работам коллег
и получите документ БЕСПЛАТНО!
Подробнее
- Предыдущая работа
- Следующая работа
Также вас может заинтересовать
- Оценка знаний по математике для 7 класса «Контрольная работа «Функция»» Математика
- Конспект занятия по математике для 2 класса «Конспект урока по математике «Час.
 Минута». 2 класс. УМК «Школа России».» Математика
Минута». 2 класс. УМК «Школа России».» Математика - Презентации по математике для 6 класса «Презентация к уроку математики в 6 классе «Арифметические действия с обыкновенными дробями (взаимно обратные числа, деление дробей).»» Математика
- Презентации по математике для «Образовательный проект: Историческое развитие науки о качестве и ее практических приложений. Политико-правовые аспекты развития систем управления качеством.» Математика
- Уроки по математике для 2 класса «КГУ «Архангельская средняя школа»» Математика
Решение уравнений с параметром | Творческие проекты и работы учащихся
Руководитель:
Поликарпова Галина Павловна
Учреждение:
ГБОУ Лицей №150 г. Санкт-Петербурга
Санкт-Петербурга
В процессе работы над индивидуальным проектом по математике «Решение уравнений с параметром» учеником 11 класса школы была поставлена и реализована цель, изучить различные способы решения задач с параметрами, решить ряд аналогичных заданий, чтобы подготовиться к решению примеров с параметрами на ЕГЭ.
Подробнее о проекте:
В ученической исследовательской работе по математике «Решение уравнений с параметром» автор рассматривает аналитический и графический метод решения уравнений с параметром, а также метод решения задачи относительно параметра. В работе подробно описаны виды уравнений с параметром и варианты решения уравнений с параметром, а также предложены задания для самостоятельного решения таких примеров.
В готовом творческом и исследовательском проекте по математике «Решение уравнений с параметром» автор анализирует задания с параметром из ЕГЭ прошлых лет, систематизирует все задания по видам, показывает способы решения в общем виде, подбирает по несколько подобных примеров на каждый вид для самостоятельного решения. К концу учебного года 19/20 автор планирует создать методичку для подготовки к решению заданий с параметром из ЕГЭ.
К концу учебного года 19/20 автор планирует создать методичку для подготовки к решению заданий с параметром из ЕГЭ.
Оглавление
Введение
1. Методы решения заданий с параметром.
1.1. Аналитический метод.
1.2. Графический метод.
1.3. Метод решения относительно параметра.
2. Виды уравнений с параметром.
3. Решение уравнений с параметром.
4. Задания для самостоятельного решения.
Заключение
Литература
Введение
В данной работе описываются основные способы решения одного из заданий ЕГЭ — задания с параметром. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений. Решение задач с параметрами способствуют формированию логического мышления, помогают в приобретении навыков исследовательской деятельности, стимулируют познавательную деятельность. Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.
На ЕГЭ встречаются два типа задач с параметрами. Первый «для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй «найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям».
И ответы в задачах этих двух типов различаются по существу. В задачах первого типа ответ выглядит так: перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответах второго типа задач с параметром перечисляются все значения параметра, при которых выполнены условия задачи.
Противоречие: многие ученики не приступают к решению задания с параметром на ЕГЭ, даже несмотря на то, что оно высоко оценивается.
Проблема: как подготовиться к решению заданий с параметрами из ЕГЭ
Цель проекта: изучение различных способов решения задач с параметрами.
Задачи:
- Проанализировать задания с параметром из ЕГЭ прошлых лет
- Систематизировать все задания по видам
- Показать способы решения в общем виде
- Подобрать по несколько подобных примеров на каждый вид для самостоятельного решения
- к концу учебного года 19/20 создать методичку для подготовки к решению заданий с параметром из ЕГЭ
Данная методическая разработка «Решение уравнений с параметрами» предназначена для учащихся 11-х классов, желающих углубить и расширить свои знания по математике. Для тех, кто готовится к поступлению в высшие учебные заведения.
Для тех, кто готовится к поступлению в высшие учебные заведения.
Актуальность проекта обусловлена тем, что многим ученикам будет гораздо легче подготовиться к ЕГЭ, используя эту разработку.
По данным только около 10% выпускников приступают к решению таких задач, и процент верного решения всего 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.
Продукт проекта: методическая разработка для подготовки к ЕГЭ (задание с параметром).
Этапы работы над проектом:
| Этап | Срок | Результат |
| Определение темы, цели, задач, актуальности проекта | Сентябрь-Октябрь 2018 | Тема проекта «Решение уравнений с параметром» Поставлены цели и задачи, определена актуальность |
| Сбор материала по проекту | Октябрь 2018-Май 2019 | Получение нужных сведений для написания проектной работы |
| Обобщение материала | Май 2019-Ноябрь 2020 | Готовый проект и презентация |
| Представление проекта | Февраль 2020 | Защита проекта |
Текст проекта представлен в формате Word внизу этой страницы!
Заключение
Во время создания данного проекта я взялся за детальное рассмотрение параметра на примерах математических задач. Ведь параметры встречаются гораздо чаще, чем мы себе представляем. Изучение многих процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Включая такое большое количество столкновений, пусть и косвенных, с параметром, я пришел к выводу, что необходимо изучать данную тему более детально. Также, решение уравнений с параметром способствует развитию логического и вариативного мышление человека, что позволит ему улучшить свои знания и умения. В моей работе рассмотрены часто встречающиеся типы уравнений, и я надеюсь, что знания, которые я получил в процессе работы, а также использовал при выполнении данной проектной работы, помогут мне и другим одиннадцатиклассникам при сдаче ЕГЭ. Выполняя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рациональных способов решения. На мой взгляд, графо-аналитический метод является самым удобным и наглядным способом решения уравнений с параметрами, так как при таком решении можно наглядно увидеть все корни и гораздо легче заметить ошибки.
Ведь параметры встречаются гораздо чаще, чем мы себе представляем. Изучение многих процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Включая такое большое количество столкновений, пусть и косвенных, с параметром, я пришел к выводу, что необходимо изучать данную тему более детально. Также, решение уравнений с параметром способствует развитию логического и вариативного мышление человека, что позволит ему улучшить свои знания и умения. В моей работе рассмотрены часто встречающиеся типы уравнений, и я надеюсь, что знания, которые я получил в процессе работы, а также использовал при выполнении данной проектной работы, помогут мне и другим одиннадцатиклассникам при сдаче ЕГЭ. Выполняя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рациональных способов решения. На мой взгляд, графо-аналитический метод является самым удобным и наглядным способом решения уравнений с параметрами, так как при таком решении можно наглядно увидеть все корни и гораздо легче заметить ошибки.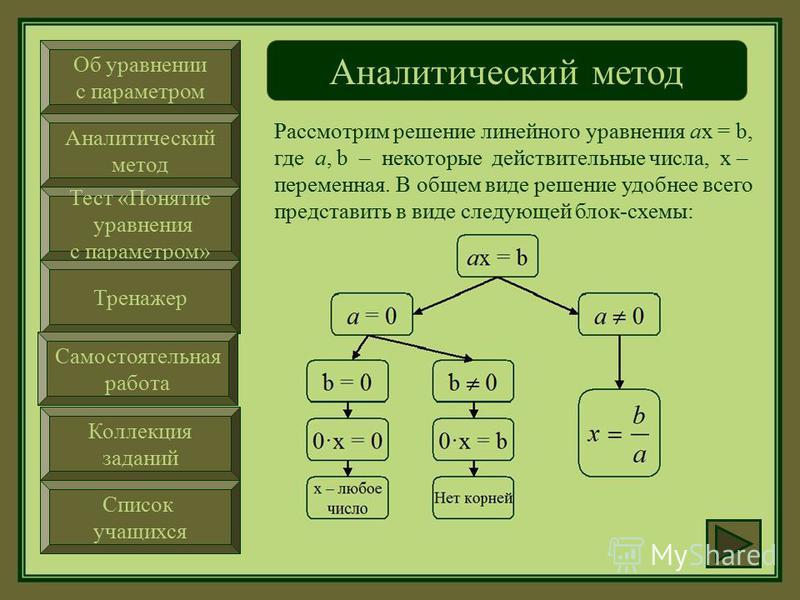
Использованная литература
- СдамГИА/РешуЕГЭ – образовательный портал для подготовки к экзаменам.
- ИНФОУРОК – ведущий образовательный портал России.
- Википедия.
- Учителя.com — учительский портал
- А. Шахмейстер «Задачи с параметрами в ЕГЭ» – «Петроглиф», №1 2004 г.
- Е.А.Ефимов «Задачи с параметром» – Самарский гос. аэрокосмический университет, 2006г.
- П.И. Горнштейн, В.Б. Полонский, М.С. Якир «Задачи с параметрами» – РИА, 2002г.
Если страница Вам понравилась, поделитесь в социальных сетях:
линейная алгебра — Как найти количество решений системы уравнений с одним параметром, которое нельзя уменьшить?
Задавать вопрос
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 1к раз 92 и 0 \\ 0 и 2+к и к \end{bmatrix} $$
Однако я не вижу, как это можно еще уменьшить. Насколько я знаю, мне нужна форма эшелона, чтобы определить, сколько существует решений. Должен ли я просто подключить $k=-2$, чтобы уменьшить его еще больше? Если да, то что можно сказать о количестве решений, если $k \neq =2$?
Насколько я знаю, мне нужна форма эшелона, чтобы определить, сколько существует решений. Должен ли я просто подключить $k=-2$, чтобы уменьшить его еще больше? Если да, то что можно сказать о количестве решений, если $k \neq =2$?
РЕДАКТИРОВАТЬ: я только начинаю курс линейной математики, поэтому я не могу использовать какие-либо передовые методы (например, определители и т. д.)
- линейная алгебра 92=0$ (т.е. $k= \pm 1$), то то, что у вас выше, равно $$ \begin{bmatrix} 1 & k & 1 \\ 0 & 0 & 0 \\ 0 и 2+к и к \end{bmatrix} \to \begin{bmatrix} 1 & k & 1 \\ 0 и 2+к и к \\ 0 и 0 и 0 \end{bmatrix} $$
- Научитесь выражать множество решений системы линейных уравнений в параметрической форме.
- Понять три возможных числа решений системы линейных уравнений.
- Рецепт: параметрическая форма.
- Словарное слово: свободная переменная .
- Запишите систему в виде расширенной матрицы.
- Уменьшение строки до уменьшенной ступенчатой формы строки.
- Запишите соответствующую (решенную) систему линейных уравнений.
- Переместите все свободные переменные в правую часть уравнений.
- Последний столбец является сводным столбцом. В этом случае система несовместима . Решений нет, т. е. множество решений пусто. Например, матрица А100010001Б получается из линейной системы без решений.
- Каждый столбец, кроме последнего, является сводным столбцом. В этом случае система имеет уникальное решение. Например, матрица A100a010b001cB говорит нам, что единственным решением является (x,y,z)=(a,b,c).
- Последний столбец не является сводным столбцом, и некоторые другие столбцы также не являются сводными столбцами. В этом случае система имеет бесконечно много решений, соответствующих бесконечному множеству возможных значений свободных переменных. Например, в системе, соответствующей матрице
С1-20310014-1Д,
любые значения x2 и x4 дают решение системы уравнений.

Можете взять отсюда в обоих случаях?
$\endgroup$
3
$\begingroup$
Назовем полученную матрицу $A$ и пусть $v = (x,y,z)$. Вы хотите решения для 92)$, это происходит, только если $k$ равно $0, 1$ или $-1$. В любом другом случае $A$ необратима, поэтому $v \to A \cdot v$ не инъективна и, следовательно, существуют $v, w$ такие, что
В любом другом случае $A$ необратима, поэтому $v \to A \cdot v$ не инъективна и, следовательно, существуют $v, w$ такие, что
$$ A\cdot v = A\cdot w \iff A\cdot (v -w) = \vec{0} $$
и любое скалярное умножение $(v-w)$ также является решением. Таким образом, в очень общем анализе система не имеет ненулевых решений при $k = 0,1,-1$ и бесконечного количества решений при любом другом значении $k$.
$\endgroup$
92 — I) = 0$Где $A$ — ваша системная матрица.
$\endgroup$
Параметрическая форма
Цели
Существует одна возможность для сокращенной по строкам формы матрицы, которую мы не видели в разделе 1. 2.
2.
Пример (Система со свободной переменной)
Рассмотрим линейную систему
E2x+y+12z=1x+2y+9z=-1.
Решаем с помощью редукции строк:
C21121129-1DR1 ←→R2—-→C129-121121D(необязательно)R2=R2-2R1——→C129-10-3-63D(шаг 1c)R2=R2÷-3—— →C129-1012-1D(Шаг 2b)R1=R1-2R2——→C1051012-1D(Шаг2c)Эта сокращенная по строкам матрица соответствует линейной системе
Ex+5z=1y+2z=-1.
В каком смысле система решена? Переписываем как
Ex=1−5zy=−1−2z.
Для любого значения z существует ровно одно значение x и y, при котором уравнения верны. Но мы можем выбрать любое значение z.
Мы нашли все решения: это множество всех значений x,y,z, где
Fx=1−5zy=−1−2zz=zzлюбое реальное число.
Это называется параметрической формой для решения линейной системы. Переменная z называется свободная переменная .
Figure2A изображение набора решений (желтая линия) линейной системы в этом примере. Существует единственное решение для каждого значения z; переместите ползунок, чтобы изменить z.
Существует единственное решение для каждого значения z; переместите ползунок, чтобы изменить z.Учитывая параметрическую форму решения линейной системы, мы можем получить конкретные решения, заменив свободные переменные любыми конкретными действительными числами. Например, установка z=0 в последнем примере дает решение (x,y,z)=(1,−1,0), а установка z=1 дает решение (x,y,z)=(−4 ,−3,1).
Определение
Рассмотрим непротиворечивую систему уравнений от переменных x1,x2,…,xn. Пусть A — ступенчатая форма расширенной матрицы для этой системы.
Мы говорим, что xi является свободной переменной , если соответствующий столбец в A не является сводным столбцом.
В приведенном выше примере переменная z была свободна, потому что уменьшенная матрица формы эшелона строк была
C1051012-1D.В матрице
C1A0AA001AAD, свободные переменные x2 и x4. (Дополненный столбец не свободен, поскольку он не соответствует переменной. )
)
Рецепт: Параметрическая форма
Параметрическая форма системы решений согласованной системы линейных уравнений получается следующим образом.
Перемещение свободных переменных в правую часть уравнений равнозначно решению для несвободных переменных (тех, которые входят в опорные столбцы) в терминах свободных переменных. Можно думать о свободных переменных как о независимых переменных, а несвободные переменные являются зависимыми .
Вы можете выбрать любое значение для свободных переменных в (непротиворечивой) линейной системе.
Свободные переменные происходят из столбцов без точек опоры в матрице в форме эшелона строк.
Пример
Пример (параметризованная плоскость)
Имеются три возможности для сокращенной ступенчатой формы расширенной матрицы линейной системы.

 Минута». 2 класс. УМК «Школа России».» Математика
Минута». 2 класс. УМК «Школа России».» Математика