Математика 4 класс Богданович. Решебник. ГДЗ. Дроби. Задание 640
Категория: —>> Математика 4 класс Богданович
Задание: —>> 640 — 659 660 — 679 680 — 692
|
|
Задание 640.
На рисунке изображены: целый круг и круг, разде¬лённый на 2 равные части. Одна такая часть — это половина. Половину обозначают двумя цифрами — 1/2 (одна вторая).
Если сложить обе половины, то получим целый круг. В жизни, для обозначения такой части часто пользуются словом половина, или пол.
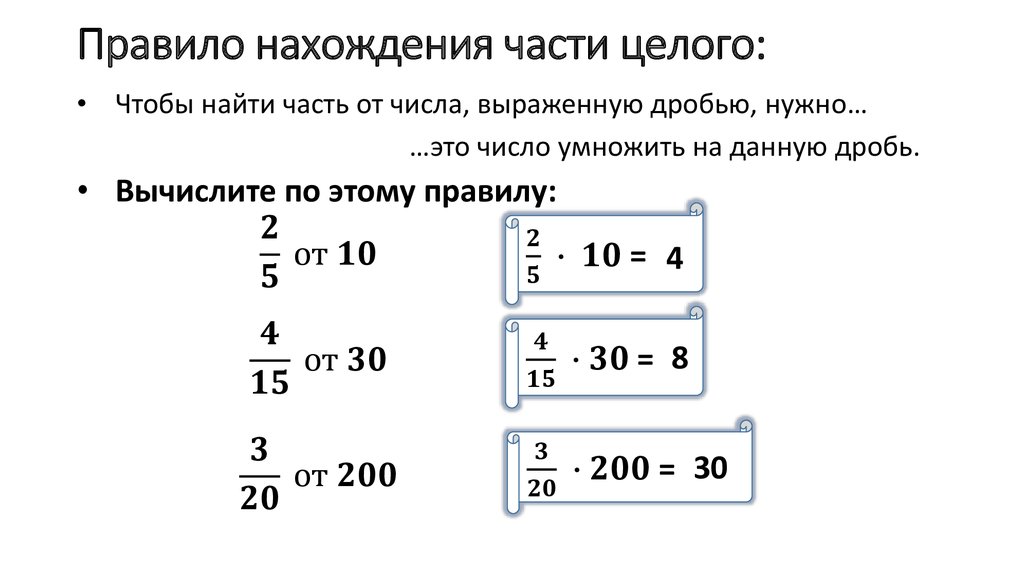
Найдите 1/2 чисел 8, 100, 1кг.
Решение:
- 1/2 — 8 = 8 : 2 = 4
- 1/2 — 100 = 100 : 2 = 50
- 1/2 — 1кг = 1кг : 2 = 500г
Задание 641.
На рисунке квадраты разделены на равные части. Какая из этих частей наибольшая, а какая наименьшая? Запишите цифрами все части от наибольшей к наи¬меньшей.
Решение: 1/2; 1/3; 1/4; 1/16.
Задание 642.
Рассмотрите задачи на нахождение части числа и чис¬ла по его части. Составьте две подобные задачи.
- Задача №1: От 12 м проволоки отрезали четвёртую часть. Сколько метров проволоки отрезали?
- Задача №2: В первый день турист прошёл 24км, что составляло 1/4 всего пути. Найдите весь путь.
Решение:
Задача №1:
- 12 : 4 = 3(м)
Ответ: — отрезали 3м проволки.
Задача №2:
- 24 * 4 = 96(км)
Ответ: весь путь составляет 96 км.
Задание 643.
- Рассмотрите задание и его решение.
- Найдите 1/6 от 720. Решение запишите.
Решение:
- Задание: Найдите 1/5 от 90.
- 90 : 5 = 18.
- Ответ: 1/5 от 90 равна 18.
- 720 : 6 = 120
- Ответ: 1/6 от 720 равна 120
Задание 644.
Длина 1/3 искомого отрезка 3см. Найдите длину искомого отрезка и начертите его в тетради.
Решение:
- 3 * 3 = 9(см) – длина искомого отрезка.
Ответ: 9см длина искомого отрезка.
Рисунок в тетради:
Задание 645.
Для школьников купили 240 билетов в цирк 420 билетов в театр.
Четвёртую часть билетов в цирк и шестую часть билетов в театр отдали ученикам начальных классов. Сколько всего билетов отдали ученикам начальных классов?
Решение:
- 240 : 4 = 60(б.) – отдали билетов в цирк начальным классам.
- 420 : 6 = 70(б.) – отдали билетов в театр начальным классам.
- 60 + 70 = 130(б.) – всего отдали билетов начальным классам.
Ответ: 130 билетов всего отдали ученикам начальных классов.
Задание 646.
Найди значения данных выражений, если а = 43.
- 989 : а — 20 = ?
- 1000 — 774 : а = ?
- 17 * а – 567 = ?
Решение:
- 989 : а — 20 = ?
- Если а = 43, то 989 : 43 — 20 = 3
- 989 : 43 = 23
- 23 – 20 = 3
- Если а = 43, то 1000 — 774 : 43 = 957
- 774 : 43 = 18
- 1000 – 43 = 957
- Если а = 43, то 17 * 43 – 567 = 164
- 17 * 43 = 731
- 731 – 567 = 164
Задание 647.
В универмаге было 280 женских и 150 мужских костюмов. На распродаже, за день, продали четвёртую часть женских и третью часть мужских костюмов. Каких костюмов продали больше и на сколько?
Решение:
- 280 : 4 = 70(к) – продали на распродаже женских костюмов.
- 150 : 3 = 50(к) – продали на распродаже женских костюмов.
- 70 – 50 = 20(к) – женских больше чем мужских.
Ответ: на 20 костюмов больше продали, для женщин, чем для мужчин.
Задание 648.
По данным рисунка найди, на сколько километров расстояние КМ меньше половины расстояния КО.
Решение:
- 320 : 2 = 160(км) – половина расстояния КО.
- 160 – 100 = 60(км) – на такое количество километров меньше расстояние КМ, половины расстояния КО.
Ответ: На 60 км километров расстояние КМ меньше половины расстояния КО.
Задание 649.
На рисунке 7 одинаковых прямоугольников.
Первый — целый, второй разделён НА 2 равные части, третий — на 3 равные части, четвёртый — на 4, пятый — на 5, шестой — на 8 и седьмой — на 10 равных частей. Сколько четвёртых частей в половине?
Используя рисунки, сравните части: 1/2 и 1/8; 1/8 и 1/10; 1/3 и 1/2; 1/4 и 1/5.
Решение:
- 1/2 меньше 1/8 в 4 раза;
- 1/8 меньше 1/10 на 2 деления;
- 1/3 меньше 1/2 на 1 деление;
- 1/4 меньше 1/5 на 1 дение.
Задание 650.
1л сока разлили в стаканы ёмкостью 1/5л. Сколько стаканов наполнили соком?
Решение:
1л = 1000мл
- 1000 : 5 = 200(мл) – емкость одного стакана.
- 1000 : 200 = 5(ст.) – количество стаканов, которые наполнили соком.
Ответ: 5 стаканов наполнили соком.
Задание 651.
4л молока разлили в пол-литровые банки. Сколько понадобилось таких банок?
Решение:
На 1л молока необходимо 2 банки, так, как каждая из них составляет половину литра.
- 4 * 2 = 8(б.) – необходимо, что бы разлить 4л молока.
Ответ: необходимо 4 пол-литровых банки что бы разлить 4л молока.
Задание 652.
Найдите:
- 1/5 от 1кг;
- 1/3 от 2мин;
- 1/4 от 1ч.
Решение:
- 1/5 от 1кг
- 1кг = 1000г
- 1000г : 5 = 200г
- 1/5 от 1кг составляет 200г.
- 2мин = 120сек
- 120 : 3 = 40сек
- 1/3 от 2мин составляет 40сек.
- 1ч = 60мин
- 60мин : 4 = 15мин
- 1/4 от 1ч составляет 15мин.
Задание 653.
В салоне штор было 450м ткани. В первый день продали пятую часть ткани, во второй — третью часть того, что осталось. Сколько метров ткани про¬дали во второй день?
Решение:
- 450 : 5 = 90(м) – продали в первый день.
- 450 – 90 = 360(м) – осталось ткани после того, как продали 90м в первый день.
- 360 : 3 = 120(м) – продали во второй день.
Ответ: 120 метров ткани продали во второй день.
Задание 654.
Длина цветника прямоугольной формы 30м, а ши¬рина 20м. 1/4 площади цветника занимают гвоздики, а остальную площадь — тюльпаны. Какая площадь засажена тюльпанами?
Решение:
- 30 * 20 = 600(м²) – площадь цветника.
- 600 : 4 = 150(м²) – занимают гвоздики.
- 600 – 150 = 450(м²) – занимают тюльпаны.
Ответ: 450м² от площади цветника занимают тюльпаны.
Задание 655.
Сквер имеет прямоугольную форму. Его длина равна 50м, а ширина 20м. 1/5 сквера занимает игровая площадка, а остальная площадь отведена под деревья и кусты. Найдите площадь, отведённую под деревья и кусты.
Решение:
- 50 * 20 = 1000(м²) – площадь сквера.
- 1000 : 5 = 200(м²) – площадь игровой площадки.
- 1000 – 200 = 800(м²) – площадь отведенная под деревья и кусты.
Ответ: 800м² — площадь отведенная под деревья и кусты.
Задание 656.
Решите примеры:
- 756 : 3 = ?
- 3 * 3027 = ?
- 100000 – 7245 * 4 + 9754 = ?
- 966 : 21 = ?
- 3027 : 3 = ?
- 100000 + 82056 : 4 – 7109 = ?
Решение:
- 756 : 3 = ?
- 756 : 3 = 252
- 3 * 3027 = 9081
- 7245 * 4 = 28980
- 100000 – 28980 = 71020
- 71020 + 9754 = 80074
- 966 : 21 = 46
- 3027 : 3 1009
- 82056 : 4 = 20514
- 100000 + 20514 = 120514
- 120514 – 7109 = 113405
Задание 657.
Запиши в тетради части в порядке возрастания.
Решение: 1/12; 1/10; 1/8; 1/6; 1/5; 1/4; 1/3; 1/2.
Задание 658.
На сколько равных частей разделён каждый квадрат? Как называется не закрашенная часть каждого квадрата? Сколько и каких частей закрашено в каждом квадрате?
Решение:
- Не закрашено: 1/2; 1/3; ¼; 1/5; 1/6.
- Закрашено: 1/2; 2/3; ¾; 4/5; 5/6.
Задание 659.
Сосчитай, на сколько равных частей разделён каждый круг. Сколько таких частей закрашено?
Числа вида 1/2, 2/3, 3/4, 1/6, 5/6 называют дробными числами. Число 5/6 дробь, 5 — числитель дроби, а 6 — знаменатель дроби. Знаменатель — число под чертой дроби — показывает, на сколько равных частей разде¬лено целое. Числитель число над чертой дроби — показывает, сколько взято равных частей целого.
Решение:
Каждый круг разделен на 6 равных частей. В первом кругу закрашено 1/6, во втором – 2/6, в третьем – 3/6, в четвертом – 4/6, в пятом 5/6.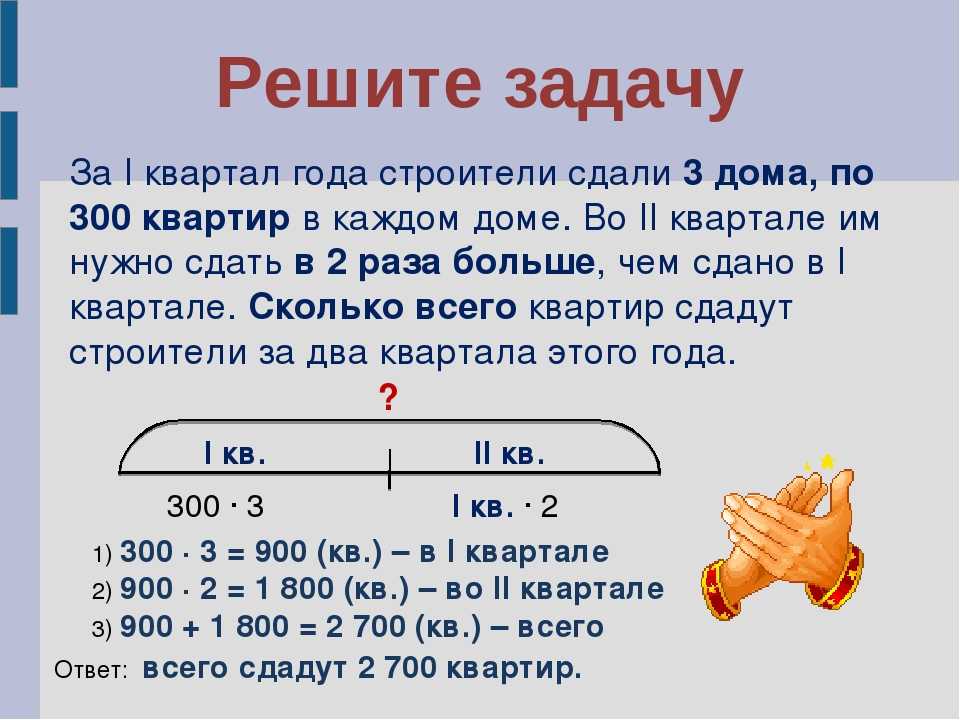
Задание: —>> 640 — 659 660 — 679 680 — 692
Старинные задачи из учебника Петерсон Л.Г.
Мар 20, 2021 | 4 класс | Нет комментариев
4.9
(74)
В учебнике Петерсон Л.Г. 4 класса ч.1 мы встречаем старинные задачи. Эти задачи простые и легкие, но для того, чтобы решить их, надо быть очень внимательными.
Итак, рассмотрим задачу 1.
Для того чтобы решить эту задачу, надо вспомнить, что унция – это двенадцатая часть – 1/12.
Чертим схему: целое делим на 12 равных частей. А 5 унций – это 5/12.
В задаче сказано, что из 5 унций вычесть 1 унцию: 5/12 – 1/12 = 4/12.
В целом – по 4 взято 3 раза. Значит, 4 унции это 1/3 от целого.
Или: 5/12 – 1/12 = 4/12.
Данную дробь можно сократить: 4/12 = 1/3.
Т.е. получится 1/3, значит, ученик решил задачу правильно.
Задача 2.
Чертим схему: у нас есть дроби 1/3 и 1/4. Чтобы отметить эти дроби на отрезке, надо привести к общему знаменателю – это 12.
Значит, целое разделим на 12 равных частей.
Треть от целого – это 4 раза по 1/12, четверть от целого – это 3 раза по 1/12.
1) 1/3 + 1/4 = 4/12 + 3/12 = 7/12 – всего вычли.
2) 12/12 – 7/12 = 5/12 – осталось.
В задаче сказано, что осталось 10, значит, 5/12 = 10.
3) находим целое по его дроби: 7/12 это 10, значит,
10 : 5 х 12 = 24.
Ответ: искомое число — 24.
Задача 3.
Чертим схему: в задаче сказано – от трети, а также – две трети от трети, значит, целое надо разделить на 3, и еще на 3. Поэтому чертим отрезок длиной 9 см, делим его на 3 равные части и одну часть делим еще на 3 равные части.
Две части от 1/3 = 70.
1) находим чему равна 1/3 от целого: 2/3 от 1/3 это 70, значит,
70 : 2 х 3 =105 (быков) – это 1/3.
2) теперь узнаем, сколько быков в стаде: 1/3 это 105, значит,
105 х 3 = 315 (быков) – в стаде.
Ответ: в стаде было 315 быков.
Задача 4.
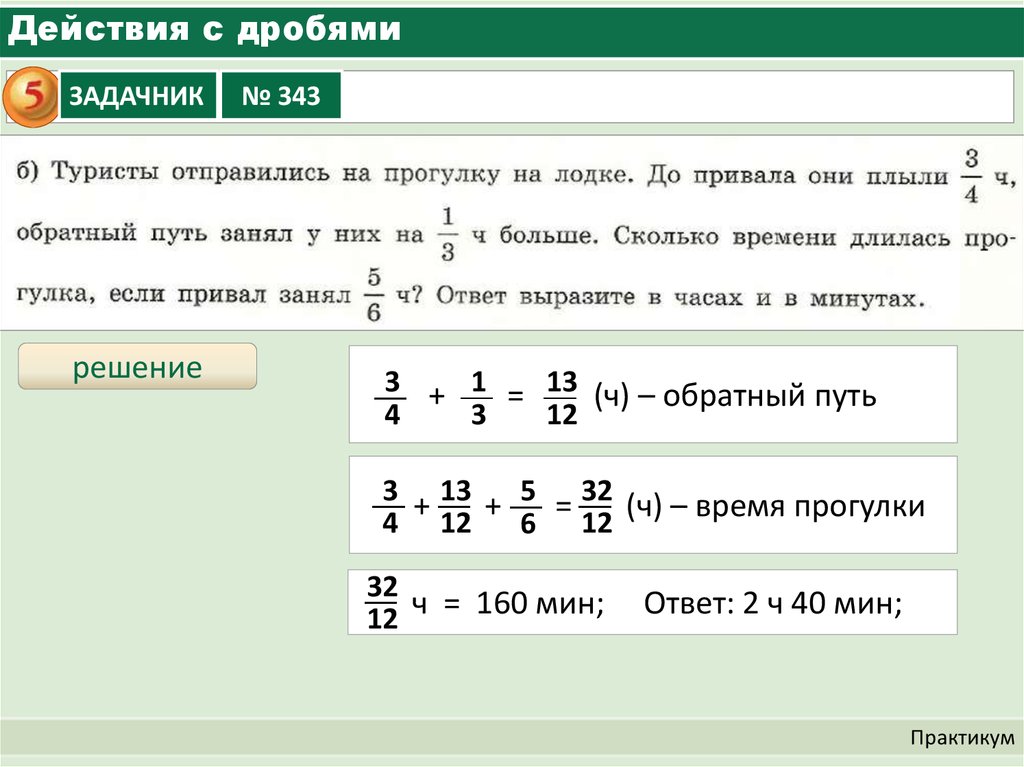
В задаче сказано, что на один лепесток третья часть пчелок опустилась, а на соседний цветок пятая часть пчелок поместилась. Чтобы найти разность, надо привести к общему знаменателю – 15, а это — 1/3 = 5/15, 1/5 = 3/15,
1) 5/15 – 3/15 = 2/15 (части) – это разность.
2) 2/15 х 3 = 6/15 (частей) – посадили на кутай.
3) теперь нужно узнать какая часть пчел летали и сидели:
5/15 + 3/15 + 6/15 = 14/15 (частей)
4) узнаем, какая часть пчел не нашли себе место:
15/15 – 14/15 = 1/15 (часть), а это 2 пчелы.
5) узнаем, сколько всего было пчел: 2 это 1/15, значит,
2 х 15 = 30 (пчел) – всего собралось.
Ответ: всего здесь собралось 30 пчел.
Задача 5.
Рассмотрим схему: мы видим, что в каждом городе купец отдавал половину и треть, значит,
1) 1/3 + 1/2 = 2/6 + 3/6 = 5/6 (частей) — взыскивали с купца.
2) 6/6 – 5/6 = 1/6 (часть) – оставалось у купца.
3) начнем разбор задачи с третьего города: в задаче сказано, что у купца осталось 11 денежков, значит, 1/6 это 11:
11 х 6 = 66 (денежков) — осталось после второго города.
4) 1/6 это 66, значит,
66 х 6 = 396 (денежков) – осталось после первого города.
5) 1/6 это 396, значит,
396 х 6 = 2376 (денежков) – было вначале у купца.
Ответ: у купца вначале было 2376 денежных знаков.
Старинные задачи являются хорошей разминкой перед решением современных задач.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.9 / 5. Количество оценок: 74
Оценок пока нет. Поставьте оценку первым.
Похожие статьи
Сложение дробей в задачах Word
Все общие основные: математические ресурсы для 4-го класса
7 диагностических тестов 189 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Common Core: Справка по математике для 4-го класса »
Числа и операции: Дроби »
Построить дроби из единичных дробей »
Решайте текстовые задачи на сложение и вычитание дробей: CCSS.
Math.Content.4.NF.B.3d »
Сложение дробей в задачах Word
В кладовой Чарли часть продуктов – картофельные чипсы, часть – чипсы из тортильи, а остальные – печенье или крекеры. Какой фракции являются фишки?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы сложим вместе картофельные чипсы и чипсы из тортильи, поэтому мы сложим дроби.
Сообщить об ошибке
В кладовой Стюарта одним из продуктов являются чипсы, а другим – хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Энди часть продуктов — это чипсы, а часть — хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Сары одним из продуктов являются чипсы и одним из продуктов являются хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Сьюзан одним из продуктов являются чипсы, а одним из блюд – хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы соединим чипсы и хлопья, поэтому мы сложим дроби.
Сообщить об ошибке
В кладовой Дэна одним из продуктов являются чипсы, а другим – хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Сьюзен одним из продуктов являются чипсы, а другим – хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Марка часть продуктов — это чипсы, а часть — хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Тима одним из продуктов являются чипсы и одним из продуктов являются хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
В кладовой Лауры одним из продуктов являются чипсы, а одним из продуктов являются хлопья. Какую часть товаров составляют чипсы или хлопья?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы складываем вместе чипсы и хлопья, поэтому складываем дроби.
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах
7 диагностических тестов 189 практических тестов Вопрос дня Карточки Учитесь по концепции
Общие базовые государственные стандарты по математике для четвертого класса: обзор
Перейти к:
Операции и алгебраическое мышление | Числа и операции с основанием десять | Число и операции-дроби | Измерения и данные | Геометрия
Операции и алгебраическое мышление
Используйте четыре операции с целыми числами для решения задач.
4.OA.A.1
Интерпретировать уравнение умножения как сравнение, например, интерпретировать 35 = 5 × 7 как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5.
Представлять вербальные утверждения мультипликативных сравнений как уравнений умножения.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
4.OA.A.2
Умножение или деление для решения текстовых задач, включающих мультипликативное сравнение, например, с помощью рисунков и уравнений с символом неизвестного числа для представления проблема, отличающая мультипликативное сравнение от аддитивного сравнения.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
4.OA.A.3
Решите многошаговые словесные задачи, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки . Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Познакомьтесь с множителями и множителями.
4.OA.B.4
Найти все пары множителей для целого числа в диапазоне от 1 до 100. Признать, что целое число является кратным каждого из его делителей. Определить, является ли заданное целое число в диапазоне от 1 до 100 кратным заданному однозначному числу. Определите, является ли заданное целое число в диапазоне от 1 до 100 простым или составным.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Создание и анализ шаблонов.
4.OA.C.5
Создание шаблона числа или формы, который следует заданному правилу. Определите очевидные особенности шаблона, которые не были явными в самом правиле.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
Числа и операции с основанием 10
Обобщить понимание разряда для многозначных целых чисел.
4.NBT.A.1
Знайте, что в многозначном целом числе цифра на одном месте в десять раз больше, чем на месте справа от нее.
См.
соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
4.NBT.A.2
Чтение и запись многозначных целых чисел с использованием десятичного основания, имен чисел и расширенной формы. Сравните два многозначных числа на основе значений цифр в каждом разряде, используя >, = и
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Используйте понимание разрядных значений и свойства операций для выполнения многозначных арифметических операций.
4.NBT.B.4
Свободно складывать и вычитать многозначные целые числа по стандартному алгоритму.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
4.NBT.B.5
Умножение целого числа, состоящего не более чем из четырех цифр, на однозначное целое число и умножение двух двузначных чисел с использованием стратегий на основе разрядности и свойств операций.
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
4.NBT.B.6
Найдите целые числа и остатки с до четырехзначными делимыми и однозначными делителями, используя стратегии, основанные на разрядном значении, свойства операций и/или отношения между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Числа и операции с дробями
Расширить понимание эквивалентности дробей и их порядка.
4.NF.A.1
Объясните, почему дробь a/b эквивалентна дроби (n × a)/(n × b), используя визуальные модели дробей, обращая внимание на то, как число и размер части различаются, хотя сами две фракции имеют одинаковый размер. Используйте этот принцип для распознавания и создания эквивалентных дробей.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
4.NF.A.2
Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнения с помощью символов >, = или
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Создавайте дроби из единичных дробей, применяя и расширяя предыдущее понимание операций над целыми числами.
4.NF.B.3
Понимать дробь a/b с a > 1 как сумму дробей 1/b.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
4.NF.B.4
Применение и расширение предыдущего понимания умножения для умножения дроби на целое число.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
Понимание десятичной записи дробей и сравнение десятичных дробей.
4.NF.C.5
Выразите дробь со знаменателем 10 в виде эквивалентной дроби со знаменателем 100 и используйте эту технику для сложения двух дробей со знаменателями 10 и 100 соответственно.
См. Связанные планы уроков
4.nf.c.6
Используйте десятичные записи для фракций с знаменателями 10 или 100.
См. Связанные рабочие листы, рабочие книги, упражнения, планы урока
4.nf.c.7
Сравните два десятичных знака с сотыми, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений символами >, = или
См. соответствующие рабочие листы, рабочие тетради, планы уроков.
Измерения и данные.
4.MD.A.1
Знать относительные величины единиц измерения в пределах одной системы единиц, в том числе км, м, см; кг, г; фунт, унция; л, мл; ч, мин, сек.
В рамках единой системы измерения выражайте измерения в большей единице через меньшую. Запишите эквиваленты измерений в таблицу из двух столбцов.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков. включая задачи, связанные с простыми дробями или десятичными знаками, и задачи, требующие выражения измерений, данных в более крупной единице, с точки зрения меньшей единицы. Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерения.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
4.MD.A.3
Применение формул площади и периметра для прямоугольников в реальных и математических задачах.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Представление и интерпретация данных.
4.MD.B.4
Постройте линейный график для отображения набора данных измерений в долях единицы (1/2, 1/4, 1/8).
Решайте задачи на сложение и вычитание дробей, используя информацию, представленную в виде линейных графиков.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
Геометрические измерения: понимание понятия угла и измерения углов.
4.MD.C.5
Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
4. MD.C.6
Измерение углов в целых числах с помощью транспортира. Эскиз углов заданной меры.
См. соответствующие рабочие листы, рабочие тетради, игры. Когда угол разлагается на непересекающиеся части, угловая мера целого равна сумме угловых мер частей. Решите задачи на сложение и вычитание, чтобы найти неизвестные углы на диаграмме в реальном мире, и математические задачи, например, используя уравнение с символом для неизвестной меры угла.