Решение задач круг эйлера: описание, примеры, для дошкольников, для школьников

Содержание

Решение задач с помощью кругов Эйлера

16,701
просмотр

Презентации / Математика / Решение задач с помощью кругов Эйлера

Скачать презентацию Понравилось | 29

Текст этой презентации

Слайд 1

Для тех , кому интересно
«Решение задач с помощью кругов Эйлера»
5-6 класс

Слайд 2

Изображение множеств в виде кругов подходит для того, чтобы облегчить рассуждения при решении задач

Слайд 3

Задача:
Все мои друзья занимаются каким-нибудь видом спорта. 17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?

Слайд 4

1.Изобразим два множества , так как два вида спорта. В одном будем фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом
2.Поскольку некоторые из друзей увлекаются и тем и другим видом спорта, то круги нарисуем так, чтобы у них была общая часть (пересечение)

Слайд 5

2
15
12
17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта.
Расставить числа , согласно условию задачи: 1)В общей части ставим цифру 2(двое увлекаются и тем и другим видом спорта)
2)В оставшейся части «футболистов» круга ставим цифру 15 (17 − 2 = 15). В свободной части «баскетболистов» круга ставим цифру12 (14 − 2 = 12).
футболом
баскетболом
3)Всего друзей 15+2+12=29 Ответ:29 друзей

Слайд 6

Задача: В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 7

1.Изобразим три множества , так как три увлечения. В одном будем фиксировать ребят из драмкружка, во втором ребят , которые поют. В третьем будем фиксировать ребят, которые увлекаются спортом.
2.Поскольку некоторые из ребят увлекаются всем , то круги нарисуем так, чтобы у них было пересечение.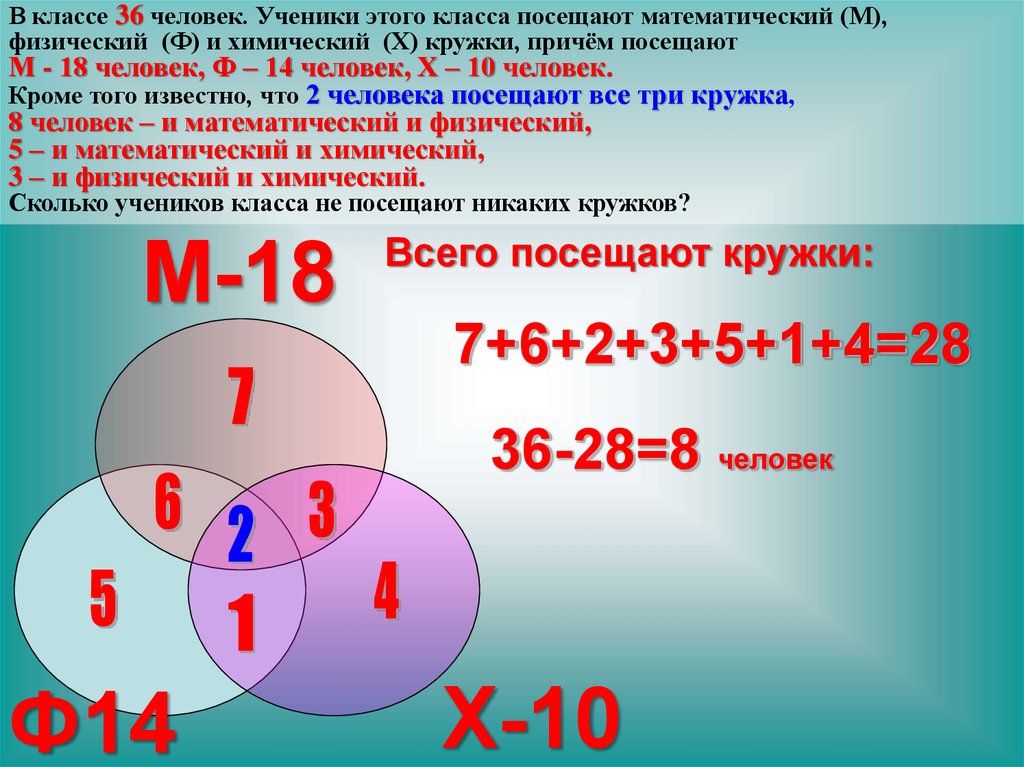

Слайд 8

драмкружок
хор
спорт

Слайд 9

драмкружок
хор
спорт
3 спортсмена посещают и драмкружок и хор , поэтому заполняем эту общую часть.
3
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 10

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает занятие ребят в драмкружке и хоре.

Слайд 11

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 10 ребят из хора . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 7 (10-3=7)

Слайд 12

Слайд 13

Слайд 14

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 8 спортсменов . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 5 (8-3=5)

Слайд 15

3
5
драмкружок
хор
спорт
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 16

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько спортсменов поют в хоре .

Слайд 17

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в хоре 6 спортсменов . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 3 (6-3=3)

Слайд 18

Слайд 19

драмкружок
хор
спорт
3
7
5
3

Слайд 20

Слайд 21

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 27 занимаются в драмкружке . А так как в предыдущих рассуждениях поставлены числа 3,5,7 ,то в оставшейся части ставим число 12 (27-(3+5+7)=12)

Слайд 22

драмкружок
хор
спорт
3
7
5
12
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 23

Слайд 24

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 32 поют в хоре . А так как в предыдущих рассуждениях поставлены числа 3,3,7 ,то в оставшейся части ставим число 19 (32-(3+3+7)=19)
3
7
3
19

Слайд 25

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят занимаются спортом.

Слайд 26

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
По условию 22 человека увлекаются спортом. А так как в предыдущих рассуждениях поставлены числа 3,5,3 ,то в оставшейся части ставим число 11 (22-(3+5+3)=11)
драмкружок
хор
спорт

Слайд 27

Слайд 28

драмкружок
хор
спорт
3
7
5
3
19
11
12

Слайд 29

Всего занимаются 12+19+11+7+3+3+5=60 человек. Не поют, не увлекаются спортом, не занимаются в драмкружке 70-60=10 человек
Ответ: 10 человек

Слайд 30

Задача:
Из 220 студентов 163 играют в шахматы,175-в футбол,22 человека не играют в эти игры . Сколько студентов одновременно играют в шахматы и в футбол?
шахматы
футбол
х
163-х
175-х
220-22=198(чел)-играют в игры
163-х+х+175-х=198 338-х=198 х=140 140 студентов одновременно играют в шахматы и в футбол

Слайд 31

Реши :
9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 бананы, апельсины и сливы. Сколько у меня друзей?

Слайд 32

Проверь решение:
бананы
апельсины
сливы
3
2
3
1
2
1
2
3+3+2+1+2+2+1=14 друзей
Ответ:14 друзей

Слайд 33

Домашнее задание:
1.Каждый из членов команды играет либо в футбол , либо в хоккей , либо в футбол и в хоккей . Сколько человек в команде ,если известно , что 18 человек играют в обе игры,22 человека играют в футбол,21 в хоккей?
2.В некоторой школе есть класс увлеченных ребят.Семь учеников из этого класса увлекаются математикой,шесть-физикой,пять-астрономией. Четверо из учеников увлекаются математикой и физикой,трое-математикой и астрономией,двое-физикой и астрономией,а один –и математикой,и физикой,и астрономией.Сколько учеников в классе?

Слайд 34

Проверь:
футбол
хоккей
1)
18
22-18=4
21-18=3
4+18+3=25(чел.)
Ответ:25 человек

Слайд 35

2)
математика
физика
астрономия
1
2
1
1
1
1
3
Ответ:10 человек
1+1+1+1+1+2+3=10(чел)

Слайд 36

Спасибо за внимание

Круги Эйлера — Учусь математике

w3.org/1999/xhtml» cellspacing=»0″>

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Решение каждой из этих задач можно красиво оформить.

Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах. Ценность задач, решаемых с помощью кругов Эйлера, состоит в том, что решения задач с громоздкими условиями и со многими данными, просты и не вызывают особых умозаключений. Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716).

В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).

Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.

Задача №1. Сколько натуральных чисел из первого десятка не делится ни на 2, ни на 3?

Решение. Для решения задачи удобно воспользоваться кругами Эйлера. В нашем случае три круга: большой круг – это множество чисел от 1 до 10, внутри большого – два меньших круга, пресекающихся друг с другом. Пусть множество чисел, кратных 2– это множество А, а множество чисел, кратных 3 – множество В. Рассуждаем. На 2 делится каждое второе число. Значит, таких чисел будет 10:2=5. На 3 делится 3 числа (10:3). На 2 и 3 делятся те числа, которые делятся на 6. Такое число только одно.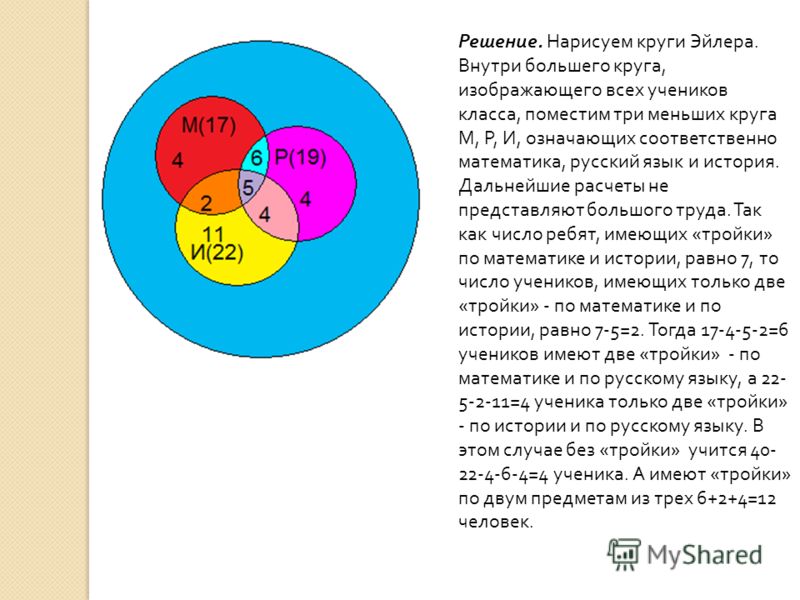 Поэтому множество А состоит из 5-1=4 чисел, множество В – 3-1=2 чисел. Отсюда следует, что в первом десятке содержится 10-(4+1+2)=3 числа.

Задача №2. С помощью кругов Эйлера можно ответить на множество вопросов, поставленных к одному условию задачи.

Пусть круг А изображает всех учащихся, говорящих по-английски, круг Н – говорящих на немецком языке, Круг Ф – говорящих по-французски. Сколько учащихся говорит: а) на всех трех языках? б) по-английски и по-немецки? в) по-французски? Сколько всего учащихся, говорящих на иностранном языке? Сколько из них не говорит по-французски? Сколько из них не говорит по-немецки? Сколько из них не говорит на иностранном языке?

Ответ: а) На всех трех языках говорят 3 ученика; б) По-английски и по-немецки – 15 человек; в) только по-французски – 8 учащихся. Всего 100 (40+7+3+15+5+22+8) ребят, говорящих на иностранных языках. По-французски не говорят 77учащихся (100-(8+5+7+3) . Решение. Для решения задачи удобно воспользоваться кругами Эйлера. В нашем случае три круга: большой круг – это множество чисел от 1 до 10, внутри большого – два меньших круга, пресекающихся друг с другом. Пусть множество чисел, кратных 2– это множество А, а множество чисел, кратных 3 – множество В. Рассуждаем. На 2 делится каждое второе число. Значит, таких чисел будет 10:2=5. На 3 делится 3 числа (10:3). На 2 и 3 делятся те числа, которые делятся на 6. Такое число только одно. Поэтому множество А состоит из 5-1=4 чисел, множество В – 3-1=2 чисел. Отсюда следует, что в первом десятке содержится 10-(4+1+2)=3 числа.

Реши самостоятельно

Задача № 3. В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам.

Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?

Решение

Задача № 4. В классе 35 учеников. В математическом кружке из них 12 занимаются, в биологическом — 9, а 16 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?

Решение.

Математика Эйлера – Круг Эйлера

На курсе Математика Эйлера (Летняя сессия 2, 2023 г.) мы изучим работу Леонарда Эйлера, одного из величайших математиков в истории, а также того, в честь которого назван круг Эйлера. Поскольку Эйлер, возможно, был самым плодовитым математиком в истории, у нас не будет возможности рассмотреть все его работы, но мы рассмотрим некоторые из его наиболее интересных работ и результатов. Эйлер был пионером во многих разделах математики, от топологии до теории графов, анализа, групп Ли, модулярных форм и вариационного исчисления, и, как следствие, он смог обнаружить некоторые из прекрасных ранних результатов в этих областях раньше, чем кто-либо другой.

до них дошло другое: он видел математику, когда другие не понимали, что она существует. В этом классе мы будем мотивированы работой Эйлера, чтобы представить некоторые из этих тем

Статьи Эйлера, по крайней мере те, которые были переведены на английский язык, приятно читать. В то время как современные авторы обычно скрывают свой мыслительный процесс и пишут только о том, что сработало, Эйлер стремился рассказать своим читателям, о чем он думал, и даже о том, что он не смог сделать. Мы все можем многому научиться, читая мысли математика такого уровня; хорошо бы последовать совету Лапласа: «Читайте Эйлера: он господин над всеми нами!» Так и будем.

Современные стандарты строгости в математике были систематизированы в девятнадцатом веке. Таким образом, Эйлер, математик восемнадцатого века, не был связан ими и не знал, насколько строгой и точной станет математика в следующем столетии. Таким образом, он был счастлив играть быстро и свободно с бесконечностями и расходящимися рядами, так, как современные математики никогда не советуют делать.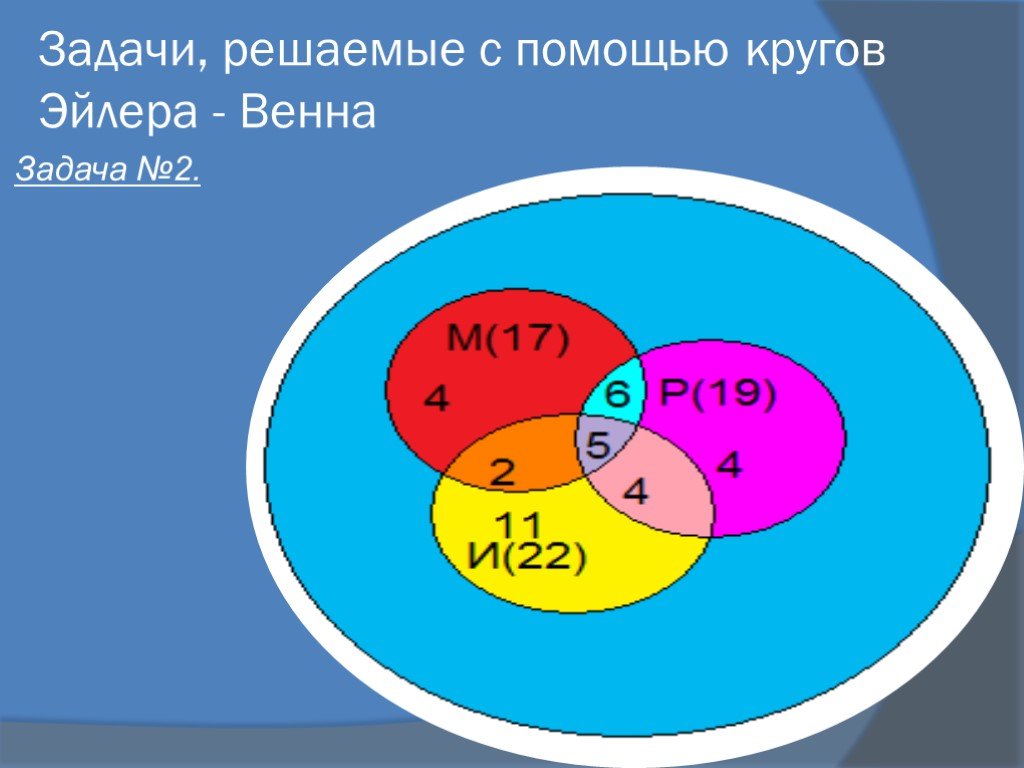

Но мы никогда не должны забывать, как весело играть с математикой и определять, что верно и как все работает, не слишком беспокоясь о точных правилах игры. Например, Эйлер был первым, кто сделал ныне известное и противоречивое наблюдение, что . Это неверно в смысле сходимости рядов, концепции девятнадцатого века. Но это намекает на очень глубокое и важное понятие аналитического продолжения. Все уловки Эйлера — намеки на глубокие концепции, которые остаются очень важными в современной математике, и мы рассмотрим (небольшой образец), что они из себя представляют и к чему привели работы Эйлера в последнее время.

На этом уроке мы предполагаем, что учащиеся знакомы с математическим анализом, либо посещая занятия по нему, либо изучая его самостоятельно.

Этот курс будет проходить в течение 5 недель, с 17 июля по 18 августа, по понедельникам, вторникам, четвергам и пятницам с 17:00 до 19:00 по тихоокеанскому времени. В другое время могут быть дополнительные необязательные (но настоятельно рекомендуемые) сеансы. Ожидается, что студенты будут выполнять значительный объем работы вне класса; Ожидается, что это будет основной деятельностью учащихся на протяжении всего занятия. Класс в основном будет проводиться в Zoom, но мы можем запланировать дополнительные личные занятия для местных студентов, если будет достаточный интерес.

Заявки на этот курс принимаются до 9 апреля. Нажмите здесь, чтобы подать заявку!

Нравится:

Нравится Загрузка…

Нажмите здесь, чтобы подписаться на рассылку!

Добро пожаловать в круг Эйлера! – Эйлеровский круг

Примечание: Euler Circle будет проводиться онлайн до тех пор, пока не станет безопасно возобновить очные занятия. Вам не обязательно проживать в районе залива Сан-Франциско, чтобы посещать онлайн-занятия. Весной мы проведем занятие по переходу к доказательствам в анализе. Летом мы проведем углубленные занятия по комбинаторике и комбинаторной теории игр.

Вы учитесь в старшей школе в районе залива Сан-Франциско и любите математику? Вы находите традиционную учебную программу по математике слишком простой? Вы хотите изучать увлекательную и сложную математику? Вы хотите работать над задачами и подружиться с математически мыслящими сверстниками? Если это так, вы пришли в нужное место!

What

Euler Circle — математический институт в районе залива Сан-Франциско для студентов продвинутого уровня, которые любят математику. Мы предлагаем ряд занятий по математике на уровне колледжа, специально адаптированных к потребностям старшеклассников, многие из которых исчерпали учебную программу по математике в своих школах и хотят узнать больше. Каждый предлагаемый нами курс эквивалентен уроку математики в колледже. На каждом занятии учащиеся решают множество задач, чтобы ознакомиться с новым материалом, а на продвинутых занятиях каждый учащийся пишет пояснительную работу по теме, связанной с материалом занятия.

Занятия устроены таким образом, чтобы обеспечить путь к независимым исследованиям. Многие из наших наборов задач в продвинутых классах включают нерешенные проблемы, которые учащиеся могут исследовать после того, как освоят материал, представленный в классе. Мы предлагаем встречи в небольших группах для студентов, заинтересованных в работе над исследовательскими проблемами, после того, как они продемонстрировали способность усердно работать над сложными задачами. Подробнее об исследованиях см. в круге Эйлера.

Почему

Математика — это больше, чем соревнования. Тем не менее, у старшеклассников мало ресурсов, чтобы узнать об остальном чудесном мире математики. Мы считаем, что многие студенты хотели бы увидеть, что еще есть, и мы хотим поделиться тем, что знаем.

Когда/где

Весной у нас будет одно открытое занятие. Это третья четверть перехода к последовательности доказательств с упором на анализ. Занятия начнутся 29 марта.и работать в течение 10 последовательных понедельников. Заявки принимаются 28 февраля . После этого мы продолжим принимать заявки по мере поступления, пока остаются места. Занятие будет проходить онлайн в Zoom. Нажмите здесь, чтобы подать заявку!

Также открыты заявки на летние занятия, которые также будут онлайн в Zoom. Мы проведем два продвинутых класса подряд. Первая сессия будет посвящена комбинаторике, а вторая — комбинаторной теории игр. Эти классы будут встречаться в понедельник, вторник, четверг и пятницу утром в течение 5 недель каждый.