2.2 Графический метод решения задач линейного программирования
Данный метод применяется для решения задач, содержащих не более трех переменных, чаще всего для задач с двумя переменными. Он базируется на следующих моментах:
целевая функция достигает своего оптимального значения в вершине области. Если она принимает это значение в двух вершинах области, то оптимум достигается в любой точке отрезка, соединяющего эти вершины;
направляющий вектор (вектор нормали) перпендикулярен прямой функции цели и всегда указывает направление ее возрастания.
Схему применения графического метода проиллюстрируем на конкретном примере, рассматривая три этапа:
построение области допустимых решений;
построение направляющего вектора и определение оптимальных точек;
нахождение оптимальных значений переменных и целевой функции.

Найти максимальное и минимальное значение функции
при ограничениях
І этап. Построение области допустимых решений
Каждому неравенству ставим в соответствие равенство, геометрическим образом которого является прямая линия. Для ее построения достаточно двух точек.
— эта прямая пройдет через точки (2; 0) и (0; 3).
0
3
2
0
— эта прямая пройдет через точки (-3; 0) и (0; 2).
0
2
– 3
0
— эта прямая пройдет через точки (4; 0) и (0; -4).

0
– 4
4
0
— эта прямая пройдет через точки (7; 0) и (0; 4).
0
4
7
0
Каждая прямая делит плоскость на две полуплоскости, в одной из которых будет справедливо соответствующее неравенство.
 Чтобы установить, точки какой полуплоскости
будут обеспечивать выполнение
неравенства, необходимо взять произвольную
точку и ее координаты подставить в
неравенство. Если для этой точки
неравенство выполнилось, то решением
неравенства будет та полуплоскость, в
которой брали точку. Если неравенство
для выбранной точки не выполнилось, то
его решением будут точки второй
полуплоскости. Рассматривая поочередно
все ограничения, получим область, в
которой будут справедливы все неравенства,
— это и есть область допустимых решений.
Чтобы установить, точки какой полуплоскости
будут обеспечивать выполнение
неравенства, необходимо взять произвольную
точку и ее координаты подставить в
неравенство. Если для этой точки
неравенство выполнилось, то решением
неравенства будет та полуплоскость, в
которой брали точку. Если неравенство
для выбранной точки не выполнилось, то
его решением будут точки второй
полуплоскости. Рассматривая поочередно
все ограничения, получим область, в
которой будут справедливы все неравенства,
— это и есть область допустимых решений.
Неравенства и означают, что область будет находиться в первой четверти. В нашем случае областью допустимых решений являются точки пятиугольника .
ІІ этап. Определение оптимальных точек
Направляющий вектор проводят из начала координат в точку с координатами, равными коэффициентам целевой функции, то есть в точку . Он всегда указывает направление возрастания функции, направление убывания целевой функции будет противоположным.

Если в задаче требуется найти максимум, прямую перемещают параллельно в сторону стрелки направляющего вектора до последней точки области – эта точка и будет точкой максимума. В примере наибольшее значение достигается в вершине .
Если требуется найти минимум, то прямую перемещают параллельно в противоположную сторону до последней точки области. В данном случае наименьшее значение достигается в вершине .
ІІІ этап. Нахождение оптимальных значений
Чтобы найти переменные, обеспечивающие экстремум, необходимо решить систему уравнений тех прямых, на пересечении которых располагается точка экстремума
а) находим | б) находим |
Таким образом, найдены
максимальное и минимальное значение
функции, все промежуточные значения
будут достигаться в других точках
области допустимых значений.
Замечание 1. Если прямая функции окажется параллельной какой-нибудь стороне многоугольника ограничений, то в этом случае задача имеет бесчисленное множество решений: координаты любой точки этой стороны многоугольника (в том числе и вершины) будут решением задачи.
Замечание 2. Если область решений не ограничена, то задача или не имеет решения, или целевая функция может принять только максимальное или только минимальное значение, или задача имеет бесконечное множество решений.
Пример решения задачи по ЭМММ
Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и mcd в архиве zip, начнется автоматически через 10 секунд.
СОДЕРЖАНИЕ
Введение ………………………………………………………………………….4
1. Постановка задачи ……………………………………………………………..5
2. Построение математической модели решения задачи………………………6
2.1. Определение вариантов раскроя рулонов…………………………………. 6
6
2.2. Математическая модель оптимизации………………………………..……..8
3. Решение задачи оптимизации в Mathcad…………………………………..…11
ВВЕДЕНИЕ
Экономико–математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала
Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.
Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющими эту область. Целевая функция в самом общем виде в свою очередь также состоит из трех элементов:
* управляемых переменных;
* неуправляемых переменных;
* формы функции (вида зависимости между ними).
Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.
Целью данной работы является применение методов линейного программирования для оптимизации раскроя материала. Основной задачей данного метода является, построение целевой функции, минимизирующей остатки материала и системы ограничений на имеющийся в запасе материал. Сама же задача линейного программирования будет реализована нами в программе Mathcad.
1. ПОСТАНОВКА ЗАДАЧИ
Предприятие для изготовления издательской продукции должно раскроить рулонный материал шириной 2 м. на заданное количество рулонов трех размеров меньшей ширины. Требуется составить все возможные варианты раскроя. Определить оптимальные варианты раскроя исходных рулонов, при которых выполняется задание по количеству раскроенных рулонов каждой ширины, и при этом получить минимум потерь материалов за счет отходов и лишних рулонов.
Исходные данные приведены в таблице 1.
Таблица 1
|
Номера раскроенных рулонов |
1 |
2 |
3 |
|
Ширина раскроенных рулонов, см. |
50 |
60 |
90 |
|
Задание по количеству раскроенных рулонов |
100 |
120 |
150 |
Задача должна решаться методом линейного программирования в Mathcad 2000/2001.
2. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
РЕШЕНИЯ ЗАДАЧИ
2.1. Определение вариантов раскроя рулонов
В курсовой работе рассматривается модель оптимального раскроя рулонного материала на рулоны меньшей ширины.
Для построения математической модели необходимо сначала определить все способы раскроя рулонов, которые возможны для заданных исходных данных, и получаемые при этом отходы (обрезки). Применяется следующее правило составления вариантов.
1. Сначала рассматривается вариант раскроя, при котором получаются только самые узкие рулоны шириной 50 см.
2. Число узких рулонов, полученное в предыдущем пункте, уменьшается на единицу и делается попытка заменить его максимальным числом рулонов, ближайших по ширине.
3. Делается попытка повторить предыдущий пункт для рулонов следующего размера (60 см.).
4. Если в предыдущих двух пунктах заменяемых размеров нет, то число узких рулонов уменьшается ещё на единицу и повторяется попытка включения всех размеров, начиная с ближайшего большего.
5. После перебора всех вариантов, получаемых по пунктам 1-2, исключаются из рассмотрения самые узкие рулоны, и все повторяется заново для рулонов с размерами 60 и 90 см. и т.д.
6. Если в результате перебора получаются заведомо худшие варианты (содержат меньшее количество разрезанных рулонов одной ширины по сравнению с ранее принятыми вариантами), то они исключаются.
В таблице 2 приводятся все возможные варианты раскроя рулонов.
Таблица 2
|
№ варианта раскроя |
Количество рулонов заданной ширины, шт. |
Отходы, см. |
||
|
42 см. |
70 см. |
84 см. |
||
|
1 |
4 |
0 |
0 |
0 |
|
2 |
2 |
0 |
1 |
10 |
|
3 |
2 |
1 |
0 |
40 |
|
4 |
1 |
2 |
0 |
30 |
|
5 |
1 |
1 |
1 |
0 |
|
6 |
0 |
3 |
0 |
20 |
|
7 |
0 |
0 |
2 |
20 |
2. 2. Математическая модель оптимизации
2. Математическая модель оптимизации
Решение задачи, обеспечивающей вычисление минимума потерь материала, производится методом линейного программирования. Целевая функция должна минимизировать потери материалов за счет отходов и за счет лишних рулонов.
Первоначально рассматривается задача линейного программирования для минимизации потерь за счет отходов. Часть целевой функции, предназначенной для минимизации потерь за счет отходов, записывается в виде:
,
где х1, х2, …, хn – вектор искомых переменных, определяющих количество рулонов, которые раскраиваются по i-му варианту, i = 1, 2, …, n, n = 7;
n – количество всех возможных вариантов раскроя рулонов;
c – вектор, элементами которого является количество отходов при раскрое по i-му варианту, i = 1, 2, …, n.
Целевую функцию можно записать в векторной форме:
Кроме целевой функции, необходимо ввести ограничения.
Ограничения построим из условия получения не менее заданного количества разрезанных рулонов каждого типа.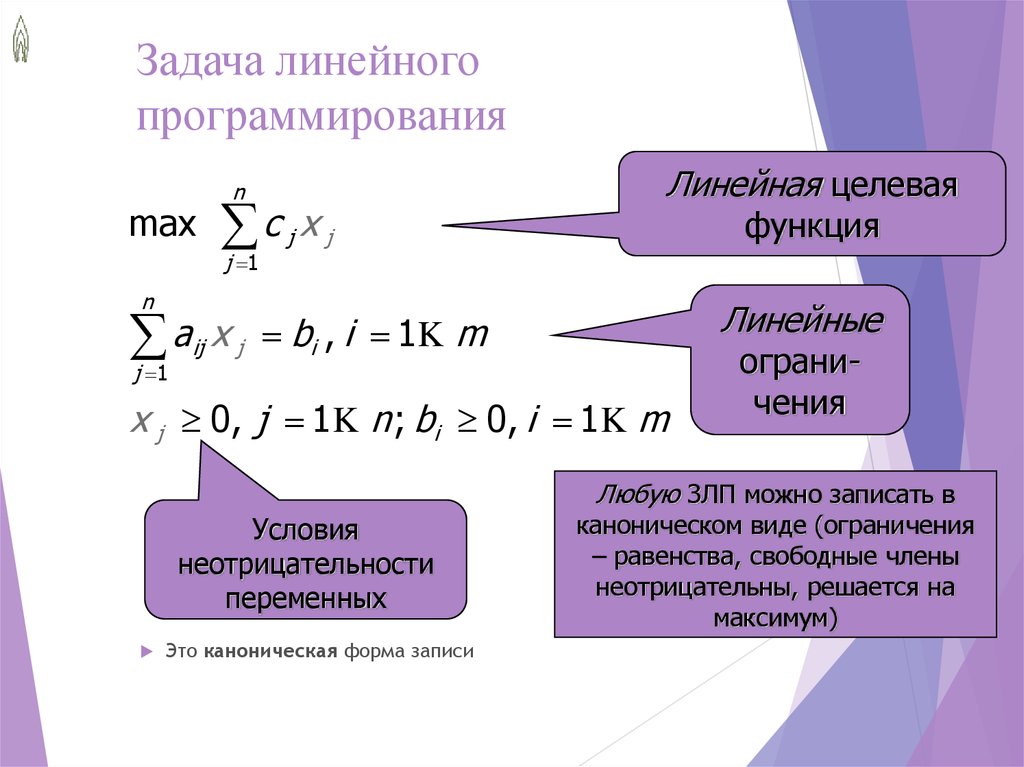
Составим их следующим образом.
Для рулонов шириной 50 см. должно быть получено по заданию не меньше чем 100 рулонов. Во втором столбце таблицы 2 указано, сколько рулонов шириной 50 см. получится из одного рулона шириной 2м. (200 см.) по каждому из вариантов раскроя. Так, по первому варианту раскроено х1 исходных рулонов – из одного рулона получается 4 рулона шириной 50 см., в итоге имеем 4х1 таких рулонов, разрезанных первым способом. Общее число рулонов шириной 50 см. равно сумме таких произведений, полученных при раскрое всеми способами. Таким образом, ограничение по количеству рулонов шириной 50 см., определяется следующим неравенством:
(1)
Следующие два ограничения построим аналогично из условия получения не менее, чем заданное количество рулонов шириной 60 и 90 см. соответственно:
(2)
(3)
Обязательным является ограничение, вытекающие из условия неотрицательности переменных:
(4)
Выражения (1) – (4) описывают математическую модель решения задачи минимизации отходов.
Вторая часть целевой функции должна минимизировать потери от лишних рулонов.
Для вывода выражения второй части целевой функции вернемся к неравенствам (1) – (3). Если умножить левые части этих неравенств на ширину соответствующих рулонов, то их сумма выражает общую ширину всех разрезанных рулонов. Часть целевой функции, минимизирующая расход материалов, выражается формулой
Целевая функция, минимизирующая общий расход материалов и соответственно минимизирующая потери за счет отходов и лишних рулонов, определяется следующим выражением:
Таким образом, математическая модель оптимизации раскроя рулонного материала по критерию минимума расхода материалов и потерь за счет отходов и лишних рулонов выражается формулой:
. (5)
3. РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ В MATHCAD
Для решения задачи используется пакет Mathcad с функцией Minimize. Данная функция определяет вектор х оптимального решения задачи:
Данная функция определяет вектор х оптимального решения задачи:
х := Minimize (Q, x),
с учетом ограничений, приведенных в системе (5).
Решение приводится в приложении. В результате решения данной задачи линейного программирования получен результат вычислений:
хТ = (0 0 0 0 100 7 25), Q(x) = 26 330.
Запись в Mathcad первого из выражений системы (5) вызывает трудности, если это выражение не помещается в видимую часть экрана. Поэтому сделаем приведение подобных членов. После приведения получается следующее выражение, которое полностью подобно первому выражению в (5):
Элементы вектора х – это оптимальное количество рулонов, которые должны быть раскроены i-м способом I = 1, 2, …, n. Решение задачи осуществляется следующим образом. в начале расчета заданы нулевые начальные значения вектора х. В векторе с заданы значения отходов для каждого из способов раскроя. В разделе между ключевым словом Given и функцией Minimize помещены ограничения.
После выражения с функцией Minimize в той же строке приводятся результаты решения задачи. Вектор х содержит оптимальное количество рулонов, раскроенных разными способами, а именно: хТ = (0 0 0 0 100 7 25). Это означает, что пятым способом должны быть раскроены 100 рулонов, шестым – 7 рулонов, седьмым – 25 рулонов. Другие способы раскроя не применяются как неэкономичные. Всего для выполнения заданий по раскрою требуется 132 рулона шириной 2 м. В метрах это значение выражается критерием оптимизации Q (x) = 263,3 м.
В трех нижних строках приложения анализируется количество лишних рулонов путем вычитания фактического количества разрезанных рулонов каждой ширины с заданием. Нулевые разности свидетельствуют, что лишних разрезанных рулонов нет. А разность равная 1 свидетельствует о том, что остается один лишний рулон шириной 60 см.
Следовательно, полученное решение задачи раскроя является оптимальным и обеспечивает минимум потерь материалов. Общие потери материала определяются как произведение векторов: с х / 100 = 6,4 м.
Линейное программирование
Модель – это
аналог (образ) оригинала, но построенный средствами и методами отличными от оригинала
подобие оригинала
копия оригинала
Экономико-математическая модель – это
математическое представление экономической системы (объектов, задачи, явлений, процессов и т. п.)
качественный анализ и интуитивное представление объектов, задач, явлений, процессов экономической системы и ее параметров
эвристические описание экономической системы (объектов, задачи, явлений, процессов и т. п.)
Метод – это
подходы, пути и способы постановки и решения той или иной задачи в различных областях человеческой деятельности
описание особенностей задачи (проблемы) и условий ее решения
требования к условиям решения той или иной задачи
ЭММ позволяют
сделать вывод о поведении объекта в будущем
управлять объектом
выявить оптимальный способ действия
выявить и формально описать связи между переменными, которые характеризуют исследования
Экономико-математическая модель межотраслевого баланса – это
макроэкономическая, детерминированная, имитационная, матричная модель
микроэкономическая, детерминированная, балансовая, регрессионная модель
макроэкономическая, детерминированная, балансовая, матричная модель
макроэкономическая, вероятностная, имитационная, матричная модель
Найти экстремум функции f(x) при выполнении ограничений Ri(x) = ai, φ (x) ≤ bj, наложенных на параметры функции – это задача
условной оптимизации
линейного программирования
безусловной оптимизации
нелинейного программирования
динамического программирования
Задача, включающая целевую функцию f и функции Ф, входящие в ограничения, является задачей линейного программирования, если
все Ф и f являются линейными функциями относительно своих аргументов
все Ф являются линейными функциями относительно своих аргументов, а функция f – нелинейна
функция f является линейной относительно своих аргументов, а функции Ф – нелинейны
только часть функций Ф и функция f являются линейными относительно своих аргументов
Множество всех допустимых решений системы задачи линейного программирования является
выпуклым
вогнутым
одновременно выпуклым и вогнутым
Если задача линейного программирования имеет оптимальное решение, то целевая функция достигает нужного экстремального значения в одной из
вершин многоугольника (многогранника) допустимых решений
внутренних точек многоугольника (многогранника) допустимых решений
точек многоугольника (многогранника) допустимых решений
В задачах линейного программирования решаемых симплекс-методом искомые переменные должны быть
Неотрицательными
положительными
свободными от ограничений
любыми
Симплексный метод решения задач линейного программирования включает
определение одного из допустимых базисных решений поставленной задачи (опорного плана)
определение правила перехода к не худшему решению
проверку оптимальности найденного решения
определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения
Графический способ решения задачи линейного программирования – это
построение прямых, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств
нахождение полуплоскости, определяемой каждым из ограничений задачи
нахождение многоугольника допустимых решений
построение прямой F = h = const >= 0, проходящей через многоугольник решений
построение вектора C, перпендикулярного прямой F = h = const
передвижение прямой F = h = const в направлении вектора C (в сторону увеличения h), в результате чего находят либо точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве допустимых решений
определение координат точки максимума функции и вычисление значения целевой функции в этой точке
Задача линейного программирования не имеет конечного оптимума, если
в точке А области допустимых значений достигается максимум целевой функции F
в точке А области допустимых значений достигается минимум целевой функции F
система ограничений задачи несовместна
целевая функция не ограничена сверху на множестве допустимых решений
При приведении задачи линейного программирования (ЛП) к виду основной задачи ЛП ограничения вида «< или =» преобразуются в ограничения равенства добавлением к его левой части дополнительной неотрицательной переменной. Вводимые дополнительные неизвестные имеют вполне определенный смысл. Так, если в ограничениях исходной задачи ЛП отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в решении задачи, записанной в виде основной имеет смысл
Вводимые дополнительные неизвестные имеют вполне определенный смысл. Так, если в ограничениях исходной задачи ЛП отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в решении задачи, записанной в виде основной имеет смысл
двойственной оценки ресурса
остатка ресурса
нехватки ресурса
стоимости ресурса
Если ресурс образует «узкое место производства», то это означает
ресурс избыточен
ресурс использован полностью
двойственная оценка ресурса равна нулю
Критерием остановки вычислений в алгоритме поиска оптимального решения методами одномерной оптимизации является условие
отношение длины текущего интервала неопределенности к длине первоначального интервала меньше заданной величины ε
значение целевой функции (ЦФ), вычисленное в текущей точке, меньше значения ЦФ, вычисленного в последующей точке
отношение длины текущего интервала неопределенности к длине первоначального интервала больше заданной величины ε
значение ЦФ, вычисленное в текущей точке, меньше значения ЦФ, вычисленного в предыдущей точке
Если целевая функция и все ограничения выражаются с помощью линейных уравнений, то рассматриваемая задача является задачей
динамического программирования
линейного программирования
целочисленного программирования
нелинейного программирования
Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений, называется
стандартной
канонической
общей
основной
нормальной
Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой неравенств, называется
стандартной
канонической
общей
основной
нормальной
В линейных оптимизационных моделях, решаемых с помощью геометрических построений число переменных должно быть
не больше двух
равно двум
не меньше двух
не больше числа ограничений 2
сколько угодно
Задача линейного программирования может достигать максимального значения
только в одной точке
в двух точках
во множестве точек
в одной или двух точках
в одной или во множестве точек
Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная
Неотрицательна
положительна
свободна от ограничений
отрицательная
Транспортная задача является задачей …. Программирования
Программирования
динамического
нелинейного
линейного
целочисленного
параметрического
Если в транспортной задаче объем спроса равен объему предложения, то такая задача называется
замкнутой
закрытой
сбалансированной
открытой
незамкнутой
Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят
фиктивный пункт производства
фиктивный пункт потребления
изменения структуры не требуются
Методы теории игр предназначены для решения задач
с конфликтными ситуациями в условиях неопределенности
с полностью детерминированными условиями
статистического моделирования
Стратегия игрока – это совокупность правил, определяющих выбор его действий при
каждом ходе в зависимости от сложившейся ситуации в одном сеансе игры
одном ходе игры
всех сеансах игры
Нижняя цена игры – это
максимин, т. е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
гарантированный выигрыш одного из игроков при любой стратегии другого игрока
минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
Верхняя цена игры – это
минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
гарантированный проигрыш одного из игроков при любой стратегии другого игрока
максимин, т.е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
Решение игры в чистых стратегиях определяется
ценой игры, равной нижней цене игры
ценой игры, равной верхней цене игры
наличием седловой точки
всем перечисленным в ответах на это задание
Решение игры в смешанных стратегиях определяется
вероятностью выбора каждой из активных (полезных) стратегий, совокупный выигрыш которых представляет случайную величину с математическим ожиданием равным цене игры
ценой игры, равной нижней цене игры
ценой игры, равной верхней цене игры
наличием седловой точки
Задача, процесс нахождения решения которой является многоэтапным, относится к задачам
линейного программирования
теории игр
динамического программирования
нелинейного программирования
параметрического программирования
Egwald Operations Research — Линейное программирование
Исследование операций — Линейное программирование — Генератор двойных симплексных таблиц
by
Элмер Г. Винс
Винс
Популярные веб-страницы Egwald предоставляются пользователям бесплатно.
Пожалуйста, проявите свою поддержку, присоединившись к Egwald Web Services в качестве поклонника Facebook:
Подпишитесь на Элмера Винса в Твиттере:
Графическое решение |
Симплексный алгоритм |
Генератор простых симплексных таблиц |
Двойной симплексный алгоритм |
Генератор двойных симплексных таблиц
Экономическое применение — максимизация прибыли |
Экономическое приложение — формула наименьшей стоимости
пример задачи | твой л.п. проблема | симплексный алгоритм | использованная литература
Метод двойного симплекса преобразует исходную таблицу в конечную таблицу, содержащую решения прямой и двойственной задач. Каждый этап алгоритма генерирует промежуточную таблицу по мере того, как алгоритм нащупывает решение.
Эта веб-страница позволяет вам ввести свою собственную задачу линейного программирования и создать эти таблицы с помощью удобного для пользователя интерфейса. Вы можете указать до 6 переменных и 10 ограничений в основной задаче с любым сочетанием ограничений = и =.
Вы можете указать до 6 переменных и 10 ограничений в основной задаче с любым сочетанием ограничений = и =.
Чтобы проиллюстрировать процедуру, которую необходимо выполнить, рассмотрим задачу:
| Основная линейная программа Максимизируйте целевую функцию (P) P = 15 х 1 + 10 х 2 + 17 х 3 с учетом L1: 1,0 x 1 + 1,0 x 2 + 1,0 x 3 L2: 1,25 x 1 + 0,5 x 2 + 1,0 x 3 >= 90 L3: 0,6 х 1 + 1,0 х 2 + 0,5 х 3 = 55 х 1 >= 0; х 2 >= 0; x 3 >= 0 |
с диаграммой:
Для формирования формы для входа в л.п. данные вы должны установить параметры, которые определяют ваш l. p. проблема, как я сделал ниже для проблемы выше.
p. проблема, как я сделал ниже для проблемы выше.
| Название задачи LP: Моя задача LP | ||||
|---|---|---|---|---|
| Количество переменных: n = 3 | Количество ограничений: м = 3 | |||
| Количество м1 = 1 | Количество >= ограничений: м2 = 1 | Количество = ограничений: м3 = 1 | ||
На параметры накладываются определенные ограничения:
м = м1 + м2 + м3; п 0;
м > 0; м1 >= 0; м2 >= 0; м3 >= 0,
Форма параметров вашего LP.
После того, как вы заполните форму и нажмете «Отправить параметры», откроется веб-страница с таблицей, подобной приведенной ниже, где вы можете ввести данные своего l.p. проблема. Обратите внимание, что вам не нужно ни умножать = constrainst на -1, ни преобразовывать >= ограничения в
Таблица форм =
| Моя проблема LP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P = | 15 | х 1 | + | 10 | x 2 | + | 17 | x 3 | при условии | |
| L 1 | 1 | x 1 | + | 1 | x 2 | + | 1 | x 3 | 85 | |
| L 2 | 1,25 | x 1 | + | 0. 5 5 | x 2 | + | 1 | x 3 | >= | 90 |
| L 3 | 0.6 | x 1 | + | 1 | x 2 | + | 0,5 | x 3 | = | 55 |
После того, как вы введете свои данные и нажмете кнопку «Отправить», программа автоматически рассчитает последовательность таблиц, которая решает прямую и двойную л.п. проблемы. Изучите следующие таблицы, чтобы увидеть, как метод двойного симплекса работает над поиском решения.
Чтобы выполнить анализ чувствительности вашей задачи линейного программирования, измените данные в таблице выше и снова нажмите Submit LP .
Двойной симплексный алгоритм.
Стандартная форма исходной двойной симплексной таблицы:
| Исходная таблица | ||
| b | A | I 3 |
| 0 9027 T | -c0062 | O 3 T |
Алгоритм двойного симплекса вычисляет последовательность таблиц. Таблица k имеет вид:
Таблица k имеет вид:
| = |
| |||||||||||||||||
после объединения центрального 2 на 2 блока матриц.
«трехфазный метод» двойного симплексного алгоритма :
Фаза 0 — свести все искусственные переменные (связанные с = ограничениями) к нулю, т. Фаза I — найти таблицу с Ø >= 0, т.е. допустимую двойную программу; Фаза II — сгенерировать таблицы, которые уменьшают значение µ, превращая ß >= 0, не возвращаясь к фазе 0 или I, т. е. находят допустимую базовую двойственную программу, которая минимизирует целевую функцию D. |
Фаза 0: Вывести искусственные переменные из основы.
| Таблица 0 | ||||||||
| б 0 | х 0 1 | х 0 2 | х 0 3 | с 0 1 | с 0 2 | с* 0 3 | row sum | |
| L 0 1 | 85 | 1 | 1 | 1 | 1 | 0 | 0 | 89 |
| L 0 2 | -90 | -1. 25 25 | -0.5 | -1 | 0 | 1 | 0 | -91.75 |
| L 0 3 | 55 | 0.6 | 1 | 0.5 | 0 | 0 | 1 | 58.1 |
| P 0 | 0 | -15 | -10 | -17 | 0 | 0 | 0 | -42 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Basis for Tableau 0 : [ с 1 , с 2 , с 3 , ]. Значение целевой функции = 0,
Значение целевой функции = 0,
Перейти к следующей таблице следующим образом:
Фаза 0: Вывести искусственные переменные из базы.
А. В таблице 0 :
1. Выбрать искусственную переменную в базе: s * 3 . Сводная строка = 3.
2. Выбрать ненулевой элемент в строке L 3 как сводная: Û 3,2 = 1. Сводная колонка = 2.
B. Для создания таблицы 1 :
3. Вычислить строку L 1 3 = L 0 3 / (1).
4. Вычесть числа, кратные строке L 1 3 , из всех остальных строк таблицы 0 так, чтобы x 1 2 = e 2 а.е. 3 в таблице
Фаза I: Цель: получить Ø >= 0.
| Таблица 1 | |||||||||||||||||||||||||||||
| б 1 | x 1 1 | x 1 2 | х 1 3 | с 1 1 | с 1 2 | с* 1 3 | row sum | ||||||||||||||||||||||
| L 1 1 = L 0 1 — (1) * L 1 3 | 30 | 0. 4 4 | 0 | 0.5 | 1 | 0 | -1 | 30,9 | |||||||||||||||||||||
| L 1 2 = L 0 2 — (-0.5) * L 1 3 | -62.5 | -0.95 | 0 | -0.75 | 0 | 1 | 0.5 | -62.7 | |||||||||||||||||||||
| L 1 3 = L 0 3 / (1) | 55 | 0. 6 6 | 1 | 0.5 | 0 | 0 | 1 | 58.1 | |||||||||||||||||||||
| Р 1 = Р 0 -(-10) * L 1 3 | 550 | -9 | 0 | -12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 5 | 0 5 | 0 | . L 1 3 L 1 3 | 0 | 15 | 0 | 24 | 0 | 0 | 0 | 0 | |||||||
Basis for Tableau 1 : [s 1 , s 2 , х 2 , ]. Значение целевой функции = 550,
Перейти к следующей таблице следующим образом:
Фаза 0: Завершена.
Этап I: Цель: получить Ø >= 0.
A. В таблице 1 :
1. Выберите целевой столбец , tcol, с Ø tcol 1 1 = -9, tcol = 1.
2. Выберите любую строку r с положительной записью в tcol = 1 в качестве опорной строки : строка = 3, связанная с Û 3,1 = 0,6 и ограничением L 3 .
3. Рассчитайте отношения -Ø / L 3 согласно последней строке. Отбросьте коэффициенты, которые не являются положительными, и коэффициенты, связанные с искусственными переменными. Выберите столбец с наименьшим положительным отношением в качестве опорного столбца : столбец = 1, связанный с 15. Таким образом, Û 3,1 = 0,6 является опорным ; переменная x 2 уйдет из базы; переменная x 1 войдет в основу.
B. Для создания Tableau 2 :
4. Вычислить строку L 2 3 = L 1 3 / (0,6).
5. Вычтите кратные строки L 2 3 из всех остальных строк Таблицы 1 так, чтобы x 1 = e 3 в Таблице 2 .
| Таблица 2 | ||||||||
| б 2 | х 2 1 | x 2 2 | x 2 3 | с 2 1 | с 2 2 | с* 2 3 | row sum | |
L 2 1 = L 1 1 — (0. 4) * L 2 3 4) * L 2 3 | -6.667 | 0 | -0.667 | 0.167 | 1 | 0 | -1.667 | -7.833 |
| L 2 2 = L 1 2 — (-0.95) * L 2 3 | 24.583 | 0 | 1.583 | 0.042 | 0 | 1 | 2.083 | 29. 292 292 |
| L 2 3 = L 1 3 / (0.6) | 91.667 | 1 | 1.667 | 0.833 | 0 | 0 | 1.667 | 96.833 |
| P 2 = P 1 — (-9) * L 2 3 | 1375 | 0 | 15 | -4.5 | 0 | 0 | 25 | 1410. 5 5 |
| -P 2 / L 2 3 | 0 | 0 | 0 | 5.4 | 0 | 0 | 0 | 0 |
Основа для таблицы 2 : [s 1 , s 2 , x 1 , ]. Значение целевой функции = 1375,
Перейти к следующей таблице следующим образом:
Фаза 0: Завершена.
Этап I: Цель: получить Ø >= 0.
A. В таблице 2 :
1. Выберите целевой столбец , tcol, с Ø tcol 2 3 = -4,5, tcol = 3.
2. Выберите любую строку r с положительной записью в tcol = 3 в качестве опорной строки : строка = 3, связанная с Û 3,3 = 0,833 и ограничением L 3 .
3. Рассчитайте отношения -Ø / L 3 согласно последней строке. Отбросьте коэффициенты, которые не являются положительными, и коэффициенты, связанные с искусственными переменными. Выберите столбец с наименьшим положительным соотношением в качестве сводного столбца : col = 3, связанный с 5.4. Таким образом х 3,3 = 0,833 — точка опоры ; переменная x 1 уйдет из базы; переменная x 3 войдет в основу.
B. Для создания таблицы 3 :
4. Вычислить строку L 3 3 = L 2 3 / (0,833).
5. Вычтите кратные строки L 3 3 из всех остальных строк Таблицы 2 так, чтобы x 3 = e 3 в Таблице 3 .
Фаза II: Цель: получить ß >= 0.
| Таблица 3 | ||||||||
| б 3 | x 3 1 | x 3 2 | x 3 3 | с 3 1 | с 3 2 | с* 3 3 | ряд сумма | |
л 3 1 = L 2 1 — (0. 167) * L 3 3 167) * L 3 3 | -25 | -0.2 | -1 | 0 | 1 | 0 | — 2 | -27.2 |
| L 3 2 = L 2 2 — (0.042) * L 3 3 | 20 | -0.05 | 1.5 | 0 | 0 | 1 | 2 | 24,45 |
L 3 3 = L 2 3 / (0. 833) 833) | 110 | 1.2 | 2 | 1 | 0 | 0 | 2 | 116.2 |
| P 3 = P 2 — (-4.5) * L 3 3 | 1870 | 5.4 | 24 | 0 | 0 | 0 | 34 | 1933.4 |
| -P 3 / L 3 1 | 0 | 27 | 24 | 0 | 0 | 0 | 0 | 0 |
Basis for Tableau 3 : [s 1 , с 2 , х 3 , ]. Значение целевой функции = 1870,
Значение целевой функции = 1870,
Перейти к следующей таблице следующим образом:
Фаза 0: Завершена.
Фаза I: Завершена.
Этап II: Цель: получить ß >= 0,
А. В таблице 3 :
1. Выберите сводную строку , строку, с помощью b 3 строку 3 1 = -25.
2. Рассчитайте отношения -Ø / L 1 согласно последней строке. Отбросьте коэффициенты, которые не являются положительными, и коэффициенты, связанные с искусственными переменными. Выберите столбец с наименьшим положительным отношением в качестве сводного столбца : столбец = 2, связанный с 24. Таким образом, Û 1,2 = -1 является сводным столбцом 9.0248 ; переменная s 1 уйдет из базы; переменная x 2 войдет в основу.
B. Для создания таблицы 4 :
3. Вычислить строку L 4 1 = L 3 1 / (-1).
4. Вычтите кратные строки L 4 1 из всех остальных строк Таблицы 3 так, чтобы x 2 = e 1 в Таблице 5 4 .
| Таблица 4 | ||||||||
| б 4 | x 4 1 | x 4 2 | x 4 3 | с 4 1 | с 4 2 | с* 4 3 | ряд сумма | |
| л 4 1 = л 3 1 / (-1) | 25 | 0. 2 2 | 1 | -0 | -1 | -0 | 2 | 27.2 |
| L 4 2 = L 3 2 — (1.5) * L 4 1 | -17.5 | -0.35 | 0 | 0 | 1.5 | 1 | -1 | -16.35 |
| L 4 3 = L 3 3 — (2) * Д 4 1 | 60 | 0. 8 8 | 0 | 1 | 2 | 0 | -2 | 61.8 |
| P 4 = P 3 — (24) * L 4 1 | 1270 | 0.6 | 0 | 0 | 24 | 0 | -14 | 1280.6 |
| -P 4 / L 4 2 | 0 | 1,714 | 0 | 0 | 0 | 0 | 0 | 0 |
для таблицы 4 : [x 2 , S 288 2 2 2 2 2 2 2 2 . Значение целевой функции = 1270,
Значение целевой функции = 1270,
Перейти к следующей таблице следующим образом:
Фаза 0: Завершена.
Фаза I: Завершена.
Фаза II: Цель: получить ß >= 0.
А. В таблице 4 :
1. Выберите сводную строку , строку, с помощью b 4 строку 4 2 = -17,5.
2. Рассчитайте отношения -Ø / L 2 согласно последней строке. Отбросьте коэффициенты, которые не являются положительными, и коэффициенты, связанные с искусственными переменными. Выберите столбец с наименьшим положительным соотношением в качестве сводного столбца : столбцов = 1, связанный с 1,714. Таким образом, х 2,1 = -0,35 является точкой опоры ; переменная с 2 покинет базу; переменная x 1 войдет в основу.
B. Для создания таблицы 5 :
3. Вычислить строку L 5 2 = L 4 2 / (-0,35).
4. Вычтите кратные строки L 5 2 из всех остальных строк Таблицы 4 так, чтобы x 1 = e 2 в Таблице 5 .
| Таблица 5 | ||||||||
| б 5 | x 5 1 | x 5 2 | x 5 3 | с 5 1 | с 5 2 | с* 5 3 | ряд сумма | |
| л 5 1 = л 4 1 — (0,2) * л 5 2 | 15 | 0 | 1 | 0 | -0. 143 143 | 0.571 | 1.429 | 17.857 |
| L 5 2 = L 4 2 / (- 0.35) | 50 | 1 | -0 | -0 | -4.286 | -2.857 | 2.857 | 46.714 |
| L 5 3 = L 4 3 — (0,8) * Л 5 2 | 20 | 0 | 0 | 1 | 5. 429 429 | 2.286 | -4.286 | 24.429 |
| P 5 = P 4 — (0.6) * L 5 2 | 1240 | 0 | 0 | 0 | 26.571 | 1.714 | -15.714 | 1252.571 |
| -P 5 / L 5 -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Basis for Tableau 5 : [x 2 , x 1 , x 3 , ]. Значение целевой функции = 1240,
Значение целевой функции = 1240,
Фаза 0: Завершена.
Фаза I: Завершена.
Фаза II: Завершена.
Первичный раствор: [x 2 , x 1 , x 3 , ] = [15, 50, 20, ]; Р = 1240,
(Первичные переменные x, не входящие в базис, имеют значение 0).
Двойное решение: [y 1 , y 2 , y 3 , ] = [26,571, 1,714, -15,714, ]; Д = 1240.
Конец двойного симплексного метода линейного программирования
Справочник по линейному программированию.
- Рестрепо, Родриго А. Теория игр и программирование: конспект лекций по математике . Ванкувер: Университет Британской Колумбии, 1967.
- Рестрепо, Родриго А. Линейное программирование и дополнительность. Ванкувер: Университет Британской Колумбии, 1994.

- Таха, Хамди А. Исследование операций: введение. 2-е издание . Нью-Йорк: Макмиллан, 1976.
- Ву, Неса и Ричард Коппинс. Линейное программирование и расширения. Нью-Йорк: Макгроу-Хилл, 1981.
Эксперты по линейному программированию, которые помогут, наставят, проверят код и многое другое
В Codementor вы найдете лучших экспертов по линейному программированию, разработчиков, консультантов и преподавателей. Создайте свой проект, проверьте код или решите проблемы проверенными фрилансерами по линейному программированию. Учитесь у опытных наставников с опытом командного обучения и коучинга. В любом случае, вы можете быстро найти необходимую помощь по линейному программированию.
Линейное программирование
Посмотреть все технологии
Абхишаке Гупта
21 долл. США / 15 мин.
5. 0 (
0 (
123
отзывы)
Писать код легко. Написание хорошего кода — это не так; требуется навык
— Используйте языки программирования, такие как Python, чтобы помочь компаниям и частным лицам решать проблемы, автоматизировать и экономить время. Вы можете ознакомиться с некоторыми из моих проектов здесь: **https://githu…
PythonDockerРазработка через тестированиеРецензенты ReactCodeОбъектно-ориентированное программирование МатематикаGitDjangoFlaskВеб-скрейпингPycharmИнтерактивные брокерыPython 3.xJavaScriptOss (программное обеспечение с открытым исходным кодом)Веб-приложениеNode.js Linear algebraCI/CDSystem designSystems architectureArchitectural designDocker swarmAlgorithmic tradingBotNseIbapiWeb developmentDevelopmentPython ideData structureData cleansingSubversionMergingCherry pickingRebaseNumpypandasData.frameRegexFindParsingBeautiful soupCode cleansingPep 8ProfilingRefactorAlgebraTablesStatisticsProbabilityCombinationsPermutationUnit testingPytest fixturesMySQLSQLGithubVersion controlCtypesRESTful Web ServicesDatabaseBugsBug fixingWith statementContext managerVariablesFunctionsClassmethodStaticmethodRepositoryGitlabProblem solving skillsObject relational mappingCommand linePython 2. 7PytestMocking
7PytestMocking
Mario Ynocente Castro
US$18 / 15 mins
5.0 (
35
reviews)
Scikit Learn (sklearn)PytorchDjangoAmazon ec2MathematicsJavaTensorFlowMachine LearningC++PythonAi (artificial intelligence)Python 3.xpandasNGINXGunicornPython /djangoCПодготовка к интервьюMatplotlibNumpyMySQLНейронные сетиГлубокое обучениеPython3Python2Навыки решения проблемСоревновательный программирование Структура данныхАлгоритмИсчислениеДискретная математика Linear Algebranlp (обработка естественного языка) Computer VisionReinforce Learning
Marcus Reaiche
US 25 /15 MINS
5.0 (
92075.0 (
9207 5. 0 (
0 (
5.0 (
92075.0 (
92075.0 . Привет! Я опытный *программист на Python*, который ежедневно работает с **Pandas**, **Numpy**, **Scipy**, **Matplotlib** и другими библиотеками. Я также люблю играть с **Ja…
Linear programming PythonData ScienceMachine LearningJuliaSQLBashMongoDBJavaScriptScikit Learn (sklearn)AlgorithmData structureData analysisUnit testingKerasTensorFlowMatplotlibpandasNumpyIpython notebookMathematicsJumpMySQLSQLitePostgreSQL
Jonathon Bell
US$15 / 15 mins
5.0 (
21
reviews)
Главный инженер-программист — Гуру языка программирования — Мастер компиляции
Превосходные навыки проектирования на C++, Haskell, Scala, FP и OO. Эксперт в разработке компиляторов, систем типов, фреймворков и встроенных языков программирования.
Strong background in pure mathe…
Эксперт в разработке компиляторов, систем типов, фреймворков и встроенных языков программирования.
Strong background in pure mathe…
C++HaskellScalaFunctionalprogrammingCode reviewersComputer scienceCompiler constructionBoostSchemeLanguage designMathcadMlCategory theory Linear algebraDesign patternModern c++FlexBisonPerformanceOOP (Object-Oriented Programming )MidiAbstract algebraPure mathematicsMathematical logicProgram transformationCode generationType inferenceType systemsYaccLexApache SparkJavafxBig DataSemantics
Leandro Medus
US$15 / 15 mins
5.0 (
20
reviews)
Embedded Firmware Engineer
During my grad school period, I developed a fascination for programming and embedded systems . С тех пор я преподаю «Embebbed C» для продвинутых студентов в университете. 2047 Linear regressionSupport vector machineShrineFfnnCnnConvolutional neural networksArtificial neural networkDeep LearningMachine LearningNanoUnoBbbBeagle boneBashScriptsHardwareSchematicsPcb designDriver developmentOsSerialCommZynqQuartusVivadoVIRTEXSpartan 6VerilogHlslHlsAutomationNeural networksOpenCVOOP (Object-Oriented Programming )State machineStlQt5QtEnterprise architectOpenGLFixed Point arithmeticSubversionGitPeripheral driver developmentSignal processingTestbenchAlteraIntelXilinxLinux kernel low Level driver developmentAnsi c
2047 Linear regressionSupport vector machineShrineFfnnCnnConvolutional neural networksArtificial neural networkDeep LearningMachine LearningNanoUnoBbbBeagle boneBashScriptsHardwareSchematicsPcb designDriver developmentOsSerialCommZynqQuartusVivadoVIRTEXSpartan 6VerilogHlslHlsAutomationNeural networksOpenCVOOP (Object-Oriented Programming )State machineStlQt5QtEnterprise architectOpenGLFixed Point arithmeticSubversionGitPeripheral driver developmentSignal processingTestbenchAlteraIntelXilinxLinux kernel low Level driver developmentAnsi c
В течение 15 минут я был в сети с опытным инженером, который редактировал мой код и указывал на мои ошибки… это был первый раз, когда я испытал потенциал Интернета для преобразования обучения.
Tomasz Tunguz
Venture capitalist at
Redpoint Ventures
Shubham Dokania
US$25 / 15 mins
5. 0 (
0 (
18
reviews)
Machine Learning Researcher
Я Шубхам Докания, бывший научный сотрудник отдела исследований и разработок Mercedes-Benz. Моя основная область работы включает, помимо прочего, глубокое обучение компьютерному зрению и искусственному интеллекту. .frameСтруктура данныхCSSОбработка данныхГлубокое обучениеTensorFlowСверточные нейронные сетиОбработка изображенийVisionDatasetScipyNumpyGameДизайнHTMLVectorsГрафикаВычислительная геометрияСтатистикаИсчисление Linear algebraAnalysisGraphsScientific computingSignal processingVersion controlGithubCollaborationWeb developmentAPIServerMVCResearchComputer VisionNLP (Natural Language Processing)BehaviourAlpha beta pruningMinimaxGame treesGametheoryJinjaBoilerplateCluster analysisNeural networksAnalyticsClusteringKnnRegressionComputer scienceAutomation
Pete
US$50 / 15 mins
5. 0 (
0 (
13
reviews)
Дружелюбный разработчик/наставник с 20-летним опытом
Пит — высококвалифицированный разработчик с 20-летним опытом руководства командой и наставничества. Он рад помочь везде, где может, и терпеливо работает с клиентами в удобном для них темпе… сетиVirtual envPipPython 3.xPython 2.7Solid PrinciplesASP.NET CoreKubernetesGcpGcp console
JOãO VITOR BOVERIO DA SILVA GOMES
US 15 /15 минут
5.0 (
6
Обзоры
Scientific Affice Affice Bases Lecement
Iates Iates Iates Iats Iats Seply Presecting
. . То же самое в университете и на работе, которую я имел. Как и многие программисты здесь, я мастер своего дела, но меня отличает…
Программирование PythonМашинное обучениеData ScienceNode. jsРазработка программного обеспеченияCloudLeadershipAPIOauth3Инженеры распределенных системConcurrent programming TerraformDeployPytorchTensorFlowJenkinsNoSQLTeam buildingCode reviewersLinuxAgilePrometheusAWS (Amazon Web Services)Data analyticsContainersMonitoringCommunicationInfrastructure as codeAzureMlopsDevOpsKubernetesScikit Learn (sklearn)Data structureLaTeXPytestDjangoFlaskMongoDB Linear algebraData visualizationGitDockerNumpyScipyPython pandaspandasMatplotlibProblem solving skillsInterview preparationCoachingRSQLStatistics
jsРазработка программного обеспеченияCloudLeadershipAPIOauth3Инженеры распределенных системConcurrent programming TerraformDeployPytorchTensorFlowJenkinsNoSQLTeam buildingCode reviewersLinuxAgilePrometheusAWS (Amazon Web Services)Data analyticsContainersMonitoringCommunicationInfrastructure as codeAzureMlopsDevOpsKubernetesScikit Learn (sklearn)Data structureLaTeXPytestDjangoFlaskMongoDB Linear algebraData visualizationGitDockerNumpyScipyPython pandaspandasMatplotlibProblem solving skillsInterview preparationCoachingRSQLStatistics
Christopher Coley
15 долларов США / 15 минут
5.0 (
4
отзывов)
Опытный инженер-программист, страстно любящий помогать другим (C, много лет опыта программирования на разных языках
, у меня более 9002 C++, MATLAB, Python и др.) на различных платформах. Большая часть моего профессионального опыта …
Большая часть моего профессионального опыта …
C++CMATLABPythonКонечная разницаScipyNumpyАнализ данныхЧисленное моделирование Линейная АлгебраАнализ данныхLapackBlasParallel Программирование
SIDHARTH GHOSHAL
US 10 /15 MINS
5.0 (
3
Обзоры).
Я работаю быстро и люблю упрощать жизнь. Полномочия: один из 800 лучших людей в мире по адресу: https://math.stackexchange.com/users/58294/frogeyedpeas. Внимание: я сейчас работаю…
Линейное программирование PythonMachine Learningscikit-learn (sklearn)Complexity Linear алгебраPython 3.xPython 2.7Теория информацииAlgorithmFlaskScipyNumpy
Посмотреть всех экспертов по линейному программированию на Codementor
Хотите стать Codementor по линейному программированию?Типы задач оптимизации — выпуклая оптимизация
- Почему выпуклость имеет значение
- Задачи выпуклой оптимизации
- Выпуклые функции
- Решение задач выпуклой оптимизации
- Другие типы задач
Почему выпуклость имеет значение
«. ..на самом деле большой водораздел в оптимизации лежит не между линейностью и нелинейностью, а между выпуклостью и невыпуклостью.»
..на самом деле большой водораздел в оптимизации лежит не между линейностью и нелинейностью, а между выпуклостью и невыпуклостью.»
— R. Tyrrell Rockafellar, in SIAM Review , 1993
Задачи выпуклой оптимизации гораздо более общие, чем задачи линейного программирования, но они обладают общими желательными свойствами задач ЛП: их можно решить быстро. и надежно до очень больших размеров — сотни тысяч переменных и ограничений. Проблема заключалась в том, что если ваша цель и ограничения не были линейными, было трудно определить независимо от того, были ли они выпуклыми. Но продукты Premium Solver Platform от Frontline System включают автоматический тест на выпуклость ваших проблемных функций.
Задачи выпуклой оптимизации
Задача выпуклой оптимизации — это задача, в которой все ограничения являются выпуклыми функциями, а цель — выпуклой функцией при минимизации или вогнутой функцией при максимизации. Линейные функции выпуклы , поэтому задачи линейного программирования являются выпуклыми задачами. Задачи конической оптимизации — естественное расширение задач линейного программирования — также являются выпуклыми задачами. В задаче выпуклой оптимизации допустимая область — пересечение выпуклых функций ограничений — является выпуклой областью, как показано ниже.
Линейные функции выпуклы , поэтому задачи линейного программирования являются выпуклыми задачами. Задачи конической оптимизации — естественное расширение задач линейного программирования — также являются выпуклыми задачами. В задаче выпуклой оптимизации допустимая область — пересечение выпуклых функций ограничений — является выпуклой областью, как показано ниже.
С выпуклой целью и выпуклой допустимой областью может быть только одно оптимальное решение, которое является глобально оптимальным . Некоторые методы, особенно методы внутренней точки, либо найдут глобально оптимальное решение, либо докажут , что не существует допустимого решения проблемы. Выпуклые задачи могут быть эффективно решены вплоть до очень больших размеров.
Задача невыпуклой оптимизации — это любая задача, в которой цель или любое из ограничений невыпуклы, как показано ниже.
Такая задача может иметь несколько допустимых областей и несколько локально оптимальных точек в каждой области. Может потребоваться время, экспоненциальное число переменных и ограничений, чтобы определить, что невыпуклая задача неразрешима, что целевая функция неограничена или что оптимальное решение является «глобальным оптимумом» во всех допустимых областях.
Может потребоваться время, экспоненциальное число переменных и ограничений, чтобы определить, что невыпуклая задача неразрешима, что целевая функция неограничена или что оптимальное решение является «глобальным оптимумом» во всех допустимых областях.
Выпуклые функции
Геометрически функция является выпуклой , если отрезок, проведенный из любой точки (x, f(x)) в другую точку (y, f(y)) — называется хорда от x до y — лежит на или выше графика f, как показано на рисунке ниже:
Алгебраически f выпукла, если для любых x и y и любого t между 0 и 1 , f( tx + (1-t)y ) <= t f(x) + (1-t) f(y). Функция является вогнутой , если -f выпукла, т. е. если хорда от x до y лежит на или ниже графика функции f. Легко видеть, что каждая линейная функция, график которой представляет собой прямую линию, одновременно выпукла и вогнута.
Невыпуклая функция «изгибается вверх и вниз» — она не является ни выпуклой, ни вогнутой. Знакомым примером является функция синуса:
Знакомым примером является функция синуса:
, но обратите внимание, что эта функция выпукла от -пи до 0 и вогнута от 0 до +пи. Если границы переменных ограничивают область цели и ограничений областью, где функции выпуклы, то общая задача является выпуклой .
Решение задач выпуклой оптимизации
Благодаря своим желаемым свойствам задачи выпуклой оптимизации можно решать различными методами. Но Методы внутренней точки или барьера особенно подходят для выпуклых задач, поскольку они обрабатывают линейные, квадратичные, конические и гладкие нелинейные функции по существу одинаково — они создают и используют гладкую выпуклую нелинейную барьерную функцию для ограничений, даже для проблем с LP.
Эти методы позволяют решать выпуклые задачи до очень больших размеров, и они особенно эффективны для задач второго порядка (квадратичных и SOCP), где гессианы функций задачи постоянны.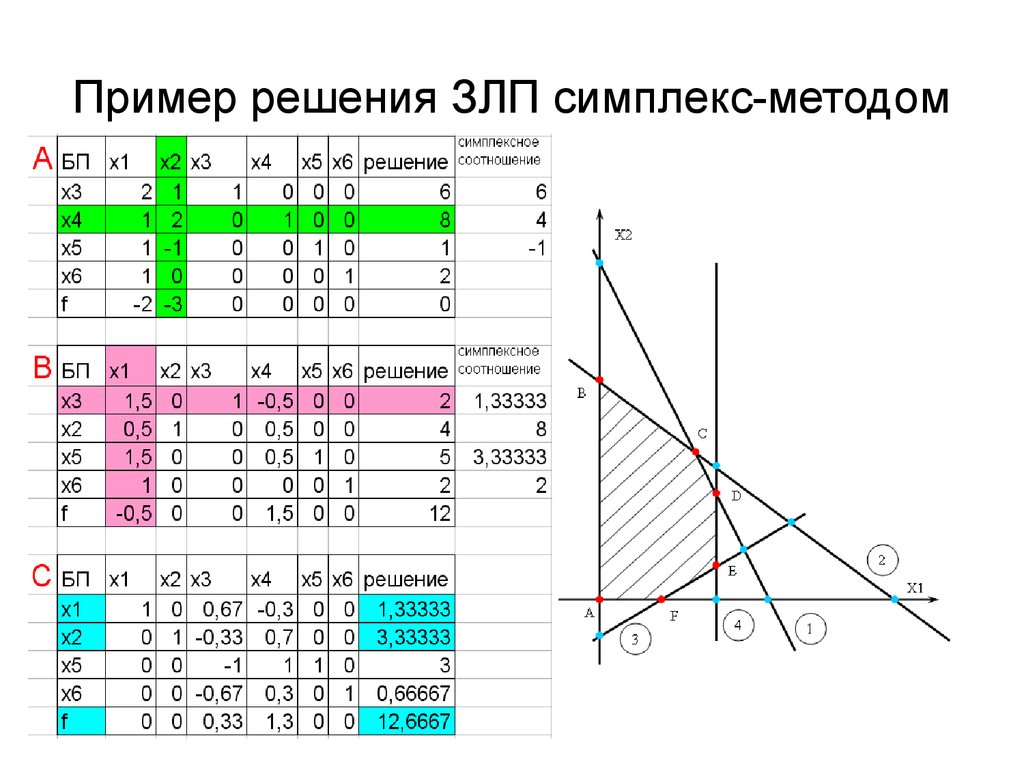



 Чтобы установить, точки какой полуплоскости
будут обеспечивать выполнение
неравенства, необходимо взять произвольную
точку и ее координаты подставить в
неравенство. Если для этой точки
неравенство выполнилось, то решением
неравенства будет та полуплоскость, в
которой брали точку. Если неравенство
для выбранной точки не выполнилось, то
его решением будут точки второй
полуплоскости. Рассматривая поочередно
все ограничения, получим область, в
которой будут справедливы все неравенства,
— это и есть область допустимых решений.
Чтобы установить, точки какой полуплоскости
будут обеспечивать выполнение
неравенства, необходимо взять произвольную
точку и ее координаты подставить в
неравенство. Если для этой точки
неравенство выполнилось, то решением
неравенства будет та полуплоскость, в
которой брали точку. Если неравенство
для выбранной точки не выполнилось, то
его решением будут точки второй
полуплоскости. Рассматривая поочередно
все ограничения, получим область, в
которой будут справедливы все неравенства,
— это и есть область допустимых решений.


 е. исключить их из базы;
е. исключить их из базы;