Решение задач на комбинаторику: К сожалению, что-то пошло не так

Содержание

«Решение задач по комбинаторике и теории вероятности.»

МБОУ «Сиалеевско-Пятинская средняя общеобразовательная школа»

Инсарского муниципального района

Республики Мордовия

Урок алгебры в 9 классе

«Решение задач по комбинаторике и теории вероятностей»

Подготовила: учитель математики

МБОУ «Сиалеевско-Пятинская

средняя общеобразовательная школа»

Инсарского муниципального района

Республики Мордовия

Ионова Наталья Михайловна

Урок по теме:

«Решение задач по комбинаторике и теории вероятности»

Здоровый образ жизни – это сила!

Ведь без здоровья в жизни никуда.

Давайте вместе будем сильны и красивы

Тогда года нам будут не беда!

Тип занятия: закрепление ЗУН по пройденному материалу.

Форма занятия: практикум по решению задач.

Цели:

Образовательные:

— Обучать решению задач по комбинаторике

Воспитательные:

Способствовать формированию:

— интереса к предмету,

— ответственности, аккуратности,

— культуры поведения, общения,

— интереса к здоровому образу жизни.

Развивающие:

Способствовать развитию:

— умения воспроизводить информацию, кратко излагать свои мысли,

— логического мышления,

— умения работать в команде,

— умения работать самостоятельно.

Задачи:

— отработать умения решать комбинаторные задачи,

— проверить понимание материала, изученного на лекции и практических занятиях,

— готовить учащихся к ГИА,

— пропаганда занятий спортом и физической культурой.

Оформление : мультимедийный проектор, экран, доска, приложение (презентация)

На классной доске плакаты с высказываниями :

Кто спортом занимается, тот силы набирается.

Кто любит спорт, тот здоров и бодр.

В здоровом теле здоровый дух.

Смолоду закалишься, на весь век сгодишься.

Со спортом не дружишь — не раз о том потужишь.

Отдай спорту время, а взамен получи здоровье.

План урока

3) Организационный момент

4) Активизация познавательной деятельности.

5) Решение комбинаторных задач.

6) Самостоятельная работа.

7) Домашнее задание.

8) Рефлексия.

Ход и содержание урока

1. Организационный момент, постановка целей и задач урока.

Учитель. В настоящее время невозможно представить спорт и физкультуру без науки. Наука — это точное знание, собирающее факты, и во всех них присутствуют цифры. Систематизация спортивных рекордов в различных видах спорта привела к установлению общего математического закона. Математическая статистика устанавливает перспективность спортсменов, условия, более благоприятные для тренировок и их эффективность. Также статистика помогает сделать объективные и научно-обоснованные выводы при анализе спортивной деятельности.

Сегодня мы проводим обобщающий урок по теме «Решение задач по комбинаторике и теории вероятности» на котором повторим различные способы решения комбинаторных задач.

Этот урок мы проведём вместе с членами сборной команды России по биатлону, которые помогут нам рассмотреть связь комбинаторики со спортом, повторить основные понятия и формулы комбинаторики и теории вероятности, а также дадут нам необходимые советы по ведению здорового образа жизни.

2. Активизация познавательной деятельности.

Перед началом любых состязаний спортсмены обязательно проводят разминку. Вот и нам они предлагают перед решением задач провести разминку в форме повторения основных понятий комбинаторики и теории вероятности.

Вся наша жизнь состоит из различных событий. В зависимости от того, произойдут они или не произойдут, события могут быть достоверными, невозможные, случайные события.

Учитель. Дайте определение этих событий.

Учащиеся. ДОСТОВЕРНОЕ СОБЫТИЕ – это событие, которое происходит всегда, и никакая случайность не может изменить исход этого события.

НЕВОЗМОЖНОЕ СОБЫТИЕ – это событие, которое никогда не может произойти в данных условиях.

СЛУЧАЙНОЕ СОБЫТИЕ – это событие, которое может произойти или не произойти, т.е. в исход вмешивается случайность.

Первая группа заданий – задания на определение вида случайного события

9) Для каждого из событий определите, каким оно является – невозможным, достоверным или случайным:

1) А = { из 12 членов сборной России по биатлону двое справляют день рождения 30 января};

2) В = { из 12 членов сборной России по биатлону двое справляют день рождения 30 февраля};

3) С = {Сочи — столица зимних олимпийских игр 2014 года };

4) D = {из списка членов сборной России по биатлону выбрали одного спортсмена и это – олимпийский чемпион};

5) Е = {из списка членов сборной России по биатлону выбрали одного спортсмена и ему – 14 месяцев};

6) F = {из списка членов сборной России по биатлону выбрали одного спортсмена и ему больше десяти лет};

7) G = {винтовка — обязательный элемент экипировки биатлониста};

8) H = {победитель этапа Кубка мира по биатлону не допустил промахов при стрельбе};

9) K = {на каждом из этапов стрельбы биатлонист должен поразить 5 мишеней};

10) L = {во время стрельбы биатлонист поразил все 5 мишеней}.

Событие	1	2	3	4	5	6	7	8	9	10
достоверное
случайное
невозможное

Вторая группа заданий – задания на применение классического определения вероятности.

(Дать определение вероятности случайного события)

1. В эстафете Кубка мира по биатлону принимают участие 22 команды. Какова вероятность того, что сборная России одержит победу в этой эстафете?

2. На старт биатлонной гонки на 15 километров вышли 96 спортсменов

среди которых 6 представителей сборной России. Какова вероятность

того, что победу одержит российский биатлонист?

3. Из 96 стартовавших спортсменов 16 чемпионы мира. Какова

вероятность того, что победителем этой гонки станет именно

чемпион мира?

— Какие способы решения комбинаторных задач вы знаете?

(перебор вариантов, дерево возможных вариантов, таблица вариантов, правило умножения)

Из этих задач видна общая схема их решения: имеются некоторые множества, содержащие n, из этих элементов составляются различные наборы, комбинации, которые можно различать:

· по порядку расположения элементов;

· по составу;

· по составу и порядку;

А значит и решения этих задач будут основываться на различных формулах комбинаторики:

Учитель. Запишите основные известные вам формулы комбинаторики, характеризующие перестановки, сочетания и размещения.

10) Размещение

Это любое упорядоченное подмножество m из элементов множества n.

11) Перестановки (). Если m = n, то эти размещения называются перестановками.

12) Сочетания () – это любое подмножество из m – элементов, которые принадлежат множеству, состоящему из n – различных элементов.

3. Решение комбинаторных задач.

(Задачи от спортсменов-биатлонистов)

Задача 1. В эстафете Кубка Мира по биатлону принимает участие 16 команд. Сколькими способами могут быть распределены золотая и серебряная медали?

Выберите букву правильного ответа. А) 256 ; Б) 31; В) 240; Г) 16.

– Мы с вами столкнулись с комбинаторной задачей.

Поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае, занят целый раздел математики, называемый комбинаторикой. Особая примета комбинаторных задач – это вопрос, который можно сформулировать таким образом, что он начинался бы словами:

Сколькими способами…?

Сколько вариантов…?

Решение: Золотую медаль может получить одна из 16 команд. После того как определен владелец золотой медали, серебряную медаль может иметь одна из 15 команд. Следовательно, общее число способов, которыми могут быть распределены золотая и серебряная медали, равно 16 * 15 = 240.

Ответ: В

Задача 2. В команде 25 спортсменов, сколькими способами можно выбрать капитана команды и его заместителя? Выберите букву правильного ответа.

А) 25 Б) 600 В) 49 Г) 625

Решение: Капитан команды может быть выбран 1 из 25 человек, значит существует 25 способов выбора капитана и 24 способа выбора его заместителя. Существует 25 * 24 = 600 способов выбора капитана команды и его заместителя.

Ответ: Б

Рекомендации спортсменов.

Для того, чтобы успешно выступать на спортивных соревнованиях спортсменам кроме хорошей физической подготовки необходимо и хорошее питание. Вот полезные советы от членов команды:

Кушай овощи и фрукты,

Рыбу, молокопродукты-

Вот полезная еда,

Витаминами полна!

На прогулку выходи,

Свежим воздухом дыши.

Только помни при уходе:

Одеваться по погоде!

В связи с этим решим следующие задачи:

Задача 3. В школьной столовой имеются 2 первых, 5 вторых и 4 третьих блюд. Сколькими способами ученик может выбрать обед, состоящий из первых, вторых и третьих блюд?

Решение: Первое блюдо можно выбрать 2 способами. Для каждого выбора первого блюда существует 5 вторых блюд. Первые два блюда можно выбрать 2 * 5 = 10 способами. И, наконец, для каждой 10 этих выборов имеются четыре возможности выбора третьего блюда, т. е. Существует 2 * 5 * 4 способов составления обеда из трех блюд. Итак, обед может быть составлен 40 способами.

Заглянем в гардероб наших девочек.

Задача 4. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы?

Решение: Получается 15 различных комбинаций одежды.

Задача 5. Сколькими способами тренер может распределить 7 спортсменов, в эстафете на первом, во втором, третьем и четвертом этапах?

Решение: А7= 7·6·5=210 Ответ: 210 способов.

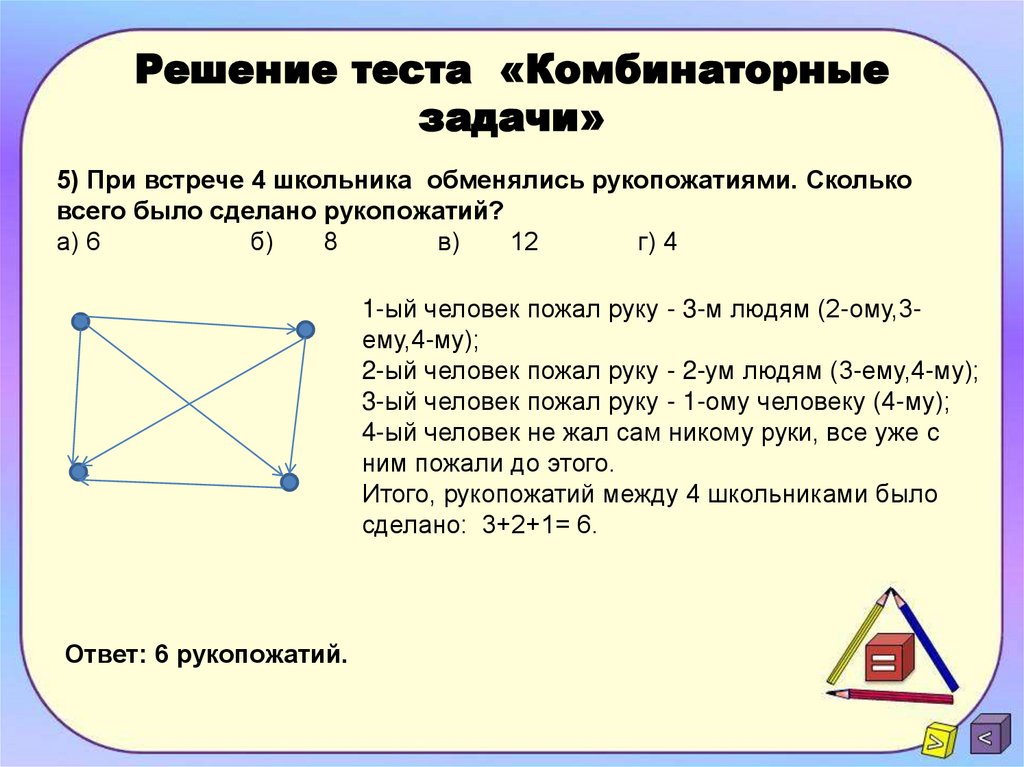
Задача 6. В эстафетную команду сборной России были отобраны Зайцева, Юрлова, Слепцова и Романова. Сколько существует возможных вариантов размещения спортсменов на четырёх этапах эстафеты?

Р=4!= 1*2*3*4=24.

Задача 6. В корзине имеются 15 груш и 7 яблок для питания спортсменов. Нужно выбрать 5 груш и 3 яблока. Сколькими способами это можно сделать?

Решение: Способов выбора 5 груш:

С15 = 1·2·…·10·11·12·13·14·15 = 360360 = 3003

1·2·3·4·5·1·2·3·4·…·10 120

Способов выбора 3 яблок:

С7 = 1·2·3·4·5·6·7 = 35

1·2·3·1·2·3·4 5 3

Всего указанный выбор можно сделать С15 ·С7 способами:

5 3

С15·С7 = 3003·35=105105 Ответ: 105105 способов.

Советы спортсменов.

Для биатлонистов очень важна хорошая стрельба по мишеням, а для этого прежде всего необходимо отличное зрение. И нам это тоже необходимо. Поэтому проведём гимнастику для глаз.

4. Самостоятельная работа.

Во время тренировок и на соревнования тренер тщательно отслеживает результаты спортсменов, ведёт статистику результатов и достижений. К основным статистическим характеристикам в математике относятся такие понятия как среднее арифметическое, медиана, размах и мода. Ребята, давайте вспомним их определение, что же такое среднее арифметическое, медиана, размах и мода?

(Учащиеся дают определение указанных понятий).

Главными соревнованиями членов сборной команды России по биатлону являются Олимпийские игры, а главными задачами любого школьника являются те, которые он должен решить на государственной итоговой аттестации (ГИА), а чтобы достойно к ней подготовиться, я предлагаю вам небольшую самостоятельную работу из задач, предлагаемых в сборниках для подготовки к экзамену по математике.

Вариант 1.

1. Во время тренировок по стрельбе биатлонист показал следующие результаты ( набранные очки из 100 возможных) :

96, 86, 89, 100, 98, 94, 96, 92, 100, 99.

Установите соответствие между статистическими характеристиками этого ряда и их значениями:

А. Среднее арифметическое; 1) 14;

Б. Медиана; 2) 96;

В. Размах. 3) 95

4) 97.

А	Б	В

2. Из 1500 ручек в среднем 90 не пишут. Какова вероятность того, что случайно выбранная ручка будет писать?

3. В сборной команде школа по биатлону занимаются 5 мальчиков и 4 девочки. Сколькими способами можно составить пару из девочки и мальчика для участия на соревнованиях в смешанной эстафете?

Вариант 2.

1. Десять участников лыжных гонок во время соревнований показали следующие результаты (в минутах):

44; 32; 29; 31; 48; 28; 42; 33; 38; 35.

Установите соответствие между статистическими характеристиками этого ряда и их значениями:

А. Среднее арифметическое; 1) 34;

Б. Медиана; 2) 20;

В. Размах. 3) 38;

4) 36.

А	Б	В

2. Из 1600 пакетов молока в среднем 80 пакетов протекают. Какова вероятность того, что случайно выбранный пакет молока не течёт?

3. В меню спортсмена 2 разных супа, 4 вторых блюда и 3 вида сока. Сколько можно составить вариантов обеда из трёх блюд?

5.Домашнее задание:

– Придумать свою комбинаторную задачу и решить её.

– Применение комбинаторики в практической деятельности людей (рассказ или эссе)

6. Рефлексия.

-Достигли ли поставленных целей на уроке?

-Что понравилось, а что бы хотели сделать по-другому?

– А какие навыки, кроме решения задач, Вы приобрели сегодня для себя? (Выслушать и обобщить ответы учащихся)

Учитель. Ребята, наш урок «Решение комбинаторных задач» нам помогли сегодня провести спортсмены-биатлонисты. С их помощью мы рассмотрели как связаны эти задачи с практической жизнью, со спортом, получили от них практические советы по ведению здорового образа жизни.

Здоровый образ жизни – это сила!

Ведь без здоровья в жизни никуда.

Давайте вместе будем сильны и красивы

Тогда года нам будут не беда!

– Спасибо всем за работу. Надеюсь, присутствующие получили много интересной и актуальной информации. Мне было очень приятно работать с вами на уроке.

Список литературы:

1. Н.Я. Виленкин, А.Н. Виленкин, П.А. Виленкин. Комбинаторика. М., 2006.

2. Ю.Н. Макарычев, Н.Г. Миндюк. Алгебра: Элементы статистики и теории вероятностей: учебное пособие для учащихся 7-9 кл. общеобразовательных учреждений/ Под ред. С.А. Тепляковского. – М.: Просвещение, 2007.

2. В. Н. Студенецкая . Решение задач по статистике, комбинаторике и теории вероятностей. 7-9 кл./ авт.-сост. В. Н. Студенецкая. Волгоград, 2006.

Решение задач по комбинаторике — презентация онлайн

Форма занятия
практикум по решению задач
Цели урока :
образовательная
— обучать решению задач по комбинаторике
развивающая
— развивать логическое мышление
— расширять математический кругозор
-развивать навыки научно — исследовательской деятельности
воспитательная
-воспитывать культуру письма, речи
-формировать чувство ответственности за принятое решение
Задачи урока :
— отработать умения решать простейшие комбинаторные задачи
— способствовать формированию и развитию вероятностного
мышления, вероятностной интуиции
— способствовать развитию творческих способностей и дарований
— создать условия для развития умений самостоятельно приобретать
и применять знания
-создать условия для расцвета личности школьника с учётом его
возрастных особенностей.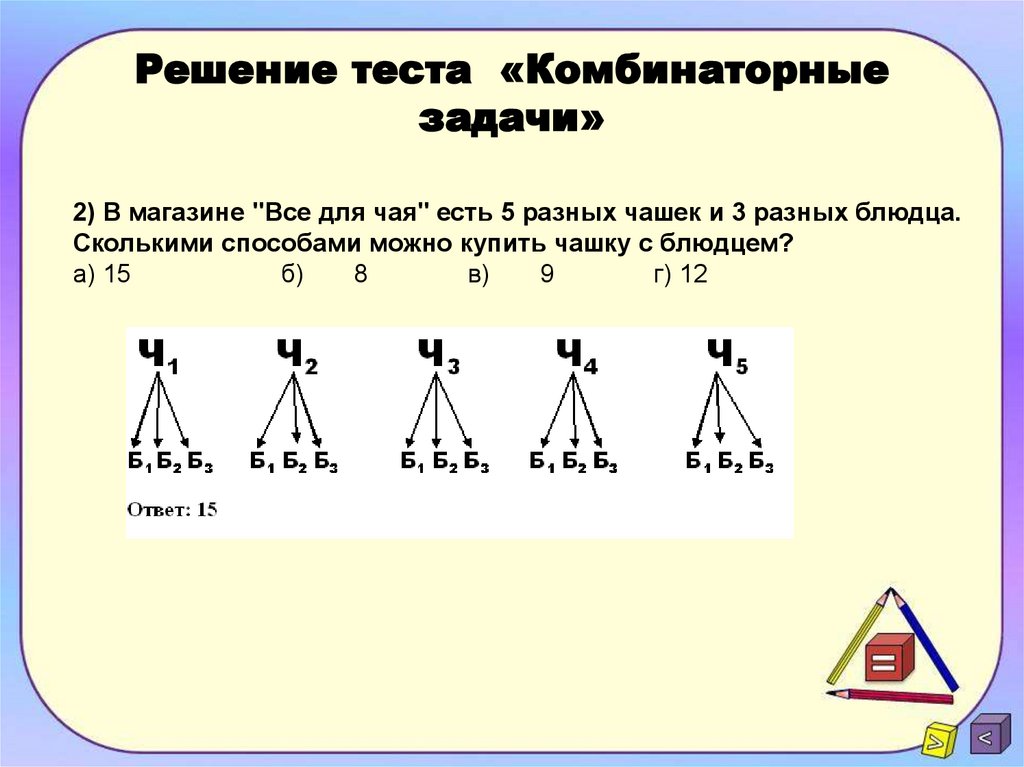

3. Немного истории

Комбинаторика является древнейшей и, возможно,
ключевой ветвью математики. В математике есть задачи, в
которых требуется из элементов составить различные наборы,
подсчитать количество всевозможных комбинаций элементов,
составленных по определённому правилу. На практике часто
приходится делать перебор определённого количества данных.
Например, учителю приходится распределять различные виды
работ между группами учащихся, офицеру выбирать из солдат
наряд, агроному размещать культуры на полях, завучу составлять
расписание и т.д. В данном случае речь идёт о всевозможных
комбинациях объектов. Задачи такого типа называются
комбинаторными задачами. Область математики, в которой
изучают комбинаторные задачи, называется комбинаторикой.
Как самостоятельный раздел математики комбинаторика
оформилась в Европе в XVIII веке. Некоторые комбинаторные
задачи решали в Индии во II веке до н. э., в Древнем Китае,
позднее в Римской империи.

Термин «комбинаторика» был введён в
математический обиход знаменитым Лейбницем.
Готфрид Вильгельм Лейбниц(1.07.1646 — 14.11.1716) всемирно известный немецкий учёный, занимался
философией, математикой, физикой, организовал
Берлинскую академию наук и стал её первым
президентом. В 1666 году Лейбниц опубликовал
«Рассуждения о комбинаторном искусстве». В своём
сочинении Лейбниц ввел специальные символы,
термины для подмножеств и операций над ними. В
течение всей своей жизни Лейбниц многократно
возвращался к идеям комбинаторного искусства.
Комбинаторику он понимал весьма широко, именно,
как составляющую любого исследования, любого
творческого акта, предполагающего сначала анализ
(расчленение целого на части), а затем синтез
(соединение частей в целое). Комбинаторике
Лейбниц предрекал блестящее будущее, широкое
применение. В XVIII веке к решению комбинаторных
задач обращались выдающиеся математики.
Г.В. Лейбниц

5.

Л. ЭйлерТак, Леонард Эйлер рассматривал задачи о
разбиении
чисел,
о
паросочетаниях,
о
циклических расстановках, о построении
магических и латинских квадратов. В 1713 году
было опубликовано сочинение Я. Бернулли
«Искусство предположений», в котором с
достаточной
полнотой
были
изложены
известные к тому времени комбинаторные
факты. Сочинение состояло из 4 частей,
комбинаторике была посвящена вторая часть, в
которой содержатся формулы. Для вывода
формул автор использовал наиболее простые и
наглядные
методы,
сопровождая
их
многочисленными таблицами и примерами. В
работах Я. Бернулли и Лейбница тщательно
изучены свойства сочетаний, размещений,
перестановок.
Я. Бернулли
РЕШЕНИЕ
КОМБИНАТОРНЫХ
ЗАДАЧ
Скажи мне – и я забуду,
Покажи мне – и я запомню,
Вовлеки меня – и я пойму.
(Древняя китайская мудрость)
Число, положение и комбинация три взаимно пересекающиеся,
но различные сферы мысли,
к которым можно отнести
все математические идеи.

Английский математик
Джеймс Джозеф Сильвестр
(1814-1897)

8. Перестановки

Комбинации из n-элементов, отличающиеся друг от
друга только порядком расположения в них элементов,
называются перестановками из n элементов
Р = n!
Р = 4! = 4 * 3 * 2 * 1 = 24

9. Задача № 1

Сколькими способами можно развесить 5
цветных шаров на гирлянде?
Решение:
Каждая расстановка будет отличаться
от предыдущей порядком следования
шаров (элементов). Поэтому это будет
перестановка из 5 элементов.
Р5 = 5! = 1·2·3·4·5= 120

10. Сочетания

Комбинации из n элементов по m , отличающиеся друг от
друга лишь составом элементов, называются сочетаниями
из n элементов по m. Количество сочетаний можно
посчитать по формуле
Число сочетаний
элементов из n по m.
Найдите:
Число сочетаний из 6 по 3:
Число сочетаний из 4 по 4:

11. Задача № 2

Из 20 учащихся надо выбрать двух дежурных.
Сколькими способами это можно сделать?
Решение:
Надо выбрать двух человек из 20.

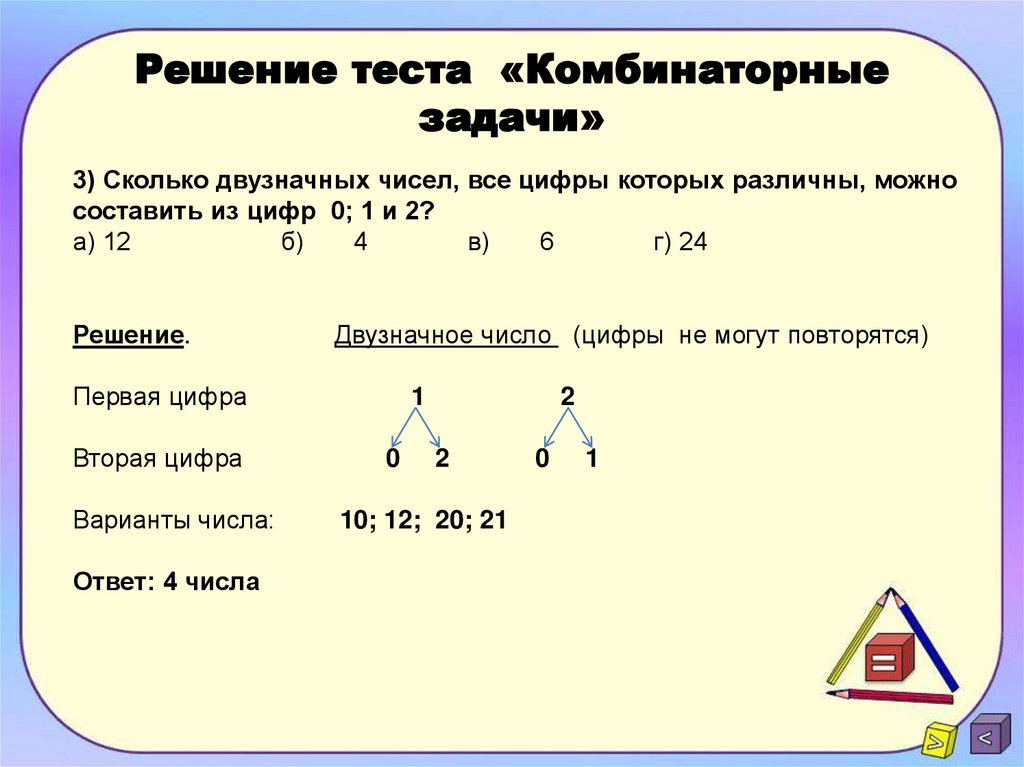
Ясно, что от порядка выбора ничего не зависит, то есть
Иванов
— Петров
или Петров
— Иванов
— это одна
и та же пара дежурных. Следовательно, это будут сочетания
из 20 по 2.

12. Задача № 3

Найдите количество отрезков,
которыми можно соединить
точки А, В, С, Е, М.
Сколько диагоналей в выпуклом десятиугольнике?
Решение:
— Найдите количество отрезков,
которыми можно соединить 10 точек.
отрезков
— Сколько из них являются сторонами?
10 являются сторонами, а остальные
45 – 10 = 35
будут диагоналями
Ответ: 35 диагоналей
Комбинации из n элементов по m, отличающиеся друг от друга либо
составом элементов, либо порядком их расположения, называются
размещениями из n элементов по m (m n).
Сколько словарей надо создать, чтобы можно
было непосредственно выполнять перевод с любого
из пяти языков на любой другой из этих языков?
Решение:
Ответ: 20 словарей.
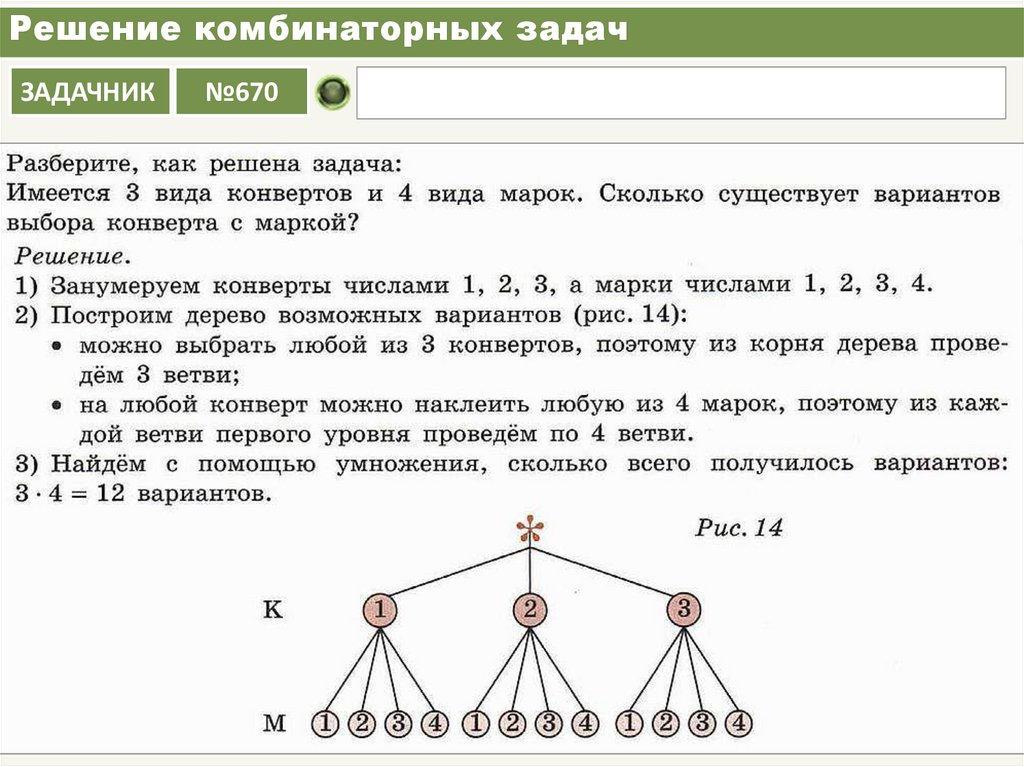
Из чисел 1, 5, 9 составить трёхзначное
число без повторяющихся цифр.

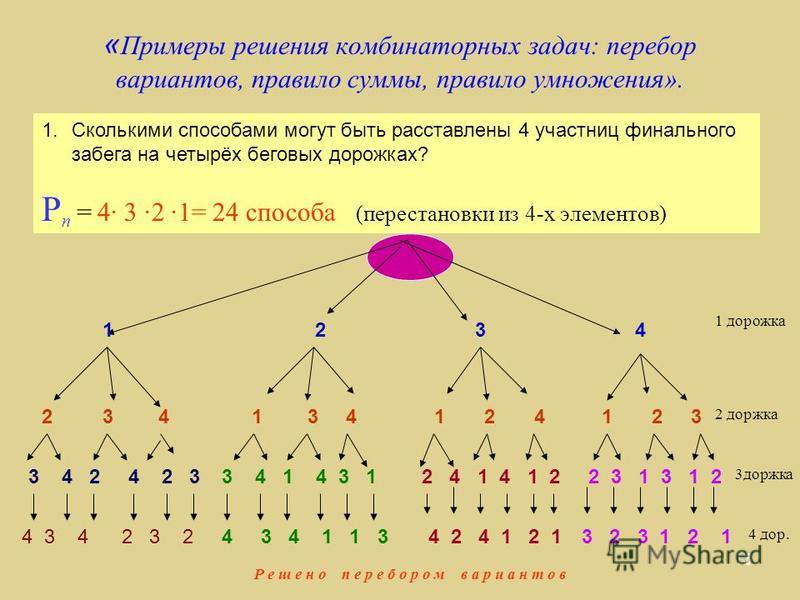
1
159
5
195
2 комбинации
1
3
519
9
591
2 комбинации
915
951
2 комбинации
Какую
часть составляют
кратные
5?
-это
вероятность
того, чточисла,
трёхзначное
число,
составленное из неповторяющихся цифр
1, 5, 9, кратно 5.

17. Понятие вероятности

Вероят ност ью событ ия называет ся число,
показывающее какую част ь сост авляют
исходы испыт ания, в кот орых наст упает
событ ие А, от всех исходов эт ого
испыт ания.
Событ ием А в т еории вероят ност и
называет ся выполнение
какого-либо свойст ва в исходах
рассмат риваемого испыт ания.

18. Понятие вероятности

Из чисел 1, 5, 9 сост авит ь т рёхзначное
число без повт оряющихся циф р.
1
159
5
195
2 комбинации
519
9
591
2 комбинации
915
951
2 комбинации
Какова
вероят
ност
ого,
чт
ополучит
получит
ся
число,
Какова
вероят
чт
число,
Какова
Какова
вероят
вероятност
ност
ностьььтьттого,
того,
ого,
чт
чтоо
ополучит
получится
ся
ся
число,
число,
квадрат ный корень
из ное
кот
орого
не больше 24?
большее
500?
крат
крат
ное
9?3?
2
1
0
13
2
Классическая вероят ност ная схема.

N ( A)
P ( A)
N
Для нахождения вероят ност и случайного событ ия
при проведении некот орого испыт ания следует :
1) Найт и число N всех возможных исходов данного
испыт ания.
2) Найт и число N(А) т ех исходов испыт ания, в
кот орых наст упает событ ие А.
3)Найт и от ношение
N ( A)
N
; оно и будет равно
вероят ност и событ ия А.
Классическое определение
вероят ност и.
Вероят ност ью событ ия А называет ся
от ношение числа т ех исходов, в
результ ат е кот орых наст упает
событ ие А, к общему числу всех
(равновозможных между собой)
исходов испыт ания.
N ( A)
P ( A)
N
В правильном 7-угольнике ABCDEFG случайным
образом провели одну из диагоналей.
В
С
А
G
D
F
а)Какова вероят ност ь т ого,
чт о по обе ст ороны от неё
лежит одинаковое
количест во вершин?
E
От вет : 0, невозможное событ ие
В правильном 7-угольнике ABCDEFG случайным
образом провели одну из диагоналей.

В
б)Какова вероят ност ь т ого,
С
А
чт о по одну ст орону от
диагонали лежит
более двух вершин?
G
D
F
E
От вет : 1, дост оверное событ ие
В правильном 7-угольнике ABCDEFG случайным
образом провели одну из диагоналей.
В
в)Какова вероят ност ь т ого,
А
С
чт о диагональ от резает от
7-угольника какой-т о
3-угольник?
G
D
Начало диагонали — 7 способов
Конец диагонали — 4 способов
E
F
Всего 7∙4=28 пар концов диагоналей
Всего диагоналей- 28:2=14, N=14
Всего диагоналей, от секающих т реугольник -7,
N(A)=7
7 1
От вет : P( A)
14
2
В правильном 7-угольнике ABCDEFG случайным
образом провели одну из диагоналей.
В
г )Какова вероят ност ь т ого,
А
С чт о один из концов диагонали вершина С, или вершина F?
G
D
Из вершины С – 4 диагонали
Из вершины F – 4 диагонали
F
E
Всего – 4 + 4 – 1 = 7 диагоналей
От вет :
P( A)
7 1
14 2

25.

Правило нахождения геометрической вероятности.Х
А
Если фигура Х целиком
содержит в себе фигуру
А, т о вероят ност ь т ого,
чт о т очка, случайно
выбранная из фигуры Х,
принадлежит фигуре А
равна от ношению
площади фигуры А к
площади фигуры Х.
S ( A)
Р
S(X )

26. Задача № 9

Случайным образом выбирают одно из
решений неравенст ва │x-1│≤3. Какова
вероят ност ь т ого, чт о оно окажет ся и
решением неравенст ва │x-2 │ ≥ 3?
х-2 ≤ -3
х-2 ≥ 3
-3 ≤ х-1 ≤ 3
-2 ≤ х ≤ 4
х ≤ -1
х≥5
х-1
-3
0
3
х-2
-3
-2 -1 0
От вет . 1/6
0
4 5
3
х

27. Задача №10

Граф ический редакт ор, уст ановленный на
компьют ере, случайно от мечает одну т очку
на монит оре – квадрат е АВСD со ст ороной
12см. Какова вероят ност ь т ого, чт о эт а т очка:
C
B
а) окажет ся в верхней
половине монит ора?
S ABCD 144
S1/ 2 ABCD 72
А
D
72 1
Р
0,5
144 2

28.

Задача №10Граф ический редакт ор, уст ановленный на
компьют ере, случайно от мечает одну т очку
на монит оре – квадрат е АВСD со ст ороной
12см. Какова вероят ност ь т ого, чт о эт а т очка:
C
B б) окажет ся одновременно
в нижней и левой
част и монит ора?
S ABCD 144
S1/ 4 ABCD 6 36
2
А
D
36 1
Р
0,25
144 4

29. Задача №10

Граф ический редакт ор, уст ановленный на
компьют ере, случайно от мечает одну т очку
на монит оре – квадрат е АВСD со ст ороной
12см. Какова вероят ност ь т ого, чт о эт а т очка:
C
B
в)будет удалена от
вершины D не более,
чем на 11см ?
S ABCD 144
S1/ 4 круга
А
D
1
2
11 30,25
4
30,25
Р
0,66
144
Предмет математики столь
серьезен, что не следует
упускать ни одной
возможности сделать его
более занимательным.
Б. Паскаль

Олимпиадная задача по комбинаторике с красивым геометрическим решением | Рассел Лим

У Эми есть такое количество камней, что масса каждого камня в килограммах является положительным целым числом. Сумма масс камней составляет 2018 килограммов. Эми понимает, что разделить камни на две кучи по 1009 килограммов невозможно. Какое максимально возможное количество камней может быть у Эми?
— Австралийская олимпиада по математике 2018

Фото Елена Можвило на Unsplash

Эта статья разделена на следующие 3 раздела:

Понимание проблемы
Мое первоначальное решение
Красивое геометрическое решение

Если вы поняли формулировку задачи, потратьте несколько минут на то, чтобы подумать над ней самостоятельно. Если вы не совсем понимаете, о чем он спрашивает, прочитайте раздел «Понимание проблемы» ниже.

Photo by Daniele Franchi on Unsplash

Чтобы понять проблему, я начал с исследования аналогичной проблемы, но где общая масса камней составляет 8 кг.

Нам нужно найти максимально возможное количество камней, чтобы камни нельзя было разделить на 2 кучки по 4 кг каждая.

Например, если есть 8 камней, каждый из них должен весить 1 кг (помните, что все они целые).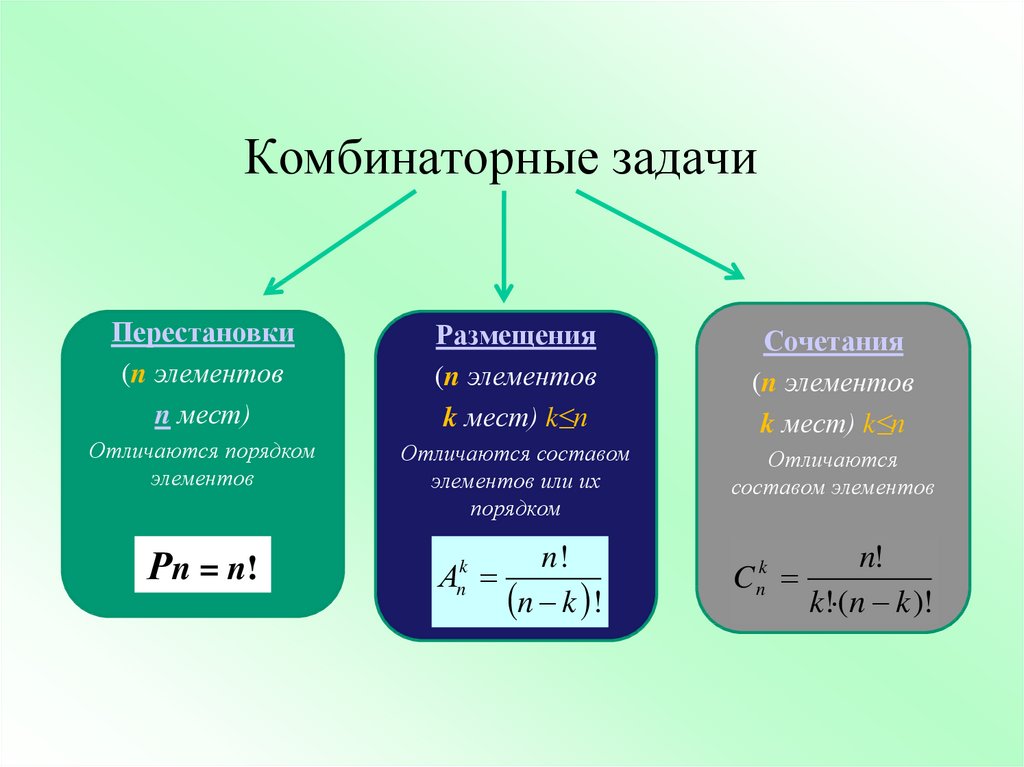 Ясно, что есть , которые можно разделить на 2 стопки по 4 кг каждая. Таким образом, максимальное количество камней должно быть меньше 8.

Ящик весом 8 кг достаточно мал, чтобы его можно было решить грубой силой. Мы ищем наибольшее количество камней, поэтому давайте составим таблицу, начиная с 8 камней, и будем двигаться дальше.

Если верить (или внимательно проверить), что я перечислил все возможные варианты от 5 до 8 камней, то ясно, что 4 — это максимальное количество камней, не позволяющее разделить на 2 равные кучки.

Вероятно, также очевидно, что набор камней {1,1,1,5} можно обобщить и применить к случаю 2018 кг: т. е. у Эми может быть 1009 камней весом {1,1,1,…1,1010 } сумма которых составляет 2018 кг и которую невозможно разделить на 2 равные стопки по 1009 кг.

Но не очевидно, как доказать, что это дает максимальное количество камней. Как мы можем быть уверены, что не существует такого расположения 1010 камней, которое также невозможно разделить на 2 равные кучи?

Мой метод заключался в использовании «доказательства от противного», чтобы показать, что у Эми не может быть более 1009 камней. Я был очень горд собой, когда завершил доказательство, но по сравнению с красивым геометрическим решением ниже оно кажется надуманным и слишком сложным 🤦‍♂️.

В любом случае, вот оно…

Пусть n будет количеством камней, которые есть у Эми. Покажем, что для n > 1009, если невозможно создать 2 кучи одинакового веса, должно быть не менее 2 камней тяжелее 1009кг каждый. Одни только эти 2 камня имеют общую массу более 2018 кг, что даст требуемое противоречие.

Пусть k будет количеством камней массой 1 кг каждый.
Из оставшихся ( n − k ) камней ни один не может иметь массу в диапазоне [1009 − k, 1009] кг, или мы могли бы объединить его с некоторыми или всеми 1-килограммовыми камнями, чтобы получить пара общей массой 1009 кг.

Но не может быть более (1008 − k ) ÷ 2 камней массой менее (1009− k ), потому что никакая пара не может иметь общую массу 1009 кг.

Остается не менее ч = ( n − k ) − (1008 − k ) ÷ 2 «тяжелых» камня весом более 1009 кг каждый. Я покажу, что если n > 1009, то h всегда не меньше 2.

Минимум n равен 1010, что дает h = (1010 − k ) − (1005 − k ) ÷ 2. Член k отрицательный, поэтому ч достигает своего минимума, когда к является максимальным, т. е. к = 1008. (Если к > 1008, то 1009 камней весом 1 кг каждая будут иметь общую массу 1009 кг).

Теперь минимальное количество тяжелых камней составляет ч = (1010 − 1008) − (1008 − 1008) ÷ 2 = 2.

Только эти 2 тяжелых камня имеют общую массу более 2 × 1009 = 2018 кг, что противоречит условию, что общая масса пород составляет 2018 кг.

Таким образом, максимальное количество камней, соответствующих заданным условиям, равно 1009..

Красивое геометрическое решение

Давайте представим камни в виде секторов круглого торта ко дню рождения (или рождественского пудинга, если хотите). Окружность торта составляет 2018 единиц, и нам разрешено разрезать торт только по линиям, соединяющим целые единицы окружности.

Эквивалентная формулировка нашей задачи о камне: «Каково максимальное количество кусочков торта, которые можно разрезать так, чтобы никакое подмножество кусочков не равнялось ровно половине торта?»

Ниже приведена диаграмма, иллюстрирующая задачу для торта с окружностью 10 единиц. Разрешается резать только по пунктирным линиям.

Для торта с окружностью 2018 единиц нам нужно доказать, что 1010 ломтиков всегда приводят к тому, что торт разрезается ровно пополам.

Вот…

Есть только 1009 диаметров, по которым нам разрешено резать. Если мы нарежем 1010 ломтиков, то должен быть хотя бы один диаметр, который был обрезан с обеих сторон. Этот диаметр делит торт на две равные половины (см. заштрихованную область на диаграмме выше).

Вот и все!

На мой взгляд, такая постановка задачи делает решение гораздо более интуитивным. Гениальность и творческий подход необходимы в первую очередь для того, чтобы найти правильную формулировку. Я был очень впечатлен, когда один из моих студентов рассказал мне об этом. Я до сих пор в восторге от учеников, которые соревнуются в олимпиаде по математике 🙇.

У этой школьной задачи по геометрии есть простое решение (его просто трудно найти!)

Пусть ABCD — квадрат, а l — отрезок прямой от B до точки на стороне AD. Если A находится в 5 см от l, а C находится в 7 см от l…

russelllim22.medium.com

Прогулка по Планарному парку — задача по теории графов с олимпиады США по математике 2021 года

Национальный парк Планар состоит из нескольких тропы, которые сходятся на перекрестках. Каждая тропа имеет две конечные точки в двух…

www.cantorsparadise.com

Материалы для обучения олимпиаде по математике | Юфэй Чжао

Раздаточные материалы канадских тренировочных лагерей IMO
Книжные рекомендации

Я вел занятия на различных учебных программах математических олимпиад. Вот некоторые из моих раздаточных материалов и учебных материалов.

Если вы не знаете, с чего начать, я рекомендую циклические четырехугольники — общая картина и три леммы в геометрии.

Алгебра

Целочисленные полиномы — MOP 2007 Black group
Целочисленные полиномы, включая различные критерии неприводимости.
Неравенство — Зимняя подготовка Канады 2008 г.
Содержит короткое эссе, посвященное неравенству ИМО 2001 г.
Полиномы — Летний тренинг 2008 г. в Канаде
Передовые методы работы с полиномами. Корни из единицы, целочисленная делимость, теорема о промежуточном значении, интерполяция Лагранжа, многочлены Чебышева, критерии неприводимости и теорема Руше.
Детерминанты: оценка и манипулирование — MIT UMA Putnam Talk
Уловки линейной алгебры для Патнэма — MIT UMA Putnam Talk

Комбинаторика

Биекции
Алгебраические методы в комбинаторике — MOP 2007 Black Group
Приложения линейной алгебры и посетов к задачам комбинаторики олимпиадного стиля.
Укладка плитки — СС 2007 Синяя группа
Обсуждение облицовки ящиков кирпичом. Содержит много проблем с окраской и мозаикой.
Подсчет двумя способами — MOP 2007 Blue and Black group
Комбинаторика: биекции, каталонские числа, счет двумя способами — Зимняя тренировка Канады 2008 г.
Комбинаторика: принцип сортировки, раскраска, биномиальные коэффициенты, биекции — AwesomeMath 2007
Комбинаторика: счет двумя способами, производящие функции, алгебраическая комбинаторика — AwesomeMath 2007

Геометрия

Леммы по евклидовой геометрии — Канадский летний курс 2007 г.
Сборник часто встречающихся конфигураций в задачах по геометрии.
Циклические четырехугольники – общая картина – Канада, 2009 г. Зимняя подготовка
Исследует многие свойства полного циклического четырехугольника и его точки Микеля, а также обсуждает несколько полезных геометрических приемов.
Три леммы по геометрии (решения) — Зимний тренинг в Канаде, 2010 г.
Power of the Point (Solutions) — UK Trinity Training 2011 (группа Mint)
кругов — Летняя тренировка в Канаде 2008 г.
No related posts.