Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376312 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
RU
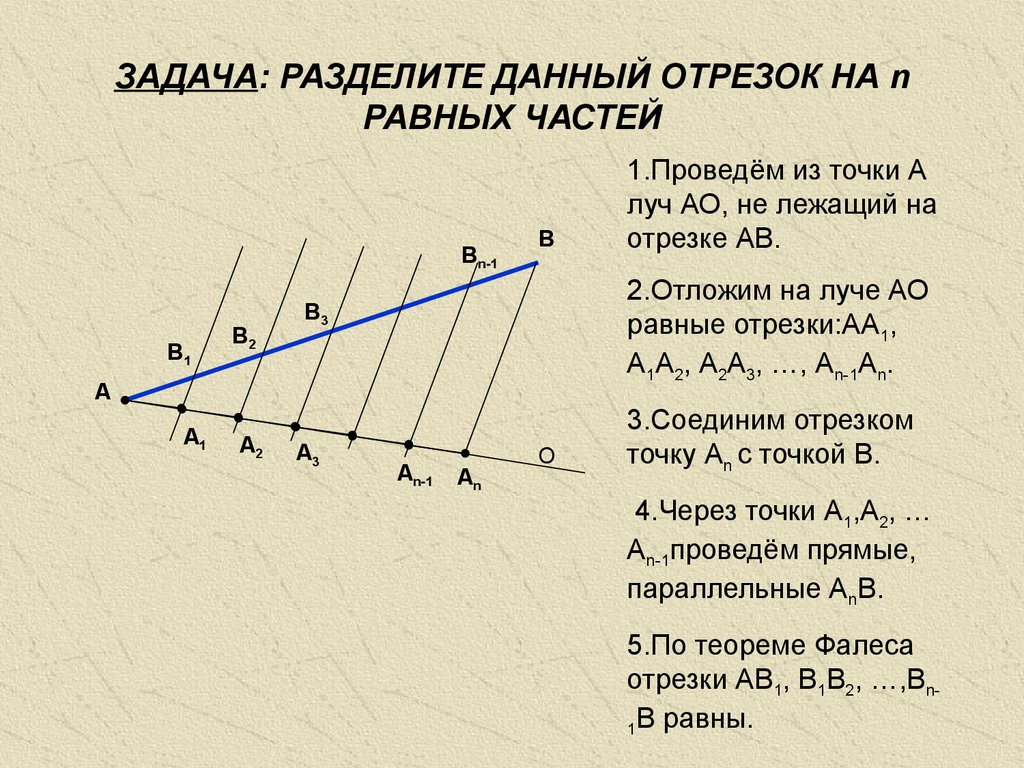
Обобщенная теорема Фалеса — ГЕОМЕТРИЯ — Уроки для 8 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок № 25
Тема. Обобщенная теорема Фалеса
Цель: сформировать у учащихся понятие о отношение отрезков, пропорциональные отрезки; сформировать осознанное понимание учащимися содержания теоремы о пропорциональных отрезках (обобщение теоремы Фалеса) и идеи ее доведения, а также возможность записи теоремы в виде двух разных равенств. Формировать у учащихся умения:
· воспроизводить содержание изученных на уроке утверждений;
· находить на рисунке пропорциональные отрезки;
· записывать равенство отношений пропорциональных отрезков по условию задачи для нахождения неизвестных длин отрезков;
· использовать теорему о пропорциональных отрезка для решения задачи на построение четвертого пропорционального отрезка.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Теорема Фалеса».
Ход урока
I. Организационный этап
Поскольку урок является первым во втором разделе курса геометрии 8 класса («Подобие треугольников. Теорема Пифагора»), то на этом этапе урока уместно будет предоставить учащимся информацию о:
· ориентировочный план изучения раздела;
· количество учебных часов, которое отведено для его изучения;
· примерное содержание материала;
· основные требования к знаниям и умениям учащихся;
· примерное содержание заданий, которые будут вынесены на контроль.
(Эту информацию можно поместить на стенде «Справочно-информационный уголок» в кабинете математики. С целью экономии времени предложить учащимся для самостоятельного ознакомления во внеурочное время).
II. Проверка домашнего задания
Если на предыдущем уроке было предложено ученикам дома решения задач контрольной работы или коррекционную работу и т.
п.), то правильность выполнения этой работы учитель проверяет, собрав тетради на проверку (для оценивания).
III. Формулировка цели и задач урока
Для понимания учащимися логики изучения материала и с целью создания мотивации учебной деятельности учащихся на уроке предлагаем им выполнить практическую работу.
Практическая работа
2. Измерьте длины всех отрезков ( АВ , АС , СВ , AY , АХ , XY), образовавшихся на рисунке 1.
3. Вычислите значение частиц: АС : ВС ; АС : АВ ; AY : XY; AY : АХ. Сравните полученные числа. Что вы заметили? Можете ли вы объяснить полученные результаты?
@ Выполняя построения, соответствующие условию задачи 1, ученики получают конфигурацию, подобную той, что изображена на рис.
1.
После выполнения измерений и вычислений в соответствии с условиями заданий 2 и 3 ученики должны заметить, что, независимо от длины отрезка АВ и градусной меры угла ХАВ и несмотря на неточность измерений, среди полученных значений долей длин образованных отрезков есть равные числа, существование которых ученики не могут объяснить. Учитель предлагает учащимся сравнить рис.1 с рисунком теореме Фалеса и найти одинаковые и отличительные черты. После этого ученики должны заметить, что, несмотря на определенное сходство (параллельные прямые пересекают стороны угла), случай на рис. 1 не полностью соответствует условию теоремы Фалеса. Таким образом формулируется проблема. Существует необходимость обобщения теоремы Фалеса для случая, когда параллельные прямые пересекают стороны угла, отхватывая на одной из сторон произвольные отрезки, а также выражение зависимости между полученными отрезками в алгебраической форме. Решения поставленной проблемы является основой целью этого урока.
IV.
Для успешного усвоения учащимися содержания понятий «отношение отрезков», «пропорциональные отрезки», содержания теоремы о пропорциональных отрезках (обобщение теоремы Фалеса) и идеи ее доведения, а также понимание учащимися возможности записи теоремы в виде двух равенств ученикам следует активизировать знания и умения относительно определения и свойства пропорции; содержания теоремы Фалеса.
Выполнение устных упражнений
1. Среди записей: , ab, a : b, а — b, а + b выбрать те, которые можно назвать отношением чисел а и b . Что может показывать это отношение?
2. Как называется запись ? Как называются числа а , b , с, d в этой записи?
3. Известно, что равенство является правильной. Какие из предложенных ниже равенств являются правильными? Почему?
а) ad = bс; b) ; в) ; г) ; д) .
4. а) АК : KB = 2 : 3 (рис. 2). Найдите: АК : АВ; ВК : АК; ВК : АВ;
б) ВК : АВ = m : n.
Найдите АК : ВК; АК : АВ.
5. Найдите NH (рис. 3), если АВ = 10.
V. Усвоение знаний
План изучения нового материала
1. Представление о содержании понятий «отношение отрезков»; «пропорциональные отрезки».
2. Теорема о пропорциональных отрезках (формулировка и идея доказательства).
3. Построение четвертого пропорционального отрезка.
@ Как показывает опыт, трудности восприятия содержания, а отсюда применение обобщенной теоремы Фалеса, возникают потому, что ученики не понимают смысла понятия «пропорциональные отрезки». Следовательно, изучение нового материала следует начинать с формирования сознательного понимания учащимися понятия пропорциональных отрезков с последующим закреплением его содержания на примерах.
За такого способа изучения материала формулировку теоремы о пропорциональных отрезках является простым обобщением результатов практической работы, поэтому, прежде чем формулировать утверждение теоремы, учитель может предложить учащимся самостоятельно составить обобщенное утверждение (исходя из равенств, которые учащиеся получили во время выполнения практической работы).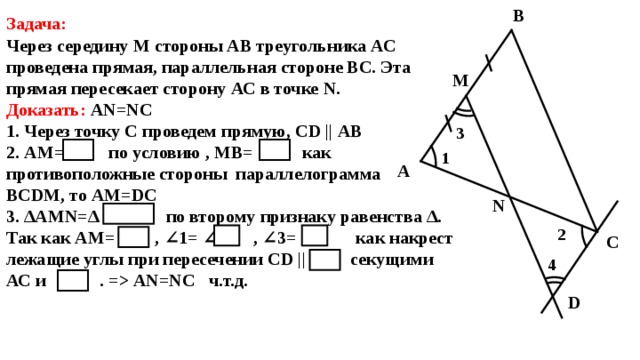
Учителю следует подчеркнуть, что выполнена построение не является доказательством утверждения (это лишь иллюстрация теоремы). Ученики должны понимать, что составленное утверждение должно быть доказанным. Поскольку строгое математическое доказательство обобщенной теоремы Фалеса является достаточно сложным для учащихся 8 класса, то предоставляется только идея доказательства утверждения теоремы о пропорциональных отрезках со ссылкой на доказанную ранее теорему Фалеса. Заметим, что, в отличие от традиционного учебника, в новом учебнике формулируется и доказывается утверждение для отрезков, которые последовательно расположены на каждой из сторон угла (за такого подхода к формулировке теоремы ссылки на теорему Фалеса становится более понятным).
Что касается пропорциональности отрезков, которые имеют общий конец в вершине угла, то в новом учебнике довольно оригинально доказан этот факт через применение к ранее доказанного утверждения одного из свойств пропорции.
После обработки понятие пропорциональных отрезков и формулировки и доказательства теоремы о пропорциональных отрезках желательно на примерах закрепить путем составления соответствующих пропорций за готовыми рисунками понимание учащимися содержания теоремы.
Если учащиеся хорошо усвоили теоретический материал, а также демонстрируют понимание содержания теорем и умение применять его на примерах, можно на этом уроке изучить схему решения базовой задачи на построение четвертого пропорционального отрезка.
VI. Закрепление знаний, формирование первоначальных умений
Выполнение письменных упражнений
1. Определите, есть отрезки длиной а и b пропорциональны отрезкам с и d , если:
а) а = 8 см, b = 24 см, с = 7 см, d = 12 см;
б) а = 9 см, b = 14 см, с = 7 см, d = 18 см.
2. По данным рисунка 4 найдите х, если а || b.
3. Прямая KM параллельна стороне АС треугольника ABC (рис. 5). Найдите отрезок MС , если АК = 2 см, KB = 6 см, ВМ = 9 см.
4. Прямая MN параллельна основаниям трапеции ABCD (рис. 6). Найдите сторону CD, если AM : AB = 4 : 5, CN = 3 см.
5. Даны отрезки а , b , с. Постройте отрезки: 1) ; 2) .
6. На рис. 7 BE : ЕА = 4 : 6, BD : DC = 6 : 7. Найдите отношение СК : КЕ .
VII. Итоги урока
На каком из приведенных рисунков допущена ошибка в изображении параллельных прямых а и b ?
1. |
2. |
||
3. |
4. |
VIII. Домашнее задание
Изучить теоретический материал.
Решить задачи.
- 1. По данным рисунка 8 найдите х, если а || b.
- 2.
2. Прямая KM параллельна стороне АС треугольника ABC (рис. 5). Найдите отрезок МС, если АК : KB = 2 : 3, ВС = 10 см.
3. Прямая MN параллельна основаниям трапеции ABCD (рис. 6). Найдите сторону АВ , если AM : ND = 3 : 2, CN = 2 см, АМ = 9 см.
4*. Даны отрезки а , b , c. Постройте отрезки: а) ; б) .
| Назад | Содержание | Вперед |
Упражнение 4.2: Теорема Фалеса и теорема о биссектрисе угла — Проблемные вопросы с ответами, решение
Построение треугольника с использованием теоремы 1: основной теоремы пропорциональности (BPT) или теоремы Фалеса, теоремы 2: обращения основной теоремы пропорциональности, теоремы 3: биссектрисы угла Теорема, Теорема 4: обращение теоремы о биссектрисе угла (ответы и решения для упражнений из учебника по математике)
Упражнение 4.
2
0008 E являются точками на сторонах AB и AC соответственно такие, что DE|| BC
(i) Если AD/DB = 3/4 и AC = 15 0
см найти
(ii). Если г. н.э. = 8 x — 7, дБ = 5 x — 3, AE = 4 x — 3 и EC = 3 x -1, найдите значение х .
2. ABCD — трапеция, в которой AB || DC и P,Q являются точками на AD и BC соответственно, так что PQ || DC если PD = 18 см, BQ = 35 см и QC = 15 см, найти AD .
3. В Δ ABC , D и E точки на сторонах AB и AC соответственно. Для каждого из следующих случаев покажите, что DE || BC
(i) AB = 12 см, AD = 8 см, AE = 12 см и AC = 18 см.
(ii) AB = 5,6 см, AD = 1,4 см, AC = 7,2 см и AE = 1,8 см.
4. На рис. если PQ || BC и PR || CD докажите, что
5. Ромб PQRB вписан в Δ ABC так, что ∠ B составляет один из его углов. P , Q и R лежат на AB , AC и BC соответственно. Если AB = 12 см и BC = 6 см, найдите стороны PQ , RB ромба.
6. В трапеции ABCD , AB || DC , E и F — точки на непараллельных сторонах AD и BC соответственно, так что EF || АВ . Покажи это .
7. На рисунке DE || BC и CD || ЭФ . Докажите, что AD 2 = AB × AF .
8. В Δ ABC , г. н.э. — это бисектор ♂ A СОЕДИНА BC AT D, , если AB 10 CM, AC = , если AB 10 CM, AC = .
0009 14 cm and BC = 6 cm, find BD and DC
9. Check whether AD is bisector of ∠ A of Δ ABC в каждом из следующих
(i) AB = 5 см, AC = 10 см, BD = 1,5 см и CD = 3,5 см.
(ii) AB = 4 см, AC = 6 см, BD = 1,6 см и CD = 2,4 см.
10. На рисунке ∠ QPR = 90°, PS — его биссектриса. Если ST ┴ PR , докажите, что ST × ( PQ + PR ) = PQ × PR.
11. ABCD — четырехугольник, в котором AB = AD, бискектор ♂ и ♂ CAD ♂ CAD ♂ CAD CAD 9000 BC и CD в точках E и F соответственно. Докажите, что EF || БД .
12. Конструкция A Δ PQR , которая основана PQ = 4,5 см, тий R = 35 и медиана от R до RG — 6 см.
13. Построить Δ PQR , в котором QR = 5 см, ∠ P = 40° и медиана PG 8 0 изот 0009 до QR составляет 4,4 см. Найдите длину высоты от P до QR .
14. Конструкция Δ PQR Такой, что QR = 6,5 см, тий P = 60 ° и высота от P до QR — длиной 4,5 см.
15. Постройте Δ ABC так, что AB = 5,5 см, ∠ C = 25° и высота от AB 9 0 до 8 009 0009 4 см.
16. Нарисуйте треугольник ABC база до н.э. = 5,6 см, тий A = 40 ° и бисектор ♂ A встречается до н.э. в D , что A = 4 см.
17. Начертите Δ PQR так, что PQ = 6,8 см, вертикальный угол равен 50°, а биссектриса вертикального угла пересекается с основанием в точке D см = 5,2
PD.
Ответы:
1.(i) 6,43 см (ii) 1
2. 60 см
5. 4 см, 4 см
8. 2,5 см, 3,5 см
9. биссектриса (ii) Биссектриса
13. 2,1 см
- Предыдущая страница
- Следующая страница
Метки : Проблемные вопросы с ответом, Решение | Математика, 10-й Математика: БЛОК 4: Геометрия
Учебный материал, Лекционные заметки, Задание, Справочник, Вики-описание, объяснение, краткая информация
10th Математика: ЧАСТЬ 4: Геометрия: Упражнение 4.2: Теорема Фалеса и теорема о биссектрисе угла | Проблемные вопросы с ответом, решение | Математика
Вписанные в круг фигуры – решение задач
В геометрии существует особая классификация, согласно которой фигуры находятся внутри других фигур, например, круг внутри треугольника, четырехугольник внутри круга и т. д. Эти фигуры называются Вписанный и описанный . Внутренняя форма известна как «вписанные формы», а внешняя форма известна как «описанные формы».
Предположим, что круг вписан в любую другую форму (многоугольник), ребра многоугольника (все касающиеся круга) являются касательными к кругу.
Прямоугольные треугольники, вписанные в окружность
Когда треугольник вставлен в окружность таким образом, что одна из сторон треугольника равна диаметру окружности, треугольник является прямоугольным.
Это также упоминается как Теорема Фалеса .
Доказательство:
На приведенной ниже диаграмме добавлен сегмент линии OC.
Поскольку отрезки OB, OC и OA являются радиусами одной окружности, все они конгруэнтны. Следовательно, оба треугольника COB и COA равнобедренные. Углы B и BCO равны, так как они лежат на противоположных сторонах равнобедренного треугольника COB. Точно так же углы A и ACO равны, потому что они являются противоположными конгруэнтными сторонами треугольника COA.
Сумма мер трех углов в треугольнике равна 180 градусам и, следовательно,
m(∠A) + m(∠B) + m(∠C) = 180
Используя эквивалентность углов из предыдущего пункт
m(∠C) = m(∠BCO) + m(∠ACO)
= m(∠CBO) + m(∠CAO)
= m(∠B) + m(∠A)
Подставляя это в предыдущую формулу, мы находим
2m(∠A) + 2m(∠B) = 180
и, таким образом, m(∠A) + m(∠B) = 90.
Поскольку меры трех углов треугольника ABC добавить к 180 это означает, что m(∠C) = 90 °, поэтому треугольник ABC является прямоугольным, как и требовалось.Вопрос: Треугольник ΔABC вписан в окружность O, а сторона AC проходит через центр окружности. Найдите диаметр круга.
Ответ:
Мы знаем, что треугольник, вписанный хордой, проходящей через центр окружности, является прямоугольным.
Дано, BC = 16 и AB = 12.
Здесь можно применить теорему о гипотенузе,
Диаметр окружности равен 20.
Вписанные углы в окружности
Вписанный в окружность угол определяется таким образом, что две его стороны/лучи действуют как хорда к окружности и вершина угол расположен на окружности окружности.
Когда добавляется еще один угол, вершина которого находится в центре, а лучи пересекаются с концами предыдущего угла, угол, образуемый центральным углом, становится в два раза больше угла, образуемого другим углом.
Циклические четырехугольники
Когда четырехугольник вписан в окружность таким образом, что все вершины четырехугольника касаются окружности окружности. Есть определенные свойства для вписанного четырехугольника.
Свойство: Сумма противоположных углов вписанного четырехугольника всегда дает 180°. ИЛИ Можно сказать, что противоположные углы являются дополнительными по своей природе.
Здесь ∠A + ∠C = 180°
∠B + ∠D = 180°
Когда все углы сложены, ∠A + ∠B + ∠C + ∠D = 180 + 180 = 360°
Вопрос 1: На рисунке ниже найдите другой угол.
Ответ:
Поскольку оба вписанных угла лежат на одной дуге, они должны быть равны.
Итак, другой угол также равен 75 o
Вопрос 2: На рисунке ниже найдите длину малой дуги AC.
Ответ:
Из ранее изученной теоремы мы знаем, что угол, вписанный в окружность дугой, равен половине угла, вписанного в центр этой же дугой.
