Решение задач с помощью уравнений. 7 класс алгебра
Нажмите для полного просмотра!
Вы можете ознакомиться и скачать Решение задач с помощью уравнений. 7 класс алгебра . Презентация содержит 8 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Решение задач с помощью уравнений.
Слайд 2
Описание слайда:
Устно. Решите уравнения 1. 3а-7=5; 2. 3х+4=х+4; 3. n-5=3n+2; 4. 3x-4=2x+1; 5. -3x=5x+16; 6. -5k=k-12.
Слайд 3
Описание слайда:
“Арифметики” Леонтия Филипповича Магницкого. Книга эта была издана в 1703 году. Задача 1. Спросил некто учителя: “Сколько у тебя в классе учеников, т.к. хочу отдать к тебе в учение своего сына?”. Учитель ответил: “Если же придет учеников столько же сколько имею, и половина, и четвертая часть класса, и твой сын, тогда будет у меня 100 учеников. Спрашивается, сколько учеников было у учителя?” Ответ: 36
Слайд 4
Задача 2.
Приходит пастух с 70 быками. Его спрашивают:– Сколько ты привозишь из своего многочисленного стада? Пастух отвечает: — Я привожу2/3от 1/3стада, сочти! Узнайте сколько быков во всем стаде.
Ответ: 315
Слайд 5
Описание слайда:
Задача 3. Если задуманное число умножить на 5, из полученного произведения вычесть его треть, остаток разделить на 10 и к результату прибавить последовательно 1/2, 1/3 и 1/4 первоначального числа, то получим 68. Чему равно задуманное число? Ответ: 48
Слайд 6
Описание слайда:
Задача 4. Отец, у которого было трое сыновей, оставил им 1600 крон. Старший сын получил на 200 крон больше, чем средний, а средний на 100 крон больше младшего. Сколько получил каждый сын? Ответ: 700, 500, 400
Слайд 7
Описание слайда:
Решение уравнений.
Слайд 8
Описание слайда:
Самостоятельная работа. Вариант I.
Теги Решение задач с помощью уравнений. 7 класс алгебра
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Email§ 6. Решение задач с помощью уравнений
Тема урока: § 6. Решение задач с помощью уравнений. Приведены все необходимые и достаточные сведения для решения текстовых задач с помощью составления уравнений.
Введение
В школьной математике есть целый кладезь текстовых задач, которые решаются универсальным методом построения уравнения (модели) исходя из условия.
Сам факт того, что огромное количество самых разнообразных задач поддаются решению с помощью составления линейного уравнения, говорит нам, что метод решений является действительно универсальным.
Обычно условия задач удается перевести на математический язык. Полученное уравнение — это следствие перевода нашего условия с русского языка на язык алгебры. Зачастую фактической стороной повествования задачи является описание реальной ситуации, какого либо процесса, события.
Чтобы получить ответ — уравнение нужно решить, полученный корень уравнения будет являться решением, разумеется необходимо еще проверить, не является ли результат противоречивым относительно условия.
Алгоритм решения текстовых задач с помощью уравнений
Для решения задачи с помощью уравнения делают следующие действия:
- Обозначают некоторое неизвестное буквой и, пользуясь условием, составляют уравнение.
- Решают уравнение.
- Истолковывают результат.
Примеры решений
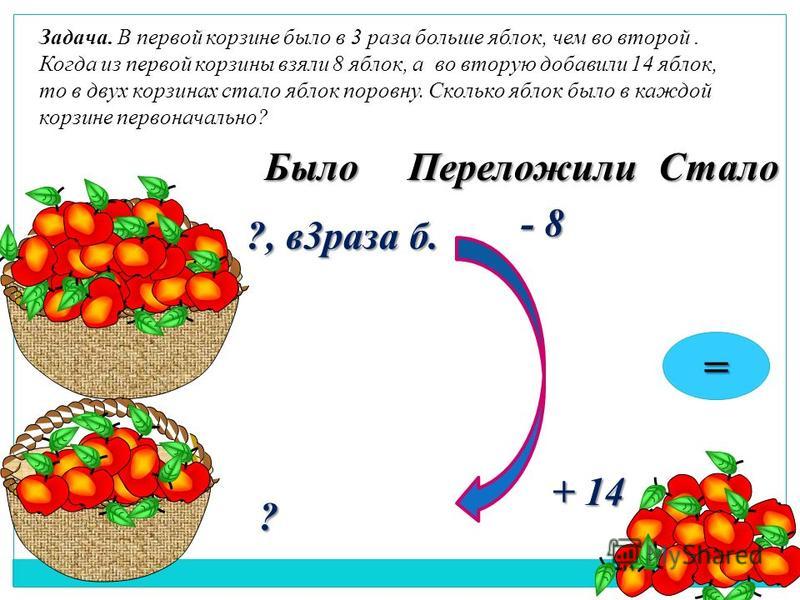
Задача 1.
В мешке было в 3 раза меньше монет, чем в сундуке. После того как из мешка переложили 24 монеты, в сундуке их стало в 7 раз больше, чем в мешке.Сколько было монет в мешке и сколько в сундуке?
Сколько было монет в мешке и сколько в сундуке?Решение:
Пусть $x$ — количество монет в мешке, а значит в сундуке: $3x$ монет. После того, как из мешка переложили $24$ монеты, в сундуке стало: $3x+24$, а в мешке $x-24$. И если в сундуке их стало в $7$ раз больше чем в мешке, то имеем: $3x+24=7(x-24)$.
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно $x$ и записать ответ.
Решим полученное уравнение: $3x+24=7(x-24)$. Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: $3x+24=7x-7\cdot 24$. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит $x$ в левую, получим: $24+7\cdot 24=7x-3x$. После упрощения получили $192=4x$, разделим обе части уравнения на коэффициент при неизвестном, т.е на $4$, тогда получим $x=48$.
Осталось истолковать ответ.
За переменную $x$ мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.Монет в мешке: $48$
Монет в сундуке: $48\cdot 3=144$
е $3x$.Задача 2.
Купили 3600 кг муки и высыпали её в три мешка. В первый мешок муки вошло в 3 раза больше, чем во второй, а в третий мешок насыпали 800 кг муки. Сколько муки насыпали в первый и сколько во второй мешок?
Решение:
Пусть в первый мешок насыпали $3x$ кг муки, тогда во второй мешок насыпали $x$ кг. Если сложим количество кг в каждом мешке, то получим $3600$ кг муки. Имеем: $3x+x+800=3600$, решим уравнение классическим методом.
Все слагаемые содержащие $x$ оставим слева, а всё остальное перенесём в правую часть равенства: $3x+x=3600-800$, упростим обе части; $4x=2800$ поделим обе части равенства на $4$ и получим ответ: $x=700$.
Ответ.
За переменную $x$ мы обозначали количество муки во втором мешке, по условию в первом в три раза больше.Муки в первом мешке: $700\cdot 3=2100$ кг.
Муки во втором мешке: $700$ кг.
Задача 3.
В первом мешке в 4 раза больше картофеля, чем во втором. После того, как из одного мешка взяли 40 кг картофеля, а во второй насыпали ещё 5 кг, в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Решение:
Пусть во втором мешке $x$ кг картофеля, тогда в первом мешке $4x$ кг. Из первого взяли $40$ кг, тогда в первом стало: $4x-40$. Во второй мешок насыпали $5$ кг и теперь в нём: $x+5$ кг картошки. Нам известно, что после этих изменений количество картофеля в мешках стало поровну, запишем это с помощью линейного уравнения:
$$4x-40=x+5$$
Решим это линейное уравнение. Все слагаемые содержащие переменную перенесём влево, а свободные члены вправо и получим:
$$4x-x=5+40$$
Упростим выражения:
$$3x=45$$
Избавимся от коэффициента при неизвестном и получим ответ:
$$x=15$$
Ответ.
За переменную $x$ мы обозначали количество кг картошки во втором мешке, по условию в первом в четыре раза больше.Картошки в первом мешке: $15\cdot 4=60$ кг.
Картошки во втором мешке: $15$ кг.
Задача 4.
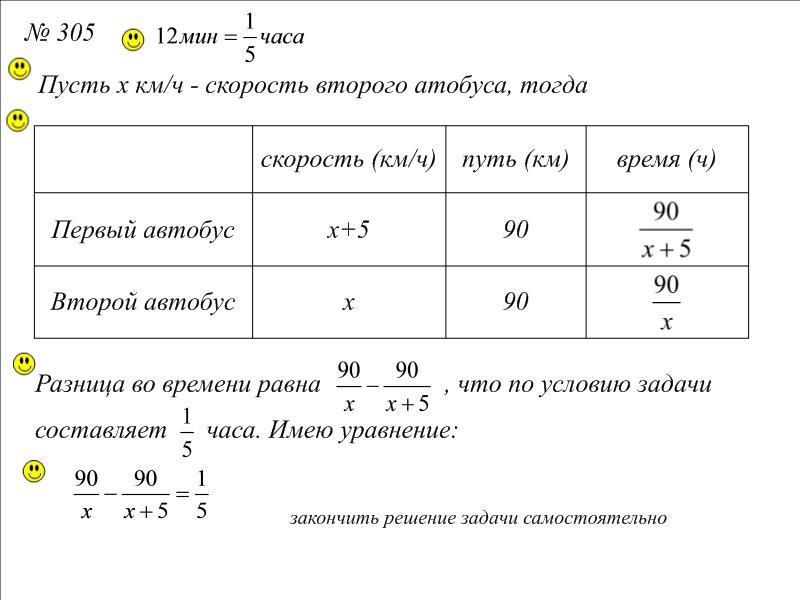
По шоссе едут две машины с одной и той же скоростью. Если первая увеличит скорость на 20 км/ч, а вторая уменьшит скорость на 20 км/ч, то первая за 2 часа пройдёт то же самое расстояние, что и вторая за 4 часа. Найдите первоначальную скорость машин.
Решение:
Пусть машины едут со скоростью $v$ км/ч, тогда после ускорения первой машины её скорость стала: $v+20$ км/ч, а скорость второй машины после замедления стала: $v-20$ км/ч. Нам известно по условию, что после изменения скоростей машин, первая проходит за два часа ровно столько, сколько вторая за четыре, тогда имеем:
По известной нам формуле $S=vt$ ($S$ — расстояние, $v$ — скорость, $t$ — время)
$$2(v+20)=4(v-20)$$
Сократим обе части равенства на $2$, тогда получим: $v+20=2(v-20)$.
Раскроем скобки в правой части уравнения и сгруппируем все переменные в правой части равенства.
$$v+20=2v-2\cdot 20$$
$$v+20=2v-40$$
$$20+40=2v-v$$
$$v=60$$
Ответ.
В качестве неизвестной величины в задаче мы взяли $v$ (первоначальную скорость машин).Первоначальная скорость машин: $v=60$ км/ч.
Задача 5.
В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Решение:
Пусть во вторую бригаду привезли $x$ кг раствора цемента, тогда в первую бригаду привезли $x-50$ кг. Через 3 часа работы у первой бригады осталось $x-50-3\cdot 150$ кг цемента, а у второй $x-3\cdot 200$ кг.
По условию известно, что через 3 часа работы в первой бригаде осталось в 1,5 раза больше цемента, чем во второй, тогда имеем:
$$x-50-3\cdot 150=1,5(x-3\cdot 200)$$
Осталось решить данное уравнение относительно $x$ и истолковать ответ.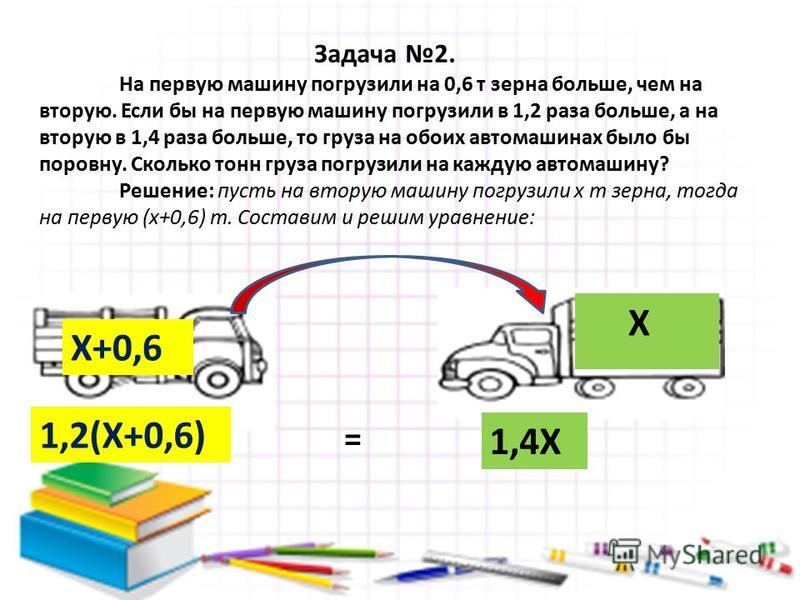
Упростим и раскроем скобки в правой части, тогда получим:
$$x-500=1,5x-1,5\cdot 600$$
Если вам неудобно работать с десятичными дробями, то вы всегда можете их переводить в рациональный вид: $1,5=\frac{15}{10}=\frac{3}{2}$.
Запишем с учётом перевода дробей и упростим:
$$x-500=\frac{3}{2}x-\frac{3}{2}\cdot \frac{600}{1}$$
$$x-500=\frac{3x}{2}-\frac{3}{1}\cdot \frac{300}{1}$$
$$x-500=\frac{3x}{2}-900$$
Перенесём слагаемые содержащие переменную в правую сторону, а всё остальное в левую:
$$900-500=\frac{3x}{2}-x$$
$$400=\frac{3x}{2}-\frac{x}{1}$$
$$400=\frac{3x-2x}{2}$$
$$400=\frac{x}{2}$$
Домножим обе части на 2 и получим ответ:
$$x=800$$
Ответ.
В качестве переменной в задаче мы взяли $x$ (кол-во кг цемента который привезли во вторую бригаду), по условию в первую привезли на 50 кг меньше, а значит $x-50$Кол-во цемента в первой бригаде: $800-50=750$ кг.
Кол-во цемента во второй бригаде: $800$ кг.
Задачи для самостоятельного решения
Условие
№1.
Задача Э. Безу.
По контракту работникам причитается 48 франков за каждый отработанный день, а за каждый неотработанный день с них вычитается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?
Решение
Пусть работники отработали $n$ дней, тогда $30-n$ дней они не отработали.
В итоге мы понимаем, что за $n$ рабочих дней они зарабатывают $48n$ франков и с них вычитается за $30-n$ не отработанных дней по $12(30-n)$ франков. Тогда ясно, что: $48n-12(30-n)=0$
$$48n-12\cdot 30+12n=0$$
$$48n+12n=12\cdot 30$$
$$60n=360$$
$$n=\frac{360}{60}$$
$$n=6$$
Ответ: Рабочие отработали 6 дней.
Условие
№2.
Задача В.И Арнольда.
Кирпич весит фунт и полкирпича. Сколько фунтов весит кирпич?
Решение
Пусть целый кирпич весит весит $k$ фунтов, тогда имеем:
1 фунт и половина кирпича = целый кирпич.
$1+0,5k=k$
$1=k-0,5k$
$0,5k=1$
$k=1:0,5$
$k=2$
Ответ: Кирпич весит 2 фунта.
Условие
№3.
Задача В.И Арнольда
Бутылка с пробкой стоит 10 копеек, причем бутылка на 9 копеек дороже пробки. Сколько стоит бутылка без пробки?
Решение
Пусть бутылка стоит $b$ копеек, а пробка $p$ копеек, тогда:
$b+p=10$ и $b=p+9$, подставив значение $b$ в первое равенство — получим:
$$p+9+p=10$$
$$2p=10-9$$
$$2p=1$$
$$p=1:2$$
$$p=0,5$$
Т.е пробка стоит пол копейки, тогда бутылка $9,5$ копеек.
Ответ: 9,5 копеек стоит бутыка без пробки.
Условие
№4.
На свитер, шапку и шарф израсходовали 555 г шерсти, причем на шапку ушло в 5 раз меньше шерсти, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?
Решение
Пусть на свитер потратили $5x$ г шерсти, тогда на шапку ушло $x$ г и на шарф потребовалось $x-5$ г, имеем:
$$5x+x+x-5=555$$
$$7x=555+5$$
$$x=560:7$$
$$x=80$$
Ответ: На шапку ушло $80$ г, на свитер $5\cdot 80=400$ г, на шарф $80-5=75$ г.
Условие
№5.
Три пионерских звена собрали для школьной библиотеки 65 книг. Первое звено собрало на 10 книг меньше, чем второе, а третье — 30% того числа книг, которое собрали первое и второе звено вместе. Сколько книг собрало каждое звено?
Решение
Пусть второе звено собрало $x$ книг, тогда первое собрало $x-10$ книг, а третье $0,3(2x-10)$, имеем:
$$2x-10+0,3(2x-10)=65$$
$$2x-10+0,3\cdot 2x-0,3\cdot 10=65$$
$$2x+0,3\cdot 2x=65+10+0,3\cdot 10$$
$$2,6x=65+13$$
$$2,6x=78$$
$$x=78:2,6$$
$$x=30$$
Ответ: Первое звено собрало $30-10=20$ книг, второе $30$ книг, третье $0,3(60-10)=15$ книг.
← Следующая тема
Standards Toolkit » Общие базовые стандарты математики для 7 класса
K123
4567
89-12
PDF для 7 класса
Launch Search
В 7 классе учебное время должно быть сосредоточено на развитии понимания:1) (1) применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работы с выражениями и линейными уравнениями; (3) решение задач, связанных с чертежами в масштабе и неформальными геометрическими построениями, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
1. Учащиеся расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одношаговых и многошаговых задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения самых разных задач на проценты, в том числе связанных со скидками, процентами, налогами, чаевыми и процентным увеличением или уменьшением.
Учащиеся решают задачи о чертежах в масштабе, связывая соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах. Учащиеся изображают пропорциональные отношения и неофициально понимают единичную норму как меру крутизны связанной линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений.
2. Учащиеся развивают единое понимание числа, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Учащиеся распространяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, а также умножением и делением. Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы долга или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами.
Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач.
3. Учащиеся продолжают работу с площадью с 6 класса, решая задачи на площадь и длину окружности и площадь поверхности трехмерных объектов. При подготовке к работе на конгруэнтность и подобие в 8 классе рассуждают об отношениях между двухмерными фигурами, используя чертежи в масштабе и неформальные геометрические построения, знакомятся с отношениями между углами, образованными пересекающимися линиями. Учащиеся работают с трехмерными фигурами, связывая их с двухмерными фигурами, рассматривая поперечные сечения. Они решают реальные и математические задачи, связанные с площадью, площадью поверхности и объемом двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
4. Учащиеся опираются на свою предыдущую работу с отдельными распределениями данных, чтобы сравнить два распределения данных и ответить на вопросы о различиях между группами населения.
Они начинают неформальную работу со случайной выборкой для создания наборов данных и узнают о важности репрезентативных выборок для получения выводов.
| Домен | Кластер | Код | Единый основной государственный стандарт |
|---|---|---|---|
| Соотношения и отношения пропорциональности | Анализировать пропорциональные отношения и использовать их для решения реальных и математических задач. | 7.РП.1 | Расчет удельных расходов, связанных с отношениями дробей, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, рассчитайте удельную скорость как комплексную дробь (1/2)/(1/4) мили в час, что эквивалентно 2 милям в час. |
| 7.RP.2 | Распознавать и отображать пропорциональные отношения между величинами. а. Определите, находятся ли две величины в пропорциональном отношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат. б. Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, схемах и словесных описаниях пропорциональных отношений. в. Представьте пропорциональные отношения уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, связь между общей стоимостью и количеством изделий может быть выражена как t = pn. д. Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки (0, 0) и (1, r) , где r — единичная ставка. | ||
| 7.РП.3 | Используйте отношения пропорциональности для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка. | ||
| Система счисления | Применять и расширять прежнее понимание операций с дробями для сложения, вычитания, умножения и деления рациональных чисел. | 7.НС.1 | Применение и расширение предыдущего понимания сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями. а. Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет заряд 0, потому что две его составляющие равны 9.0003 противоположно заряжены. б. Под p + q понимается число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Показать, что число и его противоположность имеют сумму 0 (являются аддитивными инверсиями).  Интерпретируйте суммы рациональных чисел, описывая контексты реального мира. в. Поймите вычитание рациональных чисел как добавление обратного аддитивного, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на 90 003 числовой прямой равно абсолютному значению их разности, и примените этот принцип в реальных условиях. д. Применяйте свойства операций как стратегии сложения и вычитания рациональных чисел. |
| 7.НС.2 | Применять и расширять прежнее понимание умножения и деления, а также дробей для умножения и деления рациональных чисел. а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (–1)(–1) = 1, и правилам умножения чисел со знаком. . Интерпретировать продукты рациональных чисел, описывая контексты реального мира. б. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом.  Если p и q целые числа, то –(p/q) = (–p)/q = p/(–q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира. в. Применяйте свойства операций как стратегии умножения и деления рациональных чисел. д. Преобразование рационального числа в десятичное с использованием длинного деления; знать, что десятичная форма рационального числа оканчивается на 0 или в конечном итоге повторяет | ||
| 7.НС.3 | Решите реальные и математические задачи, связанные с четырьмя операциями над рациональными числами. (Вычисления с рациональными числами расширяют правила обращения с дробями до сложных дробей.) | ||
| Выражения и уравнения | Используйте свойства операций для создания эквивалентных выражений. | 7.EE.1 | Применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами. |
| 7.EE.2 | Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5 %» равносильно «умножению на 1,05». | ||
| Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения. | 7.EE.3 | Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. | |
| 7.EE.4 | Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах. а. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих формируется плавно. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина? б. Решайте текстовые задачи, приводящие к неравенствам вида px + q > r или px + q неравенству, и интерпретируйте его в контексте задачи.  Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения. | ||
| Геометрия | Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними. | 7.G.1 | Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе. |
| 7.G.2 | Рисование (от руки, с линейкой и транспортиром и с техникой) геометрических фигур с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника. | ||
7. G.3 | Опишите двухмерные фигуры, которые получаются в результате разрезания трехмерных фигур, таких как плоские сечения прямоугольных призм и прямоугольных пирамид. | ||
| Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема. | 7.G.4 | Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга. | |
| 7.G.5 | Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многошаговой задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре. | ||
| 7.G.6 | Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм. | ||
| Статистика и вероятность | Используйте случайную выборку, чтобы делать выводы о совокупности. | 7.СП.1 | Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности. Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы. |
| 7.СП.2 | Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. | ||
| Сделайте неформальные сравнительные выводы о двух популяциях. | 7.СП.3 | Неформально оценить степень визуального перекрытия двух распределений числовых данных с похожими вариациями, измеряя разницу между центрами, выражая ее как кратное мере вариации. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот. | |
| 7.СП.4 | Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух совокупностях. Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. | ||
| Исследование случайных процессов и разработка, использование и оценка вероятностных моделей. | 7.СП.5 | Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность возникновения события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие. | |
| 7.СП.6 | Аппроксимируйте вероятность случайного события, собирая данные о случайном процессе, который его производит, и наблюдая его долгосрочную относительную частоту, и предскажите приблизительную относительную частоту с учетом вероятности. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз. | ||
7. СП.7 | Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия. а. Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, , если случайным образом выбран ученик из класса, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка. б. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты вращения копеек кажутся равновероятными? | ||
7. СП.8 | Найдите вероятности составных событий, используя упорядоченные списки, таблицы, древовидные диаграммы и моделирование. а. Поймите, что, как и в случае с простыми событиями, вероятность составного события представляет собой долю исходов в пространстве выборки, для которой происходит составных события. б. Представляйте примеры пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы. Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие. в. Разработайте и используйте симуляцию для генерации частот для составных событий. Например, используйте случайные цифры в качестве инструмента моделирования, чтобы приблизить ответ на вопрос: если 40% доноров имеют группу крови А, какова вероятность того, что потребуется не менее 4 доноров, чтобы найти одного с группой крови А? |
9 Волшебные упражнения для решения уравнений реального мира
Нет сомнений, что я должен был стать учителем средней школы.
Я люблю зомби, пиратов, единорогов, тако и авокадо. Как только я понял, что мою любовь к случайным событиям разделяют и мои ученики, я нашел способ найти с ними общий язык. Некоторые из моих студентов выходят из комнаты и просят меня съесть хороший авокадо. На самом деле это ничего не значит, но эти внутренние шутки объединяют мой класс. Когда я практикуюсь с реальными задачами или задачами со словами, я обязательно добавляю немного случайности в математические ситуации. Мы весело проводим время, решая эти страшные словесные задачи, и это помогает учащимся оставаться вовлеченными. Сегодня я поделюсь с вами девятью стратегиями и упражнениями, которые помогут учащимся попрактиковаться в решении реальных задач с помощью уравнений.
Трудно найти задачи в реальном мире, соответствующие стандартам для 7-го класса. Помнится, пару лет назад, когда я ничего не мог найти по этой теме, я просто сделал свои собственные проблемы с собственным причудливым блеском. Учащимся понравилось неожиданное появление пингвина в математической задаче, и это напомнило мне, что мы можем разнообразить занятия математикой неожиданными способами.
В этом посте вы найдете подборку реальных задач, в которых используются уравнения. Некоторые из них включают в себя несколько задач, тогда как другие берут одну проблему и превращают ее в задание на выполнение. Ваши ученики получат задание, которое им нужно для решения этих задач.
Список:
Карты задач
Реальные рабочие листы простых уравнений в реальном мире (с участием пингвинов)
Целевая игра с рабочими листами
Кубики Решения. и некоторые проблемы
Изучите миллиард головоломок с печеньем
Иллюстративная математика
Давайте погрузимся в
Решение реальных проблем — это концептуальная тема с множеством движущихся частей. Студенты должны использовать несколько концепций для постановки и решения этих задач. Это делает действия для этой темы немного отличными от других. У меня нет никаких лабиринтов или раскрасок для этой темы, потому что эта тема действительно должна быть сосредоточена на деконструкции проблемы, а затем на ее решении.
Как вы увидите, практика решения реальных проблем требует целенаправленной работы и повторения в самых разных ситуациях.
У карточек заданий так много применений. Вы можете предложить учащимся работать над ними самостоятельно, с партнерами или всем классом. Я использую их почти в каждом уроке, который преподаю. Кроме того, они отлично подходят для занятий студентов, когда у вас есть замещающий учитель. Я просто печатаю ответы на обратной стороне, и студенты могут сразу же получить обратную связь, даже когда меня нет рядом.
Этот набор карточек с заданиями «Уравнения и реальные проблемы» может быть моим любимым набором карточек с заданиями, которые я когда-либо создавал из-за предмета. Учащиеся должны прочитать, написать уравнение и решить 12 текстовых задач. Некоторые из вопросов касаются тем, которые вы, вероятно, ожидаете: распродажа выпечки, распродажа фильмов и т. д. Но другие говорят о пингвинах и семье зомби в отпуске. Я надеюсь, что они заставят детей смеяться и заниматься математикой одновременно.
Иногда я понимаю, что нам нужно много практиковаться, и это не всегда может быть очень увлекательно, но, надеюсь, такие маленькие повороты заставят детей улыбаться.
Помимо решения реальных задач, этот набор карточек с заданиями содержит 8 уравнений, которые учащиеся должны решить в качестве повторения. Он также включает в себя дополнительную деятельность, давая учащимся 4 уравнения и предлагая им написать свое собственное уравнение.
Если вам нужны еще причудливые сюжетные задачи, не ищите дальше. Этот сборник из 8 задач на тему пингвинов заставляет учащихся говорить. Учащимся необходимо составить уравнение, представленное в рассказе, а затем решить.
Похоже, мои ученики любят пингвинов, а если добавить немного математики, получается волшебство. Это отлично работает в качестве обзора или практического занятия. Часто, когда у меня есть такая деятельность, я проверяю свои ответы после каждого вопроса. Таким образом, я вижу, как у них дела, и помогаю им исправить любые неправильные представления, которые у них могут быть.
С этой темой действия могут немного отличаться от таких навыков, как распределение собственности. Выполнение задач занимает немного больше времени, и учащиеся должны уметь выполнять более одного навыка. Когда они только начинают, и я хочу, чтобы они попробовали решить некоторые задачи, мы будем использовать такую игру, как целевая игра. Он заключается в бросании шарика на присоске в цель на доске. Чтобы узнать больше об этой игре, прочтите этот пост.
Эти рабочие листы являются бесплатной практикой для учащихся. Мне нравится, что у них много примеров задач, потому что иногда детям нужно больше практики. Я использую задачи из подобных рабочих листов, чтобы играть в такие игры, как целевая игра. У них есть множество вопросов, и вы можете сделать несколько примеров с детьми всем классом. Кроме того, вы можете выбрать одну задачу для использования в качестве рабочего примера в тетрадях учащихся.
Когда мы начинаем решать задачи, наш урок математики становится уроком чтения.
Мы не можем предположить, что все учащиеся могут читать и понимать текстовые задачи, потому что многие из них испытывают затруднения. Я провел много лет, работая со студентами, которые действительно борются с чтением. Я считаю, что такие стратегии решения проблем, как C.U.B.E.S. дает учащимся структуру того, как решать проблемы. Вы можете использовать эту презентацию CUBES, чтобы увидеть, как познакомить учащихся с концепцией CUBES.
C.U.B.E.S Обозначает…
Обведите ключевые цифры
Подчеркните вопрос
Подчеркните слова-подсказки
Изучите ключевые слова, числа, вопросы и т. д.
Решите задачу
складной графический органайзер для этой презентации на TPT.
В этом посте от Mrs. E Teaches Math вы можете найти различные способы представить, как решать многошаговые уравнения в интерактивных тетрадях. Это не только отличный способ представления информации, но и дает учащимся ссылку, к которой можно вернуться. Я стараюсь убедиться, что у студентов есть пара рекомендаций, которые помогут им, когда они застрянут.
Миссис Э. Преподает математику в интерактивной тетради приводит несколько примеров того, как решать двухшаговые уравнения, и примеры того, как решать текстовые задачи.
Хотите еще больше идей для использования интерактивных тетрадей в классе математики? Ознакомьтесь с нашим БЕСПЛАТНЫМ мини-курсом о том, как максимально эффективно использовать интерактивные блокноты. Это серия из 5 частей, доставленная прямо в ваш почтовый ящик. К концу у вас будет собственный индивидуальный план запуска или расширения интерактивных тетрадей в вашем классе.
НАЖМИТЕ ЗДЕСЬ, чтобы получить бесплатный мини-курс по математике в интерактивной тетради.
Не могу дождаться встречи с вами!
Если вы хотите попрактиковаться в решении текстовых задач, вам нужно предоставить учащимся много возможностей для решения текстовых задач. Один из способов, который мне нравится оживлять нашу практику, — это игра в «Выбери карту». Когда я был ребенком, мне всегда нравилось смотреть «Правильная цена», и иногда я превращаюсь в «Боба Баркера» в своем классе.
В этой игре все учащиеся решают задачу, а затем задают им вопросы по ней. Студенты, которые ответят на вопросы, смогут выбрать карту из моей колоссальной колоды карт. Студент с самой высокой картой получает очки. Это займет всего минуту, и дети любят новизну этого.
Текстовые задачи в этом наборе из Math-Aids короткие и простые. Они отлично подходят для обзора или для работы с губкой. Они идеально подходят для того, чтобы иметь их под рукой, а затем в те моменты, когда у вас есть несколько дополнительных минут, вы можете использовать их, чтобы сыграть в игру «Выбери карту».
На веб-странице CK-12 есть записанный урок, видео и 10 задач, которые учащиеся могут выполнить, чтобы попрактиковаться в решении реальных задач с помощью многошаговых уравнений. Это дает студентам дополнительную практику, и они могут идти в своем собственном темпе. Вы также можете использовать это как ресурс для своего собственного обучения, чтобы получить некоторые идеи о том, как объяснить этот тип проблемы студентам.
Этот сайт позволяет создавать классы, и студенты могут отправлять работы через сайт. Еще один способ привлечь учащихся к ответственности — попросить их сделать скриншот страницы, когда они закончат, и отправить его вам по электронной почте.
С помощью этого задания Cookie Conundrum от Learn Zillion учащимся предстоит решить сложную проблему с видео. Учитель направляет учеников и дает подмости на ходу. Он также включает в себя некоторые дополнительные вопросы, чтобы дать студентам контроль над мышлением. Если вы войдете в Learn Zillion, что вы можете сделать с помощью своей учетной записи электронной почты Google, вы сможете получить дополнительные ресурсы. Одним из них является интервенционное задание. Задания можно назначать через Google Classroom. Одной из замечательных особенностей этого набора мероприятий является поддержка, которую программа оказывает во время работы.
Последнее действие в этом списке прекрасно подходит для повышения производительности. В этой задаче Gotham City Taxis от Illustrative Mathematics учащиеся могут прийти к решению, используя различные математические методы.
Вы можете предложить учащимся ответить на этот вопрос в качестве задачи недели или в небольших группах. Что мне нравится в этой задаче, так это то, что студенты подходят к ней по-разному. Задача заключается в том, чтобы найти цену такси, и она действительно заставляет студентов задуматься. Когда все учащиеся закончат, вы можете предложить им поделиться своим методом с классом. Как класс вы можете сравнить и сопоставить методы, которые использовали студенты. Это помогает детям увидеть, что вы можете решать проблемы разными способами.
Попробуйте что-то одно
Каждый год, когда вы снова и снова учите одному и тому же предмету, приятно добавлять что-то новое. Одна из моих коллег преподает математику уже очень давно, и она по натуре традициональна. Она всегда говорит мне, что любит пробовать что-то новое. Это бросает вызов ей как учителю, и ученики ценят ее усилия. Я надеюсь, что вы решитесь и попробуете одно из этих занятий, и, возможно, вы позволите своему внутреннему единорогу, пингвину или пирату проявить себя в течение учебного дня.