Симплексный метод решения задач линейного программирования
Симплексный метод – метод последовательного улучшения плана. Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования. Математическая модель задачи приводится к каноническому (стандартному) виду. Заполняется опорная симплекс – таблица с использованием коэффициентов целевой функции и системы ограничений. Решается задача по алгоритму.
Идея симплексного метода заключается в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по допустимым решениям к оптимальному. Значение целевой функции для задач на максимум не убывает. Так как число допустимых решений конечно, то через конечное число шагов получим оптимальное решение.
Алгоритм симплексного метода
Математическую модель задачи привести к каноническому (стандартному) виду.
Построить начальную симплекс-таблицу исходя из стандартного вида.
Найти разрешающий столбец. В строке коэффициентов ЦФ найти значение с самим маленьким отрицательным числом. Этот столбец и будет разрешающим.
Вычислить разрешающую строку и ведущий элемент (Почленно разделить столбец свободных членов на элементы разрешающего столбца, за исключением строки ЦФ. Выбрать наименьшее из частных. Эта строка будет разрешающей. Ведущий элемент будет на пересечении разрешающего столбца и разрешающей строки.).
Построить новую симплекс-таблицу-второй шаг. При построении новой таблицы убрать из базиса строку с переменной разрешающей строки в предыдущей таблице. Ввести в базис строку с названием разрешающего столбца предыдущей таблицы.
Построение ведущей строки в новой таблице. Почленно поделить всю разрешающую строку на разрешающий элемент.
Построение других строк в новой таблице. Почленно умножить ведущую строку на соответствующие этим строкам элементы разрешающего столбца из предыдущей таблицы и прибавить к соответствующим строкам в старой таблице.
Проверяем таблицу второго шага на оптимальность. Если в строке целевой функции нет отрицательных элементов, тогда таблица имеет оптимальный план, записать ответ. Если в строке ЦФ есть отрицательный элемент (элементы), тогда переходят к следующему (третьему) шагу, строят новую симплекс-таблицу в соответствии п.5 и затем проверяют ее на оптимальность. Построение таблиц заканчивается с нахождением оптимального плана.
Прямая задача на минимум решается следующим образом:
Решить двойственную модель симплекс — методом
Записать ответ.
Связь между задачами двойственной пары в том, что, решая симплексным методом одну из них, автоматически получаем решение другой.
Для этого достаточно воспользоваться соответствием переменных прямой и двойственной задач в последней симплекс-таблице.
Х1 | x2 | … | xn | S1 | S2 | … | Sm |
S1 | S2 | … | Sm | y1 | y2 | … | ym |
Пример. На предприятии имеется возможность выпускать n видов продукции (1,2,…n). При ее изготовлении используются ресурсы Р1, Р2, Р3. Размеры прямых затрат ресурсов ограничены соответственно величинами b1, b2, b3. Расход i –го ресурса на единицу продукции j-того вида составляют aij. Цена единицы продукции j-того вида равна cj ден. ед. Сформулировать прямую и двойственную задачу и раскрывать экономический смысл всех переменных.
Требуется: найти оптимальный план симплекс-методом, найти решение двойственной задачи, указать дефицитность ресурсов, обосновать эффективность плана производства, оценить целесообразность приобретения ресурса, оценить целесообразность выпуска новой продукции
Данные:
b1 = 25, b2 = 30, b3 = 42
a11= 2, a12= 3, a13= 2, a14= 1
a21= 4, a22= 1, a23= 3, a24= 2
a31= 3, a32= 5, a33= 2,a34= 2
c1= 6, c2= 5, c3= 4, c4= 3
Математическая модель прямой задачи
max(Z= 6×1+5×2+4×3+3×4)
2×1+3×2+2×3+x4<25
4×1+x2+3×3+2×4<30
3×1+5×2+2×3+2×4<42
x1,x2,x3,x4>0
Математическая модель двойственной задачи
min (Z*= 25y1+30y2+42y3)
2y1+4y2+3y3> 6
3y1+y2+5y3> 5
2y1+3y2+2y3> 4
y1+2y2+2y3> 3
y1, y2, y3, y4 > 0
Стандартный вид
min(Z= -6×1-5×2-4×3-3×4)
2×1+3×2+2×3+x4+S1=25
4×1+x2+3×3+2×4+S2=30
3×1+5×2+2×3+2×4+S3=42
x1, x2, x3, x4, S1, S2, S3 > 0
Экономический смысл переменных
Xi – количество произведенной продукции
Yj – цена ресурса
Si – количество оставшегося ресурса
базис | значение | x1 | x2 | x3 | x4 | S1 | S2 | S3 | отношение |
Z | 0 | -6 | -5 | -4 | -3 | 0 | 0 | 0 | |
S1 | 25 | 2 | 3 | 2 | 1 | 1 | 0 | 0 | 12,5 |
S2 | 30 | 4 | 1 | 3 | 2 | 0 | 1 | 0 | 7,5 |
S3 | 42 | 5 | 2 | 2 | 0 | 0 | 1 | 14 | |
Таблица 2 | |||||||||
базис | значение | x1 | x2 | x3 | x4 | S1 | S2 | S3 | отношение |
Z | 45 | 0 | -3,5 | 0,5 | 0 | 0 | 1,5 | 0 | |
S1 | 10 | 0 | 2,5 | 0,5 | 0 | 1 | -0,5 | 0 | 4 |
x1 | 7,5 | 1 | 0,25 | 0,75 | 0,5 | 0 | 0,25 | 0 | 30 |
S3 | 19,5 | 0 | 4,25 | -0,3 | 0,5 | 0 | -0,8 | 1 | 4,59 |
Таблица 3 | |||||||||
базис | значение | x1 | x2 | x3 | x4 | S1 | S2 | S3 | отношение |
Z | 59 | 0 | 0 | 1,2 | 0 | 1,4 | 0,8 | 0 | |
x2 | 4 | 0 | 1 | 0,2 | 0 | 0,4 | -0,2 | 0 | |
x1 | 6,5 | 1 | 0 | 0,7 | 0,5 | -0,1 | 0,3 | 0 | |
S3 | 2,5 | 0 | 0 | -1,1 | 0,5 | -1,7 | 0,1 | 1 | |
Анализ решения
Продукции 1 вида производим 6,5 ед., второго вида 4 единицы, третьего и четвертого вообще не производим. Прибыль при этом составит 59 ден. единиц.
Ресурс 1 типа стоит 1,4 ден. ед., 2 типа – 0,8 ден. ед. Третий тип ресурса у нас остался в количестве 2,5 ед., поэтому его покупать не нужно.
Ресурсы 1 и 2 типа дефицитны, 3 типа избыточен.
Эффективность производства:
Z = 6*6.5+5*4+4*0+3*0=59 Z*=25*1.4+30*0.8+42*0=59 Производство в целом эффективно
2*1,4+4*0,8+3*0<6 6=6 Производство 1 вида продукции эффективно
3*1,4+1*0,8+5*0<5 5=5 Производство 2 вида продукции эффективно
2*1,4+3*0,8+2*0<4 5,2> 4 Производство 3 вида продукции не эффективно
1*1,4+2*0,8+2*0<3 3=3 Т.к. x4 не входит в базис, то оптимальный план не единственен.
Оценить целесообразность покупки 5 ед. второго ресурса по цене 10 ден. ед, т.е. единица ресурса обойдется нам в 2 ден. ед. Мы же готовы покупать только по 0,8 ден. ед. за 1 единицу ресурса.
а1 = 2, а2 = 2, а3 = 4. Цена новой продукции равна 4.
2*1,4+2*0,8+2*0<4 4,4> 4 Производство 5 вида продукции не эффективно.
Пример. Для изготовления продукции используют 3 вида сырья. При этом можно применять любой из четырех способов производства. Запасы сырья, расход и количество производимой продукции за 1 час работы по каждому способу приведены в таблице.
Способ производства Сырьё | 1 | 2 | 3 | 4 | Запас сырья |
1 | 1 | 2 | 1 | 0 | 18 |
2 | 1 | 1 | 2 | 1 | 30 |
3 | 1 | 3 | 3 | 2 | 40 |
Выпуск продукции | 12 | 7 | 18 | 10 |
Требуется найти
план производства, при котором будет
выпущено наибольшее количество продукции.
Обозначим через 
время использованияj—го
способа производства (j=
1,2,3,4),получим задачу линейного
программирования:
.
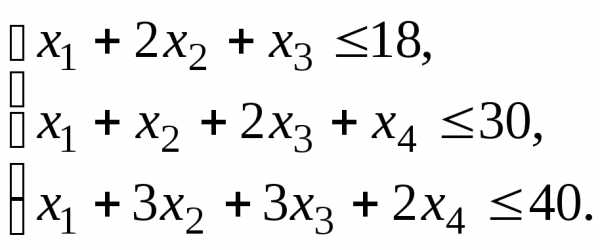
Эту задачу сведём к канонической задаче минимизации:
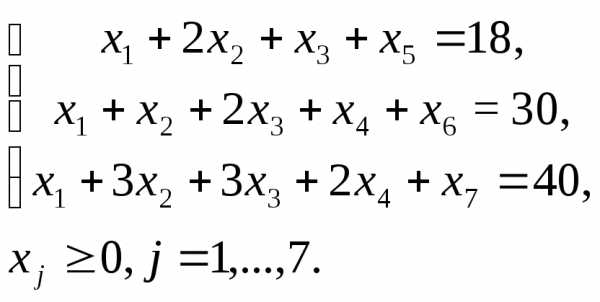
Cоставим
симплекс-таблицу. Симплекс-таблица
оказывается приведённой к базису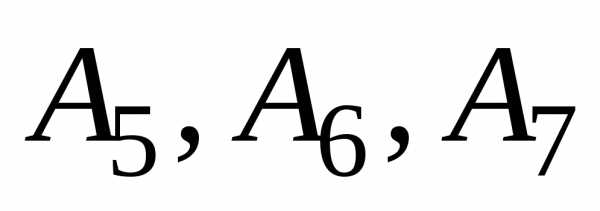
опорного решения.
x1
x2
x3
x4
x5
x6
x7
1
x
1
0
1
0
0
18
1
1
2
1
0
1
0
30
1
3
3
2
0
0
1
40
12
7
18
10
0
0
0
0
Выбираем положительную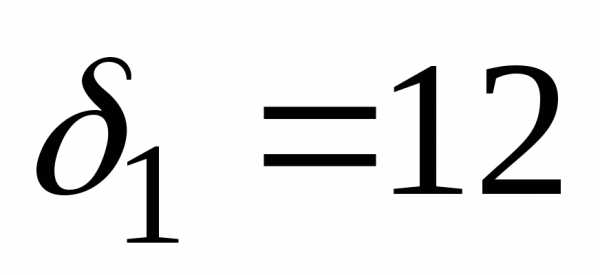 
и составляем следующие отношения: 
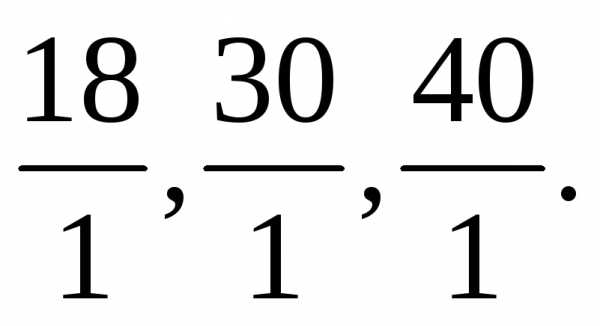Так как наименьшее среди них
то необходимо перейти к базису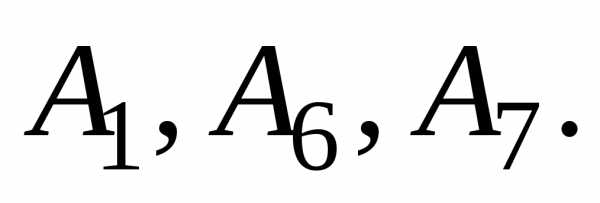
Для этого достаточно выполнить жорданово
преобразование всей таблицы с ведущим
элементом
.
x1
x2
x3
x4
x5
x6
x7
1
2
1
0
1
0
0
18
0
-1
1
1
-1
1
0
12
0
1
2
2
-1
0
1
22
0
-17
6
10
-12
0
0
-216
Базис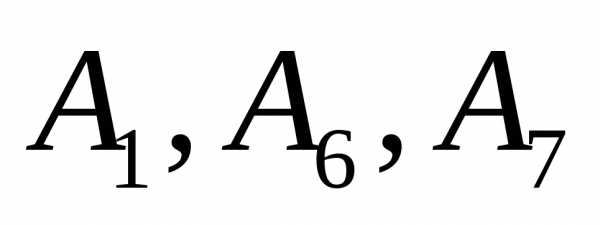 
является базисом опорного решения
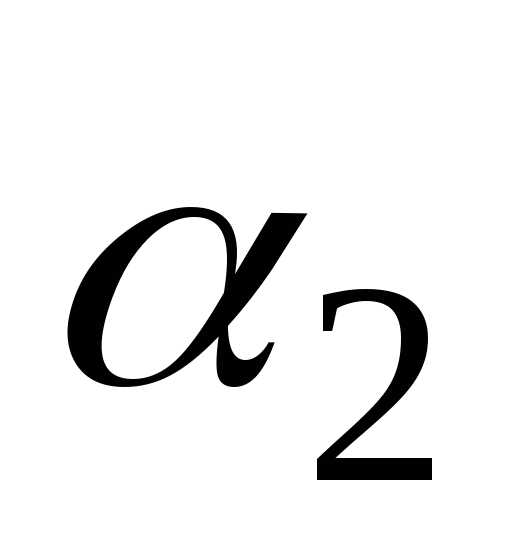=(18;0;0;0;0;12;22).
При этомв то время как
.
Выбираем оценкуи составляем отношения
Наименьшим среди них является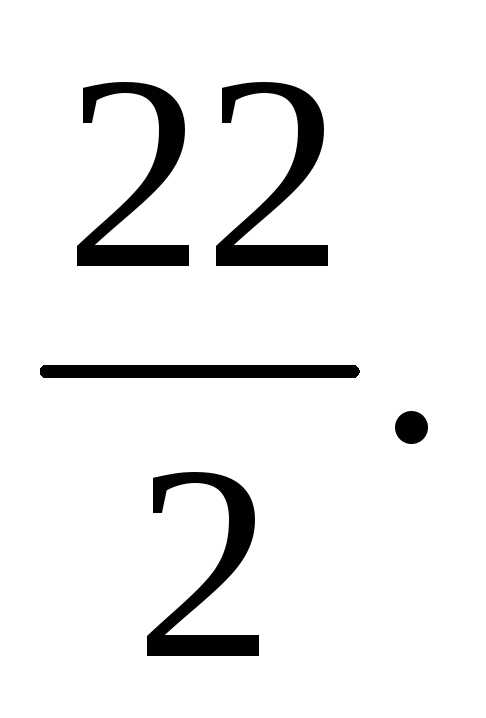
Следовательно, переходим к базису
Получим таблицу.
x1
x2
x3
x4
x5
x6
x7
1
2
1
0
1
0
0
18
0
-3/2
0
0
-1/2
1
-1/2
1
0
1/2
1
1
-1/2
0
1/2
11
0
-22
-4
0
-7
0
-5
-326
Все оценки базиса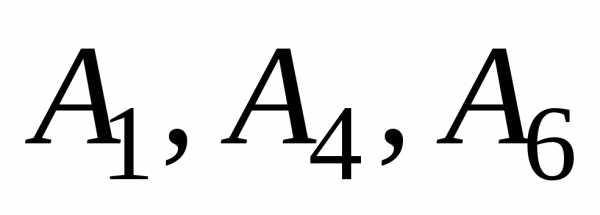 
неположительны. Следовательно,оптимальное решение канонической задачи
минимизации. Поэтомуоптимальное решение исходной задачи.
При этом
.
Таким образом, для того чтобы выпустить
наибольшее количество продукции при
имеющихся запасах сырья, необходимо в
течение 18 ч использовать первый способ
производства и в течение 11 ч – четвертый.
В результате будет произведено 326 единиц
продукции.
studfiles.net
4.2. Симплекс-метод решения задач линейного программирования
302
4.2. Симплекс-метод решения задач
линейного программирования
___________________________________________________________________________________________________________
Основная идея симплекс-метода
Основываясь на определениях данных в предыдущей лекции, мы можем найти оптимальное решение задачи линейного программирования, записанной в стандартной форме, путем простого перебора всех базисных (допустимых) решений. Но, конечно, такая процедура не эффективна. Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений [19].
Алгоритм симплекс-метода всегда начинается с некоторого допустимого базисного решения и затем пытается найти другое допустимое базисное решение, «улучшающее» значение целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в небазисные переменные. Это необходимо, чтобы новое решение содержало в точности т базисных переменных. (Напомним, что нас интересуют только базисные решения, содержащие в точности т базисных переменных.) В соответствии с терминологией симплекс-метода выбранная нулевая переменная называется вводимой (в базис), а удаляемая базисная переменная – исключаемой (из базиса).
Пример 1.
Рассмотрим детали выполнения симплекс-метода при решении следующей задачи.
Компания Тиккурила производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2. Основные данные задачи сведены в таблицу.
Расход сырья (в тоннах) на тонну краски | Максимально возможный ежедневный расход сырья | ||
Для наружных работ | Для внутренних работ | ||
Сырье М1 | 6 | 4 | 24 |
Сырье М2 | 1 | 2 | 6 |
Доход (в $1000) на тонну краски | 5 | 4 | |
Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 тонн (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.
Переменные задачи: 1= объем ежедневного производства краски для наружных работ (тонны), 2 = объем ежедневного производства краски для внутренних работ (тонны).
Краска обоих видов производится из сырья М1 и М2. Первые два ограничения задачи порождены ограниченными ежедневными запасами сырья. Другие два отображают ограниченный рыночный спрос на краску. Прибыль от одной тонны краски для наружных работ составляет $5000, а краски для внутренних работ – $4000. Целевая функция задачи должна максимизировать общую прибыль. Для удобства вычислений доходность производства красок масштабирована в тысячах долларов.
Эта задача в стандартной форме записывается так:
максимизировать
при ограничениях
Здесь s1, s2, s3, s4 – дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.
Задачу ЛП в стандартной форме можно представить в виде следующей компактной таблицы.
Нижние четыре строки этой таблицы представляют равенства ограничений; значения правых частей этих равенств даны в столбце «Решение». Строка z = W() получена из равенства
W() – 5 1– 4 2 = z – 5 1– 4 2= 0.
Дополнительные переменные s1, s2, s3 и s4 составляют очевидное начальное допустимое базисное решение. При этом, поскольку небазисные переменные 1 и 2 равны нулю, значения s1, s2, s3 и s4 автоматически отображаются в столбце «Решение»: s1 = 24, s2= 6, s3 = 1 и s4 = 2. Значение целевой функции при этом решении равно нулю.
Будет ли это начальное решение оптимальным? Конечно, нет, поскольку переменные 1 и 2 здесь равны нулю, а возрастание этих переменных даже на единицу приводит к увеличению значения целевой функции W() = 5 1+ 4 2 на 5 (при увеличении на единицу 1) или на 4 единицы (при увеличении на единицу 2). Поскольку в формуле целевой функции коэффициент при переменной 1 больше, чем коэффициент при 2, переменную 1 следует ввести в число базисных переменных (в этом случае она станет вводимой). Если обратиться к приведенной выше таблице, то вводимая переменная определяется среди множества небазисных переменных, как переменная, имеющая наибольший по модулю отрицательный коэффициент в z–строке (строке Симплекс разности).
Включаемая (вводимая) переменная 1 должна принять положительное значение. На рис. 4.2.1 видно, что, исходя из начальной точки A ( 1 = 0, 2 = 0), наибольшее значение, которое можно присвоить переменной 1 (не выходя из пространства допустимых решений), равно 4, что соответствует точке B ( 1 = 4, 2 = 0). Это означает, что решение переместилось от крайней точки A в крайнюю точку В.
Рис. 4.2.1
Поскольку симплекс-метод не должен основываться на графическом представлении задачи ЛП, необходимо определить, как выбрать точку B алгебраически. Из рисунка 4.2.1 видно, что B является одной из точек пересечения прямых, соответствующих ограничениям, с осью 1. Алгебраически точку пересечения можно найти как отношение правой части равенства (значение в столбце «Решение») к коэффициенту при переменной 1 в этом равенстве, как показано в следующей таблице.
Нас интересуют только неотрицательные отношения (или точки пересечения на положительной полуоси 1), так как они соответствуют направлению возрастания переменной 1. Отметим, что все значения в столбце «Решение» неотрицательные, поэтому вычисляемое отношение будет неотрицательным и конечным только в том случае, если знаменатель отношения строго положителен. Именно поэтому мы не рассматриваем отношения, соответствующие третьему и четвертому равенствам, так как там знаменатели или отрицательные, или равны нулю.
Минимальное неотрицательное отношение равно значению вводимой переменной 1в новом решении, а именно 1= 4 (сравните с точкой B на рис. 1). Значение целевой функции при этом значении 1 возрастет до 20 (= 54).
Теперь среди текущих базисных переменных s1, s2, s3 и s4 следует определить исключаемую переменную, которая примет нулевое значение после введения в базис переменной 1. (Напомним, что в этом примере должно быть в точности 4 базисные переменные.) Поскольку наименьшее (неотрицательное) отношение соответствует переменной s1, в точке B именно эта переменная обращается в нуль. Таким образом, переменная s1 будет исключаемой, в этом случае переменная 1 автоматически получает значение 4. Замена исключаемой переменной s1 на вводимую переменную 1 приводит к новому базисному решению ( 1, s2, s3, s4).
Вычисление нового базисного решения основывается на методе исключения переменных (методе Гаусса — Жордана). В следующей таблице, которая пока совпадает с начальной таблицей задачи ЛП, определим ведущий столбец, ассоциируемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки, назовем ведущим.
Процесс вычисления нового базисного решения состоит из двух этапов [19]:
studfiles.net
Решение задач линейного программирования симплекс-методом — Учись Как На Парах!
Использование графического способа удобно только при решении задан линейного программирования с двумя переменными. При большем числе переменных необходимо применение алгебраического аппарата. В этой ситуации используется общий метод решения задач ЛП, называемый симплекс-методом.
Симплекс-метод носит итерационный характер. Это значит, что однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение.
При использовании симплекс-метода целевая функция и ограничения на
Переменные должны быть представлены в так называемой стандартной форме. При стандартной форме линейной модели:
1) все ограничения записываются в виде равенств о неотрицательной правой частью;
2) значения всех переменных модели должны быть неотрицательны;
3) целевая функция максимизируется или минимизируется.
Исходное ограничение, записанное в виде неравенства, можно представить в виде равенства, прибавляя некоторую переменную к левой части ограничения. Например, в левую часть исходного ограничения
2×1+5×2+3×3?6
Вводится переменная xu>0, в результате чего исходное неравенство обращается в равенство
2×1+5×2+3×3 +x4=6
Если правая часть равенства отрицательна, то, умножая обе части на -1, ее можно сделать неотрицательной.
Максимизацию функции F всегда можно заменить минимизацией функции — F и наоборот.
Например,
Max F=7×1+x2+5×3
Можно заменить
Min (-F)=-7×1-x2-5×3
Если переменная, входящая в ограничения, неограниченна по знаку, то такую переменную можно представить как разность двух положительных переменных:
X1=x1′-x1», x1′?0, x1» ?0
Пример: требуется минимизировать функцию
F=3×1+4×2
При условии
X1+x2=10
-2×1+3×2?-5
7×1-4×2?6
x2?0
X1 не ограничена по знаку.
Для решения задачи неравенства превратим в равенства путем добавления новых переменных, а переменную x1 представим как разность двух положительных переменных:
Min F=3 x1′-3×1»+4×2
x1′-x1»+x2=10,
2×1′-2×1»-3×2-s1=5,
7×1′-7×1»-4×2+s2=6,
x1′, x1», x2, s1, s2 ?0
Общую идею симплекс-метода можно проиллюстрировать на примере.
Пусть требуется максимизировать функцию
F=3×1+2×2
При ограничениях
X1+2×2?6,
2×1+x2?8,
-x1+x2?1,
X2?2; x1, x2 ?0.
Приведенная линейная модель может быть сведена к стандартной форме
Max F=3×1+2×2+0x3+0x4+0x5+0x6
При ограничениях
x1+2×2+x3 =6,
4×1+2×2 +x4 =8,
— x1+ x2 +x5 =1,
x2 +x6=2
X1, x2, x3, x4, x5, x6 ?0.
На рис.2.2 представлено пространство решений данной задачи. Каждую точку этого пространства можно определить c помощью переменных, входящих в модель стандартной формы. Например, при x3=0 первое ограничение принимает вид равенства 2×1+4×2=12 , которое можно представить прямой 3-4.
Поскольку стандартная модель содержит четыре уравнения и шесть неизвестных, в каждой из экстремальных точек две переменные (=6-4) должны иметь нулевые значения. Например, в точке 1 – x1 и x2 равны нулю, в точке 2 – x4 и x2, в точке 3 – x3 и x4. Можно заметить, что экстремальные точки отличаются только одной переменной Переменные, имеющие
Отличное от нуля значение, называются базисными, остальные – небазисными переменными.
Каждую последующую экстремальную точку можно определить путем замены одной из текущих небазисных переменных текущей базисной переменной.
Алгоритм симплекс-метода состоит из следующих шагов.
Шаг 1. Используя линейную модель стандартной формы, определяют
Начальное допустимое базисное решение.
Шаг 2. Из числа текущих небазисных переменных выбирается одна, которая включается в новый базис. Увеличение этой переменной должно обеспечить улучшение значения целевой функции. Затем осуществляется переход к следующему шагу.
Шаг 3. Из числа базисных переменных выбирается одна, которая должна принять, нулевое значение (т. е. стать небазисной) при введении в состав базисных новой переменной.
Шаг 4. Находится новое базисное решение, соответствующее новым составам базисных и небазисных переменных.
В нашем примере точку I можно использовать как начальное допустимое решение. В этой точке x1=x2=0 и x3=6, x4=8, x5=1, x6=2, а функция F=0.
Преобразовав уравнение целевой функции так, чтобы его правая часть стала равна нулю
F-3×1+2×2=0
Можно убедиться, что правые части уравнений целевой функции и ограничений полностью характеризуют начальное решение.
Полученные результаты удобно представить в виде табл.2.1.
Первый столбец этой таблицы содержит переменные пробного базиса x3, x4, x5, x6, значения которых приведены в последнем столбце.
Является ли полученное решение оптимальным? Нет. Об этом свидетельствует наличие в строке целевой функции отрицательных чисел.
Таблица 2.1
Базисные Переменные | F | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
X3 | 0 | 1 | 2 | 1 | 0 | 0 | 0 | 6 |
X4 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | 8 |
X5 | 0 | -1 | 1 | 0 | 0 | 1 | 0 | 1 |
X6 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
F | 1 | -3 | -2 | 0 | 0 | 0 | 0 | 0 |
Это эквивалентно наличию положительных коэффициентов при этих переменных в исходной целевой функции. Поскольку речь идет о максимизации, значение F может быть увеличено при увеличении как x1, так и x2. Если бы в отроке целевой функции не было отрицательных чисел, это означало бы, что функция цели уже не пересекает оси в области положительных решений.
А качестве переменной, включаемой в базис, выберем x1, так как коэффициент при ней больше и функция цели изменяется сильнее. Исключаемая переменная выбирается из совокупности базисных переменных x3, x4, x5, x6. Этой переменной является та, которая первой обращается в нуль при увеличении включаемой переменной вплоть до значения, соответствующего смежной экстремальной точке. В нашем случае переменная x1 достигает максимально допустимого значения, равного 4, в точке 2, при этом исключаемой из базиса переменной становится x4.
Отношение, фиксирующее искомую точку пересечения и идентифицирующее исключаемую переменную, можно определить прямо из симплекс-таблицы. Для этого в столбце, соответствующем вводимой переменной x, вычеркиваются отрицательные и нулевые элементы ограничений. Затем вычисляются отношения постоянных, фигурирующих в правых частях этих ограничений, к оставшимся элементам столбца, соответствующего вводимой переменной x1. Исключаемой переменной будет та переменная базиса, для которой указанное выше отношение минимально.
Указанная процедура иллюстрируется табл.2.2.
Таблица 2.2
Базисные Переменные | F | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
X3 | 0 | 1 | 2 | 1 | 0 | 0 | 0 | 6 (6/1=6) |
X4 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | 8 (8/2=4) |
X5 | 0 | -1 | 1 | 0 | 0 | 1 | 0 | 1 |
X6 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
F | 1 | -3 | -2 | 0 | 0 | 0 | 0 | 0 |
Столбец симплекс-таблицы, ассоциируемый с вводимой переменной, будет называть ведущим столбцом. Строку, соответствующую исключаемой переменной, назовем ведущей строкой, а элемент таблицы, находящийся на пересечении ведущего столбца и ведущей строки, будем называть ведущим элементом.
Все элементы новой ведущей строки получаются путем деления элементов предыдущей ведущей отроки на ведущий элемент. Все остальные уравнения получаются по правилу
(Новое уравнение) = (Предыдущее уравнение) —
-(Коэффициент ведущего столбца предыдущего уравнения)*
*(Новая ведущая строка).
В новом ведущем уравнении ведущий элемент становится равным 1, а все остальные коэффициенты, фигурировавшие в ведущем столбце, становятся равными 0.
Составим по этому правилу новую симплекс-таблицу. Новая ведущая строка:
X1 | X2 | X3 | X4 | X5 | X6 | Решение | |
0 | 1 | 1/2 | 0 | 1/2 | 0 | 0 | 8/2=4 |
Для отроки получим
—
——————————————————————————
Для x3 – уравнения
0 | 1 | 2 | 1 | 0 | 0 | 0 | 6 |
1 | -1 | -1/2 | 0 | -1/2 | 0 | 0 | -4 |
——————————————————————————
Для x5 – уравнения
0 | 1 | 2 | 1 | 0 | 0 | 0 | 6 |
1 | -1 | -1/2 | 0 | -1/2 | 0 | 0 | -4 |
——————————————————————————
X6 — уравнение останется таким же, постольку соответствующий коэффициент ведущего столбца равен нулю.
Таким образом, симплекс — таблица примет вид
Таблица 2.3
Базисные Переменные | F | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
X3 | 0 | 0 | 3/2 | 1 | -1/2 | 0 | 0 | 2 (4/3) |
X1 | 0 | 1 | 1/2 | 0 | 1/2 | 0 | 0 | 4 (8) |
X5 | 0 | 0 | 3/2 | 0 | 1/2 | 1 | 0 | 5 (10/3) |
X6 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 (2) |
F | 1 | 0 | -1/2 | 0 | 3/2 | 0 | 0 | 12 |
Из последней таблицы следует, что на очередной итерации в качестве вводимой переменной следует выбрать x2, т. к. коэффициент при этой переменной в F — уравнении равен -1/2. Исключаемой переменной будет x3 , а включаемой – x2 . Новая симплекс-таблица будет иметь вид табл.2.4.
Таблица 2.4
Базисные Переменные | F | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
X3 | 0 | 0 | 1 | 2/3 | -1/3 | 0 | 0 | 4/3 |
X1 | 0 | 1 | 0 | -1/3 | 2/3 | 0 | 0 | 10/3 |
X5 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 3 |
X6 | 0 | 0 | 0 | -2/3 | 1/3 | 0 | 1 | 2/3 |
F | 1 | 0 | 0 | 1/3 | 4/3 | 0 | 0 | 38/3 |
В новом базисном решении x1=10/3 и x2=4/3. Значение F увеличилось с 12 (предыдущая таблица) до 38/3. Этот прирост целевой функции обусловлен увеличением x2 от 0 до 4/3, так как из F -строки предыдущей симплекс-таблицы следует, что возрастанию данной переменной на единицу соответствует увеличение функции на 1/2.
Последняя симплекс-таблица соответствует оптимальному решению задачи, так как в F — строке ни одна из небазисных переменных не фигурирует c отрицательным коэффициентом. На этом и завершаются вычислительные процедуры симплекс-метода.
В случае минимизации функции цели в алгоритме необходимо изменить только условие оптимальности: в качестве новой базисной переменной следует выбрать ту переменную, которая в F — строке имеет наибольший положительный коэффициент.
2.4. Частные случаи использования симплекс-метода.
Рассмотрим пример. Требуется минимизировать функцию
F=4×1+x2
При ограничениях
3×1+x2=3,
4×1+3×2?6,
x1+2×2?4,
x1, x2 ?0
Запишем задачу в стандартной форме
3×1+ x2 =3,
4×1+3×2-x3 =6,
x1+2×2 +x4=4,
Таким образом имеются три уравнения и четыре неизвестных. В отличие от случая, когда каждое уравнение содержит остаточную переменную, в заданном случае уже нельзя быть уверенным в том, что при нулевом значении одной из переменных все базисные переменные будут неотрицательными. В этом случае используется метод искусственных переменных.
Искусственные переменные вводятся только для того, чтобы получить базисное решение.
В нашем примере в первом и втором уравнениях нет переменных, выполняющих роль остаточных. Поэтому введем в каждое из этих уравнений по одной искусственной переменной (R1 и R2 ) :
3×1+x2 + R1 =3,
4×1+3×2-x3 + R2 =6,
x1+2×2 +x4=4,
За использование этих переменных в составе целевой функции нужно ввести штраф, приписывая им большой коэффициент М.
Тогда функция цели примет вид:
Min F=4×1+x2+MR1+MR2.
Начальное допустимое решение при этом будет
R1=3, R2=6 и x4=4.
Т. к. мы имеем дело о описанием минимума, а переменные R1 и R2 введены в функцию цели с большим коэффициентом М, то метод минимизации должен привести к тому, что в оптимальном решении они обратятся в ноль.
Для построения симплекс-таблицы выразим искусственные переменные через небазисные:
R1=3-3×1-x2
R2=6-4×1-3×2+x3
F=4×1+x2+M(3-3×1-x2)+M(6-4×1-3×2+x3)=(4-7M)x1+(1-4M)x2+Mx3+9M
Тогда первая симплекс-таблица будет иметь вид
Базисные переменные | X1 | X2 | X3 | X4 | Решение | ||
F | -4+7M | -1+4M | -M | 0 | 0 | 0 | 9M |
R1 | 3 | 1 | 0 | 1 | 0 | 0 | 3 |
R2 | 4 | 3 | -1 | 0 | 1 | 0 | 6 |
X4 | 1 | 2 | 0 | 0 | 0 | 1 | 4 |
Далее решение ведется обычным образом. Оптимальному решению соответствует точка x1=2/5, x2=9/5, где F=17/5.
Отметим, что при максимизации F штраф М необходимо брать c обратным знаком.
Рассмотрим другой пример.
Max F=3×1+9×2
При условии
x1+4×2?8,
x1+2×2?4,
x1, x2 ?0
Введя остаточные переменные x3 и x4, построим симплекс-таблицу
X1 | X2 | X3 | X4 | ||
F | -3 | -9 | 0 | 0 | 0 |
X3 | 1 | 4 | 1 | 0 | 8 |
X4 | 1 | 2 | 0 | 1 | 4 |
X3- выводится, x2 вводится
На следующем шаге
X1 | X2 | X3 | X4 | ||
F | -3/4 | 0 | 9/4 | 0 | 18 |
X1 | 1/4 | 1 | 1/4 | 0 | 2 |
X4 | 1/2 | 0 | -1/2 | 1 | 0 |
X4- выводится, x1 — вводится
Получим
X1 | X2 | X3 | X4 | ||
F | 0 | 0 | 3/2 | 3/2 | 18 |
X2 | 0 | 1 | 1/2 | -1/2 | 2 |
X1 | 1 | 0 | -1 | 2 | 0 |
Заметим, что после двух итераций значение функции цели не уменьшилось (18). Т. е. налицо зацикливание. Что же это означает? Рассмотрим рис.2.3. Через точку оптимума проходят три прямые, а задача содержит только две переменные. Отсюда следует вывод, что одно из ограничений лишнее.
Max F=2×1+4×2
При условии
x1+2×2?5,
x1+ x2?4,
x1, x2 ?0
Рис. 2.4 иллюстрирует суть дела. Целевая функция параллельна одной из прямой ограничений. Это означает, что задача имеет бесконечное множество решений.
Может быть случай, когда решение отсутствует вообще.
Пример:
Max F=3×1+2×2
При условии
2×1+ x2?2,
x1+4×2?12,
x1, x2 ?0.
Рис.2.5 хорошо иллюстрирует суть дела.
Записи по теме
naparah.com
Симплекс-метод решения задачи линейного программирования
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
На предприятии имеется возможность выпускать n видов продукции . При ее изготовлении используются ресурсы Р1, Р2 и Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b1, b2 и b3. Расход ресурса i-го вида на единицу продукции j-го вида составляет аij единиц. Цена единицы продукции j-го вида равна сj ден. ед.
|
|
а11 |
а12 |
а13 |
а14 |
b1 |
|
|
1 |
1 |
1 |
1 |
6000 |
|
|
а21 |
а22 |
а23 |
а24 |
b2 |
= |
|
0.5 |
1 |
5 |
0.5 |
5000 |
|
|
а31 |
а32 |
а33 |
а34 |
b3 |
|
|
0.5 |
0.5 |
20 |
0.5 |
9000 |
|
|
с1 |
с2 |
с3 |
с4 |
|
|
|
80 |
100 |
300 |
80 |
|
Требуется:
1) составить экономико-математическую модель задачи, позволяющую найти сбалансированный по ресурсам план выпуска продукции, обеспечивающий предприятию максимальный доход;
2) симплексным методом найти оптимальный план выпуска продукции по видам; (дать содержательный ответ, раскрыв экономический смысл всех переменных, приведенных в решении задачи);
3) сформулировать в экономических терминах двойственную задачу и составить ее математическою модель;
4) найти компоненты оптимального плана двойственной задачи (двойственные оценки используя решение исходной задачи и соответствие между двойственными переменными.
Решение
Обозначим через Х1 , Х2 , Х3— количество единиц продукции соответственно П1, П2, П3, планируемой к выпуску, а через f—величину прибыли от реализации этой продукции. Тогда , учитывая значение прибыли от единицы продукции П1 =80 ден. ед., П2=100 ден. ед., П3=300 ден. ед., запишем суммарную величину прибыли — целевую функцию — в следующем виде:
f = 80Х1 + 100Х2 +300Х3. (2.1)
Переменные Х1, Х2 , Х 3 должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов. Так, затраты ресурса P1 на выполнение плана (Х1 , Х2 , Х3) составят (Х1 +Х2 +Х3) ед., где Х1 — затраты ресурса P1на выпуск Х1 ед. продукции П1; Х2- затраты ресурсы P1 на выпуск Х2 ед. продукции П2 и т.д. Понятно, что указанная сумма не может превышать имеющийся запас P1 в 6000 ед., т.е.
Х1 +Х2 +Х3 ≤6000. (2.2)
Аналогично получаем ограничения по расходу ресурсов P2 и P3:
0.5 Х1 +Х2 +5Х3 ≤5000. (2.3)
0.5Х1 +0.5Х2 +20Х3 ≤9000. (2.4)
По смыслу задачи переменные Х1, Х2 , Х 3 не могут выражаться отрицательными числами, т.е.
Хj ≥0 (j=1,3) (2.5)
Соотношения (2.1) — (2.5) образуют экономико-математическую модель данной задачи.
Итак, математически задача сводится к нахождению числовых значений Х1*, Х2*, Х 3* переменных Х1, Х2 , Х 3 , удовлетворяющих линейным неравенствам (2.2) — (2.5) и доставляющих максимум линейной функции (2.1)
2. Прежде чем решать задачу линейного программирования симплекс-методом, ее модель приводят к канонической форме. Основным признаком канонической формы является запись ограничений задачи в виде равенств. В нашем же случае ограничения (2.2) — (2.4) имеют вид неравенств типа «≤». Чтобы преобразовать их в эквивалентные уравнения, введем в левые части неравенств дополнительные (балансовые) неотрицательные переменные Х4 , Х5 , Х6 , обозначающие разности между правыми и левыми частями этих неравенств. В результате модель можно записать в виде
f = 80Х1 +100Х2 +300Х3 (max) (2.6)
Х1 +Х2 +Х3 + Х4 = 6000
0,5Х1 +Х2 +5Х3 + Х5 =5000 (2.7)
0.5Х1 +0.5Х2 +20Х3 + Х6 =9000
Хj ≥0 (j=1,6) (2.8)
Заметим здесь же, что дополнительные переменные Х4 , Х5 , Х6 имеют вполне определенный экономический смысл — это возможные остатки ресурсов соответственно P1, P2, P3 . Их еще называют резервами.
Анализируя каноническую модель (2.6) — (2.8), замечаем, что каждая из переменных Х4 , Х5 , Х6 входит только в одно из уравнений системы (2.7). Это обстоятельство свидетельствует о том, что в системе (2.7) переменные Х4 , Х5 , Х6 являются базисными, а остальные переменные Х1 , Х2 , Х3 — свободными. В связи с этим в первую симплекс-таблицу систему ограничительных уравнений (2.7) можно записать в виде, разрешенном относительно базиса Х4 , Х5 , Х6 (табл. 2.1).
Таблица 2.1
|
БП |
1 |
СП |
||
|
— Х1 |
— Х2 |
— Х3 |
||
|
Х4= |
6000 |
1 |
1 |
1 |
|
Х5= |
5000 |
0.5 |
1 |
5 |
|
Х6= |
9000 |
0.5 |
0.5 |
20 |
|
f |
0 |
-80 |
-100 |
-300 |
Все элементы столбца свободных членов положительны, поэтому содержащийся в табл. 2.1 план (0; 0; 0; 6000;5000; 9000), является опорным. Однако этот план не является оптимальным: в f — строке имеются отрицательные элементы.
Чтобы получить опорный план, более близкий к оптимальному, выполним симплексное преобразование табл. 2.1. С этой целью выберем переменные, участвующие в преобразовании базиса Х4 , Х5 , Х6 в новый базис. Наибольший по модулю отрицательный элемент (-300) f-строки указывает, что в новый базис следует ввести переменную Х3 ,т.е. в качестве разрешающего в предстоящем симплексном преобразовании надо взять первый столбец. Чтобы определить переменную, выводимую из базиса, составляем симплексные отношения и выбираем наименьшее из них
Min(6000/1;5000/5;9000/20)=9000/20=450
Итак, из базиса надо исключить переменную, стоящую в третьей (разрешающей) строке, т.е. Х6. На пересечении разрешающих столбца и строки находится разрешающий элемент 20, с которым и выполняется симплексное преобразование (шаг жорданова исключения). В результате приходим к табл. 2.2.
В f-строке табл. 2.2 есть отрицательные элементы, значит, опорный
план (0;0; 450;5550;2750;0) оптимальным не является.
Таблица 2.2
|
БП |
1 |
СП |
||
|
— Х1 |
— Х2 |
— Х6 |
||
|
Х4= |
5550 |
0.975 |
||
easyhelp.su