Умножение матриц с тремя строками и тремя строками – Умножение матриц

глава 1; элементы линейной алгебры / матрицы

Глава I.

Матрицы. Основные определения и правила действия.

Определение 1.1. Матрица это прямоугольная таблица элементов, имеющаястрок истолбцов

(1.1)

Матрица (1.1) называется прямоугольной матрицей размером . Каждый элемент матрицы нумеруется двумя индексами. Первый индексобозначает номер строки. Второйиндекс обозначает номер столбца. Матрица, состоящая из одной строки, называется вектор — строкой. Матрица, состоящая из одного столбца, называется вектор – столбцом.

Если число строк равно числу столбцов, то такую матрицу называют квадратной матрицей размером.

Пример 1.1. Матрица размером имеет 2 строки и 3 столбца

Матрица размером (32) имеет 3 строки и 2 столбца .

Пример 1.2

. Элементрасположен на пересечении второй строки и третьего столбца. Элементрасположен на пересечении третьей строки и второго столбца. Элементрасположен на пересечении-ой строки и-го столбца.

Определение 1.2. Матрицы обозначаются заглавными буквами. Например, матрица, матрица.Две — матрицыиравны, если соответствующие элементы матриц равны. То естьдля всех.Между матрицами разных размеров равенства быть не может.

Элементы алгебры матриц.

Суммой двух матриц А и В одинакового размера называется -матрица , элементами которой являются суммы соответствующих элементов матриц А и В. Таким образом С=А+В еслидля всех.

Пример 1.3. Вычислить сумму матриц

Решение.

;

Замечание. Матрицы разных размеров складывать нельзя.

Определение 1.3. Чтобы умножить число на матрицу нужнокаждый элемент матрицыумножить на число.

Определение 1.4. Выражение , где-числа, а- матрицы называют линейной комбинацией матрици.

Правило 1. Умножение вектор строки на вектор – столбец.

Чтобы перемножить вектор- строку на вектор-столбец с одинаковым числом элементов нужно перемножить первый элемент строки на первый элемент столбца, второй элемент строки на второй элемент столбца ит.д. и затем полученные произведения сложить.

Пример 1.4. Пусть заданы: вектор- строкаивектор- столбецтребуется перемножитьАнаВ.

РЕШЕНИЕ. =.

Правило 2. Умножение матрицы А размером ( ) на матрицу В размером ().

При умножении матрицы А размером на матрицу В размеромполучается матрица С размером. Причем элементматрицы С получается перемножением

ой строки А матрицы иго столбца В матрицы.

Замечание. Правило 2 говорит нам о том, что если число столбцов первого сомножителя совпадает с числом строк второго сомножителя, то такие матрицы перемножать можно.

Пример 1.5.Перемножить матрицы А и В

РЕШЕНИЕ. Условия перемножения матриц выполнены. Начнём с вычисления элемента . Нужно первую строку А матрицы умножить на первый столбец В матрицы: =. Чтобы вычислить элемент нужно первую строку А матрицы умножить на второй столбец В матрицы:=.

Чтобы вычислить элемент нужно первую строку А матрицы умножить на третий столбец

матрицы В матрицы: =.

Остальные элементы С матрицы находим аналогично. Рекомендуем читателю самостоятельно их вычислить.

Ответ: .

Пример 1.6. Умножение столбца на строку. Перемножить.

Решение. Выписываем правило. В результате должна получиться матрица

С размером (сравните с результатом умножения строки на столбец ( см. пример 1.4))

Ответ: .

Пример 1.6. Умножение матрицы на столбец. Перемножить

Решение. Выписываем правило. Перемножать можно. В результате получается матрица-столбец размером. Выписываем ответ

=

Квадратные матрицы.

Матрица, у которой число строк совпадает с числом столбцов ,называется

квадратной матрицей. Матрицу размером называют матрицей 2-го порядка.

Матрицу размером называют матрицей 3-го порядка и так далее.

Определители квадратных матриц.

Определение 1.5. Определитель матрицыобозначаетсяили .

Определение 1.6. Определитель третьего порядка вычисляется разложением по первой строке по формуле

(1.2)

Определение 1.7. Определитель 2-го порядка также вычисляется разложением по первой строке по формуле

(1.3)

-называется минором элемента. Минор- это определитель, который получается из определителявычёркиванием первой строки иго столбца.

Определение 1.8. Минор элемента

— это определитель, который получается из заданного определителя вычёркиваниемой строки иго столбца.

Пример 1.7. Выписать миноры всех элементов определителя 3-го порядка и вычислить определитель

Решение.

Вычисляем миноры элементов первой строки.

О стальные миноры определителя вычисляются аналогично (проделайте это)

Вычисляем определитель по формуле (1.2)

Замечание.Определители любого порядка большего, чем третий также можно вычислять

разложением по первой строке по правилу

Здесь -это алгебраические дополнения .Вычисляемые по формуле.

Единичные матрицы

Определение 1.9. Матрицы вида

называются единичными матрицами второго и третьего порядков соответственно.

Замечание. . Матрица не изменится , если её умножить на единичную

матрицу (проверьте).

Обратные матрицы

Определение 1.10. Матрицаназывается матрицей обратной к матрицеесли

1. Определитель матрицы

Правило вычисления обратной матрицы размером даётся формулой

(1.4)

Здесь — это определитель матрицы.-миноры матрицы_.

Замечание.Обратите внимание на порядок расположения миноров и знаки миноров в формуле обратной матрицы (1.4).

_{Формула вычисления обратной матрицы}

(1.5)

Замечание.Формулы вычисления обратной матрицы порядков больших, чем три смотрите в любом курсе линейной алгебры.

Пример 1.8. Найти матрицу обратную к данной .

Решение. По определению 1.10 обратная матрица существует если .

В нашем случае определитель и все миноры найдены в примере 1.7. Подставляя найденные значения в формулу (1.4) получаем

_{Сделаем проверку} (см. определение 1.10 пункт 2)) найденного решения. Вычислим произведение

Аналогично проверяется равенство . Обратная матрица найдена верно.

Элементарные преобразования матриц

Для дальнейшего нам понадобятся следующие преобразования матриц.

Определение 1.11. Данные ниже преобразования матрицы называются элементарными преобразованиями матрицы

1. Перемена местами двух строк.

2. Умножение строки на отличное от нуля число.

3. Прибавление к элементам строки соответствующих элементов другой строки умноженной на число

Замечание. Другие элементарные преобразования матрицы можно посмотреть в курсе линейной алгебры.

Эквивалентные матрицы.

Определение 1.12. Две матрицы одинаковых размеров эквивалентны, если одну из них можно получить из другой элементарными преобразованиями.

Определение ступенчатой матрицы

У ступенчатой матрицы в первом столбце все элементы начиная со второго равны нулю. Во втором столбце все элементы, начиная с третьего равны нулю и т.д.

Пример 1.9. Матрицы

являются ступенчатыми матрицами.

Приведение матрицы к ступенчатому виду элементарными преобразованиями

Пример 1.10. Используя элементарные преобразования привести матрицу к ступенчатому виду

Решение. 1 шаг. Переставим местами первую и вторую строки данной матрицы

2 шаг. Ко второй строке прибавим первую строку, умноженную на (-7)

3 шаг. К третьей строке прибавим первую строку, умноженную на (-5)

4 шаг. К четвертой строке прибавим первую строку, умноженную на (-2)

5 шаг. К третьей строке прибавляем вторую, умноженную на (-24). А к четвёртой строке прибавляем вторую, умноженную на (-16). В результате получаем

6 шаг. Умножаем третью строку наи получаем матрицу

7 шаг. Прибавляя к четвёртой строке третью строку , умноженную на(-60) получаем ступенчатую матрицу

Контрольные вопросы.

I.Дайте определения:

1) равенства матриц ; 2) суммы матриц; 3) умножения числа на матрицуА

4) линейной комбинации матриц; 5) умножения матриц.

II.Cформулируйте правило вычисления миноров квадратной матрицы. Вычислите миноры

матрицы размером

III.Cформулируйте правила вычисления определителей квадратных матриц:

1. второго порядка; 2) третьего порядка.

IV. Дайте определения единичных матриц.

V.Cформулируйте определение обратной матрицы. Какие матрицы имеют обратные.

Напишите формулу вычисления обратной матрицы третьего порядка.

VI. Дайте определения элементарных преобразований матриц.

VII. Дайте определение ступенчатой матрицы.

Далее предлагаются упражнения по данной теме для самостоятельной работы . В разделе ответы и решения приведены краткие решения упражнений.

Матрицы.

Упражнение.1.1. Укажите среди данных матриц равные матрицы

2)Пусть даны матрицы

Напишите, какие произведения из данных пар исуществуют.

Упражнение 1.2. Укажите размерность матриц и определите, чему равны элементы

Упражнение 1.3 Определить параметры из условий

Упражнение 1.4. Вычислить линейную комбинацию матриц

1); 2).

3) ; 4).

Упражнение 1.5. Вычислить произведения матриц

Упражнение 1.6. Вычислить: , где

Упражнение 1.7. Найти миноры всех элементов матрицы

Упражнение 1.8. Вычислить данные определители

Упражнение 1.9.Проверить являются ли матрицывзаимно обратными

Упражнение 1.10. Вычислить матрицуобратную к данной матрице

и сделать проверку полученного результата.

Упражнение 1.11. Используя элементарные преобразования , привести матрицу А к ступенчатому виду

;

Упражнение 1.12. Используя решение квадратного уравнения , найдите матрицувторого порядка, которая является решением матричного уравнения.

Упражнение 1.13. Найдите матрицу третьего порядка из упражнения 1.11.

Упражнение 1.14. Перемножить матрицы

Упражнение 1.15.Перемножить матрицы

Упражнение 1.16.Решить матричное уравнение,где

Указание. Используйте обратную матрицу.

studfiles.net

Умножение матриц

1. Умножение матриц — это специфическая операция, со­ставляющая основу алгебры матриц. Строки и столбцы мат­риц можно рассматривать как векторы-строки и векторы-стол­бцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.

Пусть даны матрица А размером т х п и матрица В разме­ром п х k. Будем рассматривать матрицу А как совокупность т векторов-строк _i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов _j, каждый из которых содержит по п координат:

Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13.3). Длина строки матри­цы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.

Определение 3. Произведением матриц А и В называется матрица С, элементы которой c_ij равны скалярным произве­дениям векторов-строк _i матрицы А на векторы-столбцы _j матрицы В:

Произведение матриц А и В — матрица С — имеет размер т х k, поскольку длина п векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих век­торов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скаляр­ные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как ска­лярные произведения второй вектор-строки матрицы А на все векторы-столбцы матрицы В и так далее. Для удобства за­поминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей: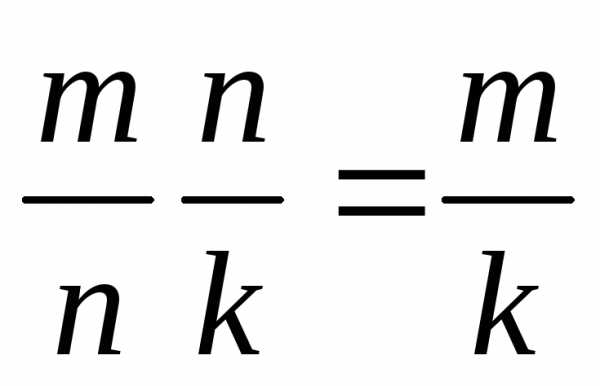, т.е. размер матрицыС равен произведению оставшихся в отношении чисел: т х k.

В операции умножения матриц есть характерная особен­ность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формиру­ющих элементы соответствующей матрицы, должны участво­вать векторы с одинаковым числом координат.

Если матрицы А и В квадратные размером n х n, то име­ет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у ис­ходных сомножителей. При этом в общем случае перемноже­ния матриц правило перестановочности не соблюдается, т.е. АВ ≠ ВА.

Рассмотрим примеры на умножение матриц.

Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:

Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.

Решение. Здесь мы найдем произведения данных матриц АВ и ВА:

Как видно из результата, матрица произведения зависит от по­рядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.

Решение. В данном случае матрица В представляет собой вектор-столбец, т.е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: век­тор-строка длины п представляет собой матрицу с одной стро­кой и п столбцами, а вектор-столбец высоты n — матрицу с n строками и одним столбцом. Размеры данных матриц соот­ветственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем

В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.

Решение. Путем последовательного умножения матриц находим

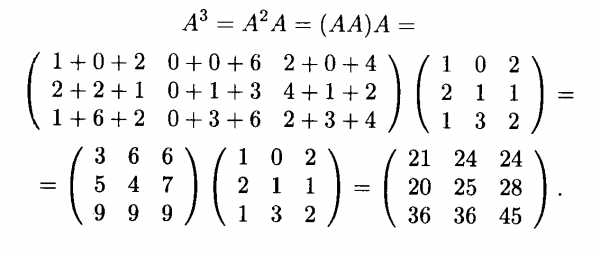
2. Свойства произведения матриц. Пусть А, В и С — мат­рицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следу­ющие свойства произведения матриц имеют место:

1) (АВ)С = А(ВС),

2) (А + В)С = AC + ВС,

3) А(В + С) = АВ + АС,

4) α(АВ) = (αА)В = А(αВ).

В п. 1 этого раздела введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т.е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадрат­ных матриц:

5) АЕ = А,

6) ЕА = А.

Иными словами, произведение любой матрицы на единич­ную матрицу, если оно имеет смысл, не меняет исходную мат­рицу.

studfiles.net

V. Умножение матрицы на матрицу-столбец.

Дано: ;

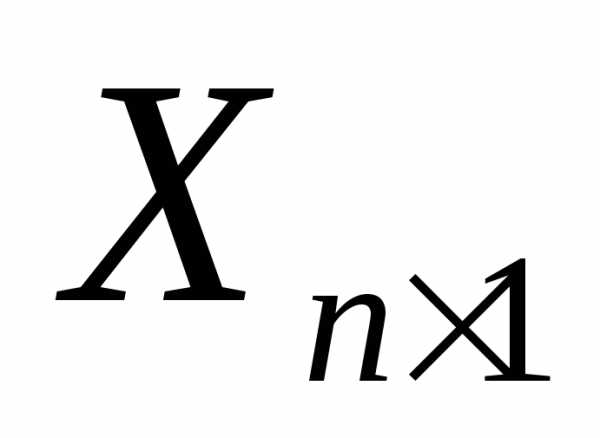
Найти: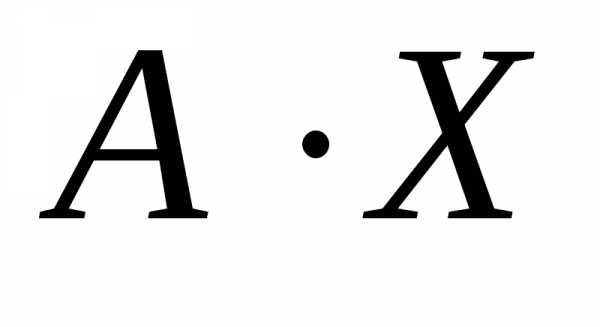

==

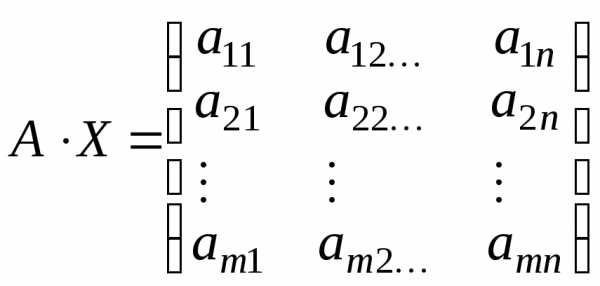
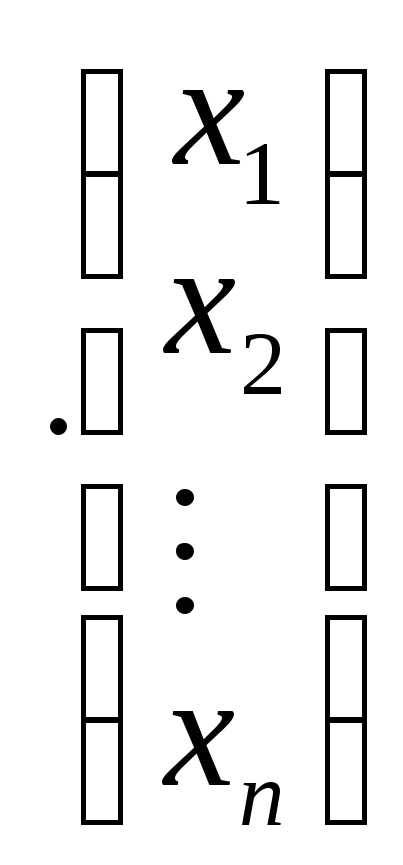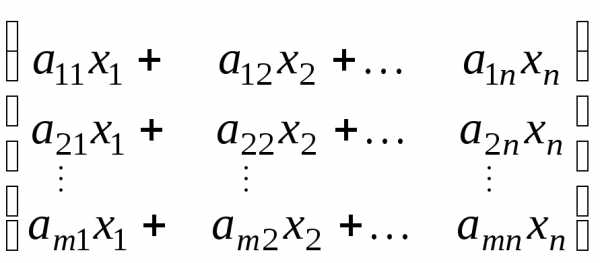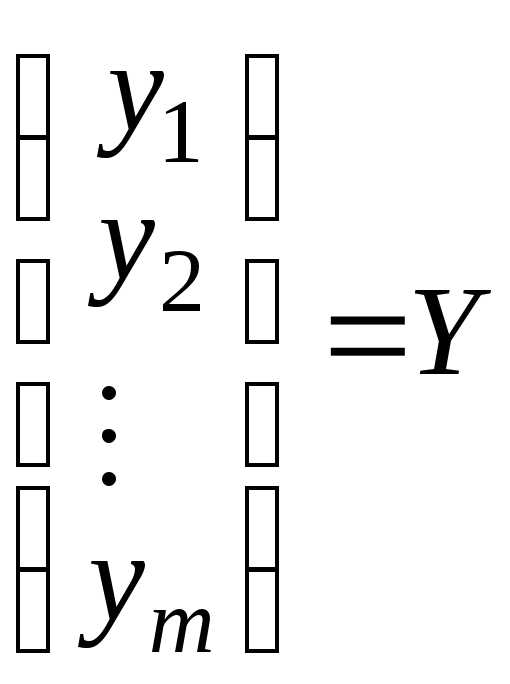
Пример 2.10

; Х =. Найти.

Решение: .

Пусть А – квадратная матрица

или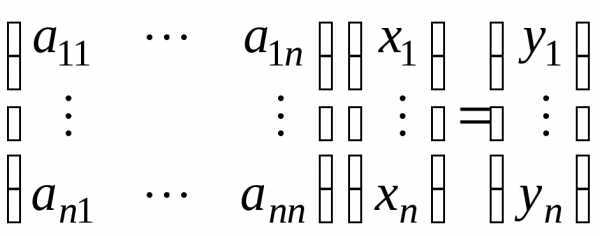

При умножении квадратной матрицы на матрицу-столбец получается матрица-столбец той же высоты.

§3. Определители

1. Определения определителей второго и третьего порядков

Понятие определителя матрицы вводится только для квадратных матриц. Любой квадратной матрице n-го порядка 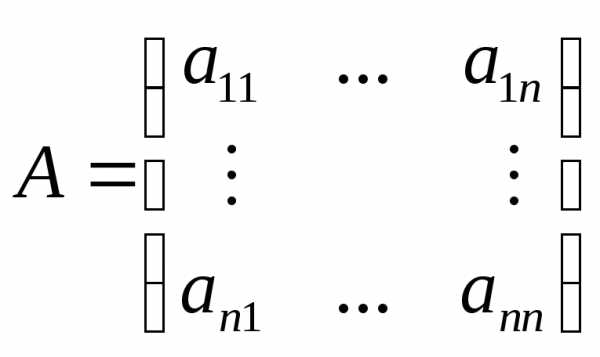можно поставить в соответствие выражение (число), которое называетсяопределителем или детерминантом матрицы и обозначается 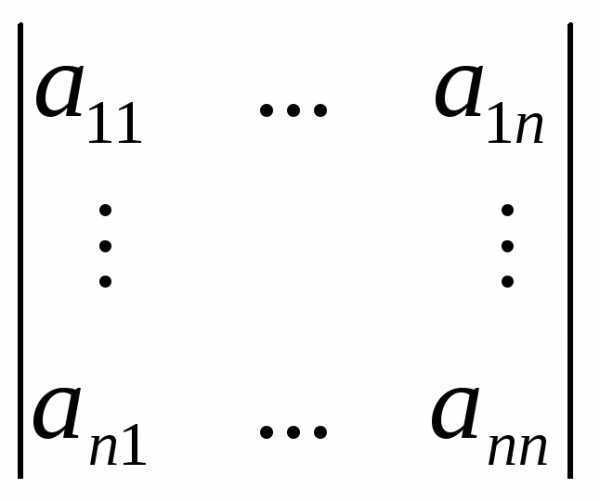илиили det A.

Опр. Определителем второго порядка называют выражение (число)

Числа а₁₁, а₁₂, а₂₁, а₂₂ называют элементами определителя, элементы а₁₁, а₂₂ образуют главную диагональ, а элементы а₁₂, а₂₁ – побочную.

Пример 3.1

Опр. Определителем третьего порядка называют выражение (число)

Числа а_ij, i=1,2,3; j=1,2,3 – элементы определителя, элементы а₁₁, а₂₂, а₃₃ образуют главную диагональ, а элементы а₁₃, а₂₂, а₃₁– побочную диагональ.

Пример 3.3

2. Свойства определителей (на примере определителя третьего порядка)

1. При замене строк столбцами величина определителя не меняется (при транспонировании матрицы ее определитель не меняется)

2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.

Например: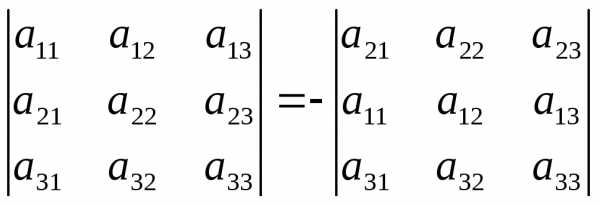

3. Если в определителе имеются две одинаковые строки (столбца), то определитель равен нулю.

4. Общий множитель элементов строки (столбца) можно вынести за знак определителя.

5. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.

6. Если элементы одной строки (столбца) пропорциональны элементам другой, то определитель равен нулю.

Доказательство: коэффициент пропорциональности выносим за знак определителя, получим определитель с двумя одинаковыми строками (столбцами), по свойству 3 определитель равен нулю.

7. Если к элементам одной строки (столбца) прибавить элементы другой строки (столбца), умноженные на любое число, то величина определителя не изменится.

3. Миноры и алгебраические дополнения. Теорема разложения определителя по элементам строки (столбца)

Рассмотрим определитель третьего порядка .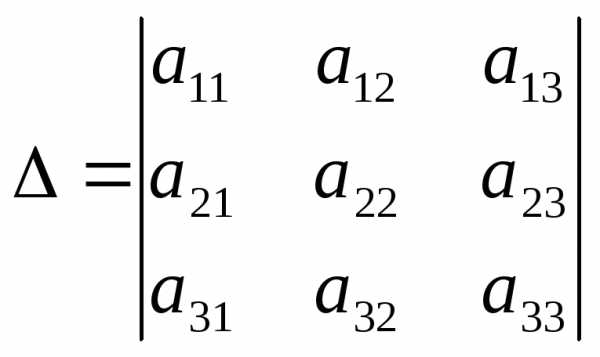

Если из определителявычеркнуть одну строку и один столбец, на пересечении которых находится некоторый элемент а_ij, то получим определитель второго порядка, который называется минором определителя , соответствующим элементу а_ij и обозначается M_ij.

Например, ,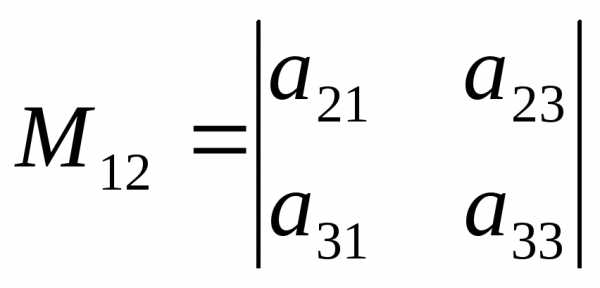

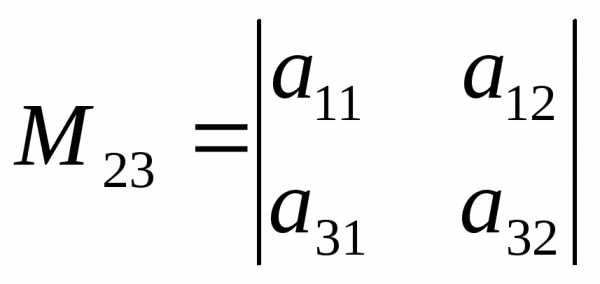
Опр. Алгебраическим дополнением элемента а_ij называется минор этого элемента, умноженный на 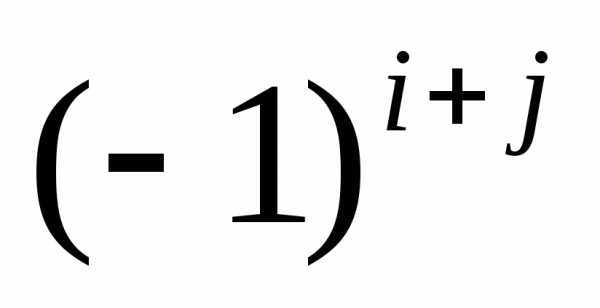и обозначается А_ij.

Пример: ,

Итак, если i+j – четно, то 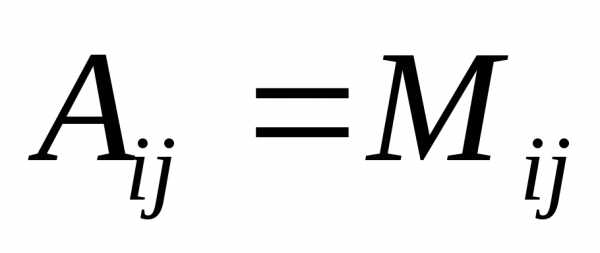, еслиi+j – нечетно, то .

Теорема разложения. Определитель третьего порядка равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения.

Например, разложение определителя по первой строке:

Замечание. Знаки, которые приписываются минору соответствующего элемента определителя: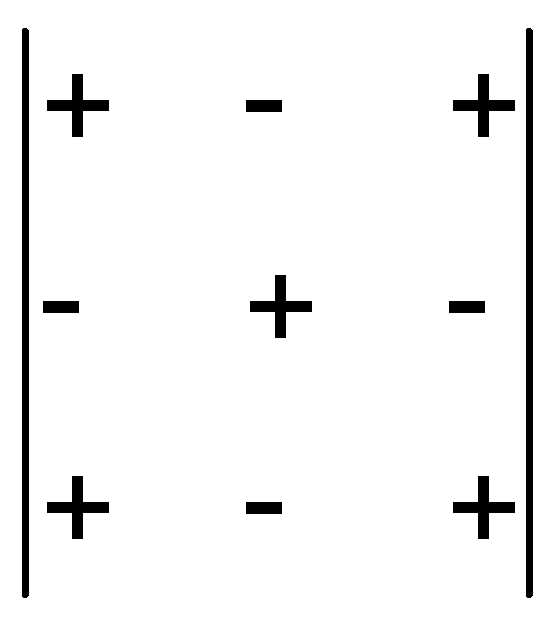

Пример 3.5

Замечание. Для определителей любых порядков остаются в силе определения минора и алгебраического дополнения, а также теорема разложения, сформулированная для определителя третьего порядка.

Например: гдеи т.д.

studfiles.net