Решения графиков функций онлайн: Построение графика функции онлайн

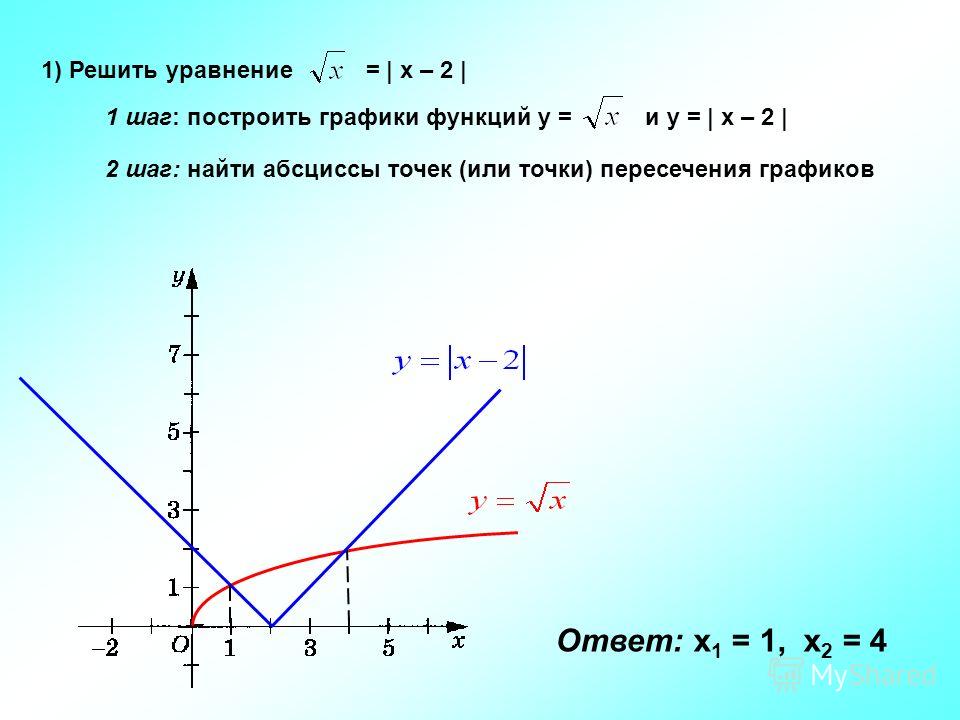
Сложение графиков функций онлайн. Функции и графики

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .

Для построения графика функции

f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) .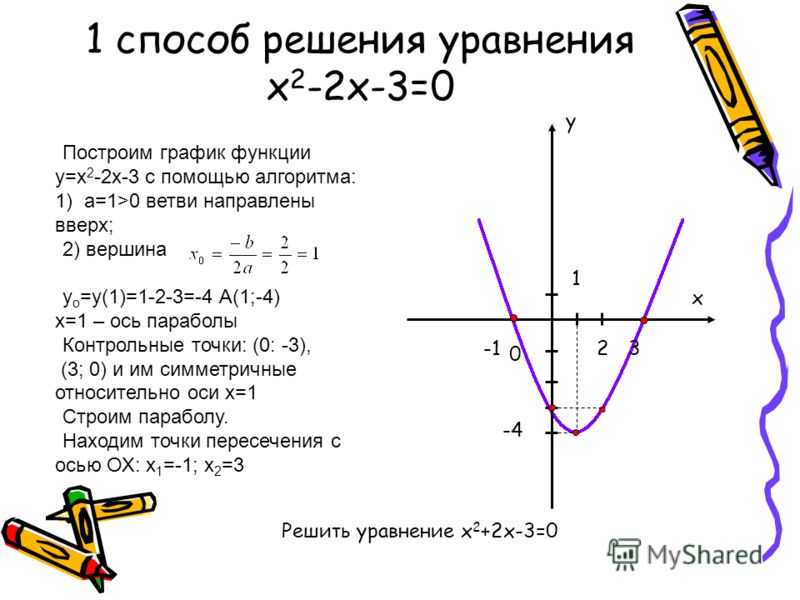 В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис.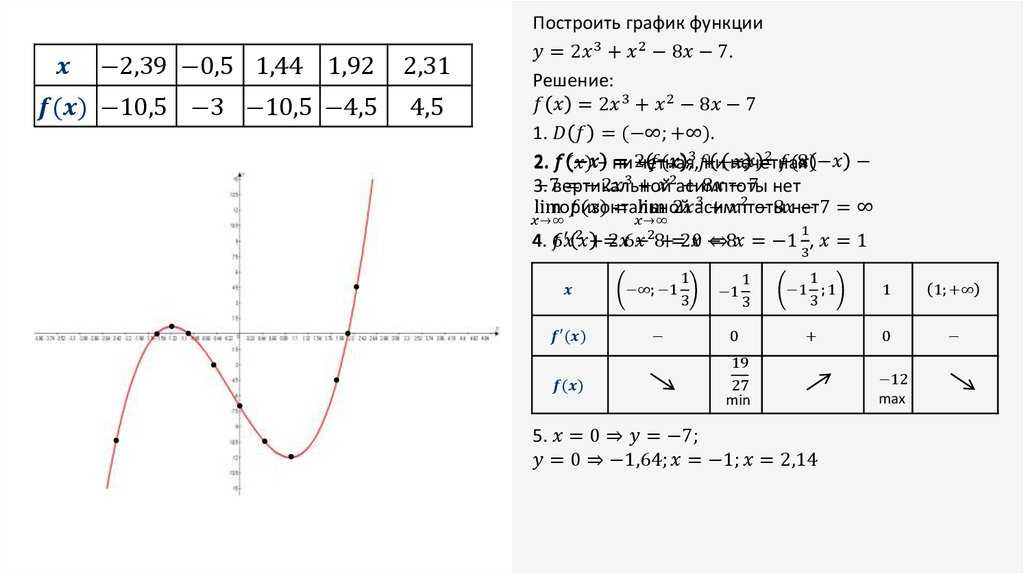 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция

y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика.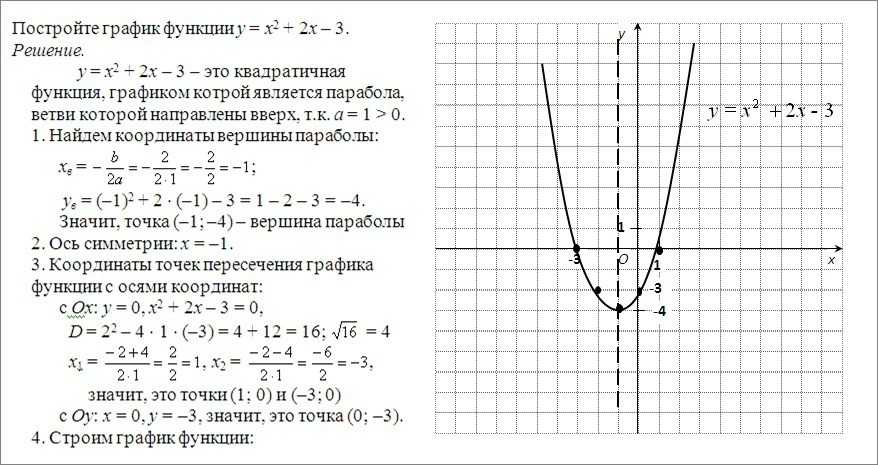 И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции

у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .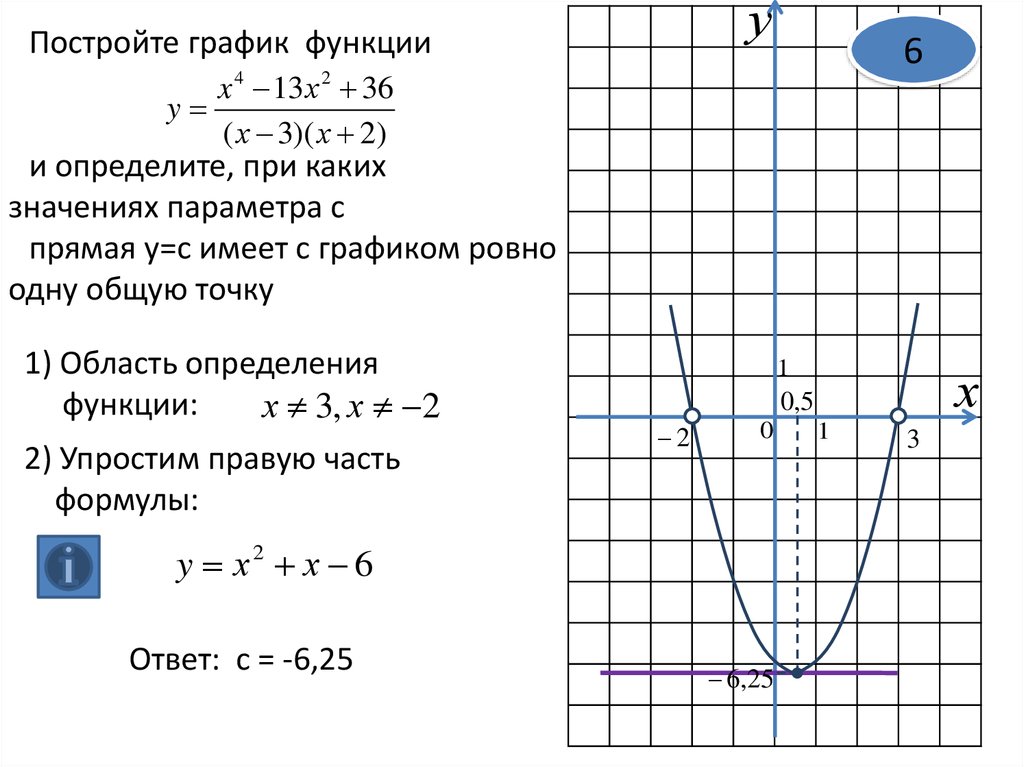

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2),

где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?

Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.

Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.

Grafikus.ru

Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.

Вот неполный перечень заданий, с которыми этот сервис успешно справляется:

• Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
• Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
• Черчение 2D-графиков в полярных координатах.
• Построение 3D-поверхностей простых функций.
• Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.

Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.

Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

Построение графиков функций онлайн презентация, доклад

Слайд 1Текст слайда:

Построение графиков функций онлайн

Инструкция по работе с сервисом «Построение графиков функций онлайн» разработана командой
10 «а» класса МОУ СОШ №3 г. Ершов Саратовской области

«Хакеры»

II Региональный конкурс «В мире точных наук, 2015»

---

Слайд 2Текст слайда:

создан в помощь
школьникам
студентам
в изучении
математики (алгебры и геометрии)
физики
и предназначен для онлайн построения графиков функций
обычных y=f(x)
параметрических x(t) и y(t)
графиков по точкам (графиков по значениям)

Построение графиков функций онлайн

---

Слайд 3Текст слайда:

yotx.ru

Зайти на сервис можно…

В поисковой системе набрать

В адресной строке браузера набрать

построение графиков онлайн

---

Слайд 4Текст слайда:

Вы оказываетесь на странице сервиса

Нажать для построения обычных графиков

Нажать для построения графиков, заданных параметрически

Нажать для построения графиков, заданных по точкам

Нажать для выбора цвета графика

Нажать для вызова справки

Раздел для задания области построения графика по координате Х

Раздел для задания области построения графика по координате Y

Кнопка для выполнения построения

---

Слайд 5Текст слайда:

Справка позволяет познакомиться с правилами ввода функций

---

Слайд 6Текст слайда:

Построение графика функции y=x2-2x-10

Нажимаете кнопку Цвет и выбираете цвет графика

x^2-2*x-10

Вводите формулу графика

Задаете интервал изменения аргумента функции

-10

10

Нажимаете кнопку Построить

---

Слайд 7Текст слайда:

Можно распечатать график

Можно скачать график

Можно сделать ссылку на график

Код для вставки на блог или сайт

График функции y=x2-2x-10

---

Слайд 8Текст слайда:

Задаете интервал изменения параметра t

Вводите формулы для X и Y

Нажимаете кнопку Построить

Построение графика функции, заданного параметрически

Выбираете вид графика

t*cos(t)

t*sin(t)

0

10

---

Слайд 9Текст слайда:

В результате получаем фигуру – спираль Архимеда

---

Слайд 10Текст слайда:

Задаете границы интервала

Вводите значения X и Y для каждой точки графика

Нажимаете кнопку Построить

Выбираете вид графика

(0;1) (1;2) (2;3) (-1;0) (-2;-1) (-3,-2)

Построение графика функции, заданного по точкам

-10

10

---

Слайд 11Текст слайда:

В результате получаем график прямой линии

---

Слайд 12Текст слайда:

Помощь в использовании сервиса вы можете получить

В разделе Примеры

В разделе Вопросы

---

Слайд 13Текст слайда:

В разделе О сервисе

Есть калькулятор матриц

}

Возможные действия с матрицами

---

Слайд 14Текст слайда:

Задаете размерность первой матрицы

Задаете элементы первой матрицы

1

2

3

3

4

1

1

2

2

Выбираете действие

Задаете размерность второй матрицы

Задаете элементы второй матрицы

Нажимаете кнопку Рассчитать

3

3

3

1

1

1

2

2

2

---

Слайд 15Текст слайда:

Результат сложения двух матриц

---

Слайд 16Текст слайда:

Достоинство данного сервиса

Проект y(x). ru предназначен для облегчения и ускорения решения многих математических задач.
y(x).ru — это онлайн-сервис, а значит, не придется искать, скачивать и устанавливать программное обеспечение. Достаточно иметь выход в Интернет с любого имеющегося под рукой устройства: стационарного компьютера, ноутбука, планшета или смартфона.

---

Слайд 17Текст слайда:

Используемые ресурсы

http://www.yotx.ru

II Региональный конкурс «В мире точных наук, 2015»

---

Скачать презентацию

Бесплатный калькулятор преобразования функций

Как преобразовать график функции?

Это зависит от направления, которое вы хотите трансформировать. В общем, преобразования в направлении y проще, чем преобразования в направлении x, см. ниже.

Как переместить функцию в направлении Y?

Просто добавьте нужное преобразование. Это оно. Например, давайте переместим этот график на единицы вверх.

Ваше упражнение: Функция должна быть перемещена на 5 вверх График до преобразования: : Функция после преобразования: на 5 в направлении вверх Добавьте 5 к функции. Перемещенная функция: Упростить новую функцию: : | добавить к

Как переместить функцию в направлении x?

Если вы хотите двигаться в направлении x, это сложнее по двум причинам:

• Вы должны заменить каждый x на
• и обратить внимание на знак: Если вы хотите двигаться в направлении x, замените x на . Но если вы хотите пойти в противоположном направлении, вы замените x на .

Вот еще один пример использования последней функции.

Ваше упражнение: Функция должна быть перемещена на 2 вправо График перед трансформацией :: Функция после трансформации: Это то, что является математикой. Расчет. Сдвинуть график на 2 вправо : Заменить каждый x на Перемещенная функция: Упростить новую функцию: : | Примените высшую биномиальную формулу с a= и b= | Рассчитать в степени . | Разверните и . | добавить к | добавить к | добавить к

Как растянуть функцию в направлении Y?

Опять же, это легко: просто умножьте всю свою функцию на коэффициент растяжения. Например, давайте растянем на Фактор в направлении Y.

Ваше упражнение: Функция должна быть перемещена на 2 в y-направлении растянута График до преобразования: : Функция после преобразования: Это то, что вычисляется по математике: Преобразование функции на 2 в y-направлении. | Разверните и .

Как растянуть функцию в направлении x?

Опять же, как и в движении, растяжка сложнее: мы должны заменить каждый x на (Учтите, что это снова не так, как вы думаете: растяжка означает не умножение на , а деление на

Ваше упражнение: Функция должна быть перемещена на 2 в x-направлении. : Преобразовать функцию на 2 в направлении растяжения x : Заменить каждый x на Растянутая функция Упростить новую функцию: : | Выписка из дроби | Решите со степенными законами: равно | Выписка из дроби

А если я хочу переместить другую функцию?

Это Мэйтпауэр. Просто введите его выше.

Калькулятор функций + онлайн-решатель с бесплатными шагами

Калькулятор функций вычисляет свойства графика, составленного из уравнения, введенного в калькулятор. Кроме того, график нарисован на декартовой плоскости, чтобы представить эту функцию f(x) визуально .

Этот калькулятор принимает любые допустимые уравнения и определяет тип функции (линейная линия, коническая форма и т. д.), а затем предоставляет таблицу, показывающую ее свойства на ее основе.

Может быть два графика, один из которых показывает увеличенное изображение , а другой выражает общий тренд функции, заданной на графике.

Более того, этот калькулятор поддерживает трехмерных уравнений , за исключением того, что он не дает подробной таблицы свойств для этих фигур и не рисует график для их визуального выражения. Для полиномов более высокого порядка результаты показывают только визуальное представление функций, а их свойства недоступен .

Что такое калькулятор функций?

Калькулятор функций — это онлайн-инструмент, который определяет тип функции и ее свойства и отображает их на основе введенного полинома в текстовом поле калькулятора. Кроме того, он рисует график для визуального представления тренда линии на декартовой плоскости. Свойства различаются от функции к функции в зависимости от типа формы, которую она выражает.

Калькулятор состоит из однострочного текстового поля с надписью «9».0014 Введите функцию, y = f(x) =, », где вы можете ввести любую законную функцию, чтобы найти ее свойства и тип. Кроме того, рекомендуется использовать калькулятор для двумерных функций, так как он правильно представляет свои свойства в этих функциях.

Как пользоваться калькулятором функций?

Вы можете правильно использовать калькулятор функций , введя нужную функцию в текстовое поле и отправив ее. Откроется новое окно, показывающее все свойства и графики для соответствующей функции ф(х) .

Ниже приведены пошаговые инструкции по использованию калькулятора:

Шаг 1

Введите нужное уравнение в текстовое поле .

Шаг 2

Убедитесь, что функция написана правильно , следуя латексному формату для вычисления калькулятором.

Шаг 3

Нажмите кнопку « Отправить », чтобы получить результаты.

Результаты

Появится всплывающее окно с подробными результатами в следующих разделах: 

• Ввод: В этом разделе показана входная функция, записанная в виде математического уравнения . Вы можете проверить уравнение, сопоставив введенную функцию с вводом, интерпретируемым калькулятором, и соответствующим образом отредактировать.
• Геометрическая фигура: В этом разделе показан тип функции и ее геометрическое имя. Основываясь на своей геометрической форме, он также показывает свои свойства, такие как точка пересечения по оси Y, градиент, направляющая, фокус, вершина, кривизна и т. д. Вы можете включить свойства, щелкнув значок «9».0014 Показать свойства » в правом верхнем углу раздела.
• Графики: Здесь построен график функций на декартовой плоскости . Линейные графики будут иметь только один график с определенным диапазоном значений x. Кроме того, коники нанесены дважды , причем один показывает увеличенный участок , а другой показывает общий тренд графика в более широком диапазоне значений x.

Решенные примеры 92 + \frac{15}{4} \]

После преобразования в стандартную форму мы можем найти свойства параболы, просто сравнив ее с уравнением стандартной формы :

\[ \Rightarrow a > 0 = 1, h= -\frac{5}{2}, k = \frac{15}{4} \]

\[ \text{vertex} = (h,\, k) = \left(-\ frac{5}{2},\, \frac{15}{4}\right) \]

Ось симметрии параллельна оси y, и парабола открывается вверх при a > 0. Таким образом полуось/фокусное расстояние находится по формуле:

\[ f = \frac{1}{4a} = \frac{1}{4} \]

\[ \text{Фокус:} \,\,  \left(\frac{5}{2} ,\, \frac{15}{4} + f\right) = \left(\mathbf{\frac{5}{2},\, 4}\right) \]

Директриса перпендикулярна к оси симметрии и, следовательно, к горизонтальной линии:

\[ \text{Directtrix :} \,\, y = -\frac{15}{4}-f = \mathbf{\frac{7}{2 }} \]

Длина полуширочайшей прямой кишки равна фокальному параметру:

\[ \text{Фокусный параметр :} \,\, p = 2f = \mathbf{\frac{1}{2 }} \]

Пример 2

Рассмотрим линейную линию с уравнением: 

\[ y = 4x + 7 \]\

Найдите свойств линии, выраженных этой функцией.

Решение

Уравнение линейной линии подчиняется общему линейному уравнению :

\[ y = mx + c \]

x-координата , м это градиент/наклон линии, а c — точка пересечения y , которая является координатой y, в которой линия пересекает ось y .

Сравнивая данное уравнение с общим уравнением линии, мы можем записать свойств линии как: 

\[\text{y-intercept = c = } 7 \]

, находим значение координаты x при $y = 0$. Отсюда:

\[ 0 = 4x + 7 \]

\[ -4x = 7 \]

\[ \mathbf{x = -\frac{7}{4}} \]

Градиент для этого выражается как м , что равно: 

\[ \text{Градиент = m = } 4 \]

Чтобы найти вектор нормали этой линии, нам нужно записать приведенное выше уравнение в виде $ax + by = 0$

\[ y = 4x ​​+ 7 \]

\[ -4x + x = 7 \]

Пренебрегая постоянным значением, мы можем взять коэффициентов , a и b, переменных x и y в качестве нормальных координат (-4 , 1).