Элементарная алгебра
Элементарная алгебра
ОглавлениеГлава I. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ§ 2. Понятия кольца и поля § 3. Упорядоченные поля § 4. Понятие функции и аналитического выражения § 5. Элементарные функции и их классификация § 6. Метод математической индукции Глава II. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНЕНИЯХ § 1. Понятие уравнения. Решения уравнения § 2. Классификация уравнений, изучаемых в элементарной математике § 3. Равносильность уравнений § 4. Преобразование уравнений при их решении Глава III. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ § 1. Алгебраические уравнения n-й степени с одним неизвестным § 2. Корни квадратного трехчлена § 3. Исследование квадратного трехчлена над полем действительных чисел § 4. Двучленные уравнения § 5. Трехчленные уравнения, приводящиеся к квадратным § 6. Симметрические уравнения § 7. Алгебраическое уравнение n-й степени с рациональными коэффициентами § 8.  Частные приемы решения уравнений высших степеней Частные приемы решения уравнений высших степеней§ 9. Дробно-рациональные уравнения Глава IV. ТЕОРИЯ СОЕДИНЕНИЙ § 2. Перестановки § 3. Сочетания § 4. Размещения § 5. Перестановки с повторениями § 6. Сочетания с повторениями § 7. Размещения с повторениями Глава V. БИНОМ НЬЮТОНА И ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА § 1. Бином Ньютона § 2. Биномиальные коэффициенты и их основные свойства § 3. Треугольник Паскаля § 4. Полиномиальная теорема § 5. Вычисление сумм степеней первых n чисел натурального ряда Глава VI. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Многочлен от нескольких переменных и его каноническая форма § 2. Однородный многочлен от n переменных и число его членов § 3. Число членов в каноническом представлении многочлена от n переменных § 5. Тождественные преобразования многочленов. Тождество Лагранжа § 6. Применение метода неопределенных коэффициентов при выполнении алгебраических действий над многочленами Глава VII.  СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ§ 1. Понятие системы уравнений § 2. Равносильность систем уравнений § 3. Уравнения и системы уравнений, являющиеся следствием данной системы уравнений § 4. Основные элементарные методы решения систем уравнений § 5. Решение нелинейных систем алгебраических уравнений элементарными методами 1. Решение системы двух уравнений с двумя неизвестными, из которых одно—второй степени, а другое — первой. 2. Решение системы двух уравнений второй степени с двумя неизвестными, которые не имеют членов первой степени. 3. Решение системы двух уравнений второй степени с двумя неизвестными в общем виде. 4. Решение системы двух однородных уравнений с двумя неизвестными. 5. Решение системы двух уравнений с двумя неизвестными, одно из которых однородное, а второе не однородное. 7. Решение нелинейной системы алгебраических уравнений, в состав которой входят линейные уравнения. 8. Решение нелинейной системы алгебраических уравнений, левая часть одного из которых представляется в виде произведения.  § 6. Графическое решение нелинейных систем алгебраических уравнений с двумя неизвестными Глава VIII. НЕРАВЕНСТВА § 1. Основные свойства неравенств § 2. Тождественные неравенства § 3. Применение неравенств для определения наибольших и наименьших значений § 4. Решение неравенств § 5. Решение алгебраических неравенств с одним неизвестным первой и второй степени § 6. Решение систем алгебраических неравенств первой степени с двумя неизвестными Глава IX. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1. Корни с натуральными показателями в поле действительных чисел § 2. Тождественные преобразования иррациональных выражений в поле действительных чисел § 3. Решение иррациональных уравнений и систем, в состав которых входят иррациональные уравнения, в поле действительных чисел Глава X. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ В ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1.  Теоретические основы решения показательных и логарифмических уравнений Теоретические основы решения показательных и логарифмических уравнений§ 2. Решение показательных уравнений с одним неизвестным § 3. Решение логарифмических уравнений с одним неизвестным § 4. Решение трансцендентных уравнений, приводящихся к показательным и логарифмическим уравнениям § 5. Решение некоторых трансцендентных систем уравнений § 6. Графические способы решения трансцендентных уравнений и систем ЛИТЕРАТУРА |
Алгебра — 11 класс. Алгебра. Уравнения и неравенства. Системы уравнений и неравенств. Равносильность неравенств, решение неравенств.
Алгебра
6занятий 3:53:13
длительность 5
тестов
2823
- Учебный план
- Отзывы ( 0 )
- Вопросы и ответы ( 0 )
1. Решение неравенств с одной переменной, равносильность неравенств. Решение неравенств с одной переменной, равносильность неравенств. | Длительность: 18 минут |
|---|---|
| 1.1
Неравенства с одной переменной. Неравенства с одной переменной. Понятие, определение, свойства. | Видео |
| 1.2
Примеры решений неравенств с одной переменной. Примеры решений неравенств с одной переменной. Понятия, определения, свойства. | Видео |
1. 3
Проверка знаний. Решение неравенств с одной переменной, равносильность неравенств. Тест. 3
Проверка знаний. Решение неравенств с одной переменной, равносильность неравенств. Тест. Решение неравенств с одной переменной, равносильность неравенств. Понятия, определения, свойства. | Тест |
| 2. Метод интервалов | Длительность: 26 минут |
|---|---|
| 2.1
Метод интервалов. Решение неравенств методом интервалов. Определения, свойства. | Видео |
2. 2
Решение квадратных неравенств методом интервалов. 2
Решение квадратных неравенств методом интервалов. Решение квадратных неравенств методом интервалов. Понятия, определения, свойства. | Видео |
| 2.3
Проверка знаний. Метод интервалов. Тест. Метод интервалов. Понятия, определения, свойства. | Тест |
| 3. Системы и совокупности неравенств. | Длительность: 40 минут |
|---|---|
3. 1
Совокупность неравенств с одной переменной. 1
Совокупность неравенств с одной переменной. Совокупность неравенств с одной переменной. Понятия, определения, свойства. Примеры решения. | Видео |
| 3.2
Системы и совокупности неравенств. | Видео |
| 3.3
Системы неравенств. Системы неравенств. Понятия, определения, свойства, примеры решения. | Видео |
4. Иррациональные неравенства. Иррациональные неравенства. | Длительность: 67 минут |
|---|---|
| 4.1
Иррациональные неравенства. Иррациональные неравенства. Понятия, определения, свойства. | Видео |
| 4.2
Примеры решения иррациональных неравенств. Примеры решения иррациональных неравенств. Понятия, определения, свойства, решения типовых задач. | Видео |
4. 3
Методы решения иррациональных неравенств. 3
Методы решения иррациональных неравенств. Методы решения иррациональных неравенств. Примеры типовых задач. | Видео |
| 4.4
Проверка знаний. Иррациональные неравенства. Тест. Иррациональные неравенства. Понятия, определения, свойства. | Тест |
| 5. Неравенства с модулями. | Длительность: 64 минуты |
|---|---|
5. 1
Неравенства и уравнения с модулем. 1
Неравенства и уравнения с модулем. Неравенства с модулем.Понятия, определения, свойства, решение типовых задач. | Видео |
| 5.2
Неравенство с модулем. Неравенство с модулем. Понятия, определения, свойства, решение задач. | Видео |
| 5.3
Проверка знаний. Решение неравенств. Тест. Решение неравенств.Понятия, определения, свойства. | Тест |
6. Уравнения и неравенства с двумя переменными. Уравнения и неравенства с двумя переменными. | Длительность: 44 минуты |
|---|---|
| 6.1
Графики неравенств с двумя переменными. Графики неравенств с двумя переменными. примеры решения типовых задач. | Видео |
| 6.2
Графическое изображение линейных неравенств с двумя переменными. Графическое изображение линейных неравенств с двумя переменными. Понятия, определения, свойства. | Видео |
6. 3
Решение неравенств с одной переменной. 3
Решение неравенств с одной переменной. Решение неравенств с одной переменной. Понятия, определения, свойства. | Видео |
| 6.4
Логарифмические неравенства. Логарифмические неравенства. Примеры решения типовых задач. | Видео |
| 6.5
Проверка знаний. Решение неравенств. Тест. Решение неравенств. Понятия, определения, свойства. | Тест |
Пока в этом курсе не задано ни одного вопроса
Задать вопрос
Описание курса
Курс «11 класс. Алгебра. Уравнения и неравенства. Системы уравнений и неравенств. Равносильность неравенств, решение неравенств.» ориентирован на раскрытие прикладного значения общих методов математики, связанных с исследованием функций, подготовке необходимого аппарата для изучения геометрии и физики. Задачи курса: раскрыть понятие, утверждения и методы, относящихся к началам анализа, выявлять их практическую значимость; развитие логического и практического мышления, культуры речи, способности к умственному эксперименту; формирование представлений о математике как части общечеловеческой культуры; развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования; овладение математическими знаниями и умениями, необходимыми для продолжения обучения в общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни. Занятия курса изучают понятие равносильности неравенств; общие методы решения неравенств.
Алгебра. Уравнения и неравенства. Системы уравнений и неравенств. Равносильность неравенств, решение неравенств.» ориентирован на раскрытие прикладного значения общих методов математики, связанных с исследованием функций, подготовке необходимого аппарата для изучения геометрии и физики. Задачи курса: раскрыть понятие, утверждения и методы, относящихся к началам анализа, выявлять их практическую значимость; развитие логического и практического мышления, культуры речи, способности к умственному эксперименту; формирование представлений о математике как части общечеловеческой культуры; развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования; овладение математическими знаниями и умениями, необходимыми для продолжения обучения в общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни. Занятия курса изучают понятие равносильности неравенств; общие методы решения неравенств.
Что будет изучено
Обсудим важное понятие равносильности неравенств, рассмотрим процесс решения таких неравенств с одной переменной путём замены более сложного неравенства более простым, но равносильным. Изучим метод интервалов, который является эффективным способом решения многих неравенств. Рассмотрим системы и совокупности различных неравенств, решение иррациональных неравенств, решение неравенств с модулями, решение уравнений и неравенств с двумя переменными. Решением типовых задач и выполнением предложенных тестов закрепим теоретический материал курса.
Требования к обучаемому
Обучаемые должны понимать значение математической науки для решения задач, возникающих в теории и практике; уметь выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; пользоваться оценкой и прикидкой при практических расчётах; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы и тригонометрические функции; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; решать уравнения, простейшие системы уравнений, используя их графики.
Курс рассчитан на обучающихся 11 классов общеобразовательных школ, абитуриентов, студентов первых курсов колледжа, техникума.
Решение систем неравенств графическим способом
В вашем браузере отключен JavaScript.
Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.
Попробуйте 30 дней бесплатно
Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!
- Математика
- Алгебра 1
- Системы уравнений и неравенств
- Решение систем неравенств графическим способом
Рейтинг
Ø 5,0 / 2 балла
Вы должны войти в систему, чтобы иметь возможность дать оценку.
Вау, спасибо!
Пожалуйста, оцените нас и в Google! Мы с нетерпением ждем этого!
Перейти в Google
Авторы
Эрик Кларк
Основы по теме
Решение систем неравенств графическим способомПодобно системам уравнений, системы неравенств представляют собой два или более неравенства с одними и теми же двумя переменными. Для определения решения системы или точки, в которой неравенства пересекаются (перекрываются), график является лучшим методом решения этих задач.
Сначала измените неравенства в системе, чтобы они были записаны в форме пересечения наклона, y = mx + b. Это облегчит вам создание графика. Для каждого неравенства в системе: Сначала поставьте точку на отрезке у, обозначенном значением b. Затем используйте значение m для рисования уклона. Чтобы соединить точки, вы будете использовать пунктирную линию для обозначения меньше или больше, а сплошную линию — для ситуаций меньше и равно или больше и равно. Заштрихуйте область набора решений.
Заштрихуйте область набора решений.
Это может быть непросто — во избежание путаницы рекомендуется выбрать контрольную точку. Вставьте координаты контрольной точки в неравенство. Если неравенство верно, заштрихуйте указанную область, а если неверно, заштрихуйте другую сторону линии. Выполните следующие шаги для каждого неравенства в системе, и пересечение заштрихованных областей станет решением, которое сделает все неравенства в системе верными.
Решайте системы уравнений, чтобы найти решения задач.
CCSS.MATH.CONTENT.HSA.REI.C.5
CCSS.MATH.CONTENT.HSA.CED.A.3
Стенограмма
Решение систем неравенств с помощью графикаФрэнк, страховой агент , летит в Перу, чтобы выследить Майка-приключенца в перуанских джунглях. Adventure Mike должен продлить свой пакет страхования Ultra Danger. В противном случае у него не будет никакой страховки от его различных приключений .
Система линейных неравенств
Фрэнк достает свой телефон, чтобы просмотреть текстовое сообщение, которое он получил несколько дней назад от Adventure Mike. Текст 9Сообщение 0087 дает подсказку о том, в каком районе джунглей Adventure Mike ищет древние реликвии. Фрэнк знает, что Майк любит общаться загадками. Он распознает послание Майка как систему из линейных неравенств .
Текст 9Сообщение 0087 дает подсказку о том, в каком районе джунглей Adventure Mike ищет древние реликвии. Фрэнк знает, что Майк любит общаться загадками. Он распознает послание Майка как систему из линейных неравенств .
Хорошо, что Фрэнк знает, как решить систему линейных неравенств с помощью построения графика . Посмотрим, как Франк решает систему линейных неравенств. Вот карта окружающего региона . Так как у нас есть система линейных неравенств, нам нужно включить оси x и y, чтобы изобразить их на графике. Наша отправная точка, или начало, — город Куско.
Нам нужно построить график системы из неравенств . Каждое неравенство записывается в форме пересечения наклона. Для первого неравенства 1 — это точка пересечения с осью y или упорядоченная пара (0, 1). Чтобы найти вторую точку, мы используем наклон линии. Наклон линии равен -2 или -2 больше 1. Мы двигаемся вниз на 2 от точки пересечения y и вправо на 1. В результате получается упорядоченное число 9.0087 пара (1, -1).
В результате получается упорядоченное число 9.0087 пара (1, -1).
Меньше или равно
Поскольку неравенство представляет собой «Меньше или равно» , график неравенства представляет собой сплошную линию . Все пункты слева от неравенства верны. Мы можем заштриховать слева от линии неравенства. Во втором неравенстве 2 — это точка пересечения с осью y или упорядоченная пара (0, -2). Чтобы найти вторую точку, мы используем наклон линии.
Меньше, чем
Наклон линии 3 больше 2. Мы двигаемся вверх на 3 от точки пересечения y и вправо на 2. В результате получается упорядоченная пара (2, 1). Поскольку неравенство представляет ‘Меньше чем’ , график неравенства представляет собой пунктирную линию. Поскольку все точки справа от неравенства равны истинным . Мы можем заштриховать справа от линии неравенства.
Решение системы неравенств состоит в том, что штриховка каждого неравенства перекрывается . Фрэнк знает, в какой части джунглей искать, поэтому он отправляется на поиски Майка-авантюриста. Ух ты! Фрэнк находит древний храм инков. Но что вырезано на его боку? Adventure Mike оставил еще одну подсказку!
Фрэнк знает, в какой части джунглей искать, поэтому он отправляется на поиски Майка-авантюриста. Ух ты! Фрэнк находит древний храм инков. Но что вырезано на его боку? Adventure Mike оставил еще одну подсказку!
Фрэнк снова достает свою карту, чтобы взломать эту подсказку и сузить круг возможных местонахождений Искателя приключений Майка. Нам нужно построить график неравенства. Неравенство записано в форме наклон-пересечение . Для первого неравенства -4 — это точка пересечения с осью y или упорядоченная пара (0, -4). Чтобы найти вторую точку, мы используем наклон линии. Наклон линии равен 1 к 4. Мы двигаемся вверх на 1 от точки пересечения y и вправо на 4. В результате получается упорядоченная пара (4, -3).
Больше или равно
Поскольку неравенство представляет собой «Больше или равно» , график неравенства представляет собой сплошную линию. Все пункты выше неравенства верны. Мы можем заштриховать над линией неравенства. Решение системы неравенств находится там, где затенение каждого неравенства перекрывается.
Теперь Фрэнк точно знает, куда идти… О, так ВОТ ПОЧЕМУ приключенческий Майк вообще отправлял эти странные сообщения.
Решение системы неравенств находится там, где затенение каждого неравенства перекрывается.
Теперь Фрэнк точно знает, куда идти… О, так ВОТ ПОЧЕМУ приключенческий Майк вообще отправлял эти странные сообщения.
Решение систем неравенств с помощью графического упражнения
Хотите применить полученные знания? Вы можете просмотреть и попрактиковаться с заданиями к видеоролику «Решение систем неравенств с помощью графика ».
Объясните, как решить систему линейных неравенств с помощью графика.
Подсказки
Имейте в виду
- $\le$ или $\ge$ $\rightarrow$ сплошная линия
- $<$ или $>$ $\rightarrow$ пунктирная линия
Оба неравенства показаны в форме пересечения наклона: $y=mx+b$.
- $m$ это наклон
- $b$ — точка пересечения с осью y.
Чтобы проверить, лежат ли решения выше или ниже линии, образованной графиком неравенства, выберите точку и подставьте координаты в соответствующее неравенство.

Решение
Имеем следующие два неравенства:
- $y\le -2x+1$
- $y<\frac32x-2$
Начните с рассмотрения неравенства $\mathbf{y\le -2x+1}$:
- Нарисуйте точку пересечения с осью Y, $1$.
- Затем нарисуйте уклон: переместитесь на две единицы вниз и на одну единицу вправо, чтобы найти вторую точку на линии.
- Соедините точки сплошной оранжевой линией, потому что в неравенстве есть «равно».
- Затенение области набора растворов. Решения лежат ниже оранжевой линии, потому что неравенство включает «меньше чем».
Аналогично поступаем со вторым неравенством, $\mathbf{y<\frac32x-2}$:
- Нарисуйте точку пересечения с осью Y, $-2$.
- Затем нарисуйте уклон: сдвиньтесь на три единицы вверх и на две единицы вправо.
- Соедините точки зеленой пунктирной линией из-за знака «меньше».
- Затенение области набора растворов.
 Решения лежат под зеленой линией.
Решения лежат под зеленой линией.
Множество всех возможных решений двух объединенных неравенств определяется пересечением заштрихованных областей.
Найдите все ответы на загадку Искателя приключений Майка.
Подсказки
Неравенства $\le$ или $\ge$ изображаются сплошными линиями, а неравенства $<$ или $>$ — пунктирными линиями.
Не забудьте:
- $\le$ или $<$ $\rightarrow$ решения лежат ниже линии
- $\ge$ или $>$ $\rightarrow$ решения лежат выше прямой
Для уравнений, записанных в форме наклона-пересечения $y=mx+b$, у-пересечение представлено членом $b $.
Решение
Здесь вы видите правильный график.
$\mathbf{y\le -2x+1}$
- оранжевая сплошная линия проходит через ось Y, $1$
- решения лежат ниже линии
$\mathbf{y<\frac32 x-2}$
- зеленая пунктирная линия проходит через точку пересечения y, $-2$
- решения лежат ниже линии
Иметь ввиду:
- рисовать сплошными линиями $\le$ или $\ge$ неравенства
- рисовать пунктирными линиями неравенства $<$ или $>$
Отметьте любую точку, чтобы проверить затенение набора решений:
- $\le$ или $<$ $\rightarrow$ ниже строки
- $\ge$ $>$ $\rightarrow$ выше линии
Определите, где будет проходить вечеринка.

Подсказки
Вы можете выбрать несколько точек и подставить их в неравенство, чтобы проверить, принадлежат ли они множеству решений.
Линии, образованные неравенствами $\le$ или $\ge$, являются частью набора решений.
Линии, образованные неравенствами $<$ или $>$, не входят в набор решений.
Решение
Начнем с неравенства $\mathbf{y\ge 2x-2}$:
- Точка пересечения с осью y равна $-2$.
- Переместите две единицы вверх и одну единицу вправо, чтобы нанести дополнительные точки.
- Соедините точки сплошной линией, так как они образованы неравенством больше или равно. Точки на линии включены в наш набор решений. Это неравенство показано зеленой линией.
- Область, заштрихованная зеленым цветом, представляет собой набор решений для этого неравенства.
Теперь построим график $\mathbf{y<-\frac12x+3}$:
- Точка пересечения с осью Y составляет $3$.

- Переместитесь на одну единицу вниз и на две единицы вправо, чтобы нанести дополнительные точки.
- Соедините точки пунктирной линией, так как они образованы неравенством меньше. Это показано оранжевой линией.
- Область, заштрихованная оранжевым цветом, представляет собой набор решений для этого неравенства.
Множество всех решений, удовлетворяющих обоим неравенствам, определяется пересечением заштрихованных областей. Не забывайте, что точки на зеленой линии $\mathbf{y\ge 2x-2}$ также принадлежат множеству решений.
Решите, находится ли местонахождение сокровища внутри области, которую ищут грабители.
Подсказки
Каждая точка в системе координат задается как $P(p_x,p_y)$, где $p_x$ — координата x, а $p_y$ — координата y точки $P$.
Подставьте каждую из заданных точек во все три неравенства. Решение должно удовлетворять каждому из неравенств.

Обратите внимание на знак $<$ во втором неравенстве.
Являются ли точки, находящиеся точно на прямой, частью набора решений?
Нарисуйте графики неравенств и посмотрите, находятся ли координаты в пределах области пересечения.
Решение
Вы можете решить систему из трех неравенств, построив график аналогично тому, как это делается для двух неравенств:
- Определить точку пересечения оси Y
- Используйте наклон для построения дополнительных точек
- Соедините точки сплошной или пунктирной линией в зависимости от знака неравенства
- Закрасьте область, принадлежащую набору решений, ниже или выше линии, в зависимости от знака неравенства
- В области пересечения всех затененных областей можно найти спрятанное сокровище
На графике справа вы можете увидеть систему трех уравнений.
Мы можем использовать этот график для нашего решения:
- Корона $(0,3)$ лежит на зеленой и на красной линиях.
 Но обратите внимание: красная линия пунктирная, что означает, что точки на линии не входят в набор решений. Поэтому грабители не могут найти это конкретное сокровище.
Но обратите внимание: красная линия пунктирная, что означает, что точки на линии не входят в набор решений. Поэтому грабители не могут найти это конкретное сокровище. - Монеты $(0,2)$ лежат внутри области решения. Это видно прямо на графике.
- Ожерелье $(2,1.75)$ лежит внутри области решения.
- Старинный меч $(-1,1)$ лежит внутри области решения.
- Бутылка любовного зелья $(2,3)$ лежит за пределами области решения. Когда мы подставляем нашу координату y, $3$, мы видим, что неравенство неверно: $3\not < \frac14\times 2+3=3,5$
Опишите, как определить множество решений неравенства.
Подсказки
Уравнение в форме пересечения наклона: $y=mx+b$
- $m$ это уклон
- $b$ — точка пересечения с осью y
Для всех $\le$ или $\ge$ неравенств нарисуйте сплошную линию, а для всех остальных — пунктирную.

Возьмем любую точку $P(x_p,y_p)$ и проверим, входят ли $x_p$ и $y_p$ в множество решений данного неравенства. Это поможет вам проверить, лежат ли решения выше или ниже линии, образованной неравенством.
Решение
Здесь вы можете увидеть график $y<\frac32x-2$:
- Y-пересечение равно $-2$
- для уклона $m=\frac32$, переместитесь на три единицы вверх и на две единицы вправо
- соедините точки $(0,-2)$ и $(2,1)$ пунктирной линией
- все наборы решений лежат ниже пунктирной линии
Присвоить неравенство.
Подсказки
Точка пересечения y легко идентифицируется в системе координат. Это место, где линия пересекает ось Y.
Вы можете рассчитать наклон, двигаясь вверх или вниз и вправо. Например, $m=-\frac34$:
- сдвинуться на три единицы вниз (из-за отрицательного знака)
- и переместитесь на четыре единицы вправо
Имейте в виду:
- $\ge$ или $\le$ $\rightarrow$ сплошная линия
- $>$ или $<$ $\rightarrow$ пунктирная линия
Как узнать, лежит ли область решения выше или ниже линии, образованной неравенством?
- $\ge$ или $>$ $\rightarrow$ выше
- $\le$ или $<$ $\rightarrow$ ниже
Решение
Восстановим три неравенства:
Начнем с красной линии и соответствующей заштрихованной области:
- Y-пересечение равно $-3$.

- Перемещаемся на три единицы вверх и на пять единиц вправо. Это дает нам наклон $m=\frac35$.
- Линия сплошная, а заштрихованная область находится над линией.
Мы можем записать неравенство:
$y\ge\frac35x-3$
$~$
Теперь посмотрим на зеленая линия :
- Пересечение по оси Y равно $3$.
- Перемещаемся на три единицы вверх и на одну единицу вправо. Это дает нам наклон $m=3$.
- Линия пунктирная, а заштрихованная область находится под линией.
Мы можем написать неравенство:
$y<3x+3$
$~$
Наконец, мы исследуем синюю линию :
- Y-пересечение составляет $4$.
- Перемещаемся на две единицы вниз и на одну единицу вправо. Это дает нам наклон $m=-2$.
- Линия сплошная, а заштрихованная область находится над линией.
Мы можем написать неравенство:
$y<-2x+4$
Еще видео по теме Системы уравнений и неравенств
Решение систем уравнений графическим способом
Решение систем уравнений подстановкой
Решение систем уравнений методом исключения
Решение систем неравенств графическим способом
Решение систем неравенств
Системы уравнений – Word задачи
Компания
- Наша команда
- Цены
- Вакансии
Платформа
Как это работает
- Обучающие видео
- Упражнения
- Диван-герой
- Рабочие листы
- Чат
Справка
- Часто задаваемые вопросы
- Дайте нам отзыв
Юридический
- Положения и условия
- Право на отзыв
- Политика конфиденциальности
- Свяжитесь с нами
- Не продавать мою личную информацию
Есть вопросы? Связаться с нами!
help@sofatutor. com
com
- дивантутор.com
- диван-репетитор.ch
- диван-репетитор.ат
- дивантутор.com
- ru.sofatutor.co.uk
Есть вопросы? Связаться с нами!
Решение системы линейных неравенств с помощью графика
Сделать 4 мин чтения
Решение системы линейных неравенств с помощью графика
Решением одного линейного неравенства является область по одну сторону от граничной линии, содержащая все точки которые делают неравенство верным. Решением системы двух линейных неравенств называется область, содержащая решения обоих неравенств. Чтобы найти эту область, мы изобразим каждое неравенство отдельно, а затем найдем область, в которой они оба верны. Решение всегда отображается в виде графика.
Пример: как решить систему линейных неравенств
Решите систему с помощью графика.
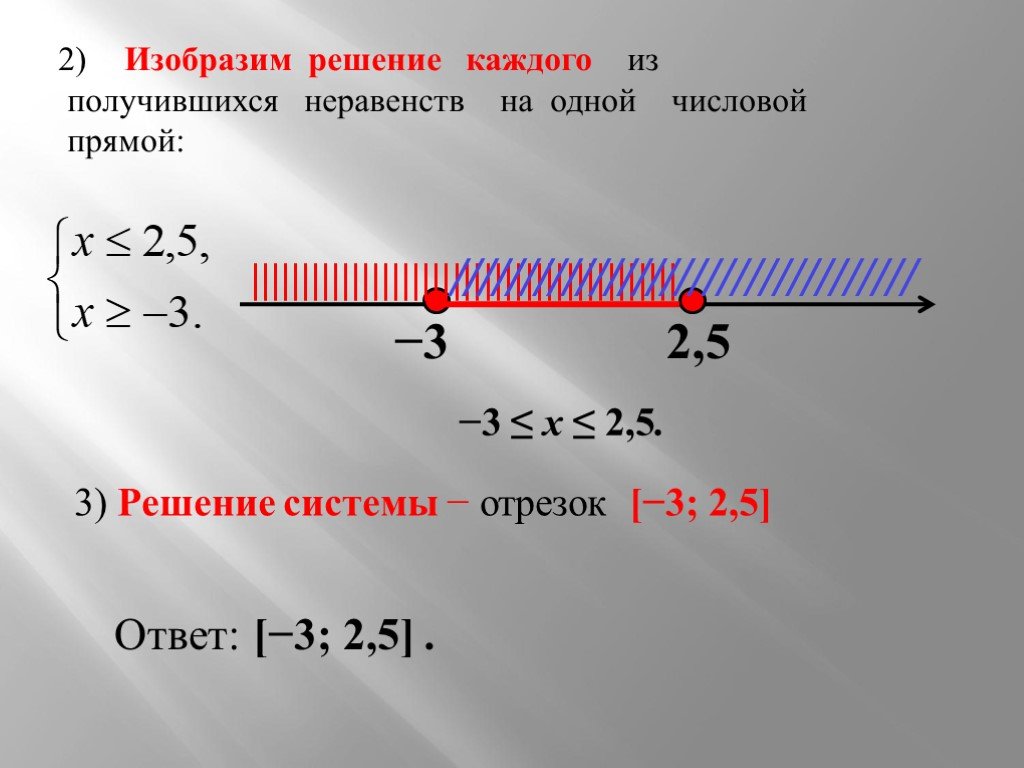
\(\begin{array}{c}y\ge 2x-1\hfill \\ y Решите систему с помощью графика. \(\begin{array}{c}x-y>3\hfill \\ y<-\frac{1}{5}x+4\hfill \end{array}\) Точка пересечения двух линий не включена, поскольку обе граничные линии были пунктирными. Решение представляет собой область, заштрихованную дважды, т. Решите систему с помощью графика. \(\begin{массив}{c}x-2y<5\hfill \\ y>-4\hfill \end{массив}\) Точка (0, 0) находится в решении, и мы уже нашли, что это решение каждого неравенства. Точка пересечения двух линий не включена, так как обе граничные линии были заштрихованы. Решение представляет собой область, заштрихованную дважды, т. Системы линейных неравенств, в которых граничные линии параллельны, могут не иметь решения. Мы увидим это в примере ниже. Решите систему с помощью графика. \(\begin{array}{c}4x+3y\ge 12\hfill \\ y<-\frac{4}{3}x+1\hfill \end{array}\) В обеих заштрихованных областях нет точек, поэтому система не имеет решения. Решите систему с помощью графика. \(\begin{массив}{c}y>\frac{1}{2}x-4\hfill \\ x-2y<-4\hfill \end{массив}\) Решение
Решите систему линейных неравенств графически.
Пример
Решение
The intercepts are x = 3 and y = -3 and the boundary line will be dashed. Test (0, 0) which makes the inequality false so shade (red) the side that does not contain (0, 0).” The graph shows a line graphed on an x y-coordinate plane. The line is dashed and the area to the right of the line is shaded.»>
График x − y > 3, по графику x − y = 3 и проверка точки.
Точки пересечения составляют x = 3 и y = −3, а граничная линия будет пунктирной.
Тест (0, 0). Это делает неравенство ложным. Итак, заштрихуйте сторону, не содержащую (0, 0) красным цветом. Choose a test point in the solution and verify that it is a solution to both inequalities.” The figure shows two lines graphed on an x y-coordinate plane. The figure shows on line that is dashed, and the area to the right is shaded. The other line is solid, and the area below it is shaded. There is an area where the two shaded areas overlap.»>
Постройте график \(y<-\frac{1}{5}x+4\), построив график \(y=-\frac{1}{5}x+4\), используя наклон \(m=-\frac{1}{5}\) и y − точка пересечения b = 4. Линия границы будет пунктирной.
Тест (0, 0). Это делает неравенство верным, поэтому закрасьте сторону, содержащую (0, 0), синим цветом.
Выберите контрольную точку в решении и убедитесь, что она является решением обоих неравенств. е. более темную заштрихованную область.
е. более темную заштрихованную область. Пример
Решение
Постройте график \(x-2y<5\), построив график \(x-2y=5\) и проверив точку.
Точки пересечения равны x = 5 и y = −2,5, а граничная линия будет пунктирной.
Тест (0, 0). Это делает неравенство верным. Итак, закрасьте сторону, содержащую (0, 0) красным цветом. The words say, “Graph y is greater than -4, by graphing y = -4 and recognizing that it is a horizontal line through y = -4. The boundary line will be dashed. Test (0, 0) which makes the inequality true so shade (blue) the side that contains (0, 0). This figure shows two line graphed in an x y-coordinate plane. One line is dashed, and the area above it is shaded. The second line is solid, and the area above it is shaded.»>
График y > −4, построение графика y = −4 и признание того, что это горизонтальная линия, проходящая через г = -4. Линия границы будет пунктирной.
Тест (0, 0). Это делает неравенство верным. Итак, закрасьте (синим) сторону, содержащую (0, 0) синего цвета. е. более темную заштрихованную область.
е. более темную заштрихованную область. Пример
Решение
The figure shows two line graphed on an x y-coordinate plane. One line is solid, and the area to the right is shaded. The other line is dashed, and the area to the left is shaded. There is no area of overlap between the two shaded areas.»>
Постройте график \(4x+3y\ge 12\), построив график \(4x+3y=12\) и проверив точку.
Точки пересечения равны x = 3 и y = 4, а линия границы будет сплошной.
Тест (0, 0). Это делает неравенство ложным. Итак, заштрихуйте сторону, не содержащую (0, 0) красным цветом. График \(y<-\frac{4}{3}x+1\) путем построения графика \(y=-\frac{4}{3}x+1\) с использованием наклона \(m=\frac {4}{3}\) и y — точка пересечения b = 1. Линия границы будет пунктирной.
Тест (0, 0). Это делает неравенство верным. Итак, закрасьте сторону, содержащую (0, 0), синим цветом. Эта система не имеет решения.
Эта система не имеет решения. Пример
Решение


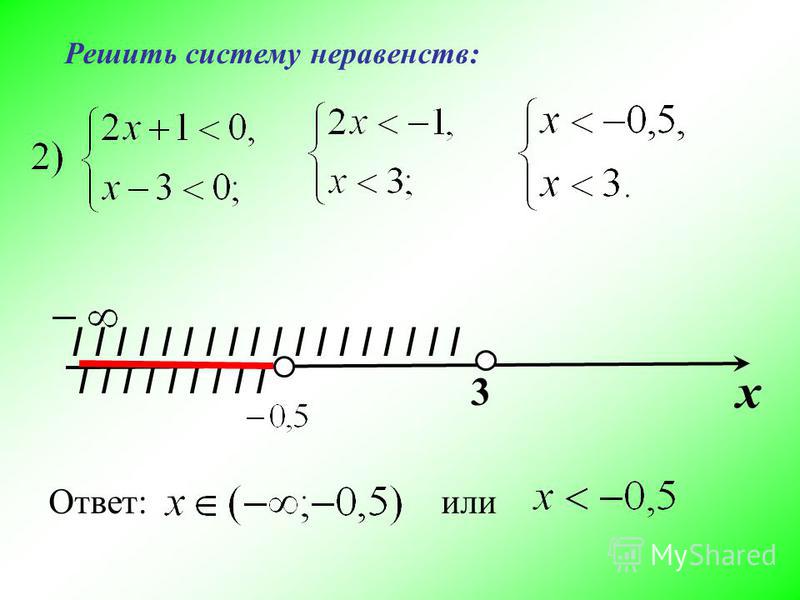
 Решения лежат под зеленой линией.
Решения лежат под зеленой линией.
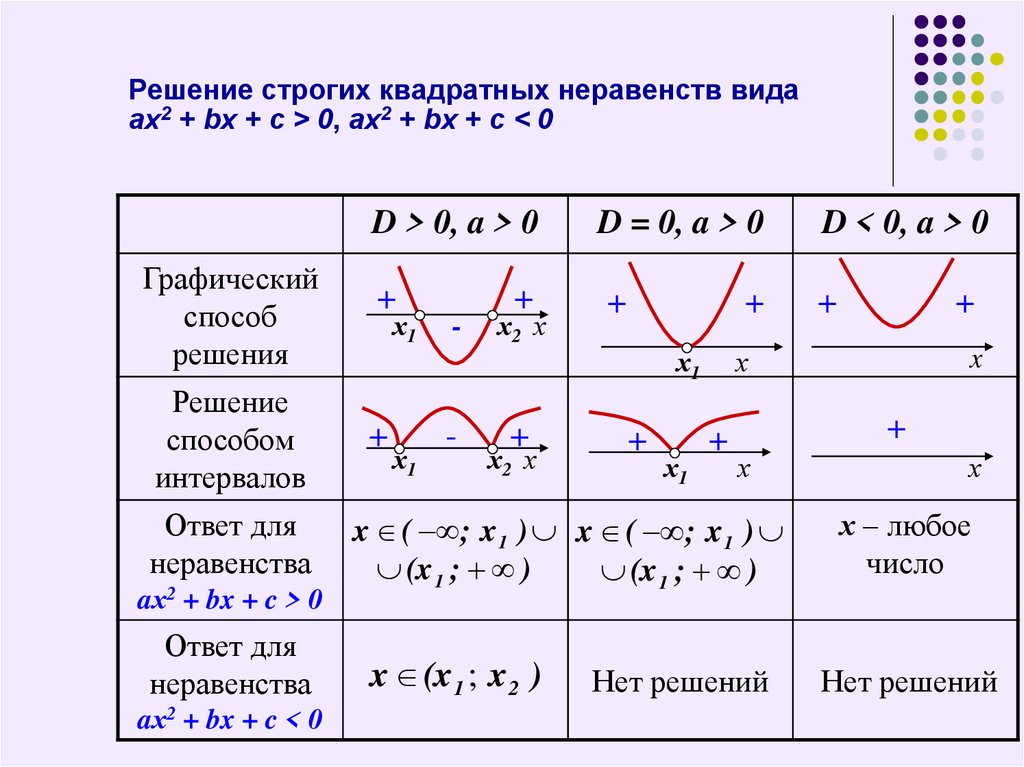
 Но обратите внимание: красная линия пунктирная, что означает, что точки на линии не входят в набор решений. Поэтому грабители не могут найти это конкретное сокровище.
Но обратите внимание: красная линия пунктирная, что означает, что точки на линии не входят в набор решений. Поэтому грабители не могут найти это конкретное сокровище.
