Точки экстремумов функции, алгебра в 10 классе, нахождение точек, урок и презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Нахождение точек экстремумов функций (PDF)
Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Как вычислять экстремумы?
5. Примеры.
Введение в экстремумы функций
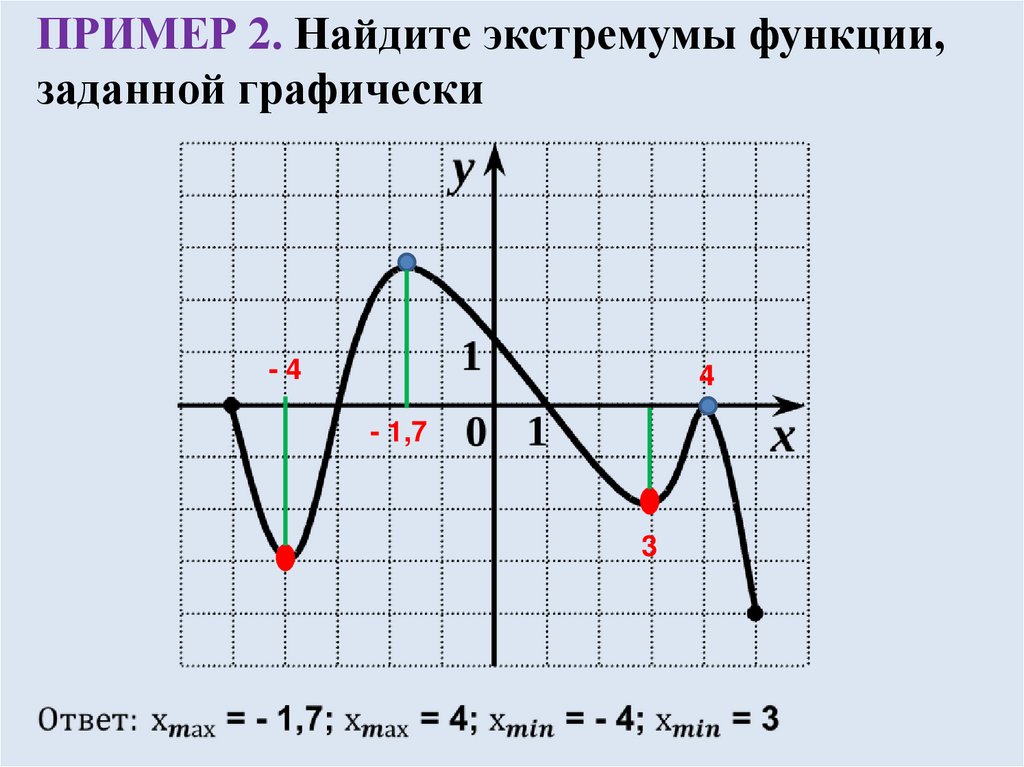
Ребята, давайте посмотрим на график некоторой функции:
Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них. До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1.
В точке x1
функция опять перегибается, и после этого — опять возрастает. Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:
Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.
Посмотрим на график вот такой функции:
Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).
Точки минимума и максимума
Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
Ребята, а что такое окрестность?
Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.
Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.
Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.
Ребята, давайте введем обозначения:
ymin — точка минимума,ymax — точка максимума.
Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.
Экстремумы функции
Для точек минимума и максимума есть общей термин – точки экстремума.
Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.
Как же искать экстремумы функции?
Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).
Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.
Точки, в которых производная равна нулю называются стационарными.
Точки, в которых производной функции не существует, называются критическими.
Как вычислять экстремумы?
Ребята, давайте опять вернемся к первому графику функции:
Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1.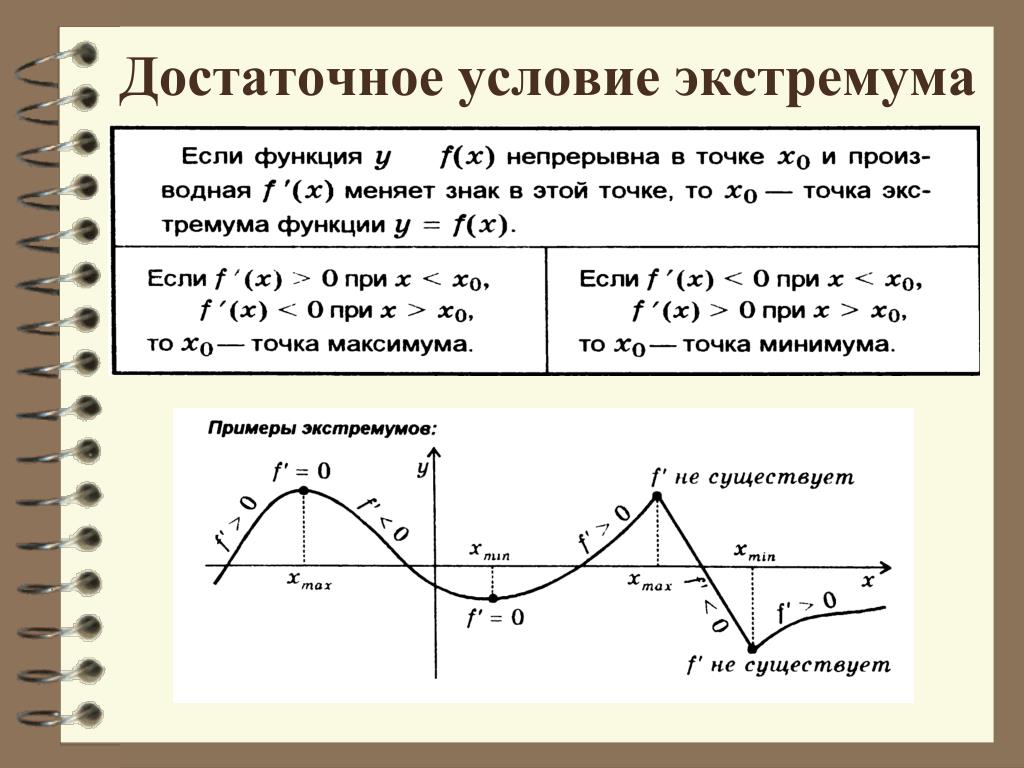
В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.
На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.
Обобщим полученные знания утверждением:
Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:
Для решении задач запомните такие правила: Если знаки производных определены то:
Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:
- Найти производную y’.
- Найти стационарные(производная равна нулю) и критические точки (производная не существует).
- Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
- По указанным выше утверждениям сделать вывод о характере точек экстремума.
Примеры нахождения точки экстремумов
1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x3
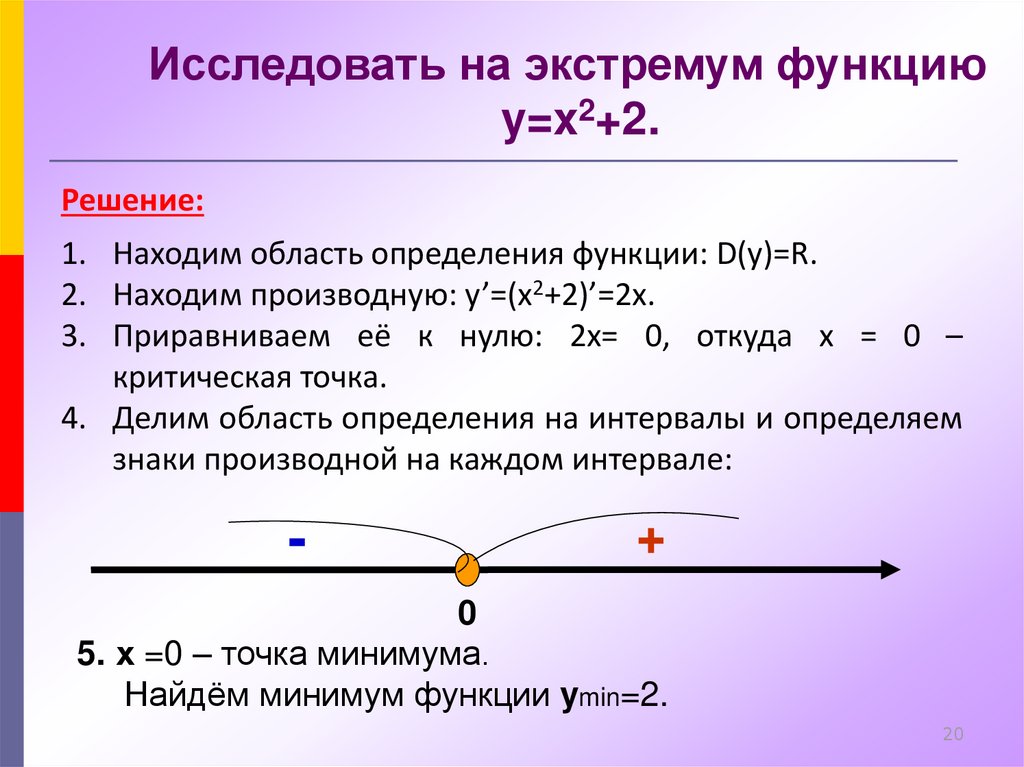
Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:а) y’= 12 — 3x2,
б) y’= 0, при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.
2) Найти точки экстремума функции и определить их характер.
Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.
3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.
Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:а) y’= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2,
т.к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
в) отметим стационарные точки на числовой прямой и определим знаки производной: г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.
4) Найти точки экстремума функции и определить их характер:
Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:а) б) найдем значения в которой производная равна нулю: y’= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции.
В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.
Задачи для самостоятельного решения
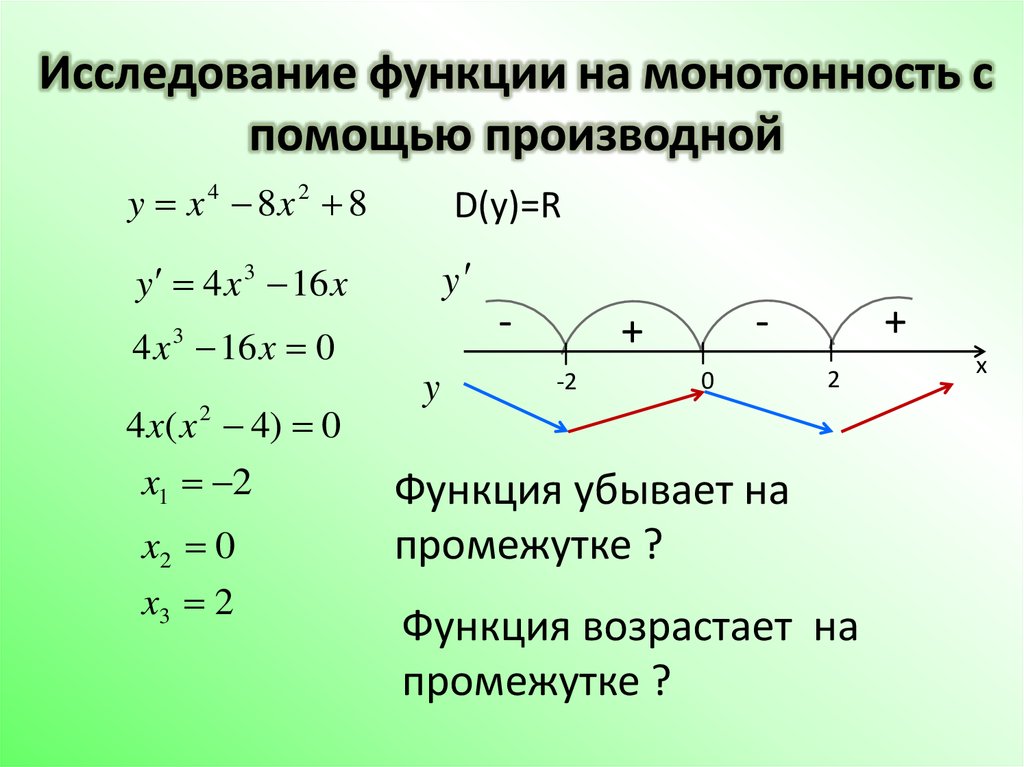
а) Найти точки экстремума функции и определить их характер: y= 5x3 — 15x — 5.
б) Найти точки экстремума функции и определить их характер:
г) Найти точки экстремума функции и определить их характер:
4.2.4. Примеры решения задач по теме «Экстремумы»
Задача 1.
Найти стационарную точку функции
Указание
В стационарной точке
Решение
Следовательно, координаты стационарной точки можно найти как решение системы
Ответ: (1,-2).
Задача 2.
Найти точку минимума функции
Указание
Пусть М0 – стационарная точка,
Тогда М0 является точкой минимума, если D > 0, A > 0.
Решение
Найдем стационарные точки функции:
Итак, стационарные точки функции –
Исследуем их на экстремум.
Нет экстремума.
Ответ:
Задача 3.
Найти экстремум функции
При условии 2Х + 5У + 3 = 0.
Указание
Найдите экстремум функции Лагранжа
Решение
Исследуем на экстремум функцию Лагранжа
Исследуем найденную точку на экстремум:
Следовательно, Точка условного максимума, и значение функции в этой точке равно
Ответ:
Задача 4.
На параболе
Найти точку, ближайшую к прямой Х – У = 2.
Указание
Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле
Следовательно, требуется найти минимум функции
При условии
Решение
Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле
Следовательно, требуется найти минимум функции
При условии
Составим функцию Лагранжа:
Не выполнено условие на знак подмодульного выражения.
Стационарная точка. При этом
Следовательно, найдена точка условного минимума.
Ответ:
Задача 5.
Найти множество значений функции
Указание
Найдите наибольшее и наименьшее значение функции в данной области,
Которые могут достигаться либо на границе, либо в стационарной точке внутри области.
Решение
Найдем стационарные точки функции:
Стационарная точка, Z(0,0) = 0.
Для определения наибольшего и наименьшего значения функции на границе области найдем условный экстремум функции Z = Xy при условии X2 + Y2 = 1.
Составим функцию Лагранжа:
Итак, найдены четыре стационарные точки:
При этом
Следовательно, наименьшее и наибольшее значения достигаются на границе области, а так как функция непрерывна, она принимает внутри области все промежуточные значения между наименьшим и наибольшим, то есть множество ее значений в данной области –
Ответ:
| < Предыдущая | Следующая > |
|---|
Уравнение \eqref{cond1} выполняется, если либо $x=0$, либо $3x+2y=0$,
т.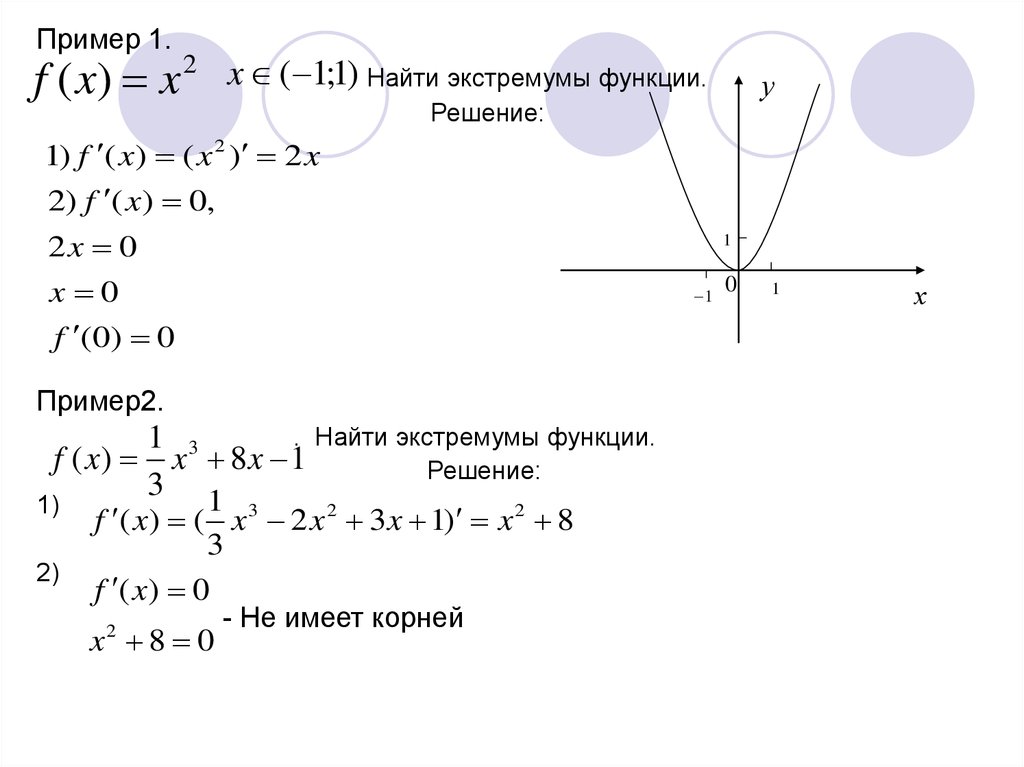
е. если $x=0$ или если $y = -3x/2$. Мы рассматриваем эти два решения как
два отдельных случая. Для каждого случая мы найдем решения для
уравнение \eqref{cond2}.
Случай 1: Пусть $x=0$. Тогда мы знаем уравнение \eqref{cond1} выполняется. Подставляем $x=0$ в уравнение \eqref{cond2}, которое становится $0-2y-4=0$, т. е. $y=-2$. Если $x=0$ и $y=-2$, то оба уравнение \eqref{cond1} и уравнение \eqref{cond2} удовлетворены. Следовательно, точка $(0,-2)$ является критическая точка. 92+3x-4&=0\\ (х-1)(х+4)&=0\\ х=1 \текст{ или } х&=-4. \конец{выравнивание*} Итак, у нас есть два решения уравнение \eqref{cond2} для случая 2. первое решение — когда $x=1$, что означает $y=-3x/2=-3/2$. Если $х=1$ и $y=-3/2$, то оба уравнение \eqref{cond1} и уравнение \eqref{cond2} удовлетворены. Поэтому точка $(1,-3/2)$ является критической точкой.
Второе решение для случая 2, когда $x=-4$, что означает $y=-3x/2=6$. Следовательно, точка $(-4,6)$ является критической точкой.
Подводя итоги по случаям 1 и 2, мы заключаем, что
$f(x,y)$ имеет три критические точки: $(0,-2)$, $(1,-3/2)$ и
$(-4,6)$.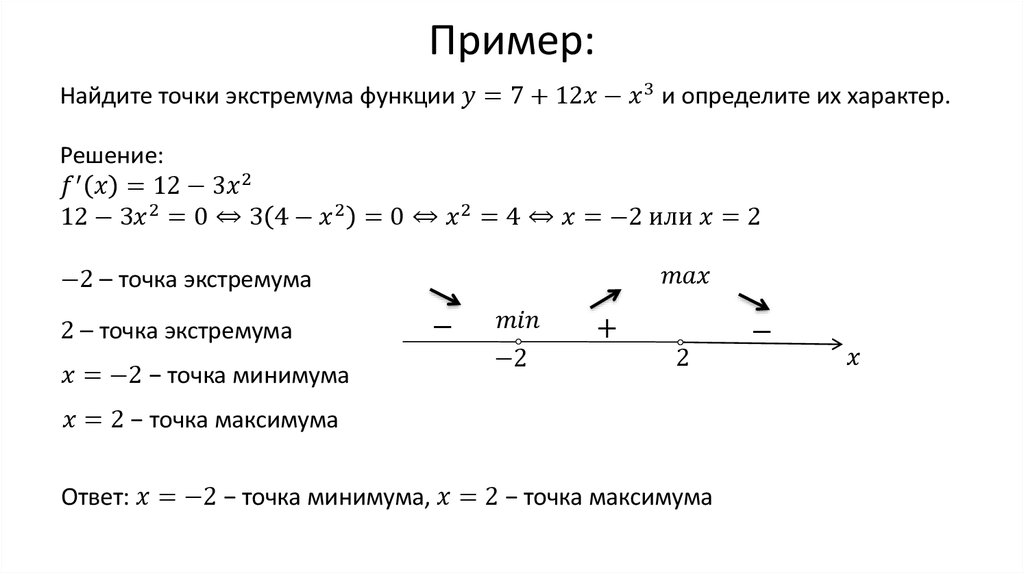
Вы должны перепроверить, что $D f(x,y)=[0 \quad 0]$ в каждой из этих точек.
Шаг 2 : Классифицируйте критические точки.
Матрица Гессе \начать{выравнивать*} Hf (х, у) = \левый[ \begin{массив}{cc} 6х+2у и 2х\\ 2x и -2 \конец{массив} \верно] \конец{выравнивание*} Нам нужно проверить определенность $Hf(x,y)$ в критической точки $(0,-2)$, $(1,-3/2)$ и $(-4,6)$.
Для критической точки $(0,-2)$, \начать{выравнивать*} Hf(0,-2) = \левый[ \begin{массив}{rr} -4 и 0\\ 0 и -2 \конец{массив} \верно] \конец{выравнивание*} $h_{11} = -4 0$. Это означает, что $Hf(0,-2)$ отрицательно определена и $f$ имеет локальный максимум в точке $(0,-2)$.
Для критической точки $(1,-3/2)$, \начать{выравнивать*} Hf(1,-3/2) = \левый[ \begin{массив}{rr} 3 и 2\\ 2 и -2 \конец{массив} \верно]. \конец{выравнивание*} $h_{11}=3>0$ и $\det(Hf) = -6-4=-10 9{-4}
Относительный экстремум — Расчет 1
Все ресурсы расчета 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept
Исчисление 1 Помощь » Функции » Графические функции » Интервалы » Относительный экстремум
Дано
Найдите -координату относительного максимума на интервале.
Возможные ответы:
Невозможно определить
Правильный ответ:
90 078 Объяснение:Чтобы найти относительные максимумы, нам нужно найти, где наша первая производная меняет знак. Для этого найдите свою первую производную, а затем найдите, где она равна нулю.
Начните с:
в
Это означает, что у нас есть экстремумы при x=0 и x=-8/3
Поскольку нас интересует только интервал от -5 до 0, нам нужно проверить точки только на этом интервале. Попробуйте точки между двумя нашими экстремумами, а также одну между -8/3 и -5.
Итак, наша первая производная переходит от отрицательной к положительной при -8/3, таким образом, это координата x нашего относительного максимума на этом интервале.
Сообщить об ошибке
Где находится максимальное значение функции
на интервале ?
Возможные ответы:
Правильный ответ:
Объяснение:
Несмотря на то, что существуют относительные максимумы в точках и (находятся путем приравнивания первой производной функции к нулю и решения для x.
), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек.
Сообщить об ошибке
Определить относительные максимумы функции:
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы определить относительные максимумы функции, мы должны определить, где первая производная функции меняется с положительной на отрицательную.
Первая производная функции
была найдена по следующему правилу:
Далее мы должны найти критические точки, значения, при которых первая производная равна нулю: первая производная:
Чтобы проверить знак первой производной, подставьте любое значение на каждом интервале в функцию первой производной.
На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.
Сообщить об ошибке
Найдите локальный максимум
, используя уравнение и/или следующий график.
Возможные ответы:
Правильный ответ:
Объяснение:
Заметим, что эта функция имеет 2 экстремума, которые расположены в точках и . Мы могли бы также найти это, взглянув на саму функцию:
.
Мы знаем, что экстремумы существуют, когда наклон функции равен нулю, поэтому мы берем производную, приравниваем ее к нулю, а затем находим x.
Производная следующая:
.
Поэтому приравнивая обе части к нулю, мы видим следующее:
и .
Чтобы выяснить, дает ли одно из этих значений x локальное минимальное или максимальное значение, требуется либо проверка первой производной, либо проверка второй производной, либо анализ графика. Мы видим, что для небольшой окрестности вокруг является наибольшим членом, следовательно, это локальный максимум. Точно так же для небольшой окрестности вокруг наименьший член, следовательно, это локальный минимум.
Следовательно, когда является единственным местом, в котором возникает локальный максимум. Помните, что не значение x должно быть самым большим, а соответствующее значение y.
Сообщить об ошибке
Ниже приведен список значений в определенных точках для непрерывного . По теореме о среднем значении сколько нулей должно быть у этой функции?
Возможные ответы:
Минимум 1
Ровно 2
Максимум 2
Ровно 1
Минимум 2
Правильный ответ:
Минимум 2
Объяснение:
Теорема о среднем значении утверждает, что если непрерывное имеет , то для всех должно быть , которое отображается в , поэтому, поскольку указанное выше значение переходит от отрицательного к положительному дважды, ноль должен быть отображен как минимум дважды.
Сообщить об ошибке
Относительный минимум функции — это все точки x в области определения функции, такие, что это наименьшее значение для некоторой окрестности. Это точки, в которых первая производная равна 0 или не существует.
Найдите относительный минимум функции
, используя следующий график и функцию.
Возможные ответы:
Правильный ответ:
Объяснение:
Заметим, что эта функция имеет 2 экстремума, расположенных в точках x=-1 и x=0. Мы могли бы также найти это, взглянув на саму функцию:
.
Мы знаем, что экстремумы существуют, когда наклон функции равен нулю, поэтому мы берем производную, приравниваем ее к нулю, а затем находим x.
Производная следующая:
.
Поэтому приравнивая обе части к нулю, мы видим следующее:
и .