Частные случаи решения систем линейных уравнений
Репетиторы ❯ Математика ❯ Частные случаи решения систем линейных уравнений
Автор: Владимир Л., онлайн репетитор по математике
●
23.10.2011
●
Раздел: Математика
Системы уравнения решаются графически. Однако такой способ решения оказывается неудобным: если точка пересечения графиков значительно удалена от начала координат. Кроме того, при графическом способе не может быть обеспечена большая точность результата. Поэтому применяют и другие методы решения.
Чаще всего для решения предлагаются такие системы линейных уравнений, в которых коэффициенты при переменных отличны от нуля. В этом случае систему необходимо преобразовать так, чтобы хотя бы в одном из уравнений коэффициент при какой-либо переменной стал равен нулю. Если коэффициент при переменной в одном из уравнений системы двух линейных уравнений равен нулю, такую систему легко решить без построения графиков.
Рассмотрим примеры решения систем уравнений с двумя переменными.
Пример 1.
Решим систему
{3х – 7у = 2,
{2х + 0у = 20.
Решение.
Уравнению 2х + 0у = 20 удовлетворяет любая пара значений переменных х и у вида (10; n), где n – любое число, и никакая другая пара.
Из множества пар вида (10; n) выделим те, которые удовлетворяют первому уравнению системы. Для этого в уравнение 3х – 7у = 2 вместо х подставим 10. Получим 3 × 10 – 7у = 2.
Пример 2.
Решим систему:
{3х = -12,
{х + у = 1.
Решение.
Первое уравнение содержит только одну переменную х и обращается в истинное равенство при х = -4.
Как известно, решением системы уравнений с двумя переменными служит пара чисел. Можно ли говорить, что первому уравнению удовлетворяет пара вида (-4; n), если в нём отсутствует переменная у?
Если условиться, что уравнение 3х = -12, входящие в данную систему, есть сокращённая запись уравнения 3х + 0у = -12, то ему будет удовлетворять любая пара значений х и у вида (-4; n), где n – какое угодно число. Подставив значение х = -4 во второе уравнение системы, найдём, что у = 5. Следовательно, пара чисел (-4; 5) является решением данной системы уравнений.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
МатематикаКурсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Высшая математика Т1
Высшая математика Т1
ОглавлениеПРЕДИСЛОВИЕ§ 1. Определители второго порядка 2.1. Определители третьего порядка. 2.2. Определители n-го порядка. §3. Матрицы 4.1 Система из n линейных уравнений с n неизвестными. 4.2. Формула Крамера 4.3. Однородная система 4.4 Правило решения системы линейных уравнений Системы линейных уравнений: 4.5 Примеры приложения правил Системы линейных уравнений: 4.6 Обоснование правил 4.7. Метод решения системы путем исключения неизвестных 4.8. Нахождение ранга матрицы 5.1. Понятие вектора 5.2. Проекция вектора 5.3. Свойства проекций векторов 5.5. Прямоугольная система координат 6.1. n-мерное пространство 6.2 Скалярное произведение в действительном пространстве 6.3 Скалярное произведение в комплексном пространстве 6.4. Неравенства Буняковского 6.5. Неравенство Минковского § 7. Отрезок.  Деление отрезка в данном отношении§ 8. Прямая линия 9.1. Уравнение плоскости в нормальном виде 9.2. Уравнение плоскости в общем виде 9.3. Уравнение плоскости в отрезках 9.4. Уравнение плоскости, роходящей через точку 9.5. Уравнение плоскости, проходящей через три точки 9.6 Угол между двумя плоскостями 9.7. Расстояние от точки до плоскости 10.1 Уравнение прямой в каноническом виде 10.2 Расположение двух плоскостей 11.1. Двумерная система координат 11.2. Трехмерная система координат 12.1. Два определения векторного произведения 12.2. Геометрический смысл определителя второго порядка 12.3. Свойства векторного произведения § 13. Смешанное (векторно-скалярное) произведение § 14. Линейно независимая система векторов § 15. Линейные операторы § 16. Базисы в Rn § 17. Ортогональные базисы в Rn § 18. Инвариантные свойства скалярного и векторного произведений § 19. Преобразование прямоугольных координат в плоскости § 20.  Линейные подпространства в Rn§ 21. Теоремы фредгольмова типа § 22. Самосопряженный оператор. Квадратичная форма § 23. Квадратичная форма в двухмерном пространстве § 24. Кривая второго порядка Эллипс Гипербола Парабола 24.3 Классификация кривых второго порядка § 25. Поверхность второго порядка в трехмерном пространстве Эллипсоид Однополостный гиперболоид Эллиптический и гиперболический параболоиды Конус второго порядка Цилиндры второго порядка Линейчатые поверхности § 26. Общая теория поверхности второго порядка в трехмерном пространстве § 27. Плоскость в Rn. Общие положения 27.2. Плоскость в Rn 27.3. Уравнение плоскости в нормальном виде 27.4. Уравнение плоскости в векторной форме 27.5. Геометрическая интерпретация уравнений 27.6. Уравнение плоскости, проходящей через n точек 27.7. Условия ортогональности и параллельности плоскостей 27.8. Уравнение плоскости, проходящей через точку 27.  9. Прямая в пространстве Rn27.10. Расположение (n-1) плоскостей 27.11. Расстояние от точки до плоскости 27.12. Различные задачи § 28. Линейное программирование 28.2. Транспортная задача 28.3.Общая задача линейного программирования 28.4. Векторно-матричная форма задачи линейного программирования 28.5. Симплекс-метод 28.7. Выбор разрешающего элемента 28.8. Условия существования базиса |
для вузов: В 3 т. / Я. С. Бугров, С. М. Никольский; Под ред. В. А. Садовничего. — 6-е изд., стереотип. — М.: Дрофа, 2004. — (Высшее образование: Современный учебник).
Решение систем и линейных уравнений (Видео)
Привет! Добро пожаловать в это видео о линейных уравнениях! Сегодня мы рассмотрим, что такое линейные уравнения и как решать системы линейных уравнений.
Прежде чем углубиться, давайте кратко рассмотрим, что такое линейное уравнение.
Помните, что линейное уравнение описывает прямую линию на графике. Обычно они выглядят примерно так: y равно mx плюс b y=mx+b. Наклон линии представлен буквой m, а точка пересечения с осью y представлена буквой b.
X и Y просто представляют собой упорядоченную пару, которая попадает на линию графика для этого уравнения. Вот пример линейного уравнения и графика для сопоставления.
Помните, что наклон представляет собой подъем над трассой. Таким образом, положительный наклон 3 представляет собой рост 3 и рост 1 (вверх 3 и более 1).
Этот пример уже был настроен в так называемой форме пересечения наклона. Однако не все линейные уравнения, с которыми вы работаете, удобно составлять таким образом. Иногда вам нужно будет манипулировать уравнением, чтобы привести его к форме пересечения наклона. Этот процесс должен произойти, прежде чем вы сможете начать построение графика.
Важно помнить, что при решении переменных в линейном уравнении цель состоит в том, чтобы использовать обратные операции, чтобы изолировать каждую переменную. Например, если вы находили y в уравнении 4, это равно отрицательному значению 2x плюс y. 4 равно отрицательному значению 2x плюс y 4=-2x+y процесс будет выглядеть следующим образом: 4 равно отрицательному значению 2x плюс y
\(4 = -2x + y\)
Чтобы изолировать переменную y, нам нужно избавиться от отрицательного члена 2x.
-2x. Для этого воспользуемся обратными операциями. Обратное отрицательному 2x равно положительному 2x. Таким образом, мы добавляем 2x к обеим частям, и мы получаем 2x плюс 4 равно y. Если мы перевернем наше уравнение, мы получим y равно 2x плюс 4.
\(Y = 2x + 4\)
Теперь линейное уравнение находится в форме пересечения наклона (y равно mx плюс b y=mx+b). Теперь это графически, потому что мы изолировали переменную y.
Теперь, когда мы рассмотрели линейные уравнения, мы можем погрузиться в процесс решения того, что мы называем системами линейных уравнений. Под «системой» мы подразумеваем более одного уравнения. Когда мы хотим решить систему уравнений, мы, по сути, ищем точку пересечения при построении уравнений. Мы решили систему, когда смогли найти точку пересечения линий. Например, решенная система линейных уравнений x минус 2y равна минусу 2 x-2y=-2 и 3x минус 2y равно 2 3x-2y=2 будет выглядеть так:
Оба уравнения изображены на графике, и линии пересекаются в точке (2,2).
Это означает, что упорядоченная пара (2,2) является нашим решением системы уравнений.
Как решать линейные уравнения
Для решения систем линейных уравнений используются три общие стратегии: построение графика, замена и исключение. Сначала остановимся на графическом методе. Этот метод состоит из трех основных этапов.
Шаг 1 состоит в том, чтобы манипулировать обоими уравнениями так, чтобы они были в форме пересечения наклона (y=mx+b).
Шаг 2 заключается в построении графиков обоих уравнений.
И Шаг 3 заключается в определении упорядоченной пары, где линии пересекаются.
Давайте подробнее рассмотрим эти три шага на примере.
Мы собираемся использовать систему y равно минус 3x минус 7 y=-3x-7 и y равно x плюс 9 y=x+9
Помните, чтобы решить эту систему, нам нужно вычислить где линии пересекаются, когда они графически.
Давайте попробуем все три шага вместе.
Шаг 1 состоит в том, чтобы манипулировать уравнениями так, чтобы они оба были в форме пересечения наклона. Для этого примера оба уравнения уже настроены в этой форме, поэтому мы готовы к шагу 2.
Шаг 2 состоит в построении графиков обоих уравнений. Давайте посмотрим на первое уравнение y равно минус 3x минус 7 y=-3x-7 . Значение -3 представляет собой наклон линии, а значение -7 представляет точку пересечения по оси Y. С помощью этих двух частей информации мы можем построить линию.
Теперь построим график второго уравнения на той же координатной сетке.
Теперь у нас есть графики обоих уравнений, так что мы готовы к Шагу 3 . Найдем упорядоченную пару в месте пересечения линий. Графический метод является удобной визуальной стратегией, потому что мы можем точно видеть, где пересекаются линии. Мы ясно видим, что линии пересекаются в точке (минус 4,5), поэтому решение этой системы линейных уравнений равно (минус 4,5) .
Давайте попробуем более сложный пример, где уравнения еще не даны нам в форме пересечения наклона. В этом примере мы будем использовать систему 3x минус y равно 4 3x-y=4 и 7x плюс 2y равно 18 7x+2y=18 .
Во-первых, нам нужно манипулировать обоими уравнениями так, чтобы они были в форме пересечения наклона (y равно mx плюс b). Начнем с первого:
Нам нужно изолировать переменную «y». Итак, сначала мы собираемся вычесть 3x с обеих сторон. Это дает нам отрицательное значение y, равное отрицательному значению 3x плюс 4. Прямо сейчас у нас есть «-y». Минус перед «y» — это, по сути, минус 1, умноженный на «y». Нам нужно избавиться от этой отрицательной 1, выполнив обратную операцию. Это означает, что нам нужно разделить обе части уравнения на минус 1. Это дает нам y равно (и когда мы делим на отрицательное число все уравнение, мы можем разделить каждую из частей числителя на минус 1). Таким образом, отрицательное значение 3x, деленное на отрицательное значение 1, дает нам 3x, а 4, деленное на отрицательное значение 1, дает отрицательное значение 4.
Итак, y равно 3x минус 4. Теперь «y» само по себе, а первое уравнение находится в форме пересечения наклона, поэтому оно графически
Теперь давайте изолируем переменную «y» во втором уравнении, чтобы мы могли построить обе линии вместе. Во-первых, мы собираемся вычесть 7x с обеих сторон. Это дает нам 2y равно минус 7x плюс 18, и мы собираемся разделить на 2 с обеих сторон. Это оставляет нас с y равным отрицательным семи половинкам x плюс 9. Мы также можем записать это так: y равно отрицательному 3,5x плюс 9.
На данный момент у нас есть два уравнения, которые оба находятся в форме пересечения наклона. Уравнение 1: y равно 3x минус 4, а уравнение 2: y равно минус 3,5x плюс 9..
Уравнение 1: y=3x-4
Уравнение 2: y=9-3,5x
Теперь нам просто нужно изобразить обе линии и определить, где они пересекаются. Вот как будет выглядеть наш график.
Система линейных уравнений решена, когда вы можете определить упорядоченную пару, где линии пересекаются.
Мы видим, что линии пересекаются по адресу (2,2) .
Если вы пытаетесь решить систему, а линии на графике оказываются параллельными и никогда не пересекаются, то система не имеет решений. Точно так же, если вы рисуете систему и линии полностью перекрывают друг друга, то система имеет бесконечные решения.
Графический метод часто является очень удобным способом решения систем. Однако иногда более эффективно решать системы с помощью метода замены или исключения. Эти два метода используют более алгебраический подход. Давайте сначала рассмотрим процесс использования метода замещения.
В этом примере мы будем использовать систему 3x плюс 5y равно 13 и 2x плюс y равно 4. 3x + 5y = 13 и 2x + y = 4 .
Второе уравнение легче решить для y, поэтому давайте решим для y, используя обратные операции и вычитая 2x из обеих частей. Итак, это дает нам y равно минус 2x плюс 4. Это шаг 1.
Шаг 2 заключается в том, что мы берем это значение y, которое является отрицательным 2x плюс 4, и подставляем его в y нашего другого уравнения (уравнение 1).
Это процесс замещения. Итак, у нас есть 3x плюс 5, умноженное на минус 2x плюс 4 равно 13.
Теперь шаг 3. Нахождение x. Вы будете использовать свойство дистрибутивности и обратные операции, чтобы найти x. Сначала распределите 5, умножив его на минус 2x и 4. Отсюда мы имеем 3x минус 10x, плюс 20, равно 13.
3x -10x +20 = 13.
Теперь объедините ваши «похожие термины». 3x минус 10x дает минус 7x плюс 20, равно 13. Теперь мы собираемся вычесть 20 с обеих сторон. Это дает нам отрицательное 7x равно отрицательному 7. Теперь мы разделим обе части на отрицательное 7 и получим x равное 1.
Мы на полпути! Теперь нам просто нужно использовать это значение x, чтобы найти y. Вот шаг 4. Мы знаем, что x равно 1, поэтому давайте подставим это вместо x в уравнение y равно отрицательному числу 2x плюс 4. y = -2x + 4.
Итак, у нас есть y равно отрицательному значению 2, умноженному на 1, плюс 4. , Теперь мы собираемся упростить. Итак, у равно минус 2 плюс 4, что равно 2.
Теперь мы видим, что у равно 2 . Таким образом, решение этой системы уравнений равно (1,2) .
Еще один способ решения систем уравнений — метод исключения. Для этого метода сначала нужно манипулировать уравнениями так, чтобы переменные были с одной стороны, а константы — с другой.
Давайте используем систему x равно y плюс 5 и 3x плюс 2y равно 5 x = y + 5 и 3x + 2y = 5 для этого уравнения.
Используя обратные операции, первое уравнение становится x минус y равно 5, а второе уравнение выглядит готовым к работе как есть. Теперь все переменные находятся с одной стороны, а константы — с другой. Цель метода исключения состоит в том, что когда вы складываете или вычитаете два уравнения, один из переменных членов будет полностью уравновешен, что даст нам гораздо более простое уравнение для решения. Например, 5x уравновешивается отрицательным 5x.
Давайте внимательно посмотрим на оба уравнения.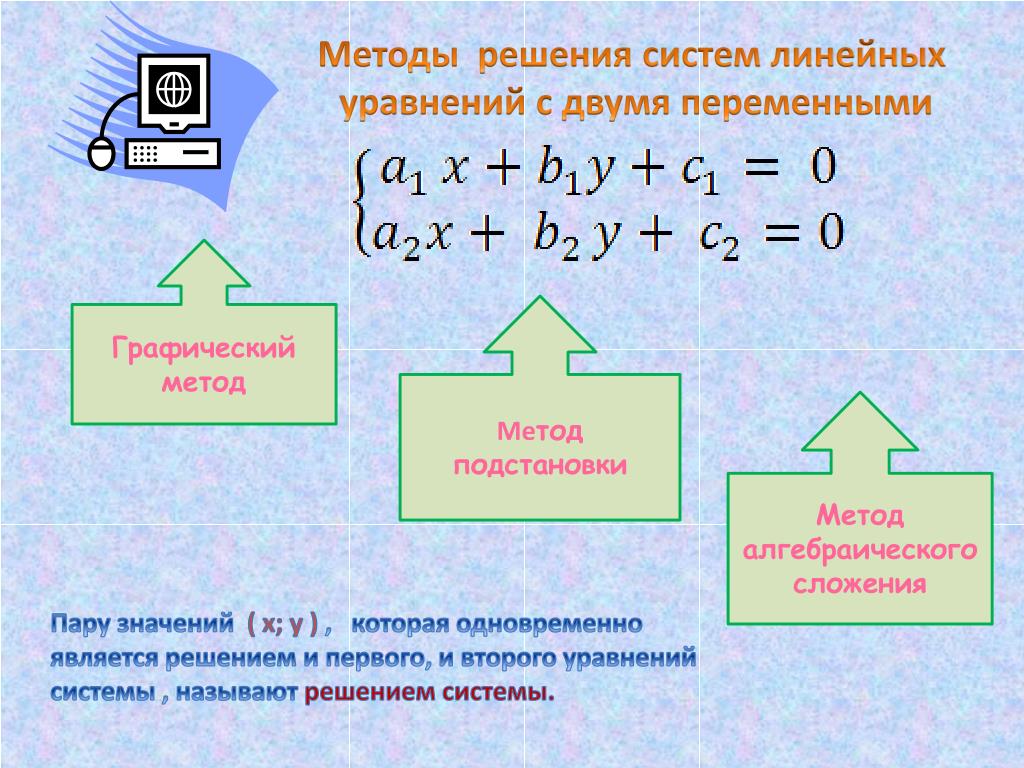
Помните, что мы собираемся выбирать, складывать или вычитать оба уравнения, чтобы исключить один из переменных членов. Исключение переменного члена просто означает наличие нулевого коэффициента.
Обратите внимание, что если мы умножим все части нашего первого уравнения на 2, отрицательный член y станет отрицательным 2y. Это полезно, потому что это отрицательное значение 2y уравновешивается переменным членом 2y в другом уравнении, а устранение переменных членов — наша цель.
Давайте попробуем. Мы умножим все части первого уравнения на 2. Это превратит это уравнение в 2x минус 2y равно 10.
Мы манипулировали уравнением таким образом, потому что теперь мы настроены на отрицательный член 2y и 2y, чтобы отменить каждый другое, когда два уравнения складываются вместе. Переменная будет исключена, и это оставит нам более простое уравнение для решения. Мы решили сложить два уравнения, а не вычесть их, потому что целью является исключение. Если мы добавим уравнения, члены сократятся.
Если бы мы вычли уравнения, у нас все равно остались бы отрицательные 4y. Итак, давайте напишем это уравнение здесь. 2x минус 2y равно 10, и мы собираемся сложить уравнения вместе. Когда 2y и отрицательное 2y сокращаются, у нас остается: 3x плюс 2x равно 5x, равно, 5 плюс 10 равно 15. Теперь нам нужно разделить обе части на 5, и мы получим x равно 3.
Теперь, когда мы знаем, что x равно 3, мы на полпути. Чтобы найти y, мы просто подставляем наше значение x в одно из наших уравнений и находим y.
X = 3 Итак, давайте подставим 3 в уравнение x минус y равно 5, вычтем 3 из обеих частей, получим отрицательное значение y равное 2 и разделим на отрицательное значение 1.
y равно отрицательному значению 2
Теперь у нас есть 3 – y = 5
Давайте воспользуемся обратными операциями, чтобы найти y.
Вычтите 3 из обеих частей, а затем разделите обе части на -1. Мы видим, что у = -2
Это означает, что решение системы равно (3, минус 2).
В этом примере мы решили добавить два уравнения, чтобы переменные члены 2y и отрицательное 2y сокращались.
Однако бывают случаи, когда вам нужно вместо этого вычесть два уравнения. * Вы бы предпочли вычесть два уравнения в ситуации, когда у вас есть два одинаковых переменных члена, например 3y и 3y.
Хорошо, прежде чем мы пойдем, давайте быстро повторим, что мы узнали:
Линейные уравнения описывают прямую линию на графике и обычно представляются в форме пересечения наклона, где y равно mx плюс b. Мы можем решать системы линейных уравнений, используя один из трех методов. При использовании графического метода вы сначала манипулируете обоими уравнениями, чтобы они были в форме пересечения наклона, затем рисуете оба уравнения и определяете упорядоченную пару, где линии пересекаются. Метод подстановки работает, беря одно из уравнений, решая одну из переменных, а затем подставляя решенную переменную в другое уравнение. При использовании метода исключения вы либо добавляете, либо вычитаете уравнения, чтобы исключить любую переменную из уравнений.
На этом обзоре все! Спасибо за просмотр и удачной учебы!
Вопрос №1:
Решите систему уравнений с помощью графика.
\(\begin{case}y=x+1\\y=-2x-8\end{case}\)
(3, -1)
(-3, -2)
(-2 , -3)
(3, 2)
Показать ответ
Ответ:
Правильный ответ (-3, -2).
Шаг 1: Убедитесь, что оба уравнения представлены в форме пересечения наклона. В этом случае оба уравнения уже имеют такой вид.
Шаг 2: Нарисуйте каждую линию.
Шаг 3: Найдите точку пересечения двух линий. В этом случае две линии пересекаются в точке (-3, -2).
Скрыть ответ
Вопрос №2:
Решите систему уравнений графически.
\(\begin{case}x+y=7\\-2x+y=1\end{case}\)
(-3, 4)
(2, 5)
(5, 2)
(-2, 5)
Показать ответ
Ответ:
Правильный ответ (2, 5).
Шаг 1: Убедитесь, что оба уравнения представлены в форме пересечения наклона.
Для этого начните с использования обратных операций, чтобы изолировать переменную y в обоих уравнениях. Для уравнения \(x+y=7\) вычтите x из обеих частей. В уравнении \(-2x+y=1\) прибавьте 2x к обеим частям. Это оставляет оба уравнения в форме пересечения наклона.
\(\begin{cases}y=-x+7\\y=2x+1\end{cases}\)
Шаг 2: Нарисуйте график каждой строки.
Шаг 3: Найдите точку пересечения двух линий. В этом случае две прямые пересекаются в точке (2, 5).
Скрыть ответ
Вопрос №3:
Решите систему уравнений графически.
\(\begin{case}2x+3y=1\\3x-y=7\end{case}\)
(3, 1)
(-1, -2)
(2, 2)
(2, -1)
Показать ответ
Ответ:
Правильный ответ (2, -1).
Шаг 1: Убедитесь, что оба уравнения представлены в форме пересечения наклона. Для этого начните с использования обратных операций, чтобы изолировать переменную y в обоих уравнениях.
Для уравнения \(2x+3y=1\) вычтите 2x с обеих сторон, а затем разделите обе части на 3. Для уравнения \(3x-y=7\) вычтите 3x с обеих сторон, а затем разделите обе части на -1. Это оставляет оба уравнения в форме пересечения наклона.
\(\begin{cases}y=\frac{-2}{3}x+\frac{1}{3}\\y=3x-7\end{cases}\)
Шаг 2. Нарисуйте график каждой строки.
Шаг 3: Найдите точку пересечения двух линий. В этом случае две прямые пересекаются в точке (2,-1).
Скрыть ответ
Вопрос №4:
Решите систему уравнений подстановкой.
\(\begin{case}2x+y=11\\7x-4y=-14\end{case}\)
(2, 6)
(4, 5)
(2, 7)
(3, 2)
Показать ответ
Ответ:
Правильный ответ (2, 7).
Шаг 1: Решите одно из уравнений для y . В этом случае решите первое уравнение. \(2x+y=11\) становится \(y=-2x+11\).
Шаг 2: Используя это только что решенное уравнение, подставьте значение y в значение y другого уравнения. Это процесс замещения.
\(7x-4(-2x+11)=-14\)
Шаг 3: Найдите x, используя обратные операции и свойство распределения. Это упрощается до \(7x+8x-44=-14\). Теперь объедините похожие термины, и результат будет \(15x-44=-14\). Отсюда прибавьте 44 к обеим сторонам, а затем разделите на 15. Остается \(x=2\).
Шаг 4: Подставьте значение x в одно из исходных уравнений. Переменная x равна 2, поэтому подставьте 2 в уравнение \(2x+y=11\). Теперь нужно решить \(2(2)+y=11\) и y . Вычтите 4 с обеих сторон и обратите внимание, что \(y=7\). \(x=2\) и \(y=7\), поэтому решением является точка (2, 7).
Скрыть Ответ
Вопрос №5:
Решите систему уравнений методом исключения.
\(\begin{case}x-4y=-18\\-x+3y=11\end{case}\)
(10, 7)
(10, 5)
(4, 18)
(3, 11)
Показать ответ
Ответ:
0 Правильный ответ (7,2).
Шаг 1: При использовании стратегии исключения ищите способ исключить член x или член y при сложении или вычитании двух уравнений. Обратите внимание на то, что x -термины сократятся ( x и – x ), если эти два уравнения будут добавлены.
Шаг 2: Сложите два уравнения, чтобы исключить x-термины.
Шаг 3: Найдите x. \(y=7\), поэтому подставьте 7 вместо y в уравнении \(-x+3y=11\). Это становится \(-x+3(7)=11\), что упрощается до \(-x+21=11\). Вычтите 21 из обеих сторон, а затем разделите на -1, чтобы изолировать переменную x. Это приводит к \(x=10\). Это означает, что решение (10, 7).
Скрыть ответ
Системы линейных уравнений и неравенств
Руководство по стимуляции > Системы линейных уравнений и неравенств w3.org/1999/xhtml» cellspacing=»0″> |
Большие идеи
Основные вопросы
Общие основные стандарты и показатели Анализ и решение линейных уравнений и пар одновременных линейных уравнений.
Создание уравнений, описывающих числа или отношения
Решить системы уравнений
Графически представлять и решать уравнения и неравенства
Стандарты для математической практики
Стандарты 3 Представление и анализ количественных взаимосвязей между зависимыми и независимыми переменными.
Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
Понимание связей между пропорциональными отношениями, линиями и линейными уравнениями.
Определение, оценка и сравнение функций.
Используйте функции для моделирования отношений между величинами.
Содержание
Навыки/стратегии Учащиеся смогут:
Key Terms/Vocabulary
Assessments
Задания/цели обучения
|
2 — Создание уравнений с двумя или более переменными для представления отношений между величинами; графические уравнения на осях координат с метками и шкалами.
11 — Объясните, почему координаты x точек пересечения графиков уравнений y = f(x) и y = g(x) являются решениями уравнения f(x) = g(x) ; находить решения приблизительно, например, используя технологии для построения графиков функций, составления таблиц значений или поиска последовательных приближений. Включите случаи, когда f(x) и/или g(x) являются линейными, полиномиальными, рациональными, абсолютными значениями, экспоненциальными и логарифмическими функциями.★
Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.