Решить 1 2 3: Решите 1,2,3 пожалуйста! — Школьные Знания.com

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.

Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто, как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1)  10 − 1 = 9

2)   9 + 2 = 11

3)  11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

---

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1)  3 + 5 = 8

2)   2 × 3 = 6

3)  8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

---

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием,  четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1)  5 − 3 = 2

2)  5 × 2 = 10

3)  2 : 2 = 1

4)  10 + 1 = 11

5)  11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

---

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1)  3250 − 2905 = 345

2)  345 :

 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1)  6 411 × 8 = 51 288

2)  51 288 − 40 799 = 10 489

3)  10 489 × 6 = 62 934

---

Пример 6.

Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

---

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

---

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Карта сайта

О центре Новости Института Наши достижения Наша команда Фотоальбом Вакансии Контакты офиса Магазин в Москве («Абрис») «Школа 2000. ..» учителям Технология ДМ Курс «Математика 1-9» Курс «Мир деятельности» Каллиграфия цифр Международный конкурс «Учу учиться» Положение о конкурсе Список конкурсных работ Правила оформления Взаимодействие с родителями Библиотека «Школа 2000. ..» родителям Важное о программе Детская Академия Петерсон Преимущества программы Детские сады и школы Шпаргалки для родителей Основные риски Курс «Мир деятельности» О надпредметном курсе и авторах Программа надпредметного курса для НШ и ОШ Письмо об использовании надпредметного курса «Мир деятельности» в основной школе Комплект для учителя Комплект для ученика Дополнительные материалы Консультации к урокам Отзывы о курсе Комплекты «Мир деятельности» Родительское собрание В кабинете психолога Библиотека для родителей Поучительные притчи Афоризмы об образовании «Решебник» к учебникам Родителям дошкольников Мы в соцсетях Учебники и методическая литература Новинки Концепция программы Дошкольная подготовка «Мир деятельности» Начальная школа Основная школа Электронные приложения Сценарии уроков на CD Курсы повышения квалификации Вебинары Выездные курсы Для работников дошкольного образования Учителям начальной школы Учителям основной школы Курсы для заведующих, ППС, методистов кафедр математического образования Стажировки Сводное расписание курсов Регистрация на курсы On-line Дистанционное обучение Отзывы о курсах Дистанционное обучение Нормативные документы, письма и программы Правоустанавливающие документы Актуальные документы ООП для школы Примерные рабочие программы по математике Курс «Мир деятельности» Государственный стандарт Рекомендованные учебники О функционировании Центра О присуждении премий Благодарственные письма ООП для детского сада Дошкольное образование

«Мир деятельности» Прошедшие мероприятия Конференции Курсы Семинары Вебинары Отзывы о курсах Текущие проекты Экспериментальная площадка Вопросы и ответы Библиотека Библиотека для учителей Из опыта работы Библиотека для родителей Контакты

Урок 27.

прибавление к числу по 1, 2, 3. вычитание из числа 1, 2, 3. решение задач: повторение — Математика — 1 класс

Математика, 1 класс

Урок 27. Прибавление к числу по 1, 2, 3. Вычитание из числа 1, 2, 3. Решение задач: повторение.

Перечень вопросов, рассматриваемых на уроке:

1. Сложение и вычитание вида  + 1,  — 1,  + 2,  — 2,  + 3,  — 3.
2. Решение задач.

Глоссарий по теме

Решить задачу – значит найти ее ответ.

Ключевые слова

Сложение, вычитание, задача.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. 2 ч. С.4 — 5

Мы повторим сложение и вычитание чисел 1, 2, 3. Сможем решать задачи.

Основное содержание урока

Ил.

Рассмотрите рисунок. На рисунке изображены яблоки на ветке. Сколько желтых яблок? Три желтых яблока. Сколько красных яблок? Два красных яблока. Составьте задачу на сложение. На ветке висело три желтых и два красных яблока. Сколько яблок висело на ветке?

Ил.

Запишем условие задачи в виде схемы. Как запишем ее решение с опорой на схему? К двум прибавить три получится пять. Как запишем ответ задачи? На ветке висело пять яблок.

Ил.

Рассмотрите рисунок. На рисунке изображены птицы. Сколько птиц сидит на земле? На земле сидит четыре птицы. Сколько птиц улетает? Одна птица улетает. Составьте задачу на вычитание. Сидело пять птиц. Одна улетела. Сколько птиц осталось?

Ил.

Запишем условие задачи в виде схемы. Как запишем ее решение с опорой на схему? Из пяти вычесть один получится четыре. Как запишем ответ задачи? Осталось четыре птицы.

Разбор тренировочных заданий

Подчеркните верное решение задачи.

На новогоднем празднике танцевали парами 5 мальчиков и столько же девочек. Сколько всего ребят танцевало?

А) 5 + 1 = 6

Б) 5 + 5 = 10

В) 10 — 5 = 5

Правильный ответ:

Б) 5 + 5 = 10

Подсказка: Обратите внимание на условие и вопрос.

Выберите верные высказывания.

А) 5 – это 4 и 1

Б) 5 – это 3 и 2

В) 5 – это 6 и 1

Правильный ответ:

А) 5 – это 4 и 1

Б) 5 – это 3 и 2

Подсказка: Вспомните состав числа 5.

6/2(2+1)= Как решается этот проклятый пример: denis_demakhin — LiveJournal

Уже давно я увлечен этим примером:

Делал по нему опросы

И сейчас попробую обосновать мою новую точку зрения, которая теперь выглядит так:

Дело в том, что между алгеброй и арифметикой есть разница в порядке действий:

Теперь понятно, почему инженерный калькулятор показывает ответ: 1.

Он не сломался. Он алгебраический.

Алгебраический калькулятор считает по правилам алгебры.

Осталось понять, алгебраический это пример или арифметический. От этого будет зависеть ответ.

Букв в примере нет, однако, в нем есть пропущенный знак умножения перед скобкой:

Случаи возможного пропуска знака умножения:

1. Между буквенными множителями;


2. Между числовым и буквенным множителем;


3. Между множителем и скобкой;


4. Между выражениями в скобках.

Тут подходит только правило №3. И тогда пропущенный знак умножения равносилен скобкам, то есть 2(2+1) = (2*(2+1)), следуя правилам из скана выше.

И получается, что если выражение (2+1) заменить на икс, то написание 6/2Х читается как «шесть, разделить на два икса».

Тогда ответ: 1.

Но почему тогда самая умная штука на Земле — Гугл-поисковик считает, что ответ 9?

Потому что и Гугл и смартфон считают по арифметическим правилам.

Но вот тут есть тонкий момент. Арифметические правила должны, по-правильному то, действовать при указании знака умножения. Так, как я написал здесь:

Тут уже нет оснований применять правила алгебры, в которых пропущенный знак умножения считается неразрывным. И ответ получается: 9.

Вывод:

Всё зависит от того, алгебра это или арифметика.

Еще интересные штуки:

Задачи, ломающие мозг (с ответами, спрятанными под спойлер)

Тренировка ума развивальщика предприятий

Подписывайся, мыслитель!

6/2(1+2)=? — Вопросы на DTF

Вы сидите тихим вечером, никого не трогаете, и тут прилетает вопрос:

16 721 просмотров

Казалось бы, ответ очевиден, но не спешите. Все зависит от того, кто спрашивает.

_____________________________________________________________________

Учительница алгебры: «6/2(1+2)=?»

В примере опущен оператор умножения, поскольку его не обязательно указывать перед скобками.

Полная запись будет выглядеть так:

Решаем слева-направо:

_____________________________________________________________________

Математик: «6/2(1+2)=?»

Отсутствие знака умножения несет смысл, это указывает на то, что ‘2(1+2)’ является отдельным выражением.

Полная запись будет выглядеть так:

Приоритет отдается скобкам, изнутри наружу.

_____________________________________________________________________

Учительница алгебры изменила задачу, додумав то, чего не было изначально. Она преобразовала выражение, и лишь затем правильно решила новое выражение.

«6/2(1+2)» не одно и то же, что «6/2*(1+2)»

Попробую объяснить.

_____________________________________________________________________

Выражение: «6/2(1+2)»

Давайте заменим скобки на переменную «a=1+2»

Выражение примет вид: «6/2a»

Что такое «2a»? Я пока не знаю. Но воспринимаю его как единое целое. Если хотите, это слово «2a».

Чтобы двигаться дальше, нужно вычислить значение переменной «a=1+2=3»

Затем я узнаю, что «2a=2*3=6»

Окончательно решаю уравнение: «6/6=1».

_____________________________________________________________________

Выражение:«6/2*(1+2)»

Заменим скобки на переменную «a=1+2»
Выражение примет вид: «6/2*a»

Я не знаю, что такое «a», но явно вижу, что «2» это отдельное число, которое пока не связано с переменной. Нам нужно будет провести операцию умножения в будущем, не обязательно делать это прямо сейчас. Деление и умножение имеют равный приоритет, значит выражение можно представить в виде «(6/2)*a».

Времени терять не будем, вычисляем «6/2=3»

Получаем выражение: «3*a»

Самое время узнать, что «a=1+2=3»

Решаем оставшееся: «3*3=9»

Ответ: «6/2*(1+2)»=9

_____________________________________________________________________

Какой ответ даст ваш калькулятор? 🙂

Вы такого не ожидали? Калькулятор не умеет читать мысли.

Если вы хотите знак умножения, то пишите его явно.

Компьютер, и большинство программ-калькуляторов, считают запись «6/2(1+2)» ошибкой.

Если одни явно исправляют формулу на «6/2*(1+2)», то другие делают это втайне от пользователя, выдавая правильный ответ 9, на измененное выражение.

Прежде чем давать ответ, убедитесь, что спрашивающий, под записью «6/2(1+2)», имеет в виду «6/2*(1+2)», а не «6/2(1+2)» 🙂

Задачи по Python 3 для начинающих от Tproger и GeekBrains

Вместе с факультетом Python-разработки GeekUniversity собрали для вас несколько простых задач по Python для обучения и тренировки. Их можно решать в любом порядке.

Обратите внимание, что у любой задачи по программированию может быть несколько способов решения. Чтобы посмотреть добавленный нами вариант решения, кликните по соответствующей кнопке. Все приведённые варианты написаны на Python 3.

***

Задача 1

Есть список a = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89].

Выведите все элементы, которые меньше 5.

Самый простой вариант, который первым приходит на ум — использовать цикл for:

for elem in a:
    if elem < 5:
        print(elem)

Также можно воспользоваться функцией filter, которая фильтрует элементы согласно заданному условию:

print(list(filter(lambda elem: elem < 5, a)))

И, вероятно, наиболее предпочтительный вариант решения этой задачи — списковое включение:

print([elem for elem in a if elem < 5])

Задача 2

Даны списки:

a = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89];

b = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13].

Нужно вернуть список, который состоит из элементов, общих для этих двух списков.

Можем воспользоваться функцией filter:

result = list(filter(lambda elem: elem in b, a))

Или списковым включением:

result = [elem for elem in a if elem in b]

А можно привести оба списка к множествам и найти их пересечение:

result = list(set(a) & set(b))

Однако в таком случае каждый элемент встретится в результирующем списке лишь один раз, т.к. множество поддерживает уникальность входящих в него элементов. Первые два решения (с фильтрацией) оставят все дубли на своих местах.

Задача 3

Отсортируйте словарь по значению в порядке возрастания и убывания.

Импортируем нужный модуль и объявляем словарь:

import operator 
d = {1: 2, 3: 4, 4: 3, 2: 1, 0: 0}

Сортируем в порядке возрастания:

result = dict(sorted(d.items(), key=operator. itemgetter(1)))

И в порядке убывания:

result = dict(sorted(d.items(), key=operator.itemgetter(1), reverse=True))

Задача 4

Напишите программу для слияния нескольких словарей в один.

Допустим, вот наши словари:

dict_a = {1:10, 2:20}
dict_b = {3:30, 4:40}
dict_c = {5:50, 6:60}

Объединить их можно вот так:

result = {}
for d in (dict_a, dict_b, dict_c):
    result.update(d)

А можно с помощью «звёздочного» синтаксиса:

result = {**dict_a, **dict_b, **dict_c}

О звёздочном синтаксисе можно прочитать в нашей статье.

Задача 5

Найдите три ключа с самыми высокими значениями в словаре my_dict = {'a':500, 'b':5874, 'c': 560,'d':400, 'e':5874, 'f': 20}.

Можно воспользоваться функцией sorted:

result = sorted(my_dict, key=my_dict.get, reverse=True)[:3]

Аналогичный результат можно получить с помощью функции nlargest из модуля heapq:

from heapq import nlargest
result = nlargest(3, my_dict, key=my_dict. get)

Читайте также: Всё о сортировке на Python

Задача 6

Напишите код, который переводит целое число в строку, при том что его можно применить в любой системе счисления.

Второй аргумент функции int отвечает за указание основания системы счисления:

print(int('ABC', 16))

Задача 7

Нужно вывести первые n строк треугольника Паскаля. В этом треугольнике на вершине и по бокам стоят единицы, а каждое число внутри равно сумме двух расположенных над ним чисел.

def pascal_triangle(n):
   row = [1]
   y = [0]
   for x in range(max(n, 0)):
      print(row)
      row = [left + right for left, right in zip(row + y, y + row)]
   
pascal_triangle(6) 

Задача 8

Напишите проверку на то, является ли строка палиндромом. Палиндром — это слово или фраза, которые одинаково читаются слева направо и справа налево.

Тут всё просто, достаточно сравнить строку с её обратной версией, для чего можно использовать встроенную функцию reversed:

def is_palindrome(string):
    return string == ''.join(reversed(string))

print(is_palindrome('abba'))

Того же эффекта можно добиться с помощью срезов:

def is_palindrome(string):
    return string == string[::-1]

print(is_palindrome('abba'))

Задача 9

Сделайте так, чтобы число секунд отображалось в виде дни:часы:минуты:секунды.

def convert(seconds):
    days = seconds // (24 * 3600)
    seconds %= 24 * 3600
    hours = seconds // 3600
    seconds %= 3600
    minutes = seconds // 60
    seconds %= 60
    print(f'{days}:{hours}:{minutes}:{seconds}')

convert(1234565)

Задача 10

Вы принимаете от пользователя последовательность чисел, разделённых запятой. Составьте список и кортеж с этими числами.

values = input('Введите числа через запятую: ')
ints_as_strings = values.split(',')
ints = map(int, ints_as_strings)
lst = list(ints)
tup = tuple(lst)
print('Список:', lst)
print('Кортеж:', tup)

Задача 11

Выведите первый и последний элемент списка.

lst = [1, 2, 3, 4, 5]
print(f'Первый: {lst[0]}; последний: {lst[-1]}')

Задача 12

Напишите программу, которая принимает имя файла и выводит его расширение. Если расширение у файла определить невозможно, выбросите исключение.

def get_extension(filename):
    filename_parts = filename.split('.')
    if len(filename_parts) < 2:  # filename has no dots
        raise ValueError('the file has no extension')
    first, *middle, last = filename_parts
    if not last or not first and not middle:
        # example filenames: . filename, filename., file.name.
        raise ValueError('the file has no extension')
    return filename_parts[-1]

print(get_extension('abc.py'))
print(get_extension('abc'))  # raises ValueError
print(get_extension('.abc'))   # raises ValueError
print(get_extension('.abc.def.'))   # raises ValueError

Задача 13

При заданном целом числе n посчитайте n + nn + nnn.

def solve(n):
    n1 = n
    n2 = int(str(n) * 2)
    n3 = int(str(n) * 3)
    print(n1 + n2 + n3)

solve(5)

Задача 14

Напишите программу, которая выводит чётные числа из заданного списка и останавливается, если встречает число 237.

numbers = [    
    386, 462, 47, 418, 907, 344, 236, 375, 823, 566, 597, 978, 328, 615, 953, 345, 
    399, 162, 758, 219, 918, 237, 412, 566, 826, 248, 866, 950, 626, 949, 687, 217, 
]

for x in numbers:
    if x == 237:
        break
    elif x % 2 == 0:
        print(x)

Задача 15

Напишите программу, которая принимает два списка и выводит все элементы первого, которых нет во втором.

set_1 = set(['White', 'Black', 'Red'])
set_2 = set(['Red', 'Green'])

print(set_1 - set_2)

Задача 16

Выведите список файлов в указанной директории.

from os import listdir
from os.path import isfile, join
files = [f for f in listdir('/home') if isfile(join('/home', f))]
print(files)

Задача 17

Сложите цифры целого числа.

def sum_digits(num):
    digits = [int(d) for d in str(num)]
    return sum(digits)

print(sum_digits(5245))

Задача 18

Посчитайте, сколько раз символ встречается в строке.

string = 'Python Software Foundation'
string.count('o')

Задача 19

Поменяйте значения переменных местами.

Можно написать монструозную конструкцию в стиле языка C:

x = 5
y = 10
temp = x
x = y
y = temp

Но в Python есть более удобный способ для решения этой задачи:

x = 5
y = 10
x, y = y, x

Задача 20

С помощью анонимной функции извлеките из списка числа, делимые на 15.

nums = [45, 55, 60, 37, 100, 105, 220]
result = list(filter(lambda x: not x % 15, nums))

Задача 21

Нужно проверить, все ли числа в последовательности уникальны.

def all_unique(numbers):
    return len(numbers) == len(set(numbers))

Задача 22

Напишите программу, которая принимает текст и выводит два слова: наиболее часто встречающееся и самое длинное.

import collections

text = 'lorem ipsum dolor sit amet amet amet'
words = text.split()
counter = collections.Counter(words)
most_common, occurrences = counter.most_common()[0]

longest = max(words, key=len)

print(most_common, longest)

***

Хотите вырасти от новичка до профессионала? Факультет Python-разработки GeekUniversity даёт год опыта для вашего резюме. Обучайтесь на практических заданиях, по-настоящему освойте Python и станьте ближе к профессии мечты.

Узнать больше

Решение пропорций | Математика

Рассмотрим решение пропорций на конкретных примерах. 

Решить уравнения с пропорцией:

 1)  25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:

   

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

   

Ответ: 45.

   

Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:

   

   

   

Ответ: 13,5.

При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.

   

Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:

   

В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100,  мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10: 

   

Сокращаем 24 и 6 на 6, 10 и 45 — на 5:

   

Еще раз сокращаем 4 и 2 на 2:

   

   

Ответ: 18.

Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.

   

Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:

   

Смешанные числа переводим в неправильные дроби:

   

   

   

Ответ: 28.

При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.

   

Произведение крайних членов пропорции равно произведению средних членов:

   

Здесь удобно упростить уравнение, разделив обе части на 5:

   

   

   

   

   

   

Ответ: 10,5.

   

Произведение крайних членов пропорции равно произведению ее средних членов:

   

Для упрощения вычислений удобно умножить каждую часть уравнения на 10:

   

   

   

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

   

Ответ: 1,12.

Калькулятор дробей

Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.

Правила для выражений с дробями:

Дроби — используйте косую черту «/» между числителем и знаменателем, т.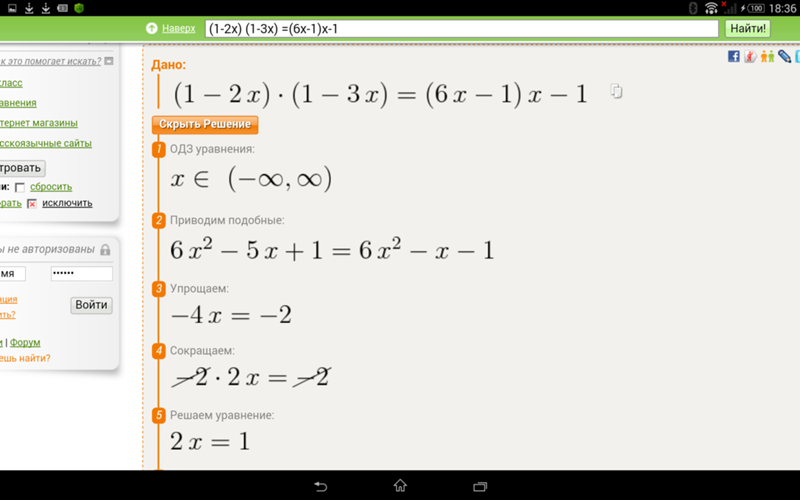 е.е., для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).

Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .

Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .

Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей i. 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3

Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.

Дроби в задачах со словами:

следующие математические задачи »

Калькулятор дробей

Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.

Правила для выражений с дробями:

Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).

Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .

Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .

Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.

Дроби в задачах со словами:

следующие математические задачи »

Как найти 1/2 из 2/3 — Видео и стенограмма урока

Проверка вашей работы

Если мы хотим убедиться, что наши вычисления верны, мы можем проверить нашу работу, используя тот факт, что умножение и деление противоположны друг другу. В некотором смысле они уничтожают друг друга. Например, если мы разделим 15 на 5, чтобы получить 3, мы можем отменить операцию, умножив 3 на 5, чтобы получить 15.В целом, следующие два факта позволяют нам проверить нашу работу в обоих методах решения.

1. Если a * b = c и a и b не равны 0, то c / a = b и c / b = a
2. Если r / s = t , то r = ts

Если мы решим найти 1/2 от 2/3 путем умножения 2/3 на 1/2, мы получим 1/2 * 2/3 = 1/3.Мы можем использовать первый факт, чтобы проверить это. Поскольку 1/2 * 2/3 = 1/3, должно быть так, что 1/3, деленная на 2/3, дает 1/2, а 1/3, деленная на 1/2, дает 2/3. Чтобы разделить дроби , мы умножаем числитель на обратную величину знаменателя, где обратная величина числа просто меняет местами числитель и знаменатель числа.

Если мы решим найти 1/2 из 2/3 путем деления 2/3 на 2, мы получим (2/3) / 2 = 1/3. Чтобы проверить наше решение, мы можем использовать второй факт. Поскольку (2/3) / 2 = 1/3, должно быть, что 1/3 * 2 = 2/3.

Конечно, как и ожидалось, это подтверждается.

Реальные приложения

Давайте рассмотрим реальное приложение задачи «найти 1/2 из 2/3». Предположим, вы готовите овсяное печенье. По вашему рецепту получается 36 печенек, но вам не нужно так много. Итак, вы решили уменьшить количество печенья, уменьшив вдвое все ингредиенты в рецепте.Рецепт требует 2/3 стакана сахара. поэтому нам просто нужно умножить 2/3 на 1/2 или разделить 2/3 на 2. В любом случае мы знаем, что 1/2 от 2/3 равно 1/3. Следовательно, для рецепта требуется 1/3 стакана сахара.

Рассмотрим другое приложение. Представьте, что вы решили заняться бегом. В парке возле вашего дома есть петля длиной 2/3 мили. Вы делаете половину пути по петле и хотите знать, как далеко вы прошли, или что составляет 1/2 от 2/3. Опять же, мы знаем, что ответ — 1/3. Это говорит нам о том, что вы пробежали 1/3 мили.Отличная работа!

Нахождение 1/2 числа — математическая задача, с которой мы часто сталкиваемся в повседневной жизни. Изучив шаги, необходимые для нахождения 1/2 из 2/3, как мы сделали в этом уроке, вы теперь знакомы с процессом и можете распространить его на другие числа.

дробей: умножение и деление дробей

Урок 4: Умножение и деление дробей

/ ru / fractions / сложение-и-вычитание-дроби / content /

Умножение дробей

Дробь — это часть целого .На последнем уроке вы узнали, как складывать и вычитать дроби. Но это не единственная математика, которую вы можете выполнять с дробями. Бывают случаи, когда будет полезно умножить и дроби.

Щелкните слайд-шоу, чтобы узнать, как написать задачу умножения с дробями.

Попробуй!

Попробуйте настроить задачу умножения ниже. Пока не беспокойтесь о ее решении!

Рецепт требует 2/3 стакана молока. Вы хотите разрезать рецепт пополам.

Примечание : Хотя наш пример говорит, что правильный ответ — 2/3 x 1/2, помните, что порядок умножения не имеет значения. 1/2 x 2/3 тоже будет правильным.

Решение задач умножения с дробями

Теперь, когда мы знаем, как ставить задачи умножения с дробями, давайте попрактикуемся в решении нескольких. Если вы чувствуете себя комфортно, умножая целые числа, вы готовы умножать дроби.

Щелкните слайд-шоу, чтобы узнать, как умножить две дроби.

Попробуй!

Попробуйте решить приведенные ниже задачи умножения.

Умножение дроби на целое число

Умножение дроби и целого числа аналогично умножению двух дробей. Есть всего один дополнительный шаг: прежде чем вы сможете умножить, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать.

Щелкните слайд-шоу, чтобы узнать, как умножить дробь на целое число.

• Умножим 2 раза на 1/3.Помните, это просто еще один способ спросить: «Что такое 1/3 из 2?»

• Прежде чем мы начнем, мы должны убедиться, что эти числа готовы к умножению.

• Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 как дробь.

• Как вы узнали из «Введение в дроби», мы также можем записать 2 как 2/1, потому что 2 можно дважды разделить на 1.

• Теперь мы готовы к умножению!

• Сначала умножим числители : на 2 и 1.

• 2 умножить на 1 равно 2. Мы выровняем 2 вместе с числителями.

• Затем мы умножим знаменателя: 1 и 3.

• 1 умножить на 3 равно 3. Совместим 3 со знаменателями.

• Итак, 2/1, умноженное на 1/3, равно 2/3. Мы также можем сказать, что 1/3 от 2 — это 2/3.

• Давайте попробуем другой пример: 4 раза по 1/5.

• Нам нужно будет записать 4 в виде дроби, прежде чем мы начнем.

• Мы перепишем 4 как 4/1. Теперь мы готовы к размножению.

• Сначала мы умножим числители: 4 и 1.

• 4 раза 1 равно 4, поэтому числитель нашего ответа будет 4.

• Затем мы умножим знаменатели: 1 и 5.

• 1 умножить на 5 равно 5, поэтому 5 является знаменателем нашего ответа.

• Итак, 4/1, умноженное на 1/5, равно 4/5.

Попробуй!

Попробуйте решить приведенные ниже задачи умножения.

Разделение на дроби

За последние несколько страниц вы узнали, как умножить дроби. Вы, наверное, догадались, что можно разделить и на дроби. Вы делите дроби, чтобы увидеть, сколько частей чего-то приходится на чего-то другого. Например, если вы хотите узнать, сколько четвертей дюйма в четырех дюймах, вы можете разделить 4 на 1/4.

Попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваша мерная чашка вмещает только 1/3, или 1/3 стакана. Сколько третей стакана нужно добавить?

Нам нужно узнать, сколько третей чашки в трех чашках. Другими словами, нам нужно разделить три на одну треть.

Задачу запишем так:

3 ÷ 1/3

Попробуй!

Попробуйте поставить эти задачи деления на дроби. Пока не беспокойтесь о их решении!

Рецепт требует 3/4 стакана воды. У вас есть только 1/8 мерного стакана.

Решение задач деления на дроби

Теперь, когда мы знаем, как писать задачи деления, давайте попрактикуемся в решении нескольких. Деление дробей во многом похоже на умножение. Требуется всего лишь один дополнительный шаг. Если вы можете умножать дроби, вы можете и их делить!

Щелкните слайд-шоу, чтобы узнать, как разделить целое число на дробь.

• Разделим 3 на 1/3. Помните, это просто еще один способ спросить: «Сколько третей в 3?»

• В нашем уроке о делении вы научились писать знак деления следующим образом (/).

• При делении дробей полезно использовать другой символ для деления (÷), чтобы не ошибочно принять его за дробь.

• Как и при умножении, мы начнем с поиска любых целых чисел в нашей задаче. Там один: 3.

• Помните, 3 — это то же самое, что и 3/1.

• Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.

• Мы заменим числителем и знаменателем дроби, которую мы делим на на: 1/3 в этом примере.

• Таким образом, 1/3 становится 3/1.

• Это называется нахождением обратного или мультипликативного , обратного , дроби.

• Поскольку мы меняем исходную дробь, мы также изменим знак деления (÷) на знак умножения знак (x).

• Это потому, что умножение — это , обратное делению.

• Теперь мы можем рассматривать это как обычную задачу умножения.

• Сначала мы умножим числители: 3 и 3.

• 3 раза 3 равно 9, поэтому мы напишем это рядом с числителями.

• Затем мы умножим знаменатели: 1 и 1.

• 1 умножить на 1 равно 1, поэтому мы запишем 1 рядом со знаменателем.
  

• Как видите, 3/1 x 1/3 = 9/1.

• Помните, любая дробь больше 1 также может быть выражена как целое число .Итак, 9/1 = 9.

• 3 ÷ 1/3 = 9. Другими словами, в 3.

• .

• Давайте попробуем другой пример: 5 разделить на 4/7.

• Как всегда, мы перепишем любые целые числа, так что 5 станет 5/1.

• Затем мы найдем , обратное 4/7. Это дробь, на которую мы делим.

• Для этого мы заменим числителем и знаменателем , так что 4/7 станет 7/4.

• Затем мы изменим знак деления (÷) на знак умножения знак (x).

• Теперь мы можем умножать как обычно. Сначала мы умножим числители: 5 и 7.

• 5 умножим на 7 равно 35, так что запишем это рядом с числителями.

• Затем мы умножим знаменатели: 1 и 4.

• 1 умножить на 4 равно 4, поэтому мы запишем это рядом со знаменателями.
  

• Итак, 5/1 x 4/7 = 35/4.
  

• Как вы узнали ранее, мы могли преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.

• 35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4.
  

Попробуй!

Попробуйте решить эти проблемы с разделением. Не беспокойтесь сейчас о сокращении ответа .

На две дроби

Мы только что научились делить целое число на дробь . Вы можете использовать тот же метод, чтобы разделить на две дроби .

Щелкните слайд-шоу, чтобы узнать, как разделить на две дроби.

• Попробуем задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.
  

• Сначала мы найдем , обратное дроби, которую мы делим на: 3/4.

• Для этого мы заменим числителем и знаменателем.Таким образом, 3/4 становится 4/3.

• Затем мы изменим знак деления (÷) на знак умножения знак (x).

• Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.

• Затем мы умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами.
  

• Итак, 2/3 x 4/3 = 8/9.
  

• Мы также можем записать это как 2/3 ÷ 3/4 = 8/9.
  

• Давайте попробуем другой пример: 4/7 разделить на 2/9.

• Целых чисел нет, поэтому мы найдем , обратное дроби, на которую мы делим. Это 2/9.

• Для этого мы заменим числителем и знаменателем. Таким образом, 2/9 становится 9/2.

• Теперь мы изменим знак деления (÷) на знак умножения знак (x) и умножим как обычно.

• Сначала умножим числители. 4 x 9 = 36.

• Затем мы умножим знаменатели. 7 x 2 = 14.

• Итак, 4/7 x 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.

• Итак, 4/7 ÷ 2/9 = 2 8/14.

Попробуй!

Попробуйте решить эти проблемы с разделением. Не беспокойтесь сейчас о сокращении ответа .

Умножение и деление смешанных чисел

Как бы вы решили такую ​​проблему?

Как вы узнали на предыдущем уроке, всякий раз, когда вы решаете задачу со смешанным числом , вам нужно сначала преобразовать его в неправильную дробь . Затем вы можете как обычно умножать или делить.

Использование отмены для упрощения задач

Иногда вам может понадобиться решить такие проблемы:

Обе эти дроби включают больших числа . Эти дроби можно умножать так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить себе 21/50 или двадцать одна пятидесятая , ?

21/50 x 25/14 = 525/700

Даже ответ кажется сложным.Это 525/700, или пятьсот двадцать пять семисотых . Какой полный рот!

Если вам не нравится работать с большими числами, вы можете упростить такую ​​задачу, используя метод под названием отмена . Когда вы отменяете дроби в задаче, вы сокращаете их обеих одновременно.

Поначалу отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз посмотрим на только что рассмотренный пример.

Шаг 1

Сначала посмотрите на числитель первой дроби и знаменатель второй. Мы хотим увидеть, можно ли разделить на на одно и то же число.

В нашем примере 21 и 14 можно разделить на 7.

Шаг 2

Затем мы разделим 21 и 14 на 7. Сначала разделим наше верхнее число слева: 21.

21 ÷ 7 = 3

Затем разделим нижнее число справа: 14.

14 ÷ 7 = 2

Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, запишем 3 вместо 21. 14 ÷ 7 равно 2, поэтому напишем 2 вместо 14. Мы можем зачеркнуть или отменить , числа, с которых мы начали.

Наша задача теперь выглядит намного проще, не так ли?

Шаг 3

Давайте посмотрим на другие числа дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй дроби.Можно ли их разделить на на одно и то же число?

Обратите внимание, что их можно разделить на 25! Вы также могли заметить, что их можно разделить на 5. Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце.

Шаг 4

Затем мы отменим , как мы это делали на шаге 2.
Мы разделим наше нижнее число слева: 50.

50 ÷ 25 = 2

Затем разделим верхнее число справа: 25.

25 ÷ 25 = 1

Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили.

Шаг 5

Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножаем числители:

3 х 1 = 3

Затем умножьте знаменатели:

2 х 2 = 4

Итак, 3/2 x 1/2 = 3/4, или три четверти .

Шаг 6

Наконец, давайте еще раз проверим нашу работу. 525/700 был бы нашим ответом, если бы мы решили проблему без отмены. Если мы разделим 525 и 700 на 175, мы увидим, что 525/700 равно 3/4.

Можно также сказать, что мы уменьшаем 525/700 до 3/4. Помните, что отмена — это еще один способ уменьшить дробь перед решением проблемы. Вы получите один и тот же ответ, независимо от того, когда вы их уменьшите.

/ ru / фракции / преобразование-десятичные-дроби-и-дроби / содержание /

Решите линейные уравнения с одним неизвестным x / 2-3 = 1 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

x / 2- 3- (1) = 0

Пошаговое решение:

Шаг 1:

 x
 Упростить -
            2
 

Уравнение в конце шага 1:

 x
  (- - 3) - 1 = 0
   2
 

Шаг 2:

Переписывание целого как эквивалентной дроби:

2.1 Вычитание целого из дроби

Перепишем целое как дробь, используя 2 в качестве знаменателя:

 3 3 • 2
    3 = - = —————
         1 2
 

Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое

Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель

  
 Сложение дробей, имеющих общий знаменатель: 
  
 
 2. 2 Сложение двух эквивалентных дробей 
 Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель 
 
 Объедините числители, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьших членов, если это возможно: 
 
 x - (3 • 2) х - 6
 знак равно
      2 2
 
 Уравнение в конце шага 2: 
 (x - 6)
  ——————— - 1 = 0
     2
 
 Шаг 3: 
 
 Переписывание целого как эквивалентной дроби: 
  
 
 3.1 Вычитание целого из дроби 
 
 Перепишем целое как дробь, используя 2 в качестве знаменателя: 
 
 1 1 • 2
    1 = - = —————
         1 2
 
 Сложение дробей с общим знаменателем: 
 
 3.2 Сложение двух эквивалентных дробей 
 
 
 (x-6) - (2) x - 8
 знак равно
      2 2
 
 Уравнение в конце шага 3: 
 x - 8
  ————— = 0
    2
 
 Шаг 4: 
 
 Когда дробь равна нулю: 
  
 4.1 Когда дробь равна нулю ... 
 Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должен быть равен нулю.
 Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
 Вот как:
 x-8
  ——— • 2 = 0 • 2
   2
 
 Теперь, с левой стороны, 2 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю.
 Уравнение теперь принимает форму: 
 x-8 = 0
 
 Решение уравнения с одной переменной: 
 
 4.2 Решите: x-8 = 0
 Добавьте 8 к обеим сторонам уравнения: 
 x = 8 
 Было найдено одно решение: 
 x = 8
 Решение задач умножением и делением дробей и смешанных чисел 
 Слово дроби Проблемы с интерактивными упражнениями 
 Пример 1. Если для изготовления платья требуется 5/6 ярдов ткани, то сколько ярдов потребуется для изготовления 8 платьев?
 Анализ: Чтобы решить эту проблему, мы преобразуем целое число в неправильную дробь.Затем мы умножим две дроби.
 Решение:
 Ответ: Для изготовления 8 платьев потребуется 6 и 2/3 ярда ткани.
 Пример 2: У Рене была коробка кексов, половину которой она отдала своему другу Хуану. Хуан отдал 3/4 своей доли своей подруге Елене. Какая дробная часть оригинальной коробки кексов досталась Елене?
 Анализ: Чтобы решить эту проблему, мы умножим эти две дроби.
 Решение:
 Ответ: Елене досталось 3/8 оригинальной коробки кексов.
 Пример 3: Класс математики Нины имеет длину 6 и 4/5 метра и ширину 1 и 3/8 метра. Какая площадь классной комнаты?
 Анализ: Чтобы решить эту проблему, мы умножим эти смешанные числа. Но сначала мы должны преобразовать каждое смешанное число в неправильную дробь.
 Решение:
 Ответ: Площадь аудитории 9 и 7/20 квадратных метров.
 Пример 4. Плитка шоколада имеет длину 3/4 дюйма. Если он разделен на части длиной 3/8 дюйма, то сколько это частей?
 Анализ: Чтобы решить эту задачу, мы разделим первую дробь на вторую.
 Решение:
 Ответ: 2 шт.
 Пример 5. У электрика есть кусок провода длиной 4 и 3/8 сантиметра. Она делит проволоку на кусочки длиной 1 и 2/3 сантиметра. Сколько у нее штук?
 Анализ: Чтобы решить эту проблему, мы разделим первое смешанное число на второе.
 Решение:
 Ответ: Электрик имеет 2 и 5/8 куска провода.
 Пример 6: На складе 1 и 3/10 метров ленты. Если они разделят ленту на куски длиной 5/8 метров, то сколько кусков у них получится?
 Анализ: Чтобы решить эту проблему, мы разделим первое смешанное число на второе. Сначала мы преобразуем каждое смешанное число в неправильную дробь.
 Решение:
 Ответ: На складе будет 2 и 2/25 кусков ленты.
 Резюме: В этом уроке мы узнали, как решать задачи со словами, связанные с умножением и делением дробей и смешанных чисел.
 Упражнения 
 Указания: вычтите смешанные числа в каждом упражнении ниже.  Обязательно упростите свой результат, если необходимо.  Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
  Примечание. Чтобы написать смешанное число четыре и две трети, введите в форму 4, пробел и 2/3.
  1. 
  Одна партия печенья содержит 1 и 3/4 стакана растопленного шоколада. Сколько чашек растопленного шоколада нужно для изготовления 8 партий печенья?  
  2. 
  Тодд выпил 5/8 банки сока объемом 24 унции. Лайла выпила на треть меньше сока, чем Тодд. Сколько унций выпила Лила?  
  3. 
  Коврик прямоугольной формы имеет длину 3 и 2/3 фута и ширину 2 и 3/4 фута. Какова площадь коврика?  
  4. 
  У Джанет 5 и 3/4 сантиметра лакричника. Она делит лакрицу на кусочки длиной 1 и 7/8 сантиметра. Сколько кусочков солодки у нее будет?  
  5. 
  Кусок дерева длиной 15 футов.Сколько 3/4 фута можно вырезать из него?  
 Что такое 1 2/3 в виде десятичной дроби? (Преобразовать 1 2/3 в десятичную форму) 
 При изучении дробей очень часто возникает желание узнать, как преобразовать смешанную дробь, например 1 2/3, в десятичную. В этом пошаговом руководстве мы покажем вам, как легко превратить любую дробь в десятичную. Давайте взглянем!
 Прежде чем мы начнем преобразование дроби в десятичную, давайте быстро рассмотрим основы дроби.Помните, что числитель — это число над дробной чертой, а знаменатель — это число под дробной чертой. Мы будем использовать это позже в руководстве.
 Когда мы используем смешанные дроби, у нас есть целое число (в данном случае 1) и дробная часть (2/3). Итак, что мы можем сделать здесь, чтобы преобразовать смешанную дробь в десятичную, это сначала преобразовать ее в неправильную дробь (где числитель больше знаменателя), а затем оттуда преобразовать неправильную дробь в десятичную /
 Шаг 1. Умножьте целое число на знаменатель 
 .
 1 х 3 = 3
 Шаг 2: Добавьте результат шага 1 в числитель 
 3 + 2 = 5
 Шаг 3. Разделите результат шага 2 на знаменатель 
 .
 5 ÷ 3 = 1. 6666666666667
  Итак, ответ состоит в том, что 1 2/3 в виде десятичной дроби составляет 1,6666666666667. 
 И это все, что нужно для преобразования 1 2/3 в десятичную дробь. Мы преобразовываем его в неправильную дробь, которая в данном случае равна 5/3, а затем делим новый числитель (5) на знаменатель, чтобы получить ответ.
 Если вы хотите попрактиковаться, возьмите ручку, блокнот и калькулятор и попробуйте самостоятельно преобразовать несколько смешанных дробей в десятичные.
 Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичную дробь, и помогло понять, насколько это просто на самом деле. Теперь вы можете переходить и переводить смешанные дроби в десятичные, сколько пожелает ваше маленькое сердце!
 Калькулятор смешанных дробей в десятичные 
 Смешанная дробь в виде десятичной дроби 
 Введите целое число, числитель и знаменатель
 Вычисление от случайной смешанной дроби к десятичной дроби 
 .
No related posts.