Двойной интеграл в прямоугольных координатах. Вопросы
Двойной интеграл в прямоугольных координатах. Вопросы
Даны несколько двойных интегралов. Требуется выяснить, какой именно способ представления двойного интеграла в виде повторного предпочтительнее с вычислительной точки зрения, и вычислить данные двойные интегралы.
Задачи такого рода решаются в следующей последовательности:
- рисуем картинку (при вычислении двойных интегралов в прямоугольных координатах без картинки никак),
- решаем, как именно мы будем представлять данный двойной интеграл в виде повторного интеграла (при вычислении двойных интегралов в прямоугольных координатах область интегрирования, как правило, оказывается правильной в направлении обеих осей, и, таким образом, есть два пути решения),
- расставляем пределы интегрирования,

Таким образом, задача на вычисление двойного интеграла в прямоугольных координатах — это, по сути, задача на вычисление повторного интеграла.
В случае необходимости пересмотрите тему «Двойной интеграл в прямоугольных координатах» еще раз. Попробуйте самостоятельно вычислить предложенные вам двойные интегралы в прямоугольных координатах, и только после этого переходите к просмотру ответов по теме «Двойной интеграл в прямоугольных координатах», чтобы проверить себя.
Тема «Двойной интеграл в прямоугольных координатах»
Вопросы по теме «Двойной интеграл в прямоугольных координатах»
Ответы на вопросы по теме «Двойной интеграл в прямоугольных координатах»
Для того чтобы лучше разобраться с темой «Двойной интеграл в прямоугольных координатах», обязательно решите все задания.
Все лекции здесь.
Популярные сообщения из этого блога
Двойной интеграл в полярных координатах. Вопросы
Даны два двойных интеграла. Требуется вычислить их путем перехода к полярным координатам.
Замена переменных в двойном интеграле. Вопросы
Даны два двойных интеграла. Требуется подобрать замены так, чтобы области интегрирования перешли в прямоугольники со сторонами, параллельными осям, и вычислить интегралы в новых координатах.
Репетиторство и консультации по Skype
$ Общее время занятий включает в себя, помимо онлайн-занятия, несколько часов видео для предварительного изучения (которые не оплачиваются). Таким образом, занимаясь фактически 3, 4, 5 и более часов, вы оплачиваете только 2 академических часа.
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| RRenfri |
| ||
19/03/15 |
| ||
| |||
| Pphantom |
| |||
09/05/12 |
| |||
| ||||
| Math_er |
| ||
02/07/11 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 4 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
— Как решить двойной интеграл с абсолютным значением?
Задавать вопрос
спросил
Изменено 3 года, 6 месяцев назад
Просмотрено 12 тысяч раз
$\begingroup$
92)\,dz\,dx=6\cdot\frac{1}{6}\cdot\frac{1}{4}=\color{red}{\frac{1}{4}}. \end{ уравнение*}$$
\end{ уравнение*}$$
$\endgroup$
3
$\begingroup$
Подумайте об этом так: вы вводите двумерные данные в плоскости $~xy~$ (если вы визуализируете, что общая площадь ввода представляет собой квадрат со стороной $~1~$) и получаете результат своей функции, предположим $~z =f(x)~$ на оси $~z~$.
Нам нужно рассчитать общий объем.
Небольшой объем равен $~(z~dx~dy )~$.
Теперь мод находится над $~x-y~$, поэтому нарисуйте его график на нашей входной плоскости $~xy~$, которую он делит на две области, если $~x-y<0~$, тогда мод открывается со знаком минус и $~x-y >0~ $, то он открывается напрямую.
Теперь вы делите интегрирование на две части и просто ставите предел, как в простом двойном интеграле.
Надеюсь помог.
$\endgroup$
3
Свойства, правила, приложения и примеры решений
Интегралы и производные являются важной частью математики, называемой исчислением.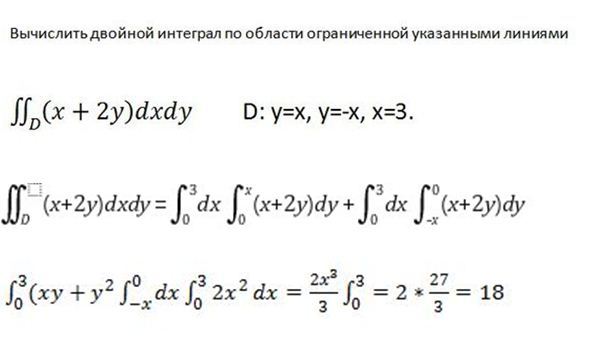 Обе они взаимосвязаны и называются основной теоремой исчисления. Интеграл — это обращение производной подобно тому, как сложение является обращением вычитания. Интеграл — это процесс, посредством которого мы находим площадь под любой кривой.
Обе они взаимосвязаны и называются основной теоремой исчисления. Интеграл — это обращение производной подобно тому, как сложение является обращением вычитания. Интеграл — это процесс, посредством которого мы находим площадь под любой кривой.
Интегралы можно в основном разделить на два типа: определенные интегралы и неопределенные интегралы.
Существует множество других специальных типов интегралов, перечисленных ниже.
- Поверхностный интеграл
- Линейный интеграл
- Двойной интеграл
- Тройной интеграл и многие другие.
В этой статье мы подробно обсудим двойной интеграл.
Двойной интеграл
Двойной интеграл — это тип интегрирования, при котором интегрирование выполняется с использованием двух переменных в определенной области. Двойной интеграл — это способ интегрирования по двумерной области. Двойной интеграл, содержащий две переменные по области \( R=\left[a,\b\right]\times\left[c,\d\right] \) может быть определен как \( \int_R^{ }f\ влево(x,\y\вправо)dA=\int_a^b\int_c^df\влево(x,\y\вправо)\dy\dx\). 1\left(8x+6y\right)dx\dy\), то 92 \\[4pt] &=20 \end{align} \)
1\left(8x+6y\right)dx\dy\), то 92 \\[4pt] &=20 \end{align} \)
Вычисление двойного интеграла
Двойные и тройные интегралы вычислялись задолго до того, как понятие интеграла было формализовано, начиная с античности, такими людьми, как Архимед и Евдокс, но для каждого частного интеграла изобретался новый аргумент. Они аппроксимировали интегралы конечными суммами, а затем пытались найти предел. Трудность заключалась в том, чтобы явно найти предел. В 17 веке был сформулирован принцип Кавальери, который помог вычислить некоторые кратные интегралы, особенно для площадей и объемов. Современные книги по математическому анализу предпочитают ссылаться на очень общую теорему Фубини, которую мы изучаем в настоящее время.
Свойства двойного интеграла
Свойства двойного интеграла очень полезны при их вычислении или другой работе с ними. Они помогают упростить данную функцию. Свойства двойного интеграла перечислены ниже.
Если мы рассмотрим функции \(f\left(x,\y\right)\ и\g\left(x,\y\right)\) интегрируемыми по прямоугольной области R , где S и T являются подобластями R и m и M — действительные числа, то мы можем описать следующие свойства.
- Сумма \( f\left(x,\y\right)\ и\ g\left(x,\y\right) \) интегрируема и \( \iint_R [f(x, y) + g(x, y)]\,dA = \iint_R f(x,y)\, dA + \iint_R g(x, y) \,dA.\nonumber \)
Свойство называется линейностью интеграла.
- Если k является константой и \( kf\left(x,\ y\right) \) интегрируемо, то \( \iint_R kf(x,y)\,dA = k\iint_R f(x ,y)\,dA.\nonumber \)
Это свойство также известно как линейность интеграла.
- Если \( R=S\cup T\ и\ S\cap T=\varничего \) кроме перекрытия на границах, то \( \iint_R f(x,y)\,dA = \iint_S f(x ,y) \,dA + \iint_T f(x,y)\, dA.\nonumber \)
Это свойство известно как аддитивность интеграла.
- Если \( f\влево(x,\y\вправо)\ge g\влево(x,\y\вправо)\ for\ \влево(x,\y\вправо)\ в\R\), тогда \( \iint_R f(x,y)\,dA \geq \iint_R g(x,y)\,dA. \nonumber \)
Это свойство называется монотонностью интеграла.
- Если \( m\le f\left(x,\ y\right) \) и A(R) = площадь R, то \( m \cdot A(R) \leq \iint_R f(x ,y)\,dA \leq M \cdot A(R).
 d h(y ) \,dy \право).\номер\) 9x}{\log a}+C \)
d h(y ) \,dy \право).\номер\) 9x}{\log a}+C \) - Тригонометрическое правило
- \( \int \sin x\ dx=-\cos x+C \)
- \( \int \cos x\ dx=\sin x+C \)
- \( \int \tan x= \log(\sec x)+C=-\log\left|(\cos x)\right|+C \)
- \( \int \cot x\ dx=\ln|\sin x|+C \ )
- \( \int \operatorname{cosec}x\ dx=\log|\operatorname{cosec}x-\cot x|+C=-\log|\operatorname{cosec}x+\cot x|+C= \log|\tan(\frac{x}{2})|+C \) 92x\ dx=-\cot x+C \)
- \( \int \sec x\tan x\ dx=\sec x+C \)
- \( \int \operatorname{cosec}x\cot x\ dx=-\operatorname{cosec}x+C \)
- Сначала запишем заданные пределы в заданном порядке или вычислим пределы, если вместо интервалов даны уравнения.
 2 \) и прямой \( y=x \ ), то мы можем нарисовать график как 91\\
2 \) и прямой \( y=x \ ), то мы можем нарисовать график как 91\\&=\frac1{2}-\frac1{3} = \frac1{6}.
\end{align*} \)
Разница между двойным и тройным интегралами
Разница между двойным и тройным интегралом указана ниже.
Двойной интеграл Тройной интеграл - Используется для интеграции 2D-области.
- Используется для интеграции трехмерной области.
Решение:
Для треугольника, определяемого \( 0 \le x \le 2 \) и \( 0 \le y \le x/2 \), пределы y зависят от x . Для заданных значений x , y находится в диапазоне от 0 до x/2 , представленных вертикальной пунктирной линией от \( \left(x,\ 0\right)\ до \left(x ,\ \frac{x}{2}\right) \).

Как и в двойном интеграле, внешние пределы должны быть постоянными, но внутренние пределы могут зависеть от внешней переменной. Это означает, что мы должны указать y как внутреннюю переменную интегрирования. 91 = \frac{{55}}{{156}}\end{align*} \)
Testbook – это универсальное хранилище всех учебных материалов и руководств, необходимых для подготовки к экзаменам. Приложение Testbook предлагает вам доступ к интерактивным живым занятиям, сериям тестов, пробным тестам и многому другому. Загрузите сейчас, чтобы получить удивительные предложения.
Часто задаваемые вопросы о двойном интеграле
В.1 В чем разница между двойным интегралом и поверхностным интегралом?
Ответ 1 Основное различие между двойным и тройным интегралом заключается в том, что двойной интеграл используется для интегрирования по двумерной области, тогда как тройной интеграл используется для трехмерной области.
Q.2 Как найти предел двойного интеграла?
Ответ 2 Пределы находятся по граничным координатам, образованным пересечением данных двух кривых.

Существует десять правил интегрирования тригонометрических функций.
Этапы решения двойных интегралов
Двойной интеграл также известен как повторный интеграл. Итак, как следует из названия, мы будем решать двойной интеграл итеративно, т. е. один за другим. Шаги перечислены ниже.


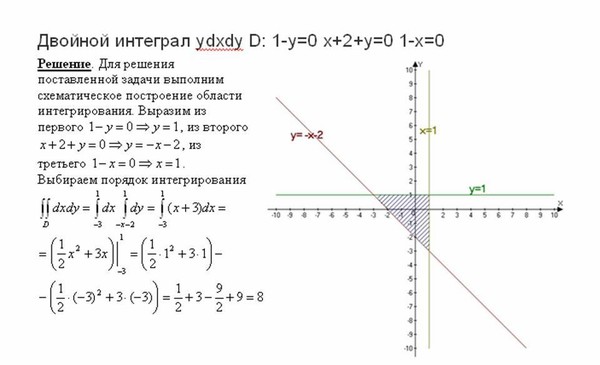 Не могу вычислить двойной интеграл следующего вида:
Не могу вычислить двойной интеграл следующего вида: Первый из двух оставшихся интегралов тривиален, второй — легко приводится к стандартной функции («интеграл/функция ошибок») с известным значением в нужной точке.
Первый из двух оставшихся интегралов тривиален, второй — легко приводится к стандартной функции («интеграл/функция ошибок») с известным значением в нужной точке. Но есть специальная функция через которую этот интеграл выражается: он равен .
Но есть специальная функция через которую этот интеграл выражается: он равен .
 d h(y ) \,dy \право).\номер\) 9x}{\log a}+C \)
d h(y ) \,dy \право).\номер\) 9x}{\log a}+C \) 2 \) и прямой \( y=x \ ), то мы можем нарисовать график как 91\\
2 \) и прямой \( y=x \ ), то мы можем нарисовать график как 91\\
