Решить двойственную задачу графически: Двойственная задача линейного программирования онлайн

Модели линейной оптимизации — Экономико-математические модели (Экономика и финансы)

Модели линейной оптимизации.

 Двойственность и основные соотношения двойственности

К моделям линейной оптимизации относятся задачи на максимум или минимум линейной целевой функции многих переменных при ограничениях на них в форме линейных равенств и неравенств.

С любой экономико-математической задачей, для которой можно построить линейную модель, либо свести к построению линейной модели, связана двойственная задача. Прямая и двойственная задача тесно взаимосвязаны, так как оптимальное решение одной задачи можно получить непосредственно, зная оптимальное решение другой задачи. Совместное изучение прямой задачи и двойственной к ней дает, как правило, значительно больше информации.

Рассмотрим решения прямой и двойственной задач графическим методом, с помощью которого легко иллюстрируются основные соотношения теории двойственности.

Пример 1. Решить графическим методом прямую и двойственную задачи (табл. 1).

Таблица 1

Решение прямой задачи.

Строим область допустимых решений задачи. Для этого нумеруем ограничения задачи

В прямоугольной декартовой системе координат (рис. 2) строим прямую  (p₁), соответствующую ограничению (1) по двум точкам, например, (– 7; 0) и (– 4; 2). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая p₁ не проходит через начало координат, подставляем координаты точки  в первое ограничение . Получаем строгое неравенство . Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем  полуплоскость, содержащую точку О. Аналогично строим прямую   (p₂) по двум точкам (0; 8) и (8; 0) и определяем область решений ограничения (2).

Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Полученная область допустимых решений на рисунке заштрихована и представляет собой ограниченный выпуклый многоугольник ОАВС.

Строим нормаль линий уровня  . Так как решается задача на отыскание максимума целевой функции, то линию уровня  перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.

Определяем координаты точки В как пересечение прямых  p₁ и  p₂. Для этого решаем систему

Получаем:

       

Следовательно, координаты точки . Оптимальное решение х₁^* = 2,         х₂^* = 6. Вычисляем максимум целевой функции:  Уравнение опорной прямой имеет вид:

Решение двойственной задачи.

Для построения области допустимых решений занумеруем ограничения задачи:

Строим прямые p₃ и p₄, уравнения которых: – 2у₁ + у₂ = 2  и  3у₁ + у₂ = 7.  Учитывая условия неотрицательности переменных, определяем область допустимых решений. Полученная область представляет неограниченный сверху выпуклый многоугольник (рис. 3). Нормаль линии уровня .

В данной задаче необходимо найти минимум целевой функции, поэтому линию уровня перемещаем в направлении, противоположном направлению нормали до опорной прямой. Эта прямая проходит через точку D пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (3) и (4), перпендикулярно нормали.

Определяем координаты точки D, как пересечение прямых p₃ и p₄. Для этого решаем систему

Получаем, что точка D имеет координаты . Оптимальное решение у₁^* = 1, у₂^* = 4. Вычисляем минимум целевой функции:  Уравнение опорной прямой имеет вид: .

Как видно из приведенных решений прямой и двойственной задач значения целевых функций равны:  

При любом допустимом решении прямой задачи значение целевой функции « » (не превосходят) значений целевой функции двойственной задачи при ее допустимом произвольном решении.

 Например, при допустимом решении прямой задачи  значение целевой функции , а при допустимом двойственной задачи  значение целевой функции , т.е. .

Пример 2. Решить графическим методом прямую и двойственную задачи (табл. 2).

                                                                                                   Таблица 2

Для решения прямой задачи вводим нумерацию ограничений задачи:

Аналогично примеру 1 строим область допустимых решений, которая представляет собой выпуклый многоугольник не ограниченный  сверху. Нормаль линии уровня  (рис. 4).

В данной задаче необходимо найти минимум целевой функции, поэтому линию уровня перемещаем в направлении, противоположном направлению нормали, которая уходит в бесконечность.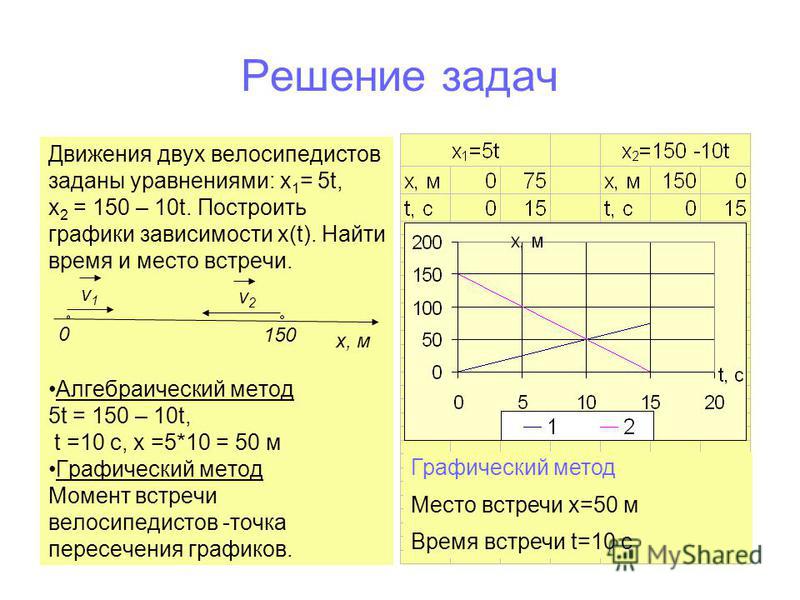 Задача не имеет оптимального решения из-за неограниченности снизу целевой функции  на множестве допустимых решений.

Решение двойственной задачи.

Область допустимых решений для данной задачи представляет собой пустое множество,  что означает противоречивость системы ограничений  (рис. 5). Следовательно, и двойственная задача, так же как и прямая задача, не имеет решения.

Взаимозависимость оптимальных решений пары двойственных задач определена следующими соотношениями:

Теорема (основное неравенство). Пусть Х – какое-нибудь допустимое решение прямой задачи, а Y – какое-нибудь допустимое решение двойственной задачи. Тогда справедливо неравенство

.

Следствие 1 (достаточный признак оптимальности). Если для каких-то допустимых решений  и  соответственно прямой и двойственной задач выполняется равенство

,

то   есть оптимальное  решение прямой задачи,  а  – оптимальное решение двойственной задачи.

Следствие 2. Если в одной из пары двойственных задач целевая  функция  не ограничена с соответствующей стороны  (т.е.  в прямой задаче  или  в двойственной задаче), то другая задача не имеет допустимых решений.

Основная теорема. Если разрешима одна из пары двойственных задач, то разрешима и другая задача, причем .

Остальные теоремы двойственности будут сформулированы в следующих разделах данного пособия.

Для понимания экономической интерпретации основных соотношений двойственности рассмотрим модель распределения ограниченных ресурсов, в которой целевая функция, отображающая прибыль или доход от производственной деятельности, подлежит максимизации.

Формулировка прямой задачи

Пусть фирма располагает m видами ресурсов Р₁ , Р₂ ,… Р_m и планирует организовать выпуск из них n видов продукции П₁ , П₂ ,…, П_n .

Известны следующие исходные данные:

a_ij– нормы расхода i—го ресурса на изготовление одной единицы j-ой продукции П_j;

c_j — прибыль от реализации одной единицы j-ой продукции П_j;

b_i—  количество ресурса i–го вида.

Требуется составить план выпуска продукции П₁, П₂,…П_n. из имеющихся объемов ресурсов Р₁, Р₂ ,…Р_m , при котором прибыль от ее реализации будет максимальной.

Построим математическую модель этой задачи.

Обозначим за x_j (j = 1,2,…,n) – число единиц продукции, запланированных к производству. Тогда прибыль от реализации j-го вида продукции составит c_j∙x_{j, а суммарная прибыль от реализации всей продукции будет равна:}

F = c₁ x₁ + c₂ x₂ + …+ c_n x_n.

 Согласно условиям задачи, она подлежит максимизации.

Затраты ресурса P_i  на выпуск всей продукции  Х = (x₁, x₂ ,…, x_n ) будут выражаться суммой произведений норм расхода a_ijна объемы выпуска и составят величину, равную a_i1 x₁ + a_i2 x₂ + . .. + a_in x_{n. Поскольку запас ресурса Рi равен bi , а расход ресурса не может превышать имеющегося его количества, то приходим к ограничениям следующего вида:}

a_i1x₁ + a_i2x₂ +… + a_inx_n £ b_i,     i = 1,2,…,m

Учитывая естественные условия неотрицательности объемов выпуска продукции,

x_j0, j=1,2,…,n,

придем к следующей задаче:

Найти такой план Х = (x₁, x₂ ,…, x_n) выпуска продукции, удовлетворяющий системе неравенств

                                               a₁₁x₁ + a₁₂x₂ + … + a_1nx_n £   b₁,

                                               a₂₁x₁ + a₂₂x₂ + … + a_2nx_n £   b₂,

                                                …   …   …   …   …   …   …

                                               a_i1x₁ + a_i2x₂ + … + a_inx_n £   b_i,

                                               …   …   …   …   …   …   …

                                               a_m1x₁ + a_m2x₂ + … + a_mnx_n £  b_m,

                                               x_j ³ 0,   j = 1, 2, …, n,

при котором функция  F = c₁x₁ + c₂x₂ + … + c_nx_n  принимает максимальное значение.

Формулировка двойственной задачи

Предположим, что некоторая организация решила закупить ресурсы Р₁ , Р₂ ,…, Р_m фирмы и необходимо определить цены на эти ресурсы у₁, у₂,…, у_m. Естественно, что покупающая организация заинтересована в том, чтобы затраты на покупку ресурсов в объеме b₁, b₂,…, b_m по ценам у₁, у₂,…, у_{m были минимальны, то есть Z = b1y1 + b2y2 + … +bmym  ®  min.}

Предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции j-го вида расходуется сырье Р₁ в объеме а_1j, сырье Р₂ в объеме а_2j…, сырье Р_m в объеме  а_mj по цене у₁, у₂,…, у_{m соответственно, то есть затраты на изготовление продукции Пjдолжны быть не меньше, чем цена ее реализации. Приходим к ограничениям следующего вида:}

а_1jу₁ + а_2jу₂  + … + а_mjу_m ≥ с_{j,     j=1,2,…,n.}

Учитывая условия неотрицательности цены единицы i-го ресурса, приходим к следующей задаче:

Найти такой вектор У = (у₁, у₂ ,…, у_m) – цен ресурсов, удовлетворяющий системе неравенств

                                               a₁₁у₁ + a₂₁у₂ + … + a_m1у_m ≥  c₁,

                                               a₁₂y₁ + a₂₂y₂ + … + a_m2y_m  ≥  c₂,

                                                …   …   …   …   …   …   …

                                               a_1jy₁ + a_2jy₂ + … + a_mjy_m ≥   c_j,

                                               …   …   …   …   …   …   …

                                               a_1ny₁ + a_2ny₂ + … + a_mny_m ≥  c_n,

                                               y_i ³ 0,   i = 1, 2, …, m,

при котором функция Z = b₁y₁ + b₂y₂ + …+ b_my_{m принимает минимальное значение.}

Цены ресурсов в экономической литературе имеют различные названия: учетные, неявные, теневые, объективно-обусловленные оценки (о-о оценки). Смысл этих названий состоит в том, что это условные (ненастоящие) цены. Эти цены определяются в ходе решения задачи, их называют оценками ресурсов.

Сопоставим общие представления прямой и двойственной задач в табл. 3, причем прямая задача – это задача модели распределения ограниченных ресурсов.

                                                                                     Таблица 3

Сравнивая рассмотренные примеры видно, что двойственная задача по отношению к исходной составляется согласно следующим правилам.

1. Если первая задача имеет размеры  (m–ограничений с n неизвестными), то вторая – размеры .

2. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих        задач являются            взаимно транспонированными.

З. В правых частях ограничений в каждой          задаче стоят коэффициенты при неизвестных в целевой функции другой задачи.

4. В прямой задаче  все ограничения представляют собой неравенства типа « », причем в этой задаче требуется достичь . Напротив, в двойственной задаче все ограничения суть неравенства типа « », причем требуется достичь .

Графически эти правила представлены в таблице 4.

                                                                                                                 Таблица 4

           

Экономическое содержание основной теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенства общей оценки продукции и ресурсов и показывают убыточность всякого другого плана, отличного от оптимального.

Из приведенных соотношений видно, что для всех допустимых решений прямой и двойственной задач значения целевой функции задачи минимизации всегда будет верхним пределом значения целевой функции задачи максимизации. Таким образом, итерационное решение задачи максимизации ведет к возрастанию значения целевой функции, а итерационное решение задач минимизации – к ее убыванию. В итоге, при успешном завершении процессов вычисления прямой и двойственной задач приходят к точке «равновесия», где значения целевых функций задач максимизации и минимизации становятся равными.

Имеет место следующая теорема равновесия, используя которую можно находить решение одной из двойственных задач, зная решение другой задачи.

Теорема равновесия. Пусть Х^* – какое-нибудь допустимое решение прямой задачи, а Y^* – какое-нибудь допустимое решение двойственной задачи. Для одновременной оптимальности этих решений необходимо и достаточно выполнение равенств:

Величины, стоящие в скобках сформулированной теоремы, равны разности между левой и правой частями ограничения одной из двойственных задач на соответствующую переменную другой задачи.

Учитывая условия неотрицательности переменных и знаки сомножителей в произведениях,  можно получить следующее:

если какое-либо ограничение одной задачи на оптимальном плане выполняется как строгое неравенство, то соответствующая координата оптимального плана другой задачи равна нулю:

  Если     a_i1 x₁^*+ a_i2 x₂^*+ . .. + a_in x_n^*< b_i , то y_i^* = 0 .

Если     a_1j y₁^*_{+ a2j y2^*}+  … + a_mj y_m^*> c_j , то x_j^* = 0 .

Если какая-либо координата оптимального плана одной задачи положительна, то соответствующее ограничение другой задачи обращается в равенство:

Если y_i^* > 0 , то a_i1 x₁^*₊ a_i2 x₂^*+  … + a_in x_n^* = b_i .                     

Если x_j^* > 0 , то a_1j y₁^*_{+ a2j y2^*}+   … + a_mj y_m^*= c_j .                      

Экономическое содержание теоремы равновесия означает, что если по некоторому оптимальному плану Х^*  производства расход i-го ресурса строго меньше его запаса bi, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равно нулю. Если же в некотором оптимальном плане оценок его i-ая координата строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует, что двойственные оценки служат мерой дефицитности ресурсов. Дефицитный ресурс, который полностью используется по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, не используемый полностью, имеет нулевую оценку.

Пример 3. Используя теорему равновесия, решить пару двойственных задач (табл.5).

Таблица 5

Решим прямую задачу графическим методом.

Рис. 6

Аналогично примеру 1 строим область допустимых решений, которая представляет собой выпуклый многоугольник ОАВСD.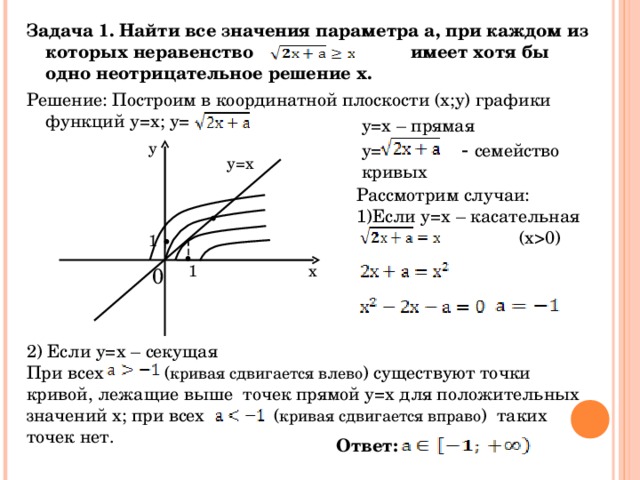 Нормаль линии уровня  (рис. 6).

Определяем координаты точки С как пересечение прямых  p₉ и  p₁₀. Для этого решаем систему

Получаем:

       

Следовательно, координаты точки . Оптимальное решение х₁^* = 4, х₂^* = 1. Вычисляем максимум целевой функции прямой задачи:

По основной теореме двойственности Z(Y^*) = F(Х^*) = 3. Подставим Х^* = (4;1) в систему ограничений прямой задачи:

 

Первое ограничение прямой задачи на оптимальном плане выполняется как строгое неравенство, следовательно, соответствующая переменная двойственной задачи  равна нулю:  y₁^*= 0.

Второе и третье ограничение прямой задачи обращается в точное равенство, следовательно, соответствующие переменные двойственной задачи положительны:  y₂^* >  0 и y₃^* >  0.

Условия равновесия можно записать в виде равенств:

Ещё посмотрите лекцию «2 Блок питания ПЭВМ» по этой теме.

Подставляя  y₁^*=0 в последнюю систему уравнений, получим систему:

 

откуда получаем, что y₂^* = , y₃^* = .

Оптимальное решение двойственной задачи Y^*= (0; 😉 при этом минимум целевой функции двойственной задачи: Z_{min= Z(Y^*) = 3.}

Графический способ решения задач показывает, что оптимальное решение задач, сводящихся к линейным моделям, всегда ассоциируется с угловой точкой области допустимых решений.

Переход от геометрического способа решения задач к симплекс-методу лежит через алгебраическое описание угловых точек области допустимых решений. Для реализации этого перехода сначала надо привести задачу к канонической  форме, преобразовав неравенства ограничений в равенства путем введения дополнительных переменных. Каноническая  форма задачи необходима, потому что она позволяет получить базисное решение, которое полностью определяет все (геометрические) крайние точки пространства решений. Симплекс-метод позволяет эффективно найти оптимальное решение среди всех базисных.

Решив графически двойственную задачу, найти решение исходной задачи. … — Учеба и наука

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

коробка с виноградом в 4 раза легче,чем коробка с бананам.Коробка с бананами на 12 кг тяжелее коробки с виноградом. Найди массу коробки с виноградом….

Решено

В корзине лежат 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик ,а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?

Решено

Вася проходит серию тестов, за каждый из которых он может получить от 0 до 100 баллов. Перед выполнением последнего теста Вася подсчитал, что если он…

в некоторой американской конторе каждый служащий считает себя либо демократом, либо республиканцем. после того как один из демократов решил стать республиканцем, тех и других стало поровну.

Пользуйтесь нашим приложением

Ответов пока нет

Михаил Александров от 0 p. Читать ответы Андрей Андреевич от 70 p. Читать ответы Eleonora Gabrielyan от 0 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Раздел 4.4 Вопрос 3. Часто задаваемые вопросы по математике

В примере 2 показано, как преобразовать стандартную задачу минимизации в стандартную задачу максимизации. Эти проблемы называются двойственными друг другу. Решения двойных задач связаны между собой и могут быть использованы для одновременного решения обеих задач.

Рассмотрим решение каждой задачи линейного программирования графически. Для каждой задачи рассмотрим график допустимой области и таблицу угловых точек с соответствующими значениями целевой функции. Из таблицы видно, что решения имеют одинаковое значение целевой функции в соответствующих решениях.

Хотя угловые точки, дающие максимум или минимум, не совпадают, значение целевой функции в оптимальной угловой точке одинаково, 100. Другими словами,

Другая связь между двойственными задачами: очевидно, если применить симплекс-метод к задаче двойной максимизации

. Если мы перестроим целевую функцию и добавим резервные переменные в ограничения, мы получим систему уравнений

Эта система соответствует начальной симплексной таблице, показанной ниже. Сводная колонка — это вторая колонка, и частные могут быть сформированы, чтобы получить

Сводная ось для этой таблицы — это 3 в первой строке, второй колонке. Если мы умножим первую строку на ¹ / ₃ , опорная точка станет 1 и приведет к таблице

. Первая симплексная итерация завершается созданием нулей в остальной части опорного столбца. Чтобы изменить эти записи, умножьте первую строку на -4 и добавьте ее ко второй строке. Затем умножьте первую строку на 24 и прибавьте к третьей строке.

Теперь, когда опорная точка равна единице, а остальная часть опорной колонки равна нулю, посмотрите на строку индикатора, чтобы увидеть, нужна ли еще одна итерация симплекс-метода. Поскольку запись в первом столбце строки индикатора, -8, является отрицательной, мы делаем первый столбец новым сводным столбцом.

Частные для каждой строки таблицы формируются ниже:

 

Наименьшее отношение находится во второй строке. Поворотный элемент ⁸ / ₃ должен быть изменен на 1 путем умножения второй строки на ,

После того, как стержень равен единице, операции со строками используются для изменения остальной части стержня на нули.

Запись в первой строке сводного столбца

изменена на ноль путем помещения суммы – ¹ / ₃ , умноженной на вторую строку и первую строку в первой строке. Запись в третьей строке сводного столбца заменяется на ноль путем помещения суммы 8 умноженной на вторую строку и третью строку в третьей строке,

Поскольку в строке индикатора больше нет отрицательных значений, мы достигли финальной таблицы. Если мы внимательно изучим окончательную симплексную таблицу, мы увидим решение стандартной задачи максимизации и стандартной задачи минимизации:

Окончательная симплексная таблица дает решение стандартной задачи максимизации и решение соответствующей двойной стандартной минимизации проблема. Это означает, что пока мы можем решить стандартную задачу максимизации с помощью симплекс-метода, мы бесплатно получаем решение двойной стандартной задачи минимизации. Это предлагает стратегию решения стандартных задач минимизации.

 

Как решить стандартную задачу минимизации с двойной задачей
1. Убедитесь, что задача минимизации имеет стандартную форму. Если она не в стандартной форме, измените задачу, чтобы привести ее в стандартную форму.2. Найдите двойную стандартную задачу максимизации.3. Примените симплекс-метод для решения задачи двойной максимизации.4. После того, как окончательная симплексная таблица была рассчитана, минимальное значение целевой функции стандартной задачи минимизации совпадает с максимальным значением целевой функции стандартной задачи максимизации. Решение стандартной задачи минимизации находится в нижней строке итоговой симплексной таблицы в столбцах, соответствующих резервным переменным.

 

Пример 3    Найти оптимальное решение

В разделе 4.2 мы решили задачу линейного программирования

с помощью графа. В примере 2 мы нашли связанную двойную задачу максимизации,

. Примените симплекс-метод к этой двойной задаче, чтобы решить задачу минимизации.

Решение В примере 1 и примере 2 мы записали эту задачу как стандартную задачу минимизации и нашли задачу двойной максимизации. В этом примере мы возьмем двойственную задачу,

и применить симплексный метод.

Исходная симплексная таблица формируется из системы уравнений

Обратите внимание, что резервные переменные s ₁ и s ₂ включены в уравнения, соответствующие ограничениям целевой функции, и были соответствующим образом переставлены.

Исходная таблица

Самая отрицательная запись в строке индикатора равна -32, поэтому второй столбец является сводным столбцом. Теперь вычислите частные, чтобы найти опорную строку,

Наименьшее частное соответствует размещению опорной точки во второй строке, во втором столбце. Чтобы изменить запись в этой позиции на единицу, умножьте вторую строку на ¹ / ₄ :

Чтобы поместить нули в оставшуюся часть сводного столбца, мы используем больше операций со строками.