Simultaneous Equations Solver
Бесплатный веб-решатель одновременных уравнений
Этот веб-решатель одновременных уравнений покажет вам, как шаг за шагом вычислять / решать одновременные уравнения онлайн. Калькулятор системы уравнений может решить любую систему уравнений, включая линейные, нелинейные, квадратичные уравнения с 2, 3, 4 или 5 переменными. Он работает с любой пользовательской переменной, например. x, y, z и т. д. Веб-калькулятор для одновременных уравнений бесплатный и простой в использовании. Его также можно использовать для решения системы с тремя неизвестными, например 2x-y+z=9.,4x-5y+8z=7; х-у+г=6. Кроме того, этот онлайн-решатель уравнений можно использовать для любой двумерной системы уравнений (нелинейной системы), например. 2ху-у=9; х-у=3. Решения любой системы уравнений можно найти методом подстановки. Другие методы включают исключение и метод исключения Гаусса.
Решатель квадратных уравнений с шагами
Этот решатель системы уравнений также поможет вам найти решение системы, включающей квадратные уравнения.
Квадратичные уравнения представляют собой уравнения с переменной степенью, равной 2. Решатель EquationCalc не только предоставляет вам корни или решения системы уравнений, но также показывает пошаговую стратегию решения. Решатель предлагает вам альтернативный способ научиться решать одновременные уравнения онлайн на решенных примерах.
Решатель одновременных уравнений с графиком
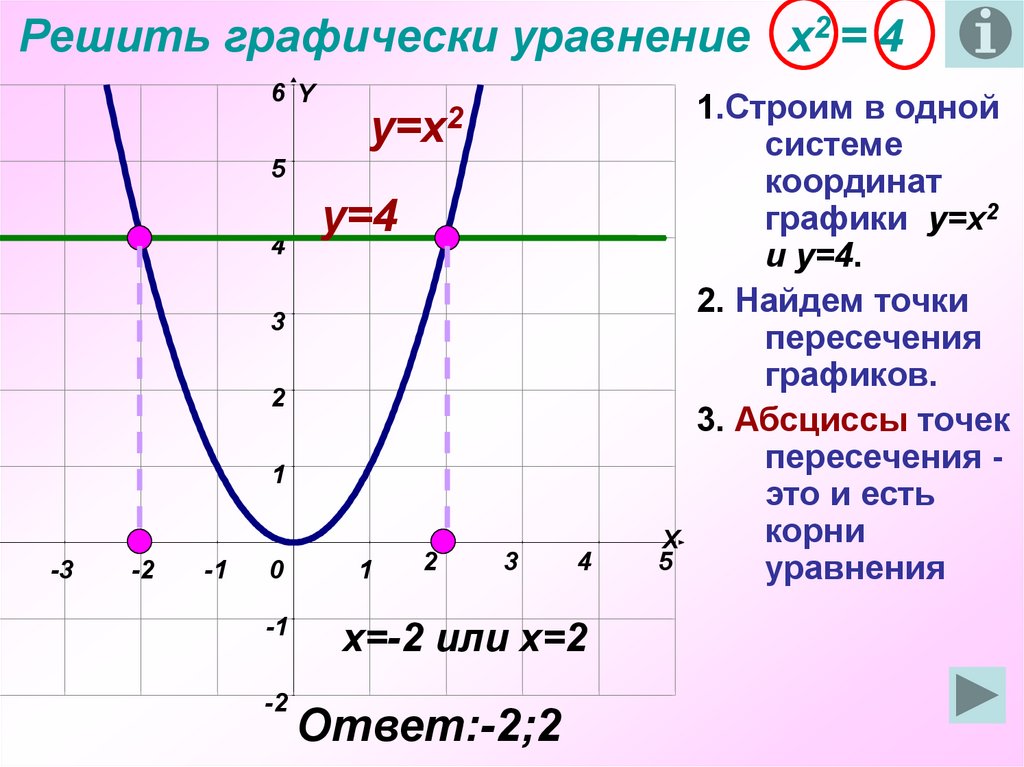
Этот онлайн-решатель для одновременных уравнений также покажет вам, как решать одновременные уравнения графически. Обратите внимание, что графические решения доступны только для двумерных систем уравнений. Это включает в себя линейную систему, а также квадратичную систему уравнений.
Графическое решение представляет собой точки пересечения графиков заданной системы уравнений. Для этого мы наносим оба уравнения в одну и ту же систему координат, а затем определяем точки пересечения между двумя уравнениями.
Онлайн-калькулятор одновременных уравнений
С помощью этого онлайн-калькулятора вы можете найти решения для любой системы уравнений.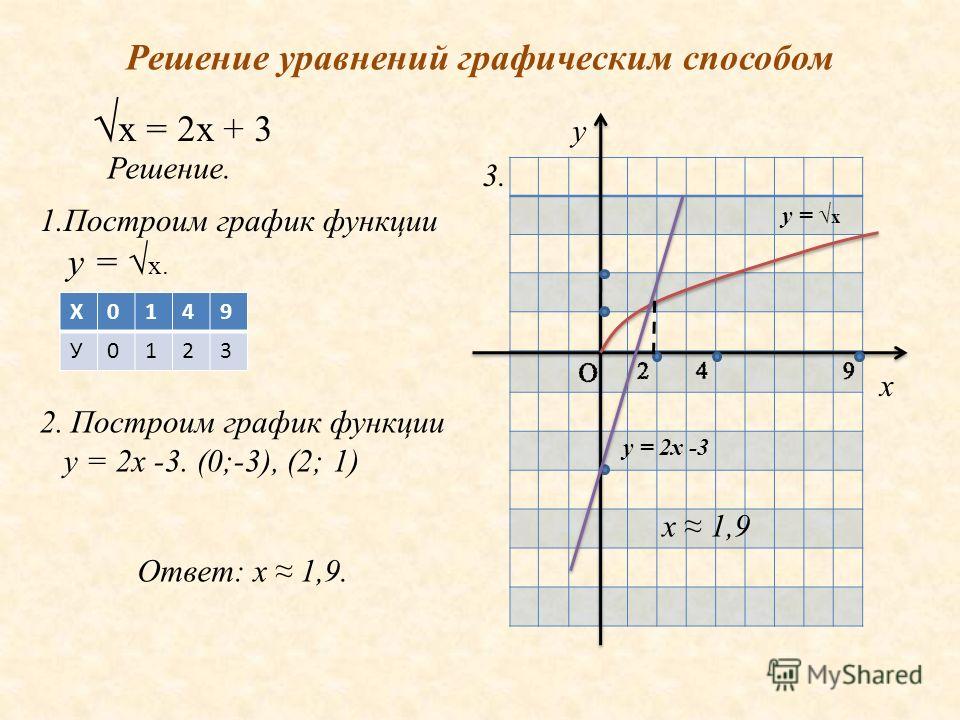
Самое приятное то, что калькулятор бесплатный и доступен для всех онлайн-пользователей. В следующем примере показано, как использовать решатель.
p>Вот рабочий пример, иллюстрирующий, как работает одновременный решатель:
Бесплатный веб-решатель уравнений. Как показано на иллюстрациях выше, использование этого онлайн-калькулятора очень простое и понятное. Для начала введите свои математические уравнения в текстовое поле выше. Ваши уравнения должны быть разделены запятыми или точкой с запятой. После того, как вы ввели свою математическую задачу/уравнение, нажмите «Решить сейчас!» кнопка для обработки решений. Обратите внимание, что при вводе уравнений следует использовать только допустимые символы. Допустимые символы перечислены внизу этой страницы.
Как решать одновременные уравнения онлайн с помощью нашего решателя
Перейти к решенным примерам одновременных уравнений с шагами
Допустимые математические символы и их использование символы и операторы.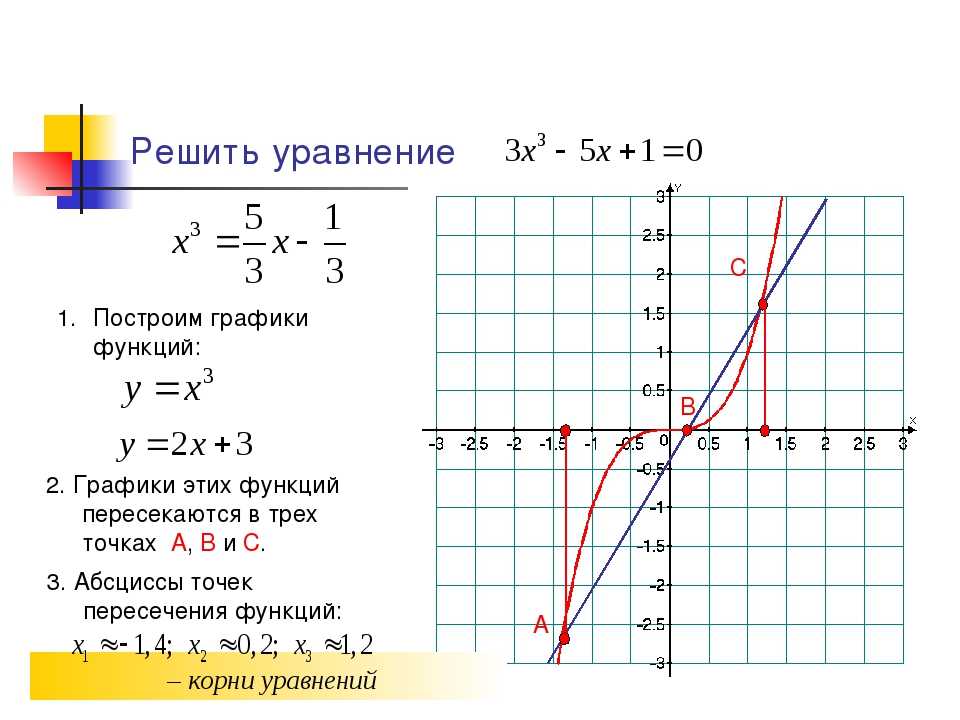
- + Используется для дополнения
- — Используется для вычитания
- *символ оператора умножения
- /Оператор отделения 9Используется для экспоненты или для возведения в степень
- sqrt Оператор квадратного корня
Pi : Представляет математическую константу pi или \pi
Что еще и каковы ограничения онлайн-решателя уравнений
Мы рады услышать ваши отзывы. Если у вас возникнут проблемы при использовании этого калькулятора, сообщите нам об этом: Хотите увидеть больше возможностей? Присылайте нам свои рекомендации и идеи приложений. Мы всегда прилагаем все усилия, чтобы сделать решение одновременных уравнений легким и увлекательным.
Графический калькулятор линейных уравнений | Как нарисовать линейный график?
Бесплатный онлайн-калькулятор для построения графиков линейных уравнений отобразит график заданного уравнения за доли секунды. Укажите допустимое выражение в поле ввода и нажмите кнопку расчета, чтобы получить результат для заданного линейного уравнения в поле вывода.
Графический калькулятор линейных уравнений: Если вы боретесь со сложными задачами линейных уравнений, обязательно попробуйте графический метод. Вы можете воспользоваться графическим методом для решения системы линейных уравнений с двумя переменными. Хотите узнать больше о построении графиков линейных уравнений, например, что это значит, как решать линейные уравнения с двумя переменными с помощью графического метода с примерами? Внимательно ознакомьтесь с этой страницей. Используйте этот удобный онлайн-калькулятор графических линейных уравнений для быстрых расчетов и пошаговых объяснений.
График линейных уравнений представляет собой график заданного линейного уравнения. Как это всегда получается в виде прямой линии. Обычно мы используем графическую форму представления, чтобы доказать взаимосвязь между двумя или более величинами. График линейных уравнений с двумя переменными представляет собой прямую.
Одним из наиболее важных понятий алгебры является построение графиков линейных уравнений.
Чтобы изобразить уравнение, оно должно быть в форме y = mx + b, также известной как форма пересечения y, где m — наклон уравнения.
Этапы решения графических линейных уравнений
Решение линейных уравнений графически и представленных в координатной плоскости называется графическими линейными уравнениями. Шаги, которые необходимо выполнить для решения линейного уравнения с помощью графического метода, перечислены ниже:
- Во-первых, убедитесь, что данное линейное уравнение находится в форме точки пересечения y, т. е. y = mx + b.
- Теперь воспользуйтесь методом проб и ошибок и найдите значения (x,y) до трех пар, которые удовлетворяют линейному уравнению.
- Вычислите точки пересечения по осям x и y уравнения. Подставьте значение x=0 в уравнение, чтобы найти пересечение y и его результаты в x=a. Ради x-пересечения подставьте значение y=0 в уравнение и получите y=c.
- В результате получаются точки (a, 0) и (0, c).
- На этом шаге вы должны нанести все точки на график.
- Теперь пришло время соединить все точки и получить прямую линию, представляющую данное линейное уравнение графически.
Пример:
Нарисовать линейное уравнение 2x+y=7 графически?
Решение:
Данное уравнение 2x+y=7
Преобразуйте данное линейное уравнение в виде y = mx + b, т. е. y = -2x + 7
Вы можете найти два решения, соответствующие к x-перехватам и y-перехватам графика, установив сначала x=0, а затем y=0.
При x=0 получаем:
y = -2(0) + 7
y = 7
При y=0 получаем:
-2x+7=0
-2x = -7
-x = -7/2
x = 3,5
Координаты плоскости (0, 7 ), (3.5, 0) для заданного линейного уравнения 2x+y=7. Графическое представление линейного уравнения показано ниже.
1.