Графический и симплекс-метод
Семинар №1
1.Построение математических моделей
выбрать переменные (неизвестные) задачи – осуществляется непосредственно из условий задачи;
построить (линейную) функцию цели – равнение различных вариантов решений и выбор наилучшего;
учесть все ограничения задачи. Этим учитывается ограниченность ресурсов, которыми необходимо распорядиться наилучшим образом.
Графический метод решения задач линейного программирования
Графическим методом можно решать задачи линейного программирования, содержащие не более трех переменных. Чаще двух переменных (плоскость).
Область определения функции цели задается системой линейных равенств и неравенств.
Во всех задачах линейного программирования
область определения функции цели всегда
выпукла, т.е. вместе с любыми двумя
точками этой же области принадлежат и
точки отрезка, соединяющие эти 2 точки.
Направляющий вектор указывает направление возрастания функции.
Задача №1.
Построение области определения целевой функции
1.
, ;
2.
, ;
3.
, .
Построение направляющего вектора:
.
Минимум находится в точке С (в пересечении прямых и ).
Решаем систему уравнений:
X1=7.5, X2=2,5
f(7,5;2,5)=-17,5.
Ответ: .
Задача №2
Построение области определения целевой функции
1.
, ;
2.
, ;
3.
, .
Построение направляющего вектора:
.
Максимум находится в точке B (в пересечении прямых и ).
Решаем систему уравнений:
X1=3, X2=4,
f(3;4)=11.
Ответ: .
Особые случаи решения задач
область определения целевой функции – пустое множество.
область определения целевой функции неограниченна.
Случай альтернативного оптимума.
Домашнее задание:
Семинар №2
Решить задачу графическим методом
Выразим X3 через третье уравнение в системе и подставим полученное выражение в четвертое:
,
Выразим Х4:
тогда:
Итого:
Подставляем выражения в первые два неравенства и получаем новую систему неравенств:
Семинар №3
Каноническая форма задач линейного программирования. Симплекс-метод
Задача №1 Привести к каноническому виду:
Задачу необходимо привести к каноническому виду:
<= — добавляем, >= — вычитаем
Задача №2 Привести к каноническому виду:
Ответ:
Симплекс-метод
Задача№3
1.
Приводим к каноническому виду:
2. Строим симплекс-таблицу:
В шапке: все коэффициенты
В первом столбце – те коэффициенты, у которых коэффициент 1, т.е. х3 и х3.
В самой нижней строке – соответствующие коэффициенты при переменных у функции, взятые с обратным знаком. Обратите внимание, что функция записанная в каноническом виде, стремится к max.
В последнем столбце записаны свободные коэффициенты.
Х1 | Х2 | Х3 | Х4 | ||
Х3 | 2 | 4 | 1 | 0 | 100 |
Х4 | 3 | 3 | 0 | 1 | 90 |
-f | -5 | -7 | 0 | 0 |
3.
Преобразовываем симплекс-таблицу:
Выбираем разрешающий столбец – где больший по модулю коэффициент в нижней строке – [-7].
Выбираем
У нас получается следующее:
Х1 | Х2 | Х3 | Х4 | ||
Х3 | 2 | 4 | 1 | 0 | 100 |
Х4 | 3 | 3 | 0 | 1 | 90 |
-f | -5 | -7 | 0 | 0 |
Где 4 – разрешающий элемент.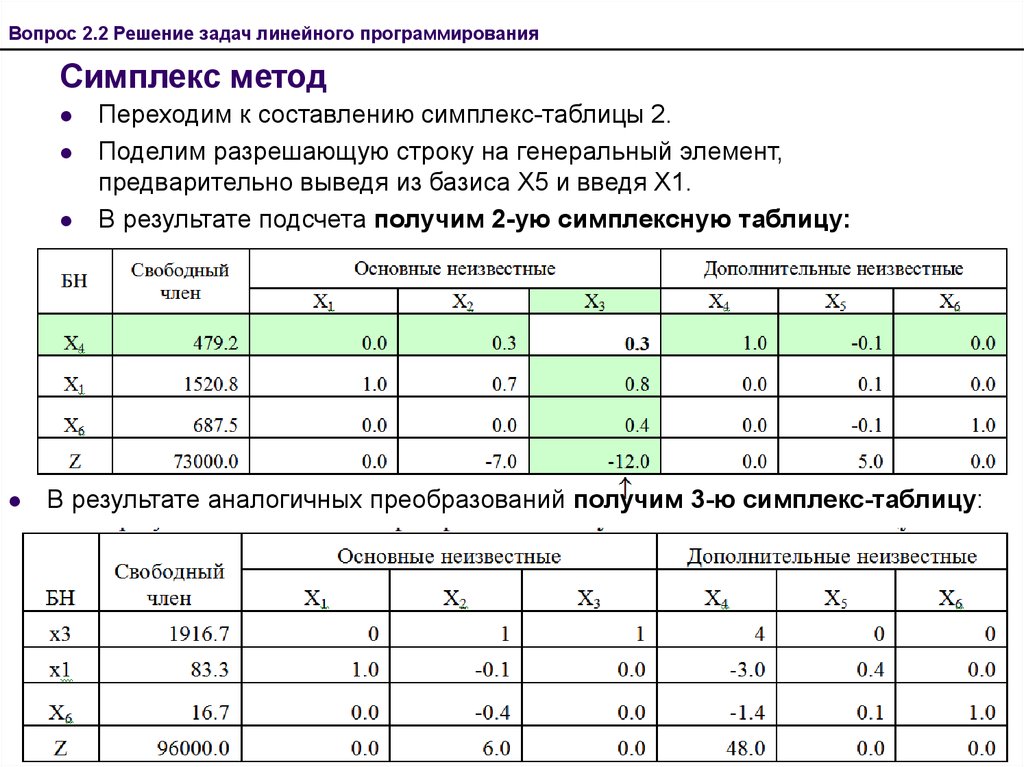
Разрешающий элемент стоит на пересечении разрешающего столбца и разрешающей строки.
Х1 | Х2 | Х3 | Х4 | ||
Х2 | |||||
Х4 | |||||
-f |
Заново считаем каждый элемент НОВОЙ таблицы по следующим правилам:
Вместо разрешающего элемента ставим 1.
Остальные элементы разрешающего столбца обнуляем.
Элементы разрешающей строки делим на разрешающий элемент: 2/4=0.5, ¼=0.25, 0/4=0, 100/4=25.
Оставшиеся элементы вычисляем по формуле треугольника:
:
, , и т.д.
а. b.
Х1 | Х2 | Х3 | Х4 | ||
Х2 | 1 | ||||
Х4 | |||||
-f |
Х1 | Х2 | Х3 | Х4 | ||
Х2 | 1 | ||||
Х4 | 0 | ||||
-f | 0 |
с.
d.
Х1 | Х2 | Х3 | Х4 | ||
Х2 | 0.5 | 1 | 0.25 | 0 | 25 |
Х4 | 0 | ||||
-f | 0 |
Х1 | Х2 | Х3 | Х4 | ||
Х2 | 0. | 1 | 0.25 | 0 | 25 |
Х4 | 1.5 | 0 | -0.75 | 1 | 15 |
-f | -1.5 | 0 | 1.75 | 0 |
5У нас получилась новая таблица:
Х1 | Х3 | Х3 | Х4 | ||
Х2 | 0. | 1 | 0.25 | 0 | 25 |
Х4 | 1.5 | 0 | -0.75 | 1 | 15 |
-f | -1.5 | 0 | 1.75 | 0 |
5Повторяем аналогичную операцию:
ищем в нижней строке таблицы максимальный
по модулю отрицательный коэффициент,
находим разрешающий столбец, разрешающую
строку и строим новую таблицу.
Х1 | Х2 | Х3 | Х4 | ||
Х2 | 0.5 | 1 | 0.25 | 0 | 25 |
Х4 | 1.5 | 0 | -0.75 | 1 | 15 |
-f | -1. | 0 | 1.75 | 0 |
5Х1 | Х2 | Х3 | Х4 | ||
Х2 | 0 | 1 | 0. 5 | -1/3 | 20 |
Х1 | 1 | 0 | -0. | 2/3 | 10 |
-f | 0 | 0 | 0 | 1 |
5В новой таблице не осталось отрицательных элементов в нижней строке. Таким образом мы пришли к оптимальному решению:
Элементы в последнем столбце показывают, чему равны Х1 и Х2 соответственно.
Обратите внимание, что, решая задачу, мы пришли к тому, что в строках остались те переменные, которые были изначально (Х1,Х2), и не осталось тех, которые мы ввели в ходе решения задачи (Х3,Х4). Если такого не произошло, то, вероятно, решение содержит ошибку.
Таким образом, оптимальное решение:
.
Ответ: 190.
Пример решения задачи — игра, графическим методом
Ниже приведено условие и решение задачи.
Закачка решения в формате doc начнется автоматически через 10 секунд.
Оптимизация мощности ателье.
Ателье по пошиву одежды рассчитано на выполнение не более 8 тыс. заявок в год. Будем считать, что поток заявок выражается цифрами 6, 8 тыс. в год. Накопленный опыт аналогичных предприятий показывает, что прибыль от выполнения одной заявки составляет 8 ден. ед., а потери, вызванные отказом из-за недостатка мощностей, оцениваются в 5 ден. ед., а убытки от простоя специалистов и оборудования при отсутствии заявок обходятся в 6 ден. ед. в расчете на каждую заявку.
1. Придать описанной ситуации игровую схему, установить характер игры и выявить ее
участников, указать возможные чистые стратегии сторон;
2. Составить платежную матрицу (матрицу затрат).
3. Решить задачу сведением ее к задаче линейного программирования и решить её графическим способом (т.е. найти оптимальные стратегии игроков и цену игры). Дать рекомендации о мощности ателье.
Решение.
1. Одним из участников рассматриваемой в задаче ситуации является руководство предприятия, озабоченное необходимостью выполнения определенного количества заявок. Если описанной ситуации придать игровую схему, то руководство ателье выступает в ней в качестве сознательного игрока А, заинтересованного в максимизации прибыли от выполнения заказов . Вторым участником является природа — совокупность объективных факторов (П), которая реализует свои состояния по присущим ей законам. Такого рода ситуация представляется типичной для стратегической игры.
Рассчитывая количество заявок, руководство предприятия может ориентироваться на величины: 6 тыс. ед. (первая чистая стратегия А1), либо 8 тыс. ед. (вторая чистая стратегия А2).
Природа (совокупность объективных неопределенных факторов) может реализовать состояния П1, П2, необходимое количество заявок 6, 8 тыс. ед. соответственно.
Таким образом, платежная матрица статистической игры будет иметь размерность 2х2.
2.
Платежная матрица игры представлена в табл. 2.1.
Таблица 2.1
|
|
П1=6 |
П2=8 |
тin aj |
|
A1=6 |
48 |
48-2·5=38 |
18 |
|
А2=8 |
48-2·6=36 |
64 |
36 |
При расчете элементов матрицы учтена прибыль за вычетом дополнительных затрат, связанных с недостатком мощностей, а также с убытком от простоя . Заметим, что в теории игр элементы aij обычно называются выигрышами игрока A, а наилучшей для А считается стратегия, при которой выигрыш максимизируется .
Рассмотрим ситуацию (а1;П2), т.е. случай, когда не хватает мощности на 2 тыс.
ед. при этом прибыль составит 64-2·5=54 . Так что «выигрыш» в этом случае равен 54 и т. д.
В ситуации (А2;П1) мощность превысит потребности на 8-6=2 (вес. ед.). Поэтому затраты связанные с простоем составят 2·6=12 (ед.). Следовательно, a21 = 48-2·6=36.
Рассуждая аналогично, находим и остальные элементы платежной матрицы.
Определим седловой элемент:
Матрица не имеет седлового элемента т.к. А ≠ В 36 ≤ v ≤ 48
3. Для определения оптимальных стратегий игроков по платежной матрице составляем пару двойственных задач.
Для игрока А:
f = Х1 + Х2 (min)
48Х1 +36Х2 ≥1
38Х1 +64Х2 ≥1 (1)
Хj ≥0 (j=1,2)
Для игрока В:
φ = Y1 + Y2 (max)
48Y1 + 38Y2 ≤ 1
36Y1 + 64Y2 ≤ 1 (2)
Yi ≥0 (i=1,2)
Решим задачу для игрока А графическим способом.
Строим прямые:
48Х1 +36Х2 =1 (I) по точкам (1/48, 0) и (0, 1/36)
38Х1 +64Х2 =1 (II) по точкам (1/38, 0) и (0, 1/64)
Долее определяем область допустимых решений. На рисунке 2.1 выделена граница области допустимых решений. Разрешающая прямая fmin, перпендикулярная вектору целевой функции 0,03С, засекает область в точке А, найдем координаты точки А, решив систему уравнений:
48Х1 +36Х2 =1 (16)
38Х1 +64Х2 =1 (-9)
Умножаем первое уравнение на 16, а второе на (-9), складывая, получаем:
426Х1=7, откуда Х1*=7/426
Х2* = (1 — 48∙(7/426) )/36= 5/852
fmin = 7/426 + 5/852 = 19/852
Цена игры: v = 1/fmin = 852/19.
Тогда оптимальные стратегии для игрока А:
Р1* = v∙X1* = (852/19)∙(7/426) = 14/19;
Р1* = v∙X2* = (852/19)∙(5/852) = 5/19.
Рис. 2.1
Следовательно, руководству надо ориентироваться на (6000∙14+8000∙5)/19 = 6526 заявок в год.
Решим задачу для игрока В. Так как неравенства в задаче для игрока А при оптимальном решении превращаются в строгие равенства, то оптимальное решение, найдем, решив систему:
48Y1 + 38Y2 =1 (-3)
36Y1 + 64Y2 =1 (4)
Умножаем первое уравнение на (-3), а второе на 4, складывая, получаем:
142Y2=1, откуда Y2*= 1/142 = 6/852
Y1* = (1 — 38∙(1/142))/48 = 104/(142∙48) = 13/852
fmin = 13/852 + 6/852 = 19/852
Цена игры: v = 1/ φ max = 852/19.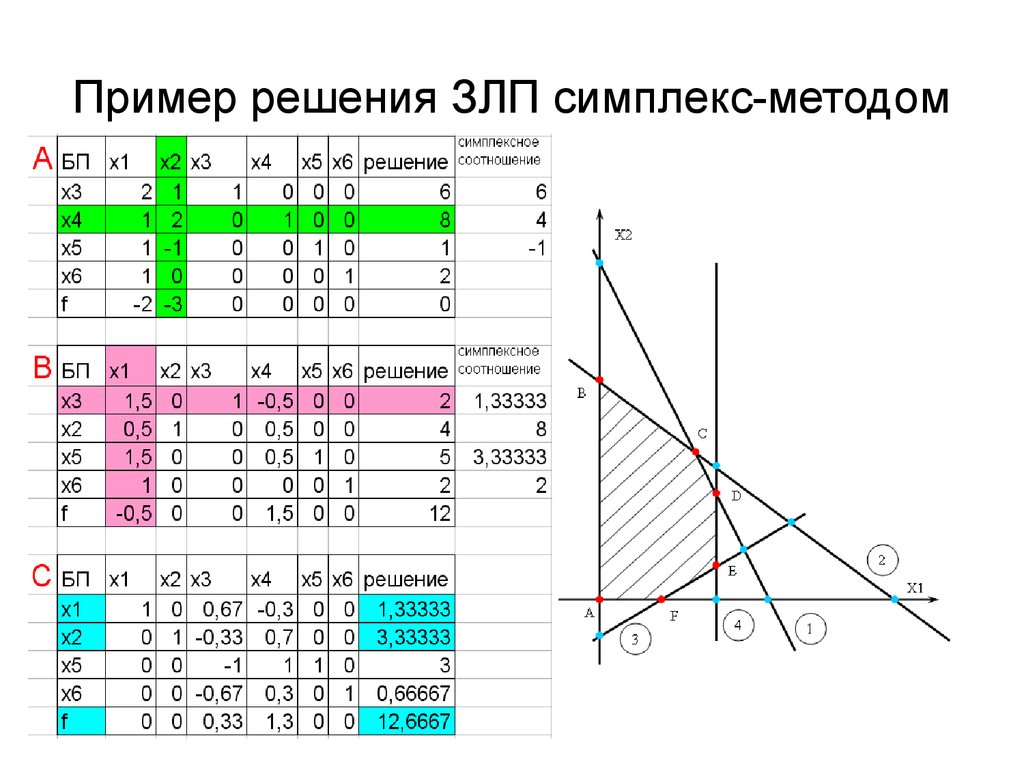
Тогда оптимальные стратегии для игрока B:
Q1* = v∙Y1* = (852/19)∙(13/852) = 13/19;
Q1* = v∙Y2* = (852/19)∙(6/852) = 6/19.
оптимизация — Графический метод в линейном программировании
спросил
Изменено 3 года, 2 месяца назад
Просмотрено 1к раз
$\begingroup$
На этой странице описывается графический метод решения линейной программы. Формулировка следующая.
$$\begin{alignat}{2} \max &\quad Z = 200W + 100B\\ \text{s.t.} &\quad 1W + 0.8B &&\leq 4000\\ &\quad 0.004W + 0.001B &&\leq 10\\ &\quad W, B &&\geq 0\end{alignat}$$
Приведенное решение:
Координаты оптимальной точки примерно 1850 з.д. и 2750 м.
в. (1850, 2750).Какой был бы простой способ вычисления оптимального решения в дополнение к оценке, видимой на графике (а не симплексным методом)? Спасибо.
- оптимизация
- линейное программирование
$\endgroup$
$\begingroup$
В примере, которым вы поделились с двумя переменными и двумя ограничениями, как вы видите на графике, ваше решение находится на пересечении двух ограничений (без учета ограничений неотрицательности). Итак, просто решите эту систему уравнений, и вы получите значения для $B$ и $W$ (что должно дать вам $B = \frac{30000}{11}$ и $W = \frac{20000}{11} $.)
Если вы хотите пойти дальше и попробовать оптимальные значения в вашей целевой функции, есть четыре угловых точки: $(0,0), (3000, 0), (0, 5000), (\frac{20000}{ 11}, \frac{30000}{11})$. Поместите эти значения в свою целевую функцию, и вы также получите целевое значение каждой точки.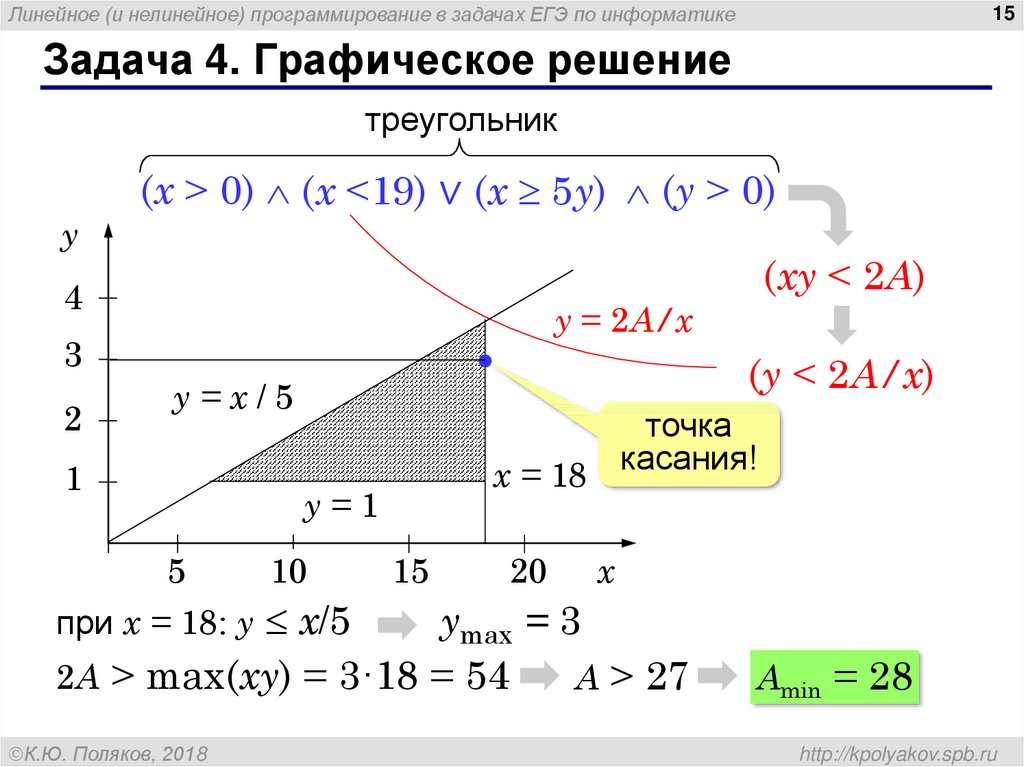
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Что такое линейное программирование и почему оно важно?30 с. В последние годы он приобрел важность из-за его применения в кодировании и искусственном интеллекте (ИИ), а также в качестве формы линейной регрессии в науке о данных. Хотя мы изучали линейное программирование в его базовой форме в школе и университете, ответ на вопрос, что такое линейное программирование, до сих пор ставит многих из нас в тупик. Этот блог поможет определить, что такое линейное программирование и как его можно использовать для решения сложных задач из реальной жизни.
Что такое линейное программирование?Линейное программирование — это способ достижения наилучшего результата, например максимальной прибыли или минимальных затрат, с использованием математической модели, представленной линейными отношениями. Он также известен как «линейная оптимизация».
Пример линейного программирования Фермер не может решить, какие культуры выращивать на участке земли размером A.
Учитывая тип почвы и погодные условия, у него есть два варианта: пшеница и просо. Однако у фермера есть ограничения с точки зрения суммы, которую он может инвестировать в удобрения (F) и пестициды (P). Предположим, что для выращивания квадратного метра урожая пшеницы требуется F1 килограммов удобрений и P1 килограммов пестицидов, а для выращивания проса требуется F2 килограммов удобрений и P2 килограммов пестицидов. Пусть S1 — цена продажи пшеницы за квадратный метр, а S2 — цена продажи проса. Если обозначить площадь земли, засеянной пшеницей и просом, соответственно за х1 и х2, то максимизировать прибыль можно, выбрав оптимальные значения х1 и х2. Его можно выразить в следующей стандартной форме:
Максимизация целевой функции (в данном случае это выручка):
S1x1+S2x2
При следующих ограничениях:
x1 +x2L
F1x1+F2x2F
P1x1+P2x2P
x10, x20 Задачи
Существует множество задач, которые можно решить с помощью линейного программирования.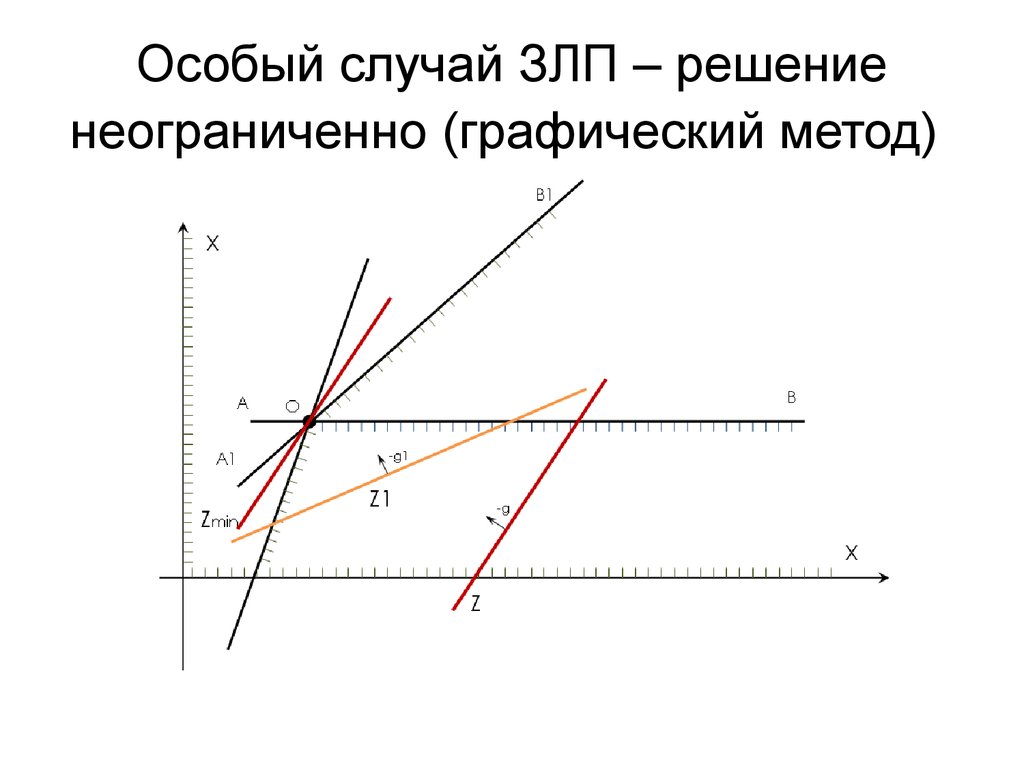
Тем не менее, наиболее распространены следующие типы:
- Производственная проблема: В основном, с которыми сталкиваются производственные компании, этот тип проблем включает в себя решение для получения максимальной прибыли или минимальных затрат с учетом различных ограничений, таких как рабочая сила, единицы продукции и время работы машины.
- Диетическая проблема: Основной целью этой проблемы является оптимизация для адекватного питания с учетом потребностей организма и связанных с этим затрат
- Транспортная задача: Этот тип задач включает в себя поиск правильных транспортных решений с учетом ограничений по стоимости и времени
- Проблема распределения ресурсов: Эта проблема связана с управлением эффективностью проекта. Основная цель состоит в том, чтобы выполнить максимальное количество задач с учетом ограничений человеко-часов и типов доступных ресурсов
Компоненты линейного программирования
1.
Переменные решенияЭто неизвестные величины в задаче оптимизации, которые необходимо решить. Например, в случае, когда компания хочет определить уровень производства на следующие двенадцать месяцев, учитывая различные ограничения, уровни производства становятся переменными решения.
2. Ограничения
Ограничения — это ограничения, которые необходимо учитывать при решении данной задачи. Например, ограничения могут касаться таких ресурсов, как время, стоимость и т. д.
3. Целевые функции
Целевые функции — это функции с действительными значениями, которые необходимо оптимизировать для достижения минимального или максимального результата при заданном наборе ограничений.
4. Ограничение неотрицательности
Переменные решения всегда должны принимать неотрицательные значения, т. е. они должны быть больше или равны 0.
Важность линейного программирования имеют простые решения. Принятие решений требует от руководителей учета множества переменных и ограничений, что затрудняет достижение ручных решений.
Программное обеспечение для линейного программирования помогает руководителям быстро и легко решать сложные проблемы, предлагая оптимальное решение.Ниже перечислены некоторые ключевые преимущества использования линейного программирования:
- Достижение оптимального использования ресурсов
- Более объективный способ принятия решений
- Обеспечение должного внимания к узким местам до возникновения проблем
- Легкая адаптация к изменениям обстоятельств
Методы решения задач линейного программирования
Общие методы, используемые для решения задач линейного программирования, включают:
- Графический метод
- Решение с использованием R
- Использование OpenSolver
- Симплексный метод
Следует отметить, что линейная программа содержит много переменных, что делает практически невозможным ее решение графическим методом.