доказать неравенство онлайн с подробным решением
Вы искали доказать неравенство онлайн с подробным решением? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и иррациональные неравенства калькулятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «доказать неравенство онлайн с подробным решением».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Где можно решить любую задачу по математике, а так же доказать неравенство онлайн с подробным решением Онлайн?
Решить задачу доказать неравенство онлайн с подробным решением вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
▶▷▶ решение неравенств с одной переменной контрольная работа
▶▷▶ решение неравенств с одной переменной контрольная работа| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 12-11-2018 |
решение неравенств с одной переменной контрольная работа — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа по линейные неравенства с одной переменной lunakids-clubru/kontrolnie-raboti/kontrolnaya Cached Контрольная работа № 8 по теме « Решение систем неравенств » 1 вариант 1Решить урок по теме «неравенства с одной переменной и их системы» При помощи линейных неравенств можно смоделироват Контрольная работа по алгебре неравенства и система doctor-qiru/kontrolnie-raboti/kontrolnaya Cached Решение линейных неравенств с одной переменной и их систем 8-й класс Уравнение с двумя переменными и его график 2 Контрольная работа по алгебре по системам неравенств sv-stefanru/kontrolnie-raboti/kontrolnaya Cached Решите неравенства: 2х НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ Контрольная работа составлена в 6 вариантах различной сложности (варианты 1 Решение Неравенств С Одной Переменной Контрольная Работа — Image Results More Решение Неравенств С Одной Переменной Контрольная Работа images Контрольная работа для 8 класса по алгебре на тему kopilkaurokovru/matematika/prochee/kontrol-naia Cached Просмотр содержимого документа « Контрольная работа для 8 класса по алгебре на тему «Неравенства с одной переменной и их системы» » Контрольная работа по алгебре неравенства с одной переменной tehnopark-tmru/kontrolnie-raboti/kontrolnaya Cached Учебно-методический материал по алгебре (8 класс) по теме: Контрольная Контрольная работа № 8 по теме « Решение систем неравенств » урок по теме «неравенства с одной переменной и их системы» Контрольная работа № 7 по теме «Неравенства» — НЕРАВЕНСТВА С wwwcompendiumsu/mathematics/algebra8/61html Cached Контрольная работа № 7 по теме «Неравенства» — НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ — НЕРАВЕНСТВА — ПОУРОЧНЫЕ РАЗРАБОТКИ ПО АЛГЕБРЕ 8 КЛАСС — поурочные разработки по алгебре для 8 Решение неравенств · Калькулятор Онлайн · с подробным решением wwwkontrolnaya-rabotaru/s/neravenstva Cached Онлайн калькулятор для решения любых уравнений, неравенств , интегралов Помощь школьникам, студентам в решении: None, можно заказать дипломную работу Решение систем неравенств с одной переменной — НЕРАВЕНСТВА С wwwcompendiumsu/mathematics/algebra8/59html Cached Глава iv НЕРАВЕНСТВА § 11 НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ Уроки 86-87 Алгебра 9 класс Контрольная работа №1 по теме: «Неравенства kopilkaurokovru/matematika/prochee/alghiebra_9 Cached Контрольная работа для 8 класса по алгебре на тему «Неравенства с одной переменной и их системы» контрольная работа по алгебре в 8 классе неравенства системы кампусятарф/blog/45180html Cached Решение неравенств с одной переменной и их систем 122 Алгебра, 8 класс, Контрольные работы, Александрова Л Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 12,100 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- которые ведут преподавание курса геометрии по учебнику ЛС Атанасяна » Геометрия 10-11″ издательства «Просвещение» Читать ещё Контрольные работы по геометриидля 9 класса ориентированы на учебник » Геометрия
- ВФ Бутузов
- 7-е изд
составлены в 4 вариантах к учебнику ЛС Атанасян контрольная работа по геометрии 9 класс контрольная работа дается учащимся как домашнее задание Контрольные работы по геометрии (7 кл) Скрыть 4 Решение контрольных | КОНТРОЛЬНЫЕ РАБОТЫ reshebnik5-11ru › Смотреть решебник › …/GDZ/geometrija9-1pdf Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы Задачи повышенной сложности АВ Тронин Решение контрольных и самостоятельных работ по геометрии за 9 класс к пособию «Дидактические материалы по геометрии для 9 класса / БГ Зив Читать ещё Контрольные работы Задачи повышенной сложности АВ Тронин Решение контрольных и самостоятельных работ по геометрии за 9 класс к пособию «Дидактические материалы по геометрии для 9 класса / БГ Зив — 7-е изд — М: Просвещение
7- 9 » (ЛС Атанасян
- можно заказать дипломную работу Решение систем неравенств с одной переменной — НЕРАВЕНСТВА С wwwcompendiumsu/mathematics/algebra8/59html Cached Глава iv НЕРАВЕНСТВА § 11 НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ Уроки 86-87 Алгебра 9 класс Контрольная работа №1 по теме: «Неравенства kopilkaurokovru/matematika/prochee/alghiebra_9 Cached Контрольная работа для 8 класса по алгебре на тему «Неравенства с одной переменной и их системы» контрольная работа по алгебре в 8 классе неравенства системы кампусятарф/blog/45180html Cached Решение неравенств с одной переменной и их систем 122 Алгебра
- студентам в решении: None
- можно заказать дипломную работу Решение систем неравенств с одной переменной — НЕРАВЕНСТВА С wwwcompendiumsu/mathematics/algebra8/59html Cached Глава iv НЕРАВЕНСТВА § 11 НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ Уроки 86-87 Алгебра 9 класс Контрольная работа №1 по теме: «Неравенства kopilkaurokovru/matematika/prochee/alghiebra_9 Cached Контрольная работа для 8 класса по алгебре на тему «Неравенства с одной переменной и их системы» контрольная работа по алгебре в 8 классе неравенства системы кампусятарф/blog/45180html Cached Решение неравенств с одной переменной и их систем 122 Алгебра
Математика
Преподаватель Никифорова Светлана Витальевна, кандидат физико-математических наук, старший преподаватель кафедры Специальной математики КНИТУ-КАИ, имеет большой опыт работы со абитуриентами, в том числе с иностранными, является автором методических указаний по подготовке к ЕГЭ.
В современной науке и технике математические методы моделирования, исследования и проектирования играют все большую роль. Это обусловлено, прежде всего, быстрым развитием вычислительной техники, благодаря которой все время существенно расширяются возможности успешного применения математики при решении задач в различных областях знаний и техники.
Цель математического образования – овладение слушателями необходимым математическим аппаратом, системой навыков и умений, дающими основание научно правильно понимать своеобразие отражения математикой простейших законов о количественных отношениях и пространственных формах в природе, обществе и производстве, помогающими моделировать, анализировать и решать прикладные инженерные задачи.
Курс предназначен для учащихся старших классов и выпускников средних школ с целью оказания им помощи при закреплении навыков и умений по решению математических задач, необходимых при сдаче экзамена, а также для всех желающих изучать математику. Учебный материал включает в себя 7 модулей, в каждом из которых содержатся краткие теоретические сведения по основным разделам математики, методические указания, необходимые теоремы и формулы, видеолекции, интересные факты из математики, примеры различного уровня сложности с подробным решением, задачи для самоконтроля с ответами (домашнее задание), контрольные задания (тесты).
Учебный материал включает в себя 7 модулей, в каждом из которых содержатся краткие теоретические сведения по основным разделам математики, методические указания, необходимые теоремы и формулы, видеолекции, интересные факты из математики, примеры различного уровня сложности с подробным решением, задачи для самоконтроля с ответами (домашнее задание), контрольные задания (тесты).
Структура курса
МОДУЛЬ 1. ЧИСЛА.
— Лекция 1.1. «Числа»
— Лекция 1.2. «Задачи повышенной сложности»
Краткое описание модуля:
Числа: натуральные, целые, рациональные, иррациональные, действительные и арифметические операции с ними. Свойства степени с натуральным показателем. Свойства степени с рациональным показателем. Свойства арифметических корней. Вычисление арифметических выражений. Формулы сокращенного умножения. Вычисление арифметических выражений. Преобразование алгебраических выражений. Решение задач повышенной сложности.
МОДУЛЬ 2. УРАВНЕНИЯ.
— Лекция 2.1. «Уравнения»
— Лекция 2.2. «Решение нестандартных уравнений»
— Лекция 2.3. «Решение нестандартных уравнений (продолжение)»
Краткое описание модуля:
Линейные уравнения, линейные уравнения с параметром. Методы решения систем линейных уравнений. Уравнения, содержащие неизвестную величину под знаком модуля. Квадратные уравнения и приводящиеся к ним. Теорема Виета. Рациональные уравнения высших степеней. Системы рациональных уравнений. Иррациональные уравнения. Замена переменных в иррациональном уравнении. Решение нестандартных уравнений.
МОДУЛЬ 3. НЕРАВЕНСТВА.
— Лекция 3.1. «Неравенства»
— Лекция 3.2. «Интересное о неравенствах»
Краткое описание модуля:
Линейные неравенства, системы линейных неравенств. Неравенства, содержащие неизвестную величину под знаком модуля.
МОДУЛЬ 4. ТРИГОНОМЕТРИЯ.
— Лекция 4. «Тригонометрия»
Краткое описание модуля:
Тригонометрические функции, их свойства. Формулы приведения. Формулы зависимости между тригонометрическими функциями одного и того же аргумента. Формулы двойного аргумента. Формулы понижения степени. Формулы сложения аргументов. Формулы преобразования суммы тригонометрических функций в произведение. Формулы преобразования произведений тригонометрических функций в сумму. Универсальная тригонометрическая подстановка. Обратные тригонометрические функции, их свойства. Тригонометрические уравнения: простейшие тригонометрические уравнения, замена переменных в тригонометрическом уравнении, однородные тригонометрические уравнения, введение вспомогательного аргумента.
МОДУЛЬ 5. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА.
— Лекция 5. «Показательные и логарифмические уравнения и неравенства»
Краткое описание модуля:
Показательная функция, ее свойства. Показательные уравнения: уравнения, содержащие одинаковые основания; уравнения, содержащие два различных основания; уравнения, содержащие три различных основания; замена переменных в показательных уравнениях. Логарифмическая функция, ее свойства. Основное логарифмическое тождество. Формула перехода к новому основанию. Логарифмические уравнения. Область допустимых значений в логарифмических уравнениях. Показательно-логарифмические и логарифмически-показательные уравнения. Показательные неравенства. Логарифмические неравенства.
МОДУЛЬ 6. ТЕКСТОВЫЕ ЗАДАЧИ.
— Лекция 6. «Текстовые задачи»
Краткое описание модуля:
Решение текстовых задач. Задачи на пропорции, проценты, смеси. Задачи на целые числа. Задачи на работу. Задачи на движение.
Задачи на пропорции, проценты, смеси. Задачи на целые числа. Задачи на работу. Задачи на движение.
МОДУЛЬ 7. ГЕОМЕТРИЯ.
— Лекция 7.1. «Геометрия»
— Лекция 7.2. «Планиметрия»
— Лекция 7.3. «Стереометрия»
Краткое описание модуля:
Основные теоретические сведения из геометрии, история её возникновения и становления. Планиметрия. Решение задач с треугольником. Четырехугольники и многоугольники. Окружность, круг, вписанные углы, касательная и секущая. Вписанные и описанные многоугольники. Комбинации геометрических тел. Стереометрия. Многогранники: призма, пирамида. Фигуры вращения: конус, цилиндр, шар. Комбинации тел вращения.
Иррациональные неравенства (ЕГЭ 2022) | YouClever
Иррациональные неравенства – коротко о главном
Определение
Иррациональное неравенство – это неравенство, содержащее переменную под корнем
Неравенства вида \( \sqrt{A}\ge \sqrt{B}\)
\( \sqrt{A}\ge \sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A\ge B\\B\ge 0\end{array} \right. \)
\)
или
\( \sqrt{A}>\sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A>B\\B\ge 0\end{array} \right.\)
Неравенства вида \( A\sqrt{B}>0\) или \( A\sqrt{B}<0\)
\( A\sqrt{B}>0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A>0\end{array} \right.\)
или
\( A\sqrt{B}<0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A<0\end{array} \right.\)
Неравенства вида \( A\sqrt{B}\ge 0\)
\( A\sqrt{B}\ge 0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}B=0\\\left\{ \begin{array}{l}A\ge 0\\B\ge 0\end{array} \right.\end{array} \right.\)
или
\( A\sqrt{B}\le 0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}B=0\\\left\{ \begin{array}{l}A\le 0\\B\ge 0\end{array} \right.\end{array} \right.\)
Неравенства вида \( \sqrt{A}\ge B\)
\( \sqrt{A}\ge B\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}\left\{ \begin{array}{l}B\le 0\\A\ge 0\end{array} \right.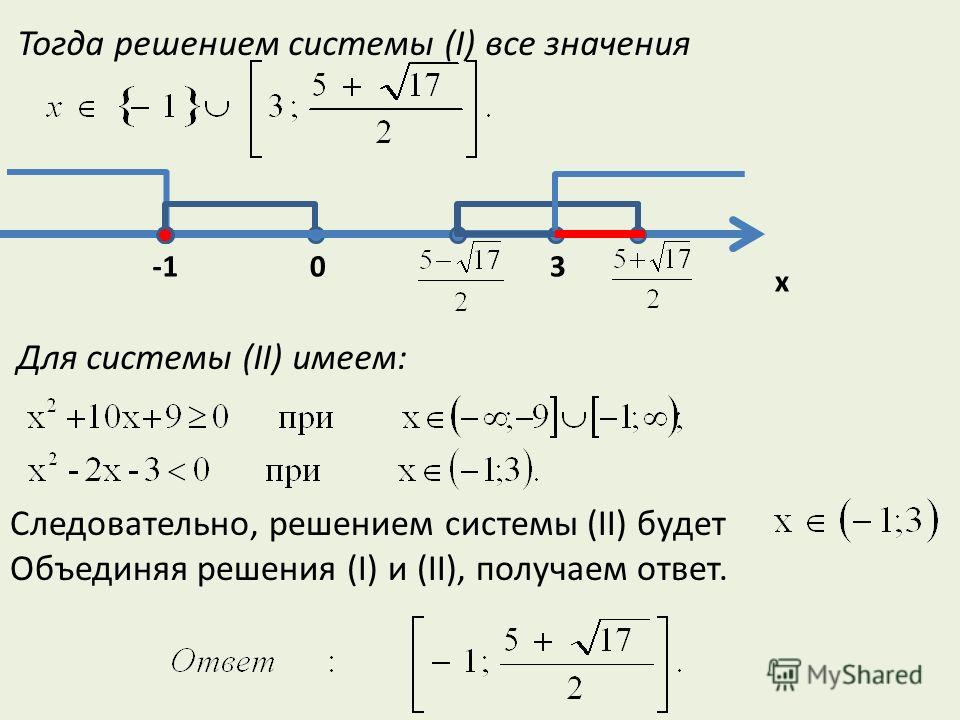 {-1}$ или $x-1<2 \Rightarrow x<3$
{-1}$ или $x-1<2 \Rightarrow x<3$
В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$
Ответ. $x \in(1 ; 3)$
Больше примеров решений2. Решение логарифмического неравенства вида $$\log _{a} f(x) \lt \log _{a} g(x)$$ равносильно решению следующих систем:
а) б)
Неравенство $\log _{a} f(x)>\log _{a} g(x)$ в каждом из двух случаев сводится к одной из систем:
$$00 \end{array}\right.$$ $$a>1:\left\{\begin{array}{l} f(x)>g(x) \\ g(x)>0 \end{array}\right.$$Слишком сложно?
Логарифмические неравенства не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Решить неравенство $\log _{5} 5>\log _{5} x$
Решение. Данное неравенство равносильно системе:
$$\left\{\begin{array}{l} 5>x, \\ x>0 \end{array} \Rightarrow\left\{\begin{array}{l} x0 \end{array} \Rightarrow x \in(0 ; 5)\right. \right.$$
\right.$$Ответ. $x \in(0 ; 5)$
Больше примеров решенийЧитать дальше: примеры решения задач с логарифмами.
Метод рационализации при решении логарифмических неравенств | Материал для подготовки к ЕГЭ (ГИА) по алгебре (11 класс) по теме:
Метод рационализации
Составитель текста – Прокофьева Т.А. (МБОУ СШ №12)
Как известно, ЕГЭ по Математике длится 235 минут, и чтобы распределить это время рационально на все задания, не помешало бы узнать короткие пути решения той или иной задачи. Так, на С3(задача №15), оцениваемое в 3 балла, рекомендовано 30 минут (при условии, что ученик намерен решать все задания). Если проводить решение согласно всем известному методу интервалов, то, возможно, вы потратите все отведенное на него время. Существует ли такой метод решения неравенств, при котором мы сможем упростить наши вычисления, тем самым сохранив время?
Это метод рационализации (оптимизации, декомпозиции, замены множителей, замены функций, обобщенный метод интервалов, правило знаков)
Теоретическое обоснование метода
Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. 0 в области определения F(x).
0 в области определения F(x).
f, g, h – выражения с переменной х, a – фиксированное число или функция ( а>0, a≠1).
Выражение F | Выражение G | |
1 | ||
2 | ||
3 | ||
4 | ||
5 | ||
6 |
Из данных выражений можно вывести некоторые следствия (с учетом области определения):
0 ⬄ 0
В указанных равносильных переходах символ ^ заменяет один из знаков неравенств: >,
Комментарий.
Стандартные ошибки, которые допускают учащиеся при использовании метода рационализации, заключаются в следующем:
а) проводят рационализацию без учета области определения данного неравенства;
б) применяют метод рационализации к неравенствам, не приведенным к стандартному виду F(x) ˅ 0;
в) формально применяют метод рационализации к выражениям вида
, заменяя на выражение ;
г) подменяют формулировку «о совпадении знаков выражений для каждого
допустимого значения х» на неверную формулировку «о совпадении значений
выражений для каждого допустимого значения х».
Для решения:
1) Рассмотрим пример решения логарифмического неравенства двумя методами
1. Метод интервалов
О.Д.З.
a) b)
-1
Ответ: ( ;
2. Метод декомпозиции (рационализации)
Метод декомпозиции (рационализации)
Ответ: ( ;
2) №17 из варианта 22 сборника Ященко И.В. 2015г.
1)
2) ,
,
,
, ,
,
,
, ;
- U U .
Ответ. , , .
3) №17 из варианта 23 сборника Ященко И.В. 2015г.
Решение.
- ,
,
,
,
;
- ,
Ответ.
4)№17 из варианта 18 сборника Ященко И.В. 2015г.
1)
2) ,
,
,
, , , ,
, .
3) U .
Ответ. , .
5) №17 из варианта 13 сборника Ященко И.В. 2015г
,
1) .
2) ,
,
, ,
.
3) .
Ответ. .
.
6)log12x2-41+35(3 – x) ≥ log2x2-5x+3(3- x).
Решение. Запишем неравенство в виде log12x2-41+35(3 – x) — log2x2-5x+3(3- x) ≥ 0 и заменим его равносильной системой, используя метод рационализации
Для решения первых трёх неравенств системы используем метод интервалов.
Ответ:
7) ≥ 0.
Решение. Заменим данное неравенство равносильной системой, используя метод рационализации
При решении неравенства (х – 1)(х – 2) x 0, x ≠ 1. Условие 1 позволяет исключить множитель x – 1 > 0 в первом неравенстве системы.
Ответ: .
Дополнительно
[0; 4]
Ответ: [0; 4]
-2
Ответ:
Решение:
Ответ: (-1;1) U (3;5)
11) Решите неравенство log 2x+3 x2
Решение. Запишем неравенство в виде log2x+3×2 – 1
Запишем неравенство в виде log2x+3×2 – 1
(2x + 2)(x2 – 2x – 3)
2x + 3 > 0
x ≠ 0
(x + 1)(x + 1)(x – 3)
x > 1,5
x ≠ 0
Ответ: (-1.5; -1) (-1; 0) (0; 3).
12) Решите неравенство log|x+2|(4 + 7x – 2×2) ≤ 2.
Решение. Запишем нераенство в виде log|x + 2|(4 + 7x – 2×2) – log|x + 2|(x + 2)2 ≤ 0 и заменим равносильной системой, используя метод рационализации
(|x + 2| — 1)(4 + 7x – 2×2 – x2 – 4x – 4) ≤ 0
4 +7x — 2×2 > 0
x + 2 ≠ 0
((x + 2)2 – 1)(-3×2 + 3x) ≤ 0
(x + 0,5)(x – 4)
x ≠ 2
x(x + 1)(x + 3)(x – 1) ≥ 0
(x + 0,5)(x – 4)
x ≠ 2
Ответ: ( -0,5; 0] [1; 4).
13) .
Решение. Получим следующую систему неравенств:
Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:
Откуда: .
Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство
.
Умножим второй сомножитель на -1 и поменяем знак неравенства:
.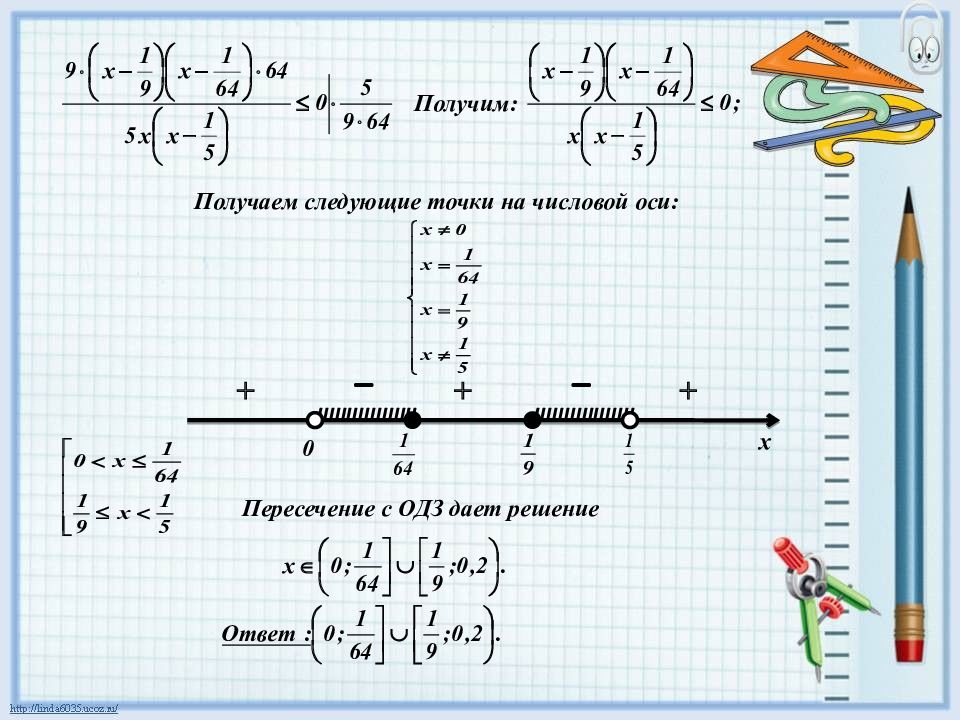
Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:
.
Это неравенство легко решить методом интервалов: .
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ: .
14) ) №17 из варианта 26 сборника Ященко И.В. 2015г.
1 способ(метод рационализации)
Решение.
- .
- ,
,
,
, ,
.
- .
Ответ. .
2 способ
,
1) Область определения
2) Логарифмическая функция с основанием большем 2 является возрастающей, тогда
а) нет решений
б) .
3)
15) №17 из варианта 4 сборника Ященко И.В. 2015г.
Решение.
- ,
,
,
,
,
,
,
,
, , ,
, , .
- , .
Ответ. , .
16) №17 из варианта 27 сборника Ященко И.В. 2015г.
- ,
,
,
,
,
,
,
,
.
- .
Ответ. .
17)
,
,
- ,
,
,
,
,
.
- , .
Ответ. .
18) .
1)
2) , ,
, ,
3) .
Ответ. .
Дополнительно для самостоятельного решения:
- . Ответ. .
- . Ответ. , .
- . Ответ.
- . Ответ. .
- . Ответ. .
- . Ответ. .
- . Ответ. .
- . Ответ. .
- . Ответ. .
- .
Ответ. .
Для работы с учениками:
Детям нужно рекомендовать использование метода рационализации в логарифмических неравенствах, когда неизвестное находится в основании степени.
Для отработки навыка решения предлагать решение в 3действия:
- Найти область определения неравенства.
- Использование замены функций по формулам рационализации.
- Решить систему всех полученных условий.
Список литературы:
- Семенов А.Л., Ященко И.В. Математика 2015. 50 вариантов. М.: Экзамен, 2015
- Корянов А.Г., Прокофьев А.А. Математике ЕГЭ 2014. Типовые задания С3. Методы решения неравенств с одной переменной. www.alexlarin.net
- Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка к ЕГЭ – 2014. Решаем задание С3 методом рационализации. Ростов-на-Дону: Легион, 2013
- Дмитрий Гущин. Математика. ЕГЭ – 2013: экспресс-курс для подготовки к экзамену. М.: Комсомольская правда, 2013
Решение логарифмических уравнений и систем уравнений. Подготовка к ЕГЭ
Ученик проходит в несколько лет дорогу, на которую человечество употребило тысячелетие.

Однако его следует вести к цели не с завязанными глазами, а зрячим:
он должен воспринимать истину, не как готовый результат, а должен её открывать.
Учитель должен руководить этой экспедицией открытий, следовательно, также присутствовать
не только в качестве простого зрителя. Но ученик должен напрягать свои силы;
ему ничто не должно доставаться даром.
Даётся только тому, кто стремится.
(А. Дистервег)
Форма урока: комбинированный урок
Тип урока:
Урок повторного контроля знаний.Обобщение и закрепление пройденного материала.
Цели урока:
- Образовательная — обобщение знаний учащихся
по теме «Логарифмические уравнения и системы
уравнений; закрепить основные приемы и методы
решения логарифмических уравнений и систем
уравнений; ознакомить учащихся с видами заданий
повышенной сложности по данной теме в ЕГЭ.

- Развивающая — развитие логического мышления для сознательного восприятия учебного материала, внимание, зрительную память, активность учащихся на уроке. Предоставить каждому из учащихся проверить свой уровень подготовки по данной теме.
- Воспитывающая — воспитание познавательной активности, формирование личностных качеств: точность и ясность словесного выражения мысли; сосредоточенность и внимание; настойчивость и ответственность, положительной мотивации к изучению предмета, аккуратности, добросовестности и чувство ответственности. Осуществить индивидуальный подход и педагогическую поддержку каждого ученика через разноуровневые задания и благоприятную психологическую атмосферу.
Задачи урока:
- выработать у учащихся умение пользоваться
алгоритмом решения логарифмических уравнений.

- осуществить формирование первоначальных знаний в виде отдельных навыков после определенной тренировки решения уравнений и систем уравнений.
- познакомить учащихся с частными случаями и отработать навыки по решению таких уравнений и систем уравнений.
Методы и педагогические приемы:
- Методы самообучения
- Приемы устного опроса.
- Приемы письменного контроля.
- Коллективная учебная деятельность.
- Организация работы в группах.
- Повышение интереса к учебному материалу.
Оборудование:
- компьютер, мультимедийный проектор и экран;
- тетради;
Раздаточный материал: задания для самостоятельной работы.
План урока:
- Организационный момент (1 мин)
- Проверка домашнего задания (3 мин)
- Входной контроль (повторение теоретического материала) (15 мин)
- Этап обобщения знаний учащихся.
 Решение
уравнений и систем уравнений (45 мин)
Решение
уравнений и систем уравнений (45 мин) - Разноуровневая самостоятельная работа (проверка знаний учащихся) (20 мин)
- Итоги урока (4 мин)
- Домашнее задание (2 мин)
Ход урока
1. Организационный момент
Взаимное приветствие; проверка готовности учащихся к уроку, организация внимания.
2. Проверка домашнего задания
Установить правильность и осознанность выполнения домашнего задания всеми учащимися; установить пробелы в знаниях.
3. Входной контроль (повторение теоретического материала)
Организация устной фронтальной работы с классом по повторению логарифмических формул и способов решения логарифмических уравнений.
Решение простейших уравнений:
Сравните числа:
а) и
б) и
2) Найдите Х, если х>0:
[1/5]
[4]
Перечислите: основные способы решения
логарифмических уравнений.
Способы решения логарифмических уравнений
- По определению логарифма.
- Метод потенцирования.
- Метод введения новой переменной.
- Решение уравнений логарифмированием его обеих частей.
- Функционально-графический способ.
На экране уравнения:
- log2(3 — 6x) = 3
- lg(х2 — 2х) = lg (2х + 12)
- 5х + 1 — 5 х — 1 = 24
- хlg х = 10000
- 32х + 5 = 3х + 2 + 2
- log32x — log3 x = 3
- log2x — log4x = 3
- 2x = x2 — 2x
Среди данных уравнений выбрать логарифмические. Определить способ решения каждого уравнения. Решите уравнения.
По окончанию работы правильность решения уравнений осуществляется с помощью экрана.
Устно ответить на следующие вопросы (если имеется не один корень):
- Найти наименьший корень уравнения.
- Найти сумму корней уравнения.
- Найти разность корней уравнения.
- Найти произведение корней уравнения.
- Найти частное корней уравнения
Самооценка и взаимооценка деятельности учащихся (результаты заносятся в листы самоконтроля).
4. Этап обобщения знаний учащихся
Решение логарифмических уравнений из заданий ЕГЭ части В и С.
№ 1 (В) Найдите корень (или сумму корней, если их несколько) уравнения log6(3x + 88) — log6 11 = log6 x. [1]
№ 2 (B) Найдите произведение всех корней уравнения
. [1]
№ 3 (B) Найдите сумму корней уравнения = log4 (x — 3) + 2. [2]
№ 4 (C) найти наибольший корень уравнения: log2(2+5)+ log0,5(-х-0,5) = 1 [-4]
№ 5 (C) Решите уравнение — log6x + 34 = ()2 + x. [2]
Уравнения №1-3 решает по два ученика на обратных крыльях доски с последующей проверкой решения всем классом.
Уравнение №4,5 решает ученик с подробным комментарием.
По окончании самооценка и взаимооценка учащихся (результаты заносятся в листы самоконтроля).
Простейшими логарифмическими уравнениями будем называть уравнения следующих видов:
log a x = b, a > 0, a 1.
log a f(x) = b, a > 0, a 1.
log f(x) b = c, b > 0.
Эти уравнения решаются на основании определения логарифма: если logb a = c, то a = b c.
Решить уравнение log2 x = 3.
Решение. Область определения уравнения x > 0. По определению логарифма x = 23, x = 8 принадлежит области определения уравнения.
Ответ: x = 8.
Уравнения вида loga f(x) = b, a > 0, a 1.
Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x).
Обычно область определения находится отдельно, и после решения уравнения f(x) = ab проверяется, принадлежат ли его корни области определения уравнения.
Пример. Решить уравнение log3(5х — 1) = 2.
Решение:
ОДЗ: 5х — 1 > 0; х > 1/5.
log3(5х- 1) = 2,
log3(5х — 1) = log332,
5х — 1 =9,
х = 2.
Ответ: 2.
Пример. Решить уравнение
Решение. Область определения уравнения находится из неравенства 2х2 — 2х — 1 > 0. Воспользуемся определением логарифма:
Применим правила действий со степенями, получим 2х2 — 2х — 1 = 3. Это уравнение имеет два корня х = -1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2х2 — 2х — 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями.
Ответ. х1 = -1, х2 = 2.
Уравнения вида logf(x) b = с, b > 0.
Уравнения этого вида решаются по определению логарифма с учётом области определения уравнения. Данное уравнение равносильно следующей системе
Чаще всего, область определения логарифмического уравнения находится отдельно, и после решения уравнения (f(x))c = b или равносильного уравнения проверяется, принадлежат ли его корни найденной области.
Пример. Решить уравнение
logx-19 = 2.
Решение. Данное уравнение равносильно системе
Ответ. x = 4.
2.. Потенцирование.
Суть метода заключается в переходе от уравнения
log a f(x) = log a g(x) к уравнению f(x) = g(x), которое обычно не равносильно исходному.
Уравнения вида
loga f(x) = loga g(x) , а > 0, а ?1.
На основании свойства монотонности логарифмической функции заключаем, что f(x) = g(x).
Переход от уравнения loga f(x) = loga g(x) к уравнению f(x) = g(x) называется потенцированием.
Нужно отметить, что при таком переходе может нарушиться равносильность уравнения. В данном уравнении f(x) > 0, g(x) > 0, а в полученном после потенцирования эти функции могут быть как положительными, так и отрицательными. Поэтому из найденных корней уравнения f(x) = g(x) нужно отобрать те, которые принадлежат области определения данного уравнения. Остальные корни будут посторонними.
Пример. Решить уравнение log3 (x2 — 3x — 5) = log3 (7 — 2x).
Решение. Область определения уравнения найдётся из системы неравенств:
x2 — 3x — 5>0, 7 — 2x>0
х> -1,5+ , х<3,5
х2 <-1,5-
Потенцируя данное уравнение, получаем х2 — 3х — 5 = 7 — 2х,
х2 — х — 12 = 0, откуда х1 = -3, х2 = 4. Число 4 не удовлетворяет системе неравенств.
Ответ. х = -3.
Cведение уравнений к виду log a f(x) = log a g(x) с помощью свойств логарифмов по одному основанию.
Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log a f(x) = log a g(x) используются следующие свойства логарифмов:
logb a + logb c = logb (a*c), где a > 0; c > 0; b > 0, b 1,
logb a — logb c = logb (a/c), где a > 0; c > 0; b > 0, b 1,
m logb a = logb a m, где a > 0; b > 0, b 1; m R.
Пример 1. Решить уравнение log6 (x — 1) = 2 — log6 (5x + 3).
Решение. Найдём область определения уравнения из системы неравенств
Применяя преобразования, приходим к уравнению
log6 (x — 1) + log6 (5x + 3) = 2,
log6 ((x — 1)(5x + 3)) = 2, далее, потенцированием, к уравнению
(х — 1)(5х + 3) = 36, имеющему два корня х = -2,6; х = 3. Учитывая область определения уравнения, х = 3.
Ответ. х = 3.
Пример 2. Решить уравнение
Решение. Найдём область определения уравнения, решив неравенство (3x — 1)(x + 3) > 0 методом интервалов.
Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log5 (x + 3) 2 = 0. По определению логарифма (х + 3) 2 = 1, х = -4, х = -2. Число х = -2 посторонний корень.
Ответ. х = -4.
Пример 3. Решить уравнение log2 (6 — x) = 2 log6 x.
Решение. На области определения 0 < x < 6 исходное уравнение равносильно уравнению 6 — x = x2, откуда х = -3, х = 2. Число х = -3 посторонний корень.
Ответ. х = 2.
Уравнения вида Alog a f(x) + Blog b g(x) + C = 0.
Метод потенцирования применяется в том случае, если все логарифмы, входящие в уравнение, имеют одинаковое основание. Для приведения логарифмов к общему основанию используются формулы:
Пример 1. Решить уравнение
Решение. Область определения уравнения 1 < x < 2. Используя формулу (3), получим
Так как 3 = log28, то на области определения получим равносильное уравнение (2-x)/(x-1) = 8, откуда x = 10/9.
Ответ. x = 10/9.
Пример 2. Решить уравнение
Решение. Область определения уравнения x > 1. Приведём логарифмы к основанию 3, используя формулу (4).
Ответ. х = 6.
Пример 3. Решить уравнение
Решение. Область определения уравнения x > -1, x 0. Приведём логарифмы к основанию 3, используя формулу (2).
Умножим обе части уравнения на log 3(x + 1) ? 0 и перенесем все слагаемые в левую часть уравнения. Получим (log 3(x + 1)-1)2 = 0, откуда log 3(x + 1) = 1 и x = 2.
Ответ. x = 2.
3. Введение новой переменной
Рассмотрим два вида логарифмических уравнений, которые введением новой переменной приводятся к квадратным.
Уравнения вида
где a > 0, a 1, A, В, С — действительные числа.
Пусть t = loga f(x), t R. Уравнение примет вид t2 + Bt + C = 0.
Решив его, найдём х из подстановки t = loga f(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.
Пример 1. Решить уравнение lg 2 x — lgx — 6 = 0.
Решение. Область определения уравнения - интервал (0; ).Введём новую переменную t = lg x, t R.
Уравнение примет вид t 2 — t — 6 = 0. Его корни t1 = -2, t2 = 3.
Вернёмся к первоначальной переменной lg x = -2 или lg x = 3, х = 10 -2 или х = 10 3.
Оба значения x удовлетворяют области определения данного уравнения (х > 0).
Ответ. х = 0,01; х = 1000.
Пример 2. Решить уравнение
Решение. Найдём область определения уравнения
Применив формулу логарифма степени, получим уравнение
Так как х < 0, то | x | = —x и следовательно
Введём новую переменную t = log3 (-x), t принадлежит R. Квадратное уравнение t 2 — 4t + 4 = 0
имеет два равных корня t1,2 = 2. Вернёмся к первоначальной переменной log3 (-x) = 2, отсюда —х = 9, х = -9. Значение неизвестной принадлежит области определения уравнения.
Ответ. х = -9.
Уравнения вида
где a > 0, a 1, A, В, С — действительные числа, A 0, В 0.
Уравнения данного вида приводятся к квадратным умножением обеих частей его на loga f(x) 0. Учитывая, что loga f(x) logf(x) a=1
(свойство logb a = 1/ loga b), получим уравнение
Замена loga f(x)=t, t R приводит его к квадратному At2 + Ct + B = 0.
Из уравнений loga f(x)= t1, logb f(x)= t2 найдем значения x и выберем среди них принадлежащие области определения уравнения:
f(x) > 0, f(x) 1.
Пример. Решить уравнение
Решение. Область определения уравнения находим из условий x+2>0, x+2 1, т.е. x >-2, x -1.
Умножим обе части уравнения на log5 (x+2) 0, получим
или, заменив log5(x+2) = t, придем к квадратному уравнению
t 2 — t — 2 = 0, t1 = -1, t2 =2.
Возвращаемся к первоначальной переменной:
log5 (x+2) = -1, x+2 = 1/5, x = -9/5,
log5 (x+2) = 2, x+2 = 25, x = 23.
Оба корня принадлежат области определения уравнения.
Ответ: x = -9/5, x = 23.
в) log2х — 2 logх2 = -1
Решение:
ОДЗ: x > 0, х 1
Используя формулу перехода к новому основанию, получим
Обозначим
Ответ:
4. Приведение некоторых уравнений к логарифмическим логарифмированием обеих частей.
Переход от уравнения вида f(x) = g(x) к уравнению loga f(x) = loga g(x), который возможен если f(x) >0, g(x) >0, a >0, a 1, называется логарифмированием.
Методом логарифмирования можно решать:
Уравнения вида
Область определения уравнения — интервал (0, ). Прологарифмируем обе части уравнения по основанию a, затем применим формулы логарифма степени и произведения
Приведем подобные и получим линейное уравнение относительно loga x.
Пример. Решить уравнение 32log4x+2=16x2.
Решение. Область определения x >0. Прологарифмируем обе части по основанию 4.
Используя свойства логарифмов, получим
Ответ: x = 1/4
Уравнения вида
Область определения уравнения — интервал (0, ). Прологарифмируем обе части уравнения по основанию a, получим
Применим формулы логарифма степени и логарифма произведения
Введем новую переменную t=loga x , t R. Решив квадратное уравнение At2 + (B-а)t-loga C=0, найдем его корни t1 и t2. Значение x найдем из уравнений t1 = loga x и t2=loga x и выберем среди них принадлежащие области определения уравнения.
Пример 1. Решить уравнение
Решение. Область определения уравнения х > 0. Так как при х > 0 обе части уравнения положительны, а функция y = log3 t монотонна, то
(1 + log3 x) log3 x = 2.
Введём новую переменную t, где t = log3 x, t R.
(1 + t) t = 2, t 2 + t — 2 = 0, t1 = -2, t2 = 1.
log3 x = -2 или log3 x = 1,
x = 1/9 или х = 3.
Ответ. х = 1/9; х = 3.
Пример 2. Решить уравнение
Решение. Область определения уравнения х >1. Обе части уравнения положительны, прологарифмируем их по основанию 2, получим
Применим формулы логарифма степени и логарифма частного:
Введем новую переменную t=log2x, получим квадратное уравнение t2 — 3t + 2 = 0,
t1 = 2, t2 = 1, тогда log2x = 2 или log2x =1.
Ответ. x = 4, x = 2.
1) Найти наибольший корень уравнения: lq(x+6) - 2 = 1/2lq(2x -3) — lq25
2) log0,5(log4(1/х)) + log4(log2(16х2)) =0
3) Пусть (х0;y0) — решение системы уравнений
Найти x0 +y0
Решение:
x0 +y0 =1,8+1,1=2,9
Ответ: 2,9.
4) Пример .Решите систему уравнений
у-1оg3х = 1,
хy=312.
Решение. Решим эту систему методом перехода к новым переменным:
u = у, v = -1оg3х.
Заметим, что x>0 и у R является областью определения данной системы.
Логарифмируя обе части второго уравнения по основанию 3, получим:
у 1оg3 х = 12 или у(- 1оg3х) = -12.
u + v = 1,
Итак,
u v = -12.
Тогда по обратной теореме Виета переменные и и v являются корнями квадратного уравнения
z2 -z-12 = 0
Следовательно, решения данной системы найдем как множество решений совокупности двух систем а) и б):
а) б)
Решениями указанных систем являются соответственно пары (27;4), (; -3).
Ответ: (27; 4), (; -3).
5) Пример. Решите систему уравнений
ху = 24
1оg22 х + 1оg22 y = 10.
Решение.
Перейдем к новым переменным:
1оg 2 х = и,
x = 2u>0, 1оg2 у = v, у = 2v >0.
В новых переменных данная система имеет вид:
Следовательно, и и v являются корнями квадратного уравнения :
z 2-42 + 3 = 0
Отсюда следует, что достаточно решить систему
Другое решение найдем из-за симметричности х и у, т. е. если (х; y) — решение, то (у; х) также является решением.
Ответ: (2; 8), (8; 2).
5. Самостоятельная работа.
1 вариант
1. Вычислите значение выражения: 11-3log3
2. Решите уравнения:
а) lg(x+3)=2lg2-lgx
б) log 736-log7(3x-12)=log7 4
3.Решите систему уравнений :
2 вариант
1. Вычислите значение выражения: 13-3log2
2. Решите уравнения:
а) 9 log 3x-x2log 3x=0
б) log5 (8-24x)-log 58=log 57.
3. Решите систему уравнений:
6.Подведение итогов урока:
Учитывая контингент учащихся данного класса, можно сделать вывод о том, что в целом учащиеся усвоили материал по данной теме.
Выставление оценок.
7. Домашнее задание:
Решите уравнения:
Приложение
Графические неравенства с программой «Пошаговое решение математических задач»
В предыдущих главах мы решали уравнения с одной неизвестной или переменной. Теперь мы изучим методы решения систем уравнений, состоящих из двух уравнений и двух переменных.
ТОЧКИ НА САМОЛЕТЕ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Представьте декартову систему координат и определите начало координат и оси.
- Для упорядоченной пары найдите эту точку в декартовой системе координат.
- Для данной точки в декартовой системе координат укажите связанную с ней упорядоченную пару.
Мы уже использовали числовую прямую, на которой мы представили числа в виде точек на прямой.
Обратите внимание, что это понятие содержит элементы из двух областей математики, строки из геометрии и чисел из алгебры. Рене Декарт (1596-1650) разработал метод соотношения точек на плоскости с алгебраическими числами. Эта схема называется декартовой системой координат (от Декарта) и иногда упоминается как прямоугольная система координат.
Эта система состоит из двух числовых линий, перпендикулярных в своих нулевых точках.
| Перпендикуляр означает, что две прямые расположены под прямым углом друг к другу. |
Внимательно изучите диаграмму, отмечая каждый из следующих фактов.
Числовые линии называются осями . Горизонтальная линия — это ось x , а вертикальная — ось y . Нулевая точка, в которой они перпендикулярны, называется исходной точкой .
| Оси множественного числа. Ось особенная. |
Положительный — справа и вверх ; отрицательный — к слева и вниз .
| Стрелки указывают, что числовые линии продолжаются бесконечно. Таким образом, плоскость бесконечно простирается во всех направлениях. |
Самолет разделен на четыре части, называемые квадрантами . Они пронумерованы в направлении против часовой стрелки, начиная с верхнего правого угла.
Точки на плоскости обозначаются упорядоченными парами чисел, записанными в скобках с запятой между ними, например (5,7). Это называется упорядоченной парой, потому что важен порядок, в котором написаны числа. Заказанная пара (5,7) — это , а не , как заказанная пара (7,5). Точки расположены на плоскости следующим образом.
Сначала начните с начала координат и посчитайте слева или справа количество пробелов, обозначенных первым числом в упорядоченной паре.Во-вторых, от точки на оси x, заданной первым числом, отсчитайте вверх или вниз количество пробелов, обозначенных вторым числом упорядоченной пары. Упорядоченные пары всегда сначала пишутся с x, а затем y, (x, y). Числа, представленные x и y, называются координатами и точки (x, y).
| Это важно. Первое число упорядоченной пары всегда относится к горизонтальному направлению, а второе число всегда относится к вертикальному направлению. |
Пример 1 В следующей декартовой системе координат точки A (3,4), B (0,5), C (-2,7), D (-4,1), E (-3 , -4), F (4, -2), G (0, -5) и H (-6,0) обозначены. Проверьте каждый, чтобы определить, как они расположены.
| Каковы координаты начала координат? |
ГРАФИЧЕСКИЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите несколько упорядоченных пар, которые делают данное линейное уравнение истинным.
- Найдите эти точки в декартовой системе координат.
- Проведите прямую линию через те точки, которые представляют график этого уравнения.
График — это графическое изображение пронумерованных фактов. Есть много типов графиков, таких как гистограммы, круговые графики, линейные графики и так далее. Примеры таких графиков обычно можно найти в финансовом разделе газеты. Графики используются, потому что изображение обычно упрощает понимание числовых фактов.
В этом разделе мы обсудим метод построения графика уравнения с двумя переменными. Другими словами, мы нарисуем картину уравнения с двумя переменными.
Рассмотрим уравнение x + y — 7 и заметим, что мы легко можем найти множество решений. Например, если x = 5, то y — 2, поскольку 5 + 2 = 7. Кроме того, если x = 3, то y = 4, поскольку 3 + 4 = 7. Если мы представим эти ответы в виде упорядоченных пар (x, y) , то у нас есть (5,2) и (3,4) как две точки на плоскости, которые представляют ответы на уравнение x + y = 7.
Все возможные ответы на это уравнение, расположенные в виде точек на плоскости, дадут нам график (или картинку) уравнения.
Конечно, мы никогда не сможем найти все числа x и y такие, что x + y = 7, поэтому мы должны довольствоваться наброском графика. Эскиз можно охарактеризовать как «кривую наилучшего соответствия». Другими словами, необходимо найти достаточно точек, чтобы получить достаточно точную картину уравнения.
| Помните, существует бесконечно много упорядоченных пар, которые удовлетворяли бы уравнению. |
Пример 1 Нарисуйте график 2x + y = 3.
Решение Мы хотим найти несколько пар чисел, которые сделают это уравнение истинным. Мы добьемся этого, выбрав число для x, а затем найдя соответствующее значение для y. Таблица значений используется для записи данных.
В верхней строке (x) мы разместим числа, которые мы выбрали для x. Затем в нижней строке (y) мы поместим соответствующее значение y, полученное из уравнения.
| Конечно, мы также могли бы начать с выбора значений для y, а затем найти соответствующие значения для x. |
В этом примере мы позволим x принимать значения -3, -2, -1,0, 1,2,3.
| Эти значения произвольны. Мы могли выбирать любые ценности. |
| Обратите внимание, что после того, как мы выбрали значение для x, значение для y определяется с помощью уравнения. |
| Эти значения x дают целые числа для значений y.Таким образом, это хороший выбор. Предположим, мы выбрали |
Эти факты дают нам следующую таблицу значений:
Теперь мы находим упорядоченные пары (-3,9), (-2,7), (-1,5), (0,3), (1,1), (2, -1), (3, -3) на координатной плоскости и соедините их линией.
Теперь у нас есть график 2x + y = 3.
| Линия указывает, что все точки на линии удовлетворяют уравнению, а также точки из таблицы.Стрелки указывают, что линия продолжается бесконечно. |
Графики всех уравнений первой степени с двумя переменными будут прямыми линиями. Этот факт будет использован здесь, хотя в математике будет намного позже, прежде чем вы сможете доказать это утверждение. Такие уравнения первой степени называются линейными уравнениями .
| Таким образом, любое уравнение вида ax + by — c, где a, b и c — действительные числа, является линейным уравнением. |
Уравнения с двумя неизвестными более высокой степени дают графики, которые представляют собой кривые разных типов.Вы изучите их на будущих курсах алгебры.
Поскольку график уравнения первой степени с двумя переменными представляет собой прямую линию, необходимо иметь только две точки. Однако ваша работа будет более точной, если вы найдете хотя бы три точки. Ошибки можно найти и исправить, если найденные точки не лежат на одной линии. Таким образом, мы называем третью точку «контрольной точкой».
| Это важно. Не пытайтесь сократить свою работу, найдя только два момента.Вы будете удивлены, как часто вы обнаружите ошибку, обнаружив все три точки. |
Пример 2 Нарисуйте график 3x — 2y — 7.
Решение Сначала составьте таблицу значений и выберите три числа, которые будут заменять x. Попробуем 0, 1,2.
| Опять же, вы также могли начать с произвольными значениями y. |
Ответ не так легко найти на графике, как целое число.Похоже, что x = 0 был не очень удачным выбором. Иногда можно заглянуть вперед и сделать лучший выбор для x.
| Поскольку и x, и y являются целыми числами, x = 1 было хорошим выбором. |
Точку (1, -2) будет легче найти. Если x = 2, у нас будет другая дробь.
Точку (3,1) легко найти.
| x = 3 был еще одним хорошим выбором. |
Скорректируем таблицу значений и будем использовать точки, дававшие целые числа.Это не всегда возможно, но попытка получить целые значения даст более точный набросок. Теперь у нас есть таблица для 3x — 2y = 7.
| Мы можем это сделать, поскольку выбор x был произвольным. |
Расположение точек (1, -2), (3,1), (- 1, -5) дает график 3x — 2y = 7.
| Сколько упорядоченных пар удовлетворяют этому уравнению? |
НАКЛОН ЛИНИИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Свяжите уклон линии с ее крутизной.
- Запишите уравнение прямой в форме пересечения наклона.
- Постройте прямую линию, используя ее наклон и точку пересечения по оси Y.
Теперь мы хотим обсудить важную концепцию, называемую наклоном линии. Интуитивно мы можем думать об уклоне как о крутизне линии по отношению к горизонтали.
Ниже приведены графики из нескольких линий. Внимательно изучите их и мысленно ответьте на следующие вопросы.
Какая линия круче?
Какова, по-видимому, связь между коэффициентом при x и крутизной Какой график будет круче: линии, когда уравнение имеет вид y = mx?
| Какой график будет круче: y = 3x или y = 7x? |
Теперь изучите следующие графики.
Какая линия круче?
Как отрицательное значение m влияет на график?
| Какой график будет круче: y = 3x или y = 7x? |
Для графика y = mx необходимо было сделать следующие наблюдения.
- Если m> 0, то
- по мере увеличения значения m крутизна линии увеличивается и
- линия поднимается вправо и опускается влево.
- Если м
- по мере увеличения значения m крутизна линии уменьшается и
- линия поднимается влево и опускается вправо
| Помните, m> 0 означает, что «m больше нуля.» |
Другими словами, в уравнении вида y — mx, m управляет крутизной линии. В математике мы используем слово наклон для обозначения крутизны и формируем следующее определение:
В уравнении вида y = mx, m — это наклон графика уравнения.
Пример 1 Нарисуйте график y = 6x и укажите наклон линии.
Решение Сначала мы составим таблицу, показывающую три набора упорядоченных пар, которые удовлетворяют уравнению.
| Помните, нам нужны только две точки для определения линии, но мы используем третью точку в качестве проверки. |
Затем мы делаем набросок графика.
Значение m равно 6, следовательно, наклон равен 6. Мы можем просто написать m — 6.
Пример 2 Нарисуйте график и укажите наклон
.Решение Выбирая значения x, которые делятся на 3, получаем таблицу
| Зачем использовать значения, которые делятся на 3? |
Тогда график
Склон
Теперь мы хотим сравнить графики двух уравнений, чтобы установить другую концепцию.
Пример 3 Нарисуйте графики y 3x и y — 3x + 2 на одном и том же наборе координатных осей.
| Сравните коэффициенты при x в этих двух уравнениях. |
Решение
В примере 3 посмотрите на таблицы значений и обратите внимание, что для данного значения x, значение y в уравнении y = 3x + 2 на два больше, чем соответствующее значение y в уравнении y = 3x.
Теперь посмотрите на графики двух уравнений и обратите внимание, что график y = 3x + 2, кажется, имеет тот же наклон, что и y = 3x.Также обратите внимание, что если весь график y = 3x перемещается вверх на две единицы, он будет идентичен графику y = 3x + 2. График y = 3x пересекает ось y в точке (0,0) , а график y = 3x + 2 пересекает ось y в точке (0,2).
| Снова сравните коэффициенты при x в двух уравнениях. |
Сравните эти таблицы и графики, как в примере 3.
| Обратите внимание: когда две линии имеют одинаковый наклон, они параллельны. |
Наклон от одной точки на линии к другой определяется отношением изменения y к изменению x. То есть
| Если вы хотите произвести впечатление на своих друзей, вы можете написать , где греческая буква (дельта) означает «изменение». |
Обратите внимание, что изменение x равно 3, а изменение y равно 2.
Изменение x равно -4, изменение y равно 1.
| Можно также сказать, что изменение x равно 4, а изменение y равно -1.Это приведет к той же строке. |
Пример 7 На графике y = 3x — 2 наклон равен 3.
Изменение x равно 1, а изменение y равно 3.
y = mx + b называется формой с пересечением наклона уравнения прямой линии. Если уравнение имеет такую форму, m — это наклон линии, а (0, b) — точка, в которой график пересекает (пересекает) ось y.
| Точка (0, b) называется точкой пересечения по оси y. |
Если уравнение прямой имеет форму пересечения наклона, можно нарисовать его график, не составляя таблицу значений. Используйте точку пересечения оси Y и наклон, чтобы нарисовать график, как показано в примере 8.
| Обратите внимание, что это уравнение имеет вид y = mx + b. |
Сначала найдите точку (0, -2). Это одна из точек на линии. Наклон показывает, что изменение x равно 4, поэтому из точки (0, -2) мы перемещаем четыре единицы в положительном направлении параллельно оси x.Поскольку изменение y равно 3, мы перемещаем три единицы в положительном направлении параллельно оси y. Полученная точка тоже находится на линии. Поскольку две точки определяют прямую линию, мы рисуем график.
| Всегда начинайте с точки пересечения оси Y. Распространенная ошибка, которую допускают многие студенты, — это путать точку пересечения по оси Y с точкой пересечения по оси x (точка, в которой линия пересекает ось x). |
Пример 9 Задайте наклон и точку пересечения по оси Y и нарисуйте график y = 3x + 4.
Решение m = -3, точка пересечения по оси y = (0,4).
Чтобы выразить наклон в виде отношения, мы можем написать -3 как или. Если мы запишем наклон как, то из точки (0,4) мы перемещаем одну единицу в положительном направлении параллельно оси x, а затем перемещаем три единицы в отрицательном направлении параллельно оси y. Затем мы проводим линию через эту точку и (0,4).
Предположим, уравнение не имеет формы y = mx + b. Сможем ли мы найти наклон и точку пересечения по оси Y? Ответ на этот вопрос — да.Однако для этого мы должны изменить форму данного уравнения, применив методы, использованные в разделе 4-2.
| Раздел 4-2 посвящен решению буквальных уравнений. Вы можете просмотреть этот раздел. |
Пример 10 Найдите наклон и точку пересечения оси Y для 3x + 4y = 12.
Решение Во-первых, мы понимаем, что уравнение не находится в форме пересечения наклона, необходимой для ответа на заданные вопросы. Чтобы получить эту форму, решите данное уравнение относительно y.
| Нарисуйте здесь график. |
Пример 11 Найдите наклон и точку пересечения оси y для 2x — y = 7.
Решение Помещая уравнение в форму пересечения наклона, получаем
| Нарисуйте график линии на сетке ниже. |
ГРАФИК ЛИНЕЙНЫХ НЕРАВЕНСТВ
ЗАДАЧИ
По завершении этого раздела вы сможете построить график линейных неравенств.
В главе 4 мы построили линейные графики неравенств, например
Это были неравенства с участием только одной переменной. Мы обнаружили, что во всех таких случаях график представлял собой часть числовой прямой. Поскольку уравнение с двумя переменными дает график на плоскости, кажется разумным предположить, что неравенство с двумя переменными будет отображаться как некоторая часть или область плоскости. На самом деле это так. Решение неравенства x + y
Пример 1 Каждая из следующих пар чисел в наборе решений x + y
Решение
| Набор решений состоит из всех упорядоченных пар, которые делают утверждение верным. |
| Подводя итог, следующие упорядоченные пары дают верное утверждение. (2,1), (3, -4), (0,0), (- 1,4) |
| Следующие упорядоченные пары дают ложное утверждение. (5,6), (3,2), (- 2,8) |
Ниже приведен график прямой x + y = 5. Точки из примера 1 указаны на графике с ответами на вопрос «Является ли x + y
| Обратите внимание, что все точки, удовлетворяющие уравнению, находятся слева и ниже линии, а все точки, которые не соответствуют, находятся сверху и справа. |
Обратите внимание, что все ответы «да» лежат на одной стороне линии x + y = 5, а все ответы «нет» лежат на другой стороне линии или на самой строке.
График прямой x + y = 5 делит плоскость на три части: саму линию и две стороны линий (называемые полуплоскостями).
х + у х + у
Если одна точка полуплоскости находится в наборе решений линейного неравенства, то все точки в этой полуплоскости входят в набор решений.Это дает нам удобный метод построения графиков линейных неравенств.
Построение графика линейного неравенства
1. Замените символ неравенства знаком равенства и нанесите на график полученную линию.
2. Отметьте одну точку, которая, очевидно, находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
3. Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений.
| Почему нужно проверять только одну точку? |
Пример 2 Нарисуйте график 2x 4- 3y> 7.
Решение Шаг 1. Сначала нарисуйте график линии 2x + 3y = 7, используя таблицу значений или форму пересечения наклона.
Шаг 2: Затем выберите точку, которая не находится на прямой 2x + 3y = 7. [Если линия не проходит через начало координат, то точка (0,0) всегда будет хорошим выбором.] Теперь обратимся к неравенство 2x + 3y>> 7, чтобы увидеть, находится ли выбранная точка в наборе решений.
Шаг 3: Точка (0,0) не входит в набор решений, поэтому полуплоскость, содержащая (0,0), не является набором решений. Следовательно, другая полуплоскость, определяемая линией 2x + 3y = 7, является множеством решений.
Поскольку сама линия не является частью решения, она показана пунктирной линией, а полуплоскость заштрихована, чтобы показать набор решений.
| Набор решений — это полуплоскость сверху и справа от линии. |
Пример 3 Изобразите график решения линейного неравенства 2x — y ≥ 4.
Решение Шаг 1. Первый график 2x — y = 4. Поскольку линейный график для 2x — y = 4 не проходит через начало координат (0,0), проверьте эту точку в линейном неравенстве.
Шаг 2:
Шаг 3: Поскольку точка (0,0) не входит в набор решений, полуплоскость, содержащая (0,0), отсутствует в наборе. Следовательно, решение — другая полуплоскость. Обратите внимание, однако, что строка 2x — y = 4 включена в набор решений. Поэтому нарисуйте сплошную линию, чтобы показать, что это часть графика.
| Набор решений — это линия и полуплоскость ниже и справа от линии. |
Пример 4 График x
Решение Первый график x = y. Затем проверьте точку не на линии. Обратите внимание, что график линии содержит точку (0,0), поэтому мы не можем использовать ее в качестве контрольной точки. Чтобы определить, какая полуплоскость является набором решений, используйте любую точку, которая явно не находится на прямой x = y. Точка (- 2,3) является такой точкой.
Используя эту информацию, график x
| Когда график линии проходит через начало координат, любая другая точка на оси x или y также будет хорошим выбором. |
ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Нарисуйте графики двух линейных уравнений в одной и той же системе координат.
- Найдите общее решение двух графиков.
Пример 1 Пара уравнений называется системой линейных уравнений.
Мы заметили, что каждое из этих уравнений имеет бесконечно много решений, и каждое из них будет образовывать прямую линию, когда мы построим его в декартовой системе координат.
Теперь мы хотим найти решения для системы. Другими словами, нам нужны все точки (x, y), которые будут на графике обоих уравнений.
Решение Мы рассуждаем следующим образом: если все решения 2x — y = 2 лежат на одной прямой, а все решения x + 2y = 11 лежат на другой прямой, то решение обоих уравнений будет их точками пересечение (если две прямые пересекаются).
| В этой таблице мы позволяем x принимать значения 0, 1 и 2. Затем мы находим значения для y, используя уравнение. Сделайте это перед тем, как продолжить. В этой таблице мы позволяем y принимать значения 2, 3 и 6. Затем мы находим x, используя уравнение. Также проверьте эти значения. |
| Две прямые пересекаются в точке (3,4). |
Обратите внимание, что точка пересечения выглядит как (3,4). Теперь мы должны проверить точку (3,4) в обоих уравнениях, чтобы убедиться, что это решение системы.
| В качестве проверки мы подставляем упорядоченную пару (3,4) в каждое уравнение, чтобы увидеть, получим ли мы истинное утверждение. Существуют ли другие точки, которые удовлетворяли бы обоим уравнениям? Почему? |
Следовательно, (3,4) является решением системы.
Не все пары уравнений дают единственное решение, как в этом примере. На самом деле существует три возможности, и вы должны знать о них.
Поскольку мы имеем дело с уравнениями, которые представляют собой прямые линии, мы можем исследовать эти возможности, наблюдая за графиками.
1. Независимые уравнения Две прямые пересекаются в одной точке. В этом случае есть единственное решение.
| Приведенный выше пример представляет собой систему независимых уравнений. |
2. Несогласованные уравнения Две линии параллельны. В этом случае решения нет.
| Независимо от того, как далеко протянуты эти линии, они никогда не пересекутся. |
3. Зависимые уравнения Два уравнения дают одну и ту же линию. В этом случае любое решение одного уравнения является решением другого.
| В этом случае общих решений будет бесконечно много. |
На более поздних курсах алгебры будут изучены методы распознавания несовместных и зависимых уравнений. Однако на этом уровне мы будем иметь дело только с независимыми уравнениями. Тогда вы можете ожидать, что для всех проблем, приведенных в этой главе, будут найдены уникальные решения.
| Это означает, что графики всех систем в этой главе будут пересекаться в одной точке. |
Чтобы решить систему двух линейных уравнений с помощью построения графиков
1. Составьте таблицу значений и нарисуйте график каждого уравнения в той же системе координат.
2. Найдите значения (x, y), которые называют точку пересечения линий.
3. Отметьте эту точку (x, y) в обоих уравнениях.
| Опять же, в этой таблице wc произвольно выбрал значения x равными — 2, 0 и 5. Здесь мы выбрали для x значения 2, 4 и 6. Вы можете выбрать любые значения, которые хотите. Мы говорим «кажущийся», потому что мы еще не проверили упорядоченную пару в обоих уравнениях. Как только он проверит, это определенно решение. |
Поскольку (3,2) проверяет оба уравнения, это решение системы.
ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Постройте два или более линейных неравенства на одном и том же наборе осей координат.
- Определите область плоскости, которая является решением системы.
Более поздние занятия по математике будут включать тему линейного программирования. Несмотря на то, что сама тема выходит за рамки этого текста, одна техника, используемая в линейном программировании, вполне доступна вам — построение графиков систем линейных неравенств — и мы обсудим это здесь.
В предыдущем разделе вы обнаружили, что решение системы линейных уравнений — это пересечение решений каждого из уравнений.Таким же образом решение системы линейных неравенств представляет собой пересечение полуплоскостей (и, возможно, прямых), которые являются решениями каждого отдельного линейного неравенства.
Другими словами, x + y> 5 имеет множество решений и 2x — y
имеет в качестве своего решения область плоскости, которая находится в наборе решений обоих неравенств.
Для построения графика решения этой системы мы наносим на график каждое линейное неравенство на одном и том же наборе координатных осей и указываем пересечение двух наборов решений.
| Обратите внимание, что решением системы линейных неравенств будет набор точек. |
| Опять же, используйте либо таблицу значений, либо форму уравнения с пересечением наклона для построения графика линий. |
Проверка точки (0,0) в неравенстве x + y> 5 показывает, что точка (0,0) не входит в набор ее решений. Мы указываем набор решений x + y> 5 экраном справа от пунктирной линии.
| Эта область находится справа и выше линии x + y = 5. |
Проверка точки (0,0) в неравенстве 2x — y
| Эта область находится слева и выше линии 2x — y = 4. |
Пересечение двух наборов решений — это та область плоскости, в которой пересекаются два экрана. Этот регион показан на графике.
| Еще раз обратите внимание, что решение не включает строки.Если, например, нас попросили изобразить решение системы , это означает, что решение включает точки на линии x + y = 5. |
Результаты показывают, что все точки в заштрихованной части графика будут в наборах решений x + y> 5 и 2x — y.
РЕШЕНИЕ СИСТЕМЫ ПУТЕМ ЗАМЕНЫ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом подстановки.
В разделе 6-5 мы решили систему двух уравнений с двумя неизвестными с помощью построения графиков. Графический метод очень полезен, но он был бы непрактичным, если бы решения были дробными. Фактическую точку пересечения определить может быть очень сложно.
Существуют алгебраические методы решения систем. В этом разделе мы обсудим метод подстановки.
Пример 1 Решить методом подстановки:
Решение
Шаг 1 Мы должны решить одну неизвестную в одном уравнении.Мы можем выбрать либо x, либо y либо в первом, либо во втором уравнении. Наш выбор может быть основан на получении простейшего выражения. В этом случае мы решим относительно x во втором уравнении, получив x = 4 + 2y, потому что любой другой выбор привел бы к дроби.
| Посмотрите на оба уравнения и посмотрите, есть ли в одном из них переменная с коэффициентом, равным единице. |
Шаг 2 Подставьте значение x в другое уравнение.В этом случае уравнение
2х + 3у = 1.
Подставляя (4 + 2y) вместо x, мы получаем 2 (4 + 2y) + 3y = 1, уравнение только с одной неизвестной.
| Причина в том, что если x = 4 + 2y в одном из уравнений, то x должен быть равен 4 + 2y в другом уравнении. |
Шаг 3 Решите неизвестное.
| Помните, сначала удалите скобки. |
Шаг 4 Подставьте y = — 1 в любое уравнение, чтобы найти соответствующее значение для x.Поскольку мы уже решили второе уравнение относительно x через y, мы можем его использовать.
| Мы можем подставить y = — 1 в любое уравнение, поскольку y имеет одинаковое значение в обоих. |
Таким образом, у нас есть решение (2, -1).
| Помните, что x записывается первым в упорядоченной паре. |
Шаг 5 Проверьте решение в обоих уравнениях. Помните, что решение системы должно быть верным для каждого уравнения в системе.С
решение (2, -1) действительно проверяет.
| Это проверяет: 2x + 3y = 1 и x — 2y = 4. |
| Проверьте эту упорядоченную пару в обоих уравнениях. Ни в одном из этих уравнений не было переменной с коэффициентом, равным единице. В этом случае решение заменой — не лучший метод, но мы сделаем это так, чтобы показать, что это возможно. В следующем разделе будет предложен более простой метод. |
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ ДОПОЛНЕНИЕМ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом сложения.
Метод сложения для решения системы линейных уравнений основан на двух фактах, которые мы использовали ранее.
Во-первых, мы знаем, что решения уравнения не меняются, если каждый член этого уравнения умножается на ненулевое число. Во-вторых, мы знаем, что если мы добавим одинаковые или равные количества к обеим сторонам уравнения, результаты все равно будут одинаковыми.
Пример 1 Решить сложением:
| Обратите внимание, что мы можем решить эту систему методом подстановки, решив первое уравнение относительно y.Решите эту систему методом подстановки и сравните свое решение с решением, полученным в этом разделе. |
Решение
Шаг 1 Наша цель — сложить два уравнения и исключить одно из неизвестных, чтобы мы могли решить полученное уравнение с одним неизвестным. Если мы сложим уравнения как есть, мы не удалим неизвестное. Это означает, что мы должны сначала умножить каждую сторону одного или обоих уравнений на число или числа, что приведет к исключению одного из неизвестных при сложении уравнений.
Внимательно изучив проблему, мы замечаем, что проще всего устранить неизвестное y. Это делается путем умножения каждой стороны первого уравнения на -2.
| Обратите внимание, что каждый член необходимо умножить на (- 2). |
Шаг 2 Добавьте уравнения.
Шаг 3 Решите полученное уравнение.
| В этом случае мы просто умножаем каждую сторону на (-1). |
Шаг 4 Найдите значение другой неизвестной, подставив это значение в одно из исходных уравнений.Используя первое уравнение,
| Подставьте x = 4 во второе уравнение и посмотрите, получите ли вы такое же значение для y. |
Шаг 5 Если мы проверим упорядоченную пару (4, -3) в обоих уравнениях, мы увидим, что это решение системы.
Пример 2 Решить сложением:
| Обратите внимание, что в этой системе ни одна переменная не имеет коэффициента, равного единице. Поэтому лучший метод решения — метод сложения. |
Решение
Шаг 1 Необходимо изменить оба уравнения, чтобы исключить одно из неизвестных. Ни одно из неизвестных не будет проще другого, поэтому удалите либо x, либо y.
Чтобы исключить x, умножьте каждую сторону первого уравнения на 3 и каждую сторону второго уравнения на -2.
| Если вы решили исключить y, умножьте первое уравнение на — 2, а второе уравнение на 3. Сделайте это и решите систему.Сравните ваше решение с полученным в примере. |
Шаг 2 Сложив уравнения, мы получаем
Шаг 3 Решение для урожайности
Шаг 4 Использование первого уравнения в исходной системе для нахождения значения другой неизвестной дает
Шаг 5 Убедитесь, что упорядоченная пара (- 1,3) является решением системы.
| Чек остается на ваше усмотрение. |
СТАНДАРТНАЯ ФОРМА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Напишите линейное уравнение в стандартной форме.
- Решите систему двух линейных уравнений, если они заданы в нестандартной форме.
Уравнения в предыдущих разделах не содержали дробей, как неизвестные в левой части уравнения, так и неизвестные в том же порядке.
Такие уравнения называются стандартными. То есть они имеют вид ax + by = c, где a, b и c — целые числа. Перед решением методом сложения уравнения необходимо привести к стандартному виду.
Пример 1 Изменить 3x = 5 + 4y на стандартную форму.
Решение 3x = 5 + 4y не в стандартной форме, потому что одно неизвестное находится справа. Если мы прибавим -4y к обеим сторонам, мы получим 3x — 4y = 5, что в стандартной форме.
| Будьте осторожны здесь. Многие студенты забывают умножить правую часть уравнения на 24. |
| Снова убедитесь, что каждый член умножен на 12. |
Теперь прибавьте — 24x к обеим сторонам, получив — 24x + 9y = -10, что в стандартной форме.Обычно уравнения пишутся так, чтобы первый член был положительным. Таким образом, мы умножаем каждый член этого уравнения на (- 1).
| Вместо того, чтобы говорить «первый член положительный», мы иногда говорим «ведущий коэффициент положительный». |
ПРОБЛЕМЫ СО СЛОВОМ С ДВУМЯ НЕИЗВЕСТНЫМИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите, когда проблема со словом может быть решена с использованием двух неизвестных.
- Составьте уравнения и решите словесную задачу.
Многие проблемы со словами можно обрисовать и решить, используя два неизвестных.
Пример 1 Сумма двух чисел равна 5. Трижды первое число, добавленное к пяти умноженным на второе число, равно 9. Найдите числа.
Решение Пусть x = первое число
y = второе число
Первое утверждение дает нам уравнение
x + y = 5.
Второе утверждение дает нам уравнение
3x + 5 y = 9.
Теперь у нас есть система
, которую мы можем решить любым из известных нам методов, давая
x = 8 и y = — 3.
| Решите систему с помощью подстановки. |
Пример 2 Два работника получают в общей сложности 136 долларов за 8-часовую работу. Если одному работнику платят на 1 доллар в час больше, чем другому, найдите почасовую ставку для каждого.
Решение Пусть x = почасовая ставка одного работника
y = почасовая ставка другого работника.
| Обратите внимание, что очень важно сказать, что представляют x и y. |
Первое утверждение дает нам уравнение
8x + 8y = 136.
Второе утверждение дает уравнение
х = у + 1.
Теперь у нас есть система (в стандартном виде)
Решение дает x = 9 и y = 8. Ставка одного рабочего составляет 9 долларов в час, а другого — 8 долларов в час.
| Решите эту систему методом сложения. |
РЕЗЮМЕ
Ключевые слова
- Декартова система координат — это метод наименования точек на плоскости.
- Упорядоченные пары чисел используются для обозначения точек на плоскости.
- Линейное уравнение представляет собой прямую линию.
- Наклон от одной точки на линии до другой — это отношение.
- Угол наклона-пересечения уравнения прямой имеет вид y = mx + b.
- Линейное неравенство отображается как часть плоскости.
- Система двух линейных уравнений состоит из линейных уравнений, для которых мы хотим найти одновременное решение.
- Независимые уравнения имеют уникальные решения.
- Противоречивые уравнения не имеют решения.
- Зависимые уравнения имеют бесконечно много решений.
- Система двух линейных неравенств состоит из линейных неравенств, для которых мы хотим найти одновременное решение.
- Стандартная форма линейного уравнения — это ax + by = c, где a, b и c — действительные числа.
Процедуры
- Чтобы нарисовать график линейного уравнения, найдите упорядоченные пары чисел, которые являются решениями этого уравнения.Найдите эти точки в декартовой системе координат и соедините их линией.
- Чтобы нарисовать график линии, используя ее наклон:
Шаг 1 Запишите уравнение прямой в форме y — mx + b.
Шаг 2 Найдите точку пересечения j (0, b).
Шаг 3 Начиная с (0, b), используйте наклон m, чтобы найти вторую точку.
Шаг 4 Соедините две точки прямой линией. - Чтобы построить график линейного неравенства:
Шаг 1 Замените символ неравенства знаком равенства и нанесите на график полученную линию.
Шаг 2 Проверьте одну точку, которая явно находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
Шаг 3 Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений. - Чтобы решить систему двух линейных уравнений с помощью построения графиков, тщательно изобразите уравнения в одной и той же системе координат.Их точка пересечения и будет решением системы.
- Чтобы решить систему двух линейных неравенств с помощью построения графиков, определите область плоскости, которая удовлетворяет обоим утверждениям неравенства.
- Чтобы решить систему двух уравнений с двумя неизвестными путем подстановки, решите одну неизвестную одного уравнения через другую неизвестную и подставьте эту величину в другое уравнение. Затем подставьте полученное таким образом числовое значение в любое уравнение, чтобы найти значение другого неизвестного.Наконец, проверьте решение в обоих уравнениях.
- Чтобы решить систему двух уравнений с двумя неизвестными путем сложения, умножьте одно или оба уравнения на необходимые числа так, чтобы при сложении уравнений одно из неизвестных было удалено. Решите оставшиеся неизвестные и подставьте это значение в одно из уравнений, чтобы найти другое неизвестное. Проверьте оба уравнения.
- Чтобы решить словесную задачу с двумя неизвестными, найдите два уравнения, которые показывают связь между неизвестными.Затем решите систему. Всегда проверяйте решение указанной проблемы.
Решение систем неравенств — Бесплатная математическая справка
Сначала нам нужно рассмотреть символы неравенства:
- Символ <означает меньше чем.
- Символ> означает больше чем.
- Символ \ (\ leq \) означает меньше или равно. Обычно на компьютерах это пишется как <=, потому что это легче вводить.
- Символ \ (\ geq \) означает больше или равно.Иногда на компьютерах это пишется как> =, потому что так легче набирать.
Есть бесконечные решения для неравенства. В свете этого факта может быть проще всего найти набор решений для неравенств, решив систему графически.
Как решить системы неравенств графически
1) Запишите неравенство в форме пересечения наклона или в форме \ (y = mx + b \).
Например, если вас попросят решить \ (x + y \ leq 10 \), мы сначала перепишем как \ (y \ leq -x + 10 \).
2) Временно замените данный символ неравенства (в данном случае \ (\ leq \)) на просто равный символ. При этом вы можете рассматривать неравенство как уравнение. НО НЕ забудьте заменить символ равенства на исходный символ неравенства в КОНЕЦ задачи!
Итак, \ (y \ leq -x + 10 \) на данный момент становится \ (y = -x + 10 \).
3) Изобразите линию, найденную на шаге 2. Это сформирует «границу» неравенства — с одной стороны линии условие будет истинным, с другой — нет.Посмотрите, как построить линию здесь.
4) Вернемся к найденному ранее неравенству как \ (y \ leq -x + 10 \). Обратите внимание, что это верно, когда y меньше или равно. На шаге 3 мы построили линию (случай равенства), поэтому теперь нам нужно учесть случай «меньше чем». Поскольку y меньше определенного значения в нижней части оси, мы закрасим область под линией, чтобы указать, что неравенство верно для всех точек ниже линии:
5) Проверить. Вставьте точку не на линии, например (0,0).Убедитесь, что неравенство выполнено. В данном случае это означает \ (0 \ leq -0 + 10 \), что явно верно. Мы заштриховали правильную сторону линии.
Пример:
Найдите все значения x и y, которые удовлетворяют: \ (y \ geq \ frac {-3} {2} x + 6 \).
Обратите внимание, что это неравенство уже имеет форму пересечения наклона. Я заменю данный символ неравенства на символ равенства для построения линии.
\ (y \ geq \ frac {-3} {2} x + 6 \) становится \ (y = \ frac {-3} {2} x + 6 \). Теперь постройте эту линию, как показано:
Так как это случай, когда неравенство верно для значений y, которые больше или равны чему-то, мы закрасили область над линией.Все точки на этой линии графика или ВЫШЕ будут удовлетворять нашему неравенству. Опять же, выберите любую точку над линией графика, чтобы убедиться, что она удовлетворяет или раскрывает ИСТИННОЕ утверждение с точки зрения исходного неравенства. Например, (5,3). Подключите это, и у нас будет \ (3 \ geq \ frac {-3} {2} * 5 + 6 \). Упростив его до \ (3 \ geq -1.5 \), мы увидим, что неравенство верно в точке (5,3). Поскольку эта точка находилась над нашей линией, она должна быть заштрихована, что подтверждает наше решение.
Множественные неравенства — система неравенств
Система неравенств содержит более одного утверждения неравенства, которое должно быть выполнено.Графически это означает, что нам нужно сделать то, что мы только что сделали — построить линию, представленную каждым неравенством, — а затем найти область графика, которая верна для ОБОИХ неравенств. Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, разделяемую двумя неравенствами.
Какой набор решений? Набор решений для ОБЕИХ неравенств будет ЛЮБОЙ ТОЧКОЙ, где ОБЕИ области закрашены вместе или где встречаются ОБЕ заштрихованные области.
Первоначально принадлежит г-ну Фелизу, © 2005
Графические системы линейных неравенств
Чтобы построить линейный неравенство в двух переменных (скажем, Икс а также у ), сначала получите у один на одной стороне.Затем рассмотрим соответствующее уравнение, полученное заменой знака неравенства на знак равенства. График этого уравнения представляет собой линию.
Если неравенство строгое ( < или же > ), начертите штриховой линией. Если неравенство не строгое ( ≤ или же ≥ ), начертите сплошной линией.
Наконец, выберите одну точку, которая не находится ни на одной строке ( ( 0 , 0 ) обычно самый простой) и решите, удовлетворяют ли эти координаты неравенству или нет.Если это так, заштрихуйте полуплоскость, содержащую эту точку. Если нет, закройте другую полуплоскость.
Аналогичным образом изобразите каждое из неравенств в системе. Решение система неравенств — область пересечения всех решений в системе.
Пример 1:
Решите систему неравенств, построив графики:
у ≤ Икс — 2 у > — 3 Икс + 5
Сначала изобразим неравенство у ≤ Икс — 2 .Связанное уравнение у знак равно Икс — 2 .
Поскольку неравенство ≤ , не строгий, граница сплошная.
Постройте прямую линию.
Рассмотрим точку, которая не находится на линии — скажем, ( 0 , 0 ) — и подставляем в неравенство у ≤ Икс — 2 .
0 ≤ 0 — 2 0 ≤ — 2
Это неправда.Итак, решение не содержит точки ( 0 , 0 ) . Заштрихуйте нижнюю половину линии.
Аналогичным образом нарисуйте пунктирную линию для соответствующего уравнения второго неравенства у > — 3 Икс + 5 которое имеет строгое неравенство. Точка ( 0 , 0 ) не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки ( 0 , 0 ) .
Решение системы неравенств — это область пересечения решений двух неравенств.
Пример 2:
Решите систему неравенств, построив графики:
2 Икс + 3 у ≥ 12 8 Икс — 4 у > 1 Икс < 4
Перепишем первые два неравенства с у один на одной стороне.
3 у ≥ — 2 Икс + 12 у ≥ — 2 3 Икс + 4 — 4 у > — 8 Икс + 1 у < 2 Икс - 1 4
Теперь изобразим неравенство у ≥ — 2 3 Икс + 4 .Связанное уравнение у знак равно — 2 3 Икс + 4 .
Поскольку неравенство ≥ , не строгий, граница сплошная.
Постройте прямую линию.
Рассмотрим точку, которая не находится на линии — скажем, ( 0 , 0 ) — и подставляем в неравенство.
0 ≥ — 2 3 ( 0 ) + 4 0 ≥ 4
Это неправда.Итак, решение не содержит точки ( 0 , 0 ) . Заштрихуйте верхнюю половину линии.
Аналогично нарисуйте пунктирную линию соответствующего уравнения второго неравенства у < 2 Икс - 1 4 которое имеет строгое неравенство. Точка ( 0 , 0 ) не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки ( 0 , 0 ) .
Нарисуйте пунктирную вертикальную линию Икс знак равно 4 которое является родственным уравнением третьего неравенства.
Здесь точка ( 0 , 0 ) удовлетворяет неравенству, поэтому заштрихуйте половину, содержащую точку.
Решение системы неравенств — это область пересечения решений трех неравенств.
Решение систем линейных неравенств
Техника решения систем линейных неравенств отличается от методов решения линейных уравнений, потому что знаки неравенства не позволяют нам выполнять замену, как мы это делаем с уравнениями.Тем не менее, мы все еще можем решить эти проблемы.
Ключевые термины
o Система линейных неравенств
o Линейная оптимизация
o Линейное программирование
Цели
o Научиться решать задачи, связанные с системами линейных неравенств
o Понять базовый подход к решению задач линейной оптимизации.
Системы линейных неравенств
Система линейных неравенств включает несколько выражений, решение которых может дать ряд решений. Многие концепции, которые мы усвоили при изучении систем линейных уравнений, можно преобразовать в решение системы линейных неравенств, но этот процесс может быть несколько сложным. Возможно, наиболее наглядный способ одновременного решения набора линейных неравенств — использование графиков.Давайте сразу рассмотрим пример в двух измерениях.
2 x -5 y ≤ 3
y — 3 x ≤ 1
Из-за неравенства мы не можем использовать подстановку так же, как мы это делали с системами линейных уравнений. Посмотрим на графики этих неравенств. Во-первых, мы упрощаемся до формы, которую легко построить графически.
2 x -5 y ≤ 3 y -3 x ≤ 1
2 x ≤ 3 + 5 y y ≤ 3 x + 1
5 y ≥ 2 x — 3
y ≥ 0.4 х — 0,6
Теперь построим график этих неравенств.
На графике видно, что есть две заштрихованные области, соответствующие решениям каждого неравенства. Линии закрашены, потому что неравенства не строгие (используются ≥ и ≤). Решением системы неравенств является более темная заштрихованная область, которая представляет собой перекрытие двух отдельных областей, и части линий (лучей), которые граничат с этой областью.Символически мы, пожалуй, лучше всего можем выразить решение в этом случае как
0,4 x — 0,6 ≤ y ≤ 3 x + 1
Решение систем неравенств в трех или более измерениях возможно, но это намного сложнее — построить графики твердых областей, которые составляют решения, также сложнее.
Практическая задача: Найдите и изобразите на графике множество решений следующей системы неравенств:
x — 5 y ≥ 6
3 x + 2 y > 1
Решение : Сначала решим выражения для y .
x — 5 y ≥ 6 3 x + 2 y > 1
x ≥ 6 + 5 y 2 y > 1-3 9 1472 x
5 y ≤ x — 6 y > 0,5 — 1,5 x
y ≤ 0,2 x — 1,2
Тогда мы можем выразить решение этой системы неравенств следующим образом:
0.5 — 1,5 x < y ≤ 0,2 x — 1,2
Построим график набора решений. Сначала мы построим график линий, соответствующих двум отдельным неравенствам (и выберем сплошную линию для первого и ломаную линию для второго), затем мы соответствующим образом закрасим две области.
Решение — это более темная заштрихованная область (которая является перекрытием двух отдельных областей решения), но давайте изобразим ее отдельно, чтобы было немного яснее.
Линейная оптимизация
Мы можем применить то, что мы узнали выше, к линейной оптимизации (также называемой линейным программированием ), которая представляет собой процесс нахождения максимального или минимального значения для некоторой функции при определенных условиях (например, линейных неравенствах). Решение задач, связанных с линейной оптимизацией, не требует от вас приобретения каких-либо новых навыков; они просто требуют, чтобы вы применяли то, что уже знаете.Итак, перейдем к практической задаче.
Практическая задача: Найдите максимальное значение y при –3 x + 2 y ≤ 4 и x + y ≤ 1 при условии, что x ≥ 0.
Решение: Нам дана система неравенств, для которой мы должны сначала найти соответствующее множество решений. В этом наборе решений мы можем найти максимальное значение y .Итак, мы можем сначала применить то, что мы уже знаем: давайте перестроим неравенства в форму, которую мы можем легко изобразить.
–3 x + 2 y ≤ 4 x + y ≤ 1 x ≥ 0
2 y ≤ 3 x + 4 y ≤ 1 — x
y ≤ 1,5 x + 2
Теперь давайте изобразим каждое из этих неравенств, отмечая, что мы должны использовать сплошные линии в каждом случае.
Самая темная заштрихованная область (клин в правом нижнем углу графика) удовлетворяет всем ограничениям задачи. Затем мы хотим найти максимальное значение y , которое явно равно 1. (Мы также можем найти это значение, подставив x = 0 в x + y ≤ 1 и найдя максимальное значение y. , что также явно 1.)
Система линейных неравенств — объяснение и примеры
Прежде чем решать системы линейных неравенств , давайте посмотрим, что означает неравенство.Слово неравенство означает математическое выражение, в котором стороны не равны друг другу.
Как правило, для представления уравнений неравенства используются пять символов неравенства.
Это меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) и символ «не равно» (≠). Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Что такое система линейных неравенств?
Система линейных неравенств — это система уравнений линейных неравенств, содержащих одинаковые переменные.
Несколько методов решения систем линейных уравнений переводятся в систему линейных неравенств. Однако решение системы линейных неравенств несколько отличается от линейных уравнений, потому что знаки неравенства мешают нам решить с помощью метода замены или исключения. Возможно, лучший метод решения систем линейных неравенств — это графическое отображение неравенств.
Как решать системы линейных неравенств?
Ранее вы научились решать простое линейное неравенство с помощью построения графиков.В этой статье мы узнаем, как найти решения для системы линейных неравенств путем одновременного построения графиков двух или более линейных неравенств.
Решением системы линейных неравенств является область, в которой пересекаются графики всех линейных неравенств в системе.
Чтобы решить систему неравенств, изобразите каждое линейное неравенство в системе на одной оси x-y, выполнив следующие шаги. :
- Изолируйте переменную y в каждом линейном неравенстве.
- Нарисуйте и заштрихуйте область над линией границы, используя пунктирные и сплошные линии для символов> и ≥ соответственно.
- Аналогичным образом нарисуйте и закрасьте область под линией границы, используя пунктирные и сплошные линии для символов <и ≤ соответственно.
- Закрасьте область, где все уравнения перекрываются или пересекаются. Если нет области пересечения, то делаем вывод, что система неравенств не имеет решения.
Давайте рассмотрим пару примеров, чтобы понять эти шаги.
Пример 1
Изобразите следующую систему линейных неравенств:
y ≤ x — 1 и y <–2x + 1
Решение
Изобразите первое неравенство y ≤ x — 1.
- Из-за символа «меньше или равно» мы нарисуем сплошную границу и сделаем штриховку под линией.
- Также изобразите второе неравенство y <–2x + 1 на той же оси x-y.
- В этом случае наша граница будет пунктирной или пунктирной из-за символа «меньше».Заштрихуйте область ниже границы.
Таким образом, решением этой системы неравенств является более темная заштрихованная область, продолжающаяся вечно в направлении вниз, как показано на рисунке ниже. ВНИМАНИЕ !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Пример 2
Решите следующую систему неравенств:
x — 5y ≥ 6
3x + 2y> 1
Решение
- Сначала выделите переменную y слева в каждом неравенстве.
Для x — 5y ≥ 6;
=> x ≥ 6 + 5y
=> 5y ≤ x — 6
=> y ≤ 0.2 x — 1,2
А для 3x + 2y> 1;
=> 2y> 1 — 3x
=> y> 0,5 — 1,5x
- Мы построим график y ≤ 2 x — 1,2 и y> 0,5 — 1,5x, используя сплошную и ломаную линии соответственно .
Решение системы неравенства — более темная заштрихованная область, которая является перекрытием двух отдельных областей решения.
Пример 3
Изобразите следующую систему линейных неравенств.
y ≤ (1/2) x + 1,
y ≥ 2x — 2,
y ≥ — (1/2) x — 3.
Решение
Эта система неравенств имеет три уравнения, которые все связаны символом «равно». Это говорит нам о том, что все границы будут прочными. График трех неравенств показан ниже.
Заштрихованная область трех уравнений перекрывается прямо в средней части. Следовательно, решения системы лежат в ограниченной области, как показано на графике.
Пример 4
Изобразите следующую систему линейных неравенств:
x + 2y <2, y> –1,
x ≥ –3.
Решение
Выделите переменную y в первом неравенстве, чтобы получить;
y <- x / 2 +1 Обратите внимание, что неравенства y> –1 и x ≥ –3 будут иметь горизонтальные и вертикальные граничные линии соответственно. Давайте изобразим три неравенства, как показано ниже.
Более темная заштрихованная область, окруженная двумя сегментами пунктирной линии и одним сегментом сплошной линии, дает три неравенства.
Пример 5
Решите следующую систему линейных неравенств:
–2x -y <-1
4x + 2y ≤-6
Решение
Изолировать переменную y неравенство.
–2x -y <-1 => y> –2x + 1
4x + 2y ≤ -6 => y ≤ -2x -3
Давайте продолжим и построим график y> –2x + 1 и y ≤ — 2x -3:
Поскольку заштрихованные области двух неравенств не перекрываются, мы можем сделать вывод, что система неравенств не имеет решения.
Предыдущий урок | Главная страница | Следующий урок
| |||||||||||||||||||||||||||||||||
| Решить | |||||||||||||||||||||||||||||||||
Графические системы линейных неравенств — Элементарная алгебра
Системы линейных уравнений
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы линейных неравенств
- Решите систему линейных неравенств, построив график
- Решите приложения систем неравенств
Прежде чем начать, пройдите тест на готовность.
- График на числовой прямой.
Если вы пропустили эту проблему, просмотрите (рисунок). - Решите неравенство.
Если вы пропустили эту проблему, просмотрите (рисунок). - Определите, является ли заказанная пара решением для системы.
Если вы пропустили эту проблему, просмотрите (рисунок)
Определить, является ли упорядоченная пара решением системы линейных неравенств
Определение системы линейных неравенств очень похоже на определение системы линейных уравнений.
Система линейных неравенств
Два или более линейных неравенства, сгруппированных вместе, образуют систему линейных неравенств.
Система линейных неравенств выглядит как система линейных уравнений, но вместо уравнений в ней есть неравенства. Ниже представлена система двух линейных неравенств.
Для решения системы линейных неравенств мы найдем значения переменных, которые являются решениями обоих неравенств. Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика.Мы найдем на плоскости область, содержащую все упорядоченные пары, удовлетворяющие обоим неравенствам.
Решения системы линейных неравенств
Решениями системы линейных неравенств являются значения переменных, которые делают все неравенства истинными.
Решение системы линейных неравенств показано заштрихованной областью в системе координат x-y , которая включает все точки, чьи упорядоченные пары делают неравенства истинными.
Чтобы определить, является ли упорядоченная пара решением системы двух неравенств, мы подставляем значения переменных в каждое неравенство. Если упорядоченная пара выполняет оба неравенства, это решение системы.
Определите, является ли заказанная пара решением для системы.
ⓐ (−2, 4) ⓑ (3,1)
Решение
- ⓐ Является ли упорядоченная пара (−2, 4) решением?
Упорядоченная пара (−2, 4) выполнила оба неравенства.Следовательно, (−2, 4) — решение этой системы.
- ⓑ Является ли упорядоченная пара (3,1) решением?
Упорядоченная пара (3,1) сделала одно неравенство истинным, а другое — ложным. Следовательно, (3,1) не является решением этой системы.
Определите, является ли заказанная пара решением для системы.
ⓐⓑ
Определите, является ли заказанная пара решением для системы.
ⓐⓑ
Решите систему линейных неравенств с помощью построения графиков
Решением единственного линейного неравенства является область на одной стороне граничной линии, которая содержит все точки, которые делают неравенство истинным.Решением системы двух линейных неравенств является область, содержащая решения обоих неравенств. Чтобы найти эту область, мы построим график каждого неравенства отдельно, а затем определим область, в которой оба неравенства верны. Решение всегда отображается в виде графика.
Как решить систему линейных неравенств
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему линейных неравенств с помощью построения графиков.
- Изобразите первое неравенство.
- Постройте граничную линию.
- Заштриховать сбоку от ограничивающей линии, где выполняется неравенство.
- На той же сетке нанесите график второго неравенства.
- Постройте граничную линию.
- Заштрихуйте сбоку от границы, на которой выполнено неравенство.
- Решением является область перекрытия штриховки.
- Проверьте, выбрав контрольную точку.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Системы линейных неравенств с параллельными линиями границ могут не иметь решения. Мы увидим это на (Рисунок).
Решите систему, построив график.
Решение
Нет смысла в обеих заштрихованных областях, поэтому у системы нет решения.У этой системы нет решения.
Решите систему, построив график.
нет решения
Решите систему, построив график.
нет решения
Решите систему, построив график.
Решение
Ни одна точка на граничных линиях не включена в решение, так как обе линии пунктирны.
Решение — это дважды заштрихованная область, которая также является решением.
Решите систему, построив график.
Решите систему, построив график.
Решение приложений систем неравенств
Первое, что нам нужно сделать для решения приложений систем неравенств, — это преобразовать каждое условие в неравенство. Затем мы строим график системы, как мы делали выше, чтобы увидеть область, содержащую решения. Многие ситуации будут реалистичными только в том случае, если обе переменные положительны, поэтому на их графиках будет отображаться только Квадрант I.
Кристи продает свои фотографии в киоске на уличной ярмарке. В начале дня она хочет, чтобы на ее стенде было не менее 25 фотографий. Каждая маленькая фотография, которую она показывает, стоит ей 4 фунта, а каждая большая фотография — 10 фунтов. Она не хочет тратить больше 200 фунтов на фотографии для показа.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему в виде графика.
ⓒ Могла ли она показать 15 маленьких и 5 больших фотографий?
ⓓ Могла ли она показать 3 больших и 22 маленьких фотографии?
Решение
- ⓐ Пусть количество маленьких фото.
количество больших фото
Чтобы найти систему неравенств, переведите информацию.
У нас есть своя система неравенства. - ⓑ
Для построения графика, график x + y = 25 в виде сплошной линии.
Выберите (0, 0) в качестве тестовой точки. Поскольку это не делает неравенство
истинным, закрасьте сторону, на которой нет точки (0, 0), красным цветом.
Для построения графика, график 4 x + 10 y = 200 в виде сплошной линии.
Выберите (0, 0) в качестве тестовой точки. Поскольку это не делает неравенство
истинным, закрасьте сторону, которая включает точку (0, 0), синим.
Решение системы — это область графика, которая закрашена дважды и, следовательно, затемнена. - ⓒ Чтобы определить, будут ли работать 10 маленьких и 20 больших фотографий, мы смотрим, находится ли точка (10, 20) в области решения. Нет. Кристи не показывала 10 маленьких и 20 больших фотографий.
- ⓓ Чтобы определить, будут ли работать 20 маленьких и 10 больших фотографий, мы смотрим, находится ли точка (20, 10) в области решения. Это. Кристи могла выбрать отображение 20 маленьких и 10 больших фотографий.
Обратите внимание, что мы также можем протестировать возможные решения, подставляя значения в каждое неравенство.
Прицеп может нести максимальный вес 160 фунтов и максимальный объем 15 кубических футов. Микроволновая печь весит 30 фунтов и имеет объем 2 кубических фута, в то время как принтер весит 20 фунтов и имеет 3 кубических фута пространства.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Можно ли перевозить на этом прицепе 4 микроволновые печи и 2 принтера?
ⓓ Можно ли в этом прицепе перевезти 7 микроволновых печей и 3 принтера?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Мэри необходимо приобрести запасы листов для ответов и карандашей для стандартного теста, который будет проводиться среди младших классов в ее средней школе. Количество необходимых листов для ответов как минимум на 5 больше, чем количество карандашей.Карандаши стоят 2 фунта, а листы ответов — 1 фунт. Бюджет Мэри на эти принадлежности предусматривает максимальную стоимость в 400 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли Мэри купить 100 карандашей и 100 листов для ответов?
ⓓ Может ли Мэри купить 150 карандашей и 150 листов для ответов?
- ⓐ
- ⓑ
- ⓒ нет
- ⓓ нет
Омару нужно съесть не менее 800 калорий, прежде чем отправиться на командную тренировку.Все, что ему нужно, — это гамбургеры и печенье, и он не хочет тратить больше пяти фунтов стерлингов. В гамбургер-ресторане рядом с его колледжем каждый гамбургер содержит 240 калорий и стоит 1,40 фунта стерлингов. Каждое печенье содержит 160 калорий и стоит 0,50 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Мог ли он съесть 3 гамбургера и 1 печенье?
ⓓ Мог ли он съесть 2 гамбургера и 4 печенья?
Решение
ⓐ Давай количество гамбургеров.
количество файлов cookie
Чтобы найти систему неравенств, переведите информацию.
Калории из гамбургеров по 240 калорий каждый плюс калорий из печенья по 160 калорий в каждом должны быть больше 800.
Сумма, потраченная на гамбургеры по 1,40 фунтов стерлингов за каждый, плюс сумма, потраченная на печенье по цене 0,50 фунтов стерлингов, должна быть не более 5,00 фунтов стерлингов.
У нас есть система неравенства.
ⓑ
Решение системы — это область графика, которая закрашена дважды и поэтому закрашена темнее.
ⓒ Чтобы определить, соответствуют ли 3 гамбургера и 2 печенья критериям Омара, мы смотрим, находится ли точка (3, 1) в области решения.Это. Он может съесть 3 гамбургера и 2 печенья.
ⓓ Чтобы определить, соответствуют ли 2 гамбургера и 4 печенья критериям Омара, мы смотрим, находится ли точка (2, 4) в области решения. Это. Он может съесть 2 гамбургера и 4 печенья.
Мы также можем проверить возможные решения, подставляя значения в каждое неравенство.
Tension необходимо съедать не менее 1000 лишних калорий в день, чтобы подготовиться к марафону. У него есть только 25 фунтов стерлингов, чтобы потратить на необходимое дополнительное питание, и он потратит их на 0 фунтов стерлингов.75 пончиков по 360 калорий в каждом и 2 энергетических напитка по 110 калорий.
ⓐ Напишите систему неравенств, моделирующую эту ситуацию.
ⓑ Изобразите систему.
ⓒ Может ли он купить 8 пончиков и 4 энергетических напитка?
ⓓ Может ли он купить 1 пончик и 3 энергетических напитка?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Врач Филиппа говорит ему, что он должен добавлять как минимум 1000 калорий в день к своему обычному рациону. Филип хочет купить протеиновые батончики по цене 1 фунт стерлингов.80 каждый и содержат 140 калорий и сок по цене 1,25 фунтов стерлингов за бутылку и содержат 125 калорий. Он не хочет тратить больше? 12.
ⓐ Напишите систему неравенств, моделирующую эту ситуацию.
ⓑ Изобразите систему.
ⓒ Может ли он купить 3 протеиновых батончика и 5 бутылок сока?
ⓓ Может ли он купить 5 протеиновых батончиков и 3 бутылки сока?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Ключевые понятия
- Решение системы линейных неравенств с помощью построения графиков
- Изобразите первое неравенство.
- Постройте граничную линию.
- Заштриховать сбоку от ограничивающей линии, где выполняется неравенство.
- На той же сетке нанесите график второго неравенства.
- Постройте граничную линию.
- Заштрихуйте сбоку от границы, на которой выполнено неравенство.
- Решением является область перекрытия штриховки.
- Проверьте, выбрав контрольную точку.
- Изобразите первое неравенство.
Упражнения по разделам
Практика ведет к совершенству
Определить, является ли упорядоченная пара решением системы линейных неравенств
В следующих упражнениях определите, является ли каждая упорядоченная пара решением для системы.
Решите систему линейных неравенств с помощью построения графиков
В следующих упражнениях решите каждую систему с помощью построения графиков.
Нет решения
Нет решения
Решение приложений систем неравенств
В следующих упражнениях переведите на систему неравенств и решите.
Кейтлин продает свои рисунки на окружной ярмарке. Она хочет продать не менее 60 рисунков, у нее есть портреты и пейзажи. Она продает портреты за 15 евро и пейзажи за 10 евро. Ей нужно продать рисунков на сумму не менее 800 фунтов стерлингов, чтобы получить прибыль.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Получит ли она прибыль, если продаст 20 портретов и 35 пейзажей?
ⓓ Получит ли она прибыль, если продаст 50 портретов и 20 пейзажей?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Джейк не хочет тратить больше 50 фунтов на мешки с удобрениями и торфяной мох для своего сада.Удобрение стоит 2 евро за мешок, а торфяной мох — 5 евро за мешок. Фургон Джейка вмещает не более 20 сумок.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли он купить 15 мешков удобрений и 4 мешка торфяного мха?
ⓓ Может ли он купить 10 мешков удобрений и 10 мешков торфяного мха?
Рэйко нужно отправлять рождественские открытки и посылки по почте, и она хочет, чтобы ее почтовые расходы не превышали 500 фунтов стерлингов. Количество карточек минимум на 4 больше, чем в два раза больше пакетов.Стоимость пересылки открытки (с картинками) — 3 евро, посылки — 7 евро.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она отправить 60 открыток и 26 пакетов?
ⓓ Может ли она отправить по почте 90 открыток и 40 пакетов?
- ⓐ
- ⓑ
- ⓒ Есть
- ⓓ Нет
Хуан готовится к выпускным экзаменам по химии и алгебре. Он знает, что у него всего 24 часа на обучение, и ему потребуется как минимум в три раза больше времени, чтобы изучать алгебру, чем химию.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли он потратить 4 часа на химию и 20 часов на алгебру?
ⓓ Может ли он потратить 6 часов на химию и 18 часов на алгебру?
Джоселин беременна и ей нужно съедать как минимум на 500 калорий в день больше, чем обычно. При покупке продуктов в один день с бюджетом в 15 фунтов на дополнительную еду, она покупает бананы, каждый из которых содержит 90 калорий, и шоколадные батончики мюсли, каждый из которых содержит 150 калорий.Бананы стоят 0,35 фунта стерлингов каждый, а батончики мюсли — 2,50 фунта стерлингов каждый.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она купить 5 бананов и 6 батончиков мюсли?
ⓓ Может ли она купить 3 банана и 4 батончика мюсли?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Марк пытается нарастить мышечную массу, поэтому ему необходимо дополнительно съедать не менее 80 граммов белка в день. Бутылка протеиновой воды стоит 3 фунта.20, а протеиновый батончик стоит 1,75 фунтов стерлингов. Белковая вода содержит 27 граммов белка, а батончик — 16 граммов. Если он есть? 10 долларов на расходы
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Мог ли он купить 3 бутылки протеиновой воды и 1 протеиновый батончик?
ⓓ Мог ли он покупать не бутылки с протеиновой водой и 5 протеиновых батончиков?
Джоселин хочет увеличить потребление белка и калорий. Она хочет есть как минимум на 35 граммов больше белка каждый день и не более чем на 200 дополнительных калорий в день.Унция сыра чеддер содержит 7 граммов белка и 110 калорий. Унция сыра пармезан содержит 11 граммов белка и 22 калории.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она съесть 30 грамм сыра чеддер и 100 грамм сыра пармезан?
ⓓ Может ли она съесть 2 унции сыра чеддер и 30 грамм сыра пармезан?
- ⓐ
- ⓑ
- ⓒ Есть
- ⓓ Нет
Марк увеличивает свои физические нагрузки, бегая и ходя не менее 4 миль каждый день.Его цель — сжечь как минимум 1500 калорий с помощью этого упражнения. Ходьба сжигает 270 калорий на милю, а бег — 650 калорий.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Сможет ли он достичь своей цели, пройдя 3 мили и пробежав 1 милю?
ⓓ Сможет ли он достичь своей цели, пройдя 2 мили и пробежав 2 мили?
Повседневная математика
Билеты на матч Американской бейсбольной лиги для 3 взрослых и 3 детей стоят менее 75 фунтов стерлингов, а билеты для 2 взрослых и 4 детей — менее 62 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой проблемы.
ⓑ Изобразите систему.
ⓒ Могут ли билеты стоить 20 евро для взрослых и 8 евро для детей?
ⓓ Могут ли билеты стоить? 15 для взрослых и 5? Для детей?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Дедушка и бабушка развлекают свою семью в кино. Билет на утренник стоит 4 евро для ребенка и 4 евро для взрослого. Вечерние билеты стоят 6 евро для ребенка и 8 евро для взрослого.Они планируют потратить не больше 80 фунтов на билеты на утренник и не более 100 на вечерние билеты.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Могут ли они взять с собой 9 детей и 4 взрослых на оба спектакля?
ⓓ Могут ли они взять с собой 8 детей и 5 взрослых на оба спектакля?
Письменные упражнения
Изобразите неравенство. Как узнать, какую сторону линии нужно растушевать?
Изобразите систему.Что означает решение?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Глава 5. Упражнения на повторение
Решение систем уравнений с помощью построения графиков
Определите, является ли упорядоченная пара решением системы уравнений .
В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
Решение системы линейных уравнений с помощью построения графиков
В следующих упражнениях решите следующие системы уравнений с помощью построения графиков.
совпадающих линий
Определите количество решений линейной системы
В следующих упражнениях без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
бесконечно много решений, непротиворечивая система, зависимые уравнения
нет решений, несовместная система, независимые уравнения
Решение приложений систем уравнений с помощью построения графиков
ЛаВелле делает кувшин кофе мокко. На каждую унцию шоколадного сиропа она использует пять унций кофе. Сколько унций шоколадного сиропа и сколько унций кофе нужно ей, чтобы приготовить 48 унций кофе мокко?
ЛаВеллю нужно 8 унций шоколадного сиропа и 40 унций кофе.
Эли готовит коктейль для вечеринок, состоящий из крендельков и чекса. На каждую чашку крендельков он использует три чашки чекса. Сколько чашек кренделей и сколько чашек чекса ему нужно, чтобы приготовить 12 чашек коктейля для вечеринок?
Решите системы уравнений подстановкой
Решите систему уравнений подстановкой
В следующих упражнениях решите системы уравнений путем подстановки.
Решите приложения систем уравнений подстановкой
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна 55. Одно число на 11 меньше другого. Найдите числа.
Цифры 22 и 33.
Периметр прямоугольника 128. Длина на 16 больше ширины. Найдите длину и ширину.
Размер одного из малых углов прямоугольного треугольника в 2 раза меньше, чем в 3 раза больше размера другого малого угла. Найдите размер обоих углов.
Размеры: 23 градуса и 67 градусов.
Габриэла работает в страховой компании, которая платит ей зарплату в размере 32 000 фунтов стерлингов плюс комиссию в размере 100 фунтов стерлингов за каждый проданный полис.Она рассматривает возможность перехода на другую работу в компанию, которая будет платить зарплату в размере 40 000 фунтов стерлингов плюс комиссию в размере 80 фунтов стерлингов за каждый проданный полис. Сколько полисов нужно продать Габриэле, чтобы общая сумма была такой же?
Решите системы уравнений методом исключения
Решите систему уравнений методом исключения В следующих упражнениях решите системы уравнений методом исключения.
Решение приложений систем уравнений методом исключения
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна. Их разница есть. Найдите числа.
Цифры и.
Омар каждый день останавливается в магазине пончиков по дороге на работу. На прошлой неделе он съел 8 пончиков и 5 капучино, что дало ему в общей сложности 3000 калорий. На этой неделе он съел 6 пончиков и 3 капучино, что в общей сложности составило 2160 калорий. Сколько калорий в одном пончике? Сколько калорий в одном капучино?
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, что было бы удобнее решить систему уравнений путем подстановки или исключения.
Решение приложений с помощью систем уравнений
Перевести в систему уравнений
В следующих упражнениях переведите в систему уравнений. Не решайте систему.
Сумма двух чисел равна. Одно число на два меньше, чем в два раза другое. Найдите числа.
Четыре раза больше числа плюс трижды второе число. Дважды первое число плюс второе число — три.Найдите числа.
В прошлом месяце Джим и Дебби заработали 7200 фунтов стерлингов. Дебби заработала на 1600 фунтов больше, чем заработал Джим. Сколько они заработали?
Анри вложил 24 000 евро в акции и облигации. Сумма в акциях на 6 000 евро больше, чем в три раза больше, чем в облигациях. Сколько стоит каждая инвестиция?
Решение задач прямого перевода
В следующих упражнениях переведите в систему уравнений и решите.
Пэм на 3 года старше своей сестры Ян.Сумма их возрастов — 99. Найдите их возраст.
Молли хочет посадить 200 луковиц в своем саду. Она хочет все ирисы и тюльпаны. Она хочет посадить в три раза больше тюльпанов, чем ирисов. Сколько ирисов и сколько тюльпанов ей следует посадить?
Приложения Solve Geometry
В следующих упражнениях переведите в систему уравнений и решите.
Разница двух дополнительных углов составляет 58 градусов. Найдите размеры углов.
Размеры: 119 градусов и 61 градус.
Два угла дополняют друг друга. Мера большего угла в пять раз больше, чем в четыре раза меньшего угла. Найдите размеры обоих углов.
Бекка вешает 28-футовую цветочную гирлянду с двух сторон и сверху беседки, чтобы подготовиться к свадьбе. Высота на четыре фута меньше ширины. Найдите высоту и ширину беседки.
Пергола 8 футов в высоту и 12 футов в ширину.
Периметр городского прямоугольного парка составляет 1428 футов. Длина на 78 футов более чем в два раза превышает ширину. Найдите длину и ширину парка.
Решение приложений с равномерным движением
В следующих упражнениях переведите в систему уравнений и решите.
Шейла и Ленор ехали в дом своей бабушки. Ленора ушла через час после Шейлы. Шейла ехала со скоростью 45 миль в час, а Ленора ехала со скоростью 60 миль в час. Сколько времени потребуется Леноре, чтобы догнать Шейлу?
Это займет у Леноры 3 часа.
Боб ушел из дома на своем велосипеде со скоростью 10 миль в час, чтобы добраться до озера. Черил, его жена, уехала через 45 минут (час) спустя, двигаясь на своей машине со скоростью 25 миль в час. Сколько времени потребуется Шерил, чтобы догнать Боба?
Маркус может проехать на своей лодке 36 миль по реке за три часа, но ему нужно четыре часа, чтобы вернуться вверх по течению. Найдите скорость лодки в стоячей воде и скорость течения.
Скорость лодки 10,5 миль в час. Скорость тока — 1.5 миль / ч.
Пассажирский реактивный самолет может пролететь 804 мили за 2 часа при попутном ветре, но только 776 миль за 2 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра.
Решение смесей приложений с помощью систем уравнений
Приложения для растворения смеси
В следующих упражнениях переведите в систему уравнений и решите.
Линн заплатила в общей сложности 2780 фунтов стерлингов за 261 билет в театр. Студенческие билеты стоят 10 евро, взрослые — 15 евро.Сколько студенческих билетов и сколько взрослых билетов купила Линн?
Линн купила 227 студенческих билетов и 34 взрослых билета.
У Приама в машине есть десять центов и центов в подстаканнике. Общая стоимость монет составляет 4,21 фунта стерлингов. Количество десятицентовиков на три меньше, чем четырехкратное количество пенсов. Сколько центов и сколько центов в чашке?
Юми хочет приготовить 12 чашек смеси для вечеринок из конфет и орехов. Ее бюджет требует, чтобы вечеринка обошлась ей в 1 фунт.29 на чашку. Конфеты стоят 2,49 фунтов за чашку, а орехи — 0,69 фунтов за чашку. Сколько чашек конфет и сколько чашек орехов ей следует съесть?
Юми следует использовать 4 чашки конфет и 8 чашек орехов.
Ученому нужно 70 литров 40% раствора спирта. У него есть 30% и 60% раствор. Сколько литров 30% и сколько литров 60% растворов он должен смешать, чтобы получить 40% раствор?
Заявки на выплату процентов
В следующих упражнениях переведите в систему уравнений и решите.
У Джека есть 12 000 евро для инвестирования, и он хочет получать 7,5% годовых. Он поместит часть денег на сберегательный счет, приносящий 4% в год, а остальную часть — на счет CD, который приносит 9% в год. Сколько денег он должен положить на каждый счет?
Джек должен положить 3600 евро в сбережения и 8400 евро на компакт-диск.
Когда она закончит колледж, Линда будет должна 43 000 фунтов стерлингов в виде студенческих ссуд. Процентная ставка по федеральным займам составляет 4,5%, а ставка по ссудам частных банков — 2%.Общая сумма процентов, которую она задолжала за один год, составила 1585 фунтов стерлингов. Какая сумма каждого кредита?
Графические системы линейных неравенств
Определить, является ли упорядоченная пара решением системы линейных неравенств
В следующих упражнениях определите, является ли каждая упорядоченная пара решением для системы.
Решите систему линейных неравенств с помощью построения графиков
В следующих упражнениях решите каждую систему с помощью построения графиков.
Нет решения
Решение приложений систем неравенств
В следующих упражнениях переведите на систему неравенств и решите.
Роксана производит браслеты и ожерелья и продает их на фермерском рынке. Браслеты она продает по 12 фунтов за штуку, а ожерелья — по 18 фунтов. На рынке в следующие выходные у нее будет место для демонстрации не более 40 штук, и ей нужно продать не менее 500 фунтов стерлингов, чтобы получить прибыль.
- ⓐ Напишите систему неравенств для моделирования этой ситуации.
- ⓑ Изобразите систему.
- ⓒ Следует ли ей показать 26 браслетов и 14 ожерелий?
- ⓓ Следует ли ей показать 39 браслетов и 1 ожерелье?
ⓐ
ⓑ
ⓒ да
ⓓ нет
У Энни есть бюджет в 600 фунтов стерлингов на покупку книг в мягкой обложке и книг в твердом переплете для своего класса. Она хочет, чтобы количество книг в твердой обложке было как минимум в 5 раз больше, чем в три раза больше книг в мягкой обложке.Книги в мягкой обложке стоят 4 фунта каждая, а книги в твердой обложке — 15 евро.
- ⓐ Напишите систему неравенств для моделирования этой ситуации.
- ⓑ Изобразите систему.
- ⓒ Может ли она купить 8 книг в мягкой обложке и 40 книг в твердой обложке?
- ⓓ Может ли она купить 10 книг в мягкой обложке и 37 книг в твердой обложке?
Практический тест
В следующих упражнениях решите следующие системы с помощью построения графиков.
В следующих упражнениях решите каждую систему уравнений.Используйте либо замену, либо исключение.
бесконечно много решений
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна −24. Одно число на 104 меньше другого. Найдите числа.
Цифры 40 и 64
Рамон хочет посадить в своем саду огурцы и помидоры.У него есть место для 16 растений, и он хочет посадить в три раза больше огурцов, чем помидоров. Сколько огурцов и сколько помидоров нужно посадить?
Два угла дополняют друг друга. Мера большего угла в шесть раз больше, чем мера меньшего угла, более чем в два раза. Найдите размеры обоих углов.
Размеры углов: 28 градусов и 62 градуса.
В понедельник Лэнс бегал 30 минут и плавал 20 минут. Его фитнес-приложение сообщило ему, что он сжег 610 калорий.В среду фитнес-приложение сообщило ему, что он сжег 695 калорий, когда бегал 25 минут и плавал 40 минут. Сколько калорий он сжег за одну минуту бега? Сколько калорий он сжег за минуту плавания?
Кэти вышла из дома, чтобы дойти до торгового центра, быстро пошла со скоростью 4 мили в час. Ее сестра Эбби вышла из дома через 15 минут и ехала на велосипеде до торгового центра со скоростью 10 миль в час. Сколько времени понадобится Эбби, чтобы догнать Кэти?
Это займет у Кэти час (или 10 минут).
Самолету требуется несколько часов, чтобы преодолеть 2475 миль при встречном ветре из Сан-Хосе, Калифорния, в Лихуэ, Гавайи. Обратный рейс из Лихуэ в Сан-Хосе с попутным ветром занимает 5 часов. Найдите скорость струи в неподвижном воздухе и скорость ветра.
Лиз заплатила 160 фунтов за 28 билетов, чтобы отвести отряд Брауни в музей науки. Детские билеты стоят 5 евро, взрослые — 9 евро. Сколько билетов для детей и сколько билетов для взрослых купила Лиз?
Лиз купила 23 детских и 5 взрослых билетов.
Фармацевту необходимо 20 литров 2% физиологического раствора. У него есть 1% и 5% раствор. Сколько литров 1% и сколько литров 5% растворов нужно смешать, чтобы получился 2% раствор?
Переведите в систему неравенств и решите.
Энди хочет потратить не более 50 фунтов стерлингов на Хэллоуинские угощения. Она хочет купить шоколадные батончики стоимостью 1 фунт каждый и леденцы стоимостью 0,50 фунтов стерлингов каждый, и она хочет, чтобы количество леденцов было как минимум в три раза больше, чем шоколадных батончиков.
- ⓐ Напишите систему неравенств для моделирования этой ситуации.
- ⓑ Изобразите систему.



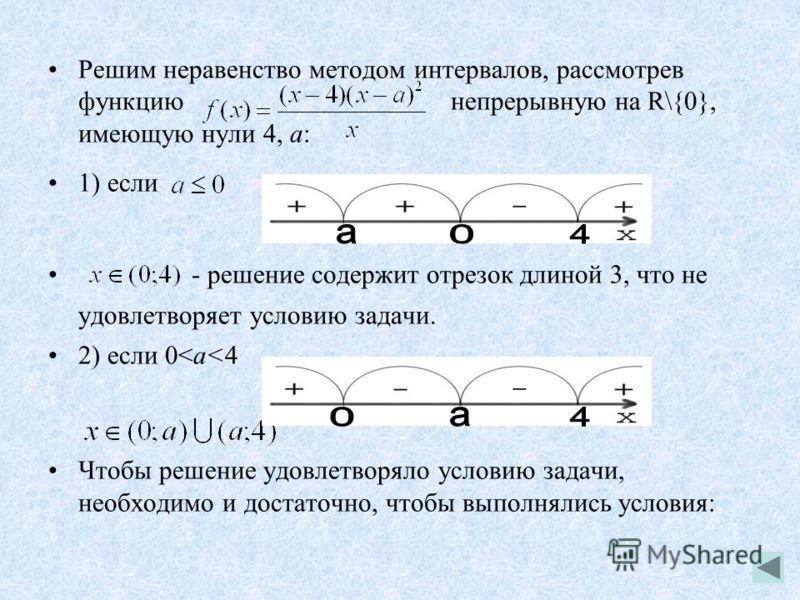
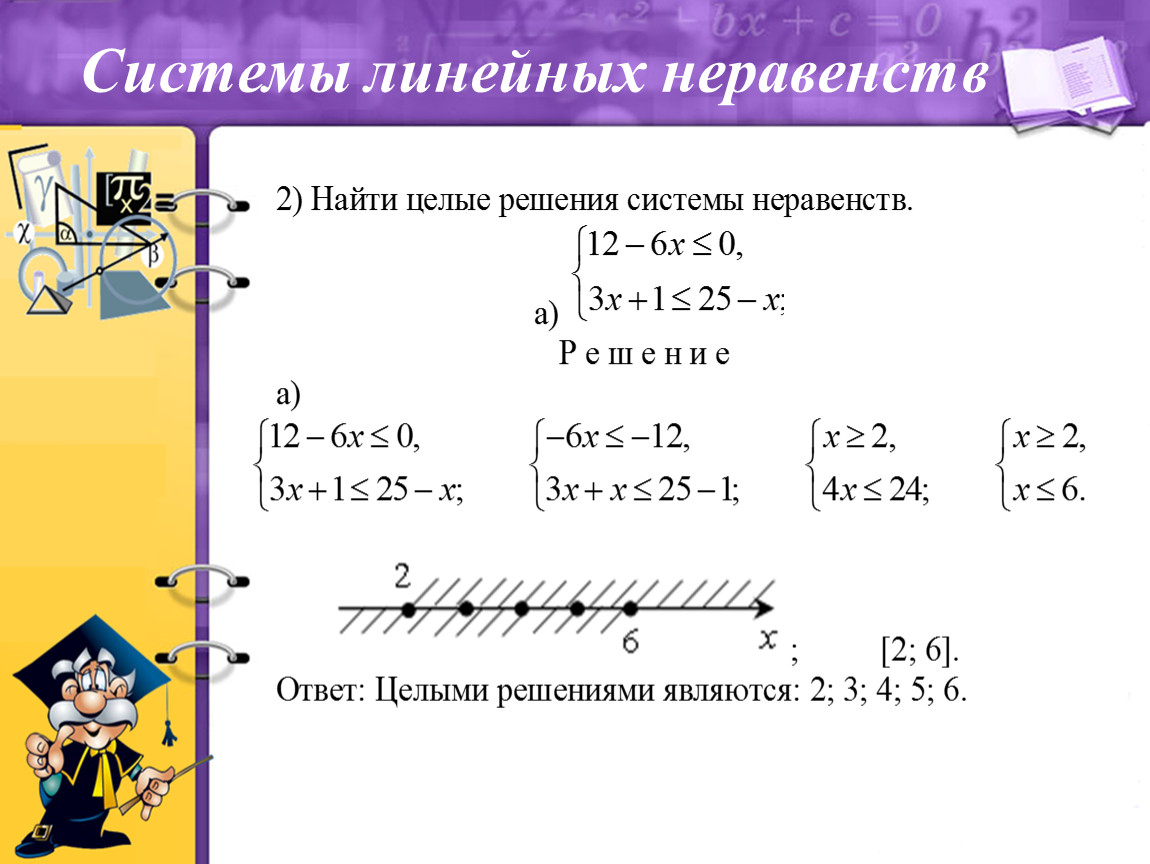 Решение
уравнений и систем уравнений (45 мин)
Решение
уравнений и систем уравнений (45 мин)