Решение системы линейных уравнений методом сложения: алгоритм, примеры
Алгоритм решения системы линейных уравнений методом сложения
Например: $ {\left\{ \begin{array}{c} 3x+y = 5 \\ x+2y = 5 \end{array} \right.}$
Шаг 1
Умножаем первое уравнение на 2
${\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right.}$
Шаг 2
Отнимаем от первого уравнения второе:
5x = 5
Шаг 3
Находим x:
x = 1
Шаг 4
Находим y из первого уравнения:
y = 5-3x = 2
Шаг 5
Ответ: (1;2)
В последовательной записи:
$$ {\left\{ \begin{array}{c} 3x+y = 5 | \times 2 \\ x+2y = 5 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x = 5 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 5-3x = 2 \end{array} \right.} $$
Ответ: (1;2)
Примеры
Пример 1. Решите систему уравнений методом сложения:
Решите систему уравнений методом сложения:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 | \times 2 \\ 2x-3y = 4 | \times 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 10x-8y = 6 \\ 10x-15y = 20 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7y = -14 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = \frac{3y+4}{2} = -1 \\ y=-2 \end{array} \right.} $
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 | \times 3 \\ 3x-4y = 0 | \times 4 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 12x-9y = 21 \\ 12x-16y = 0 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7y = 21 \\ x = \frac{4}{3} y \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 4 \\ y = 3 \end{array} \right.} $
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 | \times 2 \\ 2a+3b = -1 | \times 5 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 10a-8b = 18 \\ 10a+15b = -5 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} -23b = 23 \\ a = \frac{-3b-1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $
} \Rightarrow {\left\{ \begin{array}{c} -23b = 23 \\ a = \frac{-3b-1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $
Ответ: (1;-1)
$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 | \times (-2) \end{array} \right.} \Rightarrow (+) {\left\{ \begin{array}{c} 7a+4b = 5 \\ -6a-4b = -2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = \frac{1-3a}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -4 \end{array} \right.}$
Ответ: (3;-4)
Пример 2. Найдите решение системы уравнений:
$$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right.} \Rightarrow (+) {\left\{ \begin{array}{c} \frac{x}{4} -y = 7 \\ 6x+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 6 \frac{1}{4} x = 25 \\ y = 18-6x\end{array} \right.} \Rightarrow $$
$$\Rightarrow {\left\{ \begin{array}{c} x = 25: \frac{25}{4} = 25 \cdot \frac{4}{25} = 4 \\ y = 18-6 \cdot 4 = -6 \end{array} \right. } $$
} $$
Ответ: (4;-6)
$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 2 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 3 \end{array} \right.}\Rightarrow (-) {\left\{ \begin{array}{c} x+ \frac{2}{3} y = \frac{1}{3} \\ x+ \frac{3}{2} y = — \frac{1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} \left( \frac{2}{3}- \frac{3}{2}\right) y = \frac{1}{3}+ \frac{1}{2} \\ x = \frac{1}{3}- \frac{2}{3} y\end{array} \right.} \Rightarrow$
$$ \Rightarrow {\left\{ \begin{array}{c} y = \frac{5}{6}:\left(-\frac{5}{6}\right) = -1 \\ x = \frac{1}{3}+ \frac{2}{3} = 1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right.} $$
Ответ: (1;-1)
$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $
$$ \Rightarrow (+) {\left\{ \begin{array}{c} 10x-8y = -14 \\ x+8y = 25 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 11x = 11 \\ y = \frac{25-x}{8} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.}$$
} \Rightarrow {\left\{ \begin{array}{c} 11x = 11 \\ y = \frac{25-x}{8} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.}$$
Ответ: (1;3)
$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 | \times 7 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 7x+22y = 57 \\ 7x-21y = 14 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$
Ответ: (5;1)
Пример 3*. Найдите решение системы уравнений:
$ {\left\{ \begin{array}{c} \frac{2}{x} + \frac{3}{y} = 1 \\ \frac{3}{x} — \frac{5}{y} = 11 \end{array} \right. } $
} $
Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{x} \\ b = \frac{1}{y} \end{array} \right.} $
Перепишем систему и найдём решение для новых переменных:
$$ {\left\{ \begin{array}{c}2a+3b = 1| \times 3 \\ 3a-5b = 11 | \times 2 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 6a+9b = 3 \\ 6a-10b = 22 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 19b = -19 \\ a = \frac{1-3b}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 2 \\ b = -1 \end{array} \right.} $$
Исходные переменные:
$$ {\left\{ \begin{array}{c} x = \frac{1}{a} = \frac{1}{2} \\ y = \frac{1}{b} = -1 \end{array} \right.} $$
Ответ:$ \left(\frac{1}{2} ;-1 \right)$
Решение систем линейных уравнений способом сложения калькулятор. Решение систем уравнений способом сложения
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы — это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.
-4 — y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны. Эта пара чисел и есть решение системы уравнений. Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны, то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х, на втором у.
Ответ: (4; 3)
Пример 2 . Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
4х + 3(-2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Ответ: (1/2; — 2)
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. 
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Метод алгебраического сложения
Решить систему уравнений с двумя неизвестными можно различными способами — графическим методом или методом замены переменной.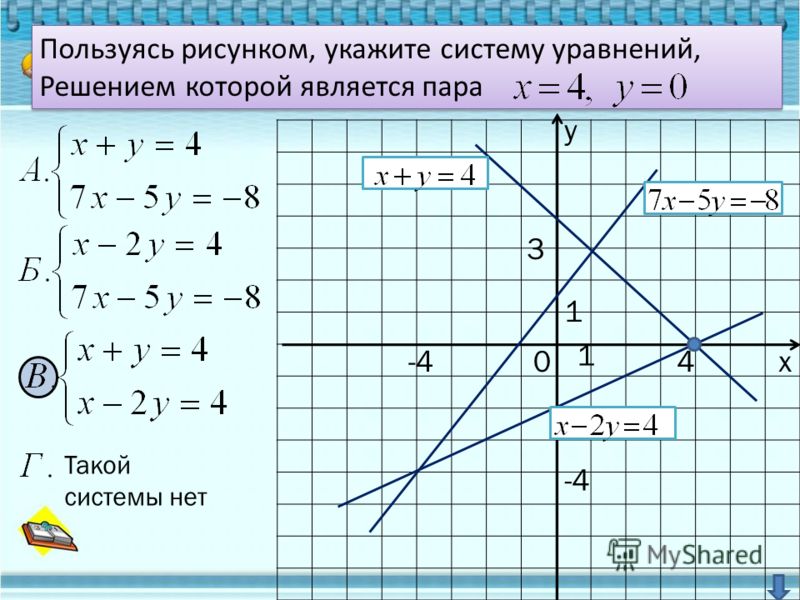
В этом уроке познакомимся с ещё одним способом решения систем, который Вам наверняка понравится — это способ алгебраического сложения.
А откуда вообще взялась идея — что-то складывать в системах? При решении систем главной проблемой является наличие двух переменных, ведь решать уравнения с двумя переменными мы не умеем. Значит, надо каким-либо законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.
Одно из таких свойств звучит так: сумма противоположных чисел равна нулю. Значит, если при одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и нам удастся исключить эту переменную из уравнения. Понятно, что складывать только слагаемые с нужной нам переменной мы не имеем право. Складывать надо уравнения целиком, т.е. по отдельности складывают подобные слагаемые в левой части, затем в правой. В результате мы получим новое уравнение, содержащее только одну переменную. Давайте рассмотрим сказанное на конкретных примерах.
Мы видим, что в первом уравнении есть переменная у, а во втором противоположное число -у. Значит, это уравнение можно решить методом сложения.
Одно из уравнений оставляют в том виде, каком оно есть. Любое, какое Вам больше нравится.
А вот второе уравнение будет получено сложением этих двух уравнений почленно. Т.е. 3х сложим с 2х, у сложим с -у, 8 сложим с 7.
Получим систему уравнений
Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = -1.
Ответ: (3; — 1).
Образец оформления:
Решить методом алгебраического сложения систему уравнений
В данной системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.
Тогда первое уравнение примет вид:
Теперь видим, что при переменной х есть противоположные коэффициенты.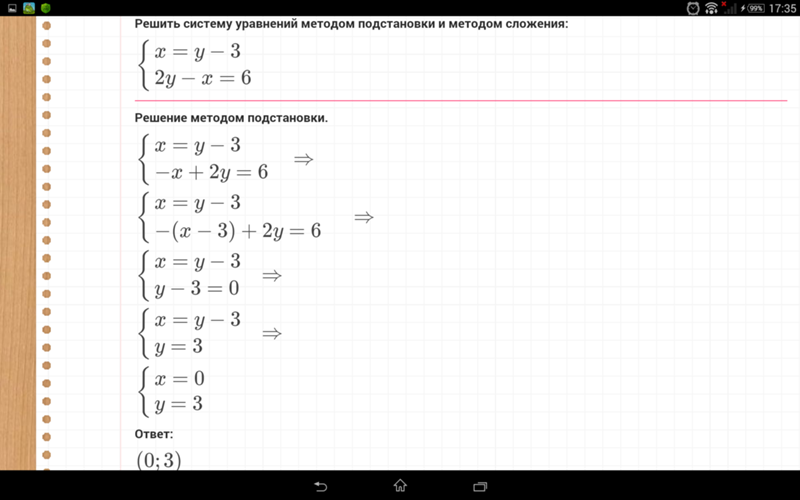 Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.
Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.
Теперь у нас система уравнений:
Легко находим из второго уравнения у = 1, а затем из первого уравнения х = 4.
Образец оформления:
Давайте подведём итоги:
Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, нам теперь известны три основных метода решения таких систем: графический, метод замены переменной и метод сложения. Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.
 Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007. - Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.
Способ сложения состоит из трёх простых шагов:
- Посмотреть на систему и выбрать переменную, у которой в каждом уравнении стоят одинаковые (либо противоположные) коэффициенты;
- Выполнить алгебраическое вычитание (для противоположных чисел — сложение) уравнений друг из друга, после чего привести подобные слагаемые;
- Решить новое уравнение, получившееся после второго шага.

Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.
Однако на практике всё не так просто. Причин тому несколько:
- Решение уравнений способом сложения подразумевает, что во всех строчках должны присутствовать переменные с одинаковыми/противоположными коэффициентами. А что делать, если это требование не выполняется?
- Далеко не всегда после сложения/вычитания уравнений указанным способом мы получим красивую конструкцию, которая легко решается. Возможно ли как-то упростить выкладки и ускорить вычисления?
Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:
Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.
Каждое из них будет являться линейным.
Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.
Вообще, существует два метода решения подобных систем:
- Метод сложения;
- Метод выражения одной переменной через другую.
Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.
Результатами подобных махинаций будет новое уравнение, которое, если и имеет корни, то они обязательно будут находиться среди корней исходного уравнения. Поэтому наша задача — сделать вычитание или сложение таким образом, чтобы или $x$, или $y$ исчез.
Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.
Решение легких задач с применением способа сложения
Итак, учимся применять метод сложения на примере двух простейших выражений.
Задача № 1
\[\left\{ \begin{align}& 5x-4y=22 \\& 7x+4y=2 \\\end{align} \right.\]
Заметим, что у $y$ коэффициент в первом уравнении $-4$, а во втором — $+4$. Они взаимно противоположны, поэтому логично предположить, что если мы их сложим, то в полученной сумме «игреки» взаимно уничтожатся. Складываем и получаем:
Решаем простейшую конструкцию:
Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:
\[-4y=12\left| :\left(-4 \right) \right.\]
Ответ: $\left(2;-3 \right)$.
Задача № 2
\[\left\{ \begin{align}& -6x+y=21 \\& 6x-11y=-51 \\\end{align} \right.\]
Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:
Сложим их:
Мы получили простейшее линейное уравнение, давайте решим его:
Теперь давайте найдем $x$:
Ответ: $\left(-3;3 \right)$.
Важные моменты
Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:
- Если есть противоположные коэффициенты при одной из переменных, то необходимо сложить все переменные в уравнении. В этом случае одна из них уничтожится.
- Найденную переменную подставляем в любое из уравнений системы, чтобы найти вторую.
- Окончательную запись ответа можно представить по-разному. Например, так — $x=…,y=…$, или в виде координаты точек — $\left(…;… \right)$. Второй вариант предпочтительней. Главное помнить, что первой координатой идет $x$, а второй — $y$.
- Правило записывать ответ в виде координат точки применимо не всегда. Например, его нельзя использовать, когда в роли переменных выступают не $x$ и $y$, а, к примеру, $a$ и $b$.
В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.
Решение легких задач с применением метода вычитания
Задача № 1
\[\left\{ \begin{align}& 10x-3y=5 \\& -6x-3y=-27 \\\end{align} \right.\]
Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:
Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:
Ответ: $\left(2;5 \right)$.
Задача № 2
\[\left\{ \begin{align}& 5x+4y=-22 \\& 5x-2y=-4 \\\end{align} \right.\]
Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:
Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:
Ответ: $\left(-3;-2 \right)$.
Нюансы решения
Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.
Мы проводим алгебраическое вычитание.
Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.
Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.
Решение задач методом домножения на коэффициент
Пример № 1
\[\left\{ \begin{align}& 5x-9y=38 \\& 3x+2y=8 \\\end{align} \right. \]
\]
Мы видим, что ни при $x$, ни при $y$ коэффициенты не только не взаимно противоположны, но и вообще никак не соотносятся с другим уравнением. Эти коэффициенты никак не исчезнут, даже если мы сложим или вычтем уравнения друг из друга. Поэтому необходимо применить домножение. Давайте попытаемся избавиться от переменной $y$. Для этого мы домножим первое уравнение на коэффициент при $y$ из второго уравнения, а второе уравнение — при $y$ из первого уравнения, при этом не трогая знак. Умножаем и получаем новую систему:
\[\left\{ \begin{align}& 10x-18y=76 \\& 27x+18y=72 \\\end{align} \right.\]
Смотрим на нее: при $y$ противоположные коэффициенты. В такой ситуации необходимо применять метод сложения. Сложим:
Теперь необходимо найти $y$. Для этого подставим $x$ в первое выражение:
\[-9y=18\left| :\left(-9 \right) \right.\]
Ответ: $\left(4;-2 \right)$.
Пример № 2
\[\left\{ \begin{align}& 11x+4y=-18 \\& 13x-6y=-32 \\\end{align} \right. \]
\]
Вновь коэффициенты ни при одной из переменных не согласованы. Домножим на коэффициенты при $y$:
\[\left\{ \begin{align}& 11x+4y=-18\left| 6 \right. \\& 13x-6y=-32\left| 4 \right. \\\end{align} \right.\]
\[\left\{ \begin{align}& 66x+24y=-108 \\& 52x-24y=-128 \\\end{align} \right.\]
Наша новая система равносильна предыдущей, однако коэффициенты при $y$ являются взаимно противоположными, и поэтому здесь легко применить метод сложения:
Теперь найдем $y$, подставив $x$ в первое уравнение:
Ответ: $\left(-2;1 \right)$.
Нюансы решения
Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:
- Смотрим на систему и анализируем каждое уравнение.
- Если мы видим, что ни при $y$, ни при $x$ коэффициенты не согласованы, т.е. они не являются ни равными, ни противоположными, то делаем следующее: выбираем переменную, от которой нужно избавиться, а затем смотрим на коэффициенты при этих уравнениях.
 Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении. - Находим одну переменную.
- Подставляем найденную переменную в одно из двух уравнений системы и находим вторую.
- Записываем ответ в виде координаты точек, если у нас переменные $x$ и $y$.
Но даже в таком нехитром алгоритме есть свои тонкости, например, коэффициенты при $x$ или $y$ могут быть дробями и прочими «некрасивыми» числами. Эти случаи мы сейчас рассмотрим отдельно, потому что в них можно действовать несколько иначе, чем по стандартному алгоритму.
Решение задач с дробными числами
Пример № 1
\[\left\{ \begin{align}& 4m-3n=32 \\& 0,8m+2,5n=-6 \\\end{align} \right.\]
Для начала заметим, что во втором уравнении присутствуют дроби. Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:
Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:
\[\left\{ \begin{align}& 4m-3n=32 \\& 4m+12,5m=-30 \\\end{align} \right.\]
Вычитаем уравнения друг из друга:
$n$ мы нашли, теперь посчитаем $m$:
Ответ: $n=-4;m=5$
Пример № 2
\[\left\{ \begin{align}& 2,5p+1,5k=-13\left| 4 \right. \\& 2p-5k=2\left| 5 \right. \\\end{align} \right.\]
Здесь, как и в предыдущей системе, присутствуют дробные коэффициенты, однако ни при одной из переменных коэффициенты в целое число раз друг в друга не укладываются. Поэтому используем стандартный алгоритм. Избавится от $p$:
\[\left\{ \begin{align}& 5p+3k=-26 \\& 5p-12,5k=5 \\\end{align} \right.\]
Применяем метод вычитания:
Давайте найдем $p$, подставив $k$ во вторую конструкцию:
Ответ: $p=-4;k=-2$.
Нюансы решения
Вот и вся оптимизация. В первом уравнении мы не стали домножать вообще ни на что, а второе уравнение домножили на $5$. В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.
В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.
Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.
В заключение хотел бы обратить ваше внимание на формат записи ответа. Как я уже и говорил, поскольку здесь у нас тут не $x$ и $y$, а другие значения, мы пользуемся нестандартной записью вида:
Решение сложных систем уравнений
В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.
Система № 1
\[\left\{ \begin{align}& 3\left(2x-y \right)+5=-2\left(x+3y \right)+4 \\& 6\left(y+1 \right)-1=5\left(2x-1 \right)+8 \\\end{align} \right. \]
\]
Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.
Итого мы получим окончательную систему, которая равносильна исходной:
\[\left\{ \begin{align}& 8x+3y=-1 \\& -10x+6y=-2 \\\end{align} \right.\]
Посмотрим на коэффициенты при $y$: $3$ укладывается в $6$ два раза, поэтому домножим первое уравнение на $2$:
\[\left\{ \begin{align}& 16x+6y=-2 \\& -10+6y=-2 \\\end{align} \right.\]
Коэффициенты при $y$ теперь равны, поэтому вычитаем из первого уравнения второе: $$
Теперь найдем $y$:
Ответ: $\left(0;-\frac{1}{3} \right)$
Система № 2
\[\left\{ \begin{align}& 4\left(a-3b \right)-2a=3\left(b+4 \right)-11 \\& -3\left(b-2a \right)-12=2\left(a-5 \right)+b \\\end{align} \right.\]
Преобразуем первое выражение:
Разбираемся со вторым:
\[-3\left(b-2a \right)-12=2\left(a-5 \right)+b\]
\[-3b+6a-12=2a-10+b\]
\[-3b+6a-2a-b=-10+12\]
Итого, наша первоначальная система примет такой вид:
\[\left\{ \begin{align}& 2a-15b=1 \\& 4a-4b=2 \\\end{align} \right. \]
\]
Посмотрев на коэффициенты при $a$, мы видим, что первое уравнение нужно домножить на $2$:
\[\left\{ \begin{align}& 4a-30b=2 \\& 4a-4b=2 \\\end{align} \right.\]
Вычитаем из первой конструкции вторую:
Теперь найдем $a$:
Ответ: $\left(a=\frac{1}{2};b=0 \right)$.
Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!
Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс. | Тренажёр по алгебре (7 класс) на тему:
Опубликовано 05.03.2017 — 23:44 — Головляницина Лидия Вадимовна
Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс.Подробное пошаговое описание работы для слабоуспевающих учащихся с тренировочными заданиями.
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.
 ру
руЗа лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
Образец решения системы уравнений методом подстановки | АЛГОРИТМ (последовательность шагов при работе) | |
1. |
3х + у = 7 -5х + 2у =3 | Выразить из первого уравнения у через х, т.е.перенести 3х в другую часть с противоположным знаком ( т.к. у записан в уравнении без числа(коэффициента)). Получится у = 7 – 3х |
2. | у = 7 – 3х | Выделить в рамочку выраженную переменную у. |
3. | у = 7 – 3х — 5х + 2(7 – 3х) = 3 | Подставить во второе уравнение вместо у выражение (7 – 3х), взяв его в скобки ! |
4. | х = у = | Приготовить знак системы уравнений и место для будущих ответов х у |
5. | -5х + 2·(7 – 3х) = 3 -5х + 14 -6х = 3 | «Выйти из системы» и решить отдельно только уравнение с одной переменной х : 1) раскрыть скобки, умножив число перед скобкой на всё что в скобках; |
6. | -5х + 14 -6х = 3 -5х — 6х = 3 — 14 | 2)Перенести число 14 в правую часть уравнения с противоположным знаком, т. |
7. | — 11х= -11 | 3)Посчитать значение в левой и правой части уравнения |
8. | х = -11:(-11) х = 1 | 4)Вычислить х как неизвестный множитель, вспомнив простой пример 2 · 3 = 6 |
9. | х = 1 у = | Заполнить место в системе уравнений для х |
10. | у = 7 – 3х = 7 — 3·1 = 7-3 = 4 | Найти значение второй переменной у |
11. | х = 1 у = 4 | Заполнить место в системе уравнений для у |
12. | Ответ: (1;4) | Записать ответ в виде координат точки (х;у) |
Решить систему уравнений методом подстановки
выбирая удобную переменную для её выражения, когда она записана без числа.
№1. у – 2х = 1 №4. 2х + у = 12
6х – у = 7 7х – 2у = 31
№2. х + у =6 №5. 4х – у = 11
3х – 5у = 2 6х – 2у = 13
№3. 7х – 3у = 13 №6. 8у – х = 4
х – 2у = 5 2х – 21у = 2
Карточка составлена учителем математики Головлянициной Лидией Вадимовной
Предварительный просмотр:
Образец решения системы уравнений методом сложения. | Алгоритм решения (последовательность шагов ) | |
1. | 4х + у = 3 6х – 2у = 1 | Рассмотрим коэффициенты перед х и у. Удобно сделать перед переменной у противоположные коэффициенты 2 и -2. |
2. |
4х + у = 3 |·2 6х – 2у = 1 |
Для этого умножим правую и левую часть первого уравнения на 2, а второе уравнение оставим без изменения. |
3. | 8х + 2у = 6 6у – 2у = 1 | Поставим знак «+» между уравнениями слева и проведем черту, как при сложении столбиком по разрядам. |
4. | 8х + 2у = 6 6х – 2у = 1 14х = 7 | Сложим подобные 8х и 6х получим 14х.Запишем это число под чертой. Подобные 2у и -2у взаимно уничтожаются и зачёркиваются. Справа (после равно) складываем числа 6 и 1 и результат записываем под чертой. |
5. | х = 7 : 14 х = 0,5 | Находим х по правилу нахождения неизвестного множителя. |
6. | 4х + у = 3 | Теперь осталось вычислить у. Выбираем и записываем то уравнение из системы, где у стоит без коэффициента, т.е. коэффициент равен 1 . |
7. | 4·0,5 + у = 3 2 + у = 3 у = 3 – 2 у = 1 | Подставить вместо х значение 0,5. |
8. | Ответ: х = 0,5; у = 1 | Записать ответ. |
Пользуясь этим алгоритмом, решите системы уравнений:
- х + у = 45
х – у = 13
- х + у = 49
— х + у = 17
- 4х – 9у = 3
х + 3у = 6
- 15х – 4у = 8
— 3х + у = 1
- 3х – у = 7
- 2х + 3у = 1 Карточка составлена учителем математики Головлянициной Лидией Вадимовной
По теме: методические разработки, презентации и конспекты
Решение систем уравнений методом подстановки 7 класс
Решение систем уравнений методом подстановки 7 класс…
Решение систем уравнений (метод подстановки)
УНЗ представлен в виде межпредметного урока, интегрированного урока, метапредметного урока (материал находится в разработке). ..
..
Урок алгебры 7 класс Решение систем уравнений методом подстановки
Тип урока: урок рефлексии.Технология: урок разработан в системе традиционного обучения с опорой на технологию деятельностного метода.Цель урока: создать условия для повторения и закрепления алгоритма …
Урок на тему «Решение систем уравнений способом подстановки и способом сложения».
Урок изучения новой темы в компетентностно- констектной модели обучения и воспитания (первый этап всей изучаемой темы)…
План-конспект урока “Решение систем уравнений” (способ подстановки и способ сложения)
Приводится план-конспект урока алгебры в 9 классе…
Презентации по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложения для решения систем уравнений» .
Презентации проедполагает использование при проведении онлайн урока по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложени. ..
..
Методическая разработка. Презентация по алгебре 7 класс по теме «Решение систем уравнений методом сложения»
В презентации рассмотрены несколько примеров рассуждения и оформления систем уравнений методом сложения. Материал можно использовать во время дистанционного обучения…
Поделиться:
Решение систем уравнений (одновременных уравнений)
Если у вас есть два разных уравнения с одними и теми же двумя неизвестными в каждом, вы можете решить для обоих неизвестных. Есть три распространенных метода решения: сложение/вычитание, замена и построение графика.
Метод сложения/вычитания
Этот метод также известен как метод исключения.
Чтобы использовать метод сложения/вычитания, сделайте следующее:
- Умножьте одно или оба уравнения на какое-либо число (числа), чтобы сделать число перед одной из букв (неизвестных) одинаковым или прямо противоположным в каждом уравнение.

- Сложите или вычтите два уравнения, чтобы исключить одну букву.
- Найдите оставшееся неизвестное.
- Найдите другое неизвестное, подставив значение найденного неизвестного в одно из исходных уравнений.
Пример 1
Найдите x и y .
Добавление уравнений устраняет y ‐членов.
Теперь подставив 5 вместо x в первое уравнение, мы получим следующее:
Ответ: x = 5, y = 2
Заменив в исходных уравнениях каждые x на 5 и каждые y на 2, вы увидите, что каждое уравнение станет верным.
В Примере и Примере существовал уникальный ответ для x и y , который делал каждое предложение верным одновременно. В некоторых ситуациях вы не получаете уникальных ответов или не получаете ответов. Вы должны знать об этом, когда используете метод сложения/вычитания.
Пример 2
Решите для x и лет.
Сначала умножьте нижнее уравнение на 3. Теперь y предшествует цифра 3 в каждом уравнении.
Уравнения можно вычесть, исключив члены y .
Вставьте x = 5 в одно из исходных уравнений, чтобы найти y .
Ответ: х = 5, y = 3
Конечно, если число перед буквой в каждом уравнении уже одно и то же, вам не нужно изменять ни одно из уравнений. Просто добавьте или вычтите.
Чтобы проверить решение, замените каждое x в каждом уравнении на 5 и замените каждое y в каждом уравнении на 3.
Пример 3
Умножьте верхнее уравнение на 2. Обратите внимание, что получится.
Теперь, если вы должны вычесть одно уравнение из другого, результат будет 0 = 0.
Это утверждение всегда верно .
Когда это происходит, система уравнений не имеет единственного решения. На самом деле, любая замена на и на , которая делает одно из уравнений верным, также делает верным другое уравнение. Например, если a = -6 и b = 5, то оба уравнения выполняются.
На самом деле, любая замена на и на , которая делает одно из уравнений верным, также делает верным другое уравнение. Например, если a = -6 и b = 5, то оба уравнения выполняются.
[3(– 6) + 4(5) = 2 И 6(– 6) + 8(5) = 4]
На самом деле у нас есть только одно уравнение, записанное двумя разными способами. В этом случае второе уравнение фактически является первым уравнением, умноженным на 2. Решением для этой ситуации является либо исходное уравнение, либо упрощенная форма любого уравнения.
Пример 4
Найдите x и y .
Умножьте верхнее уравнение на 2. Обратите внимание, что получится.
Теперь, если вы вычтете нижнее уравнение из верхнего уравнения, результат будет 0 = 1. Это утверждение равно 9.0023 никогда не верно . В этом случае система уравнений не имеет решения.
В примерах 1–4 только одно уравнение умножалось на число, чтобы числа перед буквой были одинаковыми или противоположными. Иногда каждое уравнение нужно умножать на разные числа, чтобы числа перед буквой были одинаковыми или противоположными.
Иногда каждое уравнение нужно умножать на разные числа, чтобы числа перед буквой были одинаковыми или противоположными.
Найдите x и y .
Обратите внимание, что нет простого числа, на которое можно умножить любое уравнение, чтобы получить числа перед 9.0023 x или y , чтобы стать одинаковыми или противоположными. В этом случае сделайте следующее:
- Выберите букву для исключения.
- Используйте две цифры слева от этой буквы. Найдите наименьшее общее кратное этого значения в качестве желаемого числа, которое должно стоять перед каждой буквой.
- Определите, на какое значение нужно умножить каждое уравнение, чтобы получить это значение, и умножьте уравнение на это число.
Предположим, вы хотите удалить x . Наименьшее общее кратное 3 и 5, число перед x , равно 15. Первое уравнение нужно умножить на 5, чтобы получить 15 перед x . Второе уравнение нужно умножить на 3, чтобы получить 15 перед x .
Теперь вычтите второе уравнение из первого уравнения, чтобы получить следующее:
В этот момент вы можете либо заменить y на и найти x (метод 1 ниже), либо начать с исходного два уравнения и исключить y , чтобы вычислить x (способ 2 ниже).
Метод 1
Используя верхнее уравнение: Замените y на и найдите x .
Метод 2
Исключите y и найдите x .
Наименьшее общее кратное 4 и 6 равно 12. Умножьте верхнее уравнение на 3, а нижнее уравнение на 2.
Теперь сложите два уравнения, чтобы исключить y .
Решение x = 1 и .
Метод подстановки
Иногда система легче решается методом подстановки . Этот метод включает подстановку одного уравнения в другое.
Пример 6
Решите для x и лет.
Из первого уравнения подставьте ( y + 8) вместо x во второе уравнение.
( у + 8) + 3 г = 48
Теперь найдите г. Упростите, объединив и .
Теперь подставьте y значение 10 в одно из исходных уравнений.
Ответ: y = 10, x = 18
Проверьте решение.
Пример 7
Найдите x и y методом подстановки.
Сначала найдите уравнение, в котором перед буквой стоит либо «1», либо «– 1». Решите для этой буквы через другую букву.
Затем действуйте, как в примере 6.
В этом примере в нижнем уравнении стоит «1» перед y .
Найдите y через x .
Подставьте 4 x – 17 вместо y в верхнем уравнении, а затем найдите x .
Замените x на 4 в уравнении y – 4 x = –17 и найдите y .
Решение: x = 4, y = –1.
Проверьте решение:
Графический метод
Другой метод решения уравнений заключается в построении графика каждого уравнения на координатном графике. Координаты пересечения и будут решением системы. Если вы не знакомы с построением координатных графиков, внимательно изучите статьи по координатной геометрии, прежде чем пытаться использовать этот метод.
Пример 8
Решите систему с помощью графика.
Сначала найдите три значения для x и y , которые удовлетворяют каждому уравнению. (Хотя для определения прямой линии необходимы только две точки, нахождение третьей точки является хорошим способом проверки.) Ниже приведены таблицы значений x и y :
x
и
| 4 | 0
| 2 | –2
| 5 | 1
x
и
| 1 | -1
| 4 | 0
| 7 | 1
Теперь начертите две линии на координатной плоскости, как показано на рис. 1.
Точка пересечения двух прямых (4, 0) является решением системы.
Если прямые параллельны, то они не пересекаются, а значит, у этой системы нет решений.
Рис. 1. График линий х = 4 + y и х – 3 y = 4, обозначающий решение.
Пример 9
Решите систему с помощью графика.
Найдите три значения для x и y , которые удовлетворяют каждому уравнению.
3 x + 4 y = 2 6 x + 8 y = 4
Ниже приведены таблицы значений x и 4 y 9002. См. рис. 2.
x
и
| 0 |
| 2 | – 1
| 4 |
x
и
| 0 |
| 2 | – 1
| 4 |
Обратите внимание, что одинаковые точки удовлетворяют каждому уравнению. Эти уравнения представляют одну и ту же прямую.
Следовательно, решение не является единственной точкой. Решением являются все точки на прямой.
Следовательно, решением является любое уравнение прямой, поскольку они оба представляют одну и ту же прямую.
Это похоже на пример, когда это было сделано с использованием метода сложения/вычитания.
Рис. 2. График линий 3 x + 4 y = 2 и 6 x + 8 y = 4 с указанием решения.
Пример 10
Решите систему с помощью графика.
Найдите три значения для x и y , которые удовлетворяют каждому уравнению. См. следующие таблицы значений x и y :
x
и
| 0 | 1
| 2 |
| 4 | -2
x
и
| 0 | 2
| 2 |
| 4 | -1
Обратите внимание, что на рисунке 3 два графика параллельны. Они никогда не встретятся. Следовательно, для этой системы уравнений решения нет.
Для этой системы уравнений не существует решения.
Это похоже на пример, выполненный с использованием метода сложения/вычитания.
Рис. 3. График линий 3 х + 4 у = 4 и 6 х + 8 у = 16, обозначающий решение.
Алгебраические методы решения систем
Результаты обучения
- Использовать метод подстановки
- Решить систему уравнений методом подстановки.
- Распознавать системы уравнений, которые не имеют решений или имеют бесконечное число решений
- Использовать метод исключения без умножения
- Решите систему уравнений, когда для исключения переменной не требуется умножения
- Использовать метод исключения с умножением
- Использование умножения в сочетании с методом исключения для решения системы линейных уравнений
- Распознать, когда решение системы линейных уравнений подразумевает существование бесконечного числа решений
Решение системы уравнений с помощью метода подстановки
В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики, чтобы классифицировать, сколько решений имеет система из двух линейных уравнений. Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!
Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!
В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. В этом курсе мы использовали подстановку по-разному, например, когда использовали формулы площади треугольника и простых процентов. Мы подставили значения, которые мы знали, в формулу для решения на значения, которые мы не знали. Идея аналогична применительно к решению систем, в этом процессе всего несколько разных шагов. Вы сначала определите одну переменную, а затем подставите это выражение в другое уравнение. Давайте начнем с примера, чтобы понять, что это значит.
Вы можете заменить значение переменной, даже если это выражение. Вот пример.
Помните, что решение системы уравнений должно быть решением каждого уравнения в системе. Упорядоченная пара [латекс](4,−1)[/латекс] работает для обоих уравнений, поэтому вы знаете, что она также является решением системы.
Давайте рассмотрим еще один пример, замена которого связана с распределительным свойством.
В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной х или и . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.
Иногда вам может потребоваться переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете подставить ее в другое уравнение.
В следующем видео вам будет представлен пример решения системы двух уравнений методом подстановки.
Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. На самом деле это вопрос предпочтений, потому что иногда нахождение переменной приводит к необходимости работать с дробями. Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Распознавать системы уравнений, которые не имеют решений или имеют бесконечное число решений
Когда мы изучили методы решения линейных уравнений с одной переменной, то обнаружили, что одни уравнения не имеют решений, а другие имеют бесконечное множество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.
Вспомните этот пример из Модуля 1 для решения линейных уравнений с одной переменной:
Решите для x . [латекс]12+2x–8=7x+5–5x[/латекс]
[латекс] \displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\, \,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{массив}[/латекс]
[латекс]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\, \,\,\,\,\,\,\подчеркнуть{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\ ,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,4= \,5\end{array}[/latex]
Это ложное утверждение означает, что нет решений этого уравнения. Точно так же вы можете увидеть подобный результат, когда используете метод подстановки для поиска решения системы линейных уравнений с двумя переменными. В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Точно так же вы можете увидеть подобный результат, когда используете метод подстановки для поиска решения системы линейных уравнений с двумя переменными. В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Вы получаете ложное утверждение [латекс]−8=4[/латекс]. Что это значит? График этой системы проливает некоторый свет на происходящее.
Прямые параллельны, они никогда не пересекаются и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [латекс]−8=4[/латекс] — это , а не решение. Это просто ложное утверждение, и оно указывает на то, что решения не существует.
Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное число решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.
На этот раз вы получите верное утверждение: [латекс]−4,5x=−4,5x[/латекс]. Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.
Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.
Эта система состоит из двух уравнений, представляющих одну и ту же прямую; две линии коллинеарны. Каждая точка на линии будет решением системы, поэтому метод подстановки дает истинное утверждение. В этом случае существует бесконечное множество решений.
В следующем видео вы увидите пример решения системы, которая имеет бесконечное количество решений.
В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.
Решение системы уравнений методом исключения
Метод исключения для решения систем линейных уравнений использует аддитивное свойство равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может понадобиться или не понадобиться сначала умножать члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения. В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.
Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может понадобиться или не понадобиться сначала умножать члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения. В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.
С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу перейдем к некоторым примерам.
Если вы сложите два уравнения,
[латекс]x–y=−6[/латекс] и [латекс]х+у=8[/латекс] вместе, посмотрите, что получится.
[латекс] \displaystyle \begin{array}{l}\,\,\,\,\,x-y=\,-6\\\underline{+\,x+y=\,\,\,8 }\\\,2x+0\,=\,\,\,\,2\end{array}[/latex]
Вы удалили член y , и это уравнение можно решить, используя методы для решение уравнений с одной переменной.
Посмотрим, как решается эта система методом исключения.
К сожалению, не все системы работают так легко. Как насчет такой системы, как [латекс]2x+y=12[/латекс] и [латекс]−3x+y=2[/латекс]. Если вы сложите эти два уравнения вместе, никакие переменные не будут устранены.
[латекс] \displaystyle \begin{array}{l}\,\,\,\,2x+y=12\\\underline{-3x+y=\,\,\,2}\\-x +2y=14\end{array}[/latex]
Но вы хотите удалить переменную. Итак, давайте добавим противоположное одному из уравнений к другому уравнению. Это означает, что умножьте каждый член одного из уравнений на -1, чтобы знак каждого члена был противоположным.
[латекс]\begin{array}{l}\,\,\,\,2x+\,\,y\,=12\rightarrow2x+y=12\rightarrow2x+y=12\\−3x+\,\ ,y\,=2\rightarrow-\left(-3x+y\right)=-(2)\rightarrow3x-y=-2\\\,\,\,\,5x+0y=10\end{массив }[/latex]
Вы удалили переменную y , и теперь проблема может быть решена.
В следующем видео описывается аналогичная задача, в которой можно исключить одну переменную, сложив вместе два уравнения.
youtube.com/embed/M4IEmwcqR3c?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»>Внимание! Когда вы добавляете противоположность одного полного уравнения к другому, обязательно меняйте знак КАЖДОГО члена в обеих частях уравнения. Это очень распространенная ошибка.
Ниже приведены еще два примера, показывающие, как решать линейные системы уравнений с помощью исключения.
Проверьте этот последний пример — подставьте (2, 3) в оба уравнения. Вы получаете два верных утверждения: 14=14 и 16=16!
Обратите внимание, что вы могли бы использовать противоположное первому уравнению вместо второго и получить тот же результат.
Распознавание систем, не имеющих решений или имеющих бесконечное число решений
Так же, как и метод подстановки, метод исключения иногда устраняет обе v переменных, и вы получите либо истинное утверждение, либо ложное утверждение. Напомним, что ложное утверждение означает отсутствие решения.
Давайте рассмотрим пример.
Графическое изображение этих линий показывает, что они являются параллельными линиями и поэтому не имеют общих точек, что подтверждает отсутствие решения.
Если обе переменные исключены, а у вас осталось истинное утверждение, это означает, что существует бесконечное число упорядоченных пар, удовлетворяющих обоим уравнениям. По сути, уравнения представляют собой одну и ту же строку.
Графики этих двух уравнений помогут проиллюстрировать происходящее.
В следующем видео методом исключения решается система уравнений, не имеющая решений.
Решите систему уравнений, когда умножение необходимо для исключения переменной
Много раз добавление уравнений или добавление противоположного к одному из уравнений не приводит к исключению переменной. Посмотрите на систему ниже.
Посмотрите на систему ниже.
[латекс]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex]
Если добавить приведенные выше уравнения или добавить противоположное одному из уравнения, вы получите уравнение, которое по-прежнему имеет две переменные. Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного из уравнений на число, которое позволит исключить ту же переменную в другом уравнении.
Мы делаем это с помощью умножения. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на -4, то при сложении обоих уравнений переменные y дадут в сумме 0.
Следующий пример проведет вас через все шаги, чтобы найти решение этой системы.
Внимание! Когда вы используете умножение для исключения переменной, вы должны умножать КАЖДЫЙ член в уравнении на выбранное вами число. Распространенной ошибкой является забывание умножить каждое слагаемое.
Есть и другие способы решения этой системы. Вместо того, чтобы умножать одно уравнение, чтобы исключить переменную при добавлении уравнений, вы могли бы умножить 90 559 обоих 90 560 уравнений на разные числа.
На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на [латекс]-3[/латекс].
Эти уравнения были умножены на 5 и [латекс]-3[/латекс] соответственно, потому что это дало вам члены, которые в сумме давали бы 0. Обязательно умножьте все члены уравнения.
В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.
Можно использовать метод исключения с умножением и получить результат, указывающий на отсутствие решений или на бесконечное множество решений, точно так же, как и в других изученных нами методах поиска решений систем. В следующем примере вы увидите систему, имеющую бесконечно много решений.
В следующем примере вы увидите систему, имеющую бесконечно много решений.
В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Кроме того, эта система имеет бесконечное число решений.
Резюме
Метод подстановки является одним из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных через другую переменную. Затем подставьте это выражение вместо этой переменной во второе уравнение. Затем вы можете решить это уравнение, так как теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (указывающее одно решение), неверное утверждение (указывающее отсутствие решений) или истинное утверждение (указывающее бесконечное количество решений).
Объединение уравнений — мощный инструмент для решения системы уравнений. Сложение или вычитание двух уравнений для исключения общей переменной называется методом исключения (или добавления). Как только одна переменная исключена, становится намного проще найти другую.
Умножение можно использовать для сопоставления членов в уравнениях, прежде чем они будут объединены, чтобы помочь найти решение системы. При использовании метода умножения важно умножать все члены с обеих сторон уравнения, а не только один член, который вы пытаетесь исключить.
3 лучших метода решения систем уравнений (видео)
СтенограммаFAQsPractice
Привет, ребята! Добро пожаловать в это видео, посвященное сравнению различных методов решения системы уравнений.
Если вы помните, система уравнений — это когда у вас есть более одного уравнения с неизвестными переменными в данной задаче. Итак, чтобы решить эту проблему, вам нужно найти значение всех переменных в каждом уравнении.
Это можно сделать тремя различными способами: методом замены, методом исключения и с использованием расширенной матрицы.
В этом видео я предполагаю, что вы уже знаете, как выполнять каждый метод, поэтому я хочу потратить много времени на объяснение не того, как их делать, а того, когда использовать каждый метод.
Сначала я устно скажу вам, когда использовать каждый метод, затем я напишу три разных примера, и мы вместе решим, какой метод наиболее эффективен для каждой системы.
Когда использовать метод подстановки
Вы должны использовать метод подстановки, когда один из переменные в одном из ваших уравнений уже выделены (имеет коэффициент 1).
Когда использовать метод исключения
Метод исключения следует использовать, когда одни и те же переменные во всех уравнениях имеют один и тот же коэффициент или когда они имеют один и тот же, но отрицательный коэффициент.
Когда использовать расширенную матрицу
Расширенную матрицу следует использовать, когда методы замены и исключения либо нецелесообразны, либо вообще невозможны.
Теперь давайте рассмотрим три разные системы и, используя то, что мы только что узнали, подумайте, какой метод наиболее полезен для каждой системы.
Пример системы № 1
\ (5x -58y = -883 \)
\ ( -5x + 2y = -13 \)
Пример системы #2
\ (9x + 4y. = 65\)
\(x – 18y = -2\)
ПРИМЕР СИСТЕМЫ #3
\(2x + 7y – 3z = 47\)
\(x – 4y + 8z = -33 \)
\(7x + 2y +10z = 11\)
Итак, мы пройдемся по каждой системе, решим, какой метод будет наиболее эффективным, а затем решим с помощью этого метода.
Пример метода исключения
Хорошо, давайте посмотрим на это первое уравнение.
\(5x – 58y = -883\)
\(-5x + 2y = -13\)
Теперь, возвращаясь к объяснению, которое я дал о том, когда использовать каждый метод, обратите внимание на то, что я сказал об исключении: «Вы должны использовать метод исключения, когда одни и те же переменные во всех уравнениях имеют один и тот же коэффициент или когда они имеют один и тот же, но отрицательный коэффициент».
Что ж, именно это и верно для этой конкретной системы. Итак, давайте решим эту систему, используя исключение .
\(-56y = -896\)
\(y = 16\)
Теперь мы снова подставляем нашу переменную y в одно из исходных уравнений. Подключу к первому.
\(5x – 58(16) = -883\)
\(5x – 928 = -883\)
\(5x = 45\)
\(x = 9\)
Отлично, поэтому мы решили эту систему с помощью исключения, потому что наши две одинаковые переменные имели одинаковый коэффициент или когда они имеют один и тот же, но отрицательный коэффициент (как в нашем случае).
Пример метода замены
Перейдем к системе №2.
\(9x + 4y = 65\)
\(x — 18y = -2\)
Итак, давайте еще раз вспомним, что было сказано в нашем объяснении, когда использовать каждый метод. Вспомните, что было сказано о подстановке: «Вы должны использовать метод подстановки, когда одна из переменных в одном из ваших уравнений уже изолирована».
Так обстоит дело с этой системой. Наша переменная \(x\) во втором уравнении имеет коэффициент 1. Итак, давайте решим эту систему с помощью замены.
\(9(18y – 2) + 4y = 65\)
\(162y – 18 + 4y = 65\)
\(166y = 83\)
\(y = \frac{1}{2} \)
\(x = 18(\frac{1}{2}) – 2\)
\(x = 7\)
Это было очень просто решить с помощью подстановки. Помните, означающее, которое поможет вам узнать, когда его использовать, — это если в одном из уравнений есть переменная, которая уже изолирована.
Пример расширенной матрицы
Давайте посмотрим на нашу последнюю систему, систему №3.
\(2x + 7y – 3z = 47\)
\(x – 4y + 8z = -33\)
\(7x + 2y +10z = 11\)
Помните, что мы говорили о том, когда использовать расширенную матрицу. Что ж, сейчас хорошее время. Использование исключения или замены в этом отношении потребует гораздо больше работы, чем использование расширенной матрицы.
Итак, давайте составим нашу матрицу и решим.
\(\begin{bmatrix} \left.\begin{matrix} 2& 7& -3\\ 1& -4& 8\\ 7& 2& 10 \end{matrix}\right| & \begin{matrix} 47\\ -33\\ 11 \end{matrix} \end{bmatrix}\)
\(R_{1}\leftrightarrow R_{2}\)
\(\begin{bmatrix} \left.\begin{matrix} 1& -4& 8\\ 2& 7& -3\\ 7& 2& 10 \end{matrix }\right| & \begin{matrix} -33\\ 47\\ 11 \end{matrix} \end{bmatrix}\)
\(\begin{matrix} \\ -2R_{1}+R_{2} =R_{2}\\ -7R_{1}+R_{3}=R_{3} \end{matrix}\begin{bmatrix} \left.\begin{matrix} 1& -4& 8\\ 0& 15& -19 \\ 0& 30& -46 \end{matrix}\right| & \begin{matrix} -33\\ 113\\ 242 \end{matrix} \end{bmatrix}\)
\(\begin{matrix} \\ \frac{R_{2}}{15}=R_{2}\\ \end{matrix}\begin{bmatrix} \left.\begin{matrix} 1& -4& 8\\ 0& 1& \frac{-19}{15}\\ 0& 30& -46 \end{matrix}\right| & \begin{matrix} -33\\ \frac{113}{15}\\ 242 \end{matrix} \end{bmatrix}\)
\(\begin{matrix} 4R_{2}+R_{1} =R_{1}\\ \\ -30R_{2}+R_{3}=R_{3} \end{matrix}\begin{bmatrix} \left.\begin{matrix} 1& 0& \frac{44}{ 15}\\ 0& 1& \frac{-19}{15}\\ 0& 0& -8 \end{matrix}\right| & \begin{matrix} \frac{-43}{15}\\ \frac{113 }{15}\\ 16 \end{matrix} \end{bmatrix}\)
\(\begin{matrix} \\ \\ \frac{R_{3}}{-8}=R_{3} \end {matrix}\begin{bmatrix} \left.\begin{matrix} 1& 0& \frac{44}{15}\\ 0& 1& \frac{-19}{15}\\ 0& 0& 1 \end{matrix}\right| & \begin{matrix} \frac{-43}{15}\\ \frac{113}{15}\\ -2 \end{matrix} \end{bmatrix}\)
\(\begin{matrix} — \frac{44}{15}R_{3}+R_{1}=R_{1}\\ \frac{19}{15}R_{3}+R_{2}=R_{2}\\ \end {matrix}\begin{bmatrix} \left.\begin{matrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{matrix}\right| & \begin{matrix} 3\\ 5\\ — 2 \end{matrix} \end{bmatrix}\begin{bmatrix} x\\ y\\ z \end{bmatrix}\)
\(x=3\),\(y=5\),\(z =-2\)
Надеюсь, что это видео по сравнению методов решения систем было для вас полезным.
Увидимся в следующий раз!
Часто задаваемые вопросы
Q
Что такое система уравнений?
A
Системы уравнений — это два или более уравнений, которые можно использовать для решения друг друга.
Пример. \(\begin{align*}3x+4 &= y\\ 2x+3y &= -9\end{align*}\)
Q
Как использовать метод подстановки?
A
Метод подстановки для решения линейных уравнений включает замену одного уравнения на переменную в другом уравнении, решение для одной из переменных, а затем использование этой переменной и одного из исходных уравнений для решения для другой переменной.
Пример. Решите: 2x + 3y = 15 и y = 2x + 1
Подставьте 2x + 1 вместо y
2x + 3(2x + 1) = 15
Найдите x
2x + 3(2x + 1) = 15
2x + 6x + 3 = 15
8x + 3 = 15
8x = 12
x = 3
Найдите y, подставив x в исходное уравнение на 3.
y = 2(3) + 1 = 6 + 1 = 7
Решением этих двух уравнений является точка (3, 7).
Q
Как вы используете метод исключения?
A
Чтобы использовать метод исключения для решения систем уравнений, манипулируйте одним из уравнений, чтобы его можно было добавить к другому уравнению или вычесть из него, где одна переменная аннулируется. Затем найдите другую переменную. Наконец, используйте эту переменную, чтобы найти ту, которая изначально была устранена.
пр. Решите: \(\begin{align*}3x-2y &= 14\\ 6x-7y &= 11\end{align*}\) Сначала умножьте верхнее уравнение на -2.
\(-2(3x-2y=14)\)
\(-6x+4y=-28\)
Затем сложите два уравнения.
Найдите y, разделив на -3 с обеих сторон.
\(y=\frac{17}{3}\)
Затем подставьте y в любое исходное уравнение, чтобы найти x.
\(3x-2(\frac{17}{3})=14\)
\(3x-\frac{34}{3}=14\)
\(3x-\frac{34}{4} =\frac{42}{3}\)
\(3x=\frac{76}{3}\)
\(x=\frac{76}{9}\)
Решением этой системы является точка (\(\frac{76}{9},\frac{17}{3}\)).
Q
Что такое расширенная матрица?
A
Расширенная матрица формируется путем добавления элементов одной матрицы в конец другой.
Пример. \(M=\begin{bmatrix}1&2\\3&4\end{bmatrix},I=\begin{bmatrix}1&0\\0&1\end{bmatrix}\),расширенная матрица:\(\begin{bmatrix}1&2&| 1&0\\3&4&|0&1\end{bmatrix}\)
Практические вопросы
Вопрос №1:
Решите систему уравнений с помощью замены:
\(2x-y=12\)
\(x-y=3\)
\((3, 2)\)
\((6, 9)\)
\((12, 3)\)
\((9, 6)\)
Показать ответ
Ответ:
Правильный ответ D : \((9, 6)\).
Начнем с решения второго уравнения для \(x\).
\(x−y=3\) становится \(x=3+y\).
Теперь, когда мы выделили \(x\), мы можем подставить это вместо «\(x\)» в другом уравнении, чтобы найти \(y\).
\(2x−y=12\) становится \(2(3+y)−y=12\)
Отсюда мы можем найти \(y\), потому что теперь мы имеем дело только с одной переменной.
\(2(3+y)−y=12\) становится \(y=6\)
Теперь, когда мы нашли \(y\), мы можем подставить это значение в одно из исходных уравнений, чтобы решить для \(x\). Давайте воспользуемся первым исходным уравнением: \(2x−y=12\).
Давайте воспользуемся первым исходным уравнением: \(2x−y=12\).
\(2x−y=12\) становится \(2x−6=12\), и когда мы изолируем переменную \(x\), мы получаем \(x=9\).
Наше решение — упорядоченная пара \((9, 6)\).
Скрыть ответ
Вопрос №2:
Решите систему уравнений, используя подстановку .
\(2x+3y=12\)
\(x+y=5\)
\((2, 3)\)
\((3, 2)\)
\((5, 12 )\)
\((12, 5)\)
Показать ответ
Ответ:
Правильный ответ: B: \((3, 2)\).
Начнем с решения второго уравнения для x .
\(x+y=5\) становится \(x=−y+5\)
Теперь, когда мы выделили x, мы можем заменить его на « x » в другом уравнении, чтобы найти y .
\(2x+3y=12\) становится \(2(−y+5)+3y=12\)
Отсюда мы можем найти y, потому что сейчас мы имеем дело только с одной переменной.
\(2(−y+5)+3y=12\) становится \(y=2\)
Теперь, когда мы решили для y , мы можем подставить это значение в одно из исходных уравнений, чтобы решить для х . Давайте воспользуемся вторым исходным уравнением: \(x+y=5\).
\(x+y=5\) становится \(x+(2)=5\), и когда мы изолируем переменную x , мы получаем \(x=3\).
Наше решение — упорядоченная пара \((3, 2)\).
Скрыть ответ
Вопрос №3:
Решить систему уравнений методом исключения :
\(2x+3y=15\)
\(x−3y=3\)
3 9 1, 6)\)
\((3, 5)\)
\((6, 1)\)
\((5, 3)\)
Показать ответ
Ответ:
Правильный ответ C: \((6, 1)\).
Исключение является полезной стратегией для этой системы уравнений, потому что мы можем видеть, что члены 3 y и -3>em>y сокращаются. Начнем процесс со сложения двух уравнений.
Начнем процесс со сложения двух уравнений.
Поскольку 3 y и -3 y сокращаются, у нас остается \(3x=18\), что упрощается до \(x=6\).
С этого момента мы можем просто подставить 6 вместо « x » в любом уравнении, чтобы найти « и ».
Используем второе исходное уравнение: \(x−3y=3\).
\(x−3y=3\) становится \((6)−3y=3\)
Отсюда мы можем выделить переменную y .
\(y=1\)
Решением является упорядоченная пара \((6, 1)\).
Скрыть ответ
Вопрос № 4:
Плата за вход в парк развлечений составляет 2,50 доллара США для детей и 4,50 доллара США для взрослых. В понедельник в парк развлечений вошли 2000 человек и было собрано 8000 долларов. Сколько детей и сколько взрослых ходили в парк развлечений в понедельник?
1000 детей и 1000 взрослых
500 детей и 1500 взрослых
400 детей и 1600 взрослых
800 детей и 1200 взрослых
Показать ответ
Ответ:
. Правильный ответ — 500 детей и 1,500. Взрослые люди.
Правильный ответ — 500 детей и 1,500. Взрослые люди.
Мы можем найти количество взрослых и детей, составив систему уравнений. Давайте составим два уравнения, одно для количества людей, а другое для стоимости. Пусть » а » представляют взрослых, а « c » — детей.
\(a+c=2000\)
\(4.5a+2.5c=8000\)
Отсюда следует, что метод подстановки будет наиболее эффективным, поскольку коэффициенты равны 1. Решим первое уравнение для . Теперь у нас есть \(a=2000–c\).
Мы можем подставить это значение для « a » в другое уравнение.
\(4.5(2000-c)+2.5c=8000\)
Отсюда мы можем выделить переменную c .
\(c=500\)
Теперь, когда мы нашли c , мы можем подставить 500 вместо c в любое из исходных уравнений. Используем первое уравнение.
\(a+c=2000\) становится \(a+500=2000\), что означает \(a=1500\)
Количество детей 500 и количество взрослых 1500.
Скрыть ответ
Вопрос №5:
Гончар продает миски и чашки на художественной ярмарке. Этим утром он продал 30 мисок и 4 чашки и заработал в общей сложности 1040 долларов. Позже днем он продал 8 мисок на общую сумму 256 долларов. Найдите цену за миску и чашку.
Этим утром он продал 30 мисок и 4 чашки и заработал в общей сложности 1040 долларов. Позже днем он продал 8 мисок на общую сумму 256 долларов. Найдите цену за миску и чашку.
чаша = 32 долл. США, чашка = 20 долларов
чаша = 35 долл. США, чашка = 22 долл. США
чаша = 12 долл. США, чашка = 30 долл. США
чаша = 34 долл. США, чашка = 24 долл. ответ A: чаша = 32 доллара, чашка = 20 долларов.
Мы можем найти количество чашек и мисок, составив систему уравнений. Сценарию соответствуют два уравнения: \(30B+4C=1040\) и \(8B=256\), где « B » представляет миски, а « C » представляет чашки.
Решим второе уравнение для B .
\(8B=256\) становится \(B=32\)
С этого момента мы можем подставить 32 в другое уравнение для « B ».
\(30B+4C=1040\) становится \(30(32)+4C=1040\)
Теперь мы можем найти C .
\(C=20\)
Миски стоят 32 доллара, а чашки — 20 долларов.
Скрыть ответ
Вернуться к видео по алгебре I
281590
Решение систем уравнений алгебраическими методами
Давайте начнемМетоды решения систем уравнений алгебраическиРешение систем уравнений алгебраически с помощью графикаРешение систем уравнений алгебраически с помощью подстановкиРешение систем уравнений алгебраически с помощью исключенияОсобые случаиСловарный запасЗанятие в журнале
Мы собираемся научиться использовать различные методы для решения системы уравнения.
Стандарты TEKS и ожидания учащихся
A(3) Линейные функции, уравнения и неравенства. Учащийся применяет стандарты математического процесса при использовании графиков линейных функций, ключевых функций и связанных преобразований для представления различными способами и решения уравнений, неравенств и систем уравнений с использованием технологий и без них. Ожидается, что учащийся:
A(3)(F) начертит на координатной плоскости системы двух линейных уравнений с двумя переменными и найдет решения, если они существуют
A(3)(G) графически оценивать решения систем двух линейных уравнений с двумя переменными в реальных задачах
A(5) Линейные функции, уравнения и неравенства. Учащийся применяет стандарты математического процесса для решения линейных уравнений с использованием технологий и без них и оценки обоснованности их решений. Студент должен:
A(5)(C) решать системы двух линейных уравнений с двумя переменными для решения математических и практических задач
Ресурс Цель(и)
Получив словесное и/или алгебраическое описание ситуаций, включающих системы линейных уравнений с двумя переменными, учащийся решит систему уравнений.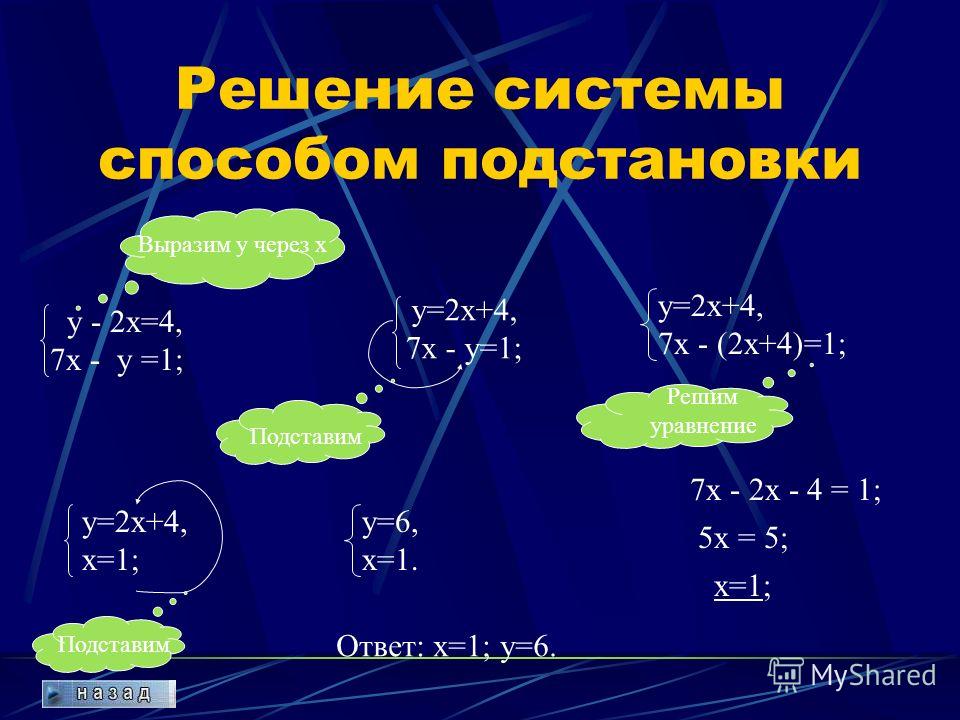
Основные вопросы
Как система уравнений может быть решена с помощью графика?
Как можно решить систему уравнений подстановкой?
Как решить систему уравнений методом исключения?
Словарь
- Согласованная система
- Зависимая система
- Несовместимая система
- Заменитель
- Система линейных уравнений
Существует три основных метода алгебраического решения систем уравнений. Они перечислены и кратко описаны ниже.
Графический метод : Когда в обоих уравнениях решается одна переменная, легко использовать графический калькулятор. В этом случае калькулятор можно использовать для построения графика обоих уравнений. Пересечение двух линий будет представлять собой решение системы уравнений.
м = -3 n
м = 10 – 4 n
Метод подстановки: Существует два различных типа систем уравнений, где подстановка является самым простым методом.
Тип 1: Одна переменная находится сама по себе или изолирована в одном из уравнений. Система решается путем подстановки уравнения с изолированным членом в другое уравнение:
x + 2 y = 7
y = x – 5
Тип 2: Одну переменную можно легко выделить. Системы решаются путем решения одной переменной в одном из уравнений, а затем подстановки этого уравнения во второе уравнение. Найдите a во втором уравнении, затем подставьте второе уравнение в первое.
2 a + 3 b = 2
a – 2 b = 8
Метод исключения 20043 : Оба уравнения имеют стандартную форму: A x + B y = C. Система уравнений решается путем исключения переменной и решения для оставшейся переменной. Сложите два уравнения вместе, чтобы исключить y, , затем найдите x .
8 x + 11 Y = 37
2 x -11 Y = -7
. вы можете подставить значения x и y, чтобы убедиться, что оба уравнения дают вам верные утверждения.
вы можете подставить значения x и y, чтобы убедиться, что оба уравнения дают вам верные утверждения.
Одним из способов алгебраического решения систем уравнений является построение графика. Нужен графический калькулятор. Если вам нужен онлайн-калькулятор, нажмите здесь.
Если два линейных уравнения равны одной и той же переменной, вам не нужно манипулировать уравнениями. Вы можете изобразить уравнения на графическом калькуляторе по мере их написания, а затем найти решение.
Помните, что этот метод работает, только если два уравнения равны одной и той же переменной.
Пример
Решите следующие системы уравнений.
Y = 2 x — 2
Y = 4 x — 4
Поместите оба уравнения в уравнение «Y =». x – 2 и Y 2 = 4 x – 4.
Проверьте, где пересекаются графики, и ответьте на следующие вопросы.
Существует два типа ситуаций, связанных с заменой.
Тип 1
Записано ли одно из уравнений с одной из переменных на одной стороне уравнения? Если это так, вы можете подставить значение этой переменной в другое уравнение и решить его.
Пример
Решите следующую систему уравнений с помощью подстановки.
b = 3
4 a + b = 7
Тип 2
Если одно из уравнений не записано с одной переменной с одной стороны уравнения, но его легко преобразовать в уравнение с одной переменной с одной стороны, подстановку все же можно использовать.
Пример
Перепишите уравнение, а затем подставьте его в другое уравнение, чтобы решить систему уравнений.
2 а + 3 б = 2
а – 2 б = 8
Когда построение графика или замена не могут быть легко выполнены, для решения системы уравнений используется исключение.
Пример
Выполните шаги, чтобы решить эту систему уравнений.
8 x + 11 Y = 37
2 x -11 Y = -7
Шаг 1: Добавьте два прибыль.
8x + 11y = 37 2x — 11y = -7 10x = 30
Шаг 2. Найдите х .
10x = 30 x = 3
Шаг 3: Чтобы найти значение y , подставьте 3 вместо x в одно из уравнений.
8(3) + 11y = 37
Шаг 4. Решите для y .
24 + 11y = 37 24 + 11y = 37- 24 — 2411y11 = 1311 y = 1311
Шаг 5: Идентифицируйте решение как упорядоченную пару.
(3, 1311)
Что делать, если добавление или вычитание не удаляет переменную?
Пример
3 x – y = 8
x + 2 y = 5
В этом случае, если добавить уравнения, переменная не будет устранена. Если y в первом уравнении заменить на 2 y , то переменные y будут аддитивными обратными, и их можно будет исключить.
Следуйте инструкциям для решения проблемы.
Большинство систем уравнений имеют хотя бы одно решение. Такие задачи называются непротиворечивыми системами.
Однако есть два таких особых случая при решении линейных систем уравнений.
Первый случай возникает при алгебраическом решении систем. Переменные исключаются, и левая часть уравнения не равна правой части уравнения. В этом случае решения нет и прямые параллельны.
Пример
-2 x + 2 y = 6
-x + y = -3 9
40002 Следуйте инструкциям для решения проблемы.
Обратите внимание, что обе переменные были удалены. Последнее утверждение, 0 ≠ 16, не равно . Это означает, что прямые никогда не пересекаются, потому что они параллельны.
В этом случае решения нет. Это называется несовместимой системой.
Второй случай также имеет место при алгебраическом решении систем. Переменные и константы исключаются, и обе части уравнения равны нулю. В этом случае любое число может быть решением, что означает, что прямые совпадают.
Переменные и константы исключаются, и обе части уравнения равны нулю. В этом случае любое число может быть решением, что означает, что прямые совпадают.
Example
3 x – 4 y = 12
— 6 x + 8 y = -24
Follow the steps to solve the проблема.
Обратите внимание, что все переменные являются аддитивными инверсиями друг друга, а левая и правая части уравнения равны нулю.
Эти уравнения представляют собой ту же самую линию . Система имеет бесконечно много решений, а линии являются зависимыми системами.
- Печать
- Поделиться
4.3 Решение систем уравнений методом исключения – Бизнес/техническая математика
4. Системы уравнений
Системы уравнений
Линн Маречек и МэриЭнн Энтони-Смит
Ожидается, что к концу этого раздела вы сможете:
- Решить систему уравнений методом исключения
- Решение приложений систем уравнений методом исключения
- Выберите наиболее удобный способ решения системы линейных уравнений
Мы решили системы линейных уравнений с помощью графиков и подстановок. Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему подстановкой, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добраться туда.
Метод исключения основан на свойстве сложения равенства. Свойство сложения равенства говорит о том, что, когда вы добавляете одно и то же количество к обеим частям уравнения, вы все равно получаете равенство. Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Для любых выражений a , b , c и d ,
Чтобы решить систему уравнений методом исключения, мы начинаем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет проще всего исключить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
и прибавляются к нулю, и мы получаем одно уравнение с одной переменной.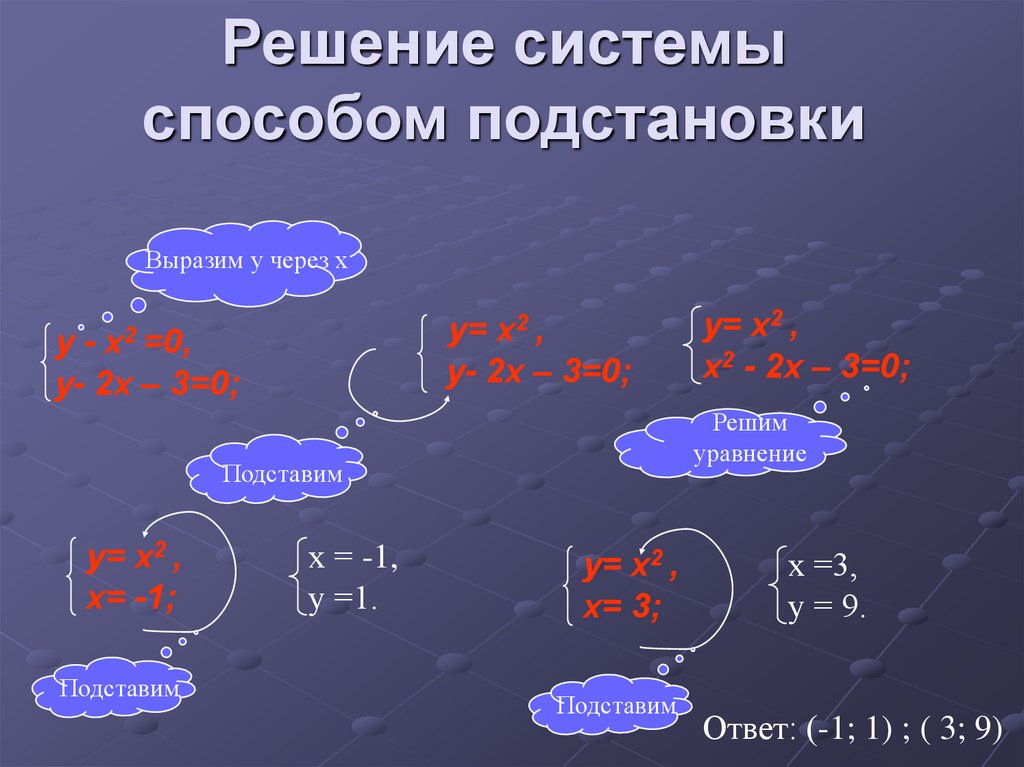
Давайте попробуем еще один:
На этот раз мы не видим переменную, которую можно сразу исключить, если мы добавим уравнения.
Но если мы умножим первое уравнение на -2, мы сделаем коэффициенты x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2.
Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будет устранено, когда мы добавим эти два уравнения.
Сложите уравнения самостоятельно — результат должен быть −3 y = −6. И это кажется легко решить, не так ли? Вот как это будет выглядеть.
Сделаем еще один:
Не похоже, чтобы коэффициенты одной переменной были противоположны, умножая одно из уравнений на константу, если только мы не используем дроби. Поэтому вместо этого нам придется умножить оба уравнения на константу.
Мы можем сделать коэффициенты x противоположными, если умножим первое уравнение на 3, а второе на -4, так что мы получим 12 x и -12 x . Это дает нам два новых уравнения: всего одна переменная, мы ее решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Это дает нам два новых уравнения: всего одна переменная, мы ее решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы посмотрим, как использовать исключение для решения той же системы уравнений, которую мы решали с помощью графика и подстановки.
Как решить систему уравнений методом исключения
Решить систему методом исключения.
Решение
Решите систему методом исключения.
Показать ответШаги перечислены ниже для удобства.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную вы удалите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.

- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Сначала мы сделаем пример, в котором мы можем сразу исключить одну переменную.
Решить систему методом исключения.
Раствор
В полученном уравнении есть только 1 переменная x .

Подставьте x = 11 в одно из исходных уравнений.
до обоих исходных уравнений.
Решите систему методом исключения.
Показать ответВ следующем примере мы сможем сделать коэффициенты одной переменной противоположными, умножив одно уравнение на константу.
Решить систему методом исключения.
Решение
 It also shows that 5x – 6y = 10 becomes 3 times -4 – 6 times -5 = 10 or -20 + 30 = 10. Thus 10 = 10. The figure then says, ‘The solutions is (-4, -5).» data-label=»»>
It also shows that 5x – 6y = 10 becomes 3 times -4 – 6 times -5 = 10 or -20 + 30 = 10. Thus 10 = 10. The figure then says, ‘The solutions is (-4, -5).» data-label=»»>в первом уравнении на −3.
Подставьте x = −4 в одно из исходных уравнений.

обоих исходных уравнений.
Решите систему методом исключения.
Показать ответТеперь сделаем пример, где нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Решить систему методом исключения.
Решение
В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты.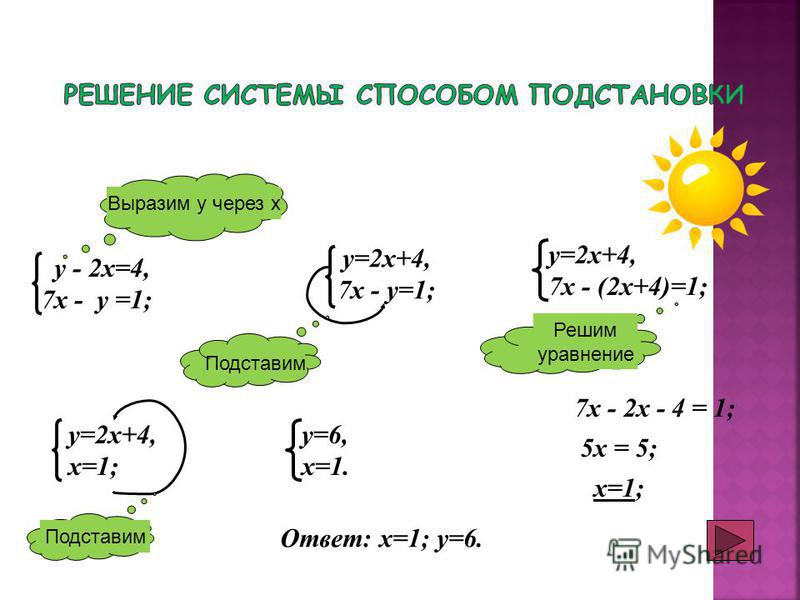 Поэтому мы стратегически умножим оба уравнения на константу, чтобы получить противоположности.
Поэтому мы стратегически умножим оба уравнения на константу, чтобы получить противоположности.
коэффициенты y , умножим первое уравнение на 2
, а второе уравнение на 3.
Подставьте x = 0 в одно из исходных уравнений.

обоих исходных уравнений.
Какие еще константы мы могли бы выбрать, чтобы исключить одну из переменных? Решение будет таким же?
Решить систему методом исключения.
Показать ответКогда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на его ЖК-дисплей.
Решить систему методом исключения.
Решение
В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на его ЖК-дисплей, чтобы очистить дроби.
оба уравнения имеют стандартную форму.

Подставьте x = 3 в одно из исходных уравнений.
до обоих исходных уравнений.
Решите систему методом исключения.
Показать ответ Когда мы решали системы линейных уравнений графически, мы увидели, что не все системы линейных уравнений имеют в качестве решения одну упорядоченную пару. Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
Решите систему путем устранения:
A)
B)
C)
D)
Решение
| A) | |
| Запишите второе уравнение в стандартной форме. | |
| Очистите дроби, умножив второе уравнение на 4. | |
| Упрощение. | |
| Чтобы исключить переменную, мы умножаем второе уравнение на . Упростить и добавить. | |
| Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений. | |
После того, как мы очистили дроби во втором уравнении, вы заметили, что эти два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии. |
| б) | |
| бесконечно много решений |
| в) | |
| бесконечно много решений |
| г) | |
| Уравнения представлены в стандартной форме. | |
| Умножьте второе уравнение на 3, чтобы исключить переменную. | |
| Упростить и добавить. | |
| Это утверждение неверно. Уравнения несовместимы, поэтому их графики будут параллельными линиями. | |
| Система не имеет решения. |
Решите систему методом исключения.
Показать ответнет решения
Некоторые прикладные задачи переводятся непосредственно в уравнения в стандартной форме, поэтому для их решения мы будем использовать метод исключения. Как и прежде, мы используем нашу Стратегию решения проблем, чтобы оставаться сосредоточенными и организованными.
Как и прежде, мы используем нашу Стратегию решения проблем, чтобы оставаться сосредоточенными и организованными.
Сумма двух чисел равна 39. Их разница равна 9. Найдите числа.
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите что мы ищем. | Ищем два числа. |
| Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества. | Пусть первое число. второй номер. |
| Шаг 4. Переведите в систему уравнений. Система: | Сумма двух чисел равна 39. Их разница равна 9. |
| Шаг 5. Решить систему уравнений. Чтобы решить систему уравнений, используйте исключение. Уравнения имеют стандартный вид, а коэффициенты противоположны. Добавлять.  Решите для . Подставьте в одно из исходных уравнений и найдите . | |
| Шаг 6. Проверьте ответ. | Так как и , ответы проверяются. |
| Шаг 7. Ответьте на вопрос. | Цифры 24 и 15. |
Сумма двух чисел равна 42. Их разница равна 8. Найдите числа.
Показать ответЧисла 25 и 17.
Каждый день по пути на работу Джо останавливается в бургерной. В понедельник он заказал один средний картофель фри и две маленькие газированные напитки, в которых было в общей сложности 620 калорий. Во вторник у него было два заказа картофеля фри среднего размера и одна маленькая газировка, всего 820 калорий. Сколько калорий в одном заказе картофеля фри среднего размера? Сколько калорий в одной маленькой газировке?
Решение
 Thus f = 340. The figure then reads, “Step 6. Check the answer. Verify that these numbers make sense in the problem and that they are solutions to both equations. We leave this to you! Step 7. Answer the question. The small soda has 140 calories and the fries have 340 calories.”» data-label=»»>
Thus f = 340. The figure then reads, “Step 6. Check the answer. Verify that these numbers make sense in the problem and that they are solutions to both equations. We leave this to you! Step 7. Answer the question. The small soda has 140 calories and the fries have 340 calories.”» data-label=»»>в одном заказе среднего картофеля фри
и в одной маленькой газировке.
1 порции картофеля фри среднего размера.
s = количество калорий в
1 маленькой газировке.

всего 620 калорий
всего 820 калорий.
Чтобы решить систему уравнений, используйте исключение
. Уравнения представлены в стандартной форме
. Чтобы получить противоположные коэффициенты f ,
, умножьте верхнее уравнение на −2.

уравнений, а затем найдите 9.1676 ф .
в задаче и что они являются
решениями обоих уравнений.
Мы оставляем это вам!
340 калорий.
Малик останавливается в продуктовом магазине, чтобы купить пакет подгузников и 2 банки детского питания. Всего он тратит 37 долларов. На следующей неделе он останавливается и покупает 2 пакета подгузников и 5 банок со смесью на общую сумму 87 долларов. Сколько стоит мешок подгузников? Сколько стоит банка смеси?
Всего он тратит 37 долларов. На следующей неделе он останавливается и покупает 2 пакета подгузников и 5 банок со смесью на общую сумму 87 долларов. Сколько стоит мешок подгузников? Сколько стоит банка смеси?
Пакет с подгузниками стоит 11 фунтов, а банка со смесью — 13 фунтов.
Когда вам нужно будет решить систему линейных уравнений на последнем уроке математики, вам обычно не говорят, какой метод использовать. Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Для каждой системы линейных уравнений решить, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.
а)
б)
Решение
а)
Поскольку оба уравнения имеют стандартный вид, наиболее удобным будет метод исключения.
б)
Так как одно уравнение уже решено для y , наиболее удобным будет использование подстановки.
Для каждой системы линейных уравнений решите, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.
а)
б)
Показать ответа) Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование исключения.
б) Так как одно уравнение уже решено для , наиболее удобным будет использование подстановки.
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения систем линейных уравнений методом исключения.
- Учебное видео по решению систем уравнений методом исключения
- Обучающее видео-решение путем устранения
- Обучающие видео-системы решения от Elimination
- Решение системы уравнений методом исключения
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.

- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную вы удалите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
В следующих упражнениях решите системы уравнений методом исключения.
В следующих упражнениях переведите систему уравнений и решите.
- Сумма двух чисел равна 65. Их разница равна 25. Найдите числа.
- Сумма двух чисел равна −27. Их разница составляет −59. Найдите числа.
- Андреа покупает новые рубашки и свитера. Она может купить 3 рубашки и 2 свитера за 114 долларов или 2 рубашки и 4 свитера за 164 доллара. Сколько стоит рубашка? Сколько стоит свитер?
- Общее количество натрия в 2 хот-догах и 3 чашках творога составляет 4720 мг. Общее количество натрия в 5 хот-догах и 2 чашках творога составляет 6300 мг. Сколько натрия в хот-доге? Сколько натрия в чашке творога?
В следующих упражнениях решите, будет ли удобнее решать систему уравнений путем замены или исключения.
- Норрис может прогрести 3 мили вверх по течению за то же время, что и 5 миль вниз по течению по течению. Решите систему.
- для , его скорость гребли в стоячей воде.

- Затем найдите , скорость течения реки.
- для , его скорость гребли в стоячей воде.
Ответы:
- (6, 9)
- (6, 1)
- (2, 3)
- (9, 5)
- бесконечно много решений
- бесконечно много решений
- бесконечно много решений
- противоречиво, нет решения
- противоречиво, нет решения
- Цифры 20 и 45.
- Числа 16 и -43.
- Рубашка стоит 16 долларов, а свитер — 33 доллара.
- В хот-доге 860 мг. В чашке творога 1000 мг.
- устранение
- замена
- замена
- устранение
Комбинация/Замена — Подготовка к тесту Каплана
Теперь, когда вы понимаете требования, которые должны быть выполнены для решения системы уравнений, давайте рассмотрим некоторые методы эффективного решения этих систем. Двумя основными методами решения системы линейных уравнений являются подстановка и комбинация (иногда называемая 9).0559 удаление добавлением ).
Двумя основными методами решения системы линейных уравнений являются подстановка и комбинация (иногда называемая 9).0559 удаление добавлением ).
Подстановка — самый простой метод решения систем, и его можно применять в любой ситуации. К сожалению, зачастую это самый длинный и трудоемкий путь решения систем уравнений. Чтобы использовать подстановку, решите более простое из двух уравнений для одной переменной, а затем подставьте результат в другое уравнение. Вы можете использовать замену, чтобы ответить на следующий вопрос, но вы увидите, что есть более быстрый способ: комбинация.
Комбинация включает сложение двух уравнений вместе для исключения переменной. Часто одно или оба уравнения должны быть умножены на константу, прежде чем они будут сложены. Комбинация часто является лучшим методом для решения системы уравнений, поскольку она обычно быстрее, чем подстановка.
К сожалению, несмотря на то, что большинство студентов предпочитают замену, задачи на PSAT часто предназначены для быстрого решения с помощью комбинации. Чтобы по-настоящему повысить свой балл в тестовый день, тренируйтесь как можно чаще на практических тестах и в домашних задачах, чтобы это стало вашей второй натурой.
Чтобы по-настоящему повысить свой балл в тестовый день, тренируйтесь как можно чаще на практических тестах и в домашних задачах, чтобы это стало вашей второй натурой.
Шаг за шагом проработайте метод Каплана для математики, чтобы решить этот вопрос. В следующей таблице слева показано стратегическое мышление Каплана, а справа предложены математические наброски.
| Стратегическое мышление | Математические наброски |
| Шаг 1: Прочтите вопрос, определяя и систематизируя важную информацию по ходу дела Вам дана система двух уравнений с двумя неизвестными, и вас просят найти значения а и б . | 6 a + 6 b = 303 a + 2 b = 14 |
Шаг 2: Выберите наилучшую стратегию для ответа на вопрос Помните, что хотя для решения этого типа задач можно использовать подстановку, комбинация часто будет быстрее. Какое преобразование позволит добавить уравнения и исключить переменную? Комбинация часто требует умножения одного из ваших уравнений на константу. В этом случае обратите внимание, что произойдет, если вы умножите второе уравнение на -3. Какое преобразование позволит добавить уравнения и исключить переменную? Комбинация часто требует умножения одного из ваших уравнений на константу. В этом случае обратите внимание, что произойдет, если вы умножите второе уравнение на -3. Какой следующий шаг в комбинации? Расположив уравнения вертикально, вы можете просто складывать их, комбинируя по пути одинаковые члены. Обратите внимание, что 6 b + (–6 b ) = 0 b = 0, и вы исключили b из своего уравнения. Ваша цель при использовании комбинации состоит в том, чтобы установить коэффициент переменной, которую вы пытаетесь исключить, равным числу, равному по величине и противоположному по знаку коэффициенту в другом уравнении. Теперь вы можете легко решить на и . | [исходный](-3)(3a +2b) = (14)(-3) -9a — 6b = -42 6a + 6b = 30+ — 9a — 6b = -42 -3a + 0b = -12 [/raw]−3 a + 0 b = −12 −3 a = −12 a = 4 |
Шаг 3. Убедитесь, что вы ответили на правильный вопрос Несмотря на то, что в вопросе вас просят указать значения a и b , каждый вариант ответа имеет разное значение и . Нет необходимости снова подключаться и находить правильное значение b . Вариант (Б) правильный. Убедитесь, что вы ответили на правильный вопрос Несмотря на то, что в вопросе вас просят указать значения a и b , каждый вариант ответа имеет разное значение и . Нет необходимости снова подключаться и находить правильное значение b . Вариант (Б) правильный. |
Комбинацию также можно использовать, когда тестировщики запрашивают у вас странное количество, как в следующей задаче:
| Стратегическое мышление | Математические наброски |
| Шаг 1. Прочтите вопрос, определяя и систематизируя важную информацию по ходу дела Вас просят найти значение b + c . Основа вопроса содержит два уравнения с участием b и c . | 5 в – 2 б = 15 3 б – 4 в = 12 |
Шаг 2. Выберите наилучшую стратегию ответа на вопрос Как быстро и точно ответить на вопрос? Почему тестировщики просят количество Выберите наилучшую стратегию ответа на вопрос Как быстро и точно ответить на вопрос? Почему тестировщики просят количество b + c а не значения b и c независимо друг от друга? Тот факт, что вы решаете для b + c , предполагает, что можно найти более короткий путь, который сэкономит время. Поскольку вы не пытаетесь избавиться от переменной, попробуйте сложить уравнения, чтобы получить результат, в котором b + c равно некоторому числовому значению. Прежде чем добавлять, не забудьте записать переменные в одном и том же порядке для каждого уравнения. | [исходное] −2b + 5c = 15+ 3b − 4c = 12 b + c = 27 [/сырье] |
| Шаг 3: Убедитесь, что вы ответили на правильный вопрос Поскольку вас попросили найти значение b + c, , здесь больше нечего делать. Вариант (Д) правильный. | б + в = 27 |
Это было намного проще и быстрее, чем замена.

 Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
 Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении. Написать её в той же строчке в системе уравнений.
Написать её в той же строчке в системе уравнений. е. сделать «сортировку» — буквы к буквам, числа к числам.
е. сделать «сортировку» — буквы к буквам, числа к числам.


 Решить уравнение, сделав перенос числа 2 в правую часть с противоположным знаком.
Решить уравнение, сделав перенос числа 2 в правую часть с противоположным знаком.
 \begin{matrix} 1& -4& 8\\ 0& 1& \frac{-19}{15}\\ 0& 30& -46 \end{matrix}\right| & \begin{matrix} -33\\ \frac{113}{15}\\ 242 \end{matrix} \end{bmatrix}\)
\begin{matrix} 1& -4& 8\\ 0& 1& \frac{-19}{15}\\ 0& 30& -46 \end{matrix}\right| & \begin{matrix} -33\\ \frac{113}{15}\\ 242 \end{matrix} \end{bmatrix}\) 