|
Окно в Мир
| |||
Тренажёр «Сложение и вычитание в пределах 20» — Kid-mama — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Примеры на сложение и вычитание в пределах 10
Протокол ошибок
В любой момент работы с тренажером вы можете перейти к разделу приложения «Протокол ошибок», кликнув на соответствующую иконку сверху, либо перелестнув страницу вниз.
Здесь вы сможете посмотреть свою статистику (количество примеров по категориям) за последние сутки и по последнему режиму.
А также увидеть список ошибок и подсказок (максимум 6 штук), либо перейти к подробной статистике.
Дополнительная информация
Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:
домен сайта + раздел приложения + кодировка данного режима
например: matematika.club/app/#12301
Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.
Таблица сложения до 20
Сложим 3 и 4. Находим число 3 по горизонтали и число 4 по вертикали. Мысленно проводим линии до места пересечения. Это и есть искомое значение. Нетрудно заметить, что если мы поменяем местами значения и отыщем по горизонтали 4, а по вертикали — 3, то также в ячейке будет 7.
Отсюда вытекает одно из свойств, справедливых для суммы чисел. Звучит оно так: «От перестановки мест слагаемых сумма не меняется». Это свойство справедливо и для большего количества слагаемых. Разберемся в вопросе о том, можно ли данной таблицей пользоваться в случае сложения нескольких слагаемых. Ответ: можно, но до определенных значений. В этом случае действия нужно производить постепенно. Сначала складываем первые два слагаемых, получаем некое число. Если это простое число, которое входит в таблицу, то мы находим его и к нему прибавляем оставшееся и так далее. То есть, ориентируемся на наличие значений в таблице. Например, 4+5+6. Начала находим результат для действия 4 + 5, в ячейке на пересечении их столбца и строки находится 9. Далее выполняем действие 9+6. Находим в таблице 9 и 6.
Звучит оно так: «От перестановки мест слагаемых сумма не меняется». Это свойство справедливо и для большего количества слагаемых. Разберемся в вопросе о том, можно ли данной таблицей пользоваться в случае сложения нескольких слагаемых. Ответ: можно, но до определенных значений. В этом случае действия нужно производить постепенно. Сначала складываем первые два слагаемых, получаем некое число. Если это простое число, которое входит в таблицу, то мы находим его и к нему прибавляем оставшееся и так далее. То есть, ориентируемся на наличие значений в таблице. Например, 4+5+6. Начала находим результат для действия 4 + 5, в ячейке на пересечении их столбца и строки находится 9. Далее выполняем действие 9+6. Находим в таблице 9 и 6.
Далее все аналогично. Для больших чисел обычно таблицы не составляются. Таблица вычитания. Этой же таблицей можно пользоваться и для операции вычитания. В этом случае производим обратные действия. В самой таблице находим значение, из которого нужно вычесть число. Затем проводим линию до того числа, которое вычитается, остается мысленно дойти до оставшегося значения. Оно и будет искомым. Совсем просто это можно осуществить при помощи линейки. В данном случае линейка подставляется от вычитаемого числа сначала вертикально, затем горизонтально. Или наоборот. Для быстрого устного счета часто запоминают результаты сложения, и со временем уже нет необходимости наличия таблицы перед глазами.
Затем проводим линию до того числа, которое вычитается, остается мысленно дойти до оставшегося значения. Оно и будет искомым. Совсем просто это можно осуществить при помощи линейки. В данном случае линейка подставляется от вычитаемого числа сначала вертикально, затем горизонтально. Или наоборот. Для быстрого устного счета часто запоминают результаты сложения, и со временем уже нет необходимости наличия таблицы перед глазами.
Для ознакомления также ниже представлены более старые варинты таблицы.
Таблицы сложения значительно упрощают повседневный счет, поэтому много лет назад люди начали их использовать и некоторые из них мы можем видеть в сохранившихся книгах. Например, так выглядела таблица сложения в книге «Арифметика» Магницкого Л.
Ф. 1703 года издания.
(на картинке фото фрагмента из оцифрованной версии книги, саму книгу найти было достаточно сложно, поэтому использована сканированная версия, которая есть в широком доступе) Так выглядит эта таблица в воспроизведении (переиздании) той же книги, сделанном в 1914 году под редакцией П. Баранова:
Баранова:
(на картинке как раз фотография тоже сканированной версии переиздания 1914 года).
Состав чисел от 2 до 10 таблица для распечатки
Если вы начали изучать и разбирать с ребенком состав чисел от 2 до 10 — таблица для распечатки от нашего Лисёнка будет вам хорошим помощником. Распечатайте бланк с таблицей и разместите его в таком месте, где он будет всегда на виду у ребенка. Малыш в любой момент сможет воспользоваться подсказками, постепенно запоминая состав каждого числа.
Желательно, обучение ребенка разбавить полезными играми, чтобы малыш не просто зубрил материал, а пытался понять его.
При желании, можно разрезать числовые таблички по контуру, используя их, как отдельные карточки. Так вам будет удобней поочередно разбирать состав каждого числа.
Таблица сложения и вычитания скачать бесплатно
Во время обучения ребенка счету до 20 вам однозначно понадобится и такая таблица сложения и вычитания, скачать которую вы можете во вложениях внизу страницы. Пользоваться ей очень просто: на таблице мы отметили стрелочками, какие действия необходимо совершить, чтобы прибавить два числа, а также, каким образом, с помощью этой же таблицы, можно от одного числа отнять другое.
Пользоваться ей очень просто: на таблице мы отметили стрелочками, какие действия необходимо совершить, чтобы прибавить два числа, а также, каким образом, с помощью этой же таблицы, можно от одного числа отнять другое.
Сложение: проводим мысленно от чисел в серых прямоугольниках, которые мы хотим сложить, линии, перпендикулярно друг другу, до пересечения. Цифра, которая находится на месте пересечения и будет являться нашим ответом.
Вычитание: проводим действие в обратном порядке. От выбранного числа, находящегося в середине таблицы, проводим линии, перпендикулярные друг другу, к числам в серых прямоугольниках. Одно число будет являться вычитаемым, а другое разницей.
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу.
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.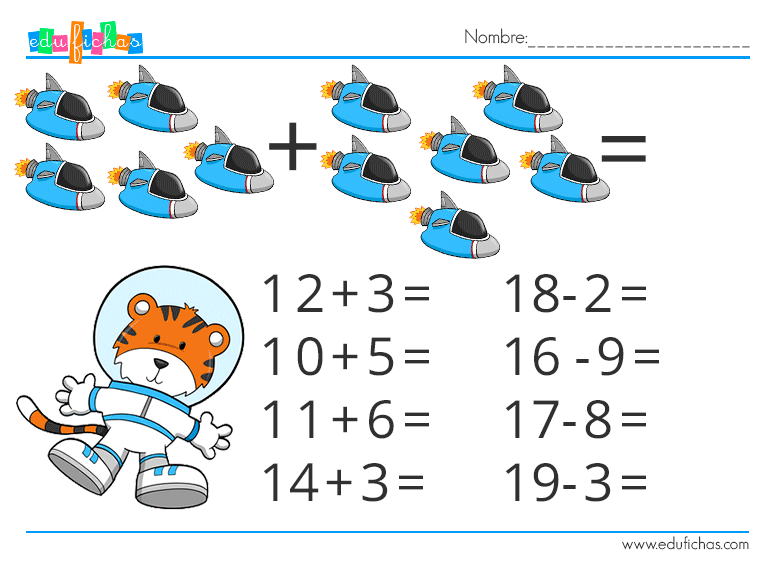
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках.
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями. Каждое задание содержит в себе картинки для раскрашивания — это стимулирует ребенка правильно выполнить задание.
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.
Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.
В игре также используется порядковый счет.
В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое.
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10.
Таблица сложения однозначных чисел до 20
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
Рис. 7
В каждом столбике первое слагаемое – одинаковое, а второе – увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
(рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
На уроке мы учились складывать и вычитать однозначные числа с переходом через десяток до 20. Знания таблицы сложения до 20 поможет вам при решении примеров и задач.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Социальная сеть работников образования (Источник).
- 5klass.net (Источник).
- Самоучка (Источник).
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
X
5klass.net
Разнообразие режимов
На странице настроек режима можно задавать необходимые параметры генерации примеров по математике для любого класса.
Тренажер устного счета позволяет отрабатывать 4 небезызвестных арифмитических действия на шести уровнях сложности.
Далее корректируете вид математического примера выбирая тип, устанавливая количество слагаемых, манипулируя числовыми множествами.
На данном этапе разработки были продуманы и реализованы режимы, позволяющие работать с двумя множествами чисел: Положительными и Отрицательными. В каждом из ним можно попрактиковаться в различных типах заданий: «Пример», «Уравнение», «Сравнение».
— этот режим включает в себя обычные арифмитические примеры по математике состоящие из двух или трёх чисел.
— режим, искомое число в котором может находиться на любой позиции.
— режим, в котором необходимо правильно поставить знак сравнения между результатами двух примеров.
Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». А когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.
Бонусом является возможность загрузить и в дальнейшем распечатать «самостоятельную работу» в формате PDF, состоящую из 26 примеров соответствующего режима, кликнум по значку Принтер.
Таблица сложения чисел до 20. Табличное сложение и вычитание натуральных чисел
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20.
У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().
- 5klass.net ().
- Самоучка ().
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу
Таблица сложения до 20 распечатать и скачать
Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.
Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.
Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.
Таблица вычитания до 20 распечатать и скачать
В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14.
На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14,
которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.
Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах.
Таблица вычитания без ответов распечатать и скачать
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
(рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().
- 5klass.net ().
- Самоучка ().
Домашнее задание
1.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Таблица сложения пифагора до 20. Табличное сложение и вычитание натуральных чисел
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
(рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().
- 5klass.net ().
- Самоучка ().
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу
Таблица сложения до 20 распечатать и скачать
Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.
Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.
Таблица вычитания до 20 распечатать и скачать
В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.
Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах.
Таблица вычитания без ответов распечатать и скачать
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.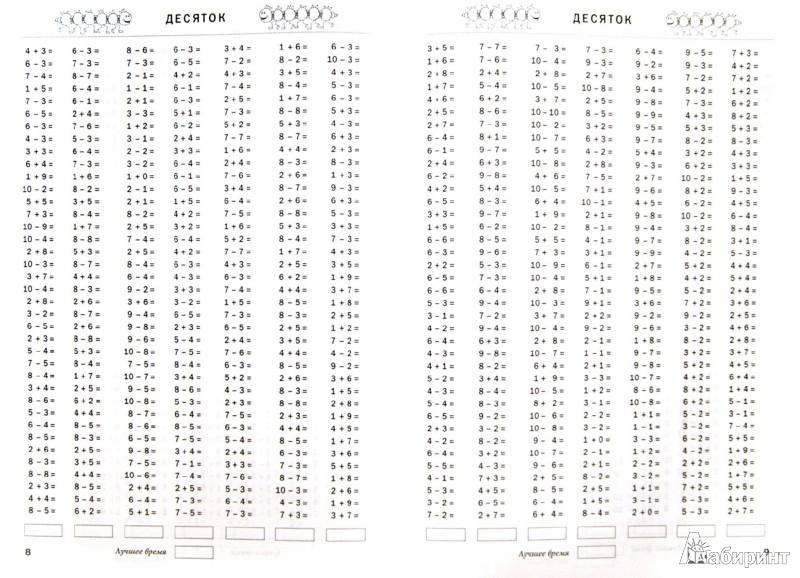
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().
- 5klass.net ().
- Самоучка ().
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Таблица сложения и вычитания натуральных чисел приведена для сложения чисел первого десятка и вычитания чисел от 1 до 18. Таблицей удобно пользоваться при сложении или вычитании по разрядам для натуральных многозначных чисел, устный счет построен на сложении по разрядам, т.е. на сложении по этой таблице.
Работа с таблицей предполагает такой результат: таблицу вы запомните, выучите наизусть в процессе вычислений, что значительно сократит время нахождения результата при сложении и вычитании натуральных чисел.
Правила пользования таблицей
Крайний левый столбец и верхняя строка — числа первого десятка — слагаемые при сложении и разность при вычитании. Чтобы сложить два числа, нужно первое слагаемое взять в крайнем левом столбце, а второе — в верхней строке. На пересечении столбца и строки в поле таблицы считывается результат сложения — сумма.
Чтобы вычесть одно число из другого, в поле таблицы нужно найти уменьшаемое и, двигаясь по этому числу по диагонали поля, выбрать строку, в которой в левом крайнем столбце помещено число вычитаемого. По месту строки и числу уменьшаемого расположен столбец, в верхней строке которого считывается разность (результат вычитания).
Примеры пользования таблицей
Сложение . 3 + 5 = 8
Первое слагаемое (3) взято в левом столбце, второе слагаемое (5) взято в верхней строке. На пересечении столбца и строки — сумма (8).
Вычитание . 8 — 3 = 5.
Уменьшаемое (8) выбираем в ноле таблицы и, двигаясь по диагонали поля с цифрой 8, останавливаемся на строке вычитаемого (3). На пересечении строки с числом 3 и столбца с числом 8 считываем разность (5) в верхней строке.
На пересечении строки с числом 3 и столбца с числом 8 считываем разность (5) в верхней строке.
Сложение и вычитание в пределах 20 фактов и рабочих листов для детей
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатный образец. Загрузить образец
Загрузить этот образец
Этот образец предназначен исключительно для участников KidsKonnect!
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь на эту страницу, чтобы начать загрузку!
Зарегистрируйтесь
Уже зарегистрировались? Авторизуйтесь, чтобы скачать.
Дети начинают разрабатывать стратегии для сложения и вычитания целых чисел на основе их более раннего использования с меньшими числами. Изучив свойства сложения и вычитания, дети теперь понимают связь между счетом и операциями.
См.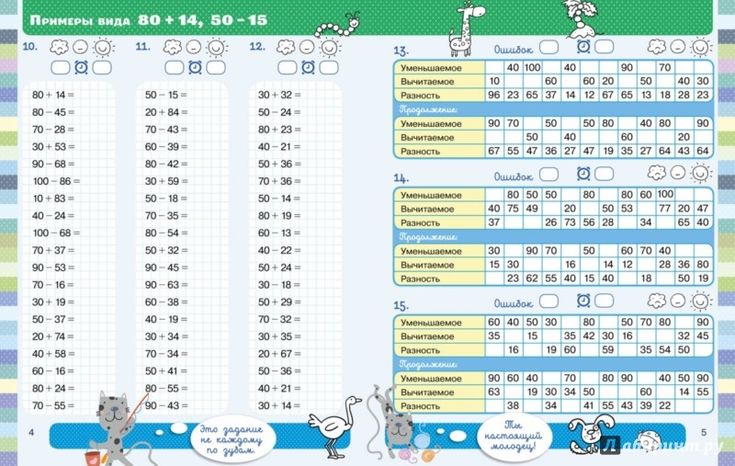 Файл фактов ниже для получения дополнительной информации о сложении и вычитании в пределах 20 или, в качестве альтернативы, вы можете загрузить наш 37-страничный пакет рабочих листов «Сложение и вычитание в пределах 20» для использования в классе или дома.
Файл фактов ниже для получения дополнительной информации о сложении и вычитании в пределах 20 или, в качестве альтернативы, вы можете загрузить наш 37-страничный пакет рабочих листов «Сложение и вычитание в пределах 20» для использования в классе или дома.
Основные факты и информация
ДОПОЛНЕНИЕ: ОБЗОР
- Ознакомьтесь с основами сложения. Первое, что нужно сделать, чтобы дети поняли сложение, — это рассказать им об этом важном символе.
- Знак «Плюс» или знак дополнения. Если вы видите этот символ, это означает, что вам нужно выполнить сложение или добавить числа или объекты до и после этого знака. Ответ на уравнение сложения называется суммой.
ДОПОЛНЕНИЕ: ПОДСЧЕТ ОБЪЕКТОВ
- Дети становятся более мотивированными, когда видят разноцветные предметы.Чтобы представить к ним дополнение, представьте предметы в качестве примеров или наглядных представлений.
- Сложение похоже на подсчет объектов. Наличие предварительных знаний о подсчете помогает детям понять сложение.

ДОПОЛНЕНИЕ: ОБЪЕКТЫ К ЧИСЛАМ
- Как только дети поймут идею подсчета предметов для сложения, познакомьте их с идеей сложения чисел. Во-первых, позвольте им записать объекты в виде чисел.
- После идентификации представьте числовую строку и начните знакомство с тем, как работает сложение, через числовую строку.
ДОБАВЛЕНИЕ ЧИСЕЛ
- Теперь дети должны иметь представление о добавлении предметов путем их подсчета и о том, как преобразовывать предметы в числа, а затем складывать их. Теперь начните знакомить с идеей сложения чисел.
- Чтобы помочь им лучше понять это, вы можете использовать объекты (введя преобразование чисел в объекты) или используя числовую линию.
- Преобразуйте числа в простые объекты, а затем вернитесь к своему прежнему пониманию сложения путем подсчета объектов.
ВЫЧИСЛЕНИЕ: ОБЗОР
- Просмотрите основы вычитания. Первое, что нужно сделать, чтобы дети поняли вычитание, — это рассказать им об этом важном символе.

- Знак «Минус» или знак вычитания. Если вы видите этот символ, это означает, что вам нужно выполнить вычитание или вычесть числа или объекты до и после этого знака. Ответ на уравнение сложения называется разностью.
ВЫЧИТАНИЕ: СЧЕТ ОБЪЕКТОВ
- Представьте задачу на вычитание слов и объясните ее с помощью рисунка.
- На столе 16 бананов. Обезьяна Марсель съела 11 бананов. Сколько бананов осталось?
- Нарисуйте 16 бананов на доске или на листе бумаги. Попросите детей сосчитать бананы и промаркировать каждый банан номером.
- Когда вы объясните, что обезьяна Марсель съела 11 бананов, вычеркните или сотрите 11 бананов, а затем спросите их, сколько бананов осталось.
- Объясните проблему с объектами. Покажите марионетку обезьяны, поставьте на стол 16 бананов и попросите ребенка пересчитать бананы.Спрячьте 11 бананов со стола, объяснив, что обезьяна Марсель уже съела бананы. Попросите детей сосчитать количество бананов, оставшихся на столе.

- При использовании предметов замените предметы, которые вы используете, чтобы учащиеся могли узнать, что математические правила универсальны. Например, решите задачу, используя бананы, а затем повторите ее с шариками.
- Напишите числовое предложение. Обсудите со своими учениками, что вы можете представить эту словесную задачу числовым предложением. Проведите их через процесс перевода слова «проблема» в числовое предложение.
ВЫЧИСЛЕНИЕ: ОБЪЕКТЫ НА НОМЕРА
- Предложите ученикам задачу на вычитание.
- Используйте числовую строку для решения проблемы. Нарисуйте числовую линию от 0 до 10.
- Напишите числовое предложение. Обсудите со своими учениками, что вы можете представить эту словесную задачу числовым предложением. Проведите их через процесс перевода слова «проблема» в числовое предложение.
ОБУЧЕНИЕ ДОБАВЛЕНИЮ И ВЫЧИСЛЕНИЮ С СЕМЕЙСТВАМИ ФАКТОВ
- Семейство фактов — это набор фактов или математических задач, в которых используются одни и те же числа.
 Три числа составляют семью фактов. Эти числа можно складывать или вычитать разными способами.
Три числа составляют семью фактов. Эти числа можно складывать или вычитать разными способами. - Например, числа 7, 8 и 15 образуют семейство фактов, которое может образовывать два предложения с числами сложения и два предложения с числами вычитания.
- Предложите ученикам задачу на вычитание.
- Всего 18 яблок. С дерева упало 3 яблока. Сколько осталось яблок?
- Используйте семейство фактов для решения проблемы. Составьте два числовых предложения сложения и два вычитания.
ДОБАВЛЕНИЕ И ВЫЧИСЛЕНИЕ ОБЩЕГО ЯДРА
- Общее ядро представляет вычитание как измерение расстояния между двумя точками. Чтобы дети могли визуализировать, нарисуйте числовую линию от 0 до 10.
- Common Core представляет сложение и вычитание как измерение расстояния между двумя точками. Чтобы ваши дети могли визуализировать, нарисуйте числовую линию от 0 до 20.
Сложение и вычитание в пределах 20 листов
Это фантастический набор, который включает в себя все, что вам нужно знать о сложении и вычитании в пределах 20 на 37 подробные страницы. Это готовых к использованию рабочих листов сложения и вычитания в пределах 20, которые идеально подходят для обучения студентов разработке стратегий сложения и вычитания целых чисел на основе их более раннего использования с меньшими числами. Изучив свойства сложения и вычитания, дети теперь понимают связь между счетом и операциями.
Это готовых к использованию рабочих листов сложения и вычитания в пределах 20, которые идеально подходят для обучения студентов разработке стратегий сложения и вычитания целых чисел на основе их более раннего использования с меньшими числами. Изучив свойства сложения и вычитания, дети теперь понимают связь между счетом и операциями.
Полный список включенных рабочих листов
- План урока
- Сложение и вычитание в пределах 20
- Сложить или вычесть?
- Количество облигаций
- Frog Jump
- Есть ли разница?
- Отсутствующие числа
- Вычесть, затем добавить
- Добавить, затем вычесть
- Решение проблем
- Magic Square
- Декодировать
Ссылка / процитировать эту страницу
Если вы ссылаетесь на любой контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник.
Сложение и вычитание в пределах 20 фактов и рабочих листов: https://kidskonnect. com — KidsKonnect, 6 мая 2020 г.
com — KidsKonnect, 6 мая 2020 г.
Ссылка будет отображаться как добавление и вычитание в пределах 20 фактов и рабочих листов: https://kidskonnect.com — KidsKonnect, 6 мая 2020 г.
Использование с любой учебной программой
Эти рабочие листы были специально разработан для использования в любой международной учебной программе.Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы.
Уравнений сложения и вычитания до 20
Научитесь складывать и вычитать числа до 20
Вау! Вы выучили много сложения и вычитания.
Давайте рассмотрим то, что вы уже узнали.
Обзор сложения и вычитания
В сумме и мы объединяем слагаемых , чтобы получить сумму .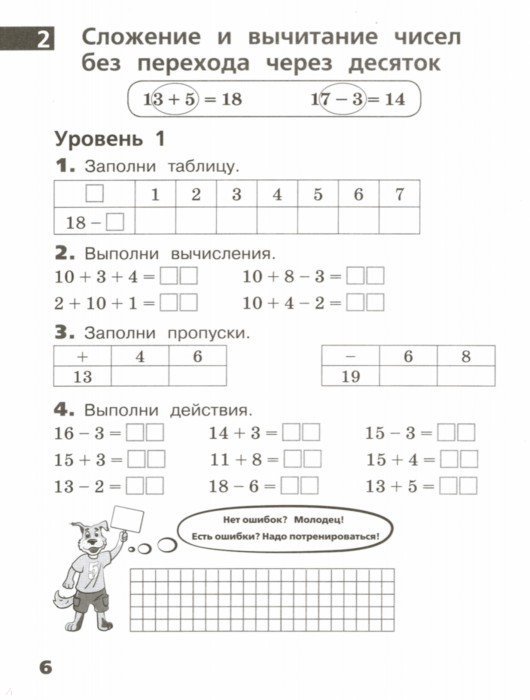
При вычитании , мы вычитаем , вычитаем из , вычитая , чтобы получить разность .
👆 Совет для запоминания:
Когда мы ‘ MINU S ‘ , порядок будет:
MINU END — S UBTRAHEND
Минут всегда равен перед вычитанием .
Сложение чисел
🤓 Попробуем сложить эти числа.
14 + 2 = ?
Как вы знаете, мы можем складывать числа разными способами. 🤗
👉 Мы можем использовать форму столбца .
👉 Мы можем добавить , используя картинки.
👉 Мы также можем добавить, используя числовую строку .
Отличная работа! 👏 Сумма равна 16.
14 + 2 = 16
Вычитание чисел
Теперь давайте попробуем вычесть два числа.
17-4 = ?
Опять же, мы можем вычитать по-разному. 😎
👉 Мы можем использовать форму столбца .
👉 Мы можем вычесть , используя картинки.
👉 Мы можем вычесть, используя числовую линию .
Отличная работа! 😎 Разница в составляет 13.
17-4 = 13
Целое и его части
Три числа в уравнении сложения или вычитания составляют группу:
👉 Наибольшее число называется целым .
👉 Два других числа — это частей.
Добавление частей дает целое.
12 + 6 = 18
6 + 12 = 18
Вычитание одной части из целого дает другую часть.
18 — 6 = 12
18 — 12 = 6
Поиск недостающих слагаемых, минусов и вычитаемых
🤓 Иногда у нас могут возникать подобные проблемы.
12 + ? = 17
15 — ? = 11
? — 3 = 10
Как мы можем найти эти недостающие числа? 🤔
Мы можем найти пропущенных чисел в уравнениях, используя целиком и по частям! 🤗
👉 Давайте посмотрим на первый пример.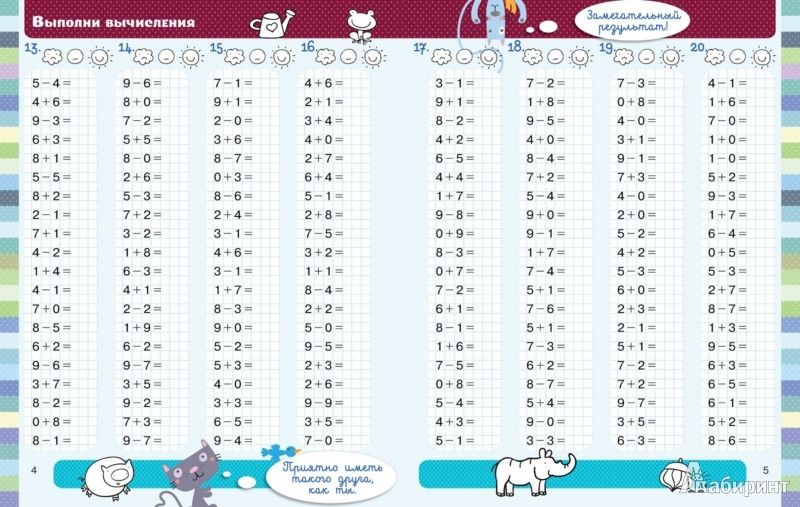
12 + ? = 17
Отсутствующий номер является частью или целым? 🤔
Поскольку мы складываем , недостающее число составляет часть.
Давайте нарисуем картинку, чтобы найти ответ.
Какая часть отсутствует? Считай звезды! 👆
😎 Верно! Это 5.
Итак, пропущено слагаемым 5.
12 + 5 = 17
👉 Давайте попробуем следующий пример.
15 — ? = 11
Здесь отсутствует второй номер уравнения вычитания.
🤓 Отсутствующий номер является частью или целым?
Отличная работа! 👍 Недостающий номер — часть.
Давайте нарисуем картинку и найдем ответ.
Что не хватает?
Отличная работа! Это 4.
Итак, недостающее вычитаемое равно 4.
15 — 4 = 11
👉 Теперь давайте посмотрим на последнюю задачу.
? — 3 = 10
На этот раз отсутствует первое число в уравнении вычитания.
Это целиком или частично? 🤔
Очень хорошо! 😃 Это целое, или меньшее.
minuend — это наибольшее число в уравнении вычитания.
Давайте нарисуем картинку, чтобы найти ответ.
Что в целом?
Сосчитайте все звезды вместе! 🙌
Отличная работа! Это 13. 🤗
🤗
.
Итак, отсутствующее значение равно 13.
13 — 3 = 10
Смотри и учись
Вы молодцы! 🤗 А теперь попробуйте задавать практические вопросы.
Рабочих листов по вычитанию
Базовое вычитание (Minuends to 10, Answers to 10)
Эти рабочие листы и задания содержат очень простые факты вычитания. У каждой задачи есть уменьшение, вычитание и разница в 10 или меньше. (примеры: 5-3 = 2 и 6-5 = 1)
Приблизительный уровень: детский сад и 1-е классы
Базовое вычитание (минус до 20, ответы на 10)
Здесь вы найдете десятки распечатанных математических заданий для обучения однозначное вычитание. Коллекция включает в себя рабочие листы, математические игры, загадочные картинки, карточки с заданиями и мероприятия учебного центра.Этот набор имеет минимальное значение до 20 и разность до 10. (примеры: 11-6 = 5 и 18-9 = 9)
Коллекция включает в себя рабочие листы, математические игры, загадочные картинки, карточки с заданиями и мероприятия учебного центра.Этот набор имеет минимальное значение до 20 и разность до 10. (примеры: 11-6 = 5 и 18-9 = 9)
Прибл. Уровень: 1-й и 2-й классы
Вычитание двух цифр (без перегруппировки / заимствования)
Загрузите и распечатайте карточки с заданиями, игры и рабочие листы для обучения сложению двузначных чисел. Это очень простые задачи, не требуют от студентов перегруппировки, переименования или заимствования.
Примерно 1-й и 2-й классы.
Вычитание двух цифр (с перегруппировкой / заимствованием)
Эти задачи на вычитание требуют, чтобы учащиеся заимствовали или перегруппировывались.На этой странице есть рабочие листы, игры в скутер, задания с магическими цифрами и математические операции с миллиметровой бумагой.
3-значное вычитание
Рабочие листы для печати, скутер, игра с магическими цифрами, карточки с заданиями, математика на миллиметровой бумаге и задачи со словами.
Вычитание 4-значных чисел
Эти упражнения можно использовать при обучении студентов вычитанию 4-значных чисел. Включает несколько PDF-файлов для вычитания нуля.
Вычитание денег
Используйте эти ресурсы, чтобы попрактиковаться в вычитании денег и внесении сдачи. Включает карточки с задачами, математику на миллиметровой бумаге и рабочие листы.
Вычитание 10 и кратное 10
Используйте модели, диаграммы сотен и математические вычисления для вычитания 10 и кратных 10 из двузначных чисел. (примеры: 56-10 = 46 и 68-40 = 28)
Создайте свой собственный
Рабочие листы вычитания Генератор однозначного вычитания (базовый)
Создайте свои собственные базовые рабочие листы вычитания с помощью этого инструмента генератора. Листы, которые вы создаете с помощью этого инструмента, можно использовать для тестов по времени или дополнительной практики.
Генератор многозначного вычитания
Создайте свои собственные рабочие листы вычитания с 2, 3, 4, 5 или 6-значными числами.Вы можете выбрать вертикальные или горизонтальные задачи.
Дробное и десятичное вычитание
Вычитание дробей и смешанных чисел
На этой странице есть серия рабочих листов для сложения и вычитания дробей и смешанных чисел.
Вычитание десятичных знаков
Научитесь складывать и вычитать десятичные дроби со значениями десятых, сотых и тысячных долей.
Смешанное сложение и вычитание
Смешанное сложение и вычитание (базовый; 0-10)
Эти рабочие листы содержат данные о сложении и вычитании.
Семейства фактов сложения-вычитания (базовые; 0-10)
Семейства лиц — это группы чисел, которые работают вместе, чтобы сформировать факты сложения и вычитания.
Целые числа (положительные и отрицательные числа)
Эта страница целочисленных рабочих листов включает несколько рабочих листов по вычитанию положительных и отрицательных чисел.
Многоступенчатые задачи со словами
Эти многоступенчатые задачи со словами требуют от учащихся использовать несколько операций.
Math Mystery Pictures
На этой странице вы найдете множество рабочих листов с загадочными картинками с базовым сложением и вычитанием.
Числовые строки
Практикуйтесь в сложении и вычитании числовых линий.
Словесные задачи (смешанные навыки)
В этих математических словесных задачах учащиеся будут использовать различные навыки, включая сложение, вычитание, определение времени, счет денег и геометрию.
Цели сложения и вычитания — Spedhelper
Цели сложения и вычитания
Кому 5:
- Стандарт Kinder: Свободно складывайте и вычитайте в пределах 5 CCSS.
 Математическое содержание.K.OA.A.5
Математическое содержание.K.OA.A.5 - Kinder цель: Учитывая 5 задач и манипуляций, ___________ будет плавно складывать и вычитать в пределах 5 CCSS.Math.Content.K.OA.A.5
- Где найти эталоны: Подсчет и мощность
Кому 20:
- Стандарт 1-го класса: Сложение и вычитание в пределах 20, демонстрируя беглость сложения и вычитания в пределах 10 CCSS.Math.Content.1.OA.C.6
- Цель 1-го класса : Учитывая пять задач, _______ будет складывать и вычитать в пределах 20 с точностью 80% CCSS.Math.Content.1.OA.C.6
- Если ученику нужны блоки, укажите это в: Учитывая пять задач и манипуляций, _______ будет добавлять и вычитать в пределах 20 с точностью 80% CCSS.Math.Content.1.OA.C.6
- Где найти стандарты: Операции и алгебраическое мышление
Кому 100:
- 1-й класс стандарт: Добавить в пределах 100 CCSS.Math.Content.1.NBT.C.4
- Цель 1-го класса: Учитывая десять задач, ______ добавит в пределах 100 с точностью 80%, как измерено учительскими записями и наблюдениями CCSS.
 Math.Content.1.NBT.C.4
Math.Content.1.NBT.C.4 - Стандарт 2-го класса: Свободно складывайте и вычитайте в пределах 100, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием CCSS.Math.Content.2.NBT.B.5
- Цель 2-го класса: Учитывая 10 задач на сложение и вычитание двух цифр, ___________ будет складывать и вычитать в пределах 100 с 80%, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием, как измерено в записях учителя. и наблюдения.CCSS.Math.Content.2.NBT.B.5
- Где найти стандарты: Числа и операции в десятичной системе координат
Кому 1000:
- Стандарт 2-го класса: Сложить и вычесть в пределах 1000 CCSS.Math.Content.2.NBT.B.7
- Цель 2-го класса : Учитывая 10 задач на сложение и вычитание трех цифр, ___________ будет складывать и вычитать в пределах 1000 с точностью 80%, как измерено записями учителя и наблюдениями CCSS.
 Math.Content.2.NBT.B.7
Math.Content.2.NBT.B.7 - Стандарт 3-го класса: Свободно складывайте и вычитайте в пределах 1000, используя стратегии и алгоритмы, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием CCSS.Math.Content.3.NBT.A.2
- Цель 3-го класса: Учитывая 10 задач сложения и вычитания из трех цифр, __________ будет складывать и вычитать в пределах 1000 с точностью 80%, используя стратегии и алгоритмы, основанные на разряде, свойствах операций и / или соотношении между сложением и вычитанием, как измеряется учительскими записями и наблюдениями CCSS.Math.Content.3.NBT.A.2
- Стандарт 4-го класса: Свободно складывайте и вычитайте многозначные целые числа, используя стандартный алгоритм CCSS.Math.Content.4.NBT.B.4
- Цель 4-го класса : Учитывая 10 задач на сложение и вычитание из трех цифр, __________ будет складывать и вычитать многозначные целые числа, используя стандартный алгоритм с точностью 80%, как измерено записями учителя и наблюдениями CCSS.
 Math.Content.4.NBT .B.4
Math.Content.4.NBT .B.4 - 5-й класс: Не существует стандарта 5-го класса для сложения и вычитания, хотя, если в вашем округе строгие требования к уровням оценок Common Core для стандартов, вы можете настроить его, чтобы он работал: складывать, вычитать, умножать и делить десятичные дроби на сотые CCSS .Math.Content.5.NBT.B.7
- Где найти стандарты: Числа и операции в десятичной системе координат
Вернуться к математическим целям
Перейти к экзаменам по математике, уровень 1
Перейти к экзаменам по математике, уровень 2
Посмотреть все цели
Сложение и вычитание на английском языке
Урок двадцать два
сложение или сложение | ||||
5 | + | 3 | ||
пять | плюс | три | равно | восемь |
2 | 4 | |||
два | и | два | это | четыре |
четыре | ||||
будут использовать «Примечание»: are »для знака равенства (=). | ||||
Учитель спрашивает ответ так:
Сколько два плюс два? (используйте глагол в единственном числе для обозначения «быть» — «есть»)
вычитание или вычитание | |||||
5 | — 9708 | = | 2 | ||
пять | минус | три | равно | два | = | 3 |
десять | отнять | семь | Примечание | первый использование «минус») предпочтительнее второго, но популярно «забрать». | |
Учитель спрашивает ответ так:
Что такое пять минус три?
Конечно, вы умеете делать математику на своем родном языке, но важно практиковаться на английском. Сложение:
Слово «сделать» часто используется при подсчете денег. Вычитание:
|
Сложение и вычитание целых чисел
Одно из применений абсолютного значения — найти расстояние между любыми двумя точками числовой прямой.Для действительных чисел a и b , формула расстояния для числовой прямой Расстояние между любыми двумя действительными числами a и b на числовой прямой можно вычислить по формуле d = | b − a |. задается как,
задается как,
Пример 9: Определите расстояние между 2 и 7 на числовой прямой.
Решение: На графике мы видим, что расстояние между двумя заданными целыми числами составляет 5 единиц.
Используя формулу расстояния, получаем тот же результат.
Пример 10: Определите расстояние между −4 и 7 на числовой прямой.
Решение: Используйте формулу расстояния для числовой прямой d = | b − a |, где a = −4 и b = 7.
Получается, что не имеет значения, какие точки используются для a и b ; абсолютное значение всегда обеспечивает положительный результат.
Попробуй! Определите расстояние между −12 и −9 на числовой прямой.
Тематические упражнения
Часть A: Сложение и вычитание
Сложить и вычесть.
1. 24 + (- 18)
2. 9 + (- 11)
3–31 + 5
4. −12 + 15
5. −30 + (- 8)
6. −50 + (- 25)
7. −7 + (- 7)
−7 + (- 7)
8. −13 — (- 13)
9. 8−12 + 5
10. −3−7 + 4
11. −1−2−3−4
12. 6 — (- 5) + (- 10) −14
13. −5 + (- 3) — (- 7)
14.2−7 + (- 9)
15. −30 + 20−8 — (- 18)
16. 10 — (- 12) + (- 8) −20
17. 5 — (- 2) + (- 6)
18. −3 + (- 17) — (- 13)
19. −10 + (- 12) — (- 20)
20. −13 + (- 5) — (- 25)
21. 20 — (- 4) — (- 5)
22. 17 + (- 12) — (- 2)
Переведите каждое предложение в математическое утверждение, а затем упростите.
23.Найдите сумму 3, 7 и −8.
24. Найдите сумму −12, −5 и 7.
25. Определите сумму первых десяти натуральных чисел.
26. Определите сумму целых чисел в наборе {−2, −1, 0, 1, 2}.
27. Найдите разницу 10 и 6.
28. Найдите разность 10 и −6.
29. Найдите разность −16 и −5.
30. Найдите разность −19 и 7.
31. Вычтем 12 из 10.
32. Вычтем −10 из −20.
33. Вычтем 5 из −31.
34. Вычтем −3 из 27.
35. Два меньше 8.
Два меньше 8.
36. Пять меньше −10.
37. Вычтем 8 из суммы 4 и 7.
38. Вычтем −5 из суммы 10 и −3.
39. Вычтите 2 из разницы 8 и 5.
40. Вычтем 6 из разницы -1 и 7.
41. Мэнди внесла депозит в размере 200 долларов на свой текущий счет во вторник. Затем она выписала 4 чека на 50, 125, 60 и 45 долларов. Насколько больше своего депозита она потратила?
42. Квотербек трижды пробежал по мячу в футбольном матче в прошлое воскресенье. Он набрал 7 ярдов за один заход, но потерял 3 и 8 ярдов за два других. Каков его общий метраж на игру?
43.Доход местного фотографа за месяц составляет 1200 долларов. Его расходы включают аренду студии в размере 600 долларов, реквизит стоимостью 105 долларов, сборы за материалы в размере 135 долларов и услуги визажиста, которые берут 120 долларов. Какова его общая прибыль за месяц?
44. Самолет, летевший на высоте 30 000 футов, потерял 2 500 футов высоты, а затем поднялся на 1 200 футов. Какая новая высота самолета?
45. Температура воздуха в 18:00 была 22 ° C. и к полуночи упал на 26 °. Какая была температура в полночь?
Температура воздуха в 18:00 была 22 ° C. и к полуночи упал на 26 °. Какая была температура в полночь?
46.У медсестры есть 30 миллилитров физиологического раствора, но необходимо 75 миллилитров раствора. Сколько еще ей нужно?
47. Ширина прямоугольника на 2 дюйма меньше его длины. Если длина составляет 16 дюймов, определите ширину.
48. Основание треугольника на 3 фута короче его высоты. Если высота составляет 5 футов, найдите длину основания.
Часть B: Расстояние на числовой прямой
Найдите расстояние между заданными числами на числовой прямой.
49. −3 и 12
50,8 и −13
51. −25 и −10
52. −100 и −130
53. −7 и −20
54,0 и -33
55. −10 и 10
56. −36 и 36
57. Самая низкая температура на Земле, –129 ° F, была зарегистрирована в 1983 году на станции Восток в Антарктиде. Самая высокая температура на Земле, 136 ° F, была зафиксирована в 1922 году в Эль-Азизии, Ливия.Рассчитайте диапазон температур Земли.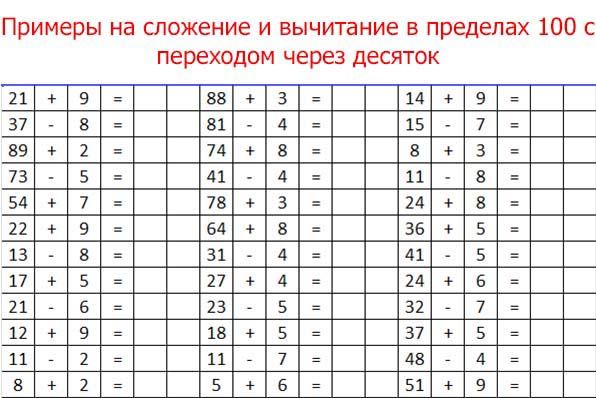
58. Ежедневная высокая температура была зафиксирована как 91 ° F, а низкая — 63 ° F. Какой был температурный диапазон в течение дня?
59. Студент набрал 67 баллов за свой самый низкий тест и 87 баллов за свой лучший. Рассчитайте диапазон его результатов теста.
60. В напряженный день определенный веб-сайт может посещаться 12 500 раз. В медленный день он может иметь всего 750 обращений. Рассчитайте диапазон количества попаданий.
Часть C: Темы дискуссионной доски
61. Поделитесь примером добавления номеров со знаком в реальном приложении.
62. Продемонстрируйте ассоциативное свойство сложения с любыми тремя действительными числами.
63. Покажите, что вычитание не коммутативно.
Ключевые слова задачи на сложение и вычитание слов
Ключевые слова сложения и вычитания
Задачи на сложение и вычитание слов обычно преподаются в классе 2 (ключевой этап 1 в Великобритании) или во втором классе (в США).
Стратегия решения проблем со словами состоит в том, чтобы, во-первых, записать задействованные числа, а во-вторых, решить, какую операцию использовать, прочитав ключевые слова в вопросе.
Чтобы решить задачи на сложение и вычитание слов, мы стараемся читать вопрос и искать ключевые слова. Приведенный ниже список ключевых слов поможет определить, есть ли у нас проблемы со словами сложения или вычитания.
Вот некоторые общие ключевые слова для сложения:
- Добавить
- плюс
- Подробнее
- Всего
- Увеличение
- Вместе / Все вместе
- Комбинированный
- Сумма
- Рост
Если мы увидим эти слова, у нас, вероятно, проблема со словом сложения.
Вот некоторые общие ключевые слова вычитания:
- Вычесть
- минус
- Забрать
- Меньше / Меньше
- Разница
- Уменьшение
- Сколько осталось / осталось?
- Раздача — денежные вопросы
- Слова, оканчивающиеся на «эр», например короче, длиннее, быстрее.
Вот наш первый пример проблемы со словом.
У Уильяма 20 жетонов, и ему дается 7 , еще .
Сколько у него всего ?
Мы видим, что у нас есть два дополнительных ключевых слова: «, еще » и «, всего ».
При обучении задачам со словами полезно сначала записать числа, которые есть в тексте вопроса.
У нас 20 и 7.
Слова « еще » и « всего » говорят нам, что это проблема сложения слов. Начинаем с 20 фишек и добавляем еще 7.
Как только мы узнаем, что у нас есть проблема со сложением слов, мы можем складывать числа.
20 + 7 = 27
Всего у Уильяма 27 счетчиков.
Вот еще один пример проблемы со словом.
У Фиби 12 см ленты, а у Джека 23 см.
Сколько у них всего всего ?
Наша стратегия состоит в том, чтобы сначала записать числа, участвующие в вопросе.
Мы записываем 12, а затем 23. Мы можем написать числа друг над другом и выровнять цифры в каждом номере.
В этом вопросе есть только одно ключевое слово — всего .
Это ключевое слово сложения, которое сообщает нам, что мы хотим объединить две суммы, чтобы получить итог.
Мы хотим сложить числа 12 и 23.
На этом этапе дети обычно записывают элементы, участвующие в вопросе.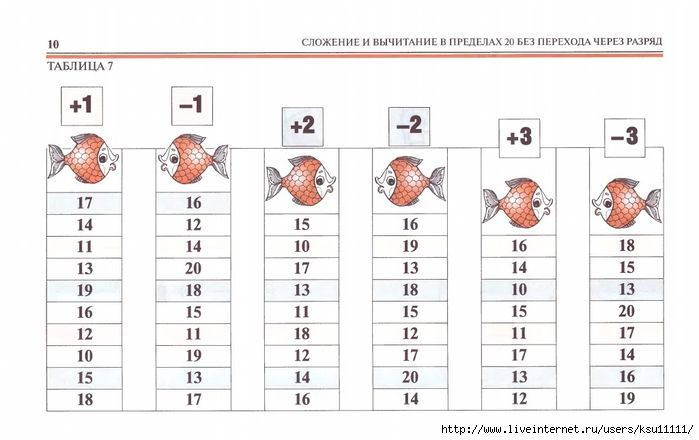 Однако проще всего просто записать сами числа, а затем указать единицы в конце вопроса, как часть проверки выполнения.
Однако проще всего просто записать сами числа, а затем указать единицы в конце вопроса, как часть проверки выполнения.
Добавляем столбец единиц, 2 + 3 = 5.
Сложив цифры в столбце десятков, 1 + 2 = 3.
Следовательно, 12 + 23 = 35 и итого у нас получается 35 см ленты.
Мы измеряем длину ленты в см, поэтому в конце ответа пишем «см».
Вот еще один пример проблемы со словом.
Я покупаю 2 сладости по 43 пенса каждая.
Сколько они стоят в итого ?
Каждая сладость стоит 43 пенса, а их два.
В этом вопросе мы дважды записываем 43.
Ключевое слово « всего » говорит нам о том, что это проблема со сложением слов.
Мы сложим две 43 суммы, написав их цифры непосредственно друг над другом, не ставя «пенсы» в конце.
Сложив единицы, 3 + 3 = 6.
Складываем десятки, 4 + 4 = 8.
Две сладости в сумме стоят 86 пенсов.
Теперь, когда расчет был произведен, мы можем написать пенсы или «р» на окончательном ответе.
В этом сформулированном вопросе у нас только одно число в самом тексте. Написана только одна буква «43».
При обучении детей задачам со словами может помочь нарисовать схему, чтобы лучше представить себе ситуацию.
Вот еще одно слово «проблема с деньгами».
У Мэтью 35 пенсов.
Он тратит 13 пенсов.
Сколько у него осталось ?
Записываем задействованные числа — 35 и 13.
В этой проблеме со словом ключевое слово осталось .
Найти, сколько осталось — ключевое слово для задачи на вычитание слов.
Это означает, что мы вычитаем меньшее число из большего числа.
Чтобы вычесть 13 из 35, мы пишем большее число над меньшим числом и выравниваем цифры.
Вычитая столбец единиц, 5 — 3 = 2.
Вычитая столбец десятков, 3 — 1 = 2.
35 — 13 = 22
Это была проблема, связанная с поиском сдачи за деньги.
Трата денег, а затем получение сдачи также очень вероятно указывает на то, что проблема со словом связана с вычитанием.
В этой задаче со следующей формулировкой у Адама 59 граммов шоколада.
Он ест 49 грамм.
Сколько у него осталось ?
Первый шаг стратегии задачи со словами — это выписать оба числа, входящих в вопрос.
У нас 59 и 49.
Второй шаг — определить ключевые слова. Слово left является ключевым словом вычитания.
Мы хотим увидеть, сколько осталось после того, как из 49 граммов было вычтено .
Мы записываем вычитание с большим числом над меньшим числом.
Вычитая цифры столбца единиц, 9 — 9 = 0.
Вычитая цифры столбца десятков, 5 — 4 = 1.
59 — 49 = 10.
Осталось 10 граммов шоколада.
Вот еще один пример проблемы со словом.
У меня есть свеча длиной 38 см.
После того, как я его зажгу, 11 см тает .
Какой длины сейчас свеча?
Эта проблема со словами усложняется тем, что в вопросе нет прямых ключевых слов.
Однако фраза « тает, » говорит нам, что мы удаляем или вычитаем.
Опять же, при обучении задачам со словами рисование диаграммы — полезный метод.
Если диаграмма или картинка не даны, это помогает нарисовать ситуацию в начале, а также ситуацию в конце.
Примеры онлайн на сложение и вычитание двузначных чисел
Онлайн примеры на сложение и вычитание в пределах позволяют довести устный счёт до автоматизма. Примеры до 20 — это сложение однозначных чисел, сумма которых переходит через десяток, а также сложение двузначных чисел из первого десятка и однозначного числа.
Переход через десяток — важная веха в освоении устного счёта: освоившись с переходом через первый десяток, можно приступать к примерам с двузначными числами.
Примеры на вычитание построены также с вычитание числа из первого десятка.
Примеры можно разделить по степени сложности: лёгкие – это примеры без перехода через десяток, сложные – с обязательным переходом, обычные – слагаемые выбираются случайным образом.
| Настройка генератора примеров |
|---|
|
|
|
Образец примеров
10 + 4
14 + 4
16 + 2
16 + 4
10 — 1
9 — 6
15 + 5
16 — 11
6 + 11
5 + 9
2 + 11
11 — 3
9 + 3
2 + 13
12 + 2
8 — 5
9 — 7
12 + 7
15 — 6
4 + 8
2 + 15
3 + 10
6 — 1
17 — 14
3 + 16
12 — 11
7 — 5
11 — 7
14 — 1
15 + 3
4 + 13
11 + 3
7 + 13
15 — 4
1 + 15
18 — 10
12 + 7
10 — 5
20 — 12
18 — 7
15 — 2
11 + 6
8 — 4
6 + 14
5 + 5
11 — 3
1 + 12
5 — 2
15 — 14
7 + 5
13 + 3
6 + 9
1 + 11
17 — 5
4 — 3
12 + 2
8 + 3
8 + 4
2 + 8
5 + 12
11 + 5
9 — 2
14 + 4
8 — 2
14 — 7
20 — 12
18 — 17
16 — 11
2 + 17
14 — 12
5 + 9
15 — 6
2 — 1
5 + 11
10 + 9
16 — 7
15 — 5
14 + 4
4 + 12
18 — 14
19 — 11
11 — 4
7 + 8
2 + 13
15 — 1
19 — 9
8 — 6
19 — 10
18 — 3
13 + 5
14 — 5
15 — 12
19 + 1
5 — 4
19 — 18
10 — 4
6 + 13
3 + 7
19 — 5
7 + 9
5 — 4
17 — 16
1 + 15
18 — 16
20 — 19
3 + 12
19 — 10
17 — 12
1 + 9
15 — 7
19 — 8
12 + 5
12 — 10
10 — 5
9 — 8
20 — 7
17 + 3
9 + 10
16 + 2
5 + 15
4 + 6
16 — 3
16 + 4
1 + 9
14 + 6
10 + 3
20 — 14
19 — 16
5 + 12
3 — 2
14 + 3
4 + 14
9 + 11
8 — 4
6 + 13
12 — 3
7 — 4
11 + 9
9 — 5
16 — 4
6 + 7
16 — 4
17 — 13
5 + 11
10 — 1
3 + 12
6 + 14
6 + 6
12 + 6
19 — 11
15 — 9
18 — 8
6 — 3
7 + 13
13 + 7
2 + 9
11 + 5
14 — 6
18 — 9
8 — 3
19 — 4
2 + 13
12 + 2
2 + 10
12 — 8
6 + 14
12 — 5
10 + 4
5 + 12
17 — 3
20 — 5
13 — 7
4 + 15
6 + 12
15 — 11
10 — 3
20 — 6
18 — 1
9 + 4
3 + 7
11 + 4
3 + 17
8 + 8
10 — 6
16 — 15
3 + 14
9 + 5
5 + 8
13 + 7
4 + 8
3 + 13
16 — 3
11 + 3
5 + 5
15 — 3
8 + 11
9 + 7
3 + 17
8 — 7
17 — 9
3 + 13
5 + 10
8 — 1
17 — 13
9 + 3
15 — 13
10 — 6
8 + 10
2 — 1
16 — 11
19 — 18
9 — 7
15 + 1
5 + 14
3 — 1
18 — 6
10 + 9
15 + 1
3 + 17
5 + 12
5 + 14
15 — 12
16 — 15
4 + 14
19 — 13
5 + 7
12 + 7
14 + 4
6 + 13
11 + 7
9 — 4
13 + 3
18 + 1
19 — 18
17 — 5
14 — 3
15 — 11
6 + 10
9 + 10
15 + 4
4 + 15
4 — 3
8 — 1
7 + 5
10 + 10
8 — 6
20 — 7
13 + 4
2 + 14
5 + 8
20 — 1
6 + 12
19 — 4
4 + 14
13 + 6
14 + 2
15 — 14
9 + 1
6 + 6
12 + 6
18 — 12
12 — 2
16 — 12
6 + 5
6 + 10
10 + 4
3 + 16
16 + 4
10 + 10
11 + 9
10 — 1
11 — 4
18 — 2
14 + 4
13 — 6
9 + 11
19 — 3
17 + 1
17 — 8
10 + 3
2 + 13
11 + 9
20 — 1
16 — 10
13 — 6
15 — 3
3 + 11
18 — 15
19 — 8
4 + 15
19 — 15
9 + 10
15 — 14
3 + 12
1 + 17
6 + 10
10 + 6
1 + 14
15 — 1
17 + 3
9 + 1
9 + 5
9 — 6
5 + 12
13 — 3
12 — 7
17 — 12
13 + 3
9 — 7
19 — 13
3 — 2
6 + 13
10 — 4
7 — 5
12 + 2
11 — 7
8 — 6
6 — 4
3 + 17
10 + 6
13 — 9
9 + 8
13 — 3
7 — 6
8 + 6
18 — 7
4 + 11
17 — 3
1 + 9
10 + 1
13 + 2
14 — 4
17 — 7
19 — 8
2 + 9
2 + 12
4 + 14
4 + 8
20 — 17
14 + 1
7 — 4
10 — 9
13 — 7
17 + 3
10 — 7
8 — 1
13 + 2
11 + 2
1 + 10
12 + 1
10 + 5
4 + 15
9 — 3
6 + 9
9 + 11
12 — 8
10 — 5
8 — 1
20 — 9
10 + 1
12 — 5
15 + 1
18 — 14
5 + 5
16 — 1
5 — 2
16 — 3
7 + 7
11 — 2
6 + 9
6 — 4
17 + 2
15 + 4
19 — 15
10 — 3
6 + 8
5 — 2
16 + 3
13 — 4
11 + 7
15 — 5
12 — 11
17 — 5
15 — 1
16 — 4
13 — 3
10 — 5
16 — 3
9 + 7
4 + 16
11 + 6
12 — 3
4 + 13
9 — 8
10 + 4
12 — 4
9 + 1
6 — 2
17 + 1
15 — 12
19 — 14
16 — 6
2 + 12
17 + 1
12 — 5
7 + 11
6 + 8
20 — 7
2 + 16
18 — 10
6 + 7
2 + 13
9 — 6
14 + 5
14 + 2
20 — 5
16 — 13
5 + 5
17 — 8
19 — 15
20 — 19
13 — 11
6 + 14
8 + 3
3 + 16
17 — 5
3 + 16
10 + 10
20 — 13
8 + 12
12 + 3
7 + 6
7 + 5
19 — 13
15 — 9
10 — 2
7 + 3
1 + 12
11 — 5
18 — 10
4 + 16
6 — 3
18 — 16
20 — 2
14 + 1
10 + 8
16 — 12
9 — 6
9 + 8
1 + 19
19 — 10
4 + 8
9 + 10
9 + 9
8 — 4
14 + 5
13 — 9
8 — 7
5 + 15
12 — 9
16 — 12
9 — 4
9 + 8
8 + 11
6 + 13
8 + 10
11 — 5
9 — 8
6 + 4
18 — 13
2 + 13
18 — 8
8 + 6
1 + 12
8 — 1
12 + 8
10 — 9
17 — 8
8 + 9
4 + 13
13 — 9
12 + 1
17 — 5
2 + 12
15 + 3
13 — 9
10 — 1
14 — 12
2 + 15
9 + 8
16 + 4
10 + 3
4 + 6
7 — 2
9 — 5
4 + 16
14 — 9
8 + 4
Сложение и вычитание в пределах 10,20.
 ..100 ФГОС
..100 ФГОС110,00 ₽
Примеры на сложение и вычитание в пределах 10,20 и т.д. до 100. Соответствует заданиям ФГОС. Без ответов. Для печати А4.
Артикул: i-1800 Категория: Для учебы Метки: Сложение и вычитание простое, 1 класс, 2 класс, 3 класс
- Описание
- Детали
- Отзывы (0)
Описание
Сложение и вычитание – это примеры, с которых начинается формирование логического мышления ребенка и совершенствование навыков счета. Практика счета таких примеров поможет развить внимательность и закрепить навыки счета дошкольникам, а также и ученикам 1 и 2 класса.
Программа представляет собой тренажер для счета. Программа имеет внутренние настройки, изменяя которые можно создать примеры для детей разного возраста и уровня подготовки. Можно сформировать примеры в пределах 10, 20, 30 и т.д. до 100. Поэтому программа будет полезна для дошкольников от 5-6 лет и для учеников начальной школы 1-2 классов.
Можно сформировать примеры в пределах 10, 20, 30 и т.д. до 100. Поэтому программа будет полезна для дошкольников от 5-6 лет и для учеников начальной школы 1-2 классов.
Особенностью карточек является соответствие пособию для начальной школы «Тренировочные примеры по математике: счет в пределах 100. 2 класс», которое соответствует федеральному государственному образовательному стандарту (второго поколения) для начальной школы. Каждая карточка рассчитана на недельную нагрузку. Систематическое выполнение заданий закрепит учебные умения и навыки в математике, доведёт до автоматизма умение решать примеры.
Программа счета написана в Excel с помощью макросов. Формируются примеры: 7 столбиков по 40 примеров на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Другие программы, которые помогут закрепить навыки счета в пределах 10,20,30 и т.д. до 100:
- Цепочки примеров в пределах 10,20…100 (сложение и вычитание)
- Найти правильные примеры (сложение и вычитание от 10 до 100)
- Числовые пирамиды в пределах 10,20…100
- Математический лабиринт (состав числа до 100)
- Арифметический маршрут 1 (сложение и вычитание в пределах 10-100)
- Математический кроссворд (сложение и вычитание до 100)
- Сравнение чисел в пределах 10,20,100
- Головоломка «Квадрат слагаемых»
- Головоломка «Геометрия чисел» (сложение и вычитание до 100)
- Умная раскраска «Слова-3»
Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.
В них можно начать с решения легких примеров, а затем перейти к более сложным.
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Цепочки примеров в пределах 100 (сложение и вычитание)
50,00 ₽В корзинуЧисловые пирамиды большие (в пределах 50,100 и больше)
100,00 ₽В корзинуГеометрия чисел (сложение и вычитание)
60,00 ₽В корзинуГоловоломка «Математический лабиринт (сложение и вычитание)»
Оценка 5.00 из 5
95,00 ₽В корзинуГоловоломка «Квадрат юного математика»
60,00 ₽В корзинуГоловоломка «Квадрат слагаемых»
Оценка 5.00 из 5
Распродажа! 50,00 ₽ В корзинуЧисловые пирамиды (в пределах 10, 20 … 100)
Оценка 5.
80,00 ₽В корзину 00 из 5
00 из 5Математический кроссворд (сложение и вычитание)
80,00 ₽В корзинуПорядок действий в пределах 100 (все действия)
80,00 ₽В корзину
Примеры на сложение и вычитание до 20
Математика сложение
Свои первые примеры ребенок начинает решать примерно в 5-6 лет. Приходя в школу, он может вычитать и складывать числа в пределах 10. Однако дальше у школьника могут возникнуть сложности, ведь следующие задания подразумевают переход на разряд. Для этого необходимо закрепление такой темы, как состав числа. Ввиду этого родители стали чаще искать специальные тренажеры для закрепления навыков счета.
Генератор примеров нашего сайта может помочь ребенку в совершенстве овладеть техникой решения заданий в пределах 20. Этот этап особенно сложен для учеников первого и второго класса, ведь приходится учиться решать примеры с разными разрядами чисел.
Тренажер удобен тем, что при каждом повторном открытии страницы ребенку будут предложены новые задания на отработку темы. Неограниченное количество заданий позволит выучить состав чисел до 20, что в дальнейшем позволит решать более сложные примеры устно, не разбивая числа для удобного сложения и вычитания.
Ребенок сможет быстро решать примеры, заданные учителем, на уроках и дома. Предлагаем воспользоваться возможностью скачивания заданий, чтобы сократить время на их переписывание. Для более легкой проверки вы можете скачать варианты с ответами.
Тренажер удобен тем, что при каждом повторном открытии страницы ребенку будут предложены новые задания на отработку темы.
O-krohe. ru
13.10.2019 16:10:47
2019-10-13 16:10:47
Источники:
Https://o-krohe. ru/math/slogenie-vychitanie/do-20/
Сложение | Математика | Fandom » /> » /> .keyword { color: red; }
Математика сложение
Где A’ обозначает натуральное число следующее за А.
Абстрактная алгебра
В абстрактной алгебре, Сложением может называться любая бинарная коммутативная и ассоциативная операция. В случае если на этом множестве определено также умножение то сложение предполагается дистрим по отношению к нему.
Свойства сложения
Сложение обладает следующими свойствами:
Запись при помощи буквы Σ
Историческая справка [1]
Знаки сложения и вычитания в их современном виде впервые появляются у Яна Видмана ( J. Widmann, 1460—XVI в.) в книге «Быстрый и красивый счёт для всего купечества» (Лецпциг, 1489). Предполагают, что знак «» width=»» height=»» />» возник из латинского et (и) из-за сходства с «t». Возможно, что знак «—» обозначал у купцов вычёркивание, убыль.
Знаки сложения и вычитания в их современном виде впервые появляются у Яна Видмана ( J. Widmann, 1460—XVI в.) в книге «Быстрый и красивый счёт для всего купечества» (Лецпциг, 1489). Предполагают, что знак «» width=»» height=»» />» возник из латинского et (и) из-за сходства с «t». Возможно, что знак «—» обозначал у купцов вычёркивание, убыль.
Возможно, что знак «—» обозначал у купцов вычёркивание, убыль.
Свойства сложения
Сложение обладает следующими свойствами:
Знаки сложения и вычитания в их современном виде впервые появляются у Яна Видмана ( J. Widmann, 1460—XVI в.) в книге «Быстрый и красивый счёт для всего купечества» (Лецпциг, 1489). Предполагают, что знак «» width=»» height=»» />» возник из латинского et (и) из-за сходства с «t». Возможно, что знак «—» обозначал у купцов вычёркивание, убыль.
В книге Быстрый и красивый счёт для всего купечества Лецпциг, 1489.
Math. fandom. com
21.07.2020 3:08:00
2020-07-21 03:08:00
Источники:
Https://math. fandom. com/ru/wiki/%D0%A1%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5
Математика. Сложение и вычитание. 3 класс — Татьяна Позднева — Google Книги » /> » /> .keyword { color: red; }
Математика сложение
Основные приёмы счёта формируются у ребёнка в первые годы обучения. Именно поэтому очень важно уделить отработке этого навыка особое внимание. В пособии представлены примеры и задания на сложение и вычитание в пределах 100 и в пределах 1000.Даны упражнения разных типов: простое и раздельное сложение и вычитание, комбинированные примеры, на письменное сложение и вычитание в пределах 1000.Примеры и задания книги помогут ребёнку отработать и закрепить до автоматизма навыки счёта, активизируют мыслительную деятельность, разовьют память, внимание и быстроту реакции. Книга подготовлена в соответствии с требованиями ФГОС начального образования. Её можно использовать при работе с любым учебником, входящим в Федеральный перечень. Пособие будет полезно на уроках математики и для самостоятельных занятий дома.
Именно поэтому очень важно уделить отработке этого навыка особое внимание. В пособии представлены примеры и задания на сложение и вычитание в пределах 100 и в пределах 1000.Даны упражнения разных типов: простое и раздельное сложение и вычитание, комбинированные примеры, на письменное сложение и вычитание в пределах 1000.Примеры и задания книги помогут ребёнку отработать и закрепить до автоматизма навыки счёта, активизируют мыслительную деятельность, разовьют память, внимание и быстроту реакции. Книга подготовлена в соответствии с требованиями ФГОС начального образования. Её можно использовать при работе с любым учебником, входящим в Федеральный перечень. Пособие будет полезно на уроках математики и для самостоятельных занятий дома.
Примеры и задания книги помогут ребёнку отработать и закрепить до автоматизма навыки счёта, активизируют мыслительную деятельность, разовьют память, внимание и быстроту реакции.
Books. google. com
28.11.2019 4:33:44
2019-11-28 04:33:44
Источники:
Https://books. google. com/books/about/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0_%D0%A1%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B8.html? id=_D5mDwAAQBAJ
google. com/books/about/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0_%D0%A1%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B8.html? id=_D5mDwAAQBAJ
Примеры на сложение и вычитание в пределах 20тренажёр по математике (1 класс) на тему — Справочник
Примеры по математике 1 класс в пределах 20
В карточке желательно указывать количество ошибок и время, потраченное на решение. Это нужно, чтобы отслеживать в динамике успехи ребенка.
По теме: методические разработки, презентации и конспекты
Урок математики 1 класс по теме «Закрепление изученного. Решение текстовых задач, примеров на сложение и вычитание в пределах 10, сравнение чисел в пределах 10»
Учащиеся учатся решать задачи изученных видов; решать примеры на сложение и вычитание чисел 1,2,3; принимать и сохранять цели и задачи учебной деятельности; находить средства и способы её осуществлени.
По теме методические разработки, презентации и конспекты.
Nsportal. ru
09.06.2019 18:35:53
2019-06-09 18:35:53
Источники:
Https://nsportal. ru/nachalnaya-shkola/matematika/2018/03/12/primery-na-slozhenie-i-vychitanie-v-predelah-20
Примеры в пределах 20, 1 класс | Тренажёр по математике (1 класс): | Образовательная социальная сеть » /> » /> .keyword { color: red; }
Примеры по математике 1 класс в пределах 20
По теме: методические разработки, презентации и конспекты
Урок по математике в 1 классе» Решение задач и примеров в пределах 10″
Урок по математике в 1 классе коррекционной школы I — II вида. Тема: «Решение задач и примеров в пределах 10»Цель: 1) закрепить знание чисел в пределах 10.
Урок математики в 1 классе «Решение задач и примеров в пределах 10»
Тема урока: « Решение задач и примеров в пределах 10».Заключительный урок по теме «Числа от 1 до 10 и число 0. Сложение и вычитание» Цель урока: отработка знаний, полученных при изучении те.
Презентация к уроку математики в 1 классе «Решение задач и примеров в пределах 10»
Тема урока: « Решение задач и примеров в пределах 10».Заключительный урок по теме «Числа от 1 до 10 и число 0. Сложение и вычитание» Цель урока: отработка знаний, полученных при изучении те.
Урок математики во 2 классе (1-4) Тема: «Решение задач и примеров в пределах 100. Закрепление».
Закрепить знания и умения решать и составлять задачи на нахождение числа, которое на несколько единиц больше или меньше данного, составлять и решать примеры;-.
Урок математики во 2 классе. Решение примеров в пределах 20 без перехода через десяток
Конспект урока математики для учащихся коррекционной школы.
Открытый урок по математике в 4 классе «Решение примеров в пределах 100»
Урок — экскурсия в город Простоквашино, встреча с его героями, которые задают ребятам различные математические задания.
1.3000 примеров по математике. 1 класс.
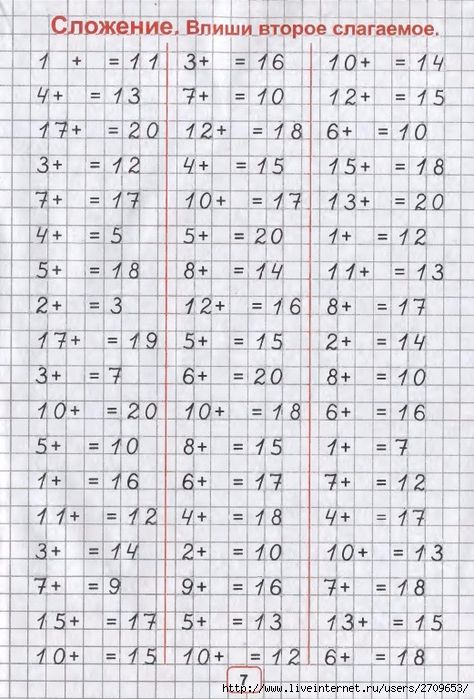 Устный счёт. Счёт в пределах 20. Узорова О. В.
Устный счёт. Счёт в пределах 20. Узорова О. В.В этом пособии представлен материал, направленный на формирование навыков устного счёта по теме «Счёт в пределах 20» для 1 класса. Устный счёт развивает сообразительность и внимание учащих.
Урок по математике в 1 классе» Решение задач и примеров в пределах 10″
Урок по математике в 1 классе коррекционной школы I — II вида. Тема: «Решение задач и примеров в пределах 10»Цель: 1) закрепить знание чисел в пределах 10.
Урок математики в 1 классе «Решение задач и примеров в пределах 10»
Тема урока: « Решение задач и примеров в пределах 10».Заключительный урок по теме «Числа от 1 до 10 и число 0. Сложение и вычитание» Цель урока: отработка знаний, полученных при изучении те.
Презентация к уроку математики в 1 классе «Решение задач и примеров в пределах 10»
Тема урока: « Решение задач и примеров в пределах 10».Заключительный урок по теме «Числа от 1 до 10 и число 0. Сложение и вычитание» Цель урока: отработка знаний, полученных при изучении те.
Урок математики во 2 классе (1-4) Тема: «Решение задач и примеров в пределах 100. Закрепление».
Закрепить знания и умения решать и составлять задачи на нахождение числа, которое на несколько единиц больше или меньше данного, составлять и решать примеры;-.
Урок математики во 2 классе. Решение примеров в пределах 20 без перехода через десяток
Конспект урока математики для учащихся коррекционной школы.
Открытый урок по математике в 4 классе «Решение примеров в пределах 100»
Урок — экскурсия в город Простоквашино, встреча с его героями, которые задают ребятам различные математические задания.
1.3000 примеров по математике. 1 класс. Устный счёт. Счёт в пределах 20. Узорова О. В.
В этом пособии представлен материал, направленный на формирование навыков устного счёта по теме «Счёт в пределах 20» для 1 класса. Устный счёт развивает сообразительность и внимание учащих.
В этом пособии представлен материал, направленный на формирование навыков устного счёта по теме Счёт в пределах 20 для 1 класса.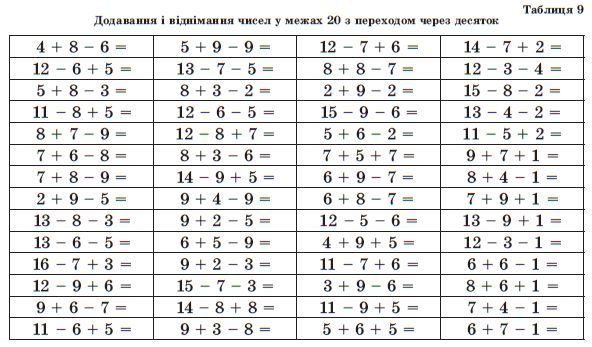
Nsportal. ru
23.12.2020 16:30:18
2020-12-23 16:30:18
Источники:
Https://nsportal. ru/nachalnaya-shkola/matematika/2021/01/12/primery-v-predelah-20-1-klass
Примеры по математике для 1 класса (скачать и распечатать) » /> » /> .keyword { color: red; }
Примеры по математике 1 класс в пределах 20
Обучение математике проходит намного легче, если тренировать навыки каждый день. Генератор примеров предлагает задания Для учеников 1 класса: тренажер позволяет усовершенствовать навыки сложения и вычитания до 20. Арифметические действия с целыми числами должен освоить каждый ученик. Именно эти знания являются базовыми для дальнейшего изучения математики.
Первоклассникам не желательно много времени проводить за компьютером, поэтому все задания можно скачать и распечатать. Очень удобно, что Генератор показывает разные примеры при каждом запуске страницы. Так родители получают доступ к неограниченному количеству заданий. Дополнительно можно распечатать лист с ответами, чтобы тратить меньше времени на проверку.
Дополнительно можно распечатать лист с ответами, чтобы тратить меньше времени на проверку.
После освоения простых арифметических действий можно переходить к более сложным. Преподаватели рекомендуют на следующем этапе осваивать умножение и деление. Тренажер разработан таким образом, что ученики 1 класса могут справиться самостоятельно со всеми примерами. Не стоит слишком сильно нагружать ребенка, максимальное количество – 1 лист в день.
Генератор примеров предлагает задания для учеников 1 класса тренажер позволяет усовершенствовать навыки сложения и вычитания до 20.
O-krohe. ru
20.10.2017 3:27:31
2017-10-20 03:27:31
Источники:
Https://o-krohe. ru/math/1-klass/
Сложение и вычитание – Элементарная математика
Сложение и вычитание целых чисел можно развивать вместе , систематически, начиная с распознавания величин и комбинаций величин, 10-основной структуры языка и символов, представляющих целые числа, удобно методы мысленных вычислений, использующие 10-основную структуру, и, наконец, формальные алгоритмы сложения и вычитания.
Цель этого поста — помочь показать часть траектории по классам.
Распознавание количества пальцев
Пальцы — прекрасный материал для манипулирования. Они прикольные и всегда под рукой! Но помните, настоящая цель любого манипулятивного материала не в том, чтобы получить ответы; это создание в уме идей и образов, позволяющих ребенку получить эти ответы без манипулятивного материала .
Скопируй меня (для самых маленьких)
Двумя руками покажи некоторое количество пальцев. Попросите детей сделать такое же изображение своими руками. Вы также можете расширить это, когда дети находят первую игру слишком легкой, чтобы «показать то же количество пальцев, но по-другому! Дети будут весьма творчески подходить к составлению правильных комбинаций.
Назовите это число (для самых маленьких детей)
Назовите число от нуля до 10. Попросите детей показать это число пальцами. Например, если вы скажете «три», они могут показать
или
или любую другую комбинацию двух рук, которая показывает три пальца.
Детям детского сада может буквально понадобиться поддержка, чтобы держать свои ручки поднятыми и видимыми для других детей!
Сколько пальцев? (первый класс)
Двумя руками показать некоторое количество пальцев. Спросите детей, сколько они видят.
Сколько пальцев
не ты видишь? (первый и второй класс)Двумя руками покажите некоторое количество пальцев, показав тыльную сторону ладони вот так.
Спросите детей, сколько они видят. Затем спросите, сколько они не видят (те, что в сложенном виде).
Из класса
Ага! Момент: Мы работали над десятью кадрами по математике и пытались найти все комбинации до десяти. Это утомительный процесс, и мы играем в игру с первого дня в школе, которую предложил координатор элементарной математики Рассел Ларсон. Я поднимал пальцы и говорил: «Сколько ты видишь?» Я только недавно начал спрашивать: «Сколько ты не видишь?» Наконец-то я смог увидеть, как он щелкает! Они, наконец, понимают, что я имею в виду, когда говорю «6 и 4 — друзья!» Терпение и настойчивость решают все! — Учитель, PISD, Техас
«Подсчет» того, чего вы не видите
Большая часть элементарной арифметики представляет собой систему ярлыков для определения «Сколько» или «Сколько» без подсчета или измерения.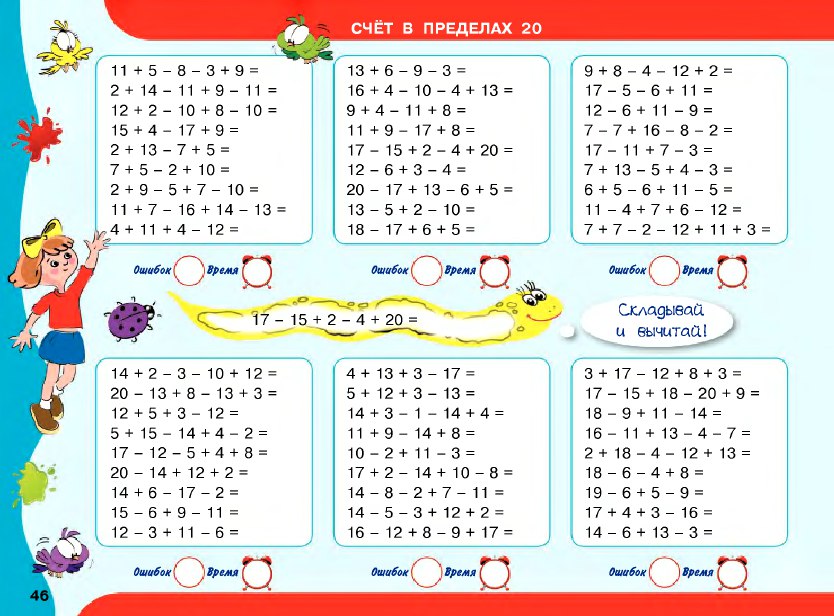
Когда все присутствуют, у нас в классе 25 человек, а сегодня только 22. Сколько отсутствует?
Мы не можем сосчитать отсутствующих людей, потому что мы их не видим. Учащиеся могут нарисовать картинку так, чтобы они могли ее увидеть, и использовать ее, чтобы понять проблему. Но мы также хотим, чтобы студенты научились решать проблему, не видя пропавших без вести.
В моем первом классе 23 ребенка, а в другом первом классе 24 ребенка. Сколько в обоих?
Опять же, если бы все дети стояли перед нами или если бы мы нарисовали изображение, мы могли бы их сосчитать. Но суть арифметики в том, что мы можем узнать, сколько их, не считая.
Создание мысленных картинок
Одна из частей помощи детям в подсчете того, чего они на самом деле не видят, заключается в том, чтобы помочь им «видеть» внутри своей головы: изображать предметы и расширять мысленное «пространство», в котором они могут работать.
Сколько окон в вашей комнате/квартире/доме?
Если вы попытаетесь решить эту задачу, вы, вероятно, прогуляетесь в уме и посчитаете! Есть много игр, которые помогают маленьким детям развивать свои способности создавать мысленные образы.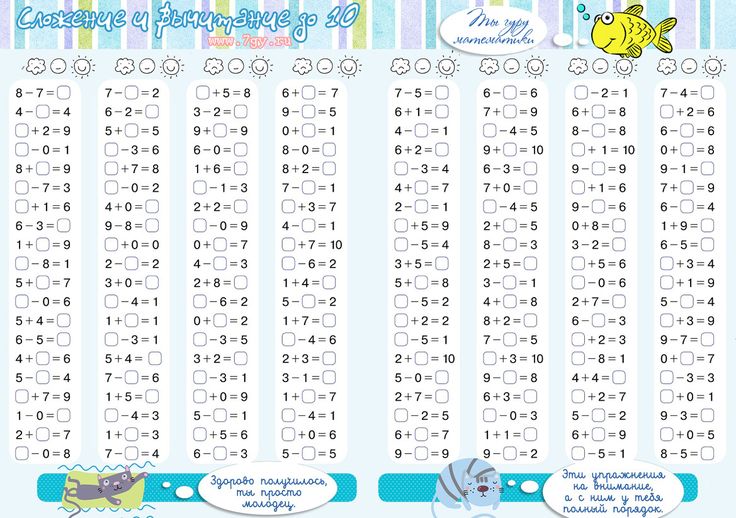 Вот три.
Вот три.
Что я увидел?
Подержите картинку в течение 15 секунд (или другого подходящего времени, достаточно долго, чтобы все увидели, и не так долго, чтобы вашим ученикам стало скучно). Это может быть большая фотография какой-то части комнаты или школы, или ребенка в классе, или это может быть известное произведение искусства.
Переверните картинку лицевой стороной вниз и попросите участников представить себе картинку и вспомнить как можно больше деталей.
Покажите, сколько
Поднимите две руки вверх, не показывая пальцев вообще, затем покажите количество пальцев (например, 7) примерно на одну секунду — достаточно долго, чтобы увидеть, но недостаточно долго, чтобы сосчитать, затем вернитесь к закрытому кулаки.
, затем
Затем попросите детей показать руками, сколько пальцев у вас было поднято. (7 в этом примере)
Считайте в уме — два способа игры
Пальцы
- Начните, как в «Покажи сколько», показывая определенное количество пальцев, достаточное для того, чтобы видеть, но не считать.

- Затем спросите: «Сколько пальцев вы видели?»
Картинки
Создавайте изображения в виде массивов — вы можете нарисовать их или использовать цветные наклейки — с небольшим количеством объектов (до четырех или пяти) в каждом из трех рядов.
- Кратко показать картинку, достаточно долго, чтобы увидеть, но не сосчитать.
- Спросите: «Сколько точек (квадратов, звездочек, наклеек…) вы видели?»
или или или
Игра для детей младшего возраста
Отлично подходит для детского сада. Первоклассникам тоже нравится!
Соберите детей на полу, чтобы они могли видеть и быть рядом. В центре разложите два десятицентовика и пять пенни в ряд, вот так, чтобы все могли видеть.
- Сколько копеек? (Некоторые дети не будут знать, какие это монеты, или даже то, что они не все монеты, поэтому вы можете уточнить: «Эти медного цвета».)
- Сколько десятицентовиков? (Опять же, вам может понадобиться уточнить, какие десятицентовики.
 )
) - Ой! Я забыл! Сколько копеек?
Это все для того, чтобы у детей была возможность наблюдать и считать, и еще раз наблюдать, прежде чем вы накроете несколько монет.
Теперь внезапно игриво лягте рукой на пол, закрывая две или три монеты с обоих концов.
- Кто-нибудь может сказать, сколько монет я спрятал?! ( Монеты могут быть для некоторых новым словом. Вы можете спросить: «Сколько копеек спрятано?» и «сколько спрятано центов ?»)
Пусть видят, проверяют. Затем сделайте это снова, возможно, на другом конце.
- Сколько монет сейчас спрятано?
Игриво меняйте то, что вы прикрываете, иногда закрывая один конец, иногда другой, иногда середину, иногда вообще ничего. Также игриво меняйте свой вопрос, иногда спрашивая о монетах, иногда только о десятицентовиках, или просто о копейках, а иногда даже о червях. (Никогда не покрывайте червей!)
Меняя вопрос и добавляя время от времени глупые вопросы (червяки!) побуждает детей не только смотреть, но и слушать.
Все о 10
Подумай о математике! закладывает прочную основу для сложения и вычитания, систематически помогая учащимся овладеть беглостью и автоматизмом с помощью
- складывать и разбивать 10 — зная «на холодную» пары счетных чисел, которые составляют десять: 1, 9; 2, 8; 3, 7; 4,6; и 5, 5
- сложение и вычитание 10, начиная с любого числа
- и использовать 10 в качестве приближения для ближайших чисел (от 8 до 12), чтобы они также могли складывать или вычитать эти числа.
Свободное владение этими навыками способствует умственным вычислениям, а также помогает учащимся приобретать другие факты и навыки сложения/вычитания.
Создание 10
Изучение 10 фактов «холодно», а затем их использование и расширение.
Сколько пальцев ты не видишь?
- Показывая тыльную сторону ладони, покажите на пальцах какое-нибудь число, например:
- Отобразить другой номер, как только учащиеся ответят.

Некоторые тонкости:
- Пока ученики еще «новички» в этой игре, когда вы показываете числа больше 5, всегда показывайте одну полную руку и остатки на другой руке.
Другими словами, а не - Начинающим часто легче понять, что два пальца невидимы, когда вы показываете 8, чем понять, что восемь пальцев невидимы, когда вы показываете 2. Время от времени чередуйте их один за другим, чтобы помочь им понять, что 2 и 8 являются парой, и то, что они видят одного из них, означает, что они не видят другого. Аналогично с 3 и 7, а также с 4 и 6.
- Несмотря на то, что вы иногда повторяете пары, чередуя отображаемые числа (как было только что описано), используйте достаточно разнообразия, чтобы игра была увлекательной.
Сколько точек ты не видишь?
- Подготовьте карточку 4×6 с двумя рядами по пять больших точек. Для этого хорошо подходят кодовые точки большого размера. Используйте один цвет, чтобы минимизировать отвлечение внимания (по крайней мере, при первом использовании).

- Закройте эту карточку разными способами, чтобы быстро ответить на вопрос «Сколько вы не видите?»
. . . . . . . . .
Пары до десяти: «Сколько ты не видишь?» игра с использованием только слов
- Ты отлично владеешь пальцами! У тебя отлично получается с точками! Можно ли это сделать только словами?!
- Назовите любое число от 0 до 10. Учащиеся отвечают «парой», которая составляет 10.
Например, если вы говорите 7, они говорят 3; если вы говорите 0, они говорят 10.
- Держите темп так живо, как может ваш класс.
Дополнительные баллы:
- Если вы делаете карточки с именами учеников, напечатанными достаточно крупным шрифтом, чтобы ученики могли их видеть, вы можете выбрать ученика, просто перевернув карточку. Таким образом, они смотрят, когда наступает их очередь, и слушают, чтобы услышать номер, который вы называете. Говорите только число, никаких других слов.
- Время от времени возвращайтесь к ученику, у которого уже была очередь, чтобы ученики оставались начеку.

Расширение «Пары до 10»
Вот несколько расширений для учащихся, которые стали быстрыми в «Парах до десяти»: Каждое из этих расширений использует навык, который уже развит у детей, а также помогает развить этот навык. тем более автоматический.
Сколько монет вы видите?
Это одно из первых расширений той же идеи.
Те же самые изображения, которые использовались для обучения пар 10, могут быть переработаны для работы с более высокими числами. Представьте, что пальцы или точки — это «пятаки».
- Сколько монет вы видите? Сколько копеек ты не видишь? Пока это точно такая же практика, как и раньше (и такая же, как если бы вы представляли пальцы или точки как яблоки, потому что вы просто считаете десятицентовики, не думая о том, сколько они стоят).
- Затем для детей, умеющих считать до 10, вы помогаете им узнать, сколько стоят три или четыре десятицентовика.
- Покажите три или четыре пальца, спросите «сколько десятицентовиков», как и раньше.

- «Кто-нибудь может сказать, сколько это денег?» Иногда дети — даже те, кто умеет считать, — не понимают, что был задан другой вопрос, поэтому вам, возможно, придется считать на пальцах «десять центов, двадцать центов, тридцать центов…», чтобы пояснить, что вы имеете в виду.
- Показать другое количество пальцев (например, 7). Сначала спросите: «Сколько десятицентовиков?» Дети, только что увидев (в предыдущем примере), что вы спрашиваете о деньгах, могут вместо «7» ответить «70». Если да, подтвердите, на какой вопрос они ответили правильно, и что это говорит вам о том, что они также знают ответ на вопрос, который вы задали, а именно «сколько десяти центов», а не «сколько денег».
- Нерегулярно переключайтесь между «сколько десятицентовиков» и «сколько денег», чтобы дети научились замечать, что это два разных вопроса, и что им нужно обращать внимание на то, какой из них вы задали.
- Покажите три или четыре пальца, спросите «сколько десятицентовиков», как и раньше.
- Когда они будут уверены в этом, добавьте еще два вопроса: «Сколько десятицентовиков вы не видите?» и «сколько денег вы не видите?»
Разнообразие вопросов также оживляет игру. Детям становится так же комфортно с 60 + 40, как и с 6 + 4, но они должны внимательно следить за тем, какой из четырех вопросов был задан. Тот факт, что это сложно, может стать хорошим поводом для смеха как у детей, так и у взрослых.
Детям становится так же комфортно с 60 + 40, как и с 6 + 4, но они должны внимательно следить за тем, какой из четырех вопросов был задан. Тот факт, что это сложно, может стать хорошим поводом для смеха как у детей, так и у взрослых.
- Наконец, отбросьте визуальные подсказки. Объявите, что всего десять десятицентовиков, и вы скажете, сколько десятицентовиков они видят или сколько денег они видят, и они скажут вам, чего не хватает.
Параллель между этими сотнями фактов и десятками фактов также создает (без каких-либо объяснений) сильное ощущение упорядоченности того, как мы пишем и называем числа.
Наряду с расширением навыков детей для работы с большими числами, это дополнительно отрабатывает тот же набор основных пар, делая их еще более автоматическими. Важно включить «десять центов» и «ноль центов» вместе с «100 центами» и «ноль центов» и, в какой-то момент, уточнить, когда они соединяют 40 с 60, они составляют пары, которые в сумме дают 100. Дети быстро учатся складывать числа, кратные 10, что дает 100.
Заработаем тысячу!
Для многих детей на этом этапе совсем не сложно сделать следующий шаг до 1000 (например, 300 + 700), и все же они чувствуют себя гордыми и умными, работая с такими большими числами! Используя те же изображения, вы можете спросить: «Сколько сотен вы видите?» — Сколько сотен ты не видишь? Игра та же, но теперь говорят, что «три сотни» плюс «семь сотен» составляют тысячу (или, с тем же успехом, говорят, «десять сотен». число «триста», но вам, вероятно, не нужно будет даже говорить это. По мере того, как дети становятся экспертами в этом, они также создают основу для того, чтобы быть способными решать гораздо более сложные задачи в уме.
Расширение «Пары-десять» до пар до 20 или 30
Другой способ расширения состоит в том, чтобы составить пары до 20. Учащиеся по-прежнему используют знакомые пары: 2 с 8; 6 с 4 и так далее, но они также должны следить за тем, нужны ли им еще 10. Это помогает, если учащиеся уже умеют прибавлять 10 к любому числу (см. ниже).
ниже).
- Часто полезно и весело начинать с конкретного изображения двух наборов рук — двадцать пальцев — и несколько опущенных пальцев.
- Пригласите двоих детей на демонстрацию. Объясните классу, что вы будете шептать двум демонстрантам, сколько пальцев опустить, и задавать классу обычные вопросы: сколько пальцев видно или сколько пальцев спрятано.
- Какое бы число вы не хотели, чтобы два ребенка «спрятали», убедитесь, что пальцы одного ребенка либо все открыты, либо все спрятаны, чтобы класс никогда не пытался складывать числа, отличные от 10, и числа меньше 10. (Например, если вы хотите, чтобы 14 пальцев были опущены, пусть два демонстранта спрячут 10 и 4, а не 7 и 7 или какую-либо другую комбинацию.)
- Варьируйте свои вопросы, убедившись, что вы спрашиваете как о том, сколько пальцев видит класс, так и о том, сколько он не видит, и что вы задаете оба типа вопросов, когда дети прячут число меньше 10, а также когда они прячут число больше 10.
- Затем играйте без пальцев, просто называя число от 0 до 20.

- Вы можете предложить одному учащемуся выбрать число от 0 до 20. Затем выберите другого учащегося, который даст свою пару. Это позволяет дифференцировать обучение, в то время как все дети участвуют в одной и той же деятельности.
- Когда дети действительно хорошо справятся с этим, попробуйте ту же идею с парами, чтобы сделать 30. Скорее всего, вам не придется повторять демонстрацию пальцев. Детям может понравиться возможность более позднего расширения до 40 или 50.
Расширение «Пары до десяти» для использования половинок
- Начните с целых чисел, как обычно: 8, 2; 3, 7; 7, 3; 6, 4; и так далее.
- После того, как класс спокойно сделает знакомое дело, после 6 (на что они отвечают 4) 6 с половиной. Студенты, скорее всего, поначалу неправильно ответят «четыре с половиной», но они также могут поймать свою ошибку, если дать ей время подумать, и ответить «нет! три с половиной!»
Второклассники к концу года, вероятно, смогут научиться делать это хорошо.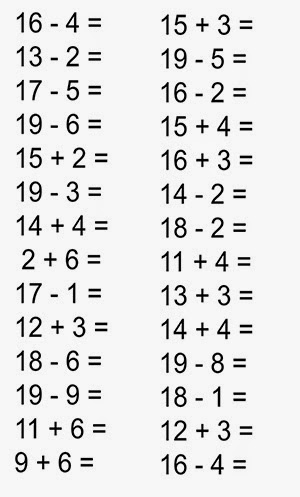 Несмотря на то, что эта игра имеет дело только с маленькими числами (10 и меньше) и использует дроби, она является отличной подготовкой к умственному сложению и вычитанию двузначных чисел и в целом легче для детей, чем соответствующее задание с двумя цифрами (после того, как они услышат 60 и ответив 40, получится 100, услышав 65 и ответив 35).
Несмотря на то, что эта игра имеет дело только с маленькими числами (10 и меньше) и использует дроби, она является отличной подготовкой к умственному сложению и вычитанию двузначных чисел и в целом легче для детей, чем соответствующее задание с двумя цифрами (после того, как они услышат 60 и ответив 40, получится 100, услышав 65 и ответив 35).
Сложение и вычитание 10
Этот раздел пересматривается с добавлением нового содержания. Оригинальное содержание этого раздела см. в разделе «Язык и математика».
Английский, как и большинство других языков, называет числа таким образом, чтобы было легко (в большинстве случаев) прибавлять или вычитать десять «в рифму». ” узор после этого просто рифмуется: двадцать два, тридцать два, сорок два, пятьдесят два… В общем, в английском языке до 20 все немного беспорядочно, но потом красиво убирается. Использование этого факта для детей — не «уловка»: в конце концов, присвоение имени было осознанным выбором!
Игра «Цепочка 10»
- Один человек называет число от 1 до 100 (например, 43), а другой называет следующие (или предыдущие) числа, считая до 10, пока они не превысят 140 или опустятся ниже нуля (например, 43).
 , 53, 63, 73, 83, 93, 103, 113, 123, 133 или, если игра идет назад, 33, 23, 13, 3).
, 53, 63, 73, 83, 93, 103, 113, 123, 133 или, если игра идет назад, 33, 23, 13, 3).
↑ Некоторые языки, такие как японский и венгерский, более регулярны; некоторые, такие как французский и датский, менее регулярны.
Приблизительно 10
В разработке: использование пар, составляющих 10, для облегчения вычислений с числами 8, 9, 11, 12, 80, 90 и т. д.
Пальцы и факты от 11 до 20 или «Остатки», задание для второго класса
Позовите двух детей и попросите одного поднять 6 пальцев, а другого — 8. Вот как это может выглядеть, если они покажут классу тыльные стороны ладоней.
. . . .
Затем вы игриво набрасываетесь на две пятерки, собираете их у себя и спрашиваете класс в быстрой последовательности.
- Сколько у меня есть? (10)
- Сколько осталось? (4)
- Сколько всего? (14)
Повторите с другими парами детей, используя каждый раз разные пары чисел от 5 до 10.
Детям это нравится, и все они захотят попробовать. Те, кто демонстрирует, чувствуют себя почти обнятыми, когда вы набрасываетесь на две пятерки и слегка сближаете их. Весь класс учится видеть «остатки» — превышение над 5 — как полезный способ смотреть на числа от 6 до 9..
Те, кто демонстрирует, чувствуют себя почти обнятыми, когда вы набрасываетесь на две пятерки и слегка сближаете их. Весь класс учится видеть «остатки» — превышение над 5 — как полезный способ смотреть на числа от 6 до 9..
Требуется большое количество важных арифметических знаний и практики. Только для того, чтобы поднять восемь пальцев, ребенок должен либо сосчитать, либо знать какой-нибудь факт, который помогает (5 + 3, 4 + 4 или, может быть, даже 10 — 8). Чтобы понять набросок учителя, ребенок практикует идею о том, что две пригоршни составляют 10. Ребенок должен уметь считать или складывать остатки (1 + 3) и должен знать, к чему приводит прибавление 10 (две пригоршни). на другое число меньше 10 (остатки).
Что делать, если ребенок использует комбинацию, в которой нет 5? Например, что, если вы попросите 6 и 8, а получите 9?0023 . . . .
Вы все еще можете играть. Вы можете, например, взять 3 и 4 и спросить
- Сколько у меня есть? (7)
- Сколько осталось? (7)
- Хммм.
 .. Итак, 7 и 7 это то же самое, что 6 и 8! (Кстати, сколько будет 7+7?)
.. Итак, 7 и 7 это то же самое, что 6 и 8! (Кстати, сколько будет 7+7?)
Но цель игры состоит в том, чтобы попрактиковаться в том, как сделать 10 и добавить остатки. Так и скажем,
С этого момента мы будем показывать как можно больше пальцев на одной руке, а потом что еще нужно на другой руке.
Сложение двумя руками
Сложение двумя руками с невидимыми пальцами, занятие для второго класса
Позовите одного ребенка. Игриво попросите ребенка показать 8 пальцев на одной руке. Конечно, это невозможно, так что, с недоумением или удивлением, скажем…
- ОК, ну покажи сколько сможешь!
- Отлично!
А теперь, игриво, к классу…
- Отлично! Она выставила восьмизначную сумму! Вы их все видите? Нет?! Ну, сколько ты видишь? (5)
- Верно! Остальные пальцы невидимы ! Сколько невидимых пальцев у Ширы? (3)
- Хорошо, Шира. На другой руке поднимите, пожалуйста, 7 пальцев!
Дети часто так быстро «понимают» глупую игру, но при необходимости снова помогите, сказав: «Покажи как можно больше».
- Итак, класс, Шира подняла 8 пальцев на этой руке и 7 пальцев на другой руке.
- Посмотрим… Сколько невидимых пальцев на этой руке? (3)
- А сколько невидимых пальцев на этой руке? (2)
- Хм… Много невидимых пальцев!
Пока не спрашивая, сколько всего невидимых пальцев, вы «продлеваете» время, в течение которого дети держат это в голове.
- Сколько видимых пальцев у Ширы? (10)
- А сколько невидимых ? (5)
- Так сколько всего вместе? (15)
- Да! Пятнадцать пальцев: восемь здесь и семь там!
Многим детям нравится, когда их меняют, и это дает классу много практики по отслеживанию в уме невидимых пальцев.
3 совета, которые помогут учащимся свободно складывать и вычитать в пределах 20
Научить учащихся свободно складывать и вычитать в пределах 20 может стать большим стандартом для учащихся 2-го класса. После многих лет преподавания я нашел 3 полезных совета, помогающих студентам освоить этот общий базовый стандарт.
Один из способов помочь учащимся свободно складывать и вычитать в пределах 20 — это развлекать их практическими занятиями. В игры очень просто помещать факты сложения и вычитания. Это могут быть простые игры, такие как Math Facts War или Math Facts Bingo.
Вы можете подумать: «У меня не так много времени в школе. Как у меня будет время, чтобы ученики практиковали математические факты в играх?»
И поверьте мне, когда я говорю, что понимаю. Нам нужно многому научить за день, и существует множество стандартов. Но я видел, что, когда я даю своим ученикам качественную математическую практику, это помогает им с более высоким уровнем математики и стандартов. Студенты растут в понимании чисел и не зацикливаются на фактах, когда я преподаю трехзначное сложение и вычитание.
Итак, я нашел несколько способов втиснуть математические игры в свое расписание занятий, которые не отнимают много времени в классе.
Во-первых, у меня есть центр, где учащиеся могут выбрать игру с математическими фактами. Они получают 10 минут или около того качественной математической практики. А так как практика проходит в игровой форме, у студентов появляется высокая мотивация к практике. Чтобы узнать больше об обучении на основе игр с математикой, прочитайте этот пост в блоге здесь.
Они получают 10 минут или около того качественной математической практики. А так как практика проходит в игровой форме, у студентов появляется высокая мотивация к практике. Чтобы узнать больше об обучении на основе игр с математикой, прочитайте этот пост в блоге здесь.
После того, как я представлю новую игру с математическими фактами, я всегда устанавливаю игры как быстрое завершающее занятие. Таким образом, когда учащиеся выполнят задание, они смогут собраться с парой одноклассников и поиграть в игру. У меня есть целая корзина с играми на математические факты, и ученики знают, что они могут выбрать любую из этих игр во время быстрого финиша.
Самое приятное в играх с математическими фактами как в упражнениях на быстрое завершение заключается в том, что они не занимают дополнительное время в классе. Список всех упражнений, которые я использую в своем классе, можно найти в этом блоге: 12 заданий на быстрое завершение, которые так забавны каждый день проводите 10-минутные математические центры. У вас есть 5 различных центров математических фактов, а затем учащиеся выбирают один, чтобы посещать его каждый день. Так что к пятнице они едут на все 5 станций. Вы можете сделать одну станцию математической игрой фактов. В другом есть студенты, изучающие компьютерную программу беглой речи. В другом есть рабочие листы, работающие над карточками задач стратегии математических фактов. В другом учащиеся работают с рабочими листами. И последним будет временная станция тестирования и мониторинга прогресса с вами.
У вас есть 5 различных центров математических фактов, а затем учащиеся выбирают один, чтобы посещать его каждый день. Так что к пятнице они едут на все 5 станций. Вы можете сделать одну станцию математической игрой фактов. В другом есть студенты, изучающие компьютерную программу беглой речи. В другом есть рабочие листы, работающие над карточками задач стратегии математических фактов. В другом учащиеся работают с рабочими листами. И последним будет временная станция тестирования и мониторинга прогресса с вами.
Поскольку учащиеся каждый день получают качественную беглую математическую практику, это поможет им свободно складывать и вычитать в пределах 20.
Студенты нуждаются не только в беглой практике, но и в том, чтобы обучать умственным приемам, чтобы свободно складывать и вычитать в пределах 20. Мне нравится учить новую стратегию каждый день и давать учащимся много практики с этими стратегиями. . Таким образом, когда они позже придут к математическому факту, у них будет целый набор стратегий, из которых они смогут выбирать.
Стратегии математических фактов помогают учащимся решить математические факты, даже если они забыли ответ в данный момент. Так меньше стресса для студентов. Они помогают учащимся развивать чувство числа. После того, как учащиеся много попрактикуются в стратегиях математических фактов, они все быстрее и быстрее используют рассуждения для поиска ответа. Помогая им достичь беглости математических фактов. Чтобы найти список стратегий математических фактов, которые я использую в своем классе, прочитайте этот пост в блоге здесь: Стратегии математических фактов, которые работают
Вот мои лучшие советы по обучению стратегиям математических фактов. После того, как вы обучите стратегию, покажите якорную диаграмму, чтобы сопровождать ее. Таким образом, когда учащийся «застрял» на математическом факте, вы можете направить его к своей стене стратегий математических фактов. Они могут выбрать тот, который они хотят использовать, и найти ответ.
После того, как вы обучите стратегии, дайте студентам много практики. Мне нравится, когда мои ученики занимаются бегом с партнером. Я раскладываю карточки с заданиями по комнате и даю каждому учащемуся собственный лист для записей. Затем они ходят со своим партнером, решая математические факты с помощью этой определенной стратегии. Мне нравится, как это заставляет студентов говорить о своих рассуждениях. Кроме того, они получают необходимую поддержку. Найдите эти карточки с заданиями для использования в классе здесь.
Мне нравится, когда мои ученики занимаются бегом с партнером. Я раскладываю карточки с заданиями по комнате и даю каждому учащемуся собственный лист для записей. Затем они ходят со своим партнером, решая математические факты с помощью этой определенной стратегии. Мне нравится, как это заставляет студентов говорить о своих рассуждениях. Кроме того, они получают необходимую поддержку. Найдите эти карточки с заданиями для использования в классе здесь.
После того, как я обучу всем стратегиям, мне нравится помогать моим ученикам продолжать практиковать их каждый день. Я делаю это с помощью процедуры, которую я называю «Математический факт дня», я помещаю математический факт на доску. Затем я даю студентам время подумать о том, как добраться до ответа.
Я предлагаю им поделиться своими идеями с партнером. Затем я позвал нескольких студентов, чтобы поделиться своими соображениями. Пока они делятся своими умственными стратегиями, я записываю их размышления на доске. Это отличная математическая разминка на весь день. Найдите мой ресурс «Математический факт дня» здесь.
Это отличная математическая разминка на весь день. Найдите мой ресурс «Математический факт дня» здесь.
Свободное сложение и вычитание в пределах 20 рабочих листов
Я не только люблю повторять стратегии математических фактов каждый день во время моей математической разминки, но также люблю бегло складывать и вычитать в пределах 20 рабочих листов в качестве основного занятия или быстро финишер деятельности для возможности практики.
У меня есть тестовые ресурсы с хронометражем, которые учащиеся используют для отсчета времени с помощью песочного таймера. Они могут пройти тесты, отметив их в своих книгах по мониторингу прогресса математических фактов. Это отличный способ для учащихся увидеть свой рост с беглостью математических фактов, а также ставить и достигать цели. Найдите мой тестовый ресурс по времени здесь и мои мониторы прогресса математических фактов здесь.
Мне нравится раскладывать другие листы с фактами по математике, чтобы быстрее их закончить. Это забавные рабочие листы, которые я излагаю каждую неделю. Я храню их в папках на стене, чтобы ученики всегда знали, где их найти. Я также включил папку «сдать». Студенты сдают свои готовые рабочие листы в эту папку, а затем я иду к ним и ставлю им перфокарту, когда они их завершают. Здесь можно найти мои хорошие перфокарты.
Это забавные рабочие листы, которые я излагаю каждую неделю. Я храню их в папках на стене, чтобы ученики всегда знали, где их найти. Я также включил папку «сдать». Студенты сдают свои готовые рабочие листы в эту папку, а затем я иду к ним и ставлю им перфокарту, когда они их завершают. Здесь можно найти мои хорошие перфокарты.
У меня есть три разных вида рабочих листов, которые я составляю каждую неделю: математические загадки, рабочие листы математических фактов I-Spy и рабочие листы математических фактов-стратегий.
Математические загадки
Они очень интересны для учащихся. Они решают все математические факты, а затем используют ключ, чтобы раскрыть забавный факт. На каждой странице есть картинка по теме факта. Так что это действительно интригует студентов, чтобы решить.
Моим ученикам это так нравится, что они часто просят сделать что-нибудь дома.
Найдите математические загадки, которые я использую в своем классе здесь.
I-Spy Math Fact Sheets
Это так весело для студентов! Каждая страница просит их найти определенные факты. Например, факты, которые составляют 10. Затем они просматривают весь клипарт и выделяют уравнения, равные 10.
Когда я хочу, чтобы учащиеся сделали больше, я копирую лист с записью на обороте страницы. Для каждого уравнения, которое они находят на странице, они пишут его на обороте и пишут сумму. Таким образом, они получают еще больше практики!
Студенты любят искать на странице и играть в «Я шпион». Они как бы забывают, что даже практикуют математические факты!
У меня есть эти рабочие листы I Spy Math Fact за весь год. У каждого месяца есть своя тема для клипарта, чтобы всегда держать студентов в напряжении! Так они никогда не надоедают, потому что клипарт меняется. Найдите комплект на год здесь.
Рабочие листы по математическим стратегиям
Я по-прежнему хочу, чтобы мои ученики попрактиковались в использовании стратегий. Поэтому я распечатываю лист стратегии на неделю. Рабочий лист знакомит их со стратегией, чтобы они установили эти ментальные связи. Мои рабочие листы по стратегии математических фактов можно найти здесь.
Поэтому я распечатываю лист стратегии на неделю. Рабочий лист знакомит их со стратегией, чтобы они установили эти ментальные связи. Мои рабочие листы по стратегии математических фактов можно найти здесь.
Свободное сложение и вычитание в пределах 20 может оказаться сложной задачей для учителей и учащихся. Но когда вы предлагаете учащимся увлекательные практические занятия, обучаете их стратегиям и позволяете учащимся практиковаться с забавными рабочими листами, они могут освоить этот общий базовый стандарт. Они могут развить чувство числа. Они могут построить основу для более высокого уровня математики. И они могут укрепить свою уверенность в своих математических способностях.
Ищете пошаговое руководство, как научить учащихся 1-го или 2-го класса владеть математическими фактами? У меня есть один для вас: 7 шагов к беглости математических фактов.
Загрузите бесплатную копию здесь.
Уравнения сложения и вычитания до 20
Ничего себе! Вы выучили много сложения и вычитания.
Давайте повторим, что вы уже узнали.
Обзор сложения и вычитания
В сложении , мы объединяем слагаемых , чтобы получить сумму .
При вычитании , мы вычитаем вычитаемое из вычитаемого , чтобы получить разница.
👆 Tip for Remembering:
When we ‘ MINU S ‘ , the order is:
MINU END — S UBTRAHEND
The minuend is always до вычитаемое.
Складываем цифры
🤓 Попробуем сложить эти цифры.
14 + 2 = ?
Как вы знаете, мы можем складывать числа разными способами. 🤗
👉 Мы можем использовать форму столбца .
👉 Мы можем добавить с помощью картинок.
👉 Мы также можем добавить, используя числовую строку .
Отличная работа! 👏 Сумма равна 16.
14 + 2 = 16Вычитание чисел
Теперь попробуем вычесть два числа.
17 — 4 = ?
Опять же, мы можем вычитать по-разному. 😎
👉 Мы можем использовать 9Форма столбца 0509.
👉 Мы можем вычесть , используя картинки.
👉 Мы можем вычитать, используя числовую строку .
Отличная работа! 😎 Разница составляет 13.
17 — 4 = 13Все и ее части
называется целым .
👉 Два других числа это части.
Добавление частей дает целое.
12 + 6 = 18
6 + 12 = 18
Subtracting One Part От участка.
18 — 6 = 12
18 — 12 = 6
99 =
6999
69
69
6999 =
69
. 0509 Поиск пропущенных слагаемых, минусов и вычитаемых
0509 Поиск пропущенных слагаемых, минусов и вычитаемых 🤓 Иногда у нас могут возникать подобные проблемы.
12 + ? = 17
15 — ? = 11
? — 3 = 10
Как мы можем найти эти недостающие числа? 🤔
Мы можем найти пропущенных чисел в уравнениях, используя целых и частей! 🤗
👉 Рассмотрим первый пример.
12 + ? = 17
Отсутствующее число — это часть или целое? 🤔
Поскольку мы добавляем , недостающее число составляет часть.
Давайте нарисуем картинку, чтобы найти ответ.
Чего не хватает? Считай звезды! 👆
😎 Правильно! Это 5.
Итак, недостающее сложение равно 5.
12 + 5 = 17
👉 Давайте попробуем следующий пример.
15 — ? = 11
Здесь отсутствует второе число уравнения вычитания.
🤓 Пропавший номер это часть или целое?
Отличная работа! 👍 Недостающее число часть.
Давайте нарисуем картинку и найдем ответ.
Чего не хватает?
Отличная работа! Это 4.
Итак, недостающие вычитаемое равно 4.
15 — 4 = 11
👉 Теперь давайте рассмотрим последнюю задачу.
? — 3 = 10
На этот раз отсутствует первое число уравнения вычитания.
Это целиком или часть? 🤔
Очень хорошо! 😃 Это целиком, или уменьшённое.
уменьшаемое — это наибольшее число в уравнении вычитания.
Давайте нарисуем картинку, чтобы найти ответ.
Что такое целое?
Сосчитай все звезды вместе! 🙌
Отличная работа! Это 13. 🤗
SO, Пропавшего Минуэнд — 13.
13 — 3 = 10
Смотреть и учиться
908! 🤗 А теперь приступайте к тренировочным вопросам.
Сложение и вычитание с использованием разрядных значений
- Учебные ресурсы
- 1-й класс
Обучение сложению и вычитанию с использованием разрядных значений — это первый класс, общий базовый математический навык: 1.NBT.4. Ниже мы показываем два видеоролика, демонстрирующих этот стандарт. Затем мы даем разбивку по конкретным шагам в видеороликах, которые помогут вам провести урок.
Предварительное обучение
Ваши учащиеся должны уметь считать от 1 до 100, используя единицы и десятки, начиная с любого числа. Они также должны уметь читать, писать и представлять объекты, используя числа от 0 до 20 (K.CC.1-3).
Future Learnings
Позже, понимание значений разрядов позволит вашим учащимся пропустить счет в пределах 1000 (считая до 5, 10 и 100). Они также смогут читать и записывать числа, используя «цифры с основанием десять, имена чисел и расширенную форму» (2. NBT.1-3).
NBT.1-3).
Общий базовый стандарт: 1.NBT.4 — Сложение в пределах 100 однозначных и двузначных чисел, кратных 10; использовать конкретные модели, чертежи и стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием
Учащиеся, понимающие этот принцип, могут:
- Использовать физические модели, рисунки и т. д., чтобы объяснить сложение в пределах 100, добавляя одно- и двузначное число.
- Используйте физические модели, чертежи и т. д., чтобы объяснить сложение в пределах 100, добавляя двузначное число и число, кратное десяти.
- Используйте физические модели, чертежи и т. д., чтобы объяснить сложение в пределах 100 путем сложения двух двузначных чисел.
- Разложите оба слагаемых, используя частичные суммы, чтобы сложить в пределах 100.
- Разбейте одно слагаемое, используя частичные суммы, чтобы сложить в пределах 100.
- Объясните, почему при сложении чисел иногда получается «новая десятка».

2 видео, которые помогут вам преподавать стандарт Common Core: 1.NBT.4
Ниже мы приводим два видео с разбивкой по ним, которые помогут вам обучать своих учеников этому стандарту.
Видео 1: Различные способы сложения больших чисел
В этом видео показаны три различных способа сложения двух больших чисел. Девушка на видео сбита с толку, потому что сначала она не знает, как решить 43 + 21. Затем она вспоминает 3 разных метода, которым она научилась в школе, как решать такие типы задач.
Первый метод использует блоки для решения уравнения.
- Сначала разбейте числа на 10 и 1.
а. На видео показаны числа 43 и 21 в виде блоков, разбитых на группы по 10 и 1. - Сложите две десятки вместе.
а. 40 + 20. - Сложите две единицы вместе.

а. 3 + 1. - Затем объедините их, чтобы получить общее количество: 64.
Следующий пример следует той же схеме, но без вспомогательных блоков.
- 40 + 20 = 60,
- 3 + 1 = 4.
- 60 + 4 = 64.
В последнем примере для решения уравнения используется числовая линия.
- Начните с 43 (большее число) в числовой строке.
- Затем добавьте 20 на 10 секунд.
а. Одну 10, чтобы получить 53, и еще 10, чтобы получить 63. - Тогда остается только еще одно число: 1.
a. 63 + 1 = 64.
Видео заканчивается напоминанием учащимся, что они могут складывать большие числа, разбивая их на десятки и единицы и используя числовую прямую.
Видео 2. Добавление больших чисел в столбцы
NBT.4)»>Видео начинается с краткого обзора разрядных значений и того, что они собой представляют: «Разрядное значение показывает позицию цифры в числе». Например, если в числе 6 десятков и 2 единицы, то это число равно 62.
Затем Боддл объясняет, что для упрощения сложения и вычитания можно использовать разрядные значения. Затем в видео представлено несколько примеров, чтобы учащиеся могли увидеть, как работает эта концепция.
- В уравнении 23 + 5 учащиеся могут выстроить их в столбец.
а. Убедитесь, что значения мест выровнены.
б. 1s над 1s и 10s над 10s. - Начните с добавления цифр в разряде 1.
а. 3 + 5 = 8. - Затем сложите числа в разряде десятков.
а. Так как 2 стоит одна на десятках, приведите ее к сумме.
б. Или подумайте об этом как 2 + 0 = 2. - 23 + 5 = 28.
Затем видео дает другой пример: 35 + 7. Оно демонстрирует, как учащиеся могут решить уравнение сложения, которое переводит новое число в 10-е место.
- Запишите уравнение в столбик.
- Добавьте значения в разряде 1.
а. 5 + 7 = 12. - Затем видео напоминает учащимся, что на одно разрядное значение можно записать только 1 число.
- Пишется только 2 из 12, и это на 1-м месте.
- 1 идет сверху 3, так как они обе на десятках.
- 1 и 3 складываются вместе.
- Ответ равен 42, поэтому 35 + 7 = 42.
Хотите больше практики?
Предложите своим учащимся дополнительную практику в соответствии со стандартами с помощью Boddle Learning. Boddle включает в себя вопросы, связанные со сравнением и измерением длин, а также награждение монетами и играми для ваших учеников, чтобы они были вовлечены. Нажмите здесь, чтобы зарегистрироваться в Boddle Learning и создать свое первое задание сегодня.
*Информация о стандартах взята с веб-сайта New Mexico Instructional Scope for Mathematics Департамента государственного образования штата Нью-Мексико и веб-сайта Common Core.
Онлайн-игры на сложение для первоклассников
Часто задаваемые вопросы:
Q1: Почему так важно обучать дополнительно?
Ответ: Сложение — один из четырех основных арифметических операторов, без которого невозможно представить ни одно вычисление. Будь то нахождение общей стоимости некоторых предметов или просто подсчет различных групп людей, подсчет предметов или денег; дополнение есть везде.
Q2: Что учатся дополнительно первоклассники?
Ответ: Первоклассники учатся складывать два однозначных числа, используя различные стратегии. Они учатся определять и составлять предложения на сложение в форме a + b = c; которые они могут решить в уме, а также считая вперед. Сложение также можно выполнить визуально с помощью числовой строки.
В3. Как добавить два номера?
Ответ: Числа можно добавлять с помощью различных стратегий. Мы можем рассчитывать с первого номера на прибавку. Числа также можно складывать с помощью числовой строки, пальцев, на диаграмме сотен и мысленно. Если вы хотите сложить 4 + 3, начните с 4 и сосчитайте еще 3 как 5,6,7; число, которое вы достигнете, является ответом. Здесь ответ 4 + 3 = 7.
Числа также можно складывать с помощью числовой строки, пальцев, на диаграмме сотен и мысленно. Если вы хотите сложить 4 + 3, начните с 4 и сосчитайте еще 3 как 5,6,7; число, которое вы достигнете, является ответом. Здесь ответ 4 + 3 = 7.
В4. Что такое простое сложение?
Ответ: Простое сложение означает сложение небольших чисел более простым способом. Самый простой способ — рассчитывать на сложение цифр. Если вы хотите сложить два числа, начните с первого числа и посчитайте второе число раз. Достигнутое число и есть ответ.
Обзор темы – Дополнение
Основная цель дошкольного образования – расширить возможности для обучения и развития необходимых навыков. в настоящее время даже на начальном этапе образования образовательная педагогика полностью основана на обучении, основанном на инструкциях или знаниях, что ограничивает область обучения ребенка.
Изучение математики не должно ограничиваться передачей только теоретических и фактических знаний с правильно определенными процедурами и задачами для выполнения; вместо этого, с точки зрения исследования, общей целью учебной программы по математике должно быть развитие математических навыков у детей.
Этот тип техники помогает ребенку установить связь со своим непосредственным окружением, развивая его область знаний, например, арифметические действия; где ребенок применяет соответствующие математические навыки при выборе правильных операций для решения задач, зная, когда выполнять сложение или вычитание.
В первые 2-3 года обучения в школе у ребенка развиваются навыки идентификации и счета чисел до 1000. Умеет упорядочивать числа в числовом ряду. в 1 классе математика фокусируется на расширении навыков подсчета чисел и идентификации объектов до сортировки похожих вещей в разных группах, а затем суммирования их вместе с помощью правильных и подходящих условий реальной жизни.
В играх-головоломках и математических рабочих листах основное внимание уделяется сложению однозначных чисел, сложению двузначных чисел, коммуникативным свойствам сложения, сложению двух цифр с перегруппировкой, связыванию чисел и т. д. Эти забавные игры помогают детям освоить навыки простого сложения без ущерба для во время их игры.
Математическое сложение
Определение сложения: сложение — это «сложение» двух групп объектов и определение их общего количества. Концепцию сложения можно легко разработать на практике с исчисляемыми объектами или блоками с разрядными значениями.
Переместительное свойство сложения:
Что такое переместительное свойство сложения?
Сначала посмотрите на картинку:
Теперь 7, добавленное к 4, будет равно 11, и так будет, когда 4 будет добавлено к 7. Таким образом, изменение порядка слагаемых не меняет сумму. Это называется коммутативным свойством сложения.
Возьмем другой пример.
Здесь необходимо помнить одну важную вещь: вычитание не является коммутативным по своей природе.
Давайте разберемся в этом больше, используя коммутативное свойство дополнительных листов или онлайн-викторин.
Таблица сложения
Таблица сложения представляет собой сетку чисел, которая помогает складывать однозначные числа. Мы можем легко найти результат в таблице.
Мы можем легко найти результат в таблице.
Дети могут использовать эту таблицу сложения и учиться с ее помощью складывать натуральные числа.
Метод числовой строки : сложение целых чисел в пределах 20
Одним из математических средств для решения математических задач является использование числовой строки. Числовая линия представляет собой градуированную прямую линию, на которой через равные промежутки нанесены целые числа или целые числа. Это полезно для сложения и вычитания чисел.
В 1 классе по математике мы ограничимся только сложением целых чисел. как складывать целые числа будут преподавать во 2 и 3 классах.
Каждая точка числового ряда является целым числом. Начальная точка линии 0,
Как складывать числа с помощью числовой строки?
- Составьте числовой ряд от 0 до 20 слева направо.
- Теперь сформулируйте математическую задачу, скажем, сложите числа 5 и 3.
Здесь 5 будет первым числом, а 3 считается вторым числом.
- Найдите первое число вашей задачи на сложение в числовой строке.
Ткните туда пальцем. В этом примере поместите палец на 5.
Отметьте номер или обведите его.
Это точка, с которой нужно начать считать, чтобы добавить 3.
- Переместите палец вправо к следующей решетке и номеру. Вы переместились на 1 место.
- Переместите палец на то же количество пробелов, что и второе число в задаче на сложение, затем остановитесь. Это гарантирует, что вы закончите с ответом на свою проблему.
Не перемещайте больше пробелов, чем второе число в задаче на сложение.
Например, если второе число в вашей математической задаче на сложение равно 3, вы переместитесь на 3 пробела. Наш ответ: 8.
Математика для детей
Математике в первую очередь учат развивать силу мышления и рассуждения. Изучение математики полностью основано на когнитивных процессах, таких как анализ, синтез, индукция, дедукция, исключение возможностей и т. д.
д.
При разработке обучающих игр на дополнении для первоклассников подход Роберта Магера был в центре внимания. По его словам, важно определить цели обучения с точки зрения поведенческих изменений, которые ожидаются у ребенка в конце урока.
Детей часто учат складывать, вычитать, умножать и делить, но они все еще не могут решить, что делать, когда сталкиваются с реальной проблемой. Основные цели этих веселых игр для детей – стимулировать у детей мотивацию к выполнению математических задач, формировать самооценку, вовлекая их в решение простых повседневных математических задач, применимых в реальной жизни. Это также облегчает их переход с одного уровня образования на другой. онлайн-решения математических задач и обучающие игры – отличный способ в игровой форме развить фундамент математических навыков, и они соответствуют основному учебному плану.
Обучение сложению с помощью простых манипуляций
1. Загрузка грузовика в Миссисипи: игра сложения одной цифры
Рональд со своей семьей переезжает в Миссисипи. Им нужно загрузить свой груз в грузовики. Помогите ему в этом.
Им нужно загрузить свой груз в грузовики. Помогите ему в этом.
Рональд упаковал свои вещи в разноцветные коробки. Ящики загружаются в грузовики соответствующего цвета. Подсчитайте количество коробок одного цвета, загруженных в каждый грузовик.
Впишите его значение в соответствующие кружки. Третий грузовик называется солнечный грузовик.
Теперь сложите числа в обоих кругах и напишите сумму в квадрате. Теперь поместите эти коробки в грузовик.
Ключевые особенности этой онлайн-игры для детей:
- Она подходит для детей в возрасте от 3 до 6 лет.
- Это отличное математическое приложение для изучения и отработки концепции сложения, а также координации цветов для детей 1 класса.
- Эта игра на сложение для 1 класса делает изучение сложения интересным и целеустремленным.
- Дети знакомы с решением задач и вычислительными навыками.
- дети подсчитывают правильное количество коробок, загруженных в каждую, и записывают это в соответствующую ячейку.

- Затем они суммируют общее количество ящиков в обоих грузовиках, перетаскивают эти ящики и загружают общий грузовик.
2. Банни хмель
Настало время Пасхи, и все расцветают от радости и празднования. Но наш маленький кролик Бусо недоволен, так как он не выполнил задание по сбору достаточного количества пасхальных яиц для празднования.
Пожалуйста, помогите ему в этом.
Подсчитайте количество яиц в каждой корзине, выбрав правильное число, указанное ниже. Добавьте общее количество яиц в обе корзины и поместите общее количество из списка чисел, приведенного ниже.
Ключевые особенности этой математической образовательной онлайн-игры для детей:
- Она подходит для детей в возрасте от 3 до 6 лет.
- Это отличное математическое приложение для изучения и отработки концепции сложения для детей 1 класса.
- Это простая математическая игра на сложение двузначных чисел.
- в игре кролик показывает путь в сад, полный пасхальных яиц и корзин, где дети изучают и практикуют концепцию сложения.

- дети определяют правильное количество изображений, а затем перетаскивают эти числа в правильные блоки.
3. Коммуникативное свойство аддитивной игры: Перестановка флагов
Сопоставьте пронумерованные флажки из соответствующих квадратов и перетащите их на свое место.
4. Сложение двух цифр с перегруппировкой
Этот математический рабочий лист/математическое задание основан на сложении двух цифр без переноса. Дети суммируют цифры по отдельности и записывают ответы в отведенном для этого месте.
Если ответ правильный, то они получают шанс отвязать шарик с таким же номером.
5. Сложение с числовой строкой: сложение одной цифры
с использованием числовой строки в сложении одной цифры.
6. Прыжок лягушки: переместительное свойство сложения с числовой прямой
Фергюс, лягушка играет со своими друзьями в пруду. Они начинают играть в прыжки.
Переместите лягушку на листья лотоса чисел, когда на экране отобразится задача на добавление слова.
7. Заставить Фергуса прыгнуть на 4 шага + 3 шага
Куда приземлился Фергус? ________
Теперь заставьте Фергуса прыгнуть сначала на 3 шага, а затем на 4 шага.
Куда приземлился Фергус? +__________
Это означает:
8. Игра с числовыми линиями: это простая математическая игра, в которую можно играть с помощью кубиков.
Раздайте детям карточки с нарисованными числовыми линиями.
Теперь бросьте кости и попросите их сложить числа, используя числовую линию.
9. Отсутствующие рабочие листы сложения
10. Отсутствующая игра сложения: ассоциативное свойство дополнения
О SplashLearn и рабочих листах по математике
Эксперт SplashLearn разработает базовые учебные листы для сложения однозначных чисел, сложения с перегруппировкой рабочих листов, сложения без перегруппировки рабочих листов и онлайн-игр для сложения для детей, необходимых для развития необходимых когнитивных навыков. Эти приобретенные навыки помогают ребенку применять изученные концепции к реальным жизненным проблемам и ситуациям.
Эти приобретенные навыки помогают ребенку применять изученные концепции к реальным жизненным проблемам и ситуациям.
Веселые игры на сложение и простые рабочие листы для сложения, разработанные экспертами, соответствуют возрасту и помогают стимулировать любознательность и развивать интерес к математическому образованию.
Лабораторные занятия SplashLearn помогают ребенку изучать математические идеи на практике. Особое внимание уделяется эвристическому подходу к обучению.
Участие себя и своего ребенка в программах SplashLearn поможет вашему ребенку развить математические образовательные навыки и важные жизненные навыки, чтобы эффективно справляться с требованиями и проблемами этого конкурентного мира, развлекаясь.
Сложение и вычитание в пределах 20
Вопросы с краткими ответами
1. Соедините линией каждую комбинацию чисел с ее суммой:
5 + 8 17
4 + 7 14
8 + 9 110005
6 + 8 13
2. Список четырех комбинаций, которые составляют 16:
Список четырех комбинаций, которые составляют 16:2. Список четырех сочеток, которые составляют 16:
2.
3. Начертите набор блоков с основанием десять, равный 9.0509 15
Более 28.
> 28
Для вопросов 4 и 5, написать <, или = в крупной коробке, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать, чтобы сделать. фраза верная.
4.
0005
5.
В вопросах 6, 7 и 8 вставьте пропущенные числа. Используйте блоки, чтобы помочь вам.
6.
7.
8.
9000 те же числа, что и в числовом предложении ниже.
94 − 27 = 67
7
3
5 бейсбольных карточек Тома. Он купил еще 25 штук. Сколько бейсбольных карточек у Тома?
Показать все свои работы.
11. В автомате Сью было 85 жевательных резинок. Она раздала 48 жевательных резинок. Сколько жевательных резинок осталось в автомате Сью
?
Показать все свои работы.
12. Сет съел 12 драже из конфетницы. В банке еще 29 драже. Сколько желейных бобов было в банке с конфетами до того, как Сет начал их есть?
Показать все свои работы.
Ключ к краткому ответу и шкала подсчета очков:
1. Соедините линией каждую комбинацию чисел с ее суммой:
5 0005
2. Перечислите четыре комбинации номера, которые составляют 16:
Ответы будут варьироваться, но будут включать любые 4 из следующих:
0 + 16, 1 +, 2 + 14, 3 + 13, 4 + 12, 5 + 11, 6 + 10, 7 + 9, 8 + 8
чем 28.
В вопросах 4 и 5 напишите <, > или = в большом поле, чтобы предложение было верным.
4.
5.
Для вопросов 6, 7 и 8, заполните пропущенные цифры. Используйте блоки, чтобы помочь вам.
6.
7.
8.
9. Напишите другое числовое предложение, используя те же числа, что и в предложении по числу ниже.
94 — 27 = 67
67 + 27 = 94 или 27 + 67 = 94 или 94 — 67 = 27
10. Том был 37. Он купил еще 25 штук. Сколько бейсбольных карточек у Тома?
Показать всю свою работу.
У Тома 62 бейсбольные карточки.
Работа будет отличаться.
11. В автомате Сью было 85 жевательных резинок. Она раздала 48 жевательных резинок. Сколько жевательных резинок осталось в автомате Сью?
Покажите все свои работы.
37 жевательных резинок все еще в автомате Сью.
Работа будет отличаться.
12. Сет съел 12 мармеладок из банки с конфетами. В банке еще 29 драже. Сколько желейных бобов было в банке с конфетами до того, как Сет начал их есть?
В банке еще 29 драже. Сколько желейных бобов было в банке с конфетами до того, как Сет начал их есть?
Покажите все свои работы.
41 мармелад был в банке до того, как Сет начал их есть.
Работа будет отличаться Очки Описание 2 1 0 У Роуленда 100 пенни. Он сложил их в две отдельные стопки. 2. Он берет 4 монеты из стопки из 50 монет и перекладывает их в другую стопку. Сколько копеек сейчас в каждой стопке? 3. Напишите числовое выражение, чтобы показать количество пенни в каждой стопке. 4. 5. Напишите числовое выражение, чтобы показать количество пенни в каждой стопке. 6. Напишите предложение вычитания, чтобы показать решение для задачи 4. 7. Напишите 5 различных чисел предложения, показывающие различные способы использования дополнения для создания 100. 8. Напишите 5 различных числовых предложений, которые показывают вычитание числа из 100. У Роуленда 100 пенни. Он сложил их в две отдельные стопки. 50 − 4 = 46 и 50 + 4 = 54 или 46 + 54 = 100 или 54 + 46 = 100 73 + 27 = 100 или 27 + 73 = 1000092 100 − 73 = 27 Баллы Описание 4 3 2 
 Роуленд снова складывает все монетки вместе и начинает сначала. Он кладет 73 пенни в одну стопку. Сколько копеек осталось для другой стопки?
Роуленд снова складывает все монетки вместе и начинает сначала. Он кладет 73 пенни в одну стопку. Сколько копеек осталось для другой стопки?
Ответы будут разными. 


 50 примеров на лист. 4 листа.
50 примеров на лист. 4 листа.
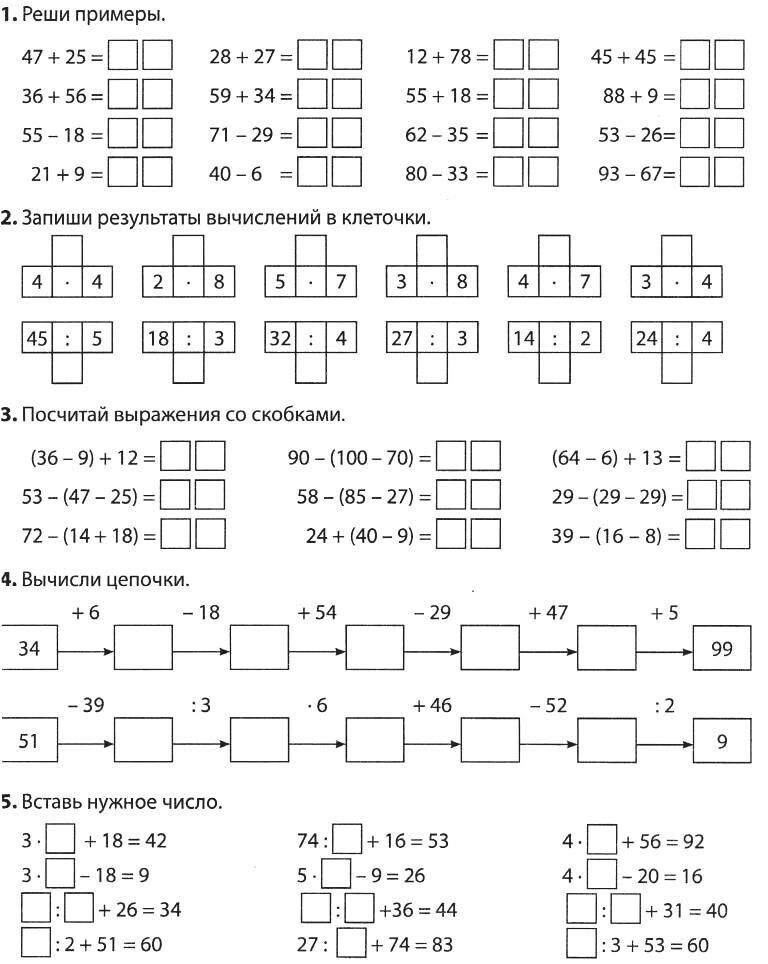


 Три числа составляют семью фактов. Эти числа можно складывать или вычитать разными способами.
Три числа составляют семью фактов. Эти числа можно складывать или вычитать разными способами. Математическое содержание.K.OA.A.5
Математическое содержание.K.OA.A.5 Math.Content.1.NBT.C.4
Math.Content.1.NBT.C.4 Math.Content.2.NBT.B.7
Math.Content.2.NBT.B.7 Math.Content.4.NBT .B.4
Math.Content.4.NBT .B.4 Грамматически это правильно, но большинство людей используют глагол единственного числа.
Грамматически это правильно, но большинство людей используют глагол единственного числа. Вот еще несколько способов говорить о сложении и вычитании:
Вот еще несколько способов говорить о сложении и вычитании:
 00 из 5
00 из 5
 )
)

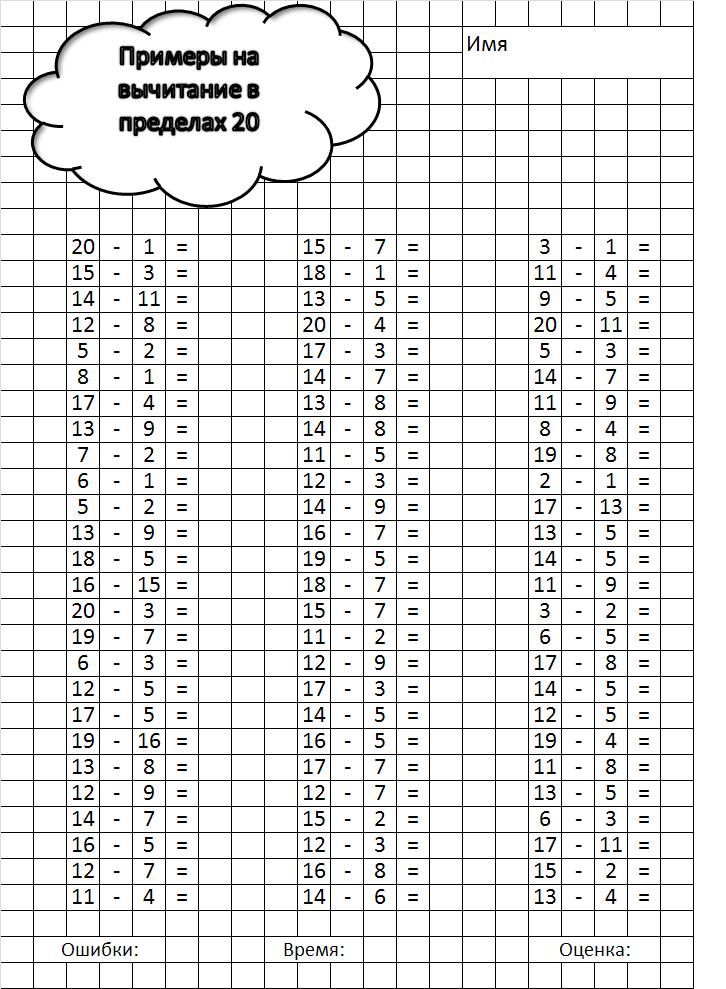


 , 53, 63, 73, 83, 93, 103, 113, 123, 133 или, если игра идет назад, 33, 23, 13, 3).
, 53, 63, 73, 83, 93, 103, 113, 123, 133 или, если игра идет назад, 33, 23, 13, 3). .. Итак, 7 и 7 это то же самое, что 6 и 8! (Кстати, сколько будет 7+7?)
.. Итак, 7 и 7 это то же самое, что 6 и 8! (Кстати, сколько будет 7+7?)