Решить систему уравнений с тремя неизвестными: Решить систему из 3-х уравнений с 3-мя неизвестными онлайн / Калькуляторы

Линейная алгебра и некоторые ее приложения

Линейная алгебра и некоторые ее приложения

Головина Л. И. Линейная алгебра и некоторые ее приложения: Учебное пособие для вузов.—4-е изд., испр,— М.: Наука, Главная редакция физико-математической литературы, 1985. — 392 с. Основное содержание книги составляют теория определителей и краткий курс собственно линейной алгебры. В качестве «приложений» линейной алгебры рассматриваются самые разные вопросы: дается краткое изложение общей теории кривых и поверхностей второго порядка, вводятся основные понятия тензорной алгебры, излагаются основные понятия теории трупп и элементы теории представлений групп. В одной из глав книги методы линейной алгебры применяются к основным понятиям физики — принципам относительности, классическому и релятивистскому. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ § 1. Системы уравнений с двумя и тремя неизвестными § 2. Перестановки и транспозиции. Определитель n-го порядка § 3. Свойства определителей § 4. Миноры и алгебраические дополнения § 5 Разложение определителя по элементам строки или столбца § 6. Системы n линейных уравнений с n неизвестными § 7. Ранг матрицы § 8. Понятие о линейной зависимости § 9. Произвольные системы линейных уравнений § 10. Однородные системы § 11. Метод Гаусса ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО § 2. Поле комплексных чисел § 3. Определение векторного пространства § 4. Размерность и базис § 5. Изоморфизм векторных пространств § 6. Переход к новому базису § 7. Подпространства векторного пространства § 8. Линейные многообразия § 9. Пересечение и сумма лодпространств § 10. Определение аффинного пространства § 11. Введение координат в аффинном пространстве § 12. Переход к новой системе координат § 13. k-мерные плоскости в аффинном пространств § 14. Выпуклые множества в аффинном пространстве ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ § 2. Действия над линейными операторами § 3. Прямоугольные матрицы § 4. Изменение матрицы линейного оператора при переходе к новому базису § 5. Ранг и дефект линейного оператора § 6. Невырожденный линейный оператор § 7. Инвариантные подпространства § 8. Собственные векторы и собственные значения линейного оператора § 9. Спектр линейного оператора § 10. Жорданова нормальная форма ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО § 1. Скалярное произведение § 2. Ортонормированный базис § 3. Ортогональное дополнение § 4. Евклидово (точечно-векторное) пространство ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ § 2. Оператор, сопряженный данному § 3. Самосопряженный оператор § 4. Ортогональный оператор § 5. Унитарный оператор § 6. Произвольный линейный оператор в евклидовом пространстве ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ § 1. Билинейный функционал. Билинейная и квадратичная формы § 2. Приведение квадратичной формы к сумме квадратов § 3. Закон инерции квадратичных форм § 4. Определенные формы § 5. Билинейные и квадратичные формы в евклидовом пространстве § 6. Билинейный функционал в комплексном векторном пространстве ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА § 1. Приведение общего уравнения кривой второго порядка к каноническому виду § 2. Инварианты кривой второго порядка § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы § 4. Исследование общего уравнения поверхности второго порядка ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ § 2. Определение и простейшие свойства тензоров § 3. Операции над тензорами § 4. Тензоры в евклидовом пространстве ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 1. Двумерные пространства со скалярным произведением § 2. Полуевклидова плоскость § 3. Псевдоевклидова плоскость § 4. Псевдоортогональный оператор § 5. Пространство событий. Принцип относительности Галилея § 6. Принцип относительности Эйнштейна § 7. Преобразования Лоренца § 8. Некоторые следствия из формул Лоренца ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП § 1. Примеры групп. Определение группы § 2. Подгруппа § 3. Группы преобразований. Симметрическая группа n-й степени § 4. Изоморфизм групп § 5. Разложение группы по подгруппе § 6. Нормальная подгруппа § 7. Фактор-группа § 8. Прямое произведение групп § 9. Классы сопряженных элементов группы § 10. Классы сопряженных элементов прямого произведения групп § 11 Гомоморфизм групп ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР § 1. Группа движений вещественного евклидова пространства и ее подгруппы § 2. Сопряженные элементы в группе вращений трехмерного пространства § 3. Группа вращений правильного n-угольника Cn § 4. Диэдральные группы Dn § 5. Группа вращений тетраэдра T § 6. Группа вращений куба О § 7. Группа симметрии тетраэдра Td § 8. Группа симметрии куба Oh § 9. Заключение ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП § 2. Изоморфные представления § 3. Подпредставление § 4. Прямая сумма представлений § 5. Унитарное представление. Приводимые и неприводимые представления § 6. Регулярное представление § 7. Функции, определенные на группе § 8. Скалярное произведение на группе § 9. Лемма Шура § 10. Следствия из леммы Шура ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ § 2. Характеры неприводимых представлений § 3. Дальнейшие свойства характеров § 4. Основное соотношение § 5. Число неприводимых представлений группы § 6. Представления коммутативной группы § 7. Представления циклических групп § 8. Представления диэдральных групп § 9. Характеры группы вращений тетраэдра § 10. Характеры группы вращений куба и группы симметрии тетраэдра § 11. Тензорное (кронекеровское) произведение матриц § 12. Тензорное произведение векторных пространств § 13. Тензорное произведение линейных операторов § 14. Тензорное произведение представлений (представления прямого произведения групп) § 15. Характеры группы симметрии куба СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ

5.1.3. Системы уравнений MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1164 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• MathCAD 12

• Нелинейные алгебраические уравнения
• 5.1. Символьное решение уравнений
  • 5.1.1. Вычислительный блок Given / Find
  • 5.1.2. Одно уравнение
  • 5.1.3. Системы уравнений
  • 5.1.4. Решение уравнений при помощи меню
• 5.2. Численное решение уравнений
  • 5.2.1. Системы уравнений: функция Find
  • 5.2.2. Уравнение с одним неизвестным: функция root
  • 5.2.3. Корни полинома: функция polyroots
  • 5. 2.4. Локализация корней
• 5.3. О численных методах
  • 5.3.1. Метод секущих: функция root
  • 5.3.2. Градиентные методы: функция Find
  • 5.3.3. Метод продолжения по параметру

Символьное решение системы алгебраических уравнений отличается от описанного случая одного уравнения только количеством соотношений, задаваемых после ключевого слова Given. Соответственно, число неизвестных также может быть любым, причем необязательно равным числу уравнений. Если система уравнений имеет не обособленные решения, а целые семейства решений, то соответствующие результаты выдаются символьным процессором Mathcad в виде выражений, формально зависящих от одной из переменных как от параметра (пример решения одного уравнения с тремя неизвестными был приведен ранее в последних двух строках листинга 5.3).

Решение системы двух нелинейных уравнений иллюстрирует листинг 5.7. Нахождение символьным процессором его обоих корней визуализируется на графике, приведенном на рис.

5.2. На нем каждое из уравнений показывается в виде зависимости у(х): первое — сплошной кривой, а второе — пунктиром. Поскольку первое уравнение является квадратичным, то оно определяет на плоскости XY параболу, и поскольку второе уравнение линейное, то оно соответствует на графике прямой линии. Очевидно, что две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений, т. е. их координаты равны искомым действительным корням системы.

Рис. 5.2. Графическая интерпретация решения системы двух уравнений (см. листинг 5.7)

Листинг 5.7. Символьное решение системы двух уравнений

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9972 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6989 0

Глава 2 Работа с файлами Mathcad 11

12543 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster. ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2134 s

9.2: Системы линейных уравнений — три переменные

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1384

• OpenStax
• OpenStax

Цели обучения

• Решать системы из трех уравнений с тремя переменными.
• Найдите несовместимые системы уравнений, содержащие три переменные.
• Выразите решение системы зависимых уравнений, содержащей три переменные.

Джон получил наследство в размере \($12,000\), которое он разделил на три части и инвестировал тремя способами: в фонд денежного рынка с выплатой \(3\%\) годовых процентов; в муниципальных облигациях с выплатой \(4\%\) годовых; и во взаимных фондах, выплачивающих \(7\%\) годовых. Джон вложил в муниципальные фонды \($4000\) больше, чем в муниципальные облигации. Он заработал \($670\) в виде процентов за первый год. Сколько Джон инвестировал в каждый тип фонда?

Рисунок \(\PageIndex{1}\): (кредит: «Elembis», Wikimedia Commons)

Понимание правильного подхода к постановке задач, подобных этой, делает поиск решения проблемой следуя шаблону. В этом разделе мы решим эту и подобные задачи с тремя уравнениями и тремя переменными. При этом используются методы, аналогичные тем, которые используются для решения систем двух уравнений с двумя переменными. Однако поиск решений систем из трех уравнений требует большей организованности и некоторой визуальной гимнастики.

Решение систем трех уравнений с тремя переменными

Для решения систем уравнений с тремя переменными, известных как системы «три на три», мы будем использовать основной инструмент, который называется методом исключения Гаусса, названным в честь плодовитого немецкого математика. Карл Фридрих Гаусс. Хотя нет определенного порядка, в котором должны выполняться операции, существуют конкретные рекомендации относительно того, какие типы движений можно выполнять. Мы можем пронумеровать уравнения, чтобы отслеживать шаги, которые мы применяем. Цель состоит в том, чтобы исключить одну переменную за раз, чтобы получить верхнетреугольную форму, идеальную форму для системы три на три, поскольку она позволяет найти решение с помощью прямой обратной подстановки \((x,y,z)\) , которую мы называем упорядоченной тройкой. Система в верхнем треугольном виде выглядит следующим образом:

\[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]

Третье уравнение можно решить относительно \(z\), а затем выполнить обратную подстановку, чтобы найти \(y\) и \(x\). Чтобы записать систему в верхнем треугольном виде, мы можем выполнить следующие операции:

1. Поменять местами любые два уравнения.
2. Умножить обе части уравнения на ненулевую константу.
3. Добавить ненулевое кратное одного уравнения к другому уравнению.

Решение множества для системы три на три представляет собой упорядоченную тройку \({(x,y,z)}\). Графически упорядоченная тройка определяет точку пересечения трех плоскостей в пространстве. Вы можете визуализировать такое пересечение, представив себе любой угол в прямоугольной комнате. Угол определяется тремя плоскостями: двумя примыкающими стенами и полом (или потолком). Любая точка, где встречаются две стены и пол, представляет собой пересечение трех плоскостей.

КОЛИЧЕСТВО ВОЗМОЖНЫХ РЕШЕНИЙ

На рисунке \(\PageIndex{2}\) и рисунке \(\PageIndex{3}\) показаны возможные сценарии решения для систем три на три.

• Системы, имеющие единственное решение, это те, которые после исключения дают множество решений, состоящее из упорядоченной тройки \({(x,y,z)}\). Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве.
• Системы, имеющие бесконечное число решений, — это те, которые после исключения приводят к всегда истинному выражению, например \(0=0\). Графически бесконечное количество решений представляет собой линию или совпадающую плоскость, которая служит пересечением трех плоскостей в пространстве.
• Системы, не имеющие решения, это те, которые после исключения приводят к утверждению, являющемуся противоречием, например \(3=0\). Графически система без решения изображается тремя плоскостями, не имеющими общих точек.

Рисунок \(\PageIndex{2}\): (a) Три плоскости пересекаются в одной точке, представляя систему три на три с единственным решением. (b) Три плоскости пересекаются по прямой, представляя систему три на три с бесконечными решениями.

Рисунок \(\PageIndex{3}\): Все три рисунка представляют системы три на три без решения. а) Три плоскости пересекаются друг с другом, но не в одной точке. (b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. в) Все три плоскости параллельны, поэтому точек пересечения нет.

Пример \(\PageIndex{1}\): определение того, является ли упорядоченная тройка решением системы

Определить, является ли упорядоченная тройка \((3,−2,1)\) решением системы.

\[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]

Решение

Мы проверим каждое уравнение, подставив значения упорядоченной тройки вместо \(x,y\) и \(z\).

\[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1) =2 \номер \\[4pt] \text{True}} & {6x−4y+5z=31 \неномер \\[4pt] 6(3)−4(−2)+5(1)=31 \неномер \\[4pt] 18+8+5=31 \не число \\[4pt] \text{True} } & { 5x+2y+2z = 13 \не число \\[4pt] 5(3)+2(−2 )+2(1)=13 \не число \\[4pt] 15−4+2=13 \не число \\[4pt] \text{True}} \end{массив}\]

Упорядоченная тройка \((3,−2,1)\) действительно является решением системы.

Как: Дана линейная система из трех уравнений, решить для трех неизвестных

1. Выберите любую пару уравнений и решите для одной переменной.
2. Выберите другую пару уравнений и решите для той же переменной.
3. Вы создали систему двух уравнений с двумя неизвестными. Решите полученную систему два на два.
4. Обратно подставьте известные переменные в любое из исходных уравнений и найдите отсутствующую переменную.

Пример \(\PageIndex{2}\): Решение системы из трех уравнений с тремя переменными методом исключения

Найдите решение следующей системы:

\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \номер \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]

Решение

Всегда будет несколько вариантов, с чего начать, но наиболее очевидным первым шагом здесь является устранение \(x\) с помощью складывая уравнения (1) и (2).

\[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(3) \nonumber \end{align} \nonumber\]

Второй шаг – умножение уравнения (1) на \(−2\) и добавление результата к уравнению (3). Эти два шага устранят переменную \(x\).

\[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ умножить на }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]

В уравнениях (4) и (5) мы создали новую систему два на два. Мы можем найти \(z\), добавив два уравнения.

\[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \номер \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]

Выбирая по одному уравнению из каждой новой системы, получаем верхнетреугольную форму:

\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \номер \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]

Затем мы снова подставляем \(z=2\) в уравнение (4) и находим \(y\).

\[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]

Наконец, мы можем обратно подставить \(z=2\) и \(y=−1\) в уравнение (1). Это даст решение для \(x\).

\[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]

Решением является упорядоченная тройка \((1,−1,2)\). См. рисунок \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\)

Пример \(\PageIndex{3}\): решение реальной задачи с использованием системы трех уравнений с тремя переменными

В проблема, поставленная в начале раздела, Джон вложил свое наследство \($12,000\) в три разных фонда: часть в фонд денежного рынка, выплачивающий \(3\%\) годовых процентов; участие в муниципальных облигациях с выплатой \(4\%\) ежегодно; а остальное в паевые инвестиционные фонды с выплатой \(7\%\) ежегодно. Джон вложил в паевые инвестиционные фонды на 4000 долларов больше, чем в муниципальные облигации. Общая сумма процентов, полученных за один год, составила \($670\). Сколько он инвестировал в каждый тип фонда?

Решение

Чтобы решить эту задачу, мы используем всю предоставленную информацию и составим три уравнения. Во-первых, мы назначаем переменную каждой из трех сумм инвестиций:

\[\begin{align} x &= \text{сумма, инвестированная в фонд денежного рынка} \nonumber \\[4pt] y &= \text{ сумма, вложенная в муниципальные облигации} \nonumber \\[4pt] z &= \text{сумма, вложенная в паевые инвестиционные фонды} \nonumber \end{align} \nonumber\]

Первое уравнение показывает, что сумма трех основных сумм составляет \($12 000\).

\[x+y+z=12,000 \nonnumber\]

Составим второе уравнение на основе информации о том, что Джон вложил \($4,000\) в паевые инвестиционные фонды больше, чем он вложил в муниципальные облигации.

\[z=y+4,000 \nonnumber\]

Третье уравнение показывает, что общая сумма процентов, полученных от каждого фонда, равна \(670$\).

\[0,03x+0,04y+0,07z=670 \нечисло\]

Затем мы записываем три уравнения в виде системы.

\[\begin{align} x+y+z &=12 000 \не число \\[4pt] −y+z &= 4 000 \не число \\[4pt] 0,03x+0,04y+0,07z &= 670 \ не номер \end{align} \nonumber\]

Чтобы упростить вычисления, мы можем умножить третье уравнение на \(100\). Таким образом,

\[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67 000 \; &(3) \nonumber \end{align} \nonumber\]

Шаг 1. Поменяйте местами уравнение (2) и уравнение (3) так, чтобы два уравнения с тремя переменными совпали.

\[\begin{align} x+y+z &= 12 000 \nonumber \\[4pt] 3x+4y+7z &= 67 000 \nonumber \\[4pt] −y+z &= 4 000 \nonumber \end {выравнивание} \ноннумеро\]

Шаг 2. Умножьте уравнение (1) на \(−3\) и добавьте к уравнению (2). Запишите результат в виде строки 2.

\[\begin{align} x+y+z &= 12 000 \nonumber \\[4pt] y+4z &= 31 000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]

Шаг 3. Добавьте уравнение (2) к уравнению (3) и запишите результат как уравнение (3).

\[\begin{align} x+y+z &= 12 000 \nonumber \\[4pt] y+4z &= 31 000 \nonumber \\[4pt] 5z &= 35 000 \nonumber \end{align} \nonumber \]

Шаг 4. Найдите \(z\) в уравнении (3). Подставьте обратно это значение в уравнение (2) и найдите \(y\). Затем подставьте обратно значения для \(z\) и \(y\) в уравнение (1) и решите для \(x\).

\[\begin{align} 5z &= 35,000 \не число \\[4pt] z &= 7,000 \не число \\[4pt] \ не число \\[4pt] y+4(7,000) &= 31,000 \не число \ \[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber \]

Джон вложил \(2000$\) в фонд денежного рынка, \(3000$\) в муниципальные облигации и \(7000$\) в паевые инвестиционные фонды.

Упражнение \(\PageIndex{1}\)

Решите систему уравнений с тремя переменными.

\[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]

Ответ

\((1,−1,1)\)

Выявление несовместных систем уравнений с тремя переменными

Так же, как и с системами уравнений с двумя переменными, мы можем столкнуться с противоречивой системой уравнений с тремя переменными, а это означает, что она не имеет решения, удовлетворяющего всем трем уравнениям. Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном и том же месте. Процесс исключения приведет к ложному утверждению, такому как \(3=7\) или какому-либо другому противоречию.

Пример \(\PageIndex{4}\): Решение противоречивой системы из трех уравнений с тремя переменными

Решите следующую систему.

\[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+ 13z &=8 \label{4.3} \end{align} \nonumber\]

Solution

Глядя на коэффициенты \(x\), мы видим, что мы можем исключить \(x\), добавив Уравнение \ref{4.1} к уравнению \ref{4.2}.

\[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]

Затем мы умножаем уравнение (1) на \(−5\) и добавляем его к уравнению (3).

\[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{умножается на }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \ end{align} \nonumber\]

Затем мы умножаем уравнение (4) на 2 и добавляем его к уравнению (5).

\[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{умножить на }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]

Итоговое уравнение \(0=2\) является противоречием, поэтому делаем вывод, что система уравнений несовместна и, следовательно, не имеет решения.

Анализ

В этой системе каждая плоскость пересекает две другие, но не в одном и том же месте. Следовательно, система несовместима.

Упражнение \(\PageIndex{2}\)

Решите систему трех уравнений с тремя переменными.

\[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{ выровнять} \номер\]

Ответить

Нет решения.

Выражение решения системы зависимых уравнений с тремя переменными

Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений. То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может быть результатом нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на прямой, имеющей бесконечные решения. Или два уравнения могут быть одинаковыми и пересекать третье по прямой.

Пример \(\PageIndex{5}\): Поиск решения зависимой системы уравнений

Найдите решение заданной системы трех уравнений с тремя переменными.

\[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y +z &= 0 &(3) \nonumber \end{align} \nonumber\]

Решение

Во-первых, мы можем умножить уравнение (1) на \(−2\) и добавить его к уравнению (2 ).

\[\begin{align} −4x−2y+6z = 0 & (1) \;\;\;\;\; \text{умножается на }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\ ]

Нам не нужно продолжать. В результате мы получаем тождество \(0=0\), которое говорит нам, что эта система имеет бесконечное число решений. Есть и другие способы начать решать эту систему, например, умножить уравнение (3) на \(−2\) и добавить его к уравнению (1). Затем мы выполняем те же шаги, что и выше, и находим тот же результат, \(0=0\).

Когда система зависима, мы можем найти общие выражения для решений. Складывая уравнения (1) и (3), имеем

\[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align } \nonumber\]

Затем мы решаем полученное уравнение относительно \(z\).

\[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]

подставьте выражение для \(z\) в одно из уравнений и найдите \(y\).

\[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]

Таким образом, общее решение: \(\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)\).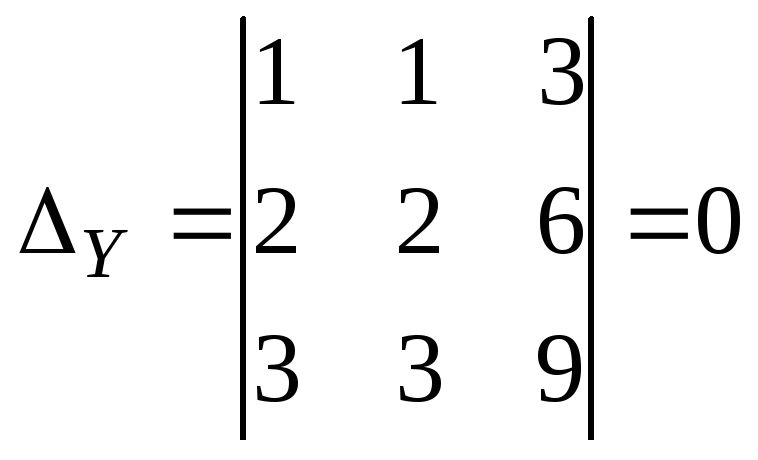 В этом решении \(x\) может быть любым вещественным числом. Значения \(y\) и \(z\) зависят от значения, выбранного для \(x\).

Анализ

Как показано на рисунке \(\PageIndex{5}\), две плоскости одинаковы и пересекают третью плоскость по прямой. Набор решений бесконечен, так как все точки вдоль линии пересечения будут удовлетворять всем трем уравнениям.

Рисунок \(\PageIndex{5}\)

Вопросы и ответы: Всегда ли общее решение для зависимой системы должно быть записано в терминах \(x\)?

Нет, общее решение можно записать в терминах любой из переменных, но обычно его записывают в терминах \(x\) и, при необходимости, \(x\) и \(y\).

Упражнение \(\PageIndex{3}\):

Решите следующую систему.

\[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \ конец {выравнивание} \nonumber\]

Ответить

Бесконечное число решений вида \((x,4x−11,−5x+18)\).

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами уравнений с тремя переменными.

• Пример 1: Система трех уравнений с тремя неизвестными с использованием исключения
• пр. 2: Система трех уравнений с тремя неизвестными с использованием исключения

• Набор решений — это упорядоченная тройка {(x,y,z)}, представляющая собой пересечение трех плоскостей в пространстве. См. пример \(\PageIndex{1}\).
• Систему из трех уравнений с тремя переменными можно решить, используя ряд шагов, которые заставляют исключить переменную. Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. См. пример \(\PageIndex{2}\).
• Системы трех уравнений с тремя переменными полезны для решения многих различных типов реальных задач. См. пример \(\PageIndex{3}\).
• Система уравнений с тремя переменными несовместна, если не существует решения. После выполнения операций исключения получается противоречие. См. пример \(\PageIndex{4}\).
• Противоречивые системы уравнений с тремя переменными могут быть результатом трех параллельных плоскостей, двух параллельных плоскостей и одной пересекающейся плоскости или трех плоскостей, которые пересекают две другие, но не в одном и том же месте.
• Система уравнений с тремя переменными является зависимой, если она имеет бесконечное число решений. После выполнения операций исключения результатом является тождество. См. пример \(\PageIndex{5}\).
• Системы уравнений с тремя переменными, которые являются зависимыми, могут быть получены из трех одинаковых плоскостей, трех плоскостей, пересекающихся по прямой, или двух одинаковых плоскостей, пересекающих третью по прямой.

Авторы

---

Эта страница под названием 9. 2: Системы линейных уравнений — три переменные распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. источник@https://openstax. org/details/books/precalculus
   2. система линейных уравнений
   3. три переменные

3 Уравнения 3 Неизвестно — Уроки математики

Всем привет и добро пожаловать обратно в MathSux! На этой неделе мы собираемся изучить, как решить 3 уравнения 3 неизвестных. Это похоже на одновременные уравнения, которые мы полюбили в алгебре, но теперь на стероидах. Раньше в алгебре нам нужно было решать только две неизвестные переменные и давали два уравнения. Но теперь, в Алгебре 2, мы сталкиваемся с тремя одновременными уравнениями, а также с тремя неизвестными переменными (обычно x, y и z), значения которых мы должны найти. Эти типы проблем могут выглядеть пугающе, но с методом устранения и некоторой практикой они не так уж плохи! Посмотрите видео, пошаговое руководство и потренируйтесь решать приведенные ниже задачи, чтобы освоить эту тему. Удачи и удачных расчетов!

Что такое 3 системы уравнений с 3 неизвестными переменными?

Три системы уравнений получаются, когда три уравнения (обычно с тремя неизвестными переменными) изображаются графически или алгебраически. График можно представить с помощью переменных x, y, z (по одной для каждой из трех отсутствующих переменных). Мы все привыкли к двухмерной координатной плоскости, в которой X идет поперек, а Y идет вверх и вниз. Но теперь, с новой неизвестной переменной z, это дает нам новую трехмерную ось. Вместо линий, к которым мы привыкли, эти уравнения будут отображаться в виде трехмерных плоскостей.

Что касается нахождения решения системы из трех уравнений, то оно одинаково для любого совместного уравнения, так как ответ находится там, где пересекаются все три плоскости. Ниже приведен пример того, как может выглядеть трехмерная плоскость в графическом виде. Не волнуйтесь, как правило, вас не попросят построить график или даже интерпретировать что-то вроде рисунка ниже.

https://www.geogebra.org/3d?lang=en

Вместо построения графика нас обычно просят найти решение с помощью алгебры! Есть три уравнения и три неизвестных переменных. Как мы должны узнать и найти значение каждой переменной? Что ж, существует несколько способов решения подобных проблем, но в этом посте блога и в видео выше мы рассмотрим 9 способов.0047 метод устранения . Это самый быстрый и простой способ решить 3 неизвестные переменные вручную.

Решение методом исключения

Основная идея Исключение состоит в том, чтобы выбрать две пары уравнений и сложить их вместе с целью исключить одну и ту же переменную . Мы делаем это, выстраивая оба уравнения одно над другим и складывая их вместе. Если сначала переменная или переменные не могут быть легко сокращены, мы затем умножаем одно из уравнений на число, чтобы оно сократилось.

Например, сложение первого уравнения (2x+2y+z=20) и второго уравнения (-3x-y-z=-18) быстро уничтожит z. Когда мы выбираем еще одну пару уравнений для добавления, выбирая второе уравнение (-3x-y-z=-18) и третье уравнение (x+y+2z=16), мы также должны сокращать z. После того как z исключено дважды, у нас появляется возможность сложить вместе два новых уравнения, которые мы только что нашли, и исключить еще больше, чтобы найти значение каждой неизвестной переменной. Если это звучит как запутанная фраза, не волнуйтесь! Мы рассмотрим этот процесс шаг за шагом ниже.

Посмотрите, как это делается шаг за шагом ниже!

Шаг 1: Во-первых, давайте еще раз взглянем на наши уравнения и пронумеруем их, чтобы мы могли отслеживать, какие уравнения мы используем и когда.

S шаг 2: Теперь давайте выберем два уравнения и попробуем исключить одну из переменных. Если мы посмотрим на первые два уравнения (помеченные 1 и 2) выше, то заметим, что мы можем легко сократить их для неизвестной переменной z.

Шаг 3: Отлично, что теперь? Теперь мы возьмем другую пару наших исходных уравнений и будем преследовать ту же цель — исключить ту же неизвестную переменную z (точно так же, как мы делали это на предыдущем шаге). Давайте выберем последние два уравнения сверху (помеченные 2 и 3). Обратите внимание, что эти два уравнения не могут легко компенсировать неизвестную переменную z, поэтому мы должны умножить все уравнение 2 в 2 раза, чтобы они компенсировали друг друга.

Шаг 4: Теперь, когда мы исключили неизвестную переменную z из двух разных пар уравнений, мы можем использовать два новых уравнения, которые мы нашли в шагах 2 и 3 (выделены фиолетовым), чтобы исключить другую переменную .

Шаг 5: Теперь, когда у нас есть значение одной переменной, x=3, мы можем подставить его в одно из наших уравнений, которые мы использовали в шаге 4.