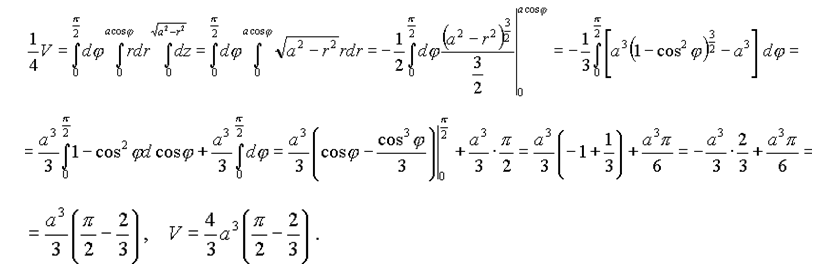Решить тройной интеграл онлайн с решением: Решение тройных интегралов онлайн / Калькуляторы

Содержание

Масса неоднородного тела. Тройной интеграл. (Лекция 2-3)

Вы можете изучить и скачать доклад-презентацию на тему Масса неоднородного тела. Тройной интеграл. (Лекция 2-3). Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Презентации» Математика» Масса неоднородного тела. Тройной интеграл. (Лекция 2-3)

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Лекция 2-3. 10. ТРОЙНЫЕ ИНТЕГРАЛЫ. 10.1. Масса неоднородного тела. Тройной интеграл. Рассмотрим тело объемом переменной плотности Разобьем тело произвольным образом на частей элементарными объемами Выберем в каждом из элементарных объемов произвольную точку Масса элементарного объема приближенно равна

Слайд 2

Описание слайда:

Просуммируем массу всех элементарных объемов Выражение в правой части называется интегральной суммой. Устремим наибольший диаметр элементарных объемов к нулю и рассмотрим предел Если этот предел интегральной суммы существует, то, очевидно, он равен массе тела и называется тройным интегралом от функции по объему

Слайд 3

Описание слайда:

Вообще, тройным интегралом от функции по объему называется предел интегральной суммы Свойства двойных интегралов переносятся на тройные интегралы: 1) 2) Тогда

Слайд 4

Описание слайда:

4) Если (x,y,z)V то 5) Если то где 6) — среднее значение f в области V.

Слайд 5

Описание слайда:

10. 2. Вычисление тройных интегралов. 1) Декартовы координаты. Пусть дан тройной интеграл Разобьем область интегрирования на элементарные объемы плоскостями, параллельными координатным плоскостям. Тогда элементарный объем равен Следовательно

Слайд 6

Описание слайда:

Установим правило вычисления тройного интеграла

Слайд 7

Описание слайда:

Пример. Вычислить тройной интеграл по области, ограниченной плоскостями: и Построим область интегрирования:

Слайд 8

Описание слайда:

2) Цилиндрические координаты. Замена переменных в тройном интеграле производится на тех же принципах, что и в двойном интеграле. Тройной интеграл в цилиндрических координатах примет вид

Слайд 9

Описание слайда:

Пример. Вычислить тройной интеграл по области, ограниченной поверхностями Перейдем к цилиндрическим координатам: Уравнение параболоида примет вид: Уравнение сферы примет вид: Линией пересечения поверхностей является окружность радиуса Переменные изменяются в следующих пределах: Интеграл запишется в виде:

Слайд 10

Описание слайда:

3) Сферические координаты. Якобиан преобразования вычисляется по формуле Тройной интеграл в сферических координатах примет вид

Слайд 11

Описание слайда:

Пример.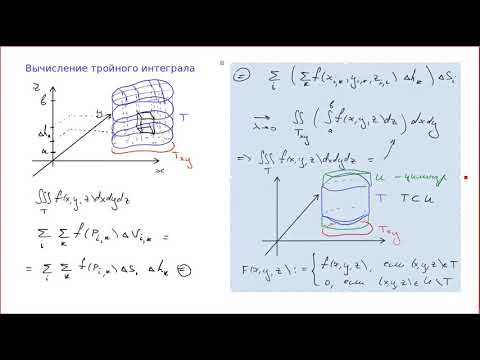 Вычислить тройной интеграл где область — верхняя половина шара Перейдем к сферическим координатам: Для данной области интегрирования, переменные изменяются в пределах: Интеграл запишется в виде:

Tags Масса неоднородного тела. Тройной интеграл. (Лекция 2-3)

Похожие презентации

Презентация успешно отправлена!

Ошибка! Введите корректный Email!

Тройной интеграл с примерами решения

Содержание:

Вычисление тройного интеграла в декартовых координатах
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.

Некоторые приложения тройного интеграла

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».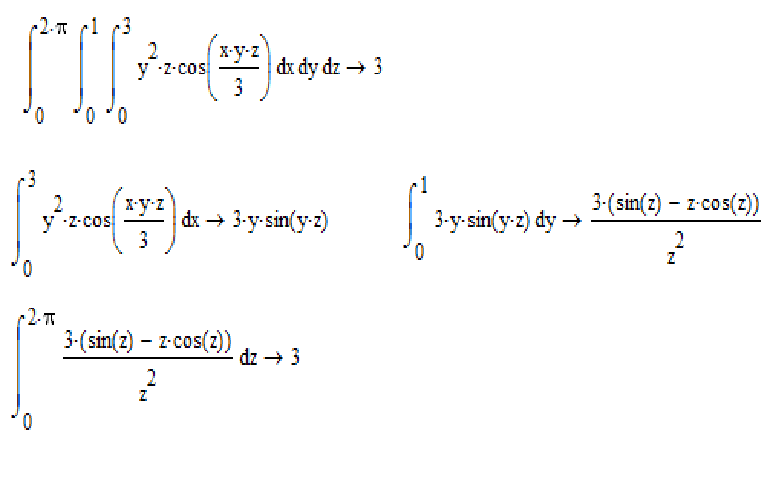

Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.

Пусть в замкнутой области пространства задана непрерывная функция Разбив область сеткой поверхностей на частей Vt (г — 1 , п) и выбрав в каждой из них произвольную точку составим интегральную сумму для функции по области (здесь — объем элементарной области

Если предел интегральной суммы существует при неограниченном увеличении числа таким образом, что каждая «элементарная область» стягивается в точку (т. е. диаметр области стремится к нулю, т.е. то его называют тройным интегралом от функции но области и обозначают

Таким образом, по определению, имеем:

Здесь — элемент объема.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Теорема 54. 1 (существования). Если функция непрерывна в ограниченной замкнутой области то предел интегральной суммы (54.1) при и существует и не зависит ни от способа разбиения области на части, ни от выбора точек

в них.

Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

а пересечение состоит из границы, их разделяющей.

4. если в области функция

Если в области интегрирования то и

5. , так как в случае любая интегральная сумма имеет вид численно равна объему тела.

Возможно вам будут полезны данные страницы:

Интегрирование двойных интегралов

Производная по направлению

Решение определённых интегралов

Интеграл произведения

6. Оценка тройного интеграла:

где и — соответственно наименьшее и наибольшее значения функции в области

7. Теорема о среднем значении: если функция непрерывна в замкнутой области то в этой области существует такая точка

что

где — объем тела.

Вычисление тройного интеграла в декартовых координатах

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

Пусть областью интегрирования является тело, ограниченное снизу поверхностью сверху — поверхностью причем и — непрерывные функции в замкнутой области являющейся проекцией тела на плоскость

(см. рис. 225). Будем считать область — правильной в направлении оси : любая прямая, параллельная оси , пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области функции имеет место формула

сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательствоформулы (54.2) не приводим).

При этом сначала вычисляется внутренний интеграл по переменной при постоянных и в пределах изменения . Нижней границей интеграла является аппликата точки — точки входа прямой, параллельной оси в область , т. е. ; верхней границей — аппликата точки — точки выхода прямой из области , т. е. — Результат вычисления этого интеграла есть функция двух переменных: и

Если область ограничена линиями и где — непрерывные на отрезке функции, причем (см. рис. 226), то, переходя от двойного интеграла по области к повторному, получаем формулу по которой вычисляется тройной интеграл в декартовых координатах.

Замечания.

1. Если область более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).

2. Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.

Пример с решением 54-1

Вычислить

где ограничена плоскостями (рис. 227).

Решение:

Область является правильной в направлении оси (как, заметим, и в направлении осей и ). Ее проекция на плоскость является правильной в направлении оси (и оси ). Согласно формуле (54.3), имеем:

Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.

При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.

Пусть совершена подстановка Если эти функции имеют в некоторой области пространства непрерывные частные производные и отличный от нуля определитель

то справедлива формула замены переменных в тройном интеграле:

Здесь — определитель Якоби, или якобиан преобразования (примем без доказательства).

Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.

Положение точки в пространстве можно определить заданием трех чисел где — длина радиуса-вектора проекции точки на плоскость — угол, образованный . этим радиусом-вектором с осью — аппликата точки (см. рис. 228).

Эти три числа называются цилиндрическими координатами точки

Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:

Возьмем в качестве цилиндрические координаты и вычислим

Формула замены переменных (54.4) принимает вид

Таким образом, вычисление тройного интеграла приводится к интегрированию по по и по аналогично тому, как это делается в декартовых координатах.

Замечание. К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

Пример 54-2.

Вычислить где — область, ограниченная верхней частью конуса и плоскостью

Решение:

На рис. 229 изображена область интегрирования Вычислим интеграл путем перехода к цилиндрическим координатам: Здесь Уравнение конуса примет вид т.е. Уравнение окружности (границы области ) запишется так: Новые

переменные изменяются в следующих пределах: — от (прямая, параллельная оси пересекающая область входит в конус и выходит из него на высоте

Таким образом, согласно формуле (54. 5), получаем:

Заметим, что, не переходя к цилиндрическим координатам, получим:

Сферическими координатами точки пространства называется тройка чисел где — длина радиуса-вектора точки — угол, образованный проекцией радиуса-вектора на плоскость и осью — угол отклонения радиуса-вектора оси (см. рис. 230).

Сферические координаты связаны с декарювыми координатами соотношениями:

В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования

Замечание. Переходить к сферическим координатам удобно, когда область интегрирования есть шар (уравнение его границы в сферических координатах имеет вид или его часть, а также если подынтегральная функция имеет вид

Пример 54-3.

Вычислить

где — шар

Решение:

Вычислим интеграл путем перехода к сферическим координатам: Тогда

Граница области — сфера и ее уравнение имеет вид подынтегральная функция после замены переменных примет вид т. е. Новые переменные изменяются в следующих пределах: -от до — от до — от до Таким образом, согласно формуле (54.6),

Некоторые приложения тройного интеграла

Объем тела

Объем области выражается формулой или

— в декартовых координатах,

— в цилиндрических координатах,

— в сферических координатах.

Масса тела

Масса тела при заданной объемной плотности вычисляется с помощью тройного интеграла как

где — объемная плотность распределения массы в точке

Статические моменты

Моменты тела отностельно координатных плоскостей вычисляются по формулам

Центр тяжести тела

Координаты центра тяжести тела находятся по формулам

Моменты инерции тела

Моменты инерции тела относительно координатных плоскостей вычисляются по формулам

а моменты инерции относительно координатных осей:

Пример 54 4.

Найти объем тела, ограниченного поверхностями

Решение:

Данное тело ограничено сверху плоскостью снизу — параболоидом (см. рис. 231). Объем тела находим, используя цилиндрические координаты:

15.4: Тройные интегралы — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2612

Гилберт Странг и Эдвин «Джед» Герман
OpenStax

Цели обучения

Распознать, когда функция трех переменных является интегрируемой по прямоугольному блоку.
Вычислите тройной интеграл, представив его в виде повторного интеграла.
Распознать, когда функция трех переменных интегрируема в замкнутой и ограниченной области.
Упростите вычисления, изменив порядок интегрирования тройного интеграла.
Вычислить среднее значение функции трех переменных. 93\) как
\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \большой\}. \nonumber \]
Мы следуем той же процедуре, что и ранее. Разделим интервал $[a,b]$ на $l$ подинтервалов $[x_{i-1},x_i]$ одинаковой длины $\Delta x$ с
\[\ Delta x = \dfrac{x_i — x_{i-1}}{l}, \nonumber \]
разделить интервал $[c,d]$ на $m$ подинтервалов $[y_{i -1}, y_i]$ одинаковой длины $\Delta y$ с
\[\Delta y = \dfrac{y_j — y_{j-1}}{m}, \nonumber \] 9*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \], если этот предел существует.
Когда тройной интеграл существует на $B$, функция $f(x,y,z)$ называется интегрируемой на $B$. Кроме того, тройной интеграл существует, если $f(x,y,z)$ непрерывен на $B$. 2)\, dx \, dy \, dz. \номер\] 92 yz \,dV \nonumber \]
где $B = \big\{(x,y,z)\,|\, — 2 \leq x \leq 1, \, 0 \leq y \leq 3 , \, 1 \leq z \leq 5 \big\} $, как показано на рисунке $\PageIndex{2}$.
Рисунок $\PageIndex{2}$: вычисление тройного интеграла по заданному прямоугольному блоку.
Решение
Порядок не указан, но повторный интеграл можно использовать в любом порядке без изменения уровня сложности. Выберите, скажем, сначала интегрировать $y$, затем $x$, а затем $z$.
93 =18(9-0) =162.\end{align*}\]
Упражнение $\PageIndex{1}$
Вычисление тройного интеграла
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]
где $B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \ dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}$.
Подсказка
Выполните действия, описанные в предыдущем примере.
Ответить
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \] 9{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber \]
Обратите внимание, что область $D$ на любой из плоскостей может относиться к типу I или типу II, как описано ранее. Если $D$ в $xy$-плоскости относится к типу I (рис. $\PageIndex{4}$), то
\[E = \big\{(x,y,z) \,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big \}. \nonumber \]
Рисунок $\PageIndex{4}$: Блок $E$, где проекция $D$ на $xy$-плоскость имеет тип I.
Тогда тройной интеграл становится 9{z=u_2(x,y)} f(x,y,z)\,dz\, dx\,dy. \nonumber \]
Пример $\PageIndex{3A}$: вычисление тройного интеграла по общей ограниченной области
Вычисление тройного интеграла функции $f(x,y,z) = 5x — 3y\ ) над сплошным тетраэдром, ограниченным плоскостями \(x = 0, \, y = 0, \, z = 0$ и $x + y + z = 1$.
Решение
На рисунке $\PageIndex{6}$ показан объемный тетраэдр $E$ и его проекция $D$ на плоскость $xy$.
Рисунок $\PageIndex{6}$: тело $E$ имеет проекцию $D$ на $xy$-плоскость типа I. 9{z=1-x-y}(5x — 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]
Так же, как мы использовали двойной интеграл \[\iint_D 1 \ ,dA \nonumber \] чтобы найти площадь общей ограниченной области $D$ мы можем использовать \[\iiint_E 1\,dV \nonumber \] чтобы найти объем общей сплошной ограниченной области $E$ . Следующий пример иллюстрирует метод.
Пример $\PageIndex{3B}$: нахождение объема путем вычисления тройного интеграла
Найдите объем правильной пирамиды с квадратным основанием в плоскости $xy$ $[-1, 1] \times [-1,1]$ и вершина в точке $(0, 0, 1)$, как показано на следующем рисунке.
Рисунок $\PageIndex{7}$: Нахождение объема пирамиды с квадратным основанием.
Решение
В этой пирамиде значение $z$ изменяется от 0 до 1 и на каждой высоте $z$ поперечное сечение пирамиды при любом значении $z$ равно квадрату
\[[-1 + z, \, 1 — z] \times [-1 + z, \, 1 — z].\nonumber \]
Следовательно, объем пирамиды равен \[\iiint_E 1\ ,dV\nonumber \] где
\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 — z, \, -1 + z \leq x \leq 1 — z \big\}. {x=3} \int_{y=-\sqrt{92}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{кубических единиц}. \конец{выравнивание*}\]
Изменение порядка интегрирования
Как мы уже видели в двойных интегралах по общим ограниченным областям, изменение порядка интегрирования делается довольно часто для упрощения вычислений. При тройном интеграле по прямоугольному ящику порядок интегрирования не меняет уровень сложности вычисления. Однако при тройном интеграле по общей ограниченной области выбор подходящего порядка интегрирования может немного упростить вычисления. Иногда изменение полярных координат также может быть очень полезным. Здесь мы демонстрируем два примера. 9{z=y} f(x,y,z)\,dz\,dy\,dx. \nonumber \]
Порядок интегрирования здесь первый относительно z , затем y , а затем x . Выразите этот интеграл, изменив порядок интегрирования так, чтобы он был сначала по $x$, затем по $z$, а затем по $y$. Убедитесь, что значение интеграла такое же, если мы допустим $f (x, y, z) = xyz$.
Решение
Лучший способ сделать это — нарисовать область $E$ и ее проекции на каждую из трех координатных плоскостей. Итак, пусть 9{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]
Среднее значение функции трех переменных
Напомним, что мы нашли среднее значение функции двух переменных путем вычисления двойного интеграла по области на плоскости и последующего деления на площадь области. Точно так же мы можем найти среднее значение функции от трех переменных, вычислив тройной интеграл по сплошной области и затем разделив его на объем твердого тела.
Среднее значение функции трех переменных
Если $f(x,y,z)$ интегрируема по твердой ограниченной области $E$ с положительным объемом $V \, (E),$, то среднее значение функции равно
\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber \]
Обратите внимание, что объем равен
\[V \, (E) = \iiint_E 1 \,dV. {z=1-xy} (xy + 8z + 20 ) \, dz \, dy \, dx = \dfrac{147}{40}. \номер\] 9{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]
Следовательно, среднее значение равно
\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441} {20} \, \text{°}\text{C} \nonumber \].
Упражнение $\PageIndex{6}$
Найдите среднее значение функции $f(x,y,z) = xyz$ по кубу со стороной 4 единицы в первом октанте с одной вершина в начале координат и ребра параллельны осям координат.
Подсказка
Выполните действия, описанные в предыдущем примере.
Ответить
$f_{ср.} = 8$
Эта страница под названием 15.4: Тройные интегралы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
1. Наверх
- Была ли эта статья полезной?
1. Тип изделия
  Раздел или Страница
  Автор
  ОпенСтакс
  Лицензия
  CC BY-NC-SA
  Версия лицензии
  4,0
  Программа OER или Publisher
  ОпенСтакс
  Показать страницу TOC
  нет
2. Теги
  1. автор @ Эдвин «Джед» Герман
  2. автор@Гилберт Странг
  3. Фубини там
  4. источник@https://openstax. 2 \le \frac{1}{2} \label{shadow} \end{выравнивание} удовлетворен. Это неравенство описывает тень рожка мороженого, которая представляет собой множество точек $(x,y)$, лежащих на диске радиуса $1/\sqrt{2}$, как показано ниже. 92}} дз\,ди\,дх. \конец{выравнивание*} Мы не будем пытаться вычислить этот интеграл в прямоугольной форме. координаты. Как только вы научитесь заменять переменные в тройных интегралах, вы сможете прочитайте, как вычислить интеграл, используя сферические координаты.
    Пример 4
    Найти объем тетраэдра, ограниченного координатой плоскости и плоскости через $(2,0,0)$, $(0,3,0)$ и $(0,0,1)$.
    Загрузка апплета
    Тетраэдр. Тетраэдр ограничен координатными плоскостями ($x=0$, $y=0$, $z=0$) и плоскостью, проходящей через три точки (2,0,0), (0,3,0 ) и (0,0,1).
    Дополнительная информация об апплете.
    Решение : Мы знаем уравнения для трех поверхностей тетраэдра, так как они являются уравнениями для координатных плоскостей: $x=0$, $y=0$ и $z=0$. В качестве начального шага мы можем найти уравнение для наклонной плоскости. Вы можете следить процедура во втором примере формирующей плоскости, чтобы вычислить, что плоскость задается уравнением \начать{выравнивать} 3x + 2y + 6z = 6. \label{plane_equation} \end{выравнивание}
    Чтобы найти пределы тетраэдра, мы снова воспользуемся методом теней, но на этот раз будем думать, что ось $y$ является вертикальной осью. Вы можете представить, что солнце, отбрасывающее тень, находится в какой-то точке далеко на положительной оси $y$.
    При такой ориентации тень тетраэдра является максимальным диапазоном $x$ и $z$ по тетраэдру. Поскольку тетраэдр расширяется в направлениях $x$ и $z$ при уменьшении $y$, тень тетраэдра является в точности основанием тетраэдра в плоскости $xz$ (плоскость $y=0$), который представляет собой треугольник, изображенный ниже.
    К интегралу по этой тени подходим как к двойному интегралу. В этой тени (и, следовательно, в самом тетраэдре) полный пробег $z$ равен \начать{выравнивать*} 0 \le z \le 1. \конец{выравнивание*} Чтобы найти диапазон $x$ для каждого значения $z$, вы можете рассчитать по фигуре тени, что верхний предел $x$ — это линия $z=1-x/2$ или $x=2 (1-я)$. Учитывая, что нижний предел $x$ равен нулю, диапазон $x$ в тени для заданного $z$ равен \начать{выравнивать*} 0 \le x \le 2(1 — z). \конец{выравнивание*} В качестве альтернативы вы могли видеть, что верхний предел $x$ соответствует плоскость, заданная уравнением \eqref{plane_equation} при $y=0$. Подключаем $y=0$ в уравнение \eqref{plane_equation} дает $3x + 6z=6$ или $x = 2(1-z)$.
    Для каждого значения $x$ и $z$ в тени нам нужно проинтегрировать $y$ снизу вверх (рассматривая $y$ как вертикальную ось). С этой точки зрения низ находится в плоскости $y=0$, а верх — наклонная плоскость уравнения \eqref{plane_equation}, которое мы можем решить для $y$ записать как $y=3(1-x/2-z)$. Следовательно, для заданных $z$ и $x$ диапазон $y$ \начать{выравнивать*} 0 \le y \le 3\left(1 — \frac{x}{2} — z\right). \конец{выравнивание*}
    Чтобы найти объем, интегрируем функцию 1 по этой области: \начать{выравнивать*} &\int_0^1 \int_0^{2(1-z)} \int_0^{3(1-x/2-z)} dy \, dx \, dz\\ &\qquad = \int_0^1 \int_0^{2(1-z)} 3\left(1 — \frac{x}{2} — z \right) dx \, дз\\ &\qquad = \int_0^1 3\left. 1\right.\\ &\qquad = 3\left(1 — 1 +\frac{1}{3}\right) = 3\left(\frac{1}{3}\right) = 1. \конец{выравнивание*} 9{3(1-x/2-z)} dy \, dx \, dz, \конец{выравнивание*} так что порядок будет $dx \, dy \, dz$.
    Решение : Один из способов изменить порядок интегрирования — построить график тетраэдра из пределов интеграла, а затем повторить процедуру примера 4, но пусть тень отбрасывается от положительного $x$ -ось. Вместо этого мы проиллюстрируем альтернативную процедуру вычисления новых пределов непосредственно из неравенств старых пределов.
    Если $y$ будет средним интегралом, нам нужны пределы $y$ через $z$ (независимо от $x$).
    Для данного $z$, насколько большим может быть диапазон $y$? Из приведенных выше пределов мы знать \начать{выравнивать*} 0 \le y \le 3\left(1 — \frac{x}{2} — z\right). \конец{выравнивание*} Диапазон самый большой, когда $x=0$, поэтому \начать{выравнивать*} 0 \le y \le 3\влево(1 — z\вправо) \конец{выравнивание*}
    Затем, учитывая $z$ и $y$, нам нужно знать диапазон $x$.
    No related posts.