| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | ||
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) |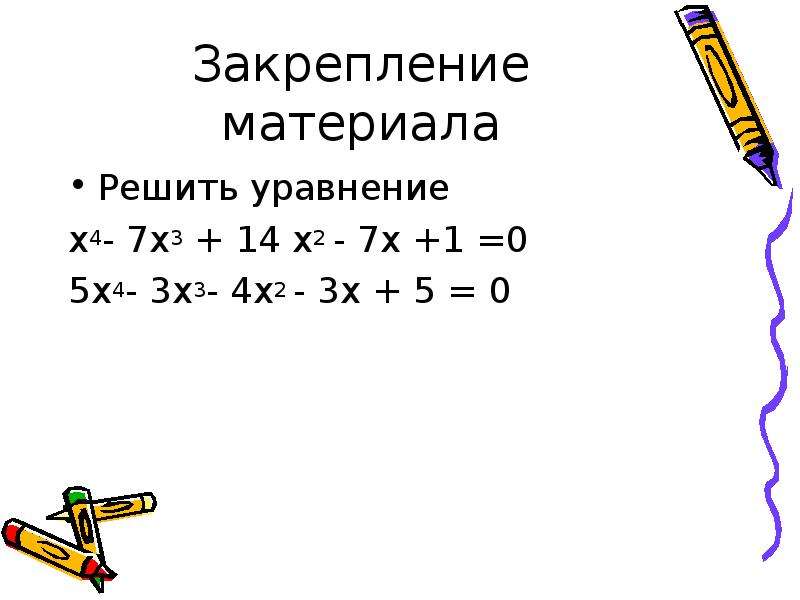
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
3 x 7 3 решение
Вы искали 3 x 7 3 решение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 3 x 7 x решение, не
исключение.
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 x 7 3 решение».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 3 x 7 3 решение,3 x 7 x решение,решите уравнение 3 x 7 x 3,решите уравнение 3 х 7 х 3,решить уравнение 3 x 7 x. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 x 7 3 решение.
Где можно решить любую задачу по математике, а так же 3 x 7 3 решение Онлайн?
Решить задачу 3 x 7 3 решение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решение простых показательных уравнений
Простые примеры на показательные уравнения позволят овладеть методикой их решения. Задания не слишком сложные и будут полезными для всех кто изучает показательные уравнения, готовится к тестированию, контрольным или вступительным экзаменам.
Пример 1. Решить уравнение (0,5)х =.
Решение: Первое что нужно сделать это свести уравнение к одному основанию. С этой целью преобразуем правую сторону показательного уравнения
В итоге уравнение сведется к виду
Теперь основы ровны, поэтому можем приравнять показатели
и найти ответ x=-2,5.
Вот такие простые вычисления.
Пример 2. Решить уравнение (2/3)х*(9/8)х =27/64.
Решение: Преобразим правую и левую сторону показательного уравнения к одной основе
Подставим в уравнение и приравняем показатели
Таким простым методом нашли решение показательного уравнения x=3.
Пример 3. Решить уравнение 52х-7х-35*52х+35*7х=0.
Решение: Сгруппируем слагаемые, содержащие 52х и 7х.
Последняя запись показательного уравнения многих заводит в тупик.
(Не всем легко найти ответ).
Тогда, давайте перепишем уравнение в виде
Согласно свойствам показательных функций решение равно нулю x=0. Только возведением к 0 степени можно получить единицу.
Для наглядности посмотрите графики показательных функций. Они пересекаются в точке x=0.
Пример 4. Решить уравнение 14х+2+5*14х-1=2749.
Решение: В подобных задачах необходимо вынести основу с наименьшим показателем. Для этого распишем уравнение к виду
Получили что решение равно единице.
Пример 5. Решить уравнение (0,6)х+2 =25/9 .
Решение: Такого рода задачи следует решать по следующей схеме.
Обязательно превратить число 0,6 к дробному виду
Далее уже поступают исходя из условия, в нашем случае превращаем правую сторону.
Приравниваем показатели, предварительно изменив знак в каком либо, чтобы получить одинаковую основу
x+2=-2; x=-2-2=-4.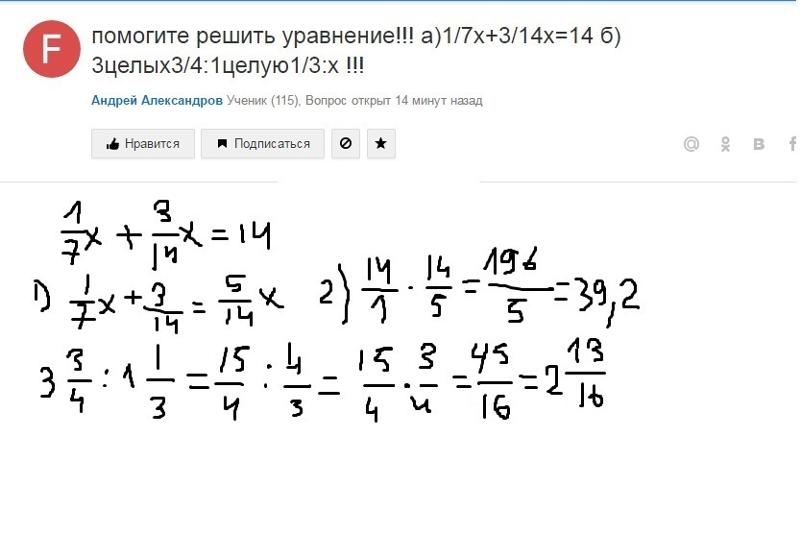
Решение показательного уравнения x=-4.
Пример 6. Решить уравнение (0,25)х-1=2*sqrt(2)
Решение: Преобразим показательное уравнение к одной основе
Подставим выражение в уравнение
Решение уравнения равно 1/4.
Пример 7. Решить уравнение (1,44)х-4=6/5.
Решение: Не сразу можно догадаться как упрощать уравнения.
Распишем сначала правую сторону 6/5=1,2.
Основу в показателе сводим к виду
После подстановки приравниваем показатели при одинаковых основаниях
2(x-4)=1; 2x-8=1; 2x=9;x=9/2=4,5.
Решения уравнения x=4,5.
Пример 8. Решить уравнение
Решение: Используем основополагающее правило для показательных уравнений — свести уравнение к слагаемым с одинаковым основанием.
Выполним манипуляции с основой
Подставляем в уравнение и приравниваем степени
Решение показательного уравнения равно x=-2.
Пример 9. Решить уравнение 3х-1+3х-2+3х-3=13.
Решение: Расписываем слагаемые так, чтобы потом сгруппировать слагаемые с одинаковим показником
Дальнейшие действия достаточно просты
Уравнение удавлетваряет значение x=3.
Пример 10. Найти сумму решений уравнения
Решение: Можно догадаться что придется вычислять квадратное уравнение. Но к нему еще нужно прийти. Для начала запишем 0,6 в виде
Подставим в показательное уравнения
Теперь можно приравнять степени при основаниях
Корни уровнения x=0; x=-1/2.
Их сумма равна
0-1/2=-0,5.
На этом знакомство с возможными примерами простых показательных уравнений завершено. Сложные примеры можно найти на страницах сайта. Оставайтесь с нами и мы подготовим Вас лучше репетиторов.
Похожие материалы:
Урок 27. решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30 — Математика — 4 класс
Математика, 4 класс
Урок № 27.
Решение уравнений вида: х · 8 = 26 + 70, х : 6 = 18 · 5,80 : х = 46 – 30
Перечень вопросов, рассматриваемых в теме:
— как решать уравнения вида: x∙ 8 = 26 + 70, x : 6 = 18 ∙ 5, 80 : x = 46 – 30
— какой алгоритм решения данных уравнений?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Алгоритм — последовательность действия (шагов)
Решить уравнение – это значит найти такое значение неизвестного числа, при котором равенство будет верным.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2017. – с.80
2. Моро М.И., Волкова С.И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.34,35
3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.44-45.
4. Волкова С.И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с.40-41.
5. Кочергина А.В. Учим математику с увлечением (Методическая библиотека). М.: 5 за знания, 2007. – с.159.
Теоретический материал для самостоятельного изучения
Вспомните, как связаны между собой числа при умножении.
Посмотрите, множитель 20, множитель 3, произведение 60.
Если 60 разделить на 20, получится 3.
Если 60 разделить на 3, получится 20.
Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей.
20 ∙ 3 = 60
60 : 20 = 3
60 : 3 = 20
Решим уравнение:
произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель. Как его найти? Для нахождения неизвестного первого множителя надо произведение 91 разделить на известный множитель 7. Делим 91 на 7 — получаем 13. Выполним проверку.
Подставим в уравнение вместо икс число 13.
13 умножить на 7 получим 91. Получили верное равенство:
91 равно девяносто одному. Значит, решили правильно.
А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка.
Вспомним, как связаны между собой числа при делении.
Посмотрите: делимое 15, делитель 3, частное равно пяти.
Если делитель 3 умножить на частное 5, получим делимое 15.
Если делимое 15 разделить на частное 5, получим делитель 3.
15 : 3 = 5
3 ∙ 5 = 15
15 : 5 = 3
Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения.
В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3.
А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно.
Задания тренировочного модуля:
1.К каждой позиции первого столбца подберите соответствующую позицию второго.
91 : х = 13 | x = 20 |
х : 21=4 | x = 7 |
24 ∙x = 96 | x = 84 |
x∙ 3 = 60 | x = 4 |
Правильный ответ:
91 : х = 13 | x = 7 |
х : 21= 4 | x = 84 |
24 ∙x = 96 | x = 4 |
x∙3 = 60 | x = 20 |
2.
Выполните вычисления и выделите верный ответ:
7 ∙x = 140 : 2
Варианты ответов: 10, 400, 2
Правильный вариант:
10
3.Решите уравнение, подчеркните правильный ответ:
(80 : у) ∙ 700 = 2800
Варианты ответов:
2, 4, 20
Правильные варианты:
20
Решите уравнение:а) 4х2 + 7х + 3 = 0; б) х2 +
Решите уравнение:
а) 4х2 + 7х + 3 = 0; б) х2 + х — 56 = 0;
в) х2 — х — 56 = 0; г) 5х2 — 18x + 16 = 0;
д) 8х2 + x — 75 = 0; е) 3х2 — 11х — 14 = 0;
ж) 3х2 + 11х — 3 4= 0; з) х2 — х — 1 = 0.
Решение:
a) 4х2 + 7х + 3 = 0; D = 49 — 4 • 4 • 3 = 49 — 48 = 1; x = (-7±1)/8; x1 = -1; x2 = -3/4;
б) х2 + х — 56 = 0; D = 1 + 4 • 56 = 255; x = (-1±15)/2; x1 = -8; x2 = 7;
в) х2 — х — 56 = 0; D = 1 + 4 • 56 = 255; x = (1±15)/2; x1 = 8; x2 = -7;
г) 5х2 — 18x + 16 = 0; D1 = 92 — 5 • 16 = 81 — 80 = 1; x = (9±15)/5; x1 = 2; x2 = 1,6;
д) 8х2 + x — 75 = 0; D = 1 + 4 • 8 • 75 = 2401; x = (-1±49)/16; x1 = 50/16 = -3 1/8; x2 = -48/16 = 3;
e) 3х2 — 11х — 14 = 0; D = 112 + 4 • 3 • 14 = 121 + 168 = 289; х = (11±17)/6; x1 = -1; x2 = 28/6 = 4 2/3;
ж) 3х2 + 11х — 3 4= 0; D = 112 + 4 • 3 • 34 = 121 + 408 = 529; х = (-11±23)/6; x1 = 2; х2 = -34/6 = -5 2/3;
з) х2 — х — 1 = 0; D = 1 + 4 = 5; х = (1±√5)/2.
Похожие задачи:
Не решая уравнения, выясните, имеет ли оно корни, и если имеет, то определите их знаки:а) х2 + 7х — 1 = 0; г) 19х2 — 23x + 5 = 0;
б) х2 — 7х + 1 = 0; д) 2х2 + 5√3х + 11 = 0;
в) 5х2 + 17x + 16 = 0; е) 11х2 — 9х + 7 — 5√2 = 0.
1) Сформулируйте теорему, на основании которой можно определить знаки корней.
2) Распределите, кто выполняет задания а), в), д), а кто — задания б), г), е), и выполните их.
3) Проверьте друг у друга, правильно ли выполнены задания. Исправьте ошибки, если они допущены.
смотреть решение >>
Ошибки в уравнениях / math5school.ru
При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней, либо появление посторонних корней.
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного, а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10)2 + lg x2 = 2lg 24.
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
lg (x – 10) + lg x = lg 24,
lg x(x – 10) = lg 24,
x2 – 10x = 24,
x2 – 10x – 24 = 0,
x1 = –2, x2 = 12.
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Ответ: –2 и 12.
Комментарий.
Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
ОДЗ: х ≠ 0, х ≠ 10,
2lg |x – 10| + 2lg|x| = 2lg 24,
lg |x – 10| + lg|x| = lg 24,
lg |x(x – 10)| = lg 24,
|x2 – 10x| = 24,
x2 – 10x = ± 24,
1) x2 – 10x – 24 = 0, x1 = –2, x2 = 12;
2) x2 – 10x + 24 = 0, x3 = 4, x4 = 6.
Ответ: –2; 4; 6 и 12.
При делении обеих частей уравнения на выражение, содержащее неизвестное, могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3х (х2 – 2х – 3) = 9 (х2 – 2х – 3).
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
3х = 9;
3х = 32;
х = 2.
Ответ: 2.
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
3х (х2 – 2х – 3) – 9 (х2 – 2х – 3) = 0;
(3х – 9) (х2 – 2х – 3) = 0;
1) 3х – 9 = 0; 3х = 32; х = 2;
2) х2 – 2х – 3 = 0; х = –1 и х = 3.
Ответ: –1; 2 и 3.
K Упражнение 2. Решить уравнение lg2 x – lg x = 0.
L Неправильное решение.
ОДЗ: х > 0.
Разделим обе части уравнения на lg x и получим:
lg x – 1 = 0;
lg x = 1;
x = 10.
Ответ: 10.
J Правильное решение.
lg2 x – lg x = 0;
ОДЗ: х > 0;
lg x (lg x – 1) = 0;
1) lg x = 0; x = 1;
2) lg x – 1 = 0; lg x = 1; x = 10.
Ответ: 1 и 10.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного.
Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину.
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0. |
| x – 1 | x2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х2 – 1 и получим:
(5 – x) (x + 1) – (5 + 3x) = 0;
–х2 + x =0;
х2 – x =0;
х (х – 1) =0.
Ответ: 0 и 1.
Комментарий. Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки.
J Правильный ответ: х = 0.
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину.
K Упражнение. Решить уравнение
| х2 – 81 |
– 2х = 0. |
| x – 9 |
L Неправильное решение.
Заметим, что х2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9. Имеем:
(x + 9) – 2х = 0;
– х + 9 = 0;
х = 9.
Ответ: 9.
Комментарий. Был приобретен посторонний корень х = 9.
J Правильный ответ: решений нет.
Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.
K Упражнение. Решить уравнение
| 2 | + х2 – | 2 | – 4х = 0. |
| 3х2 | 3х2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
х2 – 4х = 0;
х (х – 4) =0;
х = 0, х = 4.
Ответ: 0 и 4.
Комментарий. Был приобретен посторонний корень х = 0.
J Правильный ответ: 4.
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения. Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √х + 3 + √7 – х = 2.
L Неправильное решение.
ОДЗ: –3 ≤ х ≤ 7;
√х + 3 = 2 – √7 – х;
x + 3 = 4 – 4 · √7 – х + 7 – x;
2x – 8 = –4 · √7 – х;
2 · √7 – х = 4 – x;
4 (7 – x) = 16 – 8x + х2;
х2 – 4x – 12 = 0;
x1 = –2, x2 = 6.
И число –2, и число 6 содержатся в области допустимых значений переменной х, значит, являются решениями исходного уравнения.
Ответ: –2 и 6.
Комментарий. Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
√х + 3 = 2 – √7 – х
к уравнению
x + 3 = 4 – 4 · √7 – х + 7 – x.
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1. Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1, которое стало верным именно в результате возведения в квадрат, ведь 12 = (–1)2. Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
2 · √7 – х = 4 – x,
которое уже имеет один корень –2, к уравнению
4 (7 – x) = 16 – 8x + х2.
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4, которые соответствуют этим уравнениям для случая х = 6. Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
х2 – 4x – 12 = 0,
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю, прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение (x – 5) (х + 2) √х – 3 = 0.
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
х – 5 = 0, х + 2 = 0, х – 3 = 0;
х = 5, х = –2, х = 3.
Ответ: 5; –2; 3.
Комментарий. Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3.
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения. Таких равенств много, вот некоторые из них:
x = (√ х)2
√ х · y = √ х · √ y
| tg (x + y) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2x = | 2 tg x |
| 1 + tg2 x |
loga х2 = 2 loga x
loga х · y = loga x + loga y
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части.
{1/4}=3,\;\;\;\) \(x-3=81,\;\;\;\) \(x=84.\;\;\;\)
Ответ: 19 и 84.
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась.
K Упражнение. Решить уравнение х + 4√x – 5 = 0.
L Неправильное решение.
√x = t, x = t2;
t2 + 4t – 5 = 0;
t1 = 1, t2 = –5;
1) x = (t1)2 = 12 = 1;
2) x = (t2)2 = (–5)2 = 25.
Ответ: 1 и 25.
Комментарий. После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √x = t, а не x = t2.
J Правильное решение.
2}=x+3;\;\;\left|x+3 \right|=x+3\geq 0;\;\;x\geq -3.\)
Ответ: х ≥ –3.
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1.
J Правильное решение.
Находим нули модулей, для |х – 3| это 3, для |x – 4| это 4, и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
(–∞; 3), [3; 4) и [4; +∞).
На каждом из этих промежутков исходное уравнение принимает свой вид.
Так как
\[\left|x-3 \right|=\begin{cases} \;\;\;\;x-3, \;\;\;x\geq 3; \\ -(x-3), \;\;x< 3; \end{cases}\;\;\;\;\; \left|x-4 \right|=\begin{cases} \;\;\;\;x-4, \;\;x\geq 4; \\ -(x-4), \;x< 4; \end{cases}\]
то
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
– (х – 3) – (х – 4) = 1,
– х + 3 – х + 4 = 1,
2х = 6,
х = 3;
так как 3 ∉ (–∞; 3), то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
(х – 3) – (х – 4) = 1,
х – 3 – х + 4 = 1,
1 = 1;
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
(х – 3) + (х – 4) = 1,
х – 3 + х – 4 = 1,
2х = 8,
х = 4;
так как 4 ∈ [4; +∞), то 4 – корень уравнения.
Так как [3; 4)∪{4} = [3; 4], то корнями исходного уравнения являются все числа числового промежутка [3; 4].
Ответ: [3; 4].
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности.
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24.
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Ответ: 1.
Комментарий. Был подобран корень х = 1, но не обнаружен еще один корень х = –4, который соответствует разложению 24 = –4 · (–3) · (–2) · (–1). Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
х (х + 1) (х + 2) (х + 3) = 24,
(х (х + 3)) ((х + 1) (х + 2)) = 24,
(x2 + 3х) (x2 + 3х + 2) = 24,
введем новую переменную x2 + 3х + 1 = t, тогда
(t – 1) (t + 1) = 24,
t2 – 1 = 24,
t2 = 25,
t1 = –5, t2 = 5,
1) x2 + 3х + 1 = –5, x2 + 3х + 6 = 0, решений нет;
2) x2 + 3х + 1 = 5, x2 + 3х – 4 = 0, х1 = –4, х2 = 1.
Ответ: –4 и 1.
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций. Часто при этом используется производная.
K Упражнение. Решить уравнение x11 + 5х – 6 = 0.
L Неправильное решение.
Методом подбора находим корень уравнения х = 1.
Ответ: 1.
Комментарий. Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x11 + 5х – 6, что и доказывает единственность подобранного корня.
Ответ: 1.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней.
Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями, не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7x)1/3 = 1.
L Неправильное решение.
(log7 x)1/3 = (log7 x)0.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
log7 x = 1,
x = 7.
Ответ: 7.
K Упражнение 2. Решить уравнение (х + 5) х2 + х – 2 = 1.
L Неправильное решение.
(х + 5) х2 + х – 2 = (х + 5) 0,
х2 + х – 2 = 0,
х1 = –2, х2 = 1.
Ответ: –2 и 1.
Комментарий. Потерян корень х = –4. Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
х + 5 = 1,
х = –4.
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5, тогда
(х2 + х – 2) · lg (x + 5) = 0;
1) х2 + х – 2 = 0; х1 = –2, х2 = 1;
2) lg (x + 5) = 0; x + 5 = 1; x = –4.
Ответ: –4, –2 и 1.
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями. При применении этих свойств учащиеся часто допускают ошибки.
K Упражнение 1. Решить уравнение log3 x · log3 (3x) =log3 (81x).
L Неправильное решение.
log3 (3х2) =log3 (81x),
3х2 = 81x,
3х = 81,
х = 27.
Ответ: 27.
Комментарий. В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
ОДЗ: х > 0;
log3 x · (log3 3 + log3 x) = log3 81 + log3 x;
log3 x · (1 + log3 x) = 4 + log3 x;
log3 x + log32 x = 4 + log3 x;
log32 x = 4;
log3 x = ±2;
x = 9, x = 1/9.
1/_{4\sqrt[5]{8}}\;.\)
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение.
|
K Решить уравнение |
L Неправильный ответ |
J Правильный ответ |
|
sin x – cos x = 0 |
x = π/4 |
x = π/4 + πk, k ∈ Z |
|
tg x = 1/√3 |
x = π/6 + 2πk, k ∈ Z |
x = π/6 + πk, k ∈ Z |
|
sin x = 1/2 |
x = (–1)k arcsin π/6 + πk, k ∈ Z |
x = (–1)k · π/6 + πk, k ∈ Z |
|
cos x = 1/2 |
x = π/3 + 2πk, k ∈ Z |
x = ± π/3 + 2πk, k ∈ Z |
В тригонометрических уравнениях, как и в уравнениях других видов, причиной многих ошибок становится невнимательное отношение к области допустимых значений неизвестного.
K Упражнение. Решить уравнение tg 3x – tg x = 4sin x.
L Неправильное решение.
| sin (3x – x) | = 4sin x; |
| cos 3x cos x |
| sin 2x | = 4sin x; |
| cos 3x cos x |
sin 2x = 4sin x cos 3x cos x;
sin 2x = 2sin 2x cos 3x;
sin 2x – 2sin 2x cos 3x = 0;
sin 2x (1 – 2cos 3x) = 0;
1) sin 2x = 0; 2x = πn, n ∈ Z; x = πn/2, n ∈ Z;
2) 1 – 2cos 3x = 0; cos 3x = 1/2; 3x = ± π/3 + 2πk, k ∈ Z; x = ± π/9 + 2πk/3, k ∈ Z.
Ответ: πn/2 , n ∈ Z; ± π/9 + 2πk/3, k ∈ Z.
Комментарий. Была допущена серьезная ошибка. При x = πn/2 и нечетных n исходное уравнение не имеет смысла. Ошибка осталась незамеченной в результате того, что не была установлена область допустимых значений переменной.
J Правильный ответ: πn, n ∈ Z; ± π/9 + 2πk/3, k ∈ Z.
Не редкость – появление ошибок по причине невнимательного отношения ко всем заданным в уравнении условиям.
K Упражнение. Решить уравнение cos x – cos 2x = 1, если 0 < x < π/2 .
L Неправильное решение.
cos x – (2cos2 x – 1) = 1;
cos x – 2cos2 x = 0;
cos x (1 – 2cos x) = 0;
1) cos x = 0; x = π/2 + πk, k ∈ Z;
2) 1 – 2cos x = 0; cos x = 1/2; x = ± π/3 + 2πn, n ∈ Z.
Ответ: π/2 + πk, k ∈ Z; ± π/3 + 2πn, n ∈ Z.
Комментарий. Ответ не верен, так как условию 0 < x < π/2 удовлетворяют только один корень.
J Правильный ответ: π/3.
Следует не забывать, что сокращение всех членов уравнения на функцию, содержащее неизвестное не редко приводит к потере корней уравнения.
K Упражнение. Решить уравнение cos x (2sin 2x – 1) = cos x sin 2x.
L Неправильное решение.
2sin 2x – 1 = sin 2x;
sin 2x = 1;
2x = π/2 + 2πk, k ∈ Z;
x = π/4 + πk, k ∈ Z.
Ответ: π/4 + πk, k ∈ Z.
J Правильное решение.
cos x (2sin 2x – 1) – cos x sin 2x = 0;
cos x (2sin 2x – 1 – sin 2x) = 0;
cos x (sin 2x – 1) = 0;
1) cos x = 0; x = π/2 + πn, n ∈ Z;
2) sin 2x – 1 = 0; sin 2x = 1; 2x = π/2 + 2πk, k ∈ Z; x = π/4 + πk, k ∈ Z.
Ответ: π/2 + πn, n ∈ Z; π/4 + πk, k ∈ Z.
Еще одна причина появления ошибок – недостаточное внимание к проверке. Следует не забывать, что при проверке посторонних корней тригонометрических уравнений часто удобно использовать единичную окружность.
K Упражнение. Решить уравнение sin x + cos x = 1.
L Неправильное решение.
(sin x + cos x)2 = 12;
sin2 x + 2sin x cos x + cos2 x = 1;
1 + 2sin x cos x = 1;
sin 2x = 0;
2x = πn, n ∈ Z;
x = πn/2, n ∈ Z.
Ответ: πn/2, n ∈ Z.
Комментарий. Так как при решении обе части исходного уравнения возводили в квадрат, а его левая часть может быть как положительной, так и отрицательной величиной, могли появиться посторонние корни, следовательно, проверка обязательна.
J Правильное решение.
Дополним приведенное выше решение следующими рассуждениями.
Значениям x = πn/2, n ∈ Z соответствуют четыре точки, отмеченные на единичной окружности. Причем зеленые точки соответствуют корням уравнения, а красные – посторонним корням.
Так как зеленой точке на Ох соответствуют значения n = 4k, где k ∈ Z, а на оси Оу – значения n = 4m + 1, где m ∈ Z, то
1) x = 4πk/2 = 2πk, k ∈ Z;
2) x = 4πm+π/2 = π/2 + 2πm, m ∈ Z.
Ответ: 2πk, k ∈ Z и π/2 + 2πm, m ∈ Z.
Как и в любых других уравнениях, при решении тригонометрических уравнений не редкость – применение вспомогательной переменной.
Но не следует забывать, что при этом может быть сужена область определения, что может привести к потере корней.
K Упражнение. Решить уравнение sin 2x + 3cos 2x + 3 = 0.
L Неправильное решение.
Так как
| sin 2x = | 2tg x | ; |
| 1 + tg2x | ||
| cos 2x = | 1 – tg2 x | , |
| 1 + tg2 x |
то для исходного уравнения имеем:
| 2tg x | + 3 · | 1 – tg2 x | + 3 = 0; |
| 1 + tg2 x | 1 + tg2 x |
2tg x + 3 – 3tg2 x + 3 + 3tg2 x = 0;
2tg x + 6 = 0;
tg x = –3;
x = arctg (–3) + πk, k ∈ Z.
Ответ: arctg (–3) + πk, k ∈ Z.
Комментарий. Область допустимых значений неизвестного в исходном уравнении – все действительные числа. Но при x = π/2 + πn переход от sin 2x и cos 2x к tg x невозможен. Таким образом область допустимых значений неизвестного сузилась, а значит, случай x = π/2 + πn необходимо проверить отдельно.
J Правильное решение.
Продолжим решение уравнения. Подставим π/2 + πn в исходное уравнение:
sin 2(π/2 + πn) + 3cos 2(π/2 + πn) + 3 = 0;
sin (π + 2πn) + 3cos (π + 2πn) + 3 = 0;
sin π + 3cos π + 3 = 0;
0 – 3 + 3 = 0;
0 = 0 – верно и, значит, π/2 + πn, n ∈ Z – корни уравнения.
Ответ: π/2 + πn, n ∈ Z; arctg (–3) + πk, k ∈ Z.
Смотрите так же:
Ошибки в тождественных преобразованиях
Ошибки в системах уравнений
Ошибки в неравенствах
Ошибки в упражнениях с параметрами
Ошибки в упражнениях о функциях
Ошибки в упражнениях из начал анализа
Ошибки в геометрических задачах
ГДЗ. Математика 5 класс Тарасенкова. Уравнения.
Категория: —>> Математика 5 класс Тарасенкова.
Задание: —>> 553 — 569 570 — 586
наверх
|
|
Задание 553.
Какое из чисел 4. 5, 8 и 10 является корнем уравнения:
Решение:
| 1) 5; | 2) 10; | 3) 4. |
Задание 554.
Решите уравнение устно:
Решение:
| 1) 15 + x: = 55, x = 40; | 3) 60 — y = 45, y = 15; | 5) 88 : x = 8, x = 11; |
| 2) х — 22 = 42, x = 64; | 4) у * 12 = 12, y = 1; | 6) у : 10 = 40, y = 400. |
Задание 555.
Можно ли решить уравнение:
| 1) 8x = 0; | 2) 0 : y = 25; | 3) 5х = 5 | 4) 12 : y = 0? |
Решение:
1) x = 0; 2) Не имеет решений; 3) x = 1; 4) Не имеет решений;
Задание 556.
Решите уравнение:
Решение:
1)28 + (45 + х) = 100;
| 11) 121 : (х — 45) = 11;
|
Задание 557.
Решите уравнение:
Решение:
1) 65 + (х + 23) = 105;
| 6) 9х + 50 = 86;
|
Задание 558.
Составьте уравнение, корнем которого является число:
| а) 8; | б) 14. |
Решение:
| а) 2y = 16; | б) x + 7 = 21. |
Задание 559.
Составьте уравнение, корнем которого является число.
| а) 5; | б) 9. |
Решение:
| а) 25 : x = 5; | б) 5x = 45. |
Задание 560.
Некоторое число увеличили на 67 и получили число 109. Найдите это число.
Решение:
- Некоторое число — x.
- x + 67 = 109;
- x = 109 — 67;
- x = 42.
- Ответ: число 42.
Задание 561.
К некоторому числу прибавили 38 и получили число 245. Найдите это число.
Решение:
- x + 38 = 245;
- x = 245 — 38;
- x = 207.
- Ответ: 207.
Задание 562.
Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.
Решение:
- 24x = 1968;
- x = 1968 : 24;
- x = 82.
- Ответ: 82.
Задание 563.
Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.
Решение:
- x : 18 = 378;
- x = 378 * 18;
- x = 6804.
- Ответ: 6408.
Задание 564.
Некоторое число уменьшили на 22 и получили число 105. Найдите это число.
Решение:
- x — 22 = 105;
- x = 105 + 22;
- x = 127.
- Ответ: 127.
Задание 565.
Из числа 128 вычли некоторое число и получили 79. Найдите это число.
Решение:
- 128 — x = 79;
- x = 128 — 79;
- x = 49.
- Ответ: 49.
Задание 566.
Составьте и решите уравнение:
- 1) сумма удвоенного числа х и числа 39 равна 81;
- 2) разность чисел 32 и y в 2 раза меньше числа 64;
- 3) частное суммы чисел х и 12 и числа 2 равно 40;
- 4) сумма чисел х и 12 в 3 раза больше числа 15;
- 5) частное разности чисел у и 12 и числа 6 равно 18;
- 6) утроенная разность чисел у и 17 равна 63.
Решение:
- 1) 2x + 39 = 81
- 2x = 81 — 39;
- 2x = 42;
- x = 42 : 2;
- x = 21;
- 2) (32 — y) * 2 = 64
- 32 — y = 64 : 2;
- 32 — y = 32;
- y = 32 — 32;
- y = 0;
- 3) (x + 12) : 2 = 40
- x + 12 = 40 * 2;
- x + 12 = 80;
- x = 80 — 12;
- x = 68;
- 4) (x + 12) : 3 = 15
- x + 12 = 15 * 3;
- x + 12 = 45;
- x = 45 — 12;
- x = 33;
- 5) (y — 12) : 6 = 18
- y — 12 = 18 * 6;
- y — 12 = 108;
- y = 108 + 12;
- y = 120;
- 6) (y — 17) * 3 = 63
- y — 17 = 63 : 3;
- y — 17 = 21;
- y = 21 + 17;
- y = 38;
Задание 567.
Составьте и решите уравнение:
- 1) разность утроенного числа у и числа 41 равна 64;
- 2) сумма чисел 9 и х в 5 раз меньше числа 80;
- 3) частное суммы чисел у и 10 и числа 4 равно 16;
- 4) разность утроенного числа х и числа 17 равна 10.
Решение:
- 1) 3y — 41 = 64
- 3y = 64 + 41;
- 3y = 105;
- y = 105 : 3;
- y = 15;
- 2) (9 + x) * 5 = 80
- 9 + x = 80 : 5;
- 9 + x = 16;
- x = 16 — 9;
- x = 7;
- 3) (y + 10) : 4 = 16
- y + 10 = 16 * 4;
- y + 10 = 64;
- y = 64 — 10;
- y = 54;
- 4) 3x — 17 = 10
- 3x = 10 + 17;
- 3x = 27;
- x = 27 : 3;
- x = 9;
Задание 568.
Некоторое число увеличили на 5 и полученное число удвоили.
В результате получили число 22. Найдите неизвестное число.
Решение:
- (x + 5) * 2 = 22;
- x + 5 = 22 : 2;
- x + 5 = 11;
- x = 11 — 5;
- x = 6;
Задание 569.
Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.
Решение:
- 7x — 54 = 100;
- 7x = 100 + 54;
- 7x = 154;
- x = 154 : 7;
- x = 22;
Задание: —>> 553 — 569 570 — 586
Решение уравнений — методы и примеры
Понимание того, как решать уравнения, — один из самых фундаментальных навыков, которым может овладеть каждый студент, изучающий алгебру. Решения для большинства алгебраических выражений ищутся, применяя этот навык. Таким образом, учащиеся должны лучше понимать, как проводить операцию.
Эта статья научит решить уравнение , выполнив четыре основных математических операции: сложение , вычитание , умножение и деление .
Уравнение обычно состоит из двух выражений, разделенных знаком, указывающим на их взаимосвязь. Выражения в уравнении могут быть связаны знаком равенства (=), меньше (<), больше (>) или комбинацией этих знаков.
Как решать уравнения?
Решение алгебраического уравнения — это обычно процедура манипулирования уравнением. Переменная остается на одной стороне, а все остальное — на другой стороне уравнения.
Проще говоря, решить уравнение — значит изолировать его, сделав его коэффициент равным 1.Что бы вы ни делали с одной стороной уравнения, сделайте то же самое с противоположной стороной уравнения.
Решите уравнения, добавив
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 1
Решите: –7 — x = 9
Решение
–7 — x = 9
Добавьте 7 к обеим сторонам уравнения.
7 — x + 7 = 9 + 7
— x = 16
Умножить обе стороны на –1
x = –16
Пример 2
Решить 4 = x — 3
Решение
Здесь переменная находится справа в уравнении.
Добавьте 3 к обеим сторонам уравнения
4+ 3 = x — 3 + 3
7 = x
Проверьте решение, подставив ответ в исходное уравнение.
4 = x — 3
4 = 7 — 3
Следовательно, x = 7 — правильный ответ.
Решение уравнений путем вычитания
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 3
Решите относительно x в x + 10 = 16
Решение
x + 10 = 16
Вычтите 7 из обеих частей уравнения.
x + 10-10 = 16-10
x = 6
Пример 4
Решите линейное уравнение 15 = 26 — y
Решение
15 = 26 — y
Вычесть 26 с обеих сторон уравнения
15-26 = 26-26 -y
-11 = -y
Умножим обе части на –1
y = 11
Решение уравнений с переменными с обеих сторон, добавив
Давайте см. несколько примеров ниже, чтобы понять эту концепцию.
Пример 4
Рассмотрим уравнение 4x –12 = -x + 8.
Поскольку уравнение имеет две стороны, вам необходимо выполнить одну и ту же операцию с обеих сторон.
Добавьте переменную x к обеим частям уравнения
⟹ 4x –12 + x = -x + 8 + x.
Упростите
Упростите уравнение, собрав одинаковые члены с обеих сторон уравнения.
5x — 12 = 8.
Теперь уравнение имеет только одну переменную с одной стороны.
Добавьте константу 12 к обеим частям уравнения.
Константа, прикрепленная к переменной, добавляется с обеих сторон.
⟹ 5x — 12 +12 = 8 + 12
Упростить
Упростите уравнение, объединив похожие члены. И 12.
⟹ 5x = 20
Теперь разделим на коэффициент.
Деление обеих частей на коэффициент означает простое деление всего на число, присвоенное переменной.
Решение этого уравнения, следовательно,
x = 4.
Проверьте свое решение
Проверьте правильность решения, подставив ответ в исходное уравнение.
4x –12 = -x + 8
⟹ 4 (4) –12 = -4 + 8
4 = 4
Следовательно, решение верное.
Пример 5
Решить -12x -5-9 + 4x = 8x — 13x + 15-8
Решение
Упростить, объединив похожие термины
-8x-14 = -5x +7
Добавьте 5x с обеих сторон.
-8x + 5x -14 = -5x + 5x + 7
-3w -14 = 7
Теперь прибавьте 14 к обеим сторонам уравнения.
— 3x — 14 + 14 = 7 + 14
-3x = 21
Разделите обе части уравнения на -3
-3x / -3 = 21/3
x = 7.
Решение уравнений с переменными с обеих сторон путем вычитания
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 6
Решите уравнение 12x + 3 = 4x + 15
Решение
Вычтите 4x из каждой части уравнения.
12x-4x + 3 = 4x — 4x + 15
6x + 3 = 15
Вычтем константу 3 с обеих сторон.
6x + 3-3 = 15-3
6x = 12
Разделить на 6;
6x / 6 = 12/6
x = 2
Пример 7
Решите уравнение 2x — 10 = 4x + 30.
Решение
Вычтем 2x из обеих частей уравнения .
2x -2x -10 = 4x — 2x + 23
-10 = 2x + 30
Вычтем обе части уравнения на константу 30.
-10-30 = 2x + 30-30
-40 = 2x
Теперь разделите на 2
-40/2 = 2x / 2
-20 = x
Решение линейных уравнений с умножением
Линейные уравнения решаются умножением, если при написании уравнения используется деление. Как только вы заметите, что переменная делится, вы можете использовать умножение для решения уравнений.
Пример 7
Решите x / 4 = 8
Решение
Умножьте обе части уравнения на знаменатель дроби,
4 (x / 4) = 8 x 4
x = 32
Пример 8
Решите -x / 5 = 9
Решение
Умножьте обе стороны на 5.
5 (-x / 5) = 9 x 5
-x = 45
Умножьте обе стороны на -1, чтобы коэффициент переменной был положительным.
x = — 45
Решение линейных уравнений с делением
Для решения линейных уравнений с делением обе части уравнения делятся на коэффициент переменной. Давайте посмотрим на приведенные ниже примеры.
Пример 9
Решите 2x = 4
Решение
Чтобы решить это уравнение, разделите обе части на коэффициент переменной.
2x / 2 = 4/2
x = 2
Пример 10
Решите уравнение −2x = −8
Решение
Разделите обе части уравнения на 2.
−2x / 2 = −8/2
−x = — 4
Умножая обе стороны на -1, получаем;
x = 4
Как решать алгебраические уравнения, используя свойство распределения?
Решение уравнений с использованием свойства распределения влечет за собой умножение числа на выражение в круглых скобках.
Затем подобные термины объединяются, а затем выделяется переменная.
Пример 11
Решите 2x — 2 (3x — 2) = 2 (x –2) + 20
Решение
2x — 2 (3x — 2) = 2 (x –2) + 20
Используйте свойство распределения для удаления скобок
2x — 6x + 4 = 2x — 4 + 20
— 4x + 4 = 2x + 16
Сложить или вычесть с обеих сторон
–4x + 4 — 4 –2x = 2x + 16 — 4 –2x
–6x = 12
x = –2
Проверьте ответ, подставив решение в уравнение.
2x — 2 (3x — 2) = 2 (x –2) + 20
(2 * –2) — 2 ((3 * –2) –2) = 2 (–2 –2) + 20
12 = 12
Пример 12
Решите относительно x в уравнении -3x — 32 = -2 (5 — 4x)
Решение
Примените свойство распределения, чтобы удалить скобки .
–3x — 32 = — 10 + 8x
Сложение обеих частей уравнения на 3x дает
-3x + 3x — 32 = — 10 + 8x + 3x
= — 10 + 11x = -32
Сложите обе части уравнения на 10.
— 10 + 10 + 11x = -32 + 10
11x = -2
Разделите все уравнение на 11.
11x / 11 = -22/11
x = -2
Как решать уравнения с дробями?
Не паникуйте, когда увидите дроби в алгебраическом уравнении. Если вы знаете все правила сложения, вычитания, умножения и деления, это легкий кусок пирога для вас.
Чтобы решить уравнения с дробями, вам нужно преобразовать их в уравнение без дробей.
Этот метод также называется «очистка от фракций ».
При решении уравнений с дробями выполняются следующие шаги:
- Определите наименьшее общее кратное знаменателей (ЖКД) всех дробей в уравнении и умножьте на все дроби в уравнении.
- Изолировать переменную.
- Упростите обе части уравнения, применяя простые алгебраические операции.
- Примените свойство деления или умножения, чтобы коэффициент переменной был равен 1.
Пример 13
Решить (3x + 4) / 5 = (2x — 3) / 3
Решение
На ЖК-дисплее 5 и 3 будет 15, поэтому умножьте оба
(3x + 4) / 5 = (2x — 3) / 3
{(3x + 4) / 5} 15 = {(2x — 3) / 3} 15
9x +12 = 10x -15
Изолировать переменную;
9x -10x = -15-12
-x = -25
x = 25
Пример 14
Решить относительно x 3 / 2x + 6/4 = 10/3
Решение
ЖК-дисплей 2x, 4 и 3 равен 12x
Умножьте каждую дробь в уравнении на ЖК-дисплей.
(3 / 2x) 12x + (6/4) 12x = (10/3) 12x
=> 18 + 18x = 40x
Изолировать переменную
22x = 18
x = 18/22
Упростить
x = 9/11
Пример 15
Решить относительно x (2 + 2x) / 4 = (1 + 2x) / 8
Решение
LCD = 8
Умножьте каждую дробь на ЖК-дисплей,
=> 4 + 4x = 1 + 2x
Изолировать x;
2x = -3
x = -1.5
Практические вопросы1. Решите относительно x в следующих линейных уравнениях:
a. 10x — 7 = 8x + 13
б. х + 1/2 = 3
с. 0,2x = 0,24
г. 2x — 5 = x + 7
e. 11x + 5 = x + 7
2. Возраст Джареда в четыре раза старше его сына. Через 5 лет Джаред будет в 3 раза старше своего сына. Найдите настоящий возраст Джареда и его сына.
3. Стоимость 2 пар брюк и 3 рубашек — 705 долларов США. Если рубашка стоит на 40 долларов меньше пары брюк, найдите стоимость каждой рубашки и брюк.
4. Лодке требуется 6 часов при движении вверх по течению и 5 часов при движении вниз по течению. Рассчитайте скорость лодки в стоячей воде, учитывая, что скорость реки составляет 3 км / час.
5. Сумма цифр двузначного числа равна 7. Когда цифры меняются местами, полученное число на 27 меньше исходного. Найдите номер.
6. 10000 долларов распределено между 150 людьми. Если деньги достоинством 100 или 50 долларов. Подсчитайте количество денег каждого достоинства.
7. Ширина прямоугольника на 3 см меньше длины. Когда ширина и длина увеличиваются на 2, площадь прямоугольника изменяется на 70 см на 2 больше, чем у исходного прямоугольника. Вычислите размеры исходного прямоугольника.
8. Числитель дроби 8 меньше знаменателя. Когда знаменатель уменьшается на 1, а числитель увеличивается на 17, дробь становится 3/2. Определите дробь.
9. Мой отец на 12 лет больше меня, чем в два раза.Через 8 лет возраст моего отца будет на 20 лет меньше меня, чем в 3 раза.
Какого возраста сейчас мой отец?
Алгебраические доказательства вкратце
Прежде чем погрузиться в геометрические доказательства, неплохо вернуться к алгебре. Мы уже научились решать уравнения для переменной. Теперь займемся алгеброй в формате двухколоночного доказательства.
Пример задачи
Покажите, что если 3 x — 7 = 5, то x = 4.
Здесь наше данное утверждение 3 x — 7 = 5, и нас просят доказать x = 4.
| Утверждения | Причины |
| 1. 3 x — 7 = 5 | Дано |
| 2. 3 x — 7 + 7 = 5 + 7 | Добавление 7 к уравнению (1) |
| 3. 3 x + 0 = 5 + 7 | Подстановка –7 + 7 = 0 в (2) |
4. 3 x = 5 + 7 | Замена 3 x + 0 = 3 x в (3) |
| 5. 3 x = 12 | Замена 5 + 7 = 12 на ( 4) |
| 6. 3 x ⁄ 3 = 12 ⁄ 3 | Деление уравнения (5) на 3 |
| 7. x = 12 ⁄ 3 | Замена 3 x ⁄ 3 = x в (6) |
| 8. x = 4 | Подстановка 12 ⁄ 3 = 4 в (7) |
Есть такое понятие, как слишком информативное? Да, вот и все, поскольку более половины доказательства было посвящено тому, чтобы рассказать читателю, как выполнять арифметику. Обычно мы принимаем численные вычисления как должное и пишем доказательства следующим образом:
| Утверждения | Причины |
1. 3 x — 7 = 5 | Учитывая |
| 2.3 x = 12 | Добавьте 7 к обеим частям уравнения (1) |
| 3. x = 4 | Разделите уравнение (2) на 3 |
Видите? Это доказательство очень похоже на то, как мы записали бы его в алгебре. Единственная разница в том, что вы приводите причины по ходу дела, убеждая читателей (например, вашего учителя математики), что вы знаете, что делаете. Ты получил это.
Пример задачи
Покажите, что если 5 ( x + 12) = 30 и x + y = 100, то y = 106.
На этот раз наши два данных утверждения: 5 ( x + 12) = 30 и x + y = 100. Мы должны доказать, что y = 106. Итак, мы идем.
| Заявления | Причины |
| 1. 5 ( x + 12) = 30 | Дано |
2. x Дано + y6 = 100 90 | |
| 3. 5 x + 60 = 30 | Распределительная собственность (1) |
| 4.5 x = -30 | Вычтите 60 из обеих частей (3) |
| 5. x = -6 | Разделите обе стороны (4) на 5 |
| 6. -6 + y = 100 | Замените x = -6 в (2) |
| 7. y = 106 | Добавьте 6 к обеим сторонам (6) |
Как видите , есть много способов сформулировать причины. Важная часть состоит в том, что вы обосновываете каждый шаг тем, почему ваше утверждение верно.Конечно, если ваш «читатель» предпочитает, чтобы это было написано определенным образом, вероятно, было бы неплохо последовать его предложениям. Просто говорю.
8 x 4 = (? X 7) — (? X 3)
Николь,
Просто чтобы вы поняли поглубже. На этот вопрос, «как написано», есть несколько ответов.
Иногда так бывает с математикой. И это может вызвать массу недоразумений. Вы должны прочитать это очень внимательно. Если вы умножите 8 на 4, вы получите 32. Вы знаете, что (? X 7) должно быть больше этого числа, потому что вы вычитаете (? X 3).Если вы умножите 5 на 7, вы получите 35. И это больше 32. Затем возьмите 32 из 35, чтобы получить 3. Таким образом, (5 x 7) — (1 x 3) также дает 32. Если? предполагается, что это одно и то же значение для (? x 7) и (? x 3). Тогда проблему можно будет решить по правилам алгебры, как это сделала Вивиан. Любой другой анализ может дать вам другие возможные ответы. Если это так, то вопрос должен быть еще кое-что. Вам этого не сказали? знак равно Но так должно быть. А также ? это «оператор», а не просто вопросительный знак.Чтобы получить только один ответ, их обоих должно быть 8. Вы просто используете «математические правила», чтобы перемещать вещи, пока не найдете путь к ответу. Ученые иногда делают это месяцами или годами, чтобы решить сложные проблемы.
Часто ваше чувство чисел сбивается с толку из-за такого рода «несоответствий» или незнания, с чего начать ситуацию, когда вы выходите за рамки простой математики и переходите к понятиям алгебры. И это может оставить вас в растерянности и не зная, с чего начать. Если вам задают общий вопрос, решите проблему по понятиям алгебры.Вы можете предположить больше в вопросе, применяя правила алгебры. В алгебре вместо чисел используются символы. Это часть «математических правил». Затем для поиска ответа используются другие правила. Символ ? действует так же, как x или y или что-то еще. В науке иногда даже используются слова. (Так строятся задачи со словами.) Если вы знаете «математические правила». Вы можете применять логику для решения математических задач.
Я отправил этот ответ, чтобы дать вам более глубокое понимание того, что вы делаете.Теперь вы изучаете основные правила. Знание того, что вызывает у вас замешательство, может облегчить жизнь в будущем.
Просто поиграйте с математическими приемами «окей» (+, -, умножение, деление), пока вы не сможете выполнять их, не задумываясь. И математика станет легкой. Есть еще «математические правила», которые вы узнаете позже. Позже вы «увидите» ответы легче. После того, как вы получите больше опыта. Не ждите этого сейчас. Ключ к простой математике — практика.
Систем линейных уравнений — Бесплатная математическая справка
Системы линейных уравнений имеют место, когда существует более одного связанного математического выражения.Например, в \ (y = 3x + 7 \) есть только одна линия со всеми точками на этой линии, представляющая набор решений для приведенного выше уравнения.
Когда вам задают 2 уравнения в одном и том же вопросе и просят решить для единственного ответа, вы можете визуализировать проблему как две линии на одной плоскости xy. Следующие два уравнения изображены на одной плоскости xy:
$$ y = 3x + 5 $$ $$ y = — x $$ Решение любого уравнения — это место пересечения ОБЕИХ уравнений на плоскости xy.
Это место встречи называется Точкой пересечения. Если у вас есть линейное уравнение и квадратное уравнение в одной плоскости xy, могут быть ДВЕ ТОЧКИ, где график каждого уравнения будет встречаться или пересекаться. Вот геометрический вид:
Вот пример двух уравнений с двумя неизвестными переменными:
Пример
$$ x + y = 10 $$ $$ 3x + 2y = 20 $$Есть три метода решения нашего пробного вопроса.
- 1) Решаем графически
- 2) Мы можем решить это алгебраически
- 3) Мы также можем решить эту проблему с помощью алгебраического исключения
Решу вопрос всеми 3 способами.Метод 1. Решить графически:
Чтобы решить графически, лучше всего записать ОБА уравнения в форме пересечения наклона или в форме: \ (y = mx + b \), где m = наклон, а b = точка пересечения y в качестве первого шага. Таким образом, \ (x + y = 10 \) становится \ (y = — x + 10 \) (форма пересечения наклона). Затем \ (3x + 2y = 20 \) становится \ (y = — \ frac {3x} {2} + 10 \) при записи в форме пересечения наклона.
Затем нарисуйте две линии, ведущие к точке пересечения. Построив эти линии, вы обнаружите, что ОБА уравнения пересекаются в точке (0,10).Точка (0,10) означает, что если вы подставите x = 0 и y = 10 в ОБЕИ исходные уравнения, вы обнаружите, что это решает оба уравнения. Вот как эти два уравнения выглядят на плоскости xy:
Метод 2: Решить алгебраически
Шагов:
1) Решите относительно x или y в первом уравнении (\ (x + y = 10 \)). Решу за у. Итак, \ (x + y = 10 \) становится \ (y = -x + 10 \).
2) Подставьте значение y (то есть -x + 10) во второе уравнение, чтобы найти x. Наше второе уравнение было \ (3x + 2y = 20 \) и после подстановки становится \ (3x + 2 (-x + 10) = 20 \)
Далее: Решите относительно x.
$$ 3x -2x + 20 = 20 $$ $$ x + 20 = 20 $$ $$ x = 0 $$3) Подставьте x = 0 в ЛЮБОЕ исходное уравнение, чтобы найти значение y. Я буду использовать наше второе уравнение.
$$ 3x + 2y = 20 $$ $$ 3 (0) + 2y = 20 $$ $$ 0 + 2y = 20 $$ $$ y = 10 $$ Итак, наша точка пересечения снова (0,10).
Метод 3: Алгебраическое исключение
Этот метод имеет дело с сопоставлением переменных для ELIMINATE или устранением одной. Имейте в виду, что какую переменную удалить в первую очередь — это ваш выбор.
ЦЕЛЬ: исключить x и решить вместо y или наоборот. Вернемся к нашим исходным уравнениям.В нашем втором 3x + 2y = 20, вы можете исключить 3x, умножив -3 на КАЖДЫЙ член в нашем первом уравнении (x + y = 10).
x + y = 10
3x + 2y = 20
-3 (x) + -3 (y) = -3 (10)
3x + 2y = 20
-3x + -3y = -30
3x + 2y = 20
ВНИМАНИЕ, что -3x и 3x исключаются. Вижу это? Понять, почему? И вот почему: отрицательный плюс положительный = ноль.
Теперь у нас есть это:
-3y = -30
2y = 20
-3y + 2y = -30 + 20
-y = -10
y = 10.
Далее: чтобы найти x, мы подставляем y = 10 в ЛЮБОЕ из исходных уравнений. К настоящему времени вы должны увидеть, что наш ответ для x будет НУЛЬ.
Вот он:
Я буду использовать x + y = 10
x + 10 = 10
x = 0.
Вы видите то, что вижу я? Да, я снова нашел ту же самую точку пересечения, которая составляет (0,10).
Г-н Фелиз
(c) 2005
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком).
1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи с дробями:
следующие математические задачи »
Решение рациональных уравнений
Решение рациональных уравнений
Рациональное уравнение Уравнение, содержащее хотя бы одно рациональное выражение. — уравнение, содержащее хотя бы одно рациональное выражение. Рациональные выражения обычно содержат переменную в знаменателе. По этой причине мы позаботимся о том, чтобы знаменатель не был равен нулю, отметив ограничения и проверив наши решения.
Решите рациональные уравнения, удаляя дроби, умножая обе части уравнения на наименьший общий знаменатель (LCD).
Пример 1: Решить: 5x − 13 = 1x.
Решение: Сначала отметим, что x ≠ 0, а затем умножим обе стороны на ЖК-дисплей, 3 x :
Проверьте свой ответ, заменив 12 на x , чтобы убедиться, что вы получили истинное утверждение.
Ответ: Решение — 12.
После умножения обеих частей предыдущего примера на ЖК-дисплей, нам осталось решить линейное уравнение. Это не всегда так; иногда нам остается квадратное уравнение.
Пример 2: Решить: 2−1x (x + 1) = 3x + 1.
Решение: В этом примере есть два ограничения: x ≠ 0 и x ≠ −1.Начните с умножения обеих сторон на ЖК-дисплей, x (x + 1).
После распределения и деления общих множителей остается квадратное уравнение. Чтобы решить эту проблему, перепишите его в стандартной форме с коэффициентом, а затем установите каждый коэффициент равным 0.
Проверьте, решают ли эти значения исходное уравнение.
Ответ: Решения -1/2 и 1.
До этого момента все возможные решения решали исходное уравнение.Однако так бывает не всегда. Умножение обеих частей уравнения на переменные множители может привести к посторонним решениям. Решение, которое не решает исходное уравнение, то есть решения, которые не решают исходное уравнение. Полный список шагов для решения рационального уравнения представлен в следующем примере.
Пример 3: Решить: xx + 2 + 2×2 + 5x + 6 = 5x + 3.
Решение:
Шаг 1: Разложите все знаменатели на множители и определите ЖК-дисплей.
ЖК-дисплей равен (x + 2) (x + 3).
Шаг 2: Определите ограничения. В данном случае это x ≠ −2 и x ≠ −3.
Шаг 3: Умножьте обе части уравнения на ЖК-дисплей. Распространяйте осторожно, а затем упрощайте.
Шаг 4: Решите полученное уравнение. Результатом является квадратное уравнение. Перепишите его в стандартной форме, коэффициент, а затем установите каждый коэффициент равным 0.
Шаг 5: Проверьте наличие посторонних решений. Всегда подставляйте в исходное уравнение или его факторизованный эквивалент. В этом случае выберите факторизованный эквивалент для проверки:
Здесь −2 — постороннее решение, не входящее в набор решений. Важно отметить, что −2 — это ограничение.
Ответ: Решение — 4.
Если этот процесс приводит к решению, которое является ограничением, не считайте его посторонним решением.
Попробуй! Решите: xx − 5 + 3x + 2 = 7xx2−3x − 10.
Ответ: −3
Иногда все возможные решения являются посторонними, и в этом случае мы говорим, что не существует решения исходного уравнения. В следующих двух примерах мы продемонстрируем два способа, по которым рациональное уравнение может не иметь решений.
Пример 4: Решить: 3xx2−4−2x + 2 = 1x + 2.
Решение: Чтобы идентифицировать ЖК-дисплей, сначала разложите знаменатели на множители.
Умножьте обе стороны на наименьший общий знаменатель (LCD), (x + 2) (x − 2), аккуратно распределив.
Уравнение противоречит и поэтому не имеет решения.
Ответ: Нет решения, ∅
Пример 5: Решите: xx − 4−4x + 5 = 36×2 + x − 20.
Решение: Сначала разложите знаменатели на множители.
Обратите внимание, что ограничения x ≠ 4 и x ≠ −5.
Чтобы очистить дроби, умножьте на ЖК-дисплей (x − 4) (x + 5).
Оба эти значения являются ограничениями исходного уравнения; следовательно, оба посторонние.
Ответ: Нет решения, ∅
Попробуй! Решите: 1x + 1 + xx − 3 = 4xx2−2x − 3.
Ответ: ∅
Важно отметить, что этот метод очистки алгебраических дробей работает только для уравнений. Не пытайтесь очищать алгебраические дроби при упрощении выражений. Напоминаем, что у нас
Необходимо упростить выражения и решить уравнения. Если мы умножим выражение на ЖК-дисплей, x (2x + 1), мы получим другое выражение, которое не эквивалентно.
Буквенные уравнения
Буквальные уравнения или формулы часто являются рациональными уравнениями. Следовательно, методы, описанные в этом разделе, могут использоваться для решения конкретных переменных.
Предположим, что все выражения переменных в знаменателе отличны от нуля.
Пример 6: Решите относительно x : z = x − 5y.
Решение: Цель — изолировать x . Предполагая, что y отличны от нуля, умножьте обе стороны на y и затем прибавьте 5 к обеим сторонам.
Ответ: x = yz + 5
Пример 7: Решите относительно c : 1c = 1a + 1b.
Решение: В этом примере цель — изолировать c . Мы начинаем с умножения обеих сторон на ЖК-дисплей, a⋅b⋅c, осторожно распределяя.
В правой части уравнения вычтем c .
Затем разделите обе части уравнения на величину (b + a).
Ответ: c = abb + a
Попробуй! Решите относительно y : x = y + 1y − 1.
Ответ: y = x + 1x − 1
Основные выводы
- Начните решать рациональные уравнения с умножения обеих частей на ЖК-дисплей. Полученное эквивалентное уравнение можно решить, используя методы, изученные до этого момента.
- Умножение обеих частей рационального уравнения на выражение переменной вводит возможность посторонних решений. Следовательно, мы должны проверять решения на соответствие множеству ограничений.Если решение является ограничением, то оно не является частью домена и является посторонним.
- При умножении обеих частей уравнения на выражение, аккуратно распределите и умножьте каждый член на это выражение.
- Если все полученные решения являются посторонними, то исходное уравнение не имеет решений.
Тематические упражнения
Часть A: Рациональные уравнения
Решить.
1. 12 + 1x = 18
2. 13−1x = 29
3. 13x − 23 = 1x
4. 25x − 1x = 310
5. 12x + 1 = 5
6. 33x − 1 + 4 = 5
7. 2x − 3x + 5 = 2x + 5
8. 5x2x − 1 = x − 12x − 1
9. 5x − 7 = 6x − 9
10. 5x + 5 = 3x + 1
11. x6−6x = 0
12. 5x + x5 = −2
13.хх + 12 = 2х
14. 2xx + 5 = 16 − x
15. 1x + x2x + 1 = 0
16. 9x3x − 1−4x = 0
17. 1−2x = 48×2
18. 2−9x = 5×2
19. 1 + 12x = 12x − 2
20. 1−3x − 5x (3x − 4) = — 1x
21. x2 = 14x + 3
22. 3×2 = х + 13 − х
23. 6 = −3x + 3x − 1
24. 12x − 2 = 2 + 6 (4 − x) x − 2
25.
2 + 2xx − 3 = 3 (x − 1) x − 3
26. xx − 1 + 16x − 1 = x (x − 1) (6x − 1)
27. 12×2-81 = 1x + 9-2x − 9
28. 14×2−49 = 2x − 7−3x + 7
29. 6xx + 3 + 4x − 3 = 3xx2−9
30. 3xx + 2−17x − 2 = −48×2−4
31. х − 1 + 3 = 0
32. 4 − y − 1 = 0
33. y − 2−4 = 0
34. 9x − 2−1 = 0
35,3 (x − 1) −1 + 5 = 0
36,5−2 (3x + 1) −1 = 0
37.3 + 2x − 3 = 2x − 3
38. 1x = 1x + 1
39. хх + 1 = х + 1x
40. 3x − 13x = xx + 3
41. 4x − 7x − 5 = 3x − 2x − 5
42. xx2−9 = 1x − 3
43. 3x + 4x − 8−28 − x = 1
44. 1x = 6x (x + 3)
45. 3x = 1x + 1 + 13x (x + 1)
46. xx − 1−34x − 1 = 9x (4x − 1) (x − 1)
47.
1x − 4 + xx − 2 = 2×2−6x + 8
48. xx − 5 + x − 1×2−11x + 30 = 5x − 6
49.xx + 1−65×2 + 4x − 1 = −55x − 1
50. −8×2−4x − 12 + 2 (x + 2) x2 + 4x − 60 = 1x + 2
51. xx + 2−20×2 − x − 6 = −4x − 3
52. x + 7x − 1 + x − 1x + 1 = 4×2−1
53. х − 1x − 3 + x − 3x − 1 = −x + 5x − 3
54. х − 2x − 5 − x − 5x − 2 = 8 − xx − 5
55. х + 7x − 2−81×2 + 5x − 14 = 9x + 7
56. хх − 6 + 1 = 5х + 3036 − х2
57. 2xx + 1−44x − 3 = −74×2 + x − 3
58. x − 5x − 10 + 5x − 5 = −5xx2−15x + 50
59.5×2 + 5x + 4 + x + 1×2 + 3x − 4 = 5×2−1
60. 1×2−2x − 63 + x − 9×2 + 10x + 21 = 1×2−6x − 27
61. 4×2−4 + 2 (x − 2) x2−4x − 12 = x + 2×2−8x + 12
62. x + 2×2−5x + 4 + x + 2×2 + x − 2 = x − 1×2−2x − 8
63.
6xx − 1−11x + 12×2 − x − 1 = 6x2x + 1
64. 8x2x − 3 + 4x2x2−7x + 6 = 1x − 2
Часть B: Буквальные уравнения
Найдите указанную переменную.
65. Решите относительно r : t = Dr.
66. Решите относительно b : h = 2Ab.
67. Решите для P : t = IPr.
68. Решить относительно π: r = C2π.
69. Решите относительно c : 1a = 1b + 1c.
70. Решите относительно y : m = y − y1x − x1.
71. Решите относительно w : P = 2 (l + w).
72. Решите относительно t : A = P (1 + rt).
73. Решите относительно м : s = 1n + m.
74. Решить относительно S : h = S2πr − r.
75. Решите относительно x : y = xx + 2.
76.
Решите относительно x : y = 2x + 15x.
77. Решите относительно R : 1R = 1R1 + 1R2.
78. Решите относительно S1: 1f = 1S1 + 1S2.
Часть C: Обсуждение
79. Объясните, почему умножение обеих частей уравнения на ЖК-дисплей иногда дает посторонние решения.
80. Объясните связь между методом перекрестного умножения и умножением обеих частей рационального уравнения на ЖКД.
81. Объясните, как мы можем отличить рациональное выражение от рационального уравнения. Как мы относимся к ним по-другому?
Ответы
1: −8/3
3: -1
5: −2/5
7: 5/2
9: −3
11: −6, 6
13: −4, 6
15: -1
17: −6, 8
19: −4, 6
21: −7, 4
23: ∅
25:
27: −39
29: 4/3, 3/2
31: -1/3
33: -1/2, 1/2
35: 2/5
37:
39: -1/2
41: ∅
43: −7
45: 5
47: -1
49:
∅51: −4
53: 5/3
55:
57: 1/2
59: −6, 4
61: 10
63: 1/3
65: r = Dt
67: P = Itr
69: c = abb − a
71: w = P − 2l2
73: m = 1 − sns
75: х = 2y1 − y
77: R = R1R2R1 + R2
Решайте уравнения с переменными и константами с обеих сторон — Элементарная алгебра
Решение линейных уравнений и неравенств
Цели обучения
К концу этого раздела вы сможете:
- Решите уравнение с константами с обеих сторон
- Решите уравнение с переменными с обеих сторон
- Решите уравнение с переменными и константами с обеих сторон
Прежде чем начать, пройдите тест на готовность.
- Упростить:
Если вы пропустили эту проблему, просмотрите (рисунок).
Решение уравнений с константами с обеих сторон
Во всех уравнениях, которые мы решили до сих пор, все переменные члены находились только на одной стороне уравнения, а константы — на другой стороне. Это происходит не все время, поэтому теперь мы научимся решать уравнения, в которых переменные члены, или постоянные члены, или и то, и другое находятся по обе стороны уравнения.
Наша стратегия будет заключаться в том, чтобы выбрать одну сторону уравнения как «переменную сторону», а другую сторону уравнения как «постоянную сторону».Затем мы будем использовать свойства равенства вычитания и сложения, чтобы собрать все переменные члены вместе на одной стороне уравнения и постоянные члены вместе на другой стороне.
Сделав это, мы преобразуем уравнение, которое начиналось с переменных и констант с обеих сторон, в форму. Мы уже знаем, как решать уравнения этой формы, используя свойства равенства или деления или умножения.
Решить:
Решение
В этом уравнении переменная находится только в левой части.Левую часть имеет смысл называть «переменной» стороной. Следовательно, правая сторона будет «постоянной» стороной. Мы напишем метки над уравнением, чтобы помочь нам запомнить, что куда идет.
Так как левая сторона — это «» или переменная сторона, восьмерка неуместна. Мы должны «отменить» добавление 8, вычтя 8, и чтобы сохранить равенство, мы должны вычесть 8 из обеих частей.
Решить:
Решить:
Решить:
Решение
Обратите внимание, что переменная находится только в левой части уравнения, поэтому мы будем называть эту сторону стороной «переменная», а правая часть — стороной «константы».Так как левая сторона — «переменная», цифра 9 здесь неуместна. Он вычитается из числа, поэтому, чтобы «отменить» вычитание, прибавьте 9 к обеим сторонам. Помните: что бы вы ни делали слева, вы должны делать справа.
Решить:
Решить:
Решение уравнений с переменными с обеих сторон
Что, если в обеих частях уравнения есть переменные? Для таких уравнений начните, как мы делали выше — выберите сторону «переменной» и «константу», а затем используйте свойства равенства и вычитания и сложения, чтобы собрать все переменные с одной стороны и все константы с другой стороны.
Решить:
Решение
Здесь переменная находится с обеих сторон, но константы появляются только с правой стороны, поэтому давайте сделаем правую сторону «постоянной». Тогда левая сторона будет «переменной» стороной.
Решить:
Решить:
Решить:
Решение
Единственная константа слева, а с обеих сторон. Оставим константу слева, а переменные справа.
Решить:
Решить:
Решить:
Решение
Единственная константа находится справа, поэтому пусть левая сторона будет стороной «переменной».
Решить:
Решить:
Решение уравнений с переменными и константами с обеих сторон
Следующий пример будет первым, в котором переменные и константы будут по обе стороны уравнения.Для решения этого уравнения может потребоваться несколько шагов, поэтому нам нужна четкая и организованная стратегия.
Как решать уравнения с переменными и константами с обеих сторон
Решить:
Решить:
Решить:
Мы перечислим шаги ниже, чтобы вы могли легко их выполнить. Но мы назовем это «Начальной стратегией», потому что позже в этой главе мы добавим несколько шагов.
Начальная стратегия решения уравнений с переменными и константами по обе стороны уравнения.
- Выберите, какая сторона будет «переменной» стороной — другая сторона будет «постоянной» стороной.
- Соберите переменные члены в «переменную» сторону уравнения, используя свойство равенства сложения или вычитания.
- Соберите все константы с другой стороны уравнения, используя свойство равенства сложения или вычитания.
- Сделайте коэффициент переменной равным 1, используя свойство равенства умножения или деления.
- Проверьте решение, подставив его в исходное уравнение.
На шаге 1 полезный подход состоит в том, чтобы сделать сторону «переменной» стороной, имеющей переменную с большим коэффициентом. Обычно это упрощает арифметику.
Решить:
Решение
На первом этапе выберите сторону переменной, сравнивая коэффициенты переменных на каждой стороне.
Решить:
Решить:
Решить:
Решение
На первом этапе выберите сторону переменной, сравнивая коэффициенты переменных на каждой стороне.
Так как правая часть должна быть «переменной», а левая — «постоянной».
Решить:
Решить:
В последнем примере мы могли бы сделать левую часть «переменной» стороной, но это привело бы к отрицательному коэффициенту на члене переменной.
(Попробуйте!) Хотя мы можем работать с негативом, при работе с позитивом вероятность ошибок меньше. Описанная выше стратегия помогает избежать негатива!
Чтобы решить уравнение с дробями, мы просто следуем шагам нашей стратегии, чтобы получить решение!
Решить:
Решение
Так как, сделайте левую часть «переменной» стороной, а правую часть «постоянной» стороной.
Решить:
Решить:
Мы будем использовать ту же стратегию, чтобы найти решение уравнения с десятичными знаками.
Решить:
Решение
Так как, сделайте левую часть «переменной» стороной, а правую часть «постоянной» стороной.
Решить:
Решить:
Ключевые понятия
- Начальная стратегия решения уравнения с переменными и константами на обеих сторонах уравнения
- Выберите, какая сторона будет «переменной» стороной — другая сторона будет «постоянной» стороной.
- Соберите переменные члены в «переменную» сторону уравнения, используя свойство равенства сложения или вычитания.
- Соберите все константы с другой стороны уравнения, используя свойство равенства сложения или вычитания.
- Сделайте коэффициент переменной равным 1, используя свойство равенства умножения или деления.
- Проверьте решение, подставив его в исходное уравнение.
- Выберите, какая сторона будет «переменной» стороной — другая сторона будет «постоянной» стороной.
Практика ведет к совершенству
Решение уравнений с константами с обеих сторон
В следующих упражнениях решите следующие уравнения с константами с обеих сторон.
Решение уравнений с переменными с обеих сторон
В следующих упражнениях решите следующие уравнения с переменными с обеих сторон.
Решение уравнений с переменными и константами с обеих сторон
В следующих упражнениях решите следующие уравнения с переменными и константами с обеих сторон.
Повседневная математика
Билеты на концерт На школьный концерт общая стоимость проданных билетов составила 1506 евро.
Студенческие билеты продаются за 6 фунтов стерлингов, а взрослые билеты — за 9 фунтов стерлингов. Количество проданных билетов для взрослых было в 5 раз меньше, чем количество студенческих билетов. Найдите количество проданных студенческих билетов, с , решив уравнение.
Изготовление забора У Джовани есть 150 футов ограды, чтобы сделать прямоугольный сад на заднем дворе. Он хочет, чтобы длина была на 15 футов больше ширины. Найдите ширину w , решив уравнение.
Письменные упражнения
Решите уравнение, объясняющее все этапы вашего решения, как в примерах в этом разделе.
Решите уравнение, объясняющее все этапы вашего решения, как в примерах в этом разделе.
Обоснования могут быть разными.
При решении уравнения с переменными с обеих сторон, почему обычно лучше выбрать сторону с большим коэффициентом в качестве «переменной» стороны?
Это решение уравнения? Откуда вы знаете?
Да.